
Materials Processing

 | Fluid Dynamics & Materials Processing |  |
DOI: 10.32604/fdmp.2021.015961
ARTICLE
Coupled Effects of Heat and Moisture of Early-Age Concrete
1School of Urban Construction and Transportation, Hefei University, Hefei, 230601, China
2School of Electronic Science and Applied Physics, Hefei University of Technology, Hefei, 230601, China
*Corresponding Author: Hanxi Wang. Email: 2020213561@mail.hfut.edu.cn
Received: 26 January 2021; Accepted: 26 March 2021
Abstract: In order to analyze the coupled influence of temperature and humidity on early-age concrete (including cement and copper tailings), a mathematical model is introduced on the basis of the Krstulovic-Dabic hydration reaction kinetic equations. In such a framework, the influence of hydration-released heat and water consumption are also taken into account. The results provided by such a model are verified by means of experiments and related sensor measurements. The research results show that this model can adequately predict the internal temperature and the humidity temporal evolution laws.
Keywords: Composite cementitious materials; cement hydration; micro-structure; diffusion coefficient; coupled of heat and moisture
Nomenclature
| A: | empirical coefficient, m/h |
| a: | constant related to temperature |
| B: | empirical coefficient, m/h |
| b: | constant related to humidity |
| C: | specific heat capacity of concrete, J/(kg·°C) |
| D: | hydration degree, % |
| Dc: | hydration degree of cement, % |
| D28: | hydration degree when cement is hydrated for 28 days, % |
| E: | activation energy of hydration, J/mol |
| Es: | diffusion activation energy, J/mol |
| Fw: | humidity flux |
| H: | hydration relative humidity, % |
| Hs: | relative humidity induced by self-drying of concrete, % |
| Hs-max: | maximum relative humidity induced by self-drying of concrete, % |
| HE: | relative humidity of surrounding environment, % |
| h: | constant related to porosity |
| KNG: | rate constant of NG process |
| KI: | rate constant of I process |
| KD: | rate constant of D process |
| KH: | material parameter related to humidity diffusion, concrete pore structure, and temperature |
| KM: | material parameter depending on the water-binder ratio |
| mc: | mass of cement, kg |
| mt: | mass of copper tailings, kg |
| n: | constant related to mineral composition |
| P: | copper tailings mixing ratio, % |
| Q: | heat release during hydration, J |
| QT: | total heat release of cement, J |
| Qi: | total heat release of cement and copper tailings, J |
| Qc-max: | maximum heat release of cement, J |
| Qt-max: | maximum heat release of copper tailings, J |
| R0: | initial radius of cement particle, m |
| R*: | gas constant |
| S: | moisture diffusion coefficient of concrete |
| S0: | diffusion coefficient of concrete under water saturation at T0, m2/h |
| T: | hydration temperature, °C |
| TE: | ambient temperature, °C |
| T0: | standard temperature, 20°C |
| t: | reaction time, h |
| t0: | initial time of hydration, h |
| th: | time when hydration heat reaches the half of total heat, h |
| Wv: | volumetric moisture content, m3/m3 |
| α1~α6: | reduction coefficients for change rate of cement particle radius |
| α: | total porosity of cement paste mixed with copper tailings, % |
| α28: | porosity of concrete at 28 days of age, % |
| αc: | porosity of cement, % |
| αt: | porosity of copper tailings, % |
| β1~β3: | influence coefficients for change rate of copper tailings particle radius |
| βT: | exothermic coefficient of concrete surface, J/(h·m2·°C) |
| γ: | humidity exchange coefficient |
| ρ: | concrete density, kg/m3 |
| λ: | thermal conductivity of concrete, J/(h·m·°C) |
| ŋ1, ŋ2: | adjustment coefficients of hydration reaction rate |
| ΔDS: | increment of cement hydration degree, % |
| ΔDP: | increment of copper tailings hydration degree, % |
| w/b: | water-binder ratio |
Due to huge production of concrete, it is necessary to use mineral admixtures with abundant sources and low cost in practical applications. Copper tailings are waste residues discharged after the extraction of useful metals such as copper and gold. It is a typical industrial waste with large amount and small particle size.
Many researchers had been concerned the coupling effects of heat and moisture diffusion of early-age concrete. Based on cement hydration kinetics model, the coupled diffusion characteristics of temperature and humidity was studied [1,2], while the coupling mechanism of concrete at early age was not clarified yet. Based on the Weibull distribution theory, the moisture-heat chemical model from the perspective of micromechanics had been established [3], which took the coupling of dampness, heat and hydration into account. The diffusion equation of Fick’s second law was applied in simulating the relative humidity field of concrete [4], but the factor of water consumption due to self-drying was ignored. The finite difference method was used to simulate the relative humidity field of concrete [5], and self-drying and diffusion processes were considered, but the coupling effect of temperature and relative humidity was not considered.
Krstulovic et al. [6] proposed a dynamic model for hydration reaction of cement-based materials, in which hydration reaction was divided into three basic processes: crystallization nucleation and crystal growth (NG), interactions at phase boundaries (I), and diffusion process (D).
The present kinetics studies on the basis of the Krstulovic-Dabic model are mostly focused on conventional cement mixtures such as fly ash, slag and silica fume. The model was employed to study hydration heat release law of mass concrete [7], and it had been found that cement mixed with a certain amount of mineral admixtures had longer acceleration and deceleration periods. The influence on hydration kinetic parameters was discussed, and the change of hydration process after adding the admixture was analyzed [8]. The hydration process of C3S was investigated [9], in which it was found that the addition of fly ash was unable to change the type of hydration process.
However, cement active admixtures such as fly ash are becoming increasingly scarce. In view of low cost of industrial waste and production of “green cement”, in this paper, we focus on how to make full use of copper tailings as cement admixtures or concrete composite materials, which can provide a theoretical guidance for large-scale utilization of various solid industrial wastes such as quartz tailings, iron tailings, steel slag, etc.
This paper proposes an improved hydration model of mineral admixtures incorporating the effect of copper tailings on the hydration process of cement. The hydration degree, hydration rate and porosity are obtained. Related parameters are further introduced into the concrete temperature and humidity diffusion equation. The coupling model of heat and moisture for early-age concrete is created and is verified by subsequent test data.
2 Cement-Copper Tailings Hydration Kinetics
2.1 Hydration Model of Portland Cement
According to Krstulovic-Dabic model, the kinetic equations and their corresponding differential equations between hydration degree (D) and reaction time (t) are given as below (the diffusion process is calculated by the Jander reaction model [10]),
NG process:
I process:
D process:
in which KNG, KI, and KD are rate constants for the three processes, respectively, n is a constant related to cement mineral composition, and t0 is the initial time of hydration after the end of cement induction period.
Cement hydration is mainly related to some factors such as concrete components, water-binder ratio, moisture content, environmental temperature and humidity, etc. The heat release during hydration process (Q) can be expressed as a function of hydration degree [11],
where D is hydration degree, QT is the total heat release after the cement is completely hydrated.
The total heat release of Portland cement can be determined by the Knudsen extrapolation equation [12]. The relationship between heat release (Q) and cement hydration time (t) is written as below:
in which th is the time when heat release reaches the half of total heat release.
Cement hydration degree can be denoted as the ratio of heat release to the total heat release. It is assumed that copper tailings are uniformly distributed, and the heat release is proportional to the volume of the particle. Then the hydration degree of the cement particle with an initial radius R0 can be indicated as,
where Q is the heat release of cement particles after being hydrated for time t; R(t) is the radius of cement particle with initial radius of R0 at time t.
Substituting Eq. (9) into the Krstulovic-Dabic equations can attain the variation of cement particle radius per unit time of hydration:
in which dRNG, dRI, dRD are the radius reduction of cement particles with initial radius of R0 in the three processes of hydration, respectively.
According to the principle of Minimum Energy Consumption, the theoretical change rate of cement hydration particle radius (dR) takes the minimum value,
In this way, the relations among hydration heat release, hydration reaction time, hydration degree and cement particle size are set up.
2.2 Hydration Model of Cement Mixed with Copper Tailings
The hydration of composite cementitious materials consists of cement hydration and copper tailings hydration. X-ray diffraction analysis confirmed that copper tailings particles have the same microscopic hydration unit as cement particles [13], so the hydration kinetics process can be controlled by the three equations of Krstulovic-Dabic model.
The hydration degree of copper tailings can also be calculated by Eqs. (7)–(13), but the reaction constants KNG, KI, KD, n are different from those of cement. Adding copper tailings may affect cement hydration process including dilution effect, physical effect and chemical impact [13,14].
The final hydration degree of cement-based material is proportional to its effective water-cement ratio. When the proportion of copper tailings increases, the effective water-cement ratio also grows, and thus the hydration process of the composite cementitious system is delayed. This phenomenon is called dilution effect.
Copper tailings as an admixture can improve filling effect and lubrication effect of cement-based material. It exerts two physical effects on cement hydration: delaying the hydration in the early stage; increasing hydration degree of the cement particle in hydration process.
The chemical impact of copper tailings is mainly manifested as follows: copper tailings contain lots of active substances; during the hydration, cement and copper tailings need water to complete the reaction; if the dosage of copper tailings is too large, there will be a peak value in water consumption, which hinders cement hydration.
Considering the impact of copper tailings, the cement hydration degree (Dc) is represented as,
where ΔDS is the increment of cement hydration degree caused by the dilution effect of copper tailings, ΔDP is the increment induced by the physical acceleration effect of copper tailings.
In hydration process of composite cementitious materials, water reduction, pore saturation, temperature, contacting area between cement and water, copper tailings and other factors all affect the rate of change of cement particle radius. The modified change rate of cement particle radius is,
in which α1 is relevant to the water content of hydration unit, α2 concerned with pore saturation, α3 related to temperature, α4 involved with the change of hydration degree, α5 the reduction coefficient of variation of cement particle radius, α6 the retardation effect coefficient of copper tailings on cement hydration [10,14].
Likewise, considering the impact of water consumption and the reduction of the contact area between particles and water, the final change rate of the copper tailings particle radius can be presented as,
where β1 is the influence coefficient due to the decrease of water content, β2 the coefficient concerned with contact area between copper tailings and water, β3 the temperature parameter affecting particle radius, dR’ the minimum change rate of particle radius.
3 Coupled Model of Heat and Moisture
3.1 Model Controlled by Temperature Field
In this paper, the hydration microscopic model is connected with the temperature field of concrete by means of the hydration reaction rate. Taking the change of temperature and humidity, hydration degree and hydration age into account [10], the temperature control equations are written as,
in which T is the temperature, H the relative humidity, ρ the concrete density, C the specific heat capacity of concrete, λ the thermal conductivity of concrete, f(T,H) the influence coefficient of temperature and relative humidity on the hydration reaction rate [15], E the activation energy of hydration, R* the gas constant, Qi the total heat release of cement and copper tailings, ŋ1 and ŋ2 the adjustment coefficients.
in which mc is the mass of cement, mt the mass of copper tailings, Qc-max the maximum heat release of cement, and Qt-max the maximum heat release of copper tailings.
The boundary condition is presented,
where βT is the exothermic coefficient of concrete surface, and TE the ambient temperature.
Here, the humidity characteristics of concrete is described by the relative humidity of concrete. The relation between volumetric moisture content (Wv) and humidity flux (Fw) can be given as follows [16,17]:
in which KH is a parameter related to humidity diffusion, concrete pore structure, and temperature. For simplicity, neglecting the self-drying effect caused by the hydration of copper tailings, the nonlinear relative humidity diffusion equation is presented,
where S is the moisture diffusion coefficient of concrete, Hs the relative humidity induced by self-drying of concrete only. Thereby, the influence coefficient on the hydration rate f(T, H) is utilized to reflect the effect of changes on self-drying effect, and the coupling relation of temperature and humidity can be established as,
where D28 is the hydration degree when cement is hydrated for 28 days, Hs-max maximum relative humidity induced by self-drying of concrete, which can be obtained by inverse deduction from Isothermal Adsorption model [18], and KM the material parameter depending on the water-binder ratio.
The boundary condition is provided as follows:
where HE is the relative humidity of surrounding environment, γ the humidity exchange coefficient on the surface of the concrete, which represents the diffusion characteristics of moisture in the air. Here, the expression proposed in reference [19] is used: γ = A(w/b)-B, in which w/b is the water-binder ratio, A and B are the empirical coefficients, respectively.
3.3 Modification of Diffusion Coefficient Considering Coupled Effect
Apart from the influence of relative humidity and temperature on the humidity diffusion coefficient [16], the evolution of the microstructure at the early age will also affect the humidity diffusion. The effects of age and porosity were both taken into account for humidity diffusion coefficient [20]. In summary, the humidity diffusion coefficient involving the influence of porosity is listed as,
where T0 is the standard temperature (20°C), S0 the diffusion coefficient of concrete under water saturation at T0, α28 the concrete porosity at 28 days of hydration age, Es the diffusion activation energy, and P the copper tailings mixing ratio. a, b, h are constants, respectively. αc, αt are the porosities of cement and copper tailings, respectively, which can be obtained by particle size distribution function (see reference [21]).
α is the total porosity of cement paste mixed with copper tailings, which can be obtained by Eq. (29),
4 Comparison of Values between Calculation and Experiment
After the selected copper tailings are filtered by pressure, they are calcined in a rotary kiln at 1300–1500°C for 1.5–3 min, then ground into copper tailings powder with a specific surface area of 476–512 m2/kg, whose chemical composition is shown in Tab. 1 (chemical titration analysis results). The corresponding mineral composition is shown in Tab. 2 (XRF analysis results). With a water-binder ratio 0.40, the selected cement is Portland cement of grade 42.5, the proportion of copper tailings is 30%, and the mixing proportion of concrete is the following: cement: water: sand: stone: copper tailings = 0.70: 0.40: 1.61: 2.53: 0.30.
Table 1: Main chemical composition of copper tailings for experiment (wt%)

Table 2: Mineral composition of copper tailings (wt%)

Some wooden thermal insulation molds lined with plastic film have been prepared with the size 400 × 250 × 250 mm. Concrete with specified mix proportion is poured in the molds (Fig. 1a) and the thermocouple sensors (Ahlborn NiCr-Ni and FHA6x6) are directly embedded from the upper open side with embedded depths 180, 100, 30 mm, respectively (Fig. 1b). The front end of each temperature sensor is wrapped with plasticine, and the front end of the moisture sensor is wrapped with permeable and breathable fiber woven fabric and covered with porous protective tube. These sensors have high precision without data drift after long-term measurement. The back end is connected with Ahlborn MU-56901 desktop data acquisition instrument (Fig. 1c), which collects and stores data regularly and automatically [22].

Figure 1: Part of experimental devices. (a) Concrete sample. (b) Front end of temperature and humidity sensors. (c) Ahlborn MU-56901 multi-channel interfaces
According to the information of raw materials (chemical composition, particle size distribution of cement and copper tailings, water-binder ratio), one can derive the hydration degree (D), the hydration rate (dD/dt) and the particle radius change rate (dR/dt), and further temperature field (T) and humidity field (H). The hydration process can be predicted by determining whether the set time is reached through cyclic calculation.
Software FLAC3D5.0 and MATLAB-R2015a are selected to solve the nonlinear equations in the temperature and humidity coupling 1-D model [23], which can provide interactive operation interfaces. In order to simplify the calculation and set the critical value, the following steps in modeling are presented,
(1) Analysis module, select coefficient module to calculate Eqs. (17), (21–23).
(2) Geometric modeling, the upper surface of the concrete test block is treated as the boundary layer, then the mesh is divided, the model size is 400 × 250 × 250 mm, the time step is set to 0.5 h, there are 48050 grid cells and 52224 nodes (Fig. 2).
(3) Parameter setting, when the strength grade of concrete is C50, the typical values of constants, parameters and coefficients are shown in Tabs. 3–5.
(4) Boundary conditions, use Cauchy boundary conditions Eqs. (20) and (24).
Figure 2: 3D view of concrete test block and cut surface
Table 3: Hydration kinetics parameters [10,14]

Table 4: Parameters for heat and moisture coupling (R-SI) [9,10,13,14,24]

Table 5: Coefficient values in the equations [9,10,13,24]

The comparison between calculated values of the microscopic hydration model and experimental hydration values is shown in Fig. 3. The calculated results are in good agreement with the measured values. In the early stage of hydration, the calculated values are generally slightly larger than those of experiments and the error is relatively large when water-binder ratio is 0.54, which is because water content in the hydration model is sensitive to the change of the radius of cement particles. When water content is large, the hydration rate is faster and the error becomes larger. In the late period of hydration (after 7 days), the error of hydration degree with different water-binder ratios is smaller, which can demonstrate that the microscopic hydration model proposed is accurate.
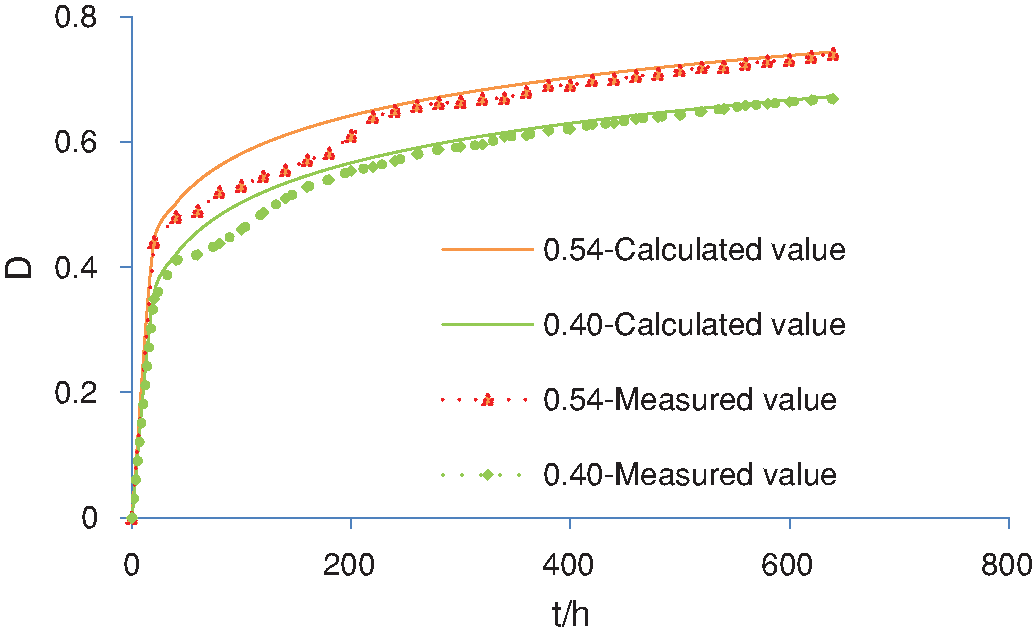
Figure 3: Comparison between calculated and measured values of hydration degree
The content of copper tailings is set to 30%, and the water-binder ratio is set to 0.4 in making C50 concrete. The comparison between calculated and measured values of temperature within 7 days is provided in Fig. 4. It can be seen that due to the exothermic effect of hydration at the initial stage, the temperature rises in a short period of time and forms a high temperature gradient, which is roughly eliminated after 90 hours. When the sensor is embedded at a depth of 30 mm, the deviation between calculated and measured values is large. That is because the measuring point is close to the surface of concrete and is greatly affected by ambient temperature, measurement error and heat dissipation.
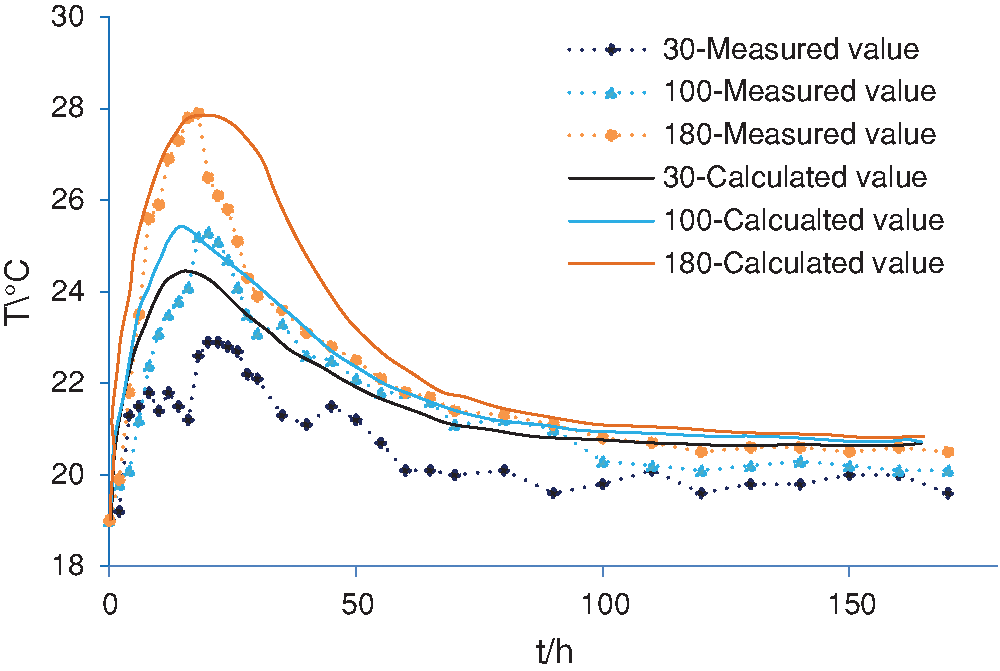
Figure 4: Comparison between calculated and measured values of temperature
The calculated and measured values of relative humidity within 28 days of each measuring point are presented in Fig. 5. Generally speaking, as the depth of the test point increases, the relative humidity of concrete rises. In accordance with the theory of free water migration, free water migrates to the direction of low humidity [25]. Since the humidity of surrounding environment is smaller than that in the interior of the concrete, free water will migrate from the inside of the concrete to the outside environment at the initial stage of setting and hardening.
In the early stage of hydration, the calculation values and measured values are quite different, the latter is significantly large. This may be due to that the temperature and the humidity are relatively high in the early stage of hydration, so that water accumulation happens in the sensors, thereby resulting in large measurement errors.
Basically, the measured and calculated results are in good agreement, especially in the middle and late stages.
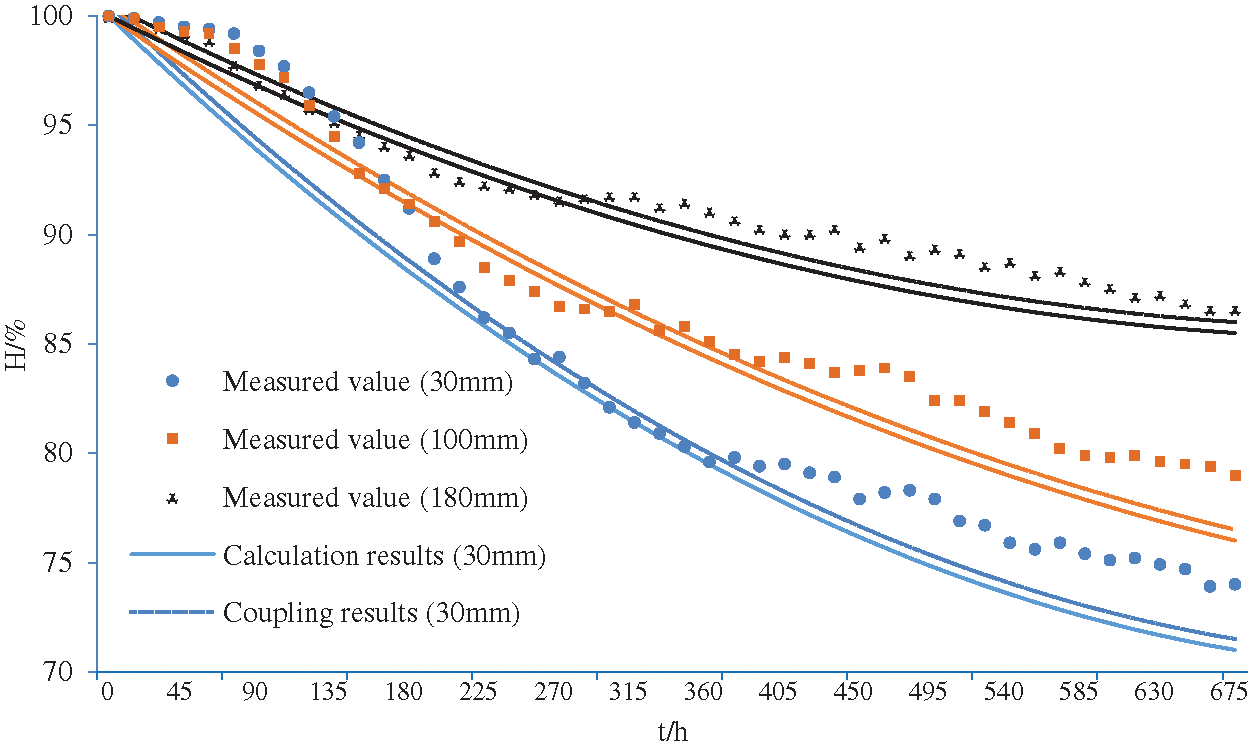
Figure 5: Comparison of calculation and experimental values of humidity
In order to explore the influences of different copper tailings content on hydration process, cementitious material pastes were prepared to observe the hydration products [26]. It can be seen from the SEM photo (Fig. 6) that pure cement paste has formed a continuous cross-linked network structure in the early stage. Adding a certain amount of copper tailings can generate more abundant hydration products, when the amount of copper tailings is large, the structural compactness and C-S-H gel are reduced and more non-gel substances appear in the hydration product, which has negative effect on hydration to a certain extent, in the meantime, the cement slurry became less dense and looser in structure. Although the strength would increase in the late stage, the overall strength of the system eventually decreased [27].
If copper tailings are applied to mass concrete, this defect could be made up by strengthening grinding and prolonging calcination, so as to enhance the activity of the materials. Further research is needed to fully remedy this defect.

Figure 6: SEM photos of the hydration products (14h) (a) Cement paste (b) Tailings content 15% (c) Tailings content 45%
For the cementitious materials slurry with 15%, 30% and 45% of copper tailings, hydration exothermic reaction rates are plotted in Fig. 7a. It can be seen that the low contents of active substances in copper tailings can extend hydration induction period. The larger the content is, the longer the second exothermic peak time will be [28], the overall hydration rate will also decline and the hydration time will be significantly prolonged, which is not suitable for the conventional structure engineering. However, copper tailings have a significant weakening effect on the early heat release rate and total heat release [29], which provides the possibility of application in mass concrete engineering.
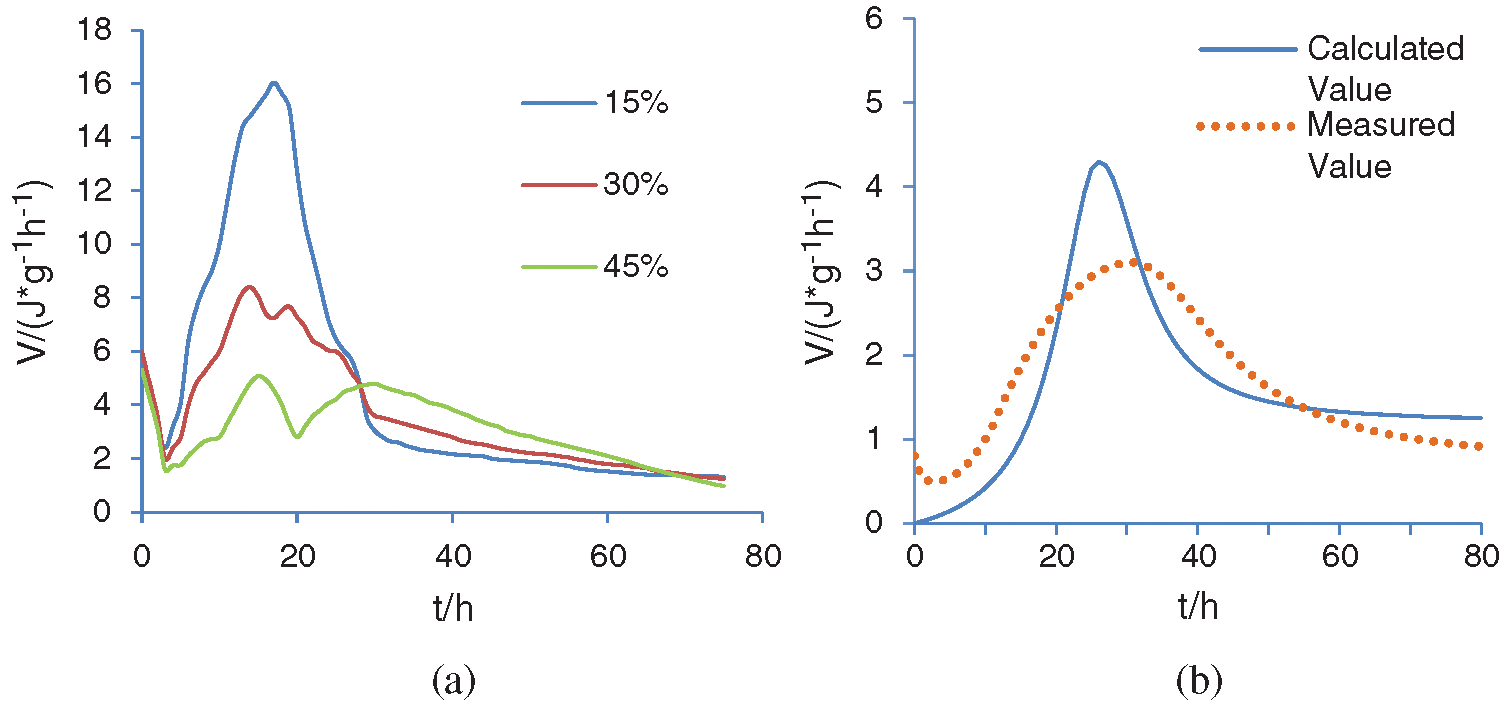
Figure 7: (a) Comparison with different contents (b) between calculated and measured value
In Fig. 7b, the content of copper tailings is 45%, the water-binder ratio of concrete is still 0.4. It can be seen from the figure that the high content of copper tailings makes the difference of peak value larger between the two curves, this shows that the admixture affects the hydration of cement. During the process of NG, the reaction resistance is relatively large, which results in the delay of the initial setting time, makes the hydration rate slower, delays the final setting time, and prolongs the acceleration period [30,31]; during the process of I, the hydration rate is faster, and the secondary hydration of the mineral admixture begins to play a leading role; in the process of D, the hydration rate is still faster, which makes the deceleration period longer.
Based on the experiment and numerical calculation, the findings of this study can be summarized as,
(1) This microscopic hydration model can accurately predict the hydration process of concrete taking cement and copper tailings as composite cementitious materials.
(2) Based on the improved microscopic hydration model, the hydration degree, hydration rate and other parameters are obtained, and then concrete macroscopic heat and moisture coupling diffusion model is established, which can predict the temperature and humidity distribution of early-age concrete.
(3) If no activator is added, the amount of copper tailings should not exceed 30%; The concrete with the larger mixing percentage of copper tailings can be attempted in mass concrete projects, which needs to be further investigated.
Funding Statement: This work was financially supported by Provincial Quality Engineering Project of Anhui Province of China [Grant Nos. 2019xfxm71 and 2020-6656].
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |