Computers, Materials & Continua DOI:10.32604/cmc.2022.019470
Article

Optimization Model for Selecting Temporary Hospital Locations During COVID-19 Pandemic

Chia-Nan Wang1, Chien-Chang Chou2,*, Hsien-Pin Hsu3, Van Thanh Nguyen4 and Viet Tinh Nguyen4

1Department of Industrial Engineering and Management, National Kaohsiung University of Science and Technology, Kaohsiung, 80778, Taiwan
2Department of Shipping Technology, National Kaohsiung University of Science and Technology, Kaohsiung, 80778, Taiwan
3Department of Supply Chain Management, National Kaohsiung University of Science and Technology, Kaohsiung, 80778, Taiwan
4Faculty of Commerce, Van Lang University, Ho Chi Minh City, 70000, Vietnam
*Corresponding Author: Chien-Chang Chou. Email: ccchou@nkust.edu.tw
Received: 14 April 2021; Accepted: 17 May 2021

Abstract: The two main approaches that countries are using to ease the strain on healthcare infrastructure is building temporary hospitals that are specialized in treating COVID-19 patients and promoting preventive measures. As such, the selection of the optimal location for a temporary hospital and the calculation of the prioritization of preventive measures are two of the most critical decisions during the pandemic, especially in densely populated areas where the risk of transmission of the virus is highest. If the location selection process or the prioritization of measures is poor, healthcare workers and patients can be harmed, and unnecessary costs may come into play. In this study, a decision support framework using a fuzzy analytic hierarchy process (FAHP) and a weighted aggregated sum product assessment model are proposed for selecting the location of a temporary hospital, and a FAHP model is proposed for calculating the prioritization of preventive measures against COVID-19. A case study is performed for Ho Chi Minh City using the proposed decision-making framework. The contribution of this work is to propose a multiple criteria decision-making model in a fuzzy environment for ranking potential locations for building temporary hospitals during the COVID-19 pandemic. The results of the study can be used to assist decision-makers, such as government authorities and infectious disease experts, in dealing with the current pandemic as well as other diseases in the future. With the entire world facing the global pandemic of COVID-19, many scientists have applied research achievements in practice to help decision-makers make accurate decisions to prevent the pandemic. As the number of cases increases exponentially, it is crucial that government authorities and infectious disease experts make optimal decisions while considering multiple quantitative and qualitative criteria. As such, the proposed approach can also be applied to support complex decision-making processes in a fuzzy environment in different countries.

Keywords: COVID-19; WHO; MCDM; preventive measures; fuzzy theory; FAHP; WASPAS

1  Introduction

COVID-19 first emerged in Wuhan, China, in December 2019. Since then, the virus has become a global health crisis causing dire social and economic consequences [1]. As of August 2020, COVID-19 has infected more than 22 million people, of which more than 700,000 died [2]. While the death rate fluctuates greatly by region [3], COVID-19's transmissibility and severe long-term health effects make it a dangerous threat to all countries, especially those with inadequate healthcare infrastructure. Active hotspot of Covid-19 cases as of April 1st 2021, shown in Fig. 1.

Several organizations, including the World Health Organization (WHO) and the U.S. Centers for Disease Control and Prevention (CDC), as well as national and federal governments, have provided warnings and guidelines to prevent the spread of COVID-19 [4]. These guidelines range from basic personal hygiene measures such as frequent washing and sanitizing of one's hands and promoting the use of face masks, to societal measures such as social distancing and shutting down public spaces [5]. While several vaccines have been developed for COVID-19, vaccine manufacturing and administration take time. Currently, public knowledge and social awareness still play important roles in limiting the spread of the deadly disease [6]. While different countries have different approaches to limiting the spread of COVID-19, it is important to identify the main way that COVID-19 spreads and to evaluate the available tools in order to prioritize effective preventive measures. This is a multicriteria decision-making problem, and to solve it requires the use of Multiple Criteria Decision-Making (MCDM) models.

Figure 1: Active hotspot of Covid-19 cases as of April 1st, 2021 [2]

Over the years, MCDM models have been developed in many fields, including ranking potential locations for renewable energy plants [7], ranking potential suppliers in various industries [8,9], and applications in healthcare [10]. Of these applications, location selection problems, which frequently involve multiple quantitative and qualitative criteria, are where MCDM models are most effective [11–14]. Location selection of a temporary hospital for COVID-19 patients is also a multicriteria decision-making problem that can be solved using an MCDM model. The incorporation of fuzzy theory allows an MCDM model to solve decision-making problems in uncertain environments.

2  Literature Review

With the entire world facing the global pandemic of COVID-19, many scientists have applied research achievements in practice to help decision-makers make accurate decisions to prevent the pandemic. As the number of cases increases exponentially, it is crucial that government authorities and infectious disease experts make optimal decisions while considering multiple quantitative and qualitative criteria. As such, MCDM models can be of great value in solving complex problems involving multiple criteria.

MCDM models have been used in many fields that involve complex decision-making problems, including third-party logistics service provider selection [15,16] green supplier evaluation and selection [17], and medial methods evaluation [18]. One disadvantage of traditional MCDM models is that they cannot convey the uncertain nature of the human decision-making process. In recent years, many researchers have integrated fuzzy set theory into their MCDM models in an attempt to overcome this disadvantage [19,20].

Through the years, many MCDM models have been developed to solve location selection problems. Chu et al. [21] have developed a fuzzy MCDM model to assist a distribution center location seclection process using fuzzy number theory. Villacreses et al. [22] developed MCDM model for deciding sustainable wind farm location using OWA, OCRA, and TOPSIS methods with intergration to Geographical Information System (GIS). Kabak et al. [23] introduced a GIS-based MCDM model for evaluation of bike-share stations. Sanchez-Lozano et al. [24] developed an GIS based Fuzzy MCDM model for deciding optimal onshore windfarm location. MDCM models are also widely applied in the healthcare sector. Afkham et al. [25] developed an MCDM model to support the service quality evaluation process of healthcare centers in Iran. Liou et al. [26] developed a hybrid DEMATEL-DANP-mVIKOR model to improve electronic health record service quality through better evaluation. Samanlioglu [27] developed a hybrid AHP-VIKOR model to evaluate influenza intervention strategies. Abbas et al. [28] introduced a framework for assessing key challenges of digital health interventions adoption during the COVID-19 pandemic under hesistant fuzzy sets. Torkzad et al. [29] created an MCDM model for evaluating and prioritizing hospital service quality.

Weighted Aggregated Sum Product Assessment (WASPAS) method was developed by Zavadskas et al. [30] in 2014 and has been applied in many decision-making problems. Zavadskas et al. [31] applied the WASPAS method to assist alternative sites for the construction of a waste incineration plant. Muhammet et al. [32] proposed a type-2 fuzzy MDCM model based on WASPAS and TOPSIS to assist in the a car sharing station selection process. Mehdi et al. [33] developed a type-2 fuzzy MCDM model using extended WASPAS method for the evaluation of green suppliers. Khubaib Amjad et al. [34] suggested a hybrid MCDM model using Fuzzy AHP-WASPAS to evaluate public cloud computing services.

Although several researchers have proposed MCDM models to investigate this problem, none have tried to solve it in a fuzzy environment. In this study, a decision support framework using fuzzy analytic hierarchy process (FAHP) and the weighted aggregated sum product assessment (WASPAS) model is proposed for selecting the location of a temporary hospital for COVID-19 patients and for the prioritization of preventive measures. The results of the study can be used to assist decision-makers, such as government authorities and infectious disease experts, in dealing with the current pandemic as well as other diseases in the future.

3  Methodology

3.1 Research Development

The model development process, shown in Fig. 2, consists of three steps:

Step 1: Analyze and evaluate the current practices (the process of selecting the location for a temporary hospital and prioritizing preventive measures). Collect additional criteria for each problem from scientific research and industry experts.

Step 2: FAHP is used to calculate the weights of all related criteria for each problem.

Step 3: Use the calculated weights from Stage 2 as the input for the rankings of potential temporary hospital locations and the COVID-19 preventive measures using WASPAS.

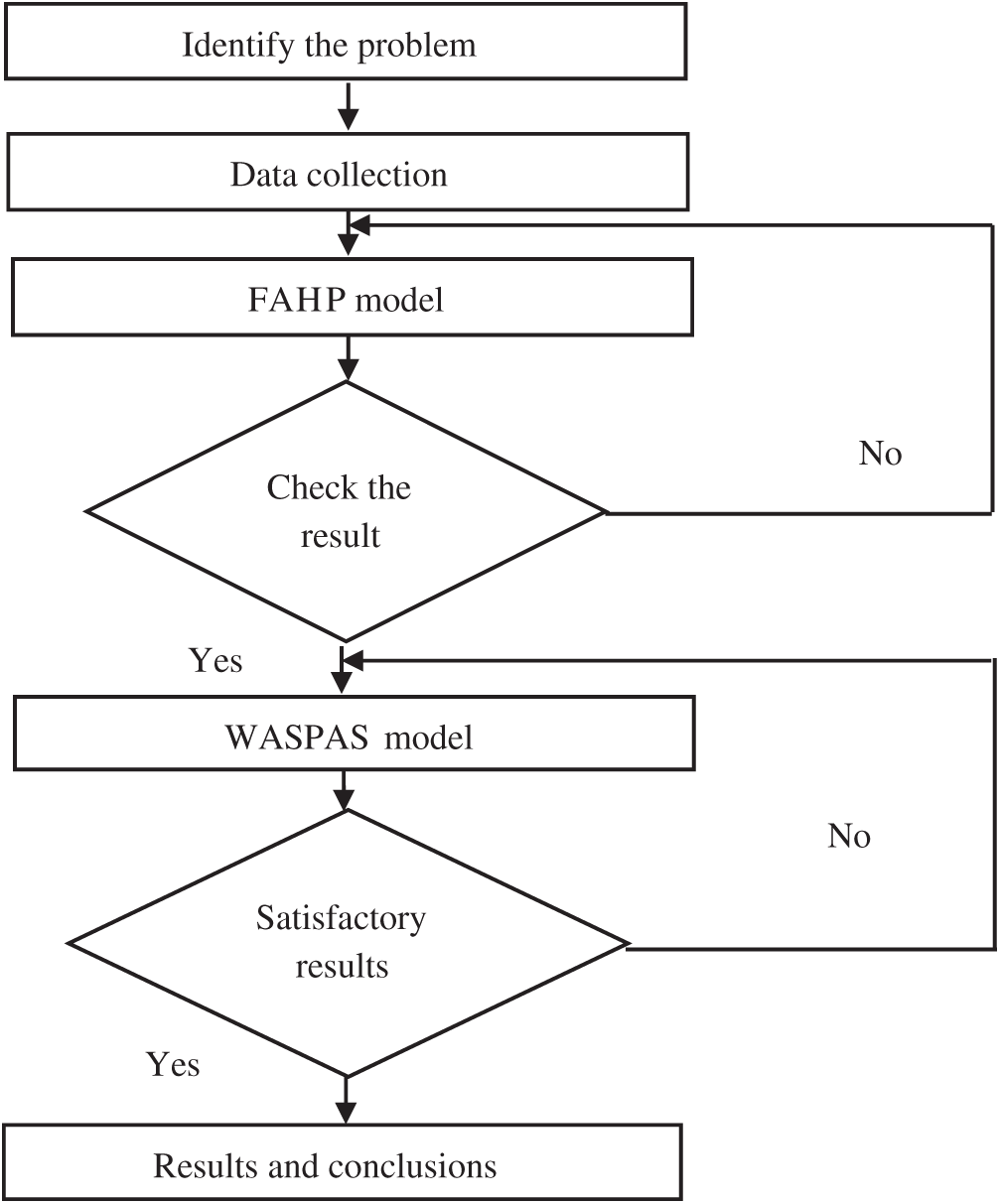
Figure 2: Research process

3.2 Basic Theory

3.2.1 Fuzzy Analytical Hierarchy Process

A Triangular Fuzzy Number (TFN) can be defined as (n, p, q), with n, p and q (n ≤p ≤ q) are parameters that specify the smallest likely value, the promising value and the largest possible value of the TFN. A typical TFN are shown in Fig. 3 and can be described as:

μ(xM˜)={0,x−np−qq−xq−p0,x<p,n≤x≤p,p≤x≤q,x>q, (1)

A fuzzy number is given as:

M~=(Mo(y),Mi(y))=[n+(p−q)y, q+(h−q)y],y∈[0,1](2)

With o(y) and i(y) represent the two sides (left and right) of the fuzzy number, respectively.

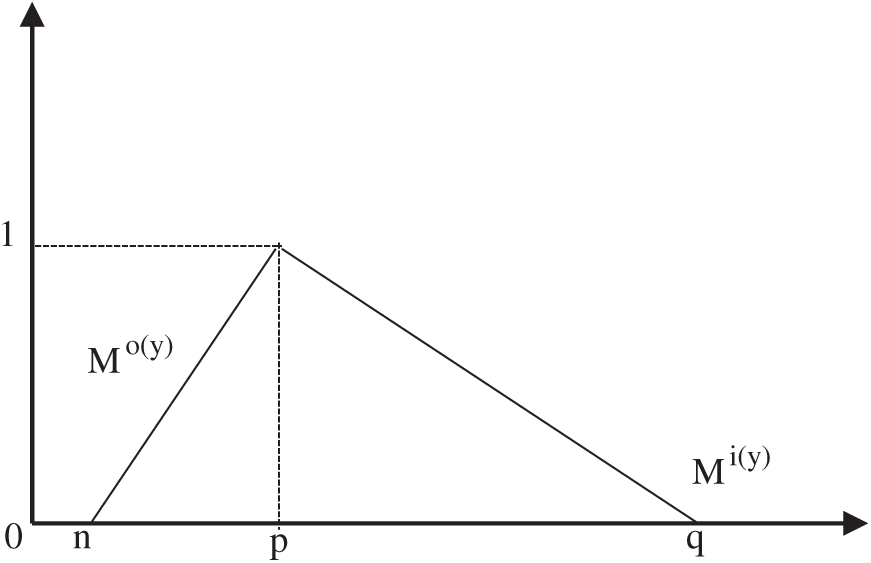
Figure 3: Triangular fuzzy number

Fuzzy Analytical Hierarchy Process (FAHP) is the fuzzy extension of AHP to handle its limitation in working with uncertain decision-making environments. Let X = \{x_1, x_2,…, x_n\} be the set of objects and K = \{k_1, k_2,…, k_n\} be the goal set. According to Chang [35] extent analysis method, each object is taken, and an extent analysis of its goals is performed. Therefore, the l extent analysis values for each object can be obtained. These values are denoted as:

Lki1,Lki2,…,Lkim,i=1,2,…,n(3)

where Lkj(j=1,2,….,m) are the TFNs

Fuzzy synthetic extent vlaue of the ith object is defined as:

Si=∑j=1m⁡Lkij⊗[∑i=1n⁡∑j=1m⁡Lkij]−1(4)

The possibility that L1≥L2 is defined as:

V(L1≥L2)=supy≥x[min(μL1(x),),(μL2(y))](5)

where the pair (x,y) exists with x≥y and μL1(x)=μL2(y), then we have V(L1≥L2)=1.

Since L1 and L2 are convex fuzzy numbers, we have:

V(L1≥L2)=1,ifl1≥l2(6)

and

V(L2≥L1)=hgt(L1∩L2)=μL1(d) (7)

where d is the ordinate of the highest intersection point L between μL1 and μL2.

With L1=(o1,p1,q1)and L2=(o2,p2,q2), the ordinate of point V is calculated by (8):

V(L2≥L1)=hgt(L1∩L2)=l1−q2(p2−q2)−(p1−o1)(8)

In order to compare L1 and L2, we need to calculate the values of V(L1≥L2) and V(L2≥L1).

The possibility for a convex fuzzy number to be greater than k convex fuzzy numbers Li(i=1,2,…k) is calculated as:

V(L≥L1,L2,…,Lk)=V[(L≥L1)and(L≥L2)](9)

and

V(L≥Lk)=minV(L≥Li),i=1,2,…,k)(10)

Under the assumption that:

d′(Bi)=minV(Si≥Sk)(11)

For k=1,2,…nandk i, the weight vector is determined as:

W′=(d′(B1),d′(B2),…d′(Bn))T(12)

where Bi are n elements.

The normalized weight vectors are shown as:

W=(d(B1),d(B2),….,d(Bn))T (13)

With W is a nonfuzzy number.

3.2.2 Fuzzy Analytical Hierarchy Process

One of the most utilized and efficient multicriteria decision making models for assessing multiple options in numerous criteria is the Weighted Sum Model (WSM). Firstly, there are a options and b decision criteria. We then define zb as the importance for the criteria and xab. is the performance level for option a evaluated in criterion b. Finally, the overall relative importance of alternative y, denoted as Py(1), is defined as [36]:

Py(1)=∑b=1n⁡x¯abzb(14)

where the linear normalization for each initial criteria value is calculated as follows,

x¯ab=xabmaxaxab(15)

if maxaxab value is preferable or

x¯ab=minaxabxab(16)

if minabxab. value is preferable.

Another method that is commonly used when assessing multiple options using the total relative importance of option y, denoted as Py(2)is the Weight Product Model (WPM). It is defined as follows [36]:

Py(2)=∏b=1n⁡(x¯ab)zb(17)

In order in incorporate both methods to evaluate further the importance of options, the weights of total relative importance are then equally divided between the WSM and WPM results for a total score:

Py=0.5Py(1)+0.5Py(2)(18)

From the study above and evaluating further regarding the accuracy and effectiveness in decision making, the coefficients that defined WSM and WPM can then be further changed in order to adapt suitably depending on the problem. This change in coefficients in called the Weighted Aggregated Sum Product Assessment method and it is used to rank the options in this research.

Py=λ∑b=1n⁡x¯abzb+(1−λ)∏j=1n⁡(x¯ab)zb(19)

4  Case Study

Because healthcare infrastructure is such an important aspect of every country, the selection of a healthcare center's location is a critical process that involves multiple quantitative and qualitative criteria, which include economic, environmental and social factors. Such decision can become even more important and more complicated during a public health crisis, such as the COVID-19 pandemic.

Due to its extremely rapid rate of transmission, COVID-19 quickly placed immense pressure on the healthcare infrastructures of countries around the world. Hospitals struggled to have enough capacity to deal with the rapid increase in the number of patients. The transmission rate of the disease also causes additional risks when COVID-19 patients are treated at regular hospitals as it can spread to the patients in other wards. Therefore, many governments have constructed temporary hospitals that are dedicated to treating COVID-19 patients, while promoting preventive measures to reduce the transmission rate, thereby reducing the pressure on healthcare infrastructures.

From international experience in building field hospitals, such as China building two field hospitals for COVID-19 patients in Wuhan, England building a field hospital in London, and Russia constructing a field hospital in Moscow, we extrapolate that the construction of a field hospital to treat patients infected with COVID-19 requires meeting multiple criteria such as a convenient location, the availability of electricity, clean water, and drainage and the ability to meet the scale and necessary medical equipment, according to the service level [37]. Other requirements are rapid construction of the facility and installation of equipment; ensuring environmental sanitation and the safety of human health in the use of construction materials; and economic efficiency and construction cost [38].

Along with building specialized temporary hospitals, WHO and government bodies around the world also promoting preventive measures to limit the transmission rate of COVID-19. These measures include basic personal hygiene such as frequent hand washing and sanitizing and promoting the use of face masks, to broader measures such as social distancing and shutting down public spaces [5]. Success stories from countries such as Vietnam, South Korea, Germany, and New Zealand [39] show that with proper implementation, these measures can help significantly reduce the transmission rate of the COVID-19 virus.

Ho Chi Minh City is the most populous city in Vietnam, and its population is averaging 2.28% annual growth. Household size is 3.51 people, and 66.4% of households have two to four people. Ho Chi Minh City is also a city where 54 ethnic groups live and work [40]. Health services have made great efforts to improve quality in order to meet the criteria issued by the Ministry of Health, and 87% of the city's hospitals have increased quality scores compared to previous years. Most hospitals have actively re-allocated resources with a focus on service improvement, resulting in quality improvement in many areas of hospital operation [41].

Figure 4: Design diagram of the screening area for COVID-19 patients who have signs of severe respiratory inflammation (SARI) [41]

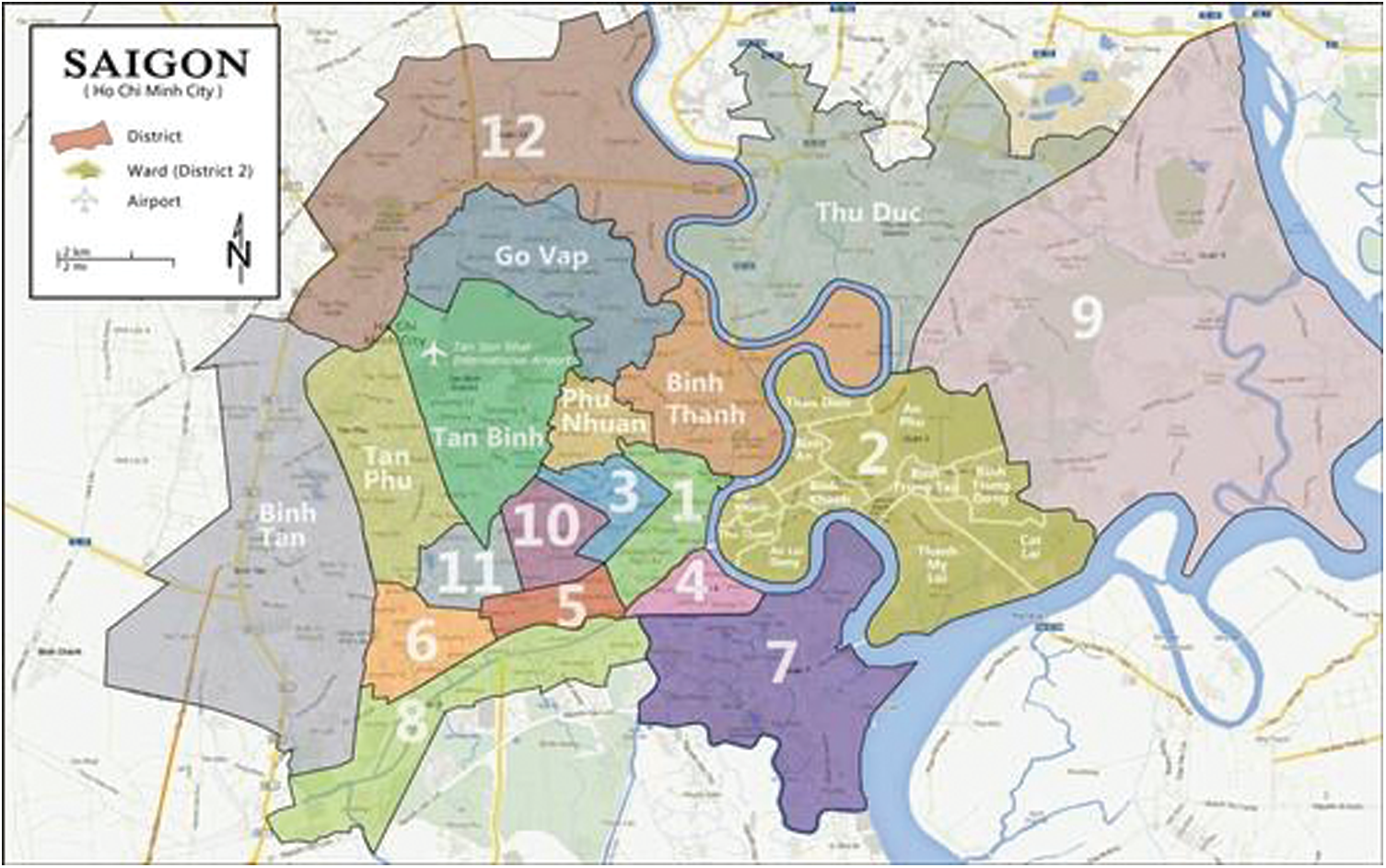
Figure 5: Detailed maps of Ho Chi Minh City [42]

Vietnam was one of the safest countries in the early days of the COVID-19 outbreak in Wuhan, China. However, recently, COVID-19 outbreaks have occurred rapidly in Vietnamese cities. Therefore, Ho Chi Minh City plans to take an active role in the preparation for the construction of field hospitals when there is an outbreak of COVID-19. In addition, preventive measures are being promoted in Vietnam, as their effectiveness was proven in the early days of the pandemic.

4.1 Temporary Hospital Location Selection Case Study

When the COVID-19 pandemic occurred, many countries discovered that they lacked the necessary facilities to screen and treat people infected with the virus and began building more field hospitals specifically for treating COVID-19. In this case study, the MCDM model is used to assist in locating temporary hospitals in Ho Chi Minh City. Design diagram of the screening area for COVID-19 patients who have signs of severe respiratory inflammation (SARI), shown in Fig. 4.

Detailed maps of Ho Chi Minh City, shown in Fig. 5. Through surveys and evaluations by experts, five locations were considered, as shown in Tab. 1.

Based on the characteristics of the decision-making problem, several criteria were identified using location selection studies in the literature and experts’ opinions. These are shown in Tab. 2.

To determine the weight of each criteria, the author used an FAHP model. The weight of each criterion is shown in Tabs. 3 and 4:

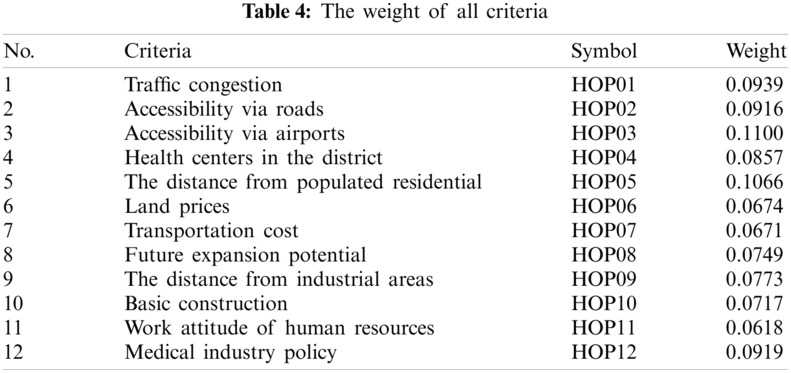
In the final stages of the process, the WASPAS model was used to rank all potential locations. The normalized matrix and normalized weighted matrix are shown in Tabs. 5 and 6:

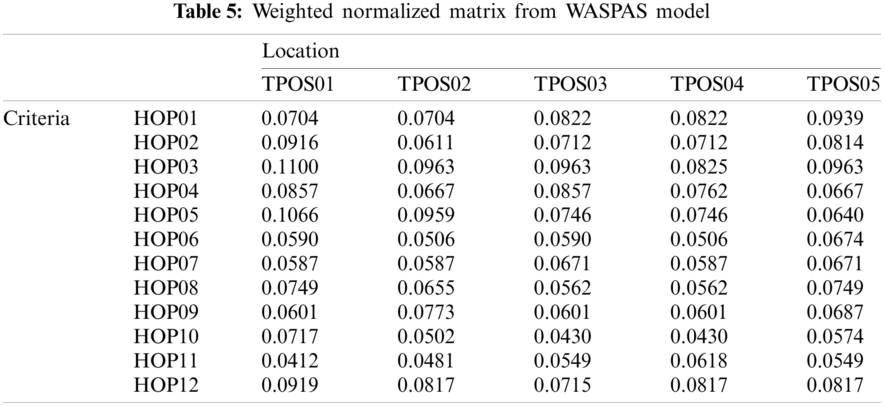
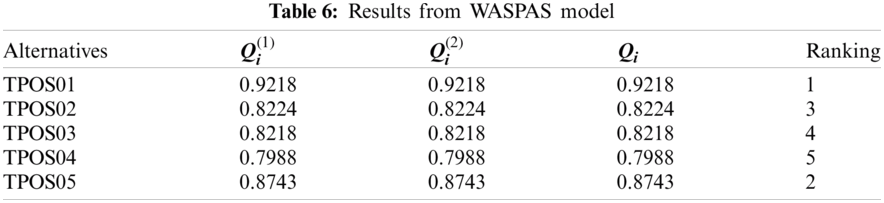
According to the proposed FAHP-WASPAS model, the optimal location for building a temporary hospital for COVID-19 patients in Ho Chi Minh City was in the Cu Chi District (TPOS01), which had the highest Qi value of 0.928. The results from the case study showed the feasibility of the model, and that it can be used alongside other MCDM methods to support better decision-making.

4.2 Prioritizing Preventive Measures Case Study

In this case study, an FAHP model was used to calculate the weight of each preventive measure, based on expert opinions. These weights were then used to create the prioritized ranking of the measures.

Through literature reviews and experts’ opinions, the list of 15 COVID-19 preventive measures is shown in Tab. 7:

The FAHP model was used to determine the weight of all subcriteria. The calculated weights are shown in Tab. 8:

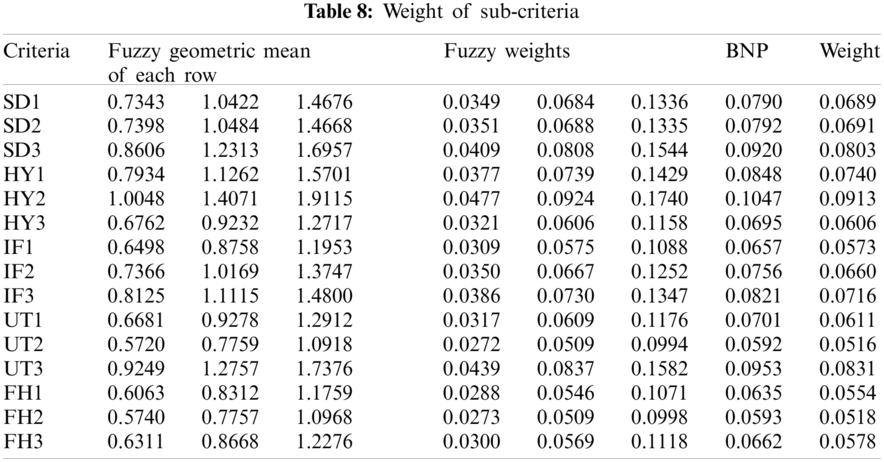
Finally, the prioritize ranking of the preventive measures are shown in Tab. 9:

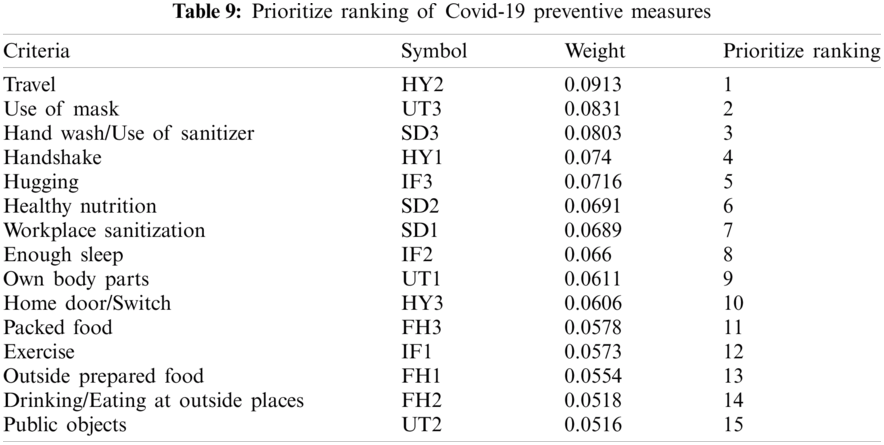
According to the proposed FAHP model, the three most effective preventive measures were 1) limiting travel; 2) the use of face masks; and 3) frequent hand washing. The results from the case study show the feasibility of the FAHP model.

5  Conclusions

The global spread of the COVID-19 virus has created one of the worst pandemics in modern history. As the virus spread, healthcare infrastructures worldwide were faced with unprecedented pressures. COVID-19's transmissibility and severe long-term health effects make it a dangerous threat to all countries, but particularly those with inadequate healthcare infrastructure.

To lessen the strain of the pandemic on existing healthcare infrastructures, two approaches have been adopted by many countries: building specialized temporary hospitals and promoting preventive measures. Each of these approaches requires a sophisticate decision-making process. In the case of building temporary hospitals, location selection is critical to the effectiveness of the facilities and involves multiple quantitative and qualitative criteria, making it an MCDM problem. Similarly, the prioritization of preventive measures can greatly reduce the transmissibility of the virus, especially in the early stage of the pandemic, and can be calculated using proper MCDM methods.

This study proposed a hybrid Fuzzy AHP-WASPAS model for the problem of selecting the best location for a temporary hospital and a Fuzzy AHP model for calculating the prioritize ranking of preventive measures. In the case study of selecting the best location for a temporary hospital in Ho Chi Minh City, the optimal location proved to be the Cu Chi District (TPOS1). In the case study of determining the preventive measures, the three most effective were limiting travel, use of face masks, and frequent hand washing.

The two proposed models can act as guidelines for creating more effective decision-making processes for temporary hospital location selection and prioritization of COVID-19 preventive measures. Future research may expand the work to related fields of study or use the work as a base for further COVID-19 related studies.

Funding Statement: The authors received no specific funding for this study.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.