DOI:10.32604/cmc.2021.017548

| Computers, Materials & Continua DOI:10.32604/cmc.2021.017548 |  |
| Article |
An Optimized Framework for Surgical Team Selection
Department of Computer Science and Engineering, Thapar Institute of Engineering and Technology, Patiala, 147004, India
*Corresponding Author: Hemant Petwal. Email: hemant.petwal@thapar.edu
Received: 02 February 2021; Accepted: 11 April 2021
Abstract: In the healthcare system, a surgical team is a unit of experienced personnel who provide medical care to surgical patients during surgery. Selecting a surgical team is challenging for a multispecialty hospital as the performance of its members affects the efficiency and reliability of the hospital’s patient care. The effectiveness of a surgical team depends not only on its individual members but also on the coordination among them. In this paper, we addressed the challenges of surgical team selection faced by a multispecialty hospital and proposed a decision-making framework for selecting the optimal list of surgical teams for a given patient. The proposed framework focused on improving the existing surgical history management system by arranging surgery-bound patients into optimal subgroups based on similar characteristics and selecting an optimal list of surgical teams for a new surgical patient based on the patient’s subgroups. For this end, two population-based meta-heuristic algorithms for clustering of mixed datasets and multi-objective optimization were proposed. The proposed algorithms were tested using different datasets and benchmark functions. Furthermore, the proposed framework was validated through a case study of a real postoperative surgical dataset obtained from the orthopedic surgery department of a multispecialty hospital in India. The results revealed that the proposed framework was efficient in arranging patients in optimal groups as well as selecting optimal surgical teams for a given patient.
Keywords: Multi-objective optimization; artificial electric field algorithm; mixed dataset clustering; surgical team; strength Pareto
During a preoperative procedure, surgical team members, surgical specialty and experience, and coordination among the members play essential roles. Although various factors can affect surgical procedures, positive outcomes mainly depend on the individual surgical team members. Appropriate coordination and cooperation among those can reduce unavoidable conflicts during the procedures [1]. Hence, the selection of an optimal surgical team is indispensable for a rapid patient recovery, decreased complications, and more favorable surgical management. However, the selection process is a considerably time-consuming and difficult task [2]. In recent years, several studies have examined the performance of surgical team members. Many vital factors, such as understanding diagnostic complications and patient characteristics, and the surgical practice environment, can result in more satisfactory outcomes. In the field of medicine, appropriate management of surgical care is a difficult task as most surgical complications occur during intra operative surgical care [3]. An efficient team can help in providing effective healthcare services [4]. Hospitals and physicians always focus on providing a safe environment for patients and enhancing their wellbeing [5]. A study investigated human factors associated with operating rooms and analyzed the relationship between their poor performance and the surgical procedures outcomes [4]. Similarly, several studies adopted approaches such as malpractice claim analysis [6], root cause analysis [7], and prospective analysis [8] to reduce intra operative surgical complications. Although these studies tried to analyze the relationship between the performance of operating room and outcomes of surgery, however, contribution of significant factors affecting the performance of operating room were not considered [3]. Studies examining factors such as teamwork in the operating room [9] and intensive care [10] focused on the effect of coordination and synergy among surgical team members. These studies have indicated the necessity and significance of surgical team selection procedure. As performing surgical procedures is often a risky and uncertain task, therefore high synergy is always expected among team members possessing different levels of experience and expertise. Various factors such as availability of surgeons, limitation of resources, and time etc. affect the surgical team selection in a multispecialty hospital; thus, selection of the surgical team is a challenging task [11]. In a surgical team, different responsibilities are assigned to different individuals [12]. As the responsibilities and the individuals to whom responsibilities are assigned change frequently with time, thus selecting an efficient team for the desired activity, considering time and resource limitation, becomes a complicated procedure. All the aforementioned studies have focused on personnel preferences for the day, shift, and units. However, none of these studies have considered the history of the surgical team, characteristics of patients, and feedback of patients who underwent surgery in the past. In this study, an optimal framework based on the characteristics of patients, history of the surgical team, and the feedback of previous surgical patients is proposed to assist in decision-making for the selection of optimal surgical teams. An optimal list of surgical teams contains more than one suitable surgical team that can be assigned to a surgical patient according to their availability.
The rest of the paper is organized as follows. Section 2 presents an overview of the existing literature. Section 3 describes preliminary and background algorithms. Section 4 discusses the proposed framework in detail. Section 5 presents a detailed case study of the orthopedic surgery department at a multispecialty hospital in India. Section 6 summarizes the findings of this research and provides concluding remarks.
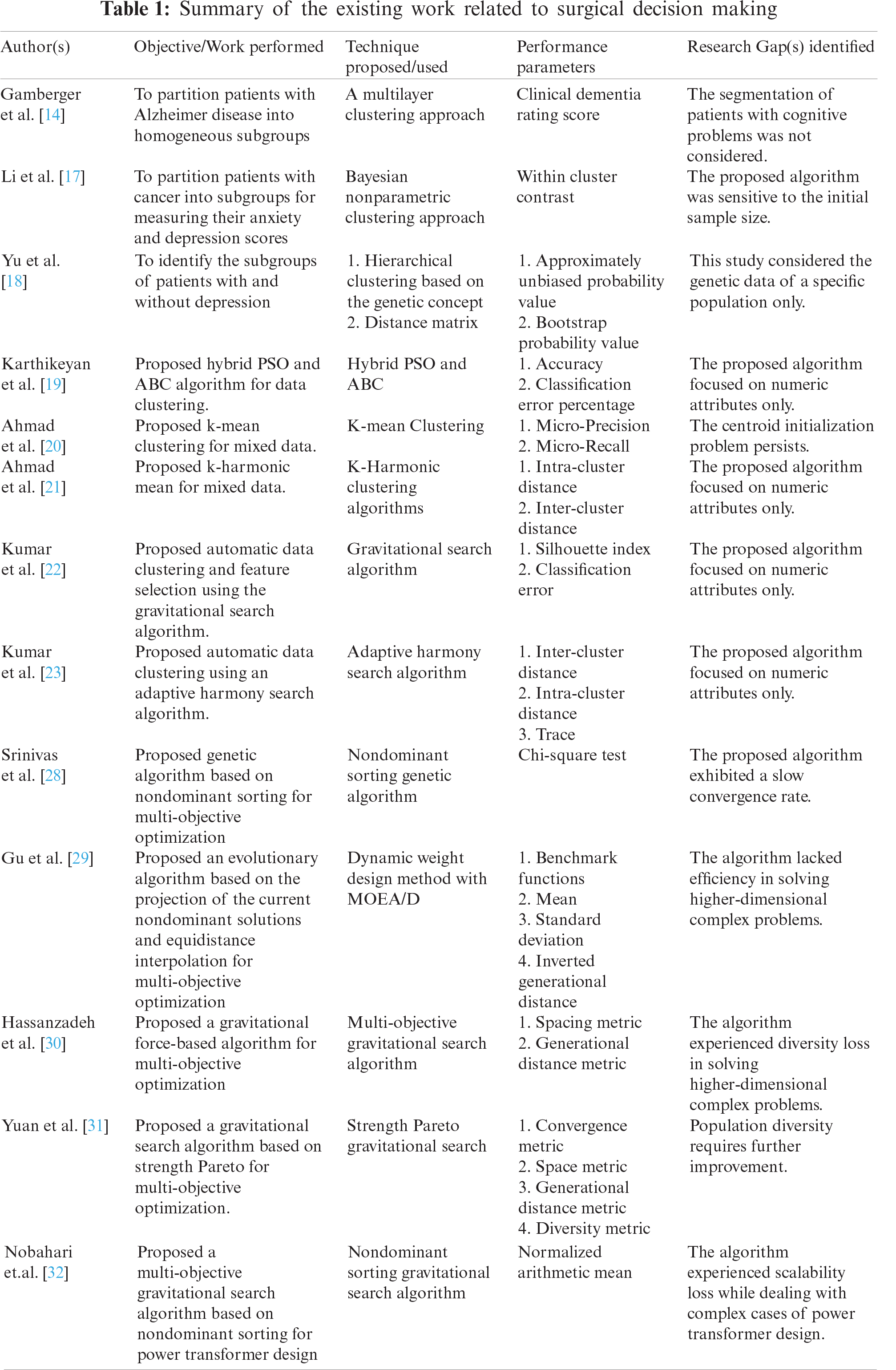
In a modern healthcare system, the provision of high-quality surgical services typically depends on symptoms of various patients. Classifying patients on the basis of their symptoms assist the decision-makers in identifying the target patient and making corresponding remedial decisions [13]. In recent years, several methods have been proposed by the authors for clustering of patients. One of the studies used k-means clustering algorithm to partition the patients based on their health status [13]. Another study used a multilayer clustering approach for partitioning of Alzheimer disease patients into male and female groups [14]. In addition, few studies have used agglomerative hierarchical clustering for partitioning of patients based on presence of comorbidities such as chronic pain and mental illness; obesity and mental illness; cancer; diabetes and renal disease [15,16]. A Bayesian nonparametric clustering approach was applied to divide patients having cancer into sub-groups to measure their anxiety and depression scores before psychotherapy [17]. Further, in a study authors proposed a hierarchical clustering algorithm incorporating genetic concept for partitioning the patients with or without depression [18]. Furthermore, many intelligent nature-inspired algorithms have also been proposed for data clustering. A study proposed a hybrid algorithm combining particle swarm optimization (PSO) and artificial bee colony (ABC) algorithms for data clustering [19]. Additionally, k-means [20] and k-harmonic means [21]—clustering algorithms have been -used for performing—clustering of mixed datasets. The functioning of most of these clustering algorithms is dependent on the predefined number of clusters. However, in real-life problems, for most of the datasets the number of clusters is not known beforehand. Hence, the accurate estimation of an optimal number of clusters is a challenging task, and can affect the performance of a clustering algorithm also. Therefore, several algorithms, such as the gravitational search algorithm [22], harmony search algorithm [23], and differential evolution algorithm [24], have been proposed for automatic clustering to address the aforementioned challenge. Automatic clustering algorithms require no prior information regarding the number of clusters. Instead, they evaluate the optimal number of clusters based on the dataset only. In this paper, an efficient clustering algorithm for mixed datasets based on the artificial electric field algorithm (AEFA) [25] is proposed to categorize patients based on their characteristics (symptoms). A recent study utilized k-prototypes algorithm for partitioning of patients and genetic algorithm (GA) for the selection of optimal surgical team [5]. Although the study reported favorable outcomes, it focused only on the complication ratio for the surgical team selection. However, the success of a surgical procedure depends on various factors also such as a lower surgical readmission rate, lower mortality and complication rates, and higher patient satisfaction (surgical feedback) etc. Therefore, this study considered the feedback of patients who underwent surgery in the past along with complication rates to select an optimal surgical team. Further, the GA [26,27] utilized by Ebadi et al. [5] is likely to experience premature convergence and diversity loss. In addition, Srinivas et al. [28], Gu et al. [29], Hassanzadeh et al. [30], Yuan et al. [31], and Nobahari et al. [32] have proposed several meta-heuristic approaches to prevent premature convergence. These algorithms have been found efficient in finding the optimal solution in a single computation. In this paper, an improved AFEA for multi-objective optimization is proposed to select optimal surgical teams. To the best of our knowledge, no study has focused on considering surgical feedback along with complication rates for selecting optimal surgical teams by utilizing AEFA. Tab. 1 summarizes the existing work related to surgical decision-making.
1. A decision-making framework is proposed to assist medical practitioners while selecting optimal surgical teams for a given patient.
2. Two population-based meta-heuristic algorithms are proposed for clustering of mixed datasets and multi-objective optimization, which are used for the partitioning of patients and the selection of optimal surgical teams, respectively.
3. The proposed algorithms are validated using a real surgical dataset of a multispecialty hospital in India.
This section briefly discusses the basic concepts of partitioning clustering, distance measure for mixed datasets, multi-objective optimization, and artificial electric field algorithm (AEFA).
In data clustering, partitioning clustering arranges data points into distinct clusters
where,
3.2 Distance Measure for Mixed Datasets
The closeness between a data point and clusters is measured by computing the distance between them. The distance measure confirms homogeneity among the data points of a cluster and heterogeneity between different clusters. Arranging a mixed dataset into distinct clusters is a challenging task. In this paper, the distance measure
where
3.3 Multi-objective Optimization
A multi-objective problem (MOOP) can be a minimization or a maximization problem. It involves
Minimize/Maximize:
Subject to constraints:
where,
3.4 Artificial Electric Field Algorithm (AEFA)
AEFA, a population-based meta-heuristic algorithm, simulates Coulomb’s law of electrostatic attraction force (EAF) and the law of motion. Each candidate solution in AEFA is represented as a charged particle. The charge present on each charged particle assists in evaluating the performance of a candidate solution. Because of EAF, each charged particle attracts another charged particle, resulting in the global movement of all charged particles toward a heavier charged particle.
This section provides a detailed description of the proposed framework. The proposed framework consists of two modules: surgical history management (SHM) and surgical team selection (STS). The SHM module involves two activities: (1) clustering of existing surgical patients based on their characteristics and (2) filtering of existing surgical team details. The STS module produces an optimal list of surgical teams for a given patient. The SHM module is designed to assist the STS module in decision-making. Fig. 1 presents the workflow of the proposed framework.
4.1 Surgical History Management (SHM) Module
Surgical history is a vital aspect of medical records and includes the social and demographic information of surgical patients, the details of surgical teams, and the outcomes of diagnostic and procedural tests. For multispecialty hospitals that provide surgical services to numerous patients, efficient management of surgical records is essential. An efficiently organized surgical history helps hospitals to enhance their patient care and resource efficiency. To utilize these surgical records, the following two activities are performed in the SHM module.
4.1.1 Clustering of the Existing Surgical Patients
Arranging existing surgical patients in disjoint clusters based on their characteristics can help hospitals to find a suitable subgroup for a newly referred surgical patient. In this study, an efficient data clustering algorithm for mixed datasets [33] is proposed to cluster surgical patients. The proposed clustering algorithm (Algorithm 1) based on the AEFA focuses on finding optimal clusters automatically. The steps of the proposed clustering algorithm are as follows:
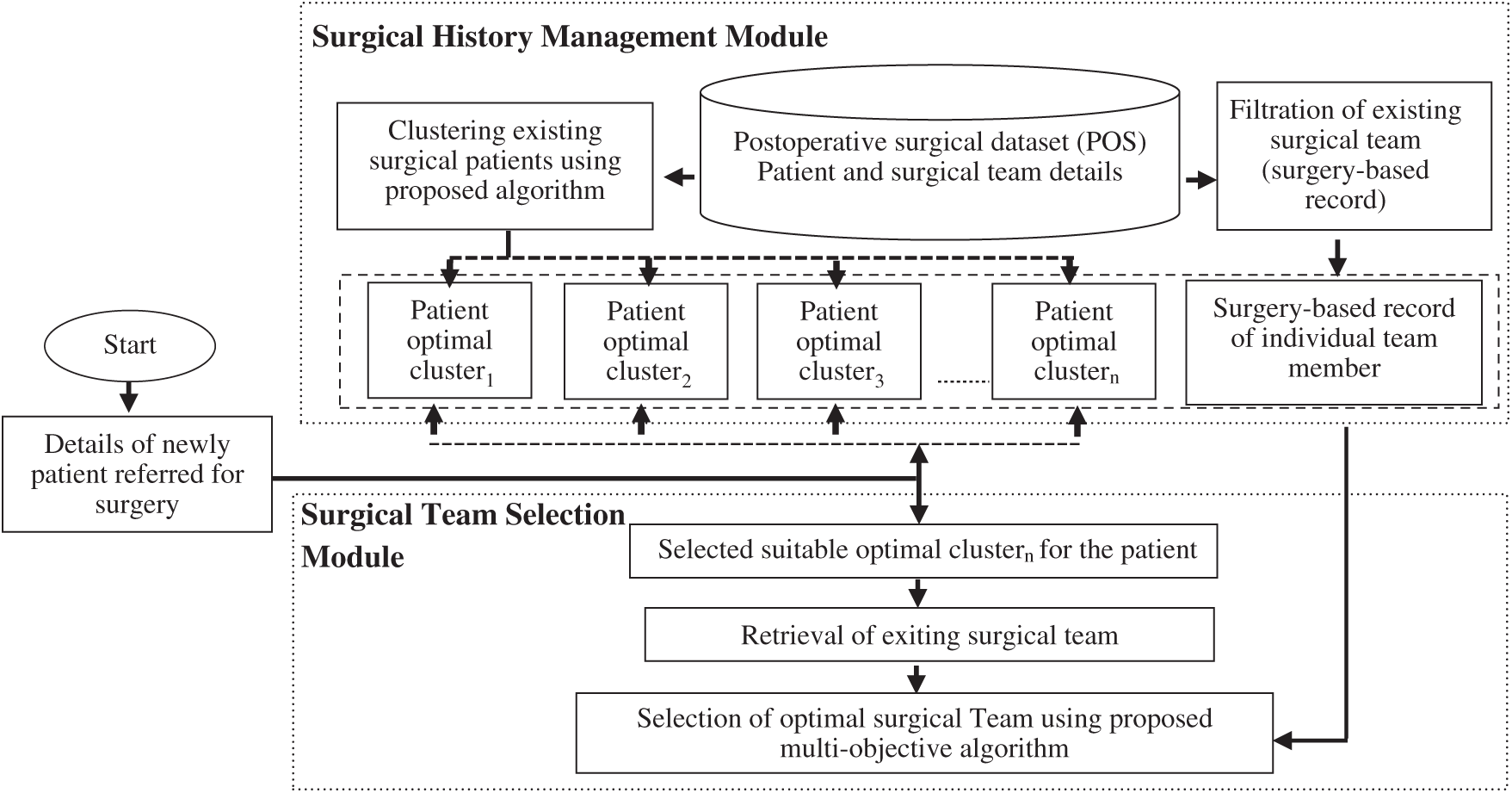
Figure 1: Workflow of the proposed framework
A. Improved Electrostatic Force Computation and Velocity Update
In a traditional AEFA, the total electrostatic attraction force (TEAF; Eq. (2)) on
where,
B. Selection of Active Centroids
For each candidate solution, active centroids are selected from
where,
where,

C. Validation of Empty Clusters
A centroid having less than two data points is termed as an empty cluster. In such cases, the corresponding centroid of the candidate solution is reinitialized, and
D. Computation of Fitness
The efficiency of a clustering algorithm depends on the cluster validation criteria. In this study, we have used silhouette index (SI) criteria for cluster validation. The fitness of the candidate solution is computed as follows:
where,
4.1.2 Filtration of the Existing Surgical Team
In this section, a postoperative surgical dataset is considered as an input. Subsequently, on the basis of the required surgery type (e.g., orthopedic surgery, neurosurgery, and pediatric surgery etc.), the details of existing surgical teams are retrieved. A surgical team involves a surgeon, a nurse circulator, and an anesthesiologist. For each retrieved surgical team, additional information such as the complication rate and patient’s surgical feedback rating -are computed and stored in a database. This stored information helps decision makers in optimizing the process of surgical team selection.
4.2 Surgical Team Selection (STS) Module
This module is invoked when the proposed framework receives details of a new surgical patient. Subsequently, an optimal cluster is selected for the new patient. The details of the corresponding surgical teams are then retrieved from the selected cluster and processed to obtain the optimal list of surgical teams. In this paper, an efficient meta-heuristic algorithm for multi-objective optimization based on AEFA is proposed to generate an optimal list of surgical teams.
4.2.1 Proposed Multi-objective Optimization Algorithm for Surgical Team Selection
The proposed multi-objective optimization (MOOA) algorithm begins with parameter initialization. Subsequently, the population of candidate solutions is generated. The proposed algorithm has two populations: search population
where,
Finally, on the basis of the fitness value of each candidate solution, the best solution is selected. This process is iteratively performed until the convergence condition is satisfied and optimum solutions are obtained. To improve convergence, bounded exponential crossover (BEX) [34] and polynomial mutation operator (PMO) [35] are used in the proposed MOOA. Furthermore, to enhance exploration and exploitation, modifications are introduced in the electrostatic force computation and velocity update (Section 4.1.1) in the proposed MOOA. The proposed MOOA is presented in Algorithm 2.

4.2.2 Fitness Evaluation of the Surgical Team
In this study, two factors are considered to evaluate the performance of a surgical team: complications associated with surgery [5] and patients’ surgical feedback rating. Surgical feedback is defined as the experience of patients during the surgical period. In this study, the feedback ratings of existing surgical teams were collected in terms of a surgical team’s behavior and activity. The fitness functions are computed as follows:
Minimize
Maximize
where,
where,
Because the definition of charge in the conventional AEFA was not found to be suitable for solving MOOPs [25], thus this study uses multi-objective function given by SPEA2 [36] as the fitness function of the AEFA.
where,
5 Experimental Results and Discussion
Experiments were performed using a real case study of a multispecialty hospital in India. The proposed framework was implemented using a postoperative surgical dataset (POS) [33], which was obtained from the orthopedic surgery department of the hospital. Sub-section 5.1 discusses the performance of the SHM module. Subsection 5.2 discusses the performance of the STS module. Performances of the SHM and STS modules are discussed in sub-sections 5.1 and 5.2 respectively. Tab. 2 lists symbols used in the proposed framework.

5.1 Performance Evaluation of the SHM Module
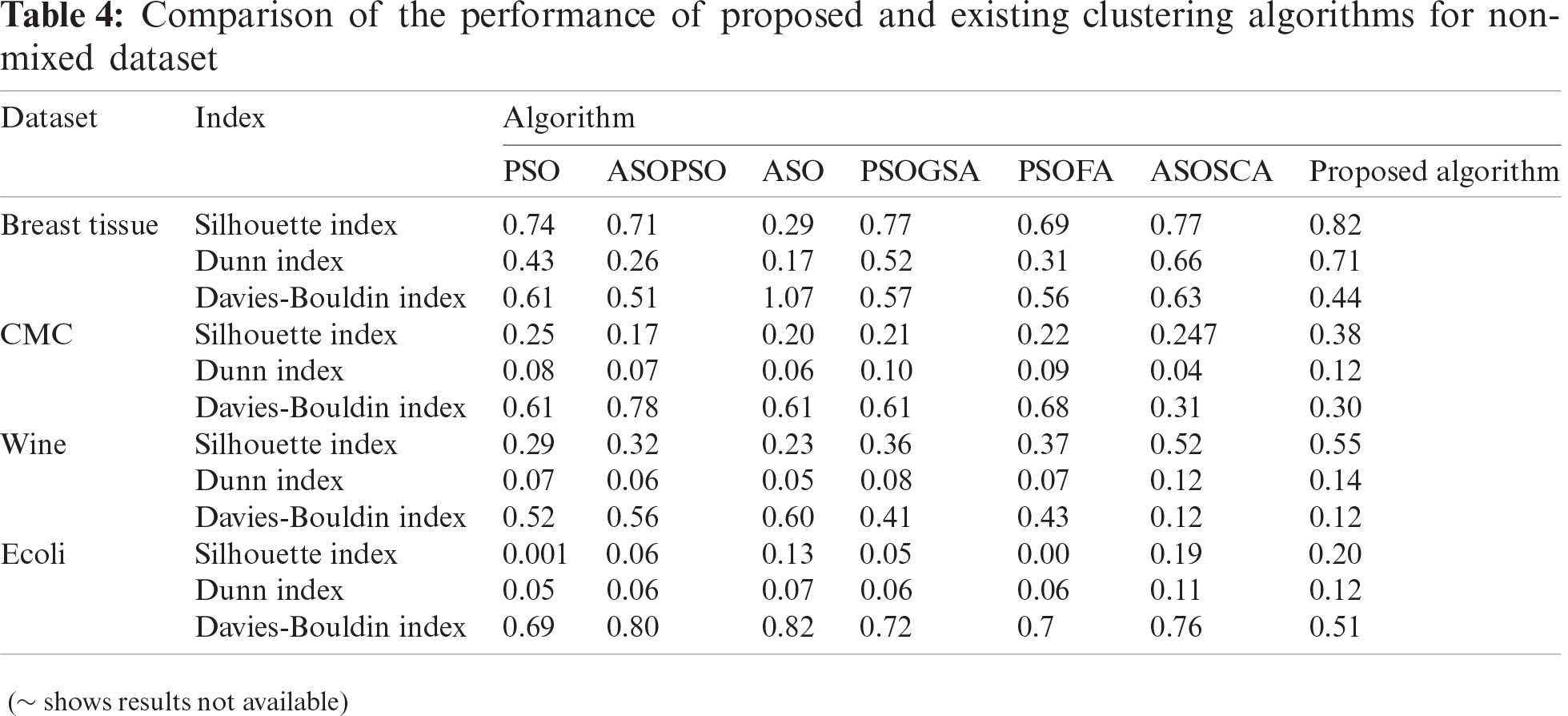
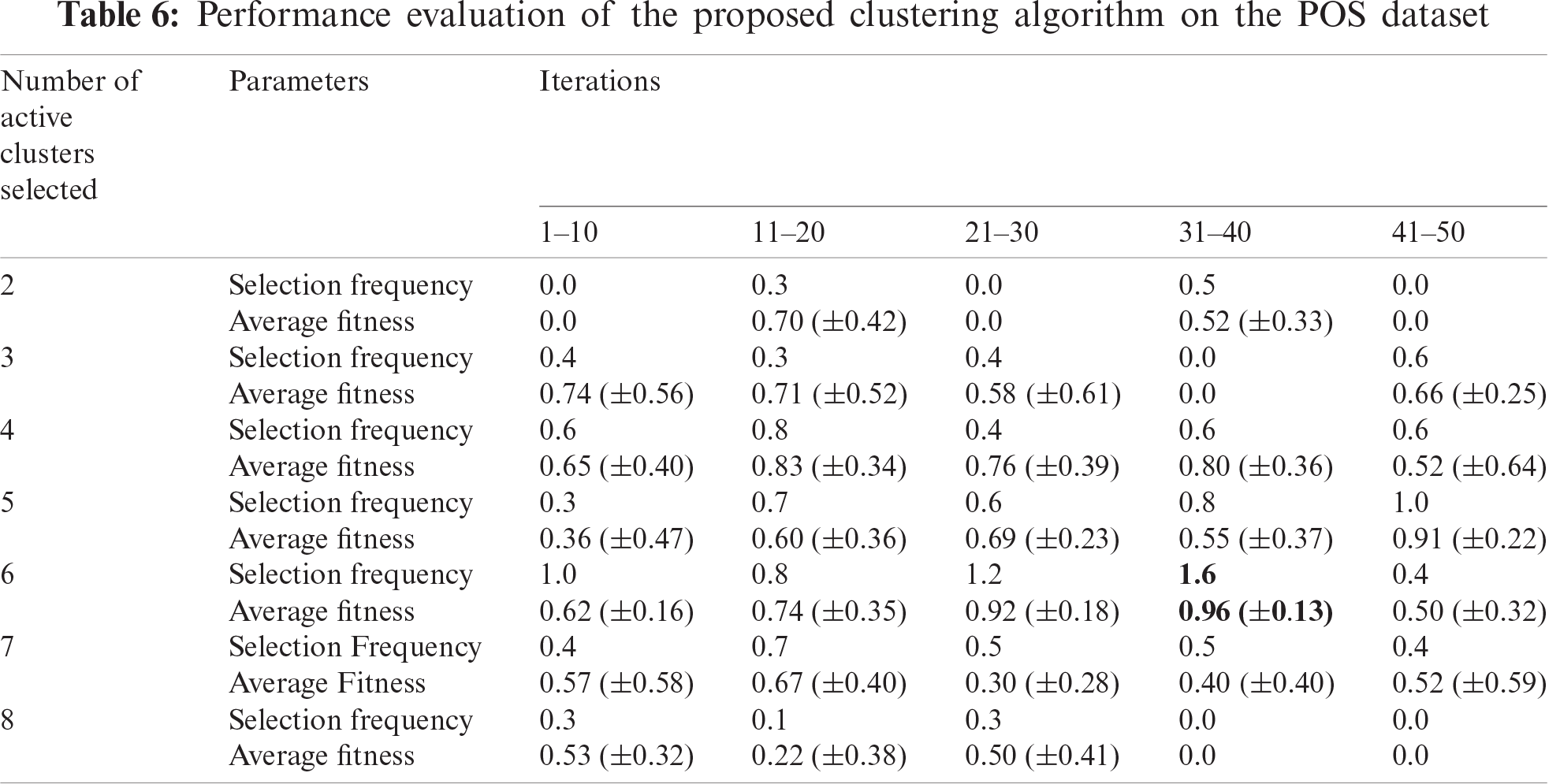
The performance of the SHM module was evaluated in three steps. Firstly, the performance of the proposed clustering algorithm was measured using nine real-life datasets (Tab. 3). Secondly, it was compared with six existing clustering for non-mixed dataset: (i) PSO, (ii) hybrid atom search optimization (ASO) and PSO (ASOPSO), (iii) ASO, (iv) hybrid PSO and gravitational search algorithm (PSOGSA), (v) hybrid PSO and firefly algorithm (PSOFA), (vi) hybrid ASO and sine-cosine algorithm (ASOSCA) [37]. The results revealed that the proposed clustering algorithm outperformed existing algorithms (Tab. 4). Subsequently, the performance of the proposed clustering algorithm was also compared with five existing clustering algorithms for mixed dataset: (i) k-means clustering algorithm, (ii) KHMCMD, (iii) k-prototypes clustering algorithm [38], (iv) Improved k-prototypes clustering algorithm [39], (v) algorithm proposed by Ji et al. [40]. The comparative results are shown in Tab. 5. Thirdly, the performance of the proposed clustering algorithm was evaluated using the POS dataset. The results revealed that considering all iterations, six active patient clusters with a selection frequency of 1.6, an average fitness of 0.96, and a standard deviation of 0.13 were selected as an optimal solution (Tab. 6).


5.2 Performance Evaluation of the STS Module
The performance of the STS module of the proposed MOOA is evaluated on the basis of parameters listed in Tab. 7 using three benchmark functions, namely SCH, FON, and ZDT1 [41]. Subsequently, the performance of the proposed MOOA was compared with four existing MOOAs: SPGSA [31], NSGA

The details related to a surgical patient (Tab. 9) were submitted as input to the STS module. Then, a suitable active patient cluster was selected from the six optimal active patient clusters (obtained from the SHM module), and associated surgical teams were extracted from it. The selected cluster contained 400 orthopedic surgical records in which 15 distinct surgeons, 40 anesthesiologists, and 30 nurses were involved. It resulted in 18000 possible combinations of surgical teams. Finally, 135 surgical teams were generated as an initial search population, and the proposed algorithm was implemented on it. The results are shown in Figs. 3 and 4. Figs. 3a and 3b show the comparison between the proposed and existing algorithms in terms of the complication ratio and surgical feedback rating, respectively. From Fig. 3a it is clear that the proposed algorithm converged faster to the optimal solution and obtained the lowest value of the complication ratio in comparison to existing algorithms. Similarly, Fig. 3b illustrates that the proposed algorithm achieved maximum value of surgical feedback rating also. The final results presented in Fig. 4 revealed that six optimal surgical teams were selected for the referred surgical patient. This can be assigned to the patient as per availability of the team members.
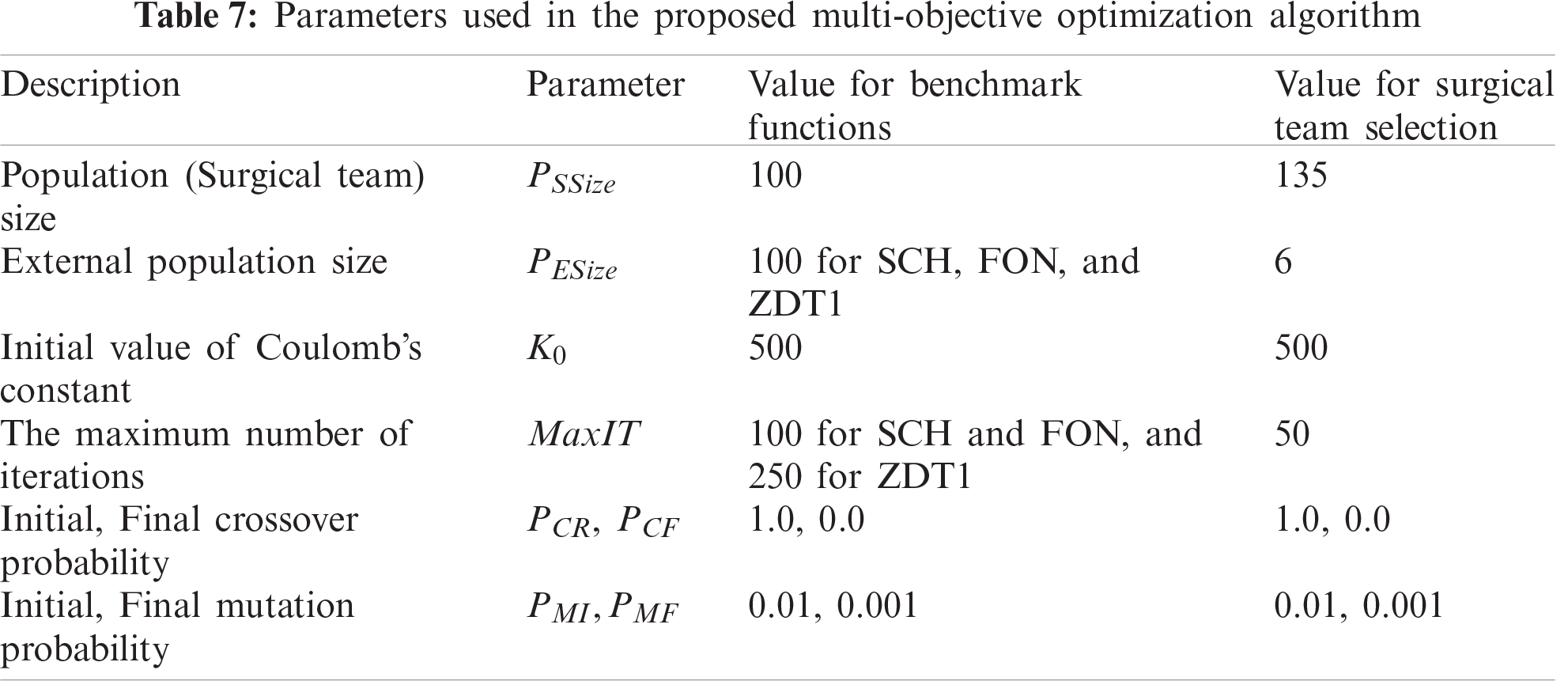
Figure 2: Comparison of performance between proposed and existing MOOAs based on (a) CM, (b) DM, and (c) GD
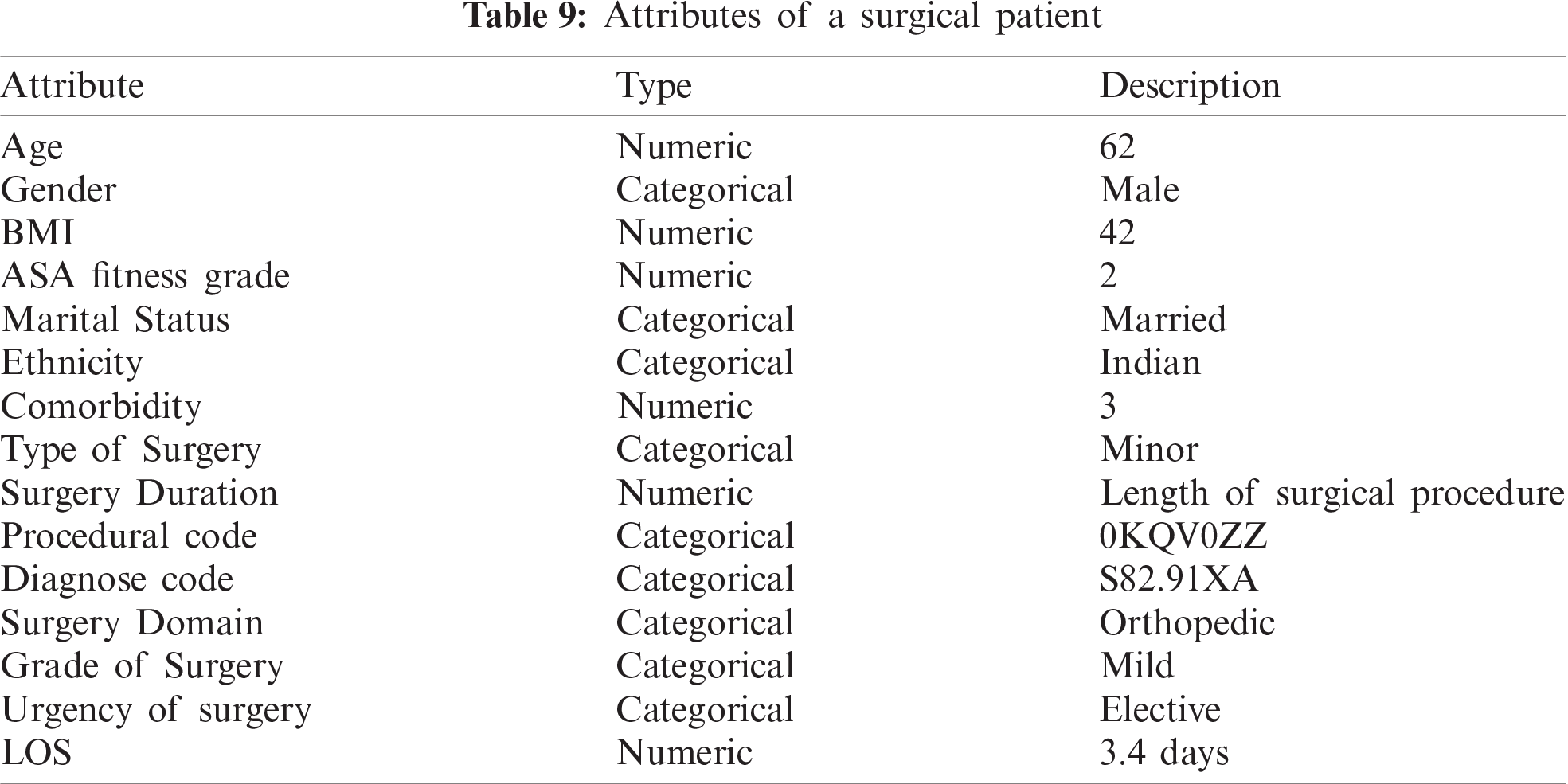
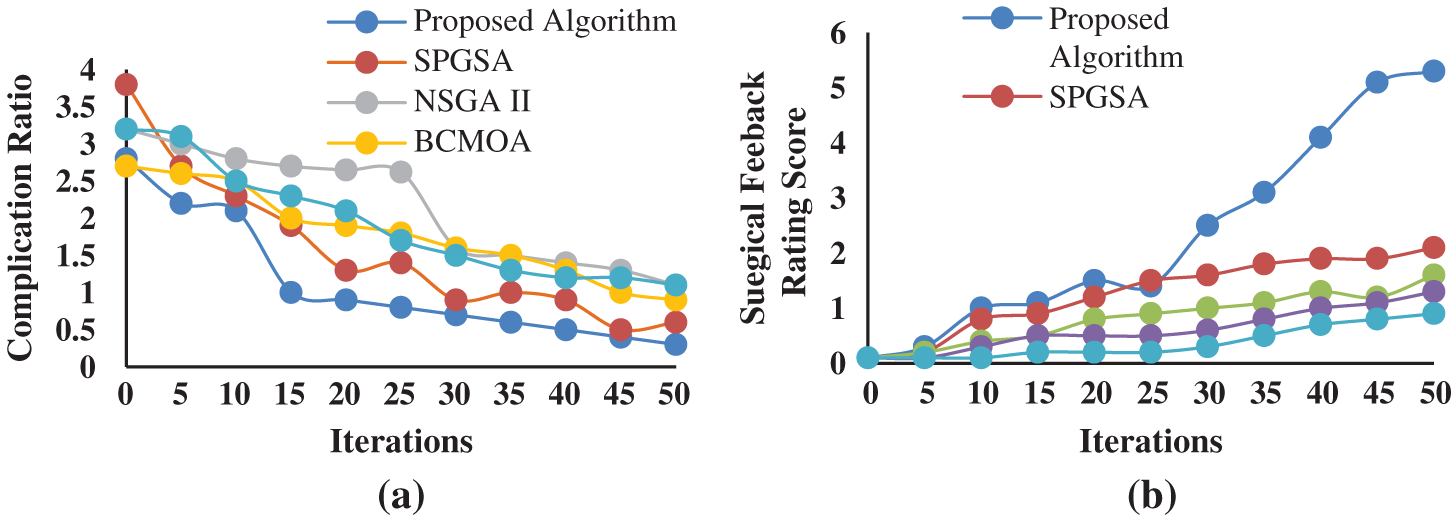
Figure 3: Comparison of performance between proposed and existing MOOAs for surgical team selection based on (a) complication ratio and (b) surgical feedback rating score

Figure 4: Optimal Pareto list of the selected surgical team
High-quality surgical services are essential from the perspective of hospitals and patients both. Surgical outcomes depend on the performance of dedicated surgical teams, which in turn affects hospital’s efficiency and patients’ trust towards that hospital. In multispecialty hospitals many surgical patients are treated concurrently. Therefore, arranging a suitable surgical team for achieving success of a surgical procedure is crucial and challenging. This study addresses the challenge of selection of an optimal list of surgical teams for a referred patient, so that each patient can receive high-quality surgical care. In this paper a framework is proposed to assist decision makers in selecting an optimal list of surgical teams. The proposed framework contains two modules: SHM and STS. SHM focuses on arranging existing surgical patients into optimal patient subgroups. This arrangement of patients further assists the STS module in selecting the optimal list of surgical teams. In this paper, an efficient clustering algorithm for mixed data is proposed to identify optimal subgroups of patients. Besides, a MOOA is proposed to select optimal surgical teams. The proposed framework is validated through a case study of the orthopedic surgery department at a multispecialty hospital in India. Data related to existing surgical records is obtained from the hospital. The performance of the proposed algorithms is evaluated based on different benchmark functions and datasets, and is compared with the existing algorithms also. The experimental evaluation revealed that the proposed algorithm yielded more favorable and significant results in comparison to the existing algorithms, indicating the efficient functionality of the proposed framework.
Funding Statement: The authors received no specific funding for this study.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |