DOI:10.32604/cmc.2021.017080

| Computers, Materials & Continua DOI:10.32604/cmc.2021.017080 |  |
| Article |
Microphone Array Speech Separation Algorithm Based on TC-ResNet
1School of Information Science and Engineering, Southeast University, Nanjing, 210096, China
2Center for Machine Vision and Signal Analysis, University of Oulu, Oulu, FI-90014, Finland
*Corresponding Author: Lin Zhou. Email: Linzhou@seu.edu.cn
Received: 20 January 2021; Accepted: 19 April 2021
Abstract: Traditional separation methods have limited ability to handle the speech separation problem in high reverberant and low signal-to-noise ratio (SNR) environments, and thus achieve unsatisfactory results. In this study, a convolutional neural network with temporal convolution and residual network (TC-ResNet) is proposed to realize speech separation in a complex acoustic environment. A simplified steered-response power phase transform, denoted as GSRP-PHAT, is employed to reduce the computational cost. The extracted features are reshaped to a special tensor as the system inputs and implements temporal convolution, which not only enlarges the receptive field of the convolution layer but also significantly reduces the network computational cost. Residual blocks are used to combine multiresolution features and accelerate the training procedure. A modified ideal ratio mask is applied as the training target. Simulation results demonstrate that the proposed microphone array speech separation algorithm based on TC-ResNet achieves a better performance in terms of distortion ratio, source-to-interference ratio, and short-time objective intelligibility in low SNR and high reverberant environments, particularly in untrained situations. This indicates that the proposed method has generalization to untrained conditions.
Keywords: Residual networks; temporal convolution; neural networks; speech separation
Speech separation, as a front-end speech signal processing system, is widely applied in various scenarios, such as smart homes [1], hearing aids, and teleconferencing. Recent studies have demonstrated that multi-channel speech separation methods are superior to monaural speech separation methods, benefiting from the full exploitation of speech spatial characteristics [2]. Moreover, various deep learning approaches, for instance, based on deep neural networks (DNNs), have garnered significant attention for speech separation, and they effectively estimate spectrum masks or directly implement a mapping operation to extract clean speech from reverberant speech [3,4].
Prior to the success of deep learning methods, speech separation methods mainly depended on spectrum masks to obtain the target speech. They extracted discriminative features from microphone array signals, thereby estimating the masks for each special time frequency unit (TF). The required speech was subsequently synthesized through these masks. Because traditional speech features, such as the mel-frequency cepstral coefficient, contain few spatial characteristics and could undermine the separation performance, additional spatial features have been developed to fully exploit the corresponding information from array signals. Among numerous spatial features, the time difference of arrival (TDOA) is preferred [5], as it can be conveniently inferred by a generalized cross-correlation (GCC) function [6]. A classic approach, known as steered-response power phase transform (SRP-PHAT), is frequently adopted to obtain a robust TDOA estimation in noisy environments [7]. However, this method is time consuming and impractical for real applications. Some advanced methods, such as LEMSalg [8] and GS [9], have been proposed to solve this problem. Unfortunately, the speech quality obtained using the aforementioned methods is still unsatisfactory.
To the best of our knowledge, various neural networks have been encouraged in speech separation in recent years. Therefore, it becomes a valuable issue to allow existing neural networks to fit for speech separation. Convolutional neural networks (CNNs) have succeeded in extracting spatial features to reconstruct required speeches, although they may suffer from a vanishing gradient phenomenon. Consequently, recurrent neural networks (RNNs) have garnered significant attention because they effectively model utterance-level speech and utilize temporal context based on time-series analysis. For instance, a popular network, known as the long short-term memory network (LSTM), is adopted to estimate the time-varied masks from reverberant speeches [10]. However, LSTM still has some shortcomings in practical applications, such as insufficient training, lack of speaker robustness, and the need for an additional permutation invariant training (PIT) procedure to match the masks on a specific utterance-level speech. To address these problems, more advanced networks have been proposed. A fully convolutional time-domain audio separation network [11,12] is presented based on a temporal convolutional network [13,14], whose task is to obtain speaker-independent speech from a single-channel reverbed speech. It modifies the long sequential model of RNN and efficiently implements the data training [15], but still requires a PIT procedure. Consequently, several deep clustering methods that extract embedding vectors from a feature space to model the characteristics of a certain speaker have been developed [16]. The PIT procedure is removed in these methods; however, embedding vector optimization is another challenge.
The general idea behind deep learning speech separation methods is to provide an appropriate training target for networks. Inspired by ideal masks, more mask variants were designed as training targets. Ideal binary mask (IBM), ideal ratio mask (IRM), and complex IRM are the commonly used training masks. IRMs achieve a higher source-to-distortion ratio (SDR) than those of other masks [17]. However, a high SDR does not always indicate a high speech quality. In some situations, IRM-based methods attain lower speech intelligibility scores, such as short-time objective intelligibility (STOI) [18] and perceptual evaluation of speech quality, compared with those of traditional methods that use phase-sensitive masks [19].
Motivated by recent progress, a speech separation algorithm based on a residual network (ResNet) is proposed, which optimizes the feature extraction and network framework. A simplified SRP-PHAT approach is adopted for the feature calculation on each time-frequency (T-F) unit, thereby significantly reducing the computational cost. A detailed ResNet network structure is introduced for feature training and transformation. Multiresolution features are effectively extracted using residual blocks. Moreover, temporal context information is employed using temporal convolution layers. These convolution layers increase the network receptive field and significantly reduce the computational cost. Simulation results demonstrate that the proposed algorithm outperforms several existing DNN algorithms in low signal-to-noise ratio (SNR) and high reverberant environments, particularly in an unmatched environment.
The remainder of this paper is organized as follows. Section 2 presents an overview of the proposed array speech separation system for temporal convolution and residual network (TC-ResNet). Section 3 describes the network structure. The simulation results and analysis are presented in Section 4. The conclusions are presented in Section 5.
2 System Overview and Feature Extraction
The proposed speech separation system is illustrated in Fig. 1. In this study, a modified SRP-PHAT feature, denoted as GSRP-PHAT, is calculated as a spatial feature. For the multi-speaker training signals with noise and reverberation, the GSRP-PHAT [20] of each T-F unit are extracted. Furthermore, to introduce the temporal context, GSRP-PHATs of several adjacent frames in the same subband are concatenated as features for the central T-F unit. These features are input into the TC-ResNet network for supervised learning to approximate the IRM target. During the testing stage, the GSRP-PHAT of each T-F unit of mixed testing signals containing multiple speakers is extracted and input to the trained network. Thereafter, the mask on the current T-F unit can be estimated. Finally, the mixed testing signals are separated to form a signal for each speaker through masking.
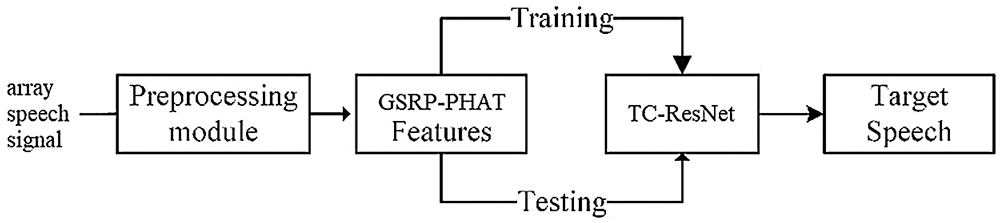
Figure 1: The block diagram of proposed algorithm
The physical model for mixed array signals with multiple speakers in reverberant and noisy environments can be formulated as follows:
where xn(t) represents the signal received by the nth microphone with a total number of N. The term sm(t) denotes the source signal of the mth speaker, with a total number of M. τmn denotes the rectilinear propagation latency. amn is the attenuation coefficient and hmn(t) is the reverberant impulse response from the mth speaker to the nth microphone. wn(t) denotes the white noise received by the nth microphone and it is assumed to be uncorrelated with the signal of another microphone. * denotes the linear convolution.
For a given azimuth of the sound source, the GCC can be calculated based on the principle of the GCC and steering vector. The extraction of the subband feature is simplified with phase transform, which removes the influence of amplitude and eliminates the need to use Gammatone filter banks [21]. The GCC can then be directly calculated from the spectrum integral. This simplification reduces the computational cost. Specifically, the extracted feature is defined as GSRP-PHAT, and is formulated as follows:
where θ represents the given azimuth of the sound source relative to the center of the microphone array. The terms ωfH and ωfL denote the upper and lower bounds of the fth subband, respectively. GSRP-PHATk, f(θ) represents the features of the kth and fth subbands. W(ω) denotes the spectrum of the rectangular window function. Xu(k, ω) and Xv(k, ω) are the spectra from the uth and vth microphones, respectively, and is formulated as follows:
where xu(k,t) and xv(k,t) represent the temporal kth frame signal received by the uth and vth microphones, respectively, and T denotes the sampling number of one frame. Moreover, in Eq. (2), τ(θ, u, v) represents the approximate rectilinear propagation latency between the uth and vth microphone given the azimuth of the sound source θ is formulated as follows:
where R denotes the radius of the microphone array, and c represents the sonic velocity. Terms ϕu and ϕv denote the azimuths of the microphone relative to the center of the array, respectively.
Angle θ varies from 0° to 350° at intervals of 10°, and GSRP-PHATk, f(θ) has 36 values for fixed k and f, that is, a T-F unit has a 36-dimensional vector to represent its spatial features. Thereafter, the features of seven sequential frames are concatenated to form a 7 × 36 matrix to represent the spatial features of the central frame. Subsequently, this matrix is reshaped into 7 × 1 × 36 as an input to TC-ResNet to realize temporal convolution. The reshaping procedure is shown in Fig. 2.
In this study, IRM was used as the ideal mask for recovering the target signal from the microphone array signal. The IRM target of each T-F unit was calculated using the following formula:
where Sm(k, f)2 denotes the source energy of the kth frame. f is the subband T-F unit from the mth speaker, and Noise(k, f)2 represents noise. IRM0 indicates the masks on the noise. All IRMs ranged from 0 to 1. Using this IRM, the ideal output of the network can be calculated. The output of the network for a 7 × 1 × 36 tensor input is a 37-dimensional vector, representing masks on the signal from 36 azimuths and noise. Most of the components of the ideal output vector are 0, indicating that the spatial position of the speakers is sparse [22].
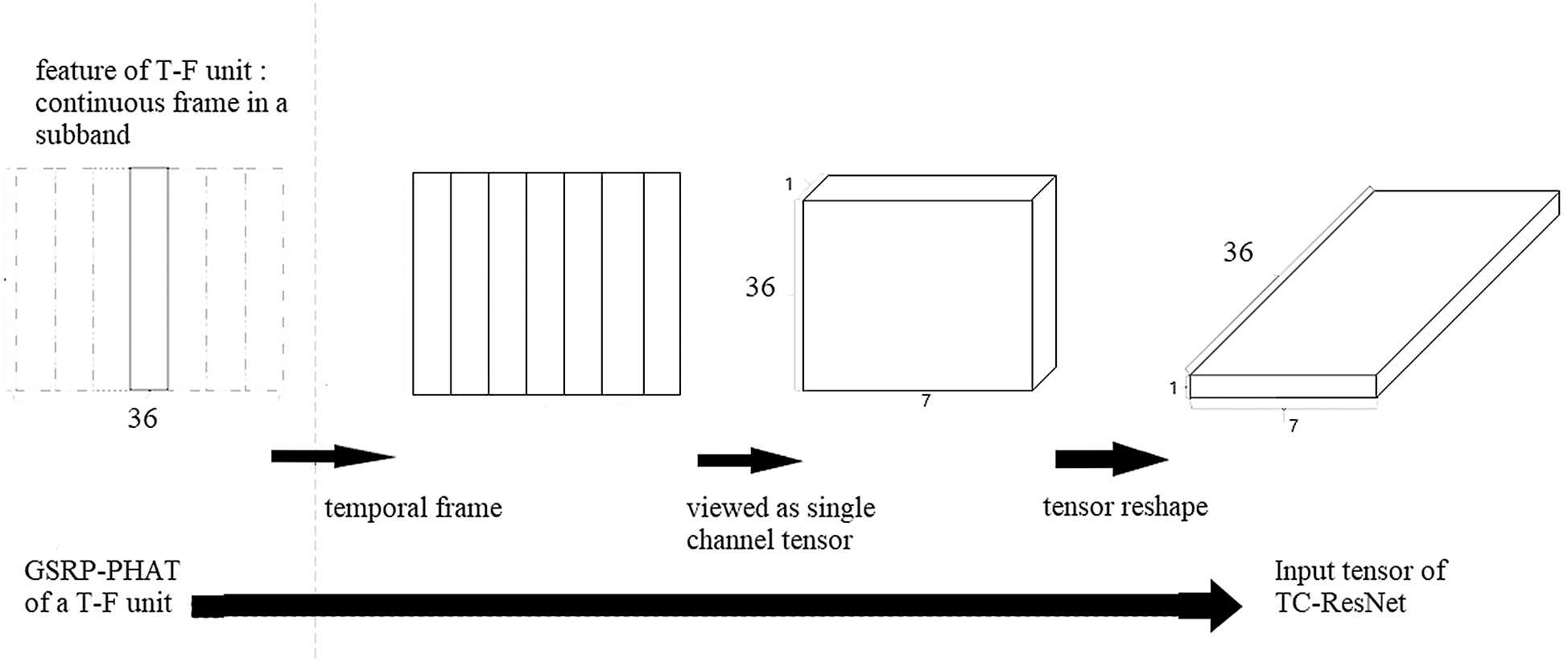
Figure 2: Procedure to structure an input tensor
3.2 Speech Separation and Reconstruction
During the testing stage, GSRP-PHAT are calculated from the testing signal to obtain the input tensor. The output vectors were regarded as the estimation of the ideal mask (ERM) for all azimuths. To handle the inferior sparsity of the ERM and determine the source azimuth, an average filter is applied to smooth the ERM in the temporal neighborhood. This filter can also apply a similar mask to sequential frames, mitigating temporal signal mutations and improving speech intelligibility. This average filter is formulated as follows:
where k0 denotes the index of the current frame, and d can assume values of 1, 2, and 3. The term Y′(k, f) represents the ERM of each T-F unit. After masking, all T-F units can be combined to reconstruct the speech.
The architecture of the network is illustrated in Fig. 3. Two different residual blocks were used. Parameter c represents the number of channels in the CNN.
TC-ResNet uses Kaiming initialization to randomly set all weights in the convolutional and fully connected layers. The training set is denoted as (Z(k, f), Y), where Z(k, f) represents the input tensor. Target Y = (y0, y1, y2,…, yMout), where yi is the ideal value of the mth output neuron, and y0 is noise. The subscripts 1, 2, …, Mout denote the indices of the azimuth. Assuming that the index of the azimuth for the mth speaker is i, then yi= IRMm, and the values of other output neurons are set to 0. For noise, y0 = IRM0. The actual output is denoted as Y′ = (y0′, y1′, y2′,…, yMout′). The mean square error is used as a loss function, formulated as follows:
A back-propagation algorithm was used to adjust the network weight. The Adam optimizer was employed, and the training phase stopped when the determined epochs were reached.
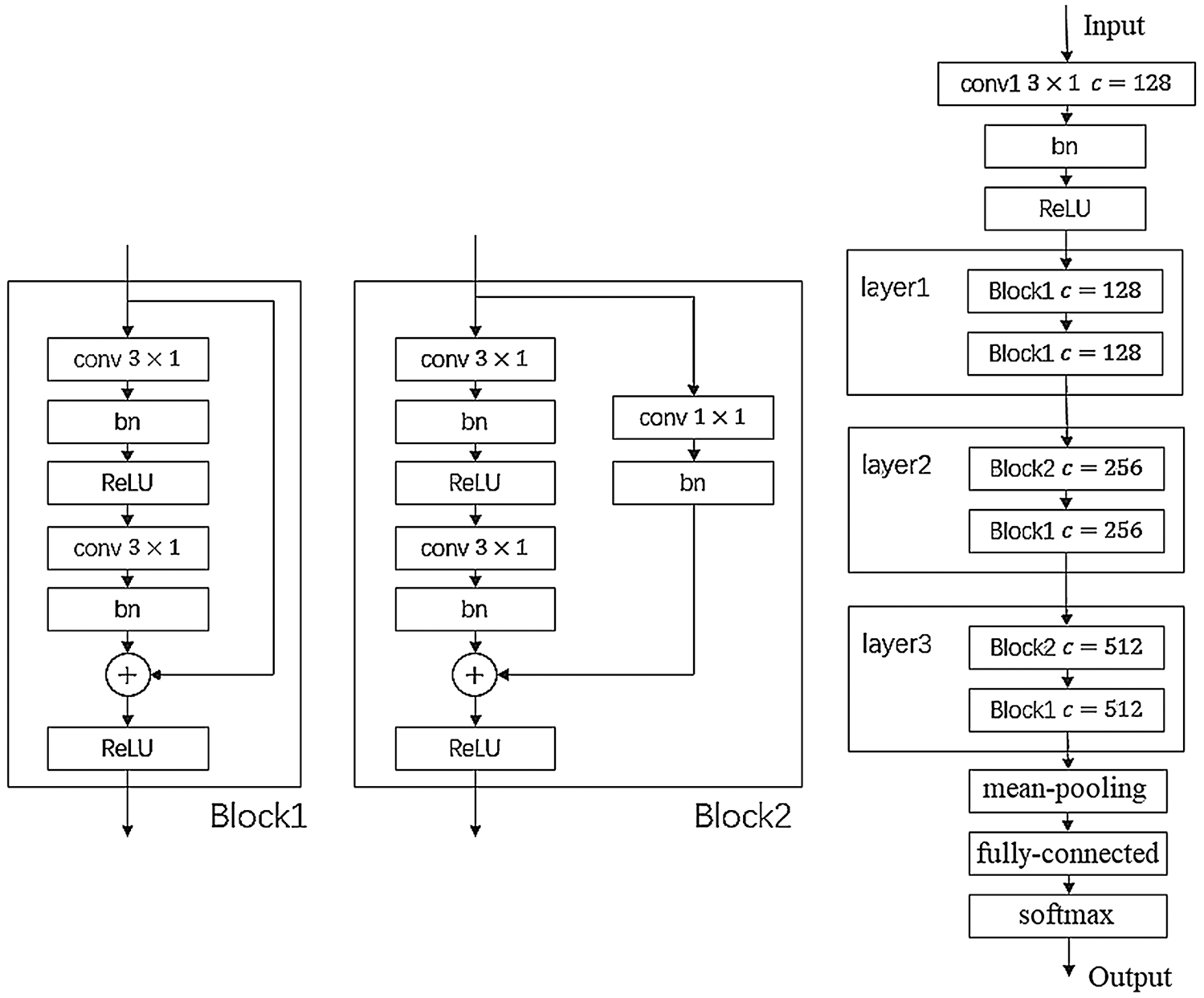
Figure 3: Architecture of TC-ResNet
4 Simulation and Result Analysis
To evaluate the proposed method, clean speech signal was taken from the TIMIT corpus. A convolution between the clean speech signal and the room impulse response of different azimuths, which is generated using the Image method [23], is executed to obtain the array signal with reverberation for different azimuths. Gaussian white noise is added to the signal at different weights to obtain different SNRs.
The detailed experimental setup is described as follows. In the Image method, the dimensions of the simulated cuboid room are 7 × 6 × 3 m. A uniform and planar circular array of six omnidirectional microphones is located at 3.5, 3, 1.5 m, and the diameter of the array is 20 cm. In addition, the SNR used in the training stage includes 0 dB, 10 dB, and 20 dB, and the reverberation time (T60) includes 0, 200, and 600 ms, totally nine different situations. During the testing stage, apart from the same situations in the training stage, a high reverberant situation, 800 ms of T60 is set with SNRs of 0 dB, 3 dB, 5 dB, 7 dB, 9 dB, 10 dB, 15 dB, and 20 dB to assess the generalization of the algorithm. The signal is segmented into frames of 32 ms with a shift of 16 ms based on a rectangular window.
To evaluate the separation performance, multiple metrics are selected, including SDR, source-to-interference ratio (SIR), and STOI. The SDR was used to objectively evaluate the entire distortion over the signal and is expressed in decibels. SIR was used to objectively evaluate other speakers’ interference over a target speaker, which is also expressed in decibels. STOI, an intelligibility metric that ranges from 0 to 1, is used to evaluate the separation performance.
We compared the performance of the proposed method, TC-ResNet-based separation using IRM, with those of several related methods for microphone array speech separation. DNN-based separation is a combination of neural networks and masks, which often uses an ideal IBM [3] or IRM. The DNN-IBM and DNN-IRM methods use the same features as those of the proposed algorithm, and all the methods use the same training and testing datasets.
4.2.1 Comparison in a Matched Environment
First, we evaluated the performance of the proposed algorithm in a matched noisy and reverberant environment, that is, when the testing and training datasets had the same SNRs and T60. The metrics for different algorithms is shown in Figs. 4–6.
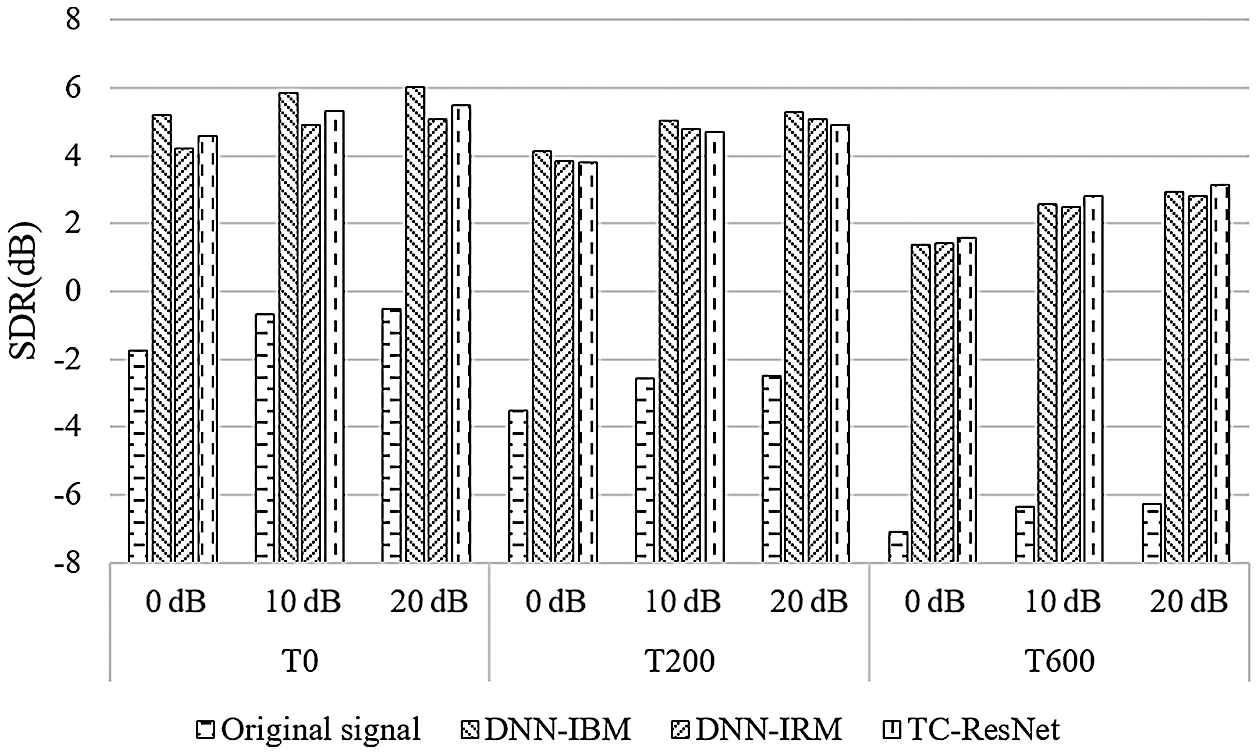
Figure 4: Comparison on SDR among different algorithms
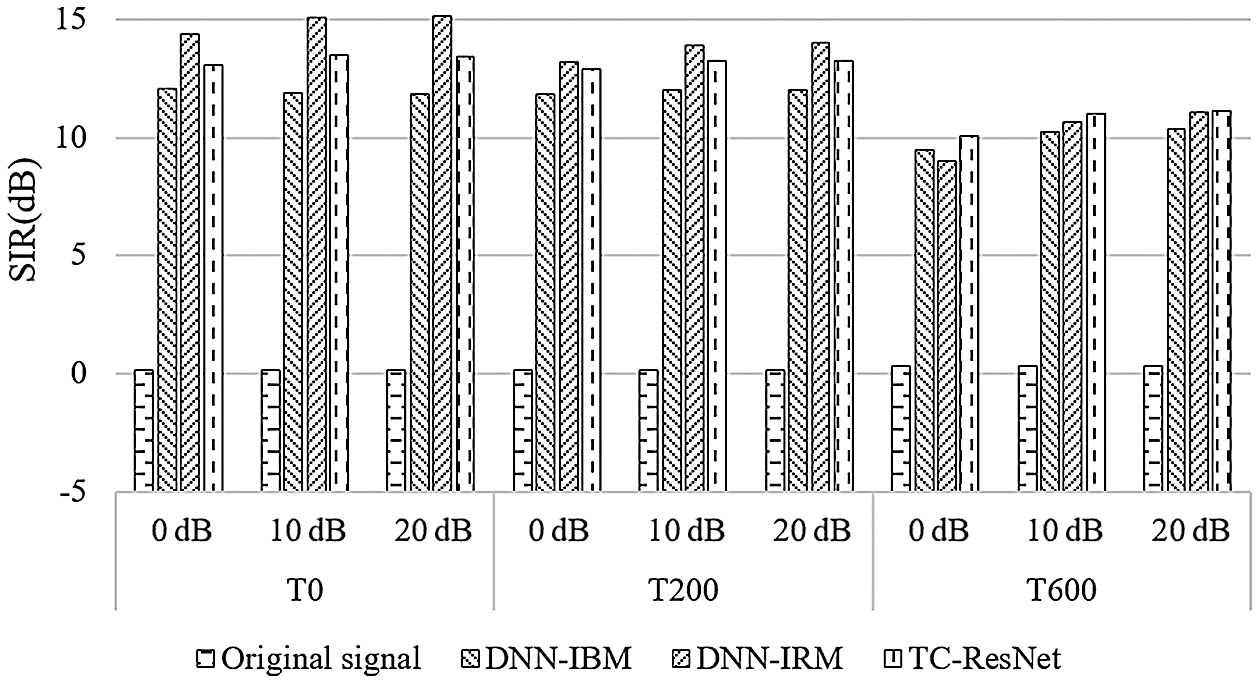
Figure 5: Comparison on SIR among different algorithms
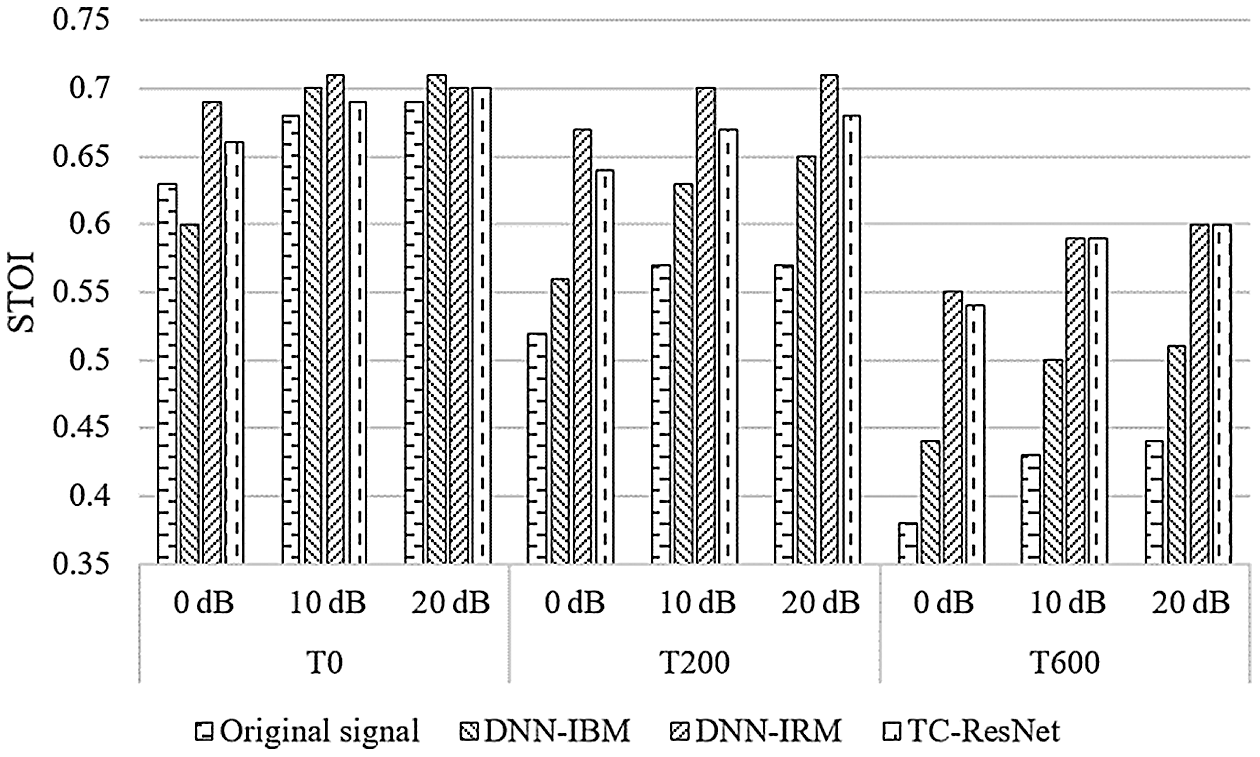
Figure 6: Comparison on STOI among different algorithms
According to Figs. 4–6, DNN-IBM has a slight advantage over SDR, but exhibit a poor performance on SIR and STOI, indicating that IBM performs poorly on multi-speaker separation and is unable to distinguish between noise and speech interference. Therefore, the following discussion ignores the DNN-IBM algorithm.
In a high reverberant situation of T60 = 600 ms, the proposed algorithm has better SDR and SIR than those of DNN-IRM, and has STOI similar to those of DNN-IRM. However, when T60 is 0 ms and 200 ms, TC-ResNet performs slightly worse than DNN-IRM. The difference between these two methods is that TC-ResNet introduces information on the front and back frames during the training phase. Although simple average smoothing on sequential frames degrades SIR, TC-ResNet does not seem to suffer from this in high reverberant situations. In our opinion, the features of the front and back frames used by TC-ResNet are for learning the trend of feature transformation between frames. This type of information is not very helpful for the prediction of the model in a low reverberant environment. In this situation, the main interference signal is interference speech and noise, and the subband method can effectively reduce the impact of interference speech and noise. However, when the reverberation is high, the reverberant compositions in the interference signal extensively affect the features of adjacent frames. TC-ResNet can utilize the trend information of the front and back frames to reduce the influence of reverberation and help the model to distinguish the target speech better. Based on the above explanation, TC-ResNet performs better in a high reverberant environment.
4.2.2 Analysis in an Unmatched Environment
For an unmatched environment in which the testing dataset has an SNR different from that of the training dataset, and the reverberation T60 is 800 ms, which is higher than that in the training data, the above explanation can be further verified. The comparison results are shown in Figs. 7–9.
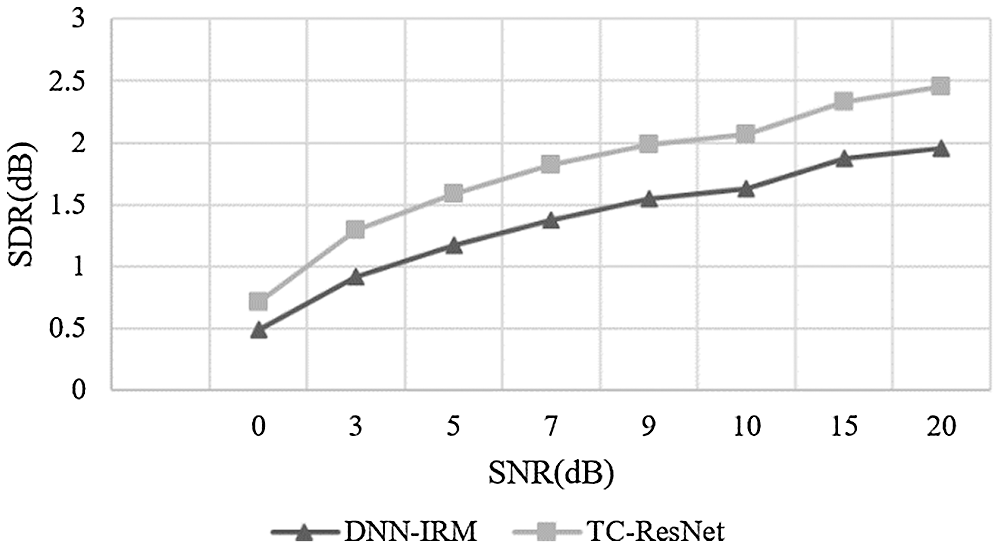
Figure 7: Comparison on SDR between DNN-IRM and TC-ResNet in high reverberation
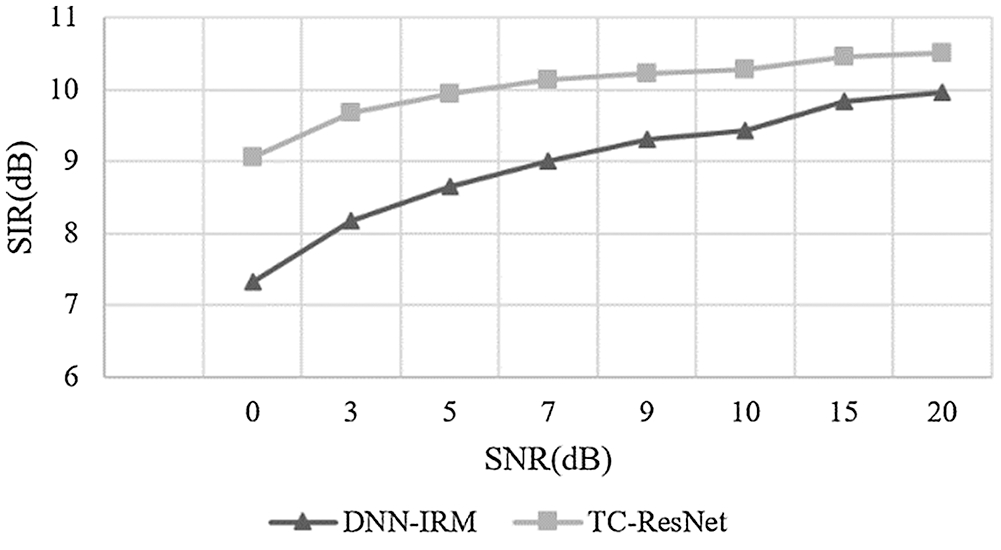
Figure 8: Comparison on SIR between DNN-IRM and TC-ResNet in high reverberation
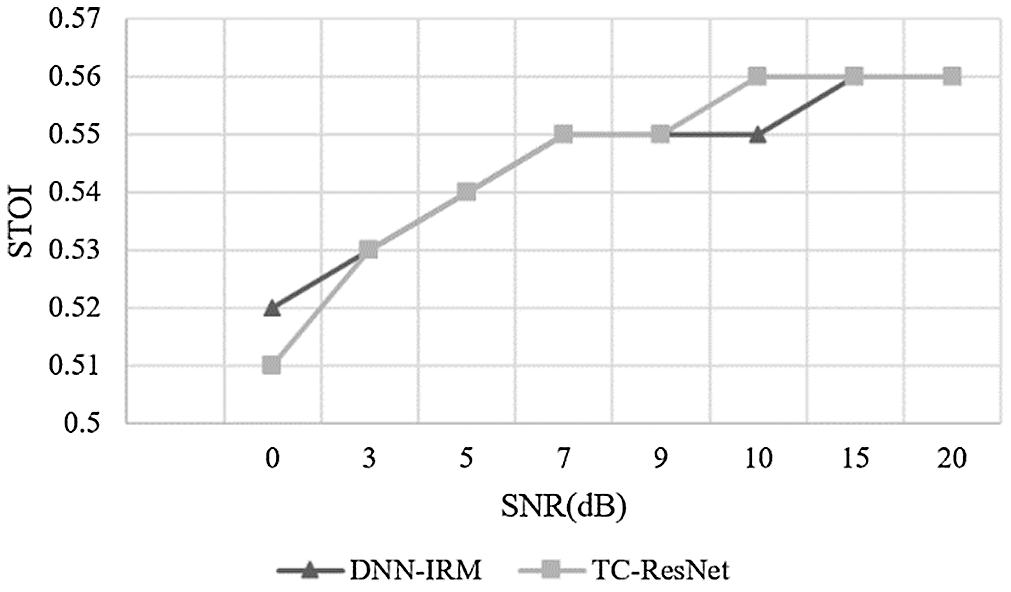
Figure 9: Comparison on STOI between DNN-IRM and TC-ResNet in high reverberation
According to Figs. 7–9, the SDR and SIR of TC-ResNet are higher than those of DNN-IRM under different SNRs when their STOI values were relatively close. This demonstrates that TC-ResNet has better generalization in a high reverberant environment as it does not degrade speech intelligibility. Therefore, TC-ResNet has a better SNR generalization than that of DNN-IRM.
Separation performance was also observed from the temporal signal. Fig. 10 shows an example of separated speech from an array signal with two speakers using DNN-IRM and TC-ResNet. For TC-ResNet, the noise and reverberation in the separated signal for each speaker are significantly reduced, particularly for speaker 1, thereby achieving better separation performance of TC-ResNet in the unmatched environment.
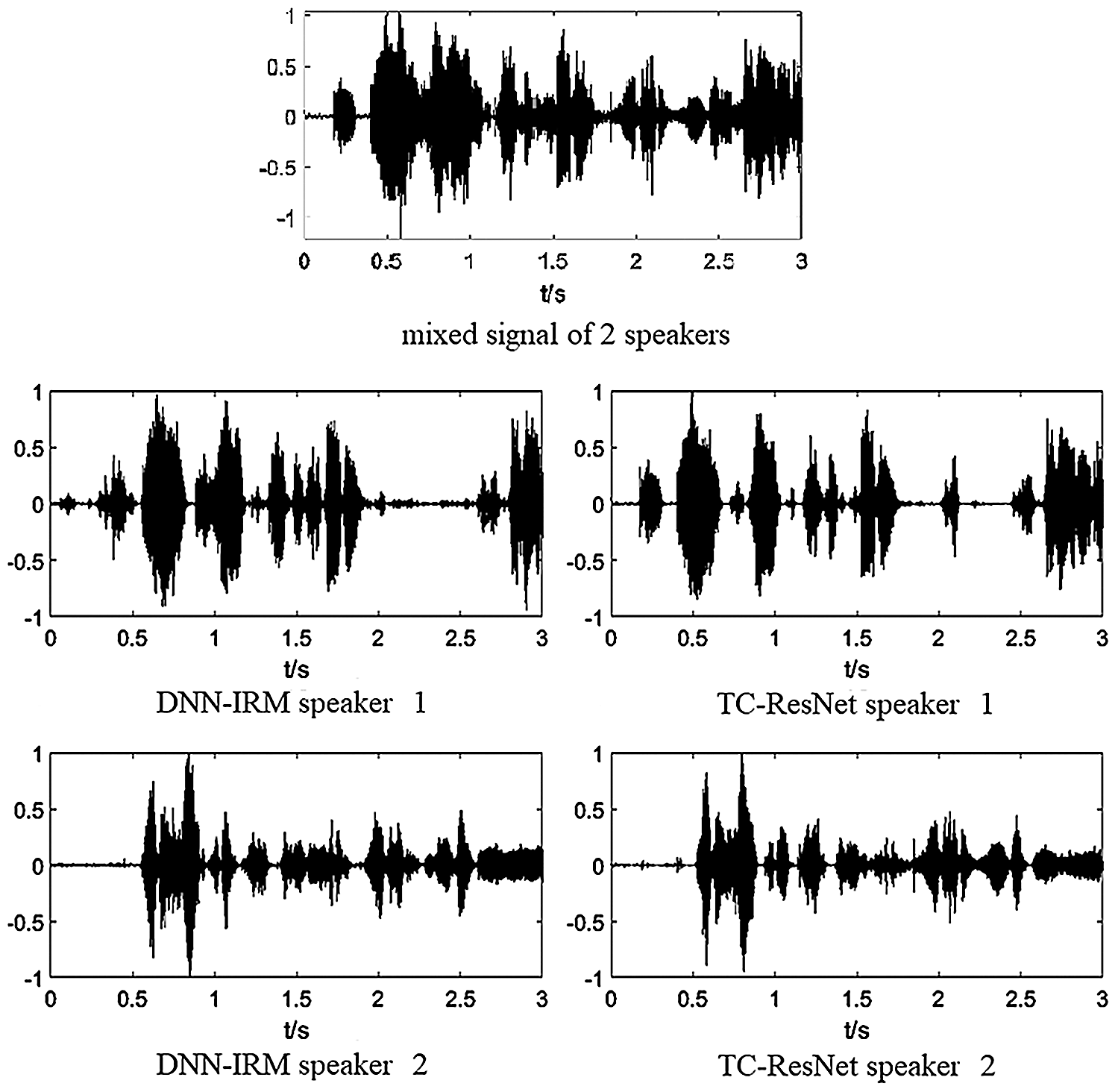
Figure 10: Comparison on signal between DNN-IRM and TC-ResNet in high reverberation
In this study, a microphone array speech separation method based on TC-ResNet is proposed. By combining spectral and spatial features, the simplified GSRP-PHAT feature is extracted and reshaped to the tensor, which reduces the computational cost. The proposed method performed temporal convolution, which expands the receptive field and significantly reduces the computational cost. Residual blocks are used to combine multiresolution features and accelerate the training procedure. Simulation results in different acoustic environments demonstrates that the microphone array speech separation method based on TC-ResNet achieves high speech intelligibility and better generalization in noisy and reverberant environments, which is superior to those of the classical algorithm using DNN.
Funding Statement: This work is supported by the National Key Research and Development Program of China under Grant 2020YFC2004003 and Grant 2020YFC2004002, and the National Nature Science Foundation of China (NSFC) under Grant No. 61571106.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. J. Park and S. Kim, “Noise cancellation based on voice activity detection using spectral variation for speech recognition in smart home devices,” Intelligent Automation & Soft Computing, vol. 26, no. 1, pp. 149–159, 2020. [Google Scholar]
2. L. Pfeifenberger, T. Schrank, M. Zohrer, M. Hagmüller and F. Pernkopf, “Multi-channel speech processing architectures for noise robust speech recognition: 3rd chime challenge results,” in Proc. IEEE ASRU, Scottsdale, AZ, USA, pp. 452–459, 2015. [Google Scholar]
3. Y. Wang and D. Wang, “Boosting classification based speech separation using temporal dynamics,” in INTERSPEECH 2012, Portland, OR, USA, pp. 1528–1531, 2012. [Google Scholar]
4. L. Zhou, S. Lu, Q. Zhong, Y. Chen, Y. Tang et al., “Binaural speech separation algorithm based on long and short time memory networks,” Computers, Materials & Continua, vol. 63, no. 3, pp. 1373–1386, 2020. [Google Scholar]
5. S. Liu, H. Cao, D. Wu and X. Chen, “Generalized array architecture with multiple sub-arrays and hole-repair algorithm for doa estimation,” Computers, Materials & Continua, vol. 64, no. 1, pp. 589–605, 2020. [Google Scholar]
6. C. Knapp and G. Carter, “The generalized correlation method for estimation of time delay,” IEEE Transactions on Acoustics, Speech, and Signal Processing, vol. 24, no. 4, pp. 320–327, 1976. [Google Scholar]
7. X. Zhao, S. Chen, L. Zhou and Y. Chen, “Sound source localization based on srp-phat spatial spectrum and deep neural network,” Computers, Materials & Continua, vol. 64, no. 1, pp. 253–271, 2020. [Google Scholar]
8. H. F. Silverman, Y. Yu, J. M. Sachar and W. R. Patterson, “Performance of real-time source-location estimators for a large-aperture microphone array,” IEEE Transactions on Speech and Audio Processing, vol. 13, no. 4, pp. 593–606, 2005. [Google Scholar]
9. M. D. Gillette and H. F. Silverman, “A linear closed-form algorithm for source localization from time-differences of arrival,” IEEE Signal Processing Letters, vol. 15, pp. 1–4, 2008. [Google Scholar]
10. M. Kolbæk, D. Yu, Z. Tan and J. Jensen, “Multitalker speech separation with utterance-level permutation invariant training of deep recurrent neural networks,” IEEE/ACM Transactions on Audio, Speech, and Language Processing, vol. 25, no. 10, pp. 1901–1913, 2017. [Google Scholar]
11. Y. Luo and N. Mesgarani, “Conv-tasNet: Surpassing ideal time–Frequency magnitude masking for speech separation,” IEEE/ACM Transactions on Audio, Speech, and Language Processing, vol. 27, no. 8, pp. 1256–1266, 2019. [Google Scholar]
12. R. Gu, S. Zhang, L. Chen, Y. Xu, M. Yu et al., “Enhancing end-to-end multi-channel speech separation via spatial feature learning,” in IEEE Int. Conf. on Acoustics, Speech and Signal Processing, Barcelona, Spain, pp. 7319–7323, 2020. [Google Scholar]
13. P. P. Bernardo, C. Gerum, A. Frischknecht, K. Lübeck and O. Bringmann, “Ultratrail: A configurable ultra-low power TC-resNet AI accelerator for efficient keyword spotting,” IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems, pp. 4240–4251, 2020. [Google Scholar]
14. S. Choi, S. Seo, B. Shin, H. Byun, M. Kersner et al., “Temporal convolution for real-time keyword spotting on mobile devices,” in INTERSPEECH 2019, Graz, Austria, pp. 3372–3376, 2019. [Google Scholar]
15. K. Yang, J. Jiang and Z. Pan, “Mixed noise removal by residual learning of deep cnn,” Journal of New Media, vol. 2, no. 1, pp. 1–10, 2020. [Google Scholar]
16. C. Han, Y. Luo and N. Mesgarani, “Online deep attractor network for real-time single-channel speech separation,” in IEEE Int. Conf. on Acoustics, Speech and Signal Processing, Brighton, UK, pp. 361–365, 2019. [Google Scholar]
17. J. L. Roux, S. Wisdom, H. Erdogan and, J. R. Hershey, “SDR–half-baked or well done?,” in IEEE Int. Conf. on Acoustics, Speech and Signal Processing, Brighton, United Kingdom, pp. 626–630, 2019. [Google Scholar]
18. Z. Wang, X. Wang, X. Li, Q. Fu and Y. Yan, “Oracle performance investigation of the ideal masks,” in IEEE Int. Workshop on Acoustic Signal Enhancement (IWAENCXi'an, China, pp. 1–5, 2016. [Google Scholar]
19. D. Yin, C. Luo, Z. Xiong and W. Zeng, “PHASEN: A phase-and-harmonics-aware speech enhancement network,” in Advancement of Artificial Intelligence, New York, USA, pp. 9458–9465, 2020. [Google Scholar]
20. A. D. Firoozabadi, P. Irarrazaval, P. Adasme, H. Durney and M. S. Olave, “A novel quasi-spherical nested microphone array and multiresolution modified SRP by gammatone filterbank for multiple speakers localization,” in Signal Processing: Algorithms, Architectures, Arrangements, and Applications, Poznan, Poland, pp. 208–213, 2019. [Google Scholar]
21. M. Pariente, S. Cornell, A. Deleforge and E. Vincent, “Filterbank design for End-to-end speech separation,” in IEEE Int. Conf. on Acoustics, Speech and Signal Processing, Barcelona, Spain, pp. 6364–6368, 2020. [Google Scholar]
22. S. Nannuru and P. Gerstoft, “2D beamforming on sparse arrays with sparse Bayesian learning,” in IEEE Int. Conf. on Acoustics, Speech and Signal Processing, Brighton, United Kingdom, pp. 4355–4359, 2019. [Google Scholar]
23. J. B. Alien and D. A. Berkley, “Image method for efficiently simulating small-room acoustics,” The Journal of the Acoustical Society of America, vol. 65, no. 4, pp. 943–950, 1979. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |