DOI:10.32604/cmc.2022.024722

| Computers, Materials & Continua DOI:10.32604/cmc.2022.024722 |  |
| Article |
Estimator-Based GPS Attitude and Angular Velocity Determination
Department of Communications, Navigation and Control Engineering, National Taiwan Ocean University, Keelung, 202301, Taiwan
*Corresponding Author: Dah-Jing Jwo. Email: djjwo@mail.ntou.edu.tw
Received: 28 October 2021; Accepted: 09 December 2021
Abstract: In this paper, the estimator-based Global Positioning System (GPS) attitude and angular velocity determination is presented. Outputs of the attitude estimator include the attitude angles and attitude rates or body angular velocities, depending on the design of estimator. Traditionally as a position, velocity and time sensor, the GPS also offers a free attitude-determination interferometer. GPS research and applications to the field of attitude determination using carrier phase or Doppler measurement has been extensively conducted. The raw attitude solution using the interferometry technique based on the least-squares approach is inherently noisy. The estimator such as the Kalman filter (KF) or extended Kalman filter (EKF) can be incorporated into the GPS interferometer, potentially providing several advantages, such as accuracy improvement, reliability enhancement, and real-time characteristics. Three estimator-based approaches are investigated for performance comparison, including (1) KF with measurement involving attitude angles only; (2) EKF with measurements based on attitude angles only; (3) EKF with measurements involving both attitude angles and body angular rates. The assistance from body mounted gyroscopes, if available, can be utilized as the measurements for further performance improvement, especially useful for the case of signal-challenged environment, such as the GPS outages. Modeling of the dynamic process involving the body angular rates and derivation of the related algorithm will be presented. Simulation results for various estimator-based approaches are conducted; performance comparison is presented for the case of GPS outages.
Keywords: Global positioning system (GPS); extended Kalman filter; attitude determination; angular velocity
Global Positioning System (GPS) [1–5] has traditionally been a position, velocity and time sensor using the code observations. Code and carrier phase observations are two types of observations that can be extracted from the GPS signals. Due to its higher accuracy and precision compared to code observations, carrier phase observations have been used to achieve very high accuracy of estimated position. It provides relative positioning in centimeter level and has been widely applied to surveying, precision approach and automatic landing, and attitude determination [6–10]. Although carrier phase observable can be very accurately measured, it is not possible to use pure carrier phase observable for absolute positioning due to inherent integer cycle ambiguity [9,10]. Positioning or attitude determination using GPS does not have the error accumulation, which happens in the inertial navigation system (INS) [11,12].
Since the carrier phase observables contain much smaller measurement noise than code observables, much effort has been given to develop a technique to utilize the carrier phase observables. By measuring the phase of the GPS carrier relative to the carrier phase at a reference site, single, double, and triple differences can be used to determine the vector between the reference (designated master) and slave antennas and subsequently solve for the attitude determination solutions. If two antennas are attached to a vehicle, a baseline vector defined as a vector from master antenna to the other antenna can be determined using relative positioning techniques. Very accurate relative position estimate will be available if the integer ambiguities are resolved. The attitude of a vehicle can be precisely determined using GPS carrier phase measurements from more than two antennas attached to the vehicle.
Two main issues, real-time integer ambiguity resolution techniques and attitude determination, are to be resolved to determine the vehicle attitude when applying GPS carrier phase double differences. There have been many efforts on real time GPS attitude determination problem. Most of the investigations have been on the real-time integer ambiguity resolution techniques and attitude determination from the baseline vectors. Some investigators utilize certain constrain factors such as baseline length or known geometry to resolve integer ambiguity in real-time manner [13,14].
This paper presents estimator-based GPS attitude and angular velocity determination. Since the attitude solution using the interferometry technique [15–18] based on the least-squares method is inherently noisy, the estimator-based method [12,19–23] using the Kalman filter or the extended Kalman filter possesses good potential for performance enhancement. Measurement for the EKF can be provided by the GPS interferometer, and possibly by the gyroscopes, depending on the availability. The assistance from body mounted gyroscopes, if available, can be utilized as the measurements for further performance improvement. This design provides the opportunity when body angular rates information from other sensor such as the gyroscopes is available for better resistance to the signal-challenged environment, such as the GPS outages.
The remainder of this paper is organized as follows. Preliminary background on GPS attitude and angular velocity determination is reviewed in Section 2. In Section 3, attitude and angular velocity estimator using the extended Kalman filter is briefly introduced. In Section 4, illustrative examples are presented to evaluation of the effectiveness of the proposed algorithm. Conclusions are given in Section 5.
2 GPS Attitude and Angular Velocity Determination
Carrier phase observables in GPS include sum of range, an unknown integer ambiguity and some ranging errors, expressed as:
where the parameters are defined as
GPS interferometry has been firstly used in precise static relative positioning, and thereafter in kinematic positioning. By using carrier phase observables, the relative positioning is obtained in centimeter level provided that the integer ambiguity is resolved. In the beginning of 1990s, Van Grass et al. [15] conducted research on the GPS to the field of aircraft attitude determination using carrier phase was developed. In their work, the receiver-satellite double difference observation was employed.
The receiver-satellite double differenced observable is formed by a linear combination of four observations:
where ‘
Double differenced observable eliminates or greatly reduces the satellite and receiver timing errors. The observation equation between two receivers and two satellites by combining phase data from master (denoted as ‘1’) and slave (denoted as ‘2’) receivers to satellites i and j can be written as
For a short baseline, e.g., less than one meter between two antennas, ionospheric and tropospheric parameters become negligible. The resulting double-difference phase equation when ignoring atmospheric, satellite ephemeris, and residual clock errors is given by
Attitude is defined by the rotation transformation that relates a coordinate system fixed in space to a coordinate system fixed in the body (body frame). The space coordinate system is typically defined to be a local level NED (north-east-down) frame. The baseline vector is defined as the vector between the antennas designated master and one of the slave antennas. The carrier phase differential GPS based on interferometer principles can solve for the antenna vector. The approach is based on the difference in the GPS carrier phase received at two or more nearby antennas connected to a rigid body. Multiple antenna vectors from an antenna array can be used to calculate the vehicle attitude. In general, to determine the three-dimensional attitude, three non-collinear antennas simultaneously receiving signals from two satellites are the minimum requirement. Referring to the configuration as in Fig. 1, when using the carrier phase signal from satellite i, the between-receiver single differenced observable is a linear combination of two phase observables received by two antennas:
Similarly, the single differenced observable received for the same antennas from satellite j is
where
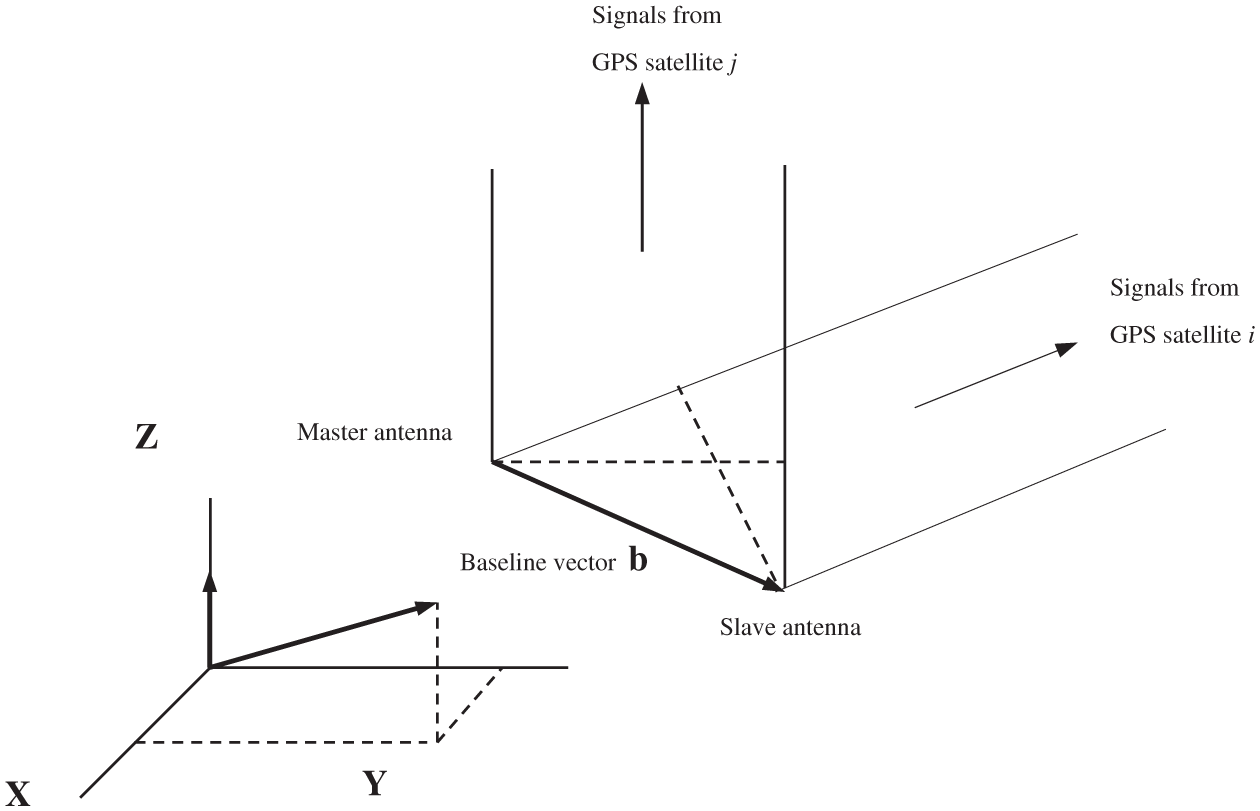
Figure 1: Receiver-satellite double differences [15]
Based on Eq. (8), signals received from
When the integer ambiguity is known, the range-equivalent of Eq. (9) is
which can be expressed in matrix form
There have been many methods proposed for the integer ambiguity resolution, typically including ambiguity function, antenna exchange/swap, baseline rotation methods. The residuals are the differences between the actual double difference measurements and those predicted based on the least-squares solution for
There are several methods available for solving vehicle attitudes, typically including Euler angle method and quaternion method [12,21]. The rotation transformation matrix that relates the NED and body frames provides the information for finding the vehicle attitude:
where the subscripts n and b represent the local and body frames, respectively, and we defined the notations
Finally, the vehicle attitude can be obtained through the relation:
To perform the calculation of attitude determination, the antennas should be set up as nonzero and are on the non-collinear vector. Once the baseline vector is determined, estimation of the coordinate frame transformation
Once the Euler attitude angle rates are available, the body angular velocity can be found
However, the attitude angle rate directly obtained from the difference of attitude angles,
is usually corrupted and too noisy. Utilization of the Kalman type of filters provides resolves some of the problem.
3 Attitude and Angular Velocity Estimator Using the Extended Kalman Filter
The EKF has been successfully applied in the GPS receiver position/velocity determination, and the integrated GPS/INS navigation system design. In this paper, the KF and EKF will be employed as the estimator for attitude, attitude rates, and body angular velocities to enhance the accuracy and reliability of the attitude solution.
3.1 Implementation of the KF and EKF as the State Estimator
Consider a dynamical system whose state is described by a linear, vector differential equation. The process model and measurement model are represented as
The Kalman filter equations are summarized in Tab. 1.

Consider a dynamical system whose state is described by a nonlinear, vector difference equation. Assuming the process to be estimated and the associated measurement relationship may be written in the form:
where the state vector
where
Without external aiding such as an inertial sensor to provide a reference trajectory, the process dynamics represent the total observer dynamics, as shown in Fig. 2. Implementation algorithm for the discrete EKF equations is provided in Tab. 2.
3.2 Modeling of Attitude Dynamics
The appropriate description of the dynamic process model depends on the type of dynamics encountered in a given application.
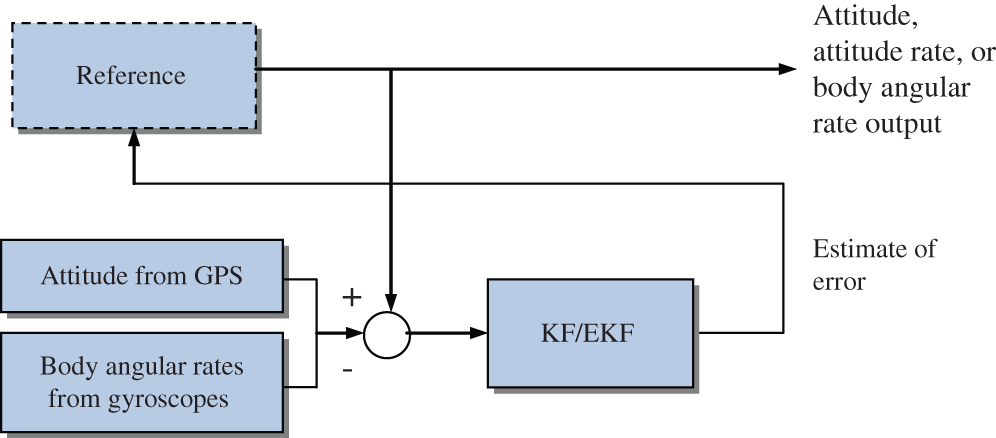
Figure 2: Attitude and angular velocity estimator as a special case of the feedback complementary filter using KF or EKF

3.2.1 Linear System Model Using the KF as the Estimator
A three-state filter model involving the state vector
(1) CAV (constant angular velocity) model for the KF
For a low to medium dynamic receiver, a six-state filter model, here referred to as the ‘constant angular velocity’ model, or ‘CAV’ model is employed. The model contains 3 attitude angles and 3 attitude rates,
In addition to a pure random walk, an alternative model using the body angular acceleration for the process model can be described as
This model is reasonable since accelerations may not be always constant, but are correlated over short time intervals. Based on Eq. (18), the dynamic process model is given by
Furthermore, they can also be modeled as the Gauss-Markov process:
(2) CAA (constant angular acceleration) model for the KF
For a high dynamic receiver, a nine-state filter model, here referred to as the ‘constant angular acceleration (CAA)’ model, with
Selecting the state vector
or
3.2.2 Nonlinear System Model Using the EKF as the Estimator
If the body angular velocity information is required, an alternative dynamic model can be applied such that the body angular velocity (
(1) CAV model for the EKF
The state vector is composed of 6 states:
The above system of equations can be written in matrix form
By combining the dynamic models of the body angular velocities:
One of the alternative models for the dynamic of body angular rate is given by:
Similarly, the Gauss-Markov can also be employed for the case of:
The Jacobian matrix
and the corresponding discrete-time model is given by
(2) CAA model for the EKF
The state vector for the CAA model involves 9 states:
Similarly, the alternative model that can be considered is given by
As mentioned, the Gauss-Markov process can also be employed when necessary:
Simulation was conducted for evaluating the estimation performance of GPS-based attitude and angular velocity determination. Computer codes were developed using the Matlab® software with assistance from the commercial software Satellite Navigation (SatNav) Toolbox by GPSoft LLC [24] employed for generation of the GPS satellite orbits/positions and thereafter, the satellite pseudorange, and carrier phase observables, required for simulation. The attitude dynamics for simulation is as follows:
with initial attitude
Three algorithms are involved for testing their performance, including
(1) KF with measurement involving attitude angles only;
(2) the first algorithm using EKF (herein referred to as the EKF1), for which the measurements involving attitude angles only;
(3) the second algorithm using EKF (herein referred to as the EKF2), for which the measurements involving both attitude angles and body angular rates (possibly from gyroscopes).
Tab. 3 summarizes the three architectures employed in this paper for comparison evaluation.
To avoid the filter divergence, it should be noticed that setting the process noise PSD to zero is not acceptable, since it can be very detrimental to the filtering performance, especially if the vehicle is maneuvering rapidly. As a result, when the system reaches steady-state condition, the steady-state gain won't become zero and, subsequently, the filter is able to follow the time-varying attitude dynamics. A small value is admissible in practical design. However, one still needs to find the appropriate values that meet the requirement. The CAV model is employed for investigation since the dynamic for the illustrative is moderate. For the CAV model, the noise strengths for the process and measurement models are selected as:
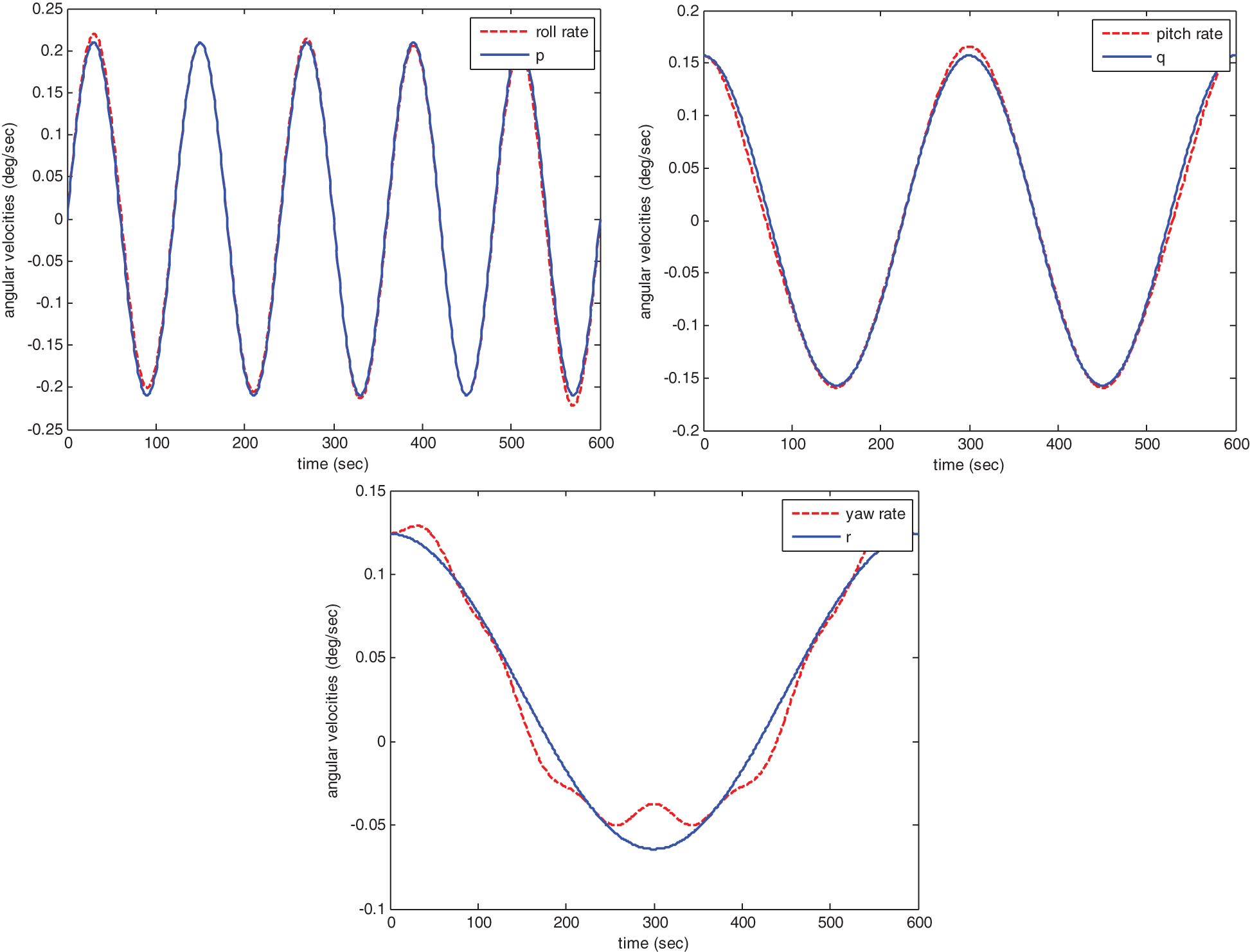
Figure 3: Attitude rates and body angular velocities in the simulation

Simulation results are shown in Figs. 4–8. Figs. 4 and 5 show the performance comparison for KF and EKF1 where Fig. 4 presents estimate of attitude angles without signal outage and Fig. 5 presents those with signal outage. It can be seen that the results from both architectures are equivalent for the case that no outage occurs while the results from EKF1 provides improved performance in some situation, but not so noticeably.
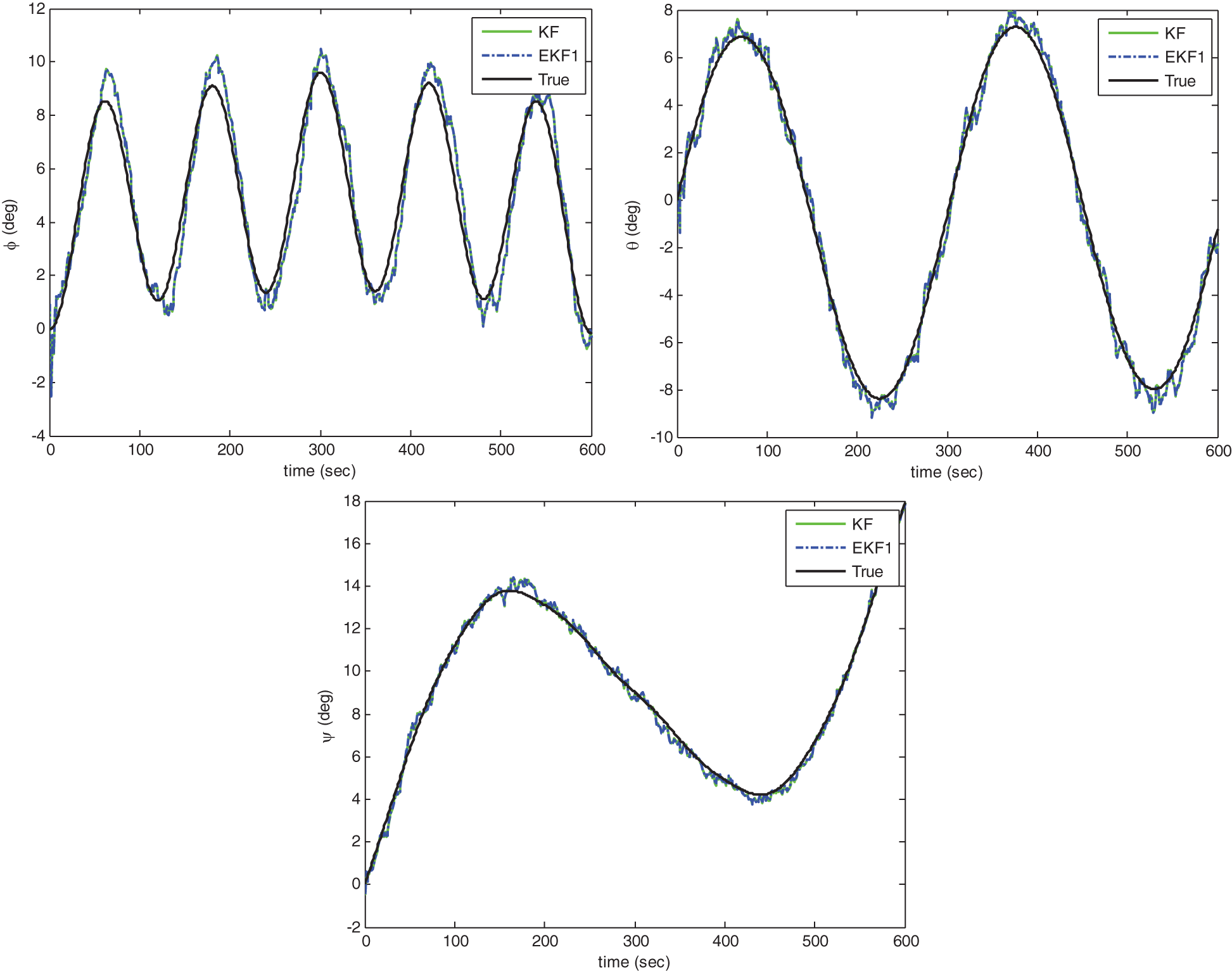
Figure 4: Estimate of attitude angles without signal outage: KF vs. EKF1
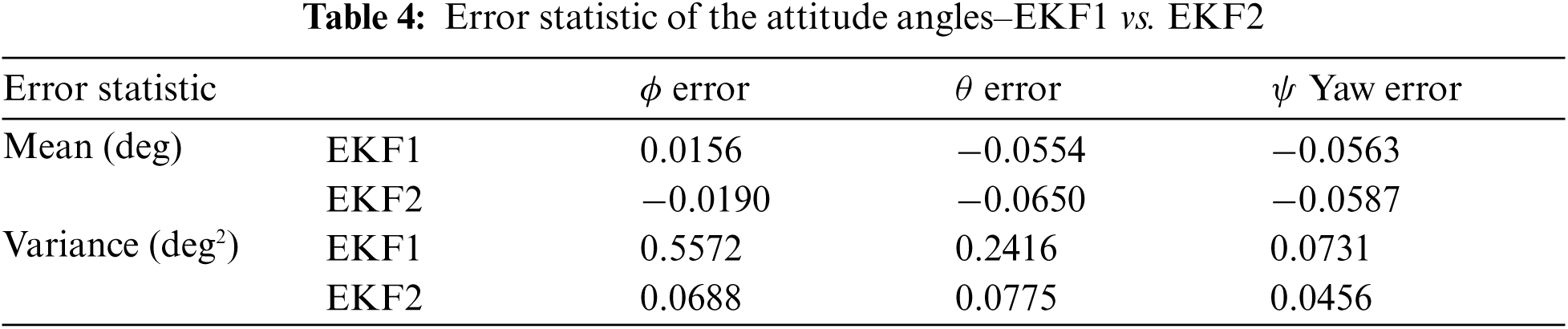
Figs. 6 and 7 show the performance comparison for EKF1 and EKF2 without signal outage. Fig. 6 shows estimate of attitude angles and Fig. 7 provides estimate of body angular rates. It can be seen that the EKF2 approach, with more measurement information available, outperforms the EKF1 approach noticeably. Notice that the solution provided by EKF2 is very close to the true states for the high quality rate gyros. Comparison of the error statistics for EKF1 and EKF2 regarding the attitude angles and body angular rates, respectively, are summarized in Tabs. 4 and 5, respectively. In addition, Fig. 8 shows estimate of attitude angles with signal outage for KF and EKF2. The assistance from body mounted gyroscopes, if available, can be utilized as the measurements for further performance improvement, especially useful for the case of GPS outages. Incorporation of the information of angular velocities into the EKF as the measurement not only achieves better accuracy but also catches the attitude dynamics well.
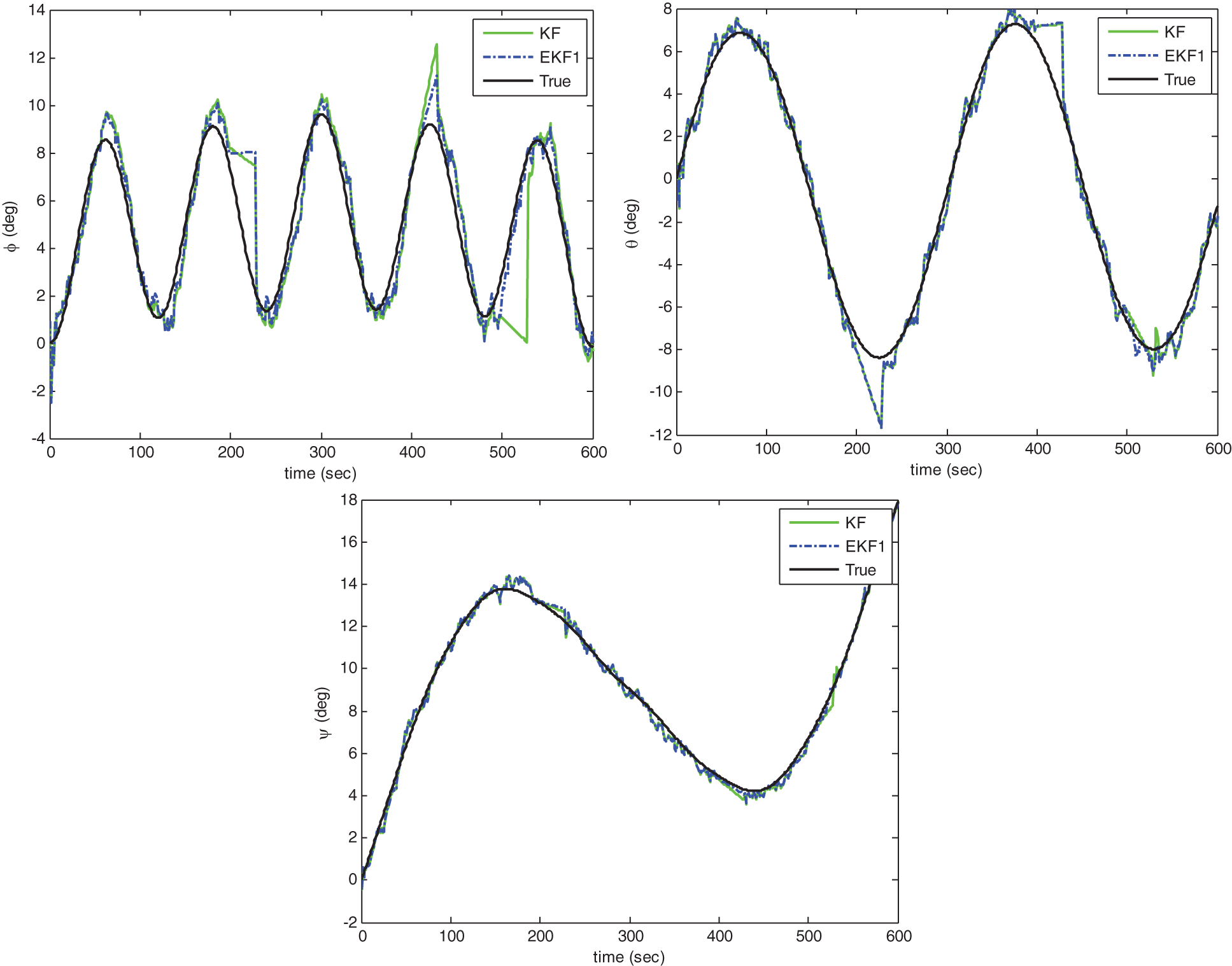
Figure 5: Estimate of attitude angles with signal outage: KF vs. EKF1

Figure 6: Estimate of attitude angles without signal outage: EKF1 vs. EKF2

Figure 7: Estimate of body angular rates without signal outage: EKF1 vs. EKF2

Figure 8: Estimate of attitude angles with signal outage: KF vs. EKF2
The above examples has demonstrated the attitude solutions obtained by KF and EKF based on measurements involving attitude angles only vs. those by EKF based on measurements involving both attitude angles and body angular velocities, possibly available from gyroscopes. In the case of signal outage, the body angular velocity is especially helpful from the view point of continuity of service and accuracy improvement.

The raw attitude solutions provided by the interferometry technique based on the least-squares approach are inherently noisy. The performance can be improved noticeably by using the Kalman family of filters. Incorporating the filter into the GPS interferometer effectively improves the performance in estimation performance. However, the case for GPS signal outage leads to performance degradation and even divergence. The proposed design provides the opportunity when body angular rates information from other sensor such as the gyroscopes is available for better resistance to the signal-challenged environment.
Details on dynamic models, including the CAV model as the second-order filter, and CAA model as the third-order filter, respectively, have been discussed. Numerical simulation has been carried out using the Kalman filter and extended Kalman filter, using the CAV model. Results involved include the estimate of attitude angles, attitude rates, and body angular velocities, for the cases with and without signal outages. Examples shown includes the attitude solutions obtained by KF and EKF based on measurements involving attitude angles only vs. those by EKF based on measurements involving both attitude angles and body angular velocities, possibly from gyroscopes. In the case of signal outage, the body angular velocity, possibly from gyroscopes is noticeably helpful from the view point of continuity of service and accuracy improvement.
Funding Statement: This work has been partially supported by the Ministry of Science and Technology, Taiwan [Grant Numbers MOST 109-2221-E-019-010 and MOST 110-2221-E-019-042].
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |