DOI:10.32604/cmc.2022.019544

| Computers, Materials & Continua DOI:10.32604/cmc.2022.019544 |  |
| Article |
Defocus Blur Segmentation Using Genetic Programming and Adaptive Threshold
Future Convergence Engineering, School of Computer Science and Engineering, Korea University of Technology and Education, Cheonan, 31253, Byeongcheon-myeon, Korea
*Corresponding Author: Muhammad Tariq Mahmood. Email: tariq@koreatech.ac.kr
Received: 16 April 2021; Accepted: 03 June 2021
Abstract: Detection and classification of the blurred and the non-blurred regions in images is a challenging task due to the limited available information about blur type, scenarios and level of blurriness. In this paper, we propose an effective method for blur detection and segmentation based on transfer learning concept. The proposed method consists of two separate steps. In the first step, genetic programming (GP) model is developed that quantify the amount of blur for each pixel in the image. The GP model method uses the multi-resolution features of the image and it provides an improved blur map. In the second phase, the blur map is segmented into blurred and non-blurred regions by using an adaptive threshold. A model based on support vector machine (SVM) is developed to compute adaptive threshold for the input blur map. The performance of the proposed method is evaluated using two different datasets and compared with various state-of-the-art methods. The comparative analysis reveals that the proposed method performs better against the state-of-the-art techniques.
Keywords: Blur measure; blur segmentation; sharpness measure; genetic programming; support vector machine
Generally, blur compromises the visual quality of images but sometimes it is induced deliberately to give the aesthetic impression or a graphical effect. Blur can be caused due to the limited depth of field of the lens, wrong focus and/or relative movement of object and camera. Unintentional defocus blur is considered as an undesirable effect because it not only decreases the quality of the image but also leads to the loss of necessary information. Hence automatic blur detection and segmentation play crucial role in many image processing and computer vision applications including forgery detection, image segmentation, object detection and scene classification, medical image processing and video surveillance system [1–3].
In literature, various blur measure operators have been proposed for blur detection and segmentation. A comprehensive study and comparative analysis of a variety of blur measures is presented in [4]. Elder et al. [5] proposed a method to estimate the blur map by calculating first and second order image gradients. Lin et al. [6] suggested the closed-form matting formulation for blur detection and classification, where the regularization term is computed through and local 1D motion of the blurred object and gradient statistics. Zhang et al. [7] suggested the double discrete wavelet transform to get the blur kernels and to process the blurred images. Zhu et al. [8] suggested the local Fourier spectrum to calculate the blur probability for each pixel and then blur map is estimated through solving a constrained energy function. Oliveira et al. [9] proposed a blur estimation technique through Radon-d transform based sinc-like structure of the motion blur kernel and then applied a non-blind deblurring algorithm to restore the blurry and noisy images. Shi et al. [10] proposed a set of blur features in multiple domains. Among them, they observed that the kurtosis varies in blurred and sharp regions. They also suggested the average power spectrum in the frequency domain as an eminent feature for blur detection. Finally, they proposed a multi-scale solution to fuse the features. In another work, Peng et al. [11] suggested the method to measure the pixel blurriness based on the difference between the original and the multi-scale Gaussian-filtered images. The blur map is then utilized to estimate the depth map. Tang et al. [12] proposed a coarse-to-fine techniques for blur map estimation. First, a coarse blur map is calculated by using the log-averaged spectrum of the image and then updated it iteratively to achieve the fine blur map by using the relevant neighbor regions in the local image. Golestaneh et al. [13] exploited the variations in the frequency domain to distinguish blur and non-blur regions in the image. They computed the spatially varying blur by applying multiscale fusion of the high-frequency discrete cosine transform (DCT) coefficients (HiFST). In another work, Takayama et al. [14] have generated the blur map by evaluating the local blur feature ANGHS (amplitude normalized gradient histogram span). Su et al. [15] have suggested the design of a blur metric by observing the connection between image blur and singular value distribution from a single image (SVD). Vu et al. [16] have measured the blur by a block-based algorithm that uses a spectral measure based on the slope of the local magnitude spectrum and a spatial measure based on maximization of local total variation (TV).
Once, blur map is generated, the next step is to segment blur and non-blur regions in the input image. Elder et al. [5] applied local scale control technique. In this technique, they calculate the zero crossing of second and third derivatives in the gradient image and use them for segmentation. Lin et al. [6] calculated the features from local 1D motion of the blurred object and used for regularization to segment the motion and blur from the images. In another method, Zhang et al. [7] computed the Double Discrete Wavelet Transform (DDWT) coefficients-based blur kernels to decouple the blurred regions from the input image. Shi et al. [10] used the graph-cut technique to segment the blurry and non-blurry regions from the blur map. Tang et al. [12] generated super pixels by using simple linear iterative clustering (SLIC) technique by adapting k-means clustering for segmentation. Yi et al. [17] proposed a new monotonic sharpness metric based on local binary patterns that rely on the observation that the non-uniform patterns are more discriminating towards blur regions. The segmentation process is done by using multi-scale alpha maps obtained through the multi-scale blur maps. Whereas, Golestaneh et al. [13] set the fixed threshold empirically, for the segmentation of in-focus and out-of-focus regions in the image. Takayama et al. [14] used Otsu’s method [18] to get the threshold for every map and then it is used to segment the blur and non-blur region of the image. Su et al. [15] extracted the blurred regions of the image by using the singular value-based blur maps. They also applied the fixed threshold to divide the in-focus and out-of-focus regions in the blurred images.
Recently, a large number of deep learning-based methods have been used for blur detection [19–23]. In [22], a convolutional neural network (CNN) based feature learning method automatically obtains the local metric map for defocus blur detection. In [20], fully convolutional network (FCN) model utilizes high-level semantic information to learn image-to-image local blur mapping. In [23], a bottom-top-bottom network (BTBNet) effectively merges high-level semantic information encoded in the bottom-top stream and low-level features encoded in the top-bottom stream. In [21], a bidirectional residual refining network (BR2Net) is proposed that encodes high-level semantic information and low-level spatial details by embedding multiple residual learning and refining modules (RLRMs) into two branches for recurrently combining and refining the residual features. In [19], a layer-output guided strategy based network exploits both high-level and low-level information to simultaneously detect in-focus and out-of-focus pixels.
The performance of the blur segmentation phase very much depends on the capability of blur detection phase. Among various blur detection methods, some perform better than the others in underlying certain conditions. Few most famous and effective methods are using multi-resolution of image in their algorithms. For example, LBP based defocus blur [17] uses three scales with window sizes
In this paper, we propose a method for blur detection and segmentation based on machine learning approaches. The block diagram of the proposed method is shown in Fig. 1. The proposed method is divided into two phases. In the first phase, a robust GP based blur detector is developed that captures the blur insight on different scales. The multi-scale resolution property is encoded into the blur measure to generate an improved blur map by fusing information at different scales through the GP technique. In the second phase, the blur map is segmented by an adaptive threshold obtained through the SVM model. The performance of the proposed method is evaluated using two different datasets and the results are compared with five state-of-the-art methods. The comparative analysis reveals that the proposed method has performed better against the state-of-the-art methods.
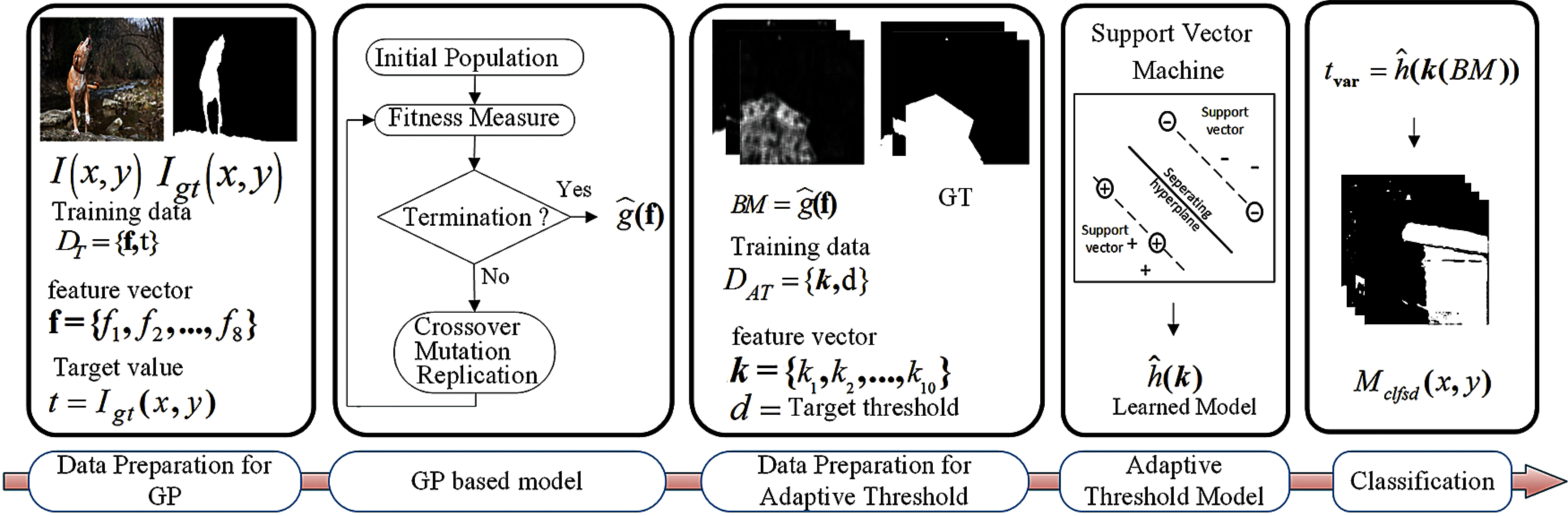
Figure 1: Block diagram for the proposed method for blur detection and segmentation
The rest of the paper is organized as follows. Section 2 discuss the basic rules for the genetic programming techniques. Section 3 presents the details of the proposed method including the details about the development of models. In Section 4, experimental setup, results, and comparative analysis are presented. Finally, Section 5 concludes the study and provides the future directions.
Multi-Gene Genetic Programming (MGGP) is a variant of GP, which provides model as a linear combination of bias coefficients and multiple genes [24]. Traditional GP, in contrast, gives a model with single gene expression. In MGGP, bias coefficients are used to scale each gene and hence play a vital role to improve the efficacy of the overall model. In MGGP symbolic regression, every prediction of the output variable is a weighted sum of each of the genes plus a bias term. The structure of the multi-gene symbolic regression model is shown in Fig. 2. Mathematically, the prediction of the training data is written as:
where
where 1 refers as a
where

Figure 2: Example of multi-gene regression model
In experiments, individuals in the population have gene restriction between 1 to
Parent 1:
The selected genes are then exchanged to produce two children for the next generation as expressed below.
Offspring 1:
The sizes of the created offspring are governed by
where
In first phase, a GP based model
In this section, GP based blur detection model is developed that generates a blur map for a partially blurred image. This section consists of two parts: (a) preparation of training data for GP, (b) learning best model form GP.
3.1.1 Data Preparation for GP Model
We prepare the training data form a random image
In this module, the first phase is to construct an initial population of predefined size. Each individual in the population is constructed with the linear combination of the bias coefficient and set of genes. The bias coefficients are determined by the least square method for each multigene individual. A gene of multigene GP is a tree-based GP model where the terminal nodes are taken from the feature set

The accuracy of individuals in the population is then evaluated with the fitness function. The best individual is then ranked and selected for the next generation by the selection method. In our experiment, we have used a tournament-based selection method to acquire individuals for the next generation. The crossover and the mutation operator are applied to the selected individuals to produce the population for the next generation. At the end of the evolutionary process the system returns an evolved program
In this section, a model for computing adaptive threshold is developed that will be applied on blur map to segment blur and non-blur pixels. This section again consists of two parts: (a) preparation of training data for SVM, (b) learning best model form SVM. Following subsections will explain the preparation of training and testing data, learning of SVM model and model evaluation.
3.2.1 Data Preparation for SVM Model
First, we create a set of useful features. We compute a feature vector
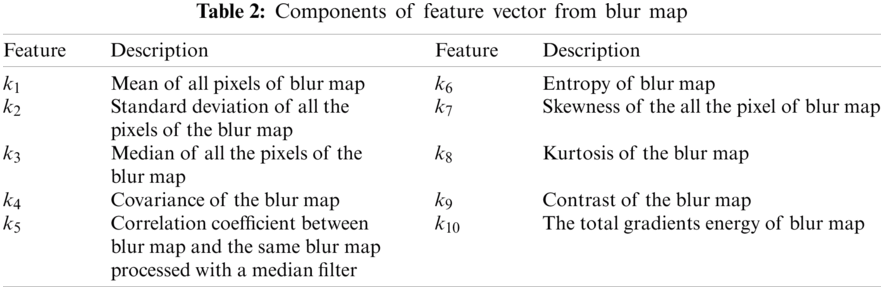
The blur map generated from the GP model is used to generate the features for training data i.e., for each blur map
Here,
Once the training data

Once the model
To evaluate the performance of the classifier, we compute classification loss
here,
In our experiment, we have used two datasets named as dataset A and dataset B. Dataset A [10] is publicly available dataset consists of 704 defocus partially blurred images. This dataset contains a variety of images, covering numerous attributes and scenarios like nature vehicles, humankind, other living, and non-living beings with different magnitude of defocus blur and resolution. Each image of this dataset is provided with a hand-segmented ground truth image-segmenting the blurred and non-blurred regions. Dataset B is a synthetic dataset which consists of 280 out of focus image from the dataset used in [26]. Each image of dataset B is synthetically created by mixing the blur and the focused part of other images of dataset A. However, we have generated the ground truth image by just segmenting the defocus blur and defocus non-blur regions of each image. There is a possibility of biasing of the particular choice of images (i.e., scenario and degree of blurriness) with the blur measure operators because the evaluation performance of the methods may differ for the different input image. Therefore, quantitative analysis on one dataset would not qualify to compare the performance of blur measure operator. There is also the possibility of model over-fitting for
where TP, TN, FP, and FN denote true positive, true negative, false positive, and false negative, respectively. If a pixel is blurred and it is detected as blurred then it is considered as true positive (TP) and if it’s not detected then it is regarded as a false negative (FN). However, if a sharp pixel is detected as a blurred pixel then it is considered as false positive (FP) otherwise it is a true negative (TN). Precision is a measure of the correct positive predictions out of all the positive predictions. It is given by;
Recall, also called as sensitivity in binary classification, is a measure of ability to retrieve the relevant results. Recall provides the proportion of actual positives that are identified correctly and it is given by the formula;
F-measure is the harmonic mean of Precision and Recall. It is defined as;
The recall gets
In order to do comparative analysis, the performance of the proposed method is compared with the five state-of-art methods including
Fig. 3 shows the quantitative comparison of the proposed method and five state-of-art methods including LBP, HiFST, LK, SVD and TV. All methods are applied on each image of two datasets
For qualitative comparison, we evaluate our method on the randomly picked images with different scenarios as well as the different degree of blur from the both datasets
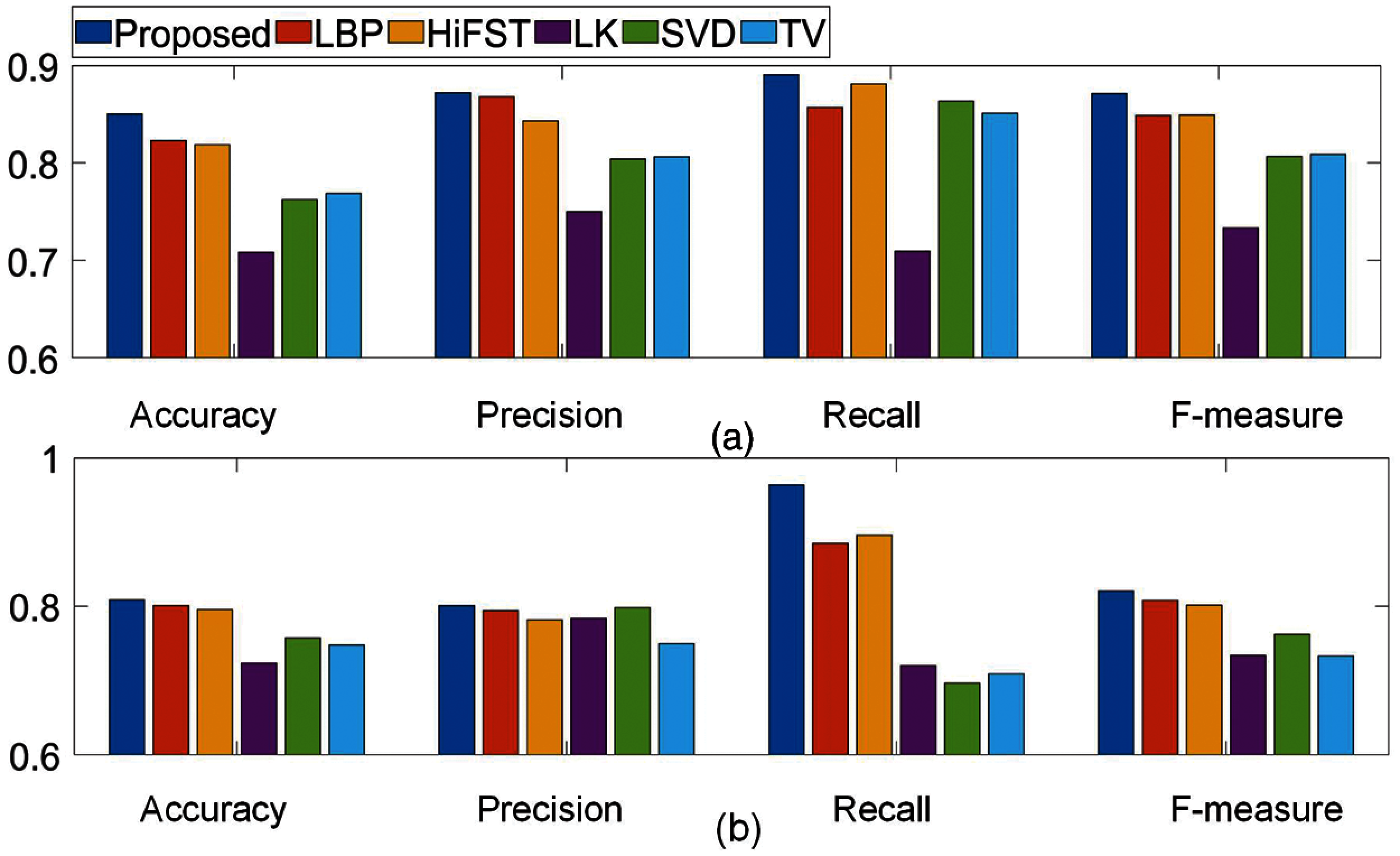
Figure 3: Comparison of the proposed method with state of art methods based on Accuracy, Precision, Recall and F-measure using images of (a) Dataset A with 704 images. (b) Dataset B with 280 images
Whereas, in blur maps produced by KL, SVD and TV methods, degree of blurriness is not correctly estimated The performances from LBP and HiFST methods are comparable with the proposed method. It is clear that the proposed method has ability to estimate degree of blurriness accurately.
The blur maps provided by the all above mentioned methods are segmented using the SVM based classifier and the results are presented in Fig. 5. It can be observed that the proposed method has segmented the blurred and unblurred regions with higher accuracy than other methods, regardless of the blur type and scenarios. Segmented results produced for the LK, SVD and TV methods have inaccuracies due to inaccurate computation of degree of blurriness. Results produced for LBP and HiFST are comparable with the proposed method, however, at few segmented parts inaccuracies are visible. Whereas, the proposed method has provided better segmented maps.
The proposed method has ability of capturing multi-scale information. Here, we analyze the multi-scale performance of the LBP-based segmentation defocus blur [17] at two sets of scale range and compared it with our proposed method. In this experiment, we have chosen scale range S1 = 11, S2 = 15 and S3 = 21 as set-1 and S1 = 23, S2 = 25 and S3 = 27 as set-2. Fig. 6b clearly shows the performance at sets-1 and 2 in their respective classified map and it varies with type of image. We observe that choosing appropriate scale for particular type of image is a challenging task. Fig. 6a shows the blur map and the segmented map of the proposed method. Our algorithm not only resolve the scale issue but also improve the segmentation results significantly.

Figure 4: Blur maps computed through for few selected images from dataset A and B. (row1), input images; (row2), ground truths; (row3~row8), blur maps that are computed through the proposed LBP [17], HiFST [13], LK [10], SVD [15] and TV [16] methods, respectively

Figure 5: Segmented maps computed through for few selected images from dataset A and B. (row1), input images; (row2), ground truths; (row3~row8), segmented maps that are computed through the proposed LBP [17], HiFST [13], LK [10], SVD [15] and TV [16] methods, respectively
The response of blur measure operator varies on different images, some operator performs better than other on same image due to different blur type, scenario, or level of blurriness. Since proposed method inherit the blur information of two methods HIFST [13] and LBP based defocus blur [17], We could not address the problem of noise propagation in this study. As shown in Fig. 7, on a particular image the performance of HIFST [13] is good and it generates a better blur map, while blur map for LBP [17] contains noise. The noise of low performer method gets propagated during the learning process of GP hence the performance for the proposed method reduced on these images. One more limitation of the proposed method is that it takes more time as compared to the other methods.
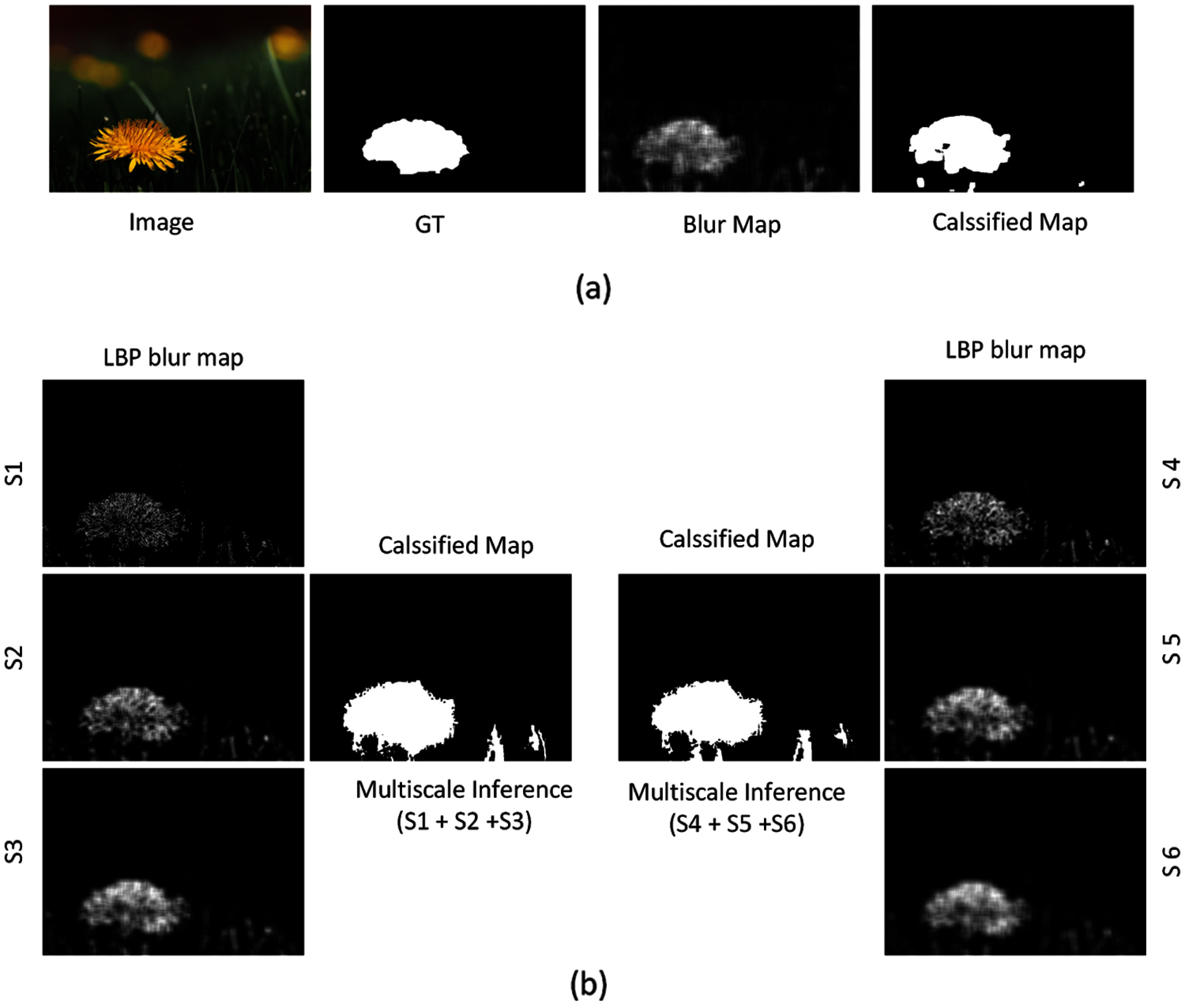
Figure 6: (a) The blur map and the classified map of proposed method (b) LBP blur maps at 2 sets of scale range (S1–S3) and (S4–S6) and their respective classified maps after multi-scale inference
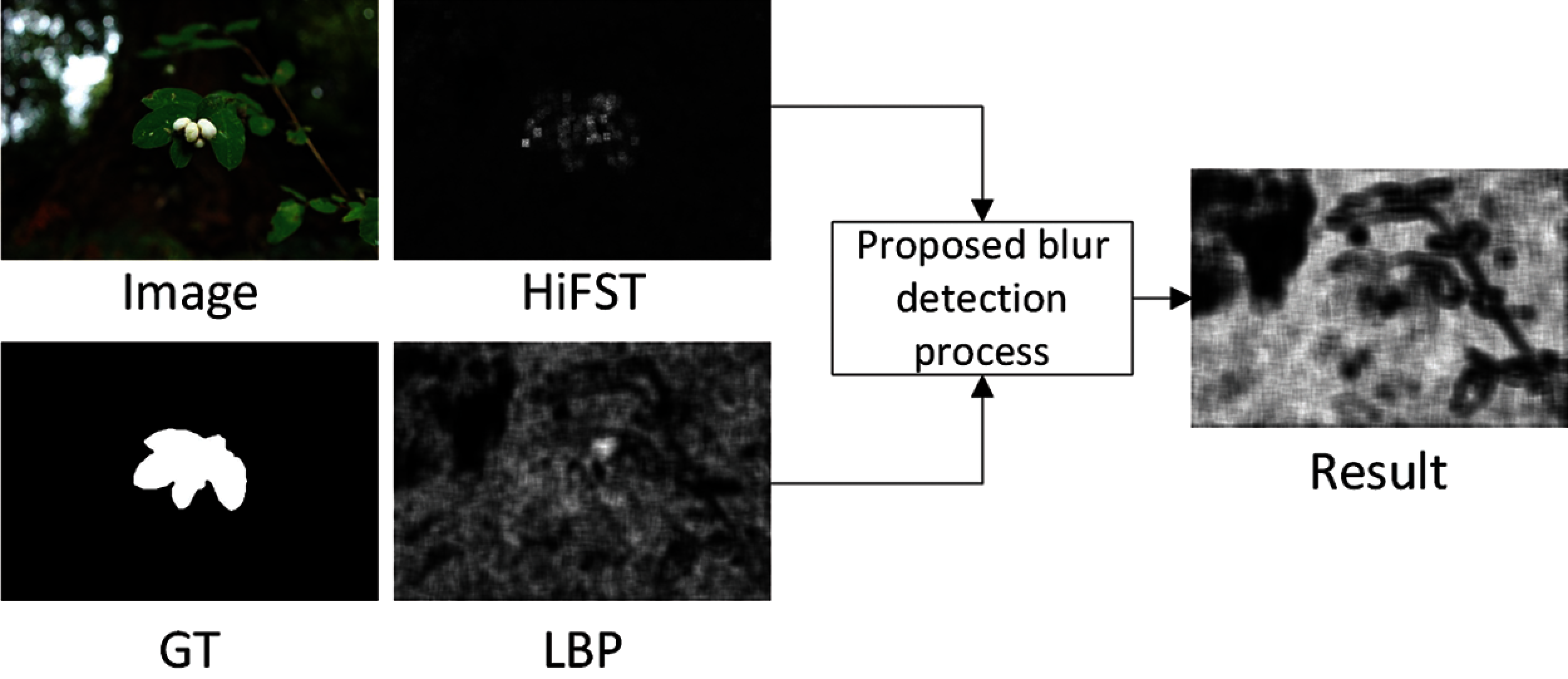
Figure 7: The blur maps of HiFST, LBP and proposed methods for an image which confirms the propagation of noise
In this article, a robust method for blur detection and segmentation is proposed. Blur detection is achieved by the GP based model, which produces a blur map. For segmentation, first, we trained a model using SVM, which can predict the threshold based on the retrieved blur map features, and then respective thresholds are used to acquire the classified map of the images. We have evaluated the performance of the proposed method in terms of accuracy, precision, Recall, and F-measure using two benchmark datasets. The results show the effectiveness of the proposed method to achieve good performance over a wide range of images, which outperforms the state-of-the-art defocus segmentation methods. In the future, we would like to expand our investigation toward different types of blur. We wish to examine the effectiveness of the proposed approach by learning the combination of motion and defocus blur.
Funding Statement: This work was supported by the BK-21 FOUR program through National Research Foundation of Korea (NRF) under Ministry of Education.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1https://github.com/xinario/defocus_segmentation
2https://github.com/isalirezag/HiFST
3http://www.cse.cuhk.edu.hk/leojia/projects/dblurdetect/index.html
4https://github.com/fled/blur_detection
5http://vision.eng.shizuoka.ac.jp/s3/
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |