DOI:10.32604/cmc.2022.017318

| Computers, Materials & Continua DOI:10.32604/cmc.2022.017318 |  |
| Article |
An Efficient Proxy Blind Signcryption Scheme for IoT
1Department of Information Technology, Abbottabad University of Science and Technology, Abbotabad, Pakistan
2Hamdard Institute of Engineering and Technology, Islamabad, 44000, Pakistan
3College of Computing and Information Technology, University of Bisha, Bisha, Saudi Arabia
4Institute of Computing, Kohat University of Science and Technology, Kohat, Pakistan
*Corresponding Author: Insaf Ullah. Email: insafktk@gmail.com
Received: 27 January 2021; Accepted: 17 April 2021
Abstract: Recent years have witnessed growing scientific research interest in the Internet of Things (IoT) technologies, which supports the development of a variety of applications such as health care, Industry 4.0, agriculture, ecological data management, and other various domains. IoT utilizes the Internet as a prime medium of communication for both single documents as well as multi-digital messages. However, due to the wide-open nature of the Internet, it is important to ensure the anonymity, untraceably, confidentiality, and unforgeability of communication with efficient computational complexity and low bandwidth. We designed a light weight and secure proxy blind signcryption for multi-digital messages based on a hyperelliptic curve (HEC). Our results outperform the available schemes in terms of computational cost and communication bandwidth. The designed scheme also has the desired authentication, unforgeability of warrants and/or plaintext, confidentiality, integrity, and blindness, respectively. Further, our scheme is more suitable for devices with low computation power such as mobiles and tablets.
Keywords: Proxy signcryption; multi-digital-documents proxy blind signcryption; hyperelliptic curve; IoT
In recent years, there has been extensive research on IoT technologies, which covers various applications such as healthcare (HC), Industry 4.0, agriculture, and ecological data management, to name a few. The IoT comprises certain devices that have the capability of sending, receiving, and storing data, in addition to being about to communicate through the Internet. Once these devices are connected to the Internet, communication can take place for single documents as well as multi-digital messages. Thus, blindness and untraceable security services are required. Chaum was the first author to coin the term blind signature for the protection of digital information privacy. The blind signature mechanism enables resistance to forgery, indisputability and anonymity [1,2]. Blindness and untraceability are the core properties which must be fulfilled by any blind signature scheme [1–4]. In addition, the blindness property allows the transmission of signed messages between the user and the signer in an interactive signature protocol. In this instance, untraceability ensures that the signer cannot link back any message-signature pairs even if the signature is revealed to the public. A blind signature scheme based on the integer factorization problem (IFP), which was initially proposed by Chaum [2], relies on the solidity of the Rivest, Shamir, and Adleman (RSA) cryptosystem assumptions. The security of this scheme is based on the appropriate selection of the underlying hash function. There have been several investigations on various schemes that examined the efficiency, security of improved blind signature techniques [3–11]. ECC-based blind signatures have been introduced in several variations; these schemes are extremely beneficial for applied applications between security and performance [12–19]. Lin et al. [20] proposed a new scheme, named the proxy blind signature, which combines proxy and blind signatures. The proxy signer is permitted with features to create blind signatures on behalf of the original signer, similar to the traditional digital signature procedure with some unique differences. Several studies have revealed considerable types of variations for this scheme to improve the desired unforgeability, untraceability, non-repudiation and efficiency [21–29].
Gamage et al. [30] provided a new approach called proxy signcryption by merging a proxy signature and encryption in a single logical step. Their approach was more secure and proficient due to the incorporation of the discrete logarithm problem (DLP). However, this approach suffered from several issues such as forward secrecy and public verifiability. Moreover, Zhang et al. [31] introduced a new proxy signcryption scheme which incorporates public verifiability and forward secrecy. Their scheme suffered from higher computational and communication costs which was later addressed by Li et al. [32]. Wang et al. [33] addressed security constraints such as forward secrecy and public verifiability with an approach called an efficient identity-based proxy-signcryption. Duan et al. [34] introduced another proxy-signcryption scheme, named secure under ROM (Random Oracle Model), which is a secure delegation-by-warrant ID- based proxy signcryption scheme. However, this scheme was challenged and negatively affected by extra computations and limited communication bandwidth. A more recent and improved proxy-signcryption scheme was provided by Elkamchouchi et al. [35–37]. The authors asserted that their techniques are publicly verifiable while achieving confidentiality, higher security levels, and authenticity using an unsecured channel.
Partial delegation rights were also provided in their technique by using bilinear pairings on elliptic curves. Their techniques suffered from a misuse of authority in the case of partial delegation. A new provable and secure proxy-signcryption scheme was designed by Lin et al. [38] by utilizing bilinear pairing. Despite the advantages of these techniques, another main drawback is their inability to ensure the warrant unforgeability requirement for security. Elkamchouchi et al. [39] introduced a proxy-signcryption based on the notion of warrants. The scheme introduced by the authors was based on elliptic curve cryptography to ensure efficiency and security, however it suffers from extra power consumption. Yanfeng et al. proposed proxy identity-based signcryption based on the elliptic curve discrete logarithm problem (ECDLP) [40]. Another proxy-signcryption scheme using DLP and ECDLP was introduced by Elkamchouchi et al. [41]. Despite their claim that the proposed scheme incurs less communication and computational costs, a major issue is that it is not sufficiently provable. More recently, a new provable and secure proxy-signcryption scheme was introduced by Lo et al. [42] based on bilinear pairing. The study addressed performance and secrecy in an effective approach in terms of unforgeability and indistinguishability. Ming et al. [43] developed a provable and secure proxy-signcryption scheme based on a standard model to improve the security service area. This approach was relatively narrow, being primarily focused on heavy computations of bilinear pairing and it also suffered from additional communication and machine control costs.
In our previous work [44], we proposed a lightweight proxy-signcryption scheme using hyperelliptic curve cryptography. This scheme ensures all security service areas that are commonly needed for proxy-signcryption in resource constrained environments due to its needs of low computational and communication costs. Our scheme was affected by utilizing additional major operations over the hyperelliptic curve. A novel proxy-signcryption scheme and its elliptic curve variant were recently proposed by Abdelfatah [45]. The author claimed that the developed technique was more secure and efficient, however, the study fails to provide security requirements such as non-repudiation, warrants, message, and message non-repudiation. The technique also incurred higher computational and communication costs. In addition, the above proxy-signcryption scheme only provides a delegation of rights with authenticity and confidentiality. Therefore, the scheme suffers in cases where the applications require anonymity.
Sadat et al. [46] proposed another proxy blind signcryption technique to provide the anonymity property together with a delegation of rights. It combines the property of proxy signcryption with blind signcryption [47–50]. More recently, Su et al. [51] proposed a new proxy blind signcryption for multiple digital documents based on elliptic curve cryptography. The scheme allows the sender to simultaneously produce a proxy blind signcryption of multi-digital documents. To the best of our knowledge, all the proxy blind signature and proxy blind signcryption approaches available in the literature are affected by higher computational cost due to RSA, bi-linear pairing and EC. A major reason for these issues is due to the fact that underlying frameworks have larger key sizes, such as 1024 bits for RSA and bilinear pairing, and 160 bits for EC.
In this paper, we propose a new provable secure proxy blind signcryption scheme for multi-digital messages based on hyperelliptic curves which provides a similar level of security with less communication and computational costs. The rest of the paper is organized as follows: Section 2 discusses the pre-requisites to understanding the formalization of our scheme, which is followed by discussions of our methodology in Section 3. Sections 4 and 5 cover the results and discussions. Finally, the conclusion is presented in Section 6.
In 1988, Koblitz introduced the generality of the elliptic curve to the advanced genus of the curve called the hyperelliptic curve cryptosystem, which performs a significant operation in comparison to the elliptic curve cryptosystem. Let
Let F0 = final field of hyper ellipticcurve cryptosystem and F
where
In contrast, the group arrangement of the hyperelliptic curve has the Jacobian (J) of a curve C. A piece element of the J is a correspondent class of divisors. A divisor is the formal sum of finite points for the curve
where
The reduced divisor is:
Eq. (3) contains one opposite point, i.e.,
and opposed point for
Polynomial expressions can be used to characterize the divisor [53]. The operative process of calculation for the whole value of C in Abelian group having a DLP.
The group operations of addition and doubling of divisors is called a scalar multiplication divisor (SMD). The operations changed elliptic curve point multiplication into divisors of the Jacobian of a hyper ellipticcurve [53–55].
3 Proposed Model in a Nutshell
Our scheme consists of five participants:
• Original user: The original signer delegates the signing capabilities to a proxy signcrypter.
• Proxy signcrypter: The proxy signcrypter verifies the delegation and blinds a message for signing and then delivers it to the anonymous signer.
• Anonymous signer: The signer generates a blind signature on a blind message and then sends it back to the proxy signcrypter. The proxy signcrypter combines the blind signature with an encrypted message and hands it over to the receiver.
• Receiver/Un-signcrypter: At the end, the receivers verify the blind signcrypted message and then decrypt it.
• The authentication server: This acts as a certificate authority which publishes all the public parameters and generates the certificates for each user.
Fig. 1 illustrates the flow of our proposed scheme.

Figure 1: Flow of our proposed scheme
The communication in the above scheme is completed in the following steps (the sequence of these steps is demonstrated in Fig. 1): Key Generation: The pre-requisite of our model (not shown in Fig. 1) is the generation of keys (public and private) by each participant of our scheme in the following manner:
All participants (Alice, Proxy, signer, Bob) first generate their keys (private, public) from the given
Alice: randomly takes a number
Proxy: randomly chooses integer
Signer: randomly chooses integer
Bob: randomly chooses integer
I. Delegation: In this step, Alice signs a warrant message and sends it to the proxy as follows:
i) Randomly pick
ii) Compute
iii) Compute
iv) Send
II. Proxy key verification phase: The proxy signcrypter first checks the validity of the warrant message, i.e., whether it was initiated by Alice or not. Only those messages which are generated by Alice are accepted.
Compute
III. Proxy blind signcryption
i Signer
a) Signer selects a random number
b) Compute
c) Send
ii Proxy
Suppose the proxy assumes that he wants to send a vector of message
a) Select three blind factors randomly
b) Select randomly a nonce
c) Compute
d) Compute the hash value like
e) Compute
f)
g)
h) Send
iii Signer
a)
b)
iv Proxy
a) Compute
b) Send
IV Bob/blind Unsigncryption
After receiving
i) Compute
ii) Compute
iii) Compute
iv) Compute
v) Accept
In this section, we divide the security of our scheme into two parts, the first part showing the correctness of the scheme and the second part showing the security services e.g., warrant authentication, unforgeability of warrants, confidentiality, integrity, and blindness, respectively. We consider a popular Dolev-Yao (DY) threat model and suppose the adversary is able to dismiss the warrant authentication, forge the warrant signature, read the exchanged messages, destroy the blindness, modify the message contents, and generate a forged signature.
Theorem 1: In this theorem, we prove how a blind unsigncrypter generates the secret key for it to decrypt a cipher text. The unsigncrypter performs the following process.
Theorem 2: In Theorem 2, we prove how the proxy signcrypter validates whether the warrant message is from the sender or not. The proxy signcrypter performs the following process.
The security attribute of the warrant authentication is another contribution of our approach. If the sender delegates their signing rights by sending a warrant message mw to the proxy, the original user first generates the digital signature mw using
Our scheme also meets the property of warrant unforgeability. When an attacker generates a forged signature
In our scheme, the encrypted multi-documents are sent to the legitimate recipient (Bob) using the secret shared key
Step 1: An intruder can easily get the secret shared key if they can solve Eq. (1). Therefore, the intruder must first get the blind random number
Step 2: Similar to step 1, an intruder can get the secret key from
We use a collision resistant hash function in our proposed scheme to ensure the integrity of multi-digital documents as
In our designed scheme, before sending the multi-document cipher text to the recipients/Bob, the signer computes a blind digital signature on the multi-documents cipher text as
Our scheme enables the proxy signer to select three blind numbers
This section elaborates on the computational cost of the proposed multi-document proxy blind signcryption scheme and the existing proxy blind signature [28,29] and signcryption schemes [46,47]. We compare our strategy with the state-of-the-art approaches by computing the time taken for proxy delegations, proxy blind signcryption and proxy blind unsigncryption. As shown in Tab. 1, we use

The computations of addition, subtraction, division and hash are ignored due to their fewer needs of computations and lower execution periods. For a more detailed illustration of the difference between the proposed and existing schemes, observations can be obtained from Ullah et al. [55], and “test the runtime of basic cryptographic operations” respectively
According to Ullah et al. [55], 1


Figure 2: Comparisons in terms of milliseconds
If the number of digital messages increases, then the computational cost will increase. Tab. 3 and Fig. 3 compare our scheme with the previous schemes for a varying number of messages. Our results show that our scheme is more computationally efficient even for a larger number of messages.


Figure 3: Comparison in terms of milliseconds for a varying number of messages
Further, we use the general formula
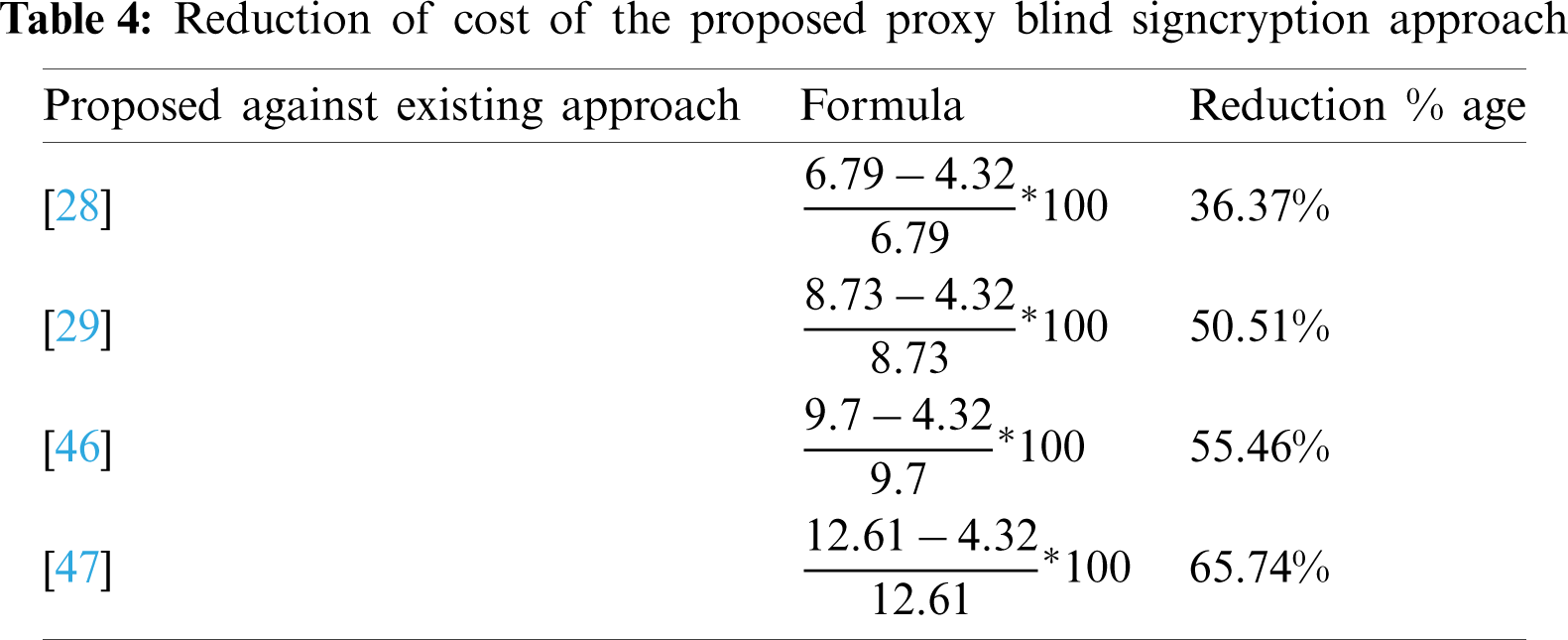
In this paper, we have developed a lightweight and secure proxy blind signcryption scheme for multi-digital messages based on a hyperelliptic curve. Our scheme consists of five participants, e.g., the authenticated server, original user, proxy signcrypter, the anonymous signer and receiver/un-signcrypter. The authenticated server performs the role of a certificate authority which publishes all public parameters and issues certificates to each user. The original signer simply delegates the signing capabilities to the proxy signcrypter. The proxy signcrypter verifies the delegation and blinds a message for signing, then delivers it to the anonymous signer. The signer only generates a blind signature on a blind message and then back sends it back to the proxy signcrypter. Finally, the proxy signcrypter combines the blind signature with the encrypted message and then hands it over to the receiver. In the final step, the receiver verifies the blind signcrypted message and then decrypts it. Further, the developed scheme provides all the security services of proxy and blind signcryption e.g., warrant authentication, unforgeability of warrants and/or plaintext, confidentiality, integrity, and blindness. Compared to the existing schemes, our scheme reduces the computational costs by about 33.28% to 64.07% in terms of milliseconds. Additionally, due to the lower parameters and the standard size of the hyperelliptic curve, our scheme is attractive to limited-resource devices such as those used in IoT environments.
Future studies are required to shed light on the development of such a scheme with different functionalities. These functionalities will be combined into a single scheme, such as encryption only, signature only, and signcryption, so that they can be utilized whenever they are required. It is also important to consider developing more efficient techniques that focus on lowering computational and communication costs.
Funding Statement: The authors received no specific funding for this study.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. D. Chaum, “Blind signatures for untraceable payments,” in Advances in cryptology, Chapter No. 3. Boston, MA, USA: Springer, pp. 199–203, 1983. [Google Scholar]
2. D. Chaum, “Security without identification: Transaction systems to make big brother obsolete,” Communications of the ACM, vol. 28, no. 10, pp. 1030–1044, 1985. [Google Scholar]
3. L. Harn, “Cryptanalysis of the blind signatures based on the discrete logarithm problem,” Electronics Letters, vol. 31, no. 14, pp. 1136–1150, 1995. [Google Scholar]
4. C. Lee, H. Min-Shiang and Y. Wei-Pang, “A new blind signature based on the discrete logarithm problem for untraceability,” Applied Mathematics and Computation, vol. 164, no. 3, pp. 837–841, 2005. [Google Scholar]
5. J. Camenisch, P. Jean-Marc and S. A. Markus, “Blind signatures based on the discrete logarithm problem,” in Workshop on the Theory and Application of Cryptographic Techniques. Berlin, Heidelberg, pp. 428–432, 1994. [Google Scholar]
6. C. I. Fan and C. L. Lei, “Efficient blind signature scheme based on quadratic residues,” Electronics Letters, vol. 32, no. 9, pp. 811–813, 1996. [Google Scholar]
7. C. I. Fan, C. Wei-Kuei and Y. Yi-Shung, “Randomization enhanced Chaum’s blind signature scheme,” Computer Communications, vol. 23, no. 17, pp. 1677–1680, 2000. [Google Scholar]
8. C. I. Fan, W. Chih-I and S. Wei-Zhe, “Fast randomization schemes for Chaum blind signatures,” International Journal of Innovative Computing, Information and Control, vol. 5, no. 11, pp. 3887–3900, 2009. [Google Scholar]
9. M. S. Hwang, L. Cheng-Chi and L. Yan-Chi, “An untraceable blind signature scheme,” IEICE Transactions on Fundamentals of Electronics, Communications and Computer Sciences, vol. 86, no. 7, pp. 1902–1906, 2003. [Google Scholar]
10. W. S. Juang and C. L. Lei, “Partially blind threshold signatures based on discrete logarithm,” Computer Communications, vol. 22, no. 1, pp. 73–86, 1999. [Google Scholar]
11. V. R. L. Shen, C. Y. Fang, C. T. Shyong and L. Y. An, “A blind signature based on discrete logarithm problem,” in ICIC International. Zhengzhou, China, pp. 5403–5416, 2011. [Google Scholar]
12. N. M. F. Tahat, E. S. Ismail and R. R. Ahmad, “A new blind signature scheme based on factoring and discrete logarithms,” International Journal of Cryptology Research, vol. 1, no. 1, pp. 1–9, 2009. [Google Scholar]
13. S. Verma and S. K. Birendra, “New proxy blind multi signature based on integer-factorization and discrete-logarithm problems,” Bulletin of Electrical Engineering and Informatics, vol. 1, no. 3, pp. 185–190, 2012. [Google Scholar]
14. K. Rabah, “Elliptic curve cryptography over binary finite field GF (2m),” Information Technology Journal, vol. 5, no. 1, pp. 204–229, 2006. [Google Scholar]
15. S. Shenghui and L. Shuwang, “A public key cryptosystem based on three new provable problems,” Theoretical Computer Science, vol. 426, no. 1, pp. 91–117, 2012. [Google Scholar]
16. I. Bütün and D. Mehmet, “A blind digital signature scheme using elliptic curve digital signature algorithm,” Turkish Journal of Electrical Engineering & Computer Sciences, vol. 21, no. 4, pp. 945–956, 2013. [Google Scholar]
17. K. Chakraborty and M. Jay, “A Stamped blind signature scheme based on elliptic curve discrete logarithm problem,” International Journal Network Security, vol. 14, no. 6, pp. 316–319, 2012. [Google Scholar]
18. J. Debasish, S. K. Jena and B. Majhi, “A novel untraceable blind signature based on elliptic curve discrete logarithm problem,” International Journal of Computer Science and Network Security, vol. 7, no. 6, pp. 1–12, 2007. [Google Scholar]
19. N. Morteza and A. Zakerolhosseini, “An efficient blind signature scheme based on the elliptic curve discrete logarithm problem,” ISC International Journal of Information Security, vol. 1, no. 2, pp. 125–131, 2009. [Google Scholar]
20. W. D. Lin and J. K. Jan, “A security personal learning tools using a proxy blind signature scheme,” in Proc. of Int. Conf. on Chinese Language Computing, Illinois, USA, pp. 273–277, 2000. [Google Scholar]
21. Z. Tan, L. Zhuojun and T. Chunmingg, “Digital proxy blind signature schemes based on DLP and ECDLP,” MM Research Preprints, vol. 21, no. 7, pp. 212–217, 2002. [Google Scholar]
22. S. Mashhadi, “A novel secure self proxy signature scheme,” International Journal Network Security, vol. 14, no. 1, pp. 22–26, 2012. [Google Scholar]
23. H. M. Sun, B. T. Hsieh and S. M. Tseng, “On the security of some proxy blind signature schemes,” Journal of Systems and Software, vol. 74, no. 3, pp. 297–302, 2005. [Google Scholar]
24. H. Wang and R. Wang, “A proxy blind signature scheme based on ECDLP,” Chinese Journal of Electronics, vol. 14, no. 2, pp. 281–284, 2005. [Google Scholar]
25. X. Yang and Y. Zhaoping, “Security analysis of a proxy blind signature scheme based on ECDLP,” in 4th Int. Conf. on Wireless Communications, Networking and Mobile Computing, WiCOM’08, Dalian, China, pp. 1–4, 2008. [Google Scholar]
26. B. Kar, P. P. Sahoo and A. K. Das, “A secure proxy blind signature scheme based on DLP,” in 2010 Int. Conf. on Multimedia Information Networking and Security, Nanjing, Jiangsu, China, pp. 477–480, 2010. [Google Scholar]
27. S. Pradhan and R. K. Mohapatra, “Proxy blind signature scheme based on ECDLP,” International Journal of Engineering Science & Technology, vol. 3, no. 3, pp. 2244–2248, 2011. [Google Scholar]
28. D. M. Alghazzawi, M. S. A. Trigui and S. H. Hasan, “A new proxy blind signature scheme based on ECDLP,” International Journal of Computer Science Issues, vol. 8, no. 3, pp. 1–14, 2011. [Google Scholar]
29. C. H. Wang and L. Meng-Zhe, “Security analysis and enhanced construction on ECDLP-based proxy blind signature scheme,” International Journal of e-Education, vol. 4, no. 1, pp. 47–64, 2014. [Google Scholar]
30. C. Gamage, L. Jussipekka and Y. Zheng, “An efficient scheme for secure message transmission using proxy-signcryption,” in Proc. of the 22nd Australasian Computer Science Conf., Auckland, Newzealand, pp. 420–431, 1999. [Google Scholar]
31. Z. Zhang, D. Qingkuan and M. Cai, “A New publicly verifiable proxy signcryption scheme,” in Progress on Cryptography. Boston, MA, USA: Springer, pp. 53–57, 2004. [Online] Available: https://link.springer.com/chapter/10.1007/1-4020-7987-7_7 [Google Scholar]
32. X. Li and K. Chen, “Identity based proxy-signcryption scheme from pairings,” in Proc. 2004 IEEE Int. Conf. on Services Computing, 2004. (SCC 2004Shanghai, China, pp. 494–497, 2004. [Google Scholar]
33. M. Wang, H. Li and Z. Liu, “Efficient identity based proxy-signcryption schemes with forward security and public verifiability,” in Networking and Mobile Computing. Berlin, Heidelberg: Springer, pp. 982–991, 2005. [Google Scholar]
34. S. Duan, Z. Cao and Y. Zhou, “Secure delegation-by-warrant ID-based proxy signcryption scheme,” in Int. Conf. on Computational and Information Science, Berlin, Heidelberg, Germany, pp. 445–450, 2005. [Google Scholar]
35. D. H. Elkamshoushy, A. K. Abouelsoud and M. Madkour, “New proxy signcryption scheme with DSA verifier,” in Radio Science Conf., 2006. NRSC 2006. Proc. of the Twenty Third National, Menouf, Egypt, pp. 1–8, 2006. [Google Scholar]
36. H. Elkamchouchi, M. Nasr and R. Ismail, “A new efficient strong proxy signcryption scheme based on a combination of hard problems,” in SMC 2009 IEEE Int. Conf. on Systems, Man and Cybernetics, San Antonio, TX, USA, pp. 5123–5127, 2009. [Google Scholar]
37. H. M. Elkamchouchi and Y. Abouelseoud, “A new proxy identity-based signcryption scheme for partial delegation of signing rights,” IACR Cryptology ePrint Archive2008, vol. 2008, pp. 1–5, 2008. [Google Scholar]
38. H. Y. Lin, W. Tzong-Sun, S. K. Huang and Y. S. Yeh, “Efficient proxy signcryption scheme with provable CCA and CMA security,” Computers & Mathematics with Applications, vol. 60, no. 7, pp. 1850–1858, 2010. [Google Scholar]
39. H. M. Elkamchouchi, Y. Abouelseoud and W. S. Shouaib, “A new proxy signcryption scheme using warrants,” International Journal of Intelligent Engineering Informatics, vol. 1, no. 3, pp. 309–327, 2011. [Google Scholar]
40. Q. Yanfeng, T. Chunming, L. Yu, X. Maozhi and G. Baoan, “Certifcateless proxy identity-based signcryption scheme without bilinear pairings,” China Communications, vol. 10, no. 11, pp. 37–41, 2013. [Google Scholar]
41. H. M. Elkamchouchi, E. F. Abuelkhair and Y. Abouelseoud, “An efficient proxy signcryption scheme based on the discrete logarithm problem,” International Journal of Information Technology, Modeling and Computing, vol. 1, no. 2, pp. 7–19, 2013. [Google Scholar]
42. N. W. Lo and J. L. Tsai, “A provably secure proxy signcryption scheme using bilinear pairings,” Journal of Applied Mathematics, vol. 2014, no. 1, pp. 1–18, 2014. [Google Scholar]
43. Y. Ming and Y. Wang, “Proxy signcryption scheme in the standard model,” Security and Communication Networks, vol. 8, no. 8, pp. 1431–1446, 2015. [Google Scholar]
44. I. Ullah, I. U. Haq, N. U. Amin and A. I. Umar, “Proxy signcrypion scheme based on hyper elliptic curves,” International Journal of Computer, vol. 20, no. 1, pp. 157–166, 2016. [Google Scholar]
45. R. Abdelfatah, “A novel proxy signcryption scheme and its elliptic curve variant,” International Journal of Computer Application, vol. 165, no. 2, pp. 36–43, 2017. [Google Scholar]
46. A. Sadat, I. Ullah, H. Khattak and S. Ullah, “Proxy blind signcrypion based on elliptic curve,” International Journal of Computer Science and Information Security, vol. 14, no. 3, pp. 257–272, 2016. [Google Scholar]
47. A. K. Awasthi and S. Lal, “An efficient scheme for sensitive message transmission using blind signcryption,” arXiv preprint cs/0504095, 2005. [Google Scholar]
48. X. Yu and D. He, “A new efficient blind signcryption,” Wuhan University Journal of Natural Sciences, vol. 13, no. 6, pp. 662–664, 2008. [Google Scholar]
49. C. H. Tsai and P. C. Su, “An ECC-based blind signcryption scheme for multiple digital documents,” Security and Communication Networks, vol. 2017, no. 1, pp. 1–12, 2017. [Google Scholar]
50. R. Ullah, A. I. Umar and N. U. Amin, “Blind signcryption scheme based on elliptic curves,” in 2014 Conf. on Information Assurance and Cyber Security, Rawalpindi, Pakistan, pp. 51–54, 2014. [Google Scholar]
51. P. C. Su and C. H. Tsai, “New proxy blind signcryption scheme for secure multiple digital messages transmission based on elliptic curve cryptography,” KSII Transactions on Internet & Information Systems, vol. 11, no. 11, pp. 1–13, 2017. [Google Scholar]
52. N. Koblitz, “A family of Jacobians suitable for discrete log cryptosystems,” in Conf. on the Theory and Application of Cryptography, New York, NY, USA, pp. 94–99, 1988. [Google Scholar]
53. A. Nelasa and T. Fedoronchak, “Usage of hyperelliptic curves in the digital signature protocol,” in MTCSET 2006. Int. Conf. Modern Problems of Radio Engineering, Telecommunications, and Computer Science, Lviv-Slavsk, Ukraine, pp. 51–53, 2006. [Google Scholar]
54. P. Kumar, A. Singh and A. D. Tyagi, “Implementation of hyperelliptic curve based sign-cryption approach,” International Journal of Scientific and Engineering Research, vol. 4, no. 7, pp. 1–15, 2013. [Google Scholar]
55. I. Ullah, N. U. Amin, A. Almogren, M. A. Khan and M. I. Uddin, “A lightweight and secured certificate-based proxy signcryption (CB-PS) scheme for e-prescription systems,” IEEE Access, vol. 8, no. 1, pp. 199197–199212, 2020. [Google Scholar]
56. A. U. Rahman, I. Ullah, M. Naeem, R. Anwar, N. U. Amin et al., “A lightweight multi-message and multi-receiver heterogeneous hybrid signcryption scheme based on hyper elliptic curve,” International Journal of Advanced Computer Science and Applications, vol. 9, no. 5, pp. 160–167, 2018. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |