 Open Access
Open Access
ARTICLE
Multi-Objective Prediction and Optimization of Vehicle Acoustic Package Based on ResNet Neural Network
1 School of Mechanical Engineering, Southwest Jiaotong University, Chengdu, 610031, China
2 Engineering Research Center of Advanced Driving Energy-Saving Technology, Ministry of Education, Chengdu, 610031, China
* Corresponding Authors: Haibo Huang. Email: ; Mingliang Yang. Email:
(This article belongs to the Special Issue: Passive and Active Noise Control for Vehicle)
Sound & Vibration 2023, 57, 73-95. https://doi.org/10.32604/sv.2023.044601
Received 03 August 2023; Accepted 11 October 2023; Issue published 10 November 2023
Abstract
Vehicle interior noise has emerged as a crucial assessment criterion for automotive NVH (Noise, Vibration, and Harshness). When analyzing the NVH performance of the vehicle body, the traditional SEA (Statistical Energy Analysis) simulation technology is usually limited by the accuracy of the material parameters obtained during the acoustic package modeling and the limitations of the application conditions. In order to effectively solve these shortcomings, based on the analysis of the vehicle noise transmission path, a multi-level objective decomposition architecture of the interior noise at the driver’s right ear is established. Combined with the data-driven method, the ResNet neural network model is introduced. The stacked residual blocks avoid the problem of gradient disappearance caused by the increasing network level of the traditional CNN network, thus establishing a higher-precision prediction model. This method alleviates the inherent limitations of traditional SEA simulation design, and enhances the prediction performance of the ResNet model by dynamically adjusting the learning rate. Finally, the proposed method is applied to a specific vehicle model and verified. The results show that the proposed method has significant advantages in prediction accuracy and robustness.Keywords
Bulleted List
| The adjacent upper-level design objective | |
| L | The proposed calculation level in the hierarchical decomposition architecture |
| The total number of layers of the hierarchical decomposition architecture | |
| k | The number of design goals of the level |
| The prediction model | |
| The design variable of the adjacent lower level | |
| I | The number of design variables of the level |
| F(X) | The optimization objective |
| p | The number of design variables of the level |
| q | The number of design variables of the level |
| The optimization objective of the adjacent upper level | |
| g | An inequality constraint condition |
| h | The equality constraint condition |
| X | The design variable |
| The upper limits of the design variable | |
| The i-th channel of the l-layer feature map | |
| The j-th kernel, and | |
| * | The convolutional layer |
| The feature map of the j-th channel of the (L + 1) layer | |
| The output feature after the pooling operation of the 0th feature map | |
| The element | |
| The weight of connecting neurons | |
| The loss of the t-th iteration is expressed | |
| N | The number of samples |
| The true value of the i-th sample | |
| X (Data pre-processing) | The data to be normalized |
| X. min(axis = 0) | A vector of rows consisting of the smallest values in each column |
| X. max(axis = 0) | The row vector consisting of the maximum value in each column |
| max | The maximum value of the interval to be mapped to, which defaults to 1 |
| min | The minimum value of the interval to map to, which defaults to 0 |
| The result of normalization | |
| The optimization constraint cost | |
| The weight | |
| The normalization constants of the optimization constraint cost | |
| The thickness parameter | |
| The area ratio parameter |
The acoustic package of a vehicle plays a critical role in determining the acoustic characteristics within the car. It not only reduces the noise level inside the vehicle but also allows for adjustments in sound quality to meet customer expectations of ride comfort. Consequently, conducting high-precision prediction research on the performance of the acoustic package is imperative for achieving the desired acoustic goals at the vehicle level. The front bulkhead package, floor package, and wheel arch package are major structural components responsible for shielding powertrain and tire noise sources, making them essential elements of the overall acoustic package. The effectiveness of their sound insulation directly impacts the overall Noise, Vibration, and Harshness (NVH) performance of the vehicle [1]. Furthermore, besides the noise reduction and acoustic quality enhancement within the vehicle, a well-designed acoustic package can contribute to vehicle lightweighting and cost reduction. Hence, investigating the enhancement of automotive acoustic package performance holds significant practical and engineering importance.
Previous studies have commonly employed the traditional acoustic finite element method to analyze in-car noise resulting from structural vibrations in automobiles [2]. However, this method is limited in its ability to address low-frequency noise. In recent years, the application of Statistical Energy Analysis (SEA) theory in automotive industry research has gained momentum [3]. SEA allows for the analysis of sound and vibration energy flow in complex structures [4,5]. Furthermore, the utilization of large-scale simulation software, such as VA-One, has contributed to the advancement of mid-to-high frequency noise analysis within vehicles. For instance, Tang et al. [6] focused on vehicle floor structures and proposed two optimization methods, namely increasing floor mat thickness and modifying their structure, to enhance the sound insulation performance of commercial vehicle floors based on SEA modeling principles. The simulation results demonstrated an error of less than 2 dB(A) when compared to experimental results, affirming the accuracy of the SEA method. Similarly, Sun et al. [7] predicted road noise propagation in automobiles, developed a comprehensive vehicle SEA model, and employed insertion loss measurement techniques to rectify predicted noise transmission paths in SEA. The SEA method is simulated based on basic parameters such as density, thickness, and pore structure of acoustic package materials [8,9] to achieve performance prediction and optimization, which shows that its effectiveness in acoustic package engineering is unquestionable. However, obtaining precise values for acoustic package material parameters (e.g., porosity, viscous characteristic length, thermal characteristic length) and characteristic parameters (e.g., modal density, internal loss factor, coupling loss factor) necessary for constructing the SEA model poses challenges [10]. Consequently, the analysis of the NVH performance of the vehicle body based on the simulation model based on the SEA method will not only reduce the research efficiency, but also increase the research cost. The SEA simulation model can only be comparable to the test results under some specific working conditions, and cannot be extended to any working conditions, thus lacking generalization and confidence.
Despite the challenges associated with accurately extracting parameter values for the material and characteristic parameters of the entire vehicle acoustic package through experimental processes, it is relatively easier to obtain underlying parameters of the acoustic package, such as the thickness of each material (e.g., sheet metal, sound insulation pads), the corresponding area proportions, coverage, and sound insulation performance of each material [11]. In recent years, the development of big data and artificial intelligence has highlighted the limitations of traditional simulation methods relying solely on conventional software, particularly in dynamic and complex operating conditions. The flourishing progress of data-driven approaches has significantly contributed to the advancement of acoustic packages. The key advantage of data-driven methods lies in their ability to establish direct mapping relationships between easily attainable underlying parameters of the acoustic package, effectively replacing the intricate derivation relationships between acoustics and structural dynamics [12]. This, in turn, facilitates the forward development of acoustic packages. Notably, researchers such as Haibo Huang have employed the AdaBoost algorithm in combination with BP neural networks, extreme learning machines, and support vector machines to analyze and predict the sound quality of in-cabin noise [13]. Additionally, Wang et al. [14] utilized a neural network method to predict the sound insulation performance of ultrafine glass wool pads. By incorporating input parameters such as thickness, surface density, and resin content of the material, and output parameters such as sound transmission loss at three frequency points (1000, 2000, 4000 Hz), they established a neural network model that achieved the required accuracy in predicting the sound insulation performance of the material. Therefore, the integration of data-driven methods offers significant advantages in accurately predicting the sound insulation performance of acoustic packages. Residual Neural Network (ResNet), an improvement over traditional CNN models [15], has demonstrated successful applications in feature extraction, image recognition, and other domains by alleviating the issue of vanishing gradients resulting from increased network depth [16]. As a result, the RseNet data-driven method can solve the mechanism problem that the material parameters and characteristic parameters of the acoustic package are difficult to accurately extract during the test process, and avoid the limitations of the prediction method of traditional simulation software in dynamic and complex application scenarios. This method provides a reference for the prediction of sound insulation performance of acoustic packages.
Moreover, the relationship between the underlying parameters of the acoustic package and its overall sound insulation performance exhibits a weak correlation. The transmission loss of components or paths associated with the acoustic package holds higher relevance. If an adaptive learning model is directly established without considering the sound insulation characteristics of the package components or paths, the complexity of the correlation between the underlying parameters and the top-level objectives significantly increases. This may lead to underfitting and adversely affect prediction accuracy [17]. This issue arises due to the lack of consideration for the sound and vibration transmission characteristics of the vehicle during the forward development process of the acoustic package [1]. In reality, the performance of the acoustic package is explicit to vehicle occupants, while its causes remain implicit. The acoustic package is not an entirely independent structure; rather, it consists of numerous subsystems and components. Hence, to predict in-cabin noise performance accurately, it is necessary to analyze and examine the key acoustic package systems of the entire vehicle and evaluate the performance of the underlying subsystems across multiple systems. Notably, researchers such as Haibo Huang from Southwest Jiaotong University conducted an analysis and prediction of the sound quality of the automotive front-end system using a multi-objective multi-level architecture [18]. They proposed a objective range optimization design and solution method based on this approach, establishing a comprehensive solution for automotive NVH forward design and fault diagnosis [19]. Furthermore, optimizing the overall vehicle acoustic package by considering its performance, weight, and cost is crucial to reduce in-cabin noise and ensure driver comfort. Therefore, in order to avoid the risk of underfitting and affecting the prediction accuracy by using ResNet network to directly construct the mapping model between the underlying design parameters and the top-level design objective (interior noise). This paper proposes a multi-objective hierarchical decomposition architecture of interior noise from the perspective of noise transfer relationship and multi-level decomposition under different working conditions. Combined with the data-driven method, the multi-objective prediction and optimization of interior noise at different frequencies are carried out, and it is applied to the interior noise at the driver’s right ear of a specific vehicle to verify, which can provide reference for the analysis and prediction of vehicle acoustic package in the future.
For the prediction of vehicle interior noise performance, many nonlinear factors will be generated from the bottom design parameters of the acoustic package to the top-level design objectives. In the research, the disadvantages of the traditional SEA method should be eliminated and the complexity of data-driven mapping should be reduced. The present study introduces two contributions: (1) The utilization of data-driven techniques and hierarchical decomposition structure to analyze the accuracy of acoustic packages in predicting in-vehicle noise under diverse operating conditions. To achieve this, ResNet residual neural networks are employed, and the prediction accuracy is enhanced by implementing a dynamic learning rate. (2) Simultaneous prediction of in-vehicle noise performance at multiple frequencies under different operating conditions. To accomplish this, the paper proposes the DLR-ResNet approach for multi-objective prediction of in-vehicle noise across 17 one-third-octave intervals.
The structure of this paper is as follows: (1) Section 2 provides a multi-level objective decomposition architecture, and establishes a multi-objective prediction and optimization model of vehicle interior noise combined with neural network, then introduces the structure of the ResNet neural network and combines it with the dynamic learning rate method to propose DLR-ResNet with better prediction accuracy. (2) Section 3 outlines the procedure for collecting noise and sound insulation data within the vehicle through testing. (3) Section 4 employs the DLR-ResNet method to predict in-vehicle noise and optimizes its performance using the Latin Hypercube experimental method. (4) Finally, Section 5 concludes the study with a summary based on the preceding results.
Fig. 1 introduces the process of using DLR-ResNet combined with multi-level target method to predict and optimize vehicle interior noise, including three steps, each of which corresponds to Section 2, 3 and 4, respectively.
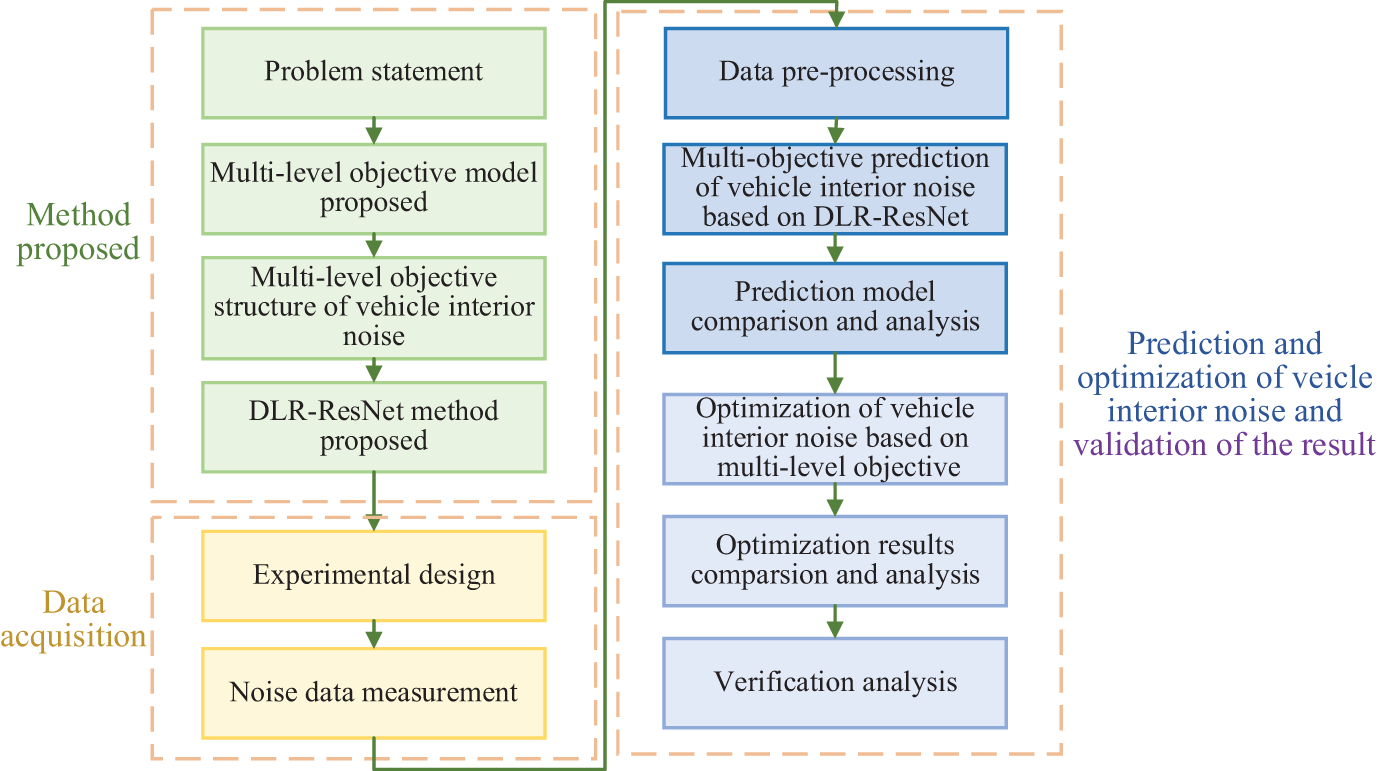
Figure 1: Process of prediction and optimization of the vehicle interior noise
2.1 Multi-Objective Predictive Model for Interior Noise
According to the noise transfer relationship of the acoustic package and the forward development process, the acoustic packages involved in the prediction of interior noise under different working conditions can be divided into system level and flat level. Based on this, the multi-level objective decomposition architecture of the interior noise acoustic package can be established as shown in Fig. 2. Among them, the top-level design objective is the interior noise performance, and the adjacent lower-level design variables connected to it are the Sound Transmission Loss (STL) performance indicators of the main system (front wall system STL, floor system STL, hub package system STL) and the tire noise sources under different working conditions. The adjacent lower-level design variables connected to the main system-level acoustic package are the material composition, block thickness, and block area of the parts. Among them, the tire noise source in the second level refers to the external noise generated by the interaction between the tire and the road surface, the interaction between the tire and the air, and the tire deformation measured by the microphone at the position of the front and rear measurement points of each tire of the car. The multi-level objective decomposition architecture [20,21] shown in Fig. 2 has the following two advantages: 1) The gradient decomposition of design objectives and design variables according to the hierarchy is beneficial to reduce the design difficulty and conforms to the development process of the acoustic package; 2) The existence of the middle layer (system layer) reduces the nonlinearity and complexity of the whole prediction model, which can more easily enhance the nonlinear prediction accuracy. In addition, it is worth mentioning that the multi-level objective decomposition architecture shown in Fig. 2 is not fully connected between the levels, which mainly depends on the overall correlation between the levels and the local coordination within the levels, which is reflected in the forward design process and the acoustic-vibration transfer relationship between the interior noise and the main system acoustic package so that the decoupling or partial decoupling between the design variables of each level can be realized, which further reduces the nonlinearity of complex problems and is conducive to improving the accuracy of analysis and calculation.
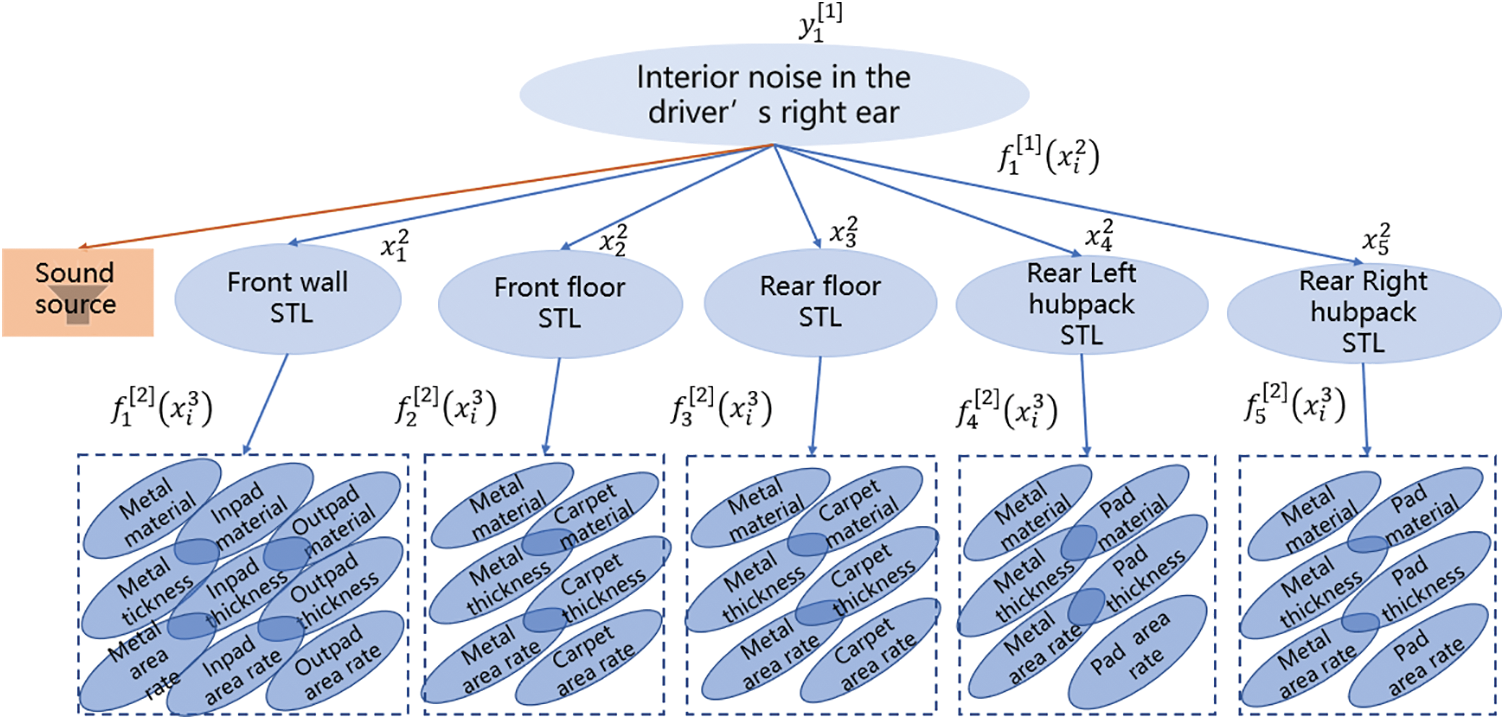
Figure 2: Multi-level objective decomposition architecture diagram of interior noise.
According to the decomposition architecture shown in Fig. 2, it is numerically modeled, that is, a multi-objective prediction model of the acoustic package is established, as shown in Eq. (1):
where,
According to the hierarchical decomposition architecture of Fig. 2, the STL of the front wall system is taken as an example. The third-level bottom design variable
2.2 Multi-Objective Optimization Model for Interior Noise
According to the multi-objective prediction model of interior noise above, it can be seen that interior noise is the prediction goal of this paper, that is, the optimization goal, and the design variable is the material composition, block thickness and block area of adjacent lower-level components connected to the main system-level acoustic package.
According to the decomposition architecture shown in Fig. 2, it is numerically modeled, that is, a multi-objective optimization model of the acoustic package is established, as shown in Eq. (2):
where,
2.3 Introduction to the Structure of the ResNet Network
In this paper, the residual network is proposed to solve the problem that the performance of neural networks decreases with the increase of network depth [22,23]. The typical residual network structure includes the convolution layer, pooling layer, and fully connected layer, and the output type is determined by using the Softmax (for classification) or Linear regression (for regression) function [24] before the output layer. The residual network autonomously detects the shape of data features and calls the activation function for convolution during the learning process through forward propagation, and this paper needs to establish a regression model so that the nonlinear activation function rule is used. The convolutional layer operates as follows:
where,
The pooling layer downsamples the input feature map to reduce the data feature dimension [25]. The commonly used pooling methods are Max pooling and Average pooling, which are respectively expressed as Eqs. (4) and (5):
where,
where,
In addition, to forward propagation, convolutional neural networks also have back propagation characteristics. The backpropagation process updates the model parameters based on the error calculated by the loss function [26]. The loss function is the core index to determine the direction of the network training process. In regression problems, the root mean square error loss is used to evaluate the error and constrain the training process, which is defined as follows:
where,
where,
Practically, as the number of layers deepens during the training process of the CNN network, the problem of network gradient disappearance occurs. Huang et al. [27] proposed the ResNet neural network, the central idea of ResNet is to slow down the gradient vanishing problem in CNN as the number of layers increases through residual blocks and Shortcuts. When the network training reaches saturation, the identity mapping layer (Residual block and Shortcut key) is added immediately afterward, which not only does not lose gradients but also further enhances the performance of the network.
Compared with the CNN network structure, ResNet uses Shortcut connections [27], and the residual block is shown in Fig. 3, and the input value a is directly passed to the final output as the initial result, and the output result is S(a) = K(a) + a, and when K(a) = 0, S(a) = a. Therefore, the ResNet learning objective changes from S(a) to S(a) − a, and the residual result K(a) = S(a) − a. If the residual blocks have different input and output dimensions, a weighted shortcut is introduced to fit the matrix dimensions. The weighted shortcut is defined by the formula S(a) = K(a) + W * a, where W is a 1 × 1 convolutional layer with the same number of filters as the K(a) output. Therefore, the residual result approaching 0 becomes the later training objective, and the accuracy no longer decreases as the network deepens.
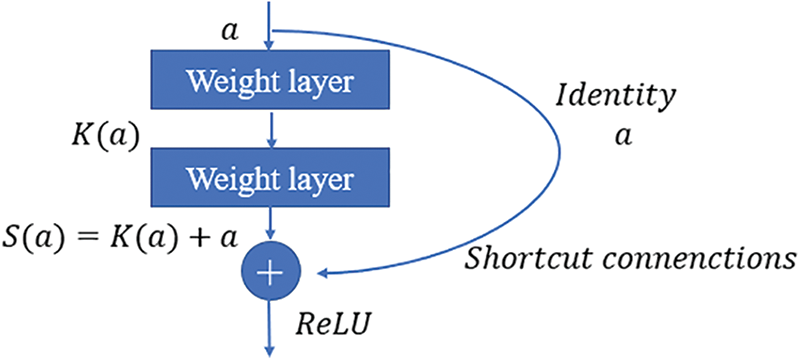
Figure 3: Structure of the residual block
The typical structure of ResNet is shown in Fig. 4, which includes the input layer, residual layer, and output layer. Each residual layer structure contains multiple residual blocks. In this paper, the commonly used residual blocks with the same input and output dimensions are shown in Fig. 4b. In the process of neural network training, adjusting the hyperparameters in the model is one of the most important factors, and the learning rate is one of the most important parameters in the hyperparameters. This paper proposes a method to optimize the model by dynamically adjusting the learning rate, to improve the accuracy of the model and improve the prediction accuracy.
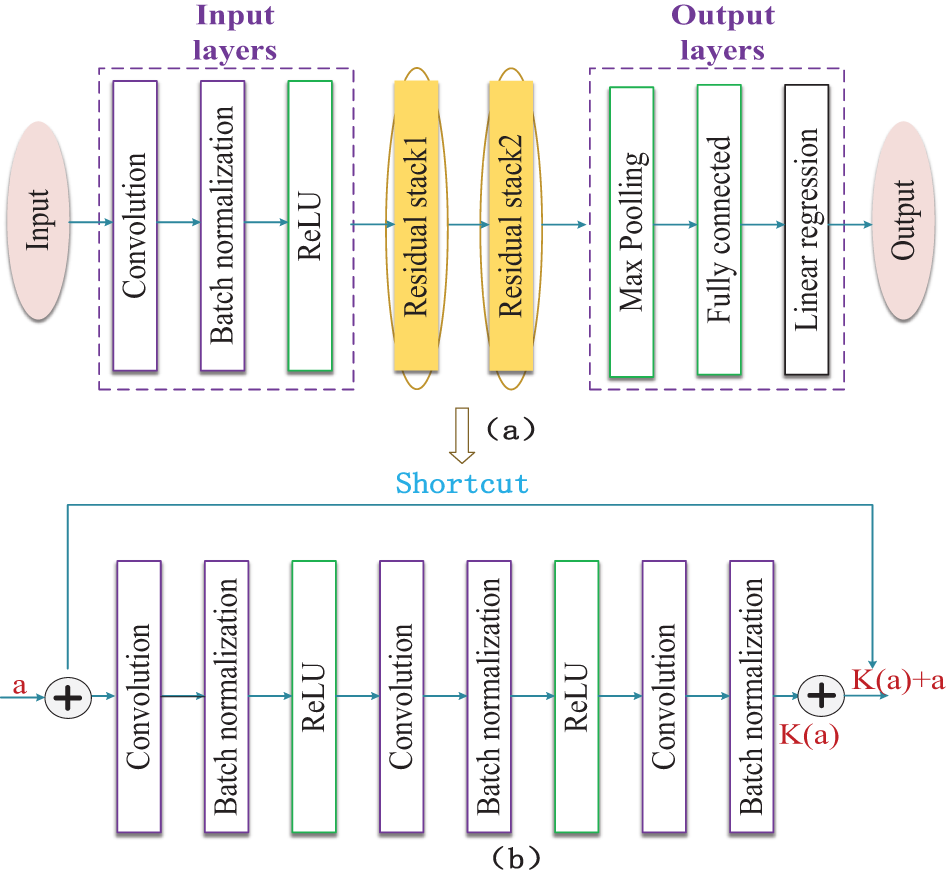
Figure 4: Structure of ResNet. (a) ResNet network with 2-layer residual blocks. (b) A residual block with the same input and output dimensions
Although ResNet deep neural networks have many of the above advantages over CNN networks, ResNet, like any model, has certain weaknesses, such as requiring a large amount of data for training and reasoning, over-reliance on data, and in some cases, ResNet may overfit, resulting in poor generalization. Therefore, this paper weakens the problem of directly using ResNet by combining the ResNet neural network with the multi-level objective decomposition architecture of the acoustic package described in Section 2.1.
The test data for this study was obtained from a real vehicle test conducted on a class A car. To minimize the impact of varying noise environments on the interior noise test data, two specific working conditions were selected: medium speed and high speed of the hub belt vehicle. The interior noise, specifically above 200 Hz, was considered as representative of the overall interior noise. In accordance with the International Society of Automotive Engineers standard SAE J1400 [28], the experiment followed a prescribed test method. A GRAS.32 HF microphone [21,29,30] was positioned to record the interior noise above the driver’s seat on the right side, as well as the interior noise above the left side of the right rear passenger seat (as depicted in Fig. 5). Given that the influence of interior noise is minimal at low speeds, the experiment was conducted at speeds of 60 and 120 km/h. The LMS Scadas data acquisition system [31] was employed, with a sampling rate of 48 kHz and a signal length of 10 s, to record the interior noise. The vehicle data test was conducted in a drum anechoic chamber, while the hub data was collected by driving the vehicle. During the experiment, the rotation speed of the hub (medium speed 60 km/h and high speed 120 km/h) was set to control the rotation speed of the tires, and the microphone was placed at the two measurement points of the four tires at the front and rear of the tires to obtain the tire noise source data at different speeds of the hub car, and a recorder was placed in the cabin.
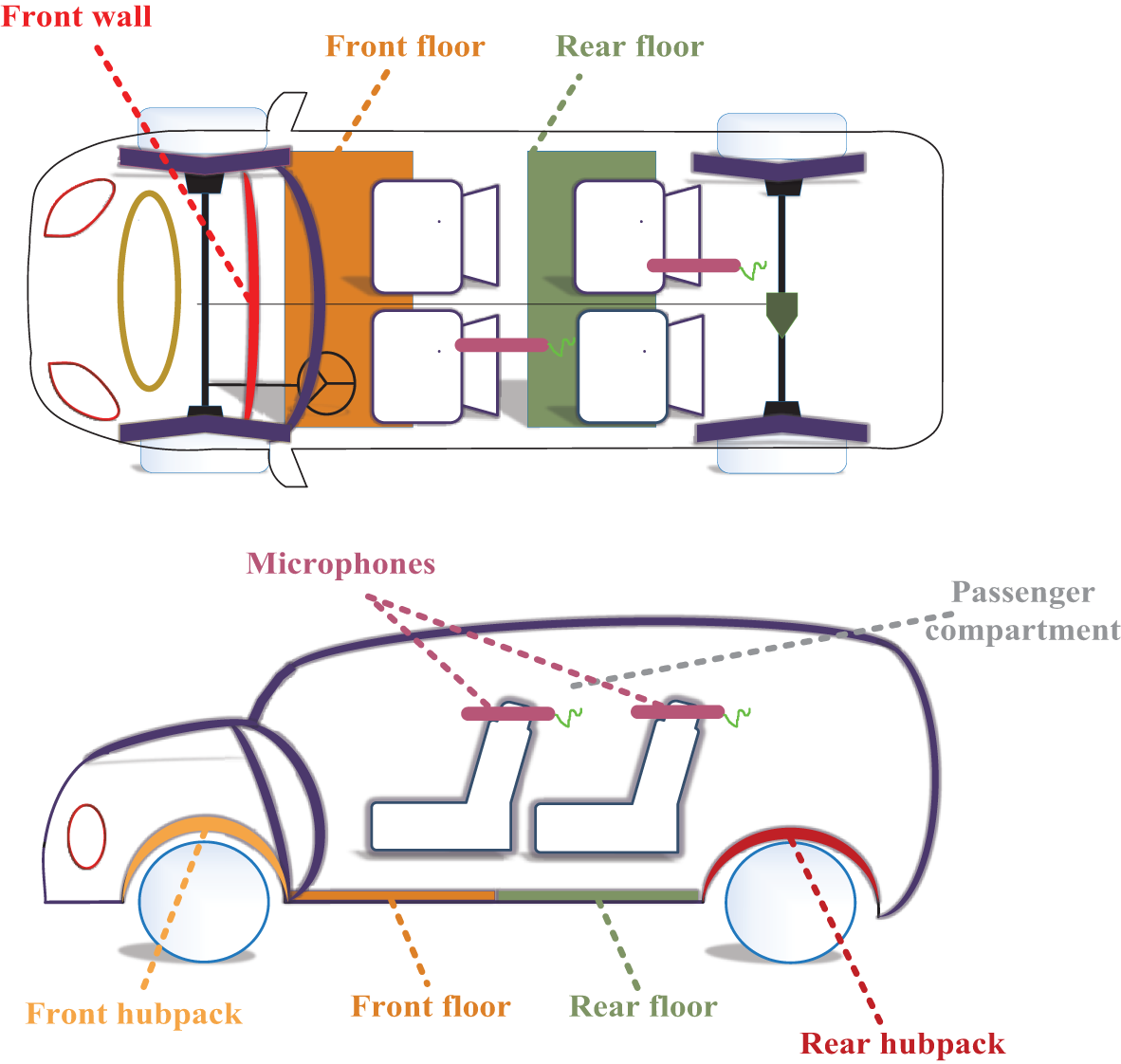
Figure 5: The acoustic package distribution of a class A car
In addition, to collect enough data to establish the mapping model between the acoustic package parameters and the interior noise of the vehicle with different frequencies, different acoustic package schemes are introduced in the test. According to the sound insulation characteristics, the main acoustic package of the test vehicle can be divided into five major systems: front panel, front floor, rear floor, front hub pack, and rear hub pack, as shown in Fig. 5. It is worth noting that the focus of this study is the tire noise from the vehicle chassis; therefore, the STL of the roof system is omitted in the analysis. Fig. 6 shows the interior noise collected at the right ear of the car driver’s seat at the speed of 60 and 120 km/h. It can be concluded from Fig. 6 that the interior noise collected on the driver’s seat has the largest noise peak at 1250 Hz frequency. Therefore, the fourth chapter explains the performance prediction accuracy at 1250 Hz and optimizes the peak.
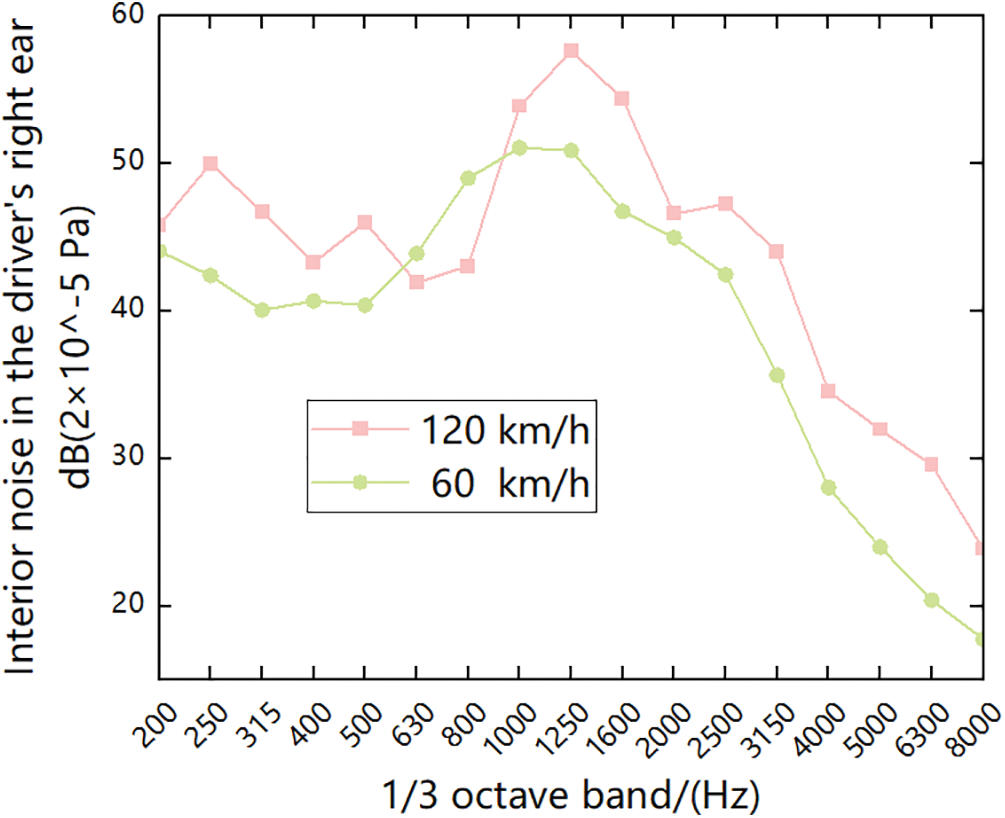
Figure 6: Interior noise under different operating conditions
To further analyze the relationship between the performance of the acoustic package and the sound quality of the interior noise, the STL characteristics of the acoustic package system and components were measured by the reverberation chamber-anechoic chamber combination [32], and the sound insulation transmission performance of the acoustic package material was evaluated [33]. Anechoic chamber is an extremely important experimental place in acoustic experiments and noise tests, its function is to provide a low-noise test environment in free field or semi-free field space, and adopt good sound insulation and seismic isolation devices to avoid interference from the external environment. The reverberation chamber is considered to be a special test chamber for the introduction of diffuse sound field. According to the test method reference to the International Society of Automotive Engineers standard SAE J1400-2017 [28], the test insulation sample is installed on the middle wall of the reverberation chamber-anechoic chamber, and clamps and sealing putty are used to prevent noise leakage. Two dodecahedron spherical sound sources are placed at two diagonal corners of the reverberation chamber to generate white noise with a total sound pressure level [34] of 100 dB. The difference between the sound power of the anechoic chamber and the reverberation chamber is the STL of the tested sample, as shown in Fig. 7. Through the test equipment (Detailed equipment information is shown in Table 1) and test location shown in Fig. 7, 5 STLs of 64 sound insulation systems were collected. Figs. 8a–8e show the sound insulation performance of the main acoustic package systems.
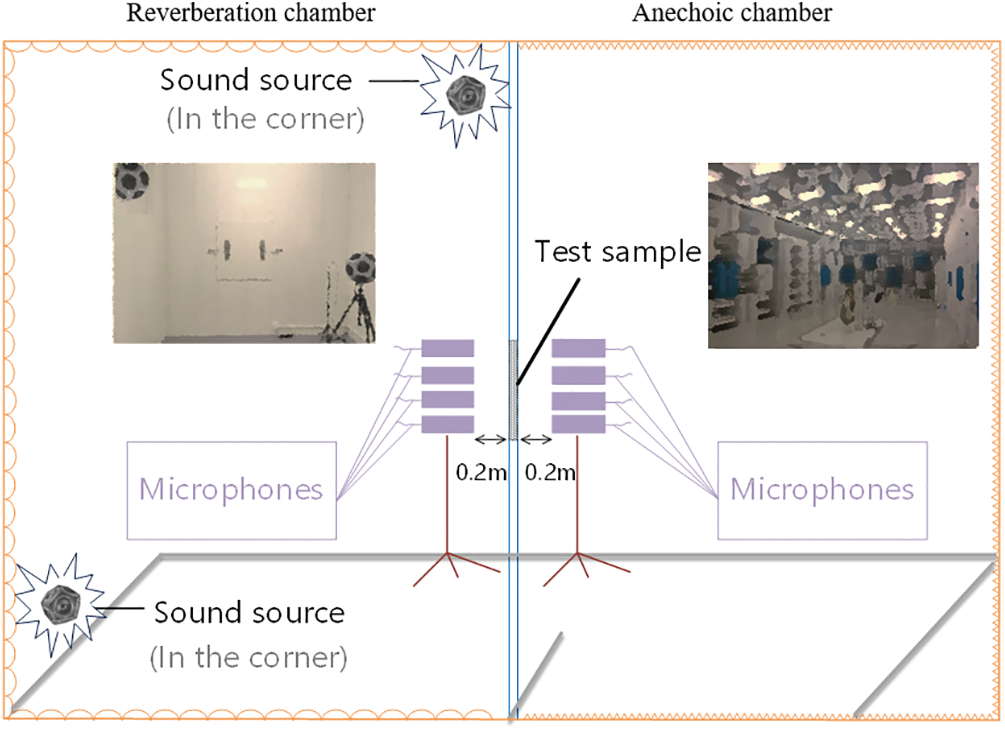
Figure 7: STL acquisition of the main acoustic package system using a reverberation chamber-anechoic chamber

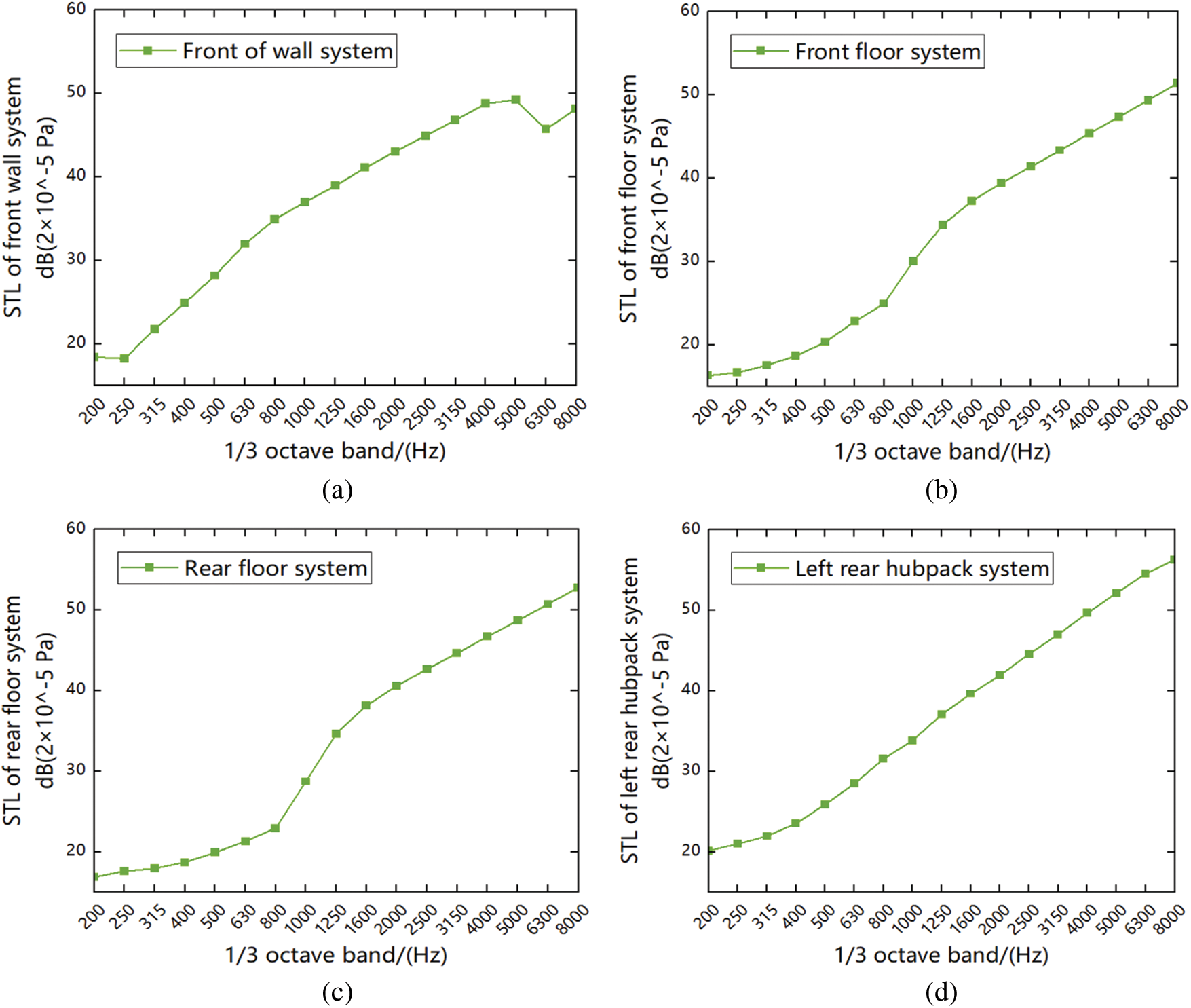
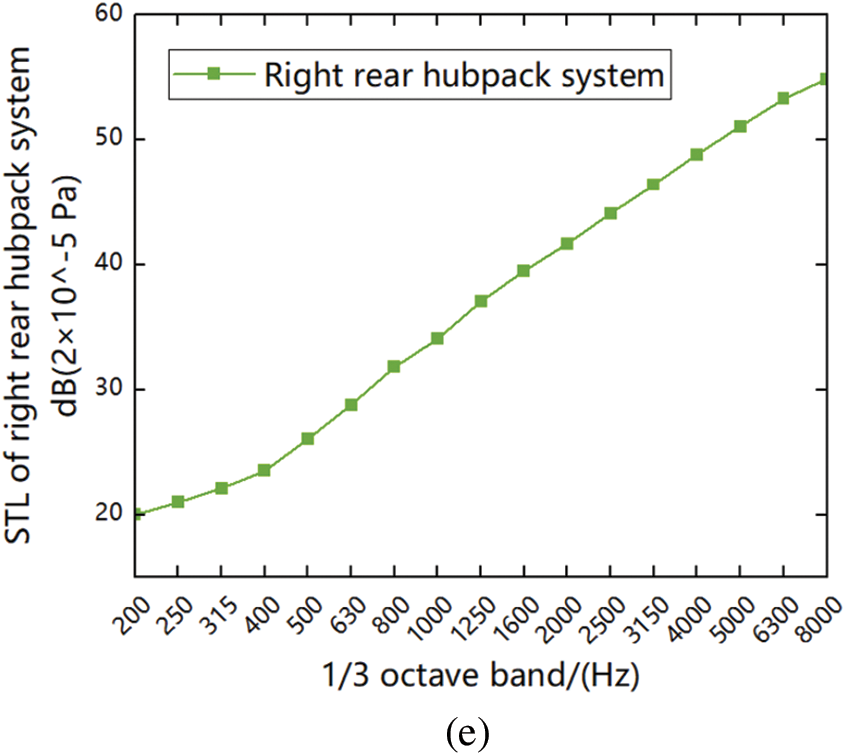
Figure 8: The acoustic insulation performance of the main system of the acoustic package. (a) STL of the front wall system. (b) STL of the front floor system. (c) STL of the rear floor system. (d) STL of the left rear hub pack system. (e) STL of the right rear hub pack system
In addition to the acoustic characteristics of acoustic package systems and components, acoustic materials consisting of acoustic package components are also crucial. Due to the large number of acoustic materials and their many general parameters, automotive companies generally build acoustic database systems for parameter invocation.
As shown in Fig. 8a, the sound insulation of the front wall system increases with the increasing layer of frequency value, but at high frequencies, the sound insulation of the front peripheral system will suddenly decrease due to the anastomosis effect of sheet metal; As shown in Figs. 8b–8c, the sound insulation of the floor system slowly increases with the increase of frequency value at low frequencies, because the material properties of carpets and acoustic insulation pads are different, and carpet materials generally have better sound insulation performance than acoustic insulation mat materials, so that the floor sound insulation amount will increase suddenly at medium frequencies, and when it comes to high frequencies, the increasing trend becomes gentle; As shown in Figs. 8d–8e, the sound insulation of the hub pack system increases linearly with frequency throughout the frequency band.
4 Application and Validation of Method
Before building the prediction model of the sound insulation performance of the vehicle body system, it is necessary to prepare relevant data and preprocess the data. The collection of samples is mainly obtained through relevant sound insulation performance tests. The tire noise source data is obtained through bench tests. The collected samples are cleaned to reduce data noise. After completing the data pre-processing, because the data dimension and value will have a certain impact on the modeling, it is necessary to further normalize the data set [35,36]. Normalization is to convert the eigenvalues of the sample to the same dimension and map the data to the [0, 1] interval. The MinMaxScaler function is used to normalize the input data and denormalize the output results. The expressions are as follows (Eqs. (9) and (10)):
where, X is the data to be normalized, usually a two-dimensional matrix; X.min(axis = 0) is a vector of rows consisting of the smallest values in each column; X.max(axis = 0) is the row vector consisting of the maximum value in each column; max is the maximum value of the interval to be mapped to, which defaults to 1; min is the minimum value of the interval to map to, which defaults to 0;
The software used for this article is Python 3.9, the deep learning library used is Pytorch 1.10.2, and the AMD Ryzen 5 4500U with Radeon Graphics and 16 G memory is configured.
4.2 Prediction of Vehicle Noise Based on ResNet Network
Through the experimental test, the accurate interior noise data under different working conditions, the transmission loss of the main system acoustic package system, and the underlying parameters obtained from the database are obtained. Based on the improvement of the data samples, the ResNet method using the dynamic learning rate is introduced and combined with the multi-level objective decomposition architecture to establish an effective acoustic package forward development model suitable for engineering applications. For the sound insulation performance objective, when constructing the third-level to the second-level model, a plate-level basic data prediction system-level transmission loss prediction model is established. The thickness area ratio of sheet metal and sound package sound insulation pad materials and the sound insulation corresponding to 17 one-third frequency doubling points of each thickness are used as inputs, and the main system-level transmission loss corresponding to each plate level is used as output. When constructing the second-level to the first-level model, the main system sound package and tire noise source are used as the input of the model, and the interior noise (the interior noise in the driver’s right ear) is used as the output of the model. In the test results, 400 groups of samples were randomly selected as the training set, the remaining 100 groups were used as the test set for learning, and the root mean square error (RMSE) index is used to test the accuracy of the model, the root mean square error formula is visible (8), the closer the RMSE index is to 0, the higher the accuracy of the model, the smaller the error of the predicted value, and the generalization of the model is strong. For the adjacent levels in the multi-level objective decomposition architecture, the two-layer DLR-ResNet network is selected as the sub-model for modeling. The number of input layer nodes of each sub-model is the input data dimension, and the output layer is the result after a full connection.
After network learning, the prediction results and model accuracy at 17 one-third frequencies can be obtained. As shown in Figs. 9 and 10, the prediction results and statistical errors of models f1[1] and f1[2] in the training set and test set are shown, respectively. Among them, the maximum relative error of the above model is 4.52% of f1[1] and 4.74% of f1[1] in the training set and the test set, respectively. Table 2 counts the accuracy of the training set and the test set of each sub-model in the multi-level model under the frequency of 1250 Hz objective, and uses the root mean square error RMSE of frequency to evaluate. Fig. 11 compares the accuracy of the second-level to top-level prediction models under different frequency objectives using the CNN network, traditional ResNet network, and DLR-ResNet network proposed in this paper. Firstly, the results of Table 2 show that the RMSE of the first-level model is lower than 0.05 at the frequency of 1250 Hz, and the RMSE value of f1[1] is less than 0.03. At the same time, the RMSE of the second-level model is not higher than 0.04. Secondly, the comparison results of Fig. 10 show that the proposed method has higher accuracy, and the introduced DLR-ResNet method is effective and generalized in the multi-objective prediction of vehicle interior noise.
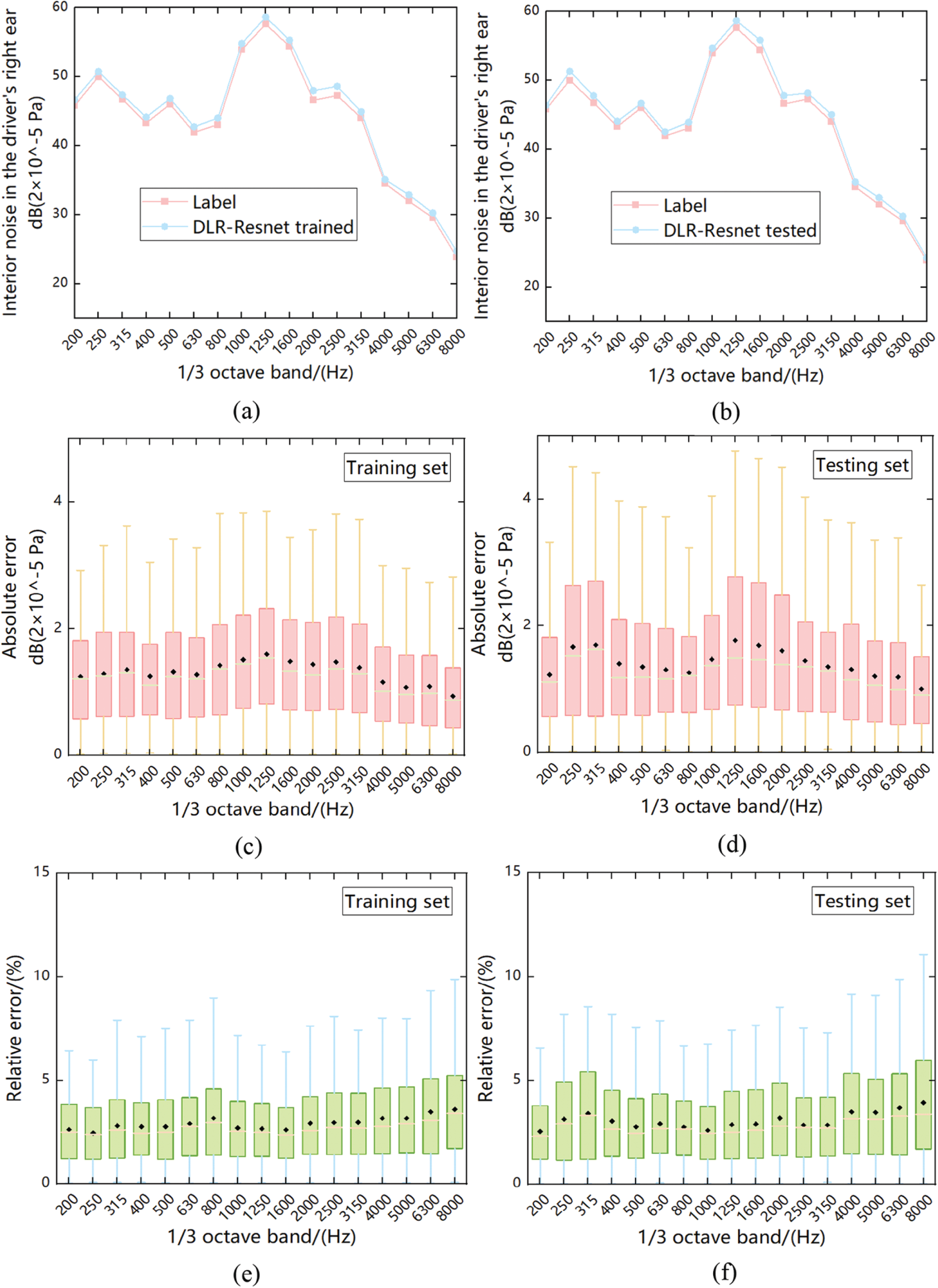
Figure 9: Trained and tested results of model f1[1] (Interior noise in the driver’s right ear). (a) Comparison of the in-vehicle noise training results with the curve of the training set label. (b) Comparison of the in-vehicle noise test results with the curve of the test set label. (c) Box plot of absolute error of training set. (d) Box plot of the absolute error of the test set. (e) Box plot of relative error of training set. (f) Box plot of relative error of test set
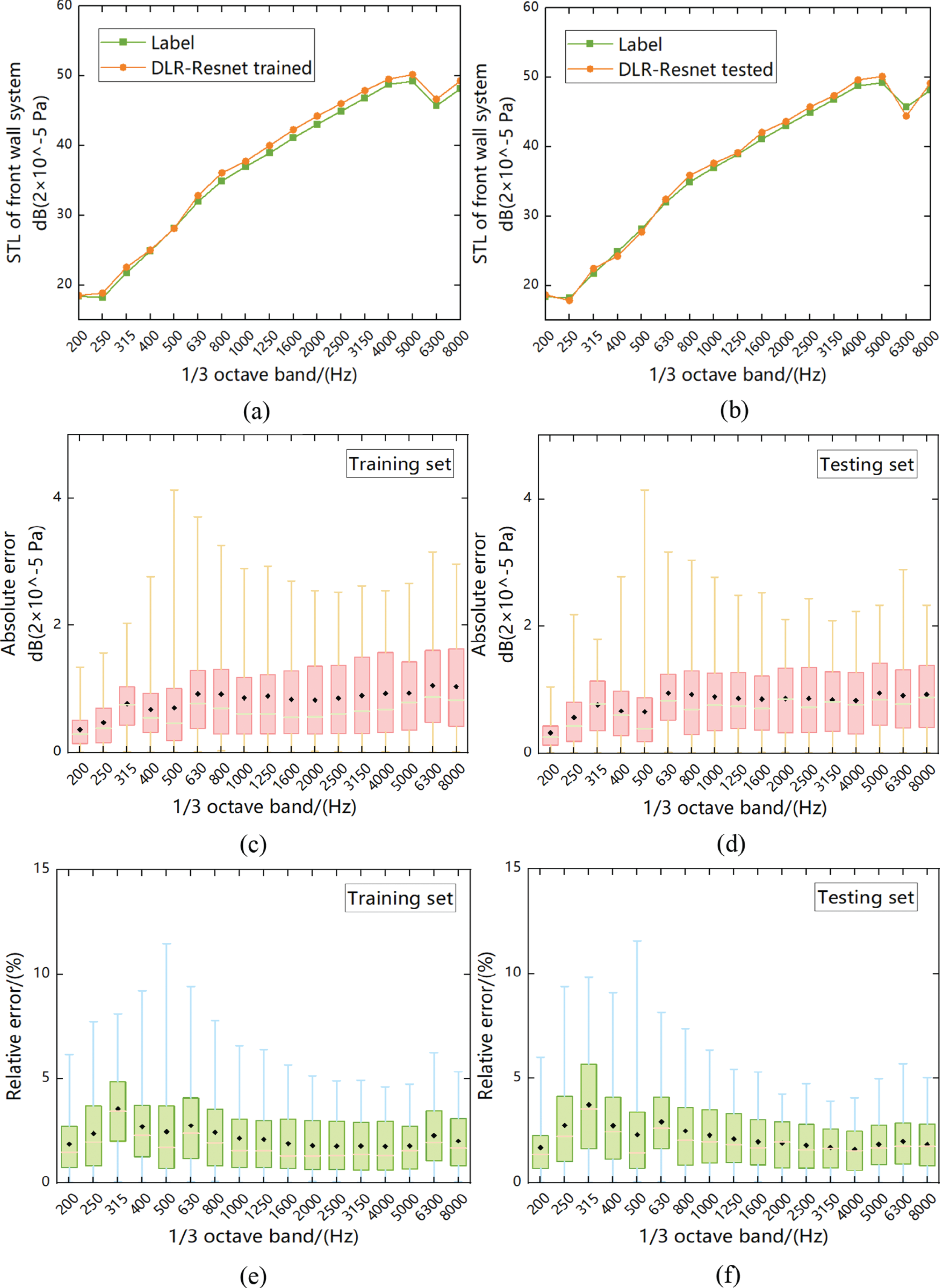
Figure 10: Trained and tested results of model f1[2] (Front wall system). (a) Comparison of the training results of the STL of the front wall system with the curves of the training set labels. (b) Comparison of test results of the STL of the front wall system with the curve of the test set label. (c) Box plot of absolute error of the training set. (d) Box plot of absolute error of the test set. (e) Box plot of the relative error of the training set. (f) Box plot of the relative error of the test set

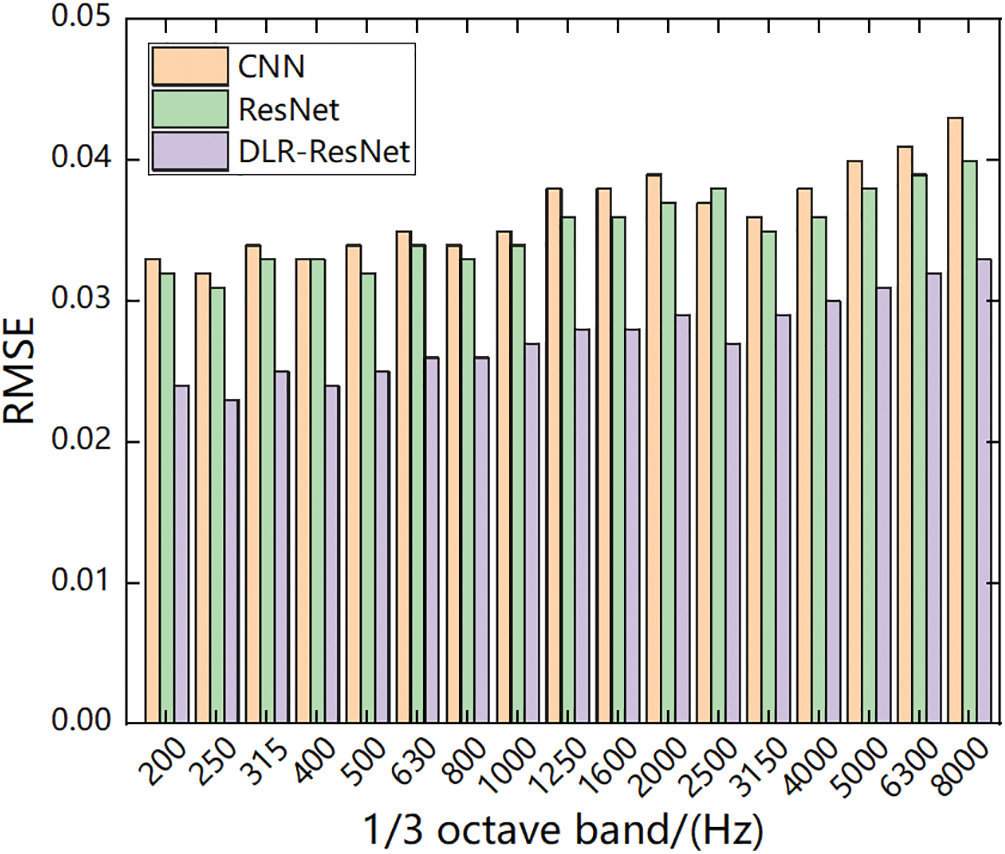
Figure 11: Comparison of prediction accuracy of the three methods (RMSE of the second-first level)
4.3 Optimization and Verification of Acoustic Package Solutions
In the previous chapter, the multi-objective prediction of vehicle interior noise has been analyzed, especially the model accuracy at 1250 Hz is explained. Therefore, both local accuracy and overall accuracy show that DLR-ResNet residual network has more prominent advantages in the performance prediction of vehicle interior noise, and has better robustness and generalization. Therefore, based on the multi-level objective decomposition architecture of vehicle interior noise and the DLR-ResNet model, the multi-objective optimization of the sound pressure level of vehicle interior noise at 17 one-third octaves is carried out, in which weight and cost are taken as constraints. Finally, an example is given according to the optimization results of vehicle interior noise peak at 1250 Hz proposed in Section 3.
Combined with the economic principle of actual acoustic package development, the weighted constraint is introduced to set different weight coefficients for cost and weight. In this study, to make the optimization results more universal, the weight coefficients of cost and weight are designed to be 0.5 and 0.5. The design variables are all five main systems: the front wall system, the front floor system, the rear floor system, the left rear hub package system, and the right rear hub package system. The block thickness and the area ratio of different thicknesses of each component of the front wall system, the front floor system, the rear floor system, the left rear hub package system, and the right rear hub package system. According to the engineering feasibility, the design space is in the range of ±20% of the variables based on the original value. There are two constraints: 1) The maximum thickness of the acoustic package of each main system is not greater than its maximum thickness in the original state, and 2) The sum of the area ratios corresponding to different thicknesses of each component is 100%. The established optimization model is shown in Eq. (11):
where,
The Latin hypercube algorithm has the advantages of good scalability and non-degeneration [37,38]. Therefore, the Latin hypercube experimental design is used for sampling, 15 factors are designed, and 500 levels are generated. The Latin hypercube experimental design is solved as Eq. (11). The optimized parameter results are shown in Table 3, and the multi-objective prediction results and measured results obtained according to the optimized parameters are shown in Table 4.


According to Table 4, the sound pressure level [39], cost, and weight of the vehicle interior noise in the original state at 1250 Hz are 59.6 dB, 502 yuan, and 251 kg, respectively. The sound pressure level of the vehicle interior noise optimized based on the multi-level architecture model is reduced by 2.4 dB. To verify the optimization effect, the main system acoustic package corresponding to the interior noise of the vehicle is adjusted according to the optimization state, and verified in the reverberation chamber-anechoic chamber. The measured interior noise is 57.4 dB, the cost is 489 yuan, and the weight is 240 kg. The predicted results are close to the measured results. The relative error of the two performances is 0.8%, which is an allowable error range in the actual project. Therefore, the accuracy and effectiveness of the proposed method are verified.
In order to reduce the problem of overfitting or over-reliance on data reasoning caused by neural networks, this section builds a multi-level objective decomposition architecture, and with the support of this mechanism, ResNet neural networks are introduced to make multi-objective prediction of top-level in-vehicle noise at different frequencies, and compare with CNN networks and the prediction results of DLR-ResNet networks proposed in this paper. The results show that the DLR-ResNet network proposed in this paper has the advantages of higher accuracy and generalization for multi-objective prediction of acoustic packets, and the DLR-ResNet network model is selected as the optimization tool for acoustic packets, and the Latin hypercube experimental design is used as a means of multi-objective optimization, and the optimization results are close to the measured results, which verifies the accuracy and effectiveness of the proposed method.
This paper presents the DLR-ResNet approach, which aims to analyze the in-cabin noise performance in automobiles across 17 one-third octave bands. By considering the noise transmission relationship and hierarchical objective decomposition, a multi-level objective prediction and optimization method for the acoustic package is proposed and validated using an actual vehicle model. The DLR-ResNet method achieves a prediction accuracy of over 98% for the interior noise performance at each frequency, surpassing both the basic CNN model and the simple ResNet model. Furthermore, the study constructs a multi-level architecture model for vehicle interior noise, reducing the nonlinearity and complexity of the overall prediction model. This approach also mitigates the limitations associated with model training caused by excessive design parameters and parameter redundancy. The optimization results based on this model closely align with the measured results, with a relative error of only 0.8% for the two performance objectives. The optimized measured results indicate improvements of 3.6%, 2.6%, and 4.4% in vehicle interior noise performance, cost, and weight, respectively, compared to the original values. These findings confirm the effectiveness and accuracy of the proposed method.
The prediction and optimization methods proposed in this paper for the multi-objective acoustic package performance research can provide some reference for subsequent scholars. However, this paper only studies the sound insulation performance and interior noise of the body system for a certain A-class model, and it is necessary to further explore and test more models in the next research to improve the migration ability and generalization ability of the model. However, the optimization of acoustic package only adopts the method of experimental design, which has certain limitations, and there may be situations where the optimization result is not optimal, so in the next step of research, multi-objective intelligent optimization algorithm can be used to explore, such as multi-objective particle swarm optimization algorithm, multi-objective genetic algorithm, NSGA-II algorithm, etc., and better combine the intelligent optimization algorithm with the machine learning prediction model.
Acknowledgement: The authors would like to acknowledge the support from the Sichuan Provincial Natural Science Foundation and the facilities provided by the Institute of Energy and Power Research at Southwest Jiaotong University for the experimental research.
Funding Statement: This research was funded by the SWJTU Science and Technology Innovation Project, Grant Number 2682022CX008; and the Natural Science Foundation of Sichuan Province, Grant Numbers 2022NSFSC1892, 2023NSFSC0395.
Author Contributions: The authors confirm contribution to the paper as follows: conceptualization, writing-original draft: Yunru Wu; resources, supervision, funding acquisition: Haibo Huang, Mingliang Yang; methodology: Xiangbo Liu; writing-review and editing: Weiping Ding. All authors reviewed the results and approved the final version of the manuscript.
Availability of Data and Materials: The data used to support the findings of this study are available from the corresponding author upon request.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
References
1. Pang, J. (2018). Noise and vibration control in automotive bodies. China: Machine Press. https://doi.org/10.1002/9781119515500 [Google Scholar] [CrossRef]
2. Munawir, A., Putra, A., Prasetiyo, I., Mohamad, W., Herawan, S. G. (2021). Corrected statistical energy analysis model in a non-reverberant acoustic space. Sound & Vibration, 55(3), 203–219. https://doi.org/10.32604/sv.2021.015938 [Google Scholar] [CrossRef]
3. Lee, H. R., Kim, H. Y., Jeon, J. H., Kang, Y. J. (2019). Application of global sensitivity analysis to statistical energy analysis: Vehicle model development and transmission path contribution. Applied Acoustics, 146, 368–389. https://doi.org/10.1016/J.APACOUST.2018.11.023 [Google Scholar] [CrossRef]
4. Fan, D., Dai, P., Yang, M., Jia, W., Jia, X. et al. (2022). Research on maglev vibration isolation technology for vehicle road noise control. SAE International Journal of Vehicle Dynamics, Stability, and NVH, 6(3), 233–245. https://doi.org/10.4271/10-06-03-0016 [Google Scholar] [CrossRef]
5. Bergen, B., Schaefer, N., Rostyne, K. V., Keppens, T. (2018). Vehicle acoustic performance analysis towards effective sound package design in mid-frequency. SAE Technical Paper Series, 2018-01-1495. https://doi.org/10.4271/2018-01-1495 [Google Scholar] [CrossRef]
6. Tang, R., Tong, Z., Li, S., Huang, L. (2020). Prediction and analysis of high-frequency noise in heavy-duty commercial vehicle interior. Mechanical Design and Manufacturing, (1), 205–208 (In Chinese). https://doi.org/10.19356/j.cnki.1001-3997.2020.01.051 [Google Scholar] [CrossRef]
7. Sun, Y., Yan, Z., Hao, Y. (2019). Prediction and control of interior noise of monorail train based on VA one. Electromechanical Information, 2019(3), 64–65. https://doi.org/10.19514/j.cnki.cn32-1628/tm.2019.03.037 [Google Scholar] [CrossRef]
8. Zong, D., Bai, W., Yin, X., Yu, J., Zhang, S. et al. (2023). Gradient pore structured elastic ceramic nanofiber aerogels with cellulose nanonets for noise absorption. Advanced Functional Materials, 33(31), 2301870. https://doi.org/10.1002/adfm.202301870 [Google Scholar] [CrossRef]
9. Zong, D., Cao, L., Yin, X. (2021). Flexible ceramic nanofibrous sponges with hierarchically entangled graphene networks enable noise absorption. Nature Communications, 12, 6599. https://doi.org/10.1038/s41467-021-26890-9 [Google Scholar] [PubMed] [CrossRef]
10. Huang, H., Huang, X., Ding, W., Yang, M., Fan, D. et al. (2022). Uncertainty optimization of pure electric vehicle interior tire/road noise comfort based on data-driven. Mechanical Systems and Signal Processing, 165, 108300. https://doi.org/10.1016/J.YMSSP.2021.108300 [Google Scholar] [CrossRef]
11. He, B. (2017). Acoustic design, optimization, and experimental study of sound barriers for high-speed railways (Ph.D. Thesis). Southwest Jiaotong University, China. [Google Scholar]
12. Dai, H., Jin, M., Chen, X., Li, N., Tu, Z. et al. (2022). A review of data-driven application adaptation techniques. Journal of Computer Research and Development, (11), 2549–2568. https://doi.org/10.7544/issn1000-1239.20210221 [Google Scholar] [CrossRef]
13. Huang, H., Huang, X., Ding, W., Zhang, S., Pang, J. (2023). Optimization of electric vehicle sound package based on LSTM with an adaptive learning rate forest and multiple-level multiple-object method. Mechanical Systems and Signal Processing, 187, 109932. https://doi.org/10.1016/j.ymssp.2022.109932 [Google Scholar] [CrossRef]
14. Wang, F., Chen, Z., Wu, C., Yang, Y. (2019). Prediction on sound insulation properties of ultrafine glass wool mats with artificial neural networks. Applied Acoustics, 146, 164–171. https://doi.org/10.1016/J.APACOUST.2018.11.018 [Google Scholar] [CrossRef]
15. Kang, X., Kun, H., Li, R. (2023). Acoustic emission recognition based on a three-streams neural network with attention. Computer Systems Science and Engineering, 46(3), 2963–2974. https://doi.org/10.32604/csse.2023.025908 [Google Scholar] [CrossRef]
16. Mohamed, A., Dahl, G. E., Hinton, G. E. (2012). Acoustic modeling using deep belief networks. IEEE Transactions on Audio, Speech, and Language Processing, 20, 14–22. https://doi.org/10.1109/TASL.2011.2109382 [Google Scholar] [CrossRef]
17. Huang, H., Wu, J., Lim, T., Yang, M., Ding, W. (2021). Pure electric vehicle nonstationary interior sound quality prediction based on deep CNNs with an adaptable learning rate tree. Mechanical Systems and Signal Processing, 148, 107170. https://doi.org/10.1016/j.ymssp.2020.107170 [Google Scholar] [CrossRef]
18. Huang, H., Zheng, Z., Zhang, S., Wu, Y., Yang, M. et al. (2023). Acoustic package optimization for automotive front bumper with multi-level objectives. Journal of Southwest Jiaotong University, (2), 287–295. https://doi.org/10.3969/j.issn.0258-2724.20211086 [Google Scholar] [CrossRef]
19. Wang, Z., Zeng, J., Shi, Y., Ling, G. (2023). MBR membrane fouling diagnosis based on improved residual neural network. Journal of Environmental Chemical Engineering, 11(3), 109742. https://doi.org/10.1016/j.jece.2023.109742 [Google Scholar] [CrossRef]
20. Qi, B., Zhang, G., Yu, L. (2023). Blind image quality assessment based on deep residual regression network and image block pre-confidence. Journal of Southwest Normal University (Natural Science Edition), 48(7), 21–30 (In Chinese). https://doi.org/10.13718/j.cnki.xsxb.2023.07.003 [Google Scholar] [CrossRef]
21. Huang, H., Lim, T. C., Wu, J., Ding, W., Pang, J. (2023). Multiobjective prediction and optimization of pure electric vehicle tire/road airborne noise sound quality based on a knowledge- and data-driven method. Mechanical Systems and Signal Processing, 197, 110361. https://doi.org/10.1016/j.ymssp.2023.110361 [Google Scholar] [CrossRef]
22. Edwin Selva Rex, C. R., Annrose, J., Jenifer Jose, J. (2022). Comparative analysis of deep convolution neural network models on small scale datasets. Optik, 271, 170238–170238. https://doi.org/10.1016/j.ijleo.2022.170238 [Google Scholar] [CrossRef]
23. Tai, Y., Yang, J., Liu, X. (2017). Image super-resolution via deep recursive residual network. 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), pp. 2790–2798. Honolulu, HI, USA. https://doi.org/10.1109/CVPR.2017.298 [Google Scholar] [CrossRef]
24. Zhou, N., Ouyang, X. (2021). Convolutional neural network development. Journal of Liaoning University of Science and Technology, 44(5), 349–356 (In Chinese). https://doi.org/10.13988/j.ustl.2021.05.004 [Google Scholar] [CrossRef]
25. Lu, X., Zhang, S., Song, Y., Wang, C., Li, W. et al. (2021). Parameter learning of convolutional neural network based on deep learning. Journal of Bohai University (Natural Science Edition), 42(4), 369–375 (In Chinese). https://doi.org/10.13831/j.cnki.issn.1673-0569.2021.04.002 [Google Scholar] [CrossRef]
26. Huang, H., Huang, X., Ding, W., Yang, M., Yu, X. et al. (2023). Vehicle vibro-acoustical comfort optimization using a multi-objective interval analysis method. Expert Systems with Applications, 213, 119001.https://doi.org/10.1016/j.eswa.2022.119001 [Google Scholar] [CrossRef]
27. Huang, H., Li, R., Huang, X., Yang, M., Ding, W. (2016). Prediction of interior noise sound quality based on adaboost algorithm. Automotive Engineering, 38(9), 1120–1125. https://doi.org/10.19562/j.chinasae.qcgc.2016.09.013 [Google Scholar] [CrossRef]
28. SAE J1400-2017: Laboratory Measurement of the Airborne Sound Barrier Performance (2017). SAE International. [Google Scholar]
29. Xu, Z., Jia, Z., Wan, W., Zeng, M., Qiu, Y. (2023). A study on hybrid active noise control system combined with remote microphone technique. Applied Acoustics, (205), 109296. https://doi.org/10.1016/j.apacoust.2023.109296 [Google Scholar] [CrossRef]
30. Biesheuvel, J., Tuinstra, M., de Santana, L. D., Venner, C. H. (2022). Acoustic lucky imaging for microphone phased arrays. Journal of Sound and Vibration, (544), 117357 (In Chinese). https://doi.org/10.1016/j.jsv.2022.117357 [Google Scholar] [CrossRef]
31. Fritz, A., Payer, J., Fuchs, A., Lieschnegg, M. (2014). Reliable noise and vibration data acquisition and processing for automotive applications. IEEE International Instrumentation and Measurement Technology Conference (I2MTC), pp. 590–594. Montevideo, Uruguay. https://doi.org/10.1109/I2MTC.2014.6860812 [Google Scholar] [CrossRef]
32. Zhang, Z., Zhao, T., Zeng, H., Liu, T., Li, W. et al. (2023). NVH performance test bench sound field characteristics test analysis. Measurement and Test Technology, 50(2), 23–26. https://doi.org/10.15988/j.cnki.1004-6941.2023.2.006 [Google Scholar] [CrossRef]
33. Thottathil Varghese, J., Thomas, S., Herbert, J., Preno Koshy, C., Venugopal, A. (2022). Airborne acoustic transmission and terrain topography at SAINTGITS amphitheatre: An analysis of outdoor auditory perception and comparison of contour plots. Sound & Vibration, 56(3), 255–274. https://doi.org/10.32604/sv.2022.016180 [Google Scholar] [CrossRef]
34. Khusnutdinov, A. N., Nuriev, M. G. (2022). The sound pressure level meter. International Russian Automation Conference (RusAutoCon), pp. 63–68. Sochi, Russian Federation. https://doi.org/10.1109/RusAutoCon54946.2022.9896267 [Google Scholar] [CrossRef]
35. Sun, Y., Liu, Y. (2022). Model-data-driven P-wave impedance inversion using ResNets and the normalized zero-lag cross-correlation objective function. Petroleum Science, 19(6), 2711–2719. https://doi.org/10.1016/j.petsci.2022.09.008 [Google Scholar] [CrossRef]
36. Maharana, K., Mondal, S. K., Nemade, B. (2022). A review: Data pre-processing and data augmentation techniques. Global Transitions Proceedings, 3(1), 91–99. https://doi.org/10.1016/j.gltp.2022.04.020 [Google Scholar] [CrossRef]
37. Du, L., Lu, L., Sun, W., Song, X. (2021). A Latin hypercube point selection strategy for constrained space. Mechanical Design and Manufacturing, 2021(8), 43–47. https://doi.org/10.19356/j.cnki.1001-3997.2021.08.011 [Google Scholar] [CrossRef]
38. Shang, X., Chao, T., Ma, P., Yang, M. (2020). An efficient local search-based genetic algorithm for constructing optimal Latin hypercube design. Engineering Optimization, 52, 271–287. https://doi.org/10.1080/0305215X.2019.1584618 [Google Scholar] [CrossRef]
39. Abd-elbasseer, M., Mohamed, H. K. (2021). Performance evaluation and effectiveness of the reverberation room. Sound & Vibration, 55(1), 43–55. https://doi.org/10.32604/sv.2021.09417 [Google Scholar] [CrossRef]
Cite This Article
 Copyright © 2023 The Author(s). Published by Tech Science Press.
Copyright © 2023 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper View Full Text
View Full Text Download PDF
Download PDF Downloads
Downloads
 Citation Tools
Citation Tools