Numerical Investigation on Vibration Performance of Flexible Plates Actuated by Pneumatic Artificial Muscle

1  Introduction

The fiber-matrix composites [1–3] have been widely used for aircraft, automobile, and other applications due to their high strength/weight ratios, superior fatigue resistance, and flexibility compared to metal materials. Many structural composite plates [4] or shells are typically flexible and possess high vibration sensitivity. Many applications require that these flexible composite plates serve in a vibration condition. The effective vibration control [5] for suppressing the oscillations of these structures is a pronounced requirement of composite materials. Compared to traditional metallic materials such as steel since composites have a lower density in order to meet strict stability, safety, and comfort requirements. The finite element (FE) methods in structural dynamic analysis play an important role and have high relevance to both validate the theoretical models and guide the structural design for vibration control. Moreover, it can highlight and discover complicated behaviors of dynamic systems [6] and structures.

Generally, it is a valid way to reduce vibrations by introducing additional damping into the designed system, such as employing seismic isolation materials [7] and adding physical damping devices. This approach is named passive vibration control (or redesign) which is a greatly developed subject area for linear vibration control [8]. Passive vibration control is preferred in practice which can be built into the system and eliminates any issues with stability or robustness as there is no control element [8]. For this merit, in face of more and more requirements of lightweight and intelligence, passive vibration control becomes an ineffective choice in the process of product design. Then whereupon active vibration control [9] is necessary and desirable to meet the requirements of lightweight and intelligence for vibration disturbances since it does not require the increase of mass due to dampeners, stiffeners and absorbers. In this paper, pneumatic artificial muscle (PAM) was introduced into a designed system to achieve active vibration control. In recent decades, PAM has received much attention in the fields of bionics [10,11], medical care [12], morphing structures [13,14], and welfare, etc., due to its significant advantages of low cost, quick response time and high power/weight and power/volume ratios.

Belalia [15] investigated the vibration behaviors of functionally graded sandwich elliptic plates using a curved hierarchical finite element. In Belalia’s study, the motion equation of bi-FGM sandwich elliptic plate is obtained using Lagrange’s equation, converted from time domain to frequency domain by means of the harmonic balance method and solved iteratively using the linearized updated mode method. Belalia also compared the model results from his proposed model with those of the literature, there was a good agreement. Akhavan et al. [16] studied the natural frequencies and vibrational mode shapes of variable stiffness composite laminate (VSCL) plates with curvilinear fibers. They found the use of curvilinear fibers instead of the traditional straight fibers introduces a greater degree of flexibility, which can be used to adjust frequencies and mode shapes. Ribeiro et al. [17] also investigated and analyzed non-linear vibrations of variable stiffness composite laminated plates based on numerical experiments and a new p-version finite element with hierarchic basis functions, which follows first order shear deformation theory and considers geometrical non-linearity. In Ribeiro and Akhavan’s study, it can be found that the variation of the fiber orientation can lead to significant differences in the amplitudes of the non-linear response.

The phase-field method [18–20] for simulation was carried out to analyze the free vibration [21] and buckling behaviors [22] of crack received plates. The results of the free vibration of cracked plate showed that when the plate thickness increases, the crack length decreases and the inclined crack angle increases then the frequencies of the cracked plate increase. Dhanda et al. [23] focused on MEMS-based vibration measuring accelerometers, they found that the contact type vibration sensors have the unique advantage of being very small, low cost, low power, less weighing, and easily accommodatable in electronics. Xu et al. [24] established an accurate series solution for the longitudinal vibration analysis of an elastically coupled nanorods system, in which artificial springs are introduced to simulate such general coupling and boundary conditions. Hu [25] established a theoretical multi-degree-of-freedom (MDOF) model and proposed a novel method of vibration mitigation based on the vibration characteristics analysis of this system.

As previously mentioned, there have been many attempts by researchers in the pursuit of studying the vibration behaviors of flexible systems or using PAMs to solve engineering problems. All of these previous attempts by researchers motivate this present work and provide great constructive ideas in this present study process. The dynamic behaviors of plates are modeled by using the finite element (FE) method. In this present finite element model, the maximum forces provided by PAM in different air pressures are adopted as controlling forces for applying for the plate. The dynamic behaviors of plates with several independent groups of controlling forces are observed and studied. The present work demonstrates the potential of the PAM actuators as valid means for damping out the vibration of flexible systems.

2  The Analysis Model for the Flexible Plate Actuated by PAM

The length (L), width (w) and thickness (t) of the flexible composite plate were 672, 50, and 4 mm respectively in this study. As seen in Fig. 1, the simply supported plate can be actuated by two PAMs. One end of the PAM was connected with the support, and the other end of the PAM was connected to the plate by a rigid cylinder. Through this connection way, the active force provided by PAM can be transferred to the plate effectively. The designed height (H) of the installation position for PAM is 100 mm. The designed length of PAM (La) is 136 mm. In Fig. 1, the Cartesian coordinate system (i, j, k) was adopted for this analysis model which is consistent with the FE model.

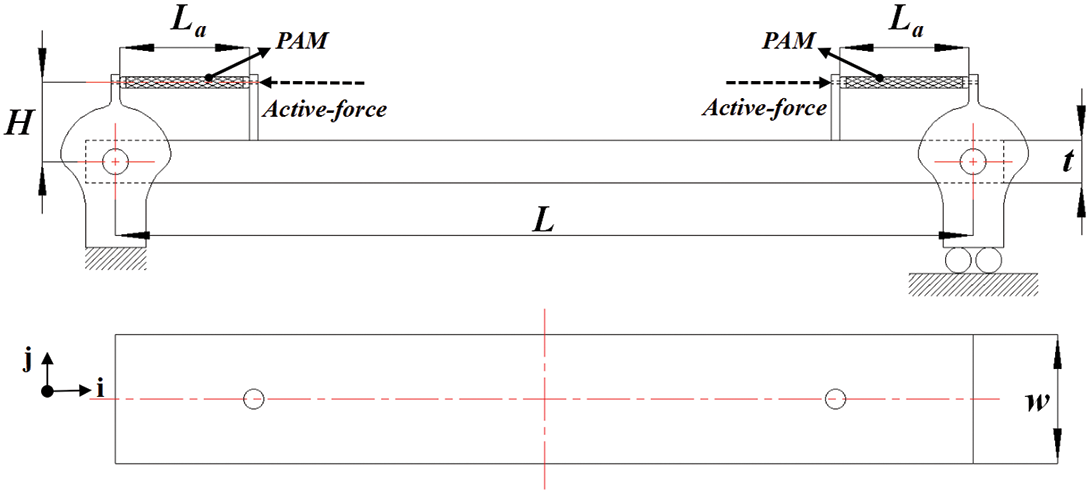
Figure 1: The model for flexible plates actuated by pneumatic artificial muscle

To simplify the plate modeling, a fiber-matrix laminated composite plate was employed in this study, which consists of sixteen fiber-matrix plies with the different fiber orientation. The thickness of each ply is 0.25 mm. Each ply possesses the same material property but is laminated as the different fiber orientation. As a matter of plane stress, the Young’s modulus (Ei, Ej) of each ply at i, j directions are 75 and 6.5 GPa, respectively. The Poisson’s ratio (μij) of each ply is 0.1. The shear elasticity modulus (Gij, Gjk, Gik) of each ply is 2.3 Gpa. The density (ρ) of each ply is 1.55 × 103 kg/m3.

As shown in the Fig. 2, the fiber-matrix laminated composite plate is consisted of four fiber-matrix laminates (I, II, III and IV), each of which contains four plies and possesses the same material property with the fiber orientations [0°, 45°, −45°, 90°].

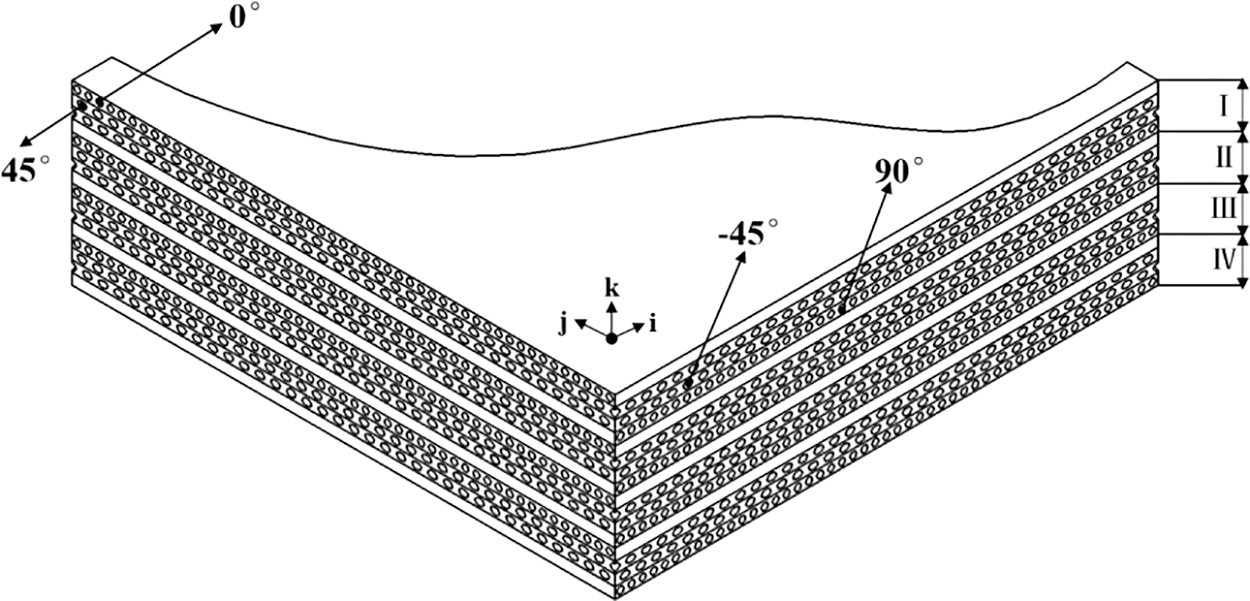
Figure 2: The fiber orientations of the fiber-matrix laminated composite plate

3  Modal Analysis of the Flexible Plate Actuated by PAM

3.1 The Pre-Stress Provided by PAMs Applied to the Flexible Plate

As seen in Fig. 1, both ends of PAMs were fixed, then the active forces can be generated when the PAMs were actuated. As the displayed connected way between the PAMs and the flexible plate, the bending moment derived from the actuated PAMs would occur in the cross section of the plate. Furthermore, the different pre-stresses can be applied to this flexible plate when the PAMs were actuated at different air pressure.

The active forces with the values of 0, 10, 20, 50, 100, 150, 200, 250 and 300 N, which are provided by PAMs, were considered respectively in this paper. 0 N represents the PAMs are not actuated, which is in the natural condition. The values of active forces are the sum of which the two settled PAMs provide. Under the active force 300 N’s stimulation, the value of the vonMises stresses that occurred in this flexible plate is 291.0 MPa in the linear elastic range of the material. Fig. 3 shows that the max vonMises stresses occurred nearby the hole which is the exact region of stress concentration. Most of the areas in the plates, the occurred vonMises stresses <120 MPa. Hence, the active force applied to the flexible plate gives permission that the flexible plate can serve within the linear elastic range of the material.

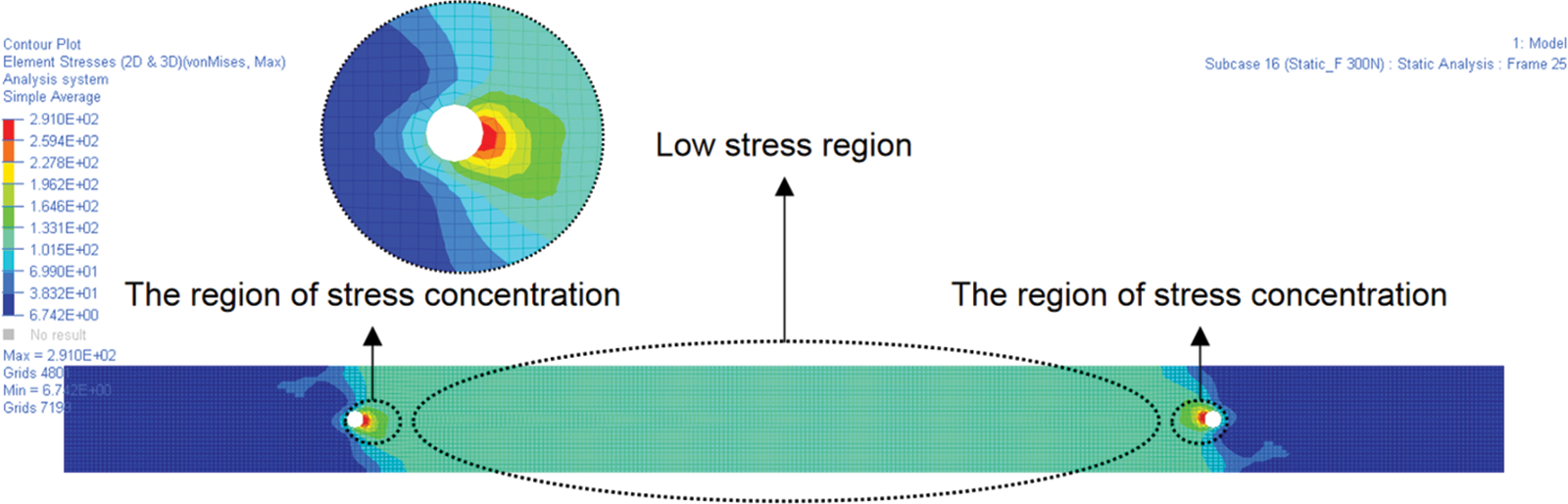
Figure 3: The stress distribution in the flexible plate when 300 N active force provided by PAMs was applied

3.2 The FE Model for the Flexible Plate Actuated by PAM

The commercial finite element software HyperWorks (Version 2017, Altair Engineering, Inc., China) is adopted for analyzing the dynamic behaviors of flexible plates under the active force’s stimulating. The plate is meshed by only quads type with the property of P-SHELL and the total element numbers are 8632. The information of each composite ply is also set as mentioned in Section 2. Here the cylinder that was connected PAMs with the plate was regarded as a rigid body using the RBE2 mesh type. In this present model, one end of the PAM was connected with the support, and the other end of the PAM was connected with the plate by a rigid cylinder. The PAMs are constrained in all degrees of freedom under the compressed air stimulating, so the PAMs can provide the maximum generative force. The active force is applied directly to the connection of PAMs in this FE model because the PAMs show light weight and softness.

3.3 Modal Analysis of the Flexible Plate Actuated by PAM

The modal analysis from 1st to 7th order was analyzed and obtained with several independent groups of controlling forces stimulating. As seen in Figs. 4–7, the modes of vibration from 1st to 7th were illustrated without active forces stimulating and the natural frequencies from 1st to 7th order vs. a series of active force were obtained. The vibration shapes of this plate under active force’s stimulating were also obtained which is almost same as the results without the stimulating.

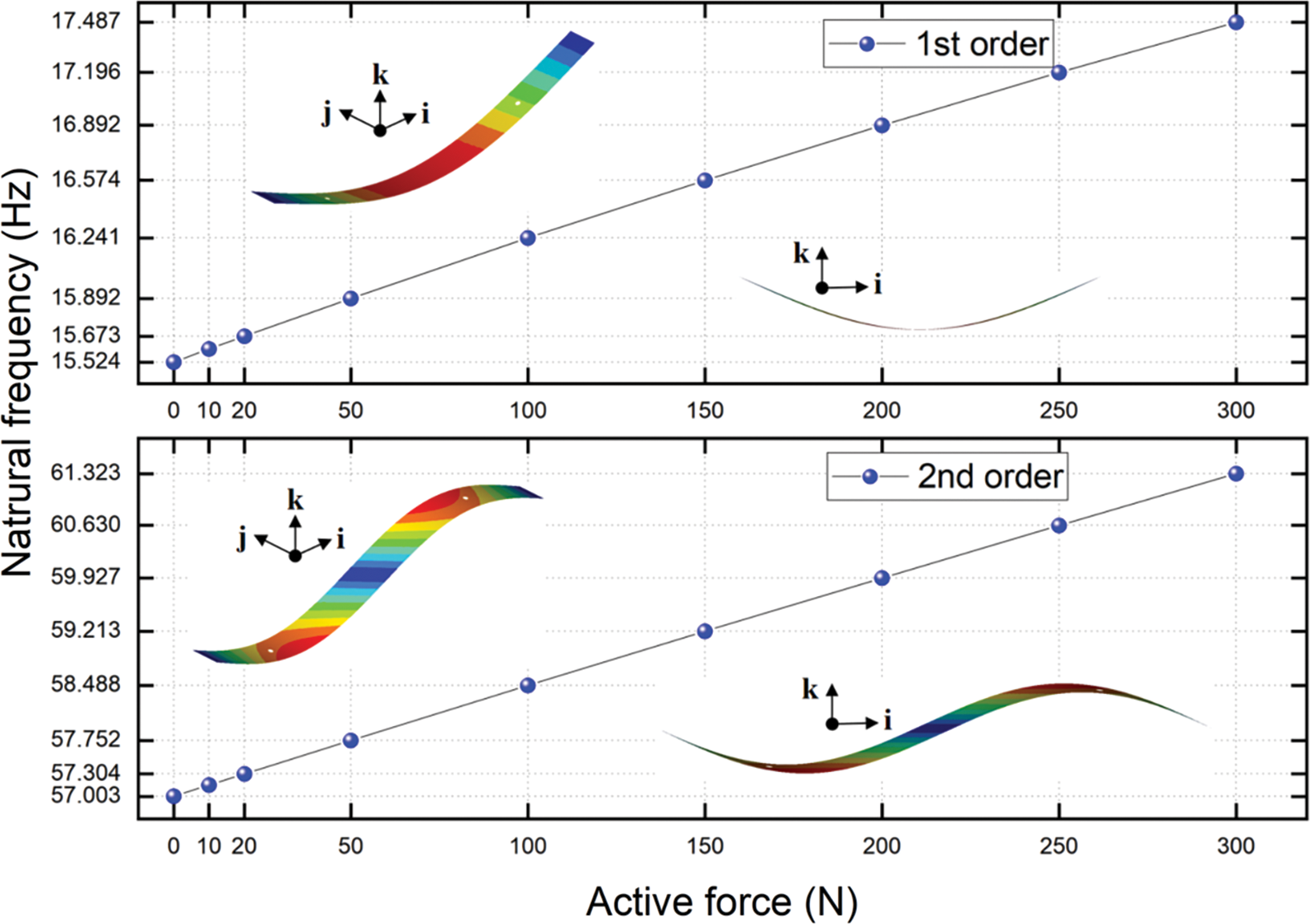
Figure 4: The natural frequencies of 1st and 2nd order vs. a series of active force

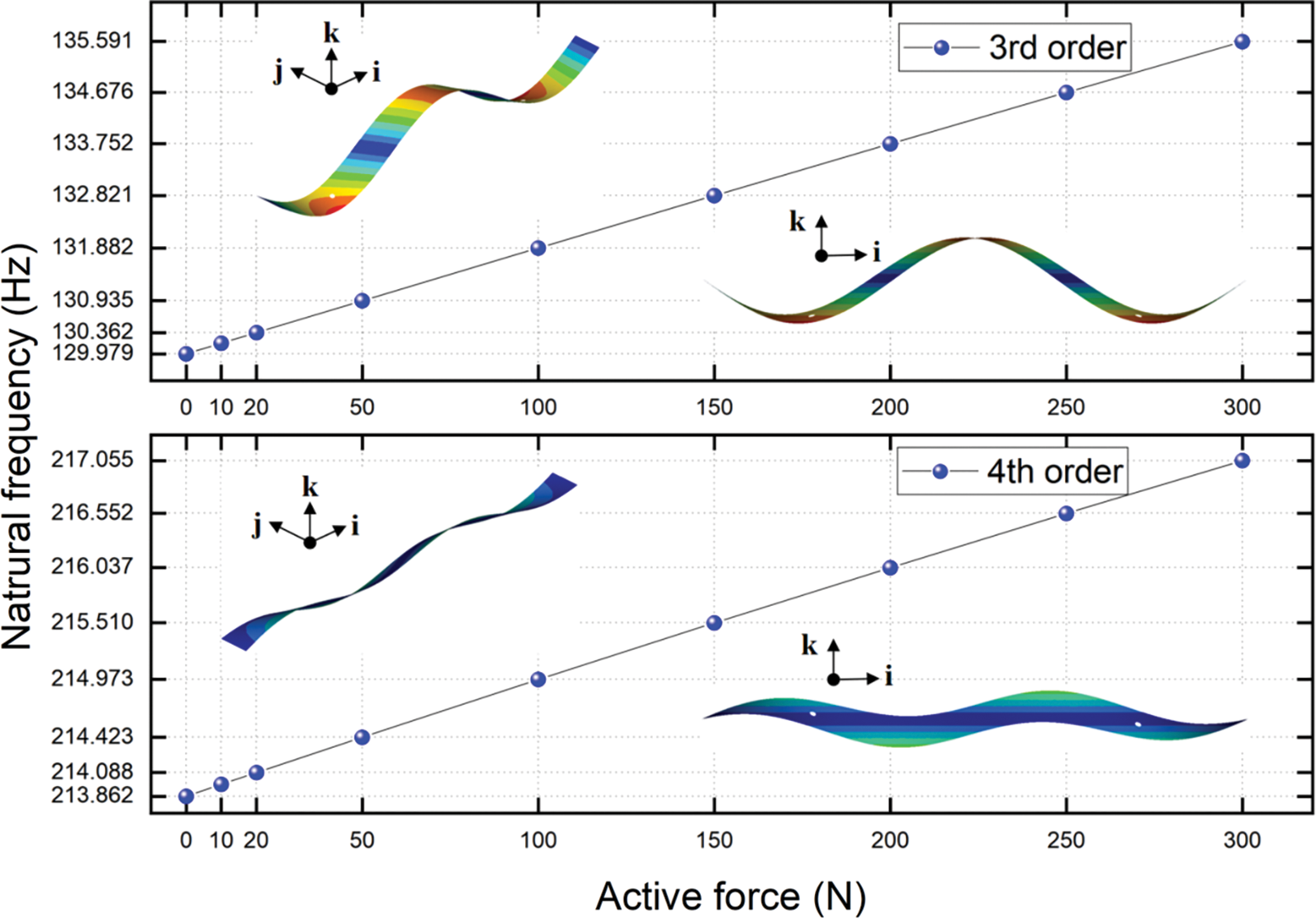
Figure 5: The natural frequencies of 3rd and 4th order vs. a series of active force

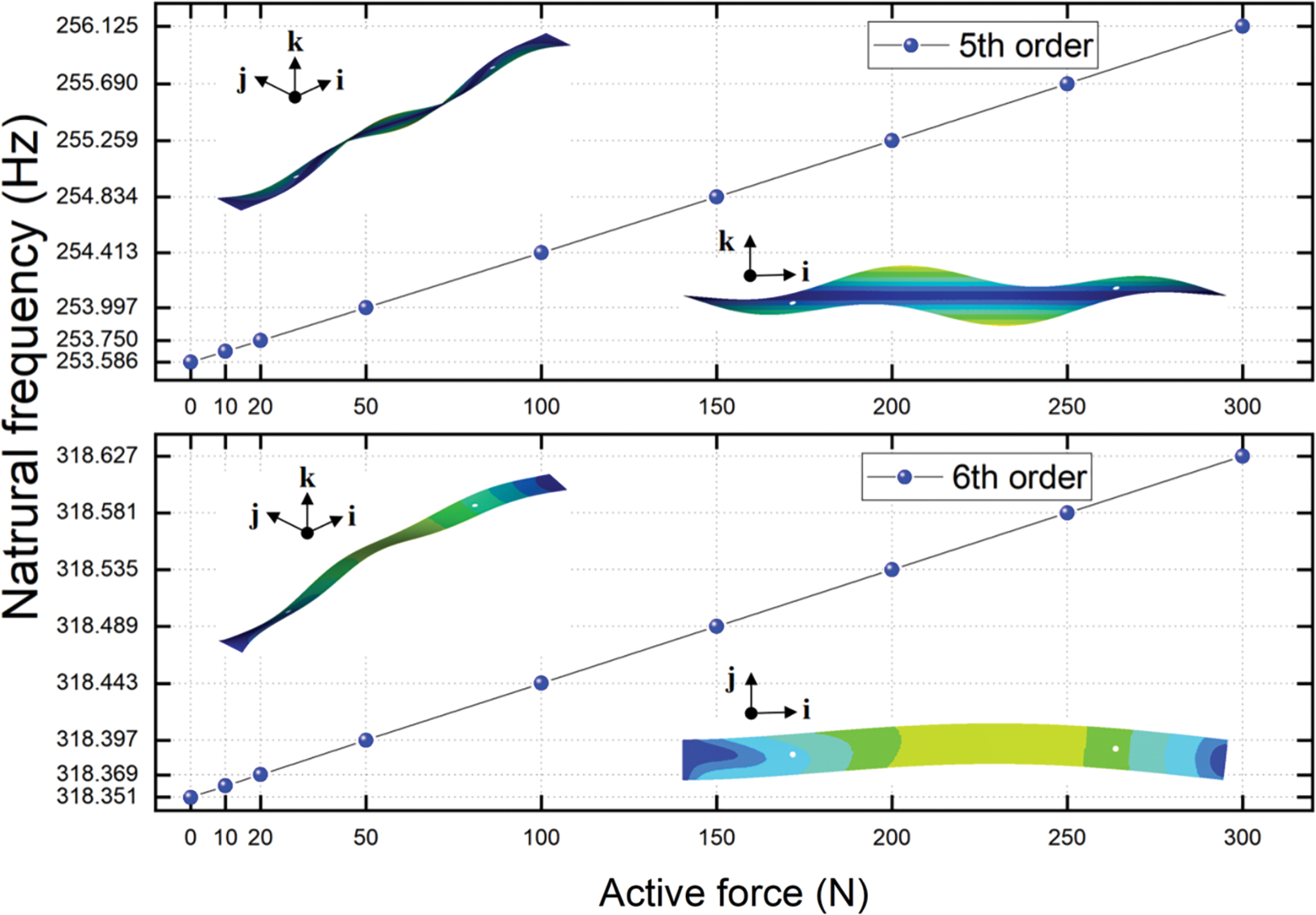
Figure 6: The natural frequencies of 5th and 6th order vs. a series of active force

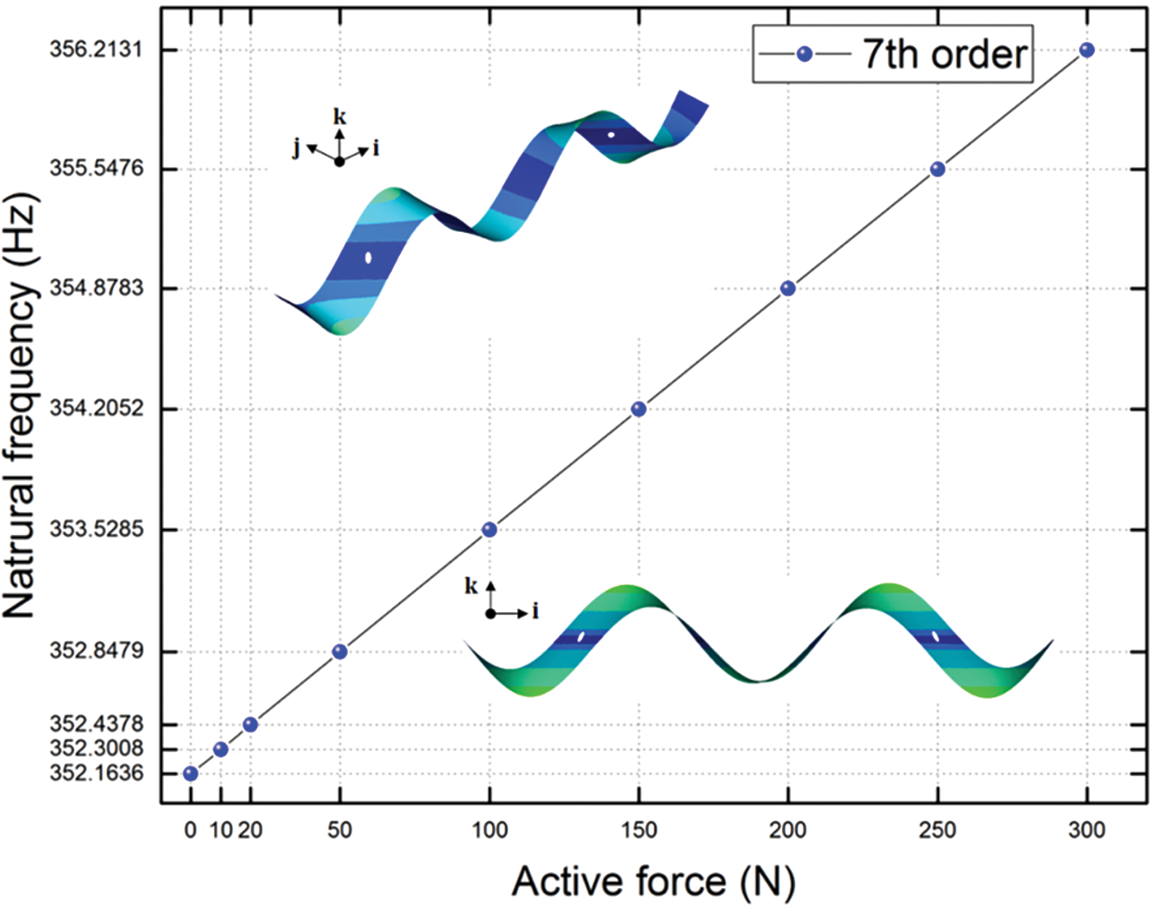
Figure 7: The 7th natural frequencies vs. a series of active force

Fig. 4 shows that, both of the 1st and 2nd order natural frequencies increase nearly linearly with the growth of active forces. When the active force reaches to 300 N, the 1st order natural frequency increases to 112.64% under the un-actuated PAMs, and the 2nd order natural frequency increases to 107.58%. Figs. 5–7 shows that the natural frequencies from 3rd to 7th also increase nearly linearly as the active forces increase. When the active force reaches to 300 N, the 3rd order natural frequency increases to 104.32% under the un-actuated PAMs, the 4th order natural frequency increases to 101.49%, the 5th order natural frequency increases to 101.00%. For the 6th order natural frequency, it is a very small improvement vs. a series of active force, and the 7th order natural frequency increases to 101.15%.

It can be found that the 1st, 2nd and 3rd order natural frequencies of the plate can be varied effectively if the controlling forces are applied. For the 4th, 5th, 6th, and 7th order natural frequencies of the plate, there is an insignificant influence when the controlling forces are applied. Meanwhile the applied active forces affect the natural frequencies of the bending modes (the 1st, 2nd and 3rd order natural frequencies) more significantly than the in-plane mode (the 6th order natural frequency).

4  Direct Frequency Response Analysis of the Flexible Plate Actuated by PAM

A frequency-dependent dynamic load is applied at the centroid of the flexible plate in order to observe the frequency response of this plate when the PAMs are stimulated at different air pressure. The applied active forces with the values of 0, 10, 20, 50, 100, 150, 200, 250 and 300 N which are provided by PAMs, were considered respectively in this section. The frequency interval of the dynamic load is from 0 to 1000 Hz, and the frequency increment is 1 Hz. The dynamic load is set as a constant displacement stimulation of 20 mm in the whole frequency interval.

The direct frequency response curve at a series of the small active force (0, 10 and 20 N) is illustrated in Fig. 8. The direct frequency response results at a series of larger active force (50, 100, 150, 200, 250 and 300 N) are compared in Fig. 9. As seen in Figs. 8 and 9, the max amplitudes decrease as the active forces increase, and the frequencies where the max displacements occur increase with the growth of active forces. The small active forces have minor impact on both the amplitudes and the frequencies where the max displacements occur (Fig. 8). The active forces have relatively significant effect on both the amplitudes and the frequencies where the max displacements occur when ≥50 N (Fig. 9).

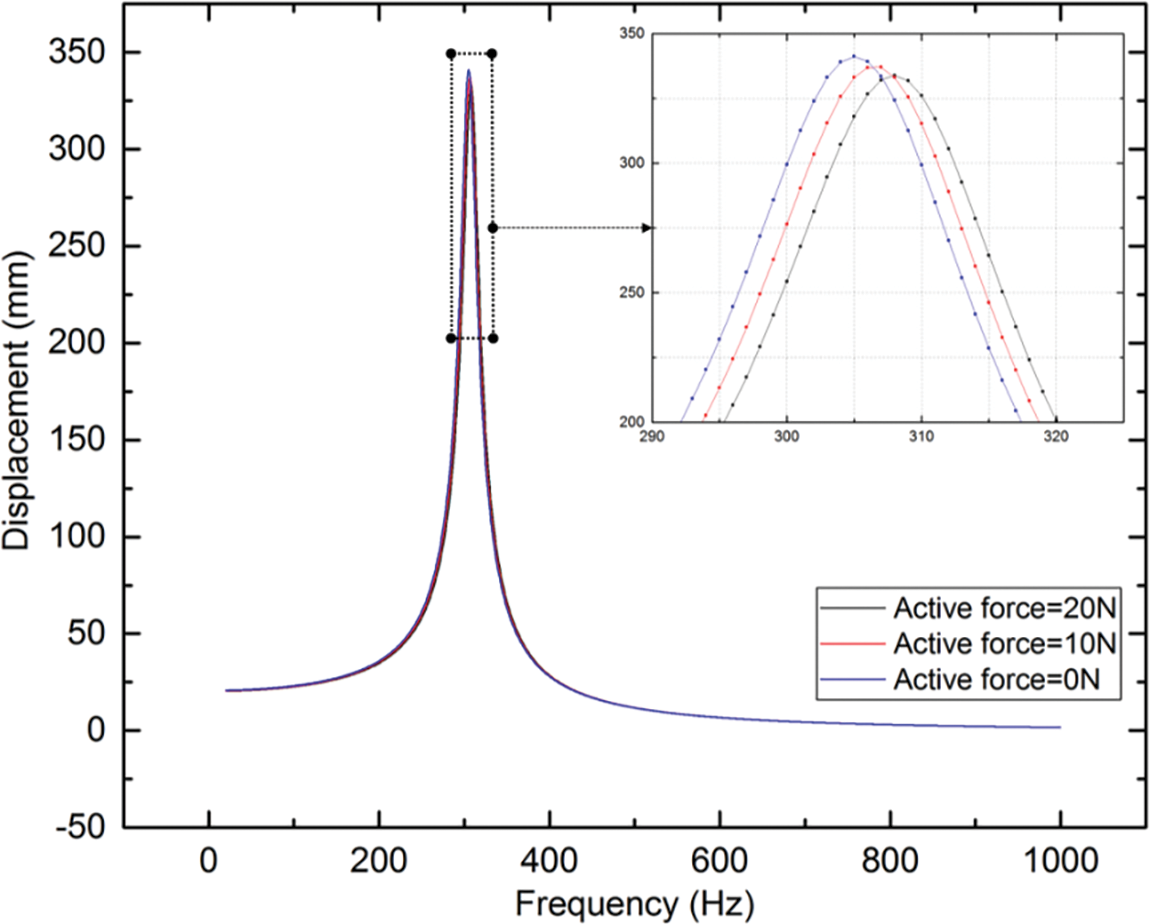
Figure 8: The amplitude-frequency characteristic curve at a series of the low active force

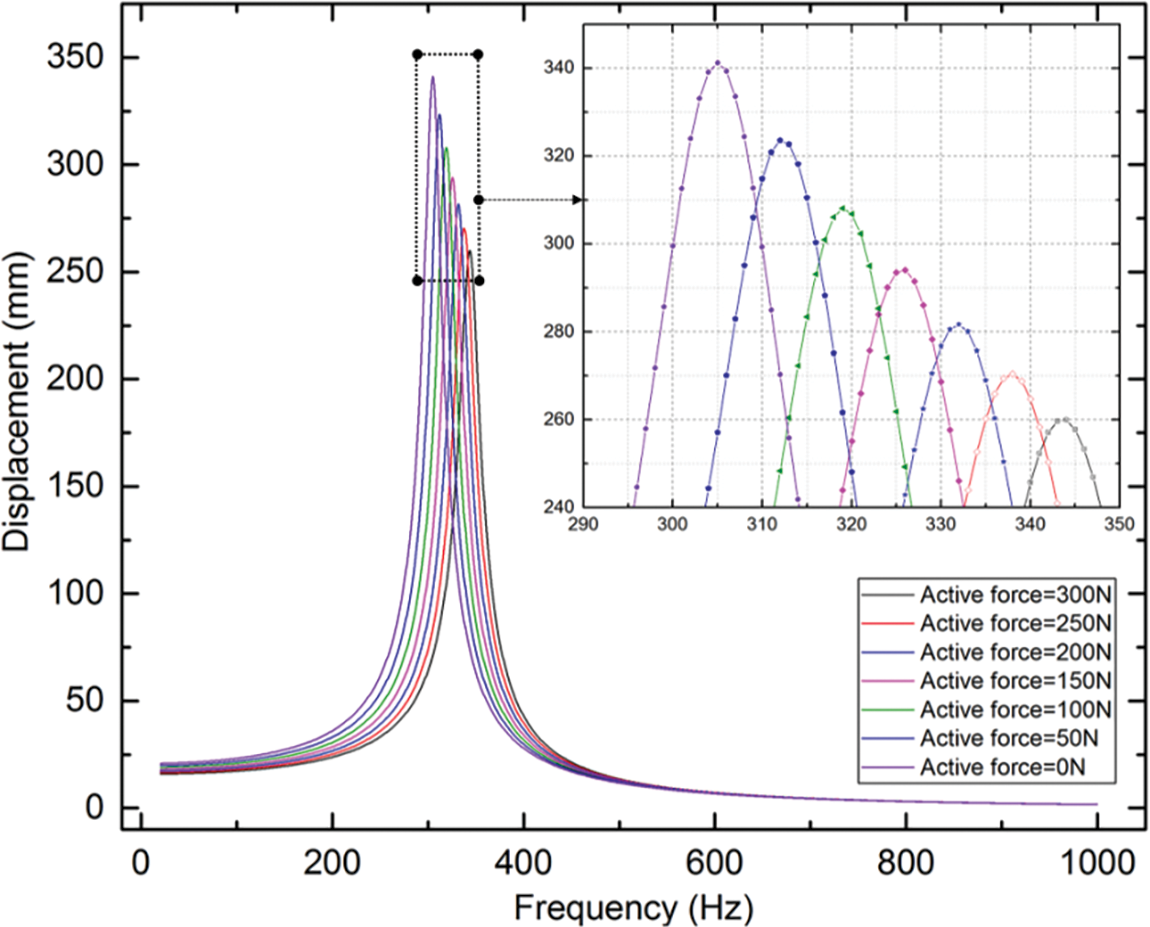
Figure 9: The amplitude-frequency characteristic curve at a series of the large active force

Figs. 10 and 11 show the max amplitudes and the frequencies where the max displacements occur vs. a series of active force at 3D and 2D Cartesian coordinate system, respectively. When the active force reaches to 150 N, the max amplitude decreases to 86.19% under the un-actuated PAMs, and the frequencies where the max displacements occur increases to 106.89%. When the active force reaches to 300 N, the max amplitude decreases to 76.18% under the un-actuated PAMs, and the frequencies where the max displacements occur increases to 112.79%. The results obtained demonstrate the potential of the PAM actuators as valid means for damping out the vibration of flexible systems.

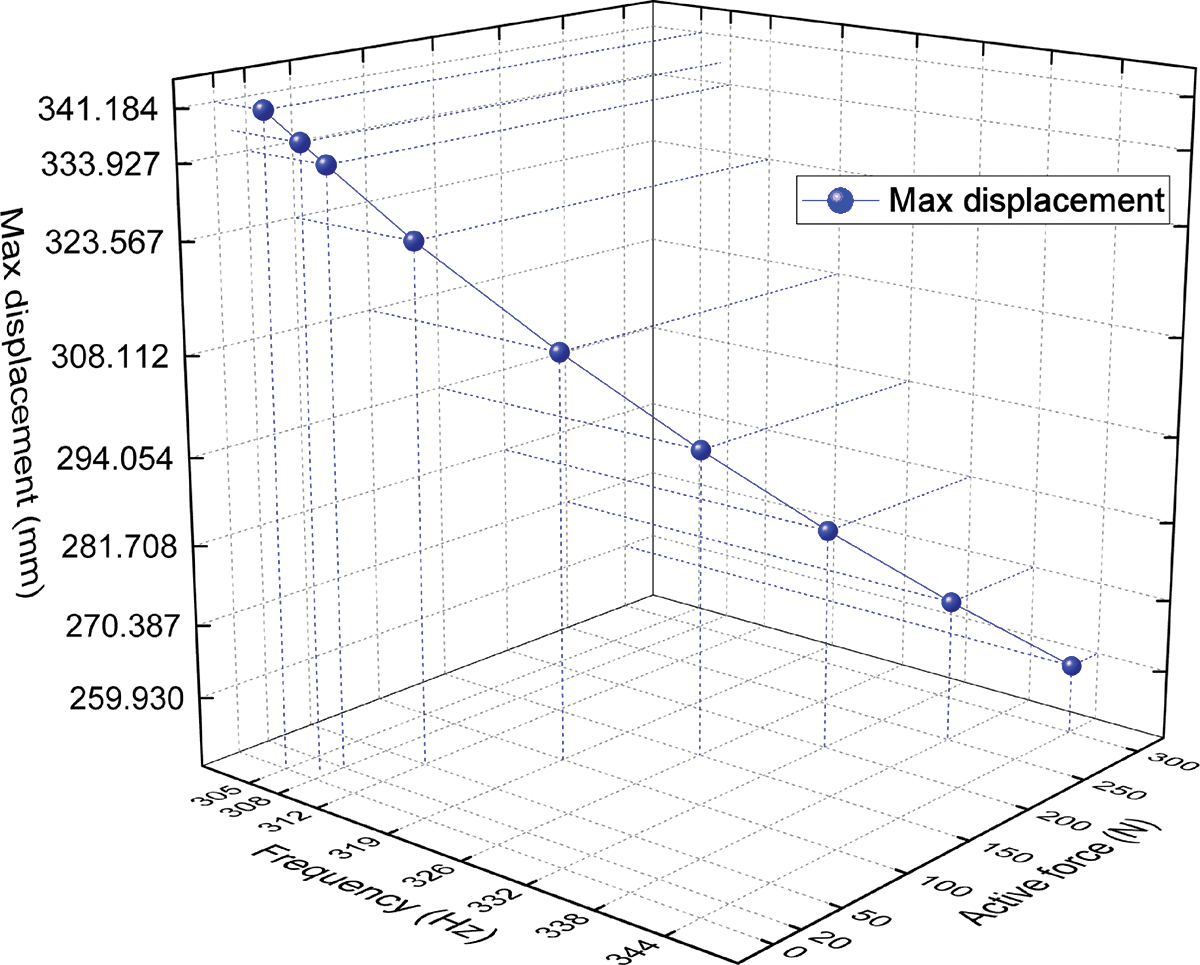
Figure 10: The max amplitudes and the frequencies where the max displacements occur vs. a series of active force at 3D Cartesian coordinate system

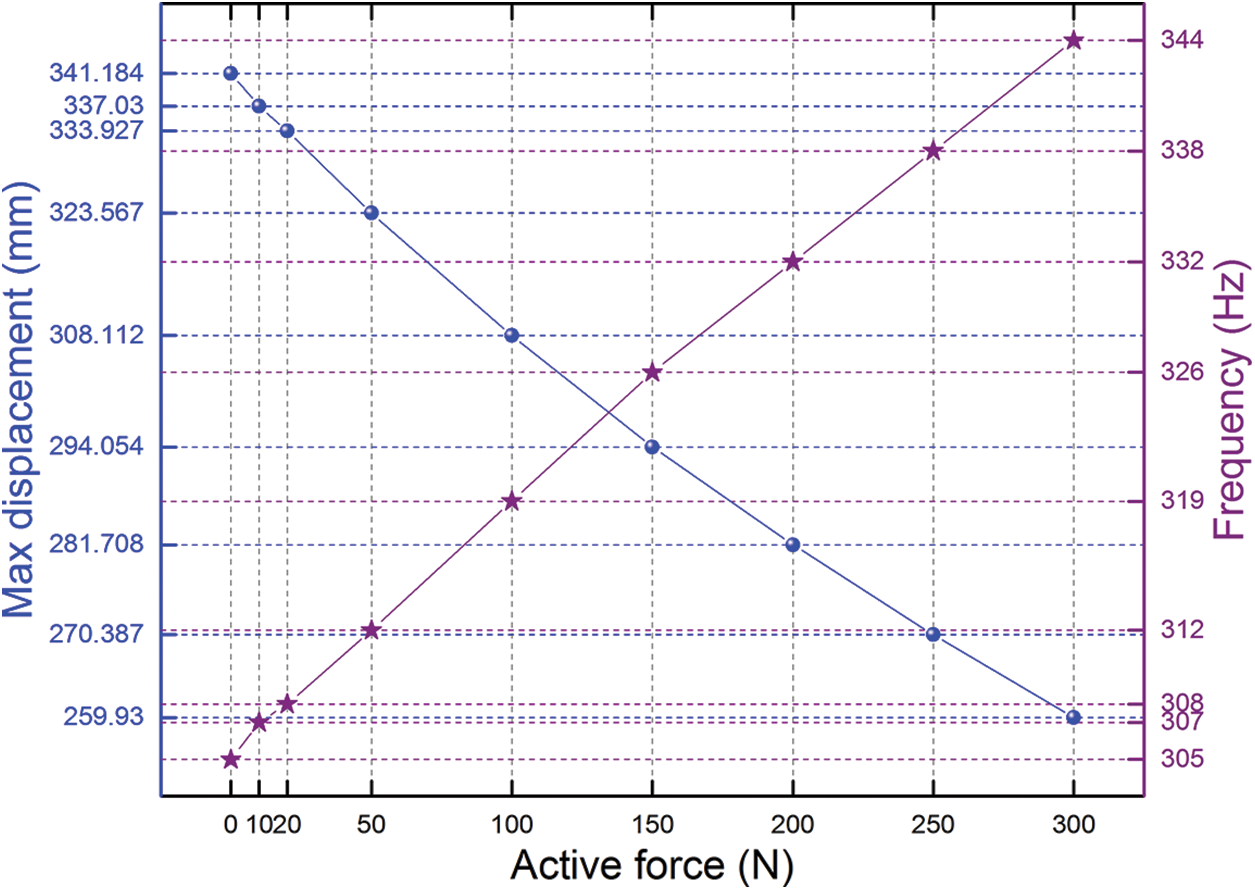
Figure 11: The max amplitudes and the frequencies where the max displacements occur vs. a series of active force

5  Conclusion

In this paper, the pressurized PAMs that can provide the active forces are employed to stimulate a flexible composite plate to vary its vibration behaviors. Firstly, the active force provided by PAMs gives permission that the flexible plate can serve in the linear elastic range of the material. The modal analysis and direct frequency response analysis of the flexible plate actuated by PAM is investigated through FE method. The natural frequencies of the plate from 1st to 7th order increase linearly as the active forces increase. The 1st, 2nd, and 3rd order natural frequencies of the plate can be varied effectively if the controlling forces are applied. When the active force reaches to 300 N, the 1st order natural frequency increases to 112.64% under the un-actuated PAMs, and the 2nd order natural frequency grows to 107.58%. For the direct frequency response analysis, when the active force reaches 300 N, the max amplitude decreases to 76.18% under the un-actuated PAMs and the frequencies where the max displacements occur increase to 112.79%. The results obtained demonstrate the potential of the PAM actuators as valid means for damping out the vibration of flexible systems.

Funding Statement: This work is supported by the Henan Provincial Science and Technology Research Project (222102220068).

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. Liu, J., Zhang, Y., Guo, Z., Liu, S., Zhang, J. et al. (2021). Enhancement of fiber-matrix adhesion in carbon fiber reinforced Al-matrix composites with an optimized electroless plating process. Composites Part A: Applied Science and Manufacturing, 142(10), 106258. https://doi.org/10.1016/j.compositesa.2020.106258 [Google Scholar] [CrossRef]

2. Deng, Y., Zhang, Z., Shi, C., Wu, Z., Zhang, C. (2022). Steel fiber-matrix interfacial bond in ultra-high performance concrete: A review. Engineering, 103(2), 8. https://doi.org/10.1016/j.eng.2021.11.019 [Google Scholar] [CrossRef]

3. Zhang, C., Chen, M., Coasne, B., Keten, S., Derome, D. et al. (2022). Hygromechanics of softwood cellulosic nanocomposite with intermolecular interactions at fiber-matrix interface investigated with molecular dynamics. Composites Part B: Engineering, 228, 109449. https://doi.org/10.1016/j.compositesb.2021.109449 [Google Scholar] [CrossRef]

4. Ding, H., Xu, B. (2021). Optimal design of vibrating composite plate considering discrete-continuous parameterization model and resonant peak constraint. International Journal of Mechanics and Materials in Design, 17(3), 679–705. https://doi.org/10.1007/s10999-021-09553-x [Google Scholar] [CrossRef]

5. Ma, R., Bi, K., Hao, H. (2021). Inerter-based structural vibration control: A state-of-the-art review. Engineering Structures, 243, 112655. https://doi.org/10.1016/j.engstruct.2021.112655 [Google Scholar] [CrossRef]

6. Chang, Y., Zhou, J., Wang, K., Xu, D. (2021). A quasi-zero-stiffness dynamic vibration absorber. Journal of Sound and Vibration, 494, 115859. https://doi.org/10.1016/j.jsv.2020.115859 [Google Scholar] [CrossRef]

7. Fraternali, F., Singh, N., Amendola, A., Benzoni, G., Milton, G. W. (2021). A biomimetic sliding-stretching approach to seismic isolation. Nonlinear Dynamics, 106(4), 3147–3159. https://doi.org/10.1007/s11071-021-06980-5 [Google Scholar] [CrossRef]

8. Zippo, A., Ferrari, G., Amabili, M., Barbieri, M., Pellicano, F. (2015). Active vibration control of a composite sandwich plate. Composite Structures, 128(8), 100–114. https://doi.org/10.1016/j.compstruct.2015.03.037 [Google Scholar] [CrossRef]

9. Wang, X., Yue, X., Wen, H., Yuan, J. (2020). Hybrid passive/active vibration control of a loosely connected spacecraft system. Computer Modeling in Engineering & Sciences, 122(1), 61–88. https://doi.org/10.32604/cmes.2020.06871 [Google Scholar] [CrossRef]

10. Ohta, P., Valle, L., King, J., Low, K., Yi, J. et al. (2018). Design of a lightweight soft robotic arm using pneumatic artificial muscles and inflatable sleeves. Soft Robotics, 5(2), 204–215. https://doi.org/10.1089/soro.2017.0044 [Google Scholar] [PubMed] [CrossRef]

11. Lei, J., Yu, H., Wang, T. (2016). Dynamic bending of bionic flexible body driven by pneumatic artificial muscles (PAMs) for spinning gait of quadruped robot. Chinese Journal of Mechanical Engineering, 29(1), 11–20. DOI https://doi.org/10.3901/CJME.2015.1016.123 [Google Scholar] [CrossRef]

12. Hitzmann, A., Masuda, H., Ikemoto, S., Hosoda, K. (2018). Anthropomorphic musculoskeletal 10 degrees-of-freedom robot arm driven by pneumatic artificial muscles. Advanced Robotics, 32(15), 865–878. https://doi.org/10.1080/01691864.2018.1494040 [Google Scholar] [CrossRef]

13. Woods, B. K., Gentry, M. F., Kothera, C. S., Wereley, N. M. (2012). Fatigue life testing of swaged pneumatic artificial muscles as actuators for aerospace applications. Journal of Intelligent Material Systems and Structures, 23(3), 327–343. https://doi.org/10.1177/1045389X11433495 [Google Scholar] [CrossRef]

14. Feng, N., Liu, L., Liu, Y., Leng, J. (2015). A bio-inspired, active morphing skin for camber morphing structures. Smart Materials and Structures, 24(3), 035023. https://doi.org/10.1088/0964-1726/24/3/035023 [Google Scholar] [CrossRef]

15. Belalia, S. A. (2019). A curved hierarchical finite element method for the nonlinear vibration analysis of functionally graded sandwich elliptic plates. Mechanics of Advanced Materials and Structures, 26(13), 1115–1129. https://doi.org/10.1080/15376494.2018.1430277 [Google Scholar] [CrossRef]

16. Akhavan, H., Ribeiro, P. (2011). Natural modes of vibration of variable stiffness composite laminates with curvilinear fibers. Composite Structures, 93(11), 3040–3047. https://doi.org/10.1016/j.compstruct.2011.04.027 [Google Scholar] [CrossRef]

17. Ribeiro, P., Akhavan, H. (2012). Non-linear vibrations of variable stiffness composite laminated plates. Composite Structures, 94(8), 2424–2432. https://doi.org/10.1016/j.compstruct.2012.03.025 [Google Scholar] [CrossRef]

18. Wu, Z., Guo, L., Hong, J. (2023). Improved staggered algorithm for phase-field brittle fracture with the local arc-length method. Computer Modeling in Engineering & Sciences, 134(1), 611–636. https://doi.org/10.32604/cmes.2022.020694 [Google Scholar] [CrossRef]

19. Liu, D., Zhao, R., Jafri, H. M., Wang, J., Huang, H. (2019). Phase-field simulations of surface charge-induced polarization switching. Applied Physics Letters, 114(11), 112903. https://doi.org/10.1063/1.5083126 [Google Scholar] [CrossRef]

20. Xu, X., Jiang, L., Zhou, Y. (2017). Reduction of leakage currents in ferroelectric thin films by flexoelectricity: A phase field study. Smart Materials and Structures, 26(11), 115024. https://doi.org/10.1088/1361-665X/aa8dc8 [Google Scholar] [CrossRef]

21. Hadji, L., Bernard, F., Zouatnia, N. (2023). Bending and free vibration analysis of porous-functionally-graded (PFG) beams resting on elastic foundations. Fluid Dynamic & Material Process, 19(4), 1043–1054. https://doi.org/10.32604/fdmp.2022.022327 [Google Scholar] [CrossRef]

22. Li, K., Qu, J., Tan, J., Wu, Z., Xu, X. (2021). A symplectic method of numerical simulation on local buckling for cylindrical long shells under axial pulse loads. Structural Durability & Health Monitoring, 15(1), 53–67. DOI https://doi.org/10.32604/sdhm.2021.014559 [Google Scholar] [CrossRef]

23. Dhanda, M., Pant, P., Dogra, S., Gupta, A., Dutt, V. (2022). Sensitivity analysis of contact type vibration measuring sensors. Sound & Vibration, 56(3), 235–243. https://doi.org/10.32604/sv.2022.015615 [Google Scholar] [CrossRef]

24. Xu, D., Du, J., Zhao, Y. (2019). Longitudinal vibration analysis of elastically coupled nanorods system with general boundary supports. Sound & Vibration, 53(2), 16–28. https://doi.org/10.32604/sv.2019.04033 [Google Scholar] [CrossRef]

25. Hu, C. (2019). A novel method for damping of complex mechanical systems. Sound & Vibration, 53(5), 199–206. https://doi.org/10.32604/sv.2019.07712 [Google Scholar] [CrossRef]