

 | Sound & Vibration |  |
DOI: 10.32604/sv.2022.014874
ARTICLE
Free Vibration Analysis of RC Box-Girder Bridges Using FEM
Motilal Nehru National Institute of Technology Allahabad, Prayagraj, 211004, India
*Corresponding Author: Preeti Agarwal. Email: gotopreetiagarwal@gmail.com
Received: 04 November 2020; Accepted: 26 January 2021
Abstract: The free vibration analysis of simply supported box-girder bridges is carried out using the finite element method. The fundamental frequency is determined in straight, skew, curved and skew-curved box-girder bridges. It is important to analyse the combined effect of skewness and curvature because skew-curved box-girder bridge behaviour cannot be predicted by simply adding the individual effects of skewness and curvature. At first, an existing model is considered to validate the present approach. A convergence study is carried out to decide the mesh size in the finite element method. An exhaustive parametric study is conducted to determine the fundamental frequency of box-girder bridges with varying skew angle, curve angle, span, span-depth ratio and cell number. The skew angle is varied from 0° to 60°, curve angle is varied from 0° to 60°, span is changed from 25 to 50 m, span-depth ratio is varied from 10 to 16, and single cell & double cell are used in the present study. A total of 420 bridge models are used for parametric study in the investigation. Mode shapes of the skew-curved bridge are also presented. The fundamental frequency of the skew-curved box-girder bridge is found to be more than the straight bridge, so, the skew-curved box-girder bridge is preferable. The present study may be useful in the design of box-girder bridges.
Keywords: Fundamental frequency; skew-curved box-girder bridge; single-cell; double-cell; curve angle; skew angle; FEM
Abbreviations
| θ | Skew angle (°) |
| α | Curve angle (°) |
| R | Radius of curve bridge (m) |
| L | Span of central bridge girder (m) |
| Lo | Span of outer girder bridge deck (m) |
| Li | Span of inner girder bridge deck (m) |
| ttf | Thickness of top flange (m) |
| tbf | Thickness of bottom flange (m) |
| tw | Thickness of web (m) |
| A | Cross-sectional area |
| L/d | Span-depth ratio |
| E | Modulus of elasticity of concrete (kN/m2) |
| I | Moment of inertia (m4) |
| | Maximum deflection (m) |
| Nf | Natural frequency (Hz) |
| g | Acceleration due to gravity (m/sec2) |
| Wd | Dead weight of bridge (kN/m) |
| a | Maximum acceleration (m/sec2) |
| ∆ | Maximum amplitude of vibration (m) |
| f | Fundamental frequency (Hz) |
In general, the box-girder bridge is used when the problems of a larger span and wider deck occur. They have high strength and more torsional and flexural stiffnesses. The deck of a straight bridge is supported orthogonally to the traffic. But due to some reasons, i.e., the site conditions and land acquisition problems, the bridge axis may not be perpendicular to the supports in the plan and such bridges are termed as skewed, as shown in Fig. 1a. Many possible straight bridges are also made curved in the plan (Fig. 1b) due to the problem of change in speed, high traffic, site restriction, and alignment layout. The combination of aforesaid two different bridges results in a skew-curved bridge, as illustrated in Fig. 1c. The responses of such types of bridges cannot be measured directly by merely adding the individual effects of skewness and curvature. So, it is necessary to combine the effects of skewness and curvature at the analysis stage itself to assess the structural behaviour of skew-curved bridges. The free vibration analysis is very important to determine the structure’s response to check whether the deck’s natural frequency is away from excitation frequencies. The free vibration occurs naturally, with no energy being added to the vibrating system. The vibration starts with some energy input but dies away with time as the energy is dissipated. The natural frequencies and vibration modes depend upon the whole system, i.e., road characteristics, the material used, cross-sectional properties, etc. As the vibration is directly proportional to the system’s mass, steel and prestressed concrete bridges are more vulnerable to vibration than the concrete bridge.
Several commercial softwares are available based on the finite element method (FEM). For a bridge being a large structure or similar structures, FEM based software can be used to assess the natural frequencies in spite of the size and complexities of such structures. Mostly the shock absorber bearing is used in the bridge. Bearings are used to transfer forces from the superstructure to the substructure while tolerating or constraining relative movement. They provide vibration isolation. Hence, the bridge deck will only influence the natural frequencies of the bridge. Therefore, only the mass of the deck is considered in the analysis while taking the effect of the bridge. However, the dynamic response will be affected under the influence of external load like vehicle’s frequency, etc. It can be determined when forced vibration analysis on such structures is performed. Several studies have been carried out to investigate the vibration behaviour of box-girder bridges, and some of the important contributions are mentioned below.
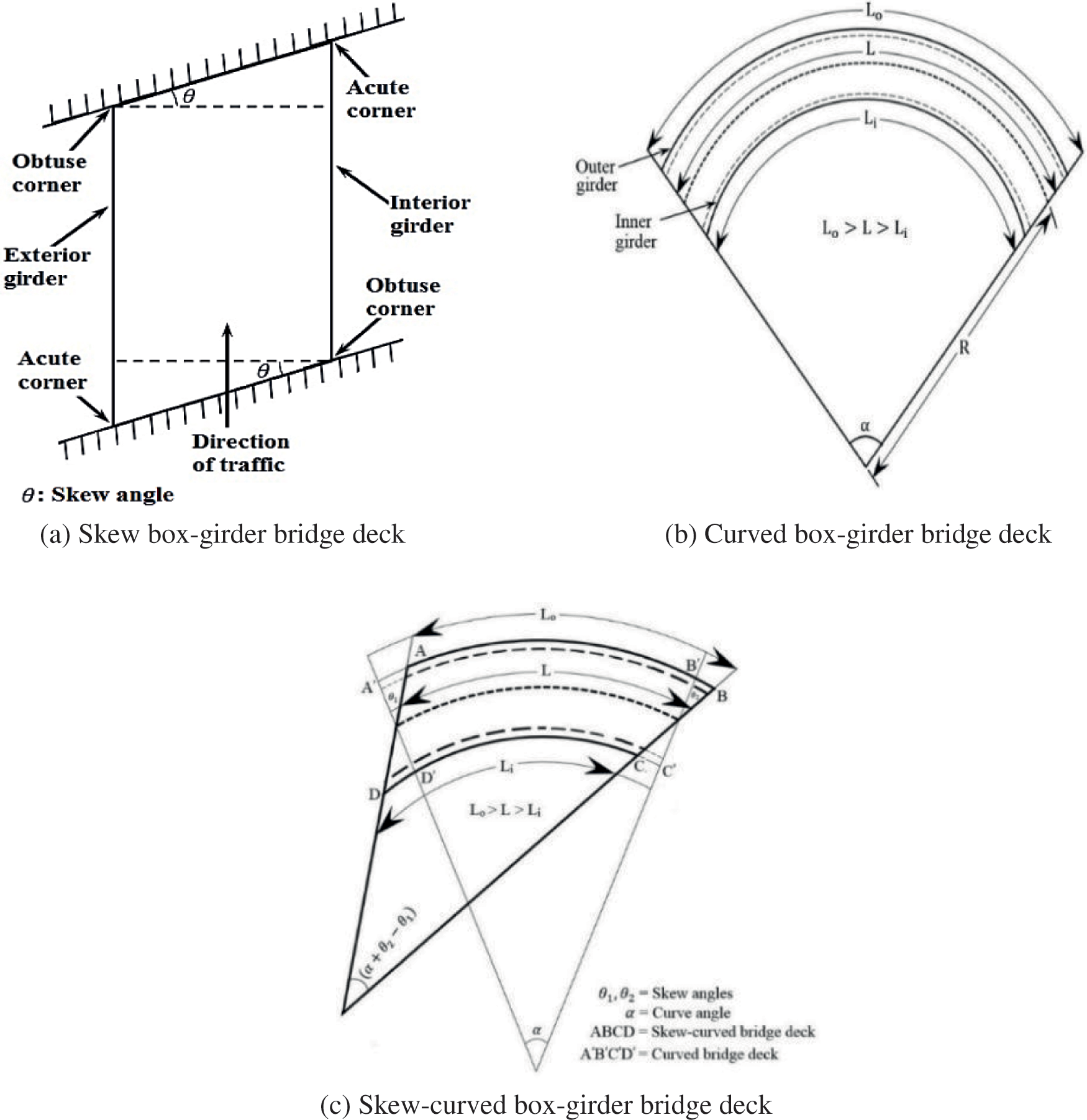
Figure 1: Box-girder bridge deck
The significant literature identified with this area is introduced as follows: A new formula is proposed for determining the natural frequency of a curved girder bridge with an asymmetrical cross-section and verified the proposed equations with the experimental studies [1]. A differential equation is derived for a curved box-girder bridge’s natural frequencies [2]. The natural frequencies of the bridge superstructure are determined by field observations and compared with the theoretical values. A comparison between the static and dynamic moduli of elasticity was made to estimate the natural frequency of vibration. It was found that the dynamic modulus of elasticity is more appropriate in finding natural frequency [3]. The dynamic response of a thin-walled curved box-girder bridge is evaluated due to the American Association of State Highway and Transportation Officials (AASHTO) HS20-44 load considering both warping torsion and distortion. Four road surface roughness classes are generated using a power spectral density function to analyse the bridges for different impact factors [4]. The skew bridge’s free vibration characteristics are presented analytically and validated with the finite element analysis results [5]. A computational tool is developed for the free vibrational analysis and the structural shape optimisation of straight and curved box-girder bridges [6]. The finite element formulation is developed for the free vibration analysis of a curved I-girder bridge considering the effects of the boundary condition and the initial curvature. The results (frequencies) are compared with the results obtained from ABAQUS software [7]. A new analytical method is proposed to determine the natural frequencies and the mode shapes of the multi-span bridge and compared the results with the numerical results obtained by ANSYS [8]. The effect of the span, number of cells, and skew angle on a box-girder bridge’s fundamental frequency are investigated using SAP2000 [9]. The static analysis is performed on skew-curved box-girder bridge experimentally [10]. The optimum performance is discussed through some parametric studies of the shape memory–alloy-based rubber bearing (SMARB). The same is compared with the lead rubber bearing (LRB) [11]. The base isolation system’s optimization is studied by incorporating excessive isolator displacement on a simply supported bridge [12]. A highway bridge’s seismic response is investigated using the finite element method subjected to six bi-directional ground motions. The bridge is isolated with passive polynomial friction pendulum isolators (PFPIs) [13]. The skew-curved box-girder bridge’s behavior is analysed under dead load and Class 70R tracked vehicular load using the finite element method [14]. The reactions of the skew-curved box-girder bridge are determined using finite element based CsiBridge software [15]. The natural frequencies of single-cell, double-cell and triple-cell box-girder bridges are determined and concluded that the triple-cell box-girder bridge is most effective [16]. The impact of span-depth ratio, span and girder spacing on the maximum bending moment and shear force in a single-cell skewed box-girder bridge are estimated [17]. The effect of curve angle on the bending moment, shear force, torsional moment and vertical deflection of the girders of single-cell, double-cell and triple-cell box-girder bridges under dead and Indian Road Congress (IRC) Class 70R track loads are evaluated [18]. The vibration characteristic of horizontal wells drillstrings using computer simulation based on the finite element method is studied [19]. The results are compared with the established experimental model based on the similarity principle. A coupling vibration analysis model of a high-speed railway simply supported beam bridge-track structure system (HSRBTS) based on energy-variational principle is established [20]. The effect of shear deformation is considered in the analysis. A hybrid passive/active vibration (HPAV) controller to mitigate the vibrations subjected to impulsive external excitations is proposed [21]. The proposed scheme is validated with the numerical simulation results. The effect of different parameters viz. skew angle, span, span-depth ratio and girder spacing on a single-cell reinforced concrete (RC) skew box-girder bridge are investigated [22]. Further, the authors investigated the combined effect of skew and curve angles on the responses of the box-girder bridge [23]. The effect of these parameters on the bending moment, shear force, torsional moment, stresses and deflection are determined.
The literature mentioned above mainly focuses on the free vibration analysis of straight box-girder bridges. It appears that the free vibration analysis of skew, curved and skew-curved RC box-girder bridges is not studied so far with the importance they deserve. Further, no such specifications and limitations for vibration are available in the literature on the skew, curved and skew-curved bridges. So, it is necessary to investigate the vibrational behaviour of such bridges. Thus, the present study aims to determine the frequencies and mode shapes of straight, skew, curved and skew-curved RC box-girder bridges using the finite element method. The comparison is also made between single-cell and double-cell box-girder bridges. The cross-section of the double-cell box-girder bridge is kept the same as that of the single-cell box-girder bridge. The bridges with different degrees of complexity can be modelled efficiently using the finite element method. Also, the results can be obtained quickly and precisely, so it is becoming quite popular nowadays compared to the experimental methods, which are rather costly and time-consuming. Thus, in the present study, a finite element based software CSiBridge [24] is used for the analysis. The present investigation aims to study the effects of skew angle, curve angle, number of cells, span, and span-depth ratios on the natural frequencies of different RC box-girder bridges.
In general, the modelling of any structure is done either in two-dimension or in three-dimension. But it should be done in three-dimension to evaluate the responses of the bridge deck. The modelling and analysis of the bridges are carried out using a finite element-based software CSiBridge v.20.0.0, as shown in Fig. 2. Simply supported boundary condition is used to constraint the bridge, and for that two roller supported bearings on one end and two pin supported bearings on the other end are considered. In the finite element modelling process, four noded shell element having six degrees of freedom (three translations and three rotations) at each node has been used. The selection of the cross-section of the bridge is a preliminary step in the analysis. The properties obtained from the trial and error method have been used in the investigation, based on the specifications mentioned in IRC 21:2000 [25], which are as follows:
1. The span of the box-girder bridge should not be less than 25 m,
2. The span-depth ratio should be around 17–18 for RC bridge,
3. Cantilever arm length is equal to 0.45 times the distance between webs,
4. The minimum soffit slab thickness should be 1/20 times the distance between the girders.
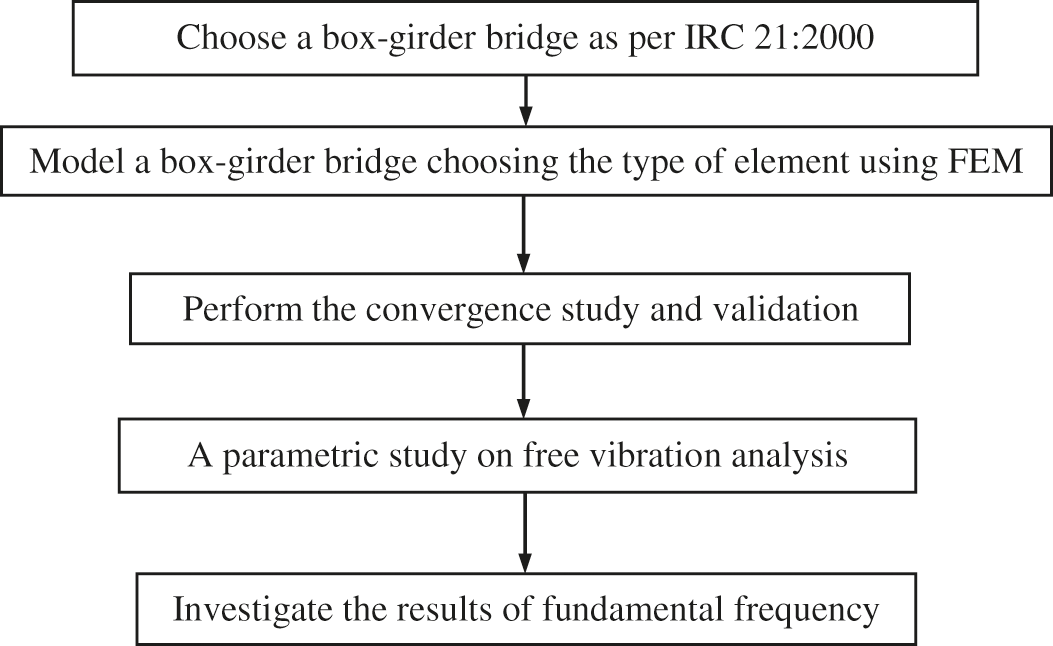
Figure 2: Flow diagram for modelling and analysis
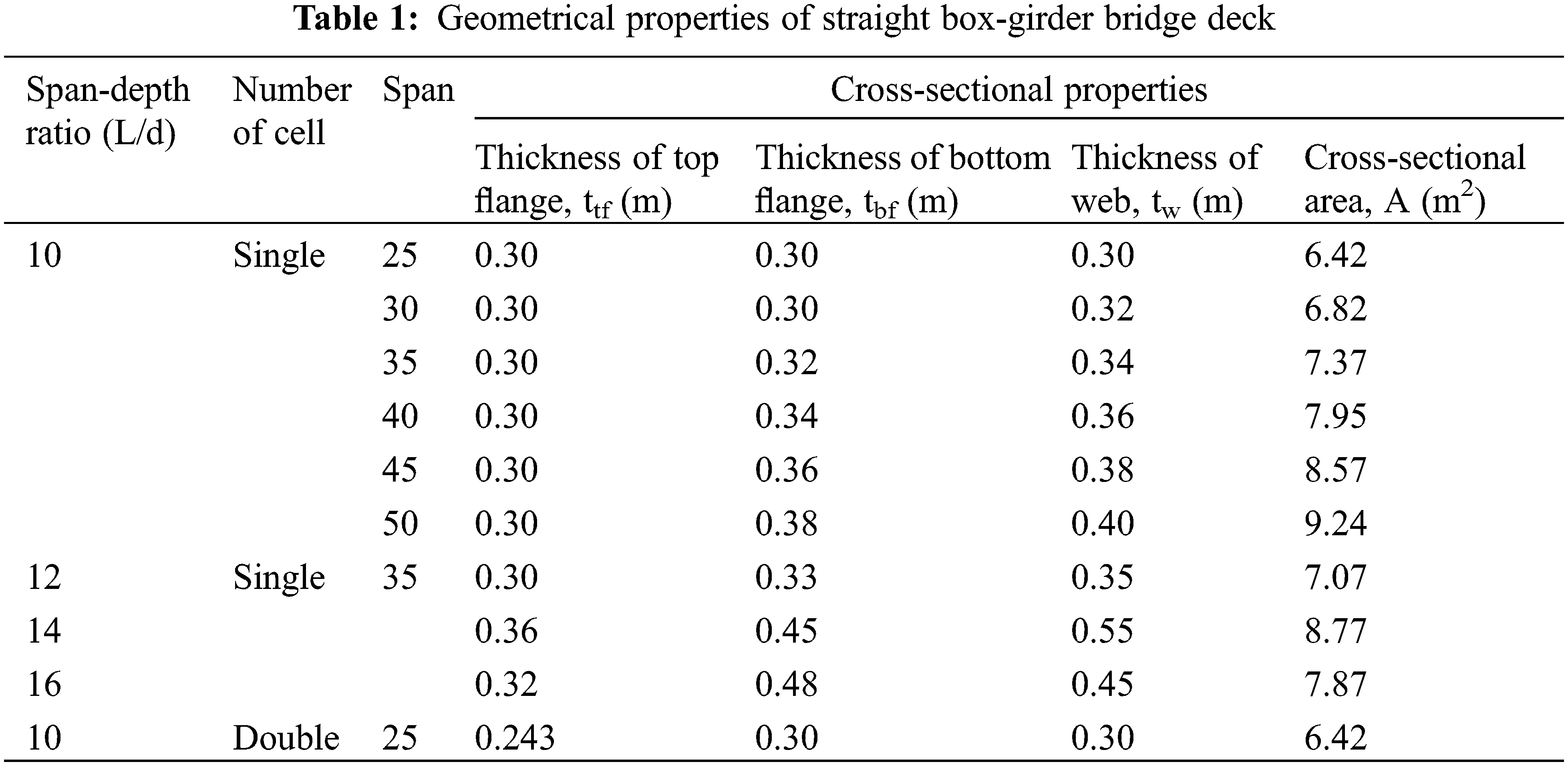
The skew angle, curve angle, span, span-depth ratio, and the cell number are geometrical parameters that directly affect the results, thereby the design. Bridges are designed to satisfy the functional requirements as well as requirements arising due to site conditions. So, these parameters are required to be considered in the estimation of frequencies of skew-curved box-girder bridges. In the present study, the cross-sectional properties of box-girder bridge deck are as follows: Total width = 11.5 m, consisting of roadway = 7.5 m, Kerb = 0.5 m on both sides and Footpath = 1.5 m on both sides. The thickness of the web, top and bottom flanges, are different for different spans and span-depth ratios. The sections are chosen based on a trial procedure. After that, the double-cell box-girder bridge is modelled, keeping the same cross-section as that of a single-cell box-girder bridge. The straight bridge models are found to be safe under limit states of collapse and serviceability, i.e., stress, deflection, and vibration, according to the specifications [25]. Fig. 3 illustrates the cross-sections of single-cell and double-cell box-girder bridge models. Table 1 presents the geometrical properties of a straight box-girder bridge deck used in the present study with different span, span-depth ratio and cell numbers. The same cross-section is used for skew, curved and skew-curved box-girder bridge models.
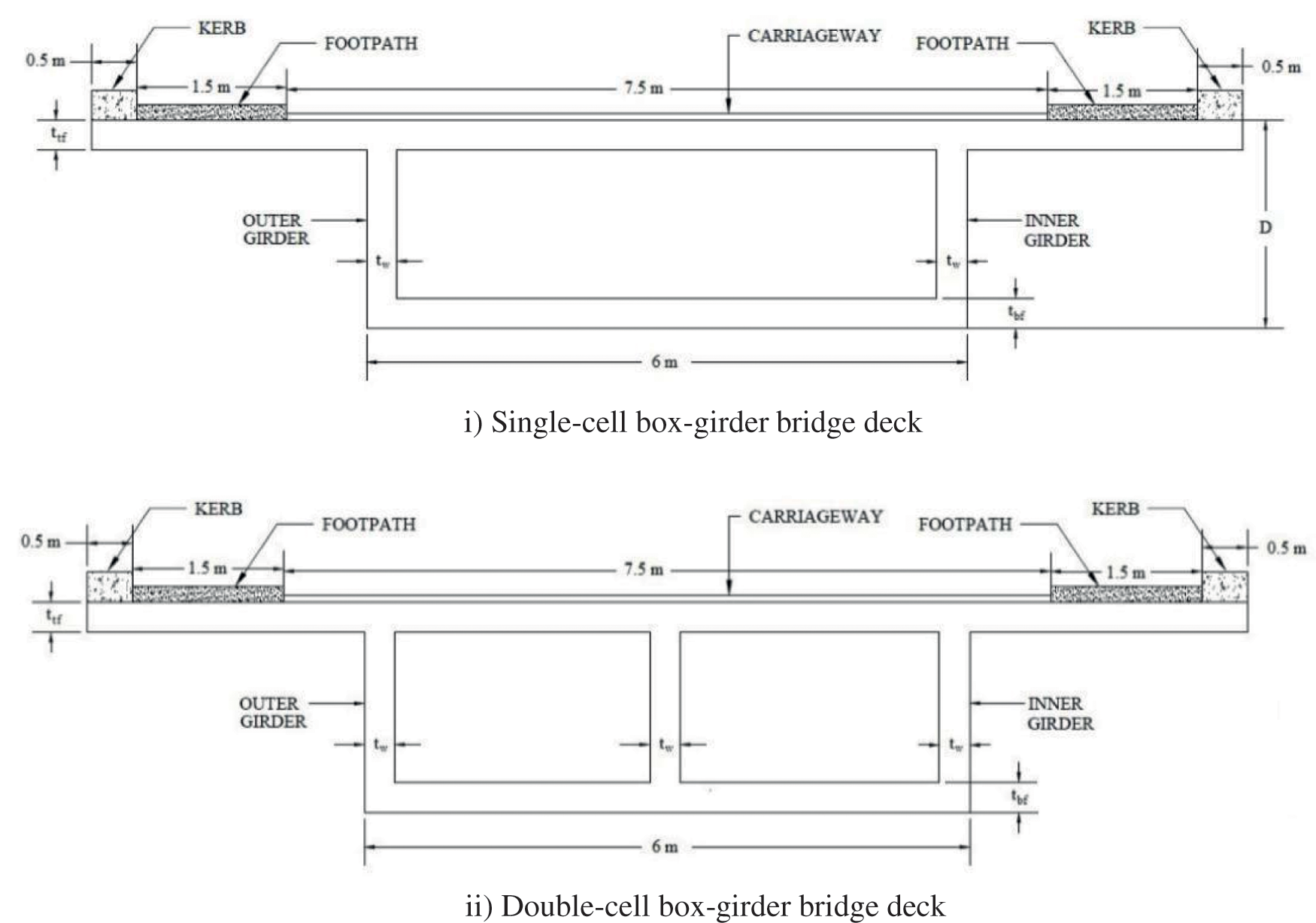
Figure 3: Model of box-girder bridge deck for present study
The material properties of concrete used in the present bridge models are: Characteristic strength = 40 MPa; Poisson’s ratio = 0.2; Density = 25 kN/m3; Modulus of elasticity = 3.16 × 107 kN/m2. The material properties of reinforcing steel are as follows: Density = 77 kN/m3; Yield strength = 500 MPa; Ultimate tensile strength = 545 MPa; Modulus of elasticity = 2 × 108 kN/m2.
Simply supported boundary condition is used to constraint the bridge, and for that two roller supported bearings on one end and two pin supported bearings on the other end are considered. For the straight bridge deck in the present study, the vibration analysis specifications are presented as per Lenzen’s criteria [26]. Lenzen’s criteria show the relationship between fundamental natural frequency and amplitude of vibration. The vibration characteristic is divided into six zones, and it is checked whether a structure is susceptible to vibration. The steps followed for the vibration analysis of the bridge deck using Lenzen’s criteria are illustrated below with a typical calculation:
i) Estimation of the maximum deflection under dead load
Span = 25 m, L/d = 10
M-40 Grade concrete, so
Maximum deflection,
Natural frequency of vibration
ii)
iv) Ensuring that the product,
v) Vibration characteristic is found from the Lenzen’s criteria using the values of
The Vibration characteristics of other spans and span-depth ratios are computed similarly and presented in Table 2. The same cross-sections are used for the parametric study on the skew-curved bridges.
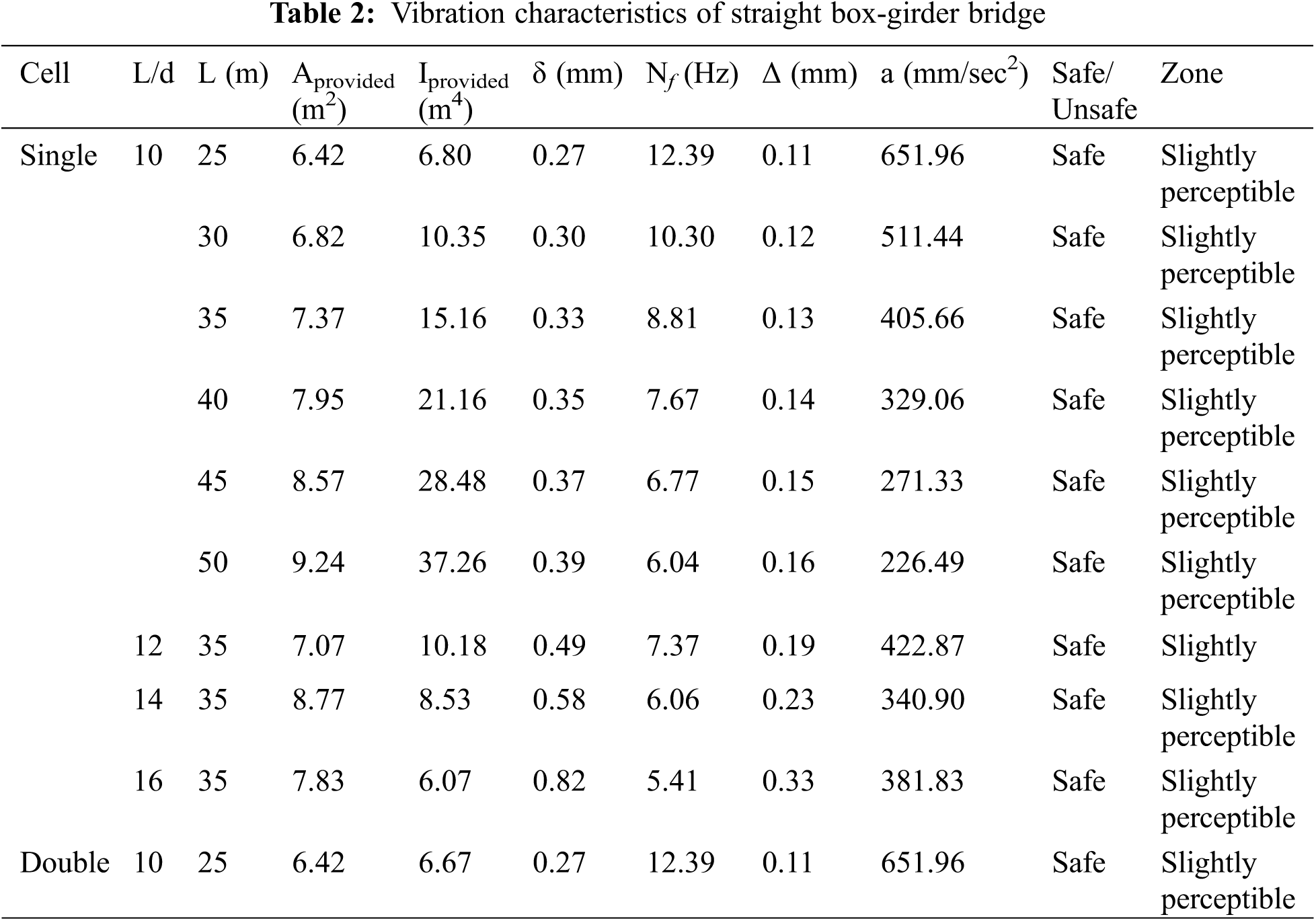
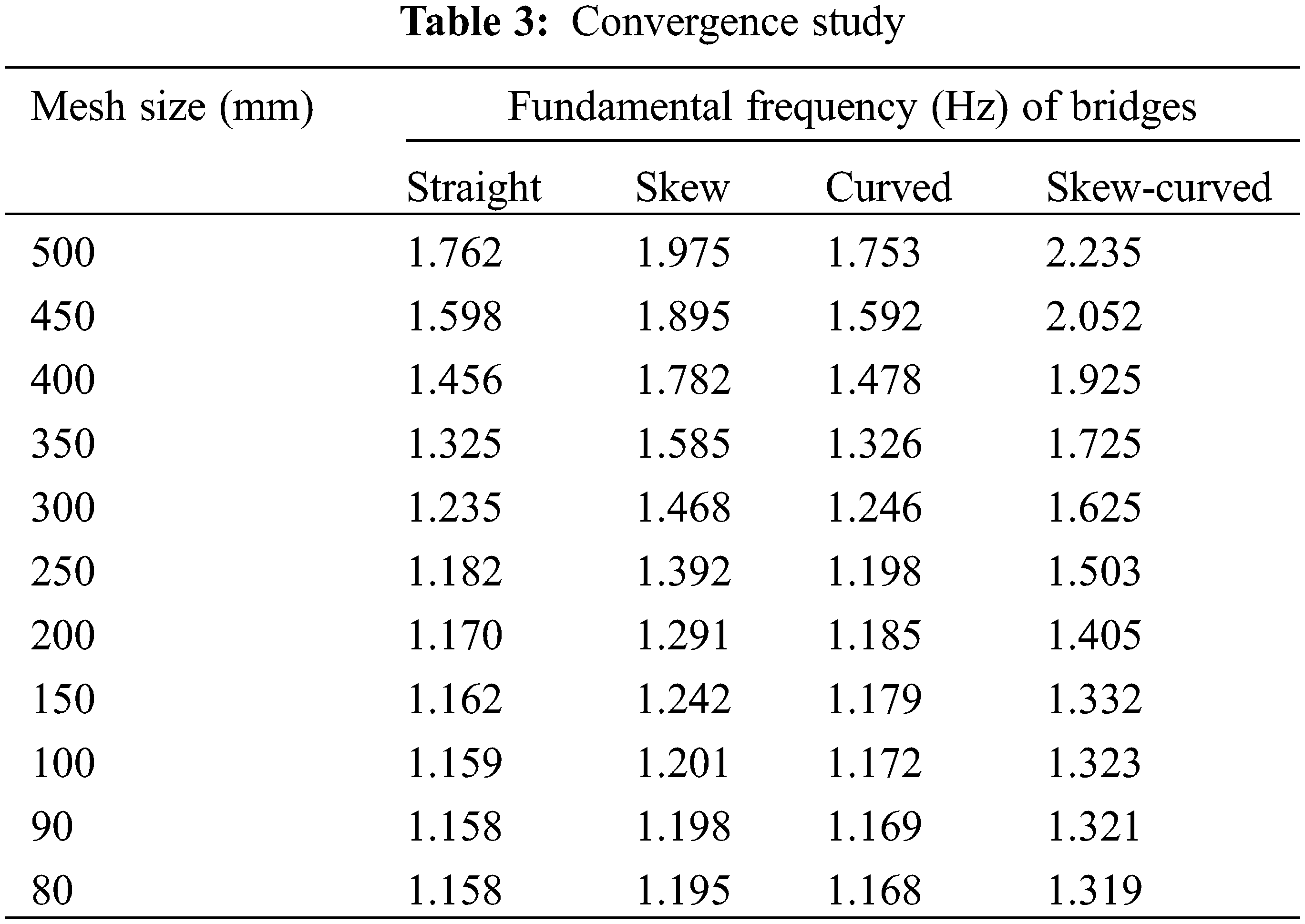
A convergence study is performed to select the refinement in mesh needed to provide the nearest solution. It gives the size of the element required to achieve the minimum error in the evaluated fundamental frequency of bridges. The different models of a single-cell box-girder bridge, i.e., straight, curved, skew and skew-curved, are considered for the study. As presented in Table 3, the results show that the results converge at the mesh size of 100 mm and less. Hence, the mesh size of 100 mm is adopted for further parametric studies.
In the analysis, a three-dimensional linear elastic finite element model is used for all the bridge models. Fig. 4 shows the discretised finite element models of a single-cell box-girder bridge generated by CSiBridge software.
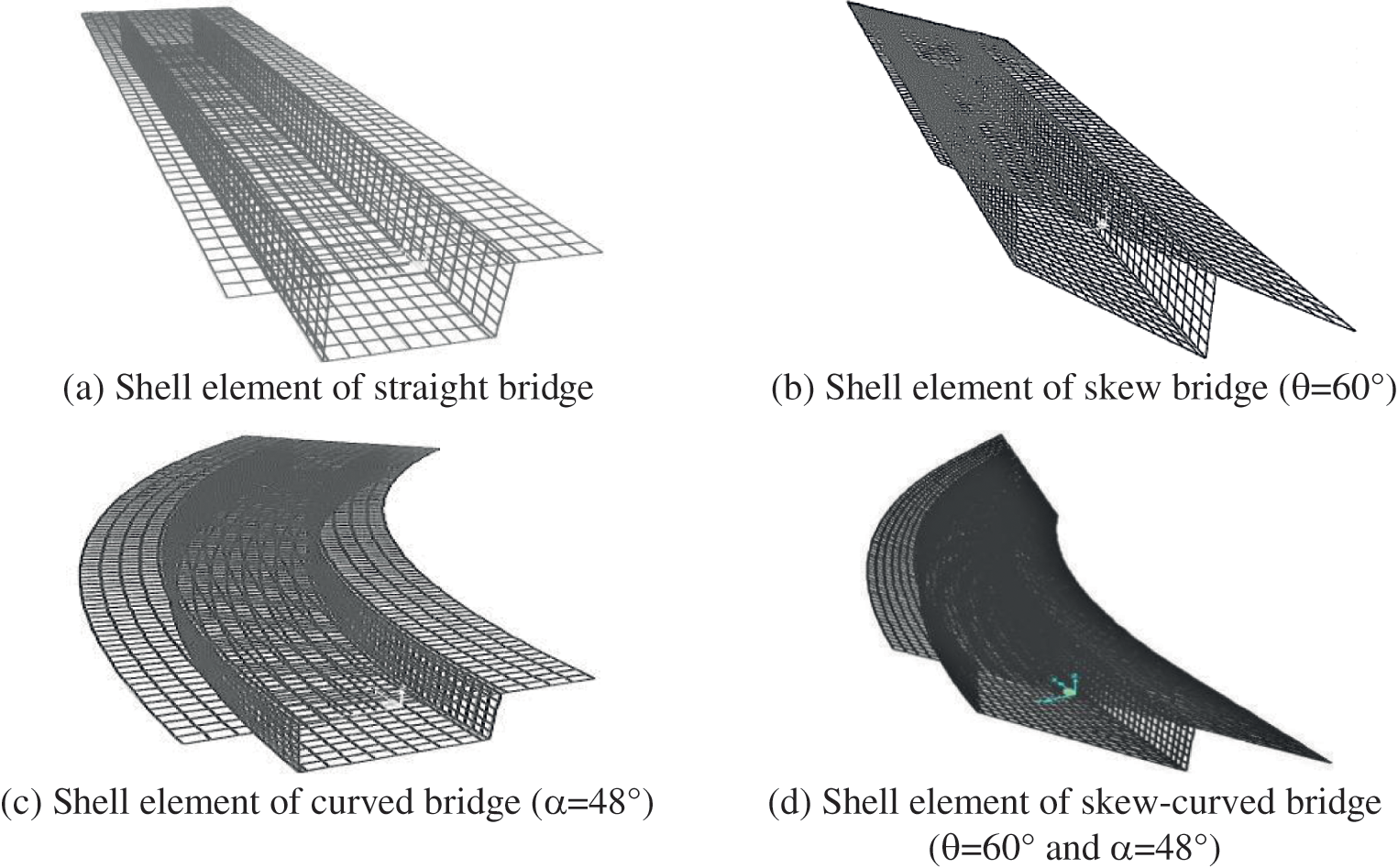
Figure 4: Finite element model of a single-cell box-girder bridge
The results on the frequencies of skew-curved RC box-girder bridges are not available in the literature. However, one may see that the present results are converged; hence, the developed modelling process can be accepted and is extended for further studies on the box-girder bridges.
A detailed parametric study is performed to investigate the natural frequencies of box-girder bridges. Skew angle, curve angle, span, span-depth ratio, and the cell number vary in the study because these are the primary factors that directly affect the bridges’ vibrational characteristics. Here, only the fundamental frequency of the bridge is presented, and the results of other modes of frequencies are circumvented for the sake of conciseness of the paper. The parameters stipulated are as follows: Skew angle (θ) = 0 to 60° at an interval of 10°; Curve angle (α) = 0 to 60° at an interval of 12°; Span (L) = 25 to 50 m at an interval of 5 m for span-depth ratio (L/d) 10; span-depth ratio = 10 to 16 at an interval of 2 for 35 m spans; and the number of cell = 1 and 2. The obtained results are presented in tabular and graphical forms; however, it is hard to interpret the results as the values are relatively closer. The effect of these parameters is shown separately in the following sections.
3.2.1 Effect on Fundamental Frequency of Skew Bridge
The skew angle effect on the fundamental frequency of bridges is investigated for different spans, span-depth ratios, and cells. A single-cell box-girder of the span-depth ratio of 10 is considered for the study. Table 4 presents the variation of fundamental frequency with the skew angle for different spans (25, 30, 35, 40, 45 and 50 m). For better understanding, fundamental frequency and skew angle for different spans are plotted in Fig. 5. The fundamental frequency is insignificant up to 20° skew angle and it is slightly increasing after that. However, it decreases with the increase in span. When the span of the bridge is increased, its mass increases, and thereby decreases frequency. For all the skew bridges considered, the frequency is maximum for the least span, i.e., 25 m, so bridges with the smaller spans are more effective when the vibration is considered. It may be because of the increased flexural stiffness of the bridge compared to the mass. For different skew angle and span, the fundamental frequency lies in the range of 0.98–3.2 Hz.
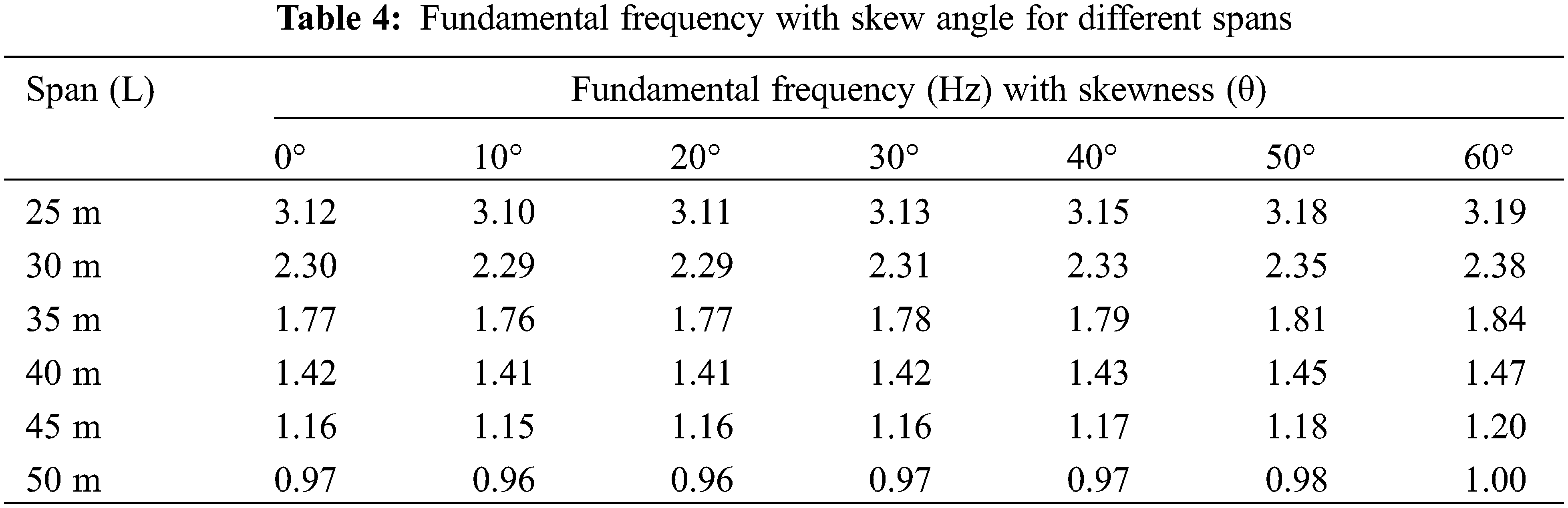
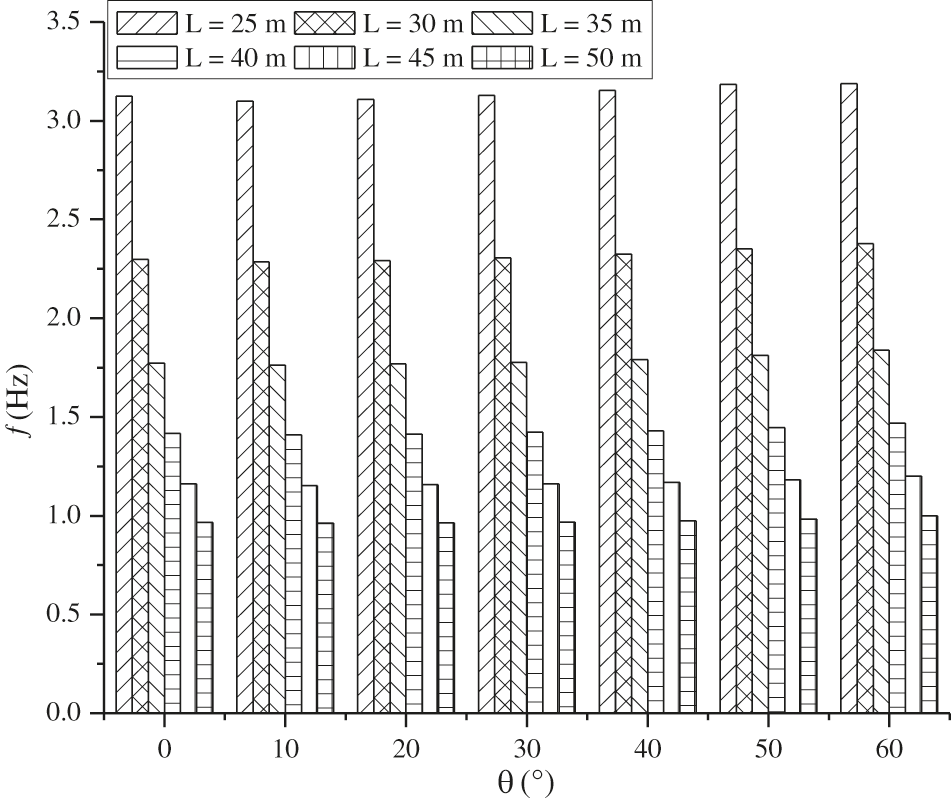
Figure 5: Variation of fundamental frequency with skew angle for different spans
The bridges’ fundamental frequency is evaluated for different skewness and span-depth ratio (10, 12, 14 and 16). A single-cell box-girder bridge of a 35 m span with varying depth is considered for the investigation. The spans less than 35 m are not considered because they do not satisfy the stress and deflection limitations (specified in IRC:21-2000) for all span-depth ratios. However, the effect of the span-depth ratios on the fundamental frequency will be similar if the spans more than 35 m are considered. Table 5 shows the variation of fundamental frequency with the skew angle for different span-depth ratios. The fundamental frequency and skew angle for different span-depth ratios are plotted in Fig. 6 for readers’ lucidity. The fundamental frequency increases slightly with the skew angle for different span-depth ratios. In the skew bridge, the support arrangement enhances its stiffness, and thus its fundamental frequency increases. Also, it increases with the span-depth ratio. For a similar span, when the span-depth ratio increases, the depth of the bridge decreases; hence, the fundamental frequency increases. When the depth of the bridge is decreased, its mass decreases and thereby increases the frequency. It is observed that the skew bridge with a higher span-depth ratio is more beneficial. For different skew angles and span to depth ratios, the fundamental frequency lies in the range of 1.7–2.0 Hz.
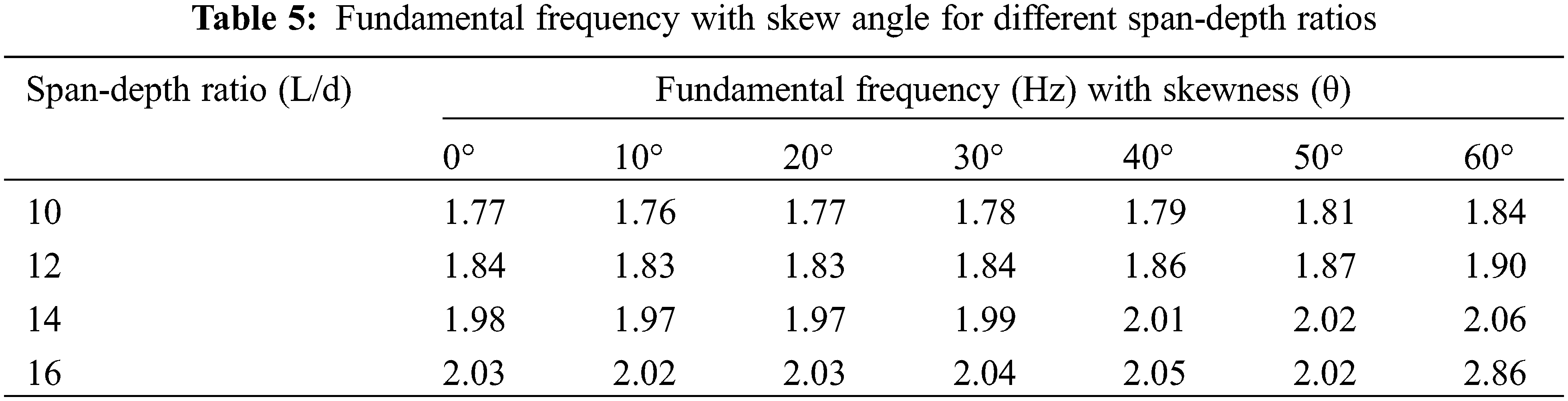

Figure 6: Variation of fundamental frequency with skew angle for different span-depth ratios
The frequency of single-cell and double-cell box-girder bridges is compared. For the investigation, a span of 25 m and a span-depth ratio of 10 are considered. A span of 25 m is considered in the study as it is specified in IRC:21-2000 to use a minimum span of 25 m for box-girder bridges. Span-depth ratios of more than 10 are not considered as they do not satisfy the serviceability criteria specified in IRC:21-2000. Table 6 presents the effect of the skew angle (0, 10, 20, 30, 40, 50 and 60°) on the bridges’ fundamental frequency with different numbers of cells. It is observed that the fundamental frequency does not change with the skew angle of single-cell, but it increases with the skew angle of double-cell. The double-cell bridge’s stiffness is more than a single-cell; hence, the double-cell bridge has more frequency. So, the double-cell skew box-girder bridge is more effective than the single-cell. For a single-cell bridge, the fundamental frequency is about 3.18 Hz for all the skew angles, while for a double-cell, it is in the range of 3.2–3.61.

3.2.2 Effect on Fundamental Frequency of Curved Bridge
The curve angle effect on the fundamental frequency of bridges is investigated for different spans, span-depth ratios, and cells. Table 7 presents the fundamental frequency of bridges for different curve angles and spans. The fundamental frequency and curve angle for different spans are plotted in Fig. 7. It is observed that the effect of the curve angle is almost insignificant. The fundamental frequency of the curved bridge is dominated by bending and torsion. With the curvature increase, both the torsional and flexural rigidities are increased but opposite in nature, and they counteract each other. Thus, the influence of the curve angle on the fundamental frequency is insignificant. The fundamental frequency decreases with the increase in span. So, the curved bridges with lesser spans are more effective. For different curve angles and spans, the fundamental frequency lies in the range of 0.98–3.1 Hz.

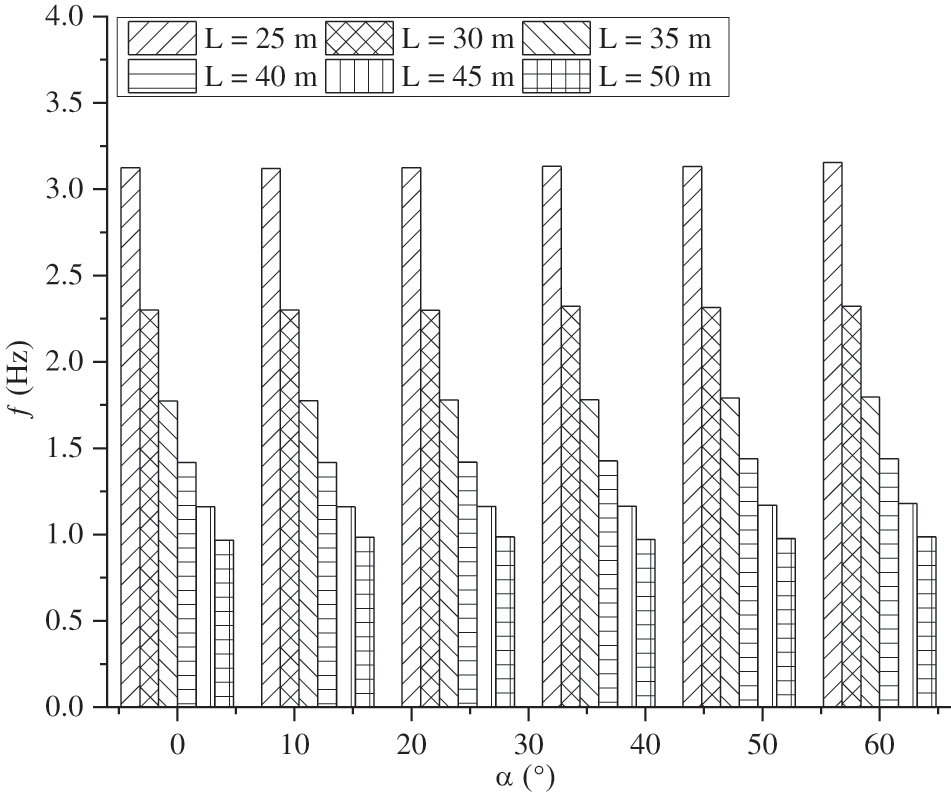
Figure 7: Variation of fundamental frequency with curve angle for different spans
The influence of curve angle and span-depth ratio on the fundamental frequency is investigated and presented in Table 8. The fundamental frequency and curve angle for different span-depth ratios is plotted in Fig. 8. The effect of the curve angle on the frequency is insignificant for any span-depth ratio. But, the frequency increases with the increment in the span-depth ratio. Thus, the curved bridge with a higher span-depth ratio is preferable. For different skew angles and span-depth ratios, the fundamental frequency lies in the range of 1.7–2.0 Hz.
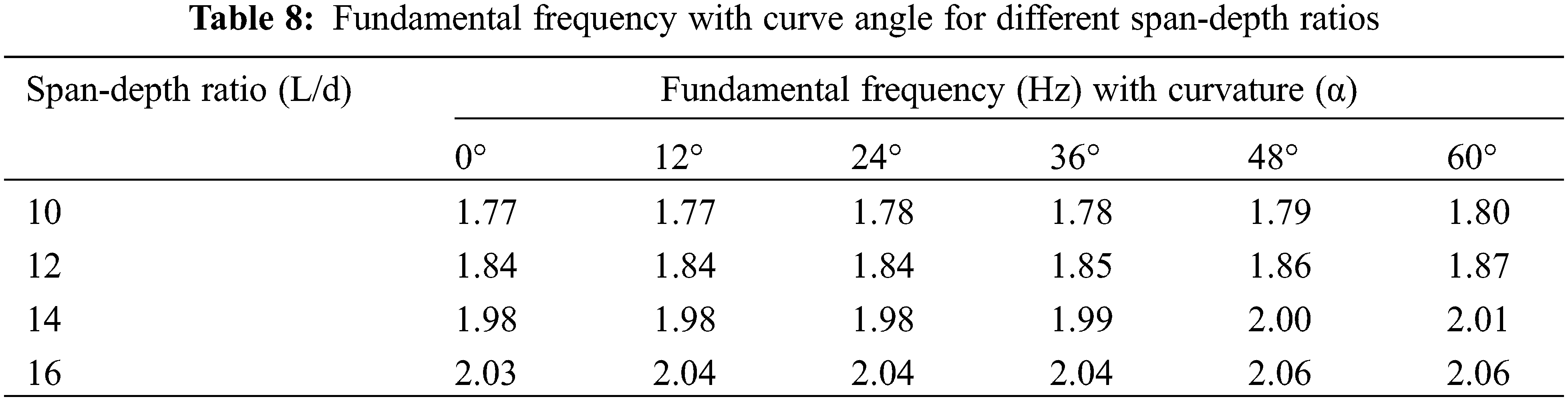
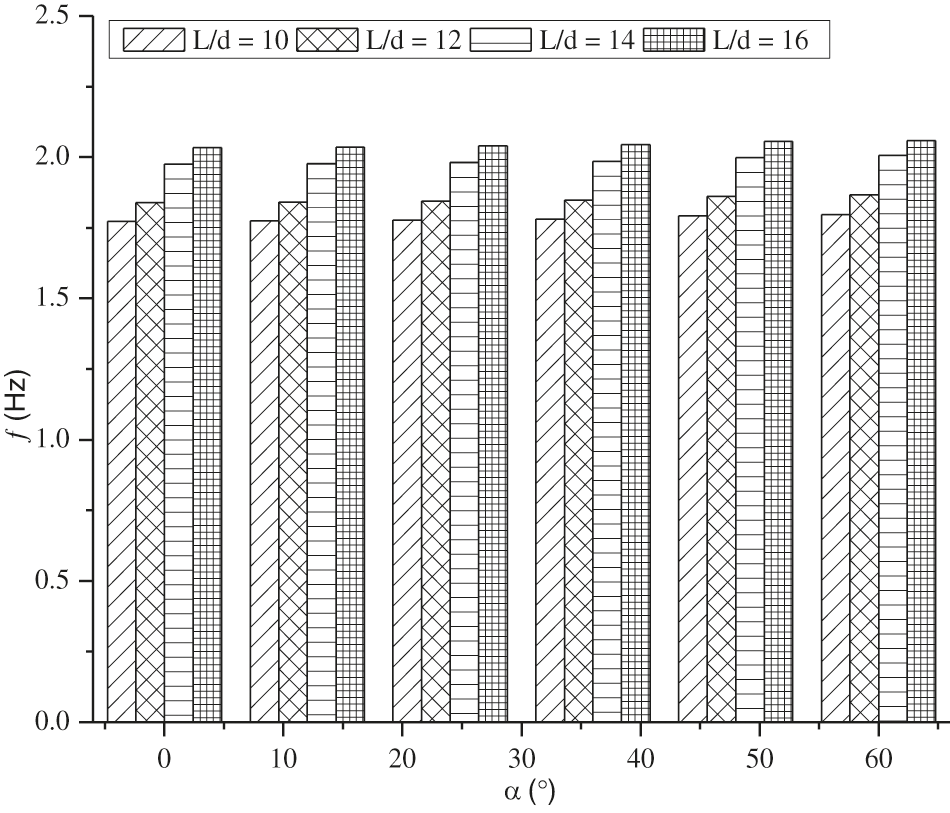
Figure 8: Variation of fundamental frequency with curve angle for different span-depth ratio
Table 9 presents the frequency of single and double-cell box-girder bridges with varying curvature. The effect of curvature on the frequency of the bridges is almost insignificant. But, the frequency 3.15 and 3.24 for single-cell and double-cell box-girder bridges, respectively.

3.2.3 Effect on Fundamental Frequency of Skew-Curved Bridge
The fundamental frequency of skew-curved bridges is investigated. Table 10 presents the combined effect of skew and curve angles on the fundamental frequency for different spans. Some of the frequency values are not shown in Table 10 because the construction of such bridges (smaller spans having high skewness and curvature) is difficult in the real situation. For straight bridges, the effect of skewness on the frequency is almost insignificant. When the curvature is introduced in the skew bridges, the fundamental frequency increases with the skew angle. The bridge’s torsional rigidity increases due to its skewness and curvature, so the fundamental frequency is improved. The frequency increment is observed only for the spans ≤40 m. Thus, the highly skew-curved bridge with a smaller span is preferable. When the span of the straight bridge is increased from 25 to 50 m, the fundamental frequency reduces from 3.1 to 0.96 Hz. For a 48° curved bridge with a skewness of 50°, the fundamental frequency reduces from 3.5 to 1.03 Hz when the span is increased from 25 to 50 m.
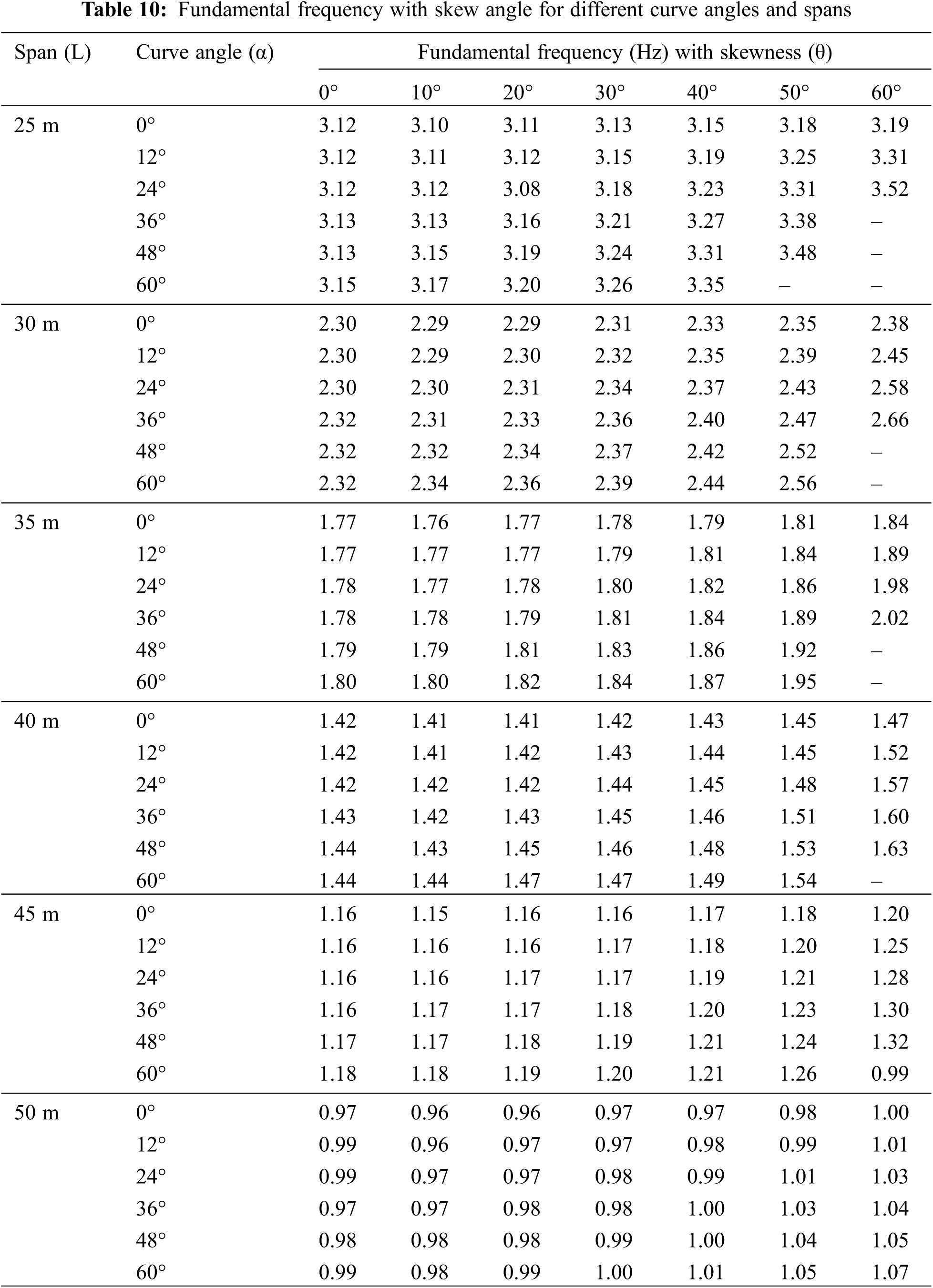
The influence of skew and curve angles on the fundamental frequency for different span-depth ratios is shown in Table 11. The bridges with skewness of 60° and the curvatures of 48° and 60° are not presented because bridges of spans ≤40 m and more skewness and curvature cannot generally be constructed. The fundamental frequency is increased slightly with the skew angle. But, the values of the fundamental frequency are significant for different span-depth ratios. When the curvature is introduced in skew bridges, the frequency increases significantly with the skew angle. So, bridges with more skewness and curvature having larger span-depth ratios are more effective than straight bridges. For straight bridges, when the span-depth ratio increases from 10 to 16, the fundamental frequency increases from 1.8 to 2.0 Hz. For a 60° curved bridge with a skewness of 50°, the fundamental frequency increases from 2.0 to 2.3 Hz when the span-depth ratio is increased from 10 to 16.
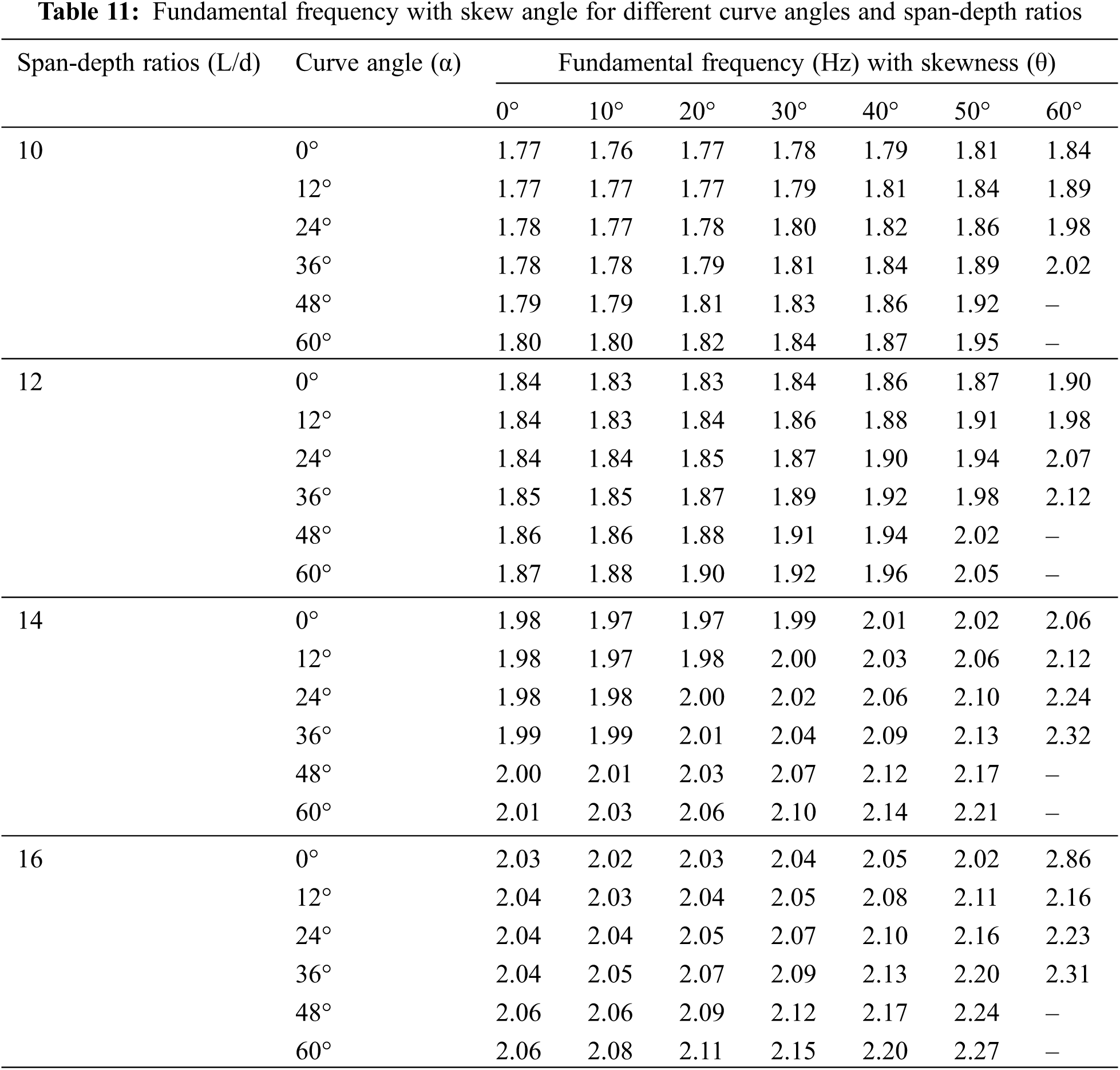
Table 12 presents the combined effect of skew and curve angles on the fundamental frequency of bridges having different numbers of cells. Some of the fundamental frequency results are not shown in Table 12, as those bridges cannot be constructed. For single-cell straight bridges, the skew angle effect on the frequency is insignificant, but it increases with the skewness for double-cell bridges. The fundamental frequency of the double-cell bridge is more compared to that of the single-cell bridge. When the curvature is introduced in skew bridges, the fundamental frequency increases significantly with the skew angle irrespective of the number of cells. So, highly skew-curved bridges having double-cell are preferable. The fundamental frequency increases to about 3.1 and 3.3 Hz for single-cell and double-cell straight bridges, respectively. For a 48° curved bridge having a skewness of 50°, the fundamental frequency increases to about 3.5 and 3.8 Hz for single-cell and double-cell straight bridges, respectively.
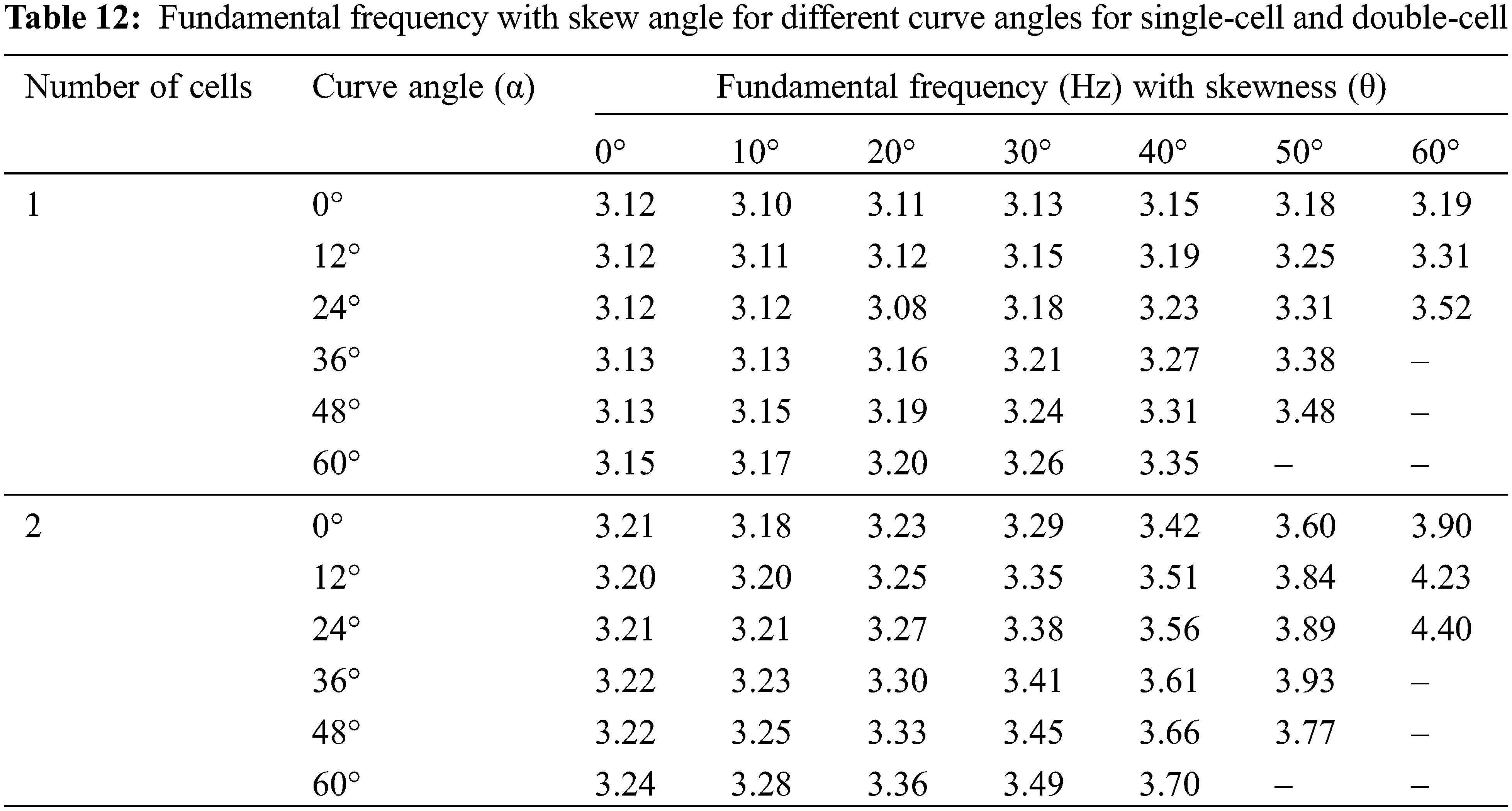
A bridge with 45 m span and a span-depth ratio of 10 is selected herein to investigate the effect of skew and curve angles. The combined effect of skew and curve angles on the fundamental frequency is illustrated in Fig. 9. For the non-skew bridge, the frequency increases slightly with the curve angle. When the skewness is introduced in the curved bridge, the frequency increases significantly with the curve angle up to 50° skew angle. But for 60° skew bridge, the fundamental frequency increases with the curve angle up to 48°; after that, it suddenly decreases. It may be due to more torsional rigidity, which affects the highly skew-curved bridge’s flexural rigidity (α = 60°, θ = 60°). So, the bridges with 60° skewness and 48° curvature are more effective than the straight bridge. For the curved bridge, the fundamental frequency is about 1.2 Hz. For 60° skew bridge, the fundamental frequency is about 1.20, 1.25, 1.28, 1.30, 1.32 and 0.99 Hz for curve angles 0, 10, 20, 30, 40, 50 and 60°, respectively.
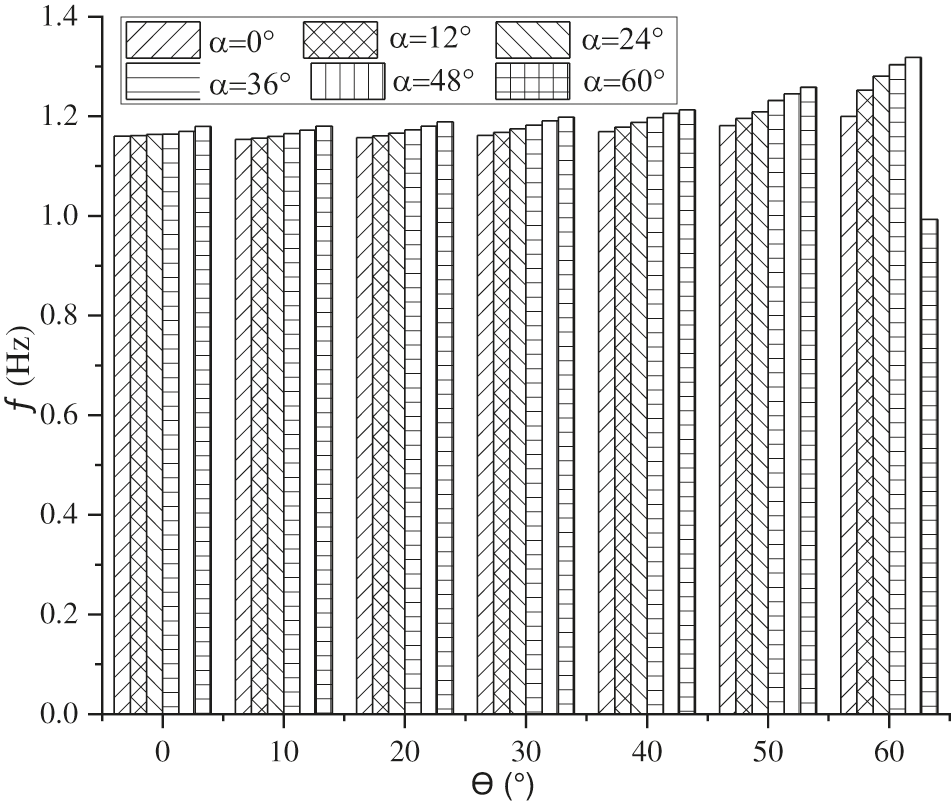
Figure 9: Fundamental frequency with skew and curve angles
The bridge has an endless number of possible modes because it has infinite degrees of freedom with continuous mass. According to IS 1893:2016, part 1 [27], the number of modes is considered up to which the cumulative modal masses are at least 90% of the total seismic mass. A typical single-cell skew-curved box-girder (span-45 m, span-depth ratio-10) bridge having 48° curvature and 60° skewness is studied to evaluate the natural frequencies. The frequencies for only the first eleven modes are presented in Table 13, considering 90% modal mass participation. The first three mode shapes are shown in Fig. 10 for a visual/qualitative comparison.
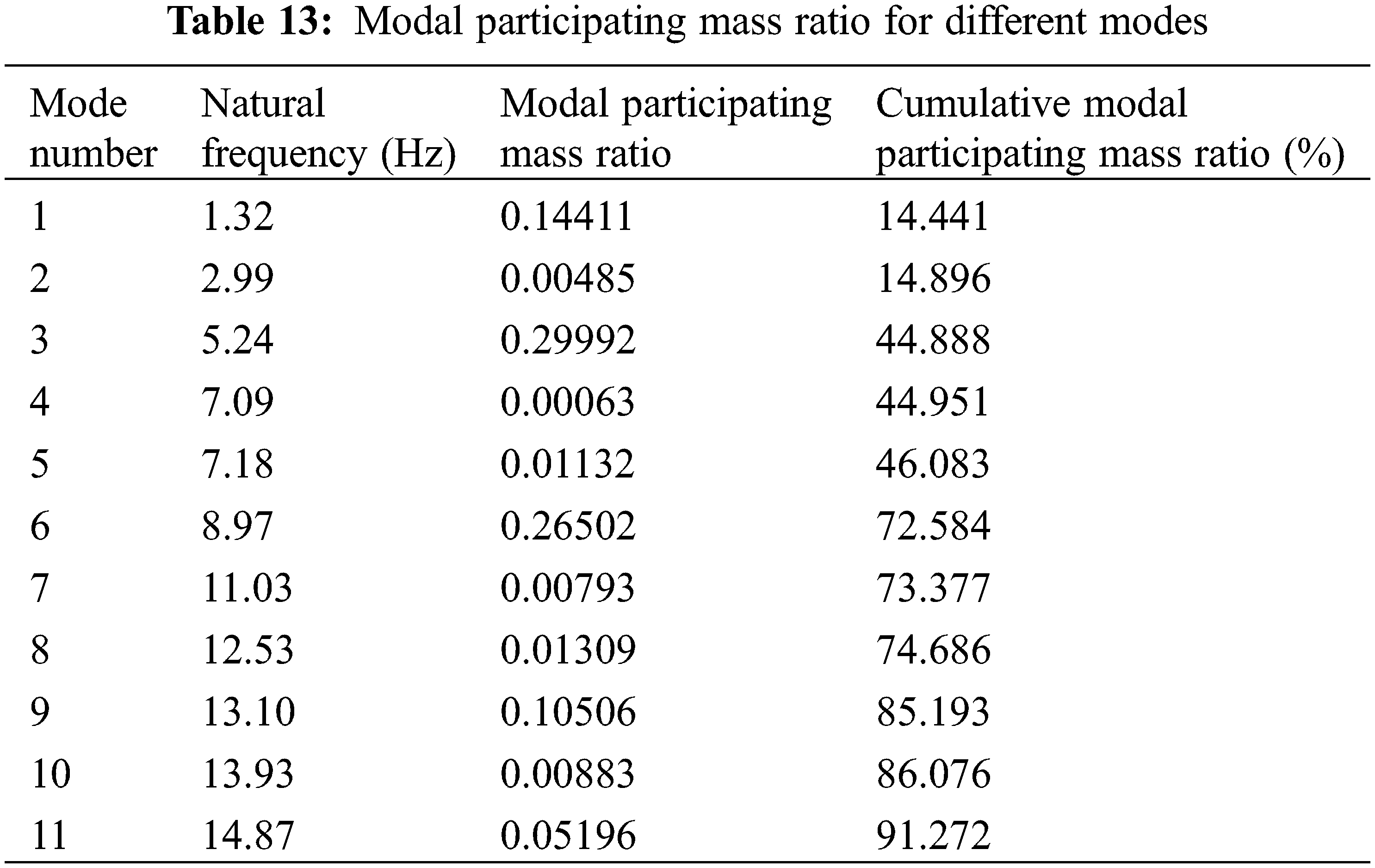
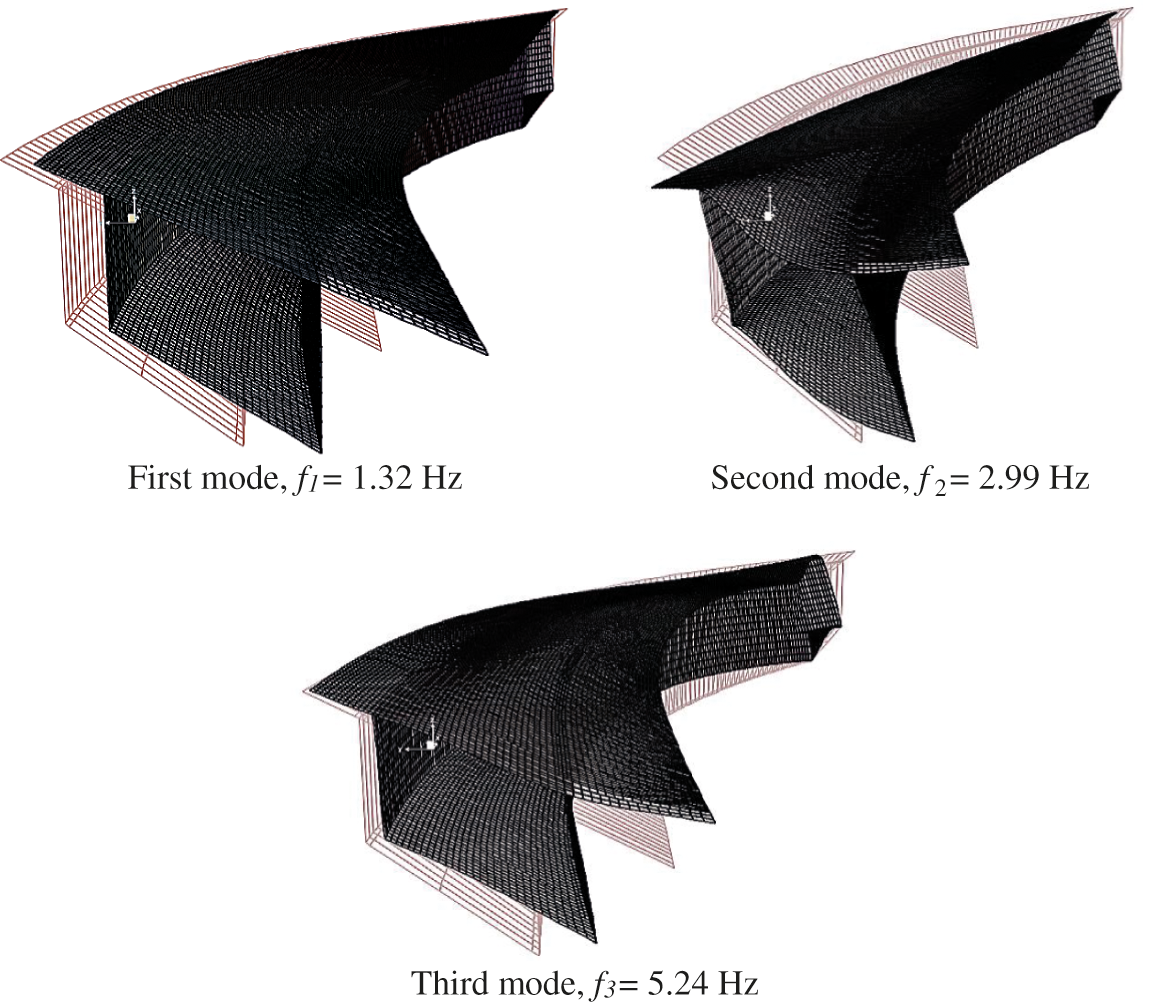
Figure 10: First three mode shapes of a skew-curved box-girder bridge
The fundamental frequency of different box-girder bridges was evaluated, and it is mostly in the range of 1 to 4.5 Hz. Here, the fundamental frequency of the bridge and the external agencies’ vibration are correlated. The bridge vibrates due to the moving loads. The exciting frequency generated due to walking over the bridge is generally in the range of 1.6 to 2.4 Hz [28]. The approximate value of exciting frequency generated due to: slow walk is 1.7 Hz; normal walk is 2 Hz; and fast walk is 2.3 Hz [29]. Mostly heavy vehicles are found to have a fundamental frequency in the range 2 to 5 Hz [30]. The fundamental frequency of the AASTHO HS20 truck is about 6.36 to 12.92 Hz [31]. Traffic-induced vibrations are generated mainly by the fluctuations of wheel contact forces, specially when vehicles travel over irregularities in the road surface. The maximum amplitude of vibration occurs when the vehicle and the bridge’s frequencies are the same, usually within the range of 2 to 5 Hz.
Also, the maximum dynamic response occurs when the vehicle’s speed is such that the time it takes to cross a span is approximately equal to the fundamental period of vibration of the structure. However, the vehicle speed is not a significant factor in determining the response of the bridges. A larger response may be produced by heavy vehicles due to accelerating or braking. That is why the vehicle speed is restricted on large span bridges as it produces maximum dynamic loading, except for a very short span (less than 15 m).
Because of the above, the box-girder bridges should be designed considering the critical range occupied by most of the vehicles, i.e., 2 to 5 Hz. Therefore, the present study is important as it provides the results of the fundamental frequency of different box-girder bridges.
The fundamental frequency of different box-girder bridges is investigated via a parametric study using the finite element method. The parameters chosen are skew angle, curve angle, span, span-depth ratio, and cell number, which influence the fundamental frequency of these bridges (skew, curved and skew-curved). The following conclusions are drawn from the present study:
• The effect of the curve angle on the fundamental frequency is insignificant. But the fundamental frequency increases with the skew angle. So, the skew bridge is more effective than the straight and curved bridges where vibrations are dominant. Hence, in those situations, skew bridges are preferable compared to straight and curved bridges.
• The fundamental frequency decreases with the increase in the span. However, it increases with the span-depth ratio.
• The fundamental frequency of the double-cell bridge is more compared to that of a single-cell bridge. So, a double-cell bridge is preferable compared to a single-cell bridge. The double-cell bridge’s fundamental frequency increases with the skew angle, but the effect of the curve angle on the double-cell bridge is insignificant.
• The fundamental frequency is more in the case of skew-curved bridges than that in the straight bridges for different spans, span-depth ratios and the number of cells. But the fundamental frequency of the bridge with more skewness (60°) and curvature (60°) is smaller in comparison to the straight bridge.
• The increment in the fundamental frequency of a skew-curved bridge (α = 48°, θ = 60°) is about 13% and 15% for single-cell and double-cell bridges, respectively, compared to the straight bridge. So, the double-cell skew-curved box-girder is preferable.
• The bridges need to be strengthened against vibration if the range of fundamental frequency is small (1.0–4.5 Hz).
Funding Statement: The authors acknowledge Motilal Nehru National Institute of Technology Allahabad for providing financial support under TEQIP-III.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. Komatsu, S., Nakai, H. (1966). Study on free vibrations of curved girder bridges. Transactions of the Japan Society of Civil Engineers, 36(1), 35–60. DOI 10.2208/jscej1949.1966.136_35. [Google Scholar] [CrossRef]
2. Tabba, M. M., Turkstra, C. J. (1997). Free vibrations on curved box girders. Journal of Sound and Vibration, 54(4), 501–514. DOI 10.1016/0022-460X(77)90608-3. [Google Scholar] [CrossRef]
3. Memory, T., Thambiratnam, D., Brameld, G. (1995). Free vibration analysis of bridges. Engineering Structures, 17(10), 705–713. DOI 10.1016/0141-0296(95)00037-8. [Google Scholar] [CrossRef]
4. Huanga, D., Wang, T. L., Shahawy, M. (1998). Vibration of horizontally curved box girder bridges due to vehicles. Computers and Structures, 68(5), 513–528. DOI 10.1016/S0045-7949(98)00065-0. [Google Scholar] [CrossRef]
5. Maleki, S. (2001). Free vibration of skewed bridges. Journal of Vibration and Control, 7(7), 935–952. DOI 10.1177/107754630100700701. [Google Scholar] [CrossRef]
6. Taysi, N., Ozakca, M. (2002). Free vibration analysis and shape optimization of box-girder bridges in straight and curved planform. Engineering Structures, 24(5), 625–637. DOI 10.1016/S0141-0296(01)00127-4. [Google Scholar] [CrossRef]
7. Yoon, K. Y., Kang, Y. J., Choi, Y. J. (2005). Free vibration analysis of horizontally curved steel I-girder bridges. Thin Walled Structures, 43(4), 679–699. DOI 10.1016/j.tws.2004.07.020. [Google Scholar] [CrossRef]
8. Guebailia, M., Ouelaa, N., Guyade, J. L. (2013). Solution of the free vibration equation of a multi span bridge deck by local estimation method. Engineering Structures, 48(4), 695–703. DOI 10.1016/j.engstruct.2012.12.004. [Google Scholar] [CrossRef]
9. Mohseni, I., Rashid, B., Junsunk, K. (2014). A simplified method to estimate the fundamental frequency of skew continues multicell box-girder bridges. Latin American Journal of Solids and Structures, 11(4), 649–658. DOI 10.1590/S1679-78252014000400006. [Google Scholar] [CrossRef]
10. Deng, Y., Phares, B. M., Greimann, L. (2015). Behavior of curved and skewed bridges with integral abutments. Journal of Constructional Steel Research, 30(109), 115–136. DOI 10.1016/j.jcsr.2015.03.003. [Google Scholar] [CrossRef]
11. Mishra, S. K., Gur, S., Roy, K., Chakraborty, S. (2016). Response of bridges isolated by shape memory-alloy rubber bearing. Journal of Bridge Engineering, 21(3), 04015071. DOI 10.1061/(ASCE)BE.1943-5592.0000837. [Google Scholar] [CrossRef]
12. Roy, B. K., Chakraborty, S., Mishra, S. K. (2016). Seismic vibration control of bridges with excessive isolator displacement. Earthquakes and Structures, 10(6), 1451–1465. DOI 10.12989/eas.2016.10.6.1451. [Google Scholar] [CrossRef]
13. Saha, A., Saha, P., Patro, S. K. (2017). Polynomial friction pendulum isolators (PFPIs) for seismic performance control of benchmark highway bridge. Earthquake Engineering and Engineering Vibration, 16(4), 827–840. DOI 10.1007/s11803-017-0418-5. [Google Scholar] [CrossRef]
14. Gupta, T., Kumar, M. (2018). Flexural response of skew-curved concrete box-girder bridges. Engineering Structures, 163(1), 358–372. DOI 10.1016/j.engstruct.2018.02.063. [Google Scholar] [CrossRef]
15. Gupta, T., Kumar, M. (2019). Reaction response of horizontally curved and skewed concrete box-girder bridges. Recent Advances in Structural Engineering, 1, 49–60. DOI 10.1007/978-981-13-0362-3. [Google Scholar] [CrossRef]
16. Gupta, N., Agarwal, P., Pal, P. (2019). Free vibration analysis of RCC curved box girder bridges. International Journal of Technology Innovation in Modern Engineering & Science, 5, 1–7. [Google Scholar]
17. Agarwal, P., Pal, P., Mehta, P. K. (2019). Analysis of RC skew box girder bridges. International Journal of Science and Innovative Engineering & Technology, 6, 1–8. [Google Scholar]
18. Gupta, N., Agarwal, P., Pal, P. (2019). Analysis of RCC curved box girder bridges. Applied Innovative Research, 1, 153–159. [Google Scholar]
19. Zhu, X., Zeng, L., Li, B. (2019). Vibration analysis of a drillstring in horizontal well. Computer Modeling in Engineering & Sciences, 122(1), 631–660. DOI 10.32604/cmes.2019.06755. [Google Scholar] [CrossRef]
20. Jiang, L., Feng, Y., Zhou, W., He, B. (2019). Vibration characteristic analysis of high-speed railway simply supported beam bridge-track structure system. Steel and Composite Structures, 31(6), 591–600. DOI 10.12989/scs.2019.31.6.591. [Google Scholar] [CrossRef]
21. Wang, X., Yue, X., Wen, H., Yuan, J. (2020). Hybrid passive/active vibration control of a loosely connected spacecraft system. Computer Modeling in Engineering & Sciences, 122(1), 61–87. DOI 10.32604/cmes.2020.06871. [Google Scholar] [CrossRef]
22. Agarwal, P., Pal, P., Mehta, P. K. (2020). Finite element analysis of skew box-girder bridges under IRC-A loading. Journal of Structural Engineering (Madras), 47, 243–258. [Google Scholar]
23. Agarwal, P., Pal, P., Mehta, P. K. (2020). Parametric study on skew-curved RC box-girder bridges. Structures, 28(4), 380–388. DOI 10.1016/j.istruc.2020.08.025. [Google Scholar] [CrossRef]
24. CSi Bridge (2016). Analysis Reference Manual Version 20.0.0. Computer Structure. Berkeley, CA. [Google Scholar]
25. Indian Road Congress (IRC) 21 (2000). Standard specification and code of practice for road bridges, section III-cement concrete (planed and reinforced3rd ed [Google Scholar]
26. Raina, V. K. (1994). Concrete bridge practice: Analysis, design and economics, 2nd ed. India: McGraw-Hill Education. [Google Scholar]
27. Indian Standard (IS) 1893 (2016). Criteria for earthquake resistant design of structures, part 1-general provisions and buildings. [Google Scholar]
28. Gheitasi, A., Ozbulut, A., Usmani, S., Alipour, M., Harris, D. K. (2016). Experimental and analytical vibration serviceability assessment of an in-service footbridge. In: Case studies in nondestructive testing and evaluation, vol. 6, pp. 79–88. DOI 10.1016/j.csndt.2016.11.001. [Google Scholar] [CrossRef]
29. Newland, D. E. (2004). Pedestrian excitation of bridges. Journal of Mechanical Engineering and Sciences, 218, 477–492. DOI 10.1243/095440604323052274. [Google Scholar] [CrossRef]
30. Li, H., Wekezer, J., Kwasniewski, L. (2008). Dynamic response of a highway bridge subjected to moving vehicles. Journal of Bridge Engineering, 13(5), 439–448. DOI 10.1061/(ASCE)1084-0702(2008)13:5(439). [Google Scholar] [CrossRef]
31. Shi, X., Cai, C. S., Chen, S. (2008). Vehicle induced dynamic behavior of short-span slab bridges considering effect of approach slab condition. Journal of Bridge Engineering, 13(1), 83–92. DOI 10.1061/(ASCE)1084-0702(2008)13:1(83). [Google Scholar] [CrossRef]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |