Sound & Vibration

DOI: 10.32604/sv.2021.015008

ARTICLE

Manipulating Chladni Patterns of Ferromagnetic Materials by an External Magnetic Field

Kenneth R. Podolak*, Vihan A.W. Wickramasinghe, Gareth A. Mansfield and Alex M. Tuller

State University of New York, Plattsburgh, 12901, USA
*Corresponding Author: Kenneth R. Podolak. Email: kpodo001@plattsburgh.edu
Received: 15 November 2020; Accepted: 23 March 2021

1  Introduction

Insights into the quantum world can be experimentally studied by driving oscillations and experimentally measuring the effects on resonant states [1,2]. An early study of these oscillations comes from a German physicist, Chladni, who discovered that a vibrating metal plate would take randomly distributed sand particles at a particular set resonant frequency and vibrate them away from the antinodes and concentrate the sand at the nodes [3]. The particles move to the nodes but the way these particles move is likely due to random motion [4,5] which may mean this motion cannot be controlled [6]. Various vibrational modes in the plate can be excited using a variety of techniques, such as a speaker [7] or a vibrating rod [8]. The size of a Chladni plate has also been investigated by Pitre [9]. Using a circular plate, Chladni concluded that the number of nodal circles in a pattern has a relation to the frequency set on the circular plate. This relationship is known as Chladni’s law as cited by Rayleigh [3] and later verified experimentally by Rossing [10]. The nodes from the circular plates have been more precisely determined by Kirchhoff based on boundary condition treatments that yield Bessel function solutions [11,12]. Many other scientists have studied Chladni patterns including Savart [13], van Gerner et al. [14,15], and Tuan et al. [16]. French scientist Savart was one of the first to use Chladni patterns in research on violin acoustics [13]. van Gerner showed that the resonating plate’s acceleration needs to be lower than the gravitational acceleration and those particles may move to the antinodes [14]. Tuan precisely determined the frequency where Chladni patterns occur through the effective impedance of the mechanical oscillator [16]. Today, the Chladni plate is used as a demonstration or laboratory exercise [17]. In this experiment, both a speaker and a violin bow were used to vibrate the plate. The plate was also struck by a hammer, and the presence of various vibrational modes was dependent on the location, force, and material of the hammer. Even Diana Cowern, “The Physics Girl,” has featured Chladni plates on PBS and on her YouTube channel in 2014 [18].

The particles used by Chladni were sand. However, anything that has a diameter above 100 microns easily form a Chladni pattern as determined by Waller [19]. We set out to create the same patterns as Chladni using iron filings which have an average size around 400 microns. We then use a localized external magnetic field to laterally move a roughly one cm segment of the iron filings from the third visible ring to the next closest ring to the center. Guiding particles on vibrating surfaces have been investigated before in air by Zhou et al. [20] and also in water by Latifi et al. [21]. After observing the Chladni patterns using the iron filings, we created a new sample with an additional 4% by weight of nickel and an average size of roughly 40 microns while keeping the total mass of the iron-nickel mixture the same. Nickel was chosen as a ferromagnetic material that can magnetically couple to the iron filings. We repeat the same experiment by applying the minimum necessary localized external magnetic field to the mixed powder and record the magnetic field required to move the mixed powder. The mass is increased further in new samples of 8% of nickel by weight in iron and 12% of nickel by weight in iron and those same experiments were also performed.

2  Procedure

A PASCO Model SF-9324 Mechanical Vibrator is connected to a 24 cm diameter circular non-magnetic coated steel plate. The plate is then covered with salt to clearly determine the frequencies at which Chladni patterns would form. Each pattern consists of a unique number of rings, thereby identifying the nodes at this frequency. The salt is then replaced with four grams of iron filings which is enough to lightly cover the plate. As the plate vibrates, Chladni circular ring patterns form from the iron filings at the same frequencies as the salt patterns that formed. A stack of ten neodymium magnets (radius of 1 cm) is next held roughly 3 cm above the iron filings of the third visible ring on the Chladni plate. The smallest necessary applied field strength is determined as the stack is lowered slowly. A roughly one cm segment of filings is guided laterally from one ring to the next inner ring by moving the magnets parallel to the plate. The same magnetic field was tested while the plate was not vibrating and no motion of the filings occurred.

A gauss meter is used at plate level to determine the applied external magnetic field. Multiple trials are taken to ensure the validity and consistency for this minimum applied external magnetic field. A constant ambient magnetic field is applied by the mechanical vibrator and is thereby measured and accounted for in the data. This field is between 9 Gauss for the lowest frequencies and 5 Gauss for the highest frequency. This variation is due to the pattern shifting farther from the center of the plate as the frequency increases. This process is repeated for 5 different frequencies. The iron filings are then replaced with a four gram mixture of iron and nickel with different amounts of nickel in each sample and the same experimental process is repeated. The uncertainty of the measurement ranges from ±0.02 g per mixture which accounts for loss of grains during transfer or in the experiment. The mass was kept the same for each trial to make sure the effects observed were not due to more magnetic materials, but from the changing magnetic materials present in the experiment.

3  Data Analysis

We begin by covering the plate with salt and gradually increasing the frequency, recording the frequencies at which Chladni resonance patterns are formed. Each new successive resonant frequency increases the number of rings by one, and the distance between each ring generally decreases. For visualization purposes, the rings can be seen in Fig. 1. The frequency of which forms the Chladni pattern rings is plotted versus the number of rings. Fig. 2 shows a parabolic relationship between the frequency and number of rings which fits Chladni’s law where the Bessel function solutions are simplified to Eq. (1) [3]:

f∼(m+2n)2 (1)

where f is the frequency, m is the diameter of the nodes, and n is the number of circles in the pattern.

Figure 1: Chladni ring patterns of salt are shown with the frequency at which they were measured with no applied external magnetic field. Salt is used here to see the patterns clearer than with the magnetic materials

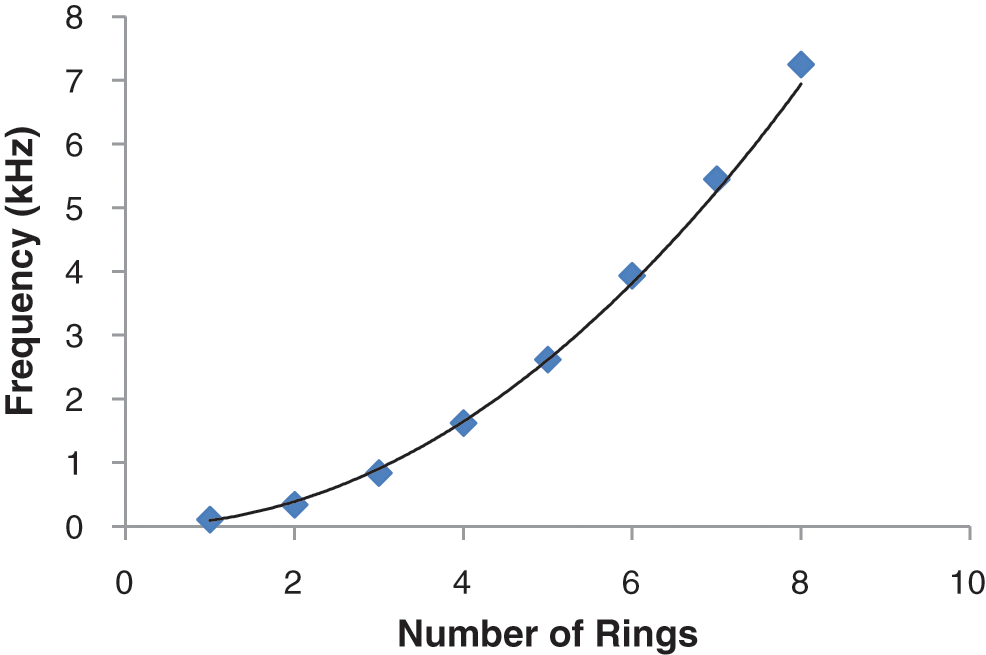
Figure 2: The frequency at which Chladni ring patterns formed by using salt were plotted versus the number of rings observed. This parabolic relationship fits as predicted

Starting with iron filings on the Chladni plate, we vibrate the plate at the earlier determined frequencies and similar patterns appear as seen for example in Fig. 3. Therefore our future results are not likely due to the torque of the filings in aligning with any applied external magnetic field, but rather the amount of external magnetic field required pulling the filings from the preferred location to a new nodal circle.

Figure 3: Chladni plate with iron filings vibrating at a frequency of 1620 Hz. The iron filings are spread out due to the Chladni vibration and not from the magnetic field produced by the vibrational apparatus

We then laterally move a one cm segment of the third ring from the center of a Chladni pattern to the second ring at each of the resonant frequencies with the necessary applied external magnetic field. Fig. 4 shows the results of the applied external magnetic field required to move a segment of the third ring vs. the resonant frequency. The decrease in the applied magnetic field required as the resonant frequency increases is likely due to less magnetic material present in the third ring at higher frequencies due to the increasing number of rings. Also, the iron filings require a substantially larger external magnetic field at the lowest resonant frequency compared to higher frequencies. As we add nickel to a new mixture of iron filings while keeping the total mass constant, we see the lowest resonant frequency takes considerably less of a difference in external magnetic field to move the magnetic material across frequencies. We attribute this likely due to the lower magnetization of the nickel compared to iron. Therefore, it is possible that there is a weaker exchange coupling between the nickel and iron powders, which allows the magnetic powder to move more readily than the pure iron powder. At the higher resonant frequencies the powder is more weakly bound to the resonant mode, allowing a less significant impact of an external magnetic field to different compositions of magnetic materials.

Figure 4: Applied magnetic field required to move a segment of magnetic material vs. the vibrational frequency where the pattern appears. We note the relatively small difference in applied magnetic field required at the highest vibrational frequency whereas the significant difference of applied magnetic field required moving magnetic materials at low frequencies

4  Conclusions

We observed the well-known Chladni patterns and added more to the work by using magnetic powders to see how much of an effect the vibration of the Chladni plate has on the motion of the powder. These results can yield further insights as to how resonant modes in waves can be manipulated externally, in our case by a magnetic field. We note that at higher frequencies, it takes a considerably less magnetic field to move the powders rather than at low frequencies. In future work, it would be interesting to see how other magnetic powders are affected by the vibration. Also, it would be fascinating to further study the magnetic interaction between individual powder grains to examine how the magnetic interaction between the individual grains changes during the plate vibration.

Funding Statement: This study was possible through the support of SUNY Plattsburgh’s Internal Research Funds.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  Gutzwiller, M. C. (1990). Chaos in classical and quantum mechanics, pp. 1–427. New York: Springer. [Google Scholar]

 2.  Chinnery, P. A., Humphrey, V. F. (1996). Experimental visualization of acoustic resonances within a stadium-shaped cavity. Physical Review E, 53, 272. [Google Scholar]

 3.  Rayleigh, L. (1911). On the calculation of Chladni’s figures for a square plate. Philosophical Magazine, 22, 225. [Google Scholar]

 4.  Arango, J., Reyes, C. (2016). Stochastic models for Chladni figures. Proceedings of the Edinburgh Mathematical Society, 59, 287. [Google Scholar]

 5.  Rayleigh, J. (1877). Theory of sound. London, UK: Macmillan. [Google Scholar]

 6.  Hu, J. (2014). Acoustic micro/nano manipulations: An editorial review. International Journal of Radiology, 1, 1. [Google Scholar]

 7.  Jensen, H. (1955). Production of Chladni figures on vibrating plates using continuous excitation. American Journal of Physics, 23, 503. [Google Scholar]

 8.  Colwell, R. (1931). The vibrations of membranes and plates. Philosophical Magazine, 12, 320. [Google Scholar]

 9.  Pitre, J. (1996). Chladni plates: How big can they be? The Physics Teacher, 34, 508. [Google Scholar]

10. Rossing, T. (1982). Chladni’s law for vibrating plates. American Journal of Physics, 50, 3. [Google Scholar]

11. Kirchhoff, G. (1850). Ueber die Schwingungen einer kreisförmigen elastischen Scheibe. Annual Review of Physical Chemistry (Poggendorf), 81, 279. [Google Scholar]

12. Kirchhoff, G. (1850). Über das Gleichgewicht und die Bewegung einer elastischen Scheibe. Journal of Mathematics (Crelle), 40, 51. [Google Scholar]

13. Savart, F. (1819). Memoire sur la construction des Instruments a cordes et a archet. Paris: Deterville. [Google Scholar]

14. van Gerner, H.,van der Hoef, M.,van der Meer, D.,van der Weele, J. (2010). Inversion of Chladni patterns by tuning the vibrational acceleration. Physical Review E, 82, 012301. [Google Scholar]

15. van Gerner, H.,van der Weele, K.,van der Hoef, M.,van der Meer, D. (2011). Air-induced inverse Chladni patterns. Journal of Fluid Mechanics, 689, 203. [Google Scholar]

16. Tuan, P., Wen, C., Chiang, C., Yu, Y., Liang, H. et al. (2015). Exploring the resonant vibration of thin plates: Reconstruction of Chladni patterns and determination of resonant wave numbers. Journal of the Acoustical Society of America, 137, 2113. [Google Scholar]

17. Graham, G. (1989). DIY physics—The paper scraper paper. Physics Education, 24, 25. [Google Scholar]

18. Cowern, D. (2014). Physics girl, singing plates—Standing waves on Chladni plates. https://www.youtube.com/watch?v=wYoxOJDrZzw. [Google Scholar]

19. Waller, M. (1961). Chladni figures: A study in symmetry. London: Bell. [Google Scholar]

20. Zhou, Q., Sariola, V., Latifi, K., Liimatainen, V. (2016). Controlling the motion of multiple objects on a Chladni plate. Nature Communications, 17, 12764. [Google Scholar]

21. Latifi, K., Wijaya, H., Zhou, Q. (2019). Motion of heavy particles on a submerged Chladni plate. Physical Review Letters, 122, 184301. [Google Scholar]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.