Sound & Vibration

DOI: 10.32604/sv.2021.014358

ARTICLE

Duffing Oscillator’s Vibration Control under Resonance with a Negative Velocity Feedback Control and Time Delay

Y. A. Amer1 and Taher A. Bahnasy2,*

1Department of Mathematics, Faculty of Science, Zagazig University, Zagazig, Egypt
2Department of Engineering Physics and Mathematics, Faculty of Engineering, Tanta University, Tanta, Egypt
*Corresponding Author: Taher A. Bahnasy. Email: taher.bahnasy@gmail.com; tbahnasy@ymail.com
Received: 21 September 2020; Accepted: 14 April 2021

1  Introduction

The existence of vibrations and dynamic chaos in machinery and structural systems is an unavoidable phenomenon, which ultimately can lead to machine failures and dangerous accidents. Different reasons lead such systems for nonlinear vibrations, as nonlinear properties of materials, geometric nonlinearities, and nonlinear excitation forces. Much time, money and efforts are spent for minimizing vibrations and oscillations for longer time life of these systems and prevent them from failures or damaging.

In the last decades resonantly forced systems with control has been investigated in various engineering fields. For control speed and system performance, the time-delay in the controllers and the actuators has become an urgent problem for increasing strict requirements. For instance, a nonlinear delayed dynamic system of one dimension which may exhibit chaotic behavior was studied in [1,2], and the stability analysis and control of nonlinear system was investigated in Yao et al. [3–5]. Vazquez-Gonzalez et al. [6] discussed the dynamic response and nonlinear frequency analysis of a damped Duffing system attached to an autoparametric pendulum absorber, operating under the external and internal resonance conditions. They deduced that is possible to reduce simultaneously the amplitude responses of the primary and secondary systems for excitation frequencies close to the exact tuning. A nonlinear active vibration absorber coupled with the plant through user-defined cubic nonlinearity was obtained in Oueni et al. [7], Moiola et al. [8] established the Hopf bifurcations resulting from nonlinear feedback systems with time delay, and they demonstrated that appropriate choices of the feedback gains and the time delay are possible for a better vibration control by using the multiple scales method [9,10]. Wenzhi et al. [11] studied active control of torsional vibration of a large turbo-generator. They found that full state feedback control with linear quadratic regulator (LQR) has significant effectiveness on attenuation of torsional vibration energy and response of the turbo-generator’s shaft system.

Wang et al. [12] investigated the dynamic response and bifurcation characteristics of blades with varying rotating speed. The results of the paper showed the interaction of the fluid and the structure that the opposite varying trends for the amplitudes and phase angles with respect to the system parameters indicate the energy transfer between the vibrations of the fluid and the structure. Thomas et al. [13] handle the large amplitude nonlinear vibratory behavior of a rotating cantilever beam, with applications to turbo machinery and turbo-propeller blades. They investigated the effect of rotation speed on nonlinear vibrations of the beam and especially on the hardening/softening behavior of its resonances and the appearance of jump phenomena at large amplitude. Rezaei et al. [14] performed an aero elastic analysis of a rotating wind turbine blade by considering the effects of geometrical nonlinearities associated with large deflection of the blade produced during wind turbine operation. They presented an aerodynamic model based on the strip theory, by applying the principles of quasi-steady and unsteady airfoil aerodynamics. The results indicated the important effect of geometrical nonlinearity, especially for larger structural deformations. El-Ganaini [15] investigated the vibration control of a harmonically excited Duffing oscillator via a simple pendulum. She studied Bifurcation analyses and applied the Lyapunov direct method to study the system stability. The analysis showed that the oscillator vibrational energy could be transferred to the pendulum parametrically when the pendulum natural frequency is equal to one-half of the oscillator natural frequency.

Kruthika et al. [16] analyzed the local stability of a gene-regulatory network and immunotherapy of cancer. They are modeled as nonlinear time-delayed systems. The effect of a high-frequency excitation on nontrivial solutions and biostability in a delayed Duffing oscillator with a delayed displacement feedback was investigated by Hamdi et al. [17]. Tusset et al. [18] studied the chaotic behaviors control of parametrically excited pendulum using two different control strategies. One of this applied control method is via the active nonlinear saturation controller, and the other via introducing a passive rotational MR damper. A one degree of freedom hybrid Rayleigh–van der Pol–Duffing oscillator is studied by [19] to minimize the vibrations induced at primary resonance case. In order to investigate the stability behavior of the Riemann-Liouville fractional derivative applied to the cubic delayed Duffing oscillator, the parameter expansion is coupled with multiple scales method introduced in Yusry [20]. Unlike the frequency expansion approach where the amplitude is supposed to be constant in time, one of the most important characteristics of the multiple time-scales method is to yield the amplitude of the wave solution as a function of time. Because of this combination of the two approaches, a differential equation associated with the algebraic frequency governs the amplitude. He extended this technique to the delayed nonlinear fractional Duffing oscillator.

To research the dynamics of the diffusive system with a cubic non-linearity time-delayed category of the damping Duffing equation, a coupling between the multiple scales approach and the homotopy disturbance was used in Yusry [21]. As well as he applied the time-scales of homotopy perturbation on the governing equation of time-periodic delay Mathieu equation in Yusry [22]. Beside the approximate periodic solutions, Numerical calculations have been done to illustrate Stability conditions are derived in both resonance and non-resonance case.

In this paper, we consider the effect of time delay in a Duffing oscillator under a parametric excitation force. The system amplitude-phase modulating equations are extracted by applying the multiple scales perturbation technique. The frequency-response curves to the system are obtained with and without delay time in control feedback. The effects of the coupling parameters, absorber, linear damping coefficient, and excitation amplitude on the frequency-response curve are explored. Numerical confirmations for the all acquired results are performed, time-histories are conducted before and after control effect. Finally, important notes are included for the optimal working conditions.

2  System Model and Mathematical Analysis

As a consequence of the motion of a body subjected to a nonlinear spring force, linear sticky damping and intermittent force, the Duffing oscillator occurs. Oscillations of mechanical systems under the action of a periodic parametric force can be revealed using Duffing oscillator. The mathematical model for the Duffing oscillator under a parametric excitation force is given in Wenlin et al. [23,24] as:

U¨(t)+2εμU˙(t)+ωo2U(t)+εωo2U3(t)−εfU(t)cos⁡(Ωt)+εBU(t−τ)+εCU˙(t−τ)=0 (1)

The terms associated with the system in Eq. (1) represents:

U˙(t) represent the small damping, 2εμ represent the ratio (coefficient) of viscous damping (it controls the size of damping), ( ωo2U(t)+εωo2U3(t) ) represent the nonlinear restoring force acting like a hard spring (with ωo2 controlling the size of stiffness and εωo2 controlling the size of nonlinearity). Where U(t) denotes the displacement, Ω,ωo are the external excitation and internal frequency, f is the parametric excitation force, B,C are feedback gains, ε is a small perturbation constant. Applying multiple time scales method (MTSM), then the second order approximation of U(t) is given in power series form as:

U(To,T1,ε)=Uo(To,T1)+εU1(To,T1)+O(ε2), (2)

where the time derivative will take the values:

ddt=D0+εD1+O(ε2),d2dt2=Do2+2εD0D1+O(ε2) (3)

and Tn=εnt,Dn=∂∂Tn,n=0,1 .

Now we will study system behavior in both cases with and without delay time in control system.

2.1 System with Delay Time, i.e., τ≠0

Applying Eqs. (2), (3) into (1) and equating same power of the coefficients of ε to obtain:

O(ε0):(Do2+ωo2)U0=0 (4)

O(ε):(Do2+ωo2)U1=−2DoD1Uo−2μDoUo−ωo2Uo3+fUocos⁡(Ωt)−BUoτ−CDoUoτ. (5)

And the homogenous solution of (4) is given by:

U0=A(T1)eiωoT0+cc, (6)

where cc represents the complex conjugate of the preceding term, and A is complex function in T1 .

Let

U(t−τ)=Uoτ(To,T1)+εU1τ(To,T1)+O(ε2), (7)

U0τ=Aτ(T1)eiωo(T0−τ)+A¯τ(T1)e−iωo(T0−τ), (8)

Expanding Aτ(T1) in Taylor series such that:

Aτ(T1)=A(T1)−ετA˙(T1)+⋯ (9)

Substituting from (21) into (20) and using only the first term approximation so:

U0τ=A(T1)eiωo(T0−τ)+A¯(T1)e−iωo(T0−τ). (10)

Introducing (6), and (10) into (5), yields:

(Do2+ωo2)U1=−2(iωoD1AeiωoTo−iωoD1A¯e−iωoTo)−2μ(iωoAeiωoTo−iωoA¯e−iωoTo)−ωo2(A3e3iωoTo+3A2A¯eiωoTo++3A¯2Ae−iωoTo+A¯3e−3iωoTo)+f2(AeiωoTo+A¯e−iωoTo)(eiΩTo+e−iΩTo)−B(Aeiωo(To−τ)+A¯e−iωo(To−τ))−C(iωoAeiωo(To−τ)−iωoA¯e−iωo(To−τ)). (11)

Now we will study the system worst operating modes due to resonance case, this worst case is the sub-harmonic resonance case:

Ω=2ωo+εσ, (12)

where σ is the detuning parameter. substituting (12) into (11) and eliminating coefficients of all secular terms, yields:

−2iωoA˙−2iωoμA−3ωo2A2A¯+fA¯2eiεσTo−BAe−iωoτ−CiωoAe−iωoτ=0 (13)

Converting the function A to the polar form then we have:

A=a2eiβ, (14)

where a,β are the system amplitude and phase respectively. Introducing Eq. (14) in Eq. (13) and equating the real and imaginary parts we get:

a˙=−μa+fasin⁡(φ)4ωo+Basin⁡(ωoτ)2ωo−Cacos⁡(ωoτ)2, (15)

aφ˙=σa−3ωoa34+facos(φ)2ωo−Bacos(ωoτ)ωo−Casin(ωoτ) (16)

where φ=σT1−2β , σ is the detuning parameter.

For obtaining the steady state solution for amplitude and phase putting a˙=φ˙=0 into Eqs. (15), (16), squaring and adding both sides, gives:

r1a4+r2a2+r3=0 (17)

where

r1=9ωo24,r2=6ωo2(Bcos⁡(ωoτ)−ωoσ+Cωosin⁡(ωoτ)),r3=[4μωo−2Bsin⁡(ωoτ)+4Cωocos⁡(ωoτ)]2+[−2ωoσ+2Bcos⁡(ωoτ)+2Cωosin⁡(ωoτ)]2−f2 (18)

To discuss the stability behavior of these solutions, linearizing Eqs. (15), (16) according to Lyapunov first (indirect) method to give the following system:

[a˙φ˙]=[∂a˙∂a∂a˙∂φ∂φ˙∂a∂φ˙∂φ][aφ]=[J11J12J21J22][aφ], (19)

where

J11=−μ+fsin⁡(φ)4ωo+Bsin⁡(ωoτ)2ωo−Ccos⁡(ωoτ)2,J12=facos⁡(φ)4ωo,J21=−9ωoa4+σa+fcos⁡(φ)2aωo−Bcos⁡(ωoτ)aωo−Csin⁡(ωoτ)a,J22=−fsin⁡(φ)2ωo (20)

Accordingly, the stability of the steady-state solution varies depending on analyzing and solving characteristic equation, the Jacobian matrix’s eigenvalues that can be obtained by:

|J11−λJ12J21J22−λ|=0, (21)

or

λ2+K1λ+K2=0, (22)

where

K1=−(J11+J22),K2=J11J22−J12J21. (23)

The state’s solution is asymptotically stable, as seen by the Routh-Huriwitz criterion, if and only if all real parts for roots of Eq. (22) are both negative, this condition be occurred if the coefficients satisfy Rn>0,n=1,2, these conditions are discussed numerically.

2.2 System without Delay Time

Applying the active velocity and displacement control without time delay, i.e., τ=0 on Eqs. (7)–(23) gives the modulation and response equations for system (1).

3  Results and Discussion

In this section we illustrate the behavior of the system amplitude and phase with and without resonance case. We will show a comparison between active and time delay control and the effect of some system parameters on its amplitude.

3.1 Time History

Fig. 1a shows the time response for the amplitude a where Fig. 1b illustrates the system phase plane, without resonance case and without applying any control system (i.e., B=C=0 ) at the following parameter variables: μ=0.1,Ω=15,ωo=1.5,f=2.5,ε=0.1 . Figs. 2a–2c also show the Time history without, with active and time delay control at sub-harmonic resonance case (Ω=2ωo+εσ) with the parameters: μ=0.1,ωo=1.5,f=2.5,ε=0.1,B=0.95, C=0.6,τ=0.015. we observe that the amplitude is reached near zero due to the effect of applied control. Effective values of the delay time that minimize system vibrations are given in Fig. 3.

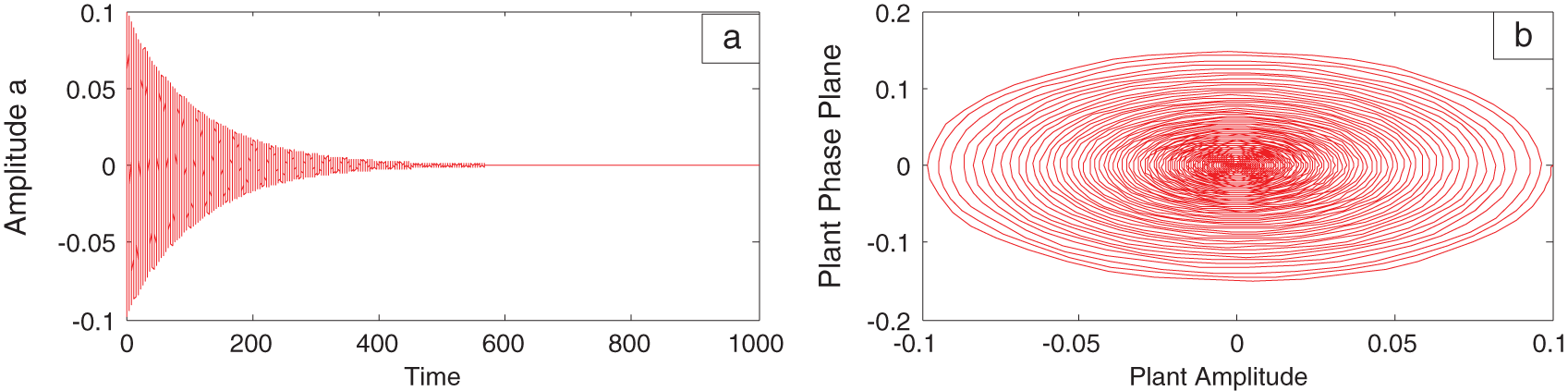
Figure 1: (a) The time response for the amplitude (without resonance and without applying control system), and (b) system phase plane

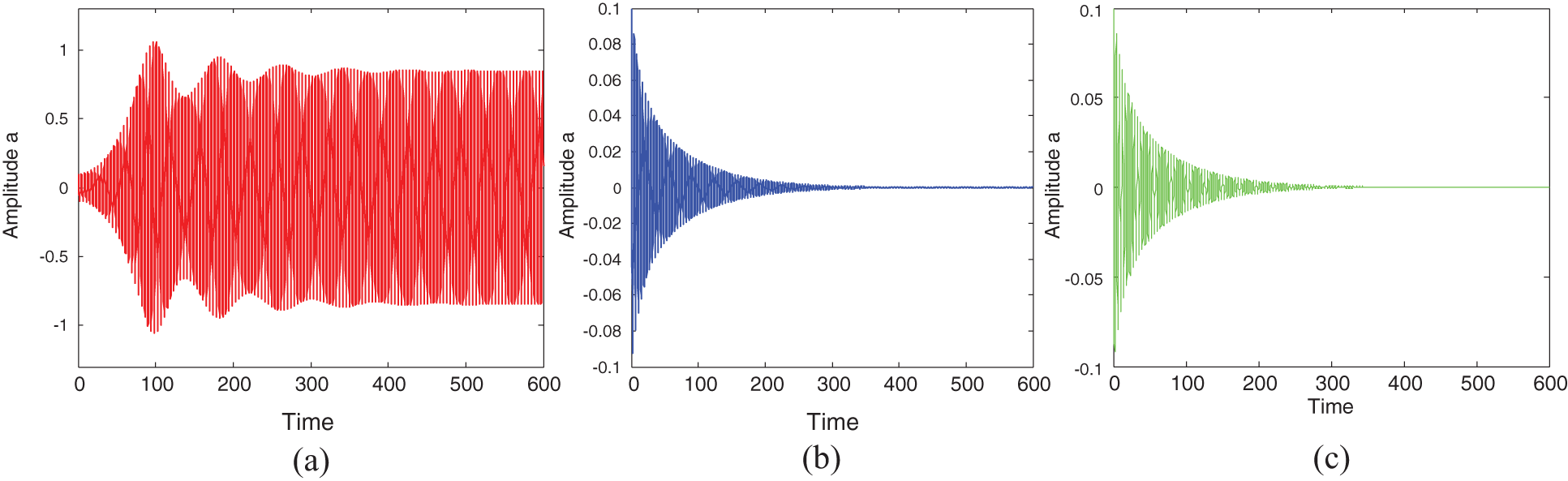
Figure 2: (a) Amplitude without control, (b) Amplitude with active control, and (c) Amplitude with time delay control

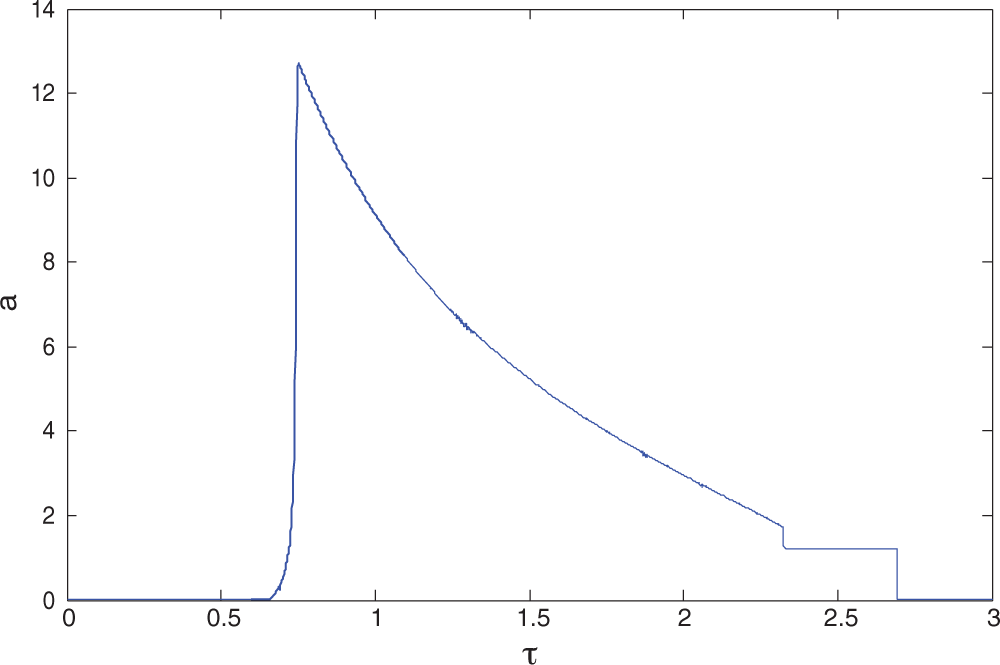
Figure 3: Amplitude (a) against the time delay ( τ )

3.2 Frequency Response

Figs. 4–6 show the system amplitude against the frequency detuning parameter σ with change in specified values for system parameters. In Fig. 4 the amplitude is plotted with the perturbation parameter σ , at resonance case with control gain C=0,0.4,0.6,B=0 we observe that the amplitude decreases with the increase of the value of C . In Figs. 5 and 6 we observe that system amplitude is proportional inversely with varying the control gain B and the damping parameter μ , respectively. The black curves denote the stable region where the red curves represent the unstable regions.

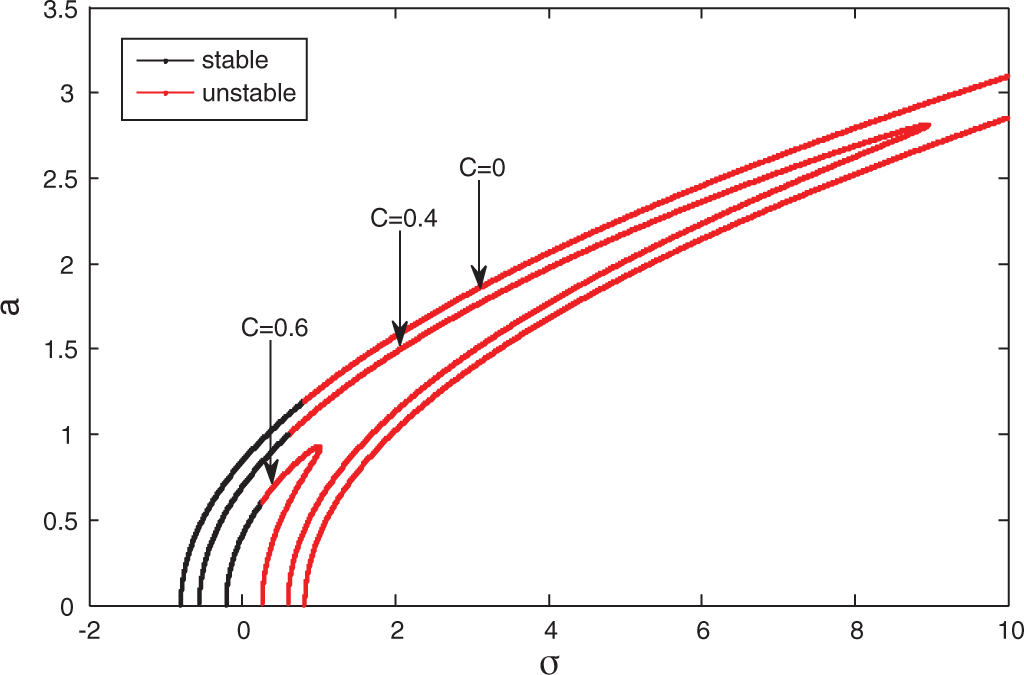
Figure 4: Frequency response curve at C = 0, 0.4, 0.6, B = 0

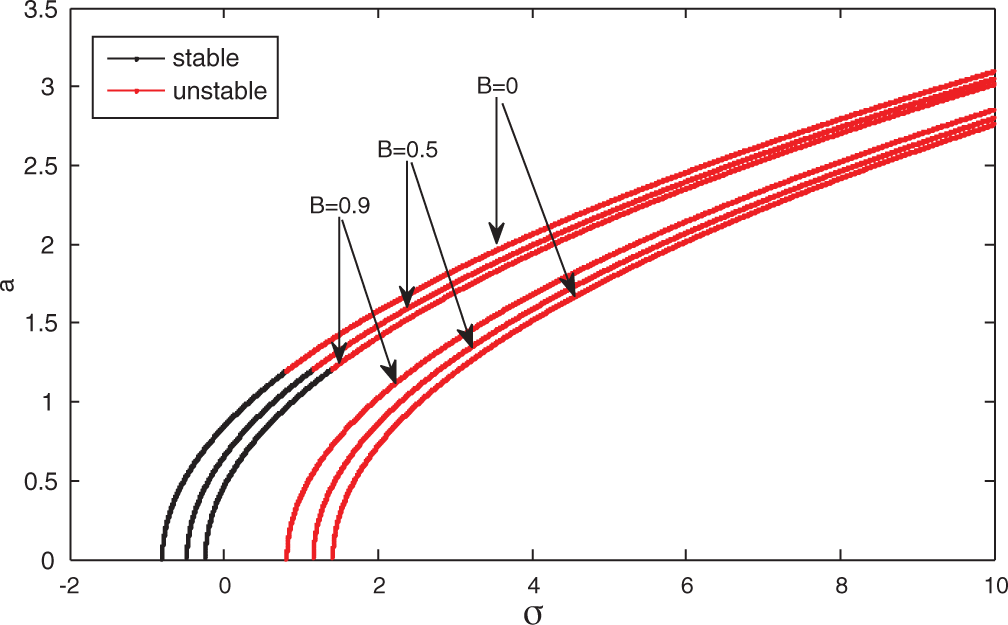
Figure 5: Frequency response curve at B = 0, 0.5, 0.9, C = 0

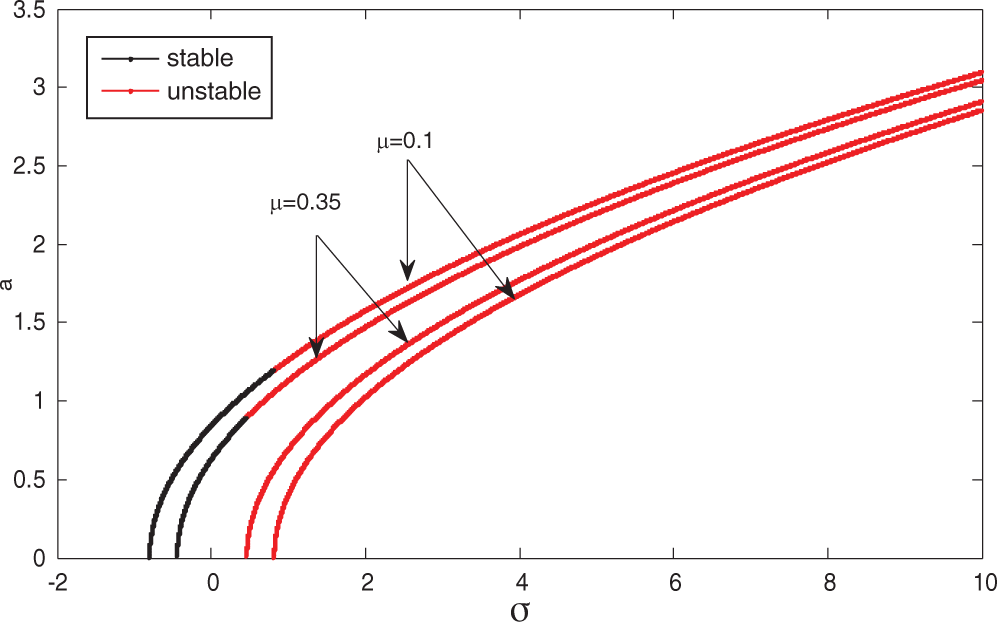
Figure 6: Frequency response curve at μ = 0.1, 0.35, B = C = 0

3.3 Comparisons with Numerical Method

In this Sub-section we compare the analytic solution of Eqs. (24), and (25) induced by (MTSM) and numerical solution of Eq. (1) using Rung-Kutta Method (RKM) of fourth order. In Fig. 7 system modes amplitudes are plotted with time in both cases of analytic and numerical method using the same parameter values in Sub-section 3.1 for Fig. 2. The response curve for the system is shown in Fig. 8. These comparisons give a good agreement between analytic and numerical solutions.

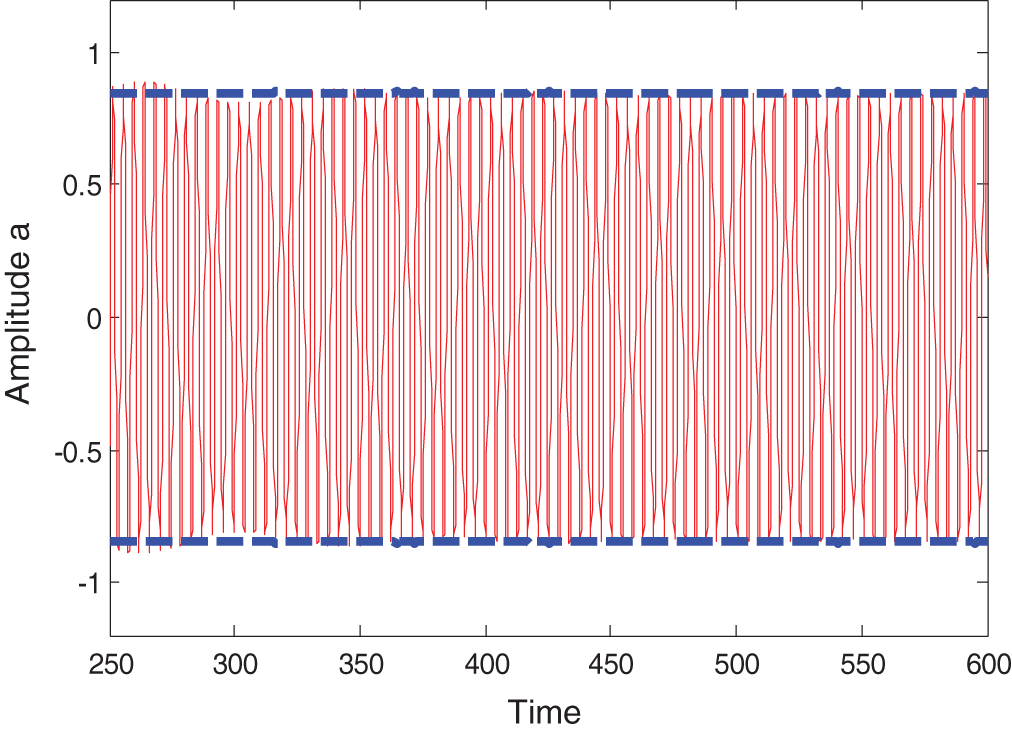
Figure 7: Comparison between the amplitude induced by analytic method (MTSM) and numerical method using Rung-Kutta Method (RKM) of fourth order (time history)

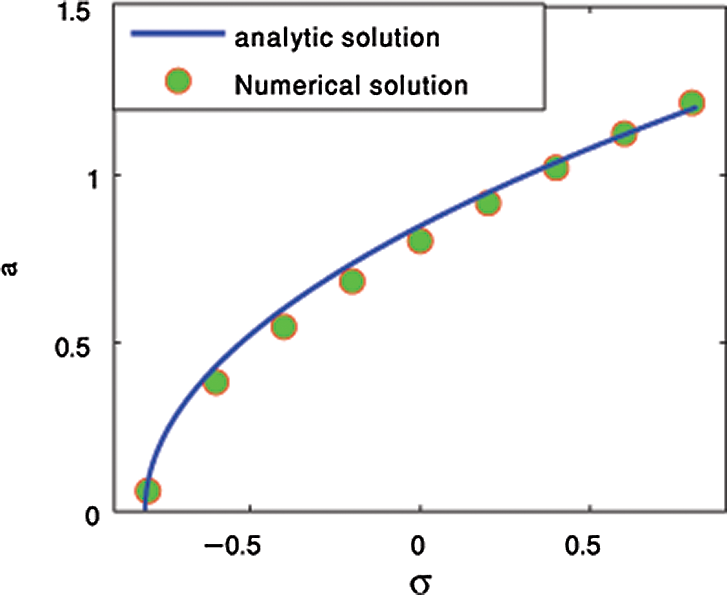
Figure 8: Comparison between analytic and numerical solutions (response curve)

3.4 Amplitude vs. Certain System Parameters

Let us consider the parameters given in Sub-section 3.1 unless otherwise specified. In this sub-section we show the change of amplitude range with varying of the system parameters. We observe that the value of a decreases by increasing of the value of μ,B, and C as shown in Figs. 9–11, respectively.

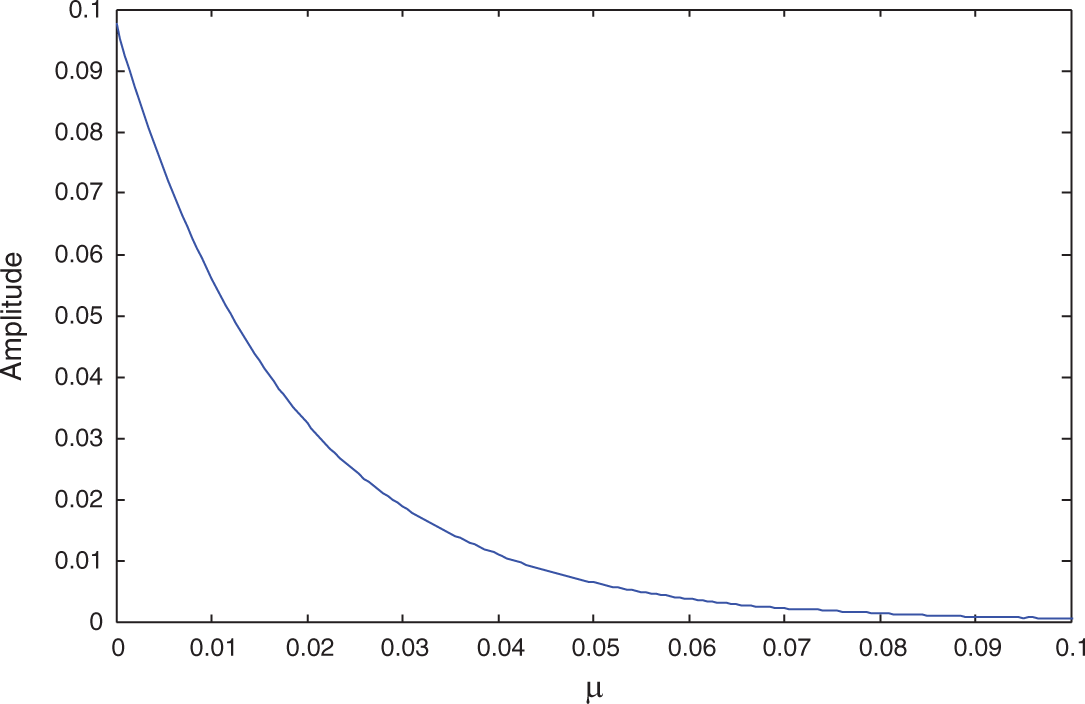
Figure 9: Amplitude against the damping parameter μ

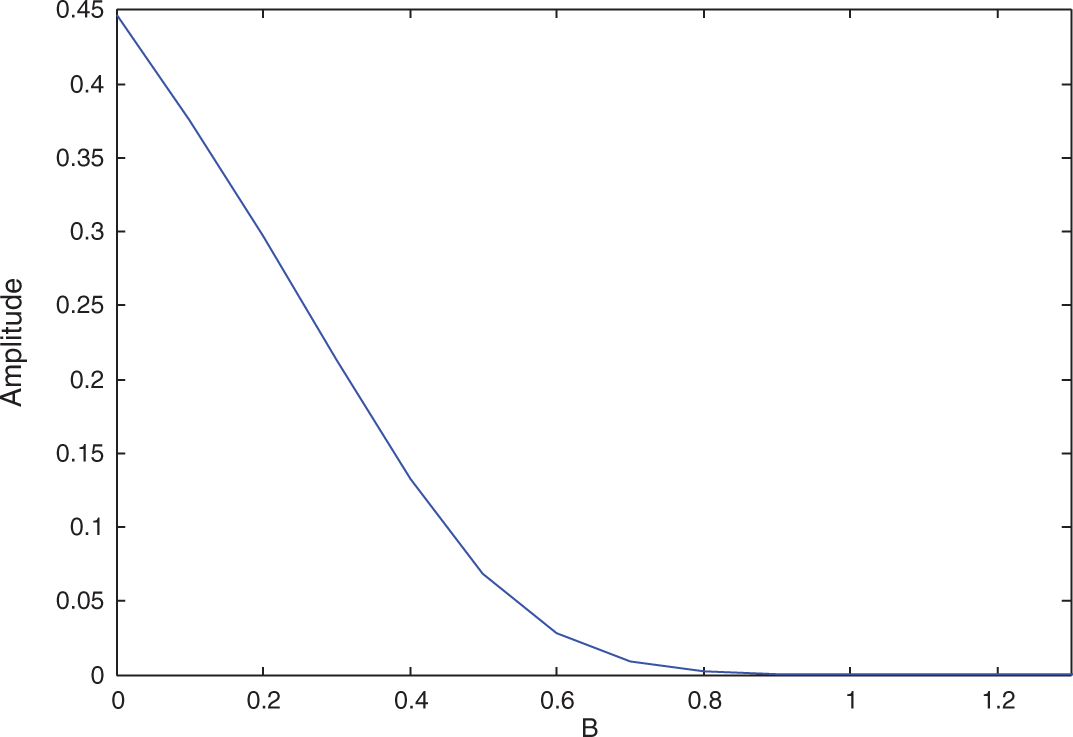
Figure 10: Amplitude against the control gain B

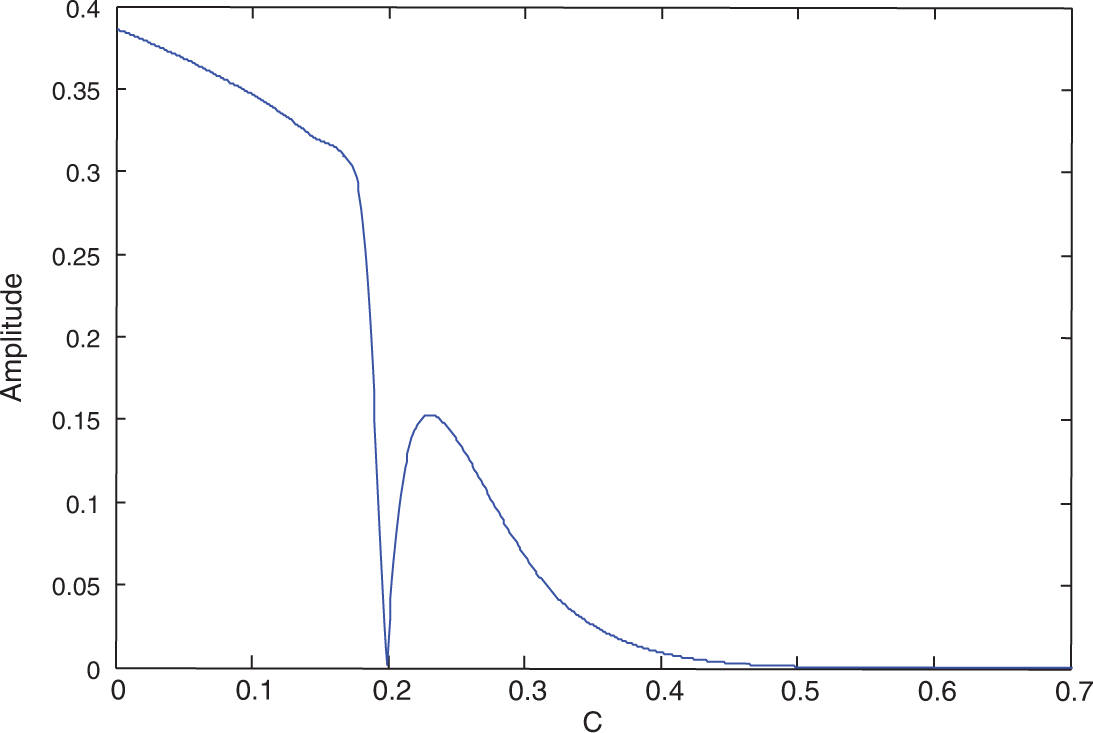
Figure 11: Amplitude against the control gain C

4  Conclusions

In this research, we use multiple time scales method to find analytic solution and discuss the worst resonance case of an externally excited Duffing oscillator under feedback control. We studied the existence and nonexistence of the time delay effect on the system amplitude in case of the worst resonance cases that were principal parametric resonance. An appropriate stability analysis has been also performed and appropriate choices for the feedback gains and the time delay have been found in order to reduce the amplitude peak. In addition, analytic solutions were compared with numerical approximation solutions using Rung-Kutta method, these comparisons give a good agreement between analytic and numerical solutions.

Funding Statement: The authors received no specific funding for this study.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.