Sound & Vibration

DOI: 10.32604/sv.2021.09729

ARTICLE

Improving the Morphological Parameters of Aluminum Foam for Maximum Sound Absorption Coefficient using Genetic Algorithm

Mohammad Javad Jafari1, Mohsen Niknam Sharak2, Ali Khavanin3, Touraj Ebadzadeh4, Mahmood Fazlali5 and Rohollah Fallah Madvari6,*

1Department of Occupational Health Engineering, School of Public Health and Safety, Shahid Beheshti University of Medical Sciences, Tehran, Iran
2Mechanical engineering, Department of Mechanical Engineering, University of Birjand, Birjand, Iran
3Department of Occupational Health Engineering, Faculty of Medical Sciences, Tarbiat Modares University, Tehran, Iran
4Department of Ceramics, Materials and Energy Research Center, Alborz, Iran
5Department of Computer Science, Shahid Beheshti University, Tehran, Iran
6Student Research Committee, Department of Occupational Health Engineering, School of Public Health and Safety, Shahid Beheshti University of Medical Sciences, Tehran, Iran
*Corresponding Author: Rohollah Fallah Madvari. Email: fallah134@gmail.com
Received: 16 January 2020; Accepted: 13 April 2020

1  Introduction

Noise control is generally carried out using passive and active methods [1]. In the passive method, the absorbing materials are used to control the noise [1]. The porous absorbent materials can be classified as foam, fibrous or granular absorbents [2]. In this regard, the metal foam has been considered as a sound absorbent since 1950 [3]. Due to its interesting features, it has attracted a lot of attention in various fields of the industry [4]. Low density, high mechanical strength, high heat resistance, and anti-corrosion are among these attractive characteristics [4–7]. The use of metal foams are rapidly expanding in engineering applications [3,4,8,9]. Generally, there are two kinds of open-cell and closed-cell metal foams [10]. Lu et al. [11], Han et al. [7]. and Hakamada et al. [12]. stated that open-cell metal foam has a better sound absorption capacity compared with closed cells; mainly because the sound wave is easily transmitted to the material in open cell foam [7]. Given that the air movement which is controlled by the morphological parameters of the cell and the cell structure, also affects the sound absorption capacity. The significant property of metal foams is their sound absorption [7].

Many parameters may affect the sound absorption coefficient (SAC) in metal foams, including porosity, pore size, pore opening, thickness, static flow resistance, and etc [13]. Some of These parameters including morphological parameters can be considered while fabricating metal foams. In other words, it is possible to fabricate metal foams with desired morphological parameters. So far, the trial and error methods are applied in laboratory to select the best metal foam for the highest sound absorption from the available metal foams. If the optimized morphological parameters could be determined in advance it would be possible to fabricate the desired metal foam for the best sound absorption using the sintering technology.

Therefore, to have a metal foam with best sound absorption, it is necessary to determine The optimized morphological parameters of the foam. For this purpose, theoretical models which describe the relationship of the sound absorption coefficient with morphological parameters are required. [14,15]. So far, such models which describe the relationship between cell structure and the sound absorption coefficient in porous materials have been proposed [7,11,16–18]. Lu model of sound absorption describes the relationship between 3 morphological parameters of porosity (Ω), pore size (D) and pore opening size (d) with sound absorption coefficient (SAC). Thus this model seems to be the best candidate for this purpose. It is expected to improve the morphological parameters of a metal foam for the best absorption coefficient using the optimization algorithms.

In the previous study (Article titled “Optimization of the Morphological Parameters of a Metal Foam for the Highest Sound Absorption Coefficient Using Local Search Algorithm” in journal of Archives of Acoustics, under publishing Vol.45, No3(2020)), the morphological parameters of metal foam were optimized using local search algorithm.

Different optimization algorithms including General Local Search (GLS) and genetic algorithm (GA) [19], Ant Colony Optimization [20] and Particle Swarm Optimization [21] have been proposed so far. GLS algorithm explores neighborhood by iteratively expanding searching domain in the neighborhood of the current solution and moving from current solution to an enhancing neighborhood [22]. This process is repeated until the current solution cannot be improved anymore. This process continues until the optimum locale is reached. The GLS approach may stuck and trapped in a local optimum disregarding other optimums in the neighboring [23]. So there need to be avoided from trapping in these local optimums [22] . Dumitrescu et al. [24] believe that the disadvantages of local search algorithms are typically 1. they cannot prove optimality, 2. they cannot provably reduce the search space, and 3. they often have problems with highly constrained problems where feasible areas of the solution space are disconnected.

For more complex problems, meta-heuristics such as genetic algorithm(GA) [19], Ant Colony Optimization [20] and Particle Swarm Optimization [21] can be considered. The meta heuristic algorithm becomes very popular because of its stability, flexibility and its ability in avoiding from trapping in local optimums [25]. The meta-heuristic GA is inspired by Darwinian evolution theory [26,27]. Today, it is widely used in solving optimization problems and learning processes [28].

The GA is a method independent from the problem domain and quickly seeks the search space for the optimized point with a qualitative function [29]. GA has a distinguished advantage compared to other stochastic methods. In this method it is extremely easy to parallelize the algorithm. It is due to the fact that the calculations of each iteration are independent of one another [30,31]. Due to different design parameters and constraints, the optimization of sound absorbents has always been a challenge in acoustic engineering [32].

Usually, the pore size, pore opening, porosity, and thickness are not known for fabricating the foam for sound absorption. Therefore, available foams with approximate dimensions are investigated through trial and error method to find the best foam absorbent. However, if it is possible to predetermine the morphology of metal foam to absorb a specific sound with best SAC, it can be claimed that a great step has been taken to fabricate porous foams intelligently. The study aimed to optimize the morphological parameters affecting the sound absorption coefficient (α) in metal foams. For this purpose, first the Genelarl Local Search approach was applied to optimize the morphological parameters of a metal foam (Article titled “Optimization of the Morphological Parameters of a Metal Foam for the Highest Sound Absorption Coefficient Using Local Search Algorithm” in journal of Archives of Acoustics, under publishing Vol.45, No3(2020)). This part of the study, discusses the applicability of the GA in improving the optimal set of metal foam parameters, including porosity, pore size and pore opening at any thickness and frequency for fabrication of an optimized foam.

2  Structure

The study was carried out according to the following flowchart (Fig. 1).

Figure 1: Study process

2.1 Lu Model

The relationship between sound absorption coefficient (α) and morphological parameters, including pore size, pore opening, and porosity are well described [11]. In present study, the equations presented in Lu model [11] were numerically solved to optimize the morphological parameters for the highest value of SAC. These equations are shown in Tab. 1.

Table 1: Equations of the Lu model

2.2 Optimization by GA

The porosity, pore size, and pore opening parameters were optimized for a frequency range of 250 Hz to 8000 Hz and a thickness of 5 mm to 40 mm. Avoiding from trapping in any local search and affirming the global optimization was essential. A typical GA flowchart is shown in Fig. 2.

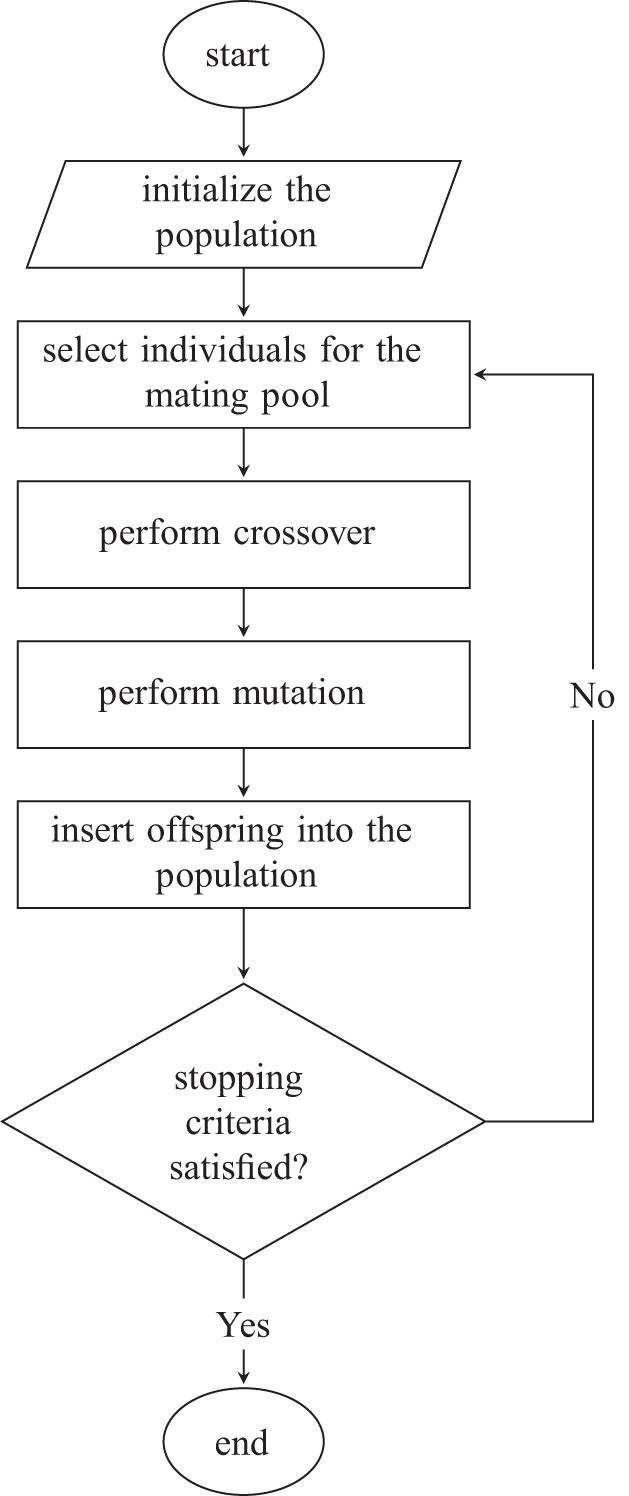
Figure 2: A typical GA flowchart [33,34]

The summary of the steps taken by the GA used in this study were [35–37]:

Step 1. Read input data

Step 2. Create primary population randomly

Step 3. Consider initial parents

Step 4. Determine mutation (considering Pm)

Step 5. Calculate all parameters

Step 6. Select the best answer

Step 7. End; if SAC=1 or the number of iteration is <150

Step 8. Else; go back to step 4

Roulette Wheel and tournament methods were used to select the members for making generation and mutation. The population included 50; the generation rate 80% (Pc = 0.8); the percentage of mutation 30% (Pm = 0.3); the mutation rate 0.02, the stopping criteria was SAC=1 or the number of iterations=150 [38]. Furthermore, the uniform crossover method was used for making generation. In order to obtain each number in the last tables, the problem solving process was used 5 times using the roulette wheel method and 5 times with the tournament method and the best result was noted. The results showed that the tournament method is better for this particular problem. The number of specified iterations (150) was used to prevent the program from hanging if there is no improvement in calculated SAC (Fitness Function).

The input data required for GA to run are summarized in Tab. 2. These parameters were selected by repeating the algorithm many times and in accordance with the best results.

Table 2: Parameters setting for GA

The searching domain for optimization of each parameter was considered according to Tab. 3. All three morphological parameters were optimized at frequencies of 0.5, 1, 2, 3, 3.5, 4, 6 and 8 kHz.

Table 3: The searching domain of each parameter

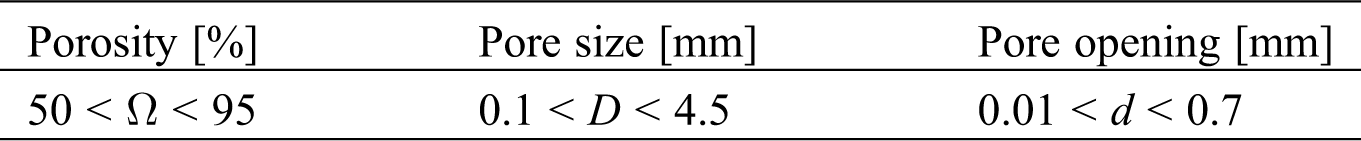
The verification and validation of the proposed codes were carried out as in Jafari et al. (Article titled “Optimization of the Morphological Parameters of a Metal Foam for the Highest Sound Absorption Coefficient Using Local Search Algorithm” in journal of Archives of Acoustics, under publishing Vol. 45, No3(2020))

3  Results

In Fig. 3, for a thickness of 5 mm to 40 mm at the frequency of 4 kHz, the convergence chart of the GA is drawn. Considering the convergence chart, it is clear that the value of the answer does not change from one iteration to the next one. Therefore, the number of iterations chosen is appropriate for achieving the desired answer. The highest value of the sound absorption coefficient is 1. Therefore, the answers must converge to the number 1.

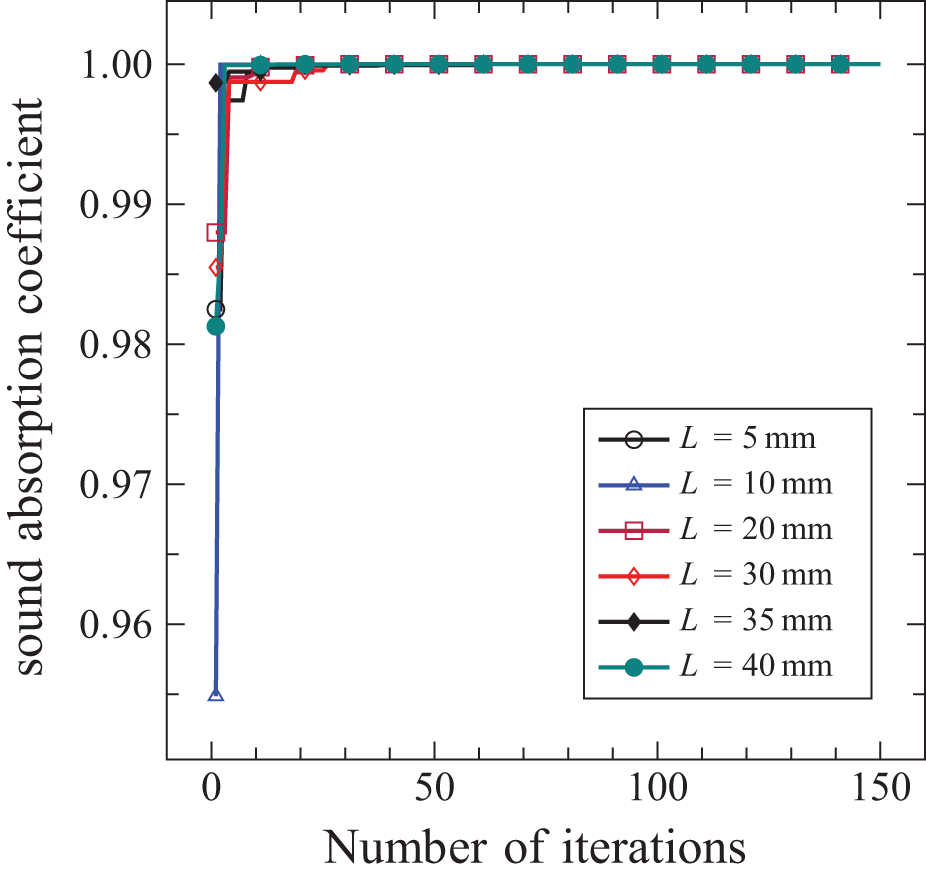
Figure 3: Convergence authentication of GA for different thicknesses at 4000 Hz

Fig. 4 depicts the optimized morphological parameters at different frequencies for the highest sound absorption coefficient (α) in an Aluminum foam barrier with 5mm thickness. Fig. 4 shows that at high frequencies (3 kHz to 8 kHz), when porosity (Ω) is between 60 to 95 percent (0.6–0.95 in figure), the pore size is 0.33 mm to 2.5 mm, the pore opening size is 0.09 mm to 0.2 mm, and the sound absorption coefficient(α) is 0.9 and 1. Furthermore, at low frequencies from 250 Hz to 2 kHz, the α is not increased; since according to previous studies, the main limitation is low thickness. Therefore, the parameters have been improved only at high frequencies. According to the results of Fig. 4 at optimized parameters, the pore size decreases as the frequency increases. Meanwhile, the porosity and pore opening do not follow a special correlation.

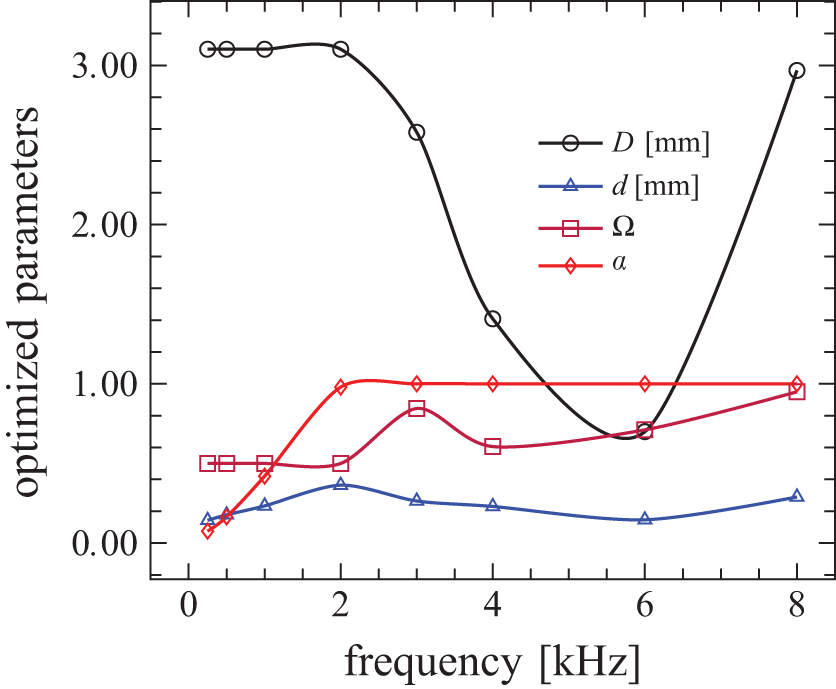
Figure 4: The optimized morphological parameters at different frequencies for the highest sound absorption coefficient (α) in an Al foam barrier with 5 mm Thickness

The optimized morphological parameters at different frequencies for the highest sound absorption coefficient (α) in an Aluminum foam barrier with 10mm thickness are shown in Fig. 5. The sound absorption coefficient (α) is close to 1 at the frequency range of 2 kHz–8 kHz when the porosity is between 70 and 95% (0.7–0.95 in figure), pore size is 0.1 mm to 2.3 mm, and pore opening is 0.07 mm to 0.3 mm. The results show that at optimized values, the pore size decreases by increasing frequency, and the porosity and pore opening size do not follow any special correlation.

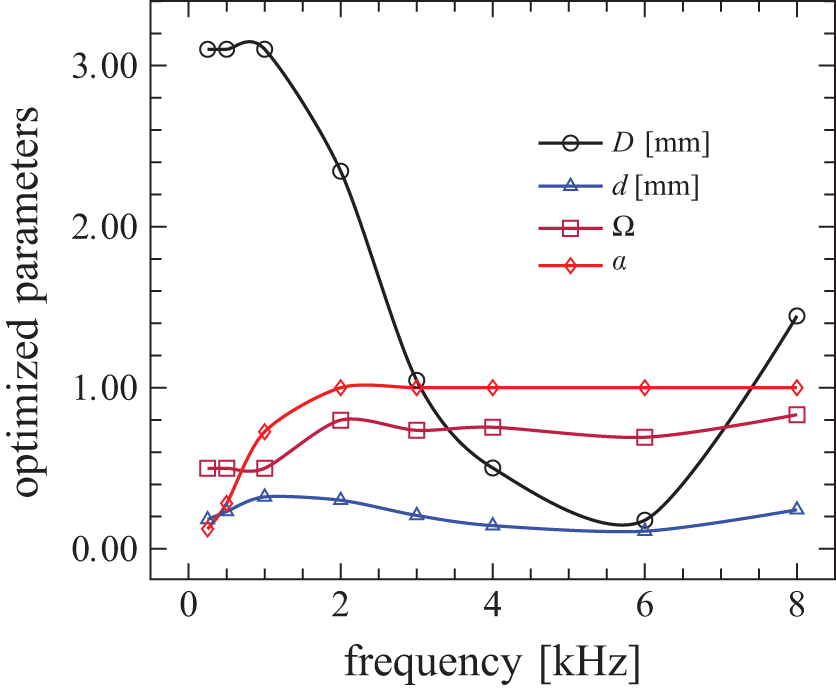
Figure 5: The optimized morphological parameters at different frequencies for the highest sound absorption coefficient (α) in an Al foam barrier with 10 mm Thickness

The optimized morphological parameters at different frequencies for the highest sound absorption coefficient (α) in an Aluminum foam barrier with 20 mm thickness are shown in Fig. 6. This figure shows that the sound absorption coefficient (α) is close to 1 at the frequency range of 2 kHz–8 kHz when the porosity is between 61% to 95 % (0.61–0.95 in figure), the pore size is 0.1 mm to 4.4 mm, and the pore opening is 0.08 mm to 0.5 mm. Fig. 6 shows that the pore size decreases by increasing frequency, while the porosity and pore opening do not follow any special correlation.

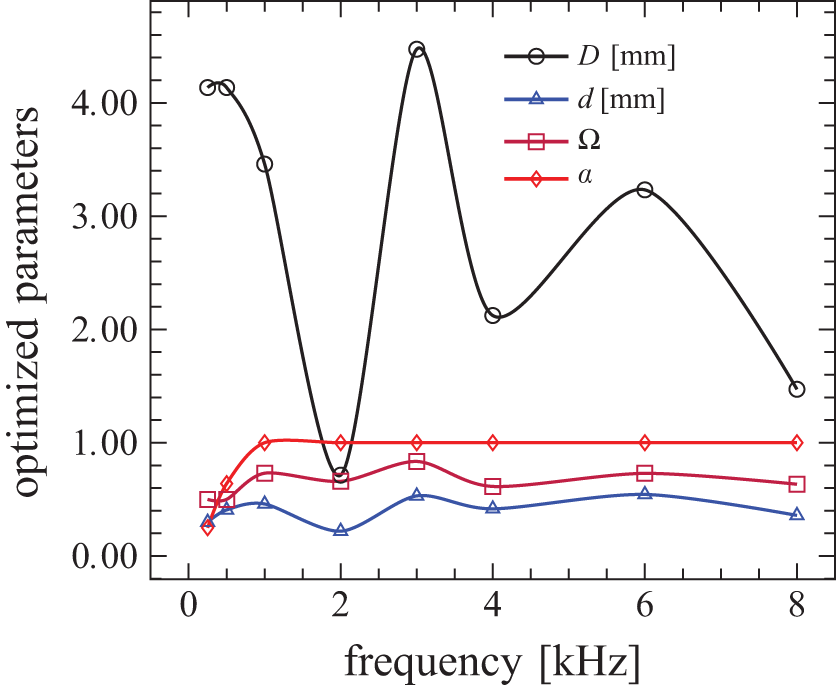
Figure 6: The optimized morphological parameters at different frequencies for the highest sound absorption coefficient (α) in an Al foam barrier with 20 mm Thickness

The results revealed that at 30 mm thickness, when the porosity is between 0.6 to 0.95, The pore size is 0.1 mm to 2.08 mm, and the pore opening is 0.09 mm to 0.43 mm, the sound absorption coefficient (α) is almost equal to 1 at the frequency range of 1 kHz to 8 kHz (Fig. 7). For most frequencies, the pore opening is 0.1 mm. Porosity, pore size, and pore opening do not follow a certain correlation, and their values vary at each studied frequency.

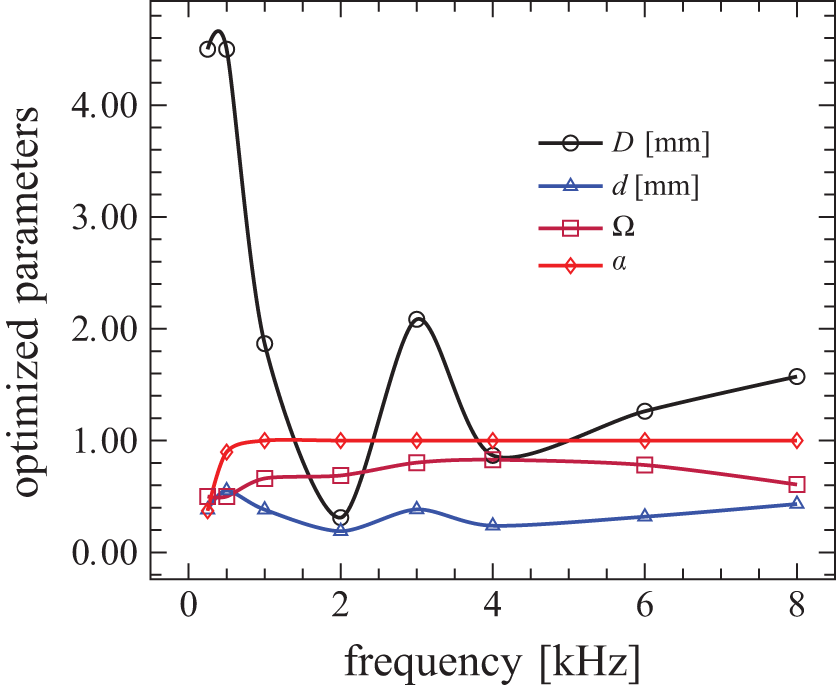
Figure 7: The optimized morphological parameters at different frequencies for the highest sound absorption coefficient (α) in an Al foam barrier with 30 mm Thickness

Fig. 8 shows the optimized morphological parameters at different frequencies for the highest sound absorption coefficient (α) in an Aluminum foam barrier with 35 mm thickness. This figure reveals that in frequencies of 0.5 kHz–8 kHz, when the porosity is between 0.5 to 0.85, the pore size is from 0.1 mm to 4.4 mm, and the pore opening is between 0.09 mm and 0.6 mm, the sound absorption coefficient (α) is close to one. Porosity, pore size, and pore opening do not follow any special correlation, and their values vary at each studied frequency.

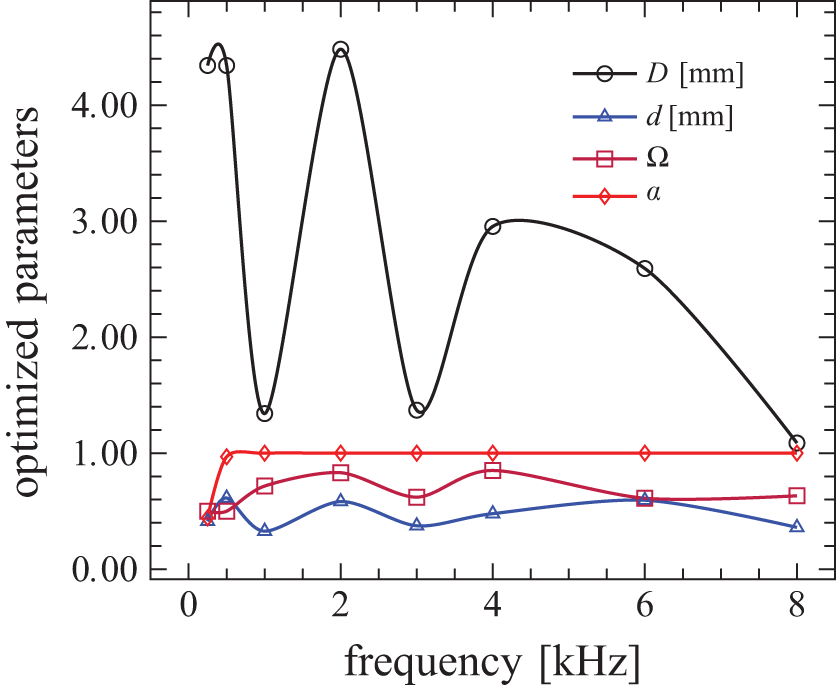
Figure 8: The optimized morphological parameters at different frequencies for the highest sound absorption coefficient (α) in an Al foam barrier with 35 mm Thickness

The results show that when the thickness is 40mm, the sound absorption is close to 1 at frequencies of 0.5-8kHz with a porosity of 0.51 to 0.95, a pore size of 0.1 mm to 4.5 mm, and a pore opening of 0.1 mm and 0.6 mm (Fig. 9). It is worth mentioning that in the thickness of 40 mm, the improved porosity and pore opening are fixed at 0.95 mm and 0.1 mm respectively. According to the results, the pore size decreases by increasing frequency, and the porosity and pore opening do not follow any special correlation. Furthermore, at a relatively low frequency of 0.5 kHz to 2 kHz, there is an increase in the sound absorption coefficient (α) relative to the thickness of 5 mm. Therefore, at low frequencies, the sound absorption coefficient (α) increases by increasing the thickness.

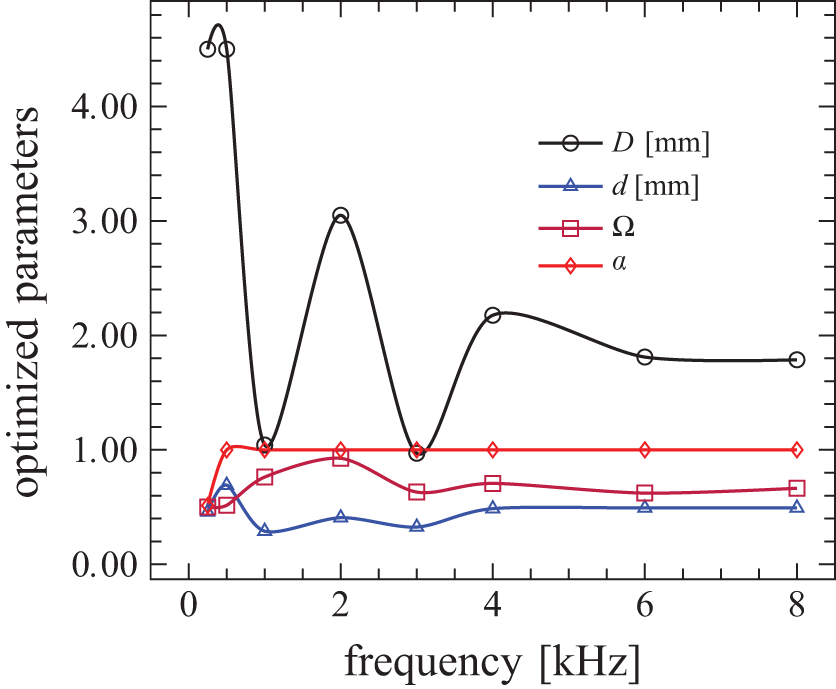
Figure 9: The optimized morphological parameters at different frequencies for the highest sound absorption coefficient(α) in an Al foam barrier with 40 mm Thickness

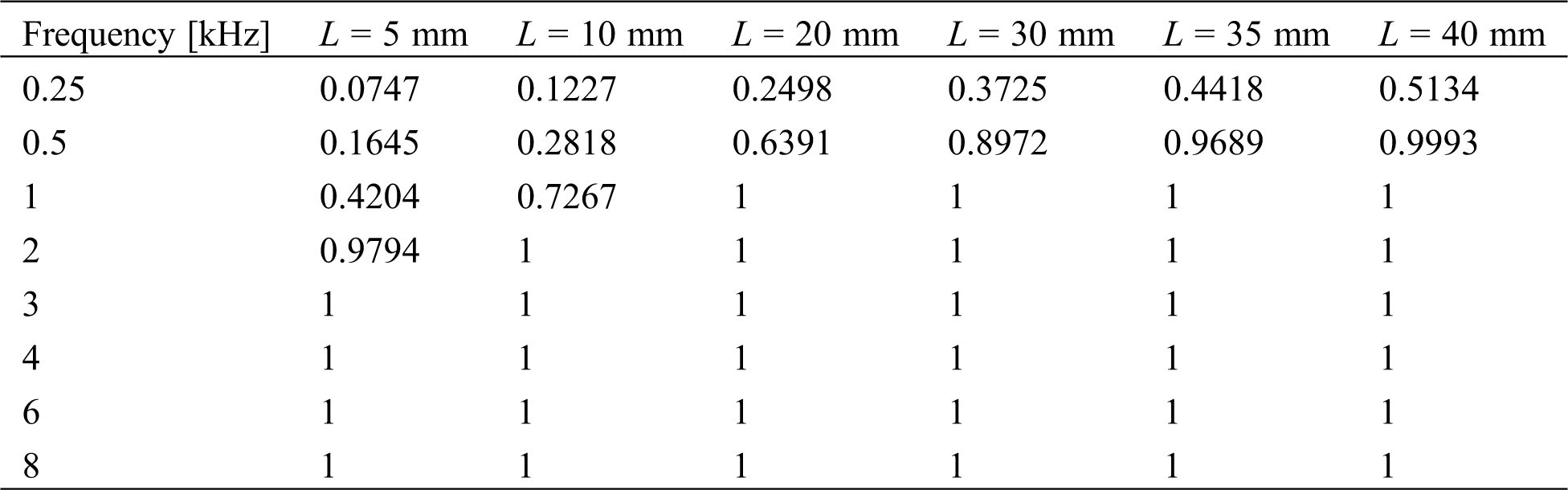
The best sound absorption coefficients (α) determined for each frequency at different thicknesses of Aluminum foam are presented in Tab. 4. The highest sound absorption coefficient (0.5134) for the challenging low frequency of 250 Hz is determined for an aluminum foam at the thickness of 40 mm.

Table 4: The highest sound absorption coefficients determined at studied frequencies for Aluminum foam at different thicknesses

4  Discussion

In this study, a novel approach was applied to improve the morphological parameters of metal foams including porosity, pore size and pore opening for the highest sound absorption coefficient at different frequencies. The method was applied to determine these parameters at different thicknesses of 5 mm to 40 mm. These improved parameters along with the highest sound absorption coefficient (α) at the frequency range of 250 Hz to 8000 Hz are presented in Figs. 4–9 for different foam thicknesses. These measures can be used to intelligently fabricate Aluminum foam for the best sound absorption coefficient using sintering technology.

Kuromura et al. [39] belive that it is very important if it would be possible to fabricate better absorbents materials that have openings connected to the adjacent cells through controlling pore opening size, pore size, and porosity. The present study shows the way it is possible to fabricate such materials.

According to the results, the sound absorption coefficients determined using this approach is almost 1 for the frequency range of 500 Hz to 8000 Hz. Controlling of low frequency sound has always been a challenging task for the engineers. The application of this approach showed that it is possible to get sound absorption coefficient of 0.5134 using Aluminum foam with 40mm thickness.

absorption for the frequencies less than for all frequencies higher it was found that for the maximum SAC at each frequency and thickness, the porosity has a certain value; however, in previous studies, it was stated that the SAC increases by increasing porosity [39–42]. In the study of Wang et al., it was found that for constant porosity, sound absorption increases by increasing cell size [43].

The results showed that in the thickness of 5, 10, 20, and 40 mm for the maximum SAC, by increasing frequency, the pore size decreases. According to the previous results, the SAC increases by decreasing pore size [7,41,42]. The study by kuromura et al. [39] stated that the SAC differs with pore size variations, which is in line with the results of the present study. In the study of Hakamada et al. [12], the sample B, with the smallest pore size of 212 μm to 300 μm, had the highest SAC, which was consistent with previous studies [7,41,42], and this pore size in the range of optimal parameters obtained in this study. In some studies including [11,43], the diameter of the pores was reported in the range of 0.5 mm to 2 mm, which were in the optimization range of this study. In the study carried out by Wang et al. [43], using computational method, the optimal amount of pore size for the best sound absorption capacity was estimated to be at least 100μm. However, in this study, the pore size differs in various frequencies and thickness.

The results of studies including [12,44,45] show that in general, reducing the pore size increases the SAC; however, according to the obtained results, for the constant SAC of nearly one, the pore size decreases by increasing frequency. Li et al. [46] stated that there is no definitive correlation between the pore size and the SAC of Aluminum foams with spherical cells, which is in line with the results of this study. Hakamada et al. [12] argued that there is no apparent correlation between the pore size and the SAC due to the significant effects of the pore opening, which is consistent with the results of this study. Recently, the importance of pore opening size in the resistance to the flow of porous metals has been emphasized [12,47].

It has been accepted that there is an apparent relationship between the SAC and the resistance to the flow [12]. Therefore, it is suggested that the pore opening size strongly affects the sound absorption behavior and controlling pore opening size is very important for achieving higher SACs [12]. When the sound wave propagates from the cells to the pore openings, the air velocity substantially increases; since pore opening channels are narrower than the cells [39]. Loss of energy increases by increasing air velocity [39]. Hence, the sound wave through friction by transferring from cell to pore opening is significant [39]. Obviously, when the pore opening size is too high, the air flow velocity changes slightly when passing through the pores, resulting in no deviation from friction [39]. Conversely, if the pore opening size is very small, the resistance to the air flow will be very high and the maximum sound waves will not be entering into the material, but reflected from the surface of the sample. It also leads to poor sound absorption [11,12,43,46]

Therefore, the pore opening size needs a certain range that needs to be optimized for each thickness and frequency. In the present study, the amount of pore opening is 0.07 mm to 0.6 mm, which has no correlation with the SAC in various thickness and frequencies. Li et al. [46] pointed out that, by increasing pore opening diameter, the SAC reduced and the pore size was within 0.3 mm–0.4 mm. It was suggested that the optimal pore opening is 0.1 mm [11,43], which is in line with the optimization results of this study. Hakamada et al. [12] stated that the presence of a pore opening smaller than 100 μm, especially for porous metals produced by the spacer method, greatly improves the sound absorption properties. In another study, they pointed out that high-sound absorption cannot be achieved when the pore opening size is 10 μm or 100 μm [48]. Therefore, it has been conclusively shown that the pore opening size strongly affects the porous Aluminum absorption behavior produced by the spacer method, and controlling the pore opening size to achieve the sound absorption capacity is very important [12].

According to the results of this study show that, in order to increase the amount of sound absorption, the thickness of the panel must be increased at frequencies below 2000 Hz. However, at higher frequencies, for each thickness (the optimal value of d, D, and Ω) can be found, so that the amount of sound absorption reaches the maximum value. According to Hakamada et al. [12], the SAC increases due to an increase in sample thickness in the frequency range of approximately less than 2000 Hz. The effect of sample thickness on sound absorption is understandable due to the long distances in relatively thick samples, which increases the interaction of the sound wave with the pores walls [46]. In the study of Li et al. [46], the peak in the SAC increases, and changes to lower frequencies by increasing the thickness of the sample. It is also found that at frequencies above 2000 Hz, increasing the sound absorption efficiency does not require an increase in thickness, and this can only be achieved by changing the amount of porosity, pore size, and pore opening. In this study, it was found that porosity, pore size, and pore opening have important factors in optimizing the SAC; however, pore size and pore opening have a more important role than porosity, which is similar to Meng study [49].

5  Conclusion

A novel method was introduced to optimize the morphological parameters of metal foams for the best sound absorption coefficients. Controlling the porosity, pore size, and pore opening is a useful strategy for sound absorption spectrum in open cell foams. The Lu model is reliable for simulating sound absorption in porous metals with difficult structures and can be used as a tool for optimizing porous structures using porosity and their permeability as variables. The results presented in Figs. 4-9 can be applied to fabricate Aluminum foams with best sound absorption coefficients at different frequencies. The GA used in this study can provide an effective way to develop optimized metal foam absorbents for any selected frequency for the industry.

Acknowledgement: This study is extracted from the PhD thesis in the field of Occupational Health Engineering. The authors wish to appreciate Shahid Beheshti University of Medical Sciences for their technical and financial support. The study proposal was registered with the grant number 9597/22. It was also approved by the university ethics committee (IR.SBMU.PHNS.REC.1397.083) prior to its execution.

Funding Statement: This paper was the output of a research project (registration number: 9597/22), which was financially supported by Shahid Beheshti University of Medical Sciences.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  Schust, M. (2004). Effects of low frequency noise up to 100 Hz. Noise and Health, 6(23), 73. [Google Scholar]

 2.  Landaluze, J., Portilla, I., Pagalday, J., Martı́nez, A., Reyero, R. (2003). Application of active noise control to an elevator cabin. Control Engineering Practice, 11(12), 1423–1431. DOI 10.1016/S0967-0661(03)00077-7. [Google Scholar] [CrossRef]

 3.  Ashby, M. F., Evans, T., Fleck, N. A., Hutchinson, J., Wadley, H. et al. (2000). Metal foams: A design guide. Elsevier. [Google Scholar]

 4.  Banhart, J. (2001). Manufacture, characterisation and application of cellular metals and metal foams. Progress in Materials Science, 46(6), 559–632. DOI 10.1016/S0079-6425(00)00002-5. [Google Scholar] [CrossRef]

 5.  Wang, Z., Li, Z., Ning, J., Zhao, L. (2009). Effect of heat treatments on the crushing behaviour and energy absorbing performance of aluminium alloy foams. Materials & Design, 30(4), 977–982. DOI 10.1016/j.matdes.2008.06.058. [Google Scholar] [CrossRef]

 6.  Campana, F., Pilone, D. (2009). Effect of heat treatments on the mechanical behaviour of aluminium alloy foams. Scripta Materialia, 60(8), 679–682. DOI 10.1016/j.scriptamat.2008.12.045. [Google Scholar] [CrossRef]

 7.  Han, F., Seiffert, G., Zhao, Y., Gibbs, B. (2003). Acoustic absorption behaviour of an open-celled aluminium foam. Journal of Physics D: Applied Physics, 36(3), 294–302. DOI 10.1088/0022-3727/36/3/312. [Google Scholar] [CrossRef]

 8.  Manalo, A. (2011). Behaviour of fibre composite sandwich structures: A case study on railway sleeper application. University of Southern Queensland. [Google Scholar]

 9.  Jang, W. y (2008). On the compressive response of open-cell aluminum foams. [Google Scholar]

10. Gibson, L. J., Ashby, M. F. (1999). Cellular solids: Structure and properties. Cambridge university press. [Google Scholar]

11. Lu, T. J., Chen, F., He, D. (2000). Sound absorption of cellular metals with semiopen cells. Journal of the Acoustical Society of America, 108(4), 1697–1709. DOI 10.1121/1.1286812. [Google Scholar] [CrossRef]

12. Hakamada, M., Kuromura, T., Chen, Y., Kusuda, H., Mabuchi, M. (2006). Sound absorption characteristics of porous aluminum fabricated by spacer method. Journal of Applied Physics, 100(11), 114908. DOI 10.1063/1.2390543. [Google Scholar] [CrossRef]

13. Guan, D., Wu, J. H., Wu, J., Li, J., Zhao, W. (2015). Acoustic performance of aluminum foams with semiopen cells. Applied Acoustics, 87, 103–108. DOI 10.1016/j.apacoust.2014.06.016. [Google Scholar] [CrossRef]

14. Meng, H., Ren, S., Xin, F., Lu, T. (2016). Sound absorption coefficient optimization of gradient sintered metal fiber felts. Science China Technological Sciences, 59(5), 699–708. DOI 10.1007/s11431-016-6042-1. [Google Scholar] [CrossRef]

15. Cobo, P., Moraes, E., Simón, F. (2015). Inverse estimation of the non-acoustical parameters of loose granular absorbers by Simulated Annealing. Building and Environment, 94, 859–866. DOI 10.1016/j.buildenv.2015.05.009. [Google Scholar] [CrossRef]

16. Allard, J. (1993). Propagation of sound in porous media, Modelling sound absorbing materials, edited by Elsevier Applied Science. New York and London: Elesevier Science Publishers LTD. [Google Scholar]

17. Biot, M. (1962). Generalized theory of acoustic propagation in porous dissipative media. Journal of the Acoustical Society of America, 34(9A), 1254–1264. DOI 10.1121/1.1918315. [Google Scholar] [CrossRef]

18. Johnson, D. L., Koplik, J., Dashen, R. (1987). Theory of dynamic permeability and tortuosity in fluid-saturated porous media. Journal of Fluid Mechanics, 176(-1), 379. DOI 10.1017/S0022112087000727. [Google Scholar] [CrossRef]

19. Goldberg, D. E. (2006). Genetic algorithms. Pearson Education India. [Google Scholar]

20. Dorigo, M., Di Caro, G. (1999). Ant colony optimization: A new meta-heuristic. Proc. of the 1999 congress on evolutionary computation-CEC99 (Cat. No. 99TH8406). IEEE. [Google Scholar]

21. Zeugmann, T., Poupart, P., Kennedy, J., Jin, X., Han, J. et al. (2011). Particle swarm optimization. Boston, MA: Springer US, 760-766. [Google Scholar]

22. Sukhbaatar, U. (2016). Un modèle de simulation pour une infrastructure logistique dédiée à la fourniture de services mobiles sensibles au contexte: Application au tourisme, Grenoble Alpes. [Google Scholar]

23. Barbulescu, L., Watson, J. P., Whitley, L. D. (2000). Dynamic representations and escaping local optima: Improving genetic algorithms and local search. AAAI/IAAI, 2000, 879–884. [Google Scholar]

24. Dumitrescu, I., Stützle, T. (2003). Combinations of local search and exact algorithms. Springer: Workshops on Applications of Evolutionary Computation. [Google Scholar]

25. Wang, T., Yang, L., Liu, Q. (2018). Beetle swarm optimization algorithm: Theory and application. arXiv preprint arXiv: 1808.00206. [Google Scholar]

26. Yeh, J. Y., Lin, W. S. (2007). Using simulation technique and genetic algorithm to improve the quality care of a hospital emergency department. Expert Systems with Applications, 32(4), 1073–1083. DOI 10.1016/j.eswa.2006.02.017. [Google Scholar] [CrossRef]

27. Yang, A., Shan, Y., Bui, L. T. (2008). Success in evolutionary computation. Springer. [Google Scholar]

28. Sheta, A., Turabieh, H. (2006). A comparison between genetic algorithms and sequential quadratic programming in solving constrained optimization problems. ICGST Int. Journal on Artificial Intelligence and Machine Learning (AIML), 6(1), 67–74. [Google Scholar]

29. Coley, D. A. (1999). An introduction to genetic algorithms for scientists and engineers. World Scientific Publishing Company. [Google Scholar]

30. Haupt, R. L., Haupt, S. E. (2004). Practical genetic algorithms. John Wiley & Sons. [Google Scholar]

31. Ou, D. (2018). An optimization method for maximizing the low frequency sound insulation of plate structures. Shock and Vibration, 2018(23), 1–8. DOI 10.1155/2018/7849327. [Google Scholar] [CrossRef]

32. Gholamipoor, M., Ghadimi, P., Alavidoost, M. H., Feizi Chekab, M. A. (2014). Application of evolution strategy algorithm for optimization of a single-layer sound absorber. Cogent Engineering, 1(1), 945820. DOI 10.1080/23311916.2014.945820. [Google Scholar] [CrossRef]

33. Ramoji, S. K., Rath, B. B., Kumar, D. V., Optimum design of a hybrid PV/Wind energy system using Genetic Algorithm (GA). [Google Scholar]

34. Nongmeikapam, K., Bandyopadhyay, S. (2016). Genetic Algorithm (GA) Implementation for Feature Selection in Manipuri POS Tagging. Proc. of the 13th Int. Conf. on Natural Language Processing. [Google Scholar]

35. Mitchell, M. (1996). An introduction to genetic algorithms mit press. Cambridge, Massachusetts. London, England. [Google Scholar]

36. Beasley, D., Bull, D. R., Martin, R. R. (1993). An overview of genetic algorithms: Part 1, fundamentals. University Computing, 15(2), 56–69. [Google Scholar]

37. Beasley, D., Bull, D. R., Martin, R. R. (1993). An overview of genetic algorithms: Part 2, research topics. University Computing, 15(4), 170–181. [Google Scholar]

38. Hassanat, A., Almohammadi, K., Alkafaween, E., Abunawas, E., Hammouri, A. et al. (2019). Choosing mutation and crossover ratios for genetic algorithms—A review with a new dynamic approach. Information-an International Interdisciplinary Journal, 10(12), 390. [Google Scholar]

39. Kuromura, T., Hakamada, M., Chen, Y., Kusuda, H., Mabuchi, M. (2007). Sound absorption behavior of porous Al produced by spacer method. Advanced Materials Research, Trans Tech Publ, 15 - 17. [Google Scholar]

40. Lu, T. J., Hess, A., Ashby, M. (1999). Sound absorption in metallic foams. Journal of applied physics, 85(11), 7528–7539. DOI 10.1063/1.370550. [Google Scholar] [CrossRef]

41. Xie, Z., Ikeda, T., Okuda, Y., Nakajima, H. (2004). Sound absorption characteristics of lotus-type porous copper fabricated by unidirectional solidification. Materials Science and Engineering: A, 386(1–2), 390–395. DOI 10.1016/S0921-5093(04)00966-9. [Google Scholar] [CrossRef]

42. Xie, Z. K., Ikeda, T., Okuda, Y., Nakajima, H. (2004). Characteristics of sound absorption in lotus-type porous magnesium. Japanese Journal of Applied Physics, 43(10), 7315–7319. DOI 10.1143/JJAP.43.7315. [Google Scholar] [CrossRef]

43. Wang, X., Lu, T. J. (1999). Optimized acoustic properties of cellular solids. Journal of the Acoustical Society of America, 106(2), 756–765. DOI 10.1121/1.427094. [Google Scholar] [CrossRef]

44. Navacerrada, M., Fernández, P., Díaz, C., Pedrero, A. (2013). Thermal and acoustic properties of aluminium foams manufactured by the infiltration process. Applied Acoustics, 74(4), 496–501. DOI 10.1016/j.apacoust.2012.10.006. [Google Scholar] [CrossRef]

45. Fang, W., Lu-cai, W., Jian-guo, W., Xiao-hong, Y. (2007). Sound absorption property of open-pore aluminum foams. Research & Development. [Google Scholar]

46. Li, Y., Wang, X., Wang, X., Ren, Y., Han, F. et al. (2011). Sound absorption characteristics of aluminum foam with spherical cells. Journal of Applied Physics, 110(11), 113525. DOI 10.1063/1.3665216. [Google Scholar] [CrossRef]

47. Despois, J. F., Mortensen, A. (2005). Permeability of open-pore microcellular materials. Acta Materialia, 53(5), 1381–1388. DOI 10.1016/j.actamat.2004.11.031. [Google Scholar] [CrossRef]

48. Hakamada, M., Kuromura, T., Chen, Y., Kusuda, H., Mabuchi, M. (2006). High sound absorption of porous aluminum fabricated by spacer method. Applied Physics Letters, 88(25), 254106. DOI 10.1063/1.2216104. [Google Scholar] [CrossRef]

49. Meng, H., Xin, F., Lu, T. (2014). Sound absorption optimization of graded semi-open cellular metals by adopting the genetic algorithm method. Journal of Vibration and Acoustics, 136(6), 114908. DOI 10.1115/1.4028377. [Google Scholar] [CrossRef]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.