 Open Access
Open Access
REVIEW
Structural Modal Parameter Recognition and Related Damage Identification Methods under Environmental Excitations: A Review
1 School of Civil Engineering and Mechanics, Lanzhou University, Lanzhou, 730000, China
2 Key Laboratory of Special Functional Materials and Structural Design, Ministry of Education, Lanzhou University, Lanzhou, 730000, China
* Corresponding Author: Hua-Ping Wang. Email:
(This article belongs to the Special Issue: Sensing Data Based Structural Health Monitoring in Engineering)
Structural Durability & Health Monitoring 2025, 19(1), 25-54. https://doi.org/10.32604/sdhm.2024.053662
Received 07 May 2024; Accepted 09 August 2024; Issue published 15 November 2024
Abstract
Modal parameters can accurately characterize the structural dynamic properties and assess the physical state of the structure. Therefore, it is particularly significant to identify the structural modal parameters according to the monitoring data information in the structural health monitoring (SHM) system, so as to provide a scientific basis for structural damage identification and dynamic model modification. In view of this, this paper reviews methods for identifying structural modal parameters under environmental excitation and briefly describes how to identify structural damages based on the derived modal parameters. The paper primarily introduces data-driven modal parameter recognition methods (e.g., time-domain, frequency-domain, and time-frequency-domain methods, etc.), briefly describes damage identification methods based on the variations of modal parameters (e.g., natural frequency, modal shapes, and curvature modal shapes, etc.) and modal validation methods (e.g., Stability Diagram and Modal Assurance Criterion, etc.). The current status of the application of artificial intelligence (AI) methods in the direction of modal parameter recognition and damage identification is further discussed. Based on the previous analysis, the main development trends of structural modal parameter recognition and damage identification methods are given to provide scientific references for the optimized design and functional upgrading of SHM systems.Keywords
Civil engineering structures such as ultra-high-rise buildings, large-span bridges, ocean platform projects, and giant dams may suffer localized damage (e.g., buckling, cracking, corrosion, etc.) due to extreme environmental factors (e.g., earthquakes, typhoons, air pollution, etc.) during long-term service, which results in a gradual degradation of the actual load-bearing capacity with the increase in operating years. The accumulation and propagation of local damage can decrease the structural load-bearing capacity. If not properly controlled, it may lead to a reduction in overall structural strength, instability, or fatigue failure [1], resulting in severe casualties, economic losses, and negative social impacts. For example, the Morandi Bridge in Genoa, Italy, collapsed during heavy rainfall on 14 August 2018, killing 43 people after the bridge structure failed to be reinforced and repaired in a timely manner after cracks appeared in the structure [2]; The Surfside condominium in Miami, USA, collapsed on 24 June 2021, killing 98 people due to water infiltration, corrosion of steel reinforcement and foundation settlement that was not repaired in time [3]. Therefore, constructing a structural health monitoring system, finding where and how much damage the structure has early on, and doing repairs and reinforcement promptly can make the structure last longer and lower the risk of major damage.
Monitoring large engineering structures needs many sensors and the ability to constantly send and process lots of data they gather right away. It also needs to pick out the structure’s health and damage details from all that data. Among them, structural damage identification is an important module. The main research areas cover detecting the presence of damage, identifying the location of damage, quantifying the extent of damage, and predicting the remaining life of the structure. Scholars have done a lot of research in this direction and much of the current research is devoted to the first three questions. Structural damage identification methods, in general, can be divided into two categories: non-destructive testing methods (NDT) and vibration-based methods [4]. NDT methods are regarded as localized methods that can directly locate structural damage, but they are only applicable to the identification of local component damage and are difficult to be used for the detection of overall structural damage in large-scale projects. Vibration-based methods, like global methods, are commonly used for finding damage in big civil engineering structures.
The identification of structural parameters can also be divided into two categories: static and dynamic identification [5]. The former identifies local damage. It arranges measurement points on the structure and applies static loads to measure the structural response. Using optimization algorithms, it obtains relevant parameter information about the structure’s actual state. Damage location is identified by comparing parameter changes before and after damage. The identified damage locations are usually within the range of the measurement points and their surroundings. For damage in the blind zone of the test, further structural theory or numerical simulation analysis is required to identify the damage [6]. The latter method uses modal frequency to determine if the structure is damaged. It then uses the modal vibration pattern to locate the damage and constructs a suitable damage identification index to diagnose the severity of structural damage [7].
Extensive research has been conducted by scholars on static identification. Cui et al. [8] identified that the stiffness parameters of rigid frame structures were able to accurately locate structural damage through a structural parameter identification method based on static strain and displacement measurements; Ghrib et al. [9] used the measured static deflections, two computational methods for reconstructing the stiffness distribution and detecting damage in Eulerian Bernoulli beams were developed, both of which were able to accurately identify the damage in the cantilever beams, but the equilibrium gap generalization-based method was closer to the actual damage state than the data discrepancy-based method. Abdo [10] studied the relationship between changes in structural displacement curvature and structural damage under static loading. They identified damage in overhanging beams and two-span continuous beams by observing changes in displacement curvature. The displacement curvature of two-span continuous beams was approximated using the center difference method. If the displacement curvature is measured directly, the accuracy of damage identification improves. Caddemi et al. [11] proposed an inverse damage identification method using a closed-form solution for transverse displacements caused by static loads and general boundary conditions. This method can identify the number of cracks, their locations, and the extent of damage on simple straight beams. It is also applicable to more complex frame structures. However, the monitoring effectiveness depends on the sensor arrangement location. Huang et al. [12] proposed a static damage identification method for beam structures based on the L1 regularization method, which can reduce the misclassification for small damages and accurately identify the damages of concrete beams compared to the least squares method. Tang et al. [13] proposed a static damage identification method based on derivative variables, which can effectively identify the damage location and damage degree of a three-span continuous beam structure when the noise level does not exceed 5%. It can be seen that: the research on static identification mainly focuses on bridges or truss structures where it is easy to apply static loads in the laboratory or in the field.
In the actual damage identification of large civil engineering structures (e.g., large-span bridges), the application of static loads for detection requires the interruption of traffic, but if the method of dynamic identification is used, a real-time monitoring system can be set up to identify the damage without affecting normal traffic. The core of structural damage identification based on dynamic response information is that changes in structural health result in changes in structural physical properties. It involves establishing functional relationships between structural modal parameters (e.g., intrinsic frequency, damping ratios, and modal shapes) and structural physical parameters (e.g., mass, damping, and stiffness) [14]. By studying the changes in parameters before and after structural damage, structural damage identification is achieved. Many scholars around the world have conducted vibration-based damage detection methods. Farrar et al. [15] described vibration-based damage detection as a statistical pattern recognition problem. This involves data acquisition and processing, feature selection, data compression, and statistical model development, with a focus on feature selection and statistical model development. Peeters et al. [16] addressed the effect of excitation and temperature on modal parameters and developed a structural damage identification method that removes the effect of temperature; Bayissa et al. [17] proposed a statistical moment of the energy density function in the time-frequency domain based on the vibration response to transform the wavelet coefficients in the spatial domain into a new damage identification parameter to accurately measure the damage in concrete slabs and steel plate beams. Cao et al. [18] reviewed the use of damping as a dynamic characteristic to identify structural damage. Huang et al. [19] summarized the basic principles of Bayesian analysis and computation and provided a summary review of recent advances in Bayesian inference for structural damage identification; Weng et al. [20] reviewed substructure methods for model correction and damage identification for large structures; Hou et al. [4] provided a review of research advances in vibration-based damage identification methods between 2010–2019. Dynamic damage identification methods are commonly used for diagnosing damage in large and complex structural systems, such as large-span bridges and high-rise buildings. These methods are divided into two main categories: physical model-driven and monitoring data-driven. The sensitivity and accuracy of their damage identification need further improvement.
The recognition of structural modal parameters under environmental excitation has the advantages of not affecting the normal operation of the structure and not requiring specialized external excitation. This is crucial for establishing structural health monitoring systems in civil engineering. In recent years, methods for identifying modal parameters under environmental excitation have made significant progress. Traditional modal parameter recognition methods, such as the SSI, FDD, and NExT-ERA, essentially decompose eigenvalues and eigenvectors from constructed characteristic matrices. However, due to the presence of noise, it is crucial to eliminate the interference of spurious modes. By combining traditional modal recognition methods with machine learning, the efficiency and accuracy of modal parameter recognition can be greatly improved. For example, neural network optimization methods can be used to solve modal equations [21–24]. Machine learning techniques such as clustering and principal component analysis can be employed to optimize the modal parameters extracted by traditional methods [25–27]. Additionally, traditional methods can be applied to the processing of computer vision data [28–30]. Additionally, non-traditional methods for obtaining modal parameters, such as the Bayesian approach [31–33] and the Blind Source Separation (BSS) technique [34–36], have also developed rapidly.
In summary, structural damage identification methods mainly include: identification methods based on structural modal analysis to obtain modal parameters, methods based on vibration test signal analysis (e.g., wavelet analysis and empirical modal decomposition, etc.), damage identification methods based on model modification and identification methods based on the analysis of physical parameters (e.g., Kalman filtering method and generalized Tikhonov regularization method, etc.). In addition, some scholars introduced artificial intelligence algorithms into the process of conventional structural parameter identification and damage diagnosis to improve the accuracy of obtaining structural modal parameters and damage identification. Among them, damage identification by obtaining modal parameters through modal analysis under environmental excitation is the current mainstream method, which has the advantages of high identification efficiency, good accuracy, and clear physical concepts. In view of this, this paper reviews methods for recognizing structural modal parameters and validating them based on modal analysis under environmental excitations. the main research progress in structural damage identification by using modal parameter estimation and the current application of artificial intelligence methods in this field have also been briefly described.
2 Research Progress of Modal Analysis Methods
2.1 Introduction to Modal Analysis
Modal analysis according to the nature of the excitation can be divided into: Experimental Modal Analysis (EMA), Operational Modal Analysis (OMA), and Computational Modal Analysis (CMA) which is often used to assist in the verification, as shown in Fig. 1. EMA uses measurable and controllable excitation such as force hammers and shakers to excite the structure, which requires vibration input and output signals. OMA mostly uses natural environmental excitation, where the excitation is unknown or unmeasurable, so only the output signal is needed. Due to the lack of input signals, it is more difficult to establish an accurate structural model when solving structural parameters, which leads to the expansion of the eigenvalue solution space and reduces the accuracy of modal identification [37,38]. With the development of artificial intelligence, big data, machine learning, and other information technologies, structural health monitoring has shifted from the paradigm based on vibration data to the paradigm based on machine learning [39], which, in combination with traditional methods, can automatically solve the structural parameters more accurately from the massive monitoring data and carry out the structural condition assessment, so as to improve the noise immunity and accuracy of the damage identification and make the monitoring system more intelligent.

Figure 1: Classification of modal analysis techniques
Modal analysis under Environmental Excitation is a kind of OMA, which only measures the output response of the structure. It has the advantages of economy, safety and does not affect the normal operation of the structure [40]. The use of manual excitation for large civil engineering structures is costly and more difficult to realize in the field, therefore, EMA is mostly carried out in the laboratory and nowadays OMA is mostly used. Environmental excitation modal identification methods, which can be categorized into time-domain, frequency-domain, and time-frequency-domain methods [37,41]. Time-domain methods, including SSI, NExT, RDT, ERA, ARMA, ITD, CEM, etc.; Frequency-domain methods, including PP, FDD, PolyLSCF (PolyMAX), BSS, Bayesian Approach, etc.; Time-frequency-domain methods, including HHT, WT, etc. As shown in Fig. 2.
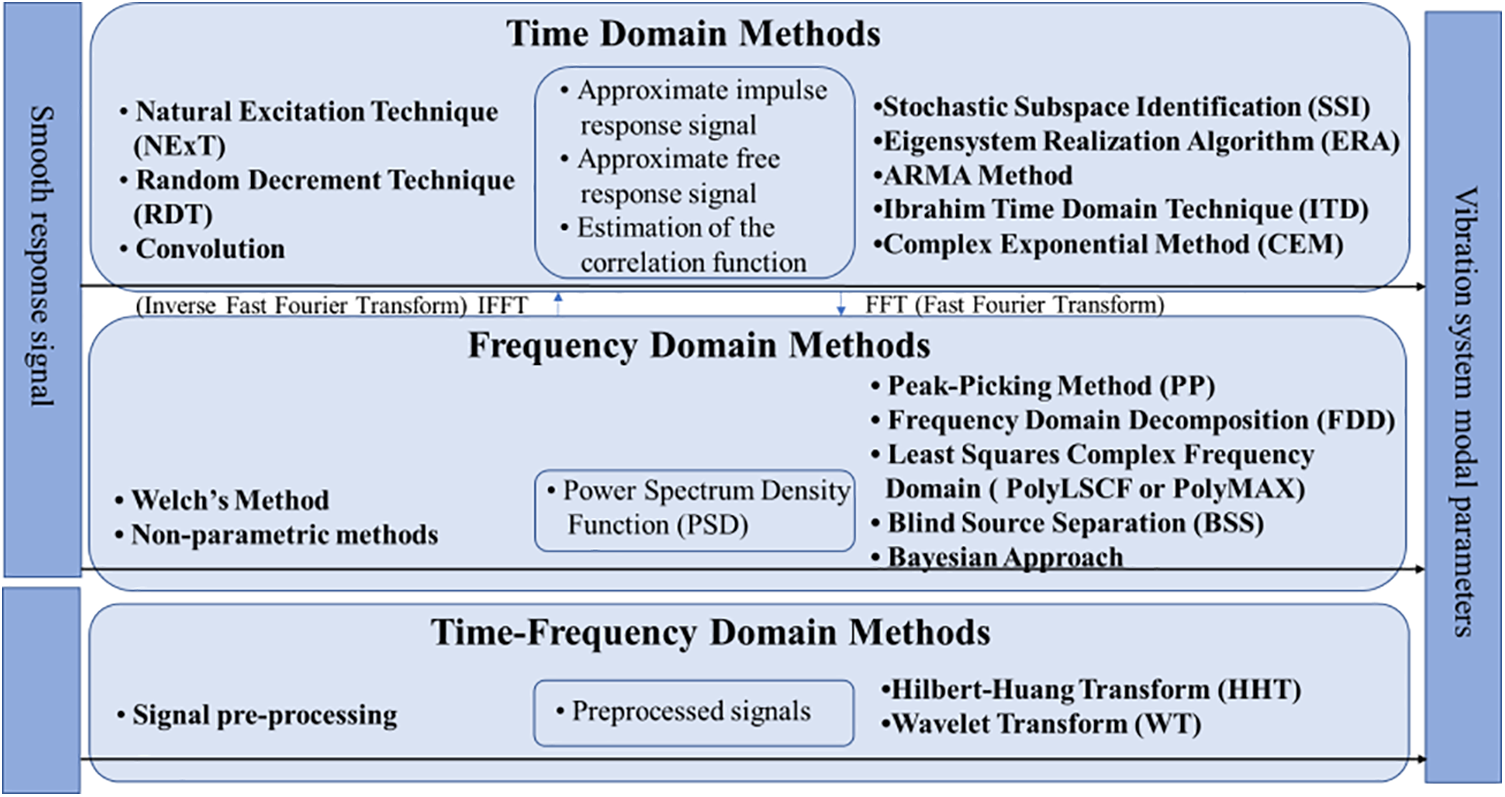
Figure 2: Classification of modal parameter recognition methods
2.2 Time Domain Methods for Modal Parameter Recognition
Environmental excitations on engineering structures are caused by natural factors. They are broadband and approximately uniformly distributed, similar to Gaussian white noise with a constant self-spectrum over an infinite bandwidth. The Time-domain method, which utilizes modern spectral analysis, is a parametric approach [41–43] and can be divided into two categories: (1) Directly using the response data of the system to derive the modal parameters (time-domain one-step method), such as the DATA-SSI and the ARMA; (2) Utilize RDT or NExT to obtain the approximate impulse function of the time-domain impulse signal, then use traditional time-domain modal identification methods like ITD and ERA for modal identification. The Time-domain method can directly process time-domain data points, avoiding errors such as frequency leakage generated by Fast Fourier Transform (FFT), resulting in high identification accuracy. However, it has poor noise resistance and is prone to generating false modes.
2.2.1 Stochastic Subspace Identification
SSI can be divided into data-driven SSI-DATA and covariance-driven SSI-COV. Peeters et al. [44] first proposed the method in 1995 and detailed its theoretical analysis process.
The SSI-DATA belongs to the methods that directly deal with the time series response of the system. Under the environmental excitation, the structural response data are measured, which are composed into a Hankel matrix as in Eq. (1). The QR Decomposition and Singular Value Decomposition (SVD) are utilized to obtain the extended observable matrix and the Kalman filtered state sequence matrix, which transforms the identification problem into a linear least-squares problem of the system matrix in the case of state determination.
where
The SSI-COV requires a decomposition projection calculation using the covariance of the measured structural response under environmental excitation to form a Toeplitze matrix, as in Eq. (2). Since the covariance and the correlation function are similar in form under white noise, the Hankel matrix can be constructed using the response’s cross-correlation function. The process is shown in Fig. 3.
where
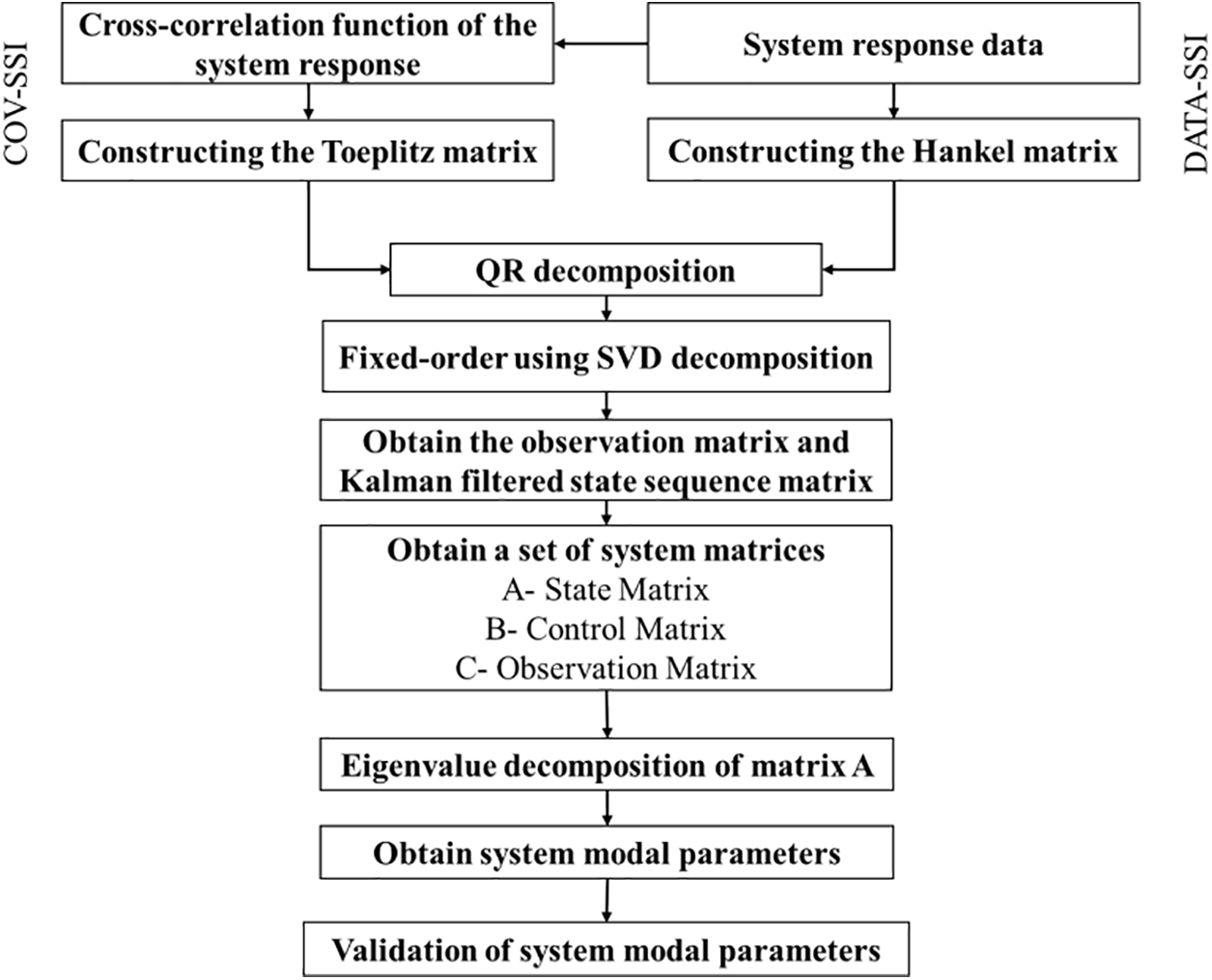
Figure 3: Flowchart of the SSI method
After decades of development, the use of SSI techniques to identify modes of engineering structures has become more mature [25]. Petters et al. [44] validated the vibration data of a steel mast under wind load excitation using the SSI method, with a substantial improvement in computational efficiency, but with high prediction errors for the unreferenced channel. Magalhaes et al. [45] developed an algorithm complementary to SSI-COV for the automatic analysis of stability diagrams to automatically identify the first 12 orders of intrinsic frequency of the Infante D. Henrique Bridge based on its 12 accelerometer data. Cheynet et al. [46–48] evaluated the effectiveness of Covariance-Driven Stochastic Subspace (SSI-COV) vs. Automatic Using Frequency-Domain Decomposition (AFDD) to identify Modal Damping Ratio (MDR) on the Lysefjord suspension bridge in the Norwegian Straits, it was observed that the AFDD algorithm’s MDR estimates are more biased. The time-domain approach is more suitable for identifying modal parameters of long suspension bridges with eigenfrequencies below 0.1 Hz. Chen et al. [49] used Peak-Picking (PP), Frequency Domain Decomposition (FDD), and SSI-DATA to extract the modal parameters of ramp bridges under environmental excitation. The PP method identified the most frequencies, while the SSI method produced the highest quality vibration shapes. Using SSI and PP provides quick preliminary results, while using SSI and FDD allows for detailed analysis. Fang et al. [50] used SSI-DATA to process dynamically distributed fiber-optic Brillouin vibration-strain data to efficiently carry out structural modal analysis. He et al. [51] used the SSI method to identify the modal parameters of environmentally excited bridges. They found that both localized damage and the presence of a moving vehicle would cause the bridge modal frequency to decrease and the vibration pattern to change. Liu et al. [23] introduced the mathematical features of modal identification into neural networks and converted modal parameter recognition into an optimization problem of Deep Neural Networks (DNN) to improve the modal identification accuracy. Li et al. [52] used the OPTICS algorithm for the SSI-COV method for modal parameter recognition to improve the noise resistance and robustness of the algorithm.
SSI has the advantages of mature theory, high identification accuracy, noise resistance, and can identify dense modes. However, it requires substantial computation, is prone to generating false modes, and needs the selection of an appropriate system order to achieve optimal results.
2.2.2 Natural Excitation Technique
The NExT was proposed by James et al. [53] of NASA in 1995, its basic principle is that for a linear time-invariant system with
where
where
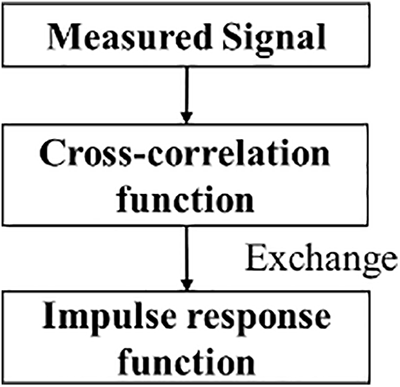
Figure 4: Flowchart of the NExT method
This method is a way to extract the free decay response of a structure. After obtaining the structural impulse response, it is combined with other methods like ERA or WT for modal parameter recognition. He et al. [54] used the NExT-ERA method to extract high-precision modal parameters from structural responses of finite length and time interval under impulse excitation and measurement noise, which was successfully verified to be effective on a suspension bridge model. Wu et al. [55] successfully obtained the self-oscillation frequency of a corner transmission tower based on the NExT-ERA technique. Yang et al. [56] combined NExT and improved empirical modal decomposition (IEMD) to attenuate the influence of the inter-correlation function due to the influence of the modes of each order between the two sides of the point and obtain more accurate modal parameters.
The essence of NExT is signal processing technology, which possesses certain noise resistance. However, it involves considerable computational complexity, is unable to identify false modes, and performs poorly in identifying low natural frequencies and high-damping structures.
2.2.3 Random Decrement Technique
The RDT was proposed by Cole [57] of NASA and theoretically analyzes the structural response signals under environmental excitation, the basic idea is to remove the random forced vibration components from the vibration response and use the averaging technique to retain only the free vibration attenuation to obtain the random reduced signal of the structure, which in turn effectively extracts the frequency and damping ratio of the structure [58–60]. The flowchart of the RDT method is shown in Fig. 5.

Figure 5: Flowchart of the RDT method
The method can better handle single-mode environmental vibration signals and poorly handle multi-mode environmental signals [61]. In order to solve this defect and improve the accuracy of modal recognition, it is often used in combination with other modal recognition methods. Huang et al. [62] combined RDT and AR time-domain algorithms to achieve dynamic feature identification of bridges subjected to environmental vibration under traffic loading. Ku et al. [63] combined RDT and Frequency Response Function (FRF) frequency domain algorithms to improve the accuracy of modal parameter recognition. Chen et al. [64] combined RDT with the ITD based on the free vibration response to extract the structural modal parameters with high noise immunity using the feature signal truncation algorithm and the minimum distance method. Areemit et al. [60] combined RDT and ERA to identify the modal parameters of high-rise buildings and obtained smaller damping ratios compared to conventional spectral analysis. Li et al. [65] identified bridge modal parameters with higher accuracy based on adaptive signal decomposition technique and Successive Variational Modal Decomposition (SVMD) combined with NExT and RDT. Yang et al. [59] proposed a RDT method based on Analytic Modal Decomposition (AMD) to effectively identify the frequency and damping ratio of a structure from the multimodal environmental vibration response. The method is based on the Empirical Modal Decomposition and Randomized Reduction Technique (EMD-RDT), firstly, the environmental vibration signal is decomposed into a series of unimodal sub-signals using AMD, then the RDT is used to extract the stochastic decimation signal from the separated sub-signals, finally the least squares method is used to identify the intrinsic modal frequencies and damping ratios of the structure. The flowchart is shown in Fig. 6.

Figure 6: Flowchart of the AMD-RDT method
The essence of RDT lies in signal processing technology, exhibiting strong robustness. Due to its reliance on the characteristic of the mean value of stationary random responses being zero, it distinguishes between deterministic and stochastic components in the original signal. Therefore, it necessitates a considerable amount of high-quality data. However, it performs poorly in identifying dense modes or high-damping structures.
2.2.4 Eigensystem Realization Algorithm
The ERA is a time-domain holistic modal identification algorithm that utilizes the principle of least-order realizations, proposed by Juang et al. [66] of NASA in 1985 and applied to the modal parameter recognition of NASA spacecraft, it is widely used for the modal parameter recognition of large structures with the advantages of small computational volume and high accuracy [67,68]. The algorithm introduces the principle of minimum realization in minimum control theory, which is constructed by determining the order of the Hankel matrix using the impulse response signal or free response signal of the system. The Hanekl matrix ordering problem was investigated by Caicedo et al. [67] and Li et al. [68] to determine a set of minimal realizations of the system parameters by performing an eigenvalue decomposition (SVD) of the matrix and performing system ordering, which in turn yields the state matrix of the original system [66]. The technical process is shown in Fig. 7.
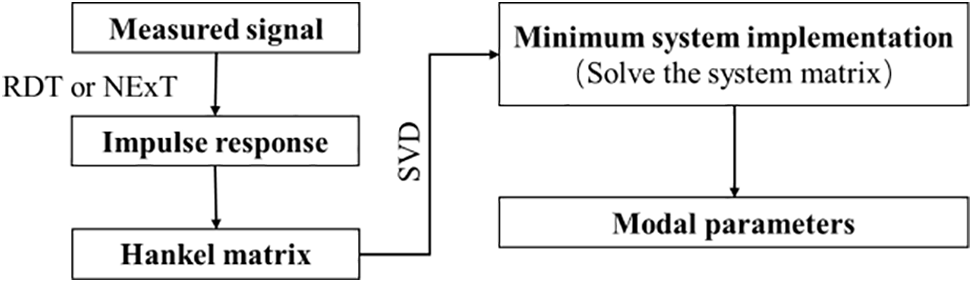
Figure 7: Flowchart of the ERA method
Under environmental excitation, either NExT or RDT can be used in conjunction with ERA to form more practical modal recognition algorithms [69]. Pu et al. [70] proposed the Fast Eigensystem Realization Algorithm (FERA) by using the constructed new symmetric matrix for eigenvalue decomposition to replace the singular value decomposition of the Hankel matrix. Zhu et al. [71] proposed a modal order fixing index called Singular Value Percentage (SVP), based on the proportion of selected order in the dynamic system. This index effectively determines the modal order, rejects spurious modes and identifies the damping ratio with high accuracy. Almunif et al. [72] improved the ERA method by SVD-based rank reduction to improve robustness.
The ERA achieves high accuracy and reduces computational complexity through model reduction techniques. It demonstrates strong practicality; however, it exhibits relatively poor robustness and is susceptible to generating false modes. Therefore, it requires the combination of noise reduction techniques and false mode elimination techniques to enhance its performance.
ARMA refers to Autoregressive Moving Average Model, which includes Auto Regressive Model (AR) and Moving Average (MA). The method is proposed by Akaike [73] in 1969, uses a parametric model to process ordered random vibration response signals to obtain structural modal parameters. The main idea is to establish the equivalent relationship between the autoregressive and sliding average parameters and the transfer function and impulse response function on the basis of the system model to solve the system modal parameters. The technical process is shown in Fig. 8. Kang et al. [74,75] proposed an uncertainty quantification method for time-varying structural operational modal analysis based on the functional series TARMA (FS-TARMA) model, which eliminates spurious modes caused by colored noise excitations and noisy modes caused by measurement noise, etc. Rezzee et al. [76] proposed an identification method for damage detection of floating wind turbines based on ARMA model and fuzzy classification.
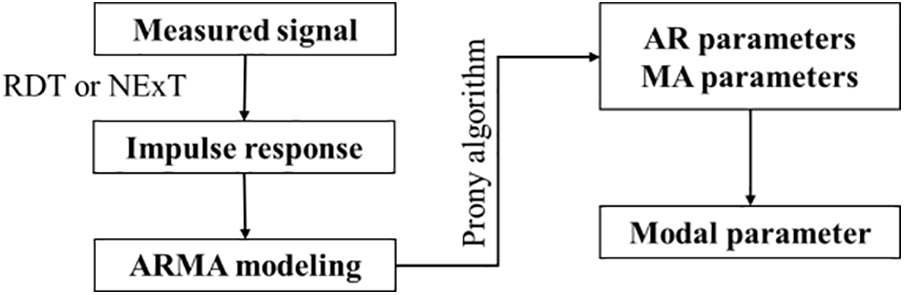
Figure 8: Flowchart of the ARMA method
The ARMA method has good applicability to both stationary and non-stationary time-domain data, high accuracy, and computational efficiency. However, it has poor robustness, suffers from model order determination issues, and is not suitable for nonlinear systems ARMA method.
2.2.6 Ibrahim Time Domain Technique
The ITD method, proposed by Ibrahim [77] in 1973, utilizes the free decaying response signal sampled at three different time delays to construct the augmentation matrix of the free response function and to solve for the modal parameters of the system from the complex exponential relationship between the response and eigenvalues, The process is shown in Fig. 9.
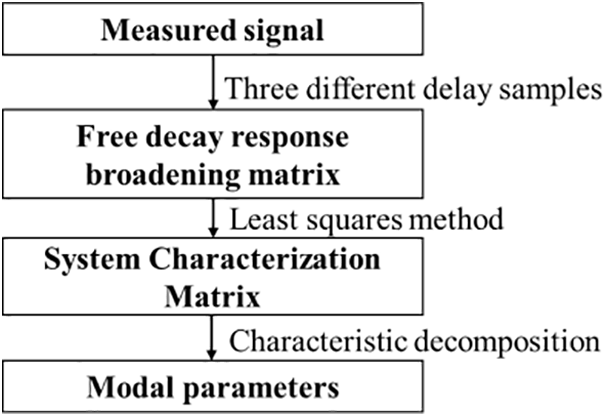
Figure 9: Flowchart of the ITD method
This method is only applicable to the single-degree-of-freedom excitation case and is computationally intensive [70]. Ibrahim [78] proposed a more practical Sparse time domain algorithm based on the ITD method in 1986, which avoids the QR decomposition of the feature matrix by ITD by constructing the Hessenbeg matrix directly. Yang et al. [79] proposed an improved ITD method by combining it with the stochastic subspace method. This method uses covariance calculation to retain all original data information while removing noise. The resulting Toeplitz matrix data is then used as input for the ITD method, improving accuracy and avoiding errors from inaccurate preprocessing, shortening computation time. Jiang et al. [80] used NExT-SSI and NExT-ITD for modal identification of wind turbine structures and used stability diagrams to reject spurious modes. The results showed that NExT-SSI has higher identification accuracy.
2.2.7 Complex Exponential Method
The CEM, or Prony polynomial method, mainly utilizes the system impulse response function to establish an autoregressive model and construct the Prony polynomials. It identifies the system parameters by solving for the system poles and the number of retentions. The advantage is that it requires less input data and computation and is independent of the initial parameter estimates, but the model ordering is difficult. The process is shown in Fig. 10.
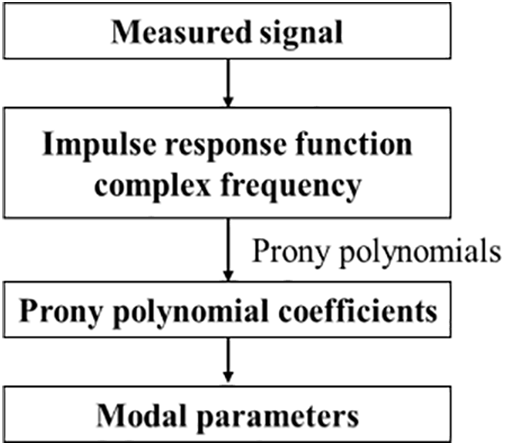
Figure 10: Flowchart of the CEM method
2.3 Frequency Domain Methods for Modal Parameter Recognition
The frequency domain method, which mostly utilises power spectrum estimation, is a non-parametric approach [41,43]. From structural dynamics, it is known that the modal parameters of a structure can be obtained by finding its frequency response function. The structural frequency response function
where
The PP method utilizes the property that the power spectral density function of the structure peaks at the intrinsic frequency of the system. It identifies the intrinsic frequency and vibration mode of the structure by picking up the peak of the power spectrum, thereby achieving the identification of the system modes [81,82]. This method is suitable for structures with small damping and few dense modes. It has high efficiency in modal parameter recognition, with a simple algorithm. However, PP suffers from subjectivity, low identification accuracy, inability to identify structural damping ratio, and difficulty in identifying dense modes.
2.3.2 Frequency Domain Decomposition Method
The FDD method is improved from the PP Method by decoupling the power spectral density function of a multi-degree-of-freedom system into a series of single-degree-of-freedom power spectra through SVD of the power spectral densities, then identifying the modal parameters of the structure by using the PP Method [83]. However, the identified modal parameters are inaccurate in the case of non-white noise excitation or non-minor damped systems [43]. Brincker et al. [84] proposed the Enhanced Frequency Domain Decomposition (EFDD) in 2001. This method involves subjecting the decomposed single-degree-of-freedom power spectral density function to Fourier Transform (FT), converting it to the time domain to derive the correlation function. Then, the logarithmic decay method is used to compute the frequency and damping ratio, as shown in Fig. 11.
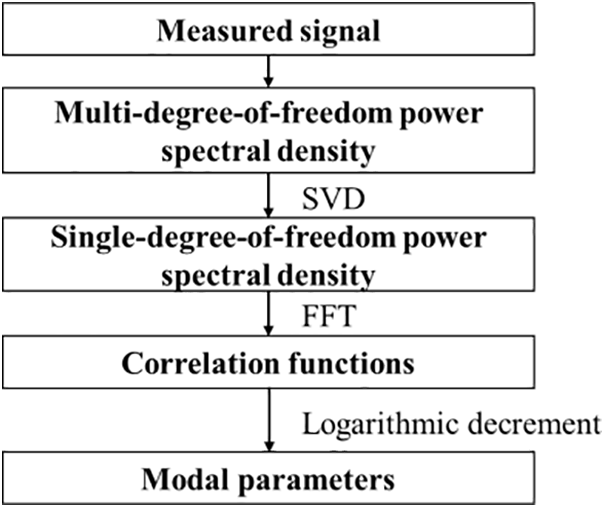
Figure 11: Flowchart of the EFDD method
2.3.3 Least Squares Complex Frequency Domain Method
The Least Squares Complex Frequency Domain (PolyMAX) method, proposed by Van Der Auweraer et al. [85] in 2001, uses an approximation of the power spectral density of the output response in place of the frequency response function, then uses a great likelihood estimation to minimize the error and achieve the identification of global modes. Guillaume et al. [86] provided a detailed account of the PolyMAX method for the computational procedure and theoretical derivation of modal parameters under Environmental Excitation in white noise environment in detail. Poly reference Least Squares Complex Frequency domain method with multiple reference points (PolyLSCF) is a multi-input and multi-output version developed on the basis of the PolyMAX method, which can overcome the shortcomings such as the degradation of the frequency response function fitting effect and the insufficient amount of information in the initial Stability Diagram when the model is decomposed by SVD by PolyMAX [87]. The Least Squares Complex Frequency Domain Method and Least Squares Complex Exponential Method both use maximum likelihood estimation for system parameter identification in the form of algorithms, but the former uses the frequency response function or the power spectral density function in the frequency domain, whereas the latter uses the impulse response function in the time domain. De Troyer et al. [88] found that if the frequency response function is uncorrelated and the information about the noise function is known (e.g., the correlation function), the modal parameter recognition values of the confidence intervals can be extracted directly from the covariance matrix of the frequency response function.
Polymax offers high computational efficiency, high accuracy, and produces high-quality stabilization diagrams, which facilitate the removal of false modes. It can be used for parameter identification of high and low damping as well as dense modes. However, it requires assuming a high trial order, and the quality of the identified modal parameters is highly dependent on the chosen order, making it susceptible to operator subjectivity.
2.3.4 Blind Source Separation Method
Blind Source Separation (BSS) was first proposed by French scholars Jutten et al. [89]. Essentially, it is a signal processing technique that can separate mixed signals without prior knowledge of the mixing process or the specific forms of the source signals. Therefore, it performs exceptionally well in handling complex signals and noisy environments. The basic principle of using BSS to identify structural modal parameters is as follows: firstly, mixed signals are collected from multiple sensors of the structure, as shown in Eq. (6):
where
where
BSS can be classified into two groups based on the number of sensors arranged on the structure and the number of active modes: determined (overdetermined) and underdetermined problems [90]. Since the available measurements for processing are usually limited (e.g., only a few sensors are available), BSS problems are largely considered underdetermined problems. Currently, scholars mainly focus on two methods to solve underdetermined BSS problems: Second Order Blind Identification (SOBI) and Sparse Component Analysis (SCA). SOBI was proposed by Belouchrani et al. [91], which identifies modes by diagonalizing the correlation matrix of responses. Yang et al. [92] first applied SCA to modal identification, demonstrating the reliability of the SCA method for underdetermined (insufficient number of sensors) BSS, particularly in structures with high damping or dense modes. Yao et al. [35] proposed an automatic frequency domain subspace segmentation method with integrated SCA to improve the modal recognition accuracy in response to the low efficiency and accuracy of SCA in handling a large number of modes; Jian et al. [36] addressed the issue of existing underdetermined BSS methods requiring sparsity assumptions on source signals and model parameter optimization, which compromises the non-parametric and blind source properties of BSS. They proposed using sinc-dictionaries for band-limited source separation, transforming the underdetermined problem into multiple determined or over-determined problems. Subsequently, they applied an improved SOBI to each band-limited signal to recover the system’s modal responses. Finally, they employed a single-degree-of-freedom fitting technique to estimate modal parameters.
The outstanding advantage of BSS is its simplicity. Its basic form is a non-parametric linear algebraic equation system, which does not involve peak picking, stabilization diagram analysis, or other procedures heavily influenced by subjectivity. However, its capability for real-time data processing still requires further research.
Bayes’ theorem was originally proposed by the British mathematician Thomas Bayes, and later elucidated by Laplace, rendering its theoretical significance clearer. In 1998, Beck et al. [93] first introduced the Bayes’ theorem into modal parameter recognition. They established posterior probability density functions containing modal parameters and utilized optimization methods to estimate the Most Probable Values (MOV) of modal parameters. The principle of Bayesian modal parameter recognation method can be summarized as follows: Firstly, it is necessary to establish the prior distribution of modal parameters based on prior knowledge or empirical assumptions; Secondly, based on the observed data, establish the likelihood function, as shown in Eq. (9); Thirdly, combine the prior distribution and the likelihood function using Bayes’ theorem to obtain the posterior distribution, as shown in Eq. (11); Finally, the posterior distribution is typically sampled using Markov Chain Monte Carlo (MCMC) methods to obtain modal parameters. The fundamental equation of the Bayesian modal parameter recognation method is represented by Eq. (8):
where
The edge probability density function of
From the above equation, it can be seen that
Au et al. [31] summarized frequency domain methods for identifying structural modal parameters under environmental excitations, providing detailed theories, computational methods, and practical experiences gleaned from on-site applications. Zhu et al. [33] addressed the issue of traditional modal analysis methods being unable to identify buried modes under environmental excitations. They proposed a Bayesian frequency domain method, which successfully identified buried modes of long-span suspension bridges, demonstrating its practicality. Luo [94] addressed the difficulties in selecting proposed distributions and the low computational efficiency of traditional MCMC methods by proposing the Simple Population-Metropolis Hastings (SP-MH) identification algorithm. This algorithm requires fewer auxiliary parameters and achieves higher computational efficiency. Additionally, Luo [94] introduced the particle position update mechanism of Particle Swarm Optimization (PSO) to improve the standard MH algorithm, resulting in the Mixed Markov Chain Monte Carlo Sampling method (MH-PSO). This method further resolves issues such as significant Monte Carlo standard error values and inaccurate Markov chain estimates in the standard MH algorithm. Sedehi et al. [95] developed a hierarchical Bayesian modeling framework that can mitigate the variability introduced by modeling errors, providing a novel approach for quantifying uncertainty.
The Bayesian modal parameter recognition method is robust and highly accurate. However, it has drawbacks such as the tendency to produce ill-conditioned matrices and the computational complexity of optimizing modal parameters.
2.4 Time-Frequency Domain Methods for Modal Parameter Recognition
Both time-domain and frequency-domain methods are based on the Fourier transform, but the Fourier transform does not respond to the instantaneous characteristics of the signal, so both of the above methods are only suitable for processing smooth response signals generated under Environmental Excitation. For the processing of non-smooth signals, time-frequency domain analysis methods, such as the Hilbert-Huang Transform (HHT) method and the Wavelet Transform (WT) method, are often used to identify modal parameters.
The HHT is an adaptive time-frequency processing technique for non-stationary signals of nonlinear systems with excellent performance, which was proposed by Huang et al. [96] of NASA in 1998. The core of the method is the Empirical Modal Decomposition (EMD) and the Hilbert Transform (HT). The EMD is a method to deal with time domain curves, the time domain signal is decomposed into multi-order Intrinsic Mode Function (IMF) and residual terms by EMD, IMF represents the vibration modes at a certain scale, then the obtained IMF is used to get the instantaneous modal parameter of the structure by using the HT. The algorithm flow is shown in Fig. 12.
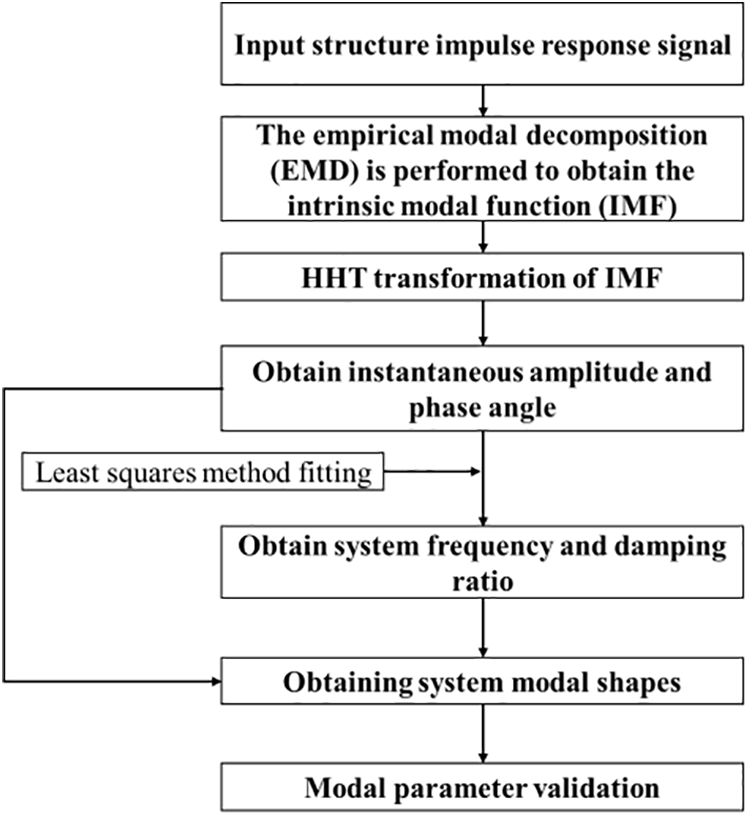
Figure 12: Flowchart of the Hilbert-Huang method
Under Environmental Excitation, the IMF components obtained from EMD include two types of signals, free vibration and forced vibration, which can be extracted for modal decomposition by processing with RDT [97]. The combination of HHT and NExT can also be used for structural modal identification under Environmental Excitation [98]. The advantage of HHT over FT and WT lies in the adaptation to the nonlinear problem. As a method of modal decomposition, EMD can also be used in conjunction with other modal identification methods, e.g., Qin et al. [99] combined the EMD with SSI, which is successfully applied to the modal analysis of dense modal structures under Environmental Excitation.
HHT has the advantage of handling nonlinear and non-stationary data. It requires only simple data collection, making it convenient for real-time data processing. HHT can identify dense modes and is relatively easy to apply in structural health monitoring systems.
The WT features an adaptive time-frequency window that adjusts the sampling step in the time domain based on different frequency components. It offers good frequency resolution in the low-frequency part of the signal and good time resolution in the high-frequency part. With multi-resolution characteristics, it can characterize the local features of the signal in both time and frequency domains. Lardies et al. [100] proposed the use of WT for identifying the modal parameters in 2002. The Empirical Wavelet Transform (EWT) technique has advantages in dealing with non-smooth, non-linear signals, but its performance relies heavily on the accuracy of the Fourier spectral segmentation. To address the susceptibility of the EWT to high-intensity noise, modulation sidebands, and the inaccurate frequency band division, Qin et al. [101] removed the high-frequency components from the Fourier wavelet transform of the vibration signal. They replaced the Fourier spectrum with the reconstructed trend spectrum of the EWT of the residual components for spectral segmentation. Combined with SET de-noising, RDT, and HT, they accurately identified the modal parameters of bridge structures. This approach showed good robustness under low Signal Noise Ratio (SNR) conditions. Wei et al. [102] utilized the projection information of Fourier spectrum to eliminate pseudo-peaks and implemented a sliding window approach to mitigate noise influence on the spectrum and enhance spectral representation. They proposed an improved EWT method, combined with NExT and HT, to efficiently assess the modal characteristics of ultra-high-rise buildings under low-amplitude Environmental Excitation. The process is shown in Fig. 13.
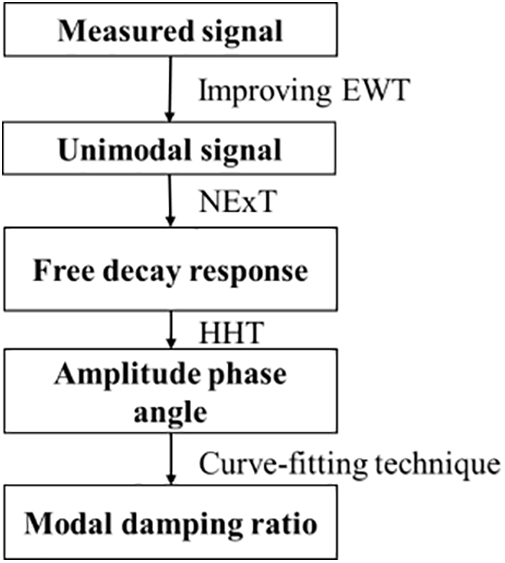
Figure 13: Flowchart of the improving EWT method
Due to OMA’s reliance on incomplete excitation and response data, it can be affected by insufficient environmental excitation and excessive noise interference. This can impact the effectiveness of modal parameter recognition and lead to the generation of spurious modes. Therefore, it is necessary to validate the results of modes identified by various modal identification algorithms. Common modal validation methods include Modal Assurance Criterion (MAC), Stability Diagram (SD), and so on.
2.5.1 Modal Assurance Criterion
Heylen et al. [103] proposed the Modal Assurance Criterion (MAC) and the Modal Phase Collineation (MPC) as a means of distinguishing between real and spurious modes. MAC is effective for evaluating the linear correlation of modal vibration vectors. Selecting modal vectors with small linear correlation ensures the completeness of modal information [104]. The MAC is commonly used to assess the similarity between them to determine whether they represent the same physical modal vibration pattern. If the two modal vibrational mode row vectors are
where
The Stability Diagram (SD) is a commonly used method to identify system poles. The horizontal coordinate represents frequency and the vertical coordinate represents system order. Different orders are chosen to complete modal identification. The authenticity of the poles is judged by identifying the stability of the system poles with respect to frequency, normalized vibration pattern, and damping ratio. The SD labels the poles corresponding to each order in the same diagram. When the interpolated values between the parameters of the higher order compared to those of the same lower order are within a certain tolerance, they can be identified as stable modal parameters. Fig. 14 shows the Stability Diagram of Cheynet et al. [46–48] using the SSI-COV method to identify the modal parameters of the Lysejord Bridge, which gives a clear picture of the first six orders of modal parameters. Chen et al. [108] addressed the issues of SSI-COV in identifying bridge modal parameters and identifying false modes with high subjectivity. They introduced a method for intelligently screening real modes. By observing that false modes change significantly with noise while structural frequency values, damping ratios, and modal vibration shapes remain stable over a short period, they proposed a discriminant matrix with modal parameters from the SD as discriminant factors. This method intelligently eliminates false modes, its feasibility and reliability were demonstrated through bridge vibration tests. Sun et al. [109] proposed a synergistic application of a modal identification system based on multiple Stability Diagrams to reduce errors and uncertainties in modal estimation. They verified the effectiveness and high robustness of the method through numerical simulations of frame structures and successfully evaluated the dynamic characteristics of 600 m high super-tall buildings during typhoons.
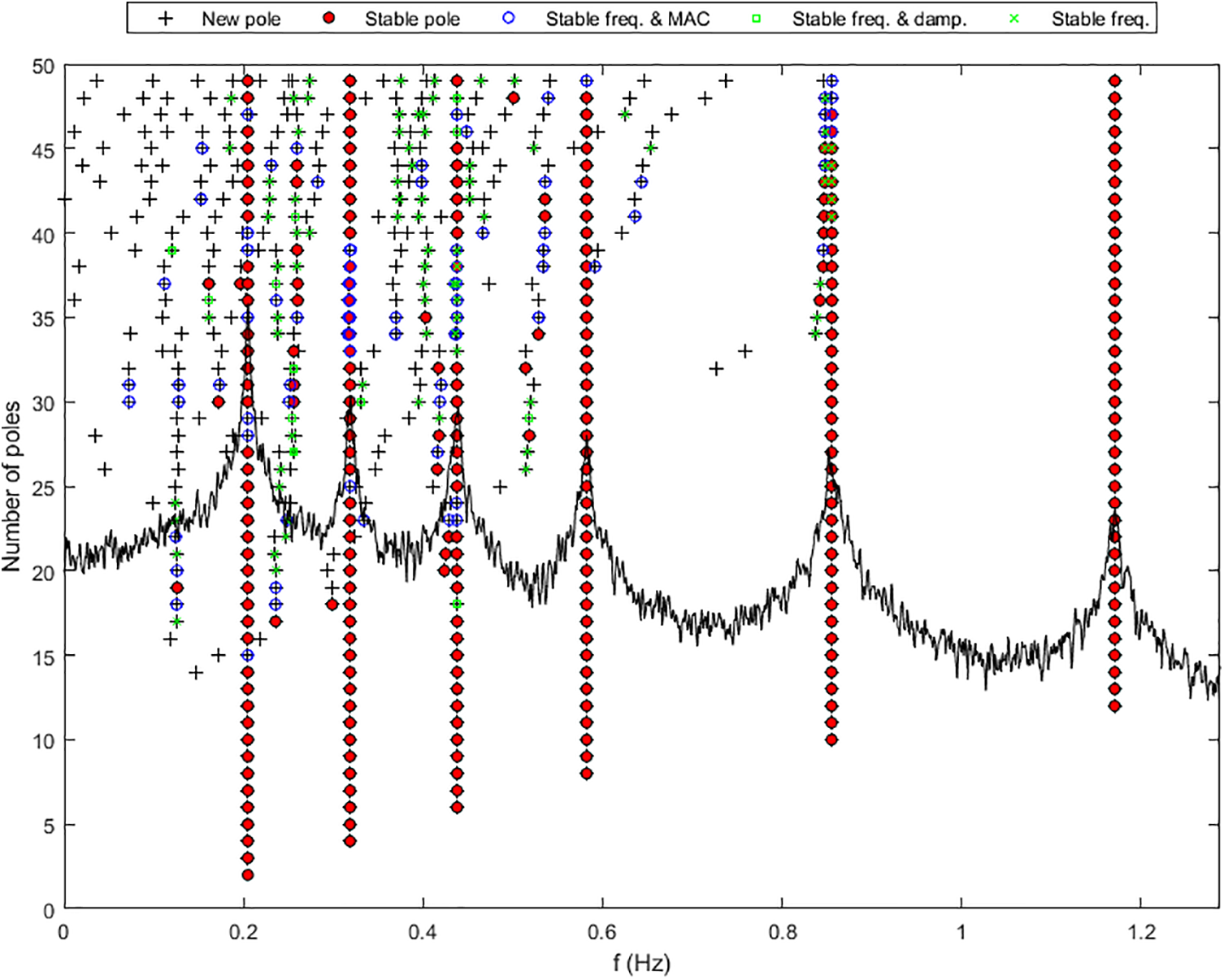
Figure 14: Stability diagram of the Lysejord bridge
1) Modal Scale Factor (MSF), orthogonality with MAC when used for different modal comparisons [110];
2) Mode Phase Collineation (MPC) checks the degree of complexity of a particular order of modes by calculating the linear relationship between the real and imaginary parts of the vibrational parameters. The MPC index is close to 0, which indicates that the modal complexity is relatively complex and there may be noisy modes [66]. The MPC can be expressed as follows:
where the range of values of
3) Mode Complexity (MOV) calculates the frequency sensitivity of the mode by increasing the added mass of the structure, with a lower MOV indicating that the mode is likely to be a noise mode [103].
3 Structural Damage Identification Based on Modal Parameters
Structural damage leads to changes in the physical parameters of the system such as stiffness and mass, which in turn leads to changes in the vibration characteristics of the structure. Damage identification methods are utilized to diagnose, locate, and assess the extent of damage by comparing changes in healthy and damaged vibration characteristics. Their core lies in finding a parameter obtained by algorithms that is sensitive to structural damage. The selection of an appropriate modal parameter is directly related to the difficulty of damage identification and the correctness of the identification results [111]. Commonly used damage characterization parameters include the natural frequency of the structure, the modal shapes, the curvature modal shapes, and so on.
3.1 Damage Identification Based on Natural Frequency Variation
When damage identification is based on natural frequency variation, the change in structural mass is usually ignored and only the reduction in structural stiffness is considered. In this case, the natural frequency of the structure decreases and the damping ratio increases. Structural damage can be identified by comparing the change in natural frequency before and after the structural damage occurs. Nguyen et al. [112] proposed a correlation coefficient with a sensitivity higher than the natural frequency based on the natural frequency-based damage identification method for monitoring and evaluating the structural damages. Li et al. [113] proposed the Particle Swarm Optimization (PSO), evaluated the performance of four natural frequency-based fitness functions in identifying structural defects in beams using the PSO-FEM method. Mekjavić et al. [114] proposed a computational method based on the nonlinear uptake theory to accurately predict the location and severity of damage by using the information about the variations of the measured natural frequencies.
There are limitations in using natural frequency variations to identify damage [4,115]:
1) Natural frequency is less sensitive to local and minor damage to the structure;
2) The same frequency variation may correspond to several different damage locations, which does not allow for localization of the damage;
3) A small degree of damage at early stages corresponds to a small rate of change of the lower-order modal frequencies and a large rate of change of the higher-order modes, but it is difficult to identify the structure under environmental excitation in the higher-order modes [116].
Therefore, damage identification based on natural frequency is often used to assist in diagnosing structural damage, while identifying the damage location requires relying on other parameters.
3.2 Damage Identification Based on Strain Modal Shapes Variation
Local damage to the structure causes a direct change in the modal shapes of the system, and it becomes possible to determine the damage by the modal shapes variation. Compared with frequency, the change of modal shapes is more sensitive to damage.
In modal analysis, both strain and displacement modes reflect the structure’s vibration characteristics, strain is the second derivative of displacement. Essentially, strain and displacement modes correspond to each other [117]. However, strain modal shapes are more sensitive to local damage, making damage identification methods based on strain modal shapes more sensitive and robust. Therefore, this paper primarily introduces damage identification methods based on strain modal shapes. There are usually three ways to identify damage based on the change of vibration strain modal shapes:
1) A direct comparison of the change in the strain modal shapes before and after damage is used to identify whether damage has occurred, e.g., the Strain Modal Shape Difference (SMSD):
where
2) Damage generation is identified by the change or value of variables of the modal shapes, such as the modal strain energy [118] and the residual tendency of the strain modal shapes;
3) Orthogonalized conditional identification of damage based on modal shapes.
Zhou et al. [118] proposed a unitary modal strain energy damage identification method to locate and quantify the damage, with significant improvement in noise immunity and identification accuracy.
3.3 Damage Identification Based on Curvature Modal Shapes
The curvature modal shapes method detects structural damage by measuring the curvature of the structure under different modal shapes. It establishes damage indicators using curvature modal shapes theory and compares the curvature of the structure under different modal shapes with the non-damaged case to determine if there is damage. For example, beam-plate structure, which mainly bears lateral external force and bending moment caused by external force, the curvature of the structure under the action of bending moment will change with the occurrence of structural damage [111].
Damage metrics based on curvature mode shapes include the strain modal shapes curvature difference SMSCD, which requires the curvature modal shapes to be obtained by first using second-order centre difference calculations:
where
The curvature modal shapes square difference (CMSSD) is improved from the SMSCD:
where
The advantage of the curvature modal shapes method is that it is capable of localizing damage to the structure and is sensitive to small areas of damage to the structure [119]. Dessi et al. [120] provided a review of curvature modal shapes based on damage identification methods. Chinka et al. [121] identified vibration characteristics through the equations of motion for healthy and damaged beams. In experimental modal testing, they located damage and estimated crack depth by analyzing the combined effects of modal shapes and frequencies on curvature modal shapes. Pooya et al. [122] located damage by using the difference between the actual curvature modal shapes of the damaged structure and the curvature modal shapes identified by the algorithm.
In terms of structural damage identification methods, there are many other damage identification methods, as shown in Table 1.
4 Application of Artificial Intelligence Methods for Modal Analysis and Damage Identification
Structural Health Monitoring (SHM) systems are capable of outputting massive amounts of monitoring data, in order to reveal the structural information embedded in the data, AI algorithms have been used for data interpretation and analysis. Sun et al. [123] summarized the application of big data and AI in processing SHM data for large span bridges, proposing a strong detailed design for data analysis. Avci et al. [124] reviewed vibration-based structural damage detection over from traditional methods to machine learning and deep learning methods. Huang et al. [125] reviewed the progress of machine learning in structural modal identification, damage identification, and reliability assessment and discussed the future trends. The application of artificial intelligence methods to modal parameters mainly includes: computer vision-based methods, methods using machine learning to solve modal equations and methods using artificial intelligence post-processing.
A computer vision based structural modal parameter recognition method is used to obtain structural modal parameters from video images of structural vibrations using computer vision techniques and blind source separation methods. Yang et al. [126] introduced a non-contact computer vision method and proposed an improved video frame interpolation algorithm EQVI-T with improved edge algorithm. Kong et al. [127] proposed a structural vibration measurement and frequency identification method based on broad-band phase-based motion magnification (BPMM) and sub-pixel template matching algorithms, with good robustness, low computational effort, and applicability. Lu et al. [28] proposed a framework for computer vision modal analysis to identify structural modal parameters. They assumed that structural micro-amplitude vibrations are smooth and directly correlate structural modal parameters with visual data. They performed visual modal analysis and obtained structural modal parameters through frequency domain decomposition. Tello-Cifuentes et al. [128] proposed a method for identifying pavement damage through pattern recognition, and image analysis and artificial intelligence algorithms, with an accuracy rate higher than 97%.
Machine learning can solve modal equations by embedding the mathematical principles of modal parameters into neural networks. This transforms the problem of solving modal parameters into an optimization problem for neural networks. Neural networks can also be used for automatic fixed-order solving of modal parameters to eliminate false modes. Liu et al. [23] embedded the mathematical features of determining modal order and identifying modal parameters in Stochastic Subspace Identification into a neural network. They proved its effectiveness through numerical simulations and bridge examples. Lei et al. [136] adopted structural response transfer data based on WT as an input of a deep convolutional neural network to eliminate the effects of different seismic excitation.
Artificial intelligence is used to automatically process the data to reduce spurious modes. For instance, in SSI and NExT-ERA methods, determining the number of ranks in the Hankel matrix directly impacts modal identification results. If the Hankel matrix is too large, it may result in spurious modes, while if it is too small, modal parameters may be lacking. Therefore, combining the deep learning and modal parameter recognition methods, by learning the huge amount of data and automatically selecting the most appropriate size of the Hankel matrix Fan et al. [25] proposed an automatic structural modal parameter recognition method based on SSI and clustering method, which uses clustering processing for the modal parameters obtained from the SSI method to eliminate false modes and accurately and automatically identify the modal parameters. He et al. [137] combined the time series model of structural monitoring data with the kernel ridge regression model in machine learning to propose a damage localization method for structures that can identify structural damages with high accuracy. Wang et al. [138] proposed a method based on the clustering model of waveforms and machine learning, which is able to efficiently and accurately identify damages in CFRP laminates.
From the above, it is evident that combining artificial intelligence algorithms with traditional modal and damage identification methods enhances their autonomous learning and data analysis capabilities. This combination effectively eliminates errors caused by human subjectivity, accurately identifies failure modes in large civil engineering structures, and revitalizes traditional methods.
This paper classifies and summarizes modal parameter recognition methods for civil engineering structures under environmental excitation. It outlines their basic principles, introduces modal verification methods, and modal parameter-based damage identification methods, and briefly describes the application of artificial intelligence methods in these areas. The synthesis can be seen: the methods of structural damage identification based on modal parameters under environmental excitation mainly have the problems of non-smooth excitation, many false modes, poor identification accuracy, inability to identify small damage, no consideration of the nonlinearity of structural damage and incomplete monitoring data. Based on the analysis of this review, the following conclusions can be obtained:
1) Environmental excitation modal identification methods often assume that the excitation signal is a smooth signal such as Gaussian white noise, while in the actual structural operating state, its Environmental Excitation is mostly non-smooth. How to deal with non-smooth signals efficiently is the key to improving the practicality and effectiveness of modal parameter recognition methods for environmental excitation.
2) For civil engineering structures subjected to large amplitude excitations like earthquakes and tsunamis, they may enter a nonlinear phase. Existing algorithms rarely consider the nonlinear behavior of the structure in the damaged state. Therefore, the identification of damage in the nonlinear phase of the structure is of important research significance.
3) Environmental excitation may not adequately excite the structure due to the impossibility of designing its excitation form and excitation energy, while for damage to small structures often requiring the use of higher order modal parameters, environmental excitation may be more difficult to realize. Structural damage detection inevitably suffers from uncertainties such as measurement noise and modelling errors due to inaccuracies in the physical parameters, unsatisfactory boundary conditions, and structural non-linearity, which can lead to false identification. In the future, it may be possible to eliminate the effect of noise by continuously learning from the data and automatically selecting the correct parameters and boundary conditions through artificial intelligence techniques.
4) Environmental excitation modal recognition methods use only the output response, which may be incomplete along with the actual structure’s modal parameters and output response. In the future, damage recognition based on unknown inputs and incomplete output data can be developed by using big data and artificial intelligence algorithms to intelligently complement and output response information.
5) Various modal parameter recognition methods and damage identification indexes are emerging. However, there is no guideline on which methods to use for specific structures due to the ever-changing conditions of engineering structures. In the future, it may be possible to develop an intelligent monitoring system for civil engineering structures, driven by the combination of big data analysis and artificial intelligence algorithms, which can efficiently process monitoring data and adaptive adjust monitoring parameters.
Acknowledgement: Special thanks are due to Jinping Ou and Zhi Zhou of Dalian University of Technology, and Youhe Zhou and Xingzhe Wang of Lanzhou University. The findings and opinions expressed in this article are only those of the authors and do not necessarily reflect the views of the sponsors.
Funding Statement: The work described in this paper was supported by the Innovation Foundation of Provincial Education Department of Gansu (2024B-005); the Gansu Province National Science Foundation (22YF7GA182); the Fundamental Research Funds for the Central Universities (No. lzujbky-2022-kb01).
Author Contributions: Study conception and design: Chao Zhang, Hua-Ping Wang; draft manuscript preparation and data collection: Chao Zhang; analysis and interpretation of results: Chao Zhang, Shang-Xi Lai; check and supervision: Hua-Ping Wang. All authors reviewed the results and approved the final version of the manuscript.
Availability of Data and Materials: The data supporting the results reported in the paper can be accessed from the first author or the corresponding author.
Ethics Approval: Not applicable.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
References
1. Li J, Hao H, Chen Z. Damage identification and optimal sensor placement for structures under unknown traffic-induced vibrations. J Aerosp Eng. 2017;30(2):B4015001. doi:10.1061/(ASCE)AS.1943-5525.0000550. [Google Scholar] [CrossRef]
2. Calvi GM, Moratti M, O’Reilly GJ, Scattarreggia N, Monteiro R, Malomo D, et al. Once upon a time in Italy: the tale of the Morandi Bridge. Struct Eng Int. 2019;29(2):198–217. doi:10.1080/10168664.2018.1558033. [Google Scholar] [CrossRef]
3. Lu X, Guan H, Sun H, Li Y, Zheng Z, Fei Y, et al. A preliminary analysis and discussion of the condominium building collapse in surfside, Florida, US, June 24, 2021. Front Struct Civ Eng. 2021;15(5):1097–110. doi:10.1007/s11709-021-0766-0. [Google Scholar] [CrossRef]
4. Hou R, Xia Y, Xia Y, Xia Y. Review on the new development of vibration-based damage identification for civil engineering structures: 2010–2019. J Sound Vib. 2020;491:115741. [Google Scholar]
5. Cai J, Wu Z, Li Z. Statistical approach to evaluating the status of an existing structure using static test data. Eng Mech. 2004;21(6):76–83 (In Chinese). [Google Scholar]
6. Sanayei M, Onipede O. Damage assessment of structures using static test data. AIAA J. 1991;29(7):1174–9. doi:10.2514/3.10720. [Google Scholar] [CrossRef]
7. Yang J, Hou P, Yang C, Yang N, Li K. Damage identification method of box girder bridges based on distributed long-gauge strain influence line under moving load. Sensors. 2021;21(3):915. doi:10.3390/s21030915. [Google Scholar] [PubMed] [CrossRef]
8. Cui F, Yuan W, Shi J. Damage detection of structures based on static response. J Tongji Univ (Nat Sci Ed). 2000;28(1):5–8 (In Chinese). [Google Scholar]
9. Ghrib F, Li L, Wilbur P. Damage identification of Euler-Bernoulli beams using static responses. J Eng Mech. 2012;138(5):405–15. doi:10.1061/(ASCE)EM.1943-7889.0000345. [Google Scholar] [CrossRef]
10. Abdo MAB. Parametric study of using only static response in structural damage detection. Eng Struct. 2012;34:124–31. doi:10.1016/j.engstruct.2011.09.027. [Google Scholar] [CrossRef]
11. Caddemi S, Caliò I, Cannizzaro F, Morassi A. A procedure for the identification of multiple cracks on beams and frames by static measurements. Struct Control Health Monit. 2018;25(8):e2194. doi:10.1002/stc.v25.8. [Google Scholar] [CrossRef]
12. Huang B, Lu Y. Static damage identification method of random beam structure based on L1 regularization. Chin J Comput Mech. 2020;37(1):69–74 (In Chinese). [Google Scholar]
13. Tang P, Wu B, Zhong H. A beam structure damage detection method using only static response. Chin J Comput Mech. 2023;40(2):289–94 (In Chinese). [Google Scholar]
14. Pandey AK, Biswas M, Samman MM. Damage detection from changes in curvature mode shapes. J Sound Vib. 1991;145(2):321–32. doi:10.1016/0022-460X(91)90595-B. [Google Scholar] [CrossRef]
15. Farrar CR, Doebling SW, Nix DA. Vibration-based structural damage identification. Philos Trans R Soc Lond Ser Math Phys Eng Sci. 2001;359(1778):131–49. doi:10.1098/rsta.2000.0717. [Google Scholar] [CrossRef]
16. Peeters B, Maeck J, Roeck GD. Vibration-based damage detection in civil engineering: excitation sources and temperature effects. Smart Mater Struct. 2001;10(3):518. doi:10.1088/0964-1726/10/3/314. [Google Scholar] [CrossRef]
17. Bayissa WL, Haritos N, Thelandersson S. Vibration-based structural damage identification using wavelet transform. Mech Syst Signal Process. 2008;22(5):1194–215. doi:10.1016/j.ymssp.2007.11.001. [Google Scholar] [CrossRef]
18. Cao MS, Sha GG, Gao YF, Ostachowicz W. Structural damage identification using damping: a compendium of uses and features. Smart Mater Struct. 2017;26(4):043001. doi:10.1088/1361-665X/aa550a. [Google Scholar] [CrossRef]
19. Huang Y, Shao C, Biao W, Wu B, Beck JL, Li H. State-of-the-art review on Bayesian inference in structural system identification and damage assessment. Adv Struct Eng. 2019;22(6):1329–51. doi:10.1177/1369433218811540. [Google Scholar] [CrossRef]
20. Weng S, Zhu H, Xia Y, Li J, Tian W. A review on dynamic substructuring methods for model updating and damage detection of large-scale structures. Adv Struct Eng. 2020;23(3):584–600. doi:10.1177/1369433219872429. [Google Scholar] [CrossRef]
21. Liu D, Tang Z, Bao Y, Li H. Machine-learning-based methods for output-only structural modal identification. Struct Control Health Monit. 2021;28(12):e2843. [Google Scholar]
22. Su L, Huang X, Song M, Michael LaFave J. Automatic identification of modal parameters for structures based on an uncertainty diagram and a convolutional neural network. Structures. 2020;28:369–79. doi:10.1016/j.istruc.2020.08.077. [Google Scholar] [CrossRef]
23. Liu D, Bao Y, Li H. Machine learning-based stochastic subspace identification method for structural modal parameters. Eng Struct. 2023;274:115178. doi:10.1016/j.engstruct.2022.115178. [Google Scholar] [CrossRef]
24. Facchini L, Betti M, Biagini P. Neural network based modal identification of structural systems through output-only measurement. Comput Struct. 2014;138:183–94. doi:10.1016/j.compstruc.2014.01.013. [Google Scholar] [CrossRef]
25. Fan G, Li J, Hao H. Improved automated operational modal identification of structures based on clustering. Struct Control Health Monit. 2019;26(12):e2450. [Google Scholar]
26. Mao JX, Wang H, Fu YG, Spencer Jr BF. Automated modal identification using principal component and cluster analysis: application to a long-span cable-stayed bridge. Struct Control Health Monit. 2019;26(10):e2430. [Google Scholar]
27. Demarie GV, Sabia D. A machine learning approach for the automatic long-term structural health monitoring. Struct Health Monit. 2019;18(3):819–37. doi:10.1177/1475921718779193. [Google Scholar] [CrossRef]
28. Lu ZR, Lin G, Wang L. Output-only modal parameter identification of structures by vision modal analysis. J Sound Vib. 2021;497:115949. doi:10.1016/j.jsv.2021.115949. [Google Scholar] [CrossRef]
29. Liu Y, Cao R, Xu S, Deng L. A deep learning-based method for structural modal analysis using computer vision. Eng Struct. 2024;301:117285. doi:10.1016/j.engstruct.2023.117285. [Google Scholar] [CrossRef]
30. Khuc T, Catbas FN. Structural identification using computer vision-based bridge health monitoring. J Struct Eng. 2018;144(2):04017202. doi:10.1061/(ASCE)ST.1943-541X.0001925. [Google Scholar] [CrossRef]
31. Au SK, Zhang FL, Ni YC. Bayesian operational modal analysis: theory, computation. Practice Comput Struct. 2013;126:3–14. doi:10.1016/j.compstruc.2012.12.015. [Google Scholar] [CrossRef]
32. Hu J, Yang JH. Operational modal analysis and bayesian model updating of a coupled building. Int J Struct Stab Dy. 2019;19(1):1940012. doi:10.1142/S0219455419400121. [Google Scholar] [CrossRef]
33. Zhu YC, Au SK, Brownjohn JMW. Bayesian operational modal analysis with buried modes. Mech Syst Signal Process. 2019;121:246–63. doi:10.1016/j.ymssp.2018.11.022. [Google Scholar] [CrossRef]
34. Li J, Bao T, Ventura CE. An automated operational modal analysis algorithm and its application to concrete dams. Mech Syst Signal Process. 2022;168:108707. doi:10.1016/j.ymssp.2021.108707. [Google Scholar] [CrossRef]
35. Yao X-J, Yi T-H, Zhao S-W. Blind modal identification for decentralized sensor network by modified sparse component analysis in frequency-domain subspace. Eng Struct. 2022;269:114794. doi:10.1016/j.engstruct.2022.114794. [Google Scholar] [CrossRef]
36. Jian J, Wang L, Lu ZR. Enhancing second-order blind identification for underdetermined operational modal analysis through bandlimited source separation. J Sound Vib. 2024;572:118179. doi:10.1016/j.jsv.2023.118179. [Google Scholar] [CrossRef]
37. Liu Y, Xin K, Fan J, Cui D. A review of structure modal identification methods through ambient excitation. Eng Mech. 2014;31(4):46–53 (In Chinese). [Google Scholar]
38. Ren W. Comparison of system identification methods using ambient vibration measurements. J Fuzhou Univ (Nat Sci Ed). 2001;29(6):80–6 (In Chinese). [Google Scholar]
39. Bao Y, Li H. Machine learning paradigm for structural health monitoring. Struct Health Monit. 2021;20(4):1353–72. doi:10.1177/1475921720972416. [Google Scholar] [CrossRef]
40. Zhang G, Tang S, Fang Z. Research on uncertainty of modal parameter identification of cable-stayed bridge by ambient excitation. Highway. 2024;69(1):93–103 (In Chinese). [Google Scholar]
41. Xu X, Hua H, Chen Z. Review of modal identification method based on ambient excitation. J Vib Shock. 2002;21(3):3–7+91 (In Chinese). [Google Scholar]
42. Zhang Y, Zhang J, Qian X, Zhang P, Yang R. Spectrum-driven methods for modal parameter identification of bridge under environmental excitation. J Jilin Univ Techno Ed. 2023;53(6):1580–91 (In Chinese). [Google Scholar]
43. Xia LX. The comparison of modal analysis methods under ambient vibration (Master Thesis). Central South University: China; 2014 (In Chinese). [Google Scholar]
44. Peeters B, De Roeck G. Reference-based stochastic subspace identification for output-only modal analysis. Mech Syst Signal Process. 1999;13(6):855–78. doi:10.1006/mssp.1999.1249. [Google Scholar] [CrossRef]
45. Magalhães F, Cunha Á, Caetano E. Online automatic identification of the modal parameters of a long span arch bridge. Mech Syst Signal Process. 2009;23(2):316–29. doi:10.1016/j.ymssp.2008.05.003. [Google Scholar] [CrossRef]
46. Cheynet E, Jakobsen JB, Snæbjörnsson J. Buffeting response of a suspension bridge in complex terrain. Eng Struct. 2016;128:474–87. doi:10.1016/j.engstruct.2016.09.060. [Google Scholar] [CrossRef]
47. Cheynet E, Jakobsen JB, Snæbjörnsson J. Damping estimation of large wind-sensitive structures. Proc Eng. 2017;199:2047–53. doi:10.1016/j.proeng.2017.09.471. [Google Scholar] [CrossRef]
48. Cheynet E, Snæbjörnsson J, Jakobsen JB. Temperature effects on the modal properties of a suspension bridge. In: Caicedo J, Pakzad S, editors. Dynamic Civil Structure. Cham: Springer International Publishing; 2017. vol. 2, p. 87–93. [Google Scholar]
49. Chen GW, Omenzetter P, Beskhyroun S. Operational modal analysis of an eleven-span concrete bridge subjected to weak ambient excitations. Eng Struct. 2017;151:839–60. doi:10.1016/j.engstruct.2017.08.066. [Google Scholar] [CrossRef]
50. Fang Z, Su H, Ansari F. Modal analysis of structures based on distributed measurement of dynamic strains with optical fibers. Mech Syst Signal Process. 2021;159:107835. doi:10.1016/j.ymssp.2021.107835. [Google Scholar] [CrossRef]
51. He W, Ding X, Ren W. Effects of moving vehicle on bridge modal parametric identification under ambient excitation. J Vib Shock. 2021;40(3):48–53 (In Chinese). [Google Scholar]
52. Li A, Zhang C, Deng Y, Zhong G, Liu S. Automatic identification method for structural modal parameters based on stochastic subspace identification. J Southeast Univ (Nat Sci Ed). 2023;53(1):53–60 (In Chinese). [Google Scholar]
53. James G, Carne T, Laufer J. The natural excitation technique (NExT) for modal parameter extraction from operating structures. J Anal Exp Modal Anal. 1995;10(4):260–77. [Google Scholar]
54. He R, Qin Q. Error analysis of time-domain modal identification methods of improved NExT-ERA. J Tsinghua Univ (Sci & Tech). 2009;49(6):803–10 (In Chinese). [Google Scholar]
55. Wu Y, Wang G, Chen B, Guo X, Wang N. Identification on natural frequencies of transmission angle-tower based on NExT through field measurement. J Wuhan Univ Technol. 2014;36(7):102–7 (In Chinese). [Google Scholar]
56. Yang J, Sun Y, Jing H, Li P. An improved NExT method for modal identification with tests validation. Eng Struct. 2023;274:115192. doi:10.1016/j.engstruct.2022.115192. [Google Scholar] [CrossRef]
57. Cole HA. On-line failure detection and damping measurement of aerospace structures by random decrement signatures. 1973. Available from: https://ntrs.nasa.gov/citations/19730010202. [Accessed 2024]. [Google Scholar]
58. Cismaşiu C, Narciso AC, Amarante Dos Santos FP. Experimental dynamic characterization and finite-element updating of a footbridge structure. J Perform Constr Facil. 2015;29(4):04014116. doi:10.1061/(ASCE)CF.1943-5509.0000615. [Google Scholar] [CrossRef]
59. Yang Y, Ning P, Wang S, Hua X, Wen Q. Analytical modal decomposition-based random decrement technique for modal parameters identification of bridge. J Railw Sci Eng. 2022;19(5):1355–63 (In Chinese). [Google Scholar]
60. Areemit N, Montgomery M, Christopoulos C, Hasan A. Identification of the dynamic properties of a reinforced concrete coupled shear wall residential high-rise building. Can J Civ Eng. 2012;39(6):631–42. doi:10.1139/l2012-047. [Google Scholar] [CrossRef]
61. Yang JN, Lei Y, Lin S, Huang N. Identification of natural frequencies and dampings of in situ tall buildings using ambient wind vibration data. J Eng Mech. 2004;130(5):570–7. doi:10.1061/(ASCE)0733-9399(2004)130:5(570). [Google Scholar] [CrossRef]
62. Huang CS. Structural identification from ambient vibration measurement using the multivariate AR model. J Sound Vib. 2001;241(3):337–59. doi:10.1006/jsvi.2000.3302. [Google Scholar] [CrossRef]
63. Ku CJ, Tamura Y. Rational fraction polynomial method and random decrement technique for force-excited acceleration responses. J Struct Eng. 2009;135(9):1134–8. doi:10.1061/(ASCE)0733-9445(2009)135:9(1134). [Google Scholar] [CrossRef]
64. Chen T, Shen W. Practical improvement of the random decrement technique in modal identification. J Vib Meas Diagn. 2019;39(6):1153–9+1355 (In Chinese). [Google Scholar]
65. Li J, Zhu X, Guo J. Bridge modal identification based on successive variational mode decomposition using a moving test vehicle. Adv Struct Eng. 2022;25(11):2284–300. doi:10.1177/13694332221092678. [Google Scholar] [CrossRef]
66. Juang JN, Pappa RS. An eigensystem realization algorithm for modal parameter identification and model reduction. J Guid Control Dyn. 1985;8(5):620–7. doi:10.2514/3.20031. [Google Scholar] [CrossRef]
67. Caicedo JM. Practical guidelines for the natural excitation technique (NExT) and the eigensystem realization algorithm (ERA) for modal identification using ambient vibration. Exp Tech. 2011;35(4):52–8. doi:10.1111/ext.2011.35.issue-4. [Google Scholar] [CrossRef]
68. Li P, Hu SLJ, Li HJ. Noise issues of modal identification using eigensystem realization algorithm. Procedia Eng. 2011;14:1681–9. doi:10.1016/j.proeng.2011.07.211. [Google Scholar] [CrossRef]
69. Cui D, Xin K, Spencer BF, Liu Y. Decentralized NExT/ERA and RDT/ERA system identification in wireless smart sensor networks. In: Applied mechanics and materials. Switzerland: Trans Tech Publications, Ltd., 2012. vol. 204, p. 4946–51. [Google Scholar]
70. Pu Q, Hong Y, Wang G, Li X. Fast eigensystem realization algorithm based structural modal parameters identification for ambient tests. J Vib Shock. 2018;37(6):55–60 (In Chinese). [Google Scholar]
71. Zhu R, Hang X, Jiang D, Fei Q, Jin W. Improved eigensystem realization algorithm and mode order determination based on SVD. J Vib Meas Diagn. 2018;38:115–22+210 (In Chinese). [Google Scholar]
72. Almunif A, Fan L, Miao Z. A tutorial on data-driven eigenvalue identification: prony analysis, matrix pencil, and eigensystem realization algorithm. Int Trans Electr Energy Syst. 2020;30(4):e12283. [Google Scholar]
73. Akaike H. Power spectrum estimation through autoregressive model fitting. Ann Inst Stat Math. 1969;21(1):407–19. doi:10.1007/BF02532269. [Google Scholar] [CrossRef]
74. Kang J, Liu L, Shao Y, Ma Q. Non-stationary signal decomposition approach for harmonic responses detection in operational modal analysis. Comput Struct. 2021;242:106377. doi:10.1016/j.compstruc.2020.106377. [Google Scholar] [CrossRef]
75. Kang J, Zeng S. Uncertainty quantification in operational modal analysis of time-varying structures based on time-dependent autoregressive moving average model. J Sound Vib. 2023;548:117549. doi:10.1016/j.jsv.2022.117549. [Google Scholar] [CrossRef]
76. Rezaee M, Fathi R, Jahangiri V, Ettefagh MM, Jamalkia A, Sadeghi MH. Detection of damages in mooring lines of spar type floating offshore wind turbines using fuzzy classification and arma parametric modeling. Int J Struct Stab Dyn. 2021;21(8):2150111. doi:10.1142/S021945542150111X. [Google Scholar] [CrossRef]
77. Ibrahim SR, Mikulcik EC. A method for the direct identification of vibration parameters from the free response. 1977. Available from: https://ntrs.nasa.gov/citations/19800070016. [Accessed 2024]. [Google Scholar]
78. Ibrahim SR. An approach for reducing computational requirements in modal identification. AIAA J. 1986;24(10):1725–7. doi:10.2514/3.9516. [Google Scholar] [CrossRef]
79. Yang Y, Li S, Li H. Improved ITD method for structural modal parameter identification under ambient excitation. J Vib Shock. 2014;33(1):194–9 (In Chinese). [Google Scholar]
80. Jiang W, Yang C, Cui H. Identification of wind turbine tower modal parameters based on stochastic subspace method. Energy Energy Conserv. 2023;6:8–13 (In Chinese). [Google Scholar]
81. Chen C, Wang HP, Ma J, Wusiman M. Dynamic feature identification of carbon-fiber-reinforced polymer laminates based on Fiber Bragg Grating sensing technology. Buildings. 2023;13(9):2292. doi:10.3390/buildings13092292. [Google Scholar] [CrossRef]
82. Wang HP, Chen C, Ni YQ, Jayawickrema M, Epaarachchi J. Computer-aided feature recognition of CFRP plates based on real-time strain fields reflected from FBG measured signals. Compos Part B Eng. 2023;263:110866. doi:10.1016/j.compositesb.2023.110866. [Google Scholar] [CrossRef]
83. Ye X, Yan Q, Wang W, Li J. Modal parameter identification of cable-stayed bridge based on multiple reference DOFs stabilization diagram. J South China Univ Technol Nat Sci Ed. 2011;39(9):41–7+53 (In Chinese). [Google Scholar]
84. Brincker R, Zhang L, Andersen P. Modal identification of output-only systems using frequency domain decomposition. Smart Mater Struct. 2001;10(3):441. doi:10.1088/0964-1726/10/3/303. [Google Scholar] [CrossRef]
85. Van Der Auweraer H, Guillaume P, Verboven P, Vanlanduit S. Application of a fast-stabilizing frequency domain parameter estimation method. J Dyn Syst Meas Control. 2001;123(4):651–8. doi:10.1115/1.1410369. [Google Scholar] [CrossRef]
86. Guillaume P, Verboven P, Vanlanduit S, Van Der Auweraer H, Peeters B. A poly-reference implementation of the least-squares complex frequency-domain estimator. Proc IMAC. 2003;21(1):183–92. [Google Scholar]
87. Peeters B, Van Der Auweraer H, Guillaume P, Leuridan J. The PolyMAX frequency-domain method: a new standard for modal parameter estimation. Shock Vib. 2004;11(3–4):395–409. [Google Scholar]
88. De Troyer T, Guillaume P, Pintelon R, Vanlanduit S. Fast calculation of confidence intervals on parameter estimates of least-squares frequency-domain estimators. Mech Syst Signal Process. 2009;23(2):261–73. doi:10.1016/j.ymssp.2008.04.009. [Google Scholar] [CrossRef]
89. Jutten C, Herault J. Blind separation of sources, part I: an adaptive algorithm based on neuromimetic architecture. Signal Process. 1991;24(1):1–10. doi:10.1016/0165-1684(91)90079-X. [Google Scholar] [CrossRef]
90. McNeill SI, Zimmerman DC. A framework for blind modal identification using joint approximate diagonalization. Mech Syst Signal Process. 2008;22(7):1526–48. doi:10.1016/j.ymssp.2008.01.010. [Google Scholar] [CrossRef]
91. Belouchrani A, Abed-Meraim K, Cardoso JF, Moulines E. A blind source separation technique using second-order statistics. IEEE Trans Signal Process. 1997;45(2):434–44. doi:10.1109/78.554307. [Google Scholar] [CrossRef]
92. Yang Y, Nagarajaiah S. Output-only modal identification with limited sensors using sparse component analysis. J Sound Vib. 2013;332(19):4741–65. doi:10.1016/j.jsv.2013.04.004. [Google Scholar] [CrossRef]
93. Beck JL, Katafygiotis LS. Updating models and their uncertainties. I: bayesian statistical framework. J Eng Mech. 1998;124(4):455–61. doi:10.1061/(ASCE)0733-9399(1998)124:4(455). [Google Scholar] [CrossRef]
94. Luo J. Bayesian damage identification based on autoregressive model and improved MCMC sampling method (Master Thesis). Wuhan Institute of Technology: China; 2023 (In Chinese). [Google Scholar]
95. Sedehi O, Katafygiotis LS, Papadimitriou C. Hierarchical Bayesian operational modal analysis: theory and computations. Mech Syst Signal Process. 2020;140:106663. doi:10.1016/j.ymssp.2020.106663. [Google Scholar] [CrossRef]
96. Huang NE, Shen Z, Long SR, Wu MC, Shih HH, Zheng Q, et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc R Soc Lond Ser Math Phys Eng Sci. 1998;454(1971):903–95. doi:10.1098/rspa.1998.0193. [Google Scholar] [CrossRef]
97. Xu YL, Chen SW, Zhang RC. Modal identification of Di Wang Building under Typhoon York using the Hilbert-Huang transform method. Struct Des Tall Spec Build. 2003;12(1):21–47. doi:10.1002/tal.v12:1. [Google Scholar] [CrossRef]
98. Ji X, Qian J, Xu H. Experimental study of modal parameter identification in a simulated ambient-excited structure. J Tsinghua Univ (Sci & Tech). 2006;46(6):769–72 (In Chinese). [Google Scholar]
99. Qin S, Pu Q, Shi Z. A method of modal parameters identification using ambient vibration measurements for a large-scale bridge. J Vib Shock. 2012;31(2):95–100 (In Chinese). [Google Scholar]
100. Lardies J, Gouttebroze S. Identification of modal parameters using the wavelet transform. Int J Mech Sci. 2002;44(11):2263–83. doi:10.1016/S0020-7403(02)00175-3. [Google Scholar] [CrossRef]
101. Qin S, Tang J, Feng J. Bridge modal parameter identification based on improved empirical wavelet transform. J Highw Transp Res Dev. 2022;39(12):94–105 (In Chinese). [Google Scholar]
102. Wei P, Li Q, Sun M, Huang J. Modal identification of high-rise buildings by combined scheme of improved empirical wavelet transform and Hilbert transform techniques. J Build Eng. 2023;63:105443. doi:10.1016/j.jobe.2022.105443. [Google Scholar] [CrossRef]
103. Heylen W, Sas P. Modal analysis theory and testing. Belgium: Katholieke Universiteit Leuven; 2005. [Google Scholar]
104. Yi T, Wang C, Li H. Optimal triaxial sensor placement using distributed wolf algorithm. J Vib Eng. 2014;27(5):668–75 (In Chinese). [Google Scholar]
105. Pastor M, Binda M, Harčarik T. Modal assurance criterion. Proc Eng. 2012;48:543–8. doi:10.1016/j.proeng.2012.09.551. [Google Scholar] [CrossRef]
106. Greś S, Döhler M, Mevel L. Uncertainty quantification of the Modal Assurance Criterion in operational modal analysis. Mech Syst Signal Process. 2021;152:107457. doi:10.1016/j.ymssp.2020.107457. [Google Scholar] [CrossRef]
107. Hızal Ç. A Bayesian approach to global mode shape identification using modal assurance criterion-based discrepancy model. J Sound Vib. 2023;558:117774. doi:10.1016/j.jsv.2023.117774. [Google Scholar] [CrossRef]
108. Chen Y, Zhong Z. Signal decomposition and modal parameter identification for bridge structural under environmental excitation. J Vib Meas Diagn. 2018;38(6):1267–74+1300 (In Chinese). [Google Scholar]
109. Sun M, Li Q. Reliable modal estimation of high-rise structures via synergistic usage of multiple stabilization diagram-based operational modal analysis techniques. Structures. 2023;56:105051. doi:10.1016/j.istruc.2023.105051. [Google Scholar] [CrossRef]
110. Ewins DJ, Saunders H. Modal testing: theory and practice. 1986. Available from: https://asmedigitalcollection.asme.org/vibrationacoustics/article/108/1/109/438421/Modal-Testing-Theory-and-Practice. [Accessed 2024]. [Google Scholar]
111. Zhu H, Yu J, Zhang J. A summary review and advantages of vibration-based damage identification methods in structural health monitoring. Eng Mech. 2011;28(2):1–11+17 (In Chinese). [Google Scholar]
112. Nguyen TQ, Nguyen HB. Detecting and evaluating defects in beams by correlation coefficients. Shock Vib. 2021;2021:e6536249. doi:10.1155/vib.v2021.1. [Google Scholar] [CrossRef]
113. Li XL, Serra R, Olivier J. Performance of fitness functions based on natural frequencies in defect detection using the standard PSO-FEM approach. Shock Vib. 2021;2021:e8863107. doi:10.1155/vib.v2021.1. [Google Scholar] [CrossRef]
114. Mekjavić I, Damjanović D. Damage assessment in bridges based on measured natural frequencies. Int J Struct Stab Dyn. 2017;17(2):1750022. doi:10.1142/S0219455417500225. [Google Scholar] [CrossRef]
115. Zhao Y, Gong M, Yang Y. A review of structural damage identification methods. World Earthq Eng. 2020;36(2):73–84 (In Chinese). [Google Scholar]
116. You S. Bridge vibration characteristics and damage identification method based on ambient excitation (Master Thesis). Beijing Jiaotong University: China; 2023 (In Chinese). [Google Scholar]
117. Peng W. Research on structural damage identification methods based on strain mode under ambient excitation (Master Thesis). Dalian University of Technology: China; 2020 (In Chinese). [Google Scholar]
118. Zhou J, Wu S, Dong E, Fei Q. Damage identification based on modal strain energy formulated by strain modes. J Vib Meas Diagn. 2019;39:25–31+218–9 (In Chinese). [Google Scholar]
119. Ma C. Research on optimal placement of bridge health monitoring sensors and damage identification method (Master Thesis). Lanzhou Jiaotong University: China; 2024 (In Chinese). [Google Scholar]
120. Dessi D, Camerlengo G. Damage identification techniques via modal curvature analysis: overview and comparison. Mech Syst Signal Process. 2015;52–53:181–205. [Google Scholar]
121. Chinka SSB, Putti SR, Adavi BK. Modal testing and evaluation of cracks on cantilever beam using mode shape curvatures and natural frequencies. Structures. 2021;32:1386–97. doi:10.1016/j.istruc.2021.03.049. [Google Scholar] [CrossRef]
122. Pooya SMH, Massumi A. A novel and efficient method for damage detection in beam-like structures solely based on damaged structure data and using mode shape curvature estimation. Appl Math Model. 2021;91:670–94. doi:10.1016/j.apm.2020.09.012. [Google Scholar] [CrossRef]
123. Sun L, Shang Z, Xia Y, Bhowmick S, Nagarajaiah S. Review of bridge structural health monitoring aided by big data and artificial intelligence: from condition assessment to damage detection. J Struct Eng. 2020;146(5):04020073. doi:10.1061/(ASCE)ST.1943-541X.0002535. [Google Scholar] [CrossRef]
124. Avci O, Abdeljaber O, Kiranyaz S, Hussein M, Gabbouj M, Inman DJ. A review of vibration-based damage detection in civil structures: from traditional methods to machine learning and deep learning applications. Mech Syst Signal Process. 2021;147:107077. doi:10.1016/j.ymssp.2020.107077. [Google Scholar] [CrossRef]
125. Huang Y, Bao Y, Li H. Research advances in machine learning for structural state identification and condition assessment. Adv Mech. 2023;53(4):774–92 (In Chinese). [Google Scholar]
126. Yang K, Li L. Structural vibration testing and mode identification based on computer vision and video frame interpolation. J Fujian Univ Technol. 2024;22(1):22–29+38 (In Chinese). [Google Scholar]
127. Kong X, Luo K, Deng L, Yi J, Yin P, Ji W. Structural frequency identification based on broad-band phase-based motion magnification and computer vision. China Civil Eng J. 2023;56(10):105–17 (In Chinese). [Google Scholar]
128. Tello-Cifuentes L, Marulanda J, Thomson P. Detection and classification of pavement damages using wavelet scattering transform, fractal dimension by box-counting method and machine learning algorithms. Road Mater Pavement Des. 2024;25(3):566–84. doi:10.1080/14680629.2023.2219338. [Google Scholar] [CrossRef]
129. Xu ZD, Zeng X, Li S. Damage detection strategy using strain-mode residual trends for long-span bridges. J Comput Civ Eng. 2015;29(5):04014064. doi:10.1061/(ASCE)CP.1943-5487.0000371. [Google Scholar] [CrossRef]
130. Xu ZD, Wu KY. Damage detection for space truss structures based on strain mode under ambient excitation. J Eng Mech. 2012;138(10):1215–23. doi:10.1061/(ASCE)EM.1943-7889.0000426. [Google Scholar] [CrossRef]
131. Kim NI, Kim S, Lee J. Vibration-based damage detection of planar and space trusses using differential evolution algorithm. Appl Acoust. 2019;148:308–21. doi:10.1016/j.apacoust.2018.08.032. [Google Scholar] [CrossRef]
132. Hou R, Beck JL, Zhou X, Xia Y. Structural damage detection of space frame structures with semi-rigid connections. Eng Struct. 2021;235:112029. doi:10.1016/j.engstruct.2021.112029. [Google Scholar] [CrossRef]
133. Hou R, Xia Y, Zhou X. Structural damage detection based on l1 regularization using natural frequencies and mode shapes. Struct Control Health Monit. 2018;25(3):e2107. doi:10.1002/stc.v25.3. [Google Scholar] [CrossRef]
134. Yoon MK, Heider D, Gillespie JW, Ratcliffe CP, Crane RM. Local damage detection with the global fitting method using operating deflection shape data. J Nondestruct Eval. 2010;29(1):25–37. doi:10.1007/s10921-010-0062-8. [Google Scholar] [CrossRef]
135. Cui H, Xu X, Peng W, Zhou Z, Hong M. A damage detection method based on strain modes for structures under ambient excitation. Measurement. 2018;125:438–46. doi:10.1016/j.measurement.2018.05.004. [Google Scholar] [CrossRef]
136. Lei Y, Zhang Y, Mi J, Liu W, Liu L. Detecting structural damage under unknown seismic excitation by deep convolutional neural network with wavelet-based transmissibility data. Struct Health Monit. 2021;20(4):1583–96. doi:10.1177/1475921720923081. [Google Scholar] [CrossRef]
137. He D, Yang J. A structural damage detection method based on time series and kernel ridge regression. China Earthq Eng J. 2022;44(5):1082–9 (In Chinese). [Google Scholar]
138. Wang J, Zhou W, Ren X, Su M, Liu J. A waveform-based clustering and machine learning method for damage mode identification in CFRP laminates. Compos Struct. 2023;312:116875. doi:10.1016/j.compstruct.2023.116875. [Google Scholar] [CrossRef]
Cite This Article
 Copyright © 2025 The Author(s). Published by Tech Science Press.
Copyright © 2025 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF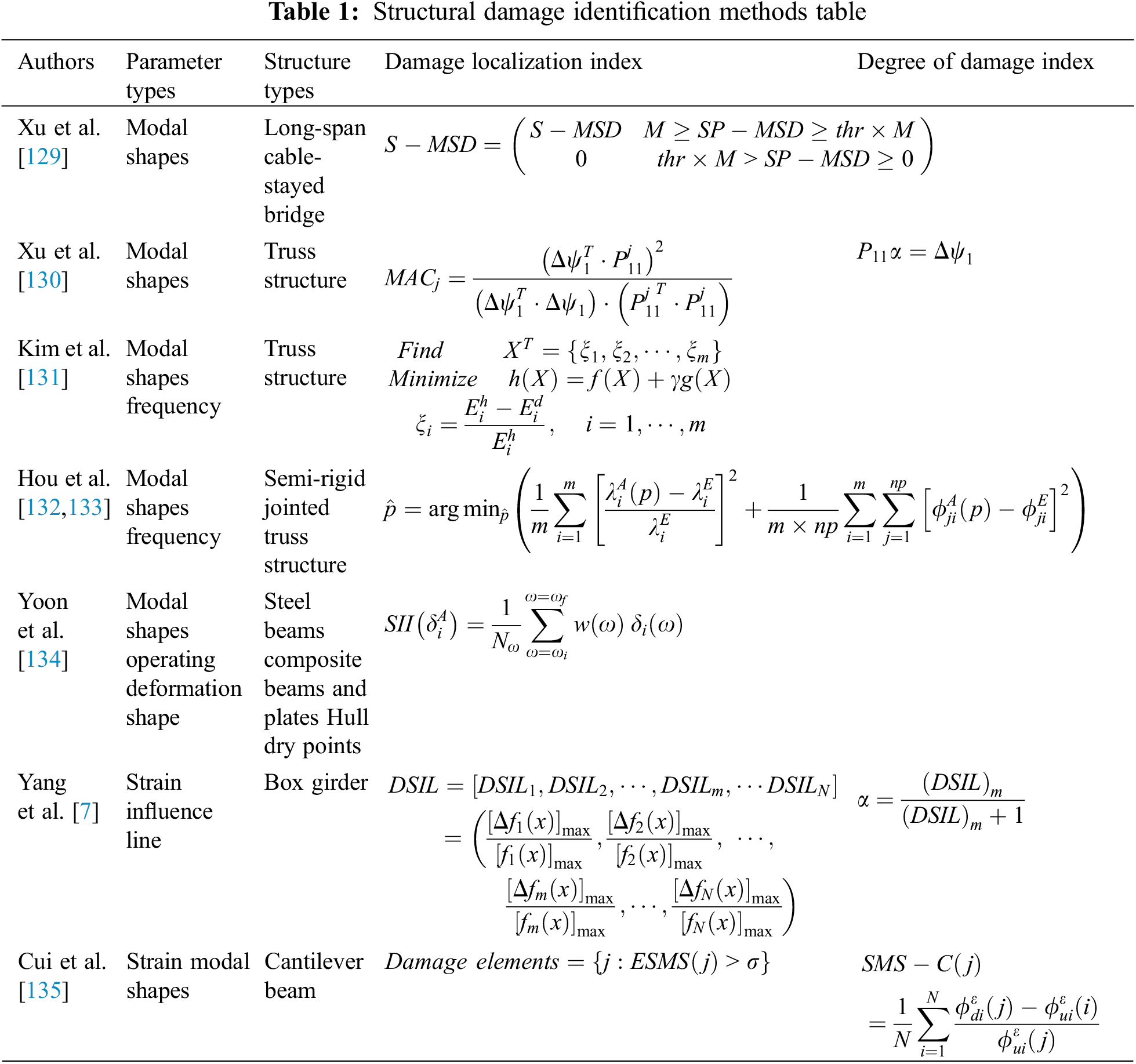
 Downloads
Downloads
 Citation Tools
Citation Tools