Discrete Numerical Study on Type II Fracture of Partially Detached Concrete Panels in Cold Region

1  Introduction

Panel earth-rock dams are widely used in water conservancy projects in cold regions. The non-uniform deformation of the concrete panel of such dams may be caused by the inhomogeneity of the deep overburden and the dam building material itself as well as the saturation change in dam’s body. Thus, the non-uniform deformation between the panel and the dam cushion layer might cause the concrete panel detachment [1,2]. The concrete panel is the key element of the panel earth-rock dam that prevents seepage, while it is subject to water pressure, ice pressure, and seismic external load [3]. The detachment of the concrete panel causes concentration in stress distribution and may even induce cracks. The initiation of such cracks badly affects the condition of the anti-seepage system and might form a pipe gushing inside the dam, which might endanger the dam safety [4,5]. The concrete panel earth-rock dam in cold regions is also affected by freeze-thaw damage, which significantly increases the cracking possibility in the concrete panel.

As shown in Fig. 1, the panel bottom of the earth-rock dam in the cold region might get detached due to the rolling of the filler, the weight of the dam, the change of the reservoir water level, and the lack of consideration of material partitioning [6]. As the upstream water surface of the panel freezes in winter, ice expansion load will be formed on the surface of the panel. After the water surface forms an ice cap, it gradually expands toward the panel and slides along the direction of the panel slope to form an ice crawling force (component 1) and form a sub-force (component 2) along the direction of the panel thickness toward the detached area. The ice expansion load and its components are generated at the water level fluctuation area [7–9], where the tensile and compression-shear stress will be formed in the panels [10]. The local concrete area may undergo a shear failure with a cyclic freeze-thaw damage as shown in Fig. 2. The mesoscale crack opening due to the freezing and expansion of internal pore water in concrete [11] as a result of freeze-thaw damage action. When concrete is subjected to external loading, macroscopic cracks tend to develop from these cracks, exhibiting a deterioration of the overall load-bearing capacity. For this reason, it is necessary to include the concrete freeze-thaw damage in this work.

Figure 1: Shear cracking of concrete panel due to the influence of partial detachment and ice expansion [7,9]

Figure 2: Mechanism of freeze-thaw damage cracking at mesoscopic scale [12,13]

The recent works [14,15] using X-ray micro-computed tomography and deep learning algorithm give more clear explanations on the strong relationship between the pore geometries and cyclic freeze-thaw damage. At present, researches on the evolution of mechanical properties of concrete considering freeze-thaw damage are mainly based on the type I cracking failure test method [16–20]. Concrete structures in cold regions may also suffer from other types of loads, such as compression-torsion [21], shear, tensile splitting [22], etc., [23–25], which requires an in-depth understanding of the mechanical behavior of freeze-thaw-damaged concrete under shear loading (type II Load).

To solve the problem of panel concrete cracking behavior in the detachment area and accurately capture the whole cracking process caused by external loads on concrete specimens, the model called LDPM-FTC (Lattice Discrete Particle Model of concrete under Freezing and Thawing Cycle) is proposed in this paper. The proposed model describes a mesoscopic tensile and compressive constitutive to accurately predict the macroscopic mechanical response within the framework of the Lattice Discrete Particle Model (LDPM) [26–30], and then obtain the crack propagation path. In the second part, LDPM-FTC is calibrated and its capability for predicting type II fracturing is verified. In the third part, the fracturing behavior of concrete panels in cold regions is investigated and the cracking pattern is discussed.

2  The LDPM-FTC

A discrete mechanical model of concrete under freeze-thaw damage is introduced in this section within the framework of the Lattice Discrete Particle Model [26,27], which is called LDPM-FTC. The discretization process of the LDPM takes the tetrahedron, which is composed of neighboring aggregates, as the computational element as it is shown in Fig. 3. The mortar matrix that wraps and binds the neighboring aggregates and the aggregates themselves constitute the polyhedral particle cells (Cells). The model uses the lattice edge to characterize the adhesion at the interface between the aggregate and the mortar. Also, it defines the interaction between the aggregates due to the external loads applied by setting the potential cracking surface between the aggregates, which is called the “Facet”.

Figure 3: Discretization of LDPM

The normal and tangential stresses are defined on the Facet k, and the mechanical response of their elasticity is defined as:

tk=[tNktMktLk]T=[ENeN∗ETeM∗ETeL∗]T (1)

where tNk is the normal stress component, tMk and tLk are the tangential strain components, the corresponding EN = E0 and ET = αE0 are the normal and tangential modulus, respectively, E0 = E∕(1 − 2 ν ) is the equivalent elastic modulus, α = (1 − 4 ν )/(1 + ν ) is the coupling coefficient of the normal and tangential modulus that is equal to 0.25 in concrete materials, E is the modulus of transience, and ν is the Poisson’s ratio.

All facets in LDPM are defined as potential crack surfaces, and their crack openings are defined as:

δ=δNn+δLl+δMm (2)

where δN=l(eN−tN/EN) is the normal crack opening, δL=l(eL−tL/EL) is the tangential crack opening, δM=l(eM−tM/EM) is the tangential crack opening, and l is the distance between the centers of adjacent aggregates.

Concrete is a porous medium, which includes internal pores, microcracks, and other congenital defects. Because of the effect of the freeze-thaw cycle, the pore water repeatedly freezes and expands, and the formation of pore pressure causes damage to concrete. This damage gradually develops into cracks, making the failure of concrete material under external loading quickly occur under stress concentration. Therefore, the freeze-thaw cycle is the main cause of amplifying this congenital defect within the concrete. The mechanical constitutive on the LDPM Facet is constructed to describe the phenomenon of freeze-thaw degradation, This can be done by considering the mesoscopic damage between the mesoscale parameter of the degradation of the mechanical properties in LDPM-FTC and the macroscale accumulation of freeze-thaw damage to the concrete. This procedure is conducted to simulate the mechanical properties of concrete under freeze-thaw damage.

It is well-known that the effective normal elastic modulus ( ENFTC ) and mesoscopic tensile strength ( σt ) control the macro-mechanical response of concrete under uniaxial tension. The effective normal modulus of elasticity satisfies the freeze-thaw degradation equation which is ENFTC=EN−2.996N2−33.42N . The mesoscopic tensile strength satisfies the freeze-thaw degradation equation:  σtFTC=1.25+2.98exp(−N/20.02) . The LDPM uses the tensile-shear coupling parameter ( rst ) to control the macroscopic mechanical response of concrete specimens subjected to uniaxial compression, i.e., (ratio of mesoscopic shear strength ( σs ) to mesoscopic tensile strength ( σt )). The mesoscopic shear strength satisfies the freeze-thaw degradation equation which is σsFTC=σs−0.0312N . Under high confinement pressure, the restricted lateral deformation caused by the collapse of internal pores results in a temporary increase in stiffness as the material densification. The model uses a compressive yield strength ( σc0 ) to characterize this phenomenon which satisfies the freeze-thaw degradation equation that is σcFTC=σc0−0.31N. More details of the LDPM constitutive law are provided in Appendix A. Fig. 4 illustrates the constitutive laws of the LDPM-FTC. The mesoscopic tensile and shear stress-strain laws are sensitive to freeze-thaw damage in the hardening stage, while the mesoscopic compressive yielding laws decrease slowly with respect to the gradual accumulation of freeze-thaw damage.

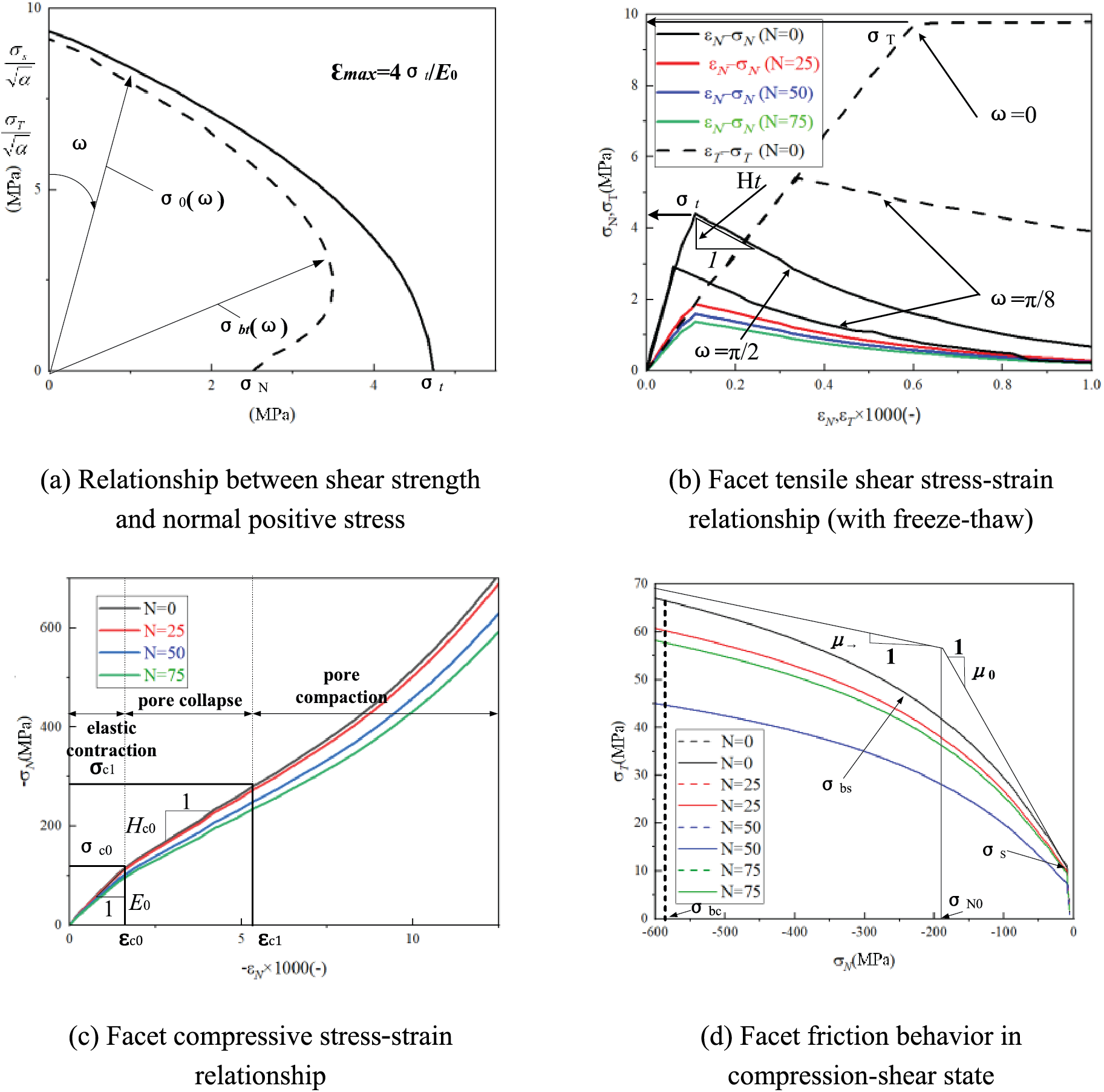
Figure 4: Schematic diagram of LDPM-FTC constitutive [26]

The LDPM governing equations are completed through the force and moment equilibrium of each LDPM cell as follows:

∑k∈ℱI⁡Aktk+VIb=0;∑k∈ℱI⁡Akck×tk=0 (3)

where ℱI is the set containing all the facets of a generic polyhedral cell I, Ak is the area of the projected facet k, ck is the vector representing the distance between the centroid of the facet k and the center of the cell, VI is the cell volume, and b is the external body forces applied on the cell. The computational framework is solved with an explicit dynamic solver. The constitutive is implemented as the VUEL subroutine [31,32] and solved by the dynamic explicit modulus in ABAQUS.

3  Model Validation and Verification

3.1 Validation: Multi-Axial Load Test

The multiaxial load specimen failure test conducted by Shang et al. [16–18] is used to verify the freeze-thaw degradation of LDPM-FTC. The test is set up with a plurality of 100 mm × 100 mm × 100 mm cube concrete specimens, where the test block mix ratio parameters are shown in Table 1. The specimens are subject to freeze-thaw cycles from 6°C to −15°C within 3 h according to GBJ82-85. It is performed on a specially designed triaxial testing machine capable of generating three independent compressive and tensile loads. In this work, the freeze-thaw cycles of 0, 25, 50, 75, and 48 stress conditions of uniaxial compression, uniaxial tensile, biaxial compression, and biaxial tension and compression are tested and simulated similar to Song et al. [16–18].

Fig. 5 shows the simulation setup. A fixed end and loading end are determined in the direction of any load on the specimen, and to measure the compressive strength in the test. Three layers of butter and three layers of plastic film are arranged between the specimen and the loading device. Hence, the low-friction parameters μ between the model specimen and the loading plate (finite element) is set to reproduce the same concrete-plate interaction in the experiments and can be calculated as μ(s)=μd+(μs−μd)s0/(s+s0) , where μ0=0 ,  μs=0.035 , and  s0=0.00005 mm . The material and LDPM parameters are provided in Table 1.

Figure 5: Schematic diagram of axial load simulation test device [18]

Fig. 6 shows the strength envelope diagram obtained from the prediction results of the biaxial load model. It can be observed that the overall good matching between experimental and numerical results demonstrates the correctness of the proposed method. It can also be observed that the specimens’ ultimate strengths of biaxial compression are higher than that of uniaxial compression. Moreover, the numerical value exceeds the uniaxial compressive strength by nearly 40% when the stress ratio is 0.5:1.0 without freeze-thaw-damage conditions. Also, the compressive strength under biaxial tensile-compressive loads decreases linearly with the increase of tensile stress in the other direction, and the biaxial tensile strength is smaller than the uniaxial tensile strength. In addition, the model predicts the strengths of concrete specimens under 100 freeze-thaw cycles. The freeze-thaw action does not change the basic shape of the envelope diagram but only shrinks inwards.

Figure 6: Strength envelope diagram of the concrete specimen under biaxial load

3.2 Validation: Compression-Shear Test

The specimen used for the compression-shear experiment is a prefabricated cylinder with a diameter of 102 mm and a height of 50 mm as shown in Fig. 7 [25]. A certain depth of circumferential notches is cut out on the top and bottom of the cylinder, and radial notches are cut out along the height at the corresponding position of the hoop notch. The specimen placement state is shown in Fig. 7a. The compressive jaw is used to fix the specimen bottom, whereas the hydraulic jack is used to restrain the specimen and apply confining pressure on the jaw. The axial loading device above the specimen is used to apply the displacement load at the position of the inner ring of the specimen. Finally, the displacement sensor (out LVDT) is attached on the top surface to measure the displacement.

Figure 7: Concrete test blocks and their placement [25] and LDPM model settings

Fig. 7b shows the load state and setting of the model. Due to the reserved notch, the crack surface is always in the form of interconnection between the upper and lower circumferential notch grooves after shear failure, and the concrete outside the circumferential notch can maintain good integrity. To make the model efficient to put aggregate pellets and run calculations, the core part of the specimen is simulated by the LDPM, and the remaining part is simulated by the finite element method (FEM) method. At the beginning, the confining pressure on its side is applied on the specimen, and then the load is applied vertically and towards the top of the circumferential notch of the specimen. The displacement rate is set to be 0.02 × 10−2 mm/s. The material and LDPM parameters are provided in Table 2.

The mesoscopic parameters of LDPM-FTC under low confining pressure are calibrated by the test results of the uniaxial compression test of cube concrete specimen with 150 mm side length (Fig. 8a), and the splitting tensile test of the concrete specimen with 150 mm diameter and 300 mm height (Fig. 8b). The mesoscopic parameters are then used to predict the compression-shear strength under various confinement pressures. Fig. 8c reports the shear stress and displacement curves of the test under 8 MPa confining pressure. The Fig. 8d compares all the shear strengths under various confining pressures. In addition, Fig. 8e shows the cracking pattern inside a specimen obtained from experiments and simulations. All the good agreements demonstrate the good ability of the LDPM to predict the shear strength of concrete when its mesoscopic parameters are calibrated by the compression and tension tests.

Figure 8: Concrete shear mechanical behavior

4  Failure Analysis of Concrete Panels

According to different dam heights, four typical dam slopes and three detached ranges conditions, and concrete with 0, 25, 50, and 75 freeze-thaw cycles are studied. The slope of earth and rock dams are designed to guarantee the dam stability. The initial selection of the upstream slope of an earth and rock dam is based on the materials and the dam height. The slope of the dams is usually recommended within the range of 1:2.0~1:3.5. This work takes four typical dam heights. The working condition settings are summarized in Table 3. N = 0 refers to intact concrete.

To study the panel concrete cracking behavior within the detached area, the core part of the concrete panel is simulated by the LDPM-FTC, and the external concrete out of the detached area is simulated by the FEM elements. The related parameters are given in the Appendix A. A rigid body finite element representing the ice expansion load is set above the LDPM-FTC specimen. Also, the ice expansion load in the figure is decomposed into the ice creeping force along the length of the specimen and the force perpendicular to the length of the specimen along the direction to the detached area (Fig. 9).

Figure 9: Schematic diagram of the shear effect of ice expansion load on the detached panel and the model settings

The displacement-bond interaction between the FEM elements and the LDPM is used. The nodes between the “ice” and the LDPM simulate the bonding of the water surface ice and the concrete panel in the actual water level fluctuation area. The simplification of finite elements on the left and right sides of the LDPM parts is adopted to save computational efforts. The ice FEM elements setting reference point is used to capture the load-bearing capacity and displacement values of the panels.

4.1 Crack Opening Modes of Concrete Panels

Fig. 10a shows the failure mode of the concrete panel subjected to ice expansion load with a detached range of 600 mm and a slope of 1:2.25. In the initial stage (stage A), the panel is in the elastic deformation stage, and microcracks initiate in the panel as the hardening stage in Fig. 10b. With the loading of ice expansion on the water surface, the concrete panel first forms a large number of layered cracks on the surface. These smeared cracks are inclined at a certain angle and concentrated together at a certain height to form a macroscopic main shear crack. The main shear crack gradually extends to the unvented edge of the panel which is known as stage B. Meanwhile, due to the increase in deflection, the tensile-shear cracks form at the lower edge of the detached area from the top to the bottom surface of the panel. As the ice surface continues to expand, a bending tensile crack at the bottom of the panel forms from the bottom to the top. At the same time, the crushed smeared cracks on the surface of the panel gradually develop in the direction of the main crack obliquely to the macroscopic main crack. The main compression-shear crack is gradually replaced by a plurality of scattered cracks until it runs through the whole panel and a certain bearing capacity still remains. Then an oblique tensile crack in the orthorhombic direction appears, termed as stage C. The oblique tensile crack imitates at the bottom of the panel near the edge of the attached edge and gradually develops towards the ice bond on the upper part of the panel. The concrete panel fails as the tension crack width increases across the whole panel (stages D–E).

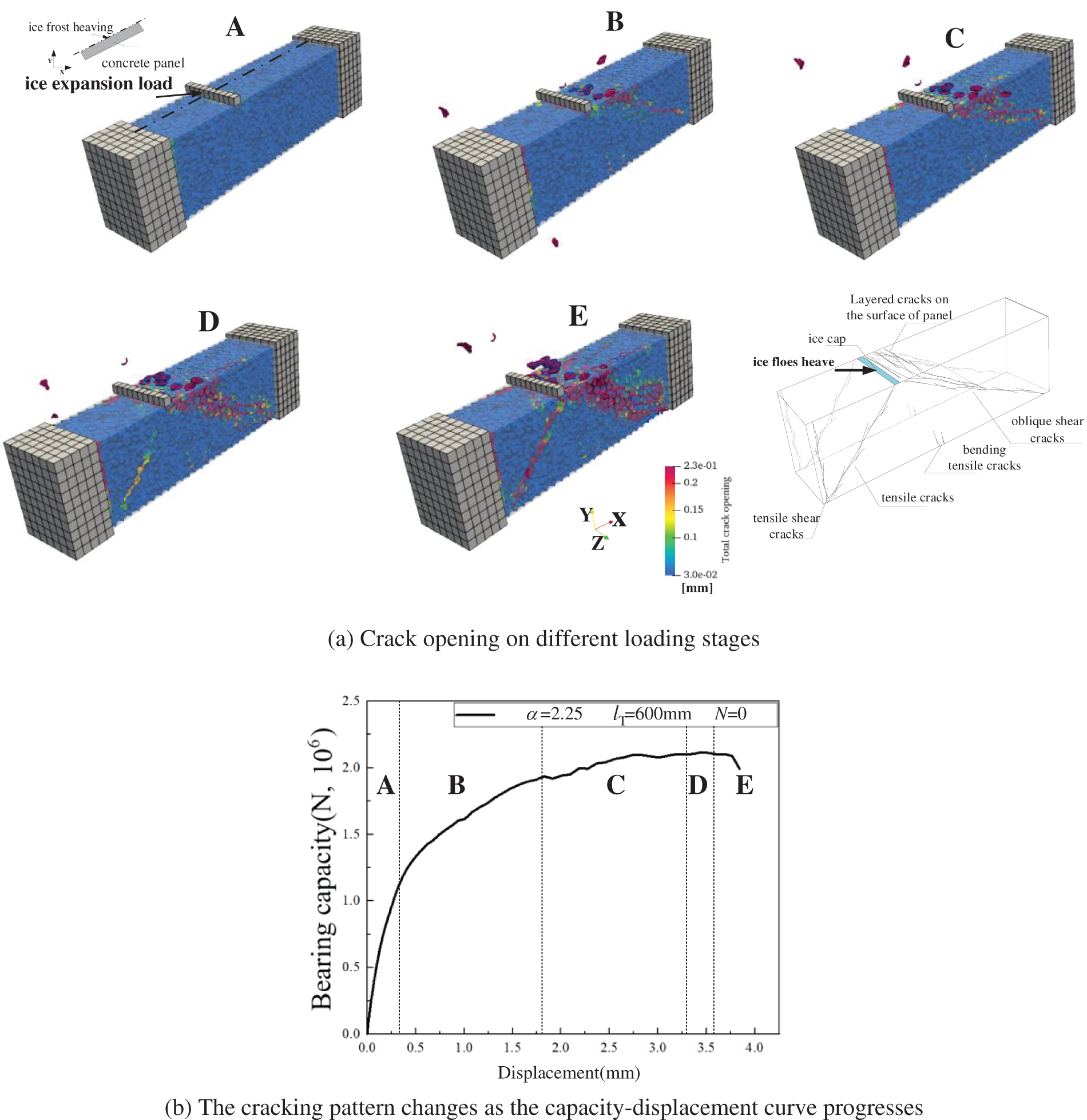
Figure 10: Crack opening modes on different loading stages

4.2 Influence of the Freeze-Thaw on Bearing Capacity

Tables 4 and 5 report the relationship between the panel capability and the slope of the panel ( α ) as well as the number of freeze-thaw cycles (N) under different detached ranges ( lT ).

Fig. 11 shows the variation of the ultimate bearing capacity of the concrete panels with the freeze-thaw damaged under different detached ranges. The load bearing capacity of the concrete panels monotonously decreases with the panel slope having the maximum reduction of 10%.

Figure 11: The relationship between the panel bearing capacity and the slope and freeze-thaw cycles under different detached ranges

The progress of freeze-thaw damage has a significant impact on the bearing capacity of concrete panels. In the case of detached range of 600 mm (Fig. 10a), the biggest reduction of 21% in the bearing capacity occurs when the concrete panel experiences 25–50 freeze-thaw cycles, while the biggest reduction of 22% occurs at 0–25 freeze-thaw cycles in the cases of detached range of 800–1000 mm (Figs. 10b and 10c).

At the slope of 1:2.25, the panel bearing capacities decrease to 95.2% after 25 freeze-thaw cycles and to 67.7% after 75 freeze-thaw cycles. When the panel slope is 1:2.75, the panel bearing capacity decreases to 95.8% after 25 freeze-thaw cycles and to 68.7% after 75 freeze-thaw cycles. In the case of 1:2.50 slope, the panel bearing capacity decreases 11.0% after 75 freeze-thaw cycles. In the case of 1:3.25 slope, the panel bearing capacity decreases to 59.5% after 75 freeze-thaw cycles.

Fig. 12 reports the relationship between the panel bearing capacity and the detachment range. The load-bearing capacity of the panels with the same slope decreases with the increase of the detachment range within the detachment range of 600 to 800 mm. The decrease of the panel bearing capacity ranges from 12.6%–14.1%, which is greater than that of the detachment range of 800–1000 mm. One can easily understand that the panel bearing capacities are closely related to the detached range and the freeze-thaw cycles. The former factor results in a large span and deflection, and the later factor results in the degradation of mesoscopic mechanical behaviors as well as the bearing capacities at the macro-scale.

Figure 12: The variation of the bearing capacity of the panel with the size of the detached range under different freeze-thaw cycles

4.3 Deformation-Bearing Capacity Relationship

Fig. 13 shows the displacement-bearing capacity curves of the panels with different detached ranges. The diagram illustrates that, for the same number of freeze-thaw cycles, panels with different slopes exhibit a high degree of consistency in curve shape, and the slope has limited influence on the mechanical properties of the panels. For the panel that experiences ice expansion load for the first time, the shape of the displacement-bearing capacity curve varies depending on the detached range. Specifically, when the detachment range is 600 mm, the deformation of the panel in the plastic yield stage is smaller compared to the detached ranges of 800 and 1000 mm. Additionally, the freeze-thaw cycle blurs the boundary between the elastic stage and the plastic stage of the curve, resulting in a gentler displacement-bearing capacity curve. However, the general curve shape of the panel remains unchanged. At this detachment range, the failure mode of the panel is not affected by the number of freeze-thaw cycles. The bearing capacity of the curve decreases more than that of other stages when the number of freeze-thaw cycles is 25 to 50 times, indicating that the accumulated freeze-thaw damage of the panels at this stage is significantly higher than that in other stages, which needs to be paid attention to.

Figure 13: The variation of the displacement-bearing capacity curve of the panel with freeze-thaw cycles under different detached ranges

For the detached ranges of 800 and 1000 mm, the panel’s toughness is significantly higher when the panel is subjected to ice expansion load for the first time compared to the detached range of 600 mm. Additionally, the panel maintains a high bearing capacity during the 1–3 mm displacement stage, after which the bearing capacity gradually decreases. Moreover, the shape of the displacement-bearing capacity curve of the panel changes significantly with the progress of freeze-thaw cycles. As a result, the bearing capacity of the panel and the deformation in the plastic stage will decrease significantly. Additionally, the bearing capacity of the panel will uniformly decrease within the range of 25–75 freeze-thaw cycles. The failure mode of the panel indicates that, for the detached range of 800 and 1000 mm, the panel is more likely to experience bending failure due to the ice expansion load. After the freeze-thaw cycle, the panel exhibits a combined failure mode of flexural and oblique shear failure.

5  Cracking Mechanism of Freeze-Thaw Damaged Panels

As it can be seen from Fig. 14, the internal “potential cracking area” is the result of ice expansion load due to freezing on the water surface when the detached-out panel is subjected to stress distribution. As the ice surface continues to advance towards the plate, the shear-cracking surface inside the panel is formed from the surface of the panel along the height direction of the panel towards the bottom of the panel. Due to the self-weight and ice expansion load action component 2, the bottom of the panel produces deflection and forms a bending tensile cracking surface. Moreover, due to the ice expansion load action, the formation of cracks begins at the bottom of the panel, along the height direction of the panel, forms an oblique pull cracking surface that develops towards the ice surface and the surface bonding area at a certain inclination angle. In addition, due to the ice expansion load component 1, the panel surface forms a layered crack. Also, due to the ice expansion load component 1 and the ice expansion load component 2, the lower edge of the detached panel will form a tensile and shear failure surface, and there is a risk of cracking. The crack arises from the outer surface of the panel and expands downward along its height. When the panel is subjected to ice expansion load for the first time, the size of the voiding range greatly affects the cracking behavior of the panel, i.e., when the detaching is 600 mm, the cracking behavior of the panel is the most abundant, and the above four cracking modes will occur. Nevertheless, the width of the oblique shear crack is the largest, and the cracking phenomenon is the most obvious. With the improvement of the detached range, the bending load of the panel rises, and the panel gradually tends to be bent cracking mode. Finally, the panel with 1000 mm of detaching shows two cracking modes, namely the oblique shear cracking and bending cracking.

Figure 14: Stress distribution in the panel under ice expansion load

Fig. 15a–c displays the internal crack distributions when the detached panels are subjected to the ice expansion load caused by the freezing of the water surface. Freeze-thaw action significantly changes the cracking behavior of the panel (see Fig. 14). Due to the mechanical degradation, the surface crushed layer becomes more serious with a smaller detached range. These smeared cracks continue to develop into the depth of the panel and become an oblique compression-shear crack. The angle between the oblique tensile crack and the bottom of the panel, which is opposite to the development direction of the oblique shear crack, decreases with the increase of the degree of freeze-thaw damage. Also, the material cohesion of the panel with 800 mm detached decreases.

Figure 15: Panel failure contour under different detached ranges

After the panel cracks, the internal mortar and aggregate are exposed. The cracking surfaces come into contact with each other and produce friction and occlusion, allowing the panels to maintain their bearing capacity. The longer the cracking surface, the stronger the bearing capacity of the panel. However, with freeze-thaw action, the mortar gradually peels off from the aggregate surface causing the cracking surface to become rougher and the aggregate occlusion to become tighter. The longer is the cracking surface, the stronger is the bearing capacity of the panel. The longer is the cracking surface, the stronger is the bearing capacity of the panel. Therefore, the bearing capacity-displacement relationship curve of the panels does not decrease rapidly after reaching the peak value. For panels with the same degree of freeze-thaw damage, the bearing capacity of the detachment of 1000 mm will be slightly stronger than the bearing capacity of the detachment range of 800 mm.

The freeze-thaw damaged panels exhibit clear shear cracking and layer cracking of the concrete on their surface. To prevent this, protective materials can be laid on the surface or steel fibers can be mixed in to increase the wear resistance of the panel surface. It is important to consider these preventive reinforcement schemes during the engineering design process. To prevent brittle failure of the concrete panel due to tension, the prestressed steel bar along the length of the panel can be embedded. This will create a state of confining compression on both sides, thereby improving the panel’s bearing capacity.

6  Conclusions

The LDPM-FTC (Lattice Discrete Particle Model of concrete under Freezing and Thawing Cycle) is proposed in this work. The fracturing process of type II fracturing behavior and the mechanical capability of the partially detached concrete panel of earth-rock dams in cold regions are then numerically studied.

(1)   The partially detached panels subjected to the ice expansion load will form tensile-shear, compressive-shear, and bending tensile stress areas. These areas are more susceptible to cracks due to the increasing degree of freeze-thaw damage. The bending tension cracks appear at the panel bottom and the smeared crack layer at the top surface appears when the freezing-thawing damage degree increases.

(2)   The detached ranges and the freeze-thaw cycle significantly weaken the bearing capacity of the panels. The panel with a small detachment is more sensitive to the freeze-thaw cycles, and the panel slope has little effect on the load-bearing capacities of the panels.

(3)   The use of shear rebar reinforcement can increase the resistance of shear cracking inside concrete panels. The protective materials can be placed on the upper surface of the waterfront panels to avoid severe layered cracking due to the freezing of the water surface.

Acknowledgement: None.

Funding Statement: This work is supported by the Project on Excellent Post-Graduate Dissertation of Hohai University, Nanjing, China (422003508), the Postgraduate Research & Practice Innovation Program of Jiangsu Province, China (SJCX23_0187;422003287), the National Natural Science Foundation of China (52250410359), and Young Elite Scientists Sponsorship Program by Jiangsu Provincial Association for Science and Technology (TJ-2023-043).

Author Contributions: The authors confirm contribution to the paper as follows. Huayi Zhang: Conceptualization, Methodology, Investigation, Validation, Writing–original draft, Writing–review & editing; Maobin Song: Conceptualization, Investigation, Validation, Writing–original draft; Lei Shen: Methodology, Software, Investigation, Writing–original draft, Writing–review & editing, Funding acquisition; Alkayem Nizar Faisal: Investigation, Writing–review & editing, Funding acquisition; Maosen Cao: Methodology, Writing–review & editing, Funding acquisition. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: Data will be made available on request.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. Jin F, Huang D, Lino M, Zhou H. A brief review of rock-filled concrete dams and prospects for next-generation concrete dam construction technology. Engineering. 2024;32(1):100–6. [Google Scholar]

2. Chen H, Liu D, Shi X. Study on long-term service behavior of concrete face rockfill dam considering actual construction quality and constitutive model improvements. Comput Geotech. 2024;168:106156. [Google Scholar]

3. Yan Y, Si Y, Lu C, Wu K. Effect of freeze-thaw cycles on chloride transportation in concrete: prediction model and experiment. Struct Durab Health Monit. 2023;17(3):225–38. [Google Scholar]

4. Li YL, Bu P, Wu HB, Wen LF, Zhou H, Lu X. Sensitivity analysis of influencing factors of separation between concrete face and cushion layer of CFRD. Chin J Appl Mech. 2022;39(6):1108–16 (In Chinese). [Google Scholar]

5. Shen CS, Li YL, Zheng FS. Causes of formation of interspace between slab and cushion layer of CFRD and measures for its prevention. J Hohai Unive (Nat Sci), 2006;34(6):635–9 (In Chinese). [Google Scholar]

6. Peng XS, Yao GZ. Analysis on cavern detection of concrete facing of earth-rock dam. Water Conserv Constr Manag. 2017;37(7):63–7 (In Chinese). [Google Scholar]

7. Han H, Shen L, Cao M, Wei L, Qian X. On the ice induced damage of reservoir drainage tower: a thermal stress-involved contact simulation. Eng Fail Anal. 2024;160:108203. [Google Scholar]

8. Hellgren R, Malm R, Fransson L, Johansson F, Nordström E, Westberg WM. Measurement of ice pressure on a concrete dam with a prototype ice load panel. Cold Reg Sci Technol. 2020;170:102923. [Google Scholar]

9. Petrich C, Sæther I, Fransson L, Sand B, Arntsen B. Time-dependent spatial distribution of thermal stresses in the ice cover of a small reservoir. Cold Reg Sci Technol. 2015;120:35–44. [Google Scholar]

10. Mingzhi L, Kui W, Hongkai L, editors. Design of concrete panel dams and freeze-thaw damage and repair of panels in alpine areas. In: Proceedings of the Technological Progress of Concrete-faced Rockfill Dams in Alpine Regions; 2013; Xinjiang, China; Altay Haba River County. [Google Scholar]

11. Zhao Z, Zhou XP. Investigating effects of pore-scale variables and pore geometries on the thermal behaviors of porous concretes. J Build Eng. 2023;75:106895. [Google Scholar]

12. Kim S, Qudoos A, Jakhrani S, Lee G, Kim H. Influence of coarse aggregates and silica fume on the mechanical properties durability, and microstructure of concrete. Materials. 2019;12(20):3324. doi:10.3390/ma12203324. [Google Scholar] [PubMed] [CrossRef]

13. Hanjari KZ, Utgenannt P, Lundgren K. Experimental study of the material and bond properties of frost-damaged concrete. Cem Concr Res. 2011;41(3):244–54. doi:10.1016/j.cemconres.2010.11.007. [Google Scholar] [CrossRef]

14. Zhao Z, Shou YD, Zhou XP. Microscopic cracking behaviors of rocks under uniaxial compression with microscopic multiphase heterogeneity by deep learning. Int J Min Sci Technol. 2023;33(4):411–22. doi:10.1016/j.ijmst.2022.12.008. [Google Scholar] [CrossRef]

15. Liu L, Qin G, Zhou Y, Chen HS, Wang XC. Freezing behavior of unsaturated porous materials. Constr Build Mater. 2021;274(8):122112. doi:10.1016/j.conbuildmat.2020.122112. [Google Scholar] [CrossRef]

16. Shang HS, Song YP. Experimental study of strength and deformation of plain concrete under biaxial compression after freezing and thawing cycles. Cem Concr Res. 2006;36(10):1857–64. doi:10.1016/j.cemconres.2006.05.018. [Google Scholar] [CrossRef]

17. Shang HS, Song YP, Qin LK. Experimental study on strength and deformation of plain concrete under triaxial compression after freeze-thaw cycles. Build Environ. 2008;43(7):1197–204. doi:10.1016/j.buildenv.2006.08.027. [Google Scholar] [CrossRef]

18. Shang HS, Song YP, Ou JP. Performance of plain concrete under biaxial tension-compression after freeze-thaw cycles. Mag Concr Res. 2010;62(2):149–55. doi:10.1680/macr.2008.62.2.149. [Google Scholar] [CrossRef]

19. Shang H, Cao WQ, Wang B. Effect of fast freeze-thaw cycles on mechanical properties of ordinary-air-entrained concrete. Sci World J. 2014;2014:923032–7. doi:10.1155/2014/923032. [Google Scholar] [PubMed] [CrossRef]

20. Zhang W, Pi Y, Kong W, Zhang Y, Wu P, Zeng W, et al. Influence of damage degree on the degradation of concrete under freezing-thawing cycles. Constr Build Mater. 2020;260(1–2):119903. doi:10.1016/j.conbuildmat.2020.119903. [Google Scholar] [CrossRef]

21. Bresler B, Pister KS. Strength of concrete under combined stress. J Am Concr Inst. 1958;30(3):321–45. [Google Scholar]

22. Bazant ZP, Kazemi MT, Hasegawa T, Mazars J. Size effect in brazilian split-cylinder tests-measurements and fracture-analysis. ACI Mater J. 1991;88(3):325–32. [Google Scholar]

23. Cong Y, Kong L, Zheng YR, Erdi AB, Wang ZQ. Experimental study on shear strength of concrete. Concrete, 2015(5):40–5 (In Chinese). [Google Scholar]

24. Shi Y, Lu Y, Cui J. Experimental study on dynamic mechanical properties of concrete under direct shear loading. Cem Concr Compos. 2023;142:105150. [Google Scholar]

25. Becks H, Aguilar M, Chudoba R, Classen M. Characterization of high-strength concrete under monotonic and fatigue mode II loading with actively controlled level of lateral compression. Mater Struct. 2022;55:252-1–252-16. [Google Scholar]

26. Cusatis G, Pelessone D, Mencarelli A. Lattice discrete particle model (LDPM) for failure behavior of concrete. I: theory. Cem Concr Compos. 2011;33(9):881–90. [Google Scholar]

27. Cusatis G, Mencarelli A, Pelessone D, Baylot J. Lattice discrete particle model (LDPM) for failure behavior of concrete. II: calibration and validation. Cem Concr Compos. 2011;33(9):891–905. [Google Scholar]

28. Alnaggar M, Pelessone D, Cusatis G. Lattice discrete particle modeling of reinforced concrete flexural behavior. J Struct Eng. 2018;145:0408231-1–0408231-14. [Google Scholar]

29. Cusatis G, Bažant Zdeněk P, Cedolin L. Confinement-shear lattice model for concrete damage in tension and compression: I. Theory. J Eng Mech. 2003;129(12):1439–48. [Google Scholar]

30. Cusatis G, Bažant Zdeněk P, Cedolin L. Confinement-shear lattice model for concrete damage in tension and compression: II. Computation and validation. J Eng Mech. 2003;129(12):1449–58. [Google Scholar]

31. Shen L, Li W, Zhou X, Feng J, Di Luzio G, Ren Q, et al. Multiphysics lattice discrete particle model for the simulation of concrete thermal spalling. Cem Concr Compos. 2020;106:103457. [Google Scholar]

32. Shen L, Lo Monte F, Di Luzio G, Cusatis G, Li W, Felicetti R, et al. On the moisture migration of concrete subject to high temperature with different heating rates. Cem Concr Res. 2021;146:106492. [Google Scholar]

Appendix A

For stresses and strains beyond the elastic limit, LDPM mesoscale failure is characterized by three mechanisms as described below:

1-   Fracture and cohesion due to tension and tension-shear

       For tensile loading ( εN > 0), the fracturing behavior is formulated through an effective strain, ε = εN2+α(εM2+εL2)2  , and stress σ = σN2+(σM+σL)2/α , which define the normal and shear stresses as σN = αεN(σ/ε) , σM = αεM(σ/ε) , and σL = αεL(σ/ε) . The effective stress σ is incrementally elastic ( σ˙ = E0ε˙ ) and must satisfy the inequality 0 < σ < σbt ( ϵ , ω ), where σbt = σ0 ( ω ) exp[− H0 ( ω ) ε−ε0(ω)/σ0 ( ω )], χ = max( χ ,0l, and tan( ω ) = εN / αεT = σN/ασT . The post peak softening modulus is defined as H0 ( ω ) = Ht (2ω/π)nt , where Ht is the softening modulus in pure tension ( ω = π /2) expressed as Ht = 2 E0 /( lt / le − 1), lt = 2 E0Gt t/ σt2 , lt is the length of the tetrahedron edge, and Gt is the mesoscale fracture energy. LDPM provides a smooth transition between pure tension and pure shear ( ω = 0) with parabolic variation for strength given by σ0 ( ω )= σtrst2 (−sin ( ω ) + sin2(ω)+4αcos2(ω)/rst2 /[  2αcos2(ω) ], where rst = σs / σt is the ratio of shear strength to tensile strength.

2-   Compaction and pore collapse from compression

       Normal stresses for compressive loading ( εN < 0) are computed through the inequality − σbt ( εD , εV ) ≤ σN ≤ 0, where σbt is a strain-dependent boundary function of the volumetric strain, εV and the deviatoric strain, εD . Beyond the elastic limit, − σbt models pore collapse as a linear evolution of stress for increasing volumetric strain with stiffness Hc , for − εV ≤ εc1 = κc0 σc0 : σbc = σc0 + (− εV−εc0 ) Hc ( rDV ); Hc ( rDV ) = Hc0 /(1 + κc2 ( rDV – κc1 )); σc0 is the mesoscale compressive yield stress; and κc1 , κc2 are the material parameters. Compaction and rehardening occur beyond the pore collapse (− εV > εc1 ). In this case one has σbc = σc0 rDV ) exp[(− εV – εc1 )  Hc ( rDV )/  σc1 ( rDV )] and σc1 ( rDV ) = σc0 + ( εc1 – εc0 ) Hc ( rDV ).

3-   Friction due to compression-shear

       The incremental shear stresses are computed as σ˙M=ET(ε˙M−ε˙Mp) and = ET(ε˙L−ε˙Lp) , where ε˙Mp = λ˙∂φ/∂σM ,  ε˙Lp = λ˙∂φ/∂σL , and λ is the plastic multiplier with loading-unloading conditions φλ˙ ≤ 0 and λ ˙≥ 0. The plastic potential is defined as φ = σM2+σL2−σbs(σN) , where the nonlinear frictional law for the shear strength is assumed to be  σbs = σs + ( μ0 − μ∞ )  σN0 [1 –exp ( σN / σN0 )] − μ∞σN , σN0 is the transitional normal stress, as well as μ0 and μ∞ are the initial and final internal friction coefficients.