Bearing Fault Diagnosis Based on the Markov Transition Field and SE-IShufflenetV2 Model

1  Introduction

In modern industry, rolling bearings are used in many machines. Because the bearing plays the role of support and movement transformation, its health directly influences mechanical equipment’s operating stability and safety. Rolling bearings are often damaged due to long-term continuous work and arduous working environments. When the rolling bearing fails, the movement of the machine is critically affected, and the vibration signal changes. When analyzing the vibration signal, features related to the failure are separated, and the category of the mechanical system failure can be determined.

The vibration signals of rolling bearings are rich in fault evolution information. The representative characteristics of faults can be obtained intuitively through signal processing. Commonly used signal processing approaches cover empirical mode decomposition (EMD) [1], improved complete ensemble empirical mode decomposition (CEEMDAN) [2], cepstrum, wavelet transform [3], and wavelet threshold denoising [4]. Different signal feature processing methods combined with various classifiers can produce different fault diagnosis effects. Li et al. [5] proposed an improved singular value decomposition (SVD) and wavelet packet transform method to address the two disadvantages of SVD: difficulty in determining the reconstruction order and poor denoising ability. This method combines both advantages to achieve optimal node selection; its effectiveness has been verified on the bearing dataset. Tang et al. [6] divided multiple time-frequency curves into interested and disinterested curves and then matched the average ratio between the interested curves with the theoretical fault characteristic coefficients to determine the fault type. Yu et al. [7] proposed a rolling bearing diagnosis approach to the EMD strength given the non-stationary vibration signals of the rolling bearing. The authors proposed the concept of energy entropy on this basis. This method uses EMD to extract the energy entropy of different frequency bands as a feature, identifying the fault types of rolling bearings. Moreover, the diagnosis effect is better than wavelet packet decomposition and reconstruction diagnosis methods. Li et al. [8] investigated the problem that the influencing parameters of variational mode decomposition (VMD) must be determined in advance. Furthermore, the sensitive intrinsic mode functions (IMF) must be selected from multiple IMFs generated by VMD. Hence, the authors proposed an optimal IMF selection method for VMD based on band entropy. This method identifies the fault type by analyzing the selected IMF using an envelope power spectrum. The authors experimentally validated the method’s effectiveness. Zhang et al. [9] proposed a bearing fault diagnosis approach based on multi-scale entropy and an adaptive neural-fuzzy inference system. Compared to the traditional single entropy value, this approach provided additional information about the operating conditions of machinery and could identify the severity of the failure.

With the consistent progress of deep learning theory, various models with strong data feature excavating capacity are diffusely applied to fault diagnosis. Zhang et al. [10] used a one-dimensional convolutional neural network (CNN) for rolling bearing fault diagnosis. The authors directly input the original one-dimensional (1D) vibration signal into the network for feature extraction and classification, obtaining the benign effect was obtained. Song et al. [11] proposed a wide convolutional neural network model to obtain a larger receptive field and enhance the model’s generalization ability. Qiao et al. [12] proposed a dual-input model for CNN and long short-term memory (LSTM) networks. This model utilizes CNN [13] to extract spatial features of data, employs LSTM [14] to capture sequential data features, and uses time-domain signals as input to enhance the diagnosis accuracy under various loads. Saghi et al. [15] designed a neural network combined with the feature attention mechanism to solve the problem of potential vibration loss of information and poor anti-noise performance in single-scale convolution. The model adopts parallel CNN with three disparate filter lengths, extracting and binding spatial and temporal features of input signals at unlike frequencies.

With the in-depth study of deep learning in the domain of bearing fault diagnosis, researchers started to explore the application of two-dimensional (2D) CNN in this field. They first used various signal processing techniques to convert 1D vibration signals into 2D feature images [16]. Then, the researchers used a 2D convolution check with stronger spatial feature extraction capability. These methods have obtained remarkable research results. Cai et al. [17] converted 1D bearing vibration signals into time-dependent 2D feature images through the Gram angle field (GAF). Moreover, the authors sent the converted data into the neural network for diagnosis. The experimental results demonstrated that high accuracy can still be obtained with varying working conditions and small samples. Lei et al. [18] addressed the issues of traditional CNN with excessive parameters, slow training speeds, and insufficient generalization by proposing a fault diagnosis approach for rolling bearing based on Markov transition field (MTF) and multi-scale feature aggregation CNN. This approach captured plentiful information from feature images at various scales and fused these features by assigning weights. Experimental results indicated that the raised approach offered faster computation speeds, better fault recognition rates, and a greater generalization nature than other approaches. In the original high-dimensional data, higher-order data can show more geometric properties and structures than lower-order data. A new type of bearing fault diagnosis method is obtained by combining the high-order data containing rich feature information with models such as CNN, ResNet [19], DenseNet [20], MobileNet [21], and VGGNet [22] achieving ideal fault diagnosis results.

In actual working situations, the bearing equipment load will constantly change, mechanical equipment generally works in a noisy environment, and the collected vibration data is always accompanied by noise, making extracting the fault characteristics of vibration signals difficult. Therefore, the model’s fault identification accuracy and generalization are poor. This paper proposed a fault diagnosis method based on MTF and an improved ShufflenetV2 [23] model for bearing fault diagnosis. Firstly, the MTF was applied to encode the collected vibration signals of rolling bearing into a 2D feature image dataset with time correlation and uniqueness. Then, the dataset was segmented into training and verification sets and sent to the improved ShufflenetV2 network for training. Finally, the availability and generalization of the proposed approach were experimentally validated under variable operating conditions and noise environments. The primary innovations of the paper are as follows:

(1) The MTF encodes the bearing vibration signal, preserving the time correlation. The color of the pixels is dark and light, which is convenient for the neural network to extract the feature information in the image. The model’s extraction ability is improved, and the recognition accuracy of the model is enhanced.

(2) The ShufflenetV2 network model is improved. The model’s accuracy is highly improved by adding a small number of parameters. Moreover, the sensitivity field of the model is enhanced, and the relationship weight between various information channels is increased, settling the matter of neuronal necrosis in the ShufflenetV2 network.

(3) The method of overlapping sampling is applied to advance the original data. Then, the adaptive learning rate method is used for training. The method proposed in this paper can obtain high recognition accuracy under variable load conditions and noise environments.

The remainder of the paper is arranged as follows. Section 2 represents MTF. Section 3 introduces ShufflenetV2 and the improved ShufflenetV2 (IShufflenetV2). Section 4 shows the fault diagnosis experiment and analyzes the experimental results. Lastly, Section 5 summarizes the paper and draws conclusions.

2  MTF

MTF [24] is based on Markov chain theory, which considers time and position information and uses Markov state transition probability to encode. In this approach, the time progression of time series is seen as a Markov process, i.e., its future evolution does not hinge on its past evolution if the current status is known. Hence, a Markov transfer matrix is constructed to convert the 1D time series signal into a 2D feature image while preserving the time correlation of the original signal.

A given time series x = {x1, x2, ..., xn}, can be divided into Q quantile regions based on the signal amplitude at different times. Then, each value of x can be quantified using quantile qj (j ∈ [1, Q]), and each xi can be mapped to qi by identifying the quantile. Finally, the Markov chain is used to calculate the transitions of each component point along the direction of the time axis, constructing the Markov transfer matrix W. The calculation formula is shown in Eq. (1):

W=[w11w12⋯w1Qw21w22⋯w2Q⋮⋮⋱⋮wQ1wQ2⋯wQQ], (1)

wij=p{xt+1∈qj|xt∈qi}, (2)

where xt is the signal amplitude corresponding to time t; qi is the quantile region corresponding to xi; wij is the probability of the quantile region qi approaching qj.

However, the Markov transfer matrix is insensitive to the timing signal x and step size. Moreover, the time and position information are ignored, reducing the cost of important information in the original signal. Therefore, the MTF, denoted as M, can be constructed via Eq. (3):

M=[ωij| x1∈qi,x1∈qj…ωij| x1∈qi,xN∈qjωij| x2∈qi,x1∈qj⋯ωij| x2∈qi,xN∈qj⋮⋱⋮ωij| xN∈qi,x1∈qj⋯ωij| xN∈qi,xN∈qj]. (3)

MTF visualizes the time series using the above coding method. Therefore, each element in the matrix is characterized by a corresponding pixel. Each generated pixel differs due to the different transfer probabilities between quantile regions. MTF retains the time and position information of the original 1D signal, making it time-dependent. Moreover, MTF is also characterized by dark and light colors of pixels, which is convenient for neural networks to extract image feature information, providing advantages in classification tasks.

Fig. 1 demonstrates the images of various bearing fault types after each sample is encoded via MTF. The 2D feature images transformed by MTF can clearly distinguish between the four bearing categories.

Figure 1: Bearing fault images generated by using MTF

3  Bearing Fault Diagnosis Method

3.1 SEnet

In deep learning, the attention mechanism is a resource allocation mechanism that mimics the human visual attention mechanism. When people browse the information they are currently reading, they pay more attention to the feature parts of the information. Also, people pay more attention to the part they are interested in and less attention to other parts.

Squeeze-and-Excitation network (SEnet) [25] is a new image recognition structure released in 2017. Its core idea is to model the interdependence between convolutional feature channels, obtain the input feature image and the weight of each channel, and set the feature channels that require attention to a higher weight for reinforcement, improving the accuracy. SEnet mainly comprises Squeeze and Excitation. The structure of SEnet is demonstrated in Fig. 2.

Figure 2: SEnet structure

Squeeze operation refers to using a global pooling method in CNN, generating a feature image of the global receptive field by performing global mean pooling on the features of each channel. The global sensitivity field enables the Squeeze operation to catch all the feature information in the input data and use a small summary value to represent the importance of the features of each channel. The Excitation operation is located at the full relation layer to demonstrate each channel’s significance. The obtained importance weight is applied to the corresponding channel.

3.2 IShufflenetV2 Network

The Shufflenet network, proposed by the MegVII Technology team in 2017, is a lightweight CNN designed for mobile devices. Shufflenet network adopts two core operations: Pointwise group convolution and channel shuffle. Compared with traditional convolution, Pointwise group convolution can reduce the network capacity and make the network lighter.

Pointwise group convolution is a technique that combines pointwise convolution with group convolution. Compared to regular group convolution, Pointwise group convolution is characterized by higher computational efficiency. However, Pointwise group convolution is still the only convolution within groups, with no information interaction between combined groups. As a result, information between groups is not exchanged, and the model cannot fully learn feature information. Channel shuffle was proposed to allow groups to communicate with each other. Its basic principle is to first group the results of Pointwise group convolution into groups within each group. Then, the subgroups within each group are exchanged to achieve cross-group feature exchange. Finally, the shuffle results are connected to form the final output feature image. Fig. 3 shows the channel shuffle process of the Shufflenet.

Figure 3: Channel shuffle process of the Shufflenet

ShufflenetV2 makes an innovation based on Shufflenet architecture and provides four criteria for constructing an efficient network. In other words, the number of input and output channels is equal, group convolution is appropriately used, the network fragmentation is reduced, and the per-element operation is decreased. The basic unit of ShufflenetV2 is demonstrated in Fig. 4.

Figure 4: The basic unit of ShufflenetV2

Fig. 4a shows the basic unit of ShufflenetV2 with stride = 1. As shown in the figure, channel segmentation is performed first. Then, Pointwise group convolution is used in the right branch header and tail for information fusion, and a 3 × 3 deep convolution kernel is used in the middle for feature extraction. Finally, the left and right branches are spliced together for channel shuffle.

Fig. 4b shows the basic unit of ShufflenetV2 with stride = 2. First, features are input into the left and right branches. In the left branch, a 3 × 3 deep convolution kernel with stride = 2 is applied for downsampling feature extraction. Information fusion is carried out after Pointwise group convolution. The first part of the right branch is the same as the basic unit operation with stride = 1. The exception is that the deep convolution kernel with stride = 2 is used in the middle for subsampling feature extraction. Then, the splicing operation is first carried out, followed by the channel shuffle.

As a lightweight convolutional network model, ShufflenetV2 performs well in image classification. However, it fails to extract fault features in image data converted from bearing data due to insufficient model complexity. Therefore, the ShufflenetV2 network is improved in this paper. The activation function plays a key role in network training. Researchers introduced the nonlinear activation function to help networks learn complex patterns in data. The ReLU activation function is applied to the ShufflenetV2 network, which is also used in most networks. Compared with other activation functions, the ReLU activation function is more efficient in computation because it only involves a simple threshold comparison operation. Being an unsaturated activation function, the ReLU only sets all negative values to zero. Eq. (4) represents the expression of the ReLU activation function:

ReLU(x)={xx>0,0x≤0. (4)

According to Eq. (4), when x is 0, the output is 0, and the gradient is 0. The network of neurons cannot update the parameters, leading to “necrosis” of the neurons in the network. Therefore, the Hardswish activation function was proposed in reference to MobileNetV3 [26], which can solve the problem of neuron necrosis in ReLU. The derivation of the Hardswish function is simple; it can prevent the saturation phenomenon caused by the gradient gradually approaching 0 during training while advancing the expression capacity of the network model. The Hardswish function is expressed in Eq. (5):

Hardswish={0x≤−3x(x+3)6−3<x<3xx≥3. (5)

This paper used the basic unit of ShufflenetV2 as the backbone for improvement. First, the basic units with stride = 1 and stride = 2 are optimized. This paper added 3 × 3 depth-wise convolutional kernels instead of 5 × 5 depth-wise convolutional kernels to add the number of parameters in the model and enhance its feature extraction capability. This approach improves the receptive field and strengthens the feature extraction capability of the model. SE module was added to the right branch of the two basic units to carry out feature weighting for different channels, strengthen the relationship between channels, and progress the model’s discrimination. The basic unit of the improved ShufflenetV2 (IShufflenetV2) is shown in Fig. 5.

Figure 5: The basic unit of IShufflenetV2

3.3 Overall Structure of Bearing Fault Diagnosis Method

The overall structure of the MTF-SE-IShufflenetV2 model is demonstrated in Fig. 6. The signal is intercepted by overlapping sampling and converted into a time-dependent two-dimensional feature image via MTF. Then, the dataset is segmented into training and validation sets. Data enhancement operations are performed on the training set (such as random rotation angle and random scaling in length and width) to stop the model from overfitting. Subsequently, the training and test sets are input into the SE-IShufflenetV2 model. The model obtains the local information of the image in the initial convolution stage; then, it goes to the deep convolution stage, where it starts to acquire complex and abstract information in the image and mixes the features through a 1 × 1 convolution layer. Finally, the Global average pool and Softmax classifier convert the classification results into probability distribution to implement the bearing’s fault diagnosis. The parameters of the SE-IShufflenetV2 model applied in this paper are shown in Table 1, where Stages 2, 3, and 4 are all stacked by the cells in Fig. 5, where Repeat demonstrates the number of stacks.

Figure 6: Overall structure of the MTF-SE-IShufflenetV2 model

4  Experiment and Analysis

4.1 Data Source and Preprocessing

The method proposed in this paper is experimentally validated by the faulty bearing dataset from Case Western Reserve University. The experimental platform mainly comprises a three-phase asynchronous motor, a torque sensor, and a load. The fault vibration signals collected from the drive end bearing of the test bench under three working conditions of 0–2 HP are selected in this paper. The signal was acceleration data of the SKF6205 deep groove ball bearing at the driving end, and the signal sampling frequency was 12 kHz. The experimental faults were segmented into four types: inner race fault, outer race fault, rolling element fault, and normal bearing. Two representative bearing faults with diameters of 0.007 inches and 0.021 inches were selected from the database. Since the collected bearing fault vibration data is limited, it is difficult to extract fault features. Hence, the paper adopts an overlapping sampling method to enhance the original collected 1D bearing fault vibration signal. First, the original data was intercepted by a sliding window with a size of 1024 and a sliding step of 341. Then, a feature image of 256 × 256 was generated by MTF. Fig. 7 demonstrates the schematic diagram of overlapping sampling. First, 2800 samples are generated under the 0–2 HP datasets. Then, the samples are divided into training and validation sets with a ratio of 8:2. The specific allocation is demonstrated in Table 2.

Figure 7: Overlapping sampling

4.2 Influence of MTF Images Generated by Different Parameters on Model Performance

MTF converts sequence data into 2D feature images. The sequence data can be quantized into different states, and MTF can be constructed by calculating the state transition probabilities. Therefore, the window length directly affects the ability of 2D feature images to express features. In the experiment, the bearing fault dataset under 1 HP was adopted. Firstly, the bearing fault signals were encoded by MTF according to different window lengths of 256, 512, and 1024, generating the MTF feature images with sizes of 128 × 128, 256 × 256, and 512 × 512, respectively. Then, the generated feature images were input into the SE-IShufflenetV2 model for training 100 Epochs. Finally, the bearing fault data under 2 HP was validated, and the training time of an epoch was recorded to analyze the effect of different parameters on the model performance under variable load.

Since excessive feature image affects model training accuracy and speed, the maximum feature image generated in the experiment was 512 × 512. The experimental results are demonstrated in Table 3. According to Table 3, when the window length is short, the larger the selected image size, the lower the accuracy, and the longer the training time. This observation can be attributed to the amount of data directly affecting the division of intervals. If the data length is insufficient and there are too few sampling points for the vibration signal, the interval will correspondingly decrease, making it difficult to capture fault characteristics. The model’s accuracy will decrease when the window length is long, and the generated image size is small. This phenomenon can be attributed to the time series data points being too dense; hence, multiple data points will be mapped to the same pixel, losing important time series information and affecting the model’s accuracy.

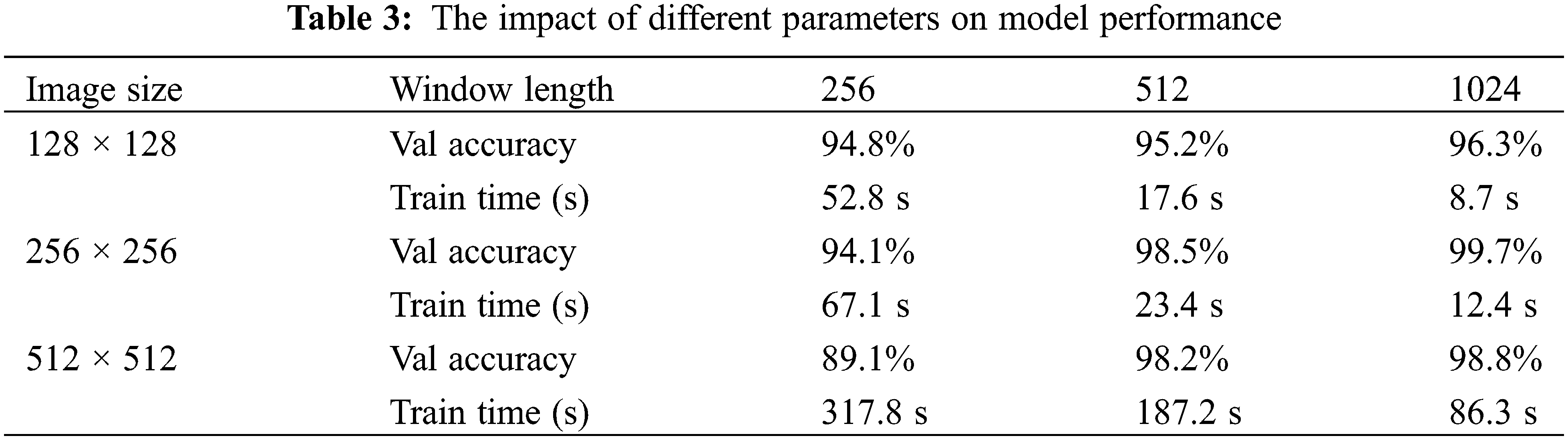
The experimental results in Table 3 demonstrate that the time of a single training Epoch is 317.8 s for the image size of 512 × 512 and the window length of 256, which is undoubtedly a very long training time. The fastest training speed is achieved when the image size is 128 × 128 and the window length is 1024. Each training Epoch only needs 8.7 s, but high training accuracy cannot be guaranteed. A higher accuracy and faster training time are achieved when the window length is 1024, and the image size is 256 × 256. The feature image size was 256 × 256, and the window length was selected as 1024 in this paper to ensure training and testing speed and high accuracy. The experimental results in the following section were obtained by training and testing using these parameters.

4.3 The Influence of Different 2D Image Generation Methods on the Model

The 2D image coding methods such as Gram angle sum field (GASF), Gram angle difference field (GADF), recursive plot (RP), and relative position matrix (RPM) were compared with the MTF proposed in this paper to investigate the influence of different 2D image coding methods on the model. In the experiment, the datasets of normal operation, rolling element fault, inner race fault, and outer race fault under 2 HP load were selected. The damage diameters of the bearings were 0.007 inch, 0.014 inch, and 0.021 inch, respectively. The SE-IShufflenetV2 network was chosen as the test model. Fig. 8 shows the verification accuracy curves of different 2D image coding methods on SE-IShufflenetV2.

Figure 8: Verification accuracy curves of different 2D image coding methods on SE-IShufflenetV2

According to Fig. 8, when generating 2D images using MTF, the accuracy can reach 100% after approximately 15 training epochs. Moreover, the training process is stable without agitation, indicating that the MTF feature image can fully display fault features. Thus, the model can better learn fault features, improving fault diagnosis accuracy. Generating 2D images using GASF and GADF can result in an accuracy of approximately 99%. Nevertheless, a gap with MTF can still be observed. Furthermore, the entire verification curve is not smooth, indicating that using Gram angle fields to generate 2D images does not display fault features well. Consequently, the model does not fully learn fault features. The 2D feature images generated by RP and RPM also fail to show the fault features. Moreover, its effect is significantly different from the MTF, making the model unable to learn effective fault information, resulting in large fluctuations in the entire accuracy curve.

4.4 Model Training

All experiments in this paper were performed by the TensorFlow deep learning framework and run on a computer with an Intel Core i5-12490F processor and an RTX 4060 graphics card. During model training, the mini-batch was set to 16, the number of Epochs was 150, and the optimizer was selected as SGD. This paper used CosineAnnealingLR to define the strategy of adjusting the learning rate. This strategy of adjusting the learning rate can gradually reduce the learning rate in the training process to make the model more stable. In the experiment, 0–2 HP (i.e., datasets A, B, and C) were selected successively to generate 2D feature images through MTF. Then, they were sent to the SE-IShufflenetV2 model for training. This process was carried out to obtain the training accuracy, test accuracy, and training loss of different load datasets.

The training results are demonstrated in Fig. 9. The horizontal coordinate represents the number of iterations in the training, and the vertical coordinate represents the accuracy. The SE-IShufflenetV2 model achieves high accuracy from the start under the MTF dataset generated under 0–2 HP load and levels off after 40 training epochs. The training and verification accuracy reaches 100% under 0 HP and 1 HP load, and the training accuracy reaches 100% under 2HP load. In comparison, the verification accuracy reaches 99.8%. The figure shows that the training process is stable, with no overfitting and a relatively fast convergence rate. This observation indicates that the model learns better feature rules, and the overall training effect is good.

Figure 9: Training accuracy, verification accuracy, and loss of MTF+SE-IShufflenetV2 under different loads

4.5 Ablation Experiment

The ablation experiment was conducted to investigate the impact of the improvement strategy raised in this paper on the network model. ShufflenetV2 was used as the basic model, and improvements to the model were added during the experimental process. The CWRU bearing dataset was used to test the model, which includes data from normal operation, rolling element fault, inner race fault, and outer race fault under 1 HP load; six repeated experiments were performed for each model, and mAP (the average accuracy of six experiments) was used as an accuracy indicator. The results of the ablation experiment are demonstrated in Table 4, in which “√” indicates module integration, and “null” indicates no module combination.

According to Table 4, when the SEnet module is added to the original ShufflenetV2, the mAP is increased by 0.4% compared with the original ShufflenetV2. When ReLU in the original ShufflenetV2 network is replaced with Hardswish, the problem of neuronal necrosis is effectively solved, and the mAP is increased by 0.2%. When the basic backbone of the ShufflenetV2 network is optimized, the sensitivity field of the model is enhanced, the feature extraction ability of the model is strengthened, and the mAP is increased by 0.5% compared with the original ShufflenetV2. The mAP has reached 100% when applying all three improvements mentioned above to the original ShufflenetV2, i.e., increased by 1.2% compared with the original ShufflenetV2. The experimental results show that the model improvement in this article is effective and can improve the model accuracy.

4.6 Generalization Performance Analysis of the Model under Variable Load Condition

During the machine’s operation, the load on rolling bearings often changes depending on the working conditions. Thus, the fault diagnosis model must accurately predict the fault after the variable load. This paper selects three kinds of fault data under disparate loads to establish the training and verification sets. In the experiment, this paper first defines the dataset under 0 HP load as dataset A, the dataset under 1 HP load as dataset B, and the dataset under 2 HP load as dataset C. Then, the proposed approach was compared with six fault diagnosis methods: MTF+MobileNetV3, MTF+ShufflenetV2, GASF+SE-IShufflenetV2, MTF+SE-ResNet50, DWT+SE-IShufflenetV2, and SVM. Table 5 shows the validation accuracy of different datasets and model sizes when the load is constant.

According to Table 5, all models except SVM can achieve relatively high accuracy under constant load, i.e., above 98%. However, the fault diagnosis approach proposed in this paper has the highest accuracy among all methods; the accuracy of other methods cannot reach 100% on datasets A and B. Although the proposed method is more complicated than the original ShufflenetV2 model, it significantly improves the diagnosis accuracy compared with the original network. This improvement can be attributed to the addition of the attention mechanism and convolutional layer. Consequently, the model increases the number of parameters, enhancing the receptive field of the model, improving the ability to extract fault features, and enabling the model to learn fault features better. Although MobileNetV3 is also a lightweight convolutional network with higher accuracy than 98%, it does not perform as well in terms of the number of parameters and accuracy compared with the proposed approach. The accuracy of the GASF+SE-IShufflenetV2 method reaches 100%, 99.4%, and 99.2% on datasets A, B, and C, respectively, indicating that the recognition method of SE-IShufflenetv2 on 2D data has good generalization. In addition, the accuracy of DWT+SE-IShufflenetV2 on three datasets is 100%, 99.5%, and 99.6% for datasets A, B, and C, respectively. Lastly, the overall effect is not as good as the method proposed in this paper, proving the effectiveness of MTF in time-domain signal processing.

Fig. 10 demonstrates the recognition accuracy of each model under variable load conditions, where A→B represents dataset A as the training dataset and dataset B as the validation dataset. Six groups of experiments were performed for each condition, and the final accuracy was represented by the average and variance of the six experiments. Fig. 10 shows that AVG is the average accuracy of six experiments under variable operating conditions. According to Fig. 10, the MTF+SE-ShufflenetV2 method that this paper proposed has the highest average accuracy among all fault diagnosis methods. Although the accuracy of conditions B→C and C→A is slightly decreased, it still reaches more than 98%. In contrast, the accuracy of other conditions is more than 99%, the variance of the overall accuracy is low, and the model is relatively stable. This observation demonstrates that MTF can retain the time correlation, enable the feature information of 1D data to be reflected in 2D feature images, and the model can fully utilize the feature extraction ability of 2D feature images.

Figure 10: Comparative experimental results under variable load conditions

According to Table 5 and Fig. 10, the DWT+SE-IShufflenetV2 can achieve a high accuracy under constant working situations. However, when the experiment is carried out under varying working conditions, the accuracy is far lower than the proposed approach, demonstrating the superiority of the MTF coding method in highlighting fault characteristics. Although MTF+MobileNetV3 is a lightweight network model, a big gap exists between its model size and the accuracy of the approach proposed in this paper. The diagnosis accuracy can only reach more than 98% on condition A→B. Although the diagnosis accuracy of the original MTF+ShufflenetV2 fault diagnosis approach can reach up to 98%, it remains insufficient compared with the proposed approach. This observation also demonstrates that the model’s ability to handle the relationships between feature channels has been enhanced after adding the SE module, allowing for better feature extraction.

The receptive field of the model improves after replacing the activation function with Hardswish and adding additional convolution kernels, greatly improving the expressibility of the model. The average accuracy of the GASF+SE-IShufflenetV2 reaches 98.42%, indicating that the SE-IShufflenetV2 model can extract the key feature information from different 2D feature images, verifying that the model can extract and learn deep-level abstract information improving the generalization of the model. The MTF+SE-ResNet50 can achieve high accuracy when the working load remains constant. However, diagnosis accuracy significantly declines when working conditions change, and diagnosis accuracy is less than 90% under condition B→C. This observation shows that the model cannot learn the deep-level feature information of the 2D feature image well, and its feature extraction ability is significantly worse than that of the proposed approach. The accuracy of SVM can still reach more than 90% when the load is constant. However, when the working condition changes, its diagnosis accuracy shows a very large decline, remains at a low accuracy, and loses the fault diagnosis ability, indicating relatively poor generalization. The experimental results show that the proposed fault diagnosis method possesses good generalization and high accuracy compared to the above approaches.

4.7 Performance Analysis of the Model under Different Noise Conditions

In actual working conditions, the machine is often accompanied by noise when running. Furthermore, the collected signal is mixed with noise, resulting in low accuracy of model fault identification. Therefore, obtaining high diagnosis accuracy in noisy environments is very important. First, Gaussian white noise with SNR of 10 dB was added to dataset A for training; the SNR calculation formula is shown in Eq. (6). Then, white Gaussian noise with SNR of 0–6 dB was added to datasets A, B, and C. Lastly, the fault diagnosis accuracy of different models was carried out under variable working load conditions.

SNRdB=10 log10(Psignal/Pnoise), (6)

where Psignal is the power of the original vibration signal, and Pnoise is the power of the added Gaussian white noise.

Table 6 shows the accuracy of each model under varying load conditions and different SNRs.

A→A indicates that after dataset A is segmented into a training set and verification set, dataset A mixed with Gaussian white noise with an SNR of 10 dB is used for training. Then, dataset A, mixed with Gaussian white noise with an SNR of 0–6 dB, is used for validation.

A→B and A→C indicate that dataset A mixed with Gaussian white noise with an SNR of 10 dB is the training set. Datasets B and C, mixed with Gaussian white noise with an SNR of 0–6 dB, are taken as the validation set. Each experiment was carried out six times, and the average accuracy and variance of the six experiments were taken as the experimental result.

According to Table 6, when SNR is 0 dB, MTF+SE-IShufflenetV2 can still achieve high accuracy in the three cases. Moreover, the overall variance value is low, demonstrating that the proposed approach is characterized by high stability. When SNR is 6 dB, the accuracy of MTF+SE-IShufflenetV2 under case A→A can reach 100%, showing that the proposed approach can still accurately extract the fault features in a noisy environment and has strong anti-noise ability. Although the accuracy of DWT+SE-IShufflenetV2 can reach more than 98% when SNR is 6 dB, the accuracy significantly decreases when SNR is 0 dB. Moreover, the overall variance fluctuates greatly, indicating that the model lacks stability.

The overall accuracy of MTF-MobileNetV3 is lower than that of the proposed method; the accuracy is higher than 98% only under cases A→A and A→B, while the overall variance fluctuates greatly. The overall accuracy of MTF+shufflenetV2 has reached over 95%. Moreover, minor changes can be observed in various situations, demonstrating that the 2D feature image transformed by MTF can better reflect the fault characteristics. Hence, the model is characterized by improved generalization.

GASF+SE-IShufflenetV2 performs well in all cases, indicating that SE-IShufflenetV2 strongly generalizes 2D data. However, the variance is too large, proving that the 2D feature image transformed by GASF does not fully represent the fault features. Hence, the model cannot learn deep abstract information, which is still far from the proposed approach. The accuracy of MTF+SE-ResNet50 does not reach 95% in most cases, and the fluctuation is relatively large. With decreased SNR, SVM cannot diagnose normal fault under variable loads. The proposed approach has better generalization and higher recognition accuracy than the above methods.

When SNR = 0 dB, MTF+SE ShufflenetV2 was trained on dataset A and validated on datasets A, B, and C; the obtained confusion matrices are shown in Fig. 11. The horizontal coordinate represents the actual labels of the different faults, the vertical coordinate demonstrates the predicted classes of the different faults, and the numbers on the primary diagonal of the matrix illustrate the number of samples correctly classified for each class of faults. It can be concluded that the model can still correctly classify rolling element faults under the condition of SNR = 0 dB.

Figure 11: Confusion matrices obtained when SNR = 0 dB, SE-IShufflenetV2 was trained on dataset A and validated on datasets A, B, and C

4.8 Variable Operating Conditions Experiment by Using a Bearing Dataset from Paderborn University

(1) Data source

The bearing dataset from Paderborn University was applied for further verification to prove the stability of the raised approach under varying working conditions. The bearing test bench at Paderborn University comprises a test motor, a torque measuring shaft, a rolling bearing test module, a flywheel, and a load motor. The experimental data were generated by installing ball bearings with different damage types in the bearing test module. The bearing is a rolling bearing (model 6203), while the model of the vibration sensor is 336c04. The detailed information on the dataset is shown in Table 7.

(2) Analysis of variable working conditions

Fig. 12 shows the experimental results of the variable operating condition on the bearing dataset from Paderborn University. Six repeated experiments were conducted under each operating condition. The average accuracy of the six experiments and its variance were taken as the experimental results. In Fig. 12, AVG is the average accuracy of six types of experiments with variable operating conditions.

Figure 12: Experimental results of variable operating conditions by using the bearing dataset from Paderborn University

According to Fig. 12, the AVG of the fault diagnosis method proposed in the paper on the bearing dataset from Paderborn University is higher than that of other fault diagnosis methods. The AVG of DWT+SE-IShufflenetV2 on the bearing dataset from Paderborn University is much lower than that of the bearing dataset from Case Western Reserve University, indicating that the feature expression ability of DWT is not as good as that of MTF. Furthermore, its performance on the insufficient purity dataset cannot meet the requirements. Consequently, DWT cannot mine the deep abstract information of one-dimensional time series data. The AVG of MTF+MobileNetV3 and MTF+ShufflenetV2 is only 71.68% and 78.19%, respectively, indicating that the depth of these two models is insufficient to extract fault information in 2D feature maps. In addition, a big gap can be observed compared with the approach proposed in this paper. The AVG of GASF+SE-IShufflenetV2 reaches 82.27%, which is superior to other methods. However, the AVG still falls short of the proposed approach, indicating that MTF coding is more able to highlight signal features than GAF coding; consequently, the model can fully learn fault features. The MTF+SE-ResNet50 and SVM fault diagnosis methods perform poorly on the bearing dataset from Paderborn University. According to the experimental results, the proposed method has higher accuracy, stability, and stronger generalization ability under varying working conditions than the methods mentioned above.

5  Conclusions

This paper proposed a fault diagnosis method based on MTF and SE-IShufflenetV2 to solve complex and variable rolling bearings loads in actual working conditions. The proposed approach also aimed to solve the difficulty of fault feature extraction, low fault diagnosis accuracy, and poor generalization due to noise on the data collected by bearings in actual work. The following conclusions can be made:

(1) The time and position information of the original one-dimensional signal can be retained by encoding the vibration signal through MTF, making it time-dependent. Once the MTF image was input into the neural network, the average accuracy of the model under variable conditions reached 99.2%.

(2) The information processing between channels was enhanced after adding the SE module, and the importance of each channel was obtained adaptively. The receptive field of the model has greatly progressed by advancing the model structure, and the feature mining ability of the model has been enhanced. The Hardswish activation function was applied instead of the ReLU activation function to solve the neuronal necrosis problem. The proposed method is characterized by higher accuracy under varying working situations than MTF+MobileNetV3, MTF+ShufflenetV2, GASF+SE-IShufflenetV2, DWT+SE-IShufflenetV2, MTF+SE-ResNet50, and SVM methods.

(3) The approach proposed in this paper can obtain high accuracy in variable operating conditions under different noise environments; the average accuracy is 98.7% under SNR = 0 dB. The proposed method has better fault identification performance and stability than other approaches.

Acknowledgement: None.

Funding Statement: This work was supported by Hebei Natural Science Foundation under Grant No. E2024402079 and Key Laboratory of Intelligent Industrial Equipment Technology of Hebei Province (Hebei University of Engineering) under Grant No. 202206.

Author Contributions: Tiexin Xu: Methodology, Software, Validation and Writing—original draft. Chaozhi Cai: Writing review and editing, Methodology, Funding acquisition. Jianhua Ren: Data collection, Formal analysis, Writing review and editing. Yingfang Xue: Software, Validation, Writing—original draft.

Availability of Data and Materials: Case Western Reserve University bearing data set. Available from: Bearing Data Center | Case School of Engineering | Case Western Reserve University. Paderborn University bearing data set. Available from: Index of /kat/BearingDataCenter (uni-paderborn.de).

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. Huang NE, Shen Z, Long SR, Wu MC, Shih HH, Zheng Q, et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc R Soc Lond Ser A Math Phys Eng Sci. 1998;454(1971):903–95. doi:10.1098/rspa.1998.0193. [Google Scholar] [CrossRef]

2. Cao J, Li Z, Li J. Financial time series forecasting model based on CEEMDAN and LSTM. Phys A Stat Mech Appl. 2021;519:127–39. doi:10.1016/j.physa.2018.11.061. [Google Scholar] [CrossRef]

3. Zhong X, Huang T, Mei Q, Gao X, Zhao X. A gearbox fault diagnosis method based on MKurt spectrum and CYCBD. Insight Non Destructive Test Condition Monit. 2021;63(8):472–8. doi:10.1784/insi.2021.63.8.472. [Google Scholar] [CrossRef]

4. Chang SG, Yu B, Vetterli M. Adaptive wavelet thresholding for image denoising and compression. IEEE Trans Image Process. 2000;9(9):1532–46. doi:10.1109/83.862633. [Google Scholar] [PubMed] [CrossRef]

5. Li H, Liu T, Wu X, Chen Q. A bearing fault diagnosis method based on enhanced singular value decomposition. IEEE Trans Ind Inform. 2020;17(5):3220–30. doi:10.1109/TII.2020.3001376. [Google Scholar] [CrossRef]

6. Tang G, Wang Y, Huang Y, Wang H. Multiple time-frequency curve classification for tacho-less and resampling-less compound bearing fault detection under time-varying speed conditions. IEEE Sens J. 2020;21(4):5091–101. doi:10.1109/JSEN.2020.3035623. [Google Scholar] [CrossRef]

7. Yu Y, Junsheng C. A roller bearing fault diagnosis method based on EMD energy entropy and ANN. J Sound Vib. 2006;294(1–2):269–77. doi:10.1016/j.jsv.2005.11.002. [Google Scholar] [CrossRef]

8. Li H, Liu T, Wu X, Chen Q. An optimized VMD method and its applications in bearing fault diagnosis. Measurement. 2020;166:108185. doi:10.1016/j.measurement.2020.108185. [Google Scholar] [CrossRef]

9. Zhang L, Xiong G, Liu H, Zou H, Guo W. Bearing fault diagnosis using multi-scale entropy and adaptive neuro-fuzzy inference. Expert Syst Appl. 2010;37(8):6077–85. doi:10.1016/j.eswa.2010.02.118. [Google Scholar] [CrossRef]

10. Zhang W, Li C, Peng G, Chen Y, Zhang Z. A deep convolutional neural network with new training methods for bearing fault diagnosis under noisy environment and different working load. Mech Syst Signal Process. 2018;100:439–53. doi:10.1016/j.ymssp.2017.06.022. [Google Scholar] [CrossRef]

11. Song X, Cong Y, Song Y, Chen Y, Liang P. A bearing fault diagnosis model based on CNN with wide convolution kernels. J Ambient Intell Humaniz Comput. 2022;13(8):4041–56. doi:10.1007/s12652-021-03177-x. [Google Scholar] [CrossRef]

12. Qiao M, Yan S, Tang X, Xu C. Deep convolutional and LSTM recurrent neural networks for rolling bearing fault diagnosis under strong noises and variable loads. IEEE Access. 2020;8:66257–69. doi:10.1109/ACCESS.2020.2985617. [Google Scholar] [CrossRef]

13. Wang D, Guo Q, Song Y, Gao S, Li Y. Application of multiscale learning neural network based on CNN in bearing fault diagnosis. J Signal Process Syst. 2019;91:1205–17. doi:10.1007/s11265-019-01461-w. [Google Scholar] [CrossRef]

14. Yu Y, Si X, Hu C, Zhang J. A review of recurrent neural networks: LSTM cells and network architectures. Neural Comput. 2019;31(7):1235–70. doi:10.1162/neco_a_01199. [Google Scholar] [PubMed] [CrossRef]

15. Saghi T, Bustan D, Aphale SS. Bearing fault diagnosis based on multi-scale CNN and bidirectional GRU. Vibration. 2022;6(1):11–28. doi:10.3390/vibration6010002. [Google Scholar] [CrossRef]

16. Kuncan M, Kaplan K, Minaz MR, Kaya Y, Ertunç HM. A novel feature extraction method for bearing fault classification with one dimensional ternary patterns. ISA Trans. 2020;100:346–57. doi:10.1016/j.isatra.2019.11.006. [Google Scholar] [PubMed] [CrossRef]

17. Cai C, Li R, Ma Q, Gao H. Bearing fault diagnosis method based on the Gramian angular field and an SE-ResNeXt50 transfer learning model. Insight Non Destructive Test Condition Monit. 2023;65(12):695–704. doi:10.1784/insi.2023.65.12.695. [Google Scholar] [CrossRef]

18. Lei C, Miao C, Wan H, Zhou J, Hao D, Feng R. Rolling bearing fault diagnosis method based on MTF-MFACNN. Meas Sci Technol. 2023;35(3):035007. doi:10.1088/1361-6501/ad11c7. [Google Scholar] [CrossRef]

19. Targ S, Almeida D, Lyman K. ResNet in ResNet: generalizing residual architectures; 2016. Available from: https://arxiv.org/abs/1603.08029. [Accessed 2023]. [Google Scholar]

20. Huang G, Liu Z, Maaten VDL, Weinberger KQ. Densely connected convolutional network. In: Proceedings of the IEEE 2017 Conference on Computer Vision and Pattern Recognition (CVPR); 2017 Jul 21–26; Honolulu, Hawaii, USA; Computer Vision Foundation; 2017. p. 4700–8. [Google Scholar]

21. Howard AG, Zhu M, Chen B, Kalenichenko D, Wang W, Weyand T, et al. Mobilenets: efficient convolutional neural networks for mobile vision applications; 2017. Available from: https://arxiv.org/abs/1704.04861. [Accessed 2023]. [Google Scholar]

22. Simonyan K, Zisserman A. Very deep convolutional networks for large-scale image recognition; 2014. Available from: https://arxiv.org/abs/1409.1556. [Accessed 2023]. [Google Scholar]

23. Ma N, Zhang X, Zheng HT, Sun J. Shufflenetv2: practical guidelines for efficient CNN architecture design. In: Proceedings of the European Conference on Computer Vision (ECCV); 2018 Sep 8–14; Munich, Germany; Computer Vision Foundation. p. 116–31. [Google Scholar]

24. He K, Xu Y, Wang Y, Wang J, Xie T. Intelligent diagnosis of rolling bearings fault based on multisignal fusion and MTF-ResNet. Sensors. 2023;23(14):6281. doi:10.3390/s23146281. [Google Scholar] [PubMed] [CrossRef]

25. Hu J, Shen L, Sun G. Squeeze-and-excitation networks. In: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR); 2018 Jun 18–22; Salt Lake City, Utah, USA; Computer Vision Foundation. p. 7132–41. [Google Scholar]

26. Du Y, Cheng X, Liu Y, Dou S, Tu J, Liu Y, et al. Gearbox fault diagnosis method based on improved MobileNetV3 and transfer learning. Tehnički Vjesnik. 2023;30(1). doi:10.17559/TV-20221025165425. [Google Scholar] [CrossRef]