 Open Access
Open Access
ARTICLE
Experimental Study on the Axial Compression Performance of Bamboo Scrimber Columns Embedded with Steel Reinforcing Bars
1 College of Civil Engineering and Transportation, Northeast Forestry University, Harbin, 150000, China
2 Department of Building Engineering, College of Civil Engineering, Tongji University, Shanghai, 200092, China
3 College of Transportation and Civil Engineering, Fujian Agriculture and Forestry University, Fuzhou, 350002, China
* Corresponding Author: Guodong Li. Email:
# Xueyan Lin and Mingtao Wu made the same contributions to this paper, they are co-first authors
Structural Durability & Health Monitoring 2024, 18(6), 805-833. https://doi.org/10.32604/sdhm.2024.051033
Received 26 February 2024; Accepted 13 May 2024; Issue published 20 September 2024
Abstract
In this paper, a new type of bamboo scrimber column embedded with steel bars (rebars) was proposed, and the compression performance was improved by pre-embedding rebars during the preparation of the columns. The effects of the slenderness ratio and the reinforcement ratio on the axial compression performance of reinforced bamboo scrimber columns were studied by axial compression tests on 28 specimens. The results showed that the increase in the slenderness ratio had a significant negative effect on the axial compression performance of the columns. When the slenderness ratio increased from 19.63 to 51.96, the failure mode changed from strength failure to buckling failure, and the maximum bearing capacity decreased by 43.03%. The axial compression performance of the reinforced bamboo scrimber columns did not significantly improve at a slenderness ratio of 19.63, but the opposite was true at slenderness ratios of 36.95 and 51.96. When the reinforcement ratio increased from 0% to 4.52%, the bearing capacity of those with a slenderness ratio of 51.96 increased by up to 16.99%, and the stiffness and ductility were also improved. Finally, based on existing specifications, two modification parameters, the overall elastic modulus Ec and the combined strength fcc, were introduced to establish a calculation method for the bearing capacity of the reinforced bamboo scrimber columns. The calculation results were compared with the test results, and the results showed that the proposed calculation models can more accurately predict the bearing capacity.Keywords
Nomenclature
| Ab | Effective area of bamboo scrimber column |
| As | Cross-section area of steel rebar |
| ac | One of the material correlation coefficients in GB 50005-2017 |
| bc | One of the material correlation coefficients in GB 50005-2017 |
| cc | One of the material correlation coefficients in GB 50005-2017 |
| c | Nonlinear constant |
| COVE | Variation coefficient of elastic modulus |
| Eb | Parallel-to-grain compression elastic modulus of bamboo scrimber |
| Ebt | Parallel-to-grain compression tangent modulus of bamboo scrimber |
| Ec | Whole elastic modulus of bamboo scrimber column |
| Ect | Whole Tangent modulus of bamboo scrimber column |
| Ecr | Whole Double modulus of bamboo scrimber column |
| Ec,0.05 | Fifth percentile value of the modulus of elasticity parallel to the grain |
| Emin | Reference and adjusted modulus of elasticity for beam stability and column stability calculations |
| Es | Tension elastic modulus of steel bar |
| Est | Tension tangent elastic modulus of steel bar |
| fc | Yield compressive strength parallel to grain of bamboo scrimber |
| fcc | Combined strength of bamboo scrimber column |
| fy | Yield strength of steel rebar |
| L | Effective length of bamboo scrimber column |
| Ncr | Critical buckling load |
| Nu | Ultimate axial compressive bearing capacity of bamboo scrimber column |
| Β | Correlation coefficient of material shear deformation |
| βc | A factor for members within the straightness limits |
| φ | Axial compression stability coefficient in GB 50005-2017 |
| Cp | Axial compression stability coefficient in ANSI/AWC NDS-2018 |
| kc | Axial compression stability coefficient in Eurocode 5 |
| λ | Slenderness ratio |
| λy | Critical slenderness ratio |
In the era of advocating a low-carbon economy, it is increasingly difficult for traditional building materials to meet the needs of people for sustainable development due to the large consumption of energy and excessive carbon emissions. As one of the earliest building materials, bamboo has gradually attracted the attention of people because of its abundant resource, green nature, and strong ability of carbon sequestration [1–4]. However, natural bamboo has an irregular shape, unstable mechanical properties, and poor durability and cannot be widely used in modern building structures [5,6]. Therefore, a series of engineered bamboo materials with good mechanical properties have been developed by natural bamboo [7,8].
Bamboo scrimber is a new type of high-strength engineered bamboo material made from a series of processing techniques [9]. During the production process, due to the compression on the bamboo fibres and the bonding of the adhesive, the internal microstructure of the bamboo becomes denser, which results in a significant improvement in the mechanical and physical properties, with the compressive strength parallel to grain being approximately 1.68, 3.07 and 2.38 times of that of glued-laminated (glulam) bamboo, spruce-pine-fir (SPF) glulam timber and China-fir, respectively [10–13].
To explore the possibility of applying bamboo scrimber to structural columns, Li et al. [14–17] studied the axial compression properties of bamboo scrimber under different fibre orientations. When the direction of the force was rotated from parallel to grain to perpendicular to grain, the failure mode changed from wrinkle failure to shear failure and then to punching failure. Subsequently, the constitutive relationship was established, simplified, and optimized, the relationships among various mechanical parameters were obtained, and the compressive strength parallel to grain is significantly higher than that in other directions, which makes it possible for bamboo scrimber to be used in structural columns. Studies have shown that the height of specimens can affect the mechanical properties of bamboo scrimber, but Li et al. [18] believed that the energy absorption capacity of the bamboo scrimber under impact load has nothing to do with the height of specimens, and the energy absorption capacity and deformation capacity of the higher specimens are independent of fibre orientation. In addition, the temperature is also an important factor affecting the mechanical properties of bamboo scrimber [19,20]. With increasing temperature, the compressive modulus and strength parallel and perpendicular to the grain decrease [19]. Therefore, Xu et al. [20] obtained the reduction coefficient of the elastic modulus and the strength concerning temperature through regression analysis, compared it with the model in the Eurocode 5, and believed that the prediction model has good accuracy and safety and can be applied in the structural design.
As the excellent mechanical properties and above benefits, bamboo scrimber is applied to structural members such as columns, and has great potential, but more attention must be paid to the prediction of bearing capacity. Most predictions are based on elastic buckling theory, i.e., the Euler formula. However, for the columns whose buckling occurs after the proportional limit, Euler’s formula no longer applies [21]. To ensure the applicable scope of elastic buckling theory, Tan et al. [22] introduced the critical slenderness ratio λy and considered that the Euler formula is more suitable for predicting the bearing capacity of columns with slenderness ratios greater than λy; for those with slenderness ratios less than λy, the inelastic Newlin-Gahagan approach can give more reasonable predictions. In addition, building codes for wood design & construction also provide calculation methods for the bearing capacity of wooden columns, but since the mechanical properties between bamboo and wood are different and bamboo is a non-uniform and anisotropic material, it is necessary to modify the calculation methods provided by the codes [23–25]. Therefore, Zhang et al. [23–25] revised the calculation formulas for the bearing capacity of wooden columns provided by Code for the Design of Timber Structures (GB 50005-2003) and National Design Specification for Wood Construction (ANSI/AWC NDS-2018), and the predicted results are closer to the real values.
In addition, due to the natural defects of bamboo and technological limitations, the elastic modulus of bamboo scrimber is low, the deformation is large during loading, and finally, brittle failures such as end splitting and fiber tearing occurs, which means that the compressive strength parallel-to-grain of bamboo scrimber cannot be fully used. Therefore, to improve the safety of bamboo structural columns, some researchers have studied various types of reinforced columns. Li et al. [26] found that the external lamination of white iron or fibre cloth can better share the lateral force generated by the axial compression on the columns, the strength and the stiffness of bamboo columns increased significantly as the spacing was reduced, and the axial compression strength of bamboo columns reinforced with glass fibre was increased by 11.9% (the highest). Wang et al. [25] found that aramid fibre-reinforced polymer (AFRP) can improve the axial compressive strength and stiffness of bamboo columns. Yang et al. [27] strengthened a rectangular wooden column by the glass fibre reinforced polymer (GFRP) lattice webs and face sheets, explained the influence of the constraint action of FRP and the change in the stiffness of core materials on the compression performance of columns, and proposed a model for calculating the enhanced load bearing capacity based on the Tsai-Wu strength criterion. Most studies on the reinforced columns considered the use of external reinforcement by attachment. Compared with external reinforcement by attachment, built-in reinforcement has the advantages of high integrity and a relatively high material utilization rate, and buildings are more aesthetically pleasing. However, there have been relatively few studies on the built-in enhancement of bamboo scrimber columns.
This paper proposed one type of novel reinforced bamboo scrimber column embedded with steel reinforcing bars (steel rebars). The axial compression performance of reinforced bamboo scrimber columns was comprehensively evaluated by comparing and analyzing the failure mode, the ultimate bearing capacity, the axial deformation, the strain, and the lateral deflection of 28 specimens with different slenderness ratios and reinforcement ratios. Finally, based on the classical models, a calculation formula for the bearing capacity of bamboo scrimber columns embedded with steel rebars was proposed and compared with the classical models and the related specifications, to determine the applicability of proposed calculation methods under different slenderness ratios and reinforcement ratios.
The bamboo scrimber in this test was made from the middle-lower part of Moso bamboo that had grown for 3–4 years. According to Standard for Test Methods of Timber Structures (GB/T 50329-2012), Standard Test Methods for Small Clear Specimens of Timber (ASTM D143-2014), and Metallic Materials-Tensile Testing-Part 1: Method of Test at Room Temperature (GBT228.1-2010), the mechanical properties of bamboo scrimber and steel rebars in this test were determined. The specific values are shown in Table 1. According to the tests, the average density of bamboo scrimber was 1211.8 kg/m3, and the moisture content was 12.3%. The tension and compression parallel to grain stress-strain relationship curves of bamboo scrimber are shown in Figs. 1 and 2. In the figures, the black line represents the test curve, and the red line represents the average curve.
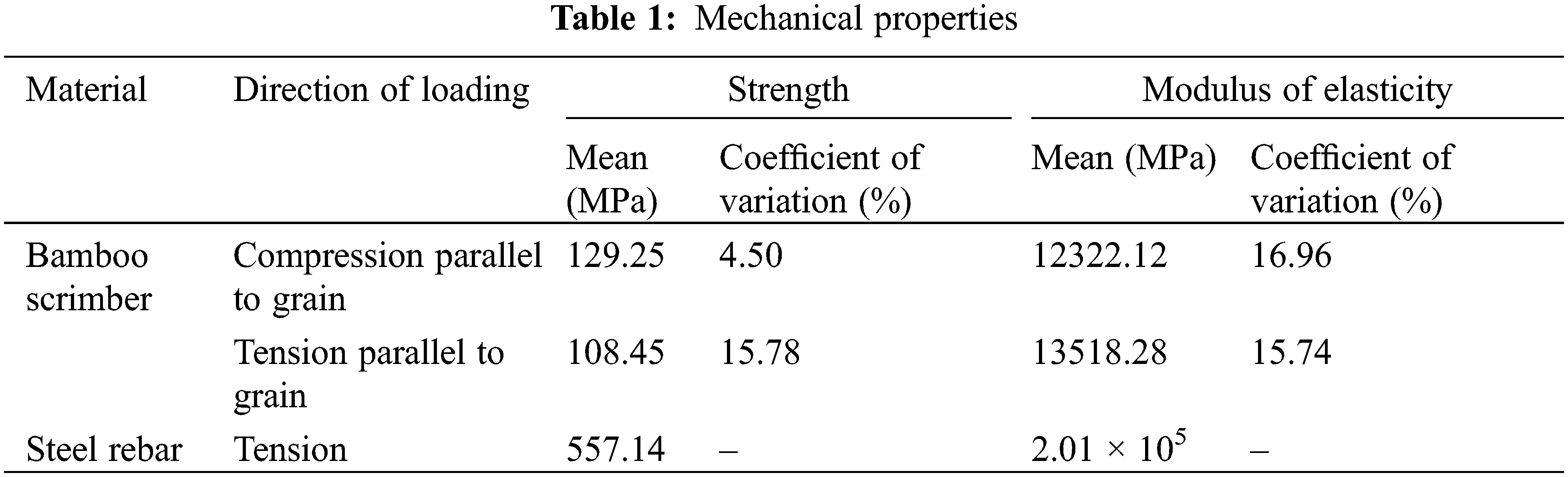
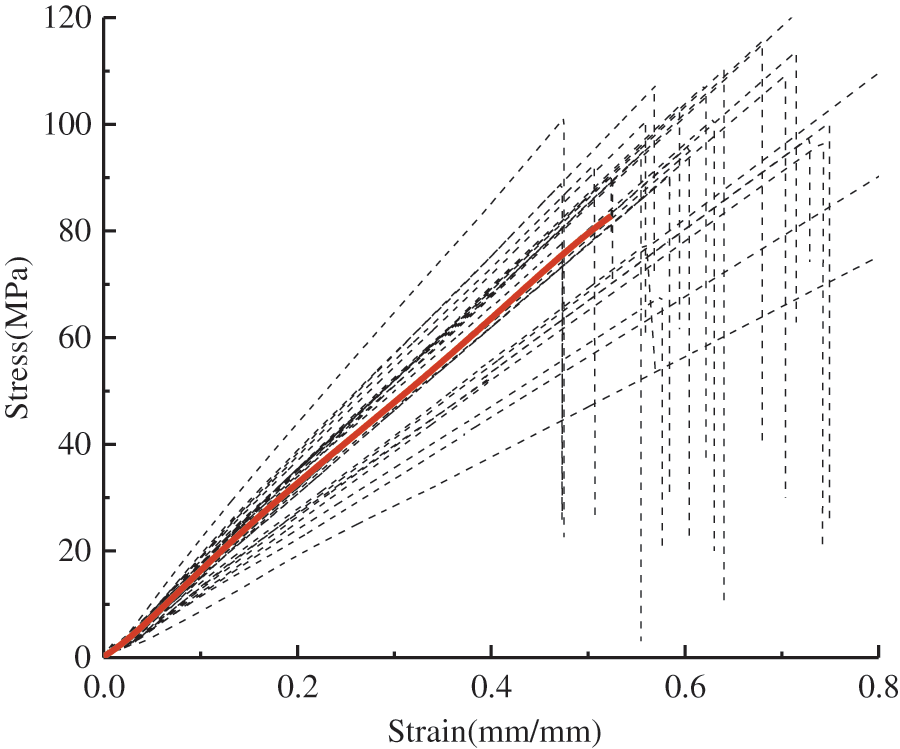
Figure 1: The tension parallel to grain stress-strain relationship curves of bamboo scrimber
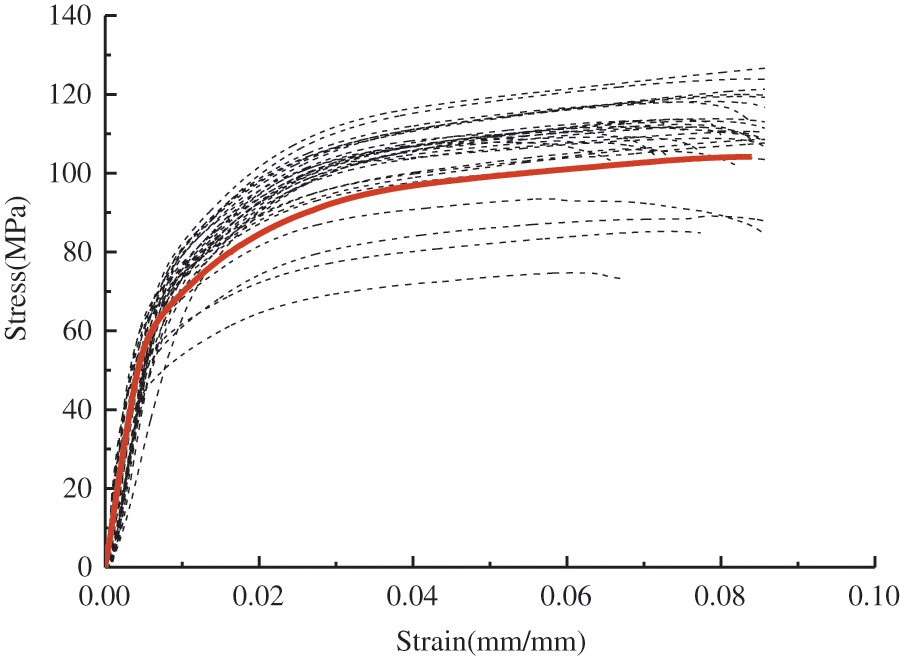
Figure 2: The compression parallel to grain stress-strain relationship curves of bamboo scrimber
2.1.2 Specimen Preparation Process
The reinforced bamboo scrimber column in this test was formed by integral hot-pressing. The natural bamboo from the middle-lower part was planed into slices and rolled into fibrous forms. After a series of processes including carbonization, drying, dipping, secondary drying, curing, hot pressing, cutting, and gluing, a reinforced bamboo scrimber column was formed. The specific steps are shown in Fig. 3.

Figure 3: Preparation process
To investigate the effect of slenderness ratios and reinforcement ratios on the axial compressive performance of reinforced bamboo scrimber columns, 28 specimens were divided into 10 working groups. Table 2 and Fig. 4 show the specifics of these specimens. The name rule is the following, the first character stands for the member type, the first number means the height of the specimen, the second number is reinforcement diameter, and the last one is the number of specimens in the group.
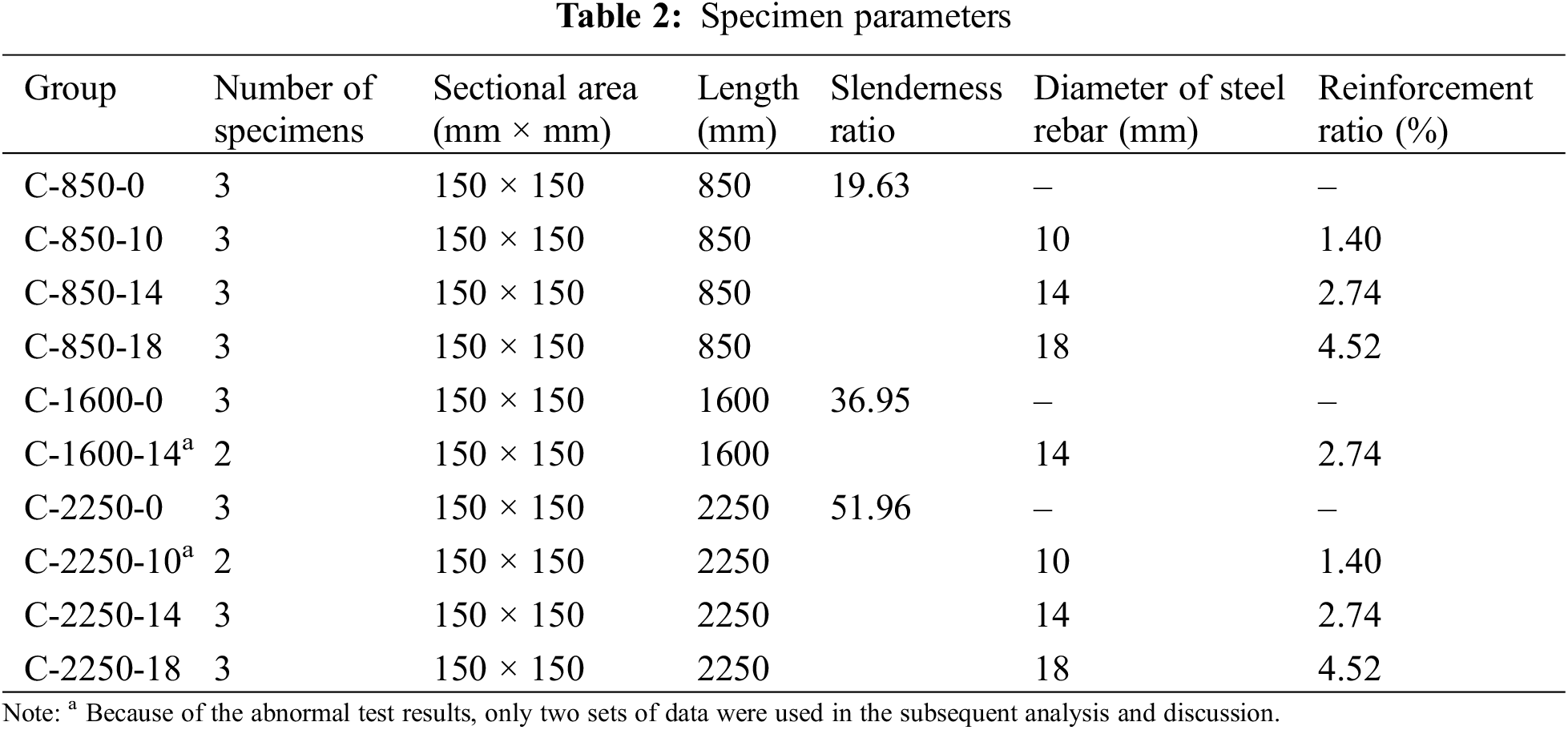
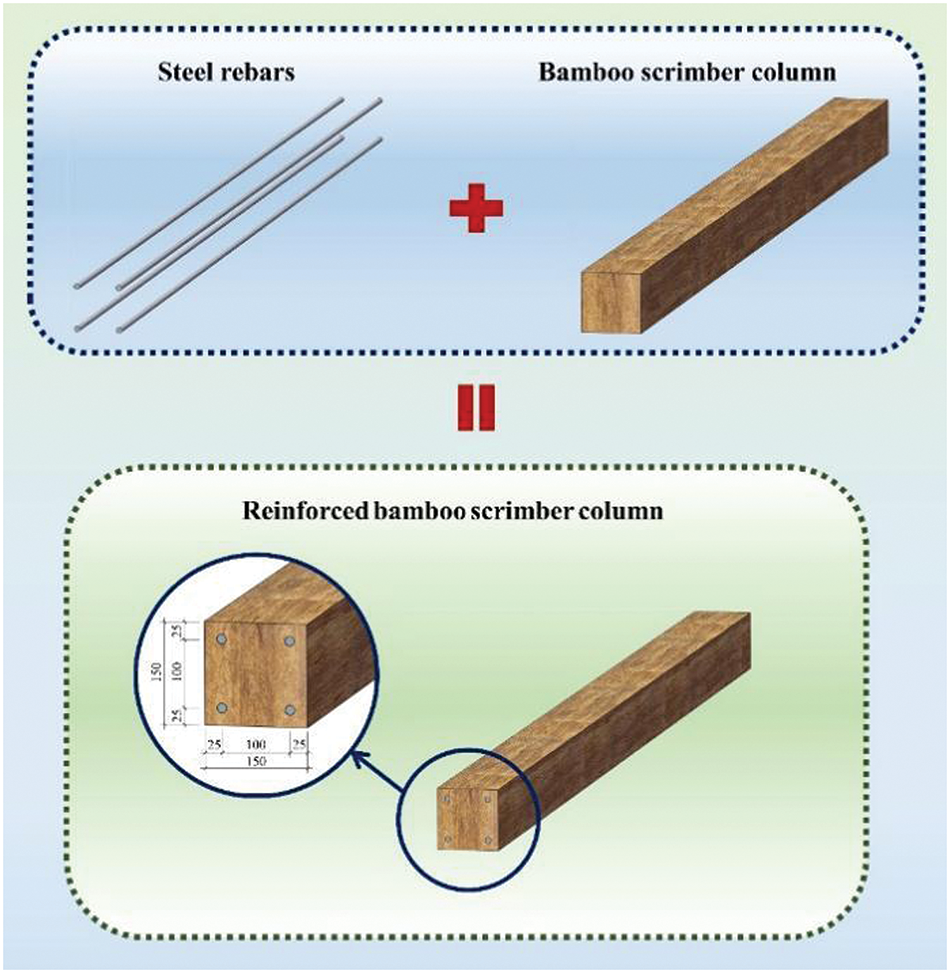
Figure 4: Specimen diagram
3000t Electro-Hydraulic Servo Press was used in this test, as shown in Fig. 5. The arrangement of instruments is shown in Fig. 6. The distance between LDVTs is 120, 225 and 320 mm respectively with increasing slenderness ratios of columns, and at the slenderness ratio of 51.96, there were 7 LDVTs used during the test which are not shown in Fig. 6. The loading process was contained two stages, the former stage was preload process including 5 cyclic loading to ensure the workability of measurements and keep the right loading position, and the last one was to measure the bearing capacities of columns, whose ratio was 0.5 mm/s.

Figure 5: 3000t Electro-Hydraulic Servo Press
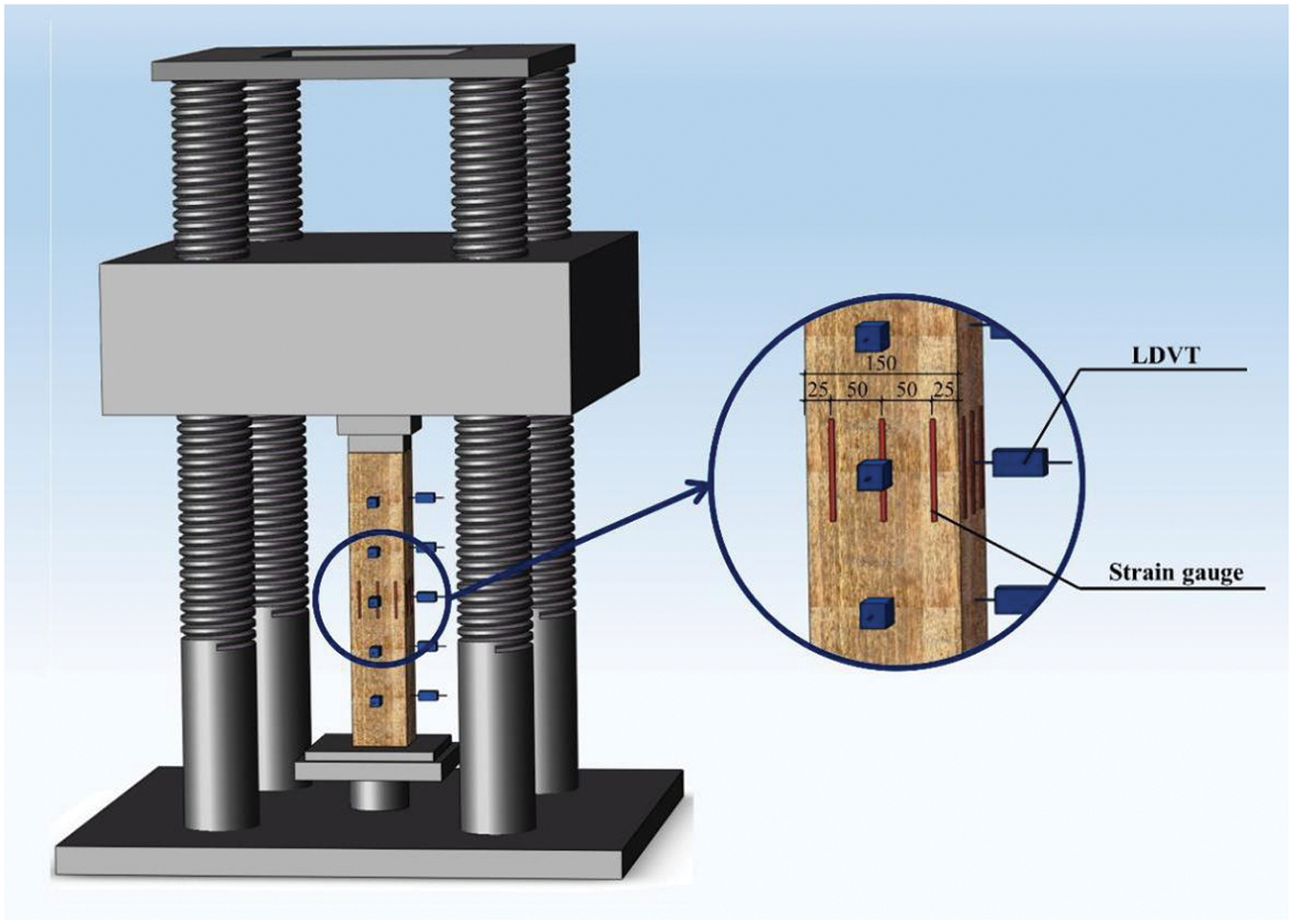
Figure 6: Diagram of the arrangement of instruments
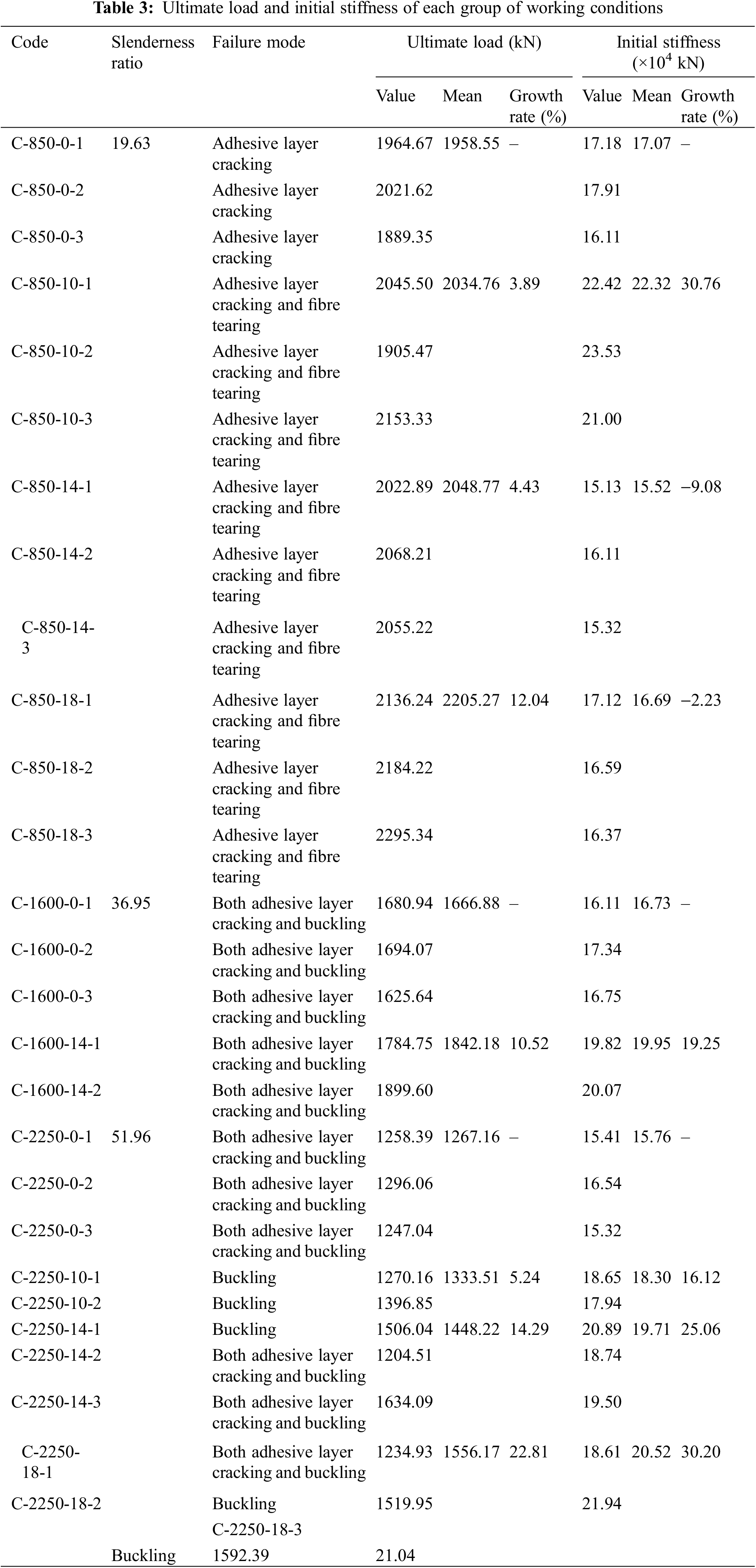
Based on the experiment phenomena, the main failure phenomena can be divided into three categories: cracking failure of adhesive layers, fibre tearing failure, and buckling failure, and these three failure phenomena appeared either alone or in combination. It should be noted that, affected by the processing technology, a 150 mm thick specimen was formed by secondary gluing of three 50 mm thick bamboo scrimber boards. Compared with bamboo scrimber, the secondary gluing strength is relatively low, so the cracking failure of adhesive layers during the loading process occurred.
3.1.1 Nonreinforced Bamboo Scrimber Column
For the nonreinforced bamboo scrimber columns, the failure modes mainly included cracking failure of adhesive layers and buckling failure, and the specific phenomena are shown in Fig. 7a,b. The cracking failure of the adhesive layer belongs to strength failure, which mainly occurred at a slenderness ratio of 19.63. Taking specimen C-850-0-1 as an example. There were no significant experimental phenomena in the early stage of loading. When the load reached 80% of the ultimate load, cracks at the secondary bonding area at the top of the column began to form and quickly extended horizontally and longitudinally until the specimen was completely separated and damaged. It is worth noting that there was no apparent deformation or tearing of specimens during the failure process.

Figure 7: Failure modes of nonreinforced bamboo scrimber columns
The bamboo scrimber columns mainly suffered buckling failure and had similar test phenomena during the loading process at slenderness ratios of 36.95 and 51.96, as shown in Fig. 7c. Taking specimen C-1600-0-1 as an example. In the early stage of the loading, there were no significant experimental phenomena. As the load increased, the specimen experienced apparent lateral deflection, and the lateral deformation rate of the column accelerated. When approaching the ultimate load, cracks developed at the bonding area at the top of the column and quickly extended until the column was broken. According to the experimental phenomena, the top of the column showed partial cracking of adhesive layers, and the cracks between adhesive layers occurred on the surface but did not run through the specimen. The whole column showed a “C” shape. The bamboo scrimber columns with a slenderness ratio of 51.96 showed more apparent lateral deformation during the failure process than those with a slenderness ratio of 36.96.
3.1.2 Reinforced Bamboo Scrimber Column
For the reinforced bamboo scrimber columns with a slenderness ratio of 19.63, compression strength parallel to grain was still the main cause of failure, and the specific phenomena were cracking of adhesive layers and tearing of fibres, as shown in Fig. 8a. Compared with the nonreinforced group, the main reason for the new fibre tearing phenomenon in the reinforced group is that the steel rebars tend to be unstable and deformed during the loading process, and under this case, the interaction between the reinforcement and the bamboo scrimber generates inter-fibre tensile stresses, since the bond stress between the rebar surface and the bamboo scrimber is relatively low. When the above-mentioned tensile stresses exceed the maximum bond stress, the bamboo scrimber surface tears. The final failure phenomena showed that tear cracks extended along the direction of rebars and ran through the column, while the cracks between adhesive layers did not penetrate the whole specimen. With increasing reinforcement ratio, the fibre tears were more apparent.

Figure 8: Failure modes of reinforcement bamboo scrimber columns
For the reinforced bamboo scrimber columns with slenderness ratios of 36.95 and 51.96, the steel rebars effectively reduced the lateral deformation and delayed the cracking of adhesive layers. Some specimens with a slenderness ratio of 51.96 did not even have the cracking of adhesive layers. The final phenomena were slight local cracking of adhesive layers at the top of the column and the “C” shape of the column body. When C-2250-18-1 was damaged, the cracks between adhesive layers instantly developed to the middle of the specimen, which is due to the insufficient bond strength between bamboo scrimber boards. The specific phenomena are shown in Fig. 8b–d. The failure modes and ultimate loads of all specimens are shown in Table 3.
The distribution of failure modes is shown in Fig. 9 and “λ” represents the slenderness ratio. From the results, it is clear that adhesive layer cracking is the main reason resulting in the damage of nonreinforced columns. Compared with the columns with a slenderness ratio of 19.63, those with slenderness ratios of 36.95 and 51.96 had additional buckling, and buckling was the decisive failure phenomenon for these two groups.
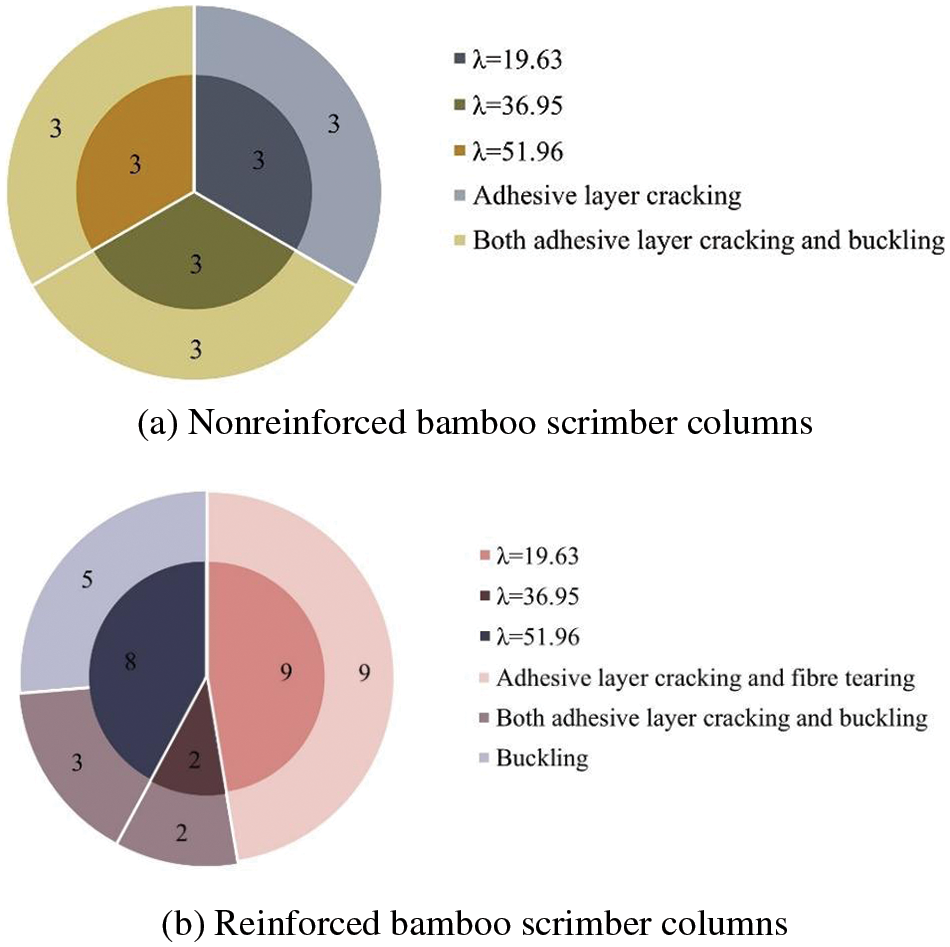
Figure 9: Failure mode proportion
For the reinforced bamboo scrimber columns with a slenderness ratio of 19.63, a new fibre tearing phenomenon occurred. In a slenderness ratio of 51.96, only part of the specimens had cracks between adhesive layers, and according to Table 3, they were always in a reinforcement ratio of 2.74%. This is because the steel-bamboo bonding effect can effectively inhibit the cracking of adhesive layers, but with the increase in the diameter of steel rebars, the bonding area between the steel rebars and the bamboo scrimber increases, which weakens the integrity of columns. When the reinforcement ratio increased to 4.52%, the stiffness of the columns was greatly improved, and only the buckling failure occurred. It indicated that the reinforcing effect of steel rebars was greater than the weakening effect at that time.
3.2.1 Influence of the Reinforcement Ratio on the Bearing Capacity
The ultimate loads, the initial stiffnesses, and the average values of each group are shown in Table 3 and Fig. 10. The results show that the reinforcement has a limited effect on the ultimate bearing capacity of columns with a slenderness ratio of 19.63 since the fibres tear along the steel rebars before making full use of the strength of bamboo scrimber. However, the reinforcement can improve bearing capacity effectively for those with slenderness ratios of 36.95 and 51.96 by limiting premature buckling. When the slenderness ratio was 51.96 and the reinforcement ratio was 2.74%, increasing the reinforcement ratio had no significant effect on bearing capacity, which is caused by material discreteness.
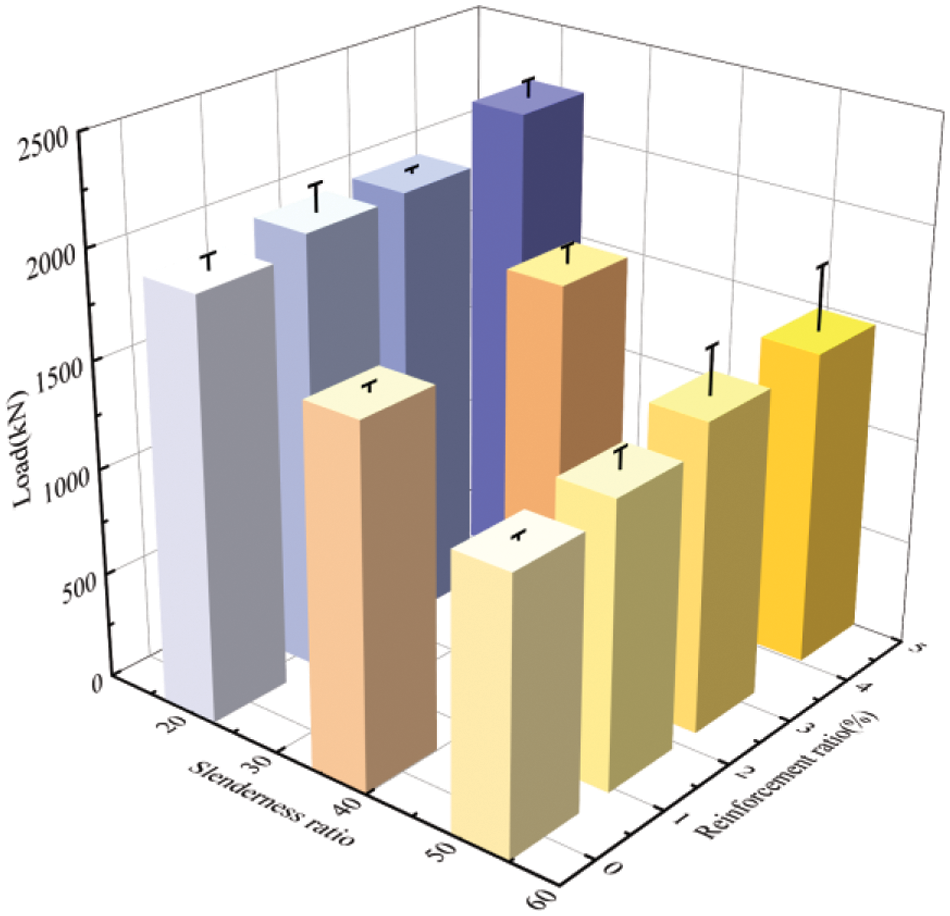
Figure 10: Average ultimate load of each group
3.2.2 Influence of the Slenderness Ratio on the Bearing Capacity
After comparison, it is clear that the bearing capacity of columns decreases as the slenderness ratio increases under the same reinforcement ratio. The difference in the bearing capacity of these three groups gradually decreases as the reinforcement ratio increases, but the overall trend has no change. It indicates that the slenderness ratio is still the determinant factor influencing the axial compressive bearing capacity of bamboo scrimber columns, while the steel rebars only delay failure.
3.3 Load-Axial Displacement Relationship Curve
3.3.1 Influence of the Reinforcement Ratio on the Axial Displacement
Due to the similarity of data, only one sample for each condition is analyzed. The effect of the reinforcement ratio on the axial deformation is shown in Fig. 11. The curve is divided into elastic stage, elastic-plastic stage, and failure stage. The slope of the elastic stage does not increase significantly as the reinforcement ratio increases when the slenderness ratio is 19.63, which indicates that the steel rebars have a limited effect on the axial stiffness of columns under this working group. Combined with Table 3, it can be seen that the stiffness shows a trend of not increasing but decreasing with the increase of the reinforcement ratio. There are two reasons: on the one hand, because the columns in this working group did not buckle under axial compression conditions, the elastic modulus has been fully used, and the increase of the initial stiffness is not obvious by adding steel bars; on the other hand, due to the limitation of processing technology, the distribution of bamboo fibers around the rebar is uneven, and with the increase of the diameter of the rebar, the negative influence on the axial compression performance of the specimen increases, and it is easier to cause fiber tears along the direction of the reinforcement bar in advance during the loading process.
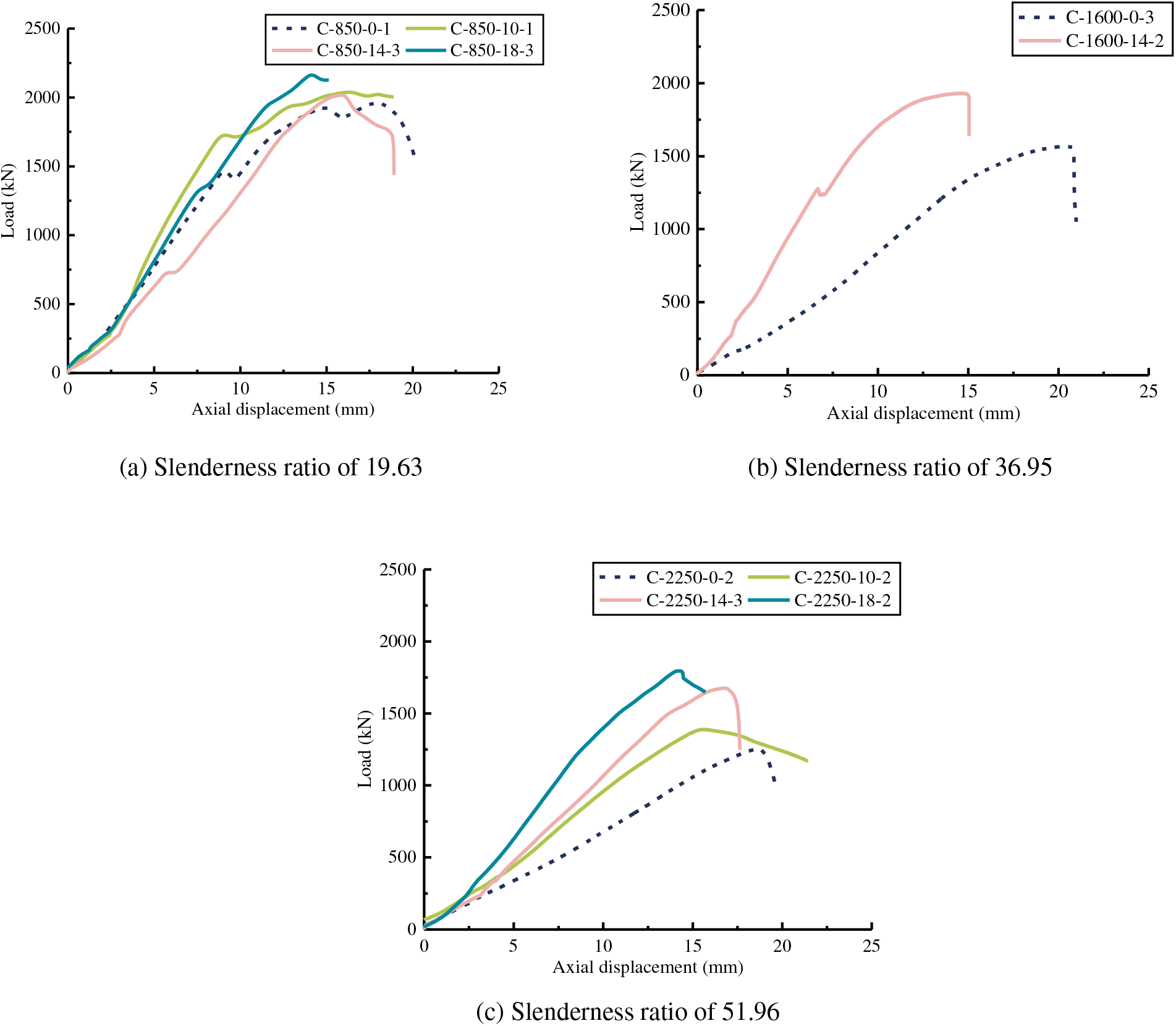
Figure 11: Load-axial displacement relationship curves under the same slenderness ratio
The slope of elastic stage in those groups with slenderness ratios of 36.95 and 51.96 increases significantly with the reinforcement ratio. Combined with Table 3, it is clear that the steel rebars can constrain the buckling during the axial compression process by exerting its tensile strength.
3.3.2 Influence of the Slenderness Ratio on the Axial Displacement
The effect of the slenderness ratio on axial displacement is shown in Fig. 12. As the slenderness ratio increases, the elastic-plastic stage becomes less apparent, which is caused by the increase in the flexibility of specimens. For the nonreinforced group, the slope of curves gradually decreases as the slenderness ratio increases, which means the rate of axial displacement development accelerates. Combined with Table 3, it is clear that when the slenderness ratio increases, the initial stiffness decreases, which is caused by the change of the failure mode. For the reinforced group, the slope difference between the three curves decreases, and the slope of curves increases significantly under the slenderness ratios of 36.95 and 51.96, which means that the rebars can constrain the lateral buckling effectively, and improve the efficiency of elasticity modulus of bamboo scrimber.
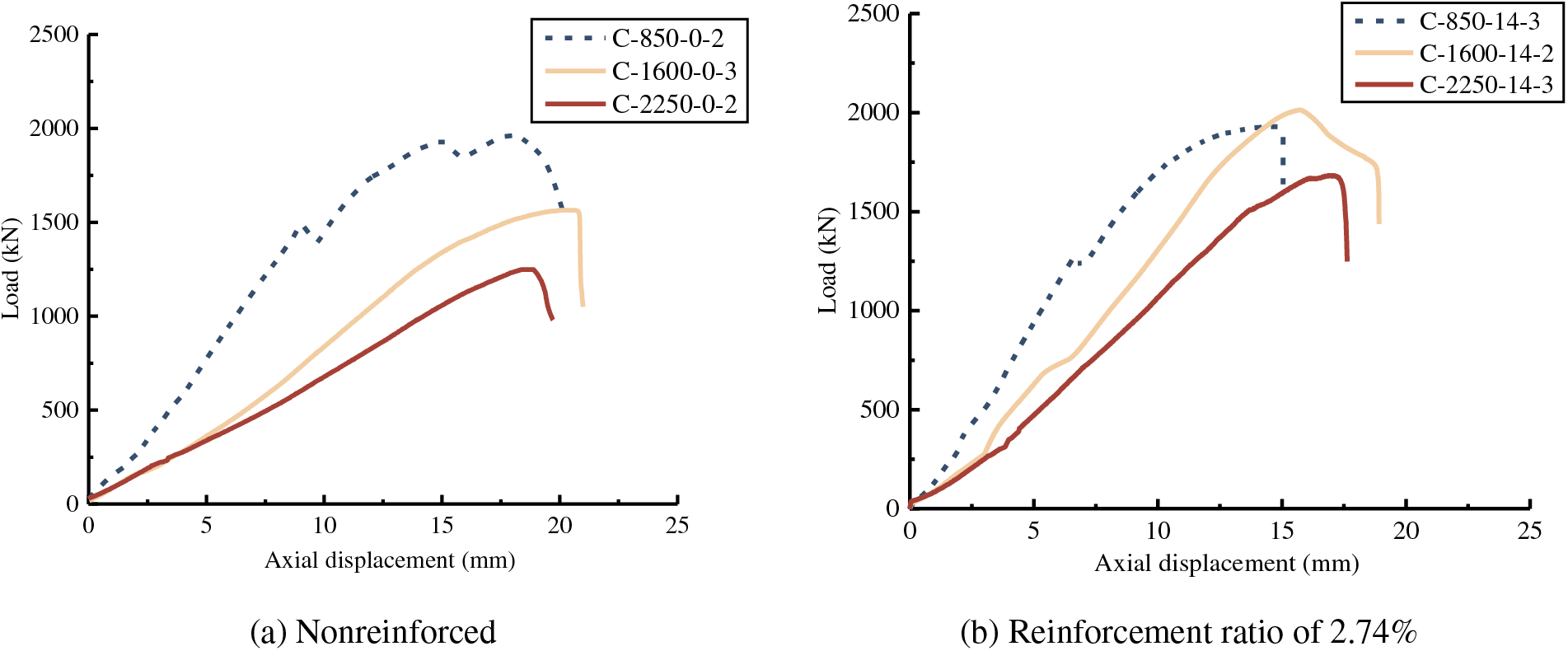
Figure 12: Load-axial displacement relationship curves under the same reinforcement ratio
3.4 Height-Lateral Displacement Relationship Curve
3.4.1 Influence of the Reinforcement Ratio on the Lateral Deflection
As the similar results, only one of each group is selected to be discussed. The effect of reinforcement ratios on the lateral deflection is shown in Fig. 13. The bamboo scrimber columns with a slenderness ratio of 19.63 do not experience apparent lateral deformation, and the lateral stiffness of columns is not greatly improved. The specimens with slenderness ratios of 36.95 and 51.96 have lateral deformation before reaching the ultimate load, but lateral deformation is not significant, and the maximum lateral deflection point is located at the upper 1/3 of the specimen, which is mainly caused by the cracks near the top of the column. After reaching the ultimate load, the lateral deformation rate is significantly accelerated, which mainly results from buckling, so the position of maximum lateral deflection returns to the middle of the specimen when loading ends. The maximum lateral deformation of columns with slenderness ratios of 36.95 and 51.96 is reduced, and the lateral stiffness is significantly improved, indicating that the steel rebars limit the lateral deformation during the axial compression process, and the effect becomes more significant as the reinforcement ratio increases.
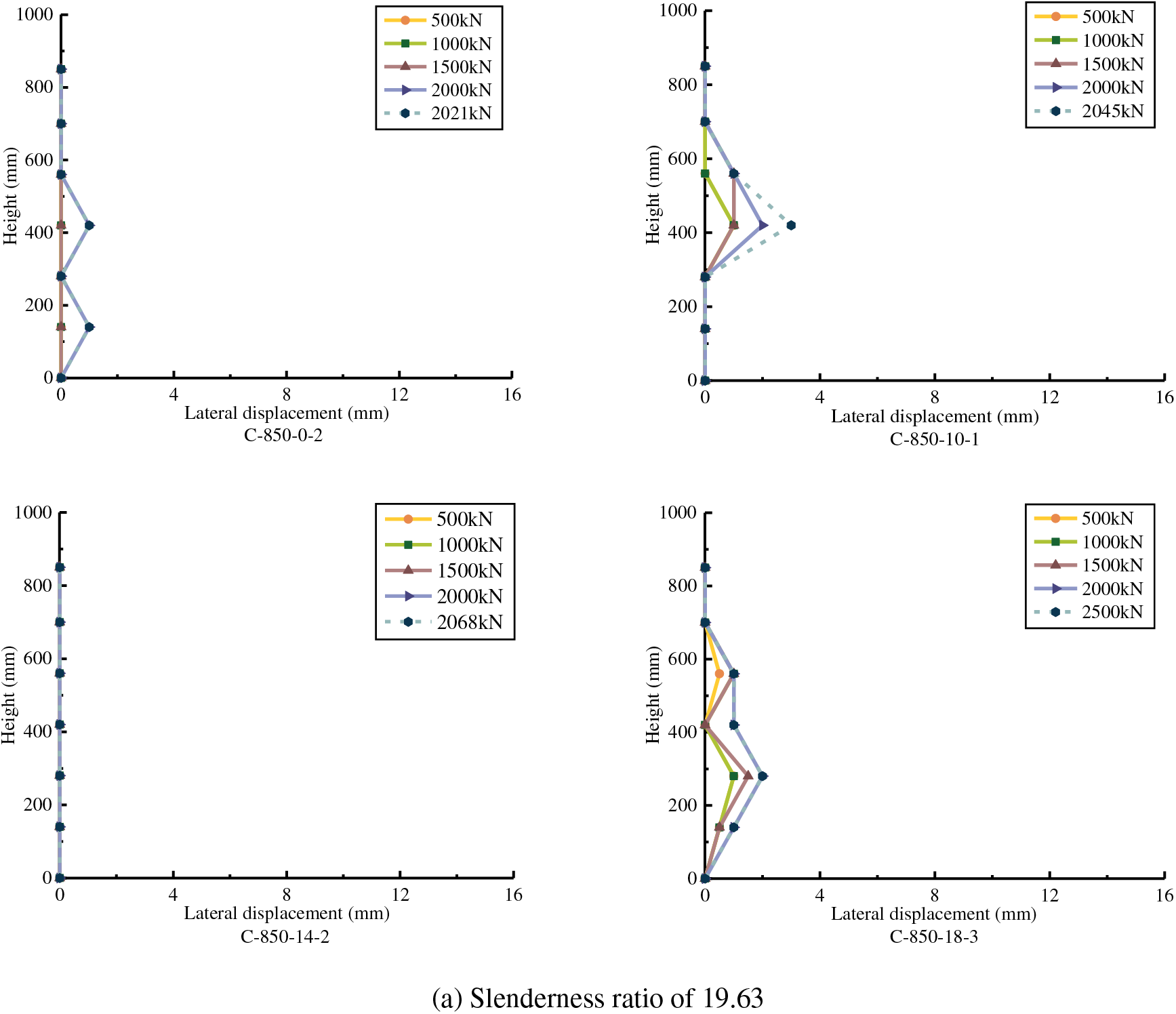
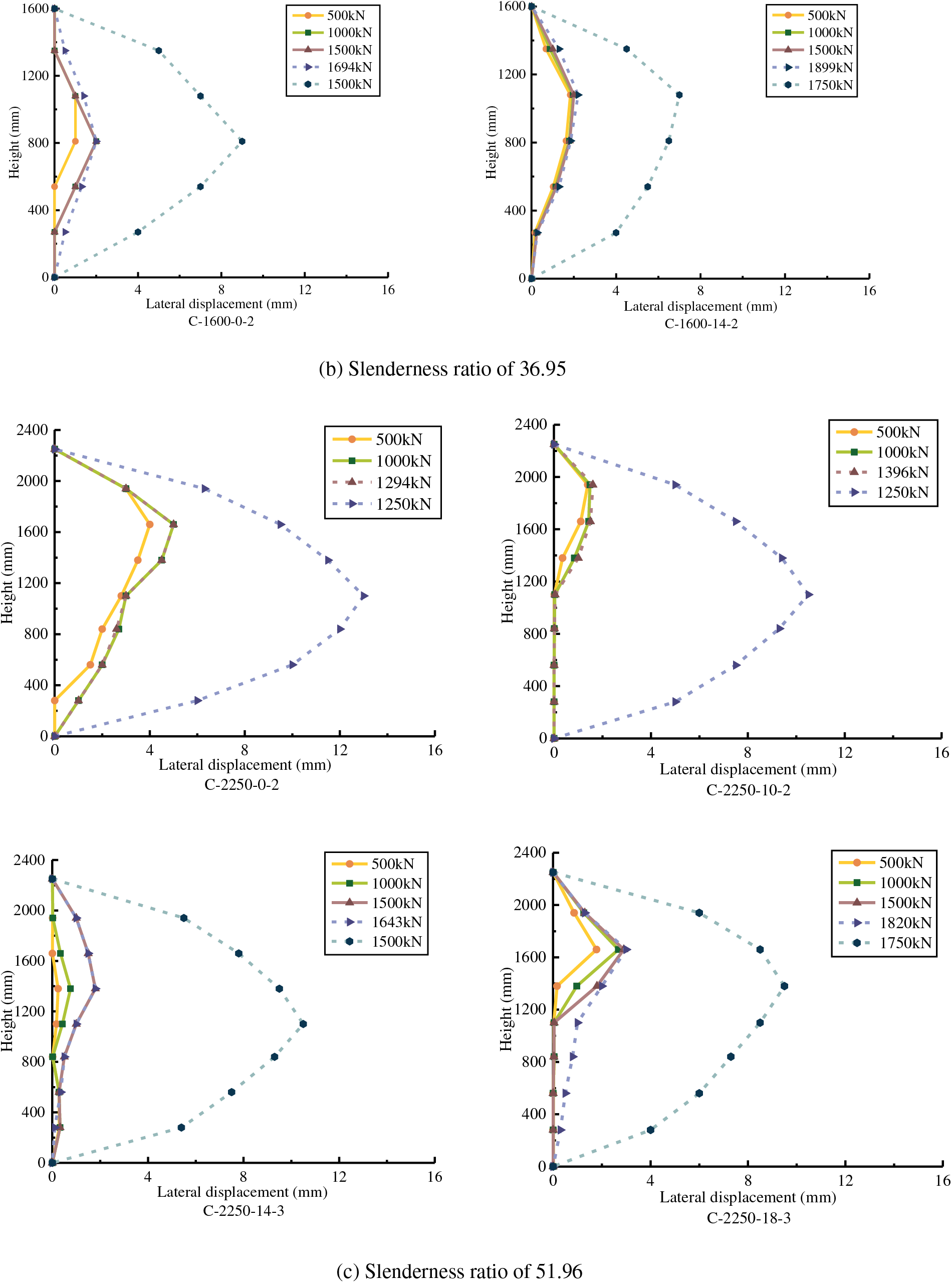
Figure 13: Height-lateral displacement relationship curve under the same slenderness ratio
3.4.2 Influence of the Slenderness Ratio on the Lateral Displacement
The effect of slenderness ratio on the lateral deflection is shown in Fig. 14. The specimens with a slenderness ratio of 19.63 maintain smaller lateral deformation, whereas those with slenderness ratios of 36.95 and 51.96 rapidly develop a large reverse “C” shape after reaching the ultimate load. The maximum lateral deflection increases as the slenderness ratio increases and lateral deformation rapidly develops until the point of failure.
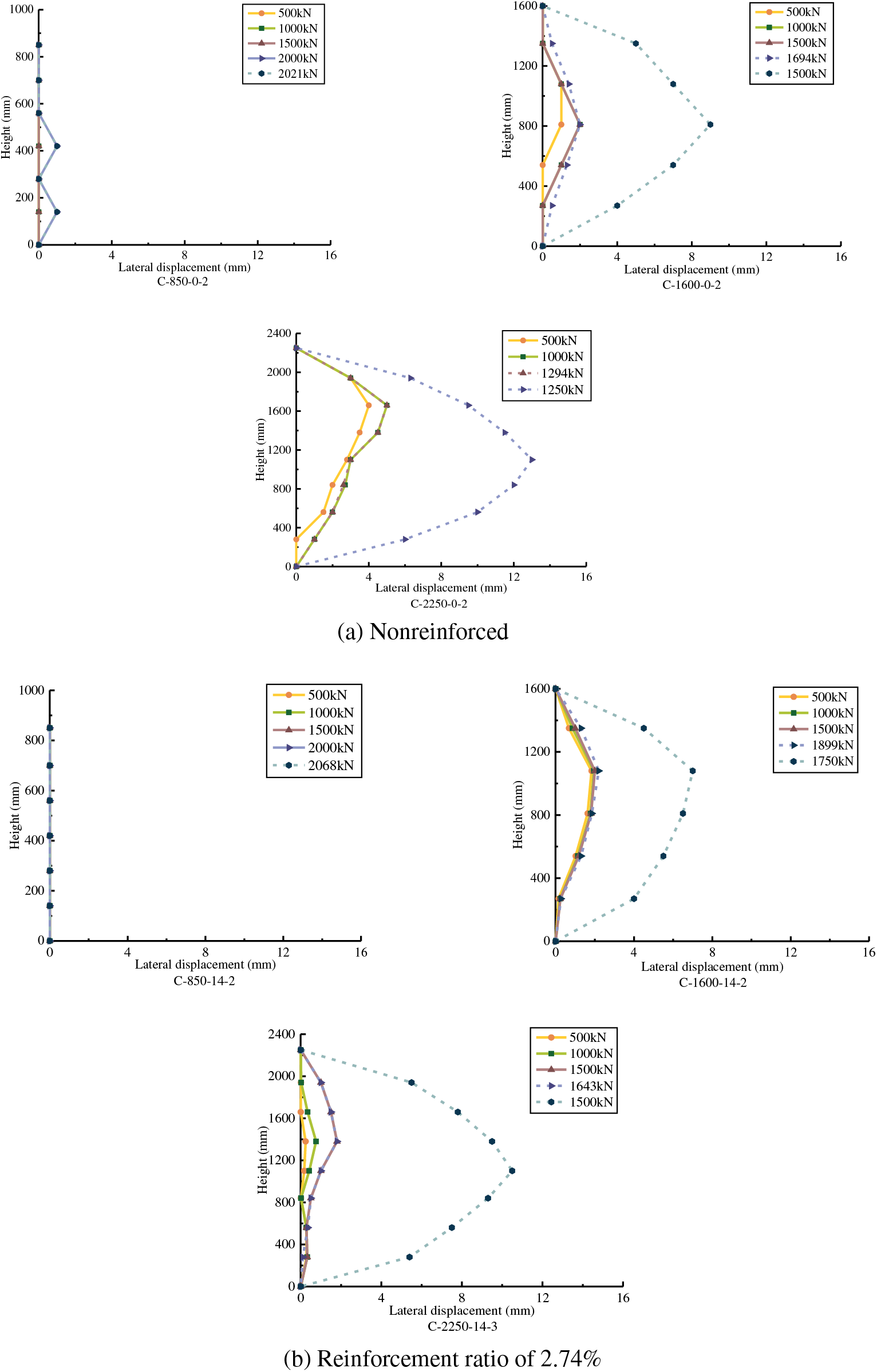
Figure 14: Height-lateral displacement relationship curve under the same reinforcement ratio
3.5 Load-Axial Strain Relationship Curve
As specimens of one group show similar results, a typical one of the group is chosen to be analyzed. The left side of the horizontal axis represents the tensile zone, while the right side represents the compressive zone. A, B, C, and D represent four arrangement surfaces of strain gauges.
3.5.1 Influence of the Reinforcement Ratio on the Axial Strain
Fig. 15 shows the effect of reinforcement ratio on the axial strain under the same slenderness ratio. When the slenderness ratio is 19.63, the curve has the elastic stage, the elastic-plastic stage, and the failure stage. The failure stage curve presents a platform, that is, the load remains stable at a certain level at this stage, and the axial strain changes sharply until the specimen fails. When the slenderness ratios are 36.95 and 51.96, the curves of specimens quickly enter the failure stage after the elastic stage, there is no apparent elastic-plastic stage in the curve, and only the brittle failure occurs.
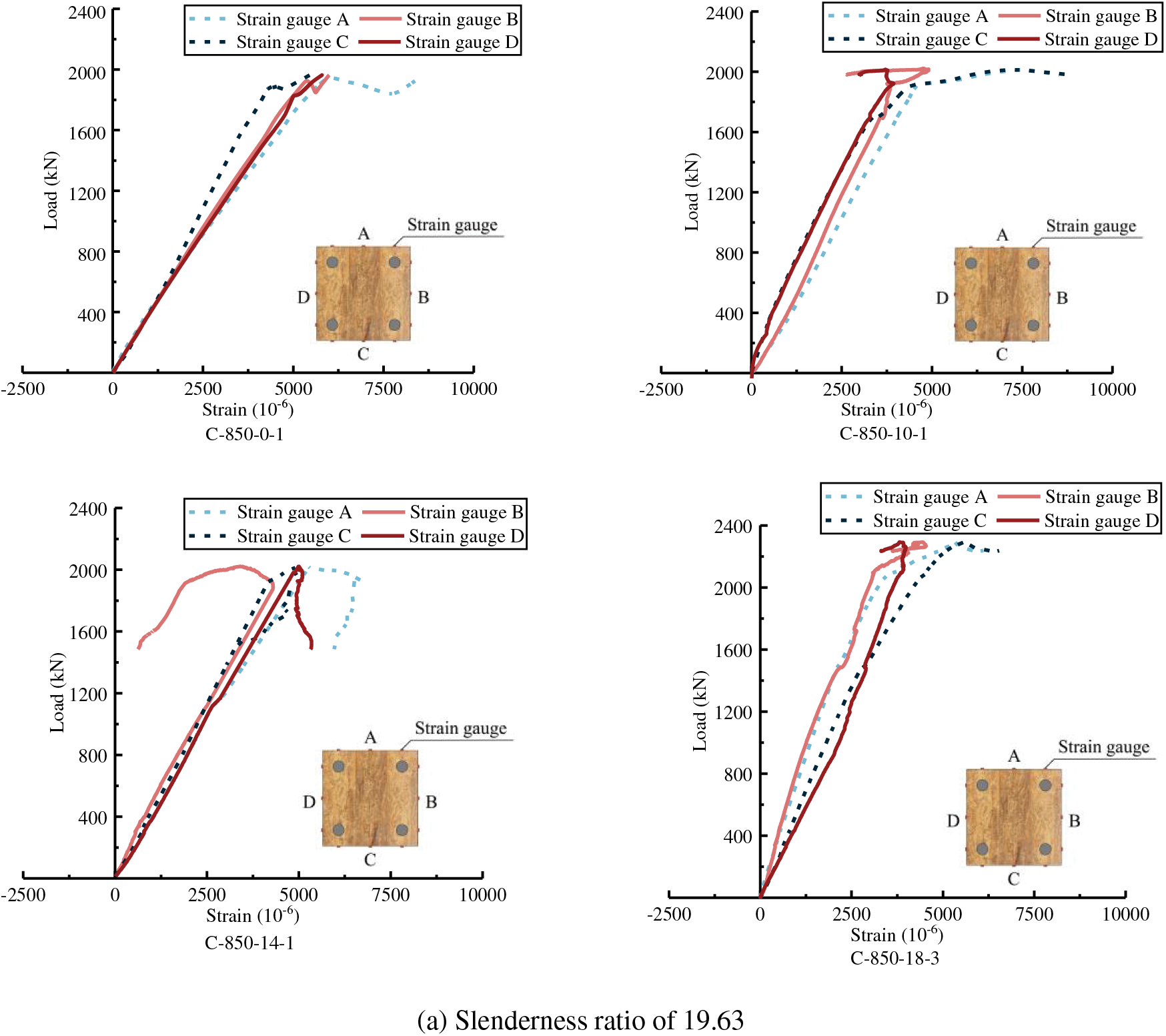
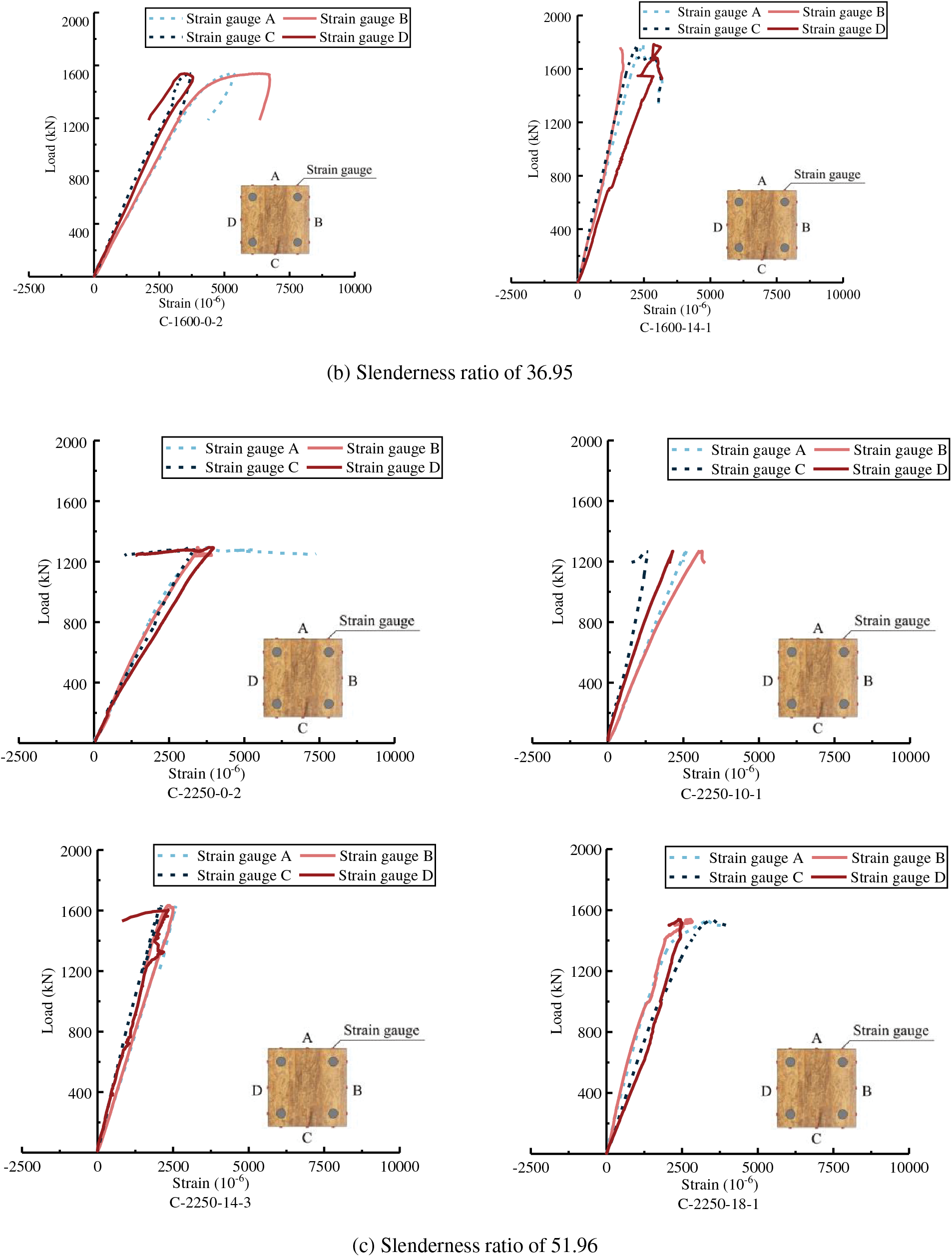
Figure 15: Load-axial strain relationship curve under the same slenderness ratio
The platform segment of curves under the slenderness ratio of 19.63 is due to the sharp increase in strain caused by the cracking of adhesive layers, and the curves develop and become flat. The curves show a negative development, which is the result of stress redistribution due to the cracking of adhesive layers. When the reinforcement ratio is 4.52%, the curves have almost no negative growth trend, indicating that the steel rebars can constrain crack extension in the lengthwise direction, thereby reducing the stress redistribution and making the stress more uniform. As the reinforcement ratio increases, the inhibitory effect becomes more significant, as shown in Fig. 15a.
The platform segment of curves of specimens with slenderness ratios of 36.95 and 51.96 is due to the large lateral deformation when reaching the ultimate load, resulting in a bending moment, which causes the strain on one side to increase rapidly and the strain on the opposite side to decrease rapidly. After reinforcement, the platform section is shortened, indicating that the steel rebars can reduce the second-order effect of columns under axial compression. In addition, the larger the reinforcement ratio is, the more significant the inhibitory effect is, as shown in Fig. 15b,c.
3.5.2 Influence of the Slenderness Ratio on the Axial Strain
The effect of the slenderness ratio on the load-axial strain relationship curve is shown in Fig. 16. The platform segment becomes longer as the slenderness ratio increases. And the amplitude of strain increase (decrease) becomes larger, indicating that the specimens become more flexible. For the nonreinforced specimens, the ultimate strain increases with the slenderness ratio. The ultimate strain in the reinforcement ratio of 2.74% gradually decreases with the increasing slenderness ratio, indicating that the axial strain can be effectively controlled by the tension of reinforcement under the higher slenderness ratio.
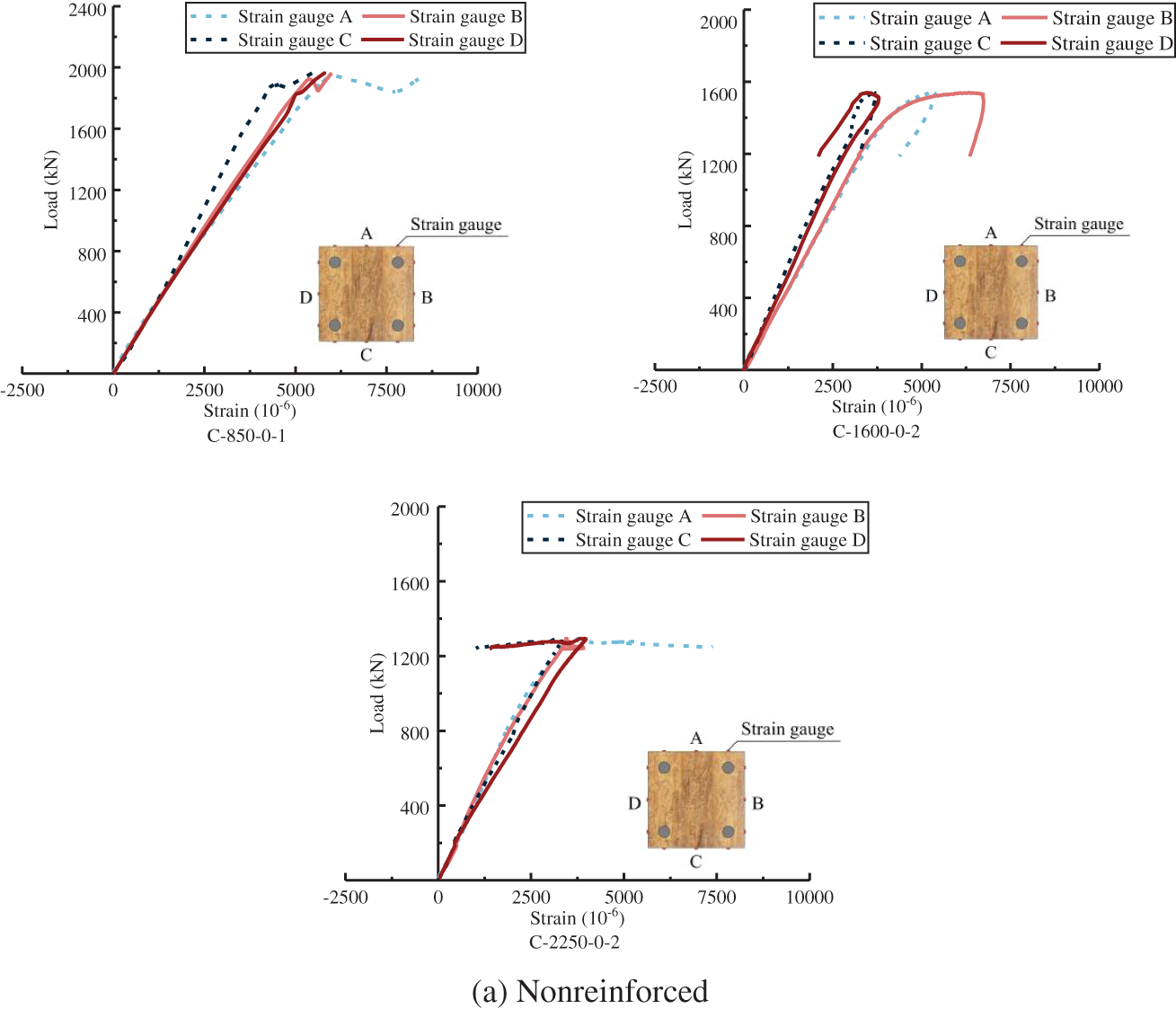
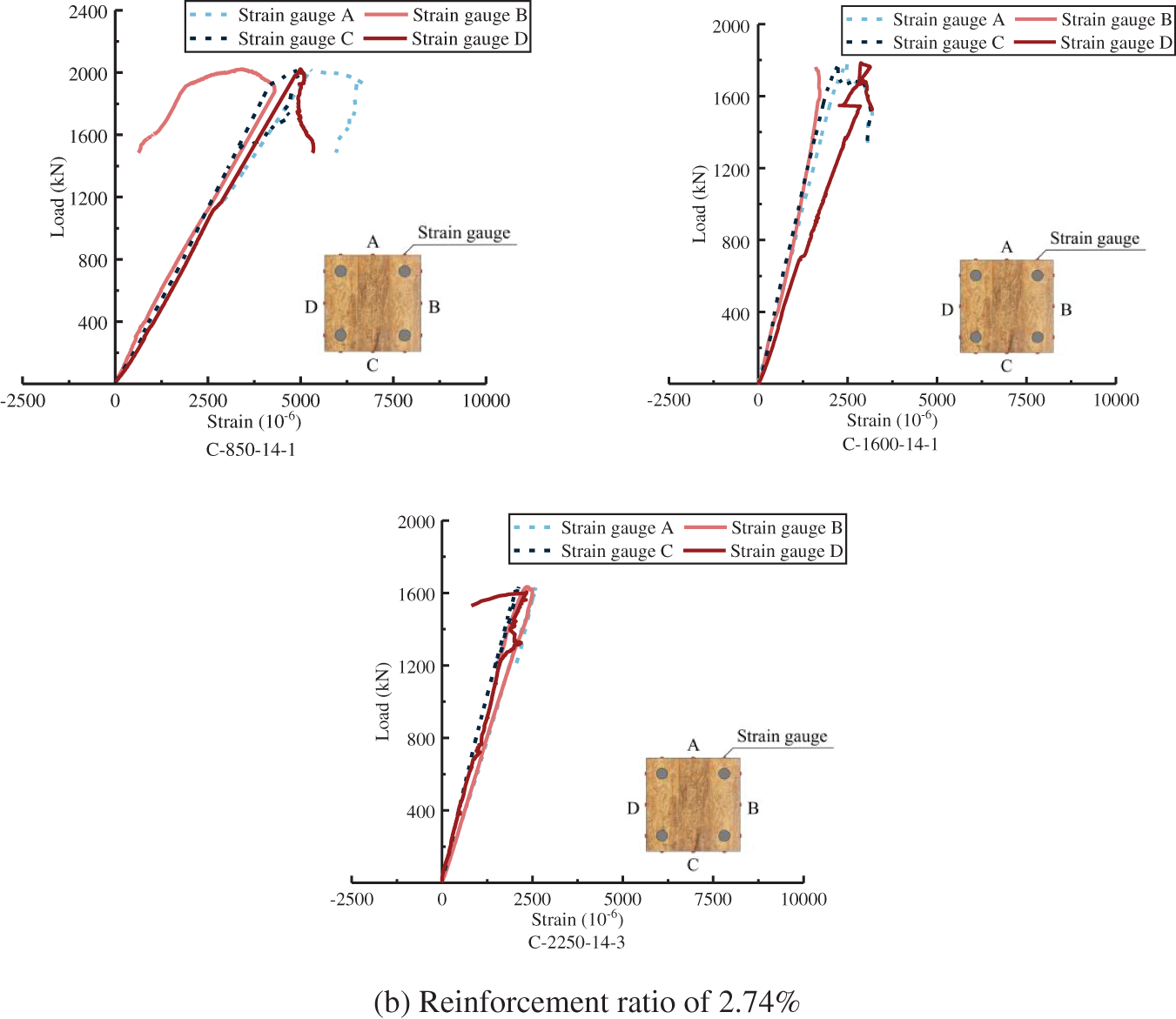
Figure 16: Load-axial strain relationship curve under the same reinforcement ratio
4 Calculation Method of Axial Bearing Capacity
The following basic assumptions must be followed before establishing and modifying the calculation formulas for the axial compressive bearing capacity of reinforced bamboo scrimber columns:
(1) The component is an equal-section straight rod;
(2) Load acts on the centroid of section;
(3) The bending deformation of components under the critical condition is tiny;
(4) The plane section assumption must be satisfied when the component is bent;
(5) The tensile stress-strain relationship model of steel used in this model is shown in Fig. 17.
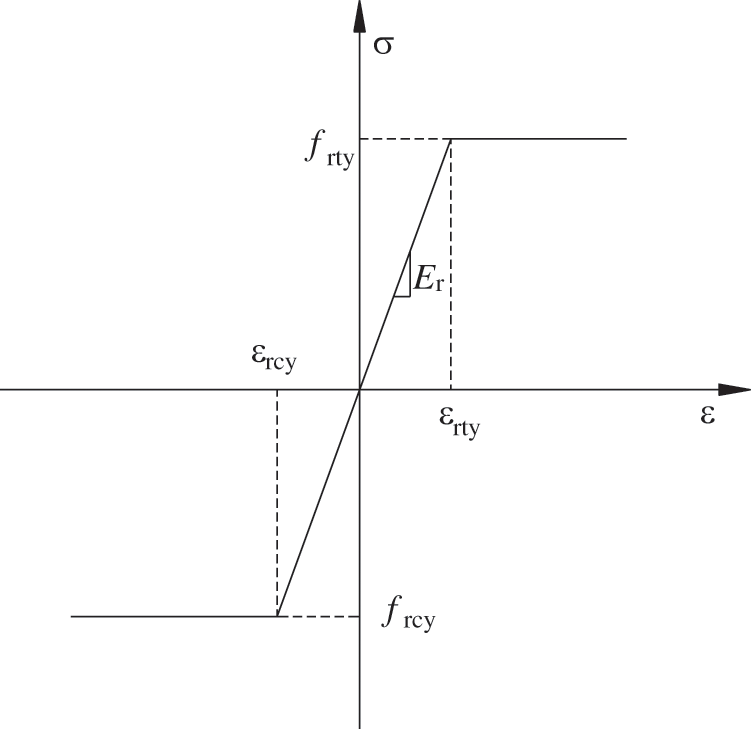
Figure 17: Stress-strain model of steel bar
The four-line model was selected as the parallel-to-grain stress-strain model of bamboo scrimber, as shown in Fig. 18 [28]. It is assumed that the tensile behavior of recombinant bamboo is linear elastic and the compressive behavior is non-linear without considering the descending stage. According to the results of material property tests, the parallel-to-grain stress-strain relationship of bamboo scrimber is shown in Eq. (1). According to the calculation results, the yield strength of steel rebar is 400 MPa, and the yield compressive strength parallel to the grain of bamboo scrimber is 100 MPa.
σ={Etb⋅εEcb⋅ε1889.60ε+64.41fc00≤ε≤εtu0≤ε<εcyεcy≤ε<εc0εc0≤ε≤εcu (1)
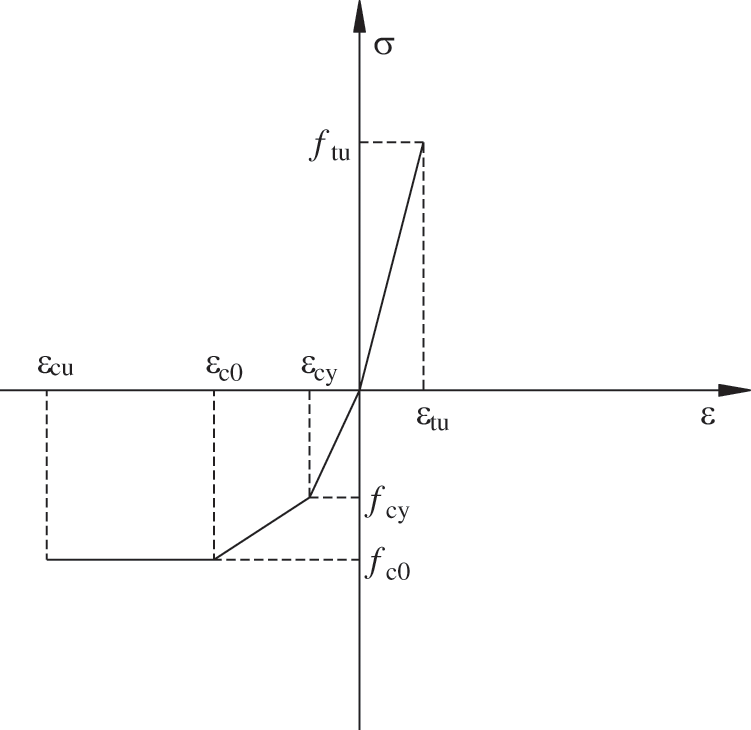
Figure 18: Parallel-to-grain stress-strain model of bamboo scrimber
4.2 Calculation Value of Axial Bearing Capacity in a Slenderness Ratio of 19.63
The failure mode for columns with a slenderness ratio of 19.63 was strength failure. Therefore, the compressive strength parallel to grain can be used directly to calculate the ultimate bearing capacity under this working group. Eq. (2) is established for the axial compressive bearing capacity of this group, assuming that the steel rebars have entered the yield stage when the specimen is broken.
Nu=fcAb+fyAs (2)
where Nu is the ultimate axial compressive bearing capacity of bamboo scrimber column; fc is the yield compressive strength parallel to the grain of bamboo scrimber; fy is the yield strength of steel rebar; Ab is the effective area of bamboo scrimber and As is the cross-section area of steel rebar.
The calculation results are shown in Table 4. It is believed that Eq. (2) can be used to predict the ultimate bearing capacity of bamboo scrimber columns with a slenderness ratio of 19.63, and the lower test value is due to the strength of adhesive layer.

4.3 Calculation Value of Axial Bearing Capacity in a Slenderness Ratio of 36.95 and 51.96
Buckling is the primary failure mode of columns with slenderness ratios of 36.95 and 51.96. Euler formula is a fundamental and widely used method for calculating the bearing capacity of those that occur buckling during the elastic stage. It calculates the ultimate bearing capacity by introducing the elastic modulus Ec and the specifics are shown in Eqs. (3) and (4).
Ec=EbAb+EsAsAb+As (3)
Ncr=π2EcIL2 (4)
Tangent Modulus Theory and Double Modulus Theory
However, the Euler formula is based on elastic theory and only applies to calculating the bearing capacity of columns whose buckling occurs before the proportion limit. For those buckling after the proportion limit, it is necessary to consider the nonlinear properties of materials during the stability analysis and calculate bearing capacity by an effective modulus rather than the elastic modulus. Tangent modulus theory and double modulus theory proposed by F. Engesser are the most widely used [29,30].
Tangent modulus theory assumes that there is no negative strain along the cross-section of the column and that the neutral axis and centroidal axis of sections do not shift during the bending process. Instead of the elastic modulus Ec, the tangent modulus Ect is used during calculating the ultimate bearing capacity, and the calculating process is as shown in Eqs. (5) and (6).
Ect=EbtAb+EstAsAb+As (5)
Ncr=π2EctIL2 (6)
According to double modulus theory, when the column is slightly bent, compressive strain increases on the concave side while tensile strain increases on the convex side, and the neutral axis shifts towards the convex side. According to these assumptions, the tangent modulus Ect is used as the deformation modulus on the concave side, the elastic modulus Ec is used on the other side, and the double modulus Ecr is the combined modulus of the two, as represented by Eq. (7), and the bearing capacity calculation formula is shown as Eq. (8).
Ecr=4EctEc(√Ec+√Ect)2 (7)
Ncr=π2EcrIL2 (8)
There have been no applicable regulations for calculating the bearing capacity of bamboo scrimber columns. As a result, to calculate the axial compressive bearing capacity of bamboo scrimber columns with non-elastic buckling, three specifications included Standard for Design of Timber Structures (GB 50005-2017), National Design Specification for Wood Construction (ANSI/AWC NDS-2018) and Eurocode 5 are referred. The elastic modulus Ec and the combined strength fcc are introduced during modifying, and the calculation of the combined strength fcc is shown as Eq. (9).
fcc=fcAb+fyAsAb+As (9)
In this code, the calculation results of the bearing capacity of columns are modified by introducing an axial compression stability coefficient φ. The revised calculation model is as follows:
φ=acπ2βEcλ2fcc, λ > λc (10)
φ=11+(λ2fcc/λ2fccbcπ2βEcbcπ2βEc), λ≤λc (11)
λc=cc√βEcfcc (12)
where ac, bc, and cc are material correlation coefficients; β is the correlation coefficient of material shear deformation; αc = 0.91, bc = 3.69, cc = 3.45, and β = 1.05 are employed in this paper.
In this code, the calculation results of the bearing capacity of columns are modified by introducing an axial compression stability coefficient Cp. The revised calculation model is as follows:
Cp=1+(fcE/fcEfccfcc)2c−√[1+(fcE/fcEfccfcc)2c]2−fcE/fcEfccfccc (13)
fcE=0.822Emin(l/lbb)2 (14)
Emin=1.05Ec[1−1.645(COVE)]/1.66 (15)
where Emin is the reference and adjusted modulus of elasticity for beam stability and column stability calculations. COVE is the variation coefficient of elastic modulus; c is the nonlinear constant; COVE = 0.10 and c = 0.9 are employed in this paper.
In this code, the calculation results of the bearing capacity of columns are modified by introducing an axial compression stability coefficient kc. The revised calculation model is as follows:
kc=1k+√k2−λrel2 (16)
k=0.5[1+βc(λrel−0.3)+λrel2] (17)
λrel=λπ√fccEc,0.05 (18)
where βc is a factor for members within the straightness limits; Ec,0.05 is the fifth percentile value of the modulus of elasticity parallel to the grain; βc = 0.1 is employed in this paper.
The calculated values of six bearing capacity models are compared with the test values, as shown in Fig. 19. When the reinforcement ratio is 0 or 2.74%, GB 50005-2017, and Eurocode can provide reasonable predicted values in the slenderness ratios of 36.95 and 51.96. For the non-reinforcement groups, both the two non-elastic classical models and NDS-2018 underestimate the bearing capacity of columns, whereas the Euler formula overestimates it. When the reinforcement ratio is 2.74%, the calculated value given by NDS-2018 is relatively conservative, while all three classical models overestimate the influence of slenderness ratio and are unsuitable for predicting bearing capacity.
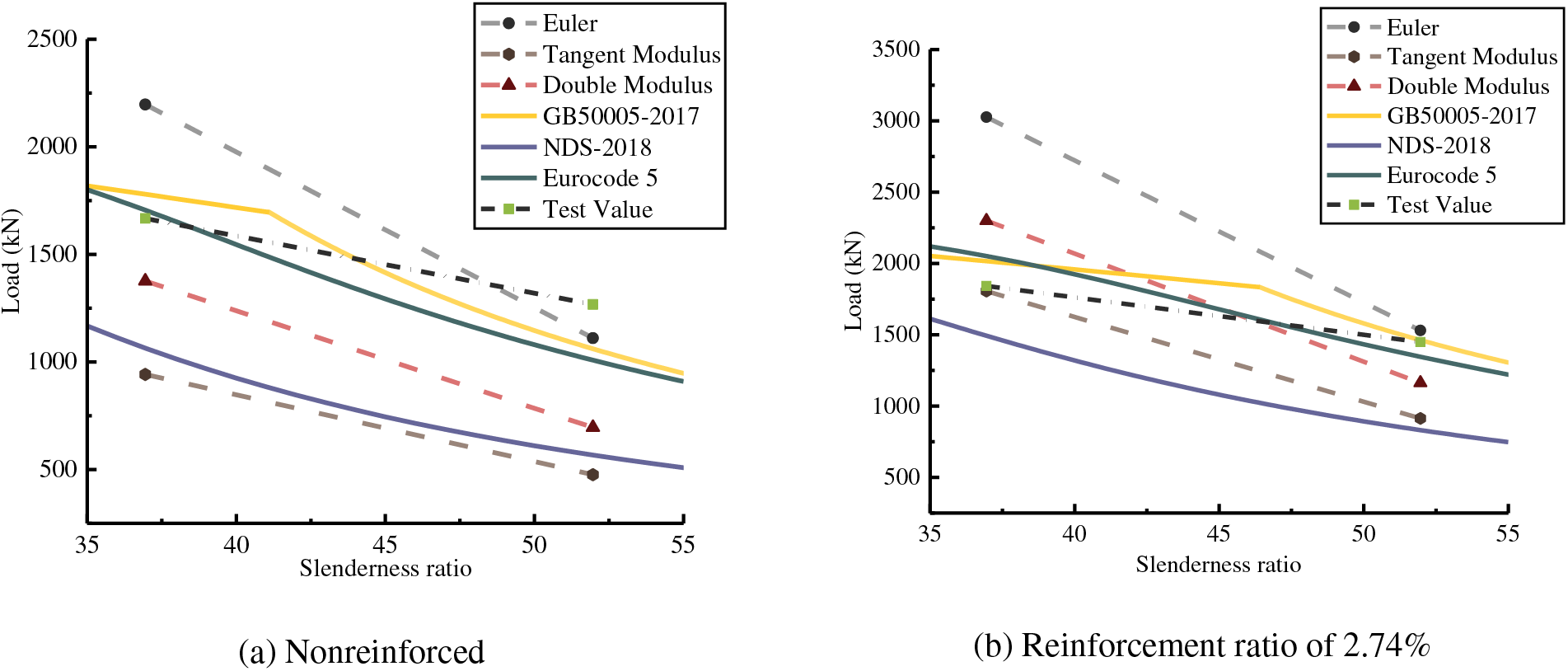
Figure 19: Comparison between calculated values and test values under various bearing capacity models
The relative error between the calculated values of six bearing capacity models and the test values is shown in Fig. 20. It is noticed that the 0 reference line and the 20% line defined in the figure are only for the convenience of comparison, which have no theoretical significance in themselves. Tangent modulus theory and NDS-2018 are unsuitable for predicting bearing capacity in the slenderness ratios of 36.95 and 51.96, and their relative errors are around −40%. In a slenderness ratio of 36.95, the average relative error of the Euler formula is about 50%, and in a slenderness ratio of 51.96, the average relative error of the double modulus model is about −25%. With slenderness ratios of 36.95 and 51.96, the maximum relative error of GB 50005-2017 is 16.28%. For Eurocode 5, the maximum relative error is −20.35%. By comparison and analysis, it can be seen that the modified GB 50005-2017 and Eurocode 5 can be used to predict the ultimate bearing capacity of reinforced bamboo scrimber columns with slenderness ratios of 36.95 and 51.96.
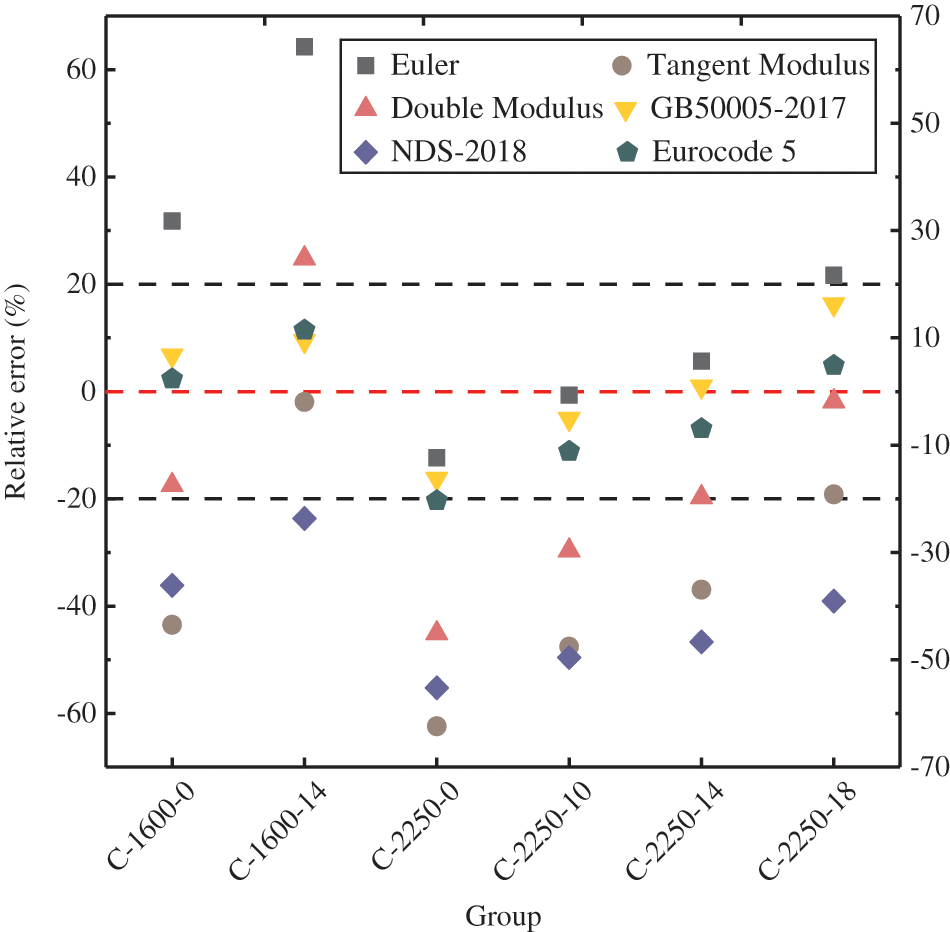
Figure 20: Relative error of each bearing capacity calculation model
In this paper, one type of novel reinforced bamboo scrimber column is presented. 28 specimens were tested to investigate the axial compressive performance, and the test values were compared with the calculated values of classical models and codes. The specific conclusions are as follows:
(1) Under axial compression, the failure modes of bamboo scrimber columns can be divided into the cracking failure of adhesive layers, the fibre tearing failure, and the buckling failure, which are influenced by the slenderness ratio and the reinforcement ratio. For the columns with a slenderness ratio of 19.63, the failure mode was strength failure for the main point, and the bearing capacity was primarily determined by the compressive strength parallel to the grain of bamboo scrimber and the yield strength of steel rebars. For those with slenderness ratios of 36.95 and 51.96, the failure mode was instability failure for the main point, and the material utilization efficiency in these two working groups was lower than that in a slenderness ratio of 19.63 due to the restriction of slenderness ratio.
(2) The beneficial effect of steel rebars on the bearing capacity of columns with a slenderness ratio of 19.63 was not noticeable, while it could significantly enhance those with slenderness ratios of 36.95 and 51.96. The axial and lateral deformation of specimens were controlled gradually as the reinforcement ratio increased, and the bearing capacity was increased by 5.24% to 16.99%.
(3) In the same reinforcement ratio, the bearing capacity of columns decreased as the slenderness ratio increased, accompanied by an increase in axial and lateral deformation. The columns with a slenderness ratio of 19.63 had no apparent lateral deformation, but those with slenderness ratios of 36.95 and 51.96 had a clear lateral “C” shape.
(4) Finally, a calculation method for the bearing capacity of reinforced bamboo scrimber columns was proposed by theoretical analysis. The results showed that the model proposed in this paper can accurately predict the ultimate bearing capacity of columns with a slenderness ratio of 19.63. For those with slenderness ratios of 36.95 and 51.96, several commonly used bearing capacity calculation models of timber columns were modified by introducing the elastic modulus Ec and the combined strength fcc. The analysis results showed that calculation models based on GB 50005-2017 and Eurocode 5 can provide more accurate predictions.
Acknowledgement: None.
Funding Statement: This work was supported by the Resources Industry Science and Technology Innovation Joint Funding Project of Nanping City (N2021Z007); and the Innovation Foundation for Doctoral Program of Forestry Engineering of Northeast Forestry University (LYGC202119).
Author Contributions: The authors confirm contribution to the paper as follows: Methodology: Xueyan Lin; Conceptualization: Mingtao Wu, Guodong Li; Investigation: Xueyan Lin, Mingtao Wu; Data curation: Xueyan Lin; Formal analysis: Xueyan Lin, Mingtao Wu, Guodong Li, Nan Guo, Lidan Mei; Writing–original draft: Xueyan Lin, Mingtao Wu; Writing–review & editing: Xueyan Lin, Mingtao Wu, Guodong Li, Nan Guo, Lidan Mei; Supervision: Guodong Li, Nan Guo; Resources: Nan Guo; Funding acquisition: Nan Guo, Lidan Mei; Project administration: Lidan Mei. All authors reviewed the results and approved the final version of the manuscript.
Availability of Data and Materials: The datasets used or analyzed during the current study are available from the corresponding author upon reasonable request.
Ethics Approval: Not applicable.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
References
1. Liu KW, Frith O. An overview of global bamboo architecture: trends and challenges. World Arch. 2013;2013(12):8 (In Chinese). [Google Scholar]
2. Chen Z, Ma R, Du Y, Wang X. State-of-the-art review on research and application of original bamboo-based composite components in structural engineering. Structures. 2022;35:1010–29. [Google Scholar]
3. Yang GS. Bamboo-from raw bamboo to glued laminated bamboo structure. Civil Eng. 2020;9(7):13 (In Chinese). [Google Scholar]
4. Zea EE, Habert G, Correal DJF, Archilla HF, Echeverry FJS, Trujillo D. Industrial or traditional bamboo construction comparative life cycle assessment (LCA) of bamboo-based buildings. Sustainability. 2018;10(9):3096. [Google Scholar]
5. Th A, Lc A, Ar A, Ck B, Dt A. The splitting of bamboo in response to changes in humidity and temperature. J Mech Behav Biomed Mater. 2020;111:103990. [Google Scholar]
6. Chen X, Xu QF, Harries KA. Research on mechanical properties and application of bamboo in civil engineer: state-of-the-art. Struct Eng. 2015;31(6):10 (In Chinese). [Google Scholar]
7. Chen J, Guagliano M, Shi M, Jiang X, Zhou H. A comprehensive overview of bamboo scrimber and its new development in China. Eur J Wood Wood Prod. 2021;79(2):363–79. [Google Scholar]
8. Ji YH, Huang YX, Zhang FD, Lei WC, Qi Y, Yu WJ. Process performance, application design, and kansei evaluation of bamboo scrimber in China: a review. World Forest Res. 2022;35(6):6 (In Chinese). [Google Scholar]
9. Chen ZF. Prefabricated structures for building construction in rural township. China: Southeast University Press; 2017. p. 182(In Chinese) [Google Scholar]
10. Li Z, He M, Tao D, Li M. Experimental buckling performance of scrimber composite columns under axial compression. Composites Part B: Eng. 2016;86:203–13. [Google Scholar]
11. Tommy YL, Cui HZ, Tang WC, Leung HC. Strength analysis of bamboo by microscopic investigation of bamboo fibre. Constr Build Mater. 2008;22(7):1532–5. [Google Scholar]
12. Yang RZ. Research on material properties of glubam and its application (Ph.D. Thesis). Hunan University: China; 2013. [Google Scholar]
13. Chen S, Wei Y, Hu Y, Zhai Z, Wang L. Behavior and strength of rectangular bamboo scrimber columns with shape and slenderness effects. Mater Today Commun. 2020;25:101392. doi:10.1016/j.mtcomm.2020.101392. [Google Scholar] [CrossRef]
14. Li H, Qiu Z, Wu G, Wei D, Lorenzo R, Yuan CG, et al. Compression behaviors of parallel bamboo strand lumber under static loading. J Renew Mater. 2019;7(7):18. doi:10.32604/jrm.2019.07592. [Google Scholar] [CrossRef]
15. Qiu Z, Wang J, Fan H, Li T. Anisotropic mechanical properties and composite model of parallel bamboo strand lumbers. Mater Today Commun. 2020;24(1):101250. doi:10.1016/j.mtcomm.2020.101250. [Google Scholar] [CrossRef]
16. Shangguan WW, Zhong Y, Xing XT, Zhao RJ, Ren HQ. Strength models of bamboo scrimber for compressive properties. J Wood Sci. 2015;61(2):120–7. doi:10.1007/s10086-014-1444-9. [Google Scholar] [CrossRef]
17. Wu M, Mei L, Guo N, Ren J, Zhang Y, Zhao Y. Mechanical properties and failure mechanisms of engineering bamboo scrimber. Constr Build Mater. 2022;344:128082. doi:10.1016/j.conbuildmat.2022.128082. [Google Scholar] [CrossRef]
18. Li X, Ashraf M, Li H, Zheng X, Hazell PJ. An experimental investigation on Parallel Bamboo Strand Lumber specimens under quasi static and impact loading. Constr Build Mater. 2019;228:116724. [Google Scholar]
19. Zhong Y, Ren HQ, Jiang ZH. Effects of temperature on the compressive strength parallel to the grain of bamboo scrimbe. Materials. 2016;9(6):436. [Google Scholar] [PubMed]
20. Xu M, Cuib Z, Chen Z, Xiang J. Experimental study on compressive and tensile properties of a bamboo scrimber at elevated temperatures. Construct & Build Mat. 2017;151:732–41. [Google Scholar]
21. Li HT, Su JW, Zhang QS, Deeks AJ, Hui D. Mechanical performance of laminated bamboo column under axial compression. Composites Part B: Eng. 2015;79:374–82. [Google Scholar]
22. Tan C, Li H, Wei D, Lorenzo R, Yuan C. Mechanical performance of parallel bamboo strand lumber columns under axial compression: experimental and numerical investigation. Constr Build Mater. 2019;231:117168. [Google Scholar]
23. Zhang SJ, Zhao ZG, Zhang WJ, Shi YY. Experimental research on axial compression of recombinant bamboo columns. Construct Technol. 2015;44(24):4(In Chinese). [Google Scholar]
24. Liu Y, Tang S, Guo Y, Xiao Z, Su X. Axial compression of three types of bamboo scrimber columns with different cross-sections. Bioresources. 2020;15(4):8093–109. doi:10.15376/biores.15.4.8093-8109. [Google Scholar] [CrossRef]
25. Wang Z, Li H, Fei B, Ashraf M, Xiong Z, Lorenzo R, et al. Axial compressive performance of laminated bamboo column with aramid fiber reinforced polymer. Compos Struct. 2021;258(8):113398. doi:10.1016/j.compstruct.2020.113398. [Google Scholar] [CrossRef]
26. Li J, Chen ST, Meng X. Compressive strength test on bamboo column reinforced by clamps. China Forest Sci Technol. 2014;28(4):113–5 (In Chinese). [Google Scholar]
27. Yang L, Li X, Fang H, Liu W, Hong J, Hui D. Compressive behaviour of wood-filled GFRP square columns with lattice-web reinforcements. Constr Build Mater. 2021;310:125129. doi:10.1016/j.conbuildmat.2021.125129. [Google Scholar] [CrossRef]
28. Li H, Zhang H, Qiu Z, Su J, Wei D, Lorenzo R, et al. Mechanical properties and stress strain relationship models for bamboo scrimber. J Renew Mater. 2020;8(1):13–27. doi:10.32604/jrm.2020.09341. [Google Scholar] [CrossRef]
29. Chen WF, Lui EM. Structural stability-theory and implementation. Amsterdam: Elsevier; 1987. [Google Scholar]
30. Goonewardena J, Subhani M, Reiner J, Kafle B, Ashraf M. Behaviour of short and long columns made from bamboo scrimber subjected to uniaxial compression. Adv Bamboo Sci. 2024;7(3):100082. doi:10.1016/j.bamboo.2024.100082. [Google Scholar] [CrossRef]
Cite This Article
 Copyright © 2024 The Author(s). Published by Tech Science Press.
Copyright © 2024 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF Downloads
Downloads
 Citation Tools
Citation Tools
