 Open Access
Open Access
ARTICLE
A Novel Method for Aging Prediction of Railway Catenary Based on Improved Kalman Filter
1 School of Electrical Engineering and Automation, Henan Institute of Technology, Xinxiang, 453003, China
2 Technology Center, Sichuan Injet Electric Co., Ltd., Deyang, 618000, China
3 Embedded System Research Institute, Xinxiang Engineering Research Center for Intelligent Condition Monitoring of Machinery, Xinxiang, 453003, China
* Corresponding Author: Jie Li. Email:
Structural Durability & Health Monitoring 2024, 18(1), 73-90. https://doi.org/10.32604/sdhm.2023.044023
Received 18 July 2023; Accepted 27 October 2023; Issue published 11 January 2024
Abstract
The aging prediction of railway catenary is of profound significance for ensuring the regular operation of electrified trains. However, in real-world scenarios, accurate predictions are challenging due to various interferences. This paper addresses this challenge by proposing a novel method for predicting the aging of railway catenary based on an improved Kalman filter (KF). The proposed method focuses on modifying the priori state estimate covariance and measurement error covariance of the KF to enhance accuracy in complex environments. By comparing the optimal displacement value with the theoretically calculated value based on the thermal expansion effect of metals, it becomes possible to ascertain the aging status of the catenary. To improve prediction accuracy, a railway catenary aging prediction model is constructed by integrating the Takagi-Sugeno (T-S) fuzzy neural network (FNN) and KF. In this model, an adaptive training method is introduced, allowing the FNN to use fewer fuzzy rules. The inputs of the model include time, temperature, and historical displacement, while the output is the predicted displacement. Furthermore, the KF is enhanced by modifying its prior state estimate covariance and measurement error covariance. These modifications contribute to more accurate predictions. Lastly, a low-power experimental platform based on FPGA is implemented to verify the effectiveness of the proposed method. The test results demonstrate that the proposed method outperforms the compared method, showcasing its superior performance.Graphic Abstract
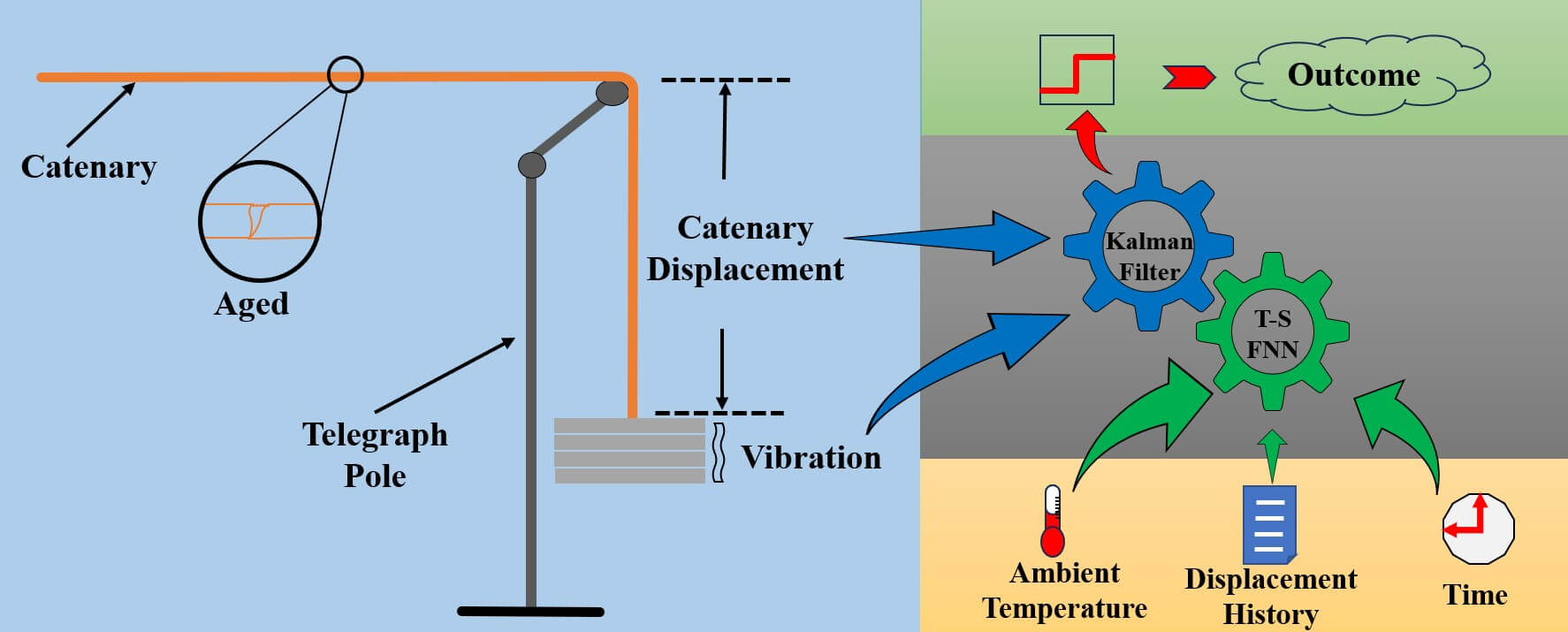
Keywords
Supplementary Material
Supplementary Material FileThe aging prediction of the railway catenary is a field of great research value, which plays a significant role in promoting the railway transportation industry [1–3]. Many researchers use a combination of image processing and artificial intelligence to determine the degree of aging of the catenary. Chen et al. [4] proposed a convolutional neural network for the detection of contact line support devices and components, using high-resolution images from cameras to continuously detect structures in various complex contact lines. Chen et al. [5] used deep neural networks to improve learning efficiency and recognition accuracy in stages. In the first stage, a neural network is established to identify the areas of the pantograph and contact network in complex scenes. In the second stage, image feature extraction algorithms are used to detect the contact points between the pantograph and the contact network. Wu et al. [6] proposed an improved convolutional neural network and a rotating retina network, which uses neural networks combined with machine vision to detect the support structure of the railway catenary. Image processing and artificial intelligence can achieve high prediction accuracy but are easily affected by environmental interference and limited training data [7]. Moreover, the engineering applicability of such equipment is not convenient, and the development cost and equipment price are not competitive.
The KF is an algorithm that uses a linear system state to perform optimal estimation of the system state [8,9]. To improve the performance of the KF, many researchers have begun to fuse neural networks with it. For example, the extended KF proposed in [10] uses a linearization method for nonlinear systems to solve the problem of inaccurate prediction of nonlinear systems. To address the problem of information loss in linearizing nonlinear systems, Liu et al. [11] used the unscented KF to handle nonlinearity. To deal with high-order nonlinear systems, Long et al. [12] used multilayer neural networks to map nonlinearity. The multilayer perceptron uses historical data to learn the dynamic representation of the observation model, replacing the rough approximation of the system state and measurement state in the KF. Revach et al. [13] proposed a neural network-aided KF, which replaces the gain with a recurrent neural network. Based on the advantages of neural networks in processing nonlinear systems, Kim et al. [14–16] used deep neural networks to improve the KF, resulting in better estimation performance in specific application areas.
The FNN combines the characteristics of fuzzy control and neural networks and has many applications in the field of nonlinear state prediction. For example, in reference [17], a particle swarm optimization algorithm was used to optimize FNN, and this model was successfully applied to dynamic environmental prediction. Yang et al. [18] proposed a method for identifying parameters of fuzzy models using recursive least squares with forgetting factors. Improved control accuracy for highly nonlinear systems. Zang et al. [19] used FNN to predict the mixed remaining service life of railway catenary, which improves the accuracy of prediction compared to traditional methods. Narges et al. [20] proposed a method for optimizing Fault Detection based Decision Tree strategy (FDDT) using neural networks and fuzzy algorithms. The neural network algorithm detects and distinguishes a type of load, and the fuzzy model serves as a modifier to determine the final output fault type. Jan et al. [21] proposed a fault detection and diagnosis system using a Fuzzy Deep Neural Network algorithm.
The KF and the FNN have many applications in health monitoring, life prediction, nonlinear state estimation, etc. Combining the KF with the FNN can greatly improve the performance of the algorithm in certain scenarios. The aging prediction of railway catenary can be transformed into a nonlinear state estimation problem. Therefore, this paper proposes a novel improved KF algorithm that uses a T-S FNN to replace the prior state estimate of the KF. The constructed T-S FNN uses an adaptive training method to increase the efficiency of prediction. In addition, the data collected by the vibration sensor is converted into measurement error covariance for the KF. The main contributions of this paper are as follows:
• Proposed a novel fusion approach. It integrates T-S FNN and KF to improve the accuracy of the aging railway catenary prediction.
• An adaptive training method is proposed, which enables the FNN to use fewer fuzzy rules while maintaining the accuracy of fitting and prediction, thus reducing the computational complexity.
• The vibration interference data is introduced into the KF to correct the measurement error covariance on the estimation of optimal values.
• An experimental platform is built to compare with some of the latest improved KF algorithms, proving the superiority of the proposed algorithm.
The rest of this paper is as follows. Section 2 explains the principle of aging prediction for the railway catenary. Section 3 illustrates the structure of the proposed method. The overall program structure is described in Section 4. Section 5 shows the comparative experiments. The conclusions are summarized in Section 6.
The railway catenary model discussed in this paper is shown in Fig. 1. Where
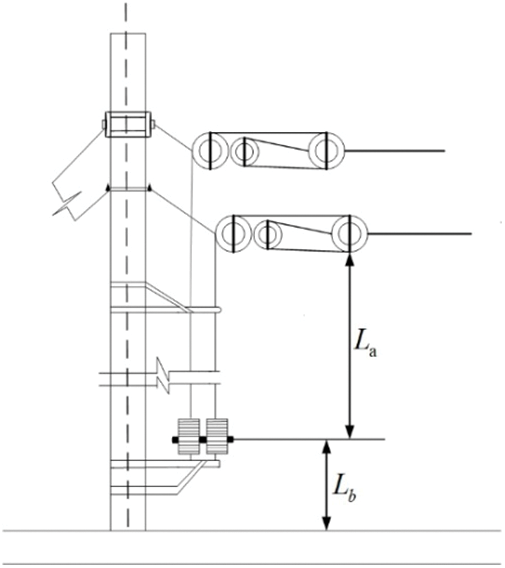
Figure 1: Railway catenary structure model
Metal cables have a specific coefficient of thermal expansion, which means that changes in ambient temperature can lead to variations in the catenary length [22]. The coefficient of thermal expansion of metals [23],
where
When no train passes by, the trend of ambient temperature and catenary displacement over time plotted based on data collected by sensors is shown in Fig. 2. The temperature curve is the temperature data within 24 h, the theory curve is the displacement change trend calculated by Eq. (1), and the actual curve is the data collected by the displacement sensor. The data sampling period is 10 min. From the statistical results, it can be seen that the theory value of the catenary displacement is correlated with temperature. Due to environmental interference, there is a certain dissimilarity between the displacement collected by the sensor and the theory value, but the correlation is still obvious.
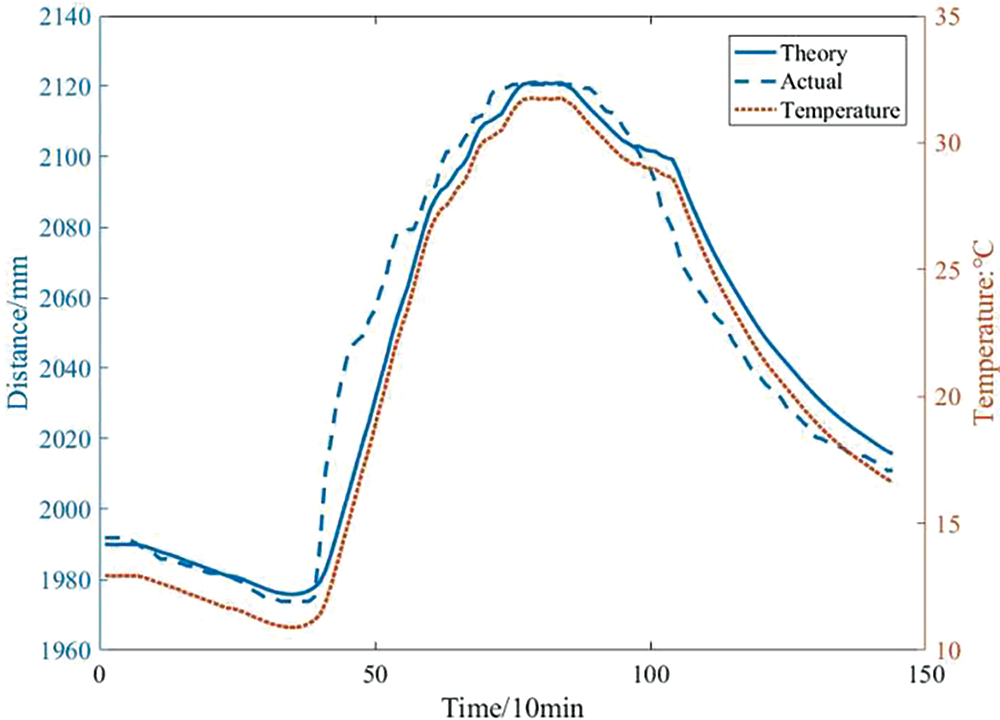
Figure 2: The relationship between catenary displacement and temperature
2.2 The Principle of Aging Prediction
After being affected by sudden interference like pantograph passing, the displacement of the catenary will experience significant fluctuations. As shown in Fig. 3, the pantograph passing effect occurred between 1000 and 2000 s. The catenary experiences significant interference resulting in a substantial deviation from the theoretical expectations. However, once the interference diminishes, they gradually realign with the theoretical predictions.
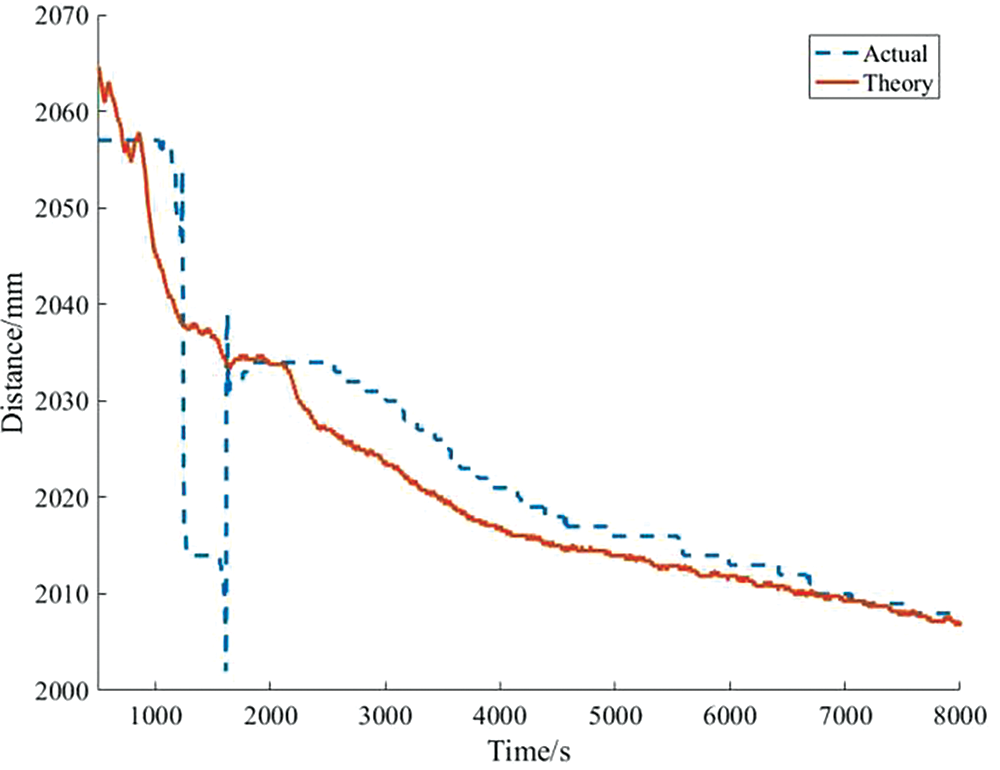
Figure 3: Pantograph interference effect
As the catenary ages, the physical properties are altered due to cable fractures. In Fig. 4, a comparison between the displacement of the aged catenary and that of a normal one is made, with the differences illustrated in Fig. 5. The results indicate a substantial disparity in the displacement distribution between the aged and normal catenaries, and this difference does not spontaneously revert to the normal state for a certain period. When the detected difference surpasses a predefined threshold and persists for a specific duration, it serves as an indicator to determine whether the catenary is indeed aged [24].
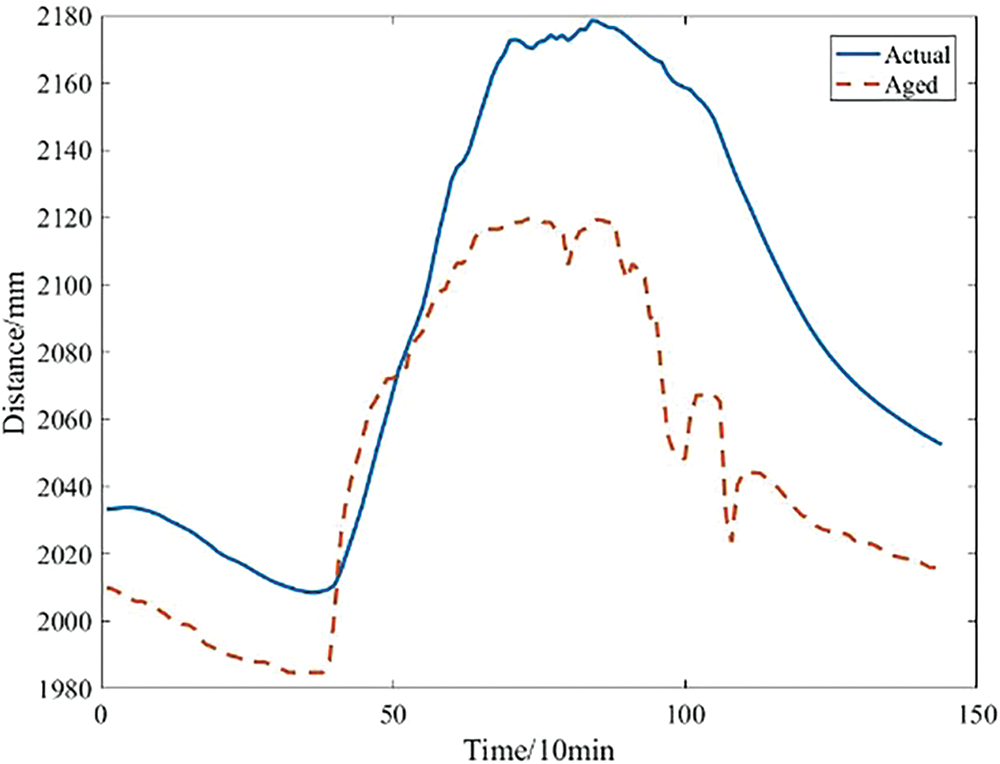
Figure 4: Comparison of displacement between aged and normal catenary
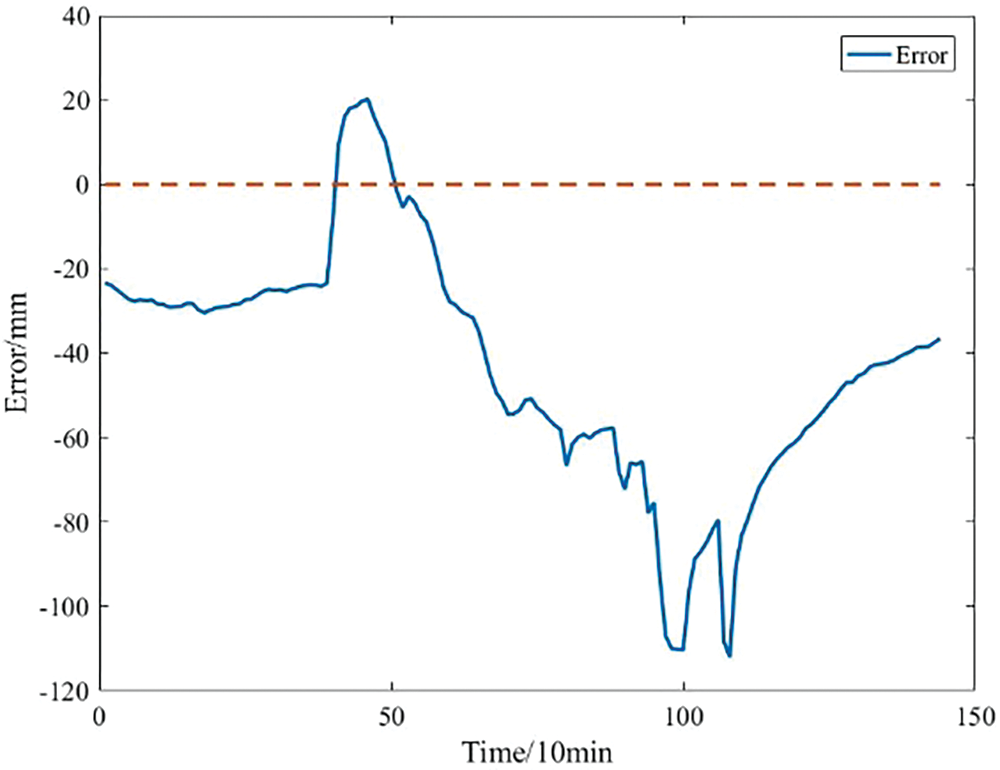
Figure 5: Displacement difference between aged and normal catenary
The values obtained from displacement sensors are susceptible to numerous influencing factors, including rain, wind, physical disturbances, etc. Without proper filtering of these observations, it can result in erroneous assessments. The aging prediction method employed in this paper relies on catenary displacement, making it crucial to account for significant interfering factors. Other factors like temperature and corrosion can manifest as changes in displacement. However, factors that do not have an abrupt impact on displacement data do not necessitate technical consideration.
The traditional KF architecture can be described as Fig. 6. The item R represents the measurement error covariance. The prior estimate error covariance is
where F indicates the state transition matrix,
where
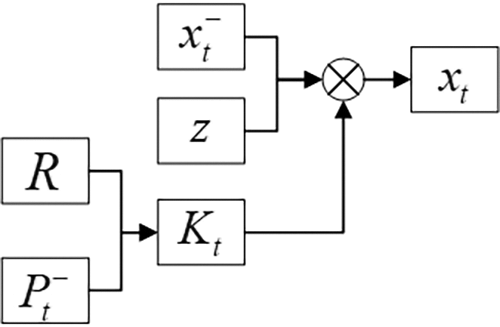
Figure 6: Traditional KF architecture
As seen in Eqs. (2) and (3), the optimal state of the KF is based on the output from the previous time, which exhibits hysteresis and is unable to effectively mitigate nonlinear interference. To enhance the anti-interference performance, this paper proposes replacing the prior state estimate equation of the KF with a T-S FNN model. The suggested structure is depicted in Fig. 7. Furthermore, the corresponding prior estimate error covariance has also been substituted. Additionally, the measurement error R has been replaced by
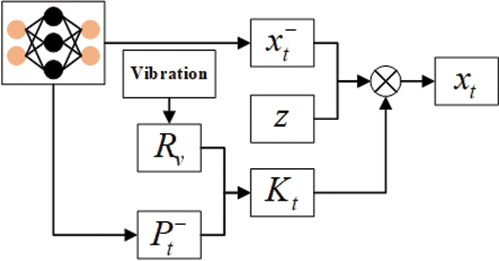
Figure 7: Proposed KF architecture
1) What are the inputs and outputs of the network?
2) How to design the structure of the network?
3) What methods are needed for training the network?
3.3 Design of the Network Structure
Compared with the traditional Mamdani fuzzy model, the T-S FNN adopts multiple linear functions for defuzzification. This enables the T-S fuzzy model combined with a back propagation neural network to reduce fuzzy rules and achieve better training results [25]. Based on the on-site collected data characteristics, this paper proposes to design the T-S fuzzy model as a three-input single-output model. As shown in Fig. 8, the model consists of the Premise Network and the Latter Network.
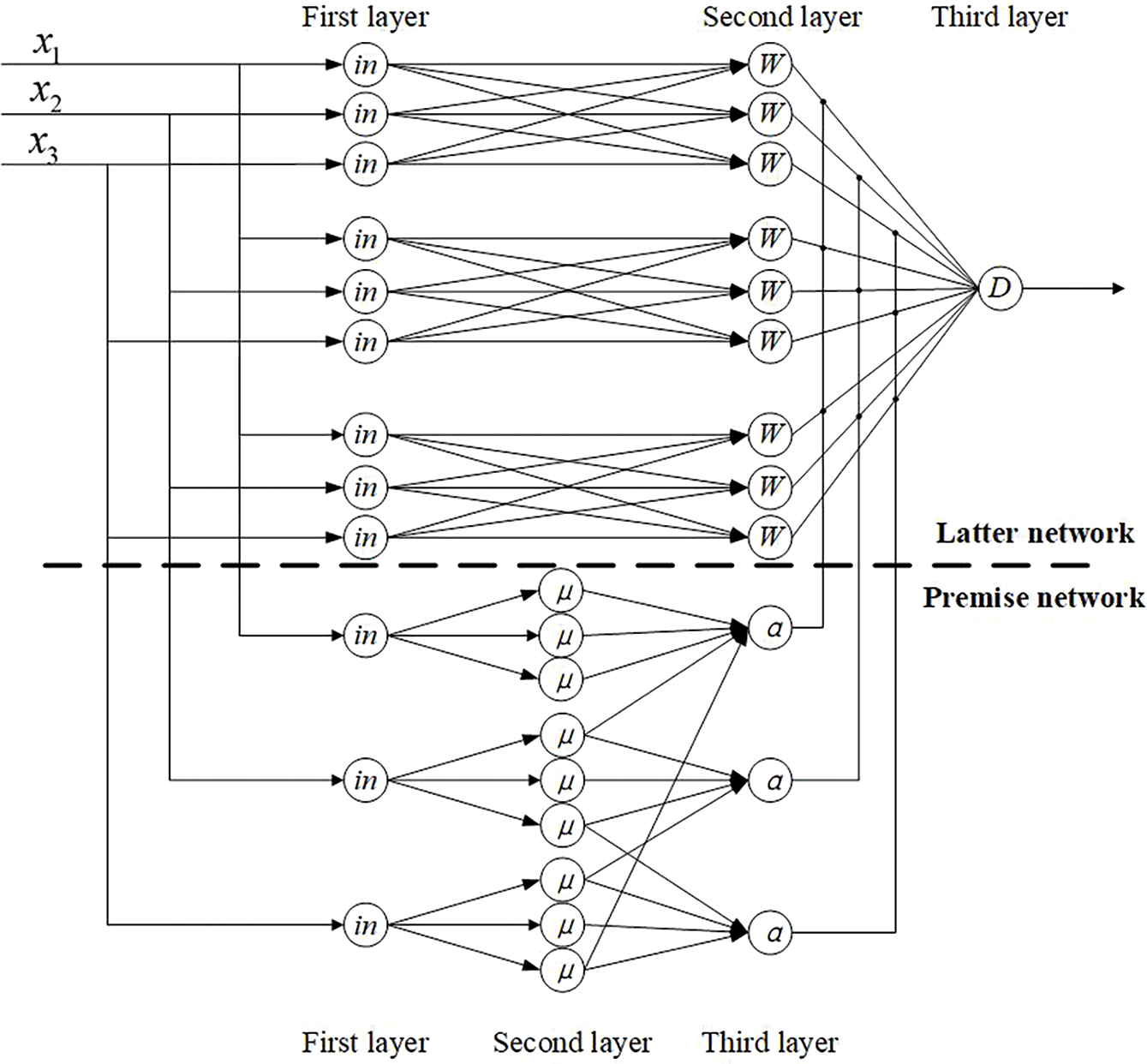
Figure 8: Proposed T-S FNN structure
The lower part shown in Fig. 8 is the Premise Network. The first layer is the input, represented by
where
where
The second layer of the Premise Network is the fuzzy language variable layer. This layer plays a primary role in computing the membership function for each component input from the first layer, which corresponds to its respective fuzzy set. This computation is carried out as follows:
where
The third layer represents the matching fuzzy rule layer, where each node corresponds to a specific fuzzy rule. The primary function of this layer is to match the fuzzy rules and compute the fitness of each rule. The fitness value is determined through the following calculation:
The third layer of the Premise Network also needs normalization. The specific calculation method is as follows:
After taking the minimum value and normalization, the coefficient vector
where a and b are the coefficients. Convert the coefficients into a linear function
Finally, take the minimum value to obtain the output
The Later Network is a fusion method based on the Premise Network and fuzzy system. It receives input signals from the Premise Network and outputs the results using fuzzy inference processing based on these signals. The network structure proposed in this paper is shown in the upper half of Fig. 8. The Later Network can be trained based on real-time data to improve the performance of fuzzy control. It consists of n subnetworks with the same structure, each of which generates an output.
The first layer of the subnetwork is the input layer, the same as the Premise Network. The second layer consists of m nodes, each of which can represent a fuzzy rule in a fuzzy model, and its main function is to calculate the consequences of each rule. The calculation method for the output of this layer is as follows:
where p indicate the usage weights of various fuzzy rules in the second layer.
The third layer is the output of the Later Network, which is the weighted sum of the Later Network of each rule. The weighted coefficients are the weights of each fuzzy rule, which means that the output of the Premise Network is used for the connection weights of the third layer of the Later Network:
In summary, FNN combines the advantages of fuzzy systems and neural networks, enabling the model to not only have self-learning and parallel processing capabilities but also handle fuzzy knowledge and utilize expert experience. In the Premise Network, the use of bell curves as input membership functions reduces training parameters while improving accuracy. Use Eqs. (7) and (8) to calculate the output of the membership function and normalize it. Output the result through Eq. (11), which has higher accuracy compared to constants. Using Eqs. (13) and (14) in the Later Network, parallel computation of the weights corresponding to each fuzzy rule is achieved.
After all, the output of the proposed T-S FNN model is
where k indicates training data volume, d represents the historical displacement of filtered. Eq. (15) elucidates that the process noise of the KF is transformed through the prediction process error of the T-S FNN model. The prior estimate error covariance and priori state estimate are defined as follows:
3.4 Adaptive Training Algorithm Design
Considering that the model of each catenary on-site is not the same, an adaptive algorithm can certainly improve the practicality of the algorithm. There are many learning algorithms for neural networks, such as Unsupervised learning algorithms based on iterative learning [26], Supervised learning algorithms [27], deep learning [28], etc. Supervised learning is suitable for big data-intensive and purposeful training. Deep learning requires a larger number of data for specific functional training. Unsupervised learning can use a small amount of data to quickly train the model. Considering real-time requirements, using an iterative Unsupervised learning algorithm to train the model can have a better effect.
The input membership function of the proposed fuzzy system is set to a bell curve. So the parameters that need to be adaptively updated in the Premise Network can be defined as the center value
where
where
Above all, the partial derivative of the error concerning the central and width of the membership function is as follows:
The learning algorithm for adjusting the parameters of the bell curve is as follows:
where
In summary, when designing adaptive algorithms for the FNN to select different fuzzy rules based on varying states, the inclusion of parameter
3.5 Measurement Error and KF Output
When the accuracy of the sensor is high, its interior error range is too small compared to the error range of the system measurement error, which cannot truly reflect the system error information. Therefore, the vibration data of the catenary is proposed as the KF measurement error. Then the measurement error covariance is calculated as follows:
where S is the vibration data. Then the KF gain is as follows:
where H is the observation matrix. Finally, the output state estimate of the KF is
The process of the aging prediction method for the railway catenary proposed in this paper is shown in Fig. 9. First, use on-site equipment to collect training data, including time, temperature, and filtered displacement data. Secondly, the trained model output used as the prior state estimate
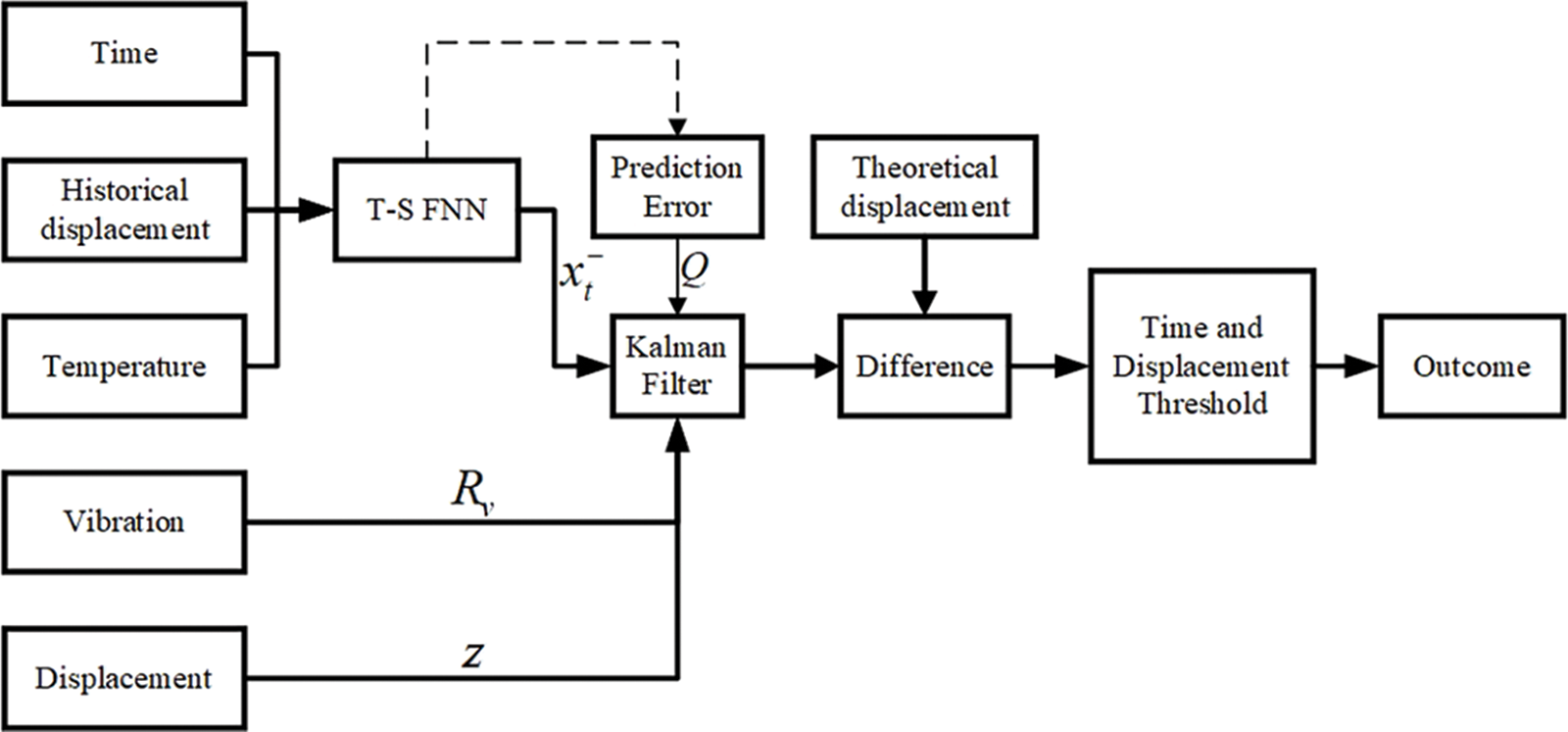
Figure 9: The structure of the proposed prediction method
5.1 Construction of Experimental Equipment
In the fields of neural networks and artificial intelligence, to validate algorithms and collect data, it is essential to establish a reasonable experimental platform [29–32]. To obtain sufficient and accurate data, as well as the authenticity of the experiment, the equipment structure used in this experiment is shown in Fig. 10. The control unit adopts a combination of MCU and FPGA, SHT30 is a high-precision temperature and humidity sensor, and 4GCAT1 is an IoT module using the CAT1 frequency band. The product is shown in Fig. 11. MCU is mainly responsible for network communication and peripheral control, and FPGA is mainly responsible for the implementation and acceleration of T-S FNN algorithms.
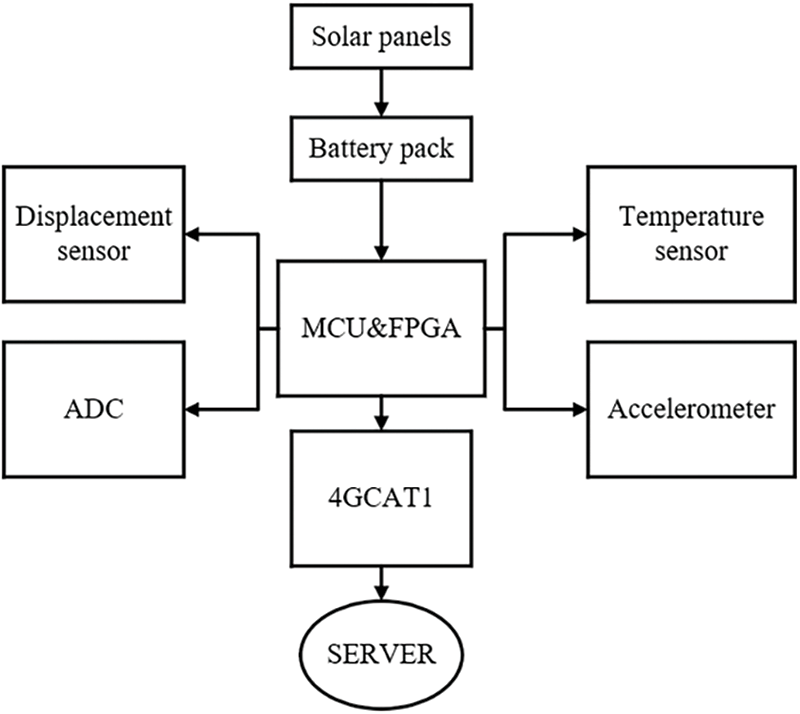
Figure 10: Topological structure of functional modules in experimental equipment

Figure 11: Experimental equipment products
To show the effectiveness of the proposed method, under the coordination of the local railway department, experimental equipment was installed in a local operating railway section for experiments. The experimental setting is shown in Fig. 12. The device within the red outline is the catenary weights, and the distance between the weights and the top pulley is the displacement of the catenary. Firstly, collect catenary data in a static state to study the vibration characteristics of the catenary. For this purpose, the equipment is installed on the weights at the end of the catenary and uses high-precision thermal resistance as a sensor to obtain temperature data. Then, a rope sensor modified by an encoder is used to measure the displacement of the catenary.

Figure 12: On-site installation of experimental equipment
Due to provisions, the complete dataset used in this experiment cannot be fully disclosed. However, for reference, some samples have been provided in the supplementary materials. The uploaded dataset sample can be found in Table S1.
5.2 Performance of the Proposed Training Method
To illustrate the effectiveness of the proposed training algorithm, we compare the performance of the proposed adaptive algorithm with the traditional backpropagation (BP) algorithm. The experimental dataset consists of 24-h data collected at a railway site. The experimental results are presented in Table 1, and the comparison of iteration times is depicted in Fig. 13.
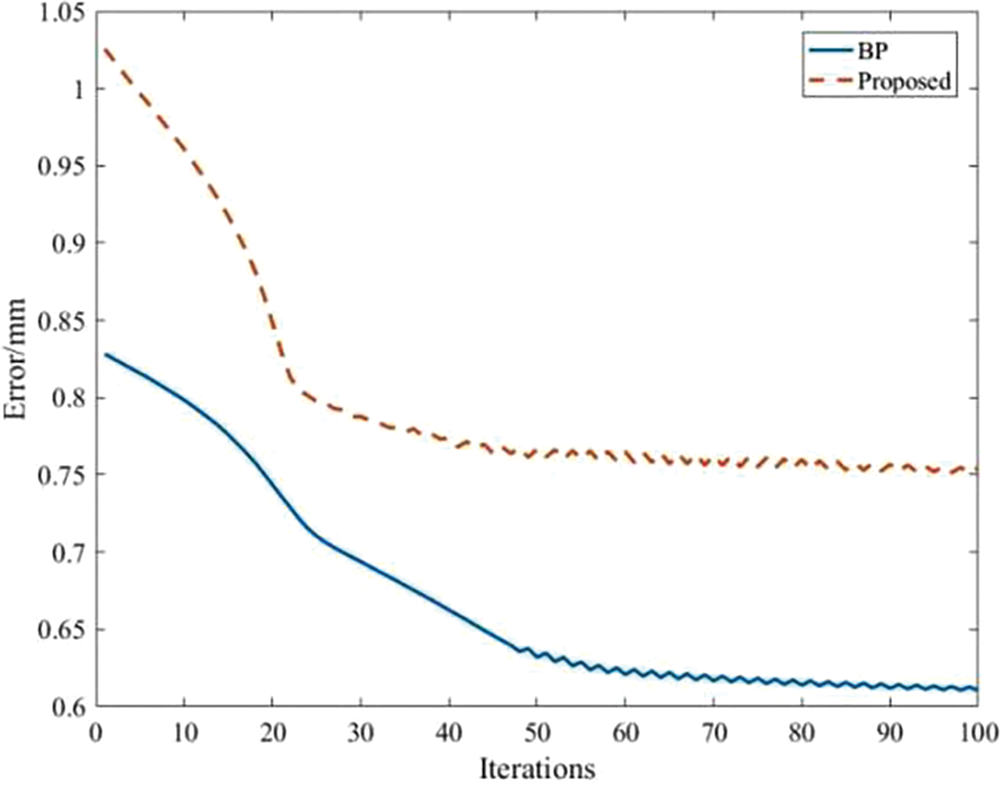
Figure 13: The proposed training algorithm training error over iterations
The results indicate that the suggested algorithm exhibits rapid convergence, with an increase in error of only 0.15 mm. Despite the slight growth in error, it has minimal effect on the prediction of aging. The purpose of this effect is to eliminate vague rules that bear minimal influence on the ultimate output result, thus enhancing computational efficiency.
5.3 Effectiveness of the Error Correction
To validate the effectiveness of replacing the KF measurement error, we conduct a comparison between using sensor internal noise and vibration information within the same dataset. The parameter of comparison is the disparity between the filtered and theoretical values. As illustrated in Fig. 14, the comparison showcases the filtering performance on three days of random data. Further details regarding the experimental data comparison can be found in Table 2, and visual comparisons of the filtered data are available in Figs. S1–S3.
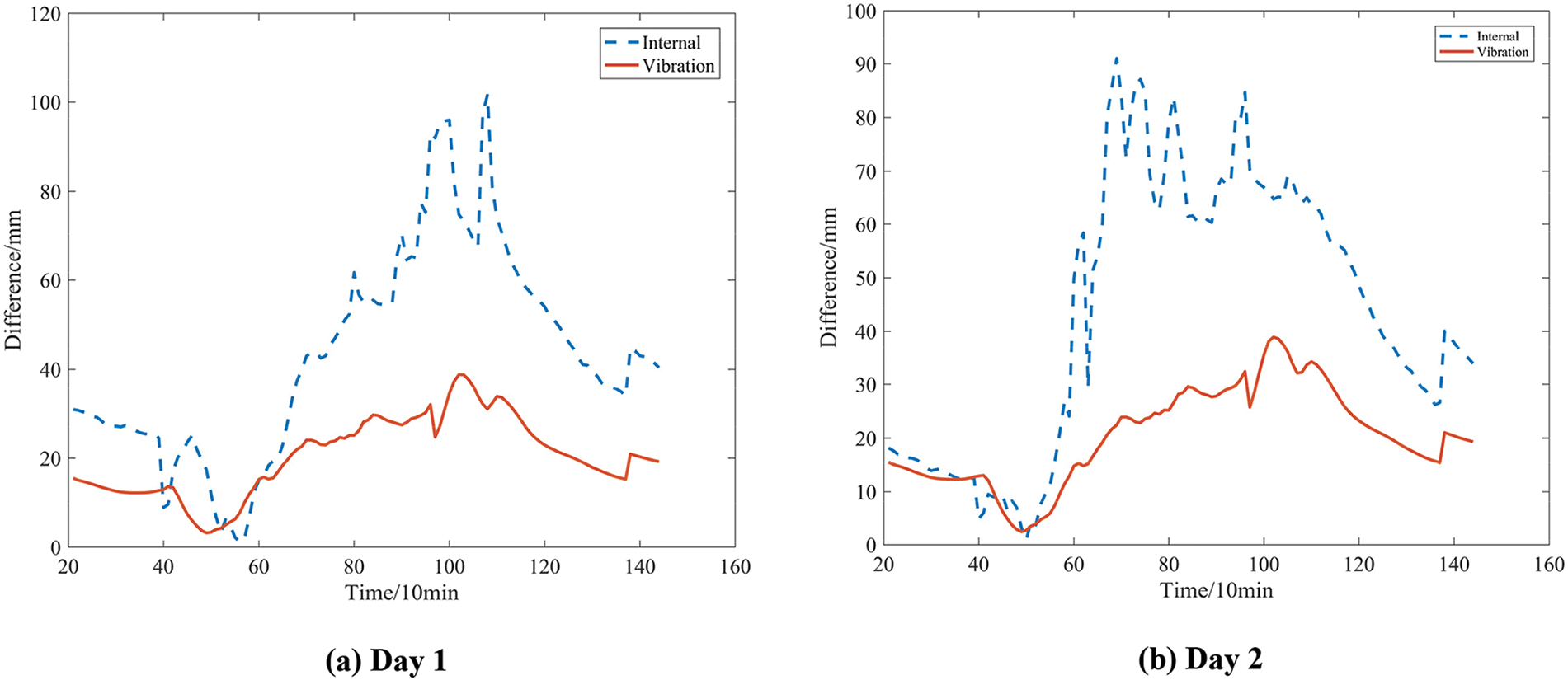
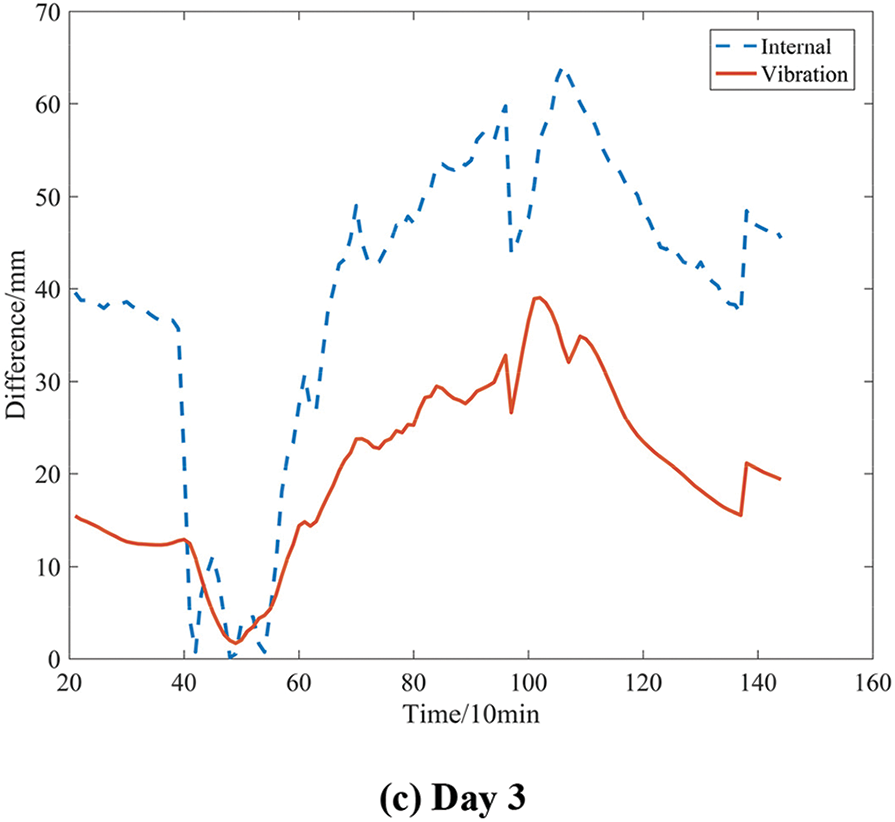
Figure 14: The impact of vibration on the KF

It can be seen from the results that using vibration information as the measurement error covariance of the KF can significantly reduce the amplitude and fluctuation of the displacement difference. The comparison of the standard deviation shows that using vibration data can significantly reduce the fluctuation of the catenary displacement. The reason for this result is that using catenary vibration information as observation noise can more accurately reflect the interference carried by sensors when detecting catenary displacement.
5.4 Comparison of the Prediction Performance
To assess the progressive nature of the proposed algorithm, we compare it with the unscented Kalman filter (UKF) in [10] and the KalmanNet in [13]. The test set comprises three days of data collected from sensors, with the comparison parameter remaining as the difference between the filtered and theoretical values. The results of this comparison are depicted in Fig. 15, and detailed experimental data can be found in Table 3. For a visual representation of the original filtered data comparison, refer to Figs. S4–S6.
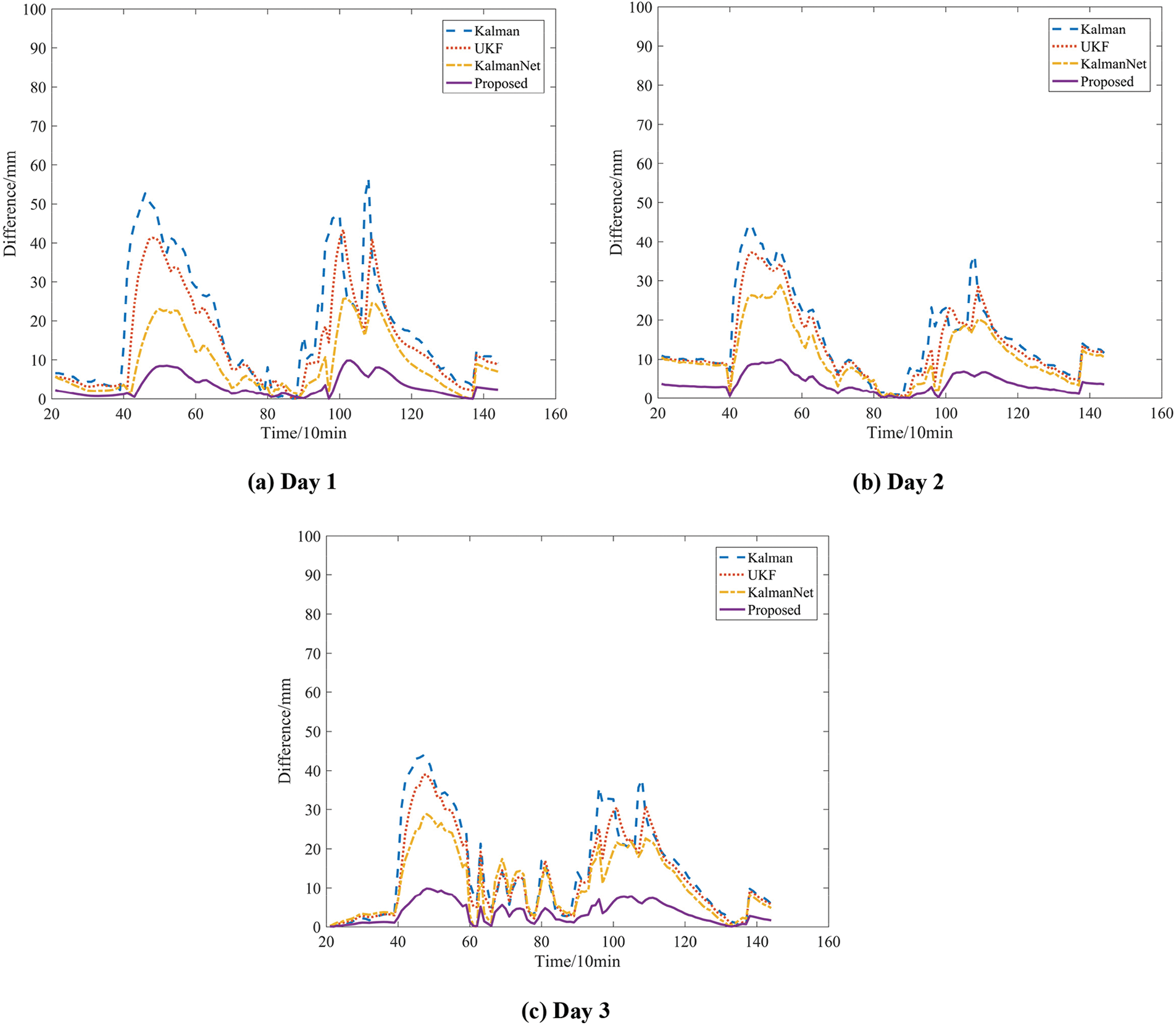
Figure 15: Comparison of filtering effects
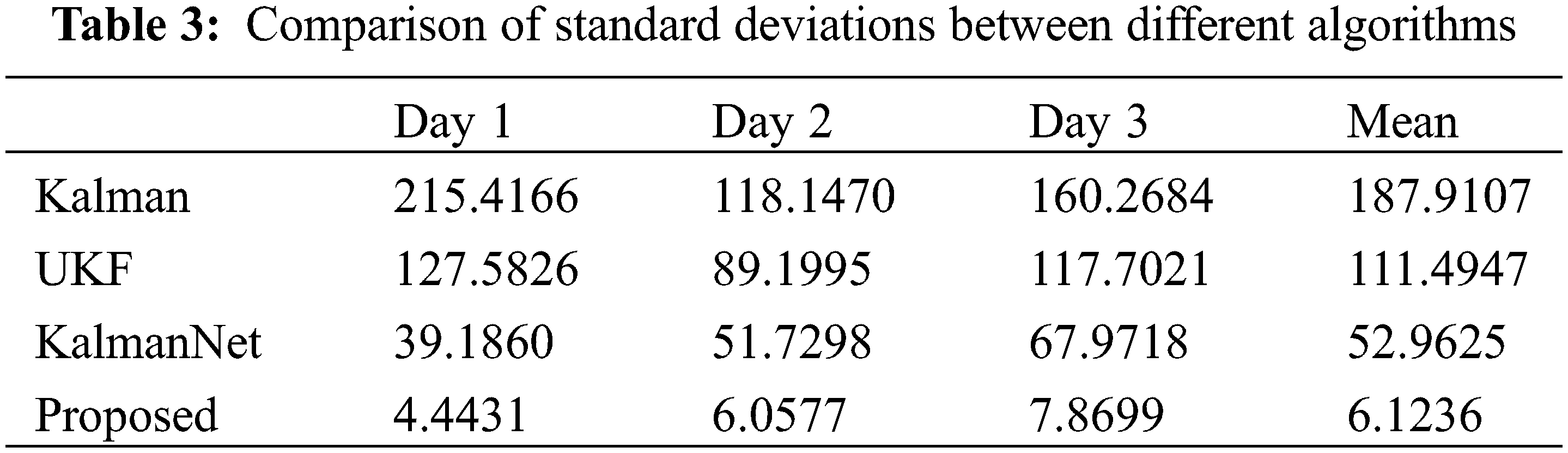
From the experimental results, compared to the traditional KF, the UKF, and the KalmanNet have a certain filtering effect. However, the filtering effect of the proposed algorithm is the most visible because it has made proprietary improvements to the problem discussed in this paper. From Fig. 15c, it can be seen that even for relatively less obvious interference, the proposed algorithm can still achieve better filtering performance.
To further verify the actual aging prediction ability of the proposed algorithm, a prediction accuracy comparison is also conducted. In this experiment, the fault diagnosis threshold is set to the displacement difference of the catenary greater than 20 mm and the duration exceeding 10 min. The comparative experimental results are shown in Table 4. The results show that the proposed algorithm greatly reduces the false alarm rate of faults caused by environmental factors or pantograph influence in the railway catenary system.
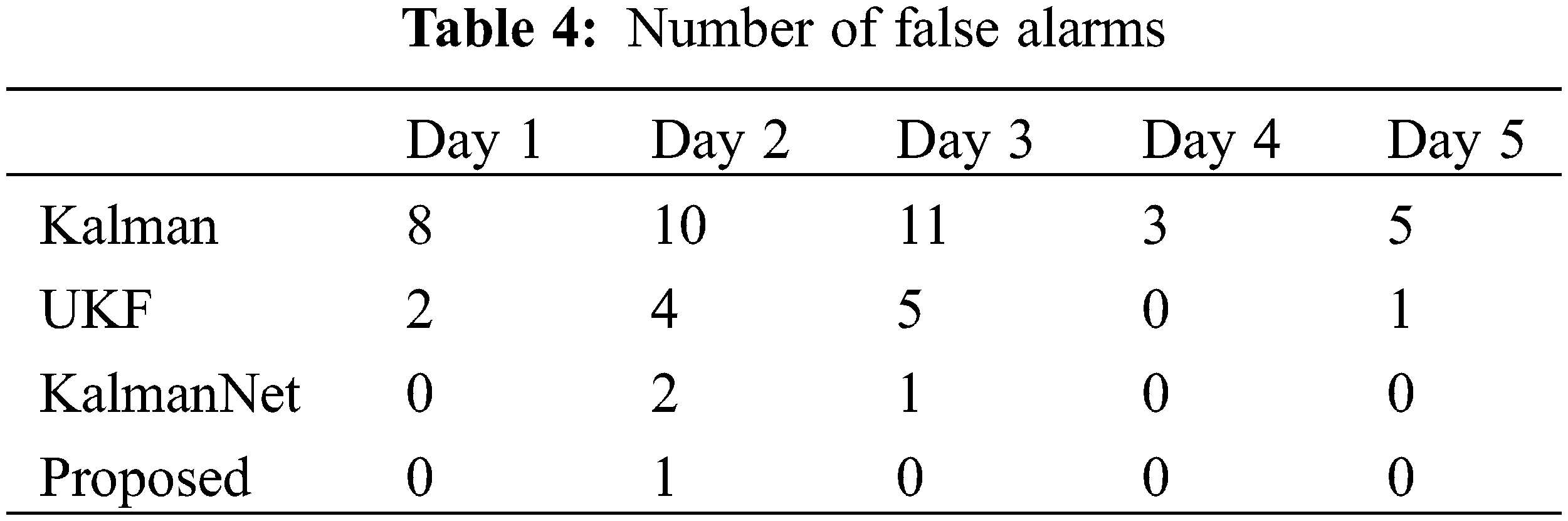
This paper proposes an improved KF algorithm to enhance the accuracy of aging prediction for the railway catenary. The suggested algorithm substitutes the priori state estimation and error in the KF procedure with the output and error of the T-S FNN model and uses the catenary vibration information as a replacement for sensor observation noise. To enhance the network’s training efficiency, an adaptive algorithm that dynamically selects fuzzy rules is suggested. Comparative experiments are conducted on an FPGA-based data acquisition and computing platform to verify the effectiveness of the proposed algorithm. The platform utilizes a modular pipeline design that enables rapid data processing. After comparing the experimental results, it is apparent that the proposed method possesses substantial advantages over other enhanced KF algorithms.
The model described in this paper is based on the study of a single railway catenary system, so the variable parameters considered are relatively few, and there may be some interference factors that are not considered in practical, resulting in a certain deviation in the prediction. So to further improve the accuracy of prediction and the universality of the model in multi-catenary systems, the future research goal will be positioned in multi-catenary systems.
Acknowledgement: The authors also thank the anonymous reviewers and referees for their valuable comments and suggestions.
Funding Statement: This work was supported by the Science and Technology Research Project of Henan Province (No. 222102210087) and the Science and Technology Research Project of Henan Province (No. 222102220102).
Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: Jie Li, Yongtao Hu; data collection: Rongwen Wang; analysis and interpretation of results: Jie Li, Rongwen Wang; draft manuscript preparation: Rongwen Wang, Jinjun Li. All authors reviewed the results and approved the final version of the manuscript.
Availability of Data and Materials: The training data used in this paper is private to the enterprise and cannot be publicly disclosed completely.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
Supplementary Materials: The supplementary material is available online at https://doi.org/10.32604/sdhm.2023.044023.
References
1. Zheng, S., Wu, Z., Xu, Y., Wei, Z. (2022). Intrusion detection of foreign objects in overhead power system for preventive maintenance in high-speed railway catenary inspection. IEEE Transactions on Instrumentation and Measurement, 71, 1–12. [Google Scholar]
2. Fan, S. (2021). Electrical control online monitoring system based on internet of things. Wireless Communications and Mobile Computing, 2021, 1–12. [Google Scholar]
3. Mao, Q., Wang, L., Nie, J., Zhao, Y. (2022). Enhancing strength and electrical conductivity of Cu–Cr composite wire by two-stage rotary swaging and aging treatments. Composites Part B: Engineering, 231, 109567. [Google Scholar]
4. Chen, J., Liu, Z., Wang, H., Liu, K. (2017). High-speed railway catenary components detection using the cascaded convolutional neural networks. 2017 IEEE International Conference on Imaging Systems and Techniques (IST), pp. 1–6. Beijing, China. [Google Scholar]
5. Chen, R., Lin, Y., Jin, T. (2022). High-speed railway pantograph-catenary anomaly detection method based on depth vision neural network. IEEE Transactions on Instrumentation and Measurement, 71, 1–10. [Google Scholar]
6. Wu, Y., Qin, Y., Qian, Y., Guo, F. (2021). Automatic detection of arbitrarily oriented fastener defect in high-speed railway. Automation in Construction, 131, 103913. [Google Scholar]
7. Kang, G., Gao, S., Yu, L., Zhang, D. (2018). Deep architecture for high-speed railway insulator surface defect detection: Denoising auto encoder with multitask learning. IEEE Transactions on Instrumentation and Measurement, 68(8), 2679–2690. [Google Scholar]
8. Xu, J., Xu, X., Li, Q. (2023). Data processing for rail level dynamic inspection based on an adaptive Kalman filter. Insight-Non-Destructive Testing and Condition Monitoring, 65(7), 373–377. [Google Scholar]
9. Cunillera, A., Bešinović, N., van Oort, N., Goverde, R. M. (2022). Real-time train motion parameter estimation using an unscented Kalman filter. Transportation Research Part C: Emerging Technologies, 143, 103794. [Google Scholar]
10. Fei, H., Liu, B., Wang, L., Fan, L. (2023). Optimal estimation of injection rate for high-pressure common rail system using the extended Kalman filter. Measurement, 220, 113385. [Google Scholar]
11. Liu, D., Jiang, W., Cai, B., Heirich, O., Wang, J. et al. (2023). Robust train localisation method based on advanced map matching measurement-augmented tightly-coupled GNSS/INS with error-state UKF. The Journal of Navigation, 76(2–3), 316–339. [Google Scholar]
12. Long, Z., Bai, M., Ren, M., Liu, J., Yu, D. (2023). Fault detection and isolation of aeroengine combustion chamber based on unscented Kalman filter method fusing artificial neural network. Energy, 272, 127068. [Google Scholar]
13. Revach, G., Shlezinger, N., Ni, X., Escoriza, A. L., Van Sloun, R. J. et al. (2022). KalmanNet: Neural network aided Kalman filtering for partially known dynamics. IEEE Transactions on Signal Processing, 70, 1532–1547. [Google Scholar]
14. Kim, D., Kim, G., Choi, S., Huh, K. (2021). An integrated deep ensemble-unscented Kalman filter for sideslip angle estimation with sensor filtering network. IEEE Access, 9, 149681–149689. [Google Scholar]
15. Liang, Y., Zhao, M., Liu, X., Jiang, J., Lu, G. et al. (2023). Image splicing compression algorithm based on the extended Kalman filter for unmanned aerial vehicles communication. Drones, 7(8), 488. [Google Scholar]
16. Deng, Z., He, C., Liu, Y. (2021). Deep neural network-based strategy for optimal sensor placement in data assimilation of turbulent flow. Physics of Fluids, 33(2), 025119. [Google Scholar]
17. Abdelrahim, E. M. (2021). Binary particle swarm optimization-based TS fuzzy predictive controller for nonlinear automotive application. Neural Computing and Applications, 33(7), 2803–2818. [Google Scholar]
18. Yang, K., Dian, S., Guo, B. (2021). Predictive control of thermal barrier coating temperature based on TS fuzzy model. 2021 6th International Conference on Automation, Control and Robotics Engineering (CACRE), pp. 145–149. Dalian, China. [Google Scholar]
19. Zang, Y., Shangguan, W., Cai, B., Wang, H., Pecht, M. G. (2021). Hybrid remaining useful life prediction method. A case study on railway D-cables. Reliability Engineering & System Safety, 213, 107746. [Google Scholar]
20. Narges, K. H., Ahmad, M., Fereydoun, G. M. (2022). A hybrid fault diagnosis scheme for railway point machines by motor current signal analysis. Proceedings of the Institution of Mechanical Engineers, Part F: Journal of Rail and Rapid Transit, 236(9), 1026–1034. [Google Scholar]
21. Jan, S. U., Lee, Y. D., Koo, I. S. (2021). A distributed sensor-fault detection and diagnosis framework using machine learning. Information Sciences, 547, 777–796. [Google Scholar]
22. Yao, Y., Huang, P., Zhou, N., Yang, Z., Zhang, W. (2023). Effect of ambient temperature on current collection quality in pantograph–Catenary interaction. International Journal of Structural Stability and Dynamics, 23(13), 2350145. [Google Scholar]
23. Fu, X., Lin, G., Yang, X. (2022). Parameter identification for current–temperature relationship of contact wire under natural convection. International Journal of Electrical Power & Energy Systems, 135, 107554. [Google Scholar]
24. Chen, Y., Song, B., Zeng, Y., Du, X., Guizani, M. (2021). Fault diagnosis based on deep learning for current-carrying ring of catenary system in sustainable railway transportation. Applied Soft Computing, 100, 106907. [Google Scholar]
25. Lv, Y., Zhou, Q., Li, Y., Li, W. (2021). A predictive maintenance system for multi-granularity faults based on AdaBelief-BP neural network and fuzzy decision making. Advanced Engineering Informatics, 49, 101318. [Google Scholar]
26. Kennedy, R. K., Salekshahrezaee, Z., Villanustre, F., Khoshgoftaar, T. M. (2023). Iterative cleaning and learning of big highly-imbalanced fraud data using unsupervised learning. Journal of Big Data, 10(1), 106. [Google Scholar]
27. Son, H., Ahn, J., Chung, A. D., Drumwright, M. E. (2023). From the black box to the glass box: Using unsupervised and supervised learning processes to predict user engagement for the airline companies. International Journal of Information Management Data Insights, 3(2), 100181. [Google Scholar]
28. Dong, S., Wang, P., Abbas, K. (2021). A survey on deep learning and its applications. Computer Science Review, 40, 100379. [Google Scholar]
29. Yu, X., Li, Y., Li, X., Wang, L., Wang, K. (2023). Research on outdoor mobile music speaker battery management algorithm based on dynamic redundancy. Technologies, 11(2), 60. [Google Scholar]
30. Yu, X., Ma, N., Zheng, L., Wang, L., Wang, K. (2023). Developments and applications of artificial intelligence in music education. Technologies, 11(2), 42. [Google Scholar]
31. Yi, Z., Chen, Z., Yin, K., Wang, L., Wang, K. (2023). Sensing as the key to the safety and sustainability of new energy storage devices. Protection and Control of Modern Power Systems, 8(1), 1–22. [Google Scholar]
32. Sun, X., Zhang, Y., Zhang, Y., Wang, L., Wang, K. (2023). Summary of health-state estimation of lithium-ion batteries based on electrochemical impedance spectroscopy. Energies, 16(15), 5682. [Google Scholar]
Cite This Article
 Copyright © 2024 The Author(s). Published by Tech Science Press.
Copyright © 2024 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF Downloads
Downloads
 Citation Tools
Citation Tools