Numerical Study on Mechanism of Blast-Induced Damage Considering Guiding Effect of Water Jet Slot

1  Introduction

Among the most commonly used rock breaking methods in China, drilling and blasting technology has been widely implemented for rock excavation in projects related to tunnel engineering, water conservancy and hydropower engineering, nuclear power infrastructure, and mine roadway engineering owing to its unique advantages of good applicability to various geotechnical conditions, cost-effectiveness, and ease of operability [1,2]. The drilling and blasting method used in excavating rock mass inevitably causes damage to the remaining rocks, which deteriorates their mechanical properties resulting in the reduction of the bearing capacity and stability of rock excavation engineering [3,4]. Therefore, studying the evolution law of rock mass damage during blasting excavation has become important.

Rock damage under blast loading is a complex dynamic evolution process. Focusing on this problem, many scholars have conducted a considerable amount of work and achieved distinct results. On the basis of previous studies, Liu et al. [5,6] successively conducted two-dimensional and three-dimensional numerical simulation studies on rock blasting damage and failure process, which further improved the blasting damage model. Li et al. [7] simulated the fluctuation of rock mass during blasting and established a relationship model that can reflect the interaction between stress wave propagation and rock mass fluctuation based on the theory of stress wave propagation in rock mass, which overcomes the difficult problem that continuous damage mechanics theory cannot be simulated in the blasting process. Li et al. [8,9] established the fractal damage constitutive relation based on fractal damage theory and verified the analytical solution of the transmission and reflection coefficient of a stress wave passing through an irregular joint on the basis of linear displacement discontinuity model. By combining numerical simulation, Xia [10] studied the scope of blasting damage in specific projects and analyzed and verified the optimal blasting parameters through field tests. Based on the damage theory and considering the inhomogeneity of rock, Liang [11] established an inhomogeneity model to analyse the rock fracture process from the mesoscopic level using numerical analysis software. The numerical simulation of the double-hole penetration process under four conditions of different blasting stress wave waveforms, hole spacings, in-situ stresses, and hole circumferential slits was performed by Wei et al. [12,13]. The influence of different lateral pressure coefficients and buried depths on the propagation law of blasting cracks is also studied. The results show that the blasting stress wave is a dominant factor in the initial blasting cracks and the detonation gas further expands and penetrates the cracks. In addition, the crack evolution process is closely related to the ground stress and the main direction of crack propagation tends toward the maximum ground stress direction. Ding et al. [14] studied the rock damage mechanism after underground excavation in water-rich soft rock and derived equations for the evolution of damage variables and deterioration of rock parameters considering time effect. A damage constitutive model of rock subjected to excavation unloading and water-weakening is then proposed considering the influence of water immersion time. The field monitoring data of a typical section in the Xujiadi tunnel is used to verify the applicability and accuracy of the proposed dual softening model and simulation method excavation in the water-rich soft rock. Meng et al. [15] investigated the evolution mechanism of rock mass damage under the empty blasthole effect by applying a tension–compression constitutive model of rock mass damage. The results indicated that existence of the empty blasthole significantly enhances the tensile stress and stress concentration factor in the rock mass that is near the empty blasthole. Meanwhile, the rock mass near the empty blasthole is mainly damaged by tension. Liu et al. [16] established an anisotropic dynamic damage constitutive model for rock materials based on the dynamic damage evolution and Hoffman failure criterion. The wave velocity of surrounding rock before and after blasting of the shallow-buried twin tunnels with small spacing is then tested using non-metallic ultrasonic detector. The damage of surrounding rock is evaluated by the change of wave velocity based on the wave measuring theory. Based on the excavation in the auxiliary tunnel of Jinping II hydropower station, Luo et al. [17] proposed a method of blasting damage simulation based on the normal direction impact load. The results also showed that the blasting damage depth of tunnel excavation has a significant correlation with the in-situ stress level and the damage depth increases after decreasing, with increase in stress level.

The above research mainly focuses on the evolution law of rock damage of ordinary circular borehole blasting under different conditions and further reveals the fracture mechanism of rock. For directional controlled blasting with water jet assistance [18], the existence of water jet slot inevitably affects the evolution law of rock blast-induced damage, which is different from the evolution law of ordinary circular borehole blasting. Therefore, an attempt was made to study the evolution mechanism of blast-induced damage under the guiding effect of water jet slot. First, the rock-like material was chosen as physical model test object, and the experiment was conducted to calibrate the numerical model parameters in ANSYS/LS-DYNA. Subsequently, the calibrated numerical models were used to simulate the blast-induced damage of ordinary circular blasthole and slotted borehole blasting. Finally, according to rock blasting theory, the blast-induced damage mechanism under the guiding effect of water jet slot was analyzed.

2  Numerical Simulation Modelling

2.1 Constitutive Model Parameters of Material and Its Validation

Single ordinary circular borehole blasting experiment was conducted to calibrate the material parameters, which will be used to verify the material model and applied in subsequent numerical simulation. The test specimen is composed of normal Portland cement (R42.5), uniform-grained sand, and water in the mass ratio of 1:2.41:0.56. The entire model has dimensions 300 × 300 × 200 mm, and the diameter of the blasthole is 8 mm. Its material mechanical parameters are as shown in Table 1. In addition, #2 rock explosive was chosen as the explosion source, the explosive charge was 0.006 kg, and the initiation mode was hole-bottom initiation.

In addition, quasi two-dimensional numerical simulation model of single ordinary circular borehole blasting was established for comparison with the experimental test results, as shown in Fig. 1b. The size of numerical model is same as that of the test specimen with a blasthole of 8 mm diameter. The total number of meshed elements is approximately 600,000.

Figure 1: Single borehole blasting and its comparation. (a) Physical model experiment; (b) Numerical simulation model

Fig. 1 shows the comparison of single ordinary circular borehole blasting physical test result and simulated result. In this study, a damage threshold D of 0.7 is reasonable for consistency between the physical test result and numerical result according to previous studies [19,20]. By comparing Fig. 1a with Fig. 1b, it can be found that the distribution of crushing zone, blast-induced damage evolution law, and blast-induced crack propagation law in numerical simulation results are similar to those in the physical test results. This is because force generated by the explosion caused by explosives is uniformly distributed along the radial direction of the blasthole, and the rock damage formed in all directions of the blasthole is approximately the same. Therefore, blast-induced cracks are also evenly distributed around blasthole. Hence, the calibrated numerical model is capable as well as feasible for studying the characteristic of blast-induced damage evolution and blast-induced crack propagation.

2.1.1 RHT Material Model for Rock-Like Material

In this study, the dynamic response and damage process of rock mass were simulated by Riedel, Hiermaier, and Thoma (RHT) in LS-DYNA, which was widely used in numerical simulation of concrete and rock [21]. The damage degree of the RHT material model is given by formula (1) and formula (2).

D=∑Δεpεf (1)

εf=D1(p∗−pspall∗)D2≥εminf (2)

here Δεp is accumulated plastic strain, εf is failure strain and εfmin is minimum failure strain, D1 and D2 are damage constant.

The effect of strain rate on the rock strength is clear. The dynamic increase factors of compression and tension can be expressed by formula (3).

Frate={1+(ε∙ε0∙)α, p>13fc, (compress)1+(ε∙ε0∙)δ, p>13ft, (tensile) (3)

here α is compressive strain rate factor and the δ is tensile strain rate factor.

In addition, P-A state equation was adopted to describe the relationship between hydrostatic pressure, material density and internal energy. The equation of state of fully compacted concrete can be described by formula (4).

{P=A1μ+A2μ2+A3μ3+(B0+B1μ)ρ0e, μ>0P=T1μ+T2μ2+B0ρ0e, μ<0 (4)

here μ = ρ/ρ0 −1 is relative coefficient of volume change, μ > 0 indicates volume compression, μ < 0 indicates volume expansion, ρ0 is initial reference density, e is specific internal energy, A1, A2, A3, B0, B1, T0, T1 is material parameters. The material parameters of constitutive model are shown in Table 2.

2.1.2 Material Model Parameters of Charge

The charge was modeled by MAT_HIGH_EXPLOSIVE_BURN in LS-DYNA, and its state equation of Jones–Wilkins–Lee (JWL) can be expressed by formula (5) [22].

Pe=A(1−ωR1V)e−R1V+B(1−ωR2V)e−R2V+ωEeV (5)

here pe is the pressure produced by the detonation products from the high explosive, ω, A, B, R1, and R2 are user-defined input parameters, V is the relative volume, and Ee is the internal energy per initial volume. The model parameters of charge are shown in Table 3.

2.1.3 Material Model Parameters of Air

Air was modelled by the material model of MAT_NULL with the Gruneisen equation in LS-DYNA, and the pressure can be calculated by formula (6) [23].

{Pa=C0+C1μ+C2μ2+C3μ3+(C4+C5μ+C6μ2)Eaμ=1Va−1 (6)

here ρa is density of air, Va is relative volume of air, Ea is internal energy of air, C0, C1, C2, C3, C4, C5, and C6 are user-defined constants, and the model parameters of charge are shown in Table 4.

2.2 Numerical Grid Model

Cylindrical charge structure was widely used in actual blasting operation, and the force generated by explosion of explosive uniformly acts on the hole wall in the axial direction of the hole during blasting. Therefore, it can be simplified as a plane strain problem in the analysis of blast-induced damage. Then, the quasi-two-dimensional numerical simulation model was established, and the total number of meshed elements is approximately 600,000. The unit system is g-mm-ms. The simulation model for double slotted blastholes and the layout of monitoring points are shown in Fig. 2, in which, the size of rock is 400 mm × 400 mm × 3 mm, R is radius of blasthole, and R is 4 mm, the length of water jet slot is 4 mm, the width of water jet slot is 0∼1 mm, the angle of water jet slot is 15°, Db is distance between the double blastholes, Dm is distance between monitoring point and blasthole.

Figure 2: Schematic numerical simulation model. (a) Layout of numerical simulation model; (b) Schematic diagram of slotted blasthole; (c) Layout of monitoring points

3  Algorithm and Solution of Blasting Model

According to rock blasting theory [24,25], shock wave interacts with the rock mass around blasthole and produces impact wave in rock mass after explosive blasts. The rock near explosion can be regarded as fluid due to the overpressure produced by explosion and large deformation occurs. Therefore, even Lagrange algorithm has the priority of less computation time and accurately describing the boundary movement of structure, it also could cause element distortion even leads to abnormal termination of calculating when dealing with the large deformation numerical calculation. In order to avoid the above problems, fluid-solid coupling algorithm was adopted for the analysis of the explosive detonation, of which, Arbitrary-Lagrangian-Eulerian algorithm (ALE) will be used for explosive and air which filled in the water jet slot, Lagrange algorithm for rock and protecting pipe. The material derivative equation and the governing equations of the ALE algorithm can be expressed as formula (7)–(10) [22].

df(X, t)dt=∂f(ξ, t)∂t+(vi−wi)∂f(x, t)∂xi (7)

∂ρ∂t=ρ∂υi∂x+ωi∂ρ∂x (8)

ρ∂υi∂t+ρωi∂υi∂xj=∂σij∂xj+ρfi (9)

ρ∂e∂t=σij∂υi∂xj−∂q∂xj−ρωi∂e∂xi (10)

here ρ is the density, υi is the velocity of particle, fi is body force, qi is heat flux, ωi is velocity of the computational grid, xi is lagrangian coordinate system, yi is eulerian coordinate system, e is Internal energy of unit mass, σij is Cauchy stress tensor, subscript i and j stand for the direction of coordinate.

At the same time, meshes of explosive and air were joined with common nodes. Then the fluid-solid coupling was defined between the meshes of the explosive, air and rock by the keyword of CONSTRAINED_LAGRANGE_IN_SOLID [26].

According to the characteristics of high-speed deformation of the material in blasting process, the calculation time is 2 ms and the time Step Scale Factor (TSSFAC) is 0.67. In addition, non-reflecting boundary condition is set around the model to simulate the blasting process of rock in infinite region.

4  Results and Analysis

4.1 Single-Hole Blasting

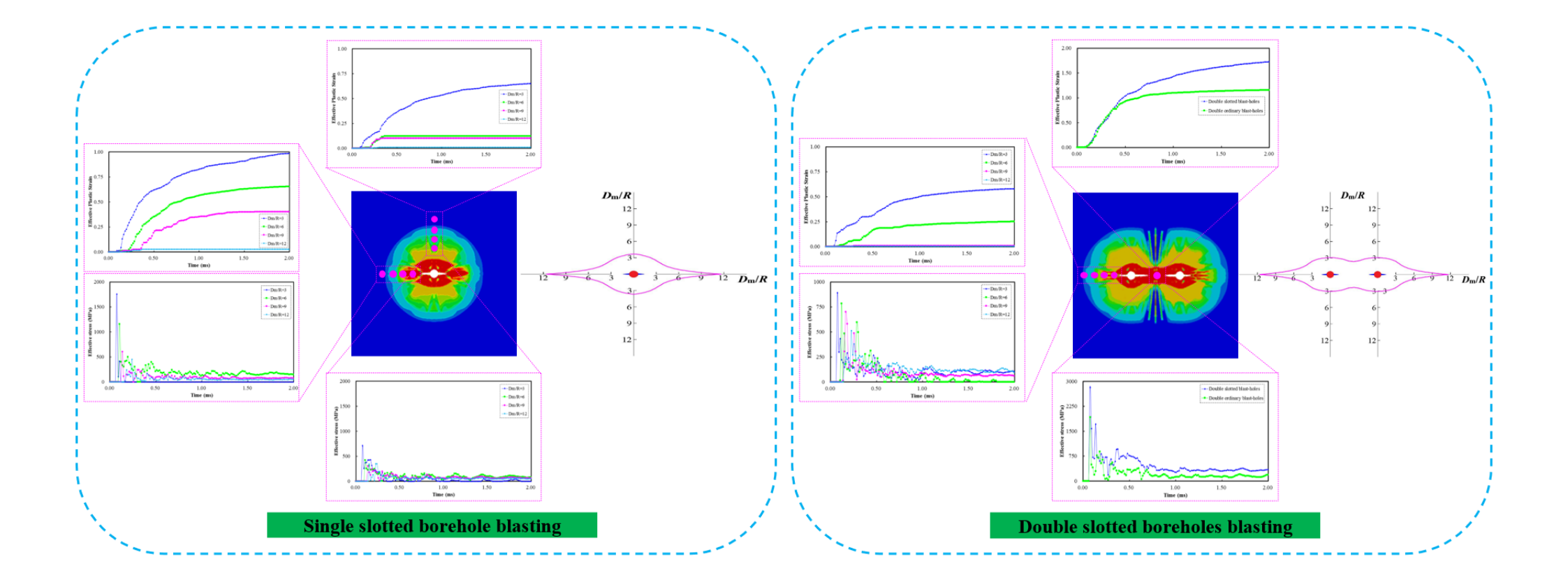
Figs. 3 and 4 indicate the schedule change rule of effective stress of different monitoring points for single ordinary circular borehole blasting and single slotted borehole blasting. According to the blasting theory [23,24], detonation gas acts on the blasthole rock mass and produces the strong shock waves at the moment after the explosive explosion, which can destroy the rock and form a certain range of crushing zones. Subsequently, blast-induced cracks further expand and penetrate under the quasi-static action of detonation gas. For single ordinary circular borehole blasting, explosive energy is approximately uniformly distributed around the blasthole, and overpressure is formed around the blasthole. Then, detonation gas wedges into the blast-induced cracks and lets the cracks expand, so that the final blast energy of a normal round hole is distributed diagonally along the center of blasthole. Fig. 3 shows that high explosion effective stress is formed near the blasthole and the effective stress decreases uniformly gradually with the increase in Dm/R. In addition, the peak value and time history variation of the effective stress of measuring points at the same distance from the blasthole are approximately the same in both horizontal and vertical directions of the blasthole.

Figure 3: Effective stress–time curves of different monitoring points for single ordinary circular borehole blasting. (a) Monitoring points in vertical direction; (b) Monitoring points in horizontal direction

Figure 4: Effective stress–time curves of different monitoring points for single slotted borehole blasting. (a) Monitoring points vertical direction; (b) Monitoring points in horizontal direction

For slotted borehole blasting, the existence of water jet slot can affect the propagation and action direction of explosion energy, especially for the detonation gas, which changes the propagation law of blast-induced cracks, and lets it expand along the direction of water jet slot [18]. Fig. 4 indicates that the effective stress of rock in horizontal direction is significantly greater than that in the vertical direction. By comparing Figs. 4a and 4b, it can be seen that when Dm/R is 3, 6, 9 and 12, respectively, the peak value of effective stress of rock in horizontal direction is 146.76%, 175.30%, 99.57% and 28.41% higher than that in vertical direction, respectively. In addition, by comparing Figs. 3 and 4, it can be seen that when Dm/R is 3, 6, 9 and 12, respectively, the peak value of effective stress of rock for single slotted borehole blasting is 117.35%, 88.42%, 4.82% and 10.93% higher than that for single ordinary circular borehole blasting in the horizontal direction, and the peak value of effective stress of rock for single slotted borehole blasting is 17.82%, 35.66%, 46.88% and 29.97% lower than that for single ordinary circular borehole blasting in the horizontal direction, which indicates that the explosion energy is focused in horizontal direction under the guiding effect of water jet slot.

Figs. 5 and 6 indicate the schedule change rule of the effective plastic strains of different monitoring points for single ordinary circular borehole blasting and single slotted borehole blasting. For single ordinary circular blasthole, due to the uniform effect of explosion energy on the blasthole wall during blasting, the schedule change rule of effective plastic strain of different monitoring points at the same distance from the blasthole are approximately the same in the vertical and horizontal directions. However, for single slotted borehole blasting, the schedule change rule of effective plastic strain of different monitoring points at the same distance from blasthole are different. By comparing Figs. 6a and 6b, it can be seen when the Dm/R values are 3, 6, 9 and 12, respectively, the peak values of effective plastic strain of rock for single slotted borehole blasting are 21.48%, 59.95%, 17.81%, and 22.10% higher than that for single ordinary circular borehole blasting in the horizontal direction, and the peak values of effective plastic strain of rock for single slotted borehole blasting are 20.61%, 75.82%, 69.73% and 35.59% lower than that for single ordinary circular borehole blasting in the horizontal direction. In addition, with increase in Dm/R, the increment of effective plastic strain becomes smaller.

Figure 5: Effective plastic strain–time curves of different monitoring points for single ordinary circular borehole blasting. (a) Monitoring points in vertical direction; (b) Monitoring points in horizontal direction

Figure 6: Effective plastic strain–time curves of different monitoring points for single slotted borehole blasting. (a) Monitoring points in vertical direction; (b) Monitoring points in horizontal direction

The evolution law of single slotted blasthole blast-induced damage is shown in Fig. 7, which shows that blast wave energy acts on the blasthole wall and forms a circular damage area in the initial stages of the explosion, as shown in Fig. 7a. Subsequently, the shape of the blast damage circle gradually changes from round to oval. In addition, the obvious damage area is formed in the direction of water jet slot. This is because the effect of blast wave on the blasthole wall is uniform in the initial explosion, and the water jet slot has little effect on the direction of explosion energy. When the explosive gas begins to act on the rock wall, the existence of the water jet slot changes the propagation direction of the explosion energy; therefore, the explosion energy is focused in the direction of the slot, and the rock mass in this direction becomes more prone to damage.

Figure 7: Damage diagram of single slotted borehole blasting. (a) t = 0.05 ms; (b) t = 0.07 ms; (c) t = 0.10 ms

In this study, the Fortran language was applied to monitor the evolution of blast-induced damage of different elements. The different blast-induced damage areas of single ordinary circular borehole blasting and single slotted borehole blasting are shown in Fig. 8. Fig. 8a shows that the shape of the blast-induced damage area of an ordinary circular blasthole is round, and its scope is larger than that of the slotted blasthole. This is because the energy generated by explosion of explosives uniformly acts on the wall of the blasthole, which results in uniform damage in the radial direction of blasthole [27–29]. Thus, a round blasting damage area is formed. By comparing Figs. 8a and 8b, we can see that the shape of blast-induced damage area of ordinary circular blasthole becomes flat. This is because the effect of the explosive explosion energy accumulates in the horizontal direction and indirectly weakens the explosion energy in the vertical direction under the guiding effect of the water jet slot, which is consistent with previous analyses.

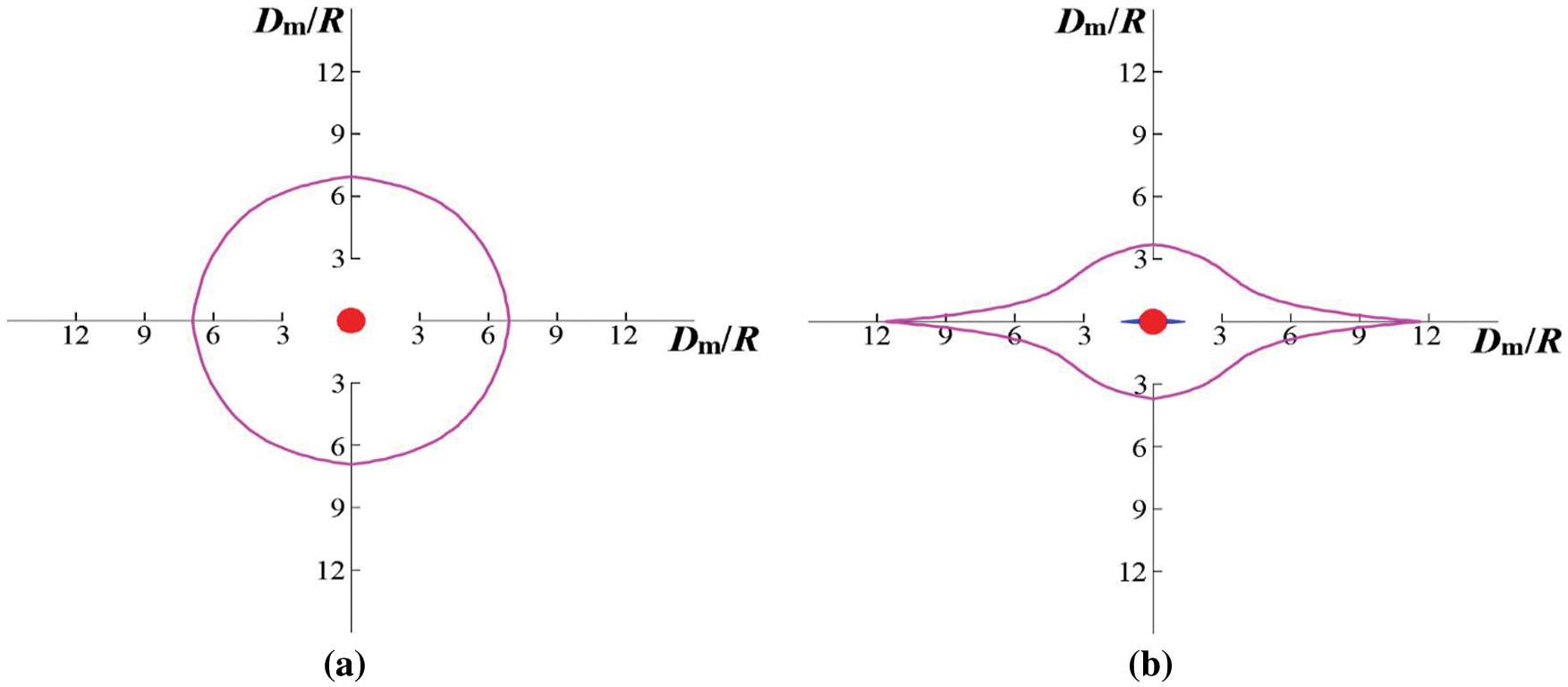
Figure 8: Diagram of blast–induced damage area. (a) Single ordinary circular borehole blasting; (b) Single slotted borehole blasting

4.2 Double-Hole Blasting

Figs. 9 and 10 indicate the schedule change rule of effective plastic strain and effective stress of different monitoring points for double borehole blasting. For double ordinary circular borehole blasting, the effective stress and strain of the measuring point in the middle of two holes are higher than those at other measuring points owing to the stress superposition effect [30]. For double slotted borehole blasting, the effective stress and effective plastic strain of the measuring point in the middle of double blastholes are evidently strengthened. By comparing with double ordinary circular boreholes blasting, the peak values of effective stress and strain of the middle measuring point of double slotted blastholes increased by 47.7% and 50.10%, respectively, as shown in Figs. 9c and 10c.

Figure 9: Effective stress time curves of different monitoring points for double-hole blasting. (a) Monitoring points in vertical direction for double ordinary circular borehole blasting; (b) Monitoring points in horizontal direction for double slotted borehole blasting; (c) Monitoring points in the middle of double blasthole

Figure 10: Effective plastic strain time curves of different monitoring points for double-hole blasting. (a) Monitoring points in vertical direction for double ordinary circular boreholes blasting; (b) Monitoring points in horizontal direction for double slotted borehole blasting; (c) Monitoring points in the middle of two blasthole

In addition, the effective stress and effective plastic strain of rock mass in the vertical direction of the hole are greatly reduced as compared to those in single borehole blasting, as shown in Figs. 9a–9b and 10a–10b. This is because the stress wave produced by double borehole blasting breaks the rock mass in the middle and the subsequent explosion gas promotes the rock mass to break, which results in easy accumulation of explosion energy in the middle.

Fig. 11 indicates the blast-induced damage diagram of double slotted boreholes blasting, and Fig. 12 indicates the different blast-induced damage areas of double ordinary circular borehole blasting and double slotted boreholes blasting, which reveal that that the shape of blast-induced damage area is a circle in the initial stage of explosion. As the explosion process progresses, the shape of the blast-induced damage area gradually changes from round to oval, as shown in Fig. 11b. Finally, the blast-induced damage spreads through the middle of the double blastholes, and blast-induced cracks are formed in the direction of the water jet slot.

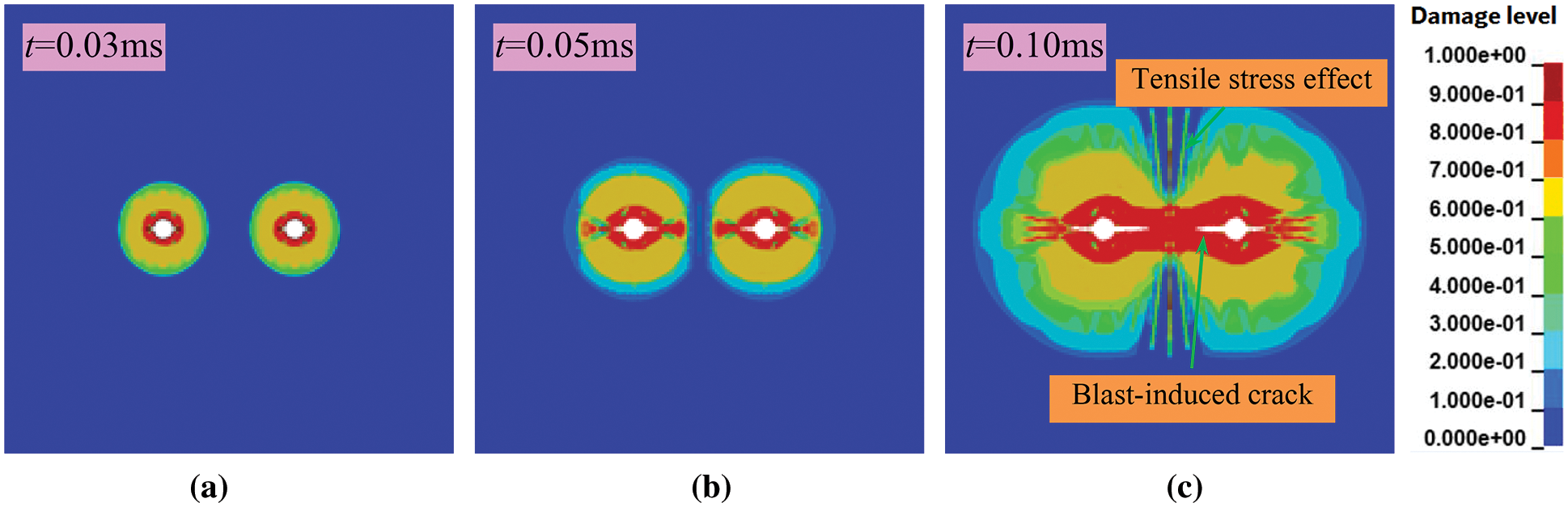
Figure 11: Damage diagram of double slotted boreholes blasting. (a) t = 0.03 ms; (b) t = 0.05 ms; (c) t = 0.10 ms

Figure 12: Diagram of blast–induced damage area. (a) Double ordinary circular boreholes blasting; (b) Double slotted boreholes blasting

According to the rock blasting theory [25], rock damage is mainly caused by the action of explosion stress wave and detonation gas during blasting. In the initial stage of blasting, rock damage is mainly caused by explosion stress wave. For slotted borehole blasting, the water jet slot has a relatively weak guiding effect on the explosion stress wave energy. Therefore, in the initial stage of blasting, the blast-induced damage area formed around slotted blasthole is circular, which is in the same range as the damage circle formed by ordinary borehole blasting, as shown in Fig. 11a. The rock damage is mainly caused by the detonation gas after the explosion stress wave. However, as the water jet slot has a strong guiding effect on the propagation of detonation gas energy [18], the rock mass in the direction of slot bears more damage, which lets the blast-induced crack expand along the direction of the water jet slot, as shown in Fig. 11b.

In addition, the superposition effect of the explosion stress wave has a guiding effect of explosive energy, which lets rock mass on the centre line of the two blastholes withstand more damage and accordingly reduce blast-induced damage of remaining rock. Therefore, the damage area of double hole blasting is larger than that of single hole blasting in the direction of two-hole connection line, and the damage area of double hole blasting is smaller than that of single hole blasting in the direction of vertical two-hole connection line, as shown in Figs. 8a and 12a.

For double slotted borehole blasting, due to the combination of the effect of the stress concentration of the explosion stress wave in the middle of the two blastholes and the guiding effect of the water jet slot on the detonation gas, the explosion energy of the explosive accumulates in the direction of the connecting line of two blastholes, so that the effective stress and strain at the measuring points in the middle of the two blastholes are significantly increased. Simultaneously, owing to the superposition effect of explosion stress wave and the guiding effect of the water jet slot, the explosive energy is focused along the direction of the connecting line. Therefore, the blast-induced damage area of double slotted borehole blasting is smaller than that of single slotted borehole blasting in the direction perpendicular to the connecting line of the two blastholes. Finally, a gourd-shaped blast-induced damage area is formed, as shown in Fig. 12b, which can provide guidance for hole spacing design of slotted blastholes.

5  Conclusions

This study mainly investigates the blast-induced damage mechanism considering the guiding effect of water jet slot. Firstly, numerical model was calibrated by comparing to the result of single ordinary circular borehole blasting. Then, the numerical simulation model of single blasthole and double blastholes were established. Finally, the blast-induced damage mechanism considering the guiding effect of water jet slot was analyzed according to rock blasting theory. The following conclusions are made:

(1)    Under the guiding effect of water jet slot, explosive energy gathers in direction of water jet slot, which let rock mass in the direction of slot easier to damage, and accordingly reduce the damage of remaining rock.

(2)    Under the combination of the superposition effect of the explosion stress wave in the middle of the two blastholes and the guiding effect of the water jet slot on the detonation gas, the explosive energy accumulates in the direction of the connecting line of the two blastholes, resulting in a significant increase in effective stress and strain at the measuring points in the middle of the two blastholes. Finally, a gourd-shaped blasting damage zone is formed.

(3)    The influence of the water jet slot on the blast-induced damage varies depending on the stages of the blasting process. In the initial stage of blasting, the blast-induced damage area formed around the slotted blasthole is circular because the water jet slot has a relatively weak guiding effect on explosion stress wave energy; this circular area is same as the damage area formed by ordinary borehole blasting. Then, the blast-induced damage area gradually becomes gourd shaped because the water jet slot has a strong guiding effect on the propagation of detonation gas energy. The blast-induced crack then expands along the direction of the water jet slot.

Funding Statement: Financial support for this work was provided by the Sichuan Natural Science Foundation Project (Youth Science Foundation Project) (No. 2022NSFSC1089), the Natural Science Foundation of Southwest University of Science and Technology (No. 18zx7124).

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. Hashemi, A. S., Katsabanis, P. (2021). Tunnel face preconditioning using destress blasting in deep underground excavations. Tunnelling and Underground Space Technology, 117, 1–17. https://doi.org/10.1016/j.tust.2021.104126 [Google Scholar] [CrossRef]

2. Deng, K., Chen, M. (2020). Blasting excavation and stability control technology for ultra-high steep rock slope of hydropower engineering in China: A review. European Journal of Remote Sensing, 54, 1–15. https://doi.org/10.1080/22797254.2020.1752811 [Google Scholar] [CrossRef]

3. Afrasiabian, B. J., Ahangari, K., Noorzad, A. (2021). Study on the effect of air deck on ground vibration and development of blast damage zone using 3D discrete element numerical method. Arabian Journal of Geosciences, 14(13), 1–12. https://doi.org/10.1007/s12517-021-07648-5 [Google Scholar] [CrossRef]

4. Xiao, S. L., Gao, W. X., Ji, J. M., Ye, M. B., Zhang, D. J. (2021). Blasting damage analysis method based on EEMD-HHT transform. Journal of Central South University (Science and Technology), 52(8), 2887–2896. https://doi.org/10.11817/j.issn.1672-7207.2021.08.033 [Google Scholar] [CrossRef]

5. Liu, D. S., Yu, B., Du, Y. L. (1999). Damage models of rock fragmentation by blasting and their progress. Engineering Blasting, 5(4), 78–84. https://doi.org/10.3969/j.issn.1006-7051.1999.04.018 [Google Scholar] [CrossRef]

6. Ling, T. L., Liu, D. S., Liang, S. F., Li, S. L. (2019). Research on damage viscoelastic dynamic constitutive model of granite. Journal of Mining Science and Technology, 4(5), 403–409. https://doi.org/10.19606/j.cnki.jmst.2019.05.004 [Google Scholar] [CrossRef]

7. Li, N., Zhang, P., Duan, Q. W., Gunter, S. (2003). Dynamic damage model of the rock mass medium with microjoints. International Journal of Damage Mechanics, 12(2), 163–173. https://doi.org/10.1177/1056789503012002004 [Google Scholar] [CrossRef]

8. Li, Y. X., Xie, H. P., Zhu, Z. M., Feng, H. D., Ye, J. J. (2009). Study on rules of transmission and reflection of stress wave across fractal joint. Chinese Journal of Rock Mechanics and Engineering, 28(1), 120–129. https://doi.org/10.3321/j.issn:1000-6915.2009.01.016 [Google Scholar] [CrossRef]

9. Li, Y. X., Zhu, Z. M., Li, B. X., Deng, J. H., Xie, H. P. (2011). Study on the transmission and reflection of stress waves across joints. International Journal of Rock Mechanics & Mining Sciences, 48(3), 364–371. https://doi.org/10.1016/j.ijrmms.2011.01.002 [Google Scholar] [CrossRef]

10. Xia, X. (2006). Study on damage characteristics and safety threshold of rock vibration by blast (Ph.D. Thesis). Wuhan, China: Institute of Rock and Soil Mechanics, Chinese Academy of Sciences, Wuhan, China. [Google Scholar]

11. Liang, Y. Y. (2011). Numerical modeling on the coalesence of blasting-induced cracking zone under simultaneous denotation of two blast-holes (Ph.D. Thesis). Northeastern University, Shenyang, China. [Google Scholar]

12. Wei, C. H., Zhu, W. C., Bai, Y., Li, S. (2016). Numerical simulation on two-hole blasting of rock under different joint angles and in-situ stress conditions. Chinese Journal of Theoretical and Applied Mechanics, 48(4), 926–935. https://doi.org/10.6052/0459-1879-15-259 [Google Scholar] [CrossRef]

13. Wei, C. H., Zhu, W. C., Bai, Y., Long, K. (2016). Numerical simulation of jointed rock mass blasting under different in-situ stress conditions. Chinese Journal of Engineering, 38(1), 19–25. https://doi.org/10.13374/j.issn2095-9389.2016.01.003 [Google Scholar] [CrossRef]

14. Ding, W., Tan, S., Zhu, R., Jiang, H., Zhang, Q. (2021). Study on the damage process and numerical simulation of tunnel excavation in water-rich soft rock. Applied Science, 11, 8906. https://doi.org/10.3390/app11198906 [Google Scholar] [CrossRef]

15. Meng, N. K., Bai, J. B., Chen, Y. (2020). Damage evolution mechanisms of rock induced by blasting with the aid of empty-hole effect. Energies, 13, 1–21. https://doi.org/10.3390/en13030756 [Google Scholar] [CrossRef]

16. Liu, M. L., Chen, S. H., Sun, J. (2021). Blasting damage detection and numerical simulation analysis of shallow-buried twin tunnels with small spacing. Explosion and Shock Waves, 41(11), 115201. https://doi.org/10.11883/bzycj-2020-0378 [Google Scholar] [CrossRef]

17. Luo, S., Yan, P., Lu, W. B. (2021). Research on the simulation of blasting damage and its mechanism of deep tunnel excavation. Chinese Journal of Rock Mechanics and Engineering, 40(S1), 2760–2772. https://doi.org/10.13722/j.cnki.jrme.2020.0817 [Google Scholar] [CrossRef]

18. Su, D. F., Kang, Y., Wang, X. C., Zheng, D. D., Li, D. Y. et al. (2016). Analysis and numerical simulation for tunnelling through coal seam assisted by water jet. Computer Modeling in Engineering & Science, 111(5), 375–393. https://doi.org/10.3970/cmes.2016.111.375 [Google Scholar] [CrossRef]

19. Yi, C., Johansson, D., Greberg, J. (2018). Effects of in-situ stresses on the fracturing of rock by blasting. Computers and Geotechnics, 104, 321–330. https://doi.org/10.1016/j.compgeo.2017.12.004 [Google Scholar] [CrossRef]

20. Huo, X., Shi, X., Qiu, X., Zhou, J., Gou, Y. et al. (2020). Rock damage control for large-diameter-hole lateral blasting excavation based on charge structure optimization. Tunnelling and Underground Space Technology, 106, 1–21. https://doi.org/10.1016/j.tust.2020.103569 [Google Scholar] [CrossRef]

21. Borrvall, T. (2011). The RHT concrete model in LS-DYNA. 8th European LS-DYNA Conference, Stuttgart. [Google Scholar]

22. Livermore Software Technology Corporation (LSTC) LS-DYNA Keyword User’s manual, Version R 10.0. (2017). http://www.lstc.com/. [Google Scholar]

23. Zhang, W. G., Zhang, R. H., Wu, C. Z., Goh, A. T. C., Lacasse, S. et al. (2020). State-of-the-art review of soft computing applications in underground excavations. Geoscience Frontiers, 11, 1095–1106. https://doi.org/10.1016/j.gsf.2019.12.003 [Google Scholar] [CrossRef]

24. Amiri, H. S., Murthy, V. M. S. R. (2019). Optimising blast pulls and controlling blast induced excavation damage zone in tunnelling through varied rock classes. Tunnelling and Underground Space Technology, 85, 307–318. https://doi.org/10.1016/j.tust.2018.11.029 [Google Scholar] [CrossRef]

25. Zhou, C. B., Jiang, N., Xia, K. W., Luo, X. D., Lu, S. W. et al. (2016). Dynamic action mechanism and response characteristics of rock blasting. Beijing, China: Science Press. [Google Scholar]

26. Bai, J. Z. (2005). Theoretical basis and example analysis of LS-DYNA 3D. Beijing: Science Press. [Google Scholar]

27. Li, C. X., Kang, Y. Q., Zhang, Y. T., Luo, H. H. (2021). Effect of double holes on crack propagation in PMMA plates under blasting load by caustics method. Theoretical and Applied Fracture Mechanics, 116, 1–11. https://doi.org/10.1016/j.tafmec.2021.103103 [Google Scholar] [CrossRef]

28. Shadabfar, M., Gokdemir, C., Zhou, M., Kordestani, H., Muho, E. V. (2021). Estimation of damage induced by single-hole rock blasting: A review on analytical, numerical, and experimental solutions. Energies, 14, 29. https://doi.org/10.3390/en14010029 [Google Scholar] [CrossRef]

29. Song, J. F., Lu, C. P., Zhang, X. F., Guo, Y., Yang, H. W. (2022). Damage mechanism and wave attenuation induced by blasting in jointed rock. Shock and Vibration, 2022, 6950335. https://doi.org/10.1155/2022/6950335 [Google Scholar] [CrossRef]

30. Zhang, J. Y., Liu, Z. G., Fu, S. G., Qiao, G. D. (2022). Damage of rock mass by double-hole blasting with slit chargeand development of stress wave under high in situ stress. Shock and Vibration, 2022, 6967057. https://doi.org/10.1155/2022/6967057 [Google Scholar] [CrossRef]