Structural Durability & Health Monitoring

DOI: 10.32604/sdhm.2021.014559

ARTICLE

A Symplectic Method of Numerical Simulation on Local Buckling for Cylindrical Long Shells under Axial Pulse Loads

Kecheng Li, Jianlong Qu, Jinqiang Tan, Zhanjun Wu and Xinsheng Xu*

State Key Laboratory of Structure Analysis for Industrial Equipment, Department of Engineering Mechanics, Dalian University of Technology, Dalian, 116024, China
*Corresponding Author: Xinsheng Xu. Email: xsxu@dlut.edu.cn
Received: 08 October 2020; Accepted: 20 November 2020

1  Introduction

Cylindrical long shell is a typical and classical structure in engineering, for example submarine pipelines, which are the core of marine oil and gas transportation [1]. In complex seabed environment, the long shell structures are more prone to instability because of ocean waves and/or currents, which is one of the main causes of structural failure [2,3]. The buckling problem of cylindrical shells has been noticed all along, and it is widely recognized that the sudden loss of capability of bending-bearing contributes to this kind of failure. More specifically speaking, the membrane stiffness is much higher than the bending stiffness for shell structures, at the beginning, external compression energy is absorbed through membrane deformation and stored as membrane strain energy, up to a point, this energy will be converted to bending strain energy, which leads to large deflection and complex bending deformation modes, and the buckling initiates. For a long shell structure, buckling usually occurs before material yielding, which could result in catastrophic consequences, hence, buckling load design is normally ahead of other kinds of strength design.

Generally, it is difficult to solve buckling problems theoretically, and therefore most research works concentrate upon experimental methods and numerical methods. At present, research trends on cylindrical shell buckling focus more on accurate experiment techniques, advanced new materials, local buckling effects and micro scale structures, literatures on these areas are enormous. Wang et al. [4] implemented experiments to analyze geometrical imperfection sensitivity of cylindrical shells buckling. Fatma et al. [5] analyzed the effect of dent variation on buckling and post-buckling behaviors for cylindrical thin shells. Skukis et al. [6] proposed an experiment based vibration correlation technique to measure buckling loads of composite cylindrical shells. Experimental studies had shown that dynamic buckling modes of cylindrical shells could be mushroom-type and petal type under high speed impact [7]. In fact, the local buckling of cylindrical shells is mainly caused by uneven stress distribution. When subjected to an impact, stress wave continually compress the shell until transverse stiffness is not capable enough to sustain lateral shape, thus may cause local buckling of shells [8]. It is worth mentioning that experimentally achieved results are effective, but they are limited to too many experiment conditions, such as experiment facilities, specimen qualities, loading methods, dispersity of test samples and so on, and thus theoretical results are needed for necessary supplement in a full comprehension of shell buckling problems. Sun et al. [9] developed a method to solve buckling problems of piezoelectric cylindrical nanoshells using Eringen’s nonlocal theory. Safarpour et al. [10] investigated buckling behavior for carbon nanotube reinforced cylindrical piezoelectric shell using a generalized differential quadrature method. In recent years, functionally graded multilayer structure is a hot topic on cylindrical shell buckling study, and many classical mathematical and mechanical methods have been applied to investigate instability of these structures [11–13]. Despite above aspects, the most commonly used method in shell buckling analysis now is finite element method (FEM), especially in engineering aeras. With its simplicity and high efficiency, FEM has been applied to solve buckling problems for all kinds of cylindrical shells ranging from nano shells to macro shell structures [4,14]. Local characteristics of cylindrical shell buckling is of great practical meaning in shell buckling analysis, on that account, researchers have studied this problem with all kinds of techniques for a long time [15–17]. Anyhow, some researchers have proposed some theoretical methods to analyze the mechanism of traditional structural buckling [18–20], but they were lack of rigorous theoretical deductions for solving buckling governing equations and directly formulated experience based solutions, which might be incomplete. What’s more, there’s an insufficiency of study on cylindrical long shell’s local buckling behaviors. And the very point that should be noted is that many works had been done on shell buckling problems using Ritz approximation, finite element codes, engineering estimation or other methods [21–28], which are all approximate solutions. However, great value can be achieved if theoretically accurate solutions to the buckling behaviors are given, by which the essence of its physical phenomena can be better understood.

Previous analytical methods mentioned are effective techniques for studying buckling of shells and are based upon the Lagrangian system. One of the mechanisms in common for these methods in solving high order partial differential governing equations is that their attentions are dedicated to approximate solutions, like inverse solutions and semi-inverse solutions. There’s another system, i.e., the Hamiltonian system, it is a dual system that has been proved to be valid for decades and it is equivalent with Lagrangian system, in addition, it has been successfully applied on many fields, such as shell buckling, dynamics, wave propagation, vibration, fluid mechanics and so on [29]. The difference is that in Hamiltonian system it is easier to get a generalized solution in solving high order buckling governing equations using the method of separation of variables to reduce the order of equations in a complete form [30]. Based on advantage of the Hamiltonian system, some problems of pre-buckling of short shells are discussed [31–34]. In this paper, the local buckling problem of cylindrical long shells under pulse load is analyzed by the symplectic method without pre-assumed analytic shape funcitons. The solutions and results can give good predictions on ultimate loads and buckling modes development for long cylindrical shells with local compression loads, and may provide guidance for failure analysis and buckling resistance design for long shell structures.

2  The Fundamental Problem and Hamiltonian System

Consider an elastic circular cylindrical shell under axial pulse loads, in which its radius is R, thick h, Young’s modulus E, Poisson’s ratio υ and density ρ . The shell has infinite length and the length of compressive load N of axial pulse is 2l. In the circular cylindrical coordinate (r, θ , x) as seen in Fig. 1. w is lateral displacement in the neutral surface along the r direction, and the boundary conditions can be expressed as

{w|x→+∞=0w|x→−∞=0 (1)

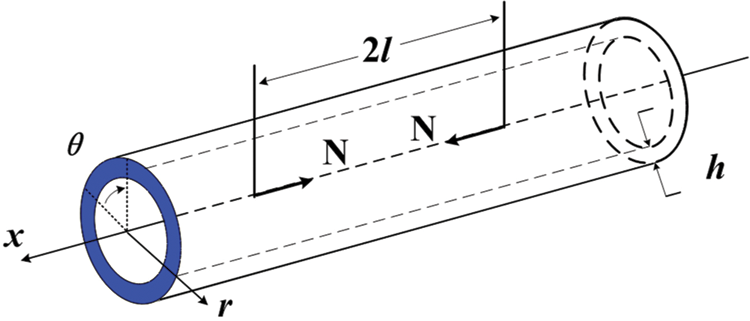
Figure 1: Coordinates and shell nomenclature

Basd on the theory of the small deformation, the Lagrangian function (deformation energy) can be written as

Le=K2(wR)2+D2[(∂2w∂x2)2+1R2(∂2w∂θ2)2+2υR2(∂2w∂x2)(∂2w∂θ2)+2(1−υ)1R2(∂2w∂x∂θ)2]−N2(∂w∂x)2 (2)

where D=Eh3/[12(1−υ2)] for bending stiffness, and K=Eh/(1−υ2) for tensile stiffness.

The circular coordinate θ is taken in analogy to the time coordinate, and ∂θ≡∂/∂θ , ∂x≡∂/∂x . Introduce φ=−∂θw/R representing circular twist angle, and denote f˙≡∂θf/R . The dual variables of the original variables q={w,φ}T can be expressed as p={p1,p2}T where

{p1=−D(∂x2w˙+w⃛)p2=−D(∂x2w−φ˙) (3)

p1 and p2 represent equivalent shear load and bending moment respectively. Then the Hamiltonian function is expressed in dual variables as

H(p,q)=pTq˙−L(p,q) (4)

Introduce the state vector

ψ={w,φ,p1,p2}T={qT,pT}T (5)

The dual equations of the Hamiltonian system can be rewritten in the form: q˙=δH/δp and p˙=−δH/δq , namely

ψ˙=Hψ (6)

H is a Hamiltonian operator matrix, and has the expression

H=[0−100∂x2001/DK+N∂x200−∂x20010] (7)

The dual equations in Hamiltonian system are equivalent with the governing equations in Lagrangian system, but they will be solved in a symplectic space.

3  Symplectic Eigenvalues and Eigensolutions

In symplectic system, the method of separation of variables can be used. The solution of Eq. (6) can be uniformly written as ψ=ψμeμθ , where μ is symplectic eigenvalue [29]. According to the closed conditions of cylindrical shells, the solution satisfies the continuity condition in circumferential direction

ψ|θ=0=ψ|θ=2π (8)

Therefore, the eigenvalues in circumferential direction are

μn=in(n=0,±1,±2,⋯) (9)

where the eigensolutions of μ0=0 and μn≠0 correspond to the axisymmetric and non-axisymmetric buckling problems, respectively.

The complete solutions of the original problem can be expressed as

ψ(n)={ψ1(n)=[C5κ5eλ3x+C6κ6eλ4x]einθ(x<−l)ψ2(n)=[C1κ1eλ1x+C2κ2e−λ1x+C3κ3eλ2x+C4κ4e−λ2x]einθ(−l≤x≤l)ψ3(n)=[C7κ7e−λ3x+C8κ8e−λ4x]einθ(x>l) (10)

where Ck(k=1,2,⋯,8) is undetermined constant, and λ is the eigensolution in axial direction, namely

{λ1,2=i{(NR2/2D−n2)∓[(NR2/2D−n2)2−γn]1/2}1/2/Rλ3,4=γn1/4{[1−n2/γn1/2]1/2±i[1+n2/γn1/2]1/2}/2R (11)

γn is intermediate coefficient related with n, which can be expressed as γn=n4+KR2/D , and constant vectors, κk(k=1,2,⋯,8) , can be shown as

{κ1=κ2={1,−in/R,−Din(λ12R2−n2)/R3,−D(λ12R2−n2)/R2}Tκ3=κ4={1,−in/R,−Din(λ22R2−n2)/R3,−D(λ22R2−n2)/R2}Tκ5=κ7={1,−in/R,−Din(λ32R2−n2)/R3,−D(λ32R2−n2)/R2}Tκ6=κ8={1,−in/R,−Din(λ42R2−n2)/R3,−D(λ42R2−n2)/R2}T (12)

4  Critical Loads and Buckling Modes

For piecewise eigensolution (10), continuity conditions can be expressed as

{D1ψ1(n)|x=−l=D2ψ2(n)|x=−lD3ψ3(n)|x=l=D2ψ2(n)|x=l (13)

where operator matrices Dk=[dk,0,0,d4](k=1,2,3) , operator vectors d1=d3={1,∂x,0,0}T , d2={1,∂x,0,N∂x}T and d4={0,0,1,∂x}T . Since eigensolution (10) should satisfy continuity conditions (13), the undetermined constants C1,C2,⋯,C8 and critical loads can be determined. Namely eight algebraic equations can be rewritten by conditions (13) as

Bc=0 (14)

where c={C1,C2,⋯,C8}T . If c is nonzero vector, there is a buckling mode at least. Therefore, the bifurcation condition is that the determinant of the coefficients equals to zero, or

|B|=0 (15)

The critical loads and the corresponding buckling modes can be determined by Eqs. (10), (13) and (14). It should be noted that critical load has many roots from Eq. (14) for a fixed n, so denote m (m=1,2,⋯) and n (n=0,1,2,⋯) as the axial order and circumferential order of the shell buckling. Rewrite the eigensolution (10) as ψnm(α)(X)einθ for n and ψnm(β)(X)e−inθ for –n while n ≠ 0. For n = 0, ψ0m(β)(X,θ) is the Jordan form of ψ0m(α)(X) . Introduce the inner product of the function as

<ψ1,ψ2>=∫−∞−L∫02πψ1TJψ2dθdX+∫−LL∫02πψ1TJψ2dθdX+∫L∞∫02πψ1TJψ2dθdX (16)

where J is a unit rotational matrix [29]. By orthogonalizing, it can be proved that there are adjoint symplectic orthogonal relations between the eigensolutions as following

{<ψnm(α)(X,θ),ψkj(β)(X,θ)>=−<ψnm(β)(X,θ),ψkj(α)(X,θ)>=δnkδmj<ψnm(α)(X,θ),ψkj(α)(X,θ)>=<ψnm(β)(X,θ),ψkj(β)(X,θ)>=0 (17)

Since the symplectic space is complete, the mode of buckling can be obtained by expanding the eigensolutions (10) as

ψ=∑n,m=1∞[Anmψnm(α)(X)einθ+Bnmψnm(β)(X)e−inθ]+∑m=1∞Cmψ0m(α)(X) (18)

where the unknown coefficients, Anm , Bnm and Cm , can be determined from boundary conditions.

5  Numerical Results

For simplicity, define the following dimensionless terms: X=x/R , W=w/R , L=l/R , H=h/R , Ncr=NR2/D and γ=KR2/D . Consider an infinite elastic circular cylindrical shell with Poisson’s ratio υ=0.25 and H = 0.01. Numerical results are discussed below.

As the first example, take L from 0.1 to 1, the relationship between critical loads of the first five orders and the length of axial load is depicted in Fig. 2. The figures show downward trends of critical loads with the length for n = 0,1,2,3 and m = 1,2,3,4,5. For branches m with odd numbers, the trends are noemonotonic decreasing, for m with the even numbers, the trends are basically monotonic decreasing. From this result we can see the complexity of buckling problem and difference between axisymmetric buckling behaviors and non-axisymmetric behaviors. What’s more, the curve patterns are nearly the same for a specific m with different n on the whole. Another interesting point is that the critical loads have similar values for a specific n with different m, which illustrates that buckling modes can be various while the critical loads are similar. For given loading length and circumferential order n, the critical load becomes higher while the branch order m increases, the reason for this is that the more complex the buckling mode is the more energy or larger load is needed. Furthermore, there are limit loads when the length L becomes infinite, but the influence of loading length is different for each m, in the large, the higher the m becomes, the bigger the length value is when the curve approaches smooth.

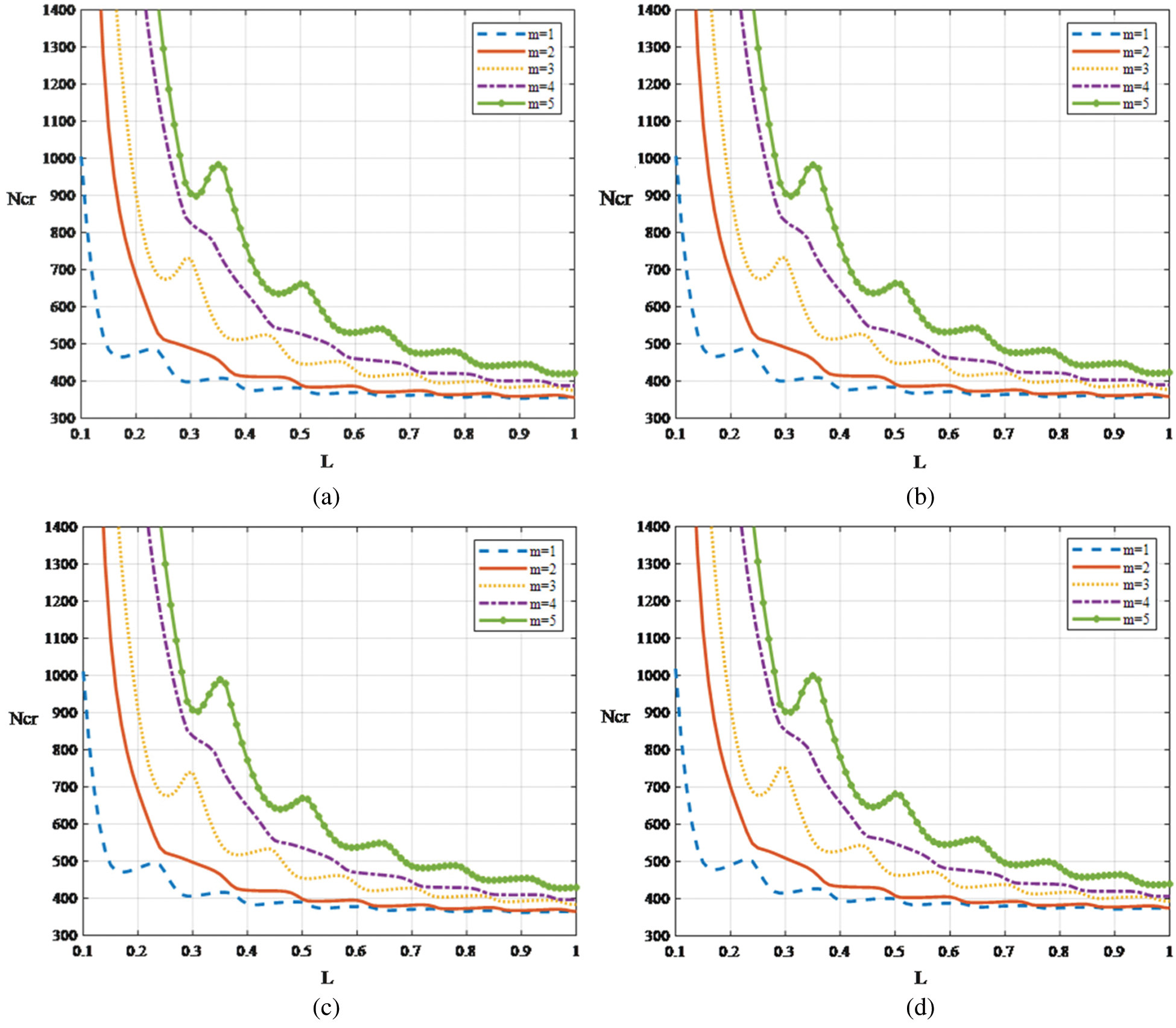
Figure 2: The relationship between critical loads and the length of axial load for n = 0,1,2,3. (a) n = 1, (b) n = 1, (c) n = 2 and (d) n = 3

To reveal the internal law of buckling with respect to circumferential orders n, Fig. 3 gives the curves of critical loads for the first ten circumferential orders n. The results shows that the higher the order n is the higher the critical load becomes, and it is more obvious for higher orders. The critical loads present a wave trend for a given n, and then become gentle as length of axial load increases, and finally reach stable values. With the form of eigensolutions in (7), it is easy to find that there are infinite theoretical solutions for every n, however, only the top-ranking solutions are of great importance, especially the first one which is also the lowest and usually occurs the first. While the length of axial load is small, particularly when L < 0.1, critical loads for different n are very close, with which some experimental phenomena can be illustrated, for example, sometimes several buckling modes of a short shell can coexist in one specimen, and in some other cases, the first buckling mode of the same batch of specimen can be different. As the length of loading area grows, particularly when L > 0.3, the critical loads are distinctly separated for different order n.

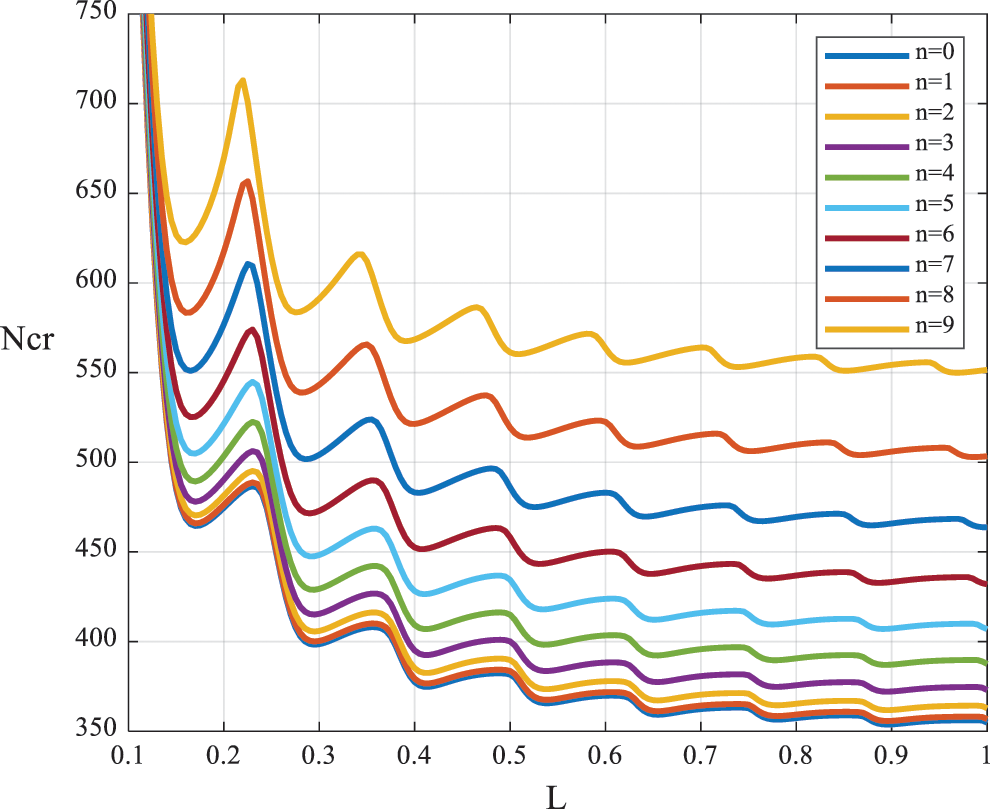
Figure 3: The curves of critical loads for the first ten circumferential orders n

The buckling modes are shown in Figs. 4–7, which correspond to buckling modes for circumferential orders n = 0,1,2,3 when L = 0.1, and the first five axial orders m = 1,2,3,4,5 are chosen in particular. It is obvious that Fig. 4 gives axisymmetric buckling modes when n = 0, and the number of circumferential waves is 0. The shape of the buckling region is similar to bamboo node, and some researchers call it bamboo node-type buckling. Moreover, as the axial branch number m grows, in other words, as the axial load increases, the number of axial waves goes up. Even though the taken L = 0.1 is relatively small, it is still easy to recognize the axial wave mode when m < 5 in Fig. 4, which would be a problem in FEM simulations since element size may be larger than the axial wave distance. For engineering cylindrical structures under axial compression, the bamboo node-type mode is the most common seen buckling form.

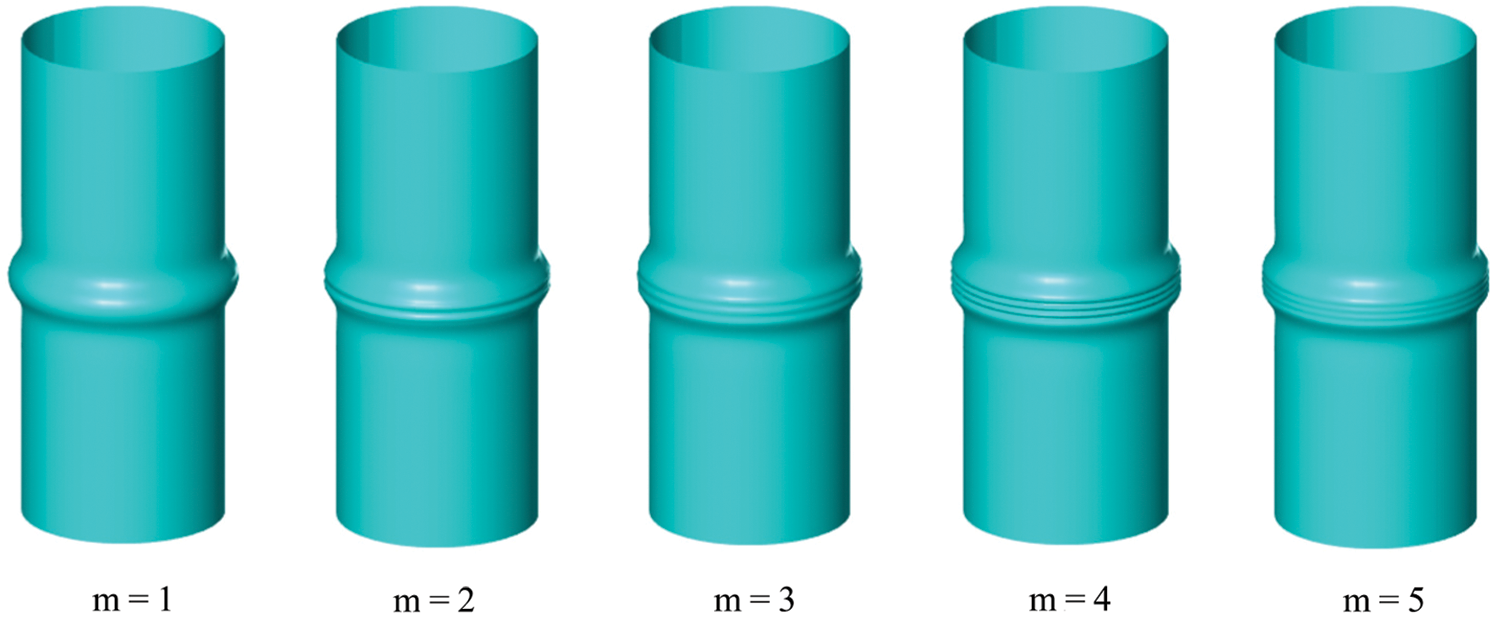
Figure 4: Shell buckling modes of the first 5 branches with circumferential order n = 0

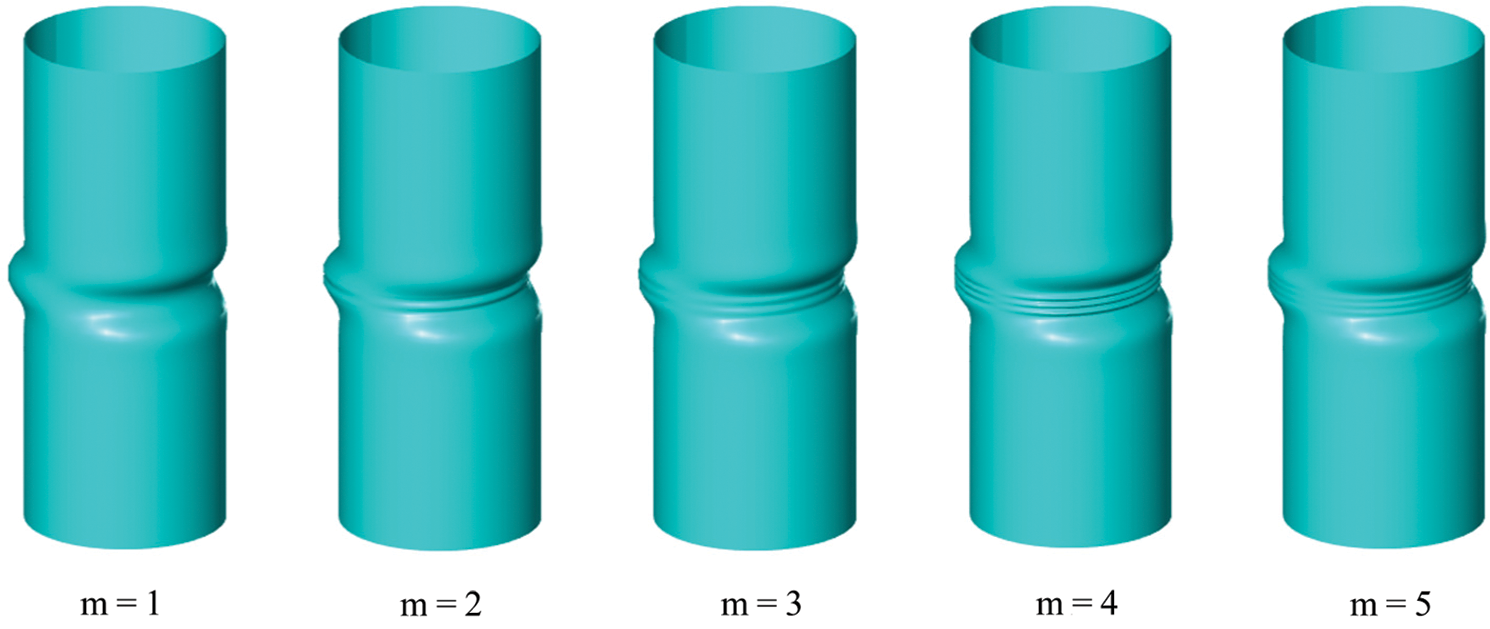
Figure 5: Shell buckling modes of the first 5 branches with circumferential order n = 1

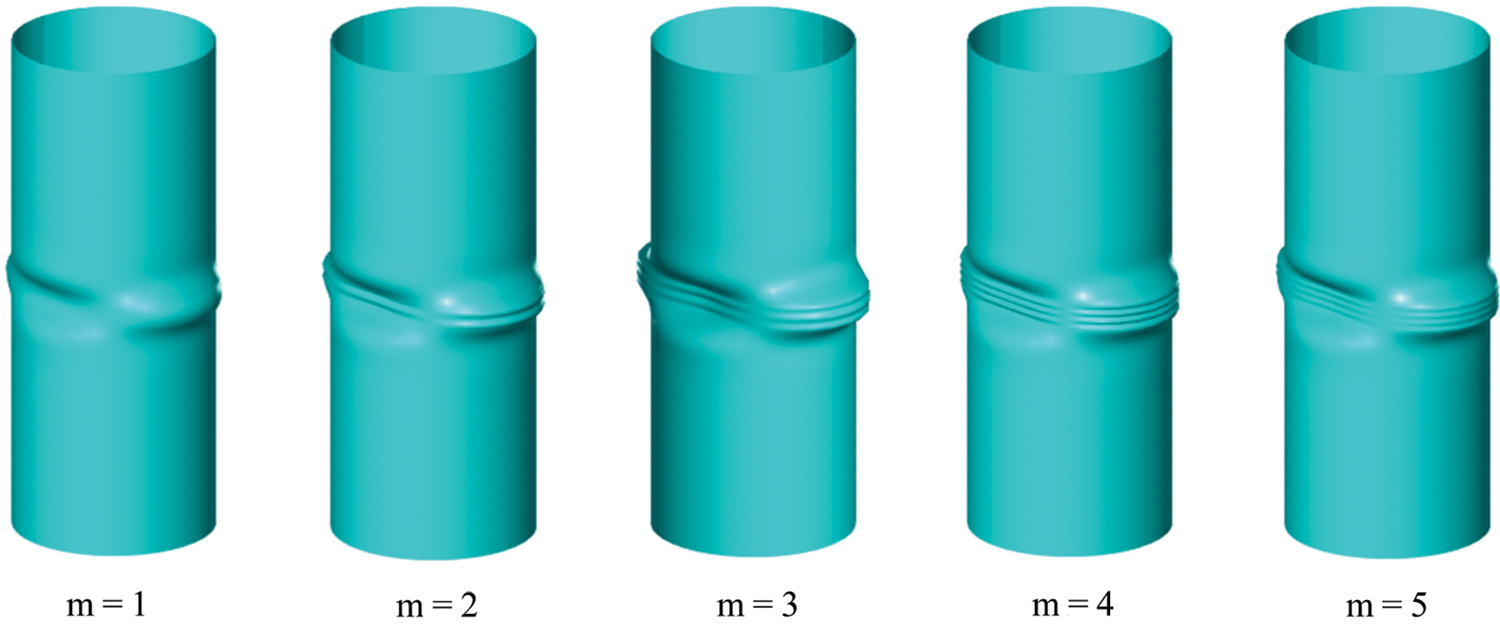
Figure 6: Shell buckling modes of the first 5 branches with circumferential order n = 2

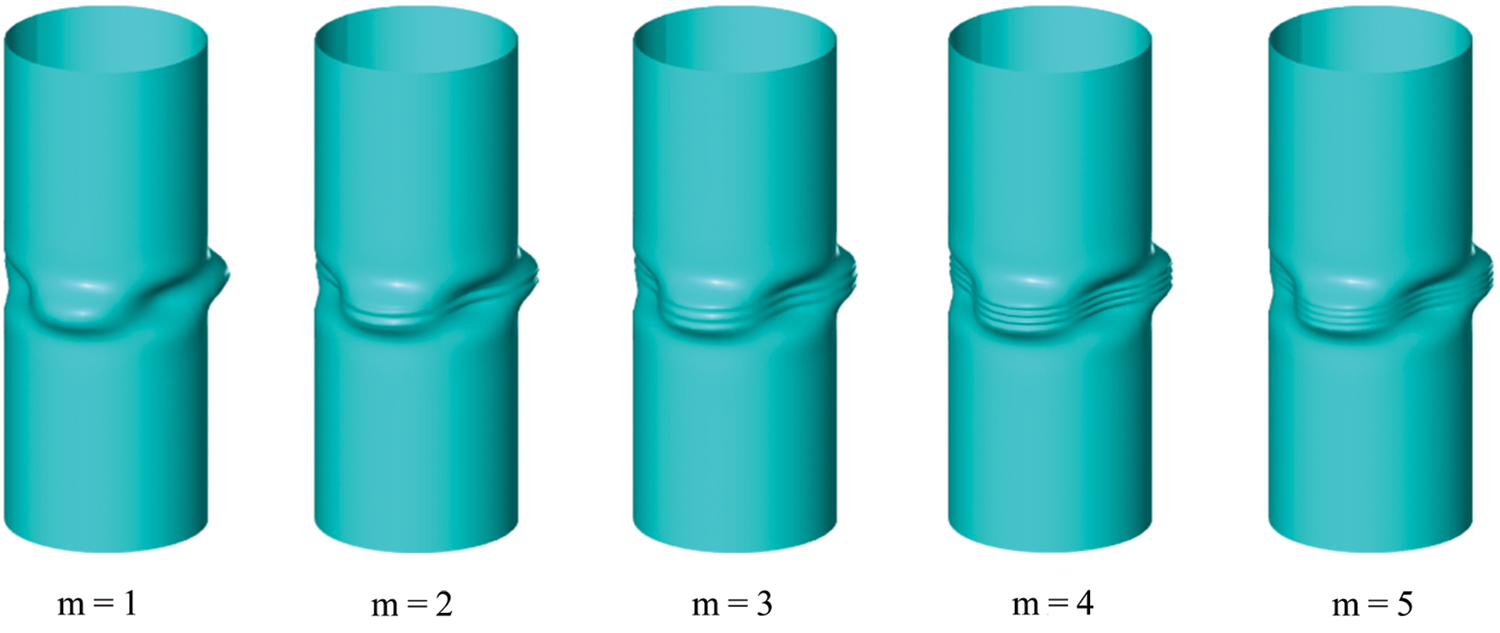
Figure 7: Shell buckling modes of the first 5 branches with circumferential order n = 3

Fig. 5 shows anti-symmetrical buckling modes for n = 1 with m = 1,2,3,4,5. The number of circumferential waves is 1, and the axial wave number also goes up along with increasing of m. The shape of the buckling region is similar to a bending tube, thus some researchers call it bending type buckling. This type of mode is also a common buckling mode in cylindrical long shell structures, especially for that with local defects.

Figs. 6 and 7 show higher order buckling modes for n = 2 and n = 3 with m = 1,2,3,4,5. Their circumferential wave numbers are 2 and 3, respectively. The increasing of number of buckling waves has similar law with cases above. The shape of the buckling region is similar to periodically arranged concaves, thus some researchers call the buckling modes of n ≥ 2 concave type buckling. These kinds of buckling often occur in anisotropic material shells. Specially, the circumferential mode for n = 2 is orthogonally symmetric.

Take L = 0.11, Fig. 8 gives the first branch buckling modes of shells for circumferential orders n = 0–9. The result indicates that the circumferential wave numbers match the circumferential orders and high order buckling modes display more complicated deformation shapes. The figures also demonstrate that the buckling modes evolve from simple bamboo node-type to bending type and concave types, which correspond to mode characteristics of buckling states of n = 0, n = 1 and n ≥ 2, respectively. All these modes exhibit characteristics of locality.

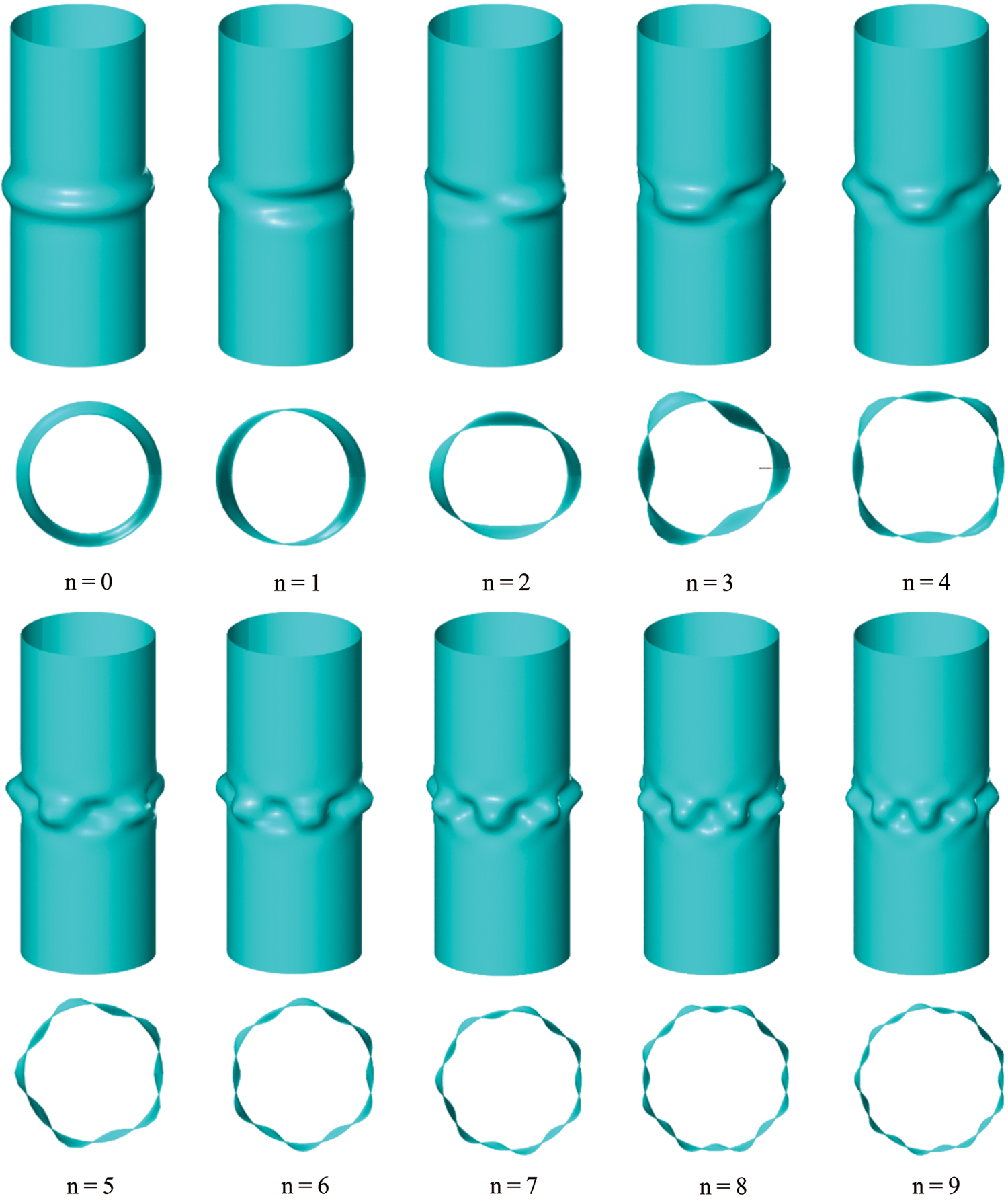
Figure 8: Buckling modes of shells for circumferential order n from 0 to 9

Take the axisymmetric buckling mode (n = 0) and the first bifurcation mode (m = 1) for example to study the influence of length of axial load. And buckling modes for loading length L = 0.1, 0.2, …, 1.0 are plotted in Fig. 9, respectively. From the images, it is obvious to see that buckling wrinkles located in the region where axial load is applied, and thus the number of the axial wrinkle waves increases with the scale of loading area. It should be noted that the number of axial wrinkles waves does not increase linearly with the length of axial load on account of the significant influence of material properties. To investigate the evolution pattern of the wrinkle waves in axial direction, numbers of axial wrinkle waves are listed in Tab. 1 for different kinds of buckling modes.

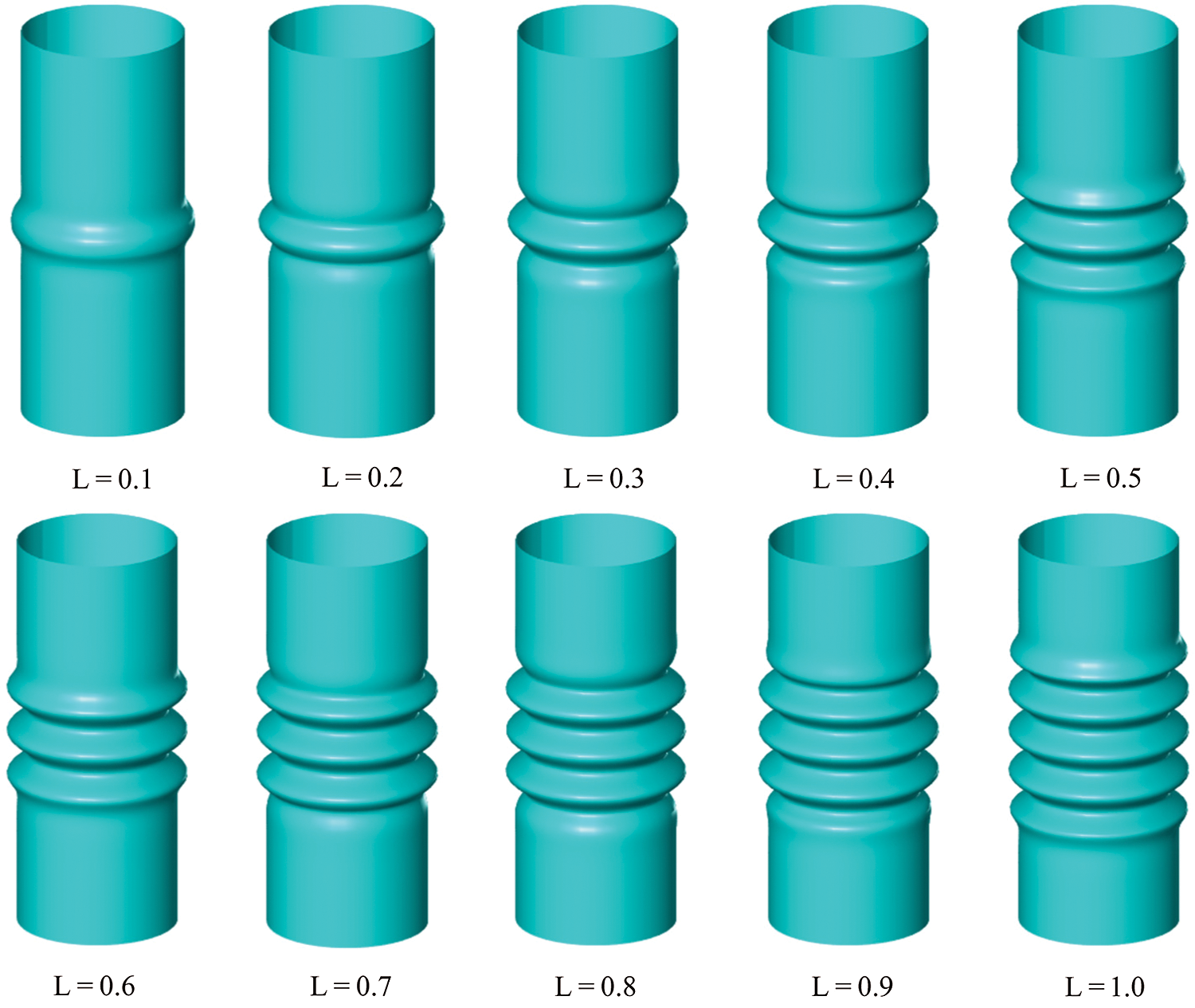
Figure 9: Buckling modes of shells with length of load from 0.1 to 1.0

Table 1: Number of axial wrinkle waves for different length of load region

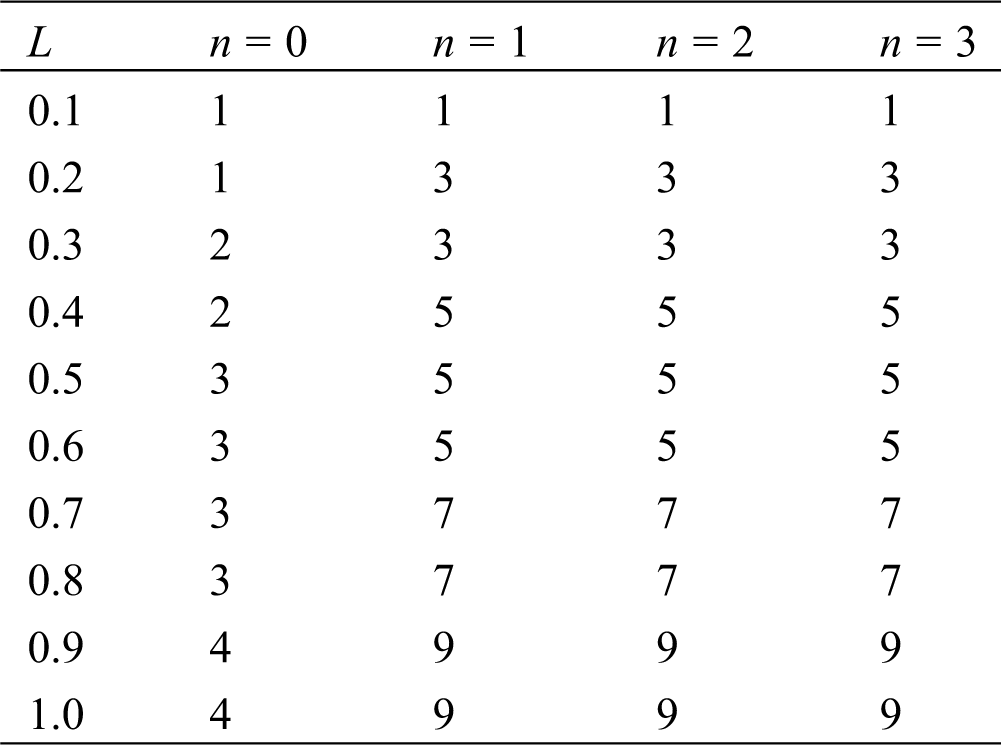
As seen in Tab. 1, the number of axial wrinkle waves are positively correlated with the length of axial load. In cases that L is small, such as L ≤ 0.1, the axial wrinkle wave number is always 1 for different n. As the L increases, it gets easier for the shells to buckle, accordingly, the axial wrinkle wave number goes up. And it is not difficult to conclude from the data that the axial wrinkle number grows in a natural order in the axial symmetric buckling cases and grows in an odd sequence order in the non-symmetric buckling cases. This conclusion can be useful for prediction of collapsing modes for cylindrical thin shells and helpful for geometry and loading design of cylindrical shell structures.

To discuss the thickness effect, define another dimensionless critical load, Pcr=N/ER , which is independent of thickness, while the dimensionless load Ncr=NR2/D has something to do with thickness. In fact, the relationship between Pcr and Ncr can be expressed as NcrH3=12(1−υ2)Pcr . Take the critical load of bending type buckling (n = 1) as an example, Fig. 10 illustrates the relation of critical loads with thickness of shells from two perspectives. Fig. 10a presents the curves of critical load Pcr and the length of load L with 5 different thickness values, which indicates that the critical loads decrease with the length of load in a non-monotonic way, the critical load curves drop sharply when L < 0.2, and vary smoothly when L > 0.2, and finally approach flat. Fig. 10b presents Pcr and the shell thickness with four different length of load, which depicts that the critical loads increase with growth of shell thickness in a monotonic way. What’s more, the trend of the curves varies from a quadratic type to a linear type when the length of load grows. Further, load curve for L = 0.1 is much higher than the other curves, and load curves for L = 0.2, 0.4, 0.5 are quite close, from which we can obtain that buckling mode of a very short shell needs quite big energy or compressive load to arouse, when the length grows to a critical value, the buckling load will sharply decrease and the buckling deformation becomes more easily.

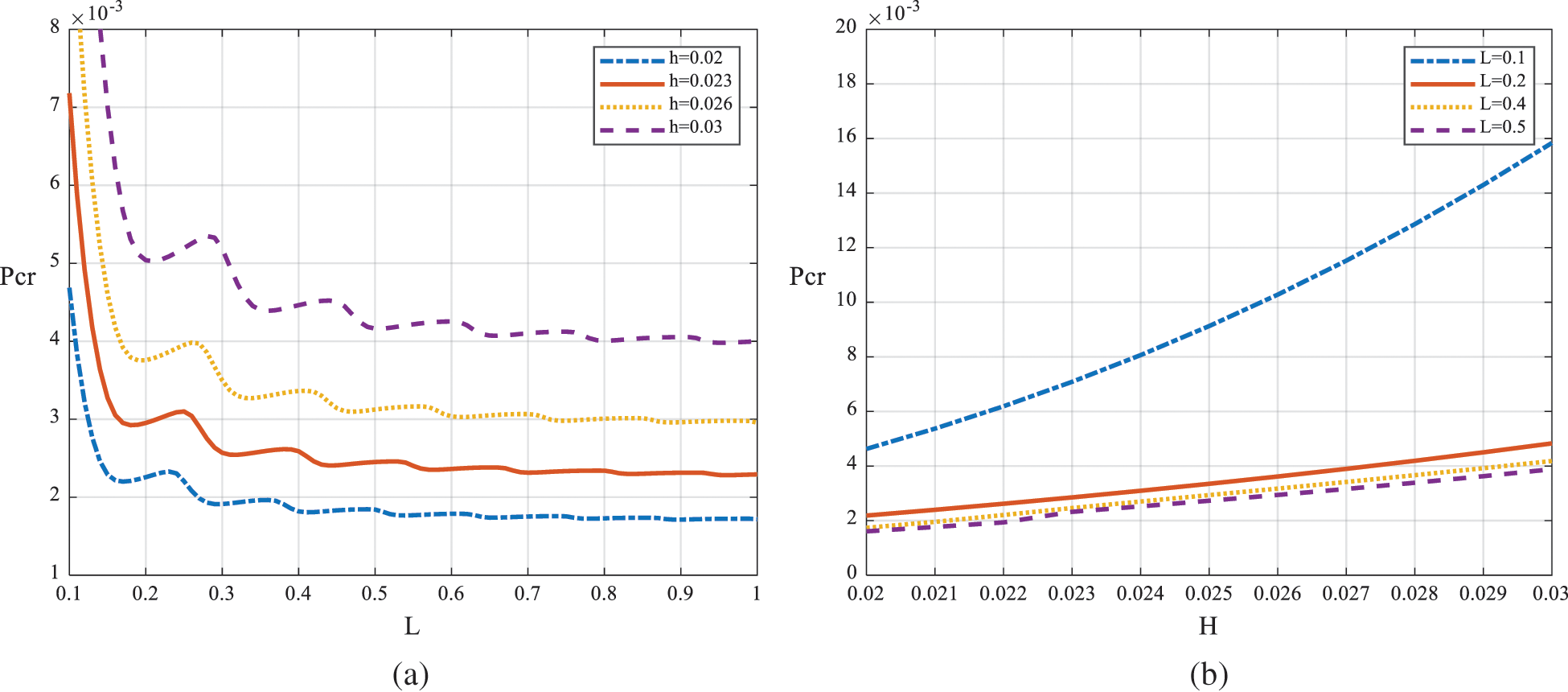
Figure 10: Critical loads with pulse length and thickness of shells when n = 1. (a) Pcr vs. normalized length of load and (b) Pcr vs. normalized thickness

6  Solution Verification by Comparison with FEM Results

To verify the effectiveness of the method used for buckling prediction above, a comparison between the FEM results and the results of this paper are implemented. In the FEM simulation an infinite long cylindrical shell is simplified to a finite long shell with L/R = 20, and set the R = 1, H = 0.01, E = 200 GPa, ν = 0.25. The ends of the shell are far enough from the loading region, so that end boundary conditions hardly effect the local buckling in the middle region, and then set the end boundary conditions to be simply supported. Set the ends of the loading region to be free of external constraints, and only exert a pair of axial compressive loads. 3 FEM models were established, in which 3 values of the length of loading region were taken: L = 0.6 R, L = 0.8 R, and L = 1 R. Due to the mesh size effect, the length of the mesh was taken to be 0.1, which is small enough to get accurate results. The overall mesh quantity is 12600. A 4-node doubly curved thin shell mesh strategy was adopted with reduced integration and hourglass control. The FEM model is shown in Fig. 11.

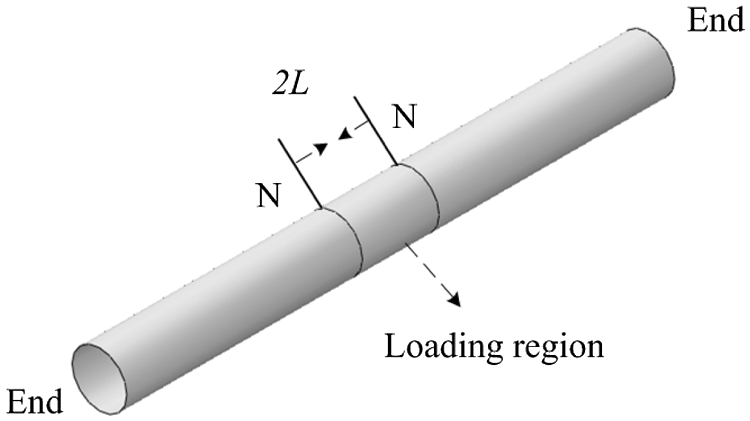
Figure 11: FEM model of cylindrical long shell

The generalized critical buckling load of the first branch for each FEM model is employed in contrast to the results in this paper as shown in Tab. 2 below. From the statistics in Tab. 2, we can see that the results in this paper are consistent with FEM results, and the results are more accordant for the cases in which L is large.

Table 2: Critical buckling loads of results from FEM and present method

Corresponding to Figs. 12a and 12b, the selected cylindrical shell buckling patterns are the same for FEM and present results, and thus the reliability and accuracy are verified.

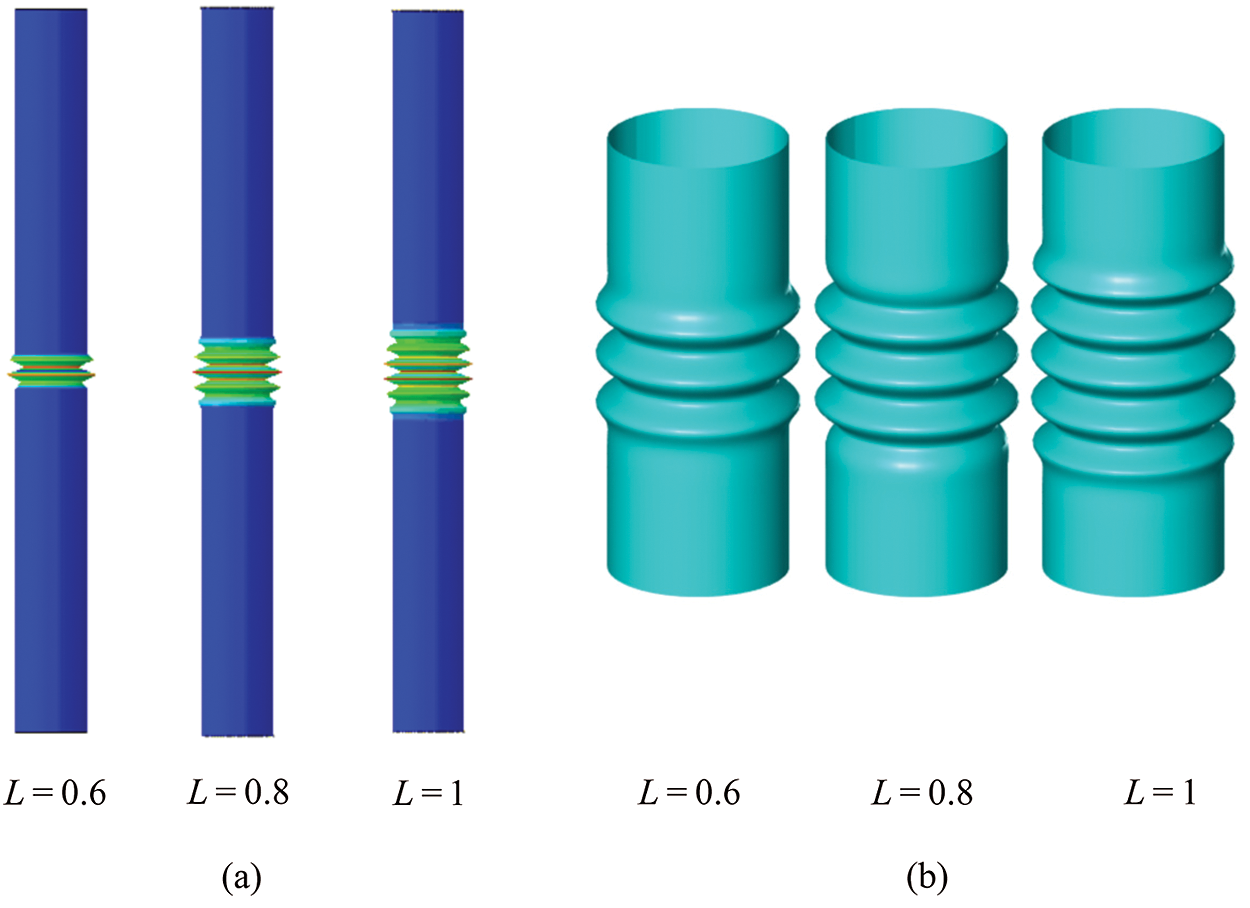
Figure 12: Shell buckling modes for FEM and present results when L = 0.6, 0.8, 1. (a) FEM results and (b) Present results

7  Conclusions

In Hamiltonian system, critical loads and modes of buckling of long shells are reduced to symplectic generalized eigenvalues and eigensolutions respectively. Under axial pulse loads, buckling of cylindrical long shells may happen and the main reason for the local buckling of shells is the pulse load. The critical load of local buckling of long shells is related to material constants and geometric parameters of shells and the pulse length of loads. The eigensolutions, modes of local buckling of shells, can be expressed by two parameters, namely axial order m and circumferential order n of buckling modes. The modes corresponding to these parameters show special phenomena. Eigensolutions of the zero eigenvalue represent the axisymmetric buckling modes and eigensolutions of the non-zero eigenvalues represent non-axisymmetric modes. The number of wrinkles along axial and circumferential directions and the buckling types depend on the parameters n and m. Numerical analysis reveals that the modes of local buckling of long shells mainly include bamboo node-type modes (n = 0), bending type modes (n = 1), concave type buckling modes (n ≥ 2) and so on. Results from this paper show good agreement with FEM results, and thus the reliability of the methodology imposed in this paper is verified. The symplectic method can also provide an analytical support to solve the problem of post-buckling of shells.

Funding Statement: This research is funded by the grants from Dalian Project of Innovation Foundation of Science and Technology (No. 2018J11CY005) and Research Program of State Key Laboratory of Structural Analysis for Industrial Equipment (No. S18313).

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.