 Open Access
Open Access
ARTICLE
Biomechanical Response of the Root System in Tomato Seedlings under Wind Disturbance
1 College of Mechanical and Electronic Engineering, Northwest A&F University, Yangling, 712100, China
2 Postharvest Research Laboratory, Department of Botany and Plant Biotechnology, University of Johannesburg, Johannesburg, 2006, South Africa
3 Institute of Agricultural Engineering, Jiangsu University, Zhenjiang, 212002, China
* Corresponding Author: Zhiguo Li. Email:
Phyton-International Journal of Experimental Botany 2023, 92(4), 1071-1090. https://doi.org/10.32604/phyton.2023.026408
Received 02 September 2022; Accepted 31 October 2022; Issue published 06 January 2023
Abstract
Wind disturbance as a green method can effectively prevent the overgrowth of tomato seedlings, and its mechanism may be related to root system mechanics. This study characterized the biophysical mechanical properties of taproot and lateral roots of tomato seedlings at five seedling ages and seedling substrates with three different moisture content. The corresponding root system-substrate finite element (FE) model was then developed and validated. The study showed that seedling age significantly affected the biomechanical properties of the taproot and lateral roots of the seedlings and that moisture content significantly affected the biomechanical properties of the seedling substrate (p < 0.05). The established FE model was sensitive to wind speed, substrate moisture content, strong seedling index, and seedling age and was robust. The multiple linear regression equations obtained could predict the maximum stress and strain of the root system of tomato seedlings in the wind field. The strong seedling index had the greatest impact on the biomechanical response of the seedling root system during wind disturbance, followed by wind speed. In contrast, seedling age had no significant effect on the biomechanical response of the root system during wind disturbance. In the simulation, no mechanical damage was observed on the tissue of the seedling root system, but there were some strain behaviors. Based on the plant stress resistance, wind disturbance may affect the growth and development of the root system in the later growth stage. In this study, finite element and statistical analysis methods were combined to provide an effective approach for in-depth analysis of the biomechanical mechanisms of wind disturbances that inhibit tomato seedlings’ growth from the root system’s perspective.Keywords
Nomenclature
| A | cross-sectional area of the sample, mm2 |
| d1 | diameter of taproot, mm |
| dt | diameter of lateral root, mm |
| E | tensile modulus of elasticity of sample, MPa |
| El | elastic modulus of lateral root, MPa |
| Es | modulus of elasticity of substrate, MPa |
| Et | elastic modulus of taproot, MPa |
| Elt | tangent modulus of lateral root, MPa |
| Est | tangent modulus of seedling substrate, MPa |
| Ett | tangent modulus of taproot, MPa |
| Em | modulus of elasticity of taproot, MPa |
| Etm | tangent modulus of taproot, MPa |
| Er | modulus of elasticity of lateral root, MPa |
| Etr | tangent modulus of lateral root, MPa |
| Fmax | elastic peak force, N |
| L1 | initial length of the sample, mm |
| ΔL | difference in sample length before and after the test, mm |
| Lt | length of taproot, mm |
| Ms | moisture content of substrate, % |
| M1 | mass of substrate during compression test, g |
| M2 | mass of seedling substrate after drying, g |
| n1 | number of lateral root |
| P | initial position point |
| SA | seedling age, day |
| S1 | initial growth point of root system, mm |
| SSI | strong seedling index |
| VW | wind velocity, m/s |
| ε1 | maximum yield strain of lateral root, MPa |
| εs | yield strain of the seedling substrate, MPa |
| εt | maximum yield strain of taproot, MPa |
| εy | fracture strain of the sample, % |
| α | tangent swing angle of the bottom of stem, ° |
| β | tangent swing angle of the top of taproot, ° |
| σl | maximum yield stress of lateral root, MPa |
| σm | yield stress of the taproot, MPa |
| σr | yield stress of lateral root, MPa |
| σs | yield stress of the seedling substrate, MPa |
| σt | maximum yield stress of taproot, MPa |
| σy | fracture stress of the sample, MPa |
| αA | axial angle, ° |
| λs | Poisson’s ratio of the seedling substrate |
| λt | Poisson’s ratio of the taproot |
| λl | Poisson’s ratio of the lateral root |
| ρs | density of the seedling substrate, g/cm3 |
| ρl | density of lateral root, g/cm3 |
| ρt | density of the taproot, g/cm3 |
| | angle of inclination |
Overgrowth is one of the most common technical issues in fruit and vegetable factory breeding; seedling enterprises must use a variety of growth regulators to control overgrowth. Potential chemical residues pollute the environment and affect food safety [1]. Wind disturbance is a green physical control method that is gradually being implemented in seedling factories to limit the overgrowth of tomato seedlings [2]. When wind disturbance was used to restrain the overgrowth of tomato seedlings, the wind disturbance directly acted on the seedling’s leaves and stems in the form of force and was transmitted through the stem to the root system (taproot and lateral root) [3]. Consequently, it produces some pressure on the root system, which leads to a physiological-biochemical response in the seedling and slows down the axial direction growth of the tomato plant seedling [4]. The root system of fruit and vegetables (such as tomatoes) mainly includes taproot and lateral root, which are the most important organs for plants to absorb water and nutrients and maintain life activities [5]. Under wind disturbances, the root system of seedlings can stretch or break, adversely affecting seedlings’ growth and development. Therefore, studying the biomechanical behavior of tomato seedling roots under the influence of wind disturbance is of great scientific value.
The existing literature on plant root mechanics mainly focuses on the root’s cell hardness and elastoplastic mechanical characterization. Nicolás-Álvarez et al. [6,7] found that the elastic modulus of epidermal cells of tomato seedling roots increased from 9.19 ± 0.68 to 13.90 ± 1.68 MPa while the elastic modulus of parenchyma cells and vascular bundle cells decreased from 1.74 ± 0.49 and 10.60 ± 0.58 to 0.48 ± 0.55 and 6.37 ± 0.53 MPa, respectively from day 7 to day 21. Fernandes et al. [8] discovered that the inherent surface mechanical properties of living Arabidopsis thaliana whole-root epidermal cells showed nanoscale heterogeneity. Plavcová et al. [9] found that roots’ bending and structural torsional modulus varied greatly between 9 species of woody angiosperms, with the bending modulus ranging from 558 to 2913 MN/m2 and the torsion modulus ranging from 48 to 254 mN/m2. Ali [10] revealed that the maximum tensile force of Leucaena leucocephala roots with diameters of 0.0–2.5, 2.5–5.0, and 5.0–8.0 mm is about 60, 135, and 310 N, respectively, and that of Acacia mangium and Melastoma malabathricum is approximately 40, 90, 110 N and 20, 55, 210 N, respectively. Sanchez-Castillo et al. [11] found a negative correlation between root diameter, tensile strength, and elastic modulus of the roots of Quercus rysophylla, Pinus pseudostrobus, and A. berlandieri, implying that the larger the root diameter, the lower the tensile strength and elasticity. Xu et al. [12] found that the elastic moduli of the root system of Populus simonii treated by trampling, defoliation, and physiological integration were 0.84, 0.88, and 4.4 GPa, respectively, while the breaking stresses were 0.15, 0.01 and 1.67 MPa, respectively. Ma et al. [13] determined that Bermuda grass roots’ peak tensile breaking force was 15.21 N. Li et al. [14] found that the tensile strength of roots of Amorpha fruticose Linn., Swida alba Opiz and Lespedeza bicolor Turcz increased as root diameter decreased. Zhang et al. [15] found that the maximum tensile force of the root system of K. scoparia and A. sacrorum reached maximum values of 9.49 ± 1.62 and 16.12 ± 2.24 N, respectively, when the gauge length was 50 mm, and minimum values of 5.96 ± 0.95 and 10.92 ± 1.49 N, respectively at a gauge length of 200 mm, which indicated that the maximum pulling force of K. scoparia and A. sacrorum roots decreased in a power function as gauge length increased.
To summarize, the existing literature has greatly progressed in exploring the multiscale biomechanics of different plant roots. However, less attention has been paid to the effects of wind disturbances on the biomechanical behavior of tomato seedling roots. The process of suppressing the overgrowth of tomato seedlings by wind disturbance in the seedling factory includes: the wind blows the tomato seedlings, causing the above-ground tissues and organs to swing, and the stem drives its root movement and mechanically interacts with the seedling substrate, which may cause root system damage and slow seedling growth. The seedling root system-substrate shares all external wind disturbance forces, and there is an indirect interaction between the wind disturbance and the root system. However, it is unclear how wind disturbance parameters, tomato seedling morphology, and substrate mechanical parameters affect the mechanical laws of tomato seedling roots. Therefore, this study aimed to investigate the effect of wind disturbance on the biomechanical behavior of the root system of tomato seedlings. The study further elucidates the mechanical action mechanism of wind disturbance restraining the overgrowth of tomato seedlings and establishes a set of green seedling theories and methods for repressing the overgrowth of tomato seedlings due to wind disturbance.
The popular ‘improved 802 F1’ tomato seeds with high stress and disease resistance were selected for seedlings in a modern glass greenhouse of the Plant Mechanics Research Group at the National (Yangling) Agricultural Hi-tech Industries Demonstration Zone (E 108°.07145′, N 34°.27175′), China. To promote rapid seed germination, the seeds were first immersed in water for 24 h at an environment temperature of about 25°C to absorb water quickly and reach a moisture content that allows them to germinate properly. Subsequently, the seeds were dispersed in Petri dishes lined with moist filter paper and preserved in a greenhouse with an environment temperature of about 25°C. At the same time, the seedling substrate (Yangling Linke Ecological Technology Co., Ltd., Shaanxi, China) was taken out, and the water was mixed in a 2:1 ratio to form a wet substrate. Then, it was placed in a seedling tray and smoothed out with a blade to make the thickness approximately 3–4 cm. After each seed had grown a radicle in the glass garden, the seed was gently sown on the upper surface of the moist substrate in the tray with a tweezer. Then, another portion of the moist substrate was scattered over the seeds to cover them with a thickness of approximately 0.5–1.0 cm. After the seedlings in the tray grew into a stem with two compound leaves and one apical bud, each seedling was transplanted into a plastic bowl measuring 6.5 cm × 6.5 cm × 6.5 cm (length × width × height). One seedling for each plastic bowl, and then 48 plastic bowls were placed in 2 seedling trays with a density of 4 rows by 6 columns. Finally, tomato seedlings were cultivated in a normal growth environment with a temperature of 28°C/15°C (day/night), a photoperiod of 14 h/10 h (day/night), and a light intensity of 10,000–40,000 Lux (9:00–17:00).
2.2 Determination of the Morphological and Biomechanical Parameters of the Root
When the tomato seedlings had grown to 3–4 compound leaves (tomato seedling was at 25 days old), five tomato seedlings with no surface damage and worm infestation were chosen randomly, and their leaves and stems were picked off to determine the morphological and biomechanical parameters. Given that tomato seedlings are usually transplanted after 45 days and that the preliminary experiment revealed that young seedlings (SA < 25 days) are easily lodged during wind flow, the root systems of tomato seedlings at the ages of 25, 30, 35, 40, and 45 days were chosen for investigation. Following that, the root morphological and biomechanical parameters were determined on five seedlings every five days. Tomato seedlings’ morphological and biomechanical parameters were measured five times during their growth period.
2.2.1 Determination of the Morphological Parameters of the Root
The following root system morphological parameters were determined in tomato seedlings: length Lt and diameter dt of the taproot, length L1 and diameter d1 of the lateral root, number nl of the lateral root, initial position point P, and angle of inclination
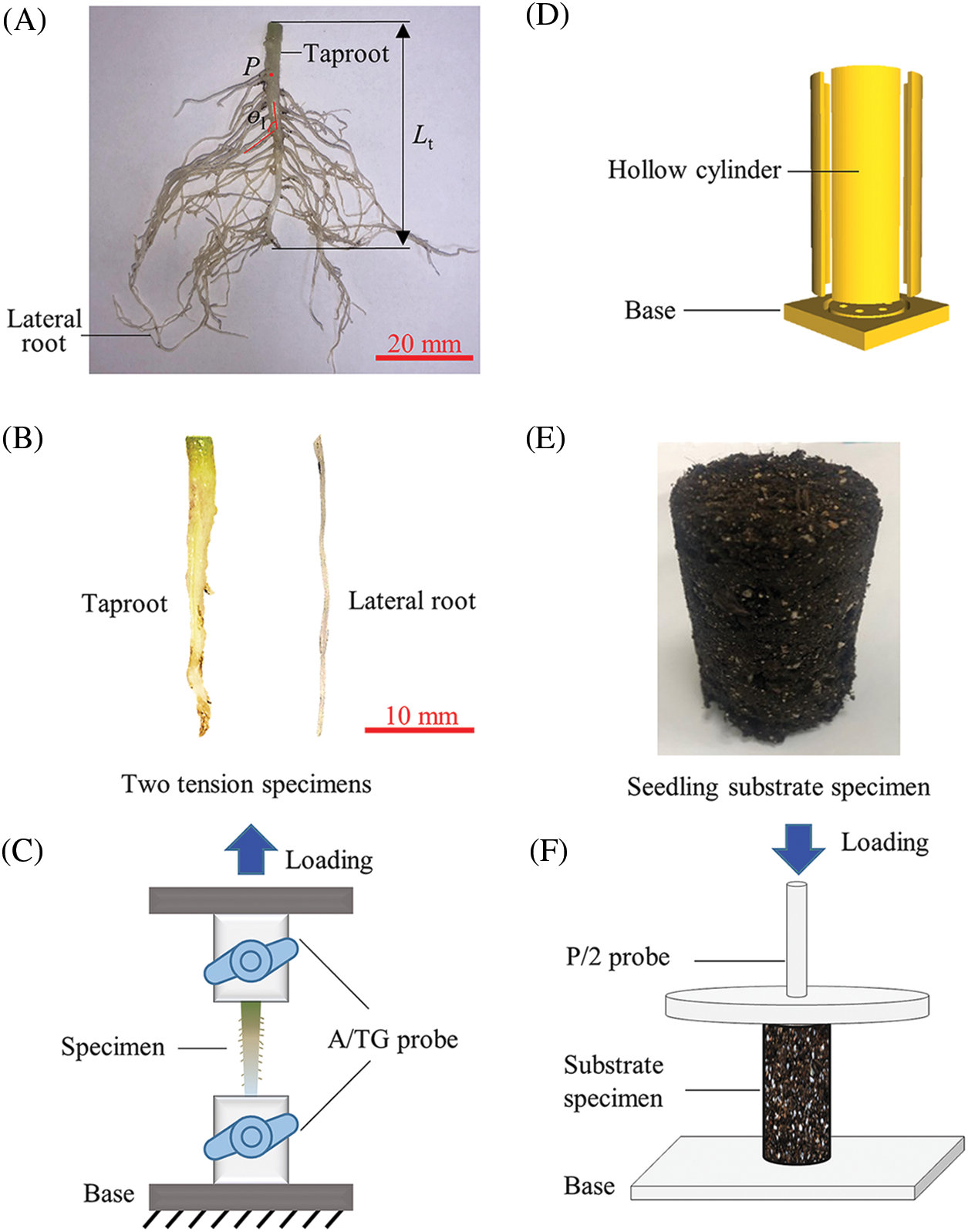
Figure 1: Morphological determination of tomato seedling roots and determination of mechanical parameters of the root system and seedling substrate. (A) morphological determination of tomato root system, (B) taproot and lateral root specimens, (C) tension test, (D) hollow plastic cylinder, (E) seedling substrate specimen, (F) compression test
2.2.2 Determination of the Biomechanical Parameters of the Root
Tomatoes have a straight root system with a taproot and many slender lateral roots. Since the tomato seedling stage was grown in a plastic bowl and the taproot was short, the biomechanical variations between different parts of the taproot were ignored. During the test, a tomato seedling was removed from the plastic bowl, and running water was used to clean out the root system of the mixed seedling substrate. Subsequently, a sample of about 3 cm in length was cut from the middle of each seedling’s taproot using a FEATHER R35 blade to determine the tensile mechanics of the seedling’s taproot. Similarly, a sample with a length of about 3 cm was cut from the middle of the lateral root to measure the tensile mechanics of the seedling’s lateral root (Fig. 1B). Finally, according to the GB/T 228-2002 tensile test method, both ends of each sample were fixed between the upper and lower probe fixtures of A/TG of the texture analyzer (Universal TA, Tengba Instrument Technology Co., Ltd., Shanghai, China), stretching upward to fracture (Fig. 1C). Before the tensile test, a 1 kg weight was used to calibrate the texture analyzer. Then, the initial position of the upper stretch probe of A/TG was calibrated by setting the contact distance between the upper and lower fixtures to 0. The initial separation distance of the upper and lower stretching clamps was 15 mm, and the stretching speed was 1 mm/s. The force-displacement curve data of each tensile test was recorded by computer in real-time. Finally, Eqs.(1)–(3) were used to deduce the mechanical parameters of the taproot and the lateral root. The parameters include fracture stress σy, fracture strain εy, and elasticity modulus E [16–19].
2.3 Determination of the Biomechanical Parameters of the Seedling Substrate
Variations in environmental temperature within the seedling greenhouse may necessitate varying amounts of irrigation required for tomato seedling growth, and seedling substrates with different moisture content can affect their biomechanical properties. Therefore, the biomechanical properties of the seedling substrate under various water content conditions were determined in this section. The following is the procedure for preparing the seedling substrate sample: firstly, to prepare the breeding substrate sample, 175 g of the dry substrate and 350 g of water were mixed evenly in a beaker at a mass ratio of 1:2 and then poured into five hollow plastic cylinders (inner diameter: 25 mm, height: 64 mm) printed by a 3D printer [20] (Figs. 1D and 1E). Then, the samples were stored in a constant temperature and humidity chamber (SPX80B, Tianjin Henuo Instrument Co., Ltd., Tianjin, China) with the temperature set at 25°C and the relative humidity set at 50%. Finally, after 24 h of storage, five seedling substrate samples were taken out to determine the mechanical parameters of the substrate. Similarly, the seedling substrate samples were prepared and stored for 72 and 120 h, respectively, to determine the mechanical parameters of the substrate. The water content of seedling substrate samples after 24 , 72, and 120 h storage differed due to the same storage temperature set in the constant temperature and humidity chamber. Following each sample preparation, a substrate was chosen, and its mass, M1, was determined using an electronic balance (accuracy 0.01 g). After weighing, the substrate was placed in the oven and dried at 60°C until the mass became constant. At this point, the mass of the substrate was designated as M2, and the moisture content w of the prepared seedling substrate was calculated using Eq. (4).
The biomechanical measurement procedure was as follows: firstly, according to the GB/T 228-2002 standard compression test method, each seedling substrate sample was sequentially placed on the base plate of a Texture Analyzer (Universal TA, Tengba Instrument Technology Co., Ltd., Shanghai, China) before being compressed downward with a 15 cm diameter P/2 compression probe. A 1 kg weight was used to calibrate the Texture Analyzer before the compression test, and the base plate was used for height calibration of the P/2 probe. The initial separation distance between the substrate and the compression probe was 80 mm, and the compressive velocity was 1 mm/s. The force-displacement curve data during the compression test was recorded by a computer in real-time. Then, Eqs. (1)–(3) were used to deduce the relevant mechanical parameters of the seedling substrate: fracture strain Es, fracture stress σs, and fracture strain εs [16–18].
2.4 Modeling and Simulation of the Seedling Root System under Wind Disturbance
2.4.1 3D Finite Element Modeling of the Root and Substrate
Step 1: Geometric modeling. Firstly, five ages (25, 30, 35, 40, and 45 days old) of tomato seedlings were geometrically modeled using the Pro/ENGINEER software (Version: 5.0, American Parametric Technologies Corp., USA), respectively, based on the morphological parameters of seedlings obtained in Section 2.2.1. In each case, a seedling geometric model was imported into the ANSYS software (2021R/Workbench, American Ansys Co., Canonsburg, USA). After that, a substrate model was created to surround the root system based on the geometric model of the root system of a specific growth stage. Consequently, the geometric model of the root system-substrate of five different seedling ages was formed. The geometric model of each tomato seedling’s root system consists primarily of 1 taproot and 34 lateral roots. The dimensions (length × width × height) of the substrate geometry surrounding the seedling root system were set as 0.065 m × 0.065 m × 0.065 m, with the following method of operation: Design Modeler-Tool-Enclosure.
Step 2: Definition of interactions. In practice, the lateral roots and seedling substrate will envelop each other; therefore, in the simulation, the root system of the tomato seedling and the seedling substrate were set as binding links. The contact surface of the tomato seedling roots system (contact geometry) was bound to the substrate contact surface (target geometry). The maximum offset of the contact surface to the target surface in the bonding constraint was set to 0.01 mm. During initialization, binding pairs were established by bonding all nodes on the contact surface of the seedling substrate less than 0.01 mm away from the root system’s contact surface to the substrate’s contact surface using the automatic search algorithm. A “penalty forces” operation ensured that the relative position of the nodes of the root system’s contact surface on the seedling substrate’s contact surface did not change during the simulation.
Step 3: Boundary condition setting and meshing. Firstly, the other five surfaces of the seedling substrate, except for the upper surface, were set as fixed support, limiting its translation along the x, y, and z axes and rotation around the x, y, and z axes. The boundary condition indicated that the plastic bowl of the cultivated tomato seedling did not deform or move throughout the analysis. Subsequently, in consideration that: i) the deformation of the tomato seedling root system and partial substrate was large under the action of the wind field, the root system and substrate geometry model should be meshed as finely as possible, and its element type should be robust during simulation, with minimal shear and volume locking properties; ii) the shape of the root system in the tomato seedling was irregular, using the structured meshing technique of the tetrahedral element type can obtain better mesh orthogonal quality; therefore, the taproot, lateral root and seedling substrate of the tomato seedling were meshed by “Tet 4” (four-node linear tetrahedral unit) cells, with cell sizes of 1.5 mm for the taproot and lateral root and 5 mm for the seedling substrate. Finally, Table 1 shows the meshing results of five tomato root-substrate geometric models (5 seedling stages). Fig. 2A depicts the finite element model of the root system-substrate of tomato seedlings aged 25 days.
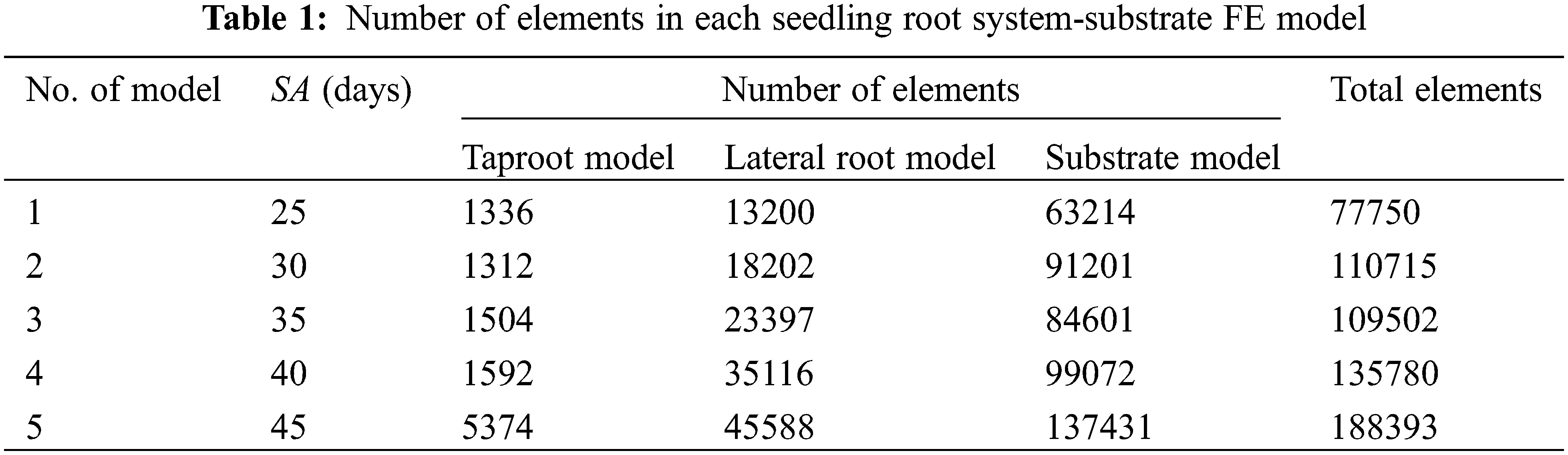
Figure 2: Modeling and validation of the seedling root-substrate system. (A) a root system (age: 25 days)-substrate FE model, (B) a previous seedling FE model, (C) the swing angle of stem base, (D) root system FE model, (E) taproot head swing angle-time curves in experiment and simulations, the green area is the error band of 5 experiment results
2.4.2 Validation of the Tomato Seedling Root System-Substrate FE Model
Validation: To validate the accuracy of the established root system of the tomato seedling FE model, given that a tomato seedling had the same movement at the junction of the stem and the root systems (Figs. 2B–2D), the experimental results of the base movement of the taproot of the 25-day-old tomato seedling disturbed by the wind-flow with a velocity of 2 m/s and the simulation results of the top movement of the taproot, such as the seedling swing angle-time curve, were compared.
Experimental method: Firstly, a previously designed test platform for wind-flow disturbed tomato seedlings was used [21]; a cartesian coordinate system, xyz, was established on the base at 100 mm away from the fan’s air outlet, and five 25-day-old tomato seedlings contained in plastic bowls were placed at the origin o of the coordinate system. Subsequently, after each seedling was securely placed, the fan was turned on, and its average wind velocity could maintain 2 m/s within 120 s to blow the seedlings. Real-time video of the swing process of the base of the taproot of the tomato seedling disturbed by wind flow was captured using a high-definition camera. Following the experiment, the recorded videos were imported into Kinovea-0.9.5, an open-source motion analysis software. Then, the angle between the tangent line and the vertical line at the base of the stem was automatically tracked over time using the “Angle to horizontal” function (Fig. 2C). In addition, a part of the substrate was removed from the plastic bowl, and the moisture content was determined through drying.
Simulation method: the swing process of the 25-day-old tomato seedling under external force was simulated using the established root system-substrate finite element model No. 12 (Table 2) in Section 2.4.1. The elastic modulus and tangent modulus of the taproot were set to 16.37 and 2.09 MPa, respectively; the elastic modulus and tangent modulus of the lateral root were set to 18.22 and 1.08 MPa, respectively; and the elastic modulus and tangent modulus of the seedling substrate were set to 0.15 and 0.013 MPa, respectively. Based on the previous research results of Liu [21], the force-time data of the base of the stem were extracted when the wind speed was 2 m/s for a 25-day-old seedling of tomato (Fig. 2B). It was simulated by applying it to the cap of the taproot of the tomato seedlings’ root substrate finite element model. Finally, the swing angle-time data curve of the top of the taproot was extracted from the simulation results (Figs. 2D and 2E). The prediction accuracy of the root system-substrate finite element model was assessed by comparing the above indexes from the simulation and experimental results.

To investigate the effects of wind speeds, strong seedling indexes, and humidity substrates on the biomechanical response of tomato seedlings at different seedling ages, the wind velocity at the wind field’s inlet was set to two levels, 1 and 2 m/s. Similarly, the strong seedling index was set to 0.01 and 0.02. Based on the previous research findings of Liu [21], force-time data of the seedling’s root cap were extracted when the wind speed was 1 and 2 m/s, and the strong seedling index was 0.01 and 0.02. Then, it was applied to the cap of the taproot for simulation. The seedling age was set to five levels: 25, 30, 35, 40, and 45 days old. The seedling substrate’s moisture content was set at 16.52%, 30.54%, and 50.06%. After that, corresponding biomechanical parameters were assigned to the constructed root system-substrate geometric model during the simulation (Table 2). In addition, the Poisson’s ratio of most root systems approximates 0.25~0.4 [22,23], so the Poisson’s ratio of the taproot and lateral roots of the tomato seedling were set to 0.3. Finally, the comprehensive simulation experiments design method was used (Table 2). 60 (5 seedling age levels × 3 water content levels × 2 wind velocity levels × 2 strong seedling index levels) FE simulation calculations of root system-substrate biomechanics interaction were performed based on the tomato seedling root system-substrate finite element model.
The following assumptions were made to simplify the FE analysis: (1) the taproot and lateral roots of the root system, as well as the substrate materials, are considered homogeneous, ignoring the intercellular cavity, pit cavity, and other gaps in seedling tissue; the biomechanical parameters of the root system, such as stress and strain, and displacement, can be expressed by a continuous function; (2) the material properties of the taproot and lateral roots of the tomato seedlings are orthogonal and isotropic, which means that the mechanical properties in three mutually perpendicular directions (longitudinal, radial and chordal directions) are the same; (3) the taproot and lateral roots of a tomato seedling are elastic-plastic materials that follow the plastic increment theory in elastic-plastic theory, which divides an object’s strain in the elastic-plastic deformation stage into two parts: elastic strain and plastic strain. The elastic strain can be calculated using Hooke’s law, and the plastic strain can be calculated using the yield surface theory, flow rule theory, and process hardening theory from the plastic increment theory.
The SAS software (version 9.2, SAS Institute Inc., USA) was used to perform the multiple linear regression analysis on the 60 simulation results, with the significance level set at 0.05. The swing Angle of the cap of the taproot, maximum strain, and stress of the root system in the simulation results were extracted and set as dependent variables, respectively. The seedling age, strong seedling index, wind speed, and substrate moisture content were set as independent variables. The backward elimination method was used to establish the multiple linear regression equations between dependent and independent variables.
3.1 Biomechanics of the Taproot and Lateral Root in Tomato Seedlings during Growth
As shown in Fig. 3A, the image described the biomechanical parameters of tomato seedlings’ taproot and lateral roots at five seedling ages. The results of the variance analysis showed that the seedling age significantly affected the elastic modulus and failure stress of tomato seedlings’ taproot and lateral roots (p < 0.05). When the seedling age was less than 30 days, the elastic modulus of the taproot of tomato seedlings was lower than that of the lateral root. Whereas, when the seedling age was more than 30 days, the elastic modulus of the taproot and lateral root of tomato seedlings increased with seedling age, with a greater elastic modulus observed for the taproot than the lateral root. Additionally, when the seedling age was more than 30 days, the failure stress of the tomato seedling’s taproot and lateral roots did not change significantly with the increase in seedling age (p < 0.05). In all five seedling ages, the failure stress of the taproot was greater than that of the lateral root. In addition, humidity had adverse and significant effects on the elastic modulus and failure stress of the seedling substrate (p < 0.05) (Fig. 3B). The measured elastic modulus of the seedling root is much lower than the 2.3 GPa proposed by Wang et al. [24] for a 2-week single suspension-cultured cell in the root meristem of tomato seedlings. There is no information in the literature about the biomechanics of the macroscopic taproot and lateral root in tomato seedlings during growth, so no comparisons are possible.
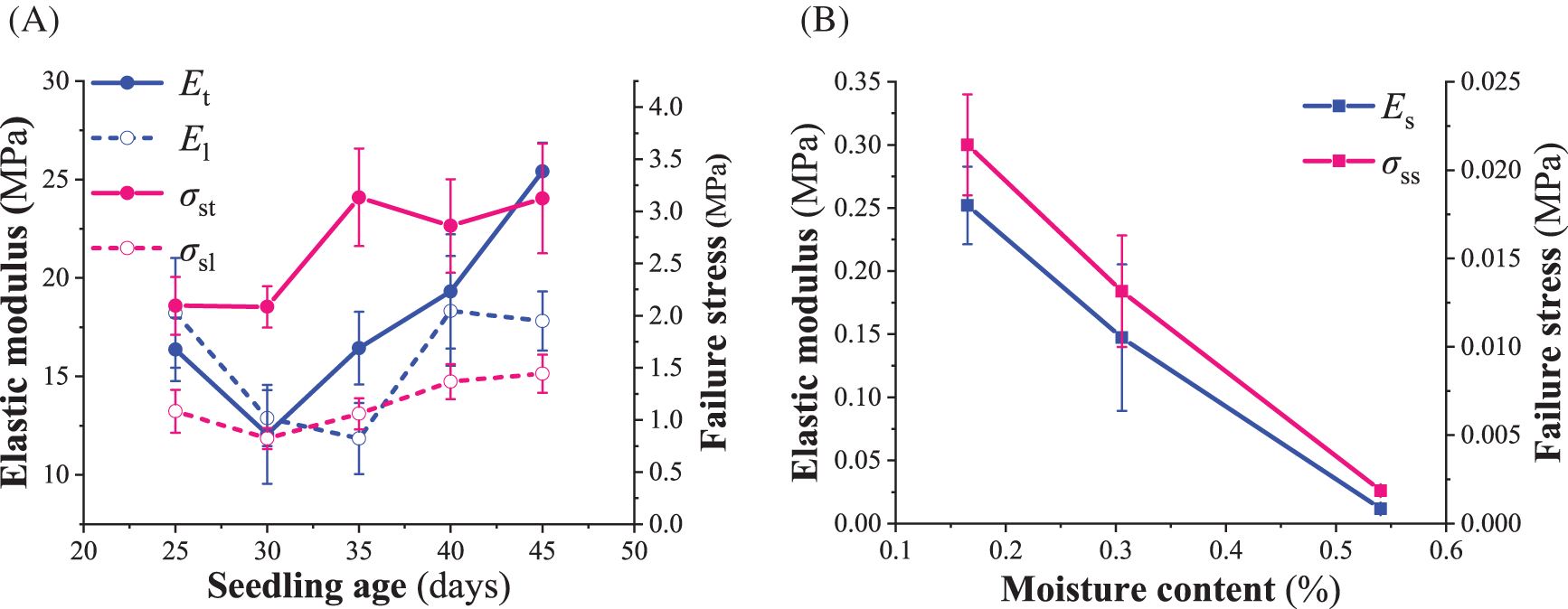
Figure 3: Biomechanics of the seedling root system and substrate. (A) elastic modulus and failure stress of the taproot and lateral root during growth; (B) elastic modulus and failure stress of the substrate at different moisture contents.
3.2 Performance of the Tomato Seedling Root System-Substrate FE Model
When the tomato seedling was 25 days old, and the wind was blowing at 2 m/s, the swing angle-time curves of tomato seedlings are shown in Fig. 2E, which includes the experimental data of swing angle-time at the stem base and simulation results using the seedling root system-substrate finite element model. The green area represents the error band of the swing angle of the base of the stem of tomato seedlings changing with increasing blowing time during the five experiments. Evidently, the simulation results obtained using the seedling root system-substrate finite element model, that is, the variation curve of root cap swing angle with blowing time, was within the error range of actual test results. Therefore, the established finite element model of the tomato seedling root system has a high prediction accuracy and can be applied to the subsequent analyses of the tomato seedling root system-substrate biomechanical interactions.
Fig. 4 shows the Von Mises stress contour of the root system in the tomato seedling FE model (seedling age = 30 days, substrate moisture content = 30.54%, wind speed = 1 m/s). The stress of the taproot is mainly distributed in its top region during wind disturbance. The stress in the connection region between the taproot and a lateral root was much higher than in the distal end of the lateral root, indicating that the lateral roots, particularly those surrounding the top region of the taproot, play an important role in the taproot’s fixation in the substrate. The results obtained corroborate those reported earlier by Yang et al., Stokes, and Watson [23,25,26]. Because lateral roots have a soft texture, they can only withstand tension but not compression, and the contribution (stress distribution) of the lateral root to the taproot on the windward side is significantly greater than on the leeward side [25–28].
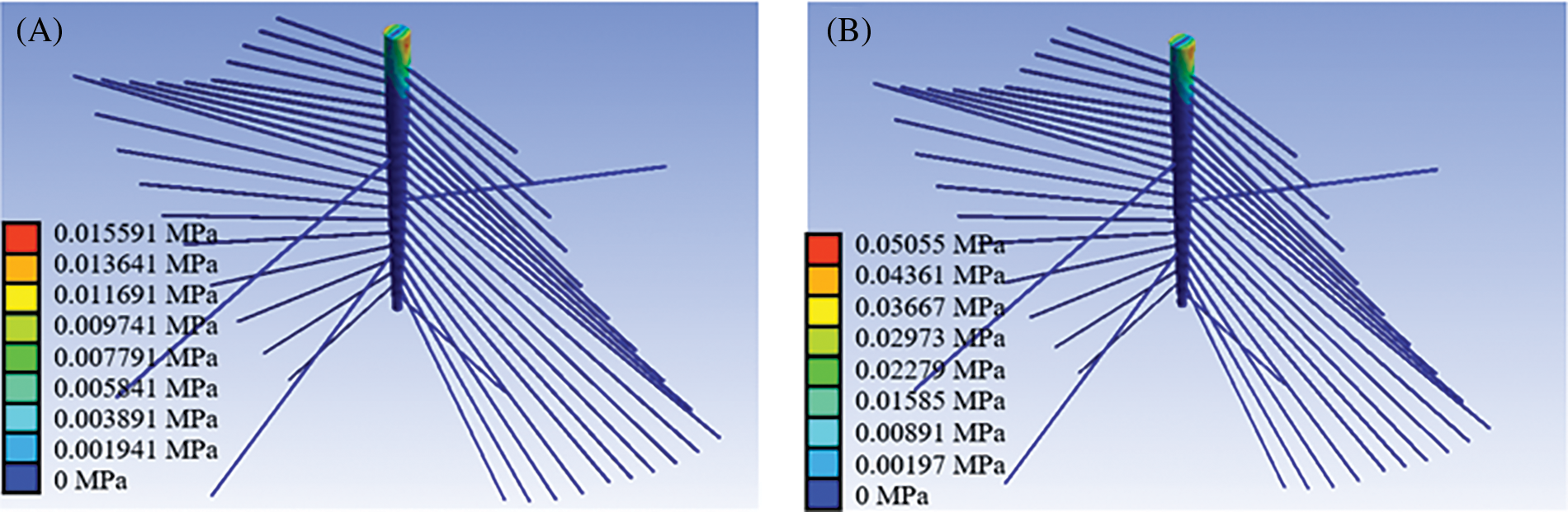
Figure 4: Von Mises stress contour of the root system in a tomato seedling (seedling age = 30 days, substrate moisture content = 30.54%, wind speed = 1 m/s). (A) Von Mises stress contour of the root system (strong seedling index = 0.01), (B) Von Mises stress contour of the root system (strong seedling index = 0.02)
3.3 Sensitivity of the FE Model to the Wind Velocity, Substrate Moisture Content, Strong Seedling Index, and Seedling Age
The model as described above was investigated for its sensitivity to four potential variables: wind velocity, substrate moisture content, strong seedling index, and seedling age, respectively, to assess the robustness of the developed tomato seedling root system-substrate FE model to various external factors and tomato seedling properties.
3.3.1 Sensitivity to the Wind Velocity
Figs. 5A and 5B show the curves of maximum stress on taproot and lateral roots with time when the seedling age was 30 days, the strong seedling index was 0.02, the moisture content of the substrate was 30.54%, and the wind speed was 1 and 2 m/s, respectively. The taproot model was more sensitive to wind speed than the lateral root model. Under the two wind speeds, the maximum stress of tomato seedling taproot and lateral root showed an approximate fluctuation period with increasing blowing time. When the wind speed was 2 m/s, the maximum stress of tomato seedlings’ taproot and lateral root increased sharply and reached the first peak at 170 ms, which were 0.142 and 0.0766 MPa, respectively, and were 2.81 and 2.75 times more than the peak stress under 1 m/s wind speed. The maximum strains of tomato seedlings’ taproot and lateral root tissues were 0.00414 and 0.00205 when the wind speed was 1 m/s and 0.0117 and 0.00557 when the wind speed was 2 m/s, respectively. Under the wind disturbance, the aboveground organs of tomato seedlings experienced a damped harmonic motion of “swing (stem bending) → deformation (leaf torsion and bending, collateral bending) → recovery (primary and lateral stem restore, leaf returning to initial shape)” [29], with the peak value of the maximum stress transmitted from the stem to the taproot and lateral root gradually decreasing with the increase in wind disturbance time (decay).
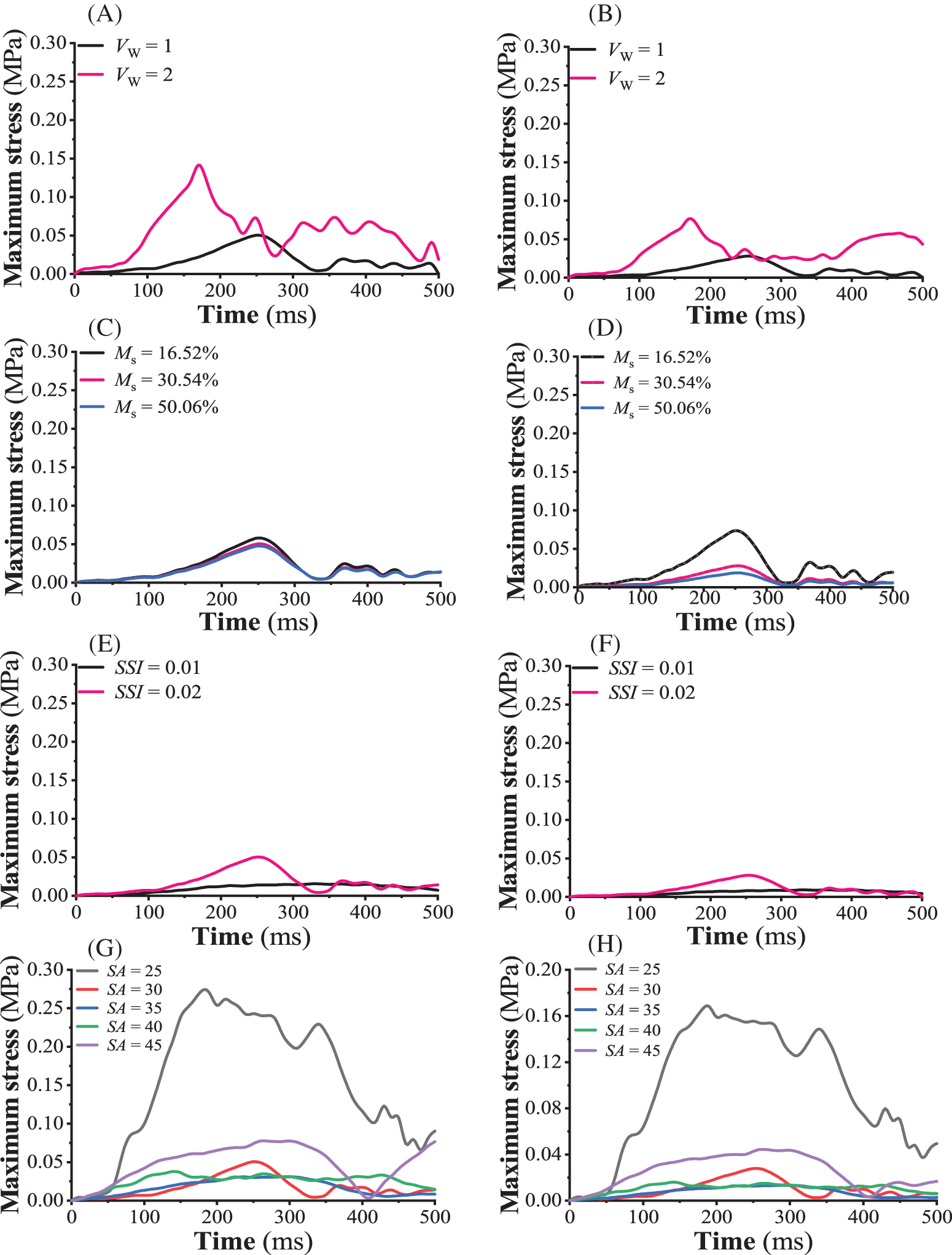
Figure 5: Sensitivity of the FE model. (A, B) sensitivity of the taproot and lateral root models to the wind velocity, respectively, (C, D) sensitivity of the taproot and lateral root models to the moisture content within the seedling substrate, respectively, (E, F) sensitivity of the taproot and lateral root models to the strong seedling index, respectively, (G, H) sensitivity of the taproot and lateral root models to the seedling age, respectively
3.3.2 Sensitivity to the Moisture Content within the Seedling Substrate
Figs. 5C and 5D depict the time-dependent maximum stress curves on taproot and lateral roots when the seedling age was 30 days, the strong seedling index was 0.02, the wind speed was 1 m/s, and the substrate moisture content was 16.52%, 30.54%, and 50.06%, respectively. The sensitivity of taproots to substrate moisture content was lower than that of lateral roots in the finite element model. Under the humidity conditions of three seedling substrates, the maximum stress of tomato seedlings’ primary and lateral roots fluctuated similarly with increasing blowing time. When the moisture content of the seedling substrate was 16.52%, the maximum stress of the taproot and lateral root of tomato seedlings gradually increased with an increase in wind disturbance time, reaching the first peak at 250 ms, which were 0.058 and 0.0737 MPa, respectively, and were 1.22 and 3.96 times more under 50.06% humidity. The maximum strains produced by tomato seedlings’ main and lateral root tissues were 0.00476 and 0.00562 under 16.52% humidity, 0.00414 and 0.00205 under 30.54% humidity, and 0.00391 and 0.00141 under 50.06% humidity, respectively.
3.3.3 Sensitivity to the Strong Seedling Index
Figs. 5E and 5F show the change in maximum stress curves of tomato seedling taproot and lateral roots with time when the seedling age was 30 days, the substrate water content was 30.54%, the wind speed was 1 m/s, and the strong seedling index was 0.01 and 0.02, respectively. The taproot model was more sensitive to the strong seedling index than the lateral root. The maximum stress of taproot and lateral root of two types of healthy tomato seedlings fluctuated differently as blowing time increased. When the strong seedling index was 0.02, the maximum stress of tomato seedlings’ taproot and lateral roots gradually increased with increasing wind disturbance time, reaching the first peak at 250 ms, which were 0.0505 and 0.0278 MPa, respectively, and were 3.24 and 3.06 times higher than the peak stress under 0.01 strong seedling index. The maximum strains of taproot and lateral root tissues were 0.00127 and 0.000669 when the strong seedling index was 0.01 and 0.00414 and 0.00205 when the strong seedling index was 0.02, respectively.
3.3.4 Sensitivity to the Seedling Age
Figs. 5G and 5H show the change in maximum stress curves of tomato seedling taproot and lateral roots with time when the strong seedling index was 0.02, substrate water content was 30.54%, wind speed was 1 m/s, and seedling age was 25 days, 30 days, 35 days, 40 days, and 45 days, respectively. The sensitivity of the taproot model to the seedling age in the established root system-substrate finite element model was higher than the lateral root. The maximum stress of tomato seedling taproot and lateral root at five seedling ages revealed fluctuating scenarios as blowing time increased. When the seedling age was 25 days, the maximum stress of the taproot and lateral root of the tomato seedlings increased gradually with the wind’s disturbed time, reaching the first peak at 170 and 180 ms, which were 0.273 and 0.168 MPa, respectively, and were 3.543 and 3.79 times more than when the seedling age was 45 days. When the seedling age was 25 days, the maximum strains produced by the tomato seedlings’ primary and lateral root tissues were 0.0166 and 0.00928, respectively. Similarly, the maximum strains produced by the tomato seedlings’ primary and lateral root tissues were 0.00414 and 0.00205 by day 30, 0.00176 and 0.00115 under by day 35, 0.00194 and 0.000836 by day 40, 0.00302 and 0.00249 by day 45, respectively.
3.4 Prediction of the Maximum Stress and Strain in the Root System of Tomato Seedling
The multiple linear regression analysis results showed that the maximum stress and strain of the taproot and lateral roots of tomato seedlings could be predicted by mathematical Eqs.(5)–(8). Two factors: strong seedling index and wind speed, significantly influenced the maximum stress and strain of tomato seedlings’ taproots (p < 0.05). Three significant factors affected the maximum stress and strain of the lateral roots of the tomato seedlings: strong seedling index, wind speed, and water content of seedling substrate (p < 0.05).
When the strong seedling index increased by 0.01, the maximum stress and strain of tomato seedling taproot increased by 0.0876 and 0.00534 MPa, respectively, and the maximum stress and strain of tomato seedling lateral root increased by 0.0553 and 0.00356 MPa, respectively. The greater the strong seedling index, the greater the maximum stress and strain of tomato seedling’s taproot and lateral root. The reason was that tomato seedlings with different growth degrees have different resistance to wind disturbance in the same wind field. The larger the strong seedling index, the stronger the tomato seedling, the more luxuriant the stem and leaf, and the greater the resistance to wind field. Therefore, the maximum stress and strain generated by the internal tissues of the taproot and lateral root of the seedling were larger.
When the wind velocity increased by 1 mm/s, the maximum stress and strain of tomato seedling taproot increased by 0.0799 and 0.000367 MPa, respectively, and the maximum stress of tomato seedling lateral root increased by 0.0435 and 0.00227 MPa. The maximum stress of tomato seedling taproot and lateral root increased as wind velocity increased.
The reason was that the greater the wind velocity, the greater the force exerted on the overground organs of the tomato seedling, and the greater the force transmitted from the stem to the root system. In addition to performing physiological and biochemical tasks like transmitting water and nutrients and synthesizing amino acids [30–32], the plant root system also fixes and supports tomato seedlings [33,34]. Under a wind speed of 2 m/s, the maximum stress in the taproot and lateral root reached 0.142 and 0.0766 MPa, which were 0.68% and 9.33% of the yield strength, respectively, and no mechanical damage occurred in the taproot and lateral root tissues. The maximum stress of the lateral root was significantly lower than that of the taproot, at only 53.94% of the taproot’s maximum stress. Under the support of the stem and leaves, the tomato seedling’s taproot was bent and deformed in the direction of the wind, and the lateral roots were bound to both the taproot and the seedling substrate. Due to the inhibition of taproot deformation, the lateral root tissues located in the same direction as the taproot were subjected to greater tensile stress, whereas the lateral root tissues located in the opposite direction of the taproot were subjected to a certain degree of compressive stress [35,36]. Although such mechanical stress does not cause mechanical damage to the root system, it may have specific effects on the root system’s subsequent growth and development, such as increasing the number, length, and strength of the root system [33].
In the wind field, as long as a tomato seedling’s aboveground organs can withstand external forces and moments, the entire load acting on the aboveground will be transferred to the root-substrate system [25]. Therefore, it is necessary to coordinate the three factors, namely root-substrate structure, root strength, and substrate strength, to fix the tomato seedling and prevent uprooting [27,37–39]. The substrate strength mainly depends on the water content, which affects the anchorage strength and plays a crucial role in forming the root-substrate structure [25,40]. Based on the root system-substrate FE model, the moisture content of the seedling substrate had a significant effect on the maximum stress of tomato seedling lateral roots (p < 0.05) but had no significant impact on the maximum stress and strain of taproots (p > 0.05). This observation can be attributed to the contact area between the lateral root and substrate, which is much larger than that between the taproot and substrate [35]. Models (7–8) revealed that as the seedling substrate’s moisture content increased, the lateral root tissue’s maximum stress and strain decreased. This observation is because the moisture content of the seedling substrate was closely related to the mechanical properties of the substrate. It can be seen from Table 2 that the elastic modulus and failure modulus of the seedling substrate increased with increasing moisture content, and this agrees with the research results of Chenari et al. [41], Shen et al [42], Huang et al. [43], and Wei et al. [44] on the relationship between soil moisture content and strength. Moisture content is one of the most critical factors affecting the stability of substrate structure, and it can directly affect the connection mode and cementation strength between substrate particles [45]. When the moisture content in the substrate increases, the combined moisture film on the substrate particles’ surface will thicken, so the adhesion of the substrate particle-moisture-air interface decreases, and the cohesion between substrate particles weakens [46]. In addition, more moisture will form a moisture film between the particles, reducing the resistance to relative sliding between substrate particles, reducing the internal friction angle of the substrate, and decreasing the substrate’s stability [47–48].
Seedling age had no significant effect on the maximum stress and strain of the taproot and lateral roots of the tomato seedling. The reason may be that the external force on the root system of the tomato seedling and its geometric characteristics synchronously change with the change in seedling age. That is, in the same wind field, the geometric size of the tomato seedling’s root system was smaller at the younger seedling stage, as was the external force on the taproot’s top [49]. Additionally, the geometric size of the root system of the tomato seedling at the younger seedling stage was larger, as was the external force on the taproot’s top. According to statics theory, the stress on an object is positively correlated with the ratio of the external force and the geometric size of the object; thus, synchronous changes in the external force and geometric size of the object result in no significant difference in the maximum stress of the tomato seedling root system at different seedling ages.
In this study, the seedling age had a significant effect on the biomechanical characteristics of the tomato seedling root system (p < 0.05), and the elastic modulus and failure modulus of the taproot were greater than those of the lateral roots (seedling age > 20 days). The established root system-substrate FE model was robust and was sensitive to wind speed, substrate moisture content, strong seedling index, and seedling age. The multivariate linear mathematical model could predict tomato seedling roots’ maximum stress and strain under wind field action. The strong seedling index had the greatest effect on the biomechanical response of the seedling root system under wind disturbance, followed by wind speed. In contrast, the seedling age had no significant impact on the biomechanical response of the root system under wind disturbance. The tissue of the seedling root system did not suffer biomechanical damage in the simulation, but some strain behaviors were observed. Based on plant stress tolerance, wind disturbance may affect root growth and development in later growth stages. This study will help to reveal the biomechanical mechanism of wind disturbance inhibiting the overgrowth of tomato seedlings from the perspective of the root system.
Authorship: Zhengguang Liu: Writing-original draft. Jun Yang and Tobi Fadiji: Writing-review & editing. Zhiguo Li and Jiheng Ni: Writing-review & editing, funding acquisition.
Funding Statement: This work was supported by a European Marie Curie International Incoming Fellowship (326847 and 912847), a Chinese Universities Scientific Fund (2452018313), a High-End Foreign Expert Recruitment Program (G2022172006L), and an Agricultural Science Innovation and Transformation Project of Shaanxi Province (NYKJ-2022-YL(XN)12).
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
References
1. Chanclud, E., Lacombe, B. (2017). Plant hormones: Key players in gut microbiota and human diseases? Trends in Plant Science, 22(9), 754–758. [Google Scholar]
2. Sparke, M. A., Pujner, K., Müller, J., Ruttensperger, U., Heesch, F. et al. (2022). Growth regulation by air stream-based mechanical stimulation in tomato (Solanum lycopersicum L.)–Part II: Phenotypic and physiological responses. Scientia Horticulturae, 305, 111359. [Google Scholar]
3. Gardiner, B., Berry, P., Moulia, B. (2016). Review: Wind impacts on plant growth, mechanics and damage. Plant Science, 245, 94–118. [Google Scholar]
4. Tamasi, E., Stokes, A., Lasserre, B., Danjon, F., Berthier, S. et al. (2005). Influence of wind loading on root system development and architecture in oak (Quercus robur L.) seedlings. Trees, 19(4), 374–384. [Google Scholar]
5. Michel-Aceves, A. C., Díaz-Nájera1, J. F., Ariza-Flores, R., Otero-Sánchez, M. A., Escobar, R. M. et al. (2019). Control alternatives for damping-off in tomato seedling production. Phyton-International Journal of Experimental Botany, 88(3), 325–333. [Google Scholar]
6. Nicolás-Álvarez, D. E., Andraca-Adame, J. A., Chanona-Pérez, J. J., Méndez-Méndez, J. V., Borja-Urby, R. et al. (2021). Effects of TiO2 nanoparticles incorporation into cells of tomato roots. Nanomater, 11(5), 1127. [Google Scholar]
7. Nicolás-Álvarez, D. E., Andraca-Adame, J. A., Chanona-Pérez, J. J., Méndez-Méndez, J. V., Cárdenas-Pérez, S. et al. (2019). Evaluation of nanomechanical properties of tomato root by atomic force microscopy. Microscopy and Microanalysis, 25(4), 989–997. [Google Scholar]
8. Fernandes, A. N., Chen, X., Scotchford, C. A., Walker, J., Wells, D. M. et al. (2012). Mechanical properties of epidermal cells of whole living roots of Arabidopsis thaliana: An atomic force microscopy study. Physical Review E, 85, 021916. [Google Scholar]
9. Plavcová, L., Gallenmüller, F., Morris, H., Khatamirad, M., Jansen, S. et al. (2019). Mechanical properties and structure-function trade-offs in secondary xylem of young roots and stems. Journal of Experimental Botany, 70(14), 3679–3691. [Google Scholar]
10. Ali, F. (2010). Use of vegetation for slope protection: Root mechanical properties of some tropical plants. International Journal of Physical Sciences, 5(5), 496–506. [Google Scholar]
11. Sanchez-Castillo, L., Kubota, T., Silva, I. C., Yáñez, I. (2017). Comparisons of the root mechanical properties of three native mexican tree species for soil bioengineering practices. Botanical Sciences, 95(2), 259–269. [Google Scholar]
12. Xu, L., Yu, F., Drunen, E. V., Schieving, F., Dong, M. et al. (2012). Trampling, defoliation and physiological integration affect growth, morphological and mechanical properties of a root-suckering clonal tree. Annals of Botany, 109(5), 1001–1008. [Google Scholar]
13. Ma, Q., Wu, N., Xiao, H., Li, Z., Li, W. (2021). Effect of Bermuda grass root on mechanical properties of soil under dry-wet cycles. Bulletin of Engineering Geology and the Environment, 80(9), 1–15. [Google Scholar]
14. Li, Y., Zhou, M., Zuo, H., Wang, Q., Xing, Y. et al. (2021). Root traits and mechanical properties of three shrubland species: Implications for bioengineered slope stability. Environmental Engineering Science, 38(12), 1176–1187. [Google Scholar]
15. Zhang, C., Ma, X., Liu, Y., Jiang, J. (2021). Influence of various gauge lengths, root spacing and root numbers on root tensile properties of herbaceous plants. Sains Malaysiana, 50(9), 2499–2510. [Google Scholar]
16. An, X., Li, Z., Zude-Sasse, M., Tchuenbou-Magaia, F., Yang, Y. (2020). Characterization of textural failure mechanics of strawberry fruit. Journal of Food Engineering, 282(3), 110016. DOI 10.1016/j.jfoodeng.2020.110016. [Google Scholar] [CrossRef]
17. Li, Z., Li, P., Yang, H., Liu, J., Xu, Y. (2012). Mechanical properties of tomato exocarp, mesocarp and locular gel tissues. Journal of Food Engineering, 111(1), 82–91. DOI 10.1016/j.jfoodeng.2012.01.023. [Google Scholar] [CrossRef]
18. Stopa, R., Szyjewicz, D., Komarnicki, P., Kuta, Ł. (2018). Determining the resistance to mechanical damage of apples under impact loads. Postharvest Biology and Technology, 146(11), 79–89. DOI 10.1016/j.postharvbio.2018.08.016. [Google Scholar] [CrossRef]
19. Han, X., An, X., Fadiji, T., Li, Z., Khojastehpour, M. (2022). Textural thermo-mechanical properties of sweet cherry for postharvest damage analysis. Journal of Texture Studies, 53(4), 453–464. DOI 10.1111/jtxs.12661. [Google Scholar] [CrossRef]
20. Tassinari, D., Junior, M. D. S. D., Silva, B. M., Oliveira, G. C. D., Carvalho, T. S. D. et al. (2021). Determination method and strain-attribute interact in the calculation of precompression stress from soil compression curves. Biosystems Engineering, 210, 33–47. DOI 10.1016/j.biosystemseng.2021.07.016. [Google Scholar] [CrossRef]
21. Liu, Z. G. (2022). Research on the correlation mechanism among mechanics, physiology and growth in the over-growth inhibition of tomato seedling by wind flowing. Northwest A&F University, Shaanxi, China. [Google Scholar]
22. Dupuy, L. X., Fourcaud, T., Lac, P., Stokes, A. (2007). A generic 3D finite element model of tree anchorage integrating soil mechanics and real root system architecture. American Journal of Botany, 94(9), 1506–1514. [Google Scholar]
23. Yang, M., Défossez, P., Danjon, F., Fourcaud, T. (2014). Tree stability under wind: Simulating uprooting with root breakage using a finite element method. Annals of Botany, 114(4), 695–709. [Google Scholar]
24. Wang, C. X., Wang, L., Thomas, C. R. (2004). Modelling the mechanical properties of single suspension-cultured tomato cells. Annals of Botany, 93(4), 443–453. [Google Scholar]
25. Stokes, A. (2000). Strain distribution during anchorage failure of Pinus pinaster Ait. at different ages and tree growth response to wind-induced root movement. Plant and Solid, 87(1–2), 19–29. [Google Scholar]
26. Watson, A. (2000). Wind-induced forces in the near-surface lateral roots of radiata pine. Forest Ecology and Management, 135(1–3), 133–142. [Google Scholar]
27. Crook, M. P., Ennos, A. R. (1996). The anchorage mechanics of deep rooted larch, Larix europea × L. japonica. Journal of Experimental Botany, 47(303), 1509–1517. [Google Scholar]
28. Crook, M. P., Ennos, A. R., Banks, J. R. (1997). The function of buttress roots: A comparative study of the anchorage systems of buttressed (Aglaia and Nephelium ramboutan species) and non-buttressed (Mallotus wrayi) tropical trees. Journal of Experimental Botany, 48(9), 1703–1716. [Google Scholar]
29. Tadrist, L., Julio, K., Saudreau, M., Langre, E. D. (2015). Leaf flutter by torsional galloping: Experiments and mode. Journal of Fluids & Structures, 56, 1–10. [Google Scholar]
30. Bertin, C., Yang, X., Weston, L. A. (2003). The role of root exudates and allelochemicals in the rhizosphere. Plant and Soil, 256, 67–83. [Google Scholar]
31. Sakiko, O., Guillaume, P. (2011). Amino acid export in plants: A missing link in nitrogen cycling. Molecular Plant, 4(3), 453–463. [Google Scholar]
32. Walker, T. S., Bais, H. P., Grotewold, E., Vivanco, J. M. (2003). Root exudation and rhizosphere biology. Plant Physiology, 132(1), 44–51. DOI 10.1104/pp.102.019661. [Google Scholar] [CrossRef]
33. Danjon, F., Fourcaud, T., Bert, D. (2005). Root architecture and wind-firmness of mature Pinus pinaster. New Phytologist, 168(2), 387–400. DOI 10.1111/j.1469-8137.2005.01497.x. [Google Scholar] [CrossRef]
34. Waisel, Y., Eshel, A., Beeckman, T., Kafkafi, U. (2002). Plant roots: The hidden half. 3rd edition Boca Raton: CRC Press. [Google Scholar]
35. Stokes, A., Ball, J., Fitter, A. H., Brain, P., Coutts, M. P. (1996). An experimental investigation of the resistance of model root systems to uprooting. Annals of Botany, 78(4), 415–421. DOI 10.1006/anbo.1996.0137. [Google Scholar] [CrossRef]
36. de Langre, E. (2008). Effects of wind on plants. Annual Review of Fluid Mechanics, 40(1), 141–168. DOI 10.1146/annurev.fluid.40.111406.102135. [Google Scholar] [CrossRef]
37. Coutts, M. P. (1983). Root architecture and tree stability. Plant and Solid, 71(1–3), 171–188. DOI 10.1007/BF02182653. [Google Scholar] [CrossRef]
38. Coutts, M. P. (1986). Components of tree stability in Sitka spruce on peaty gley soil. Forestry, 59(2), 173–197. [Google Scholar]
39. Moore, J. R. (2000). Differences in maximum resistive bending moments of Pinus radiata trees grown on a range of soil types. Forest Ecology and Management, 135(1–3), 63–71. [Google Scholar]
40. Mergen, F. (1954). Mechanical aspects of wind-breakage and wind firmness. Journal of Forestry, 52(2), 119–125. [Google Scholar]
41. Chenari, R. J., Fatahi, B., Ghoreishi, M., Taleb, A. (2019). Physical and numerical modelling of the inherent variability of shear strength in soil mechanics. Geomechanics and Engineering, 17(1), 31–45. [Google Scholar]
42. Shen, C., Fang, X., Wang, H., Sun, S., Guo, J. (2009). Research on effects of suction, water content and dry density on shear strength of remolded unsaturated soils. Rock and Soil Mechanics, 30(5), 1347–1351+1342. [Google Scholar]
43. Huang, K., Wan, J., Chen, G., Zeng, Y. (2012). Testing study of relationship between water content and shear strength of unsaturated soils. Rock and Soil Mechanics, 33(9), 2600–2604. [Google Scholar]
44. Wei, H., Xu, W., Wei, C., Meng, Q. (2018). Influence of water content and shear rate on the mechanical behavior of soil-rock mixtures. Science China Technological Sciences, 61(8), 1127–1136. DOI 10.1007/s11431-017-9277-5. [Google Scholar] [CrossRef]
45. Fredlund, D., Morgenstern, N. (1977). Stress state variables for unsaturated soils. Journal of Geotechnical and Geoenvironmental Engineering, 103(5), 447–466. [Google Scholar]
46. Rahardjo, H., Kim, Y., Satyanaga, A. (2019). Role of unsaturated soil mechanics in geotechnical engineering. International Journal of Geo-Engineering, 10(1), 1–23. DOI 10.1186/s40703-019-0104-8. [Google Scholar] [CrossRef]
47. Hu, F., Wei, C., Xu, C., Wei, N., Zhong, M. et al. (2013). Water sensitivity of shear strength of purple paddy soils. Transactions of the Chinese Society of Agricultural Engineering, 29(3), 107–114. [Google Scholar]
48. Jeong, S., Lee, K., Kim, J., Kim, Y. (2017). Analysis of rainfall-induced landslide on unsaturated soil slopes. Sustainability, 9(7), 1280–1299. [Google Scholar]
49. Ennos, A. R. (1991). The mechanics of anchorage in Wheat Triticum aestivum L.: I. The anchorage of wheat seedlings. Journal of Experimental Botany, 42(12), 1601–1606. [Google Scholar]
Cite This Article
 Copyright © 2023 The Author(s). Published by Tech Science Press.
Copyright © 2023 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF Downloads
Downloads
 Citation Tools
Citation Tools