Anatomical Feature Segmentation of Femur Point Cloud Based on Medical Semantics

1  Introduction

As the longest and hardest tubular bone in the human skeletal system, the femur starts at the hip joint at the top and ends at the knee joint at the bottom, and bears all the weight of the upper body [1]. With the increasing trend of global aging, femoral surgery accounts for a large proportion of all surgical clinics. For the treatment of local bone damage and necrosis, the most common method for doctors is to use orthopedic implants to replace the original part of the bone [2], so as to achieve the restoration of bone anatomical morphology and specific biological functions.

Fortunately, the integration of digital technology and interdisciplinary fusion, such as orthopedics continuously drives the transformation of clinical treatment patterns and the promotion of postoperative quality in orthopedics [3]. Three dimensional (3D) digital models have become an important reference for doctors in femur pathological diagnosis and preoperative planning of surgical treatment [4,5]. However, we found that in the clinical surgical treatment of medical orthopedics, especially in joint replacement surgery, surgeons usually pay more attention to the anatomical morphological characteristics of the local lesion area than the complete bone shape to achieve better personalized treatment.

For medical device manufacturers, a good match between the shape structure and mechanical property of implant product and individual patient’s bone is the research direction and ultimate goal. Therefore, during orthopedic implant and prosthesis development, designers need to acquire the complete bone structure and local shape characteristics of the specific population or an individual patient, and then complete serial or customized product development according to routine standards and individual needs, respectively [6,7]. In hip prosthetic replacement, the selected implant should match the original femoral head shape as closely as possible. While in knee arthroplasty, the shape of artificial joint must approximate that of distal femoral condyle. Therefore, dividing the entire femoral model into multiple regions according to the semantic of medical anatomy, especially complex regions involving joints, is critical for the design and development of prosthesis and joint replacement surgery.

The surface contour of the femur is very complex and contains a large number of irregular curved surfaces with varying degrees of freedom. At the same time, the local anatomy of the femur has important medical functional and physio-mechanical properties, such as the external shape of the femoral head is directly related to hip stability, which in turn affects the normal movement and life of patients. However, existing segmentation algorithms have much uncertainty for femoral model segmentation because of the smooth surface of bone, fewer geometrical characteristics, and individual differences. 3D segmentation of human bone is still challenging work, especially for general medical researchers lacking computer modeling expertise. Therefore, according to the typical topography and structure of the human femur, we hypothesize that anatomical feature objects with important medical anatomical semantics could be used to represent the global structure and describe the local anatomy [8–12], thereby guiding the watershed algorithm for the anatomical segmentation of femur model based on the reference object.

In this study, we propose a novel segmentation methodology for anatomical features of femur model based on medical semantics. Firstly, anatomical reference objects (ARO) are created to represent typical characteristics of femur anatomy in combination with medical priori knowledge. Secondly, local point clouds between adjacent anatomies are selected according to the AROs to extract boundary feature point (BFP)s. Thirdly, the complete model of femur is divided into anatomical regions by executing the enhanced watershed algorithm guided with BFPs. Our contributions to this paper are three-fold:

•   First, we introduce a novel representation mechanism of femur anatomy in two-level feature points, including structural feature points and shape feature points with anatomical referential objects (AROs) to describe the overall structure and local details.

•   Second, we improve a watershed 3D segmentation algorithm guided by boundary feature points (BFPs) to achieve fast segmentation of complex regions.

•   Finally, we implement the segmentation algorithms and evaluate the effectiveness and feasibility in a prototype platform.

The paper is organized as follows. Section 2 reviews some of the existing segmentation works. Section 3 describes the materials and detailed algorithms for feature description, feature point extraction, registration of segments and surface reconstruction. In Section 4, the methodology is implemented, and experimental results are summarized and analyzed. Section 5 discusses the results and algorithms. Section 6 concludes with a summary of the content of this study and proposes future research directions.

2  Related Works

In this section, we start by surveying existing techniques, including unsupervised segmentation and supervision segmentation [13,14]. Then, we discuss the segmentation methods and their shortcomings in existing femur related, and propose a medical semantic based idea for anatomical feature segmentation in point cloud models.

2.1 Unsupervised Segmentation

In unsupervised studies, 3D model segmentations are achieved without using any label information by using classical algorithms include clustering [15], region growth [16], spectrum analysis, topological segmentation, surface fitting, spatial subdivision and others [17]. The core idea of unsupervised segmentation is to cluster related objects with consistent geometric features or shapes into the same class, and then obtain segmentation models. Relying on consistent geometric similarity matching algorithms in sets, existing studies have achieved good performance. However, in the case of different shapes and topologies of objects of the same class, it is very hard to obtain satisfactory segmentation by only relying on a small number of features to match objects. Previous techniques used handmade features, which are usually concentrated on specific attributes of 3D objects, so it is difficult to extend them to other application environments.

2.2 Supervision Segmentation

Supervised segmentation uses machine learning to map local features to labels, and its advantage lies in solving geometric problems with algebra [18]. Typical supervised segmentation algorithms can be roughly divided into point cloud segmentation, kd tree point cloud segmentation, image segmentation projection to shape, hierarchical segmentation and graphical neural network [13]. In the process of execution of such methods, a large number of shape features need to be input, and on this basis, the underlying objects constituting the model are classified according to labels [19]. When data sets are diversified, network prediction labels based on image convolution could effectively solve the problem of difficult segmentation [20]. Because 3D point cloud data can be regarded as graphical data, many ideas of graphical network have been applied to feature learning of point cloud data and achieved good results. Yi et al. [21] used spectrum based graph convolution to perform semantic segmentation of 3D object models, proposed a spectrum conversion network to achieve better parameter sharing, and introduced the concept of gap convolution to increase multi-scale information. Compared with unsupervised segmentation, supervised segmentation methods could achieve higher accuracy. However, the segmentation accuracy of the existing method object boundary still needs to be strengthened [22], and the global information and local information cannot be effectively integrated.

In summary, existing research has made significant contributions to model segmentation innovation. However, existing methods usually focus on aspects such as geometric features and mathematical statistics, while ignoring concerns and constraints on typical structures and specific functions in specific types of models. Therefore, the existing segmentation algorithms are difficult to be used for the segmentation of models with smooth surfaces and less prominent geometric features, and the rationality of the final segmentation results cannot be guaranteed.

2.3 Bone Segmentation

Through semantic segmentation, medical users can more clearly locate and represent the detailed shape and morphology of local regions in bone models. Unlike other standard segmentation test case models, the anatomy and local shape of the human femur are irregular. At present, there are few reports on the semantic segmentation of bone models combined with medical anatomy. Zhang et al. [23] proposed a normal vector election method to solve the Gaussian curvature of vertices, and divided the femoral mesh model into multiple regions automatically according to vertex clustering. Wu et al. [24] suggested the feature point guided regional growth algorithm to segment the femoral and tibia mesh, and obtained the experimental results related to medical understanding. However, due to the smooth surface and irregular shape of femur, it is a challenge to incorporate the specific needs of medical anatomy into the segmentation strategy or rules of existing research methods. Therefore, the existing research on femur segmentation cannot avoid the problems of over-segmentation and under-segmentation of local regions caused by automatic execution, and it is difficult to meet the requirements of medical semantic segmentation.

To overcome the above-mentioned anatomical segmentation challenge of femur, we propose a novel anatomical feature segmentation method for point cloud model based on medical semantics. In this study, anatomical reference object (ARO) was used to describe typical anatomical features and medical anatomical semantics of femur, and the enhanced watershed algorithm was combined with a few semantic interactive operations to segment the femur into five components with significant medical significance.

3  Materials and Methods

In this study, 50 healthy femurs of Chinese female volunteers living in Southern Jiangsu of China with no previous trauma were scanned by 64-slice CT (MSCT, Aquilion 64, Toshiba, Zoetermeer, Netherlands) to acquire 3D surface models, and each femur was preprocessed by removing tendons and other attachments around the bone, then point cloud models were obtained. The average height of the samples was 159.8 ± 4.6 mm (range from 157.2 to 163.7 mm). In addition, an averaged femur model constructed in our previous studies [17–20] was used to represent the typical skeletal anatomy of femur.

3.1 Overview of Proposed Approach

To achieve the satisfaction of the segmentation results of femoral surface features to medical needs, it is essential to describe the typical anatomical characteristics of femur as accurately as possible in combination with medical prior knowledge. Fig. 1 shows the overall workflow of anatomical feature segmentation and key processes of our method, namely ARO creation, BFP extraction, automatic segmentation and interactive modification. First of all, the femoral anatomical reference object (ARO)s are used to represent the typical anatomical structure information of femur. Next, considering the difference of boundary features between regions, we select boundary feature point (BFP)s to guide bone segmentation based on the existing marker-controlled watershed algorithm [24,25]. Then, the slight modification of segmentation results can be achieved by adjusting a few threshold parameter values.

Figure 1: Overall workflow of feature segmentation based on femoral medical semantics

3.2 Creation of Anatomical Referential Object

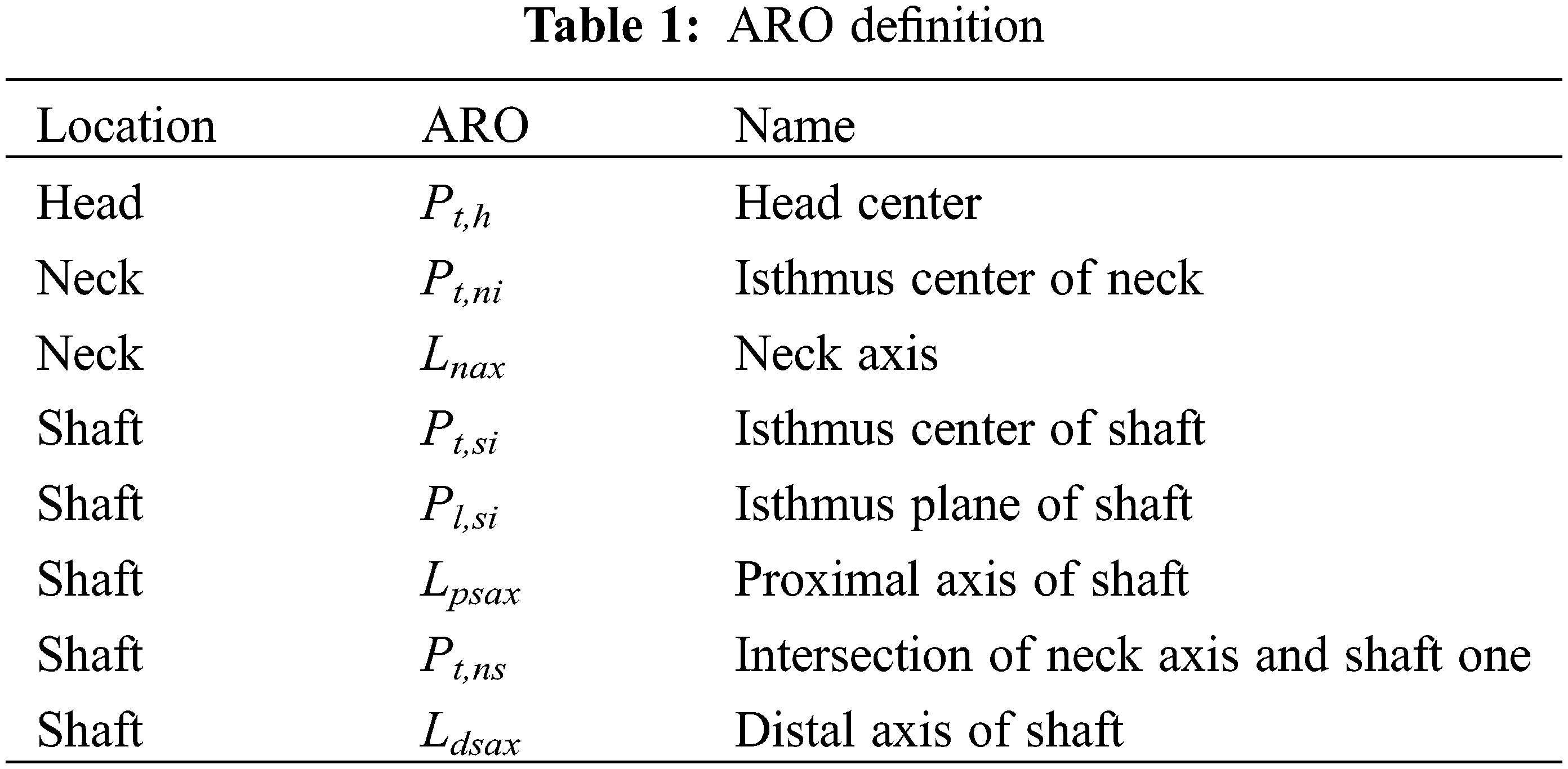
In the studies of human bone morphology, the representation of femoral anatomical structure and the recognition of shape features generally rely on a series of anatomical reference object (ARO)s with significant medical semantics, including points, axes, planes, etc. The AROs are commonly located on the surface or inside of the 3D model. On the basis of existing research works [26,27], 3D point fitting strategy is adopted to create the AROs corresponding to the head, neck, shaft and other features [9,10,12], and to guide subsequent segmentation of femoral anatomical features.

The point set of femoral head area Ph is fitted to a spherical surface by using the least squares method, as shown in Fig. 2a.

Figure 2: Anatomical reference object of femur

Jh(Pt,h, Rh)=∑Pi∈Ph(||Pi−Pt,h||−Rh)2 (1)

in which, Pt,h and Rh are the head center and head radius of femoral spherical, respectively.

The center point of the neck isthmus Pt,ni is created by the minimum interface fitting method [27] as shown in Fig. 2b, and the neck axes line Lnax is generated by connect Pt,h and Pt,ni.

Jn(Pt,e, xd, yd, α)=∑(||Pi−Pt,e||−xd2yd2xd2sin2α+yd2cos⁡2α)2 (2)

According to the center point of the femoral isthmus, the femur is divided into two parts, namely the proximal part and the distal one, and the anatomical axis is created by means of cross-section fitting circle as follows:

Step 1. Create the center of femur center Vc (the average value of all vertices in the point cloud) as shown in Fig. 2c.

Step 2. Generate the cross plane Pl,mc which has the smallest area and passes Vc, and its corresponding plane Pl,m.

Step 3. Obtain the cross plane Pl,sc which has the smallest area size parallel to Pl,m, and create the center Pt,si and its isthmus plane Pl,si by fitting contour curves.

Step 4. Create multiple cutting contour curves parallel to Pl,si, and generate the proximal axis Lpsax and the distal axis Ldsax by fitting corresponding circle centers.

The detailed information of AROs is listed in Table 1, and the detailed creation methods can be found in our previous studies [11,12].

3.3 Extraction of Boundary Feature Point

Boundary feature point (BFP) refers to a concave or convex vertex located at the boundary of adjacent anatomical regions of femur. The strategy adopted in this work for BFP extraction is to preliminarily determine the range of adjacent boundary feature points based on the above-mentioned AROs, and extract the BFPs of adjacent area through geometric attribute calculation of the vertex. In view of the fact that the local height of vertex can effectively describe the curved shape, we describe the concavity and convexity of the vertex position with the vertex height with average normal, and realize BFP extraction based on the vertex height screening principle. The main steps of height calculation [11] are as follows:

Step 1. Calculate the area AT and normal NT of the triangular surface where the vertex V and the adjacent vertices Vi and Vi+1 are located, and obtain the normal vector NV of vertex V as shown in Fig. 3a.

Figure 3: Height definition of vertex

NV(V)=∑i=1m−1(NT(Ti)∗AT(Ti)∑i=1m−1AT(Ti) (3)

in which, m is the number of triangles associated with point V.

Step 2. Calculate the normal vector NB of the edge where the two adjacent vertices are located, and obtain the height HV between two adjacent vertices.

NB(V,Vi)=NV(V)+NV(Vi)||NV(V)+NV(Vi)|| (4)

HV(V,Vi)=(V−Vi)∗NB(V,Vi) (5)

Step 3. Calculate the height H of V.

H(V)=T∑i=1mHV(V,Vi)S2|NV(V)| (6)

in which, T is the height coefficient. For the fine point cloud model, the local height difference of vertices is very close, and increasing the value of T can appropriately increase the height difference between adjacent vertices, and then is beneficial to solve the local maximum height. The T value can be adjusted in the interval.

Combining the femoral anatomy visual features and medical anatomical semantics, we adopt the local height value as the extraction criterion of BFP. First, a significant feature point is manually marked in the adjacent area. Then, the feature point is traversed by breadth, and the BFP point with a larger height value is selected. The detailed execution process is shown in Algorithm 1.

Take the head and neck as an example, the BFP extraction steps are as follows:

Step 1. Extract a significant feature point Fpi in the area to be segmented as shown in Fig. 4a, and calculate the distance from Fpi to the head center Pt,h;

Step 2. Define the local cloud range of BFP (Lc) between head and neck according to the initial value of threshold α as shown in Fig. 4a, and traverse all adjacent vertices Fpij, then remove vertices which values of height H are negative;

Step 3. Extract the vertices Fpij with larger height value, and add it into the BFP set as shown in Fig. 4b.

Figure 4: BFP extraction between head and neck

3.4 Segmentation of Femoral Anatomical Feature

Different from the existing marker-controlled watershed algorithm [23], we adopt BFP to guide the segmentation process, and define geodesic distance [28] as the segmentation criterion. The segmentation process is detailed in Algorithm 2.

First, a salient feature point is selected as the seed Si in each adjacent point cloud area Lc. Next, the Si is traversed with breadth-first, if the neighbor Sij is a non-boundary point and its geodesic distance value is smaller, expand the anatomical area by flooding, and remove Si from Lc. Finally, repeat the above steps until Lc is empty, stop the seed area expansion, and obtain the point set Sp.

The segment result of the head, neck, and trochanter is shown in Fig. 5.

Figure 5: Segmentation of head, neck, and trochanter

For the regions namely connection trochanter and shaft, connection shaft and condyle with smooth shape and hard to extract effectively by BFP, a small amount of semantic interactions are used for segmentation based on BFP and ARO. The femoral shaft is the part between the lesser trochanter point Pt,lt and the supracondylar point Pt,mt, through the two points, the femur model is cut orthogonal to the axis of the shaft Lsx as shown in Fig. 6.

Figure 6: Segmentation of trochanter, shaft, and condyle with semantic interaction

4  Experiments and Results

4.1 Experiment Environment

The proposed segmentation methodology and algorithms were implemented in the prototype experimental platform with the hardware environment consisting of 3.0 GHz i7-9700 CPU with 16G RAM, and the software environment including Microsoft Visual Studio 2008 and CATIA V5 R21 integrated with CAA V5 and RADE V5 toolkits, as shown in Fig. 7.

Figure 7: Implementation interfaces of prototype platform

4.2 Automatic Segmentation

In the experiments, 50 femur samples and 1 average model were used to evaluate the segmentation algorithm.

With the interface as shown in Fig. 7a, we selected the objects predefined in the ABO label, including HeadCt, NeckAxs, NectCt, ShaftPl, ShaftCt, ShaftAxs, TPt and NeckShaftPt to create corresponding AROs. Then, in the Segmentation Controll label, the distance thresholds between features were set to 0.50, and the height values of BFP were set to be twice the average height of the searched area. Finally, the feature segmentation results of the femur samples were obtained automatically; the segment results of one average model and six samples are shown in Fig. 8.

Figure 8: Segmentation results of one average model and six femur samples

4.3 Interactive Modification

In order to verify the segmentation modification function of the proposed method, a few interactive operations were performed on the averaged femur model.

As mentioned above, after editing the value of proximal ARO (Pt,lt ) as shown in Fig. 7 to the center of shaft isthmus by 5 mm, the segmentation results between the trochanter and shaft are shown in Fig. 9b. With a similar interactive adjustment method, the fine-tuning results of the distal boundary segmentation were obtained as shown in Fig. 9c. Subsequently, the threshold α of the distance searched for the neck and intertrochanteric BFP was adjusted from 0.50 to 0.30 mm, and the segmentation result is shown in Fig. 9d. The experimental results show that the BFP extraction range can be effectively controlled by adjusting the distance threshold and ARO in the region where the boundary feature points are located through a small amount of interactive operations.

Figure 9: Segmentation adjustment based on interactions

4.4 Comparison of Existing Methods

To evaluate the effectiveness of anatomical segmentation, the segmentation results of our method are compared with existing methods in semantic segmentation. The experimental results are listed and compared as shown in Fig. 10.

Figure 10: Result comparison with existing methods

5  Discussions

From the experiments, we can find that femur surfaces can be segmented into significant regions, including head, neck, intertrochanter, shaft, and condyle as shown in Fig. 8. Unlike other real femur samples, the segmented boundaries of the averaged model are relatively smooth, because that the surface of averaged femur is smoother and the individual features are weaker than other samples. The segmentation results of several real femoral sample models show that there are some differences in local detailed anatomy (such as head, neck, etc.) between individual femoral samples. However, the segmentation results of individual bone models are very similar. Especially for the complex shape of neck and intertrochanter, the automatic segmentation results of the watershed algorithm based on feature point marking can basically keep the same feature shape. On one side, the results could meet the needs of visual features and medical anatomy, and can be used to locate and describe the local anatomical shape in preoperative planning of patients, so as to improve the accuracy of bone pathological diagnosis. On the other hand, the head, condyle and other areas separated from the whole femur can not only independently represent the complex shape of individual local anatomy, but also be used to quickly and batch obtain the anatomical information of specific people’s bones, and then improve the design efficiency of orthopedic implant and prosthesis and the matching of the implant to the patient’s bone. Therefore, representing anatomical semantics based on ARO and BFP can effectively achieve medical semantic segmentation of 3D femur model.

During the entire process of BFP extraction, the feature point search range and height threshold settings directly affect the final extraction result, which in turn determines the anatomical segmentation effect of femur model. Taking into account various factors such as the shape characteristics of each region of femur and the quality of model, we define the threshold within 0.1 and 0.5 mm, and set the BFP extraction height to be 3 to 10 times the average height of vertices in the search area. In fact, due to the significant differences in the shape of human bones, the above parameter value settings must be reasonably adjusted for the specific characteristic shape of the individual femur region in order to more effectively extract regional BFPs. Therefore, combined with a few interactive interventions, the method can intuitively fine-tune femoral feature segmentation results, so as to meet the actual needs of femoral feature segmentation in different medical applications.

For the complex shape and smooth surface of femur, existing femoral segmentation research cannot avoid the problem of local region transition segmentation or insufficient segmentation caused by the automatic implementation of different algorithms. Some studies proposed various evaluation metrics for 3D mesh segmentation [29]; however, for the evaluation of femur feature segmentation results, there is still no unified measurement indicator. Existing related works mainly analyze the segmentation results based on medical semantics and boundary shape comparison. To evaluate the effectiveness of anatomical segmentation, the results of our method were compared with those of other similar methods in semantic segmentation. The comparison of the experimental results is shown in Fig. 10. We can find that the proposed method can address the issue of under-segmentation caused by the curvature calculation in the literature [15], and the feature boundary after segmentation is clearer. BFP extraction based on AROs achieves the semantic description of femoral anatomy and femoral medical function. Our segmentation method makes up for the insufficiency of the uncontrollable BFPs in the literature [24], and effectively solves the problem of meaningless over-segmentation in regions such as intertrochanter in Fig. 10c, and then the segmentation results are more in line with medical understanding. The representation and localization of the anatomical morphology and surface anatomical features of human long bones are of great significance for many medical research and clinical applications, and the segmentation of bone models has great research space.

6  Conclusions

In this study, we propose a novel segmentation method for anatomical features of femoral point cloud model based on medical semantics. This research has the following three contributions. (1) The boundary feature points and the local height of vertices are used as markers and geometric measures, and the fast watershed algorithm is improved to effectively control the expansion range of seed vertices and realize automatic semantic segmentation of complex anatomical shapes. (2) Combined with anatomical reference entities, it supports segmentation adjustment based on a small amount of semantic interaction, which can solve the problem of over segmentation and under segmentation, and the segmentation result has more medical anatomical semantics. (3) The effectiveness and feasibility of segmentation algorithms are implemented and evaluated in a prototype platform.

The surface of femur is smooth, and the shape complexity of feature regions is obviously different. In different clinical applications or medical researches, medical personnel has different concerns about feature segmentation of the same region. Therefore, how to refine the model segmentation according to the medical anatomy semantics and personality requirements of each local feature area will be the key research work in the future.

Funding Statement: This work was supported by Changzhou Science and Technology Support Plan Project (Grant No. CE20205006), the Qing Lan Project of Jiangsu Province (Grant No. 2022CZIE), and the Key Project of Educational Science in Jiangsu Province (Grant No. B/2021/03/37).

Conflicts of Interest: The author declares that they have no conflicts of interest to report regarding the present study.

References

1. Terry, S., James, H., Frederick, M. (2021). Campbell’s core orthopaedic procedures. Beijing, China: Peking University Medical Press. [Google Scholar]

2. Bogdan, Y., Vallier, H. (2022). What’s new in orthopaedic trauma. The Journal of Bone and Joint Surgery, 104(23), 1131–1137. https://doi.org/10.2106/JBJS.22.00261 [Google Scholar] [PubMed] [CrossRef]

3. Kubicek, J., Tomanec, F., Cerny, M. (2019). Recent trends, technical concepts and components of computer-assisted orthopedic surgery systems: A comprehensive review. Sensors, 19(23), 1–33. https://doi.org/10.3390/s19235199 [Google Scholar] [PubMed] [CrossRef]

4. Jacquet, C., Flecher, X., Pioger, C. (2020). Long-term results of custom-made femoral stems. Orthopedics, 49(5), 408–416. [Google Scholar]

5. Deng, Z., Jiang, J., Liu, H. (2020). A data-driven approach for assembling intertrochanteric fractures by axis-position alignment. IEEE Access, 8, 137549–137563. https://doi.org/10.1109/ACCESS.2020.3012047 [Google Scholar] [CrossRef]

6. Darwish, S., Al-Samhan, A. (2009). Optimization of artificial hip joint parameters. Materialwissenschaft und Werkstofftechnik, 40(3), 218–223. https://doi.org/10.1002/mawe.200900430 [Google Scholar] [CrossRef]

7. Vitkovic, N., Veselinovic, M., Misic, D. (2012). Geometrical models of human bones and implants, and their usage in application for preoperative planning in orthopedics. Journal of Production Engineering, 15(2), 87–90. [Google Scholar]

8. Chen, X., Mao, Z., Jiang, X. (2021). Feature-based design of personalized anatomical plates for the treatment of femoral fractures. IEEE Access, 9, 43824–43836. https://doi.org/10.1109/ACCESS.2021.3065390 [Google Scholar] [CrossRef]

9. Chen, X. (2020). Reconstruction individual three-dimensional model of fractured long bone based on feature points. Computational and Applied Mathematics, 39(2), 1–14. https://doi.org/10.1007/s40314-020-01165-z [Google Scholar] [CrossRef]

10. Chen, X., Zhu, B., Mao, Z. (2019). Construction of restored model of fractured femurs based on anatomic features. Biotechnology & Biotechnological Equipment, 33(1), 988–999. https://doi.org/10.1080/13102818.2019.1637277 [Google Scholar] [CrossRef]

11. Chen, X. (2021). Feature point extraction of femur surface based on reference object. Proceedings of IEEE International Conference on Power, Intelligent Computing and Systems, pp. 761–765. Shenyang, China. https://doi.org/10.1109/ICPICS52425.2021.9524129 [Google Scholar] [CrossRef]

12. Chen, X., He, K., Chen, Z. (2016). A parametric approach to construct femur models and their fixation plates. Biotechnology & Biotechnological Equipment, 30(3), 529–537. https://doi.org/10.1080/13102818.2016.1145555 [Google Scholar] [CrossRef]

13. Youness, A., Omar, H., Lahcen, M., Taoufiq, G. (2020). A hybrid CNN-CRF inference models for 3D mesh segmentation. Proceedings of 2020 6th IEEE Congress on Information Science and Technology, pp. 296–301. https://doi.org/10.1109/CiSt49399.2021.9357275 [Google Scholar] [CrossRef]

14. Vieira, M., Shimada, K. (2005). Surface mesh segmentation and smooth surface extraction through region growing. Computer Aided Geometry Design, 22(8), 771–792. https://doi.org/10.1016/j.cagd.2005.03.006 [Google Scholar] [CrossRef]

15. Sagi, K., Ayellet, T. (2003). Hierarchical mesh decomposition using fuzzy clustering and cuts. Association for Computing Machinery Transactions on Graphs, 22(3), 954–961. https://doi.org/10.1145/1201775.882369 [Google Scholar] [CrossRef]

16. David, G., Xie, X., Gary, K. (2018). 3D mesh segmentation via multi-branch 1D convolutional neural networks. Graphical Models, 96(2–3), 1–10. https://doi.org/10.1016/j.gmod.2018.01.001 [Google Scholar] [CrossRef]

17. Gezawa, A., Wang, Q., Chiroma, H., Lei, Y. (2022). A deep learning approach to mesh segmentation. Computer Modeling in Engineering & Sciences, 135(2), 1–19. https://doi.org/10.32604/cmes.2022.021351 [Google Scholar] [CrossRef]

18. Patane, G. (2017). An introduction to laplacian spectral distances and kernels: theory, computation, and application. Proceedings of ACM Siggraph, Los Angeles, California, USA. https://doi.org/10.1145/3084873.3084919 [Google Scholar] [CrossRef]

19. Xie, Z., Xu, K., Shan, W., Liu, L., Xiong, Y. et al. (2015). Projective feature learning for 3D shapes with multi-view depth images. Computer Graphics Forum, 34(7), 1–11. https://doi.org/10.1111/cgf.12740 [Google Scholar] [CrossRef]

20. Guo, K., Zou, D., Chen, X., Paepcke, A. (2015). 3D mesh labeling via deep convolutional neural networks. ACM Transactions on Graphics, 35(1), 1–12. https://doi.org/10.1145/2835487 [Google Scholar] [CrossRef]

21. Yi, L., Su, H., Guo, X. (2017). SyncSpecCNN: Synchronized spectral CNN for 3D shape segmentation. Proceedings of Computer Vision and Pattern Recognition, pp. 2282–2290. Honolulu Hawaii, USA. [Google Scholar]

22. Abubakar, S., Wang, Q., Haruna, C., Lei, Y. (2022). Study on the 3D point cloud semantic segmentation method of fusion semantic edge detection. Computer Modeling in Engineering & Sciences, 135(2), 1745–1763. https://doi.org/10.32604/cmes.2022.021351 [Google Scholar] [CrossRef]

23. Zhang, J., Malcolm, D., Hislopjambrich, J. (2014). An anatomical region-based statistical shape model of the human femur. Computer Methods in Biomechanics and Biomedical Engineering: Imaging and Visualization, 2(3), 176–185. https://doi.org/10.1080/21681163.2013.878668 [Google Scholar] [CrossRef]

24. Wu, Y., Chen, Z., He, K. (2016). Rapid generation of human femur models based on morphological parameters and mesh deformation. Biotechnology & Biotechnological Equipment, 31(1), 1–13. https://doi.org/10.1080/13102818.2016.1255156 [Google Scholar] [CrossRef]

25. Li, C., Zhang, C., Wang, G. (2006). Fast marker-controlled interactive mesh segmentation. Acta Scientiarum Naturalium Universitatis Pekinensis, 42(5), 662–667. https://doi.org/10.13209/j.0479-8023.2006.118 [Google Scholar] [CrossRef]

26. Mahaisavariya, B., Sitthiseripratip, K., Tongdee, T. (2002). Morphological study of the proximal femur: A new method of geometrical assessment using 3-dimensional reverse engineering. Medical Engineering and Physics, 24(9), 617–622. https://doi.org/10.1016/S1350-4533(02)00113-3 [Google Scholar] [PubMed] [CrossRef]

27. Byoung-Keon, P., Ji-hoon, B., Bon-Yeol, K. (2014). Function-based morphing methodology for parameterizing patient-specific models of human proximal femurs. Computer-Aided Design, 51(7), 31–38. https://doi.org/10.1016/j.cad.2014.02.003 [Google Scholar] [CrossRef]

28. Agathos, A., Pratikakis, I., Perantonis, S. (2010). Protrusion-oriented 3D mesh segmentation. The Visual Computer, 26(1), 63–81. https://doi.org/10.1007/s00371-009-0383-8 [Google Scholar] [CrossRef]

29. Arhid, K., Mohcine, B., Fatima, R. (2017). An overview of existing evaluation metrics for 3D mesh segmentation. ARPN Journal of Engineering and Applied Science, 12(23), 6883–6894. [Google Scholar]