Molecular & Cellular Biomechanics

DOI: 10.32604/mcb.2021.015605

ARTICLE

The Influence of Drag on Nonlinear Oscillatory Flow through Concentric Annulus

B. Umadevi1,*, C. V. Vinay1 and P. A. Dinesh2

1Department of Mathematics, JSS Academy of Technical Education, Bangalore, India
2Department of Mathematics, Ramaiah Institute of Technology, Bangalore, India
*Corresponding Author: B. Umadevi. Email: bumadevi@jssateb.ac.in
Received: 30 December 2020; Accepted: 13 August 2021

1  Introduction

Oscillatory flow is a widespread phenomenon and plays an important role in many fields, e.g. pneumatic propulsion, piston—driven flow, and acoustic oscillation are commonly used in mechanical engineering; pulsatile blood circulation, respiratory flow in lung, and capillary waves are of much interest in bio-mechanics; seasonal reversing wind, ocean circulations as well as tide flow are of high concern in meteorology, etc. More than mere oscillation or repetition, mass, momentum, and energy may be transferred via these reciprocating movements. Oscillatory flow of fluid enclosed in distensible vessels is of substantial significance due to its applications to various fields. The model can be used to understand (i) Blood flow in large arteries, (ii) wave propagation in fluid filled flexible tubes, which is essential for the study of acoustics or pulse propagation in arteries, (iii) flow in collapsible veins and (iv) peristaltic motion in the intestines. Many researchers for over 180 years are investigating the blood flow in arteries. Comparison of experimental measurements and mathematical modeling of these problems have been investigated. Recently, the study of flow with periodic variations has attracted much attention of researchers due to its various engineering and physiological applications. Oscillatory motion of a viscous liquid in a thin-walled elastic tube is investigated by Womersley [1]. Further, Womersley [2] studied the elastic tube theory of pulse conduction and oscillatory flow in mammalian arteries. Saffman [3] studied the stability of laminar flow of dusty gas. Rubinow et al. [4] analyzed the flow of a viscous fluid in an elastic tube with application to blood flow. RamachandraRao et al. [5] studied the pulsatile flow in tubes of various cross section. Taylor et al. [6] presented a mathematical model to analyze the blood flow through arteries and expressed the different pressure radius relationships for elastic tube. RamachandraRao [7] investigated the oscillatory flow in an elastic tube of variable cross section. Analytical solution by the method of linear approximation to describe the velocity distribution for laminar periodic flow through porous walls is proposed by Chang et al. [8]. Wang et al. [9] studied non-linear analysis of oscillatory flow with a non zero mean, in an elastic tube (artery). Srivastava [10] investigated the two phase model of blood flow through stenosed tubes in the presence of peripheral layer. Sarkar et al. [11] investigated the Correction to Flow Rate-Pressure Drop in Coronary Angioplasty: Steady Streaming Effect. Sarkar et al. [12] discussed the nonlinear analysis of oscillatory flow in the annulus of an elastic tube. In addition, they noticed that the velocity distribution in a small vessel depend significantly on geometry of the wall and its elastic nature. Jayaraman et al. [13] studied the Nonlinear analysis of arterial blood flow—steady streaming effect. Vajravelu et al. [14] considered the case of inserting a catheter into an elastic tube to observe the changes in blood flow pattern by taking Herschel–Bulkley fluid. Unsteady flow of a Jeffrey fluid in an elastic tube with a stenosis was considered by Sreedharamalle et al. [15]. Sochi [16] projected the expression for the volumetric flow as a function of pressure in elastic tube using two pressure area constitutive relationships. Sankar et al. [17] analyzed the cooling of heat sources by natural convection heat transfer in a vertical annulus, Siddiquiet al. [18] investigated mathematical analysis on pulsatile flow through a catheterized stenosedartery. Khudayarov et al. [19] investigated the mathematical simulation of nonlinear oscillations of viscoelastic pipelines conveying fluid. Do et al. [20] studied the Navier’s slip condition on time dependent Darcy—Forchheimer nano fluid using Spectral relaxation method. Tsimpoukis et al. [21] investigated the nonlinear oscillatory fully-developed rarefied gas flow in plane geometry. Kiran et al. [22] studied the Computational analysis of conjugate buoyant convective transport in an annulus. Naveed et al. [23] investigated the mathematical analysis of novel coronavirus (2019-nCov) delay pandemic model. Azam et al. [24] studied the numerical modeling and theoretical analysis of a nonlinear advection-reaction epidemic system. Saqib et al. [25] investigated the Symmetric MHD channel flow of nonlocal fractional model of BTF containing hybrid nanoparticles. Bilal et al. [26] investigated Finite element method about heat transfer analysis of Newtonian material in triangular cavity with square cylinder. Rasool et al. [27] studied the MHD squeezed Darcy-Forchheimer nano fluid flow between two h-distance apart horizontal plates. Lu et al. [28] studied the oscillatory two-phase flow in microchannels. Bilal et al. [29] studied the Analytical treatment of radiative Casson fluid over an isothermal inclined Riga surface with aspects of chemically reactive species.

Blood is a concentrated suspension of several formed cellular elements, red blood cells (RBCs or erythrocytes), white blood cells (WBCs or leukocytes) and platelets (thrombocytes), in an aqueous polymeric and ionic solution, the plasma, composed of 93% water and 3% particles, namely electrolytes, organic molecules, numerous proteins (albumin, globulins and fibrinogen) and waste products. Plasma’s central physiological function is to transport these dissolved substances, nutrients, wastes and the formed cellular elements throughout the circulatory system. The primary function of erythrocytes is to transport oxygen and carbon dioxide. Leukocytes are roughly spherical and much larger than erythrocytes, but they exist in a smaller number in blood. Leukocytes are subdivided into granulocytes (65%), lymphocytes (30%), monocytes (5%) and natural killer cells. Granulocytes are further subdivided into neutrophils (95%), eosinophils (4%) and basophils (1%). The leukocytes play a vital role in fighting infection and thus are able to migrate out of the blood vessels and into the tissues. Thrombocytes are small discoid non-nucleated cell fragments, much smaller than erythrocytes and leukocytes. Thrombocytes are a vital component of the blood clotting mechanism. The total volume concentration of leukocytes and thrombocytes is only about 1%. Blood cells are continually produced by the bone marrow over a human’s life.

In the present investigation Blood is modeled as an incompressible particulate viscous Newtonian fluid, and the flow will be fully developed. A mathematical model has been developed to view the oscillatory nonlinear flow in the annulus formed by catheterized artery. The analysis of the problem has been given by perturbation method. The variation of velocity and pressure observed with the influence of the parameters such as elastic parameter, Womersley number and drag parameter.

2  Mathematical Formulation

The artery modeled as an isotropic thin walled elastic tube with mean radius R0 and the catheter as a coaxial flexible tube with radius kR0(k<1). Blood is considered as an incompressible particulate viscous Newtonian fluid. The flow is oscillatory and axial-symmetric. The oscillatory nature of the flow will have an influence on the instant position of the flexible catheter. The catheter movement will influence the flow there it is assumed that to have small constant amplitude and a small phase lead over the rate flow. This is necessary because, in general, in the case of unsteady boundary layer flows, the stress has a phase lead over the rate of velocity such that the amplitude is taken as very small. The oscillatory phenomena of the wall will generate longitudinal movement in the tube wall, on the other hand vascular tethering of the arteries has a damping effect on this longitudinal movement and it is assumed to be negligible, leading to simplification of the equations describing the wall motion.

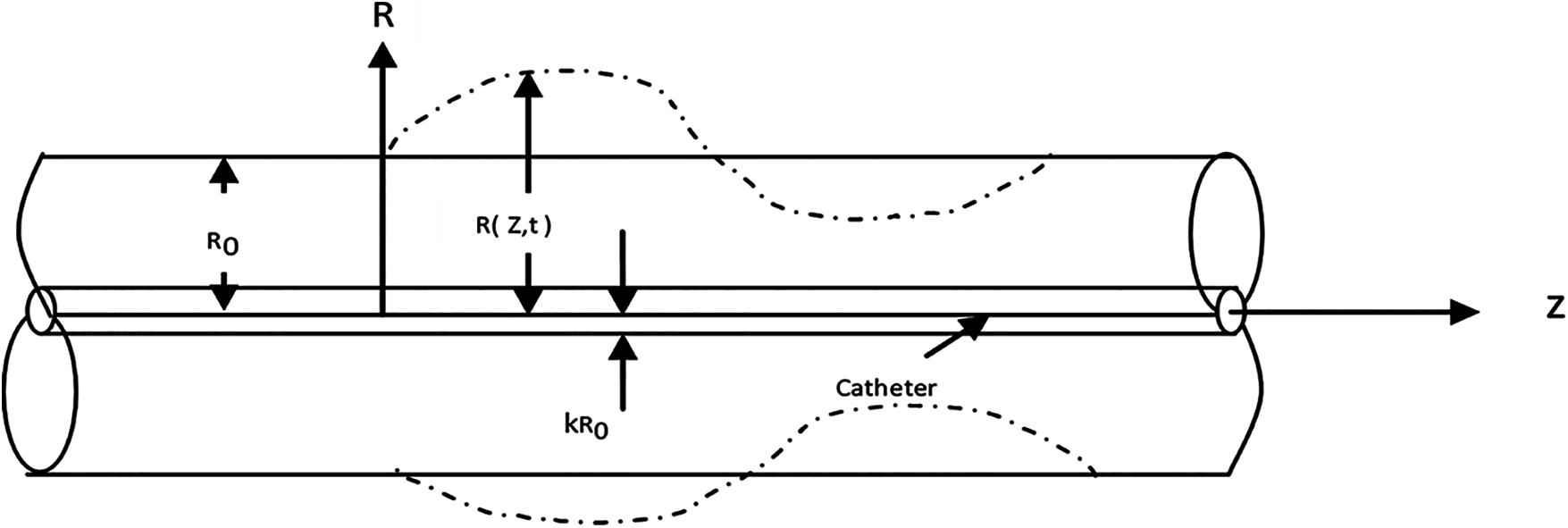
Figure 1: Physical configuration

Fig. 1 shows a schematic diagram of the annular geometry and the cylindrical coordinate system (R,θ,Z) with Z along the axis of the tube. (U,0,W) be the velocity vector of the fluid phase and (U′,0,W′) be the velocity vector of particulate phase corresponding to the cylindrical coordinate system (R,θ,Z) . The Navier–Stokes equations corresponding to this phenomenon from Saffman [3], Srivastava [10] and Sarkar et al. [12] are given by

∂W∂t+U∂W∂R+W∂W∂Z=−1ρ∂P∂Z+ν(∂2W∂R2+1R∂W∂R+∂2W∂Z2)+KNρ(W′−W), (1)

Nm∂W′∂t=KN(W−W′), (2)

∂U∂t+U∂U∂R+W∂U∂Z=−1ρ∂P∂R+ν(∂2U∂R2+1R∂U∂R−UR2+∂2U∂Z2)+KNρ(U′−U), (3)

Nm∂U′∂t=KN(U−U′), (4)

1R∂(RU)∂R+∂W∂Z=0, (5)

where P is the pressure, ρ is the density the fluid, t is the time, N is the number density of the particles, ν is the kinematic viscosity of the fluid, K=3μπd is the stokes drag term, m is the mass of the each particulate and d is diameter of the particulate.

The radius of the tube R~(Z,t), varies with the pressure pulse due to the elastic nature of the wall. Therefore radius is given by R~=R~(P), or the pressure can be expressed as P=P(R~). The no slip boundary conditions at the outer wall and at the inner tube wall are

W=Wc(t),U=0 atR=kR0, (6)

W=0, U=∂R~∂t atR=R~, (7)

where Wc(t) represents the pulsatile movement of the flexible catheter.

Non-dimensional transformation variables given as follows:

where (u,0,w) be the non dimensional velocity of fluid phase, (u′,0,w′) be the non dimensional velocity of particulate phase, (r,θ,z) be the non dimensional coordinates, P0 is the mean pressure, C0 denotes a characteristic wave speed, Ω is the angular velocity, D is the distensibility of the flexible tube, b is the non-dimensional boundary radius is function of pressure p, q is the flow rate, R~max is the maximum radius attained by the tube wall due to the influence of the oscillatory pressure on the elastic wall of the tube. We thus describe the parameters governing to the flow as Womersley number, α=R0Ω/Ωνν and steady streaming Reynolds number as Rst=ε2α2. If Rst is small, the steady streaming is the same to Stokes flow and when it is large the steady streaming may also have a tractable form.

Let us assume |ΩR0/ΩR0C0C0|≤1 (long wave length approximation). This assumption reduces the dimensionless form of the Eq. (4) with the condition ∂p/∂p∂r∂r=0 that is pressure is independent of the radial position. The other governing equations in non dimensional form for fluid phase and particulate phase reduces to

∂w∂τ=−∂p∂z+1α2(∂2w∂r2+1r∂w∂r)−u∂w∂r−w∂w∂z+KN(w−w′), (8)

Nm∂w′∂τ=KN(w′−w), (9)

1r∂∂r(ru)+∂w∂z=0. (10)

In the Eq. (8) the axial viscous transport term ∂2w/∂2w∂z∂z2 is ignored because |ΩR0/ΩR0C0C0|≤1 .

The boundary conditions are

w=w~c,u=0atr=k, (11)

w=0,u=∂b(p)∂τatr=b(p). (12)

Introducing the non dimensional transformation to overcome the difficulty of moving boundary as

s=k+(1−k)(r−k)(b(p)−k). (13)

Thus the equations of motion and continuity in the transformed coordinate are

∂w∂τ=−∂p∂z+(1−k)2α2b12(∂2w∂s2+b1(1−k)((s−k)b1(1−k)+k)∂w∂s)−(u(1−k)−(s−k)∂b∂τ)1b1∂w∂s−w(∂w∂z−(s−k)b1∂b∂z∂w∂s)+KN(w−w′), (14)

Nm∂w′∂τ=KN(w′−w), (15)

(1−k)((s−k)b1(1−k)+k)∂∂s(((s−k)b1(1−k)+k)u)+b1∂w∂z−(s−k)∂b∂z∂w∂s=0, (16)

where b1(s,z,τ)=(b(p)−k).

The consequent boundary conditions are given by

w=w~c,u=0ats=k, (17)

w=0,u=∂b(p)∂τats=1. (18)

The relation between the cross sectional area of the tube and the transmutable pressure difference—has to be specified to understand the flow in inert tubes. That is in the present problem, specifying b(p) will be given in tube law.

3  Method of Solution

Being nonlinear in nature, the Eq. (14) does not provide the closed form solution. By using perturbation method, the approximate solutions for velocity and pressure distribution up to second order have been analyzed. The diameter variation in arteries, resulting from the effect of pressure pulse, represented by ε is considered very small. This enables us to seek a solution by expanding for fluid velocity, particulate velocity in axial direction and radial direction, pressure and non-dimensional boundary radius i.e., w,w′,p,b,u,u′ in terms of ε≤1 given below:

w=εw11+ε2(w20+w21+w22)+O(ε3),

w′=εw11′+ε2(w′20+w′21+w′22)+O(ε3),

p=εp11+ε2(p20+p21+p22)+O(ε3),

b=1+εb11(p)+ε2(b20(p)+b21(p)+b22(p))+O(ε3),

u=εu11+ε2(u20+u21+u22)+O(ε3),  u′=εu11′+ε2(u′20+u′21+u′22)+O(ε3). (19)

wij represents the j th harmonic of the i th order term in the perturbed expansion of w. Similar definitions hold for wij′,pij,bij,uij&uij′. ε≤1 allows the frequency parameter α, to take moderate values with Rst≈O(1). Again, considering purely oscillatory flow rate we can consider

w11=Re[W11eiτ], (20)

where Re [ ] denotes the real part of a complex variable. Associated expressions can be written for w11′,u11,u11′,p11,b11. We take w~c=wccos(τ−τ0) where wc≤1 is the maximum amplitude of the flexible annular wall. τ0 is the phase lead of this wall oscillation over the flow. In general the wc will depend on the elastic properties of the catheter material and the tangential stress exerted by the fluid flow. However, in the present study we treat wc&τ0 given. Implementing the Eqs. (19) and (20) in Eqs. (14)–(18) and equating the terms of varying orders of ε, we get a system of differential equations for various order terms.

3.1 Solution of O(ε)

The equations corresponding to first order O(ε) terms which are proportional to eiτ are the following:

∂2W11∂s2+1s∂W11∂s−α12W11=α2P11, (21)

1s∂∂s(sU11)+∂W11∂z=0, (22)

α12=iα2(1+KNΓ(1+iΓ)(1+Γ2)),Γ=mK. (23)

(1+KNΓ(1+iΓ)(1+Γ2))=ω is the drag parameter.

The corresponding boundary conditions are

W11=wce−iτ0,U11=0ats=k, (24)

W11=0ats=1. (25)

After solving for U11&W11 in terms of modified Bessel functions of complex arguments, solutions of O(ε) for the Eqs. (14) and (19) are obtained as

p11′=Re[f(z)eiτ], (26)

w11=Re[(−wce−iτ0F1(s)+f(z)i(1−F2(s)))eiτ], (27)

u11=Re[(−f′(z)i(s2−F4(s)+A4s))eiτ]. (28)

The boundary conditions on radial velocity, i.e., Eq. (12), is

u11=∂b11∂τats=1, gives b11=Re[B1(z)eiτ],

where

B1(z)=−12f′(z)C12. (29)

The ( `) denotes derivative with respect to z . F1(s),F2(s),F4(s),A4,C12 are defined in the Appendix. f(z) be the unknown function which depends on the elastic nature of the tube and its response to the pressure gradient.

3.2 Steady Streaming Solution of O(ε2) for Arbitrary α and Small Rst

The O(ε2) equations for the steady streaming components are given by

1α2(∂2w20∂s2+1s∂w20∂s)=p20′(z)+G1(z,s), (30)

1s∂∂s(su20)+∂w20∂z=0, (31)

where

G2(z,s)=s11∂b11∂z∂w11∂s−b111−k∂w11∂z+kb11u11s2(1−k), and s1=s−k1−kwithk<1.

A double over bar denotes time averaged solution.

Boundary conditions:

w20=0ats=kands=1, (32)

u20=0ats=kands=1. (33)

The solution for pressure and velocity are obtained as follows:

p20′=Re[D1iwceiτC12f′(z)+D2iwceiτC12C12¯f′(z)f(z)¯], (34)

w20=Re[α2(p′20(z)4s2+iwceiτC12f′(z)(H1(s)−H1(k)ln(k)−(1−1ln⁡(k))H1(1))+iC12C12¯f′(z)f(z)¯∗(H2(s)−H2(k)ln(k)−(1−1ln⁡(k))H2(1)))], (35)

where s2=s2−1+1−k2lnkwithk<1.

H1(s),H2(s), defined in the Appendix. D1 and D2 are pure constants which are evaluated using the Eqs. (31) and (33). It is to be distinguished that the first term in Eq. (34) component due to the movement of the flexible inner tube. It is to be identified that p20′ is the correction to the mean pressure—an important result from the nonlinear steady streaming study. The effect of p20′ will depend on α,ε,wc,τ0,f′(z) and the function F(z)=iC12C12¯f′(z)f¯(z). In addition, it was revealed that F(z) is proportional to the wall movement and flow rate amplitude at O(ε) .

In the current study, the longitudinal oscillations of the catheter give rise to an additional term whose magnitude will depend upon wc,τ0,f′(z) . Thus the interface of the amplitude of catheter oscillation (wc) and the amplitude of the wall movement which is proportional to f′(z) is first felt at the O(ε2) through p20′ and w20.

3.3 Dependence on Axial Position

f(z) f(z) is an unknown function and it is related to both pressure gradient and diameter variation, is assumed as

f(z)=A1e(i/iC1C1)z+A2e−(i/iC1C1)z. (36)

where the constants of integration of A1,A2 complex in nature and can be determined from the dynamic conditions of the flow.

The flow rate of wave form is determined by the pressure wave, movement of the wall, and in a small measure by the movement of the catheter. The non dimensional form of the flow rate can be written as

q(z,t)=Re[Q1ei(τ−τ0)+Q2(z)ei(τ+φ(z))]. (37)

where the first term is due to the catheter movement and the second is due to the oscillatory pressure gradient. Q1 will depend on wc, contributes to the modified amplitude, Q2 is the amplitude in the absence of the oscillations of the flexible inner tube and φ(z) is the phase angle difference between the wall motion and flow rate in the absence of oscillation of the flexible inner tube at O(ε).

A1,A2 are estimated by setting up the flow rate amplitude when the inner tube is at rest and amplitude of wall motion. Q1 has been fixed from the given values for wc. From experiments with and without the presence of the movement of the annulus and know the flow rate and diameter deviation at a particular point in the axial direction.

4  Results and Discussion

The present investigation reveals the influence of the particle drag parameter on nonlinear oscillatory flow through concentric annulus. The variation of velocity profile and pressure gradient have been analyzed with respect to the effects of drag parameter, frequency parameter and phase angle. In this section we discuss our results corresponding to values for the parameters in the model suitable to the physiological system. The frequency parameter α is taken from a small value of 5 to a moderate value up to 15, k is the ratio of the radii of the inner tube is varied from 0.2 to 0.5 and wc is given values from 0 to 0.4 and drag parameter ω is taken in the range 0.5–0.8. Here Q2(z) fixed as 0.5 and the amplitude of wall variation B1(z) as 0.05 at z=0 for the purpose of analyzing the results of our mathematical model. The phase difference angle φ be the notion as an indicator of the impedance to the flow. Values for φ ranging from 0° to 90° are given to study the influence of wave reflections on the steady streaming induced mean pressure gradient and velocity profile.

4.1 Mean Pressure Gradient and Velocity Distribution

The induced mean pressure gradient p20′(z) along the axial direction for different values of ω drag parameter have been presented in the Figs. 2–5. From these it reveals that as drag parameter increases mean pressure gradient decreases. It is seen from Fig. 6 that the phase lead τ0 of the wall of the oscillating catheter to flow, it does not have considerable influence on pressure gradient. The effect of catheter radius on mean pressure gradient p20′(z) can be seen in the Figs. 7 and 8. From these, it reveals that as catheter radius k increases mean pressure gradient decreases.

Variations of mean axial velocity w11 and w20 along the radial direction for various values of drag parameter have been presented in the Figs. 9–12, for various values of drag parameter and frequency parameter with fixed values of phase angle, and catheter radius. It discloses that the parabolic profile has been maintained that similar to annular flow in a rigid tube. It can be observed that as drag parameter increases then the velocity decreases, that is particulate drag resists the flow of the fluid. But as frequency parameter increases the parabolic profile shows kinks near the outer wall (artery wall) of the tube suggesting the influence of the elastic nature of the tube wall on the flow. The obtained results have been agreed with that of Wang et al. [9] and also Sarkar et al. [12].

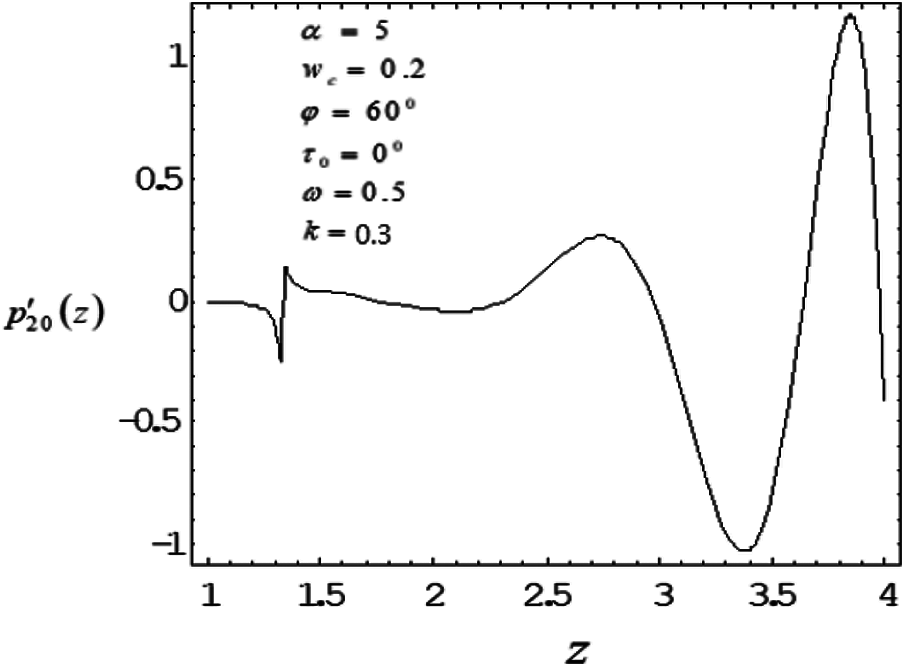
Figure 2: Variation of mean pressure gradient along the axial length with drag parameter 0.5

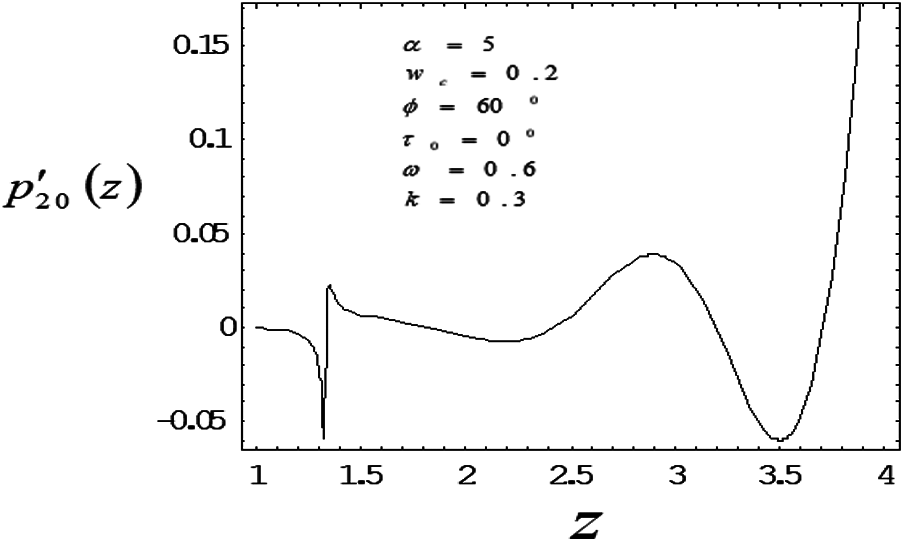
Figure 3: Variation of mean pressure gradient along the axial length with drag parameter 0.6

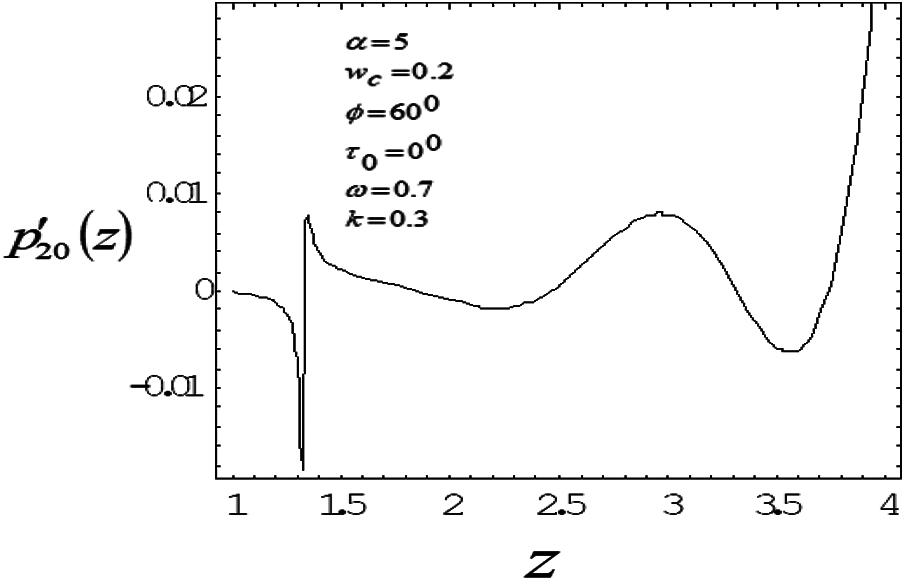
Figure 4: Variation of mean pressure gradient along the axial length with drag parameter 0.7

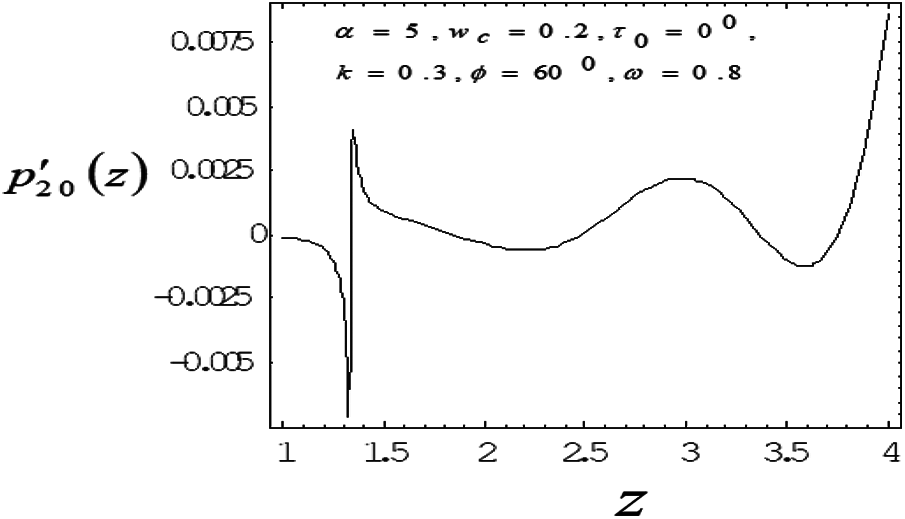
Figure 5: Variation of mean pressure gradient along the axial length with drag parameter 0.8

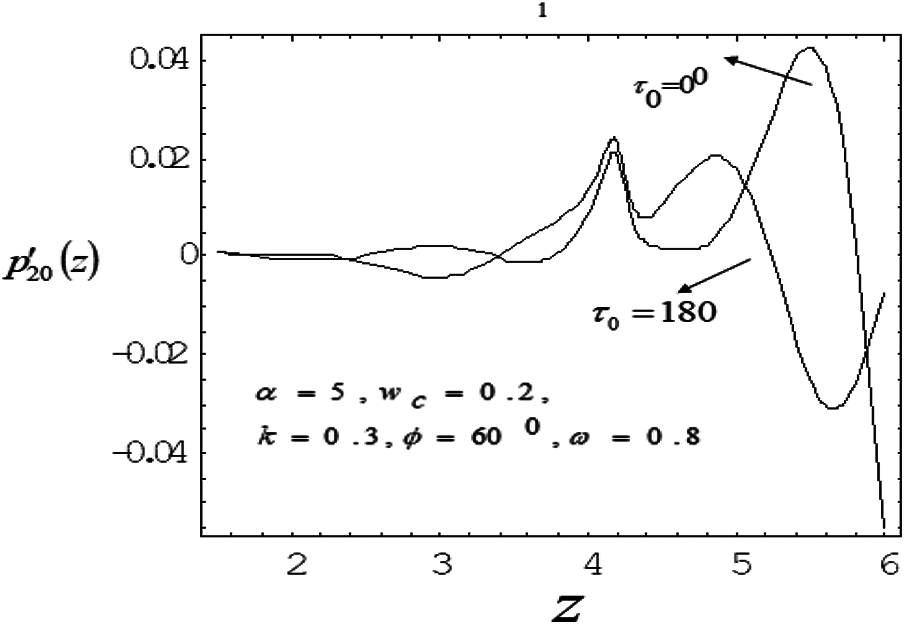
Figure 6: Variation of mean pressure gradient along the axial length for different phase lead angles

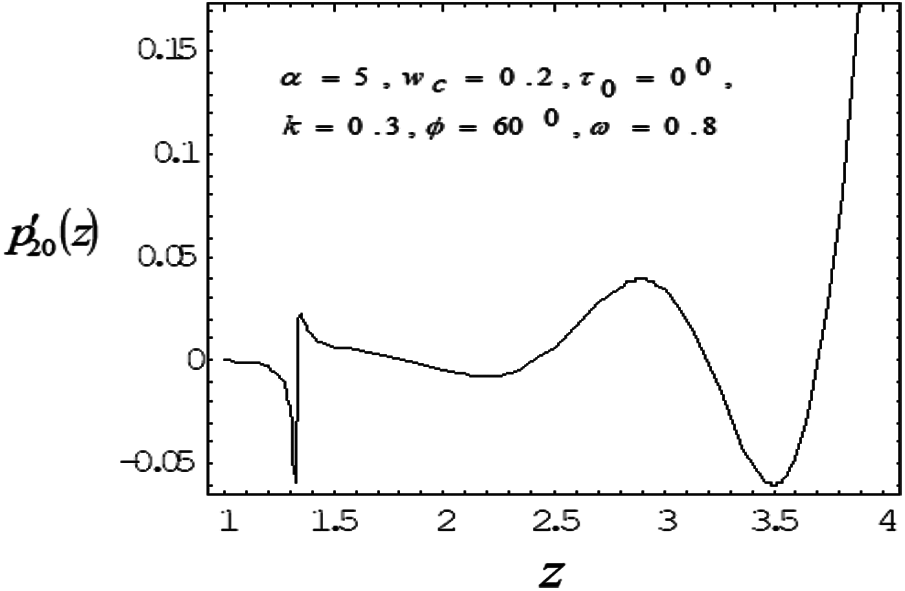
Figure 7: Variation of mean pressure gradient along the axial length with Catheter radius 0.3

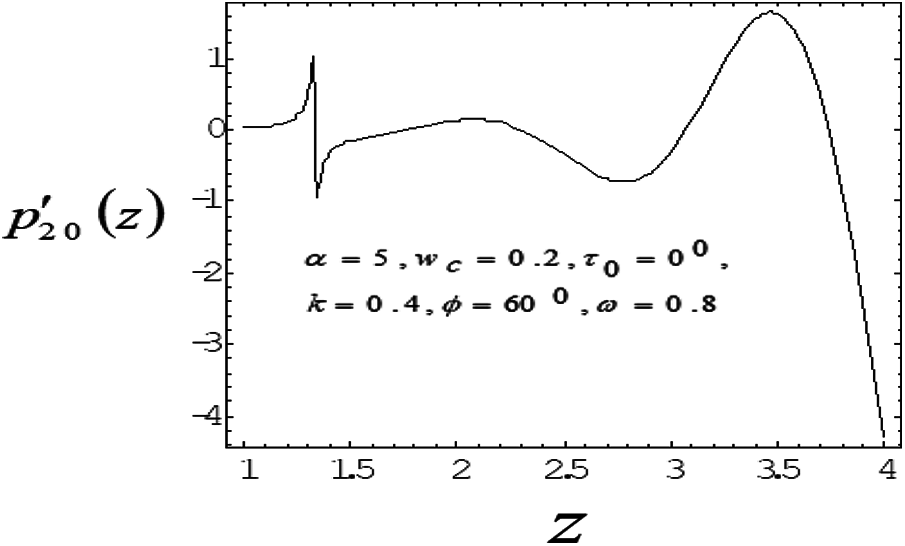
Figure 8: Variation of mean pressure gradient along the axial length with Catheter radius 0.4

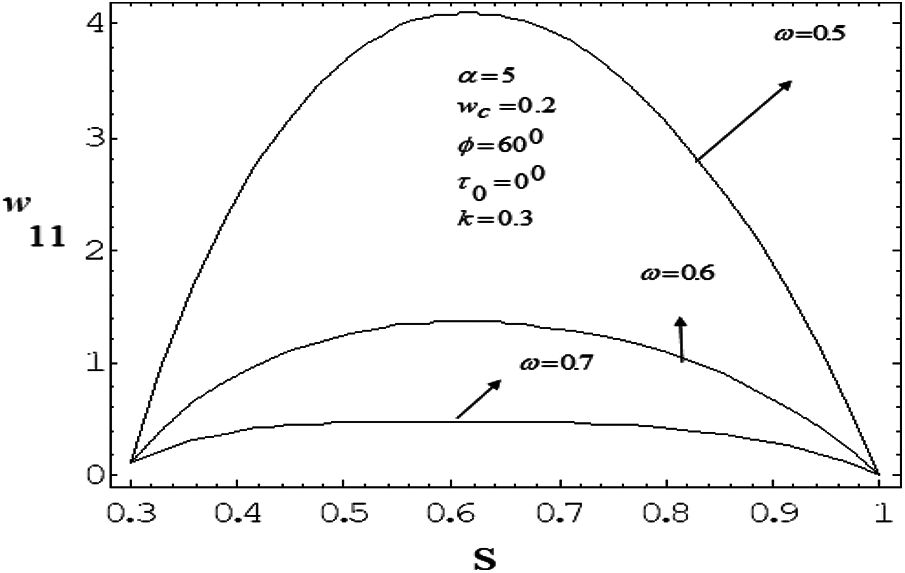
Figure 9: Variation of mean axial velocity of first order along the radial direction for various values of drag parameter with frequency parameter value 5

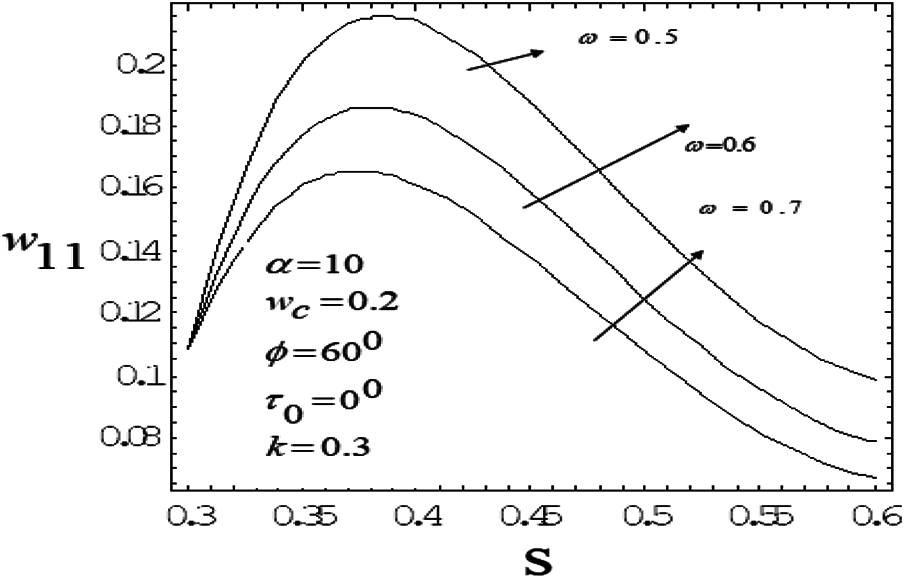
Figure 10: Variation of mean axial velocity of first order along the radial-direction for various vales of drag parameter with frequency parameter value 10

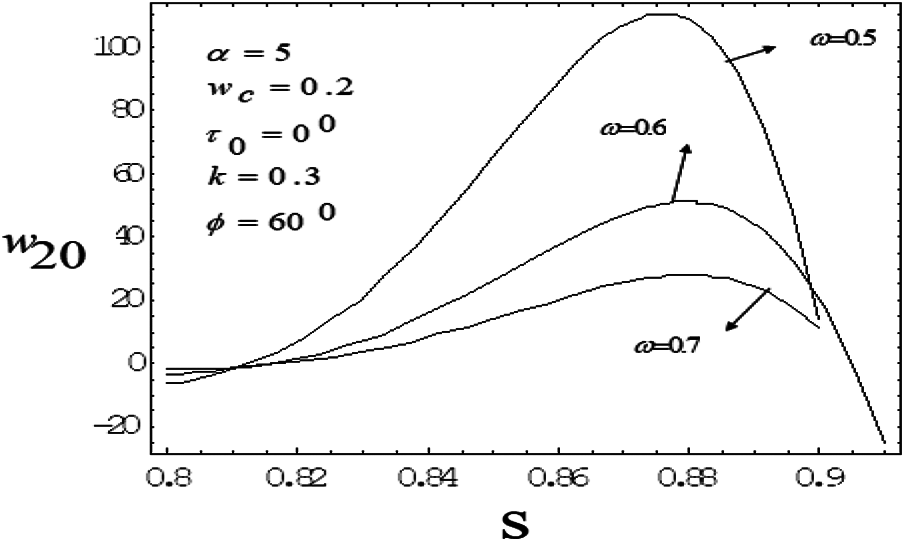
Figure 11: Variation of mean axial velocity of second order along the radial-direction for various vales of drag parameter with frequency parameter value 5

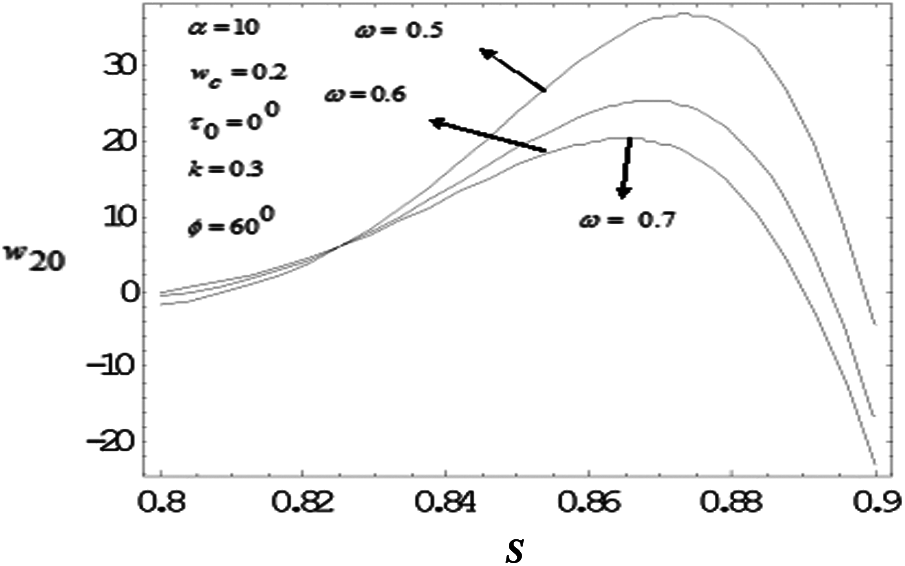
Figure 12: Variation of mean axial velocity of second order along the radial-direction for various vales of drag parameter with frequency parameter value 10

5  Conclusion

To study the nonlinear oscillatory flow in the concentric annulus with the influence of particle drag and frequency parameter, a mathematical model has been developed. The model has been applied to investigate induced mean pressure gradient, mean velocity distribution—vary noticeably along axial, radial correspondingly. The computational results were found in good agreement with the bench mark results. As particle drag parameter increases then mean pressure gradient and mean velocity distribution decreases. Mean velocity profile bends near the outer wall (artery wall) of the tube, as frequency parameter increases, suggesting the influence of the elastic nature of the tube wall on the flow. Also depending on catheter size, a slim catheter experience the minute oscillations due to the flow conditions is likely to influence in the same way as thicker catheter which remains quite stationary inside the artery.

This study gives an insight to enormous applications in the field of diagnosing, treating and certain surgical procedures related to the disorders/diseases which originate in the body relating to COVID-19 symptoms, cardiovascular, pulmonary, synovial systems etc., where as the different types of cardiovascular diseases include Aneurysms, Angina, Atherosclerosis, Stroke, different types of cerebrovascular disease, Heart Failure, Coronary Heart diseases and Myocardial infarction or Heart attacks.

Acknowledgement: The authors acknowledge the support of JSS Academy of Technical Education, Bangalore and Ramaiah Institute of Technology, Bangalore.

Funding Statement: The authors received no specific funding for this study.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  Womersely, J. R. (1955). Oscillatory motion of a viscous liquid in a thin-walled elastic tube-I: The linear approximation of long waves. Philosophical Magazine Series, 46(373), 199–221. DOI 10.1080/14786440208520564. [Google Scholar] [CrossRef]

 2.  Womersely, J. R. (1957). An elastic tube theory of pulse transmission and oscillatory flow in mammalian arteries, WADCTR-56-614. Ohio: Wright Air Development Center, Wright Patterson Air Force Base. [Google Scholar]

 3.  Saffman, P. G. (1962). On the stability of laminar flow of dusty gas. Journal of Fluid Mechanics, 120(13), 120–128. DOI 10.1017/S0022112062000555. [Google Scholar] [CrossRef]

 4.  Rubinow, S. I., Keller, J. B. (1972). Flow of a viscous fluid through an elastic tube with applications to blood flow. Journal of Theoretical Biology, 35(2), 299–313. DOI 10.1016/0022-5193(72)90041-0. [Google Scholar] [CrossRef]

 5.  Rao, A. R., Devanathan, R. (1973). Pulsatile flow in tubes of varying cross-section. Journal of Aplied Mathematics and Physics, 24(2), 203–213. [Google Scholar]

 6.  Taylor, L. A., Gerrard, J. H. (1977). Pressure-radius relationships for elastic tubes and their application to arteries. Part 1—Theoretical relationships. Medical and Biological Engineering and Computing, 15(5), 11–17. DOI 10.1007/BF02441569. [Google Scholar] [CrossRef]

 7.  RamachandraRao, A. (1983). Oscillatory flow in an elastic tube of variable cross-section. ActaMechanica, 46, 155–165. [Google Scholar]

 8.  Chang, H. C., Ha, S. C., Park, J. K., Kim, I. H., Shin, H. D. (1989). Velocity field of pulsatile flow in a porous tube. Journal of Biomechanics, 22(11-12), 1257–1262. DOI 10.1016/0021-9290(89)90228-5. [Google Scholar] [CrossRef]

 9.  Wang, D. M., Tarbell, J. M. (1995). Non-linear analysis of oscillatory flow with a non zero mean, in an elastictube(artery). Journal of Biomechanical of Engineering, 117(1), 127–135. DOI 10.1115/1.2792260. [Google Scholar] [CrossRef]

10. Srivastava, V. P. (1996). Two phase model of blood flow through stenosed tubes in the presence of peripheral layer. Journal of Biomechanics, 1377(29), 1377–1382. DOI 10.1016/0021-9290(96)00037-1. [Google Scholar] [CrossRef]

11. Sarkar, A., Jayaraman, G. (1998). Correction to flow rate-pressure drop in coronary angioplasty: Steady streaming effect. Journal of Biomechanics, 31(9), 781–791. DOI 10.1016/S0021-9290(98)00053-0. [Google Scholar] [CrossRef]

12. Sarkar, A., Jayaraman, G. (2001). Nonlinear analysis of oscillatory flow of in the annulus of an elastic tube: Application to catheterized artery. Physics of the Fluids, 13(10), 2901–2911. DOI 10.1063/1.1389285. [Google Scholar] [CrossRef]

13. Jayaraman, G., Sarkar, A. (2005). Nonlinear analysis of arterial blood flow—Steady streaming effect. Nonlinear Analysis: Theory, Methods & Applications, 63(5–7), 880–890. DOI 10.1016/j.na.2005.01.016. [Google Scholar] [CrossRef]

14. Vajravelu, K., Sreenadh, S., Devaki, P., Prasad, K. V. (2011). Mathematical model for a Herschel-Bulkley fluid flow in an elastic tube. Central European Journal of Physics, 9, 1357–1365. [Google Scholar]

15. Sreedharamalle, S., Palluru, D., Diwakar Reddy, D., Krishnaiah (2012). Unsteady flow of a Jeffrey fluid in an elastic tube with a stenosis. International Conference of Fluid dynamics and Thermodynamics Technologies, vol. 33. Singapore, IPCSIT. [Google Scholar]

16. Sochi, T. (2014). The flow of Newtonian and power-law fluids in elastic tubes. International Journal of Non-Linear Mechanics, 67(6), 245–250. DOI 10.1016/j.ijnonlinmec.2014.09.013. [Google Scholar] [CrossRef]

17. Sankar, M., Do, Y., Ryu, S., Jang, B. (2015). Cooling of heat sources by natural convection heat transfer in a vertical annulus. An International Journal Computation and Methodology, 68(6), 847–869. DOI 10.1080/10407782.2015.1023097. [Google Scholar] [CrossRef]

18. Siddiqui, S. U., Awasthi, C. (2017). Mathematical analysis on pulsatile flow through a catheterized stenosed artery. Journal of Applied Mathematical Physics, 5(9), 1874–1886. DOI 10.4236/jamp.2017.59157. [Google Scholar] [CrossRef]

19. Khudayarov, B. A., Turaev, F. Z. (2019). Mathematical simultion of nonlinear oscillations of viscoelastic pipelines conveying fluid. Applied Mathematical Modelling, 66, 662–679. DOI 10.1016/j.apm.2018.10.008. [Google Scholar] [CrossRef]

20. Do, Y., Ramesh., G. K., Roopa, G. S., Sankar, M. (2019). Navier’s slip condition on time dependent Darcy-Forchheimer nano fluid using spectral relaxation method. Journal of South Central University, 26(7), 2000–2010. DOI 10.1007/s11771-019-4147-y. [Google Scholar] [CrossRef]

21. Tsimpoukis, A., Vasileiadis, N., Tatsios, G., Valougeorgis, D. (2019). Nonlinear oscillatory fully-developed rarefied gas flow in plane geometry. Physics of Fluids, 31(6), 06108. DOI 10.1063/1.5099051. [Google Scholar] [CrossRef]

22. Kiran, S., Keerthi, R., Sankar, M., Do, Y. (2020). Computational analysis of conjugate buoyant convective transport in an annulus. Advances in Fluid Mechanics, 26, 889–905. [Google Scholar]

23. Naveed, M., Rafiq, M., Raza, A., Ahmed, N., Khan, I. et al. (2020). Mathematical analysis of novel coronavirus (2019-nCov) delay pandemic model. Computers, Materials & Continua, 64(3), 1401–1414. DOI 10.32604/cmc.2020.011314. [Google Scholar] [CrossRef]

24. Azam, S., Macius-Diaz, J. E., Ahmed, N., Khan, I., Iqbal, M. S. et al. (2020). Numerical modeling and theoretical analysis of a nonlinear advection-reaction epidemic system. Computer Methods and Programs in Biomedicine, 193(772), 105429. DOI 10.1016/j.cmpb.2020.105429. [Google Scholar] [CrossRef]

25. Saqib, M., Shafie, S., Khan, I., Chu, Y. M., Nisar, K. S. (2020). Symmetric MHD channel flow of nonlocal fractional model of BTF containing hybrid nanoparticles. Symmetry, 663(12), 12040663. DOI 10.3390/sym12040663. [Google Scholar] [CrossRef]

26. Bilal, S., Mahmood, R., Majeed, A. H., Khan, I., Nisar, K. S. (2020). Finite element method about heat transfer analysis of Newtonian material in triangular cavity with square cylinder. Journal of Materials Research and Technology, 9(3), 4904–4918. DOI 10.1016/j.jmrt.2020.03.010. [Google Scholar] [CrossRef]

27. Rasool, G., Khan, W. A., Bilal, S. M., Khan, I. (2020). MHD squeezed Darcy-Forchheimer nanofluid flow between two h-distance apart horizontal plates. Open Physics, 18(1), 1100–1107. DOI 10.1515/phys-2020-0191. [Google Scholar] [CrossRef]

28. Lu, Z., Dupuis, E. D., Patel, V. K., Momen, A. M., Shahab, S. (2021). Ultrasonic oscillatory two-phase flow in microchannels. Physics of Fluids, 33(3), 032003. DOI 10.1063/5.0039971. [Google Scholar] [CrossRef]

29. Bilal, S., Asogwa, K., Alotaibi, H., Malik, M. Y., Khan, I. (2021). Analytical treatment of radiative Casson fluid over an isothermal inclined Riga surface with aspects of chemically reactive species. Alexandria Engineering Journal, 60(5), 4243–4253. DOI 10.1016/j.aej.2021.03.015. [Google Scholar] [CrossRef]

Appendix

F1(s)=1D(K0(α1s)I0(α1)−I0(α1s)K0(α1)),

F2(s)=1D(I0(α1k)K0(α1s)−K0(α1k)I0(α1s))−F1(s),

F3(s)=−1α1D(I0(α1)K1(α1s)+K0(α1)I1(α1s)),

F4(s)=−1α1D(I0(α1k)K1(α1s)+K0(α1)I1(α1s))−F3(s),

D=(K0(α1)I0(α1k)−K0(α1k)I0(α1)),

C12=1+2α1D(I0(α1k)K1(α1)−K0(α1k)I1(α1)−1α1)+2A4,

H1(s)=∫dss∫sH3(s)ds,H2(s)=∫dss∫sH4(s)ds,

where

H3(s)=−F1(s)C12−s12∂F1¯∂s(s)+F1¯(s)C12(s2−F4(s)+A4)−iα2(1−k)((1−k)∂2F1¯∂s2(s)−(2s−k2s2)∂F1¯∂s(s)),

H4 (s) =   − (1− F2 (s))(1− F2 ¯ (s)) i C12 C1¯2 − (s12 C1¯2)  ∂ F2¯ ∂ s (s) +  i  (1− F2 ¯ (s)) i C12 C1¯2   (s2 − F4 (s) + A4) − 1α2 (1−k)   ((1−kC1¯2) ∂ 2 F2¯ ∂ s2 (s)  −  (2s−k2 s2 C1¯2)∂ F2¯ ∂ s (s))  .

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.