Static Bending Creep Properties of Glass Fiber Surface Composite Wood

1  Introduction

Poplar is an artificial fast-growing tree that is planted on a large scale in China. Due to the growth period being short, Poplar has a low density and poor mechanical properties, so it cannot be directly used in the field of structural building materials [1]. To widen the application scope of artificial fast-growing forests in the field of structural building materials, many enhancement methods have been proposed. Among them, fiber composite reinforcement is one of the cheaper and more effective ways to enhance the materials of artificial fast-growing forests [2–4]. Fiber Reinforced Polymer (FRP) technology refers to the application of adhesives and coupling agents to composite fiber materials in/outside the substrate to improve the overall mechanical properties of the original substrate [5–8]. After the FRP composite is created, the bearing capacity of wood materials can be increased by 17.7%­­–77.3% [9,10]; the static bending strength can be increased by 12.3%–24.6%; and the elastic modulus can be increased by 10.3%–57.6% [11–13]; the shear strength increased by 2.9%–38.0% [14]; the joint strength increased by 33.0% when combining glass fiber reinforced composite and reinforced bolts [15]; the flexural strength and modulus increased by 14.6% and 51.4% and can significantly reduce the water-absorbing thickness expansion rate when combined with wood-based panels [16–18]. The above studies mainly focus on the instantaneous physical and mechanical properties of wood materials reinforced by fibers, but it is important to examine the properties of heavy-duty wood building materials under long-term external loads, that is, creep resistance (Generally, the total creep deformation is used to measure or predict), service stability, reliability, and safety during its life cycle of wood. When the wood is under load, it can be divided into Normal Creep (NC) and Mechanical Sorptive Creep (MSC) according to the Relative Humidity (RH). When the relative humidity is constant, it is called NC, and when the relative humidity changes cyclically, it is called MSC (load and ambient temperature are constant) [19–21]. It is generally believed that under the same external load conditions, the total deflection of wood or wood material produced by MSC is much larger than that of NC [22]. Considering that the RH in the service environment of generally heavy-duty wood materials changes dynamically, the resistance to MSC is particularly important for the service performance of heavy-duty wood materials. After the upper and lower surfaces of the wood are reinforced with fibers, on the one hand, the overall bending stiffness will be significantly improved; on the other hand, the adhesive will hinder the moisture absorption and desorption of the wood (absorbing water vapor from the air or releasing water vapor) and weaken its mechanical adsorption effect, theoretically speaking, these two improvements can improve the anti-MSC ability of FRP reinforced wood.

For this reason, this paper takes the artificial fast-growing tree Poplar, which is widely planted and industrialized in China, as the subject of interest, and examines the static-bending creep law of GFRP composted with glass fiber surface reinforcement under the action of different loads and different environmental relative humidity. Then, the mechanism of GFRP is explored based on the static-bending force analysis using the Abaqus finite element software. Finally, NC of GFRP is simulated by Burgers’ 4-factor model and Weibull distribution equation. The research results will provide a new way for the scientific evaluation of the long-term service performance of GFRP and the feasibility of its application in the field of load-bearing timber.

2  Materials and Methods

2.1 Materials

The ten-year-old plantation-grown Poplar (Populus euramevicana cv, origin Jiangsu) was processed into a sample size of 120 mm × 10 mm × 5 mm (length × width × Thickness) [23]. The full dry density of the specimen was 448.21 kg/m3, and the bending strength and modulus of elasticity of 115 MPa (5.23) and 7,900 MPa (621). E-type glass fiber cloth (thickness 1 mm, elastic modulus 72,000 MPa) was purchased from Jiangxi Dahuaboxian Co., Ltd., China adhesive (2:1 transparent epoxy resin type A and B) was purchased from Manzhouli Beiya Chemical Co., Ltd. (China), and coupling reagent (KH550) was purchased from Nanjing USI Chemical Co., Ltd., China.

2.2 Preparation of Glass Fiber Reinforced Poplar Specimens

To improve the bonding properties of wood and glass fiber, the dewaxed glass fiber cloth was dried in a drum drying oven at 103°C ± 2°C for 72 h. A coupling reagent with a mass fraction of 1% was added to the epoxy resin, and the epoxy resin with a coating amount of 320 g/m2 was evenly brushed on the upper and lower surfaces of the specimen. The pre-tensioned glass fiber cloth was pasted on the upper and lower surfaces of the specimen to give full play to the tensile strength of glass fiber cloth and to improve the overall bearing capacity of the glass fiber-reinforced composite specimen. Finally, the specimens were cold-pressed and solidified for 72 hours (h) to obtain glass Fiber-reinforced Poplar specimens GFRP. The mechanical properties of P and GFRP were tested according to GB/T 1927.9-2021 “Determination of bending strength” and GB/T1927.10-2021 “Determination of modulus of elasticity in bending” [24,25].

2.3 Static-Bending Creep Test Designs

The static bending test was designed based on ASTM D 6815, GB/T 31291-2014, and LY/T 1975-2011, and the two-point loading method was used to test the creep of GFRP and the deflection during the creep recovery process [26–28]. The test equipment consists of an environmental system, a creep test system, and a creep deflection monitoring system. The environmental system is controlled by a Binder climate chamber to accurately control the ambient temperature and RH of the creep test (temperature range 0°C∼70°C (accuracy ± 1°C), relative humidity range 10%∼98% (accuracy ± 2%)). The creep test system adopts the wood static bending creep developed by the course group. The creep deflection monitoring system records the creep deflection of the specimen in real-time using the linear displacement sensor (the test accuracy is ± 0.01 mm) and automatically generates images. The details of the whole set of test equipment are shown in [29]. The experimental designs of NC and MSC are shown in Tables 1 and 2, respectively.

2.4 Finite Element Analysis

To analyze the bending performance of poplar and glass fiber reinforced poplar more accurately, the material parameters of poplar were obtained based on the four-point bending material property test, and the finite element model of poplar and glass fiber reinforced poplar bending stress test was established by combining with the general finite element ABAQUS [30,31]. The three-dimensional eight-node solid unit C3D8 was selected, with a total of 6000 units and a unit size of 1 mm × 1 mm × 1 mm as shown in Fig. 1. Neglecting the glue line, the wood is bound directly to the fiberglass cloth. To realistically simulate the support and loading points of the specimen, steel roller support, and loading points are used, four RP reference points are set up at the specimen, and the concentrated force load is applied through the reference loading points (the top two RPs of the specimen) points. Reference points RP (two RP points below the specimen) are established at the specimen support points.

Figure 1: Meshing of the test specimen

3  Results and Analysis

3.1 Influence of Glass Fiber Reinforcement on Mechanical Properties of Poplar

As can be observed from Table 3, compared with the control material P, the MOE, and MOR of GFRP increased by 17.06%, and 10%, respectively. This effect is caused by the GFRP specimen being subjected to lateral load, the maximum compressive stress, and tensile stress on the upper and lower surface layers being borne by the high-strength glass fiber layer, causing the strength and stiffness of GFRP to be significantly improved.

3.2 Effect of Load on NC and MSC

From Fig. 2a, it can be observed that the variation law of NC and recovery of GFRP under different loads are similar to that of classical wood NC. The NC of GFRP under different loads has the following characteristics: 1) It exhibits three stages: transient creep stage (0–5 h), steady-state creep stage (6–90 h), and creep recovery stage (91–125 h); 2) The load has a great influence on the NC of GFRP. The greater the load, the greater the creep deflection, initial elastic deformation, and viscous deformation of the specimen (Table 4). At high stress levels (35% in this study), excessive creep deflection may lead to fracture failure of wood in a short time; 3) When the loading level of GFRP and P is 10% of their static bending failure strength, the GFRP maximum creep deflection is reduced by 26.17% compared to the maximum creep deflection of P.

Figure 2: NC (a) and MSC (b) curves of GFRP under different loads

It can be observed from Fig. 2b that P under MSC, the creep deflection of the first moisture absorption and desorption increased, but the creep deflection decreased in the subsequent moisture absorption process and increased during the desorption process. However, the creep deflection of GPRP under MSC does not change with the change of relative humidity, the MSC of GFRP only exhibits NC characteristics of wood. When the loading level of GFRP and P was 10% of the static bending failure strength of each group, the maximum creep deflection of GFRP was reduced by 73.23% compared with that of untreated stilts.

When comparing Figs. 2a and 2b, on the one hand, the MSC of GFRP is similar to the NC characteristics of GFRP, and their creep deflection is the same. On the other hand, when the load is 10%, the MSC creep deflection of GFRP (0.4025 mm) is only 7.41% higher than that of NC (0.3747 mm). However, the MSC (RH98%–65%) creep deflection of P (1.5187 mm) is 199.25% higher than the maximum creep deflection (0.5075 mm) of NC (RH65%). It is worth noting that the change law of relative humidity in the natural atmospheric environment is similar to the cyclic change of relative humidity in MSC, so we should be alert to the problem of rapid destruction of wood caused by MSC.

3.3 The Effect of RH on NC and MSC

It can be observed from Fig. 3a that the NC of GFRP under different relative humidity has the following characteristics: 1) It exhibits a transient creep stage (0–10 h), a steady-state creep stage (11–89 h), and a creep recovery stage (90–125 h); 2) Relative humidity has a certain influence on the NC of GFRP, the specimen exposed to higher relative humidity has greater creep deflection and viscous deformation.

Figure 3: NC (a) and MSC (b) curves of GFRP under different relative humidity

It can be observed from Fig. 3b that the MSC of GFRP under different relative humidity cycles only exhibits NC characteristics. The MSC of GFRP under different relative humidity cycles has the following characteristics: 1) It exhibits a transient creep stage (0–10 h) and a steady-state creep stage (11–60 h); 2) Different relative humidity cycles have different effects on the mechanical properties of GFRP the adsorption creep has no obvious effect, and the MSC of GFRP shows the characteristics of NC; 3) Under RH 98%–65% cycle, the maximum creep deflection of GFRP was reduced by 288.17% compared with the maximum creep deflection of P. Comparing Figs. 3a and 3b, it can be observed that, the MSC of GFRP is similar to the NC characteristics of GFRP, and the creep deflection is the same.

The main reasons why glass fiber surface reinforced wood can effectively reduce the static bending creep deflection of wood and change the MSC characteristics are as follows: 1) When the P bending stress is applied, the upper and lower surfaces bear the maximum compressive/tensile stress, and the maximum. It is easily affected by ambient temperature and humidity, as shown in Figs. 4 and 5a, causing the upper and lower parts of the wood to be most easily damaged in static bending creep (without considering internal factors such as wood defects). When the glass fiber cloth is pasted on the upper and lower surfaces of the wood, on the one hand, the glass fiber cloth with the high elastic modulus (72000 MPa) bears the maximum compressive/tensile stress of the composite material, and Poplar bears lesser stress. On the other hand, for GFRP the stress is much smaller than that of P as shown in Figs. 4a and 4b, thus improving the overall bearing capacity of GFRP; 2) The influence of ambient temperature and humidity on the mechanical properties of glass fiber is much less than that of wood; 3) The epoxy resin layer on the surface of the prevents moisture from entering the interior of the wood which reduces the moisture content of the GFRP specimen as shown in Fig. 6. Therefore, the MSC phenomenon of GFRP is greatly weakened or not present, and MSC only exhibits NC characteristics.

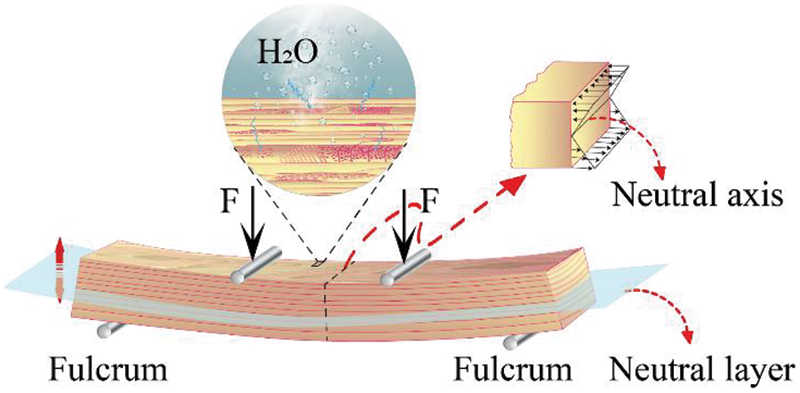
Figure 4: Schematic diagram of the static bending force and water entry into the surface of the wood

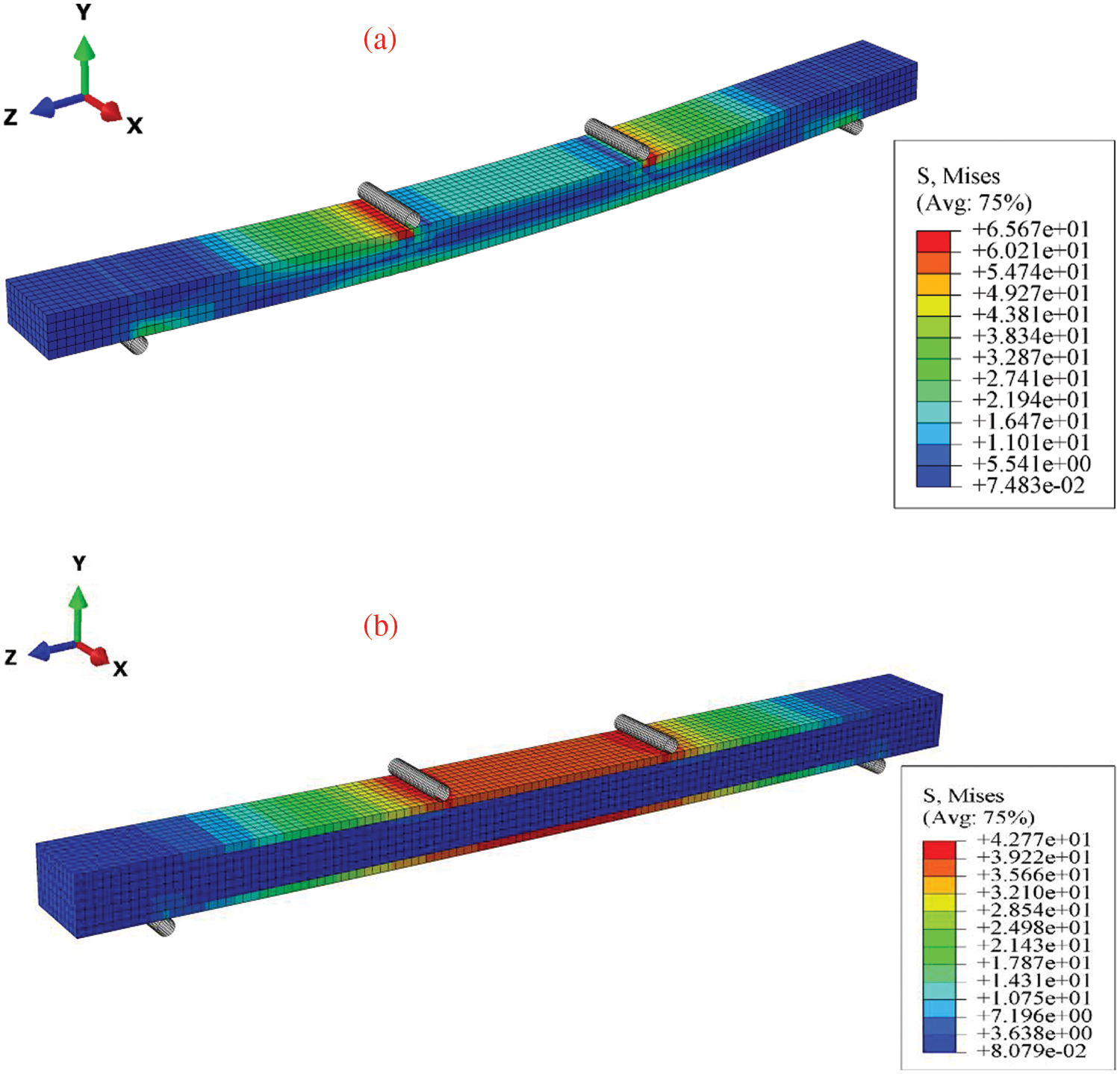
Figure 5: (a) P stress cloud diagram of P static bending failure strength of 35% (74 N); (b) GFRP Stress cloud diagram of P static bending failure strength of 35% (144 N)

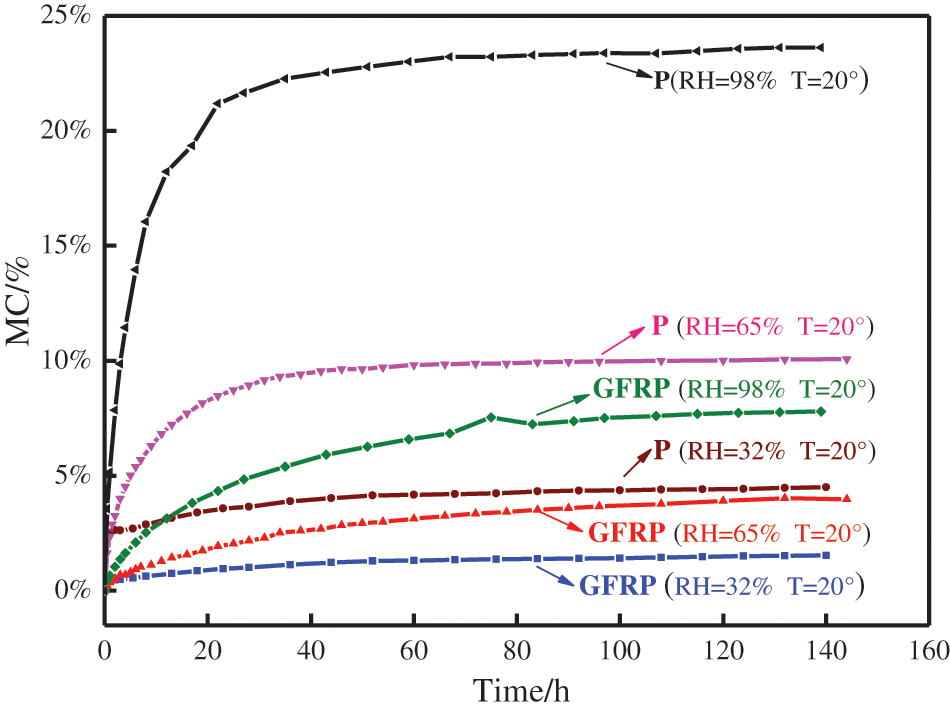
Figure 6: Moisture content of GFRP and P at different relative humidity

3.4 Parameter Fitting and Analysis of GFRP Common Creep Model

The next stage of this project was selecting an appropriate creep model that could obtain the creep function of wood with the creep influence factor as the independent variable. The most important thing is to predict the long-term creep behavior of wood and provide a scientific evaluation of its long-term service performance. The Burgers 4-factor model (Eq. (1)) is a model based on the rheological theory of wood materials that can predict the NC of wood materials, but the Burgers 4-factor model will not converge in the calculation of creep recovery, while the Weibull distribution equation (Eq. (2)) reliably predicting NC recovery of wood. The Weibull distribution equation was originally used to simulate the creep behavior of composite solid materials [32], but many previous studies have shown that the Weibull distribution equation can also accurately reflect the creep recovery behavior of polymer materials [33–35].

ε(t)=β1+β2[1−exp⁡(−β3t)]+β4t (1)

In Eq. (1), ε(t) is the creep deflection, mm; t is the time, s; β1 is the instantaneous elastic strain, mm; β2 is the delayed elastic strain, mm; β3 is the shape parameter determined by the characteristic life, mm; β4 is the non-recoverable creep components, mm.

εr(t)=ε2+ε3[exp⁡(−(tη2)k)] (2)

In Eq. (2), εr is the creep recovery deflection (mm); ε2 is the permanent deformation due to the viscous effect (mm); ε3 is the delayed elastic strain (mm); k is the shape parameter that changes with the recovery time; η2 is the characteristic life; and t is the load removal time (s).

It can be observed from Figs. 7 and 8 that the Burgers 4-factor model and the Weibull distribution equation can better fit the NC curve of GFRP, where the correlation coefficient R2 of the former is above 0.82, and the correlation coefficient R2 of the latter is both 0.98 The fitting curves of the two models are in good agreement with the experimental curves.

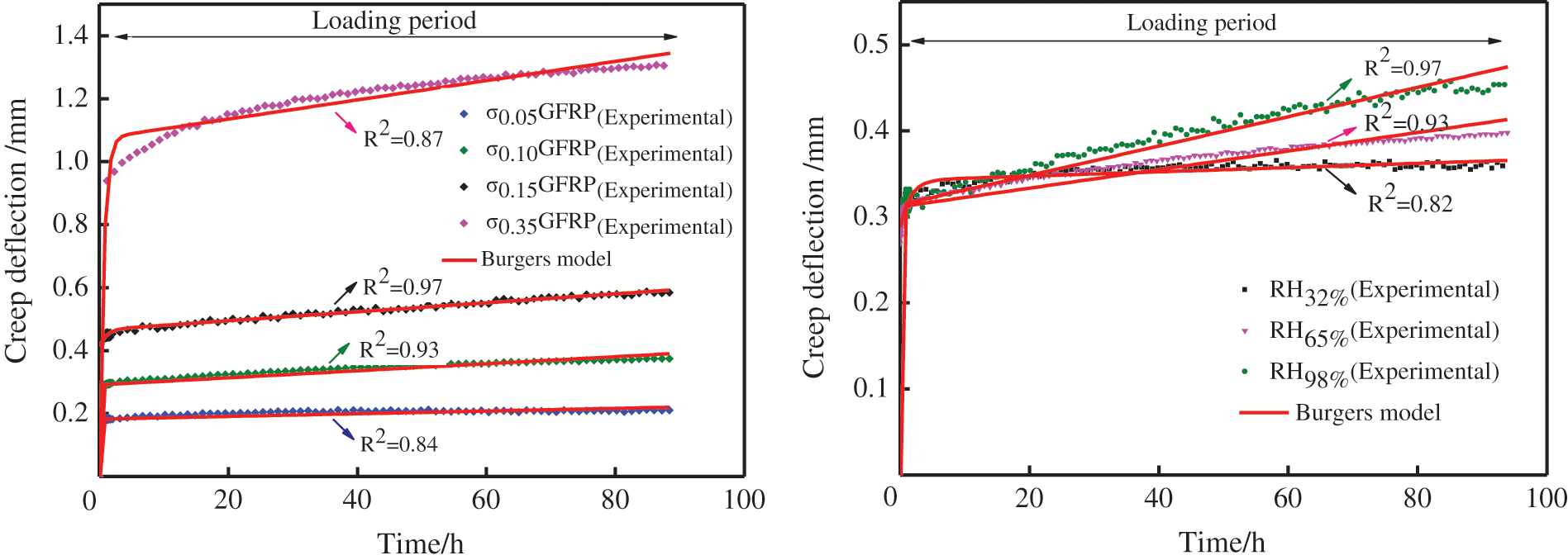
Figure 7: Fitting curve of GFRP during NC applied pressure period

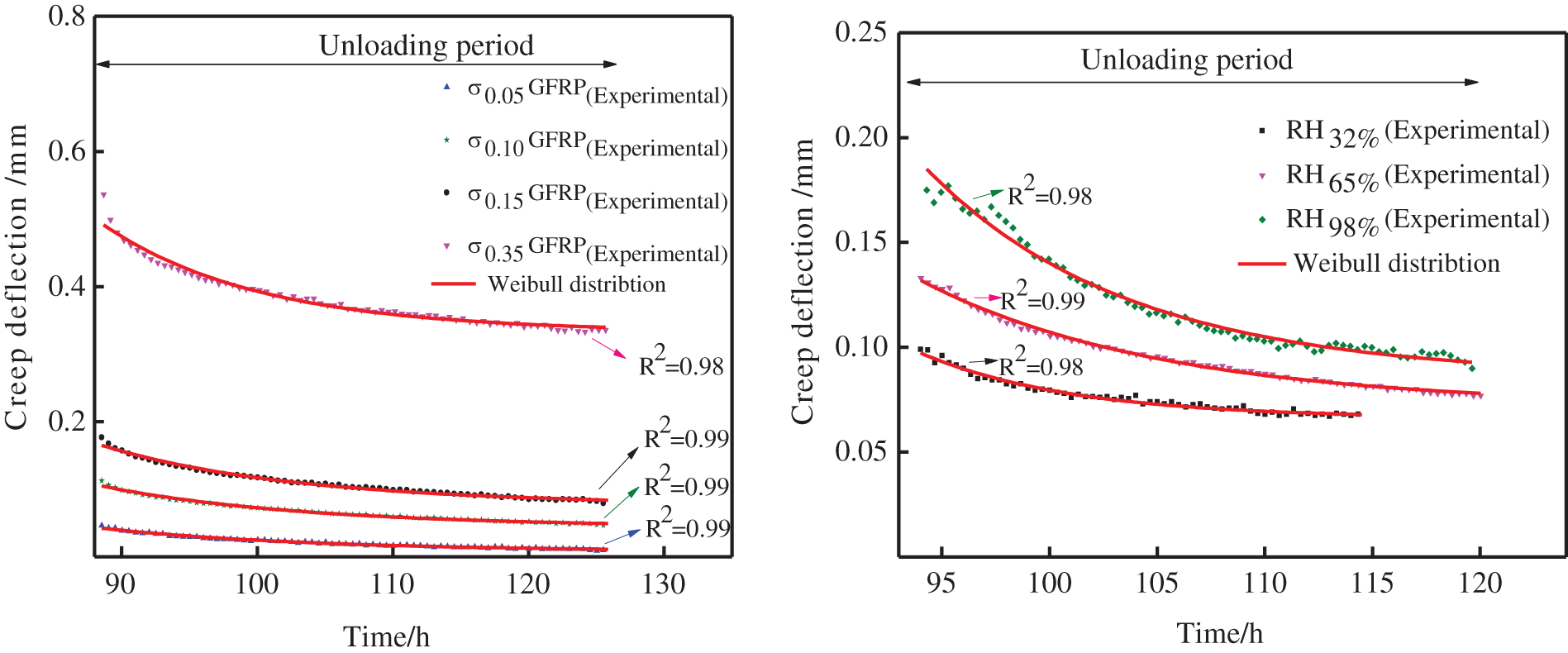
Figure 8: Fitting curve of NC unloading pressure period of GFRP

4  Conclusion

The poplar reinforced by the glass fiber surface, no matter if the ambient humidity is constant or alternately changed, only shows the NC law of wood, and loses the MSC characteristics of wood at the same time. On the one hand, the instantaneous elastic deformation, viscoelastic deformation, viscous deformation, and total creep deflection of GFRP have positively correlated with the external load stress level of the specimen but the creep recovery rate is related to the external load stress level of the specimen. On the other hand, the static bending creep deflection and viscous deformation of GFRP increase with the increase of the relative humidity of the environment. In addition, Burgers’ 4-factor model and Weibull distribution equation can reliably fit the NC and NC creep recovery process of GFRP. In addition, the maximum creep deflection of MSC of GFRP is only 7.41% higher than that of NC, but the maximum creep deflection of MSC of P is 199.25% higher than that of NC. It is worth noting that the relative humidity in the natural atmospheric environment, the change rule is similar to the cyclic change of relative humidity in mechanical sorptive creep, therefore, we should be alert to damage caused by mechanical sorptive creep.

Funding Statement: The present work was financially sponsored by the National Natural Science Foundation of China (Grant No. 31960291).

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. Zhang, L., Song, F. F. (2020). Research progress on high value utilization of fast-growing wood in plantation. China Forest Products Industry, 57(5), 53–55. [Google Scholar]

2. Prashanth, S., Subbaya, K. M., Nithin, K., Sachhidananda, S. (2017). Fiber reinforced composites–A review. Journal of Material Science & Engineering, 6(3), 2–6. [Google Scholar]

3. Kilinçarslan, Ş., Türker, Y. Ş. (2020). Investigation of wooden beam behaviors reinforced with fiber reinforced polymers. Organic Polymer Material Research, 2(1), 1–7. https://doi.org/10.30564/opmr.v2i1.1783 [Google Scholar] [CrossRef]

4. Balla, V. K., Kate, K. H., Satyavolu, J., Singh, P., Tadimeti, J. G. D. (2019). Additive manufacturing of natural fiber reinforced polymer composites: Processing and prospects. Composites Part B: Engineering, 174, 1–29. https://doi.org/10.1016/j.compositesb.2019.106956 [Google Scholar] [CrossRef]

5. Chaiyasarn, K., Ali, N., Phuphasuwan, P., Poovarodom, N., Joyklad, P. et al. (2021). Flexural behavior of natural hybrid frp-strengthened RC beams and strain measurements using BOTDA. Polymers, 13(20), 3604. https://doi.org/10.3390/polym13203604 [Google Scholar] [PubMed] [CrossRef]

6. Corradi, M., Vemury, C. M., Edmondson, V., Poologanathan, K., Nagaratnam, B. (2021). Local FRP reinforcement of existing timber beams. Composite Structures, 258, 113363. https://doi.org/10.1016/j.compstruct.2020.113363 [Google Scholar] [CrossRef]

7. Novosel, A., Sedlar, T., Čizmar, D., Turkulin, H., Živković, V. (2023). Improvement of mechanical properties of oak-wood by bi-directional laminations–Efficacy of standard and pre-stressed glass fibre implants. Composite Structures, 304, 116465. https://doi.org/10.1016/j.compstruct.2022.116465 [Google Scholar] [CrossRef]

8. Novosel, A., Sedlar, T., Miklečić, J., Turkulin, H., Lučić, L. et al. (2022). Analysis of bonding mechanisms of various implants and adhesives in laminated Oak-wood elements. Polymers, 14(24), 53–73. https://doi.org/10.3390/polym14245373 [Google Scholar] [PubMed] [CrossRef]

9. Shekarchi, M., Oskouei, A. V., Raftery, G. M. (2020). Bending behavior of timber beams strengthened with pultruded glass fiber reinforced polymer profiles. Composite Structures, 241, 112062. https://doi.org/10.1016/j.compstruct.2020.112062 [Google Scholar] [CrossRef]

10. Gao, Y., Guo, L., Zhang, X., Wang, Y., Yang, X. et al. (2022). Mechanical properties of fast-growing poplar reinforced with carbon fiber. Advances in Civil Engineering, 2022. https://doi.org/10.1155/2022/7051194 [Google Scholar] [CrossRef]

11. Brunetti, M., Christovasilis, I. P., Micheloni, M., Nocetti, M., Pizzo, B. (2019). Production feasibility and performance of carbon fibre reinforced glulam beams manufactured with polyurethane adhesive. Composites Part B: Engineering, 156, 212–219. https://doi.org/10.1016/j.compositesb.2018.08.075 [Google Scholar] [CrossRef]

12. He, M., Wang, Y., Li, Z., Zhou, L., Tong, Y. et al. (2022). An experimental and analytical study on the bending performance of CFRP-reinforced glulam beams. Frontiers in Materials, 8, 607. https://doi.org/10.3389/fmats.2021.802249 [Google Scholar] [CrossRef]

13. Zhang, S., Dong, C. L., Dou, L., Rong, C. L., Zhang, B. G. (2020). The effect of furfuryl alcohol and glass fiber treatment on the flexural creep of wood. Journal of Building Materials, 23(1), 162–167. [Google Scholar]

14. Triantafillou, T. C. (1997). Shear reinforcement of wood using FRP materials. Journal of Materials in Civil Engineering, 9(2), 65–69. https://doi.org/10.1061/(ASCE)0899-1561(1997)9:2(65) [Google Scholar] [CrossRef]

15. Soltis, L. A., Ross, R. J., Windorski, D. F. (1998). Fiberglass-reinforced bolted wood connections. Forest Products Journal, 48(9), 63. [Google Scholar]

16. Fucheng, B., Shuanghao, Z., Li, Z. (2004). Study on the improvement of properties of wood-fiberglass panel. Scientia Silvae Sinicae, 40, 117–122. [Google Scholar]

17. Zhang, J., Wang, H., Ou, R., Wang, Q. (2018). The properties of flax fiber reinforced wood flour/high density polyethylene composites. Journal of Forestry Research, 29(2), 533–540. https://doi.org/10.1007/s11676-017-0461-0 [Google Scholar] [CrossRef]

18. Zhang, S., Zhao, L., Bao, F., Zhou, H. (2001). Study on triploid populus tomentosa wood (shavings) composite materials reinforced by glass fiber and flax chips. Forestry Industry, 28(4), 9–12 + 16. [Google Scholar]

19. Armstrong, L. D., Kingston, R. S. T. (1960). Effect of moisture changes on creep in wood. Nature, 185, 862–863. https://doi.org/10.1038/185862c0 [Google Scholar] [CrossRef]

20. Armstrong, L. D., Christensen, G. N. (1961). Influence of moisture changes on deformation of wood under stress. Nature, 191(4791), 869–870. https://doi.org/10.1038/191869a0 [Google Scholar] [CrossRef]

21. Huang, Y. (2016). Creep behavior of wood under cyclic moisture changes: Interaction between load effect and moisture effect. Journal of Wood Science, 62, 392–399. https://doi.org/10.1007/s10086-016-1565-4 [Google Scholar] [CrossRef]

22. Curtu, I., Stanciu, M. D. (2015). Rheology in wood engineering. Procedia Technology, 19, 77–84. https://doi.org/10.1016/j.protcy.2015.02.012 [Google Scholar] [CrossRef]

23. GB/T1927.2 (2021). Test method for physical and mechanical properties of small clear specimens-Part 2: Sampling methods and general requirement. Beijing: Standards Press of China. [Google Scholar]

24. GB/T1927.9 (2021). Test method for physical and mechanical properties of small clear specimens-Part 9: Determination of bending strength. Beijing: Standards Press of China. [Google Scholar]

25. GB/T1927.10 (2021). Test method for physical and mechanical properties of small clear specimens-Part 10: Determination of modulus of elasticity in bending. Beijing: Standards Press of China. [Google Scholar]

26. ASTM-D6815. (2015). Standard specification for evaluation of duration of load andcreep effects of wood and wood-based products. ASTM International, West Conshohocken, PA. [Google Scholar]

27. GB/T 31291 (2014). Standard for evaluation of duration of load and creep effects of wood and wood-based products. Beijing: Standards Press of China. [Google Scholar]

28. LY/T 1975 (2011). Standard for evaluation of duration of load and creep effects of wood and wood-based products. Beijing: Standards Press of China. [Google Scholar]

29. Dong, C., Bao, K., Huang, Y., Zhang, H. (2021). Research and development of a set of test systems for wood static bending and creeping. Journal of Forestry Engineering, 6(1), 147–154. [Google Scholar]

30. Zhou, Y. (2020). Experimental research on fatigue performance of CFRP reinforced glulam beams (Master’s Thesis). Central South University of Forestry and Technology, China. https://kns.cnki.net/KCMS/detail/detail.aspx?dbname=CMFD202201&filename=1021128483.nh [Google Scholar]

31. Pan, Y., An, R., Zhang, C., Wang, Y. (2019). Experimental study on the flexural behavior of circular cross-section wooden beams strengthened with BFRP cloth. Journal of Building Structures, 40(10), 197–206. [Google Scholar]

32. Huč, S., Svensson, S. (2018). Coupled two-dimensional modeling of viscoelastic creep of wood. Wood Science and Technology, 52, 29–43. https://doi.org/10.1007/s00226-017-0944-3 [Google Scholar] [CrossRef]

33. Fancey, K. S. (2005). A mechanical model for creep, recovery and stress relaxation in polymeric materials. Journal of Materials Science, 40(18), 27–31. https://doi.org/10.1007/s10853-005-2020-x [Google Scholar] [CrossRef]

34. Ma, X., Shi, S. Q., Wang, G., Fei, B., Jiang, Z. (2018). Long creep-recovery behavior of bamboo-based products. Journal of Wood Science, 64, 119–125. https://doi.org/10.1007/s10086-017-1683-7 [Google Scholar] [CrossRef]

35. Dong, C., Zhang, S., Wang, J., Chui, Y. H. (2021). Static bending creep properties of furfurylated poplar wood. Construction and Building Materials, 269, 121308. https://doi.org/10.1016/j.conbuildmat.2020.121308 [Google Scholar] [CrossRef]