 Open Access
Open Access
ARTICLE
Compressive Performance of Fiber Reinforced Recycled Aggregate Concrete by Basalt Fiber Reinforced Polymer-Polyvinyl Chloride Composite Jackets
1 Civil Engineering & Architecture College, Liaoning University of Technology, Jinzhou, 121001, China
2 School of Civil Engineering & Architecture, Ningbo Tech University, Ningbo, 315100, China
* Corresponding Author: Genjin Liu. Email:
(This article belongs to the Special Issue: Natural Fibre Composites: Design, Materials Selection and Fabrication)
Journal of Renewable Materials 2023, 11(4), 1763-1791. https://doi.org/10.32604/jrm.2023.024319
Received 31 May 2022; Accepted 09 August 2022; Issue published 01 December 2022
Abstract
The development of recycled aggregate concrete (RAC) provides a new approach to limiting the waste of natural resources. In the present study, the mechanical properties and deformability of RACs were improved by adding basalt fibers (BFs) and using external restraints, such as a fiber-reinforced polymer (FRP) jacket or a PVC pipe. Samples were tested under axial compression. The results showed that RAC (50% replacement of aggregate) containing 0.2% BFs had the best mechanical properties. Using either BFs or PVC reinforcement had a slight effect on the loadbearing capacity and mode of failure. With different levels of BFs, the compressive strengths of the specimens reinforced with 1-layer and 3-layer basalt fiber reinforced polymer (BFRP) increased by 6.7%–10.5% and 16.5%–23.7%, respectively, and the ultimate strains increased by 48.5%–80.7% and 97.1%–141.1%, respectively. The peak stress of the 3-layer BFRP-PVC increased by 42.2%, and the ultimate strain improved by 131.3%, relative to the control. This reinforcement combined the high tensile strength of BFRP, which improved the post-peak behavior, and PVC, which enhanced the structural durability. In addition, to investigate the influence of the various constraints on compressive behavior, the stress-strain response was analyzed. Based on the analysis of experimental results, a peak stress-strain model and an amended ultimate stress-strain model were proposed. The models were verified as well; the result showed that the predictions from calculations are generally consistent with the experimental data (error within 10%). The results of this study provide a theoretical basis and reference for future applications of fiber-reinforced recycled concrete.Graphic Abstract
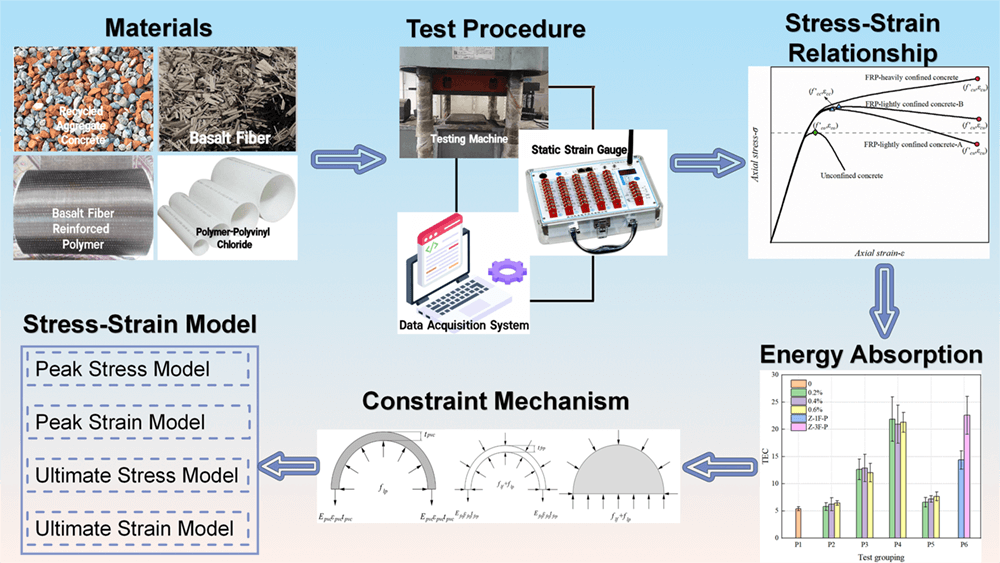
Keywords
Nomenclature
| | Lateral confining pressure of actively confined concrete (MPa) |
| | Lateral confining pressure of PVC confined concrete (MPa) |
| | Lateral confining pressure of BFRP confined concrete (MPa) |
| | Elastic modulus of PVC (MPa) |
| | Mono-axial tensile strain of PVC |
| | Thickness of PVC material (mm) |
| | Elastic modulus of FRP (GPa) |
| | Mono-axial tensile strain of FRP |
| | Total thickness of FRP material (mm) |
| d | Diameter of the concrete specimen (mm) |
| | Lateral confining pressure at ultimate (MPa) |
| | Circumferential tensile strength of FRP material (MPa) |
| | Circumferential tensile strength of PVC material (MPa) |
| | Eigenvalues related to the elastic modulus of concrete |
| | Eigenvalues related to peak stress |
| | Elastic modulus of recycled aggregate concrete (MPa) |
| | Lateral confining stiffness at peak (MPa) |
| | Ultimate stress of the confining specimen (MPa) |
| | Peak stress of the confining specimen (MPa) |
| | Axial compressive strength of unconfined specimen (MPa) |
| | Increase factor of laterally confined stiffness ratio |
| | Stiffness reduction factor |
| | Ultimate strain of the confining specimen |
| | Peak strain of the confining specimen |
| | Peak strain of the unconfined specimen |
| | Increase factor of lateral confined strength |
| N | Sample size |
| | Calculated value (predicted) |
| | Test value, mean test value |
| | Constant |
Construction and demolition (C&D) waste pollution and shortage of coarse aggregate have become increasingly serious problems nowadays [1,2]. In this case, the emergence of recycled aggregate concrete (RAC) helps reduce the pollution of C&D waste and contributes to the sustainable development of the construction industry [3–6].
However, studies have shown that RAC has deficiencies such as a high crushing index, low aggregate hardness, and large porosity, which restrict its engineering application [7–9]. Therefore, it is essential to improve the functional performance of RAC. Literature has also proved that the mechanical behavior of recycled concrete can be improved by incorporating short chopped fibers [10–12].
Xiao et al. [13] found that adding 1% fibers in the mortar with 100% recycled aggregate can change the specimen failure from brittle to ductile, which was attributed to the fibers enhancing the interfacial bond between fibers and matrix. Based on the fiber reinforcement theory, Zhang et al. [14] proposed the combined effect of basalt fiber (BF) with RCA and focused on the fiber effect on the mechanical property of concrete before and after cracking. Tests showed that BF significantly improved the interfacial transition zone of recycled concrete and effectively restricted the crack development when the RCA replacement rate was 50%. Ortega-López et al. [15] utilized synthetic fibers as reinforcing materials in concrete. It was found that the presence of fibers inhibited the specimen’s lateral expansion deformation and improved lateral deformation capacity compared to conventional concretes; thus, it significantly improved the post-cracking behavior of concrete.
One way to increase the utilization of recycled concrete is to produce fiber-reinforced recycled concrete structural members like columns and beams. In addition, the strength and ductility of RAC can be improved by additional fiber-reinforced polymers (FRP) sheets [16–20]. Basalt fiber (BF) is a green, inorganic, high-performance fiber material with excellent tensile strength material. Basalt fiber-reinforced polymer (BFRP) is widely used because of its lightweight and high strength [21,22]. However, BFRP showed poor acid resistance and was easily broken in an unfriendly environment. In order to protect the BFRP sheet reinforced recycled concrete cylinder, polyvinyl chloride (PVC) tube was introduced to serve as a safe jacket to protect the core concrete [23–26]. For instance, Gupta [24] applied PVC pipe as a safety jacket for concrete, improving its strength and ductility. However, whether the PVC tube benefits the mechanical behavior of the BFRP-confined cylinder was unclear.
In this work, a new BFRP-PVC confined recycled concrete cylinder was proposed. This reinforcement combined the high tensile strength of BFRP, which improved the post-peak behavior, and the outer PVC, which enhanced the structural durability and protected the internal materials. The compressive behavior of the cylinder under uniaxial compressive tests was studied. As is well known, the stress-strain relationship of the structural member was essential for compressive behavior [27–30]. For instance, Chang et al. [31] investigated the effect of the recycled aggregate (RA) replacement ratio on the stress-strain behavior of different concrete strengths. The test results showed that the incorporation of RA had a more significant effect on low-strength concrete, which agreed with prior test results [32–34]. Revilla-Cuesta et al. [35,36] researched the compressive deformation behavior of concrete with various RA. The test showed that using RA resulted in lower peak and fracture strains.
Furthermore, the external reinforced materials strongly influence the structural properties [37–39]. Although some models have been proposed to predict the monotonic compressive response of FRP-confined concrete, there are few models for BFRP-PVC confined fiber recycled concrete [40,41]. Meanwhile, to obtain an accurate idea of the responses between the concrete and restraining materials, studying the mechanical properties of BFRP and PVC is worthwhile [42]. Given pertinent classical models, the experimental data and the composite structure’s force characteristics were considered as well. It is a worthwhile endeavor to establish an accurate model for FRCs in conjunction with BFRP-PVC.
This study investigated the compressive behavior of the basalt fiber reinforced recycled concrete confined by BFRP-PVC composite jackets. The variables include the shortcut BF content, the number of BFRP layers, and external constraint types. The peak stress-strain model and the amended ultimate stress-strain model are proposed based on the experimental results.
To investigate the axial compression performance of BFRP-PVC composite reinforced fiber-recycled concrete, 45 recycled concrete cylinders with different BF volume fractions (Vf) were designed in this experiment.
Among them, there were 12 fiber-recycled concrete cylinders without lateral restraint. A total of 27 fiber-recycled concrete cylinders were restrained by BFRP (1 layer, 3 layers) overall wrapping or PVC pipe, and 6 specimens were reinforced by both BFRP (1 layer, 3 layers) and PVC pipe overall wrapping. The specific parameters of the specimen classification design are shown in Table 1.

This test used ordinary Portland cement (PO.42.5) and natural water. Fine aggregate is natural river sand, and the fineness modulus is 2.7, belonging to zone II gradation. Natural coarse aggregate (NCA) is granite crushed stone. The recycled coarse aggregate (RCA) replacement rate is 50%, and the aggregate particle size is 5-20 mm, which is crushed and screened from waste concrete. The basic properties of RAC are shown in Table 2. The density of primary fly ash is 2.55 g/cm3, water content is 0.85%, and the burn loss rate is 4.7%. Using PC Polycarboxylic acid superplasticizer with a water reduction rate of 30%. The characteristics of fibers are shown in Table 3. The PVC type is D160×4, nominal outer diameter 160 mm, wall thickness 4 mm, density 1350–1550 kg/m3. The impregnating adhesive is based on converted EP-type epoxy resin, and the aliphatic amine is the curing agent. The tensile strength of the adhesive is 60 MPa, the tensile modulus of elasticity is 3.2 GPa, elongation is 2.5%, flexural strength is 75 MPa, and compressive strength is 83.6 MPa. The manufacturer provides all the above data. According to the concrete ratio design standard JGJ55-2011 [43], the design ratio is shown in Table 4.


The height of the concrete cylinder was 300 mm, and the outer diameter was 150 mm. Before the mixing process, considering the high-water absorption of recycled aggregates, the recycled aggregates were prepared in saturated surface dry condition (SSD) [44–46]. Cut the BFRP sheet to the required size according to the wrapped layers and the height of the specimen. Polish the surface of the cylinder to keep it smooth and wipe it with acetone solution. The end was flattened with primers to ensure good contact between the cylinder and BFRP. The surface of the specimen and the BFRP are evenly brushed with bonding adhesive with a dosage of 0.6–0.75 kg/m3 [47].
In this paper, the tests were performed at different time intervals. The axial compression test selected 0.2% BF as the optimal dosage. The preparation process of the unidirectional tensile test of BFRP materials refers to the Chinese guideline GB/T 3354-2014 [48]. Two layers of impregnating adhesive are applied to each side of the BFRP sheet to ensure complete saturation of epoxy resin between the BFRP and aluminum flat bar.
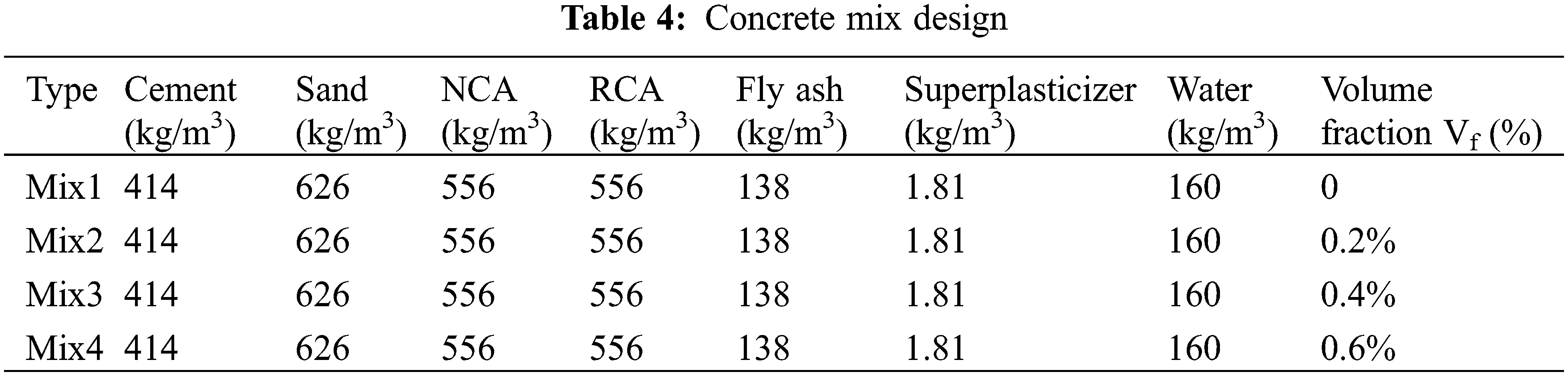
The BFRP tensile performance test was prepared in two groups, and 5 samples were in each group. The total thickness (

Figure 1: (a) BFRP stripe; (b) Schematic diagram of the unidirectional tensile test of BFRP material
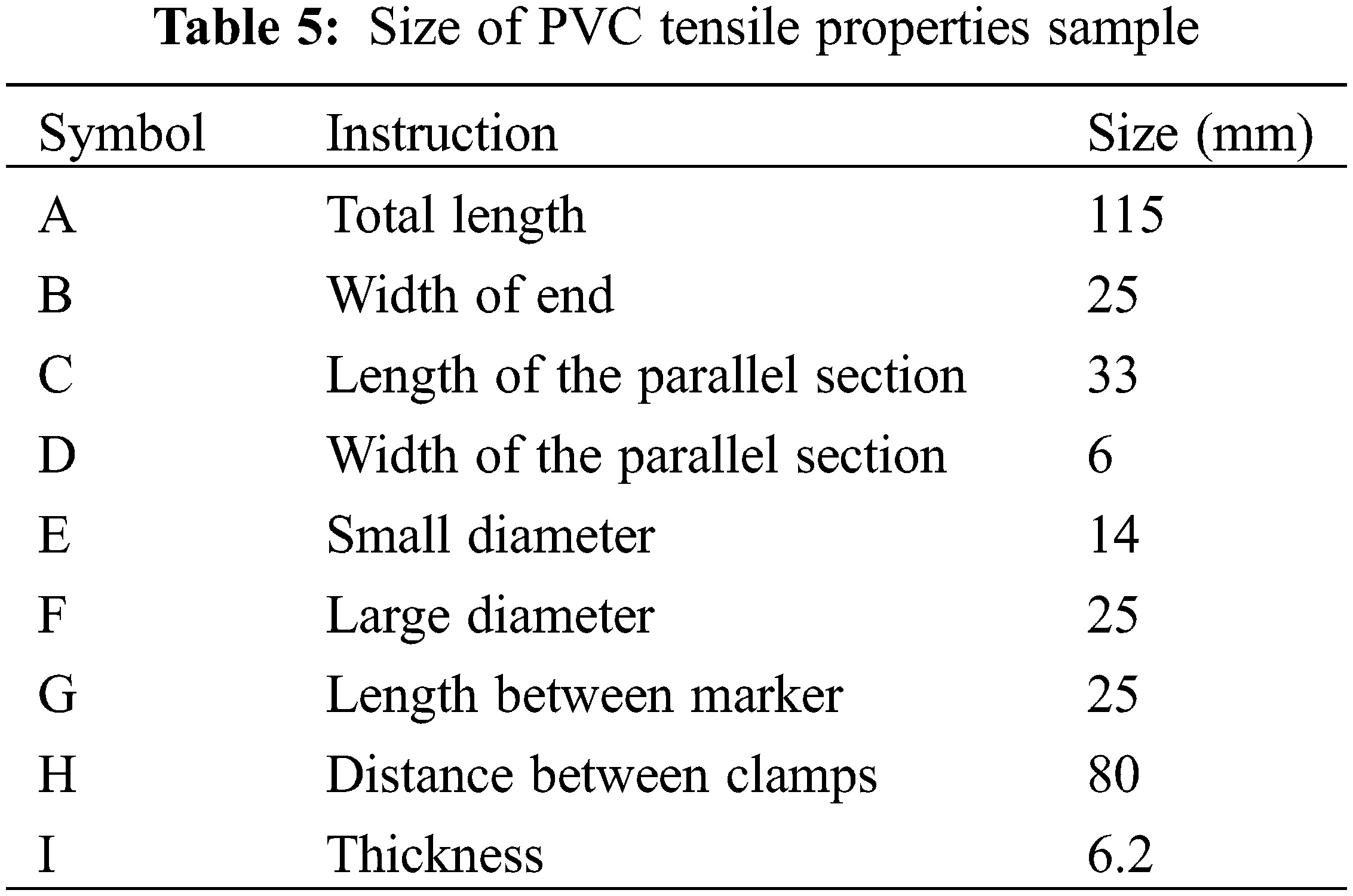
The test of PVC material properties was operated according to “Determination of Tensile Properties of Thermoplastic Pipes” (GB/T 8804.2-2003) [49], and the PVC sample used in this test is shown in Fig. 2a. Dumbbell-type samples were taken from the PVC pipe to investigate its tensile properties. The specific dimensions of the test pieces are shown in Fig. 2b and Table 5.
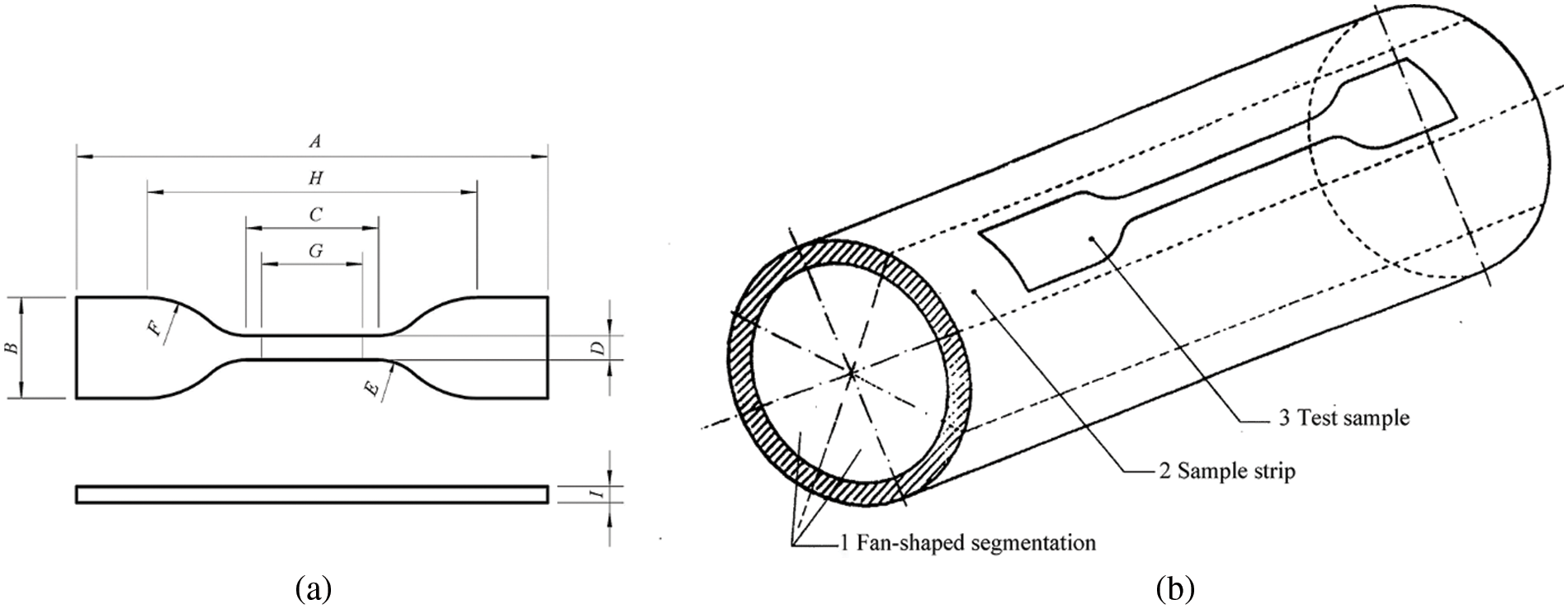
Figure 2: (a) PVC sample; (b) Schematic diagram of the unidirectional tensile test of PVC sample
2.4 Instrumentation and Testing Procedure
In order to investigate the monotonic behavior of the specimens, a 5000 kN hydraulic compressive testing machine was employed for testing the specimens according to GB 50152-2012 [50]. In addition, all the cylindrical samples were axially loaded with the loading device as in Fig. 3. The specimens were loaded using a graded loading system with 100 kN per stage and a loading speed of 1 kN/s. When the load achieved about 80% of the ultimate load, the rate was slowly changed to 0.5 kN/s until the specimen failed. The longitudinal displacement was measured by the linear variable differential transformer (LVDT) arranged symmetrically on both sides. In addition, the longitudinal and circumferential deformations of the specimens are measured by the longitudinal and circumferential strain gauges. The positions of each layer of strain gauges should be staggered to ensure the maximum accuracy of the test, as shown in Fig. 4.

Figure 3: Loading device: (a) Load schematic; (b) Test machine
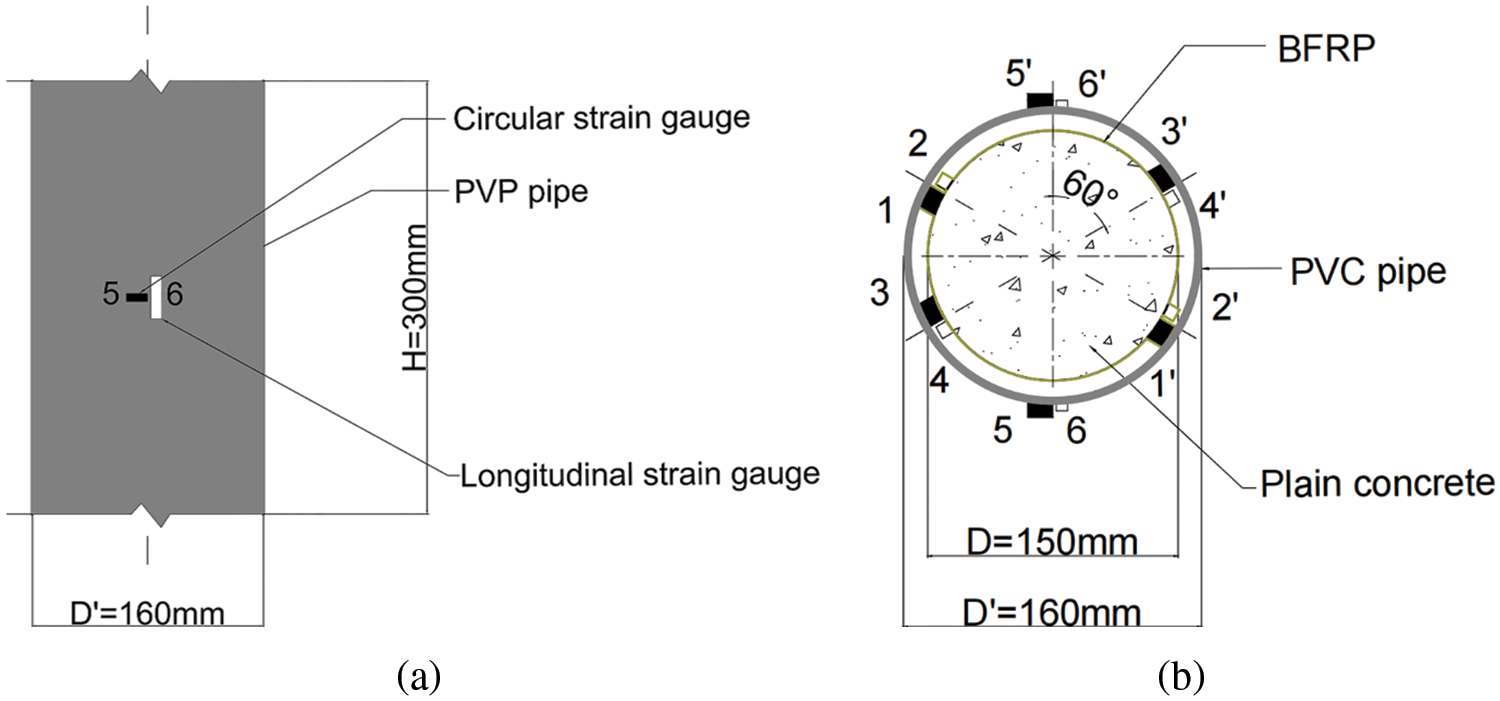
Figure 4: Instrumentation details: (a) Elevation of P6; (b) Planform of P6
The unidirectional stretching device was a WDW-100 electronic universal testing machine manufactured by MTS Industrial Systems Co., Ltd., China as shown in Fig. 5. The loading rates of BFRP samples and PVC material were 2 mm/min and 5 mm/min, respectively. The results of the unidirectional tensile performance of the materials were: the average tensile strength of the 1-layer and 3-layer sheets were 2033.6 and 1891.0 MPa, respectively. The modulus of elasticity was 82.4 and 99.0 GPa, respectively, and the elongation at break was 2.47% and 2.01%, respectively. The average tensile strength of the PVC was 28.2 MPa, and the modulus of elasticity was 282.6 MPa. There is a certain discrepancy with the data provided by the manufacturer.

Figure 5: WDW-100 electronic universal testing machine
3 Experimental Results and Discussions
The specimens with basalt fiber (P2) showed no significant changes at the beginning of loading. Micro cracks appeared and developed continuously along the longitudinal direction with the further increasing load. After approaching the ultimate load, cracks developed rapidly and penetrated the entire specimen, eventually crushing with the phenomenon of concrete spalling. The failure process is a brittle failure. Similar results were reported by Xiao et al. [51] and Zhang et al. [14]. In addition, the failure mode of the plain concrete cylinder specimen (P1) is like that of P2.
The specimens wrapped with 1 layer of BFRP sheet (P3) had slight transverse deformation at the beginning of loading, and the BFRP sheet did not play a role. As the load increased, the circumferential deformation in the middle of the specimen increased and began to bulge significantly. The upper epoxy cracked and pulled apart, and the BFRP sheet whitened and made a continuous crackling sound. When increasing to ultimate load, the BFRP in the middle and top of the specimen was propped up and started to fall off. The sample wrapped with 3 layers of BFRP sheets (P4) was like P3 specimens in the initial loading stage. When close to the ultimate load, the 3 layers of BFRP suddenly collapsed. However, they showed a thin filamentary connection between each other, did not wholly separate, and still tended to protect the specimen inward. Such behavior belongs to ductile damage. The damage results show that the 3 layers of BFRP sheets inhibit the internal damage of the specimen. This phenomenon is the same as the test process of Jiang et al. [52] and Zeng et al. [53]. Moreover, Zhang et al. [54] also reported a similar result: multilayer BFRP materials can inhibit the internal damage of the specimens. In these cases, improving the BF percentage will enhance the stability of the specimen during failure progress.
For the P5 specimen, there was no noticeable change in the initial stage of loading. When the loading was close to its ultimate bearing capacity, the color of the PVC pipe changed locally. The pipe hoop at the end of the specimen was suddenly propped up and cracked as the pressure increased, then the concrete core was crushed, while it fell off and scattered with the crushed instant. The damage process has no prominent warning—the collapse of the PVC hoop and the damage to the specimen occurred almost simultaneously, which belongs to brittle damage. Similarly, the study of Saadoon et al. [55] confirmed that the PVC pipe’s low strength and high brittleness and the uneven lateral deformation produced by the core concrete resulted in a reduced adhesion between the PVC and the concrete cylinder, which ultimately could not provide sufficient lateral circumferential pressure.
The P6 specimen did not change significantly at the beginning of the loading. When the load reached 70%–80% of its ultimate bearing capacity, the PVC pipe protruded outward as the core area concrete and the BFRP sheets deformed circumferential expansion. After that, the vertical cracks increased with some local concrete crushed, and finally, the pipe hoop collapsed and ruptured. This damaging process has apparent predictability and belongs to ductile damage. Feng et al. [40] similarly presented the experimental phenomena and results: the PVC pipe provided external circumferential compressive stress, which transferred uniformly to the cylinder through the BFRP sheet. The combination not only keeps sufficient compressive strength of BFRP to resist the lateral expansion but also increases the elasticity; the PVC has superior corrosion resistance and plays a protective role for the internal materials in harsh environments. The damage morphology of each group is shown in Fig. 6.

Figure 6: Failure modes of specimens: (a) P1; (b) P2; (c) P3; (d) P4; (e) P5; (f) P6
3.2 Shape of the Stress-Strain Curve
Referring to the analysis of Lam et al. [56], the stress-strain response of the FRP reinforced concrete specimens depends on the strength utilization of the FRP. Additionally, the stress-strain response of FRP-confined concrete is a monotonically rising bilinear curve when the FRP wrapping exceeds a specific critical value, as shown in Fig. 7 for FRP-heavily confined concrete. Some scholars also proposed the bilinear curve behavior [57–60]. The peak point of such curves is the ultimate point, and the ultimate strain (
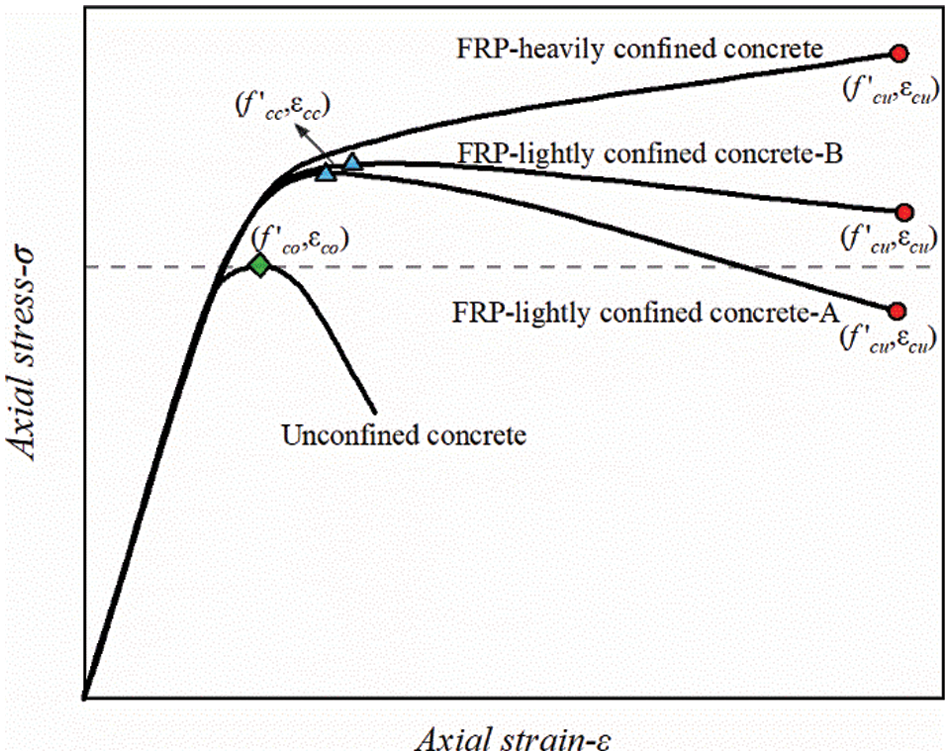
Figure 7: FRP-confined concrete behavior typical response
While most research results show the bilinear character of FRP confinement, some experiments also show that FRP-lightly confined curves emerge when the level of FRP confinement is insufficient to cause a post-peak strain hardening behavior, as shown in Fig. 7. In such cases, the specimen reaches the peak point (
3.3 Stress-Strain Relationships
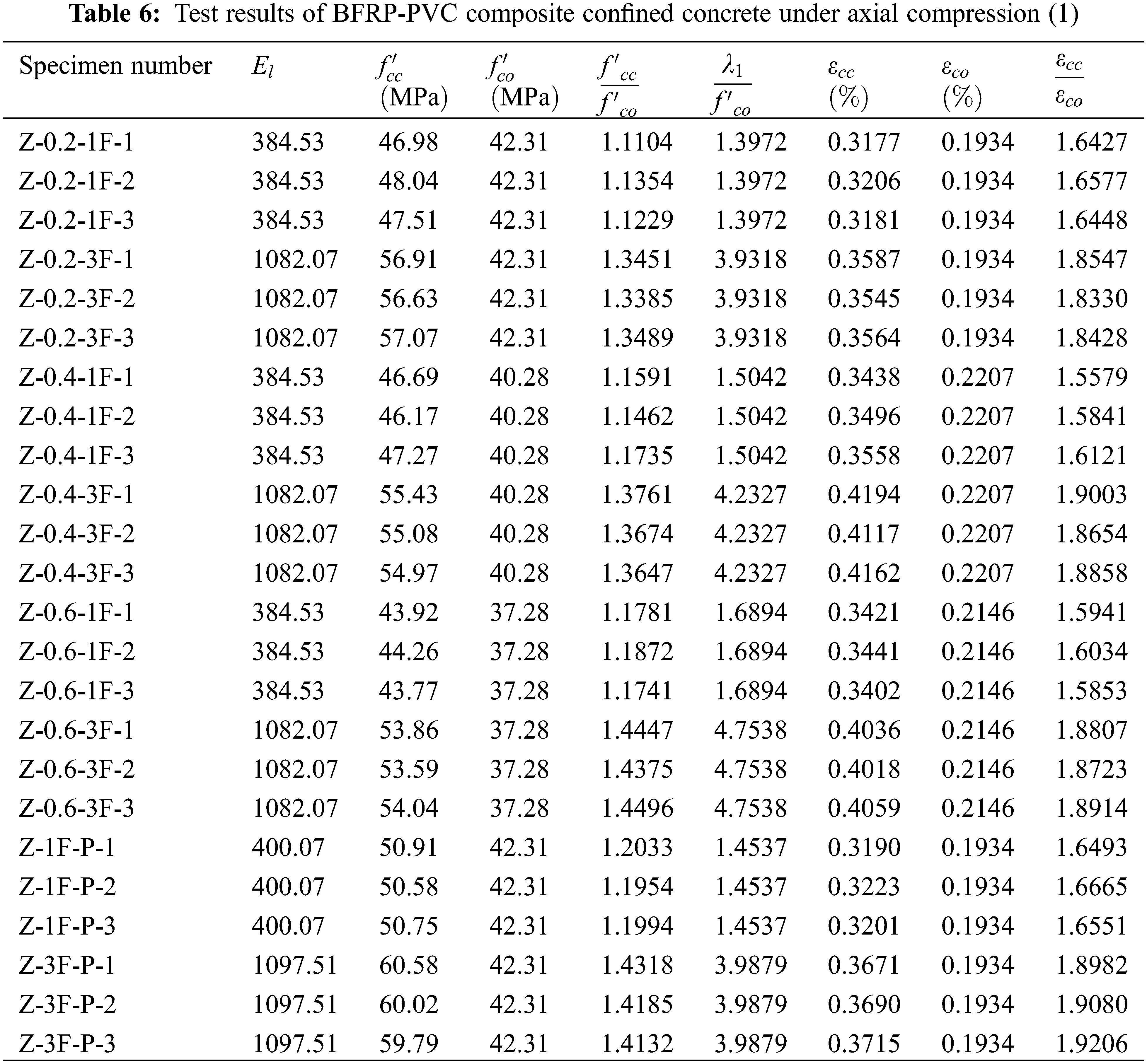
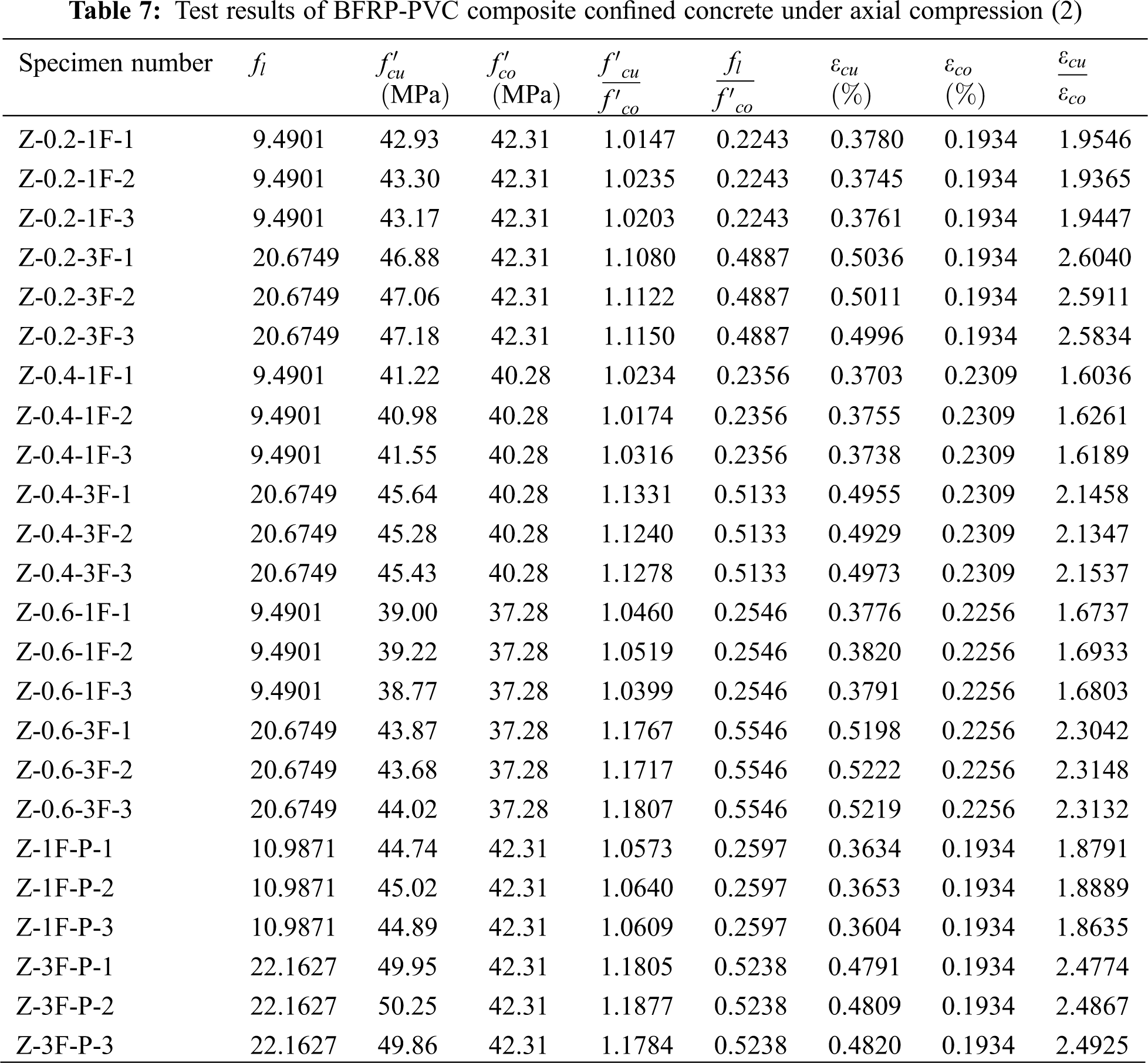
A compression test on BFRP-PVC restrained fiber-recycled concrete was conducted in this work. The axial stress-strain curves were obtained, as shown in Fig. 8.
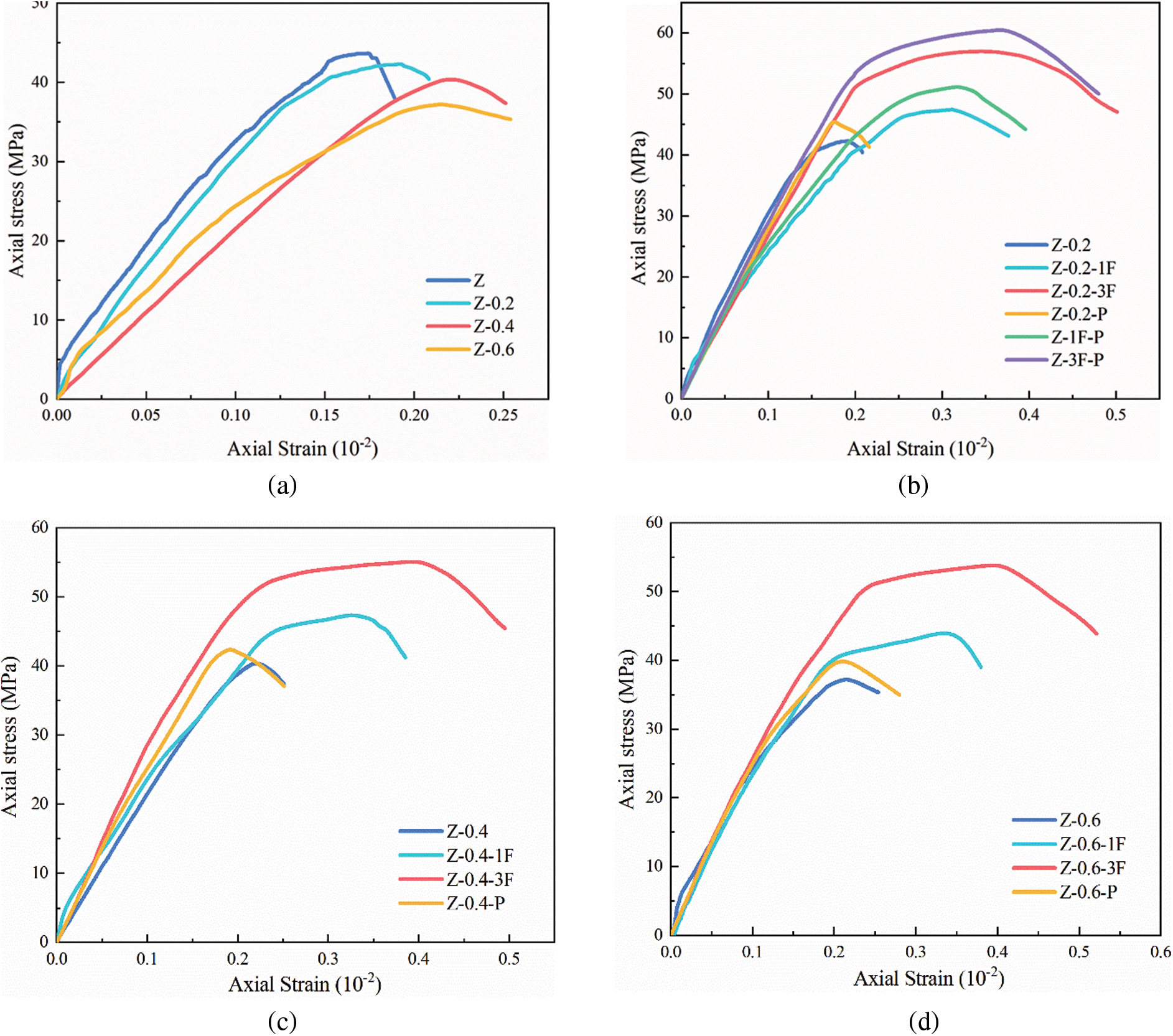
Figure 8: Stress-strain curves: (a) Stress-strain curve of unconfined concrete; (b) Stress-strain curve with 0.2% basalt fiber; (c) Stress-strain curve with 0.4% basalt fiber; (d) Stress-strain curve with 0.6% basalt fiber
At the initial loading stage, the various specimens are in the elastic stage, and the stress-strain curves are similar. When the load increases to the peak point, the compressive strain in the middle of most specimens reaches or exceeds 0.2%. With the development of lateral deformation of RAC, various types of cylinders showed different stress-strain curves.
After reaching the peak point (
Specimens P3, P4, and P5 with unconfined concrete strength of 42.31, 40.28, and 37.28 MPa, respectively, incorporating into 0.2%, 0.4%, and 0.6% volume fractions of BF, respectively. Compared with the unconfined specimens, the ultimate stresses in the one-layer BFRP sheet-confined specimens were not significantly higher; however, the curves of one-layer BFRP specimens in the transition period were smoother. For PVC-confined concrete, the curve dramatically drops after reaching the peak point
The P6 specimens have the most pronounced peak stress enhancement; among them, Z-1F-P has an insignificant increase in the compressive strength (
Further details of these specimens can be found in Tables 6 and 7.
3.4 Breaking Mechanism Analysis
The first stage is before the stresses reach the compressive strength of the unconfined FRC cylinder, the specimen is in the elastic stage, and the curve is linear. After reaching the compressive strength of unconfined recycled concrete (
3.5 Toughness Indexes and Energy Absorption
In this paper, five indexes are introduced to describe the energy absorption capacity of the specimens based on the literatures [67–69].
(1) Pre-crack energy (PEC)
PEC is the energy absorption capacity of the specimen before cracking. Mathematically, the PEC can be calculated by integrating the stress-strain curve, i.e., the area enclosed from the starting point to the yield stress point. The yield stress point is the stress at which first visual cracks observing during the axial compression test. The PEC values of each group of specimens are shown in Fig. 9a. Among them, the PEC of plain concrete is 3.782. Mono-doped BFs rarely contribute to pre-cracking energy absorption, as in the case of the P2 specimens. Khan et al. [65] proposed the same conclusion that the higher dosage of fibers decreases bond strength. The PEC of the P6 specimen is substantially enhanced and increases with the number of BFRP layers. The solid restraining sustainability of Z-3F-P nicely improved the PEC value. This result may be due to the strong deformation confining effect of multilayer BFRP and the confining pressure provided by the PVC, which transfers to the concrete surface through the fiber sheet, inhibiting the pre-cracking expansion behavior. Therefore, these specimens can absorb more energy and considerably improve the PEC value. There is a similar situation observed in P3 and P4 specimens.
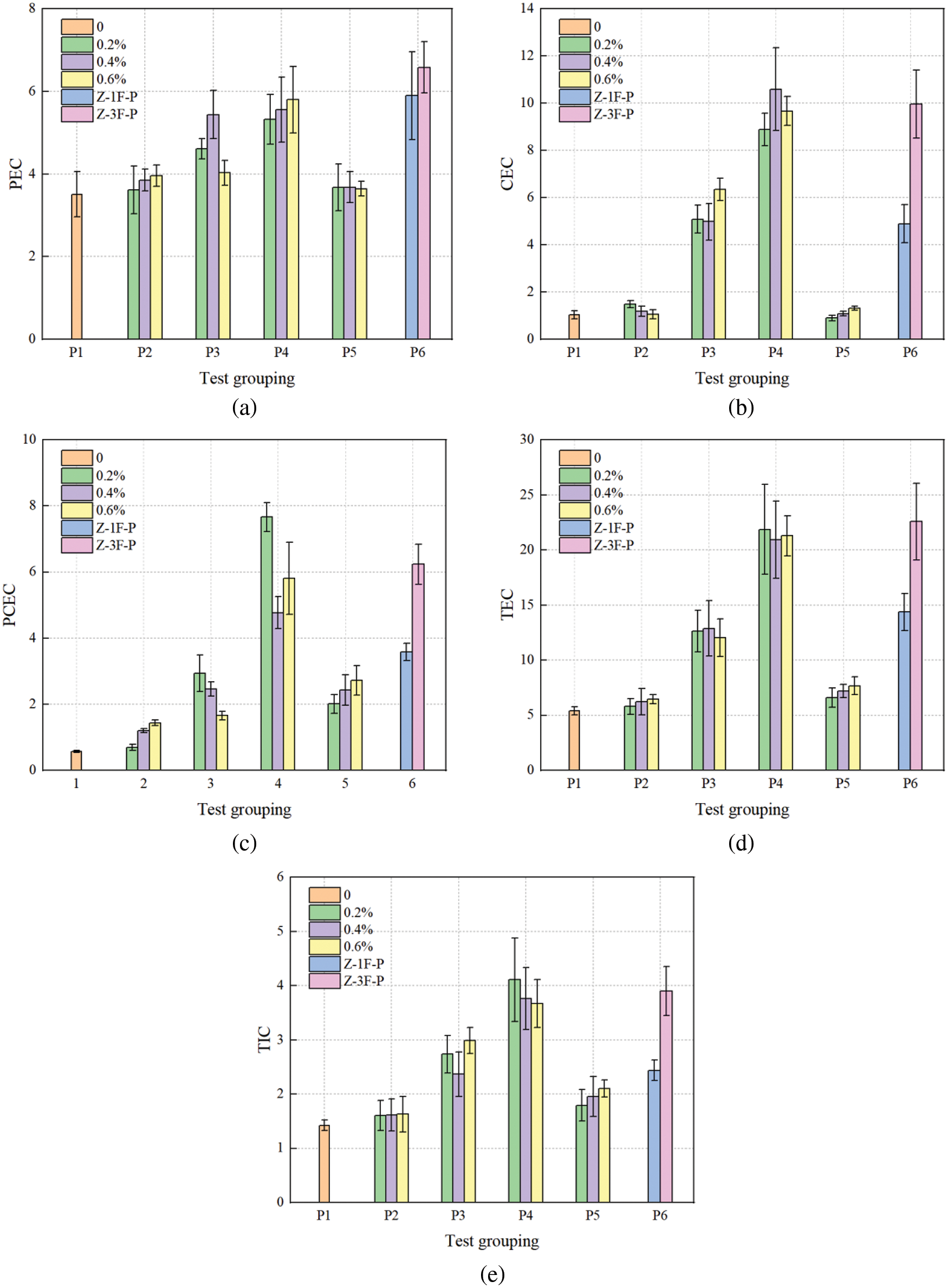
Figure 9: Energy absorption and toughness index: (a) PEC; (b) CEC; (c) PCEC; (d) TEC; (e) TIC
(2) Cracked energy absorbed in compression (CEC)
CEC is the amount of energy absorbed from the beginning of the cracks to the peak stress, i.e., the size of the curve from the yield stress point to the peak stress point, as shown in Fig. 9b. The CEC of the plain concrete sample is 1.037, and its improvement is not significant with adding basalt fibers. At this stage, the reinforcement with a three-layer BFRP helped most significantly to resist the crack development. Among them, the CEC of Z-0.4-3F is up to 10.596, which is much higher than all other trial specimens. It shows that mixed 0.4% basalt fiber in RAC with three-layer BFRP can work well together. However, the CEC elevation of the P5 specimen was negative because the PVC pipe and concrete bonding interface failed in advance due to the construction process, and the PVC pipe with a wall thickness of 4 mm has a weak strength. Finally, the PVC pipe cannot provide sufficient compressive capacity and fails to restrain the cylinder effectively.
(3) Post-crack energy absorbed in compression (PCEC)
PCEC is the energy absorbed by the specimen from cracking to failure, i.e., the area of the curve from the peak stress to the ultimate stress. The PCEC is shown in Fig. 9c. The cylinders without lateral restraint at this stage have the lowest energy absorption, e.g., P1 and P2 cylinders. One-layer BFRP restraint and the application of PVC considerably enhanced the energy absorption during these stages. In particular, the best PECE elevation is the three-layer BFRP sheet restraint method. The multilayer FRP has the most excellent elevation of the axial compressive strength for the center core concrete. Moreover, duo to the FRP restraint is a passive restraint, once the axial strength exceeds the compressive strength of unconfined concrete, the lateral restraint effect of FRP is activated and leads to the maximum energy absorption capacity at this stage.
(4) Total energy absorbed in compression (TEC)
TEC is the total energy absorbed by the specimen before final damage and is the sum of the PEC, CEC, and PCEC. As shown in Fig. 9d, the TEC value of the plain concrete cylinder is 5.385. The BF incorporation only slightly helps in its energy absorption capacity. One-layer BFRP restraint can better augment the TEC by approximately twice as much as that of plain concrete. The triple layers BFRP and the BFRP-PVC composite constraint can substantially improve the energy absorption capacity of the cylinder. Among these values, the TECs of Z-0.2-3F and Z-3F-P are as high as 21.873 and 22.784, respectively. This conclusion is agreeable with that of Dabbagh et al. [42], where different energy values obtaining from various stress or strain levels on the monotonic curve, and the energy absorption increases dramatically with the enhancement of confinement capacity.
(5) Toughness index in compression (TIC)
TIC is the ability of a material to withstand repeated twisting and bending, and the size is equal to the total energy value absorbed by the specimen divided by the absorbed energy value before cracking, i.e., TEC/PEC. The TIC value of the plain concrete specimen is 1.424, as shown in Fig. 9e. The multilayer BPFR can significantly enhance the ductile flexural capacity and contribute to absorbing more energy, and the findings are consistent with Dabbagh et al. [42]. Therefore, the TIC value of the strengthened specimens is presumed to be strongly related to the outer wrapping materials.
4.1 Mechanism of BFRP-PVC Confinement
The FRP-PVC composite restrained concrete develops based on the steel-FRP restrained concrete. For FRP-constrained or BFRP-PVC composite restrained concrete cylinder under axial pressure, the lateral expansion of the core of concrete will increase with the load. Meanwhile, the restraining stress of the FRP will constrain the expansion-deformation. Since the concrete core is under triaxial compression, the load bearing capacity and deformation capacity of the concrete cylinder can be improved. The stress distribution of the concrete core is shown in Fig. 10.
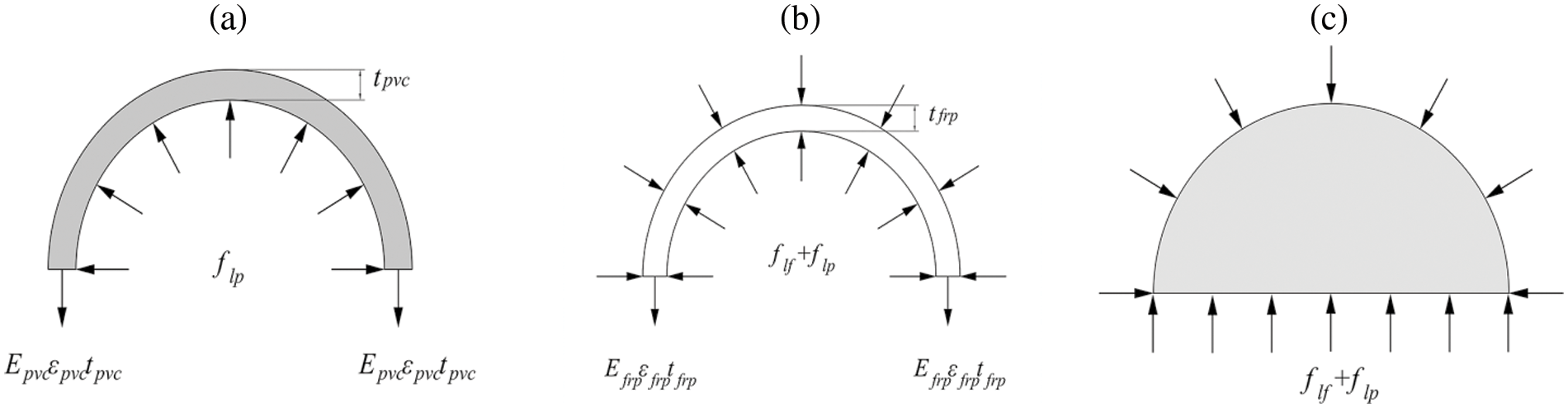
Figure 10: Schematic diagram of BFRP-PVC composite confined concrete under axial compression: (a) PVC; (b) BFRP; (c) Core concrete
From the damage mechanism, the stress elevation for the BFRP-PVC composite confined specimens is contributed by both BFRP and PVC materials. Among them, the multilayer BFRP fabric plays an essential role in improving compressive properties, while the lateral restraint provided by the PVC is relatively minor. When the FRP subjected to the expansion force in the circumferential direction, the lateral confining pressure
The mechanical relationship of the PVC is given by the following expression:
The mechanical relationship of the BFRP is given as follows:
Thus, for the BFRP-PVC composite confined specimens:
When the lateral confining pressure of the actively confined concrete (
According to the damage mechanism in Chapter 3 and the above analysis of the pressure characteristics of composite confined concrete, the PVC has a marginal contribution to axial compressive strength, while the multilayer BFRP material plays a decisive role. Therefore, this section is based on the FRP’s classical strength model while considering the PVC’s contribution to the ultimate lateral confining pressure (
4.2 Existing Stress-Strain Model
A large amount of academic study has concentrated on FRP-confined concrete in recent years. Lam et al. [66] classified these models into design-oriented and analysis-oriented models. The former models were obtained by regression analysis of experimental data. Newman et al. [70] proposed a nonlinear expression to calculate the inefficient constraint under high-lateral pressure stresses, and the model is shown as follows:
Fardis et al. [71] proposed the models for calculating the compressive strength and ultimate strain of hoop-confined concrete, which express as follows:
Saadatmanesh et al. [72] simplified and modified the existing analytical model to calculate the compressive strength and ultimate strain of FRP-confined concrete. The strength model is consistent with Mander et al. [73], and the ultimate strain model is consistent with that proposed by Richart et al. [74]. The expressions are as follows:
After analyzing numerous models, Karbhari et al. [75] developed the models for FRP-confined concrete based on the formulations of Gusson and Paultre:
The other category is an analytical model obtained by the numerical methods of incremental iterative considering the interaction between FRP and concrete. Mander et al. [73] proposed a well-used strength model based on William et al. [76] and modified by Mirmiran [77], i.e., the modified strength and the ultimate strain calculation models are as follows:
Harries et al. [78] modified the strength expressions proposed by Richart et al. [74], and Mirmiran [77] established the following models:
Binici [79] proposed modified strength and ultimate strain models based on the work of Richart et al. [74] through a theoretical analysis approach:
4.3 Peak Stress and Peak Strain Models
Because the stress-strain curve of the BFRP-PVC composite confined FRC exhibited strain-softening behavior, that is, when reached the peak stress (
When the internal concrete reaches the compressive strength (
Referring to the investigation of Wu et al. [80], when the stress-strain relationship has no strain-softening behavior, the maximum stress point corresponds to the FRP material fracture. Thus, the ultimate stress is mainly dependent on the lateral confining strength. For the curve has a softening section, the FRP does not break when the axial pressure reaches the peak point; therefore, the peak stress relates mainly to the lateral confining stiffness.
In summary, the peak stress of the BFRP-PVC composite confined FRC is relevant to the lateral confining stiffness (
4.3.2 Modeling of the Peak Stress-Strain
Ozbakkaloglu et al. [82] proposed the ultimate condition models based on Richart et al. [74] initiative constraint (steel constraint) models; however, these models are not suitable for the specimens in this experiment due to the greater lateral restraint stiffness provided by steel tubes than FRP. In order to model the strain-softening behavior based on the active constraint, this work will introduce a stiffness reduction factor (b) into the stiffness variable. Combining Newman et al. [70] and Saadatmanesh et al. [72], hereby we establish that the expressions of peak stress and strain are as follows:
Regression analysis and iterative calculations show that when k1 = 0.36, b1 = −5.9941, α = 0.5828, k2 = 1.204, b2 = −1.8905, and β = 0.2449, the calculated value of the peak model is closer to the trial result, and R2 is 0.94 and 0.92, respectively. Moreover, the fitting curve is shown in Fig. 11.
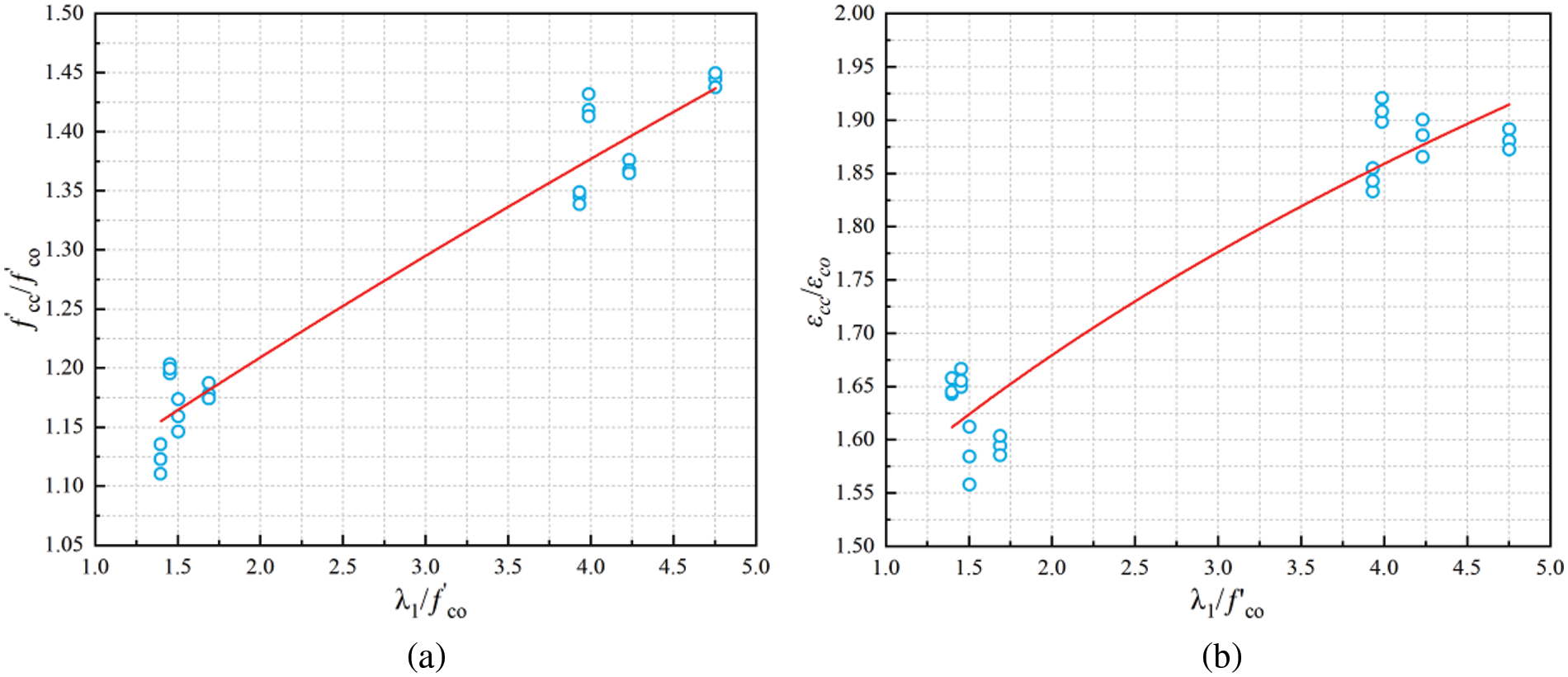
Figure 11: Model fitting curve: (a) Peak stress model fitting curve; (b) Peak strain model fitting curve
In summary, the peak stress and peak strain models are proposed for BFRP-PVC composite confined fiber-recycled concrete as follows:
Most existing FRP-confined concrete strength models are based on strain-hardening behavior, which means that the axial stress of the confined specimen can continue to ascend until the FRP fractures. The classical models presented in the previous section are based on such a case, characterized by the ultimate stress equal to the peak stress. The present model curve has a falling segment after the peak point, i.e., the ultimate axial pressure is generally weaker than the peak stress. The following models mainly reflect the feature of this weak constraint.
Lam et al. [56] model:
Pantelides et al. [83] model:
Youssef et al. [81] model:
Wei et al. [84] model:
A review of the classical FRP-constrained concrete strength models shows that the expressions for the ultimate stresses have converged to top-performing expressions, regardless of whether they are strongly or weakly confined models. In addition, the specimen is destroyed in the end state due to the collapse of the externally binding material. Thus, it is rational to propose an equation related to
The experimental data (Table 7) are substituted into the above expression, and after iterative computer operations with k3 = 0.5348 and b3 = 1.93126, the equation obtained at this time fits better with the present experimental data, with R2 = 0.92. The fitting curve is shown in Fig. 12a. The simplistic and straightforward formulation with high accuracy helps researchers quickly and easily grasp the material’s properties. Therefore, in this paper, the ultimate stress model of the BFRP-PVC composite confined fiber-recycled concrete is simplified as follows:
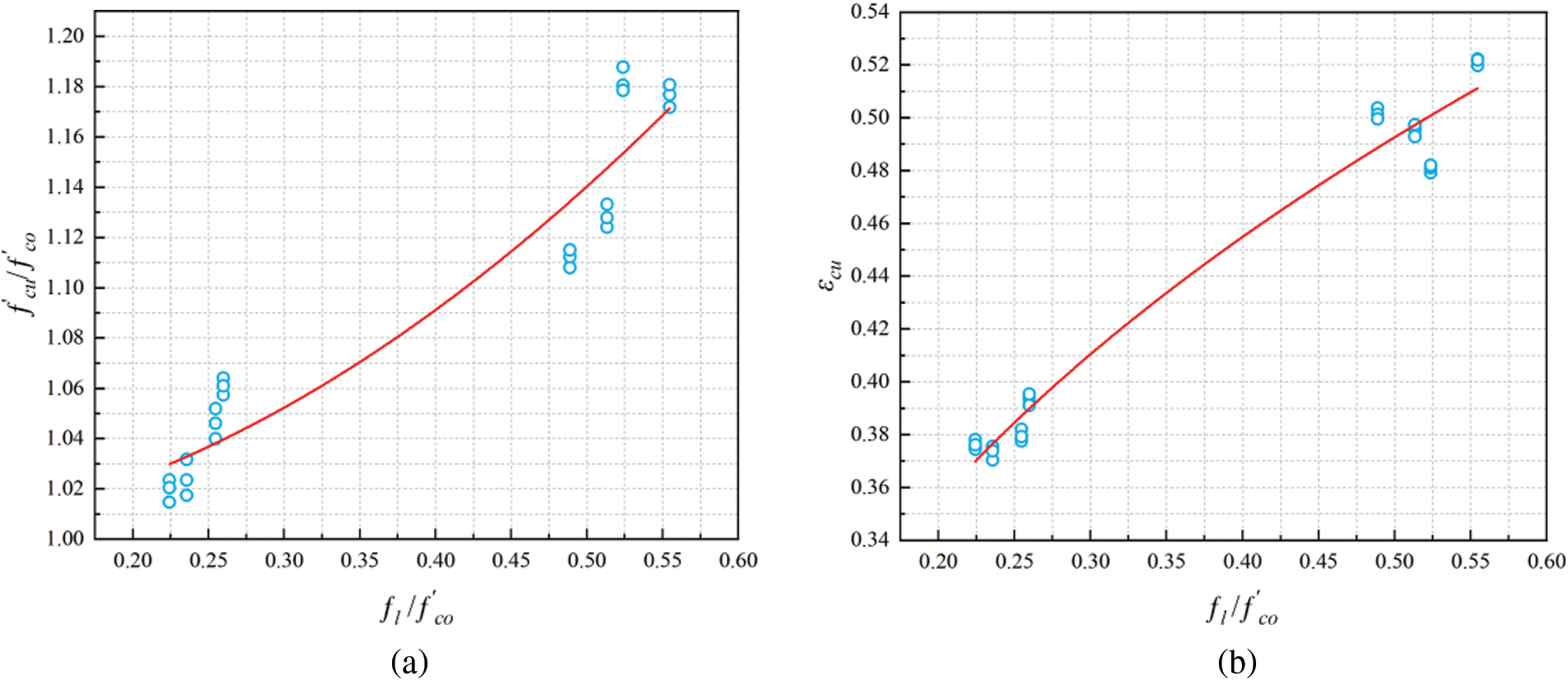
Figure 12: Model fitting curve: (a) Ultimate stress model fitting curve; (b) Ultimate strain model fitting curve
In order to establish the most suitable ultimate strain model, the following classical models include Fardis et al. [71], Saadatmanesh et al. [72], Karbhari et al. [75], Youssef et al. [81], and Vintzileou et al. [85] model are selected for comparison. The calculated value (Cal.) based on the above model is compared with the experimental value (Exp.), and the relative error (RE) is also calculated. Finally, a precise and suitable ultimate strain model of the BFRP-PVC composite restrained fiber-recycled concrete is proposed. The comparison of each model is shown in Table 8.
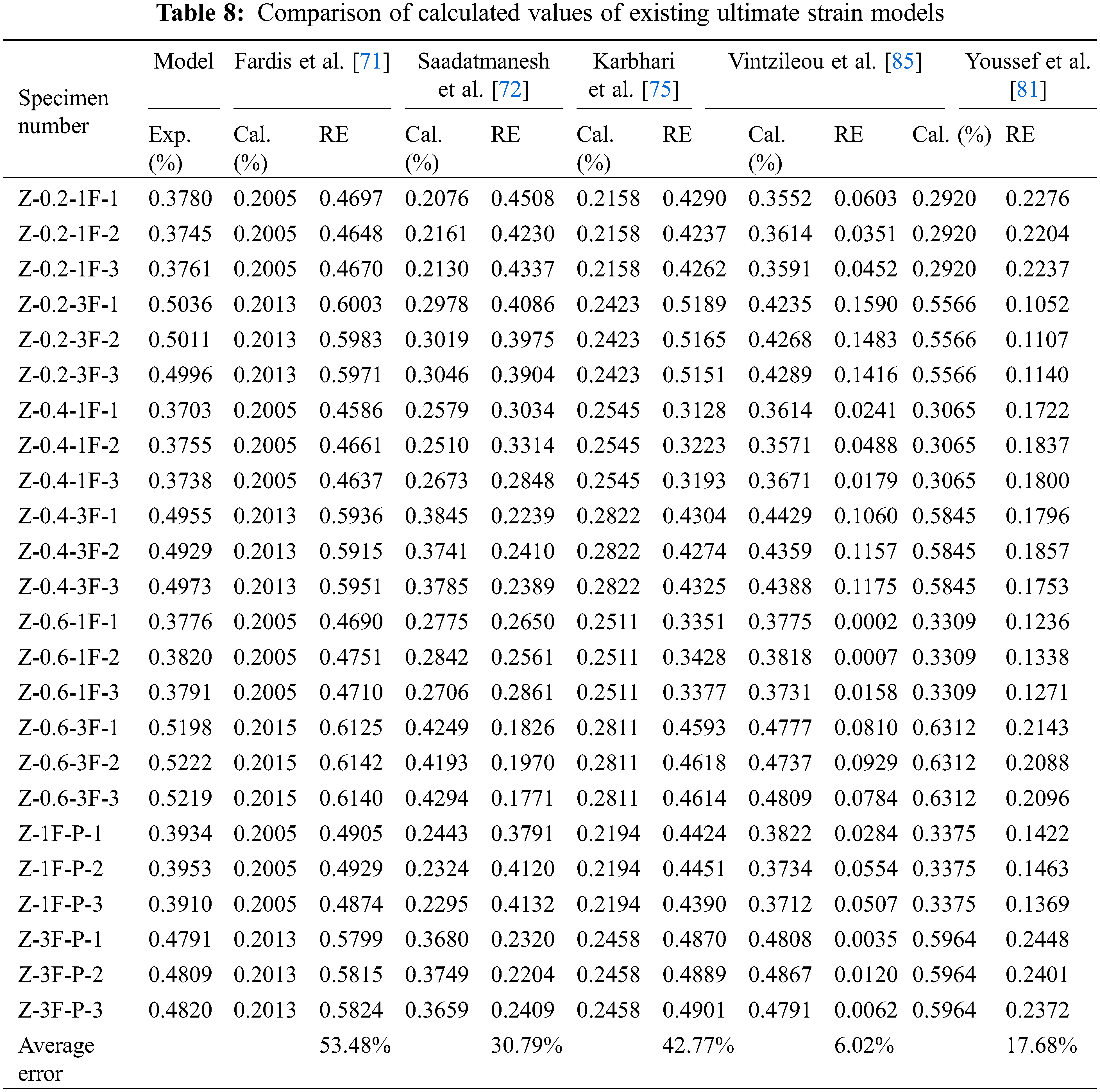
There is a large discrepancy between the experimental and calculated values, as shown in Table 8. One reason may be that the BFRP material has a more excellent elongation at fracture, and the modulus of elasticity is only one-third of that of the CFRP material. Hence, the specimen can have a considerable ductility enhancement even at the ultimate strength. Existing models cannot accurately predict the restraint performance of fiber-reinforced composites with weak elastic modulus and easily deformed property.
The Vintzileou et al. model [85] with relatively minor errors is selected and combined with the analysis of the previous chapter for the constraint mechanism in the ultimate conditions. Furthermore, the following ultimate strain model is proposed:
By regression analysis, when k4 = 0.54869 and b4 = 0.35731, the deviation of the calculated value from the experimental value is minor. At this time, R2 = 0.97, and the fitting curve is shown in Fig. 12b.
The modified expression for the ultimate strain is simplified as follows:
4.6 Comparison of the Predicted Values with Experimental Values
Fig. 13. shows the comparisons of the results under experimental axial pressure with the predicted by the equations. This paper chooses various assessment values to analyze the performance of different expression formulas, and the values are shown in Fig. 13. The mean absolute error (MAE) and the mean absolute percentage error (MAPE) are used to assess the accuracy of the model. In addition, the standard deviation (SD) was used to determine the scatter size of model predictions. The formulas are as follows.
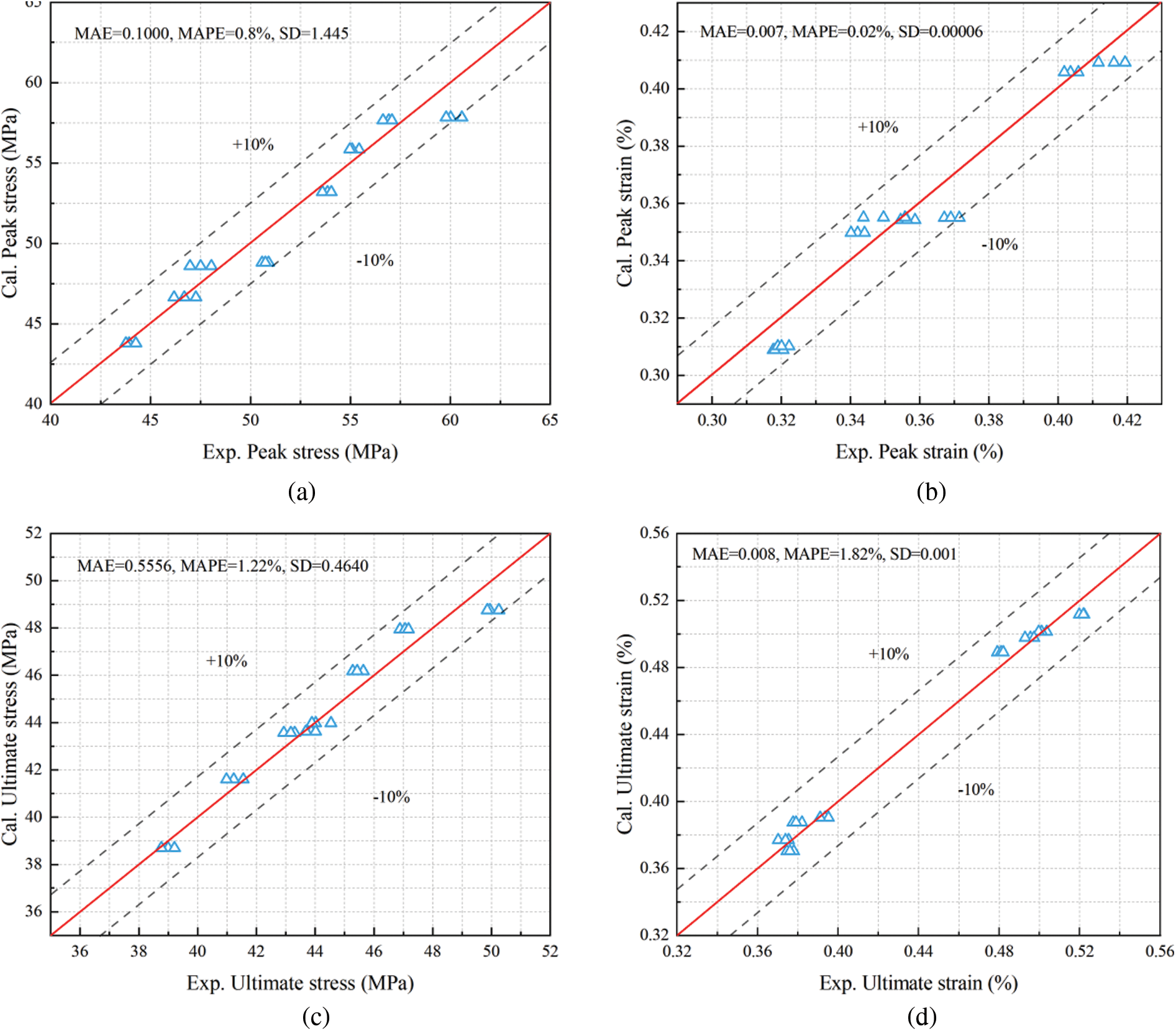
Figure 13: Comparison of model predictions with experimental data: (a) Peak stress; (b) peak strain; (c) Ultimate stress; (d) Ultimate strain
In Fig. 13, the 45° line corresponds to a perfect agreement between the predictions and experimental results. A trend that spans above the 45° reference line represents model predictions’ overestimating the experimental results. In contrast, a trend below the reference line indicates an underestimation of the test results. By installing error lines (EL ± 10%), the data points that deviate from the main trend line can be observed.
The result shows that the model fits well with the test data. However, it is worth noting that there are still some samples with large deviations between the predicted values and the test values. Therefore, more test data and further research are needed to propose a higher accuracy model.
In this experiment, BF fibers were added to RAC at various contents (0.2%, 0.4%, and 0.6%), and the fiber-reinforced recycled concrete was restrained by different materials (BFRP, PVC, and BFRP-PVC). All the samples were tested in axial compression. The damage modes, load bearing capacity, stress-strain relationships, and energy absorption capacity of the specimens were analyzed. Based on the discussion, the following conclusions can be drawn:
1. The brittle failure mode of the RAC cylinder can be transformed into ductile failure due to the restraining effect of the BFRP sheet.
2. The compressive strength of RAC was increased by 6.7%–10.5% and 16.5%–23.7%, respectively, for the 1 layer and 3 layers BFRP reinforced specimens. The most considerable strength improvement was 42.2% when reinforced with 3-layer BFRP-PVC.
3. The BFRP-constrained samples and the composite-constrained specimens had an apparent transition plateau after the initial rising branch in the stress-strain curves. For samples constrained by PVC pipe, the stress-strain curves decreased sharply after the peak load due to brittleness and low strength.
4. Ductility was an essential parameter evaluated in this study. The ultimate strain of the specimens with 1-layer BFRP reinforcement was elevated by 48.5%–80.9%. The most significant enhancement was observed for the 3-layer BFRP reinforcement, which increased by 97.1%–141.1%.
5. The mono addition of BF or PVC had little effect on the mechanical properties of RAC.
6. The peak stress-strain and ultimate stress-strain models of BFRP-PVC restrained FRC were established. The predicted values of the proposed models are in good agreement with the experimental data.
In summary, the recycled aggregate concrete (50% replacement) containing 0.2% BF provided the best mechanical properties, and its stress-strain behavior was closest to that of ordinary concrete. The simultaneous use of 0.2% BFs and external restraints (BFRP and PVC) increased the energy absorption, toughness index, and post-peak response. Using BFRP and PVC as reinforcement materials were cost-effective in combining the high tensile strength of BFRP and the outer PVC pipe, which enhanced the structural durability and protected the internal concrete.
Funding Statement: This research was supported by the Natural Science Foundation Project of Liaoning Provincial Department of Education of China under Grant No. JJL201915404, Zhejiang Provincial Natural Science Foundation of China under Grant No. LQ22E080024 and Zhejiang Province Department of Education Fund of China under Grant No. Y202146776.
Conflicts of Interest: The authors have no conflicts of interest to declare, have all read and approved the manuscript, and agree with its submission. There are no other persons who satisfy the criteria for authorship.
References
1. Xiao, J., Tang, Y., Chen, H., Zhang, H., Xia, B. (2022). Effects of recycled aggregate combinations and recycled powder contents on fracture behavior of fully recycled aggregate concrete. Journal of Cleaner Production, 366(9), 132895. DOI 10.1016/j.jclepro.2022.132895. [Google Scholar] [CrossRef]
2. Pacheco, J., de Brito, J., Chastre, C., Evangelista, L. (2019). Experimental investigation on the variability of the main mechanical properties of concrete produced with coarse recycled concrete aggregates. Construction and Building Materials, 201(2), 110–120. DOI 10.1016/j.conbuildmat.2018.12.200. [Google Scholar] [CrossRef]
3. Xiao, J., Zou, S., Yu, Y., Wang, Y., Ding, T. et al. (2020). 3D recycled mortar printing: System development, process design, material properties and on-site printing. Journal of Building Engineering, 32, 101779. DOI 10.1016/j.jobe.2020.101779. [Google Scholar] [CrossRef]
4. Kim, J., Jang, H. (2022). Closed-loop recycling of C&D waste: Mechanical properties of concrete with the repeatedly recycled C&D powder as partial cement replacement. Journal of Cleaner Production, 343, 130977. DOI 10.1016/j.jclepro.2022.130977. [Google Scholar] [CrossRef]
5. Duan, Z., Singh, A., Xiao, J., Hou, S. (2020). Combined use of recycled powder and recycled coarse aggregate derived from construction and demolition waste in self-compacting concrete. Construction and Building Materials, 254, 119323. DOI 10.1016/j.conbuildmat.2020.119323. [Google Scholar] [CrossRef]
6. Chen, W., Jin, R., Xu, Y., Wanatowski, D., Li, B. et al. (2019). Adopting recycled aggregates as sustainable construction materials: A review of the scientific literature. Construction and Building Materials, 218(4), 483–496. DOI 10.1016/j.conbuildmat.2019.05.130. [Google Scholar] [CrossRef]
7. Tang, Q., Ma, Z., Wu, H., Wang, W. (2020). The utilization of eco-friendly recycled powder from concrete and brick waste in new concrete: A critical review. Cement and Concrete Composites, 114(4), 103807. DOI 10.1016/j.cemconcomp.2020.103807. [Google Scholar] [CrossRef]
8. Chen, X., Capiau, L., Reynaert, I., Zheng, K., Gruyaert, E. et al. (2022). Comparative study on modelling concrete properties using physical and mechanical properties of recycled coarse aggregate. Construction and Building Materials, 345(6), 128249. DOI 10.1016/j.conbuildmat.2022.128249. [Google Scholar] [CrossRef]
9. Tam, V. W. Y., Soomro, M., Evangelista, A. C. J. (2021). Quality improvement of recycled concrete aggregate by removal of residual mortar: A comprehensive review of approaches adopted. Construction and Building Materials, 288(1940), 123066. DOI 10.1016/j.conbuildmat.2021.123066. [Google Scholar] [CrossRef]
10. Wang, W., Wang, Y., Chen, Q., Liu, Y., Zhang, Y. et al. (2022). Bond properties of basalt fiber reinforced polymer (BFRP) bars in recycled aggregate thermal insulation concrete under freeze-thaw cycles. Construction and Building Materials, 329(6), 127197. DOI 10.1016/j.conbuildmat.2022.127197. [Google Scholar] [CrossRef]
11. Lima, G. T. D. S., Rocha, J. C., Cheriaf, M. (2022). Investigation of the properties of pervious concrete with a recycled aggregate designed with a new combination of admixture. Construction and Building Materials, 340, 127710. DOI 10.1016/j.conbuildmat.2022.127710. [Google Scholar] [CrossRef]
12. Du, X., Li, Y., Si, Z., Huang, L., Chen, X. (2022). Effects of basalt fiber and polyvinyl alcohol fiber on the properties of recycled aggregate concrete and optimization of fiber contents. Construction and Building Materials, 340(1), 127646. DOI 10.1016/j.conbuildmat.2022.127646. [Google Scholar] [CrossRef]
13. Xiao, J., Zou, S., Ding, T., Duan, Z., Liu, Q. (2021). Fiber-reinforced mortar with 100% recycled fine aggregates: A cleaner perspective on 3D printing. Journal of Cleaner Production, 319, 102548. DOI 10.1016/j.jclepro.2021.128720. [Google Scholar] [CrossRef]
14. Zhang, C., Wang, Y., Zhang, X., Ding, Y., Xu, P. (2021). Mechanical properties and microstructure of basalt fiber-reinforced recycled concrete. Journal of Cleaner Production, 278(10), 123252. DOI 10.1016/j.jclepro.2020.123252. [Google Scholar] [CrossRef]
15. Ortega-López, V., García-Llona, A., Revilla-Cuesta, V., Santamaría, A., San-José, J. T. (2021). Fiber-reinforcement and its effects on the mechanical properties of high-workability concretes manufactured with slag as aggregate and binder. Journal of Building Engineering, 43(5), 102548. DOI 10.1016/j.jobe.2021.102548. [Google Scholar] [CrossRef]
16. Hao, L., Xiao, J., Sun, J., Xia, B., Cao, W. (2022). Thermal conductivity of 3D printed concrete with recycled fine aggregate composite phase change materials. Journal of Cleaner Production, 364, 132598. DOI 10.1016/j.jclepro.2022.132598. [Google Scholar] [CrossRef]
17. Zhang, W. H., Wang, R., Zhao, H., Lam, D., Chen, P. (2022). Axial-load response of CFST stub columns with external stainless steel and recycled aggregate concrete: Testing, mechanism analysis and design. Engineering Structures, 256(5), 113968. DOI 10.1016/j.engstruct.2022.113968. [Google Scholar] [CrossRef]
18. Zhang, H., Geng, Y., Wang, Y. Y., Li, X. Z. (2022). Experimental study and prediction model for bond behaviour of steel-recycled aggregate concrete composite slabs. Journal of Building Engineering, 53, 104585. DOI 10.1016/j.jobe.2022.104585. [Google Scholar] [CrossRef]
19. Fiore, V., Scalici, T., Di Bella, G., Valenza, A. (2015). A review on basalt fibre and its composites. Composites Part B: Engineering, 74(26), 74–94. DOI 10.1016/j.compositesb.2014.12.034. [Google Scholar] [CrossRef]
20. Nepomuceno, E., Sena-Cruz, J., Correia, L., D’Antino, T. (2021). Review on the bond behavior and durability of FRP bars to concrete. Construction and Building Materials, 287(3), 123042. DOI 10.1016/j.conbuildmat.2021.123042. [Google Scholar] [CrossRef]
21. He, J., Lu, Z., Tan, S., Ueda, T., Pan, Y. et al. (2020). Effect of temperature variation and pre-sustained loading on the bond between basalt FRP sheets and concrete. Materials, 13(7), 1530. DOI 10.3390/ma13071530. [Google Scholar] [CrossRef]
22. Lopresto, V., Leone, C., De Iorio, I. (2011). Mechanical characterisation of basalt fibre reinforced plastic. Composites Part B: Engineering, 42(4), 717–723. DOI 10.1016/j.compositesb.2011.01.030. [Google Scholar] [CrossRef]
23. Kurt, C. E. (1978). Concrete filled structural plastic columns. Journal of the Structural Division, 104(1), 55–63. DOI 10.1061/JSDEAG.0004849. [Google Scholar] [CrossRef]
24. Gupta, P. K., Verma, V. K. (2016). Study of concrete-filled unplasticized polyvinyl chloride tubes in marine environment. Journal of Engineering for the Maritime Environment, 230(2), 229–240. DOI 10.1177/1475090214560448. [Google Scholar] [CrossRef]
25. Wang, J., Yang, Q. (2010). Experimental study on mechanical properties of concrete confined with plastic pipe. ACI Materials Journal, 107(2), 132–137. DOI 10.14359/51663576. [Google Scholar] [CrossRef]
26. Gupta, P. K. (2013). Confinement of concrete columns with unplasticized Polyvinyl chloride tubes. International Journal of Advanced Structural Engineering, 5(9), 1–8. DOI 10.1186/2008-6695-5-19. [Google Scholar] [CrossRef]
27. Tang, Y., Xiao, J., Zhang, H., Duan, Z., Xia, B. (2022). Mechanical properties and uniaxial compressive stress-strain behavior of fully recycled aggregate concrete. Construction and Building Materials, 323(5), 126546. DOI 10.1016/j.conbuildmat.2022.126546. [Google Scholar] [CrossRef]
28. Sivamani, J., Renganathan, N. T. (2021). Effect of fine recycled aggregate on the strength and durability properties of concrete modified through two-stage mixing approach. Environmental Science and Pollution Research, 30(8), 1–14. DOI 10.1007/s11356-021-14420-5. [Google Scholar] [CrossRef]
29. Yang, S., Li, L., Sun, Z., Wang, J., Guo, Q. et al. (2021). A closed-form fracture model to predict tensile strength and fracture toughness of alkali-activated slag and fly ash blended concrete made by sea sand and recycled coarse aggregate. Construction and Building Materials, 300(5), 123976. DOI 10.1016/j.conbuildmat.2021.123976. [Google Scholar] [CrossRef]
30. Wang, C., Xiao, J. (2018). Evaluation of the stress-strain behavior of confined recycled aggregate concrete under monotonic dynamic loadings. Cement and Concrete Composites, 87(4), 149–163. DOI 10.1016/j.cemconcomp.2017.12.012. [Google Scholar] [CrossRef]
31. Chang, Y. C., Wang, Y. Y., Zhang, H., Chen, J., Geng, Y. (2022). Different influence of replacement ratio of recycled aggregate on uniaxial stress-strain relationship for recycled concrete with different concrete strengths. Structures, 42(4), 284–308. DOI 10.1016/j.istruc.2022.05.117. [Google Scholar] [CrossRef]
32. Xiao, J., Li, J., Zhang, C. (2005). Mechanical properties of recycled aggregate concrete under uniaxial loading. Cement and Concrete Research, 35(6), 1187–1194. DOI 10.1016/j.cemconres.2004.09.020. [Google Scholar] [CrossRef]
33. Belén, G. F., Fernando, M. A., Diego, C. L., Sindy, S. P. (2011). Stress-strain relationship in axial compression for concrete using recycled saturated coarse aggregate. Construction and Building Materials, 25(5), 2335–2342. DOI 10.1016/j.conbuildmat.2010.11.031. [Google Scholar] [CrossRef]
34. Rahal, K. (2007). Mechanical properties of concrete with recycled coarse aggregate. Building and Environment, 42(1), 407–415. DOI 10.1016/j.buildenv.2005.07.033. [Google Scholar] [CrossRef]
35. Revilla-Cuesta, V., Ortega-López, V., Skaf, M., Khan, A. U. R., Manso, J. M. (2022). Deformational behavior of self-compacting concrete containing recycled aggregate, slag cement and green powders under compression and bending: Description and prediction adjustment. Journal of Building Engineering, 54(3), 104611. DOI 10.1016/j.jobe.2022.104611. [Google Scholar] [CrossRef]
36. Revilla-Cuesta, V., Skaf, M., Santamaría, A., Ortega-López, V., Manso, J. M. (2021). Assessment of longitudinal and transversal plastic behavior of recycled aggregate self-compacting concrete: A two-way study. Construction and Building Materials, 292(7), 123426. DOI 10.1016/j.conbuildmat.2021.123426. [Google Scholar] [CrossRef]
37. Teng, J. G., Zhao, J. L., Yu, T., Li, L. J., Guo, Y. C. (2016). Behavior of FRP-confined compound concrete containing recycled concrete lumps. Journal of Composites for Construction, 20(1), 04015038. DOI 10.1061/(ASCE)CC.1943-5614.0000602. [Google Scholar] [CrossRef]
38. Gao, C., Huang, L., Yan, L., Jin, R., Kasal, B. (2019). Strength and ductility improvement of recycled aggregate concrete by polyester FRP-PVC tube confinement. Composites Part B: Engineering, 162(12), 178–197. DOI 10.1016/j.compositesb.2018.10.102. [Google Scholar] [CrossRef]
39. Toutanji, H., Saafi, M. (2001). Durability studies on concrete columns encased in PVC-FRP composite tubes. Composite Structures, 54(1), 27–35. DOI 10.1016/S0263-8223(01)00067-8. [Google Scholar] [CrossRef]
40. Feng, C., Yu, F., Fang, Y. (2021). Mechanical behavior of PVC tube confined concrete and PVC-FRP confined concrete: A review. Structures, 31(3), 613–635. DOI 10.1016/j.istruc.2021.01.093. [Google Scholar] [CrossRef]
41. Lu, Y., Li, N., Li, S. (2014). Behavior of FRP-confined concrete-filled steel tube columns. Polymers, 6(5), 1333–1349. DOI 10.3390/polym6051333. [Google Scholar] [CrossRef]
42. Dabbagh, H., Delshad, M., Amoorezaei, K. (2021). Design-oriented stress-strain model for FRP-confined lightweight aggregate concrete. KSCE Journal of Civil Engineering, 25(1), 219–234. DOI 10.1007/s12205-020-0233-9. [Google Scholar] [CrossRef]
43. JGJ 55-2011 (2011). Specification for mix proportion design of ordinary concrete. Beijing, China: China Architecture & Building Press. [Google Scholar]
44. Suryawanshi, S., Singh, B., Bhargava, P. (2018). Equation for stress-strain relationship of recycled aggregate concrete in axial compression. Magazine of Concrete Research, 70(4), 163–171. DOI 10.1680/jmacr.16.00108. [Google Scholar] [CrossRef]
45. Chang, Y. C., Wang, Y. Y., Zhang, H., Chen, J., Geng, Y. (2022). Different influence of replacement ratio of recycled aggregate on uniaxial stress-strain relationship for recycled concrete with different concrete strengths. Structures, 42(4), 284–308. DOI 10.1016/j.istruc.2022.05.117. [Google Scholar] [CrossRef]
46. Omary, S., Ghorbel, E., Wardeh, G., Nguyen, M. D. (2018). Mix design and recycled aggregates effects on the concrete’s properties. International Journal of Civil Engineering, 16(8), 973–992. DOI 10.1007/s40999-017-0247-y. [Google Scholar] [CrossRef]
47. Omer, A. I. I. (2016). Experimental and theoretical study on seismic behavior of concrete columns reinforced with steel-basalt frp composite bars and hybrid stirrups (Master Thesis). Nanjing, China: Southeast University. [Google Scholar]
48. GB/T 3354-2014 (2014). Test method for tensile properties of orientation fiber reinforced polymer matrix composite materials. Beijing, China: China Standard Press. [Google Scholar]
49. GB/T 8804.2-2003 (2003). Hermoplastic pipes-determination of tensile properties–Part 2: Pipes made of unplasticize poly (vinyl chloride) (PVC-Uchlorinated poly (vinyl chloride) (PVC-C) and high-impact-poly (vinyl chloride) (PVC-HI). National Standards of the People’s Republic. Beijing, China: China Standard Press. [Google Scholar]
50. GB/T50152-2012 (2012). Standard for test methods for concrete structures. Beijing, China: China Architecture & Building Press. [Google Scholar]
51. Xiao, J., Li, W., Sun, Z., Shah, S. P. (2012). Crack propagation in recycled aggregate concrete under uniaxial compressive loading. ACI Materials Journal, 109(4), 451–462. DOI 10.14359/51683920. [Google Scholar] [CrossRef]
52. Jiang, J. F., Wu, Y. F. (2016). Plasticity-based criterion for confinement design of FRP jacketed concrete columns. Materials and Structures/Materiaux et Constructions, 49(6), 2035–2051. DOI 10.1617/s11527-015-0632-4. [Google Scholar] [CrossRef]
53. Zeng, J. J., Liang, S. D., Li, Y. L., Guo, Y. C., Shan, G. Y. (2021). Compressive behavior of FRP-confined elliptical concrete-filled high-strength steel tube columns. Composite Structures, 266(7), 113808. DOI 10.1016/j.compstruct.2021.113808. [Google Scholar] [CrossRef]
54. Zhang, P., Chen, B., Liu, Y., Tu, Y., Gao, D. et al. (2021). Experimental study on the axial compression behavior of columns confined by BFRP ties. Composite Structures, 258(3), 113302. DOI 10.1016/j.compstruct.2020.113302. [Google Scholar] [CrossRef]
55. Saadoon, A. S., Jasim, N. A. (2019). Experimental investigation of partially reinforced concrete-filled plastic tubular columns. Methods, 129, 53033–53036. [Google Scholar]
56. Lam, L., Teng, J. G. (2003). Design-oriented stress-strain model for FRP-confined concrete in rectangular columns. Journal of Reinforced Plastics and Composites, 22(13), 1149–1186. DOI 10.1177/0731684403035429. [Google Scholar] [CrossRef]
57. Nanni, A., Bradford, N. M. (1995). FRP jacketed concrete under uniaxial compression. Construction and Building Materials, 9(2), 115–124. DOI 10.1016/0950-0618(95)00004-Y. [Google Scholar] [CrossRef]
58. Mirmiran, A., Shahawy, M., Samaan, M., Echary, H. E., Mastrapa, J. C. et al. (1998). Effect of column parameters on FRP-confined concrete. Journal of Composites for Construction, 2(4), 175–185. DOI 10.1061/(ASCE)1090-0268(1998)2:4(175). [Google Scholar] [CrossRef]
59. Campione, G., Miraglia, N. (2003). Strength and strain capacities of concrete compression members reinforced with FRP. Cement and Concrete Composites, 25(1), 31–41. DOI 10.1016/S0958-9465(01)00048-8. [Google Scholar] [CrossRef]
60. Shahawy, M., Mirmiran, A., Beitelman, T. (2000). Tests and modeling of carbon-wrapped concrete columns. Composites Part B: Engineering, 31(6–7), 471–480. DOI 10.1016/S1359-8368(00)00021-4. [Google Scholar] [CrossRef]
61. Xiao, Y., Wu, H. (2000). Compressive behavior of concrete confined by carbon fiber composite jackets. Journal of Materials in Civil Engineering, 12(2), 139–146. DOI 10.1061/(ASCE)0899-1561(2000)12:2(139). [Google Scholar] [CrossRef]
62. Aire, C., Gettu, R., Casas, J. (2001). Study of the compressive behavior of concrete confined by fiber reinforced composites. Proceedings of the International Conference, pp. 239–243. Porto, Portugal. [Google Scholar]
63. Khan, M., Ali, M. (2018). Effect of super plasticizer on the properties of medium strength concrete prepared with coconut fiber. Construction and Building Materials, 182(19), 703–715. DOI 10.1016/j.conbuildmat.2018.06.150. [Google Scholar] [CrossRef]
64. Zia, A., Ali, M. (2017). Behavior of fiber reinforced concrete for controlling the rate of cracking in canal-lining. Construction and Building Materials, 155(3), 726–739. DOI 10.1016/j.conbuildmat.2017.08.078. [Google Scholar] [CrossRef]
65. Khan, M., Cao, M., Ali, M. (2018). Effect of basalt fibers on mechanical properties of calcium carbonate whisker-steel fiber reinforced concrete. Construction and Building Materials, 192(7), 742–753. DOI 10.1016/j.conbuildmat.2018.10.159. [Google Scholar] [CrossRef]
66. Lam, L., Teng, J. G. (2003). Design-oriented stress-strain model for FRP-confined concrete. Construction and Building Materials, 17(6–7), 471–489. DOI 10.1016/S0950-0618(03)00045-X. [Google Scholar] [CrossRef]
67. Danish, A., Mosaberpanah, M. A. (2020). Formation mechanism and applications of cenospheres: A review. Journal of Materials Science, 55(11), 4539–4557. DOI 10.1007/s10853-019-04341-7. [Google Scholar] [CrossRef]
68. Khan, M. I., Usman, M., Rizwan, S. A., Hanif, A. (2019). Self-consolidating lightweight concrete incorporating limestone powder and fly ash as supplementary cementing material. Materials, 12(18), 3050. DOI 10.3390/ma12183050. [Google Scholar] [CrossRef]
69. Hanif, A., Cheng, Y., Lu, Z., Li, Z. (2018). Mechanical behavior of thin-laminated cementitious composites incorporating cenosphere fillers. ACI Materials Journal, 115(1), 117–127. DOI 10.14359/51701007. [Google Scholar] [CrossRef]
70. Newman, K., Newman, J. B. (1971). Failure theories and design criteria for plain concrete. In: Structure, solid mechanics and engineering design, pp. 963–995. London: Wiley. [Google Scholar]
71. Fardis, M. N., Khalili, H. H. (1982). FRP-encased concrete as a structural material. Magazine of Concrete Research, 34(121), 191–202. DOI 10.1680/macr.1982.34.121.191. [Google Scholar] [CrossRef]
72. Saadatmanesh, H., Ehsani, M. R., Li, M. W. (1994). Strength and ductility of concrete columns externally reinforced with fiber composite straps. Structural Journal, 91(4), 434–447. DOI 10.14359/4151. [Google Scholar] [CrossRef]
73. Mander, J. B., Priestley, M. J. N., Park, R. (1988). Theoretical stress-strain model for confined concrete. Journal of Structural Engineering, 114(8), 1804–1826. DOI 10.1061/(ASCE)0733-9445(1988)114:8(1804). [Google Scholar] [CrossRef]
74. Richart, F. E., Brandtzæg, A., Brown, R. L. (1928). A study of the failure of concrete under combined compressive stresses. University of Illinois, Engineering Experiment Station, Bulletin, 26, 80–90. [Google Scholar]
75. Karbhari, V. M., Gao, Y. (1997). Composite jacketed concrete under uniaxial compression—verification of simple design equations. Journal of Materials in Civil Engineering, 9(4), 185–193. DOI 10.1061/(ASCE)0899-1561(1997)9:4(185). [Google Scholar] [CrossRef]
76. William, K. J., Warnke, E. P. (1975). Constitutive models for the triaxial behavior of concrete. Proceedings of the International Association for Bridge and Structural, pp. 1–30. Bergamo, Italy. [Google Scholar]
77. Mirmiran, A. (1997). Analytical and experimental investigation of reinforced concrete columns encased in fiberglass tubular jacket and use of fiber jacket for pile splicing. Florida Department of Transportation, Report number: B-9135. Tallahassee, Florida. [Google Scholar]
78. Harries, K. A., Kharel, G. (2002). Behavior and modeling of concrete subject to variable confining pressure. Materials Journal, 99(2), 180–189. DOI 10.14359/11711. [Google Scholar] [CrossRef]
79. Binici, B. (2005). An analytical model for stress-strain behavior of confined concrete. Engineering Structures, 27(7), 1040–1051. DOI 10.1016/j.engstruct.2005.03.002. [Google Scholar] [CrossRef]
80. Wu, G., Wu, Z. S., Lu, Z. T. (2006). Study on the stress-strain relationship of FRP-confined concrete cylinder with softening section. Journal of Civil Engineering, 39(11), 7–14. DOI 10.3321/j.issn:1000-131X.2006.11.002. [Google Scholar] [CrossRef]
81. Youssef, M. N., Feng, M. Q., Mosallam, A. S. (2007). Stress-strain model for concrete confined by FRP composites. Composites Part B: Engineering, 38(5–6), 614–628. DOI 10.1016/j.compositesb.2006.07.020. [Google Scholar] [CrossRef]
82. Ozbakkaloglu, T., Lim, J. C., Vincent, T. (2013). FRP-confined concrete in circular sections: Review and assessment of stress-strain models. Engineering Structures, 49(122), 1068–1088. DOI 10.1016/j.engstruct.2012.06.010. [Google Scholar] [CrossRef]
83. Pantelides, C. P., Yan, Z. (2007). Confinement model of concrete with externally bonded FRP jackets or posttensioned FRP shells. Journal of Structural Engineering, 133(9), 1288–1296. DOI 10.1061/(ASCE)0733-9445(2007)133:9(1288). [Google Scholar] [CrossRef]
84. Wei, Y. Y., Wu, Y. F. (2012). Unified stress-strain model of concrete for FRP-confined columns. Construction and Building Materials, 26(1), 381–392. DOI 10.1016/j.conbuildmat.2011.06.037. [Google Scholar] [CrossRef]
85. Vintzileou, E., Panagiotidou, E. (2008). An empirical model for predicting the mechanical properties of FRP-confined concrete. Construction and Building Materials, 22(5), 841–854. DOI 10.1016/j.conbuildmat.2006.12.009. [Google Scholar] [CrossRef]
Cite This Article
 Copyright © 2023 The Author(s). Published by Tech Science Press.
Copyright © 2023 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF Downloads
Downloads
 Citation Tools
Citation Tools