Dynamic Testing of Elastic Modulus, Shear Modulus, and Poisson’s Ratio of Bamboo Scrimber

1  Introduction

Bamboo is a green, fast-growing, easily renewable, and degradable biomass material. Compared to traditional structural materials, bamboo requires lower energy during its processing. As the most important bamboo-producing country in the world, China ranks first in terms of bamboo resources, bamboo forest area, bamboo stock, bamboo output, and foreign trade volume of bamboo products. At present, bamboo products such as bamboo scrimber, bamboo scrimber floor, and bamboo-wood composite container floor have been widely used in municipal, construction, furniture, water conservancy, energy, transportation, packaging, sports, military, and leisure fields [1]. Bamboo fiber has high strength [2]. However, bamboo is a sort of hollow plant. It is rarely used directly in mainstream architecture.

The bamboo scrimber is a board made of bamboo bundles as a unit, which is assembled so that all the fibers are aligned in the longitudinal direction and glued together by hot pressing (or cold pressing), which completely compensates for the structural defects of the original bamboo. Its high utilization rate of raw materials has completely changed the original properties of bamboo, with excellent mechanical properties and great changes in physical properties [3,4]. The excellent grain orientation mechanical properties of bamboo scrimber can also meet the needs of building materials, as has recently been achieved many results in this direction [5–7]. The elastic constant is an important parameter reflecting the mechanical properties of materials and is more important for building materials. In China’s current specification GB/T 40247-2021 “Bamboo scrimber” [8] and LY/T 3194-2020 “Structural bamboo scrimber” [9] for structural bamboo scrimber, the product quality of the bamboo scrimber was graded according to the elastic modulus value. At present, the test method for the elastic constant of bamboo scrimber in the academic circle is mainly the static method [10–12]. In 2012, Zhang et al. [13] measured basic mechanical parameters such as elastic modulus and Poisson’s ratio of Neosinocalamus affinis (Bambusaemeiensis L. C. Chia & H. L. Fung) reconstituted wood by static tensile test method and static axial compression test method. The results show that the tensile elastic modulus of the bamboo scrimber is 32.84 GPa, and the compressive elastic modulus is 37.73 GPa. Although the elastic modulus and Poisson’s ratio variation coefficient of the bamboo scrimber are all small and the stability performance is good, the conventional statics method is destructive to the bamboo scrimber specimen, so the test process is rather cumbersome, and the dynamic test method has become a hot research direction at present as it can accurately test the elastic constant of the material without destroying the specimen. Thus making research work on dynamic testing of bamboo scrimbers’ modulus of elasticity, shear modulus, and Poisson’s ratio is particularly important.

At present, the main methods to dynamically test the elastic constant of the bamboo scrimber are the wave velocity method and the vibration method [14–16]. In 2014, Zhou et al. [17] measured the elastic constant of bamboo scrimber using the lateral free vibration method of the cantilever and explored the effects of density and aspect ratio on the elastic modulus. The research results showed that when the length-thickness ratio of the bamboo scrimber specimen is less than 15, the elastic modulus measured by the vibration method is low, and the elastic modulus increases with the increase of the density. In 2015, Armandei et al. [18] used spectrum analysis on the vibration data of bamboo cantilever beams, proving that spectrum analysis has the advantages of low cost and high accuracy. Dynamic testing of wood-based panel elastic constant testing has the advantages of rapidity, simplicity, and high reliability [19–21]. It has been proven to be a commonly used and successful method, and its measurement results are in good agreement with those of traditional static methods. Furthermore, many types of research used probabilistic approach methods to study the mechanical properties of materials [22–24]. At present, the cantilever method and the wave velocity method are mostly used in the dynamic testing research of bamboo scrimber. The former can test the elastic modulus and shear modulus, but most of the research only tests the elastic modulus of the bamboo scrimber, failing to measure the shear modulus at the same time. And the formula used does not consider the size effect, so the length-width ratio and width-thickness ratio have a great influence on the test results of the elastic modulus and shear modulus. The latter can only measure the elastic modulus, and there is a strain rate effect; that is, its strength gradually increases with the increase of the strain rate [25]. In addition, the test has strict requirements on the size of the specimen.

Through previous studies, this paper proposes a free-plate transient excitation method to dynamically test the elastic modulus and shear modulus of reconstituted bamboo specimens, and uses the cantilever plate torsional vibration method to simultaneously test the elasticity, modulus shear modulus, and Poisson’s ratio. The test method used in this paper considers the effects of dimensional effects and material densities, the specimens do not require special customization, and the measured elastic constants results are more accurate. The accuracy and reliability of dynamic testing of the elastic modulus, shear modulus and Poisson’s ratio of reconstituted bamboo were also verified using static four-point bending method tests.

2  Materials and Methods

2.1 Materials

A bamboo scrimber, its size is 1860 mm (l) × 1310 mm (b) × 18 mm (h), produced by Fujian Bamboo Voya Co., Ltd., China. The material is made of moso bamboo (Phyllostachys edulis (Carriere) J. Houzeau) as the basic material and is processed by sawing, rolling, drying, dipping, and hot pressing. Send the bamboo to the bamboo rolling and splitting machine to flatten and remove the outer layer and inner layer. The flattened bamboo splits are processed by a bamboo thinning machine to obtain bamboo bundles with different degrees of thinning. Dry the loosened bamboo bundle to a moisture content of 7%~10%, then immerse it in phenolic resin adhesive, and press it into a plate with a hot-pressing pressure of 4~6 MPa.

As shown in Fig. 1, from the same 18 mm thick board, 7 pieces of 756 mm (l) × 126 mm (b) × 18 mm (h) longitudinal specimens were cut out in the direction parallel to the bamboo bundles, marked AZ specimens. 7 pieces of 756 mm (l) × 126 mm (b) × 18 mm (h) transverse specimens were cut out in the vertical direction of bamboo bundles and were recorded as AH specimens. 14 specimens were subjected to a free plate transient excitation test and cantilever plate dynamic test, and their elastic modulus, shear modulus, and Poisson’s ratio were measured.

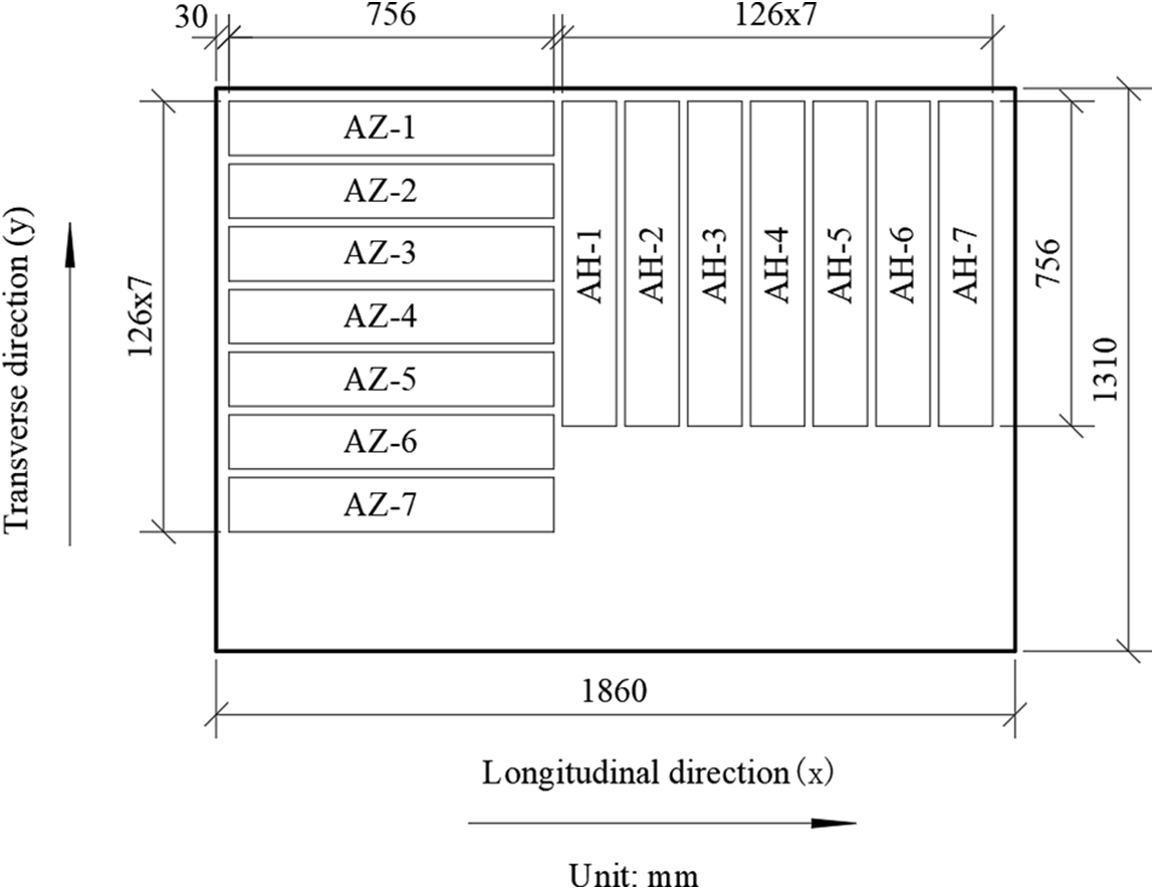
Figure 1: The blanking diagram of the bamboo scrimber plate

The elastic modulus, shear modulus, and Poisson’s ratio of AZ and AH specimens were dynamically measured then one longitudinal plate and one transverse plate were sawn into beam specimens for static verification test of symmetrical four-point bending and asymmetrical four-point bending method. In this test, AZ-6 and AH-5 specimens were taken and made into 5 beam specimens of 380 mm (l) × 18 mm (b) × 18 mm (h) each, the longitudinal number was BZ, and the transverse number was BH.

2.2 Test Instruments and Accessories

One set of CRAS vibration and dynamic signal acquisition and analysis systems, mainly including signal conditioning instrument, signal acquisition box and its supporting analysis software, 1 CA-YD-125 voltage acceleration sensor, mass 1.5 g, sensitivity 0.089 pc/m·s−2. The main accessories include 1 JY-501 electronic balance (0.1 g), 1 vernier caliper (0.02 mm), 1 steel ruler (0–500 mm), 1 HK-30 induction wood moisture tester, and 1 rubber hammer.

2.3 Dynamic Testing of Elastic Modulus, Shear Modulus and Poisson’s Ratio of Bamboo Scrimber Specimens

2.3.1 Dynamic Testing of Elastic Modulus and Shear Modulus of Free Plates

Dynamic measurement of elastic modulus and shear modulus by the dynamic method: the elastic modulus value is obtained by the free-plate transient excitation method according to the transverse bending theory of Euler beams [26]. The relationship between the first-order bending frequency of the free beam and the elastic modulus E is shown in Eq. (1).

E=0.9462ρl4f1b2h2 (1)

where ρ is density (kg/m3); l is the length of the free plate (m); f1b first-order bending frequency of the free plate (Hz); h is the thickness of the free plate (m).

Using the free plate mode coefficient γ in the free plate torsional mode method, the free plate mode coefficient of bamboo scrimber is calculated, and the shear modulus G is obtained.

The relationship between the first-order torsional frequency of the free plate and the shear modulus is shown in Eq. (2).

G=π2ρ(l/2)2b2f1t2γβh2(l/b=1∼8) (2)

where ρ is density (kg/m3); l is the length of the free plate (m); b is the width of free plate (m); f1t is the first-order torsional frequency of cantilever plate (Hz); γ is mode shape coefficients of the free plate which can be calculated by width-to-length and thickness-to-width ratios of the free plate; β≈1/16[16/3−3.36hb(1−h412b4)].

The free plate mode coefficient γ adopts the Eq. (3) [27]:

γ=7.1153(1+0.3583bl+0.0417hb) (3)

The experimental process [28,29] is shown in Fig. 2.

Figure 2: Block diagram of the free plate transient excitation test system

2.3.2 Dynamic Testing of Elastic Modulus, Shear Modulus, and Poisson’s Ratio of Cantilever Plates

Based on the transverse bending theory of Euler beams, the relationship between the first-order bending frequency of a cantilever plate and the elastic modulus E is shown in Eq. (4):

E=48π2l4f1b2(1.875)4h2 (4)

where l is the outrigger length of the cantilever plate (m); f1b is the first-order bending frequency of the cantilever plate (Hz); h is the thickness of the cantilever plate (m).

The relationship between the first-order torsional frequency of the cantilever plate and the shear modulus is shown in Eq. (5):

G=π2ρl2b2f1t2C1βh2−C2E (5)

where ρ is density (kg/m3); l is the outrigger length of the cantilever plate (m); b is the width of the cantilever plate (m); f1t is the first-order torsional frequency of the cantilever plate (Hz); C1, C2 is mode shape coefficients of the cantilever plate which can be calculated by width-to-length and thickness-to-width ratios of the cantilever plate; β≈116[163−3.36hb(1−h412b4)]; h is the thickness of the cantilever plate (m).

The mode shape coefficients C1 and C2 of the cantilever plate [28] are shown in Eqs. (6) and (7):

C1=7.4809+4.462bl−2.9980hb (6)

C2=0.00763+0.04032bl−0.05351hb (7)

The Poisson’s ratio of the cantilever plate is shown in Eq. (8):

μ=ε90∘ε0∘ (8)

where Δεx is the longitudinal strain increment (μm/m); Δεy is the transverse strain increment (μm/m).

In Fig. 3, the 126 mm end of the bamboo scrimber specimen is clamped with a splint to achieve a fixed restraint method, forming a cantilever with a length of 630 mm, a width of 126 mm, and a thickness of 18 mm, achieving an aspect ratio of 5 and a width-to-thickness ratio of 7. An accelerometer is placed at a distance of 0.8 l from the fixed end of the board to connect to the CRAS vibration and dynamic signal acquisition and analysis system and its SsCras signal analysis software.

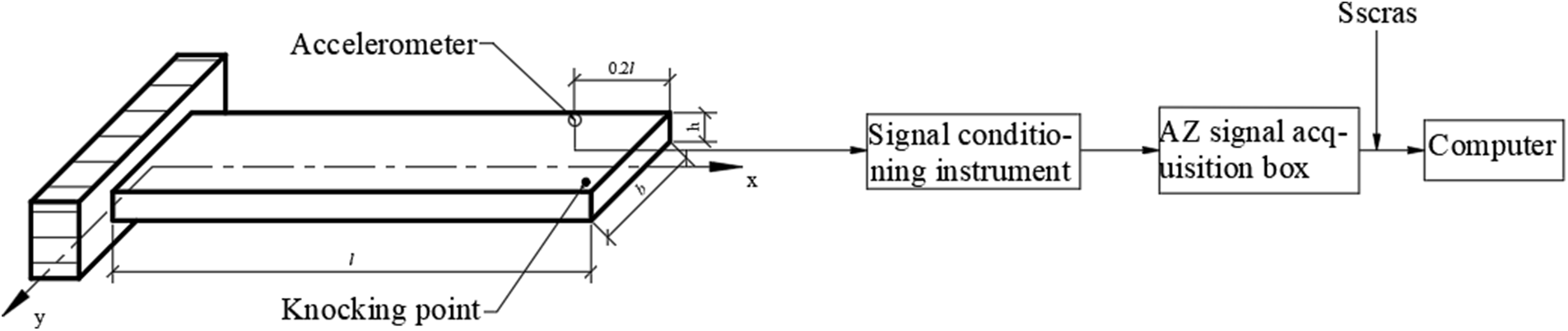
Figure 3: Transient excitation test block diagram of the bamboo scrimber cantilever plate specimen

When dynamically testing the Poisson’s ratio of the cantilever plate specimen, the mid-span patch method is selected, as shown in Fig. 4. The longitudinal strain gauge on the upper surface of the cantilever plate occupies one channel (1ch) of the dynamic strain gauge according to the half-bridge method, and the transverse strain gauge on the lower plate of the cantilever plate occupies the other channel (2ch) of the dynamic strain gauge according to the half-bridge method, that is, dual-channel measurement. The output signal of the signal conditioner converts the analog signal into a digital signal through the signal acquisition box, and then through the signal analysis software and computer calculation, the spectrum of the cantilever plate is displayed.

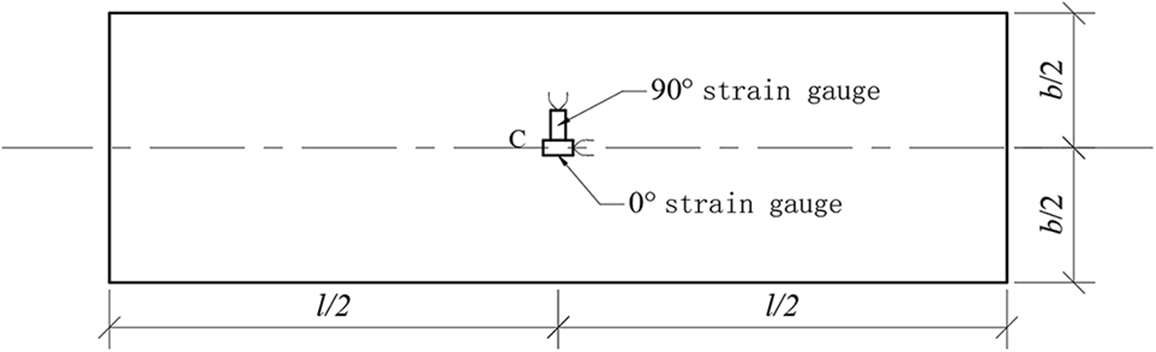
Figure 4: Strain gauge midspan patches for cantilever specimens

2.4 Static Verification Test of Elastic Modulus, Shear Modulus, and Poisson’s Ratio

2.4.1 Static Verification Test of Elastic Modulus and Poisson’s Ratio for the Symmetrical Four-Point Bending Beam Method

The loading schematic diagram of the symmetrical four-point bending beam is shown in Fig. 5.

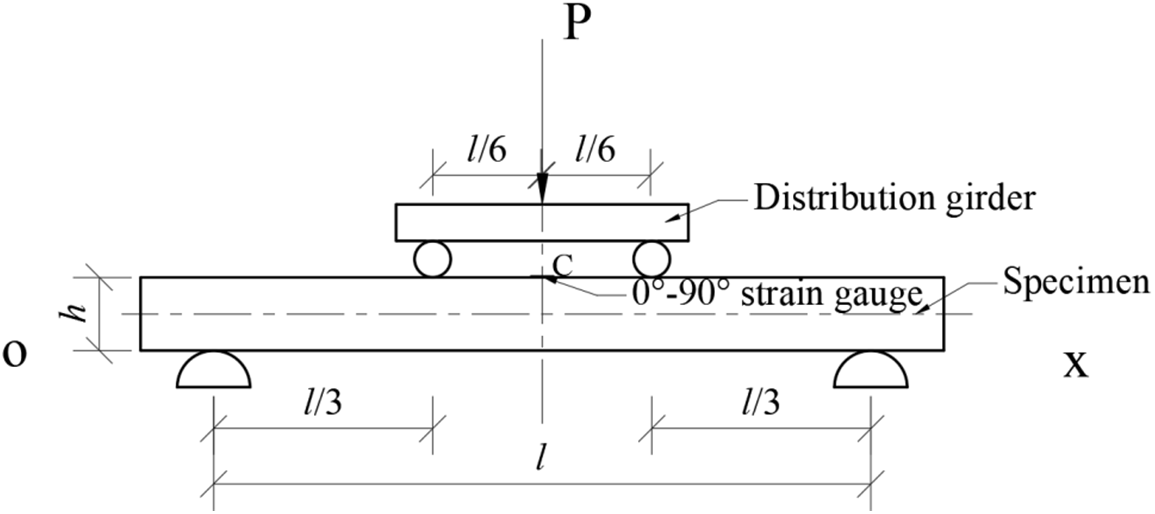
Figure 5: Schematic diagram of loading of the symmetrical four-point bending beam

In the symmetrical four-point bending beam (l/3-l/3-l/3 loading), the normal stress at each point on the upper and lower surfaces of the beam in the pure bending section is as shown in Eq. (9).

σ=Plbh2 (9)

If the longitudinal strain at the center point of the upper and lower surfaces of the beam is εx, then according to Hooke’s law, its elastic modulus E can be expressed as E=Plbh2εx, written in incremental form:

E=ΔP⋅lbh2Δεx (10)

where ΔP is the load increment (N); l is the length of beam (m); b is the width of beam (m); h is the thickness of beam (m); Δεx is the longitudinal strain increment ( μm/m).

If the test values of transverse strain and longitudinal strain at the center point of the upper and lower surfaces of the beam in the pure bending section are εy and εx while using the symmetrical four-point bending beam (l/3-l/3-l/3 loading), the Poisson’s ratio can be written as:

μ=−ΔεyΔεx (11)

where Δεx is longitudinal strain increment ( μm/m); Δεy is transverse strain increment ( μm/m).

Attach 90° (longitudinal) and 0° (transverse) strain gauges at the center points of the upper and lower surfaces of the beam specimen, a symmetrical four-point bending load was applied to the beam (Fig. 5), and the longitudinal and transverse strains at the center point were measured. Two sets of half-bridge tests were carried out by the symmetrical four-point bending method. Place the specimen on the support and position it as shown in Fig. 5 and place the auxiliary beam so that the loading point is above the center of the 90° strain gauge. A weight of 2.55 kg was placed on the auxiliary beam three times to apply a load to the four-point bending system, and the software was used to record the strain value of the specimen after each placement of the weight for subsequent calculation.

2.4.2 Static Verification Test for Shear Modulus of Asymmetric Four-Point Bending Beam Method

The loading schematic diagram of the asymmetric four-point bending beam is shown in Fig. 6. The asymmetric four-point bending beam method tests the shear modulus of a material based on Hooke’s law in shear and the formula for calculating the maximum shear stress at a point on the neutral axis of a beam with a rectangular section. The shear modulus is derived by measuring the shear strain at a point on the neutral axis.

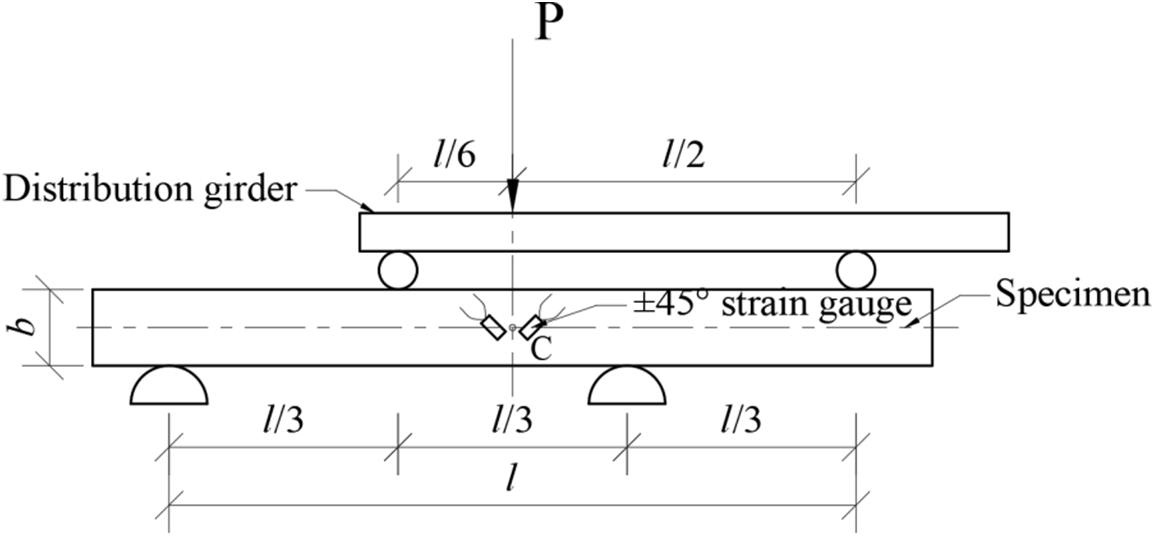
Figure 6: Schematic diagram of the four-point bending beam test device with asymmetric loading

Since the shear stress τmax=3Q2bh at the point on the neutral axis of the beam cross-section, the shear stress τ=3P4bh at the center point of the side surface of the beam under asymmetrical bending loading, and the shear strain υ=ε−45∘−ε45∘.

According to Hooke’s law of shearing, its shear modulus G can be expressed as G=3ΔP4bh|Δε−45∘−Δε45∘|, which can be written in an incremental form that is convenient for testing.

G=3ΔP4bh|Δε−45∘−Δε45∘| (12)

where ΔP is load increment (N); b is the width of beam (m); h is the thickness of beam (m); Δε−45∘ and Δε+45∘ are strain increments in the minus 45° and plus 45° directions at the center point of the beam side ( με).

If the full bridge method is adopted, then |Δε−45o−Δε45∘|=2Δε, Eq. (13) can be written as

G=3ΔP8bhΔε (13)

where Δε is strain increment readings for full bridge measurements ( μm/m).

Attach 45° strain gauges at the center points of the front and rear side surfaces of the beam specimen. In Fig. 6, the beam was subjected to an asymmetrical four-point bending load, and the shear strain at the center point was measured. The +45° and −45° strain gauged on the front and rear side surfaces of the beam occupy one channel of the strain gauge according to the full bridge method.

Place the specimen on the support and position it as shown in Fig. 6 and place the auxiliary beam so that the loading point was above the center of the ±45° strain gauge. A weight of 1.275 kg was placed on the auxiliary beam three times to apply a load to the four-point bending system, and the software was used to record the strain value of the specimen after each placement of the weight for subsequent calculation.

3  Results and Analysis

3.1 Dynamic Test Results and Analysis of Elastic Modulus and Shear Modulus of Bamboo Curtain Plywood

3.1.1 Results and Analysis of Free Plate Specimen

The average elastic modulus value of the AZ specimen measured by the transient test is 12019 MPa (CoV: 5.3%), and the shear modulus value is 1559 MPa (CoV: 6.6%); the average elastic modulus value of the AH specimen measured It was 3230 MPa (CoV: 18.4%), and the shear modulus was 1551 MPa (CoV: 10.6%). Apparently, the bamboo scrimber longitudinal plate has an elastic modulus about 3.7 times that of its transverse plate, and the shear modulus is the same. There is a large error in the test results of the transverse plate by the transient excitation method of the free plate. The main reason is that the bamboo bundles of the bamboo scrimber have different paving patterns, some are in a parallel pavement state, and some are in a folded state. Pavement state, so the obtained elastic constants vary greatly.

Bamboo scrimber is composed of bamboo bundle units, which are assembled according to the grain and glued together by hot pressing (or cold pressing). The bamboo bundle unit is a vascular bundle structure, and its arrangement is unidirectional. The elastic modulus of bamboo is very high along the grain. It not only maintains the advantages of the high strength of bamboo but also overcomes the disadvantage of the thin wall of bamboo. Moreover, the adhesive interface of the bamboo scrimber after hot pressing is mainly distributed on the yz and xz planes, which determines that the elastic modulus Ex of the bamboo scrimber along the grain direction will be much larger than the elastic modulus Ey in the transverse grain direction, which is consistent with the test results.

Since the shear modulus is an elastic constant that reflects the in-plane properties of the material, the shear modulus measured in this test is the torsional shear modulus of the xy plane.

3.1.2 Results and Analysis of Free Beam Specimen

To verify the correctness and reliability of the elastic modulus and shear modulus results of the dynamic test of the bamboo scrimber specimen in this study, the longitudinal beam specimens BZ and transverse beam specimens BH were sawn from two plate specimens AZ-6 and AH-5.

It can be seen from Table 1 that the elastic modulus of the beam specimens processed by AZ-6 and AH-5 is not much different from the original plate specimens. Due to the small cross-section, the torsional frequency was not captured during the test, so the results did not reflect the shear modulus. There is also a relationship between the longitudinal elastic modulus and the transverse elastic modulus of 3.1 times for the beam specimen, which is consistent with the result of the plate specimen. Among them, the coefficient of variation of the BH specimen is larger and similar to the average result of the transverse plate specimen AH. This is related to the way of assembling the bamboo scrimber. The bamboo bundles are assembled along the grain, resulting in the bamboo scrimber being compact in the longitudinal direction, while in the transverse direction, due to the large number of glue layers and the uneven distribution, there is also a certain difference between the materials in the same direction. And the beam whose cutting position is close to the edge of the plate is relatively easier to deform. During the test, among the 5 BH specimens, the first-order bending frequencies of the 3 beam specimens whose blanking positions were located at the edge of the original plate were relatively small, which resulted in a large variation coefficient of the average results of the BH specimens.

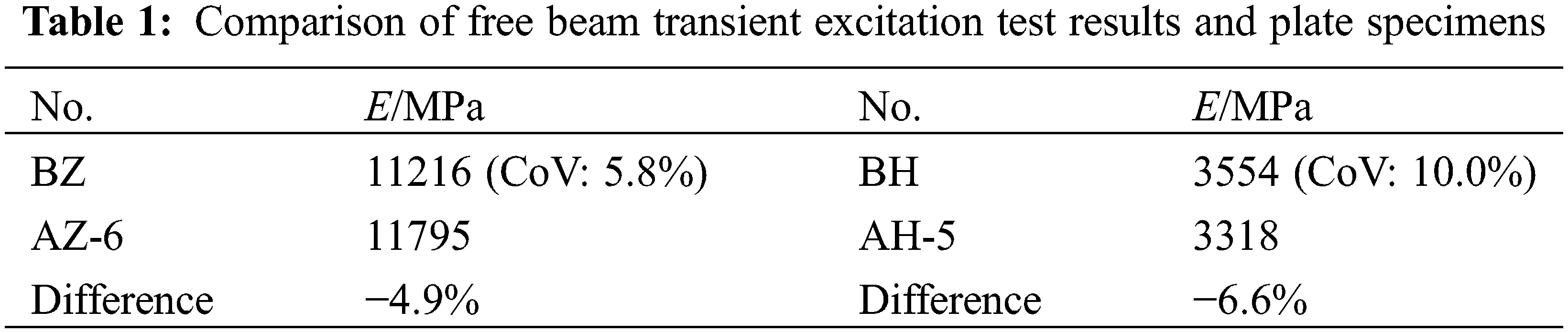
3.2 Dynamic Test Results and Analysis of Elastic Modulus, Shear Modulus, and Poisson’s Ratio for Cantilever Plates

The elastic modulus, shear modulus, and Poisson’s ratio of the bamboo scrimber were measured simultaneously by the cantilever transient excitation method, which was verified with the free suspension test results. The first-order frequency and the corresponding x-direction strain and y-direction strain are obtained, and the corresponding elastic constants are calculated. The results of the cantilever method and the free plate method are compared in Table 2.

It can be seen from Table 2 that the elastic modulus Ex of the longitudinal plate AZ measured by the cantilever method is 11797 MPa, the shear modulus Gxy is 1579 MPa, and the Poisson’s ratio μxy is 0.311. The elastic modulus Ey of the transverse plate AH was 3401 MPa, the shear modulus Gyx was 1561 MPa, and the Poisson’s ratio μyx was 0.105. The results measured by the cantilever plate transient excitation method are consistent with the results of the free plate transient excitation test method, the relative error is within 5%, and the Poisson’s ratio also has a quantitative relationship that the longitudinal plate is 3 times that of the transverse plate. This result shows that it is feasible to dynamically test E, G, and μ of the bamboo scrimber, and the test results are accurate. Substitute the test results into the isotropic verification formula G=E/2(1+μ), the equation does not hold, so the bamboo scrimber is identified as an anisotropic material.

3.3 Static Verification Test Results and Analysis of Elastic Modulus, Shear Modulus, and Poisson’s Ratio

To verify the accuracy of the elastic constant of the bamboo scrimber specimen in the dynamic test, a static four-point bending test was carried out. This study mainly compares the dynamic and static elastic moduli of BZ and BH beam specimens and tests the static Poisson’s ratio of the beam specimens, which is used as the basis for judging whether the bamboo scrimber is anisotropic [29,30]. Since in the symmetrical four-point bending test, the upper surface is compressed and the lower surface is tensioned, the test result is the average value of the tensile elastic modulus and the compression elastic modulus, that is, the bending elastic modulus. The texture of the material will change the measured amount of strain due to different stress conditions. To exclude the influence of bamboo bundle texture on the elastic modulus of bamboo scrimber, the upper and lower surfaces are defined as U surface and D surface in the test, and two sets of tests are carried out, denoted as I and II. In group I experiments, the U face was upward, and in the second group experiment, the D face was upward.

It can be seen from Fig. 7 that the average longitudinal elastic modulus Ex of the beam specimen measured by the symmetrical four-point bending test method is 12317 MPa (CoV: 7.80%), and the average transverse elastic modulus Ey is 3408 MPa (CoV: 10.11%). The ratio of the elastic modulus of the longitudinal beam to the elastic modulus of the beam is 3.6:1, and the ratio of Poisson’s ratio of the longitudinal beam to the Poisson of the beam is 3.5:1. During the test, flipping the upper and lower surfaces of the specimen has little effect on the test results.

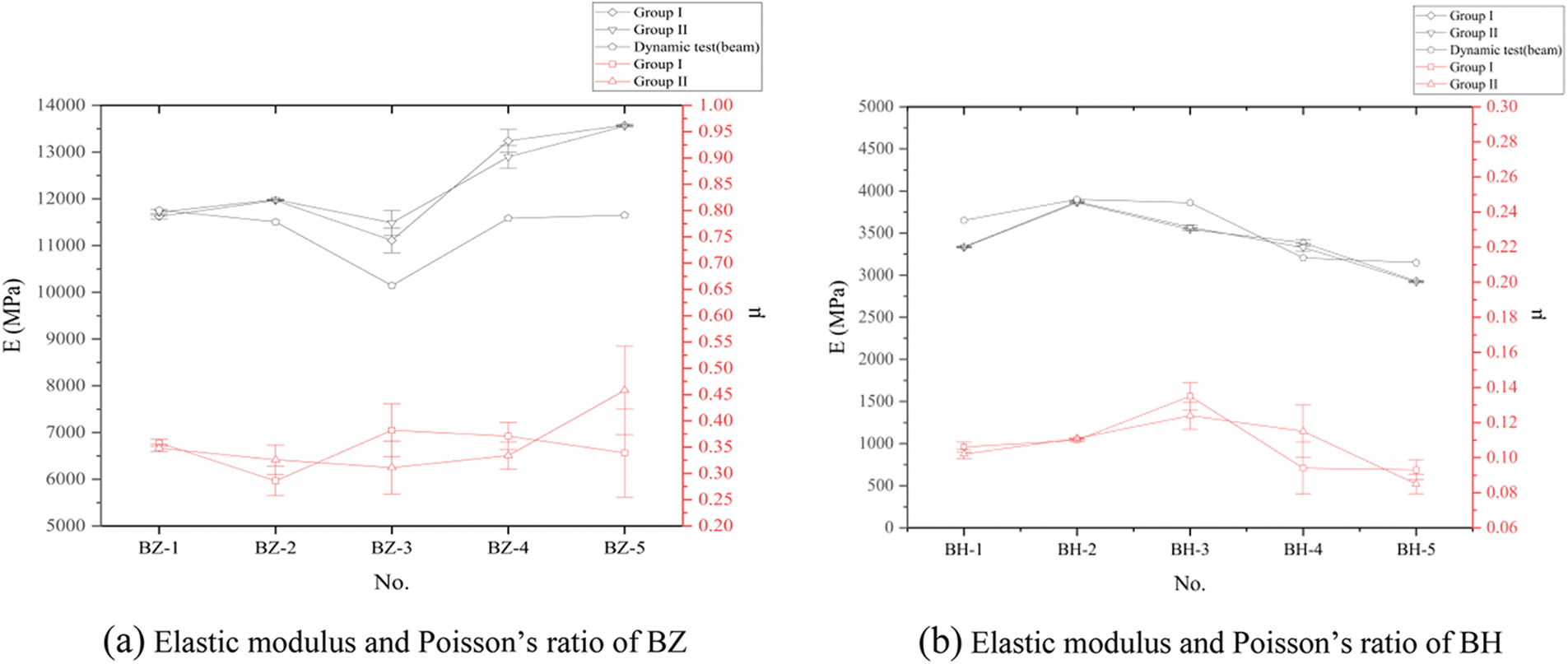
Figure 7: Summary of static symmetric four-point bend test results

To verify the accuracy of the dynamic test, a static asymmetric four-point bending test was carried out. Substitute into Eq. (10) to calculate the shear modulus of each plate specimen. The average value of Gxy of the longitudinal plate measured by the asymmetric four-point bending test is 1639 MPa, and the average value of Gyx of the transverse plate is 1407 MPa, and the test results differ by 14.2%. The coefficients of variation of the test values of Gxy and Gyx were all less than 9%, which confirmed the reliability of the test.

3.4 Comparison of E, G, μ Dynamic Testing and Static Verification Experiments

The dynamic test and static test results of the beam specimen are shown in Tables 3 and 4.

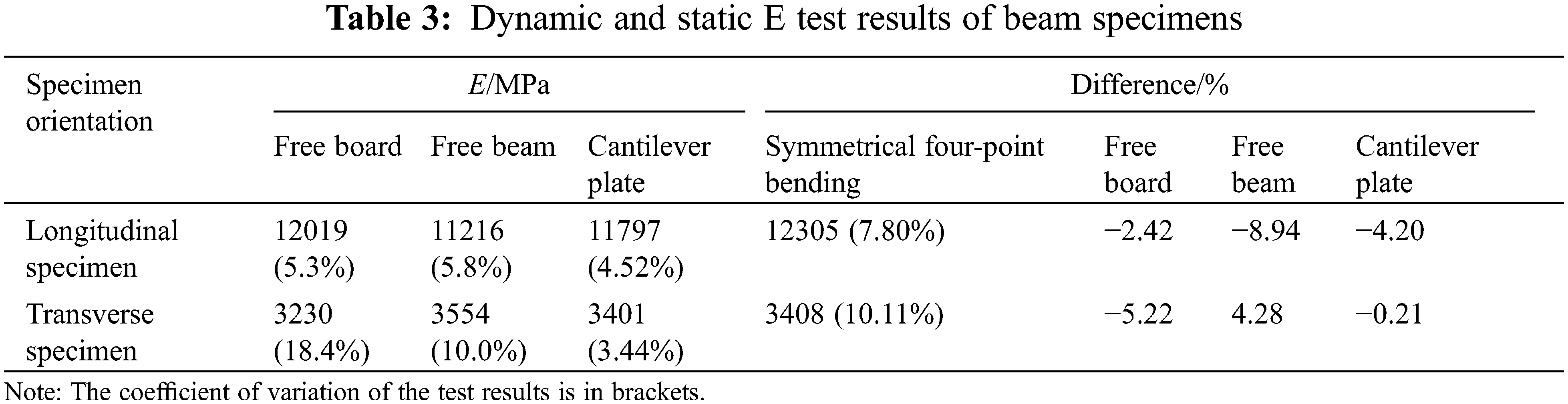
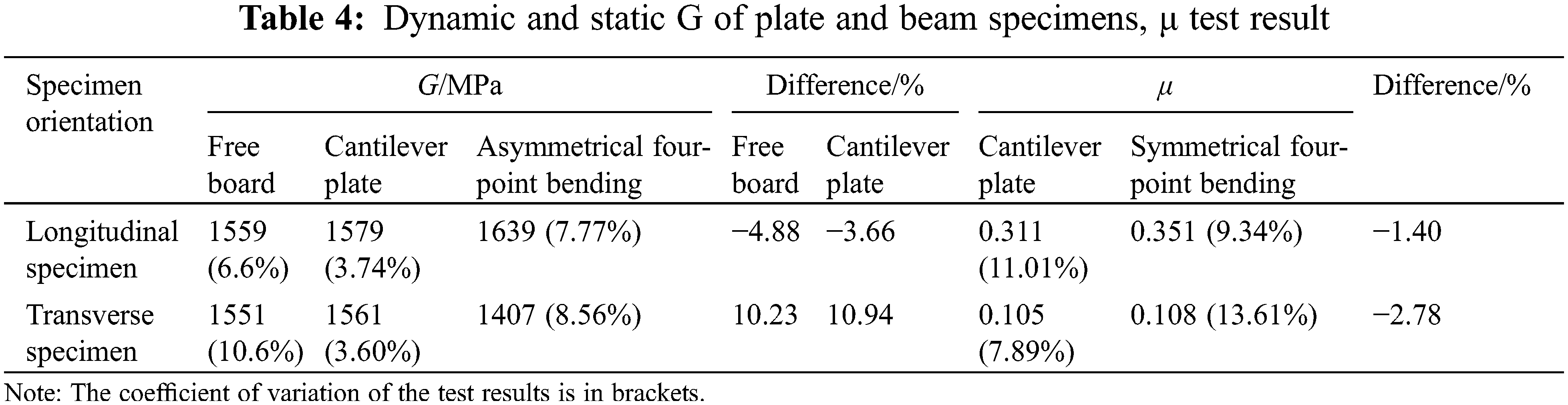
It can be seen from Table 3 that the transient elastic modulus of the free plate of the longitudinal specimen is 2.42% smaller than the static elastic modulus, and the dynamic elastic modulus of the transverse specimen is 5.22% smaller than the static elastic modulus. The accuracy of the dynamic free-hanging transient excitation test can be confirmed. The longitudinal elastic modulus of the cantilever plate is 4.20% smaller than the static elastic modulus, and the dynamic elastic modulus of the transverse specimen is 0.21% smaller than the static elastic modulus, so the accuracy of the transient excitation test of the dynamic cantilever plate can be confirmed. The test deviations of the longitudinal and transverse elastic modulus values in each test are similar, which confirms the reliability of each test.

It can be seen from Table 4 that the shear modulus of the free-hanging longitudinal plate is 4.88% smaller than that of the asymmetric longitudinal beam. The longitudinal shear modulus of the cantilever plate is 3.66% smaller than that of the asymmetric four-point bending longitudinal beam. The difference in transverse shear modulus is larger, with a difference of 10.23% and 10.94%, respectively. The transverse beam specimen used here is taken from the plate specimen AH-5 and its dynamic shear modulus is 1492 MPa and its shear modulus measured by the static asymmetric four-point bending transverse beam specimen has a 6% difference, which can also prove that dynamic and static anastomosis. The average shear modulus of the AH specimen is quite different from that of the asymmetric four-point bending specimen. The reason is that the shear modulus of the AH-5 specimen itself is poor, which affects the shear modulus of the BH specimen made from it.

The dynamic test results are generally lower than the static test results, but the difference is not large. The test results of the free-plate transient excitation method are higher than those of the cantilever plate torsional vibration method and are closer to the static test results. The results are consistent with those in the OSB test and wood test.

In addition, according to the existing research [31,32], it can be seen that the bonding strength also has a certain influence on the material strength. The fiber roughness, porosity, wettability, and adhesive density of the glued interface will all affect the mechanical strength. For the bamboo scrimber, the transverse bonding interface is densely distributed, and the bamboo fiber is not subjected to transverse force, resulting in a particularly obvious effect of the bonding strength on the elastic constants (E, G). In the current world, the surface treatment of bamboo bundles is still in the laboratory stage. In actual production, the surface of bamboo bundles is rarely treated, which also leads to the greater variability of the bonding strength of bamboo scrimber, which affects the E and G of the material, and the effect on the transverse direction of bamboo scrimber is more obvious. This leads to a large error in the test results of the transverse plate, about 10%. However, according to research in the field of wood, there is a certain difference between the measured value and the theoretical value of the elastic constant of natural materials such as wood, and the error is generally between 15% and 25% [33]. Therefore, the deviation between the dynamic and static test results is 10%, which confirms the reliability of the dynamic test results.

3.5 Anisotropic Analysis of Bamboo Scrimber

Substitute the dynamic and static measured E, G, and μ into the relationship of G=E/2(1+μ) and the equation does not hold because the bamboo scrimber in this test is an anisotropic material and the test deviations of the longitudinal and transverse elastic modulus values in each test are similar, which confirms the reliability of the dynamic test.

Bamboo scrimber can be divided into bamboo bundles and adhesives according to the process of bamboo scrimber. Bamboo bundles can be subdivided into bamboo fibers (vascular bundle structure composed of thick-walled cells) and matrix (parenchyma cells). According to the existing research on bamboo [29], the mechanical properties of bamboo fiber in bamboo scrimber are far better than those of bamboo matrix, and the properties of matrix are better than those of adhesive.The longitudinal direction of the board is along the grain direction, and its elastic modulus can be understood as the weighting of the elastic modulus of the bamboo fiber, the matrix, and the adhesive after curing, while the transverse direction of the board is perpendicular to the grain, and its elastic modulus is the weighting of the matrix and the adhesive. From the perspective of a microscopic three-dimensional structure, bamboo fibers exist in a linear structure, the matrix is a honeycomb structure, and the interface and the interface between the two are the weak points of the overall structure. These interfaces exist more in the transverse direction, and the transverse bamboo fibers are not stressed, so the longitudinal elastic modulus is much larger than the transverse elastic modulus. In addition, there are inevitably micro-voids that are invisible to the naked eye at the bonding interface of composite materials. This phenomenon leads to the failure of effective stress conduction, and the material weak point appears on the bonding interface, which seriously weakens the elastic properties of the material. For the bamboo scrimber, the dense arrangement of the lateral adhesive layer also amplifies this defect, resulting in stronger variability and a slightly larger difference in the elastic modulus values of the same specifications and the same direction.

4  Conclusion

The results of the Bamboo Scrimber elastic constant dynamic test using the free plate and the cantilever plate transient excitation method are the same. In this paper, the principal elastic modulus, shear modulus, and Poisson’s ratio of the bamboo scrimber in the dynamic test are about 12 GPa, 1500 MPa, and 0.31, respectively, which meet the technical requirements of the bamboo scrimber for structural use in GB/T 40247-2021. The minimum standard of elastic modulus of reconstituted bamboo in GB/T 40247-2021 is 9 GPa. The bamboo scrimber in this paper has reached the level of 120 Ec.

The elastic constant value of bamboo scrimber in the dynamic test does not satisfy the relation of G=E/2(1+μ), so bamboo scrimber is an anisotropic material. The longitudinal E and G variability of bamboo scrimber is small, and the lateral mechanical property variability is large. The longitudinal elastic modulus is 3-4 times that of the transverse direction, the longitudinal Poisson’s ratio is 3 times that of the transverse direction, and the shear modulus of the transverse and longitudinal directions are similar.

The dynamic test method is suitable for the determination of the elastic modulus, shear modulus, and Poisson’s ratio of the bamboo scrimber. The beam specimen tested by the static four-point bending method is directly sawed from the same plate specimen tested by the dynamic test, and the error of the dynamic and static test results is 10%, which proves the accuracy of the dynamic test. The free-plate transient excitation method is more accurate.

The method of dynamically testing the elastic constant of bamboo scrimber has the advantages of quickness, simplicity, good repeatability, and high precision.

Funding Statement: The authors received no specific funding for this study.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. Mimendi, L., Lorenzo, R., Li, H. (2022). An innovative digital workflow to design, build and manage bamboo structures. Sustainable Structures, 2(1), 000011. https://doi.org/10.54113/j.sust.2022.000011 [Google Scholar] [CrossRef]

2. Su, J., Li, H., Xiong, Z., Lorenzo, R. (2021). Structural design and construction of an office building with laminated bamboo lumber. Sustainable Structures, 1(2), 000010. https://doi.org/10.54113/j.sust.2021.000010 [Google Scholar] [CrossRef]

3. Yu, W. (2012). Current status and future development of bamboo scrimber industry in China. Chinese Journal of Wood Scien1ce and Technology, 26(1), 11–14. https://doi.org/10.19455/j.mcgy.2012.01.005 [Google Scholar] [CrossRef]

4. Yang, F. (2014). Processing technology of bamboo scrimber and OSB composite and its performance prediction. Chines Academy of Forestry. https://doi.org/10.7666/d.Y2629885 [Google Scholar] [CrossRef]

5. Zhang, J., Li, Y., Liu, R., Xu, D., Bian, X. (2018). Examining bonding stress and slippage at steel-bamboo interface. Composite Structures, 194, 584–597. https://doi.org/10.1016/j.compstruct.2018.04.037 [Google Scholar] [CrossRef]

6. Dauletbek, A., Li, H., Xiong, Z., Lorenzo, R. (2021). A review of mechanical behavior of structural laminated bamboo lumber. Sustainable Structures, 1(1), 000004. https://doi.org/10.54113/j.sust.2021.000004 [Google Scholar] [CrossRef]

7. Guan, M., Zhu, Y., Zhang, X. (2006). Comparison of bending properties of scrimber and bamboo scrimber. Journal of Northeast Forestry University, 1(4), 7–21. https://doi.org/10.3969/j.issn.1000-5382.2006.04.003 [Google Scholar] [CrossRef]

8. GB/T 40247-2021 (2021). Bamboo scrimber. China: China Quality and Standards Publishing and Media Co., Ltd. [Google Scholar]

9. LY/T 3194-2020 (2020). Structural bamboo scrimber. China: China Quality and Standards Publishing and Media Co., Ltd. [Google Scholar]

10. Wang, T., Di, J., Zuo, H. (2021). Experimental study on bending behavior of glulam beams strengthened with bamboo scrimber. International Journal of Structural Integrity, 13(1). https://doi.org/10.1108/IJSI-03-2021-0037 [Google Scholar] [CrossRef]

11. Liang, D., Chen, H. S., Yu, X. H. (2016). Advance on joint types of recombined bamboo timber. Journal of Zhejiang Forestry Science and Technology, 36(4), 81–84. https://doi.org/10.3969/j.issn.1001-3776.2016.04.016 [Google Scholar] [CrossRef]

12. Liu, K., Jayaraman, D., Shi, Y., Harries, K., Yang, J. et al. (2022). “Bamboo: A very sustainable construction material”—2021 international online seminar summary report. Sustainable Structures, 2(1), 000015. https://doi.org/10.54113/j.sust.2022.000015 [Google Scholar] [CrossRef]

13. Zhang, J., Ren, Q., Zhong, Y., Zhao, R. (2012). Analysis of compressive and tensile mechanical properties of recombinant bamboo. Journal of Nanjing Forestry University (Natural Sciences Edition), 36(4), 107–111. https://doi.org/10.3969/j.issn.1000-2006.2012.04.022 [Google Scholar] [CrossRef]

14. Quintero, M. A. M., Tam, C. P. T., Li, H. (2022). Structural analysis of a Guadua bamboo bridge in Colombia. Sustainable Structures, 2(2), 000020. https://doi.org/10.54113/j.sust.2022.000020 [Google Scholar] [CrossRef]

15. Chung, M. J., Wang, S. Y. (2018). Effects of peeling and steam-heating treatment on mechanical properties and dimensional stability of oriented Phyllostachys makinoi and Phyllostachys pubescens scrimber boards. Journal of Wood Science, 64(5), 625–634. https://doi.org/10.1007/s10086-018-1731-y [Google Scholar] [CrossRef]

16. Kubojima, Y., Inokuchi, Y., Suzuki, Y., Tonosaki, M. (2010). Shear modulus of several kinds of Japanese bamboo obtained by flexural vibration test. Journal of Wood Science, 56(1), 64–70. https://doi.org/10.1007/s10086-009-1047-z [Google Scholar] [CrossRef]

17. Zhou, X., Tang, W., Wang, Z., Cao, L. (2014). Study on transverse free vibration of bamboo wood. Journal of Central South University of Forestry and Technology, 34(5), 75–78. https://doi.org/10.14067/j.cnki.1673-923x.2014.05.006 [Google Scholar] [CrossRef]

18. Armandei, M., Darwish, I. F., Ghavami, K. (2015). Experimental study on variation of mechanical properties of a cantilever beam of bamboo. Construction and Building Materials, 101, 784–790. https://doi.org/10.1016/j.conbuildmat.2015.10.078 [Google Scholar] [CrossRef]

19. Wang, Z. H., Wang, Z., Wang, B. J., Wang, Y., Liu, B. et al. (2014). Dynamic testing and evaluation of modulus of elasticity (MOE) of SPF dimension lumber. BioResources, 9(3), 3869–3882. https://doi.org/10.15376/biores.9.3.3869-3882 [Google Scholar] [CrossRef]

20. Wang, Z., Xie, W. B., Wang, Z. H., Cao, Y. (2018). Strain method for synchronous dynamic measurement of elastic, shear modulus and Poisson’s ratio of wood and wood composites. Construction and Building Materials, 182, 608–619. https://doi.org/10.1016/j.conbuildmat.2018.06.139 [Google Scholar] [CrossRef]

21. Wang, Z. H., Gao, Z. Z., Wang, Y. L., Cao, Y., Wang, G. G. et al. (2015). A new dynamic testing method for elastic, shear modulus and Poisson’s ratio of concrete. Construction and Building Materials, 100(1), 129–135. https://doi.org/10.1016/j.conbuildmat.2015.09.060 [Google Scholar] [CrossRef]

22. Wang, Z. H., Ghanem, R. (2022). A functional global sensitivity measure and efficient reliability sensitivity analysis with respect to statistical parameters. Computer Methods in Applied Mechanics and Engineering, 115175. https://doi.org/10.1016/j.cma.2022.115175 [Google Scholar] [CrossRef]

23. Wang, Z. H., Ghanem, R. (2021). An extended polynomial chaos expansion for PDF characterization and variation with aleatory and epistemic uncertainties. Computer Methods in Applied Mechanics and Engineering, 382, 113854. https://doi.org/10.1016/j.cma.2021.113854 [Google Scholar] [CrossRef]

24. Peng, Y. B., Wang, Z. H., Ai, X. Q. (2018). Wind-induced fragility assessment of urban trees with structural uncertainties. Wind and Structures, 26(1), 45–56. https://doi.org/10.12989/was.2018.26.1.045 [Google Scholar] [CrossRef]

25. Wang, M. (2022). Study on quasi-static and dynamic mechanical properties and failure mechanism of bamboo scrimber. North University of China, China. https://doi.org/10.27470/d.cnki.ghbgc.2022.000643 [Google Scholar] [CrossRef]

26. Timoshenko, S. (1965). Mechanical vibration, pp. 316–333. Beijing, China: Engineering Industry Press. [Google Scholar]

27. Wang, Z., Xie, W. B., Lu, Y., Li, H. T., Wang, Z. H. et al. (2019). Dynamic and static testing methods for shear modulus of oriented strand board. Construction and Building Materials, 216, 542–551. https://doi.org/10.1016/j.conbuildmat.2019.05.004 [Google Scholar] [CrossRef]

28. Wang, Z. H., Wang, Y. L., Cao, Y., Wang, Z. (2016). Measurement of shear modulus of materials based on the torsional mode of cantilever plate. Construction and Building Materials, 124, 1059–1071. https://doi.org/10.1016/j.conbuildmat.2016.08.104 [Google Scholar] [CrossRef]

29. Wang Y. Z., Zhang C. L., Chen W. Q. (2017). An analytical model to predict material gradient and anisotropy in bamboo. Acta Mechanica, 228(8), 2819–2833. https://doi.org/10.1007/s00707-015-1514-0 [Google Scholar] [CrossRef]

30. Qiu, Z., Wang, J., Fan, H. (2021). Impact bending behaviors of parallel bamboo strand lumber beams: Velocity sensitivity and anisotropy. Composite Structures, 263, 113711. https://doi.org/10.1016/j.compstruct.2021.113711 [Google Scholar] [CrossRef]

31. Xu, J., Liu, R., Wu, H., Qiu, H., Yu, Y. et al. (2019). Coating performance of water-based polyurethane-acrylate coating on bamboo/bamboo scrimber substrates. Advances in Polymer Technology, 4264701. https://doi.org/10.1155/2019/4264701 [Google Scholar] [CrossRef]

32. Wu, J., Zhang, Y., Ji, Y., Zhu, R., Sun, Y. et al. (2022). Engineering the surface properties of bamboo scrimber to enhance the gluing properties. Polymer Composites, 43(8), 5465–5475. https://doi.org/10.1002/pc.26852 [Google Scholar] [CrossRef]

33. Kollmann, F. P. (1991). Principles of wood science and technology. Beijing, China: China Forestry Publishing House. [Google Scholar]