 Open Access
Open Access
ARTICLE
Coordinate-Parametric Matrix Model Inspired Square-Conjoint Pattern in Cross Woven for Conventional Bamboo Mat
1
College of Furniture and Art Design, Central South University of Forestry and Technology, Changsha, 410004, China
2
College of Materials Science and Engineering, Central South University of Forestry and Technology, Changsha, 410004, China
3
Hunan Taohuajiang Bamboo Science & Technology Co., Ltd., Yiyang, 413400, China
* Corresponding Authors: Liwen Deng. Email: ; Jinbo Hu. Email:
(This article belongs to the Special Issue: Computational Tools for Renewable Materials)
Journal of Renewable Materials 2023, 11(12), 4025-4038. https://doi.org/10.32604/jrm.2023.028454
Received 19 December 2022; Accepted 07 February 2023; Issue published 10 November 2023
Abstract
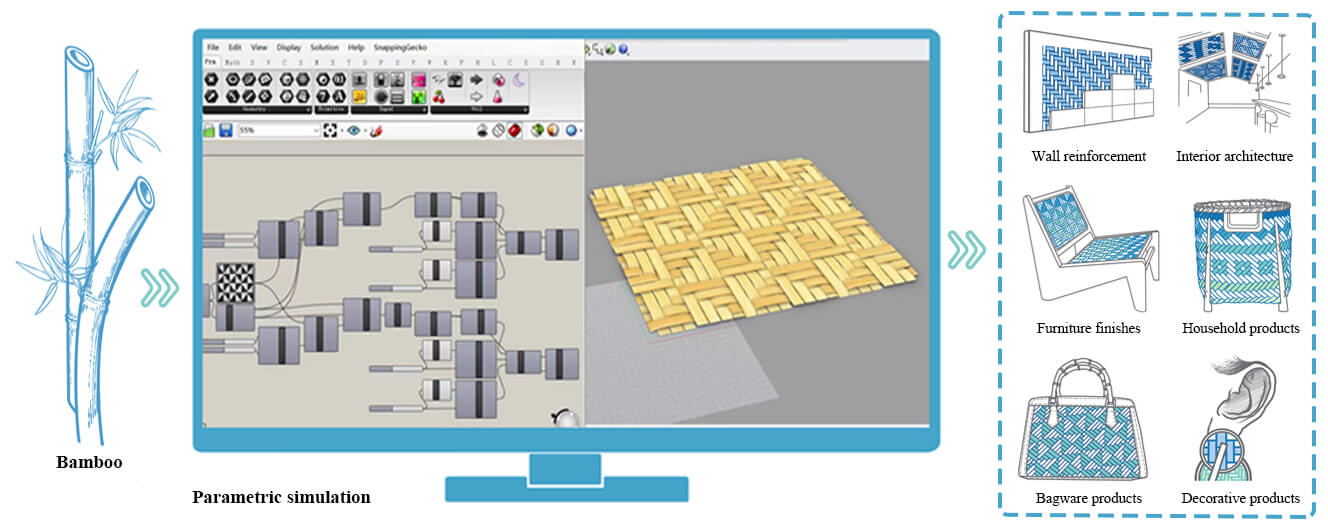
In the study, it is proposed that a coordinate-parametric matrix model is performed to a square-conjoint pattern of cross woven (SCPCW) in the bamboo mat. The patterns of SCPCW are firstly detected according to the perspective of configuration, which is divided into the basic-monomer shape and the basic combination shape. Secondly, the compositions of design patterns in SCPCW are analyzed to attain the trend of curve shape. Based on the coordinate-parametric matrix model, the specimens of SCPCW are subsequently accomplished to elaborate the woven logic of bamboo mats. The digital innovation of SCPCW, defined by a mathematical resolution, is implemented by the software of Grasshopper (GH), which plays a crucial role in capturing image information by the Image Sampler component. Successively, the weaving logic of coordinated matrix is referred to apply in the computing component of Grasshopper software. Finally, the computer simulation could demonstrate that the coordinate-parametric matrix model of SCPCW would be realized to analyze the micro-weaving structure and overall weaving effect in the bamboo mat.Graphic Abstract
Keywords
In the Asia-Pacific region, some conventional bamboo products are abundant [1–3], e.g., bamboo houses, bamboo furniture, bamboo ornamentation, bamboo necessities, and so on. It is especially prominent that bamboo weaving is inset into these bamboo productions. In architectural or furniture decoration, household products, and stationery, bamboo wovens could be sought because the bending strength of the bamboo is applied to weave in various ways [4–9]. Bamboo weaving techniques are classified as polygonal woven and cross-woven [10–12]. The unit of the polygonal-woven pattern (Fig. 1a) is often constructed by three or more bamboo strips (Figs. 1b and 1c), which are interwoven via several angles to make a hollow polygonal-woven structure. However, a single-geometric shape is only anchored into the polygonal-woven pattern (Figs. 1b and 1c). The cell of the cross-woven pattern (Fig. 1d) is made up of two bamboo strips vertically interwoven to pick and press between the warp direction and the weft direction (Fig. 1e). Consequently, a cross woven could emerge many rectangular blocks (Fig. 1d) in a bamboo mat pattern [9,12]. Hence, the cross-woven bamboo design is comparatively applied in furniture and fixtures, specially constructed sophisticated woven patterns [11]. The quadrilateral-chambray mat is composed of some continuous shapes, which are arranged in the bamboo as follows connected type, scattered type, and overlapping type [13]. Usually, a basic shape is centered in the mat pattern to obtain the emissive-decoration effect [14]. Among them, the connected type of square-conjoint pattern is regarded as simple, single, or multiple-constituent patterns, which can be fabricated the visual image in a harmonious and comfortable atmosphere by means of arrangement and repetition [15]. SCPCW in the bamboo mat could be more easily architectural aesthetics, which is more and more popular in decorative applications of household products [11,14,16].
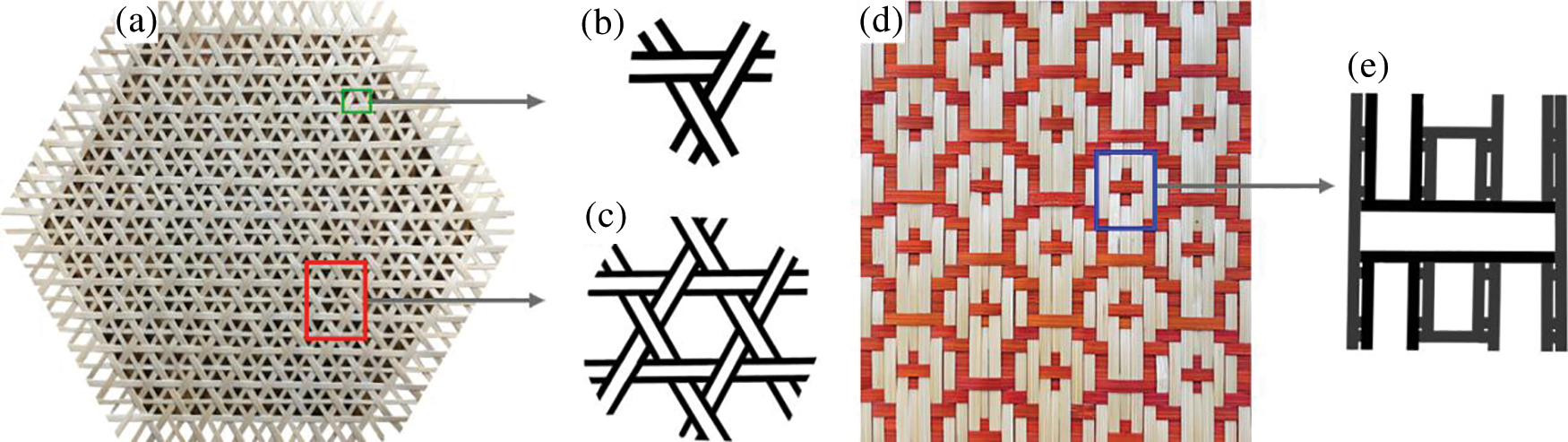
Figure 1: Polygonal and cross-woven structure: (a) Real bamboo mat by the polygonal-woven style. (b) Polygonal-woven structure I. (c) Polygonal-woven structure II. (d) Real bamboo mat by the cross-woven style. (e) Cross-woven structure
Many brands have popularized the design elements of woven bamboo due to their natural material texture, woven patterns, color matching, and other aesthetic values [16]. The Japanese Nendo studio has released the Tokyo Tribal Collection of woven bamboo and wooden furniture products [17]. Swedish IKEA has launched the MISTERHULT woven bamboo lighting and home product line [18]. The French clothing brand, CHANEL, has even released a woven bamboo handbag [19]. Several interesting furnishings embellished with bamboo weaving were displayed during the 2022 Milan Design Week [20,21] by the Spanish leather goods company LOEWE, the French luxury brand LOUIS VUITTON, etc. These anecdotes confirm that the bamboo weaving collection has a strong international market value. Therefore, the diversification of bamboo weaving is more and more important in fostering a novel design fabrication [22,23]. The adjustment could spontaneously arise in the process if the actual weaving effect can not satisfy the designer’s expectations [22,23]. However, the amendment during the design and process is very complex and different. It is well known that bamboo weaving is a traditional handicraft, with the weaving process being temporal, geospatial, lingual, and cultural limitations [22–26]. The communicated obstacles between the artisan and designer should be removed in an intuitive way [22–26], then the bamboo weaving would be preferably applied in modern life.
There are a lot of digitized and visualized means to help designers preview partial woven structures and holistic aesthetic effects [27,28], such as Autodesk’s 3ds Max, Maya design programs, CorelDRAW’s Rhinoceros, and so on. As previously mentioned, some heavily regular orderliness and intricate structural logic are investigated in the pattern compositions of woven bamboo. Although these aforementioned modeling tools could be performed in the structure of woven bamboo, their fundamental methods are tremendous and inefficient [27,28]. The parametric design concepts are first applied in architecture, such as Antonio Gaudi’s the Sagrada Família, Zaha Hadid’s the Circle at Zurich Airport exhibition hall in Germany, Ma Yansong’s the Absolute Towers, and so on [29]. The complex structural systems perform a parametric design to quickly accomplish the design intent by controlling some variables in a three-dimensional workspace, such as points, lines, and surfaces [30–33]. GH is developed by implanting the algorithm plug-in for Rhino to address many problems encountered in the parametric design cycle of architecture by extending the program to achieve more parametric functions [29–31].
In this study, the dogtooth pattern and the fish-style pattern of SCPCW will be investigated by the coordinate-parametric matrix model, configurated by the basic-monomer shape and basic-combination shape, respectively. It could be reinterpreted woven logic of SCPCW through the coordinate sequences of the bamboo mat. Compared to bamboo weaving and jacquard fabric, the image information is likewise digitalized to realize the freely desired effects. Namely, the matrix coordinate of the bamboo mat pattern is similar to the digital weaving software of the jacquard fabric [34–36]. Subsequently, the gradients of the weaving units in the bamboo-mat description can be adjusted and regulated for some weaving textures in various patterns [27,28,37]. Actually, the coordinate-parametric matrix model can be attained by the coordinate image of the floating point pixel in the Image Sampler component of the GH. Finally, the designers can lightheartedly discern and review the effects of the bamboo-mat pattern by installing this coordinate-parametric matrix model, which can be freely restructured and modified until getting a satisfied prospect [29–31].
2 Composition Form of SCPCW in the Bamboo Mat
A basic shape is the unit of pattern in a bamboo mat, which can be divided into two forms, namely monomeric and duplex-style shapes. The primary skeletal framework of basic shape is made up of visible and invisible lines or geometric shapes. The skeleton-framework joints are seamless and can be continuously stretched toward four directions-top of the woven bamboo mat [13]. In this way, a visual impression of the bamboo-mat pattern can be displayed, which is the regular effect of unity, proportionality, repetition, and continuity. The explanatory subsections would be elaborated to better understand this concept.
2.1 Configuration of Basic Shapes in SCPCW
Fig. 2a describes a picture of real products decorated with a dogtooth pattern in the bamboo mat. The basic-monomer shape of SCPCW in the bamboo mat is shown in a dogtooth pattern, which is a single geometric shape in an independent form (Fig. 2b). The variational cluster of a basic-monomer shape is exhibited in Figs. 2c–2h. In bamboo mats, some prospects of the SCPCW are configured by a single monomer. Others are configured by the combination of two or more monomers. The graphic rule of variational clusters to the basic monomer shape is investigated as follows in Fig. 2: the dogtooth pattern of Fig. 2b is regarded as the original monomer. The monomer is horizontally flipped in Fig. 2c. The monomer is vertically flipped in Fig. 2d. The monomer is rotated 180° in Fig. 2e. Furthermore, these monomers can be dynamically arranged to some of the basic-combination shapes of the SCPCW in Figs. 2f–2h. It is explored that the monomer is gyrated, deconstructed, and rotationally reorganized, respectively.
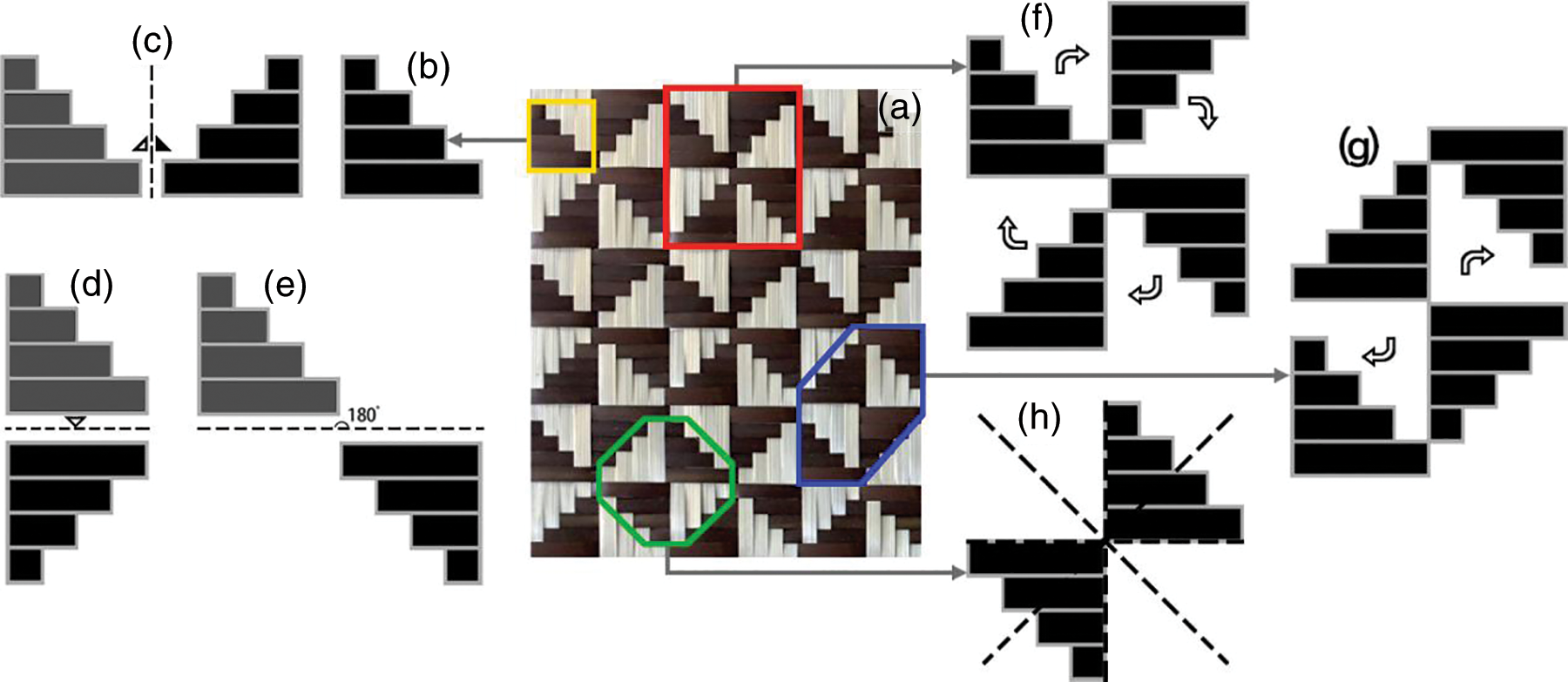
Figure 2: Variational-cluster representations of the basic-monomer shape in SCPCW bamboo mat: (a) Picture of real bamboo mat filled by the dogtooth pattern of SCPCW. (b) Dogtooth pattern. (c) Basic-monomer shape I. (d) Basic-monomer shape II. (e) Basic-monomer shape III. (f) Basic-combination shape I. (g) Basic-combination shape II. (h) Basic-combination shape III
In Figs. 2f–2h, these basic-combination shapes are produced by recomposing the same initial basic shape, which is transformed at the quantitative locations and angles. The basic-combination form is also possible to be created by two or more distinct morphologies (Fig. 3a, a fish-style pattern). In Fig. 3b, it is seen that two monolithic geometries of different shapes are juxtaposed along the center axis. After that, it is inspected that a monolithic pattern is made up of two basic-combination shapes.
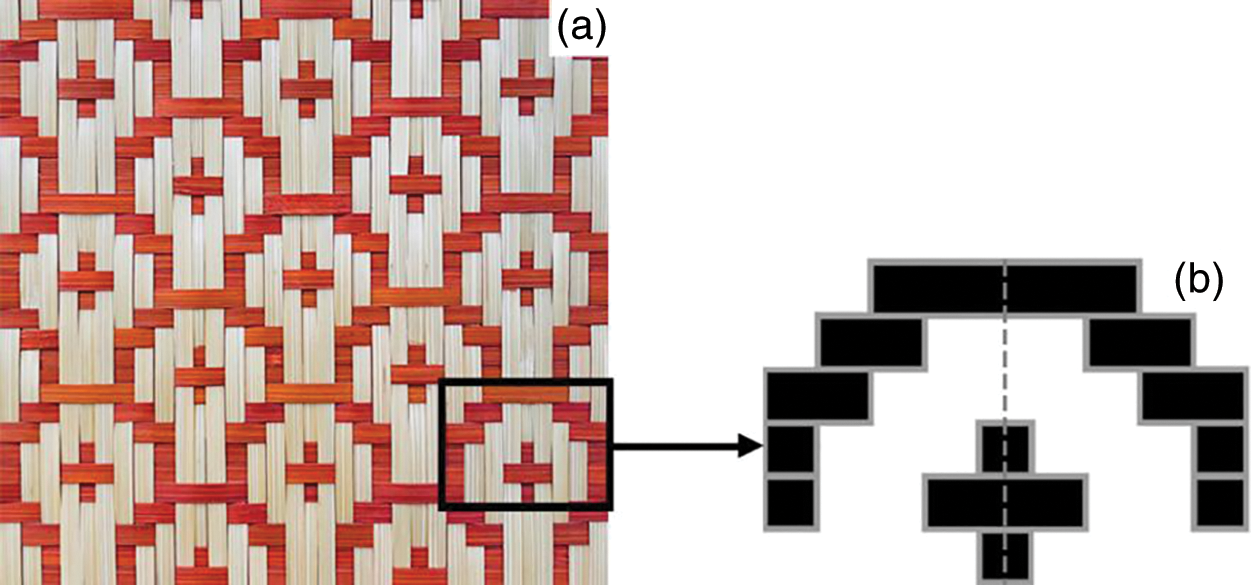
Figure 3: Multi-body configuration representations of the SCPCW in bamboo mat: (a) Picture of real bamboo mat filled by the fish-style pattern of SCPCW. (b) Basic-combination shape
2.2 Composition of SCPCW in the Bamboo Mat
From different viewpoints, the continuous patterns of SCPCW are regarded as varied apperceptions [13]. Then, some tendencies of skeleton frameworks are observed, which can indicate the continuous patterns stretching across these different basic shapes. SCPCWs in the bamboo mat can be distinguished into linear and geometric skeletal frameworks (Fig. 4). In Figs. 4a–4c, the dogtooth pattern is formed by the skeletons framework of quadrilateral, hexagonal, and polygonal shapes to form three new basic-combination shape units, which are the skeletons framework of these basic-combination shape units are then repeatedly arranged in four directions in a juxtaposed or step-type to enhance the visual recognition and awareness of the basic-combination shape units. In addition, the fish-style patterns in Figs. 4d–4f are repeatedly continued in four directions through three different linear skeletal frameworks of linear equidistance, the diagonal-conjoint, and the wavy curve, respectively, thus forming a visual identification and awareness of the fish-style patterns. Hence, the visual impact of SCPCWs can enhance pattern identification and awareness [13,15].

Figure 4: Skeletal frameworks representations of SCPCW in bamboo mat: (a) Geometric skeletal frameworks I. (b) Geometric skeletal frameworks II. (c) Geometric skeletal frameworks III. (d) Linear skeletal frameworks I. (e) Linear skeletal frameworks II. (f) Linear skeletal frameworks III
3 Coordinate and Parameters of SCPCW in the Bamboo Mat
3.1 Elements of Model Building to the Bamboo-Mat Pattern of SCPCW
The longitudinal strips picked and pressed in the cross-woven bamboo mat are known as warp strips, while the horizontal strips weaved in sequence are known as weft strips [10,11,38,39]. In the cross-woven bamboo mats, warp strips and weft strips are perpendicularly intersected and woven into the bamboo, which could fabricate the effect of a rectangularly geometric block [12,40]. The gaps between the warp strips and weft strips are arranged in a quadrilateral pattern [40], where the cross-section structures are presented in a wavy pattern [28]. In the bamboo mat, several color strips can be sought, namely a dyed strip and a nature-color strip [39]. In that way, these polychrome bamboo strips can make a tremendous visual impact. Usually, the colored strip is employed as a weft strip. The natural strip is applied to a warp strip. In this study, if the weft is pushed above the non-dyed warp strips to regard as a positive pattern, other than if the colored strip is pressed below the non-dyed strip it regards as a negative pattern. To rapidly capture pictorial information of woven patterns, a recognition of colour design on the bamboo mat is defined as the black-and-white grid pictures, which is analogous to a binary image matrix division construct [35,36,41].
In Fig. 5, a vertical column is represented by a warp strip, and a weft strip represents a horizontal row. Hence, a matrix coordinate system of each block containing positive or negative shape information is modeled. Dogtooth (Fig. 5a) and fish-style (Fig. 5c) patterns are converted into binary representations (Figs. 5b and 5d), respectively, in which the positive and negative shapes of the patterns are sequentially filled with black and white rectangles. As to the binary matrix, the parameters of P and N have denoted the coordinate array of the positive and negative shapes in the pattern, respectively.
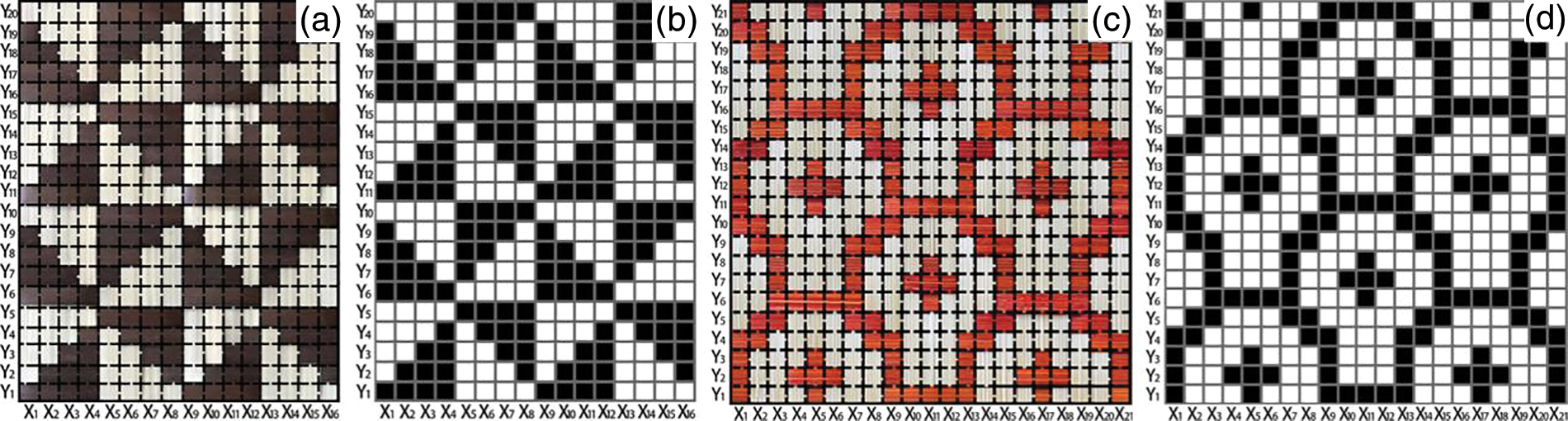
Figure 5: Binary representations of matrix coordinates of SCPCW bamboo mat: (a) Picture of real bamboo mat filled by the dogtooth pattern of SCPCW. (b) Binary matrix coordinate image I. (c) Picture of real bamboo mat filled by the fish-style of pattern SCPCW. (d) Binary matrix coordinate image II
In the practical performance, the minimum width and thickness of the strip in the weaving bamboo mats are 1.5 and 0.1 mm, respectively. In the study, the design of the weaving model is conducted with bamboo strips of 1.5 mm width and 0.1 mm thickness. It is explored that the uneven surface of the bamboo mat would emerge if a weft strip is sequentially weaved in 7 warp strips (Fig. 6a) [12,42]. The elasticity modulus of the bamboo strip could possibly generate this phenomenon. Thus the variates of the binary matrix are maximized up to 7, which are the parameters in the vertical column and horizontal row. In this study, the matrix coordinates of the basic-monomeric and basic-combination shapes are selected as examples to supervise standardized weaving.

Figure 6: Unit lengths representations of strip picking and pressing in cross-woven bamboo mats: (a) Picture of the real bamboo mat by the cross-woven. (b) Binary matrix image
The coordinate array C in Eq. (1) [41,43] is represented the bamboo mat of SCPCW based on the binary matrix:
where X is the warp strips of woven bamboo, Y is the weft strips of woven bamboo, Xw represents the variable of the warp strips of woven bamboo, Yh represents the variable of the weft strips of woven bamboo, P is the positive shape coordinate, and N is the negative shape coordinate. As construct C combines positive and negative shapes, the patterns in the matrix take values in the vertical direction from left to simas X1, X2, ..., Xw and in the horizontal direction from bottom to top as Y1, Y2, ..., Yh.
Based on C, the matrix coordinate arrays of P and N (Eq. (2)) corresponding to the positive and negative pattern shapes can now be established:
where X is the warp strips of woven bamboo, Y is the weft strips of woven bamboo, Yh represents the variable of the weft strips of woven bamboo, Xs is the starting warp variable, and subscript a is the pattern-width increment. The rectangular coordinates of the pattern’s positive or negative shape information in the horizontal Yh matrix take values in the range of Xs
3.2 Coordinate Matrix of Monomer Shape
According to Eq. (2), Eq. (3) represented the coordinate array of positive shapes is deduced to illustrate the dogtooth pattern, which is exemplified by the basic-monomer shape CDT = (X1
where PDT is the coordinate matrix of positive shapes of the dogtooth pattern, X is warp strips of the positive shapes, and Y is weft strips of the positive shapes.

Figure 7: The schematic of binary matrix coordinate to dogtooth pattern
In the same way, the coordinate array of negative shapes in the dogtooth pattern is reflected in Eq. (4):
where NDT is the coordinate matrix of negative shapes of the dogtooth pattern, X is warp strips of the negative shapes, and Y is weft strips of the negative shapes.
According to Eqs. (3) and (4), Eq. (5) represented the coordinate array of the combination of positive and negative shapes in the dogtooth pattern:
where CDT is the coordinate combination of positive and negative shapes of the dogtooth pattern, P is the coordinate matrix of positive shapes of the dogtooth pattern, and N is the coordinate matrix of negative shapes of the dogtooth pattern.
In the dogtooth pattern (Fig. 7), the P1 = (X1
3.3 Coordinate Matrix of Combination Shape
According to Eq. (2), Eq. (6) represented the coordinate array of positive shapes is deduced to illustrate the fish-style pattern, which is exemplified by the basic-combination shape CFS = (X1
in the coordinate matrix, where PFS is the positive shape of the fish-style pattern, X is warp strips of the positive shapes, and Y is the weft strips of the positive shape.
In the same way, the coordinate array of negative shapes in the fish-style pattern is reflected in Eq. (7):
in the coordinate matrix, where NFS is the negative shapes of the fish-style pattern, X is warp strips of the negative shapes, and Y is the weft strips of the negative shapes.

Figure 8: The schematic of binary matrix coordinate to fish-style pattern
In Fig. 8, it is seen that two geometries of different shapes are juxtaposed along the center axis, which is inspected as a monolithic pattern. Namely, the coordinates of the central axis in the pattern are P1, P2.2, P3.2, N4, N5.2, and P6, respectively. After that, it forms multiple sets of symmetric matrices with the coordinates of the central axis. In the fish-style pattern, Eq. (8) represented the coordinate array of the positive and negative shapes indicated as follows:
in the fish-style pattern, where CFS is the coordinate combination of positive and negative shapes, P is the coordinate matrix of positive shapes, and N is the coordinate matrix of negative shapes.
4 Perform a Parametric Simulation Modeled with GH to the Weaving Pattern of SCPCW
4.1 Coordinate-Parametric Transformation Logic of SCPCW
Especially, the weaving logic of the coordinated matrix is referred to apply in the computing component of GH software, which is realized to predict the micro-weaving structure and weaving effect in the bamboo mat. First, the bamboo-mat pattern is segmented to the binary image, similar to when a jacquard fabric’s pattern matrix [34–36,43]. In fact, the Image Sampler component of GH could recognize the coordinate information of the SCPCW in the bamboo mat, which could recognize the array output of the jacquard pattern oppositely from the textile-information identification. The Image Sampler component can transform the image’s color characteristics to the numerical digitization by floating-point pixel coordinates in the range [0,1], where a high b\simess recognition of the output parameter is defined as 1, and a low brightness recognition of output value is defined as of 0. In Fig. 9, the Image Sampler component has separately gathered the lightness and darkness of the binary image in the dogtooth pattern (Fig. 9a) and the fish-style pattern (Fig. 9c), which is referred the Eqs. (5) and (8). Successively, the parameter matrix (Fig. 9b) of the dogtooth pattern and the parameter matrix (Fig. 9d) of the fish-style pattern can respectively be obtained as follows. ‘P = 0’ and ‘N = 1’ are represented by the black rectangle (positive shape P) and the white rectangle (negative shape N).

Figure 9: The schematic of binary and parameter matrix of basic shapes: (a) Binary matrix I. (b) Parameter matrix I. (c) Binary matrix II. (d) Parameter matrix II
4.2 Parametric Modeled of SCPCW Structure in the Bamboo Mats
In Table 1, it can be seen to indicate the parametric-modeling logic of the SCPCW in the bamboo mat, which is based on the coordinate weaving method, pattern coordinate-parametric transformation logic, and SCPCW composition form. Firstly, in the cross-woven bamboo mats, the warp strip and weft strip are perpendicularly intersected and woven, which are fabricated with the effect of a rectangularly geometric block [40]. Therefore, in the GH plug-in, the matrix parameters of X × Y in Figs. 10a and 10e can be input to form a 2D matrix lattices of CDT = X16 × Y20 and CFS = X21 × Y21, which realize the matrix space of the bamboo mats pattern (Figs. 10b and 10f). In 2D matrix lattices, lightness and darkness detection of the Image Sampler component in GH can be captured, which are the parameters representing the weaving structure’s nodes (Figs. 10c and 10g).


Figure 10: The schematic of binary and parameter matrix of SCPCW: (a) Binary matrix of dogtooth pattern in SCPCW. (b) 2D grid framework I. (c) Parameter matrix I. (d) Weaving Nodes I. (e) Binary matrix of fish-style pattern in SCPCW. (f) 2D grid framework II. (g) Parameter matrix II. (h) Weaving Nodes II
Secondly, the Z-axis value mapped for the image acquisition is input into the Image Sampler component to generate upward and downward altitudes floating on the 2D matrix lattices. Hence, the wave-like variation (Figs. 10d and 10h) of the warp strips and weft strips along the Z-axis can take shape on the cross-sectional surface [28] of the SCPCW bamboo mat. Thus, the black rectangle’s center will jump on the surface of the bamboo mat when the white rectangle’s center is kept still. Whereas the white rectangle’s center is going to grow tall when the black rectangle’s center is kept static. As a result, the 3D warp and weft weaving nodes of the dogtooth pattern (Fig. 10d) and fish-style pattern (Fig. 10h) appeared following the prescribed order.
Successively, the interpolation lines are pointed into after connecting some woven nodes along the warp direction, and the weft direction, respectively (Fig. 11a). Based on the centroid of the interpolation curves, the length, width, and thickness of the woven surface are arranged by customizing the parameter variables of the warp and weft woven surface. Afterward, the custom parameter squares extend along the interpolation curves in the warp directions and weft directions, which form an up-and-down interwoven woven surface (Fig. 11c). Finally, the parametric model of the SCPCW in the bamboo mat can be made as follows, the model of the dogtooth pattern (Fig. 11b) and the model of the fish-style pattern (Fig. 11d).

Figure 11: The schematic of parametric model schematic by the interpolation curves in GH plug-ins: (a) Woven interpolation curve I. (b) Parametric model I. (c) Woven interpolation curve II. (d) Parametric model II
In order to realize the digitization of bamboo mats, a mathematical resolution has been substantially elaborated by extracting the configuration form and composition form of SCPCW in the traditional bamboo mat. In the future, parametric technology in bamboo mats will not only attain some diverse landscape designs but also efficiently fabricate beautiful bamboo decoration. In the project, some analyses have been presented as follows:
(1) The image configuration of the cross woven in the bamboo mat could be explicitly defined as follows, the basic-monomer shape and the basic combination shape. At the same time, the compositions of design patterns in the bamboo mat of SCPCW are analyzed to attain the trend of curve shape.
(2) The coordinate-parametric matrix model has been executed to inspire a digital analysis of the cross-woven delineation in a bamboo mat.
(3) A computer simulation carried out by GH software could confirm that the coordinate-parametric matrix model of SCPCW in the bamboo mat would be effective.
Funding Statement: This work acknowledges the financial support from the Hunan Provincial Key Research and Development Program (2020WK2018); the Arts Crafts Industrial Design Center of Hunan Province (No. 2022GYMSZ2); and the Scientific Innovation Fund for Post-Graduates of Central South University of Forestry and Technology (No. 2022CX02079).
Author Contributions: Conceived and designed the experiments: Ye Fu, Jinbo Hu; performed the experiment: Ye Fu, Liwen Deng, Ting Li; supervised the work: Jinbo Hu, Shanshan Chang; wrote the paper: Ye Fu, Liwen Deng, Jinbo Hu; revised the paper: Jinbo Hu, Shanshan Chang.
Availability of Data and Materials: Data generated or analyzed during this study were included in this published article and its supplementary information files.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
References
1. Fang, C. H., Jiang, Z. H., Sun, Z. J., Liu, H. R., Zhang, X. B. et al. (2018). An overview on bamboo culm flattening. Construction and Building Materials, 171(9), 65–74. https://doi.org/10.1016/j.conbuildmat.2018.03.085 [Google Scholar] [CrossRef]
2. Dlamini, L. C., Fakudze, S., Makombe, G. G., Muse, S., Zhu, J. (2022). Bamboo as a valuable resource and its utilization in historical and modern-day China. BioResources, 17(1), 1926–1938. https://doi.org/10.15376/biores.17.1.Dlamini [Google Scholar] [CrossRef]
3. Huang, Z., Sun, Y. (2021). Hygrothermal performance comparison study on bamboo and timber construction in Asia-Pacific bamboo areas. Construction and Building Materials, 271(9), 121602. https://doi.org/10.1016/j.conbuildmat.2020.121602 [Google Scholar] [CrossRef]
4. Dixon, P. G., Ahvenainen, P., Aijazi, A. N., Chen, S. H., Lin, S. et al. (2015). Comparison of the structure and flexural properties of Moso, Guadua and Tre Gai bamboo. Construction and Building Materials, 90, 11–17. https://doi.org/10.1016/j.conbuildmat.2015.04.042 [Google Scholar] [CrossRef]
5. Malkowska, D., Norman, J., Trujillo, D. (2022). Theoretical and experimental study on laterally loaded nailed bamboo connection. Construction and Building Materials, 342(4), 127971. https://doi.org/10.1016/j.conbuildmat.2022.127971 [Google Scholar] [CrossRef]
6. Chen, H., Wu, J., Shi, J., Zhang, W., Wang, H. (2021). Effect of alkali treatment on microstructure and thermal stability of parenchyma cell compared with bamboo fiber. Industrial Crops and Products, 164(1), 113380. https://doi.org/10.1016/j.indcrop.2021.113380 [Google Scholar] [CrossRef]
7. Sharma, B., Gatóo, A., Bock, M., Ramage, M. (2015). Engineered bamboo for structural applications. Construction and Building Materials, 81(4), 66–73. https://doi.org/10.1016/j.conbuildmat.2015.01.077 [Google Scholar] [CrossRef]
8. Li, Z. H., Chen, C. J., Xie, H., Zhang, Y., Brozena, A. et al. (2022). Sustainable high-strength macrofibres extracted from natural bamboo. Nature Sustainability, 5(3), 235–244. https://doi.org/10.1038/s41893-021-00831-2 [Google Scholar] [CrossRef]
9. Xu, Q., Chen, X., Chen, J. F., Chen, K. A., Wang, Z. (2019). Seismic strengthening of masonry walls using bamboo components. Advances in Structural Engineering, 22(14), 2982–2997. https://doi.org/10.1177/1369433219855902 [Google Scholar] [CrossRef]
10. Li, L., Chen, Y. H. (2019). Chinese bamboo weaving techniques: Plane weaving. China: China Forestry Publishing House. [Google Scholar]
11. Chen, Z. J., He, X. Q. (2016). Design and analysis of materials of bamboo weaving veneer furniture. Furniture & Interior Design, (6), 13–15. https://doi.org/10.16771/j.cnki.cn43-1247/ts.2016.06.003 [Google Scholar] [CrossRef]
12. Wang, B. J., Young, W. B. (2022). The natural fiber reinforced thermoplastic composite made of woven bamboo fiber and polypropylene. Fibers and Polymers, 23(1), 155–163. https://doi.org/10.1007/s12221-021-0982-1 [Google Scholar] [CrossRef]
13. Chen, Z. F., Chen, C. Y. (2020). The complete works of Chen Zhi Fo. In: Design method ABC design composition method, vol. 1, pp. 230–276. China: Nanjing Normal University Press. [Google Scholar]
14. Zhang, Z. D. (2014). Design culture of folk bamboo utensils in Hunan (Ph.D. Thesis). Central South University of Forestry and Technology, China. [Google Scholar]
15. Zhang, W. D. (2015). Inheritance and innovation of Chinese ethnic pattern composition forms (Master Thesis). LuXun Academy of Fine Arts, China. [Google Scholar]
16. Zheng, Y., Zhu, J. (2021). The application of bamboo weaving in modern furniture. BioResources, 16(3), 5024–5035. https://doi.org/10.15376/biores.16.3.5024-5035 [Google Scholar] [CrossRef]
17. Nendo (2015). Tokyo tribal collection. https://www.nendo.jp/en/works/tokyo-tribal-collection-2. [Google Scholar]
18. IKEA (2020). From waste to ambient lighting-MISTERHULT. https://www.ikea.cn/cn/zh/p/misterhult-mi-si-te-hu-tai-deng-zhu-shou-gong-zhi-zuo-10437628/. [Google Scholar]
19. Kang, J. X., Li, X. L. (2021). Research on the cross border design of bags and traditional bamboo weaving. China Leather, 50(7), 101–104. https://doi.org/10.13536/j.cnki.issn1001-6813.2021-007-023 [Google Scholar] [CrossRef]
20. Data Park (2022). Milan design week 2022: A home design for luxury brands. https://new.qq.com/rain/a/20220617A098EH00/. [Google Scholar]
21. Loewe (2019). Home-loewe foundation craft prize. https://craftprize.loewe.com/en/craftprize2019. [Google Scholar]
22. Yao, J. (2021). Research on digital inheritance and communication innovation of traditional craftsmanship intangible cultural heritage--A case study of Zhangjiagang houcheng weaving. China National Exhibition, 7(13), 89–91. [Google Scholar]
23. Zhang, W. L., Zou, Q. (2018). VR in solving communication for bamboo weaving product’s design. Packaging Engineering, 39(18), 203–208. https://doi.org/10.19554/j.cnki.1001-3563.2018.18.038 [Google Scholar] [CrossRef]
24. Shen, J. C. (2020). Research on rework risk of prefabricated construction process (Ph.D. Thesis). Tsinghua University, China. [Google Scholar]
25. Li, X. J. (2013). Research on inner design communication pattern of home decoration enterprise (Master Thesis). Central South University, China. [Google Scholar]
26. Zhao, B., Wang, Y. Q., Niu, B. S. (2011). Application of 4D-virtual construction technology based on BIM in schedule management of construction project. Construction Economy, (9), 93–95. https://doi.org/10.14181/j.cnki.1002-851x.2011.09.025 [Google Scholar] [CrossRef]
27. Chang, H. C. (2021). Parametric design used in the creation of 3D models with weaving characteristics. Journal of Computer and Communications, 9(11), 112–127. https://doi.org/10.4236/jcc.2021.911008 [Google Scholar] [CrossRef]
28. Gong, R. H., Ozgen, B., Soleimani, M. (2009). Modeling of yarn cross-section in plain woven fabric. Textile Research Journal, 79(11), 1014–1020. https://doi.org/10.1177/0040517508101799 [Google Scholar] [CrossRef]
29. Qi, F. (2018). Application of parametric method based on grasshopperin structure design. Journal of Information Technology in Civil Engineering and Architecture, 10, 105–110. https://doi.org/10.16670/j.cnki.cn11–5823/tu [Google Scholar] [CrossRef]
30. Pedersen, C. (2020). The parametric process: A strategic analysis on digital design technology in landscape architecture (Master Thesis). University of Guelph, Canada. [Google Scholar]
31. Hernandez, C. R. B. (2006). Thinking parametric design: Introducing parametric Gaudi. Design Studies, 27(3), 309–324. https://doi.org/10.1016/j.destud.2005.11.006 [Google Scholar] [CrossRef]
32. Monedero, J. (2000). Parametric design: A review and some experiences. Automation in Construction, 9(4), 369–377. https://doi.org/10.1016/S0926-5805(99)00020-5 [Google Scholar] [CrossRef]
33. Stavric, M., Marina, O. (2011). Parametric modeling for advanced architectur. International Journal of Applied Mathematics and Informatics, 5(1), 9–16. [Google Scholar]
34. Zhong, P., Shi, Z. F., Jiang, M., Yang, F., Zheng, H. et al. (2017). Research on the modeling method for digital weaving based on the information of physical yarns and Fabric pattern. Journal of Fashion Technology & Textile Engineering, 5(2). https://doi.org/10.4172/2329-9568.1000149 [Google Scholar] [CrossRef]
35. Chen, S., Toyoura, M., Terada, T., Mao, X., Xu, G. (2021). Image-based textile decoding. Integrated Computer-Aided Engineering, 28(2), 177–190. https://doi.org/10.3233/ICA-200647 [Google Scholar] [CrossRef]
36. Liang, J., Cong, H., Gao, Z., Zhang, A., Dong, Z. (2020). Computer-aided design of weft-knitted two-side jacquard fabric. International Journal of Clothing Science and Technology, 33(1), 122–136. https://doi.org/10.1108/IJCST-04-2019-0061 [Google Scholar] [CrossRef]
37. Gao, C. (2021). Research on parametric modeling technology of weaving in micro-architecture manufacture. CONVERTER, 2021(4), 198–205. [Google Scholar]
38. Adumitroaie, A., Barbero, E. J. (2011). Beyond plain weave fabrics–I. Geometrical model. Composite Structures, 93(5), 1424–1432. https://doi.org/10.1016/j.compstruct.2010.11.014 [Google Scholar] [CrossRef]
39. Luo, B., Ahmed, S., Long, C. (2020). Bamboos for weaving and relevant traditional knowledge in Sansui, Southwest China. Journal of Ethnobiology and Ethnomedicine, 16(1), 1–9. https://doi.org/10.1186/s13002-020-00418-9 [Google Scholar] [PubMed] [CrossRef]
40. Akhil, K. S., Sankar, N., Chandrakaran, S. (2021). Effect of aperture size on the performance of bamboo mat reinforced soil bed. Journal of Natural Fibers, 1–12(13), 6909–6920. https://doi.org/10.1080/15440478.2021.1941480 [Google Scholar] [CrossRef]
41. He, L., Ren, X., Zhao, X., Yao, B., Kasuya, H. et al. (2019). An efficient two-scan algorithm for computing basic shape features of objects in a binary image. Journal of Real-Time Image Processing, 16(4), 1277–1287. https://doi.org/10.1007/s11554-016-0626-7 [Google Scholar] [CrossRef]
42. Kanaginahal, G. M., Hebbar, H. S., Kulkarni, S. M. (2019). Influence of weave pattern and composite thickness on mechanical properties of bamboo/epoxy composites. Materials Research Express, 6(12), 125334. https://doi.org/10.1088/2053-1591/ab5a90 [Google Scholar] [CrossRef]
43. Wang, W., Jiang, G., Gao, Z. Y., Yang, M. T. (2018). Computer aided design system model and algorithm of weft knitted jacquard fabrics. Journal of Textile Research, 39(3), 161–166. https://doi.org/10.13475/j.Fzxb.20170607606 [Google Scholar] [CrossRef]
Cite This Article
 Copyright © 2023 The Author(s). Published by Tech Science Press.
Copyright © 2023 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF Downloads
Downloads
 Citation Tools
Citation Tools