Journal of Renewable Materials

DOI: 10.32604/jrm.2022.020829

ARTICLE

CO2 and Cost-Based Optimum Design of Sustainable Metakaolin-Modified Concrete

Xiaoyong Wang*

Department of Architectural Engineering, Department of Integrated Energy and Infra System, Kangwon National University, Chuncheon-si, 24341, Korea
*Corresponding Author: Xiaoyong Wang. Email: wxbrave@kangwon.ac.kr
Received: 15 December 2021; Accepted: 14 February 2022

1  Introduction

Metakaolin is an artificial pozzolanic material that can react with calcium hydroxide to form secondary calcium silicate hydrate. Metakaolin-modified concrete shows many benefits, such as low CO2 emissions, low chloride permeability, high strength, and good workability [1–4]. Due to these benefits, metakaolin is widely utilized in concrete manufacture.

Many experimental tests have been carried out on the strength, durability, and workability of metakaolin-modified concrete. Ding et al. [5] found that metakaolin-composite concrete presented a comparable strength to silica-fume-composite concrete. Dinakar et al. [6] found that as the metakaolin percentage increased, the resistance to chloride permeability, absorption, and water penetration was improved. Li et al. [7] found that metakaolin can decrease the shrinkage of cement paste. Chen et al. [8] proposed that metakaolin can improve the cohesiveness and compressive strength of concrete. Meddah et al. [9] and Bucher et al. [10] found that metakaolin-modified concrete has a higher carbonation depth than plain concrete. Liu et al. [11] reported carbonation curing of cement-based materials could densify the microstructure and enhance the mechanical and durability properties.

In addition to various experimental tests, some models have been proposed for evaluating the performance of metakaolin-modified concrete. Bai et al. [12] used neural networks to evaluate the workability performance of metakaolin-and fly-ash-composite concrete. Papadakis et al. [13–15] used the efficiency factor to evaluate the strength and chloride and carbonation durability of composite concrete. Safarzadegan Gilan et al. [16] used support vector regression to evaluate the strength and chloride ingress resistance of composite concrete containing metakaolin. Sharifi et al. [4] used neural networks to evaluate the strength of composite mortar containing metakaolin. Al-alaily et al. [17] statistically modeled the strength and chloride permeability of concrete with metakaolin.

Moreover, based on performance evaluation models, some work has been carried out to investigate the optimal design of metakaolin-modified concrete. Dvorkin et al. [18] designed low-cost metakaolin-modified concrete considering its strength. Güneyisi et al. [19] used the response surface method to optimally design metakaolin-fly-ash-modified concrete considering its strength, water absorption, and chloride ingress resistance. Long et al. [20] designed sustainable self-compacting concrete considering its strength and environmental impact. Dinakar et al. [21] designed a concrete mixture for metakaolin-modified concrete, considering its strength and workability. Ashish et al. [22] determined the optimal mixture for composite concrete considering both strength and self-compacting ability.

Although various work has been performed on the optimal mixture design of metakaolin-modified concrete, this work shows weak points. First, most of the previous work focuses on strength and workability. Yet, as the addition of metakaolin impairs the carbonation resistance of concrete, the carbonation service life may be the dominant constraint factor of metakaolin-modified concrete [13,14], though previous mixture design methods did not consider carbonation. Second, previous works mainly concentrated on the material costs of metakaolin-modified concrete. Yet, in addition to costs, CO2 emissions are an important index for concrete sustainability. Low-CO2 concrete and low-cost concrete may be different. Previous studies did not clarify the differences between low-cost concrete and low-CO2 concrete [23,24]. Third, climate change is an urgent problem that may accelerate carbonation, and accordingly, affect concrete mixture design. Previous studies did not offer a mixture design protocol to account for the risks of climate change.

This study offers a framework for the mixture design of sustainable metakaolin-modified concrete with low CO2 emissions and costs. A genetic algorithm is used to determine the optimal mixtures. The strength of the concrete, its workability (slump), and its carbonation service life with climate change are set as the constraints of the genetic algorithm. Five design cases are considered: low-CO2 concrete with no carbonation, low-CO2 concrete with carbonation, low-material-cost concrete with carbonation, low-total-cost concrete with carbonation, and low-total-cost concrete with climate change. Based on an analysis of design cases, the importance of carbonation and climate change is highlighted, and the difference between low-cost concrete and low-CO2 concrete is clarified.

The structure of this study is as follows: first, there is an introduction, and then, the second and third sections cover the mixture design method and provide illustrative examples, respectively; following this, the fourth section offers a discussion of the topic, before the last section concludes the study.

2  Mixture Design Method

2.1 Aim of Mixture Design

The sustainability of concrete is a product of many factors, such as CO2 emissions and material costs. An optimal mixture design is dependent on the selected index of sustainability. The CO2 emissions of metakaolin-modified concrete can be calculated according to the following formula:

MCO2=CO2−C×C+CO2−MK×MK+CO2−W×W+CO2−S×S+CO2−CA×CA+CO2−SP×SP (1)

where MCO2 represents the CO2 emissions of concrete; CO2-C;, CO2-MK;, CO2-W;, CO2-S;, CO2-CA;, and CO2-SP; are the CO2 emissions from 1 kg cement, metakaolin, water, sand, coarse aggregate, and superplasticizer, respectively (shown in Table 1) [20,24]. Further to this, C, MK, W, S, CA, and SP are the masses of cement, metakaolin, water, sand, coarse aggregate, and superplasticizer in concrete, respectively.

Similarly, the material cost of metakaolin-modified concrete can be calculated according to the following formula:

COSTM=PrC×C+PrMK×MK+PrW×W+PrS×S+PrCA×CA+PrSP×SP (2)

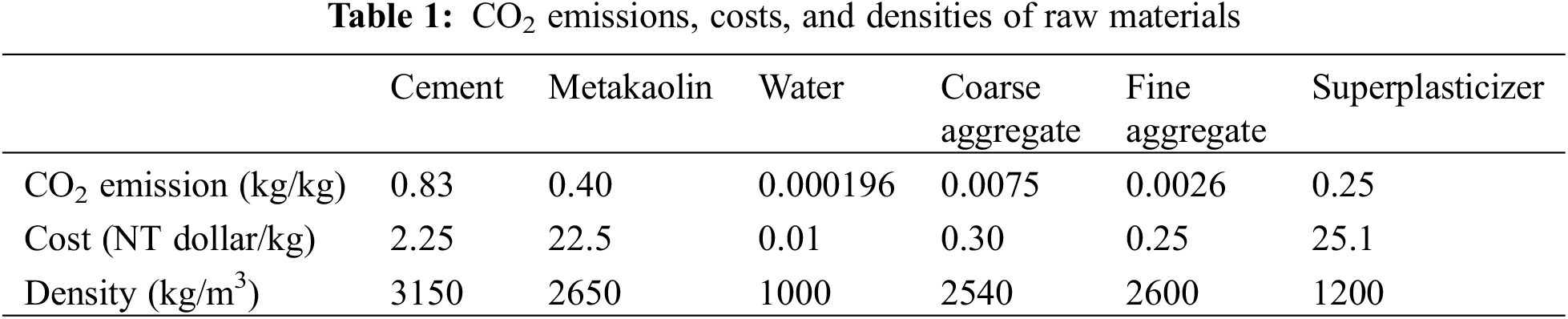
where COSTM is the material cost of concrete; PrC, PrMK, PrW, PrS, PrCA, and PrSP are the prices of 1 kg cement, metakaolin, water, sand, coarse aggregate, and superplasticizer, respectively (shown in Table 1) [25,26]. Fig. 1 shows the gradation of metakaolin powder. The diameter of metakaolin powder corresponding to 50% cumulative distribution is 3.84 μm.

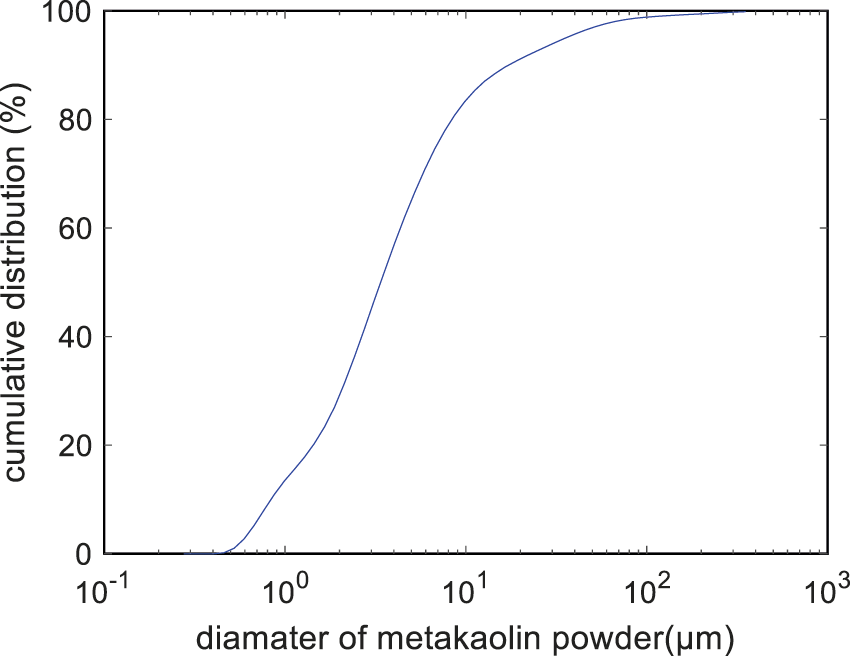
Figure 1: Gradation of metakaolin powder

The CO2 emission cost can be determined using the mass of the CO2 emissions of concrete multiplied by the unit price of CO2 emissions [23]. Moreover, the total cost can be determined as the sum of the material costs and CO2 emissions costs [23]. The total cost can be calculated according to the following formula:

COST=COSTM+COSTCO2= COSTM+PrCO2×MCO2 (3)

where COST is total cost; COSTCO2 is the CO2 emissions costs; PrCO2 is the unit price of CO2 ( PrCO2 = 862.897 NT dollar/ton) [27].

2.2 Constraints on Mixture Design

The mixture design of concrete is subject to various constraints, such as the component range of concrete, the component ratio between concrete components, the strength, slump, absolute volume, and carbonation durability [25].

(1)    The constraint of component range of concrete means that the mass of the concrete component should fall between the upper mass boundary and lower mass boundary. The constraint of the component range of concrete can be written as follows:

lowermass≤componentmass≤uppermass (4)

where the lower and upper masses represent the lower and upper boundaries of the components of concrete, respectively. The lower and upper masses are shown in Table 2 [25].

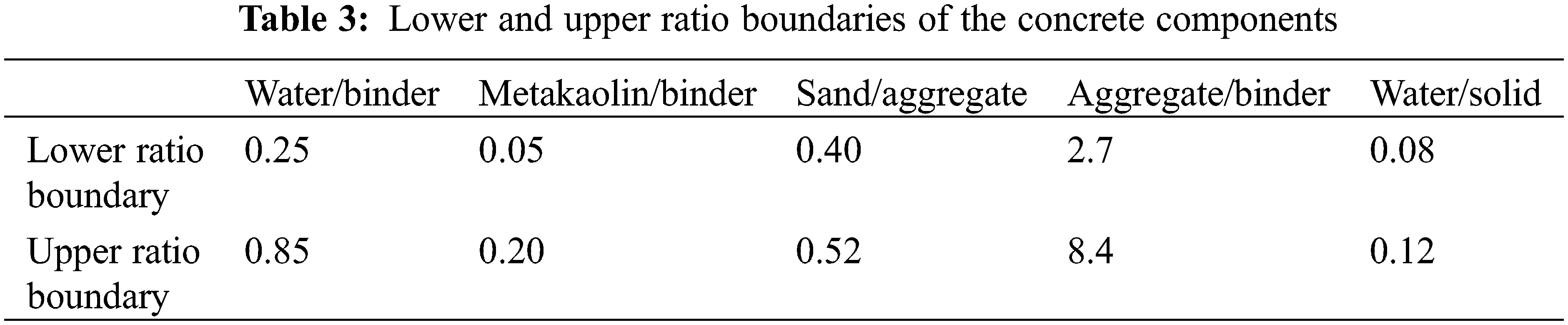
(2)   The component ratio constraint denotes the ratios among concrete components, such as the water/binder ratio, sand/aggregate ratio, metakaolin/binder ratio, water/solid ratio, and aggregate/binder ratio; should fall between the lower and upper boundaries. The component ratio constraint can be written as follows:

lowerratio≤componentratio≤upperratio (5)

where the lower and upper ratios represent the lower and upper ratio boundaries of the concrete components. The lower and upper ratios are shown in Table 3 [25].

(3)    The strength constraint denotes that the real strength should exceed the aimed strength. The strength constraint can be written as follows:

fc(t)≥fcr(t) (6)

where fc is the real strength; fcr is the design strength. Moreover, the 28-day strength of metakaolin-modified concrete can be calculated according to the following formula [15,21,28]:

fc=11.145×(W/(C+2.5×MK))−1.528 (7)

where 2.5 is the strength efficiency factor of metakaolin. The addition of metakaolin can improve concrete strength [29,30].

(4)   The slump constraint denotes that the real slump should exceed the aimed slump. For metakaolin-modified concrete, the slump constraint can be written as follows:

Slump≥Slumpr (8)

where Slump is real slump; Slumpr is design slump. Moreover, the slump can be calculated according to the following formula [6,25,31]:

Slump=209.27×WC+MK+1.34×W−325.1×SS+CA−69.28×MKC+MK+1.29×SP+63.3 (9)

Eq. (9) shows that as the water/binder ratio, water content, and superplasticizer content increase, the slump of the concrete increases, while as the metakaolin/binder ratio and sand ratio increase, the concrete slump decreases [32].

The superplasticizer content can be calculated according to the following formula [6,25,33]:

SP=(9.20−7.74×WC+MK)×(1+5×MKC+MK) (10)

Eq. (10) shows that as the water/binder ratio increases or the metakaolin/binder ratio decreases, the superplasticizer content decreases.

(5)   The absolute volume constraint denotes that the sum of the individual volumes of the concrete components should total 1 cubic meter. The absolute volume constraint can be written as follows:

WρW+CρC+MKρMK+CAρCA+SρS+SPρSP+Vair=1 (11)

where ρW, ρC, ρMK, ρCA, ρS, and ρSP are the densities of water, cement, metakaolin, coarse aggregate, sand, and superplasticizer, respectively; Vair is the volume of the entrapped air of the concrete.

(6)    For metakaolin-modified concrete, the carbonation depth increases as the metakaolin content increases [2,10,13,14]. Hence, carbonation durability may limit the application of metakaolin in the concrete industry. The carbonation durability can be written as follows:

xc(t)≤CV (12)

where xc(t) means the concrete carbonation depth; CV denotes the cover depth of the concrete.

The carbonation depth of metakaolin-modified concrete can be determined based on the concept of the carbonation efficiency factor. The calculation equation for carbonation depth is as follows [13,14]:

xc=2D[CO2]0t0.218×(C+0.4×MK)×αH (13)

D=6.1×10−6([W−0.267×(C+0.40×MK)×αH]/1000C+0.4×MKρc+Wρw)3(1−RH100)2.2exp⁡[β(1Tref−1T)] (14)

where [CO2]0 is the CO2 concentration; D is the CO2 diffusivity; αH is the degree of hydration (αH = 1 − exp (− 3.38 × W/(C + 0.4 × MK)) [34,35]; RH is the relative humidity of the environment; Tref is the reference temperature (Tref = 293 K); T is the temperature of the environment; β is the temperature sensitivity coefficient of the CO2 diffusion (β = 4300) [36]. In Eqs. (13) and (14), the [CO2]0, RH, and T are factors of the environment. The denominator of Eq. (13), 0.218 × (C + 0.4 × MK) × αH, means the content of carbonatable substances [13,14]. ([W−0.267×(C+0.40×MK)×αH]/1000C+0.4×MKρc+Wρw) in Eq. (14) means the concrete’s porosity [13,14]. Thus, diffusivity (D) relates to both the concrete’s material properties and its exposure environment. In addition, Eqs. (13) and (14) show that as the CO2 concentration and temperature increase, the carbonation depth of the concrete increases. This is relevant as increasing CO2 concentrations and temperatures are forecast to occur as climate change proceeds [37].

2.3 Genetic Algorithm

Mixture design means finding the individual mass of a component of concrete (such as cement, metakaolin, water, sand, stone, or superplasticizer) that can achieve the desired function and simultaneously satisfy various constraints. Feasible concrete components can be found using numerical analysis methods, such as the genetic algorithm. The genetic algorithm is a universal method of making global optimizations [31,38]. The calculation process of the genetic algorithm is not dependent on the specific desired functions or constraint equations. The toolbox of global optimization in the MATLAB program can be used to find the optimal mixtures.

The flowchart of the genetic algorithm is shown in Fig. 2. Optimization is aimed at the CO2 emissions, material costs, or total cost. The constraints on optimization are the compressive strength, slump, carbonation, component range, component ratio, and absolute volume. After inputting the desired functions and the constraints, the optimal mixtures for various design cases are found.

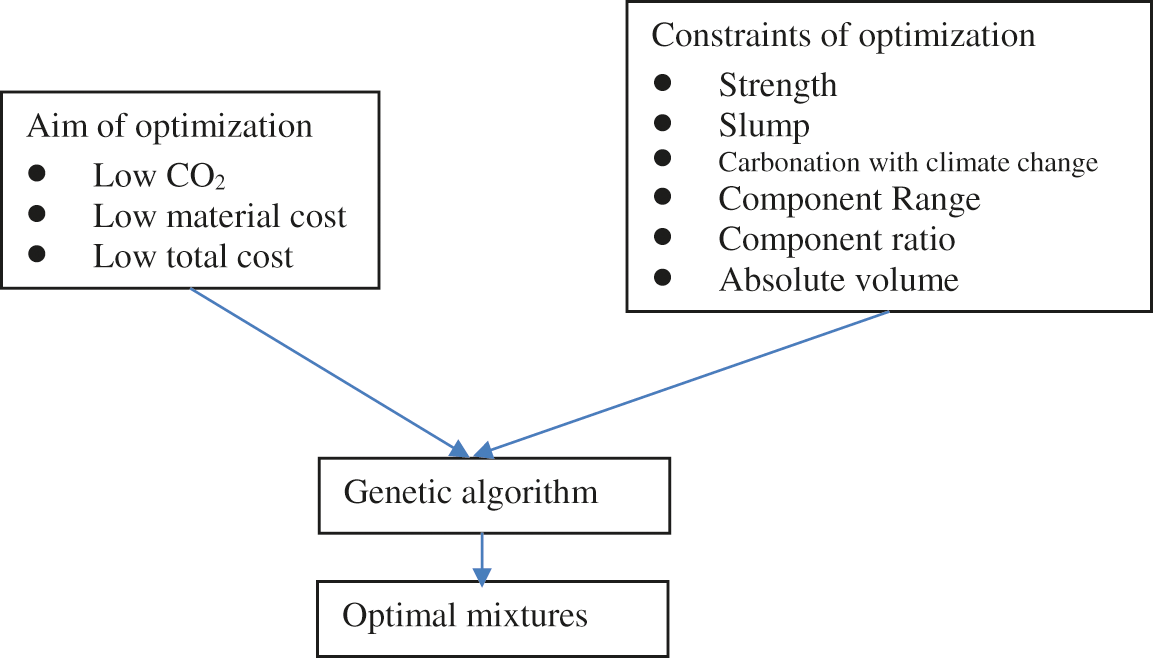
Figure 2: Flowchart of optimal design

3  Design Examples

This section illustrates design cases with different strengths. The 28-day design strengths are set as 30, 40, 50, and 60 MPa. The required slump is set as 180 mm. According to the design code, the cover depth is set as 25 mm [39]. The environmental temperature is set as 20°C. The relative humidity of the environment is set as 0.65. The CO2 concentration is set as 0.037%, which is a common CO2 concentration of suburban zone [1,3]. For other zones, the CO2 concentration may be different. The service life is assumed to be 50 years [39]. The entrapped air content is assumed to be 2%.

As shown in Table 4, five design cases are considered: low-CO2 concrete with no carbonation, low-CO2 concrete with carbonation, low-material-cost concrete with carbonation, low-total-cost concrete with carbonation, and low-total-cost concrete with climate change and carbonation.

As shown in Table 5, the following points can be clarified based on the comparison of cases: from Case 1 to Case 2, the impact of carbonation durability on mixture design can be clarified; from Case 2 to Case 3, we can find the difference between low-CO2 concrete and low-material-cost concrete; from Case 3 to Case 4, we can find the difference between low-material-cost concrete and low-total-cost concrete; from Case 4 to Case 5, the impact of climate change on the mixture design can be clarified. Moreover, based on the comparisons of design strength levels from 30 to 60 MPa, we can find the impact of design strength on optimal design.

3.1 Case 1: Low-CO2 Concrete with No Carbonation

Based on the genetic algorithm, we can find mixtures with low CO2 emissions. The carbonation durability constraint is not considered in this section. The optimal mixtures of Case 1 are shown in Table 6. The performance of the optimal mixtures of Case 1 is shown in Table 7. The water contents for Mixes 1 to 4 are similar; this is due to the constraint of the water/solid ratio. The water/solid ratio for Mixes 1 to 4 is at the lower limit. Table 7 shows that the metakaolin/binder ratio for Mixes 1 to 4 is at the upper limit; this is because the CO2 emissions for 1 kg metakaolin are much lower than those for 1 kg cement. When the aim of the optimization is set to low CO2 emissions, the metakaolin/binder ratio reaches the upper limit. In addition, as shown in Fig. 3, as the strength of the concrete increases, the CO2 emissions of the concrete increase (Fig. 3a) and the water/binder ratio decreases (Fig. 3b). This trend agrees with the results in [23].

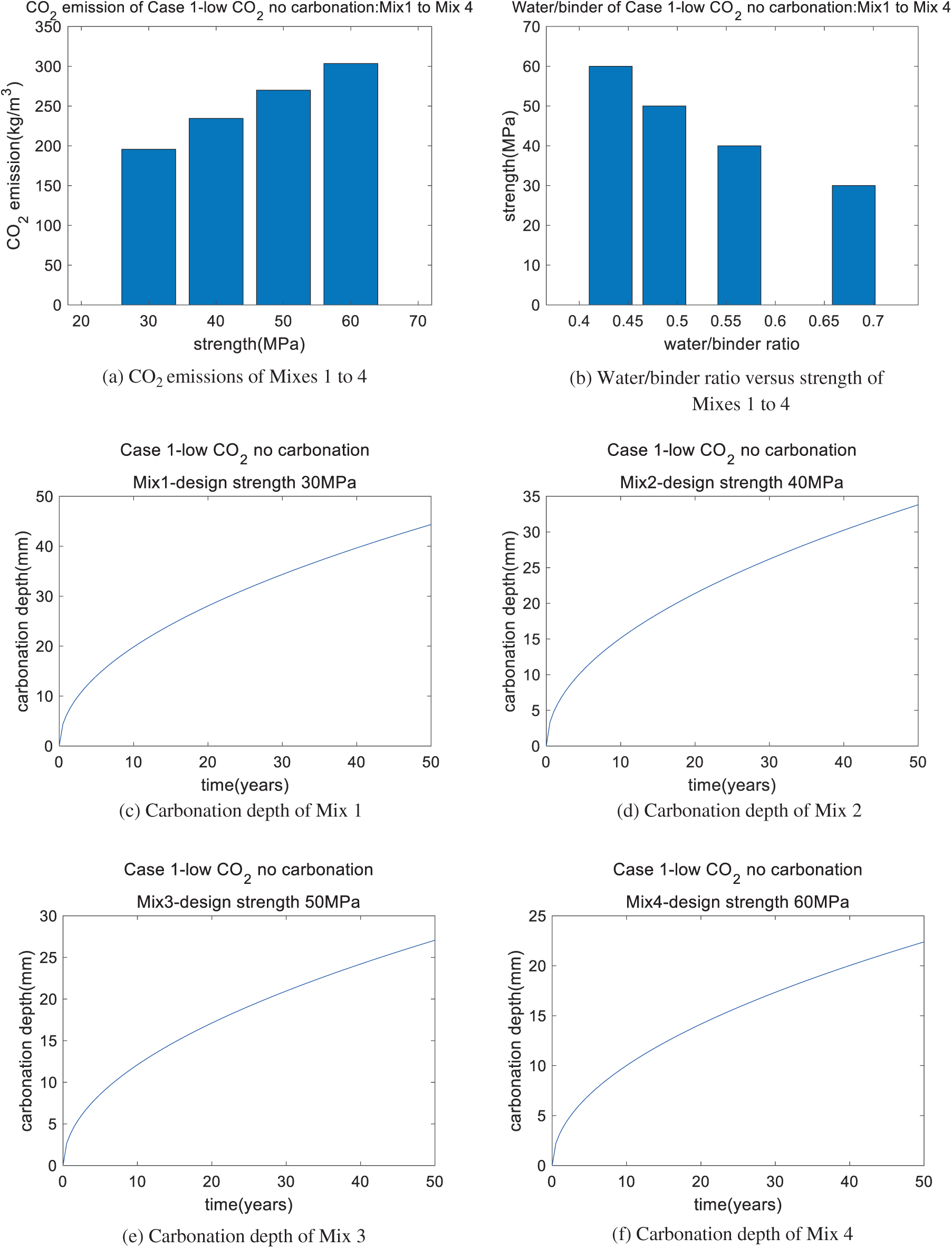
Figure 3: Performance of Case 1 (low CO2 with no carbonation): Mix 1, Mix 2, Mix 3, and Mix 4

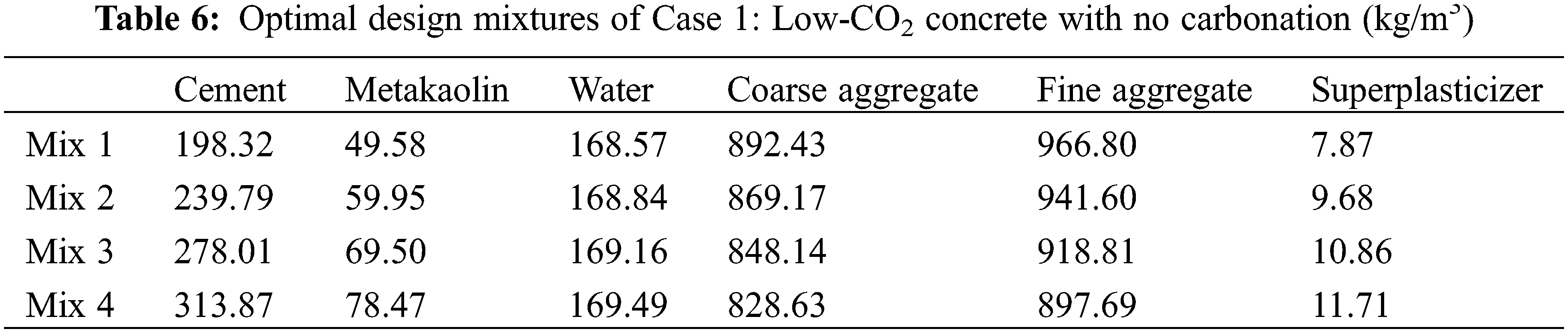
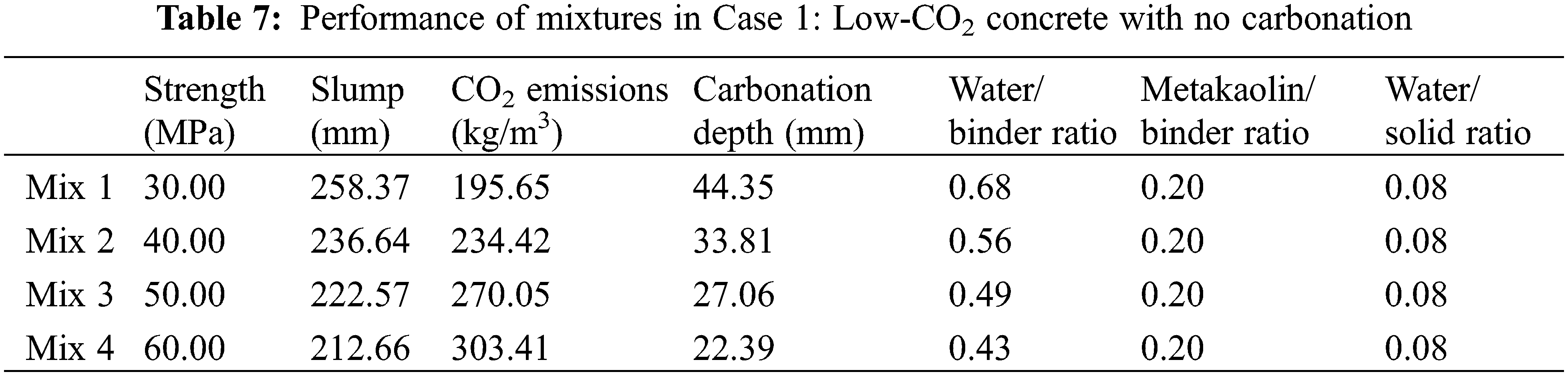
Carbonation depth vs. time for Mixes 1 to 4 is shown in Figs. 3c to 3f. After a service life of 50 years, the depths of carbonation of Mixes 1 to 3 exceed the cover depth of 25 mm (shown in Figs. 3c to 3e), while the depth of carbonation of Mix 4 is less than the cover depth (shown in Fig. 3f). This means that for concrete with high strength and a high binder content (Mix 4; 60 MPa), the carbonation durability can be satisfied, while for concrete of an ordinary content and medium strength (Mixes 1 to 3; 30, 40, and 50 MPa), the carbonation durability cannot be satisfied. Hence, the carbonation constraint should be considered for the design strengths of 30, 40, and 50 MPa.

3.2 Case 2: Low-CO2 Concrete with Carbonation

Section 3.1 presents the importance and necessity of the durability of carbonation for mixture design. Hence, this section adds the durability of carbonation as a constraint on mixture design. The difference between the previous section and this section is that the previous Section 3.1 does not include carbonation, while this Section 3.2 does. All the other constraints are the same in both sections.

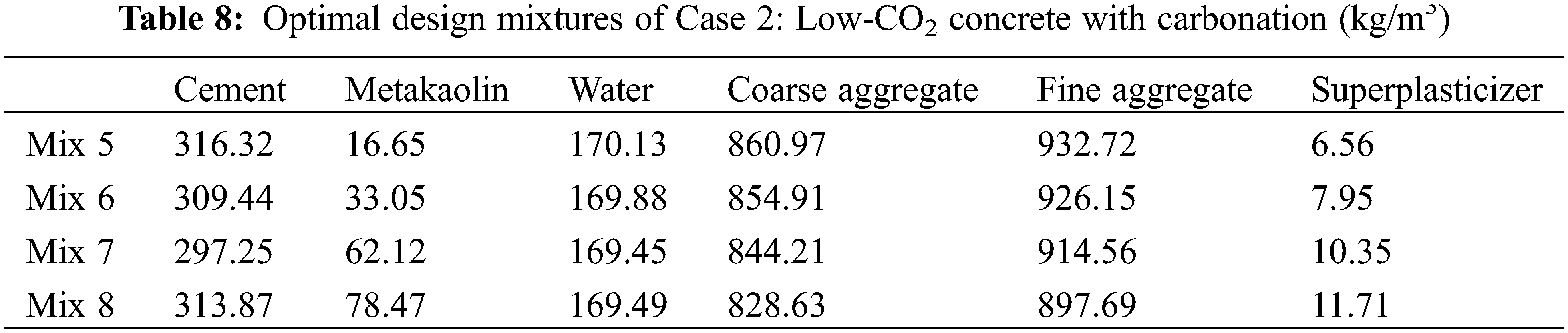
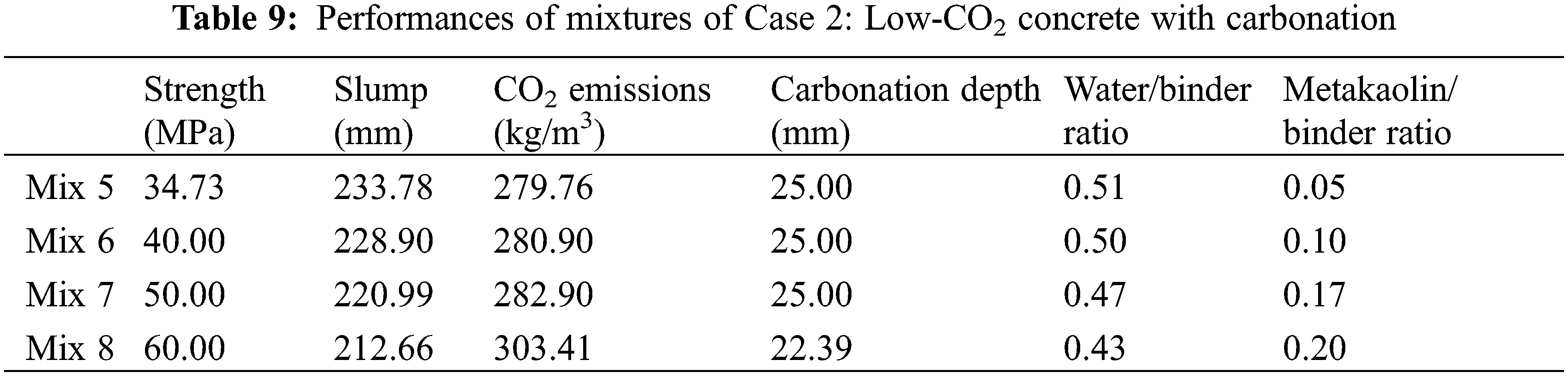
The optimal mixtures and their performances are presented in Tables 8 and 9, respectively. For ordinary-strength concrete Mix 5, the design strength is 30 MPa but the real strength is 34.73 MPa. This means the durability of carbonation is the dominant factor of the design for Mix 5. For carbonation durability, a higher strength must be used. The metakaolin/binder ratio of Mix 5 reaches the lower limit as the addition of metakaolin impairs carbonation resistance. Moreover, for medium-strength concrete, Mixes 6 and 7 have the same strengths as Mixes 2 and 3, respectively. However, the metakaolin/binder ratios of Mixes 6 and 7 are lower than those of Mixes 2 and 3, respectively. This is because a higher metakaolin content can impair carbonation durability. Lastly, for high-strength concrete, Mix 8 is the same as Mix 4. This means that carbonation does not influence the mixture design of concrete with high strength. As shown in Fig. 4, as the strength of concrete increases, the CO2 emissions increase (shown in Fig. 4a) and the water/binder ratio decreases (shown in Fig. 4b). This trend agrees with results in [25,31]. For Mixes 5 to 7, the depth of carbonation equals the cover depth of the concrete (shown in Figs. 4c to 4e), while for Mix 8, the depth of the carbonation is less than the cover depth of the concrete (shown in Fig. 4f).

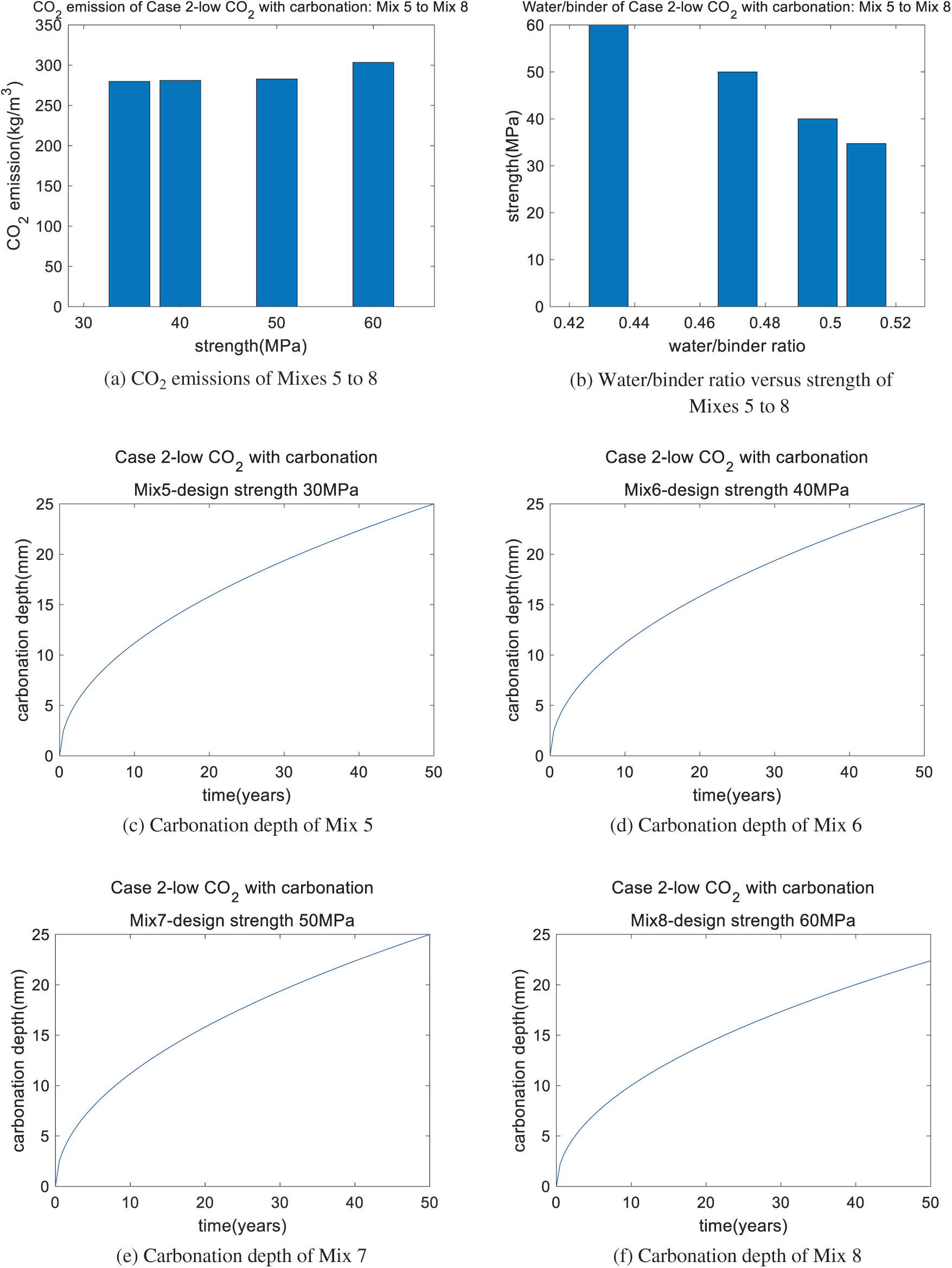
Figure 4: Performance of Case 2 (low CO2 with carbonation): Mix 5, Mix 6, Mix 7, and Mix 8

3.3 Case 3: Low-Material-Cost Concrete with Carbonation

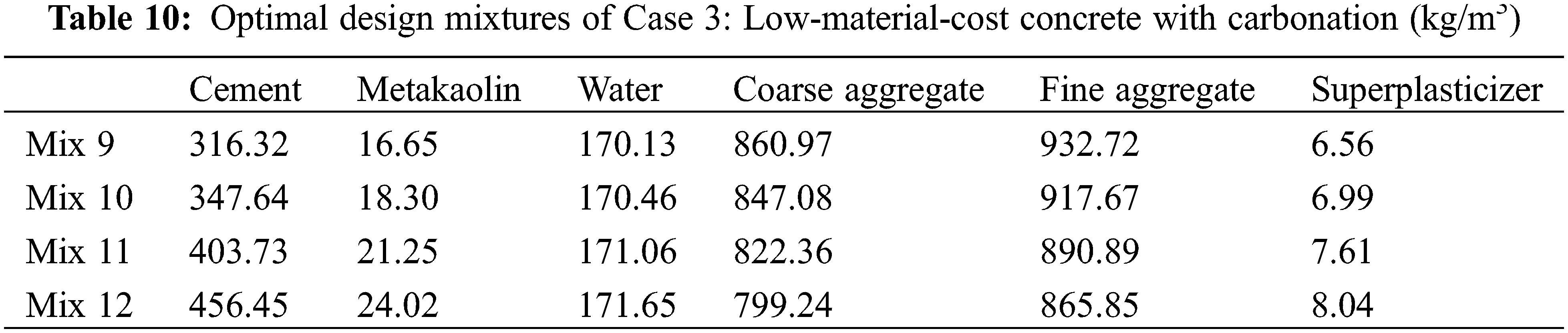
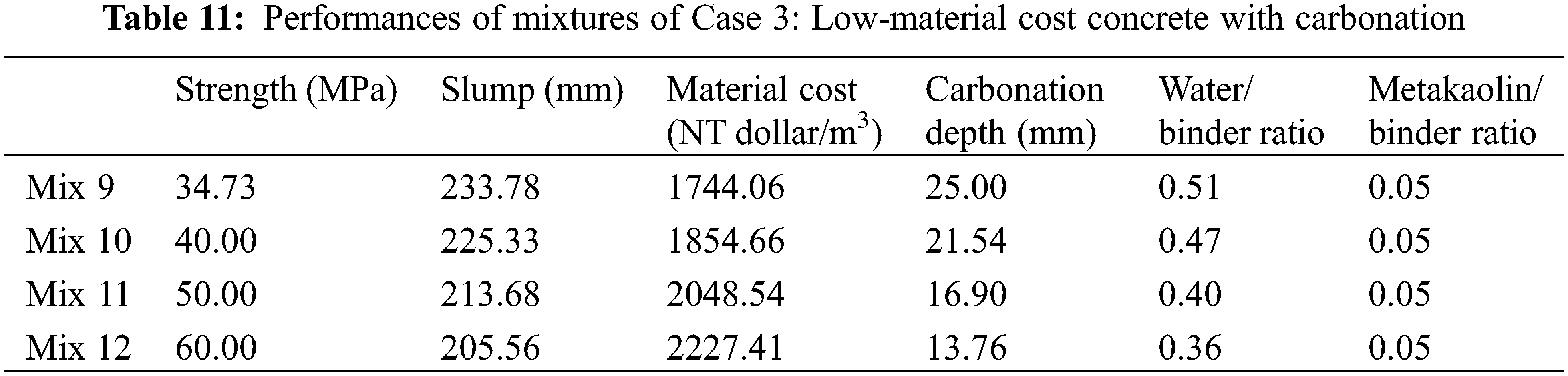
In the previous Sections 3.1 and 3.2, the aim of the optimal design was low CO2. Besides CO2 emissions, material costs are an important index of concrete sustainability [25]. In this section, a minimal material cost of the concrete is set as the aim of the optimal design. By using the genetic algorithm, the optimal mixtures with low material costs are calculated and presented in Table 10. The performance of the optimal mixtures in Case 3 is shown in Table 11. First, we can see that Mix 9 is the same as Mix 5, though the aim of the optimal design for Mix 9 is low material cost, while the aim for Mix 5 is low cost. This is because carbonation durability is the dominant factor for the optimal design of Mixes 9 and 5, which have an ordinary strength of 30 MPa. Second, for Mixes 10 to 12, the metakaolin/binder ratio is at the lower limit. This is because the unit material cost of metakaolin is much higher than that of cement. When the aim is set as low cost, the content of metakaolin will be as low as possible. Third, as shown in Fig. 5, as the strength of concrete increases, the cost of materials increases (shown in Fig. 5a), the water/binder ratio of the concrete decreases (shown in Fig. 5b), and the depth of carbonation of the concrete decreases (shown in Figs. 5c to 5f). This shows agreement with references [13–14,28]. For Mixes 10 to Mix 12, the depth of carbonation after 50 years is lower than the cover depth of the concrete (shown in Figs. 5d to 5f, respectively).

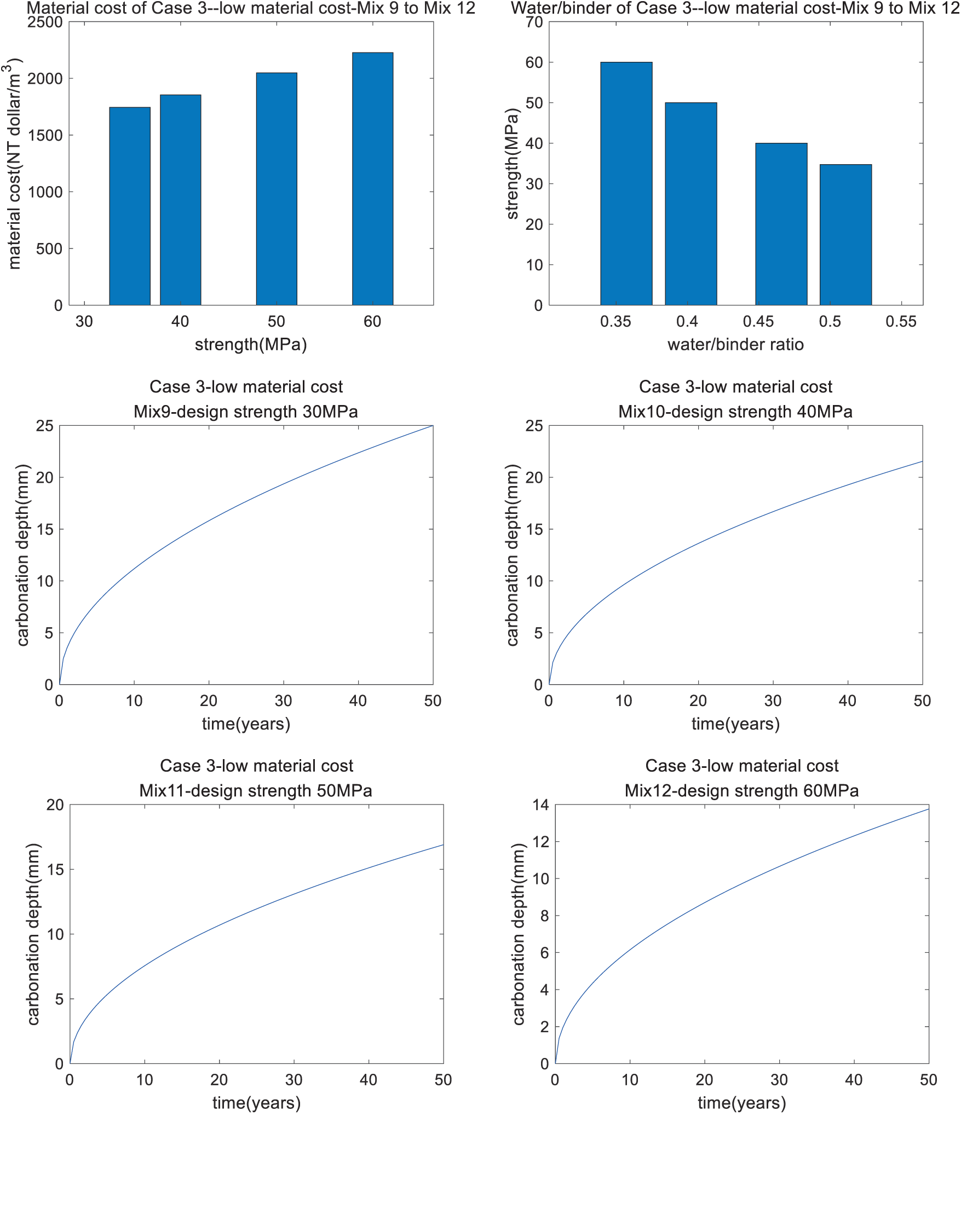
Figure 5: Performance of Case 3 (low material cost): Mix 9, Mix 10, Mix 11, and Mix 12

3.4 Case 4: Low-Total-Cost Concrete with Carbonation

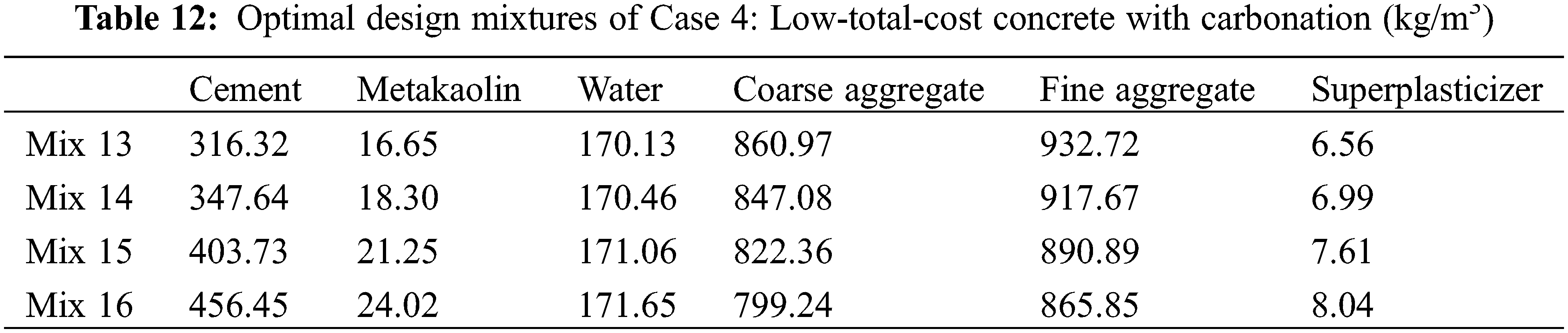
Sections 3.2 and 3.3 show the optimal design of low-CO2 and low-material-cost concrete, respectively. Because CO2 emissions have a different unit to material costs, this study uses the carbon price to convert the unit of CO2 emissions into that of cost [27]. In other words, the total cost equals the cost of materials plus CO2 emission costs [27]. Based on the genetic algorithm, we produce an optimal design for a low total cost with carbonation. We find that the results for the optimal design (shown in Table 12) are the same as those shown in Section 3.3. This is because the cost of CO2 emissions is much lower than the material costs. As shown in Fig. 6a, the ratio of CO2 emission costs to total cost is about 13%. This low ratio is not enough to affect the results of the optimal design. In addition, as shown in Fig. 6b, as the concrete strength increases, the total cost also increases.

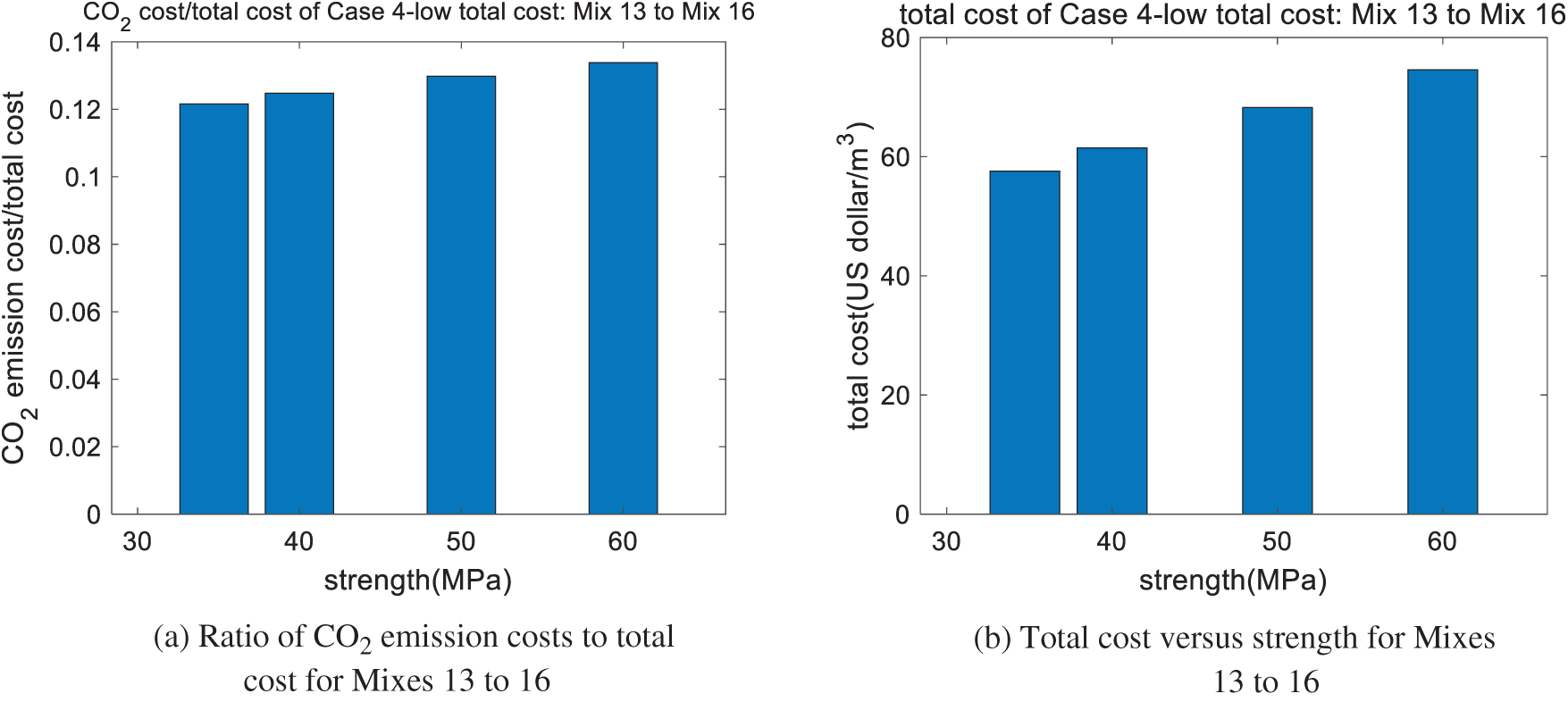
Figure 6: Performance of Case 4 (low total cost): Mix 13, Mix 14, Mix 15, Mix 16

3.5 Case 5: Low-Total-Cost Concrete with Climate Change

In Sections 3.2 to 3.4, the effect of carbonation on the optimal design was considered. Carbonation is a complex physical-chemical process. The rate of carbonation is closely related to environmental conditions, such as the CO2 concentration and environmental temperature. Because of climate change, CO2 concentrations and temperatures are increasing. Consequently, climate change will affect the carbonation service life. Furthermore, concrete mixture design may be affected by climate change.

The Intergovernmental Panel on Climate Change (IPCC) has proposed various Representative Concentration Pathways (RCPs), such as RCP 2.6, RCP 4.5, RCP 6.0, and RCP 8.5. These climate change scenarios represent various directions global warming could take [37]. RCP 8.5 has greater increases in the CO2 concentration and temperature than the other scenarios. This section considers the effect of climate change scenario RCP 8.5 on the optimal design. The difference between Sections 3.4 and 3.5 is Section 3.5 considers climate change, while Section 3.4 does not.

The increases in CO2 concentration and temperature in RCP 8.5 are shown in Figs. 7a and 7b, respectively. To determine the carbonation depth with climate change, the time average of CO2 concentration ∫0t[CO2]tdtt and the time average of CO2 diffusivity ∫0t[D]tdtt are used [40].

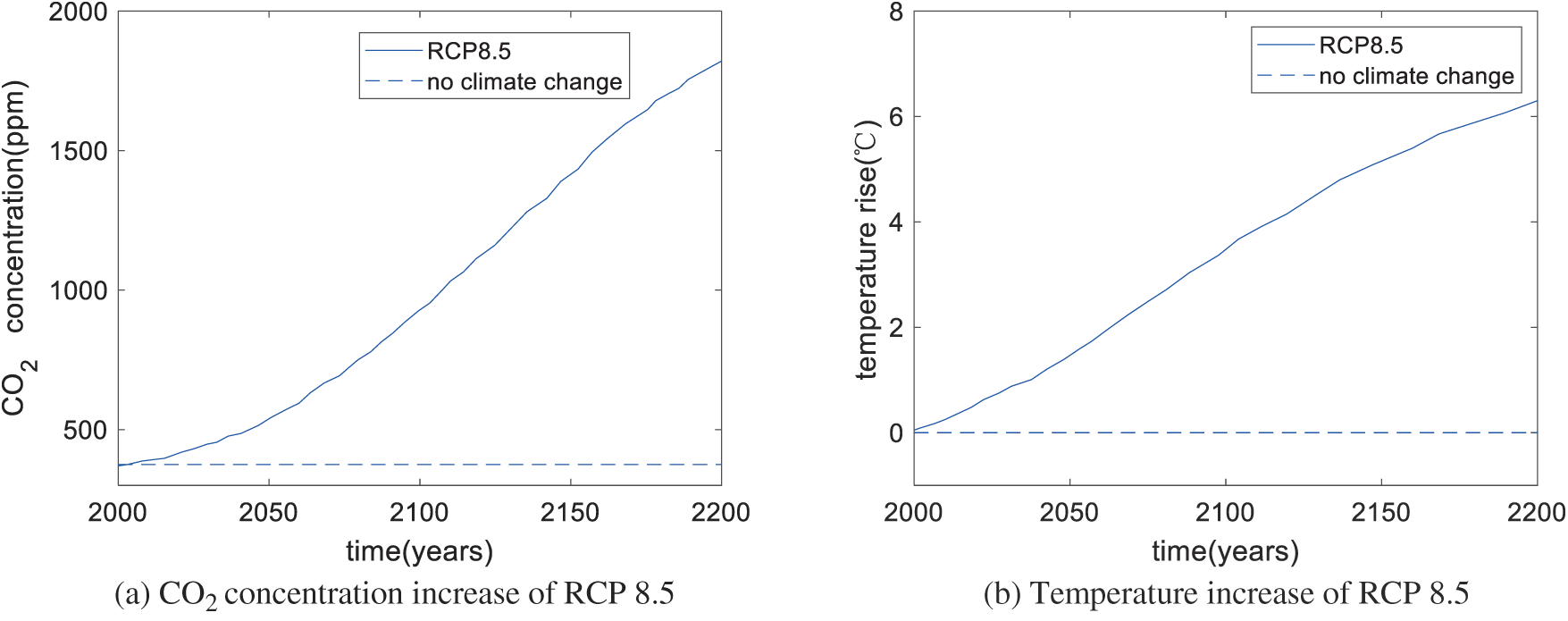
Figure 7: CO2 concentration and temperature increases of RCP 8.5

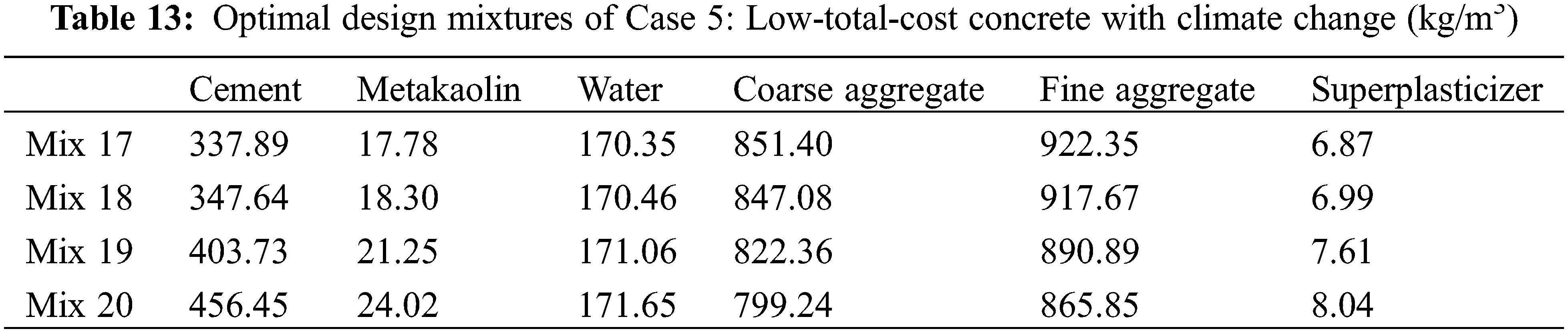
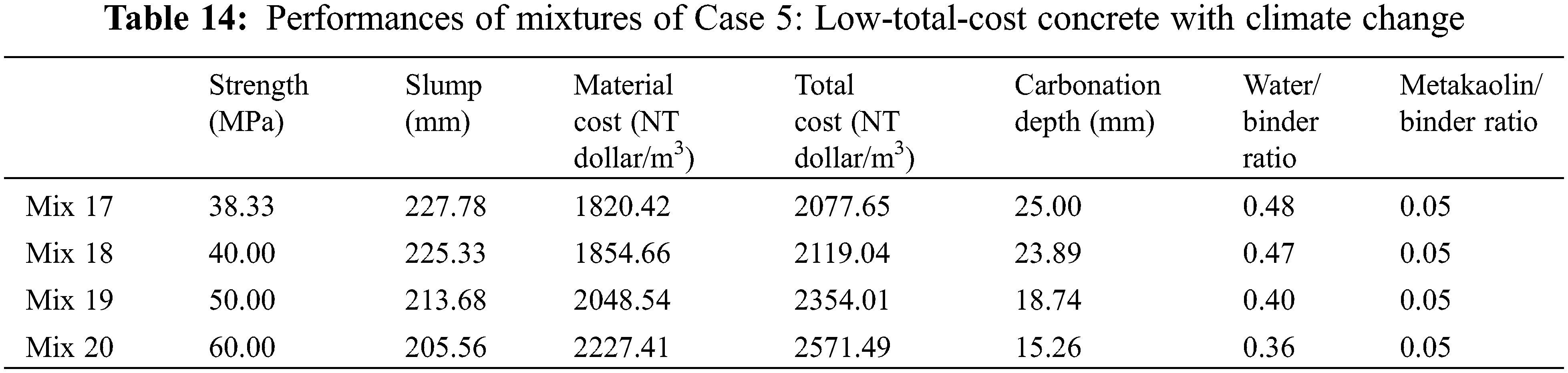
Based on the genetic algorithm, the optimal mixtures are determined and presented in Table 13. The performances of the optimal mixtures of case 5 are shown in Table 14. First, the design strength of Mix 17 is 30 MPa, while the real strength of Mix 17 is 38.33 MPa. This is because the durability of carbonation dominates the mixture design of Mix 17. Moreover, Mixes 17 and 13 have the same design strength, while the real strength of Mix 17 is higher than that of Mix 13 because Mix 17 considers climate change. To satisfy the demand for carbonation with climate change, a higher binder content and higher strength should be used. Second, Mixes 18 to 20 are the same as Mixes 10 to 12, respectively. In other words, climate change does not influence the mixture design of Mixes 18 to 20. This is because Mixes 18 to 20 have a high binder content and show sufficient resistance to carbonation even if climate change occurs. Third, as shown in Fig. 8, as the strength of the concrete increases, the total cost of the concrete increases (shown in Fig. 8a), the water/binder ratio decreases (shown in Fig. 8b), and the depth of carbonation decreases (shown in Figs. 8c to 8f). Moreover, the analysis results show that the carbonation depth of concrete under climate change is much higher than that without climate change, especially at a late age of service life (shown in Figs. 8c to 8f).

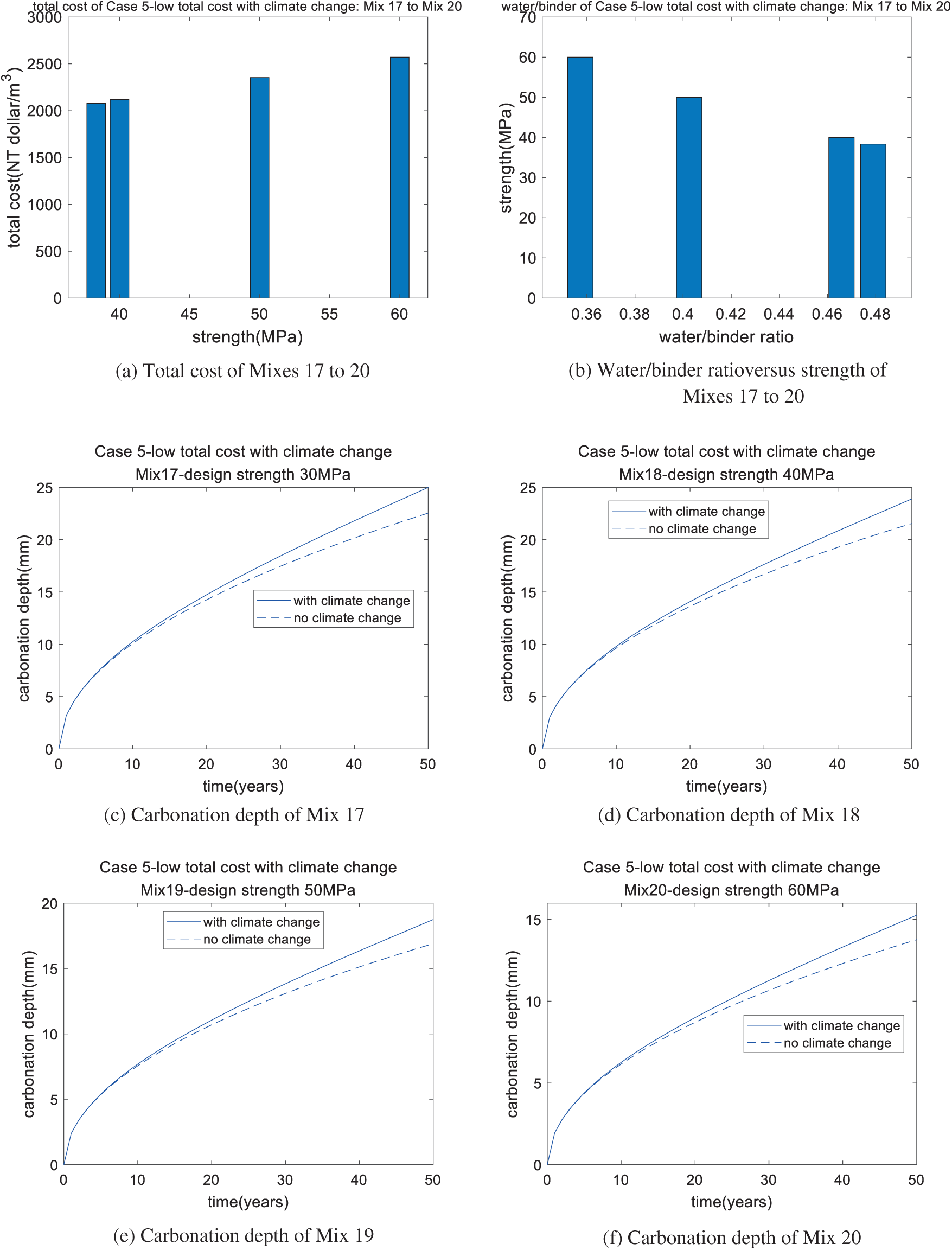
Figure 8: Performance of Case 5 (low total cost with climate change): Mix 17, Mix 18, Mix 19, Mix 20

4  Discussions

Compared with previous studies, the proposed design framework shows some benefits as follows:

First, previous studies mainly focused on low-cost concrete [25] or low-CO2 concrete [23,24]. The difference between low-cost concrete and low-CO2 concrete was not clearly clarified. In this study, the proposed method can design low-cost concrete (Case 3) or low-CO2 concrete (Case 2). We find that when the design strength is 30 MPa, the low-cost concrete is the same as the low-CO2 concrete because the durability of carbonation dominates the mixture design. Yet, for the cases of the design strengths 40, 50, and 60 MPa, low-cost concrete is different from low-CO2 concrete. To summarize, the proposed method is flexible and thus suited to finding optimal mixtures with different aims.

Second, previous mixture design studies did not pay enough attention to carbonation durability [23,24]. This study finds that when the design strength is 30 MPa, after considering carbonation durability (from Case 1 to Case 2), the real strength should be higher than 30 MPa. Moreover, when carbonation proceeds with climate change (from Case 4 to Case 5), the real strength of the concrete should be further improved. Next, when the design strength is 40 and 50 MPa, after considering carbonation durability (from Case 1 to Case 2), the metakaolin/binder ratio is lowered because the addition of metakaolin can impair carbonation resistance. Finally, when the design strength is 60 MPa, after considering carbonation durability (from Case 1 to Case 2), the optimal mixtures do not change. In summary, carbonation durability mainly affects the optimal design of ordinary-strength (30 MPa) and medium-strength (40 and 50 MPa) concrete, and does not affect the optimal design of high-strength concrete (60 MPa).

Third, for different design codes, the calculation equations of strength, slump, and carbonation depth for metakaolin-modified concrete may be different [13,14,23,24,41,42]. However, because the genetic algorithm is a common optimization process that can be used for different constraints equations, based on the proposed integrated design framework, other researchers can determine the optimal mixture design for their local situations.

Fourth, in this study, a genetic algorithm was used to determine optimal mixtures. As shown in Table 4, five case studies were performed, and each case study consists of four mix ratios. The performance of the optimal results, such as strength, slump, and carbonation depth, were calculated using Eqs. (7), (9) and (13), respectively. Because these performance evaluation equations have been verified from the relevant experimental studies, the accuracy of optimal results is acceptable. In addition, in this study, we made case studies about making low-CO2 concrete or low-cost concrete using MK. In previous literature, the differences between low-CO2 concrete and low-cost concrete were not studied in detail. The results of this study can fill the gap. The analysis results of Section 3.3 of this study show that it is not wise to produce low-cost concrete using MK.

5  Conclusions

This study offers an integrated mixture design framework for sustainable metakaolin-modified concrete. The genetic algorithm is used to determine the optimal mixtures. Strength, slump, and carbonation with or without climate change are considered as constraints of optimization, and CO2 emissions, material costs, and the total cost are set as the aims of optimization. Based on an analysis of five design cases, the following conclusions can be drawn:

(1)   Case 1 (low-CO2 concrete with no carbonation) shows that for concrete with high strength and a high binder content (Mix 4; 60 MPa), the carbonation durability can be satisfied, while for concrete with an ordinary and medium strengths (Mixes 1 to 3; 30, 40, and 50 MPa, respectively), the carbonation durability cannot be satisfied. For Mixes 1 to 4, the metakaolin/binder ratio is at the upper limit because the CO2 emissions of metakaolin are much lower than those of cement.

(2)   Case 2 (low-CO2 concrete with carbonation) shows that for ordinary-strength concrete Mix 5, the design strength is 30 MPa but the real strength is 34.73 MPa. This means that carbonation, not strength dominates the mixture design for Mix 5. To meet the carbonation durability, a higher real strength must be used. For medium-strength concrete Mixes 6 and 7 (design strengths 40 and 50 MPa, respectively), the metakaolin/binder ratio is lower than that for Case 1 (low-CO2 concrete with no carbonation) because metakaolin can impair carbonation resistance.

(3)   Case 3 (low-material cost concrete with carbonation) shows that for Mixes 9 to 12, the metakaolin/binder ratio is at the lower limit. This is because the unit material cost of metakaolin is higher than that of cement. In addition, when the design strength is 30 MPa, low-material-cost concrete Mix 9 is the same as low-CO2 concrete Mix 5. Thus, carbonation durability is the control factor for the mixture design of ordinary-strength concrete Mix 9 (design strength 30 MPa).

(4)   Case 4 (low-total cost concrete with carbonation) shows that low-total-cost concrete Mixes 13 to 16 are the same as low-material-cost concrete Mixes 9 to 12, respectively. This is because the costs of CO2 emissions are much lower than the material costs. The ratio of CO2 emission costs to the total cost is about 13%. This low ratio is not enough to affect the results of the optimal design.

(5)   Case 5 (low-total cost concrete with carbonation and climate change) shows that when the design strength is 30 MPa (Mix 17), due to considerations of climate change, the concrete’s real strength increases from 34.73 to 38.33 MPa. For ordinary-strength concrete (design strength 30 MPa), to satisfy the demand of carbonation with climate change, a higher binder content and higher strength should be used. On the other hand, climate change does not influence the mixture design of concrete with the design strengths of 40, 50, and 60 MPa.

To conclude, the proposed framework covers various aims (minimized CO2 emissions, material costs, and total cost) and considers different constraints (strength, workability, and durability with climate change). The proposed method can be used as a general process for the optimal design of sustainable metakaolin-modified concrete.

Funding Statement: This research was supported by the National Research Foundation of Korea (NRF-2020R1A2C4002093).

Conflicts of Interest: The author declares that they have no conflicts of interest to report regarding the present study.

References

 1.  Wang, X. (2017). Analysis of hydration-mechanical-durability properties of metakaolin blended concrete. Applied Sciences, 7(10), 1087–1102. DOI 10.3390/app7101087. [Google Scholar] [CrossRef]

 2.  Bakera, A., Alexander, M. (2019). Use of metakaolin as supplementary cementitious material in concrete, with focus on durability properties. RILEM Technical Letters, 4, 89–102. DOI 10.21809/rilemtechlett.2019.94. [Google Scholar] [CrossRef]

 3.  Wang, X., Lee, H. (2019). Microstructure modeling of carbonation of metakaolin blended concrete. Advances in Concrete Construction, 7(3), 167–174. DOI 10.12989/acc.2019.7.3.167 [Google Scholar] [CrossRef]

 4.  Sharifi, Y., Hosseinpour, M. (2020). A predictive model based ANN for compressive strength assessment of the mortars containing metakaolin. Journal of Soft Computing in Civil Engineering, 4, 1–12. DOI 10.22115/scce.2020.214444.1157. [Google Scholar] [CrossRef]

 5.  Ding, J., Li, Z. (2002). Effects of metakaolin and silica fume on properties of concrete. ACI Materials Journal, 99, 393–398. DOI 10.14359/12222. [Google Scholar] [CrossRef]

 6.  Dinakar, P., Sahoo, P., Sriram, G. (2013). Effect of metakaolin content on the properties of high strength concrete. International Journal of Concrete Structures and Materials, 7(3), 215–223. DOI 10.1007/s40069-013-0045-0. [Google Scholar] [CrossRef]

 7.  Li, Z. (2016). Drying shrinkage prediction of paste containing meta-kaolin and ultrafine fly ash for developing ultra-high performance concrete. Materials Today Communications, 6, 74–80. DOI 10.1016/j.mtcomm.2016.01.001. [Google Scholar] [CrossRef]

 8.  Chen, J., Li, Q., Ng, P., Li, L., Kwan, A. (2020). Cement equivalence of metakaolin for workability, cohesiveness, strength and sorptivity of concrete. Materials, 13(7), 1646–1667. DOI 10.3390/ma13071646. [Google Scholar] [CrossRef]

 9.  Meddah, M., Ismail, M., El-Gamal, S., Fitriani, H. (2018). Performances evaluation of binary concrete designed with silica fume and metakaolin. Construction and Building Materials, 166, 400–412. DOI 10.1016/j.conbuildmat.2018.01.138. [Google Scholar] [CrossRef]

10. Bucher, R., Diederich, P., Escadeillas, G., Cyr, M. (2017). Service life of metakaolin-based concrete exposed to carbonation. Cement and Concrete Research, 99, 18–29. DOI 10.1016/j.cemconres.2017.04.013. [Google Scholar] [CrossRef]

11. Liu, B., Qin, J., Shi, J., Jiang, J., Wu, X. et al. (2021). New perspectives on utilization of CO2 sequestration technologies in cement-based materials. Construction and Building Materials, 272, 121660. DOI 10.1016/j.conbuildmat.2020.121660. [Google Scholar] [CrossRef]

12. Bai, J., Wild, S., Ware, J., Sabir, B. (2003). Using neural networks to predict workability of concrete incorporating metakaolin and fly ash. Advances in Engineering Software, 34(11–12), 663–669. DOI 10.1016/S0965-9978(03)00102-9. [Google Scholar] [CrossRef]

13. Papadakis, V., Antiohos, S., Tsimas, S. (2002). Supplementary cementing materials in concrete: Part II: A fundamental estimation of the efficiency factor. Cement and Concrete Research, 32, 1533–1538. DOI 10.1016/S0008-8846(02)00829-3. [Google Scholar] [CrossRef]

14. Papadakis, V., Tsimas, S. (2002). Supplementary cementing materials in concrete: Part I: Efficiency and design. Cement and Concrete Research, 32, 1525–1532. DOI 10.1016/S0008-8846(02)00827-X. [Google Scholar] [CrossRef]

15. Papadakis, V., Demis, S. (2013). Predictive modeling of concrete compressive strength based on cement strength class. Computers and Concrete, 11 (6), 587–602. DOI 10.12989/cac.2013.11.6.587. [Google Scholar] [CrossRef]

16. Safarzadegan Gilan, S., Bahrami Jovein, H., Ramezanianpour, A. (2012). Hybrid support vector regression–particle swarm optimization for prediction of compressive strength and RCPT of concretes containing metakaolin. Construction and Building Materials, 34, 321–329. DOI 10.1016/j.conbuildmat.2012.02.038. [Google Scholar] [CrossRef]

17. Al-alaily, H., Hassan, A. (2016). Refined statistical modeling for chloride permeability and strength of concrete containing metakaolin. Construction and Building Materials, 114, 564–579. DOI 10.1016/j.conbuildmat.2016.03.187. [Google Scholar] [CrossRef]

18. Dvorkin, L., Bezusyak, A., Lushnikova, N., Ribakov, Y. (2012). Using mathematical modeling for design of self compacting high strength concrete with metakaolin admixture. Construction and Building Materials, 37, 851–864. DOI 10.1016/j.conbuildmat.2012.04.019. [Google Scholar] [CrossRef]

19. Güneyisi, E., Gesoğlu, M., Algın, Z., Mermerdaş, K. (2014). Optimization of concrete mixture with hybrid blends of metakaolin and fly ash using response surface method. Composites Part B: Engineering, 60, 707–715. DOI 10.1016/j.compositesb.2014.01.017. [Google Scholar] [CrossRef]

20. Long, G., Gao, Y., Xie, Y. (2015). Designing more sustainable and greener self-compacting concrete. Construction and Building Materials, 84, 301–306. DOI 10.1016/j.conbuildmat.2015.02.072. [Google Scholar] [CrossRef]

21. Dinakar, P., Manu, S. (2014). Concrete mix design for high strength self-compacting concrete using metakaolin. Materials & Design, 60, 661–668. DOI 10.1016/j.matdes.2014.03.053. [Google Scholar] [CrossRef]

22. Ashish, D., Verma, S. (2019). Determination of optimum mixture design method for self-compacting concrete: Validation of method with experimental results. Construction and Building Materials, 217, 664–678. DOI 10.1016/j.conbuildmat.2019.05.034. [Google Scholar] [CrossRef]

23. Kim, T., Tae, S., Roh, S. (2013). Assessment of the CO2 emission and cost reduction performance of a low-carbon-emission concrete mix design using an optimal mix design system. Renewable and Sustainable Energy Reviews, 25, 729–741. DOI 10.1016/j.rser.2013.05.013. [Google Scholar] [CrossRef]

24. Yang, K., Tae, S., Choi, D. (2016). Mixture proportioning approach for low-CO2 concrete using supplementary cementitious materials. ACI Materials Journal, 113 (4), 533–542. DOI 10.14359/51688992. [Google Scholar] [CrossRef]

25. Yeh, I. (2007). Computer-aided design for optimum concrete mixtures. Cement and Concrete Composites, 29(3), 193–202. DOI 10.1016/j.cemconcomp.2006.11.001. [Google Scholar] [CrossRef]

26. Huang, W., Kazemi-Kamyab, H., Sun, W., Scrivener, K. (2017). Effect of replacement of silica fume with calcined clay on the hydration and microstructural development of eco-UHPFRC. Materials & Design, 121, 36–46. DOI 10.1016/j.matdes.2017.02.052. [Google Scholar] [CrossRef]

27. Park, H., Kwon, B., Shin, Y., Kim, Y., Hong, T. et al. (2013). Cost and CO2 emission optimization of steel reinforced concrete columns in high-rise buildings. Energies, 6, 5609–5624. DOI 10.3390/en6115609. [Google Scholar] [CrossRef]

28. Thomas, M. (2013). Supplementary cementing materials in concrete. Boca Raton: CRC Press. [Google Scholar]

29. Ashish, D., Verma, S. (2019). Cementing efficiency of flash and rotary-calcined metakaolin in concrete. Journal of Materials in Civil Engineering, 31(12), 4019307. DOI 10.1061/(ASCE)MT.1943-5533.0002953. [Google Scholar] [CrossRef]

30. Rezaifar, O., Hasanzadeh, M., Gholhaki, M. (2016). Concrete made with hybrid blends of crumb rubber and metakaolin: Optimization using response surface method. Construction and Building Materials, 123, 59–68. DOI 10.1016/j.conbuildmat.2016.06.047. [Google Scholar] [CrossRef]

31. Lim, C., Yoon, Y., Kim, J. (2004). Genetic algorithm in mix proportioning of high-performance concrete. Cement and Concrete Research, 34(3), 409–420. DOI 10.1016/j.cemconres.2003.08.018. [Google Scholar] [CrossRef]

32. Nazário Santos, F., Raquel Gomes de Sousa, S., José Faria Bombard, A., Lopes Vieira, S. (2017). Rheological study of cement paste with metakaolin and/or limestone filler using mixture design of experiments. Construction and Building Materials, 143, 92–103. DOI 10.1016/j.conbuildmat.2017.03.001. [Google Scholar] [CrossRef]

33. Rashwan, M., Megahed, A., Essa, M. (2015). Effect of local metakaolin on properties of concrete and its sulphuric acid resistance. Journal of Engineering Sciences, 43 (2), 183–199. DOI 10.21608/jesaun.2015.115165. [Google Scholar] [CrossRef]

34. Oh, B., Jang, S. (2004). Prediction of diffusivity of concrete based on simple analytic equations. Cement and Concrete Research, 34, 463–480. DOI 10.1016/j.cemconres.2003.08.026. [Google Scholar] [CrossRef]

35. Larrard, F. (1999) Concrete Mixture Proportioning-A scientific approach. London: E&FN Spon. [Google Scholar]

36. Song, H., Kwon, S. (2007). Permeability characteristics of carbonated concrete considering capillary pore structure. Cement and Concrete Research, 37, 909–915. DOI 10.1016/j.cemconres.2007.03.011. [Google Scholar] [CrossRef]

37. IPCC (2014). Climate Change 2014: Synthesis Report. Contribution of Working Groups I, II and III to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change [Core Writing Team, R.K. Pachauri and L.A. Meyer (eds.)], pp. 151, IPCC, Geneva, Switzerland. [Google Scholar]

38. Noguchi, T., Maruyama, I., Kanematsu, M. (2003). Performance based design system for concrete mixture with multi-optimizing genetic algorithm. Proceedings of the 11th International Congress on the Chemistry of Cement, South Africa, South Africa, pp. 1921–1930. The Cement and Concrete Institute of South Africa. [Google Scholar]

39. CEN (2006). Eurocode 2: Design of concrete structures. UK: British standards institution. [Google Scholar]

40. Kwon, S., Na, U., Park, S., Jung, S. (2009). Service life prediction of concrete wharves with early-aged crack: Probabilistic approach for chloride diffusion. Structural Safety, 31, 75–83. DOI 10.1016/j.strusafe.2008.03.004. [Google Scholar] [CrossRef]

41. Zhang, H., Xu, Y., Gan, Y., Chang, Z., Schlangen, E. et al. (2019). Combined experimental and numerical study of uniaxial compression failure of hardened cement paste at micrometre length scale. Cement and Concrete Research, 126, 105925. DOI 10.1016/j.cemconres.2019.105925. [Google Scholar] [CrossRef]

42. Ge, Z., Tawfek, A., Zhang, H., Yang, Y., Yuan, H. et al. (2021). Influence of an extrusion approach on the fiber orientation and mechanical properties of engineering cementitious composite. Construction and Building Materials, 306, 124876. DOI 10.1016/j.conbuildmat.2021.124876. [Google Scholar] [CrossRef]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.