Journal of Renewable Materials

DOI: 10.32604/jrm.2022.018467

ARTICLE

Mechanism behind Time Dependent Elasticity of Crumb Rubber-Nano-Asphalt Hybrids Using Discrete Relaxation Spectrum

Lili Han1,2, Mulian Zheng2,*, Hongbing Guo1, Tao Wang3, Jiajian Zhu4 and Pouria Hajikarimi5

1Shaanxi College of Communication Technology, Xi’an, 710018, China
2Key Laboratory for Special Area Highway Engineering of Ministry of Education, Chang’an University, Xi’an, 710064, China
3Huabang Construction & Investment Group Co., Ltd., Guangzhou, 510030, China
4Gansu Road and Bridge Construction Group Co., Ltd., Lanzhou, 730000, China
5Department of Civil and Environmental Engineering, Amirkabir University of Technology, Tehran, 1591634311, Iran
*Corresponding Author: Mulian Zheng. Email: zhengml@chd.edu.cn
Received: 30 July 2021; Accepted: 08 September 2021

1  Introduction

Currently, most countries and regions in the world are facing increasingly severe challenges of waste tires from automobile industry. Rather than simply stockpiling or burning waste tires which may bring about serious environmental issues, crumb rubber powder is a successfully renewable material from recycling waste rubber tire. By shredding and chipping a whole tire into pieces and then removing the steel and fabric inside, tire chips are obtained and then ground at ambient temperature or cryogenically to produce crumb rubber powder which can be used as bitumen modifier in pavement engineering. Crumb rubber powder has been incorporated into paving asphalt since the 1930s due to its good resistance to deformation and fatigue as well as its eco-friendly performance [1].

Rutting has been recognized as the most serious asphalt pavement distress caused by heavy traffic loads as well as harsh weather. Generally, this distress is acknowledged as an accumulation of mixture non-recoverable deformations under repeated vehicle loads, which is highly dependent on viscoelastic nature of asphalt binder [2–4]. Asphalt binder demonstrates elasticity and viscosity simultaneously within its service temperature, and thus characterizing its rutting resistance using viscoelastic theory is currently a common practice [5–10]. In terms of characterizing viscoelasticity of asphalt binders, both the linear viscoelastic (LVE) theory and nonlinear viscoelastic (NLVE) theory were used. The LVE theory was applicable to small stress or strain level, which describes material mechanical responses using combinations basic mechanical analogue elements. Whereas the NLVE theory was suitable for large stress or strain level, which takes into account the nonlinear relationship of stress vs. strain by adopting more complex constitutive equations. Although the NLVE theory seemed to be more accurate than the LVE theory, the latter was more popular in practice due to clear physical meaning, model simplicity as well as sufficient accuracy [5–6,9].

To enhance the rutting resistance of asphalt mixture, a great number of modified asphalts have been investigated and have been put into practice successfully. Among which, the crumb rubber modified asphalt has been commonly used due to excellent anti-deformation capability, enough fatigue resistance as well as environment-friendly advantages [11–14]. Plenty of publications were reported in the literature concerning the manufacturing process, material blending proportion as well as physical and rheological properties of this modified asphalt [13–19].

In the literature, various nano materials have also been reported to use in order to improve the rutting resistance of asphalt binders. Commonly adopted nano materials included nano clay, nano silica, carbon nanotubes, etc. with at least one particle dimension no more than 100 nm [20–23]. The logic behind nano reinforcement of asphalt binder lies in the unique physical and chemical properties resulted from nano-scale materials and their huge surface area-to-volume ratio. It has been verified that most nano materials were able to increase the high temperature stiffness of asphalt binder [21–23].

Researchers have acknowledged that high viscosity and good elasticity were two main reasons which might explain excellent road performances of crumb rubber modified asphalt [11,24,25]. Currently two kinds of experimental methods were applied to evaluate the elasticity of modified asphalt. One is the empirical elastic recovery or resilience test method which could not reflect viscoelastic nature of the asphalt [25]. Another one is the viscoelastic mechanical method, which could reveal the viscoelastic nature of asphalt binder accurately. A case in point for the latter is the repeated creep and recovery (RCR) test which was initially proposed by Bahia in an attempt to analyze the rutting performance of modified asphalt [2]. Based on the RCR test, some changes were made by researcher in the Federal Highway Administration and the well-known multiple stress creep and recovery test (MSCR) was proposed to evaluate the rutting resistance and elasticity of modified asphalts. The elastic recovery obtained in the MSCR test can directly represent the elastic responses of modified asphalt [2,26–28], which has been widely accepted in the characterization of crumb rubber modified asphalts. However, there is a gap in the experimental investigation into the elastic properties of crumb rubber modified asphalt using MSCR test. That is the percent recovery is still a phenomenologically description of the elasticity of modified asphalt. Further experimental research on the high temperature elastic mechanism using Dynamic Mechanical Analysis (DMA) and more intrinsic viscoelastic functions were needed to better explain good elastic properties of crumb rubber modified asphalt.

As a result, this research presented the feasibility of characterizing delayed elasticity of the crumb rubber-nano-asphalt hybrids experimentally using discrete relaxation spectrum which is a true reflection of material viscoelastic nature in broader frequency domain. By performing the generalized Maxwell (GM) model fitting on the 60°C complex modulus curves, the asphalt discrete relaxation spectra were obtained and then the main relaxation time was calculated to characterize time dependent elasticity of the hybrids. To show the model effectiveness, comparisons between the GM model and two other models were made in the fitting process. Good agreements between the main relaxation time and the 60°C zero shear viscosity as well as the percent recovery verified the feasibility of the proposed method. This research was expected to shed some light on the time dependent elasticity mechanism of crumb rubber modified asphalt from the perspective of polymer physics.

2  Methodology

The excellent road performance of crumb rubber-nano-asphalt hybrid was highly related to good elastic property and adequate viscosity. Upon testing their high temperature dynamic viscoelastic responses, this research characterized the delayed elastic performance of crumb rubber-nano-asphalt hybrids using material discrete relaxation spectra based on linear viscoelastic theory. Furthermore, correlation between the relaxation spectrum results with the commonly accepted MSCR test was also analyzed. Fig. 1 illustrates the overall materials, experiments and procedure.

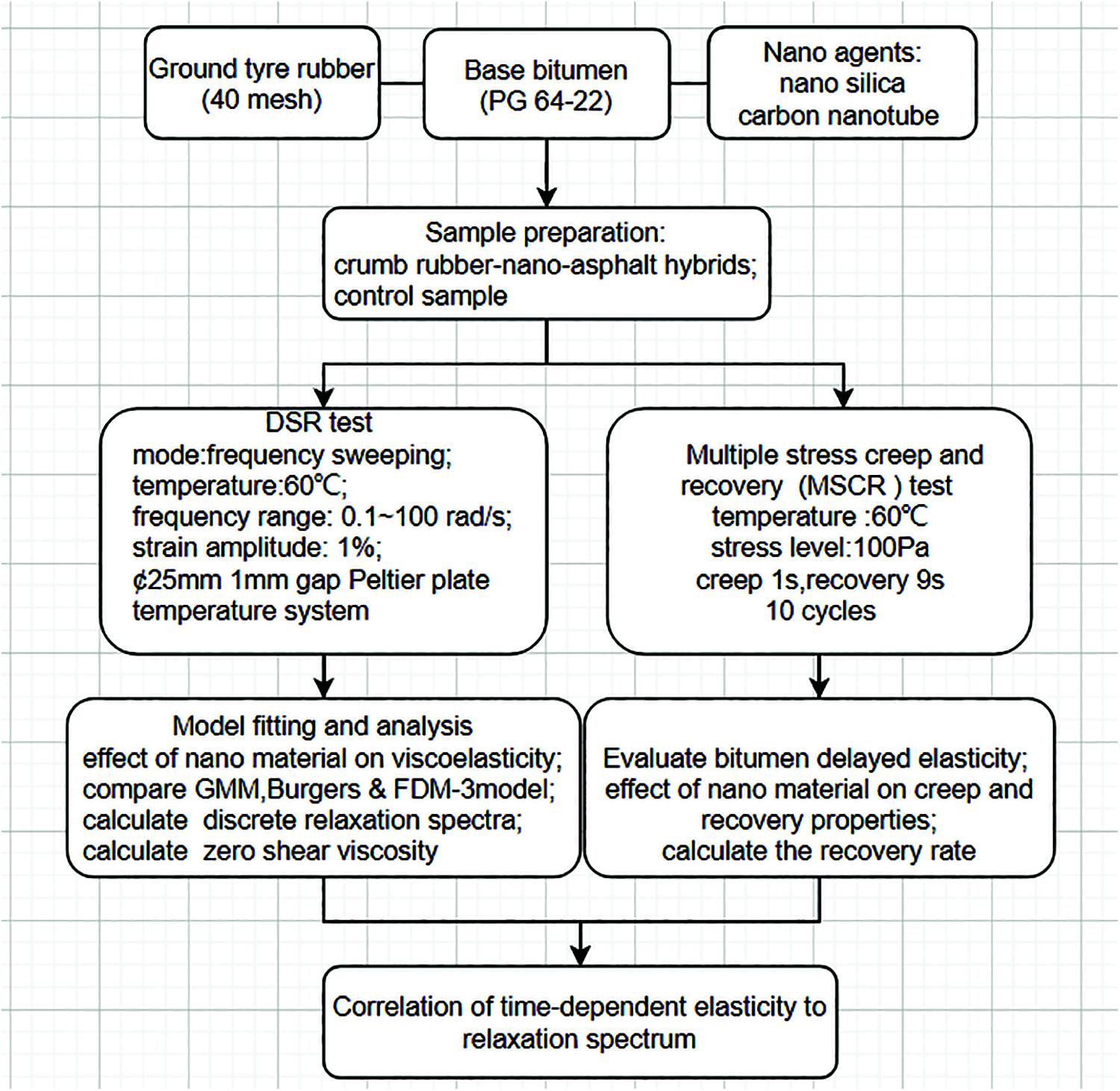
Figure 1: Methods and procedure used in this research

2.1 Materials

In this study, multiple sets of crumb rubber-nano-asphalt hybrids were prepared by adopting the terminal blend technique. All the raw materials are presented below.

2.1.1 Crumb Rubber

The terminal blend technique was adopted to prepare crumb rubber-nano-asphalt hybrids in the lab due to adequate viscosity and good homogeneity [1,13]. Finely ground tire rubber (GTR) powder was adopted to prepare the mentioned hybrids. Its particle gradation is shown in Table 1.

2.1.2 Matrix Asphalt

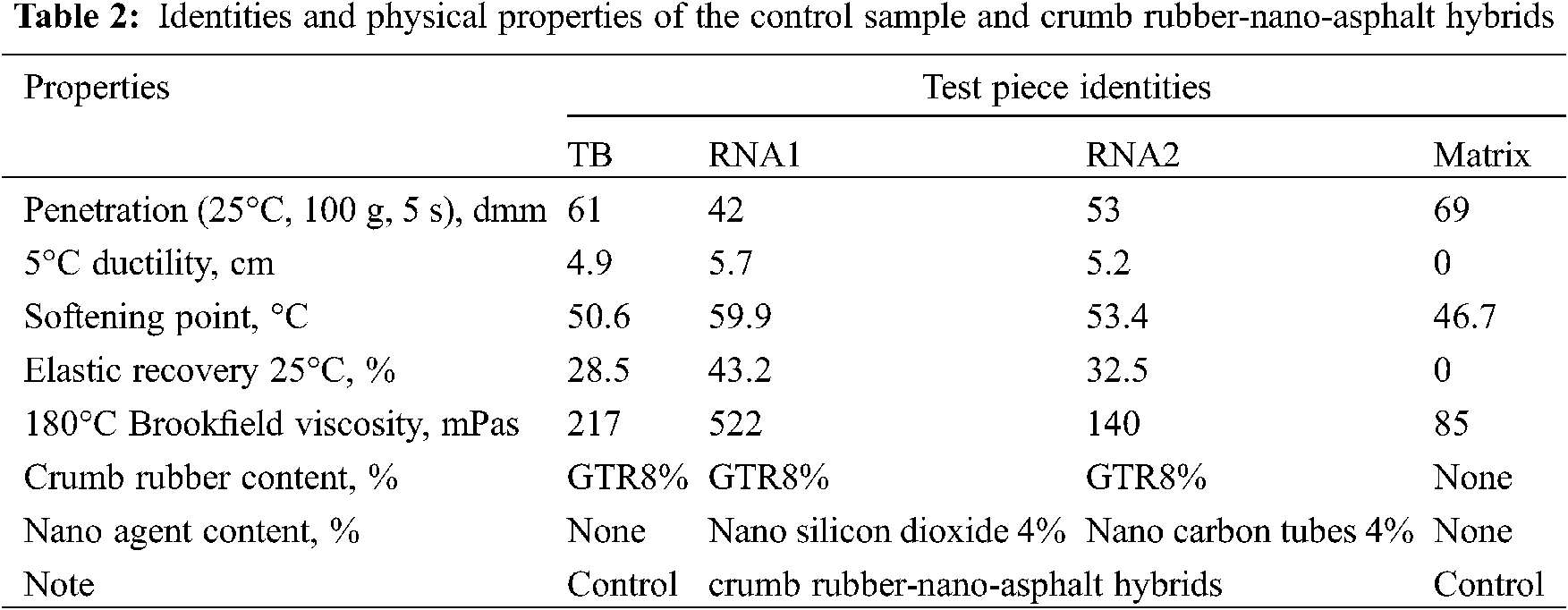
The matrix was A-70 penetration grade asphalt (PG64-22) obtained from the Petro China Karamay Petrochemical Company, Xinjiang Uygur Autonomous Region, China. Physical properties of the matrix asphalt were tested according to the technical code of the Ministry of Transport of China [29] and were given in Table 2.

2.1.3 Nano Reinforcing Agents

The reason for introducing crumb rubber-nano-asphalt hybrids in this research is to make up the defects of terminal blend crumb rubber modified asphalt resulted from excessive desulfurization and degradation of GTR. The main feature of terminal blend technique is smaller crumb rubber content (less than 10% by weight of base binder) and finer rubber mesh (finer than 30 mesh). Two nano agents as shown in Figs. 2a and 2b were added in the hybrids. One is the multi-walled carbon nanotubes pre-dispersed in high-density polyethylene fabricated in Chengdu city, Sichuan Province. Its carbon nanotube concentration is 25% by weight of base polyethylene and the outer and inner diameter of carbon nanotubes are 10∼30 nm and 5∼10 nm, respectively. The other nano agent is nano silicon dioxide manufactured in Qingdao City, Shandong Province, with an average particle size of 80 nm and a specific area of 20∼45 m2/g.

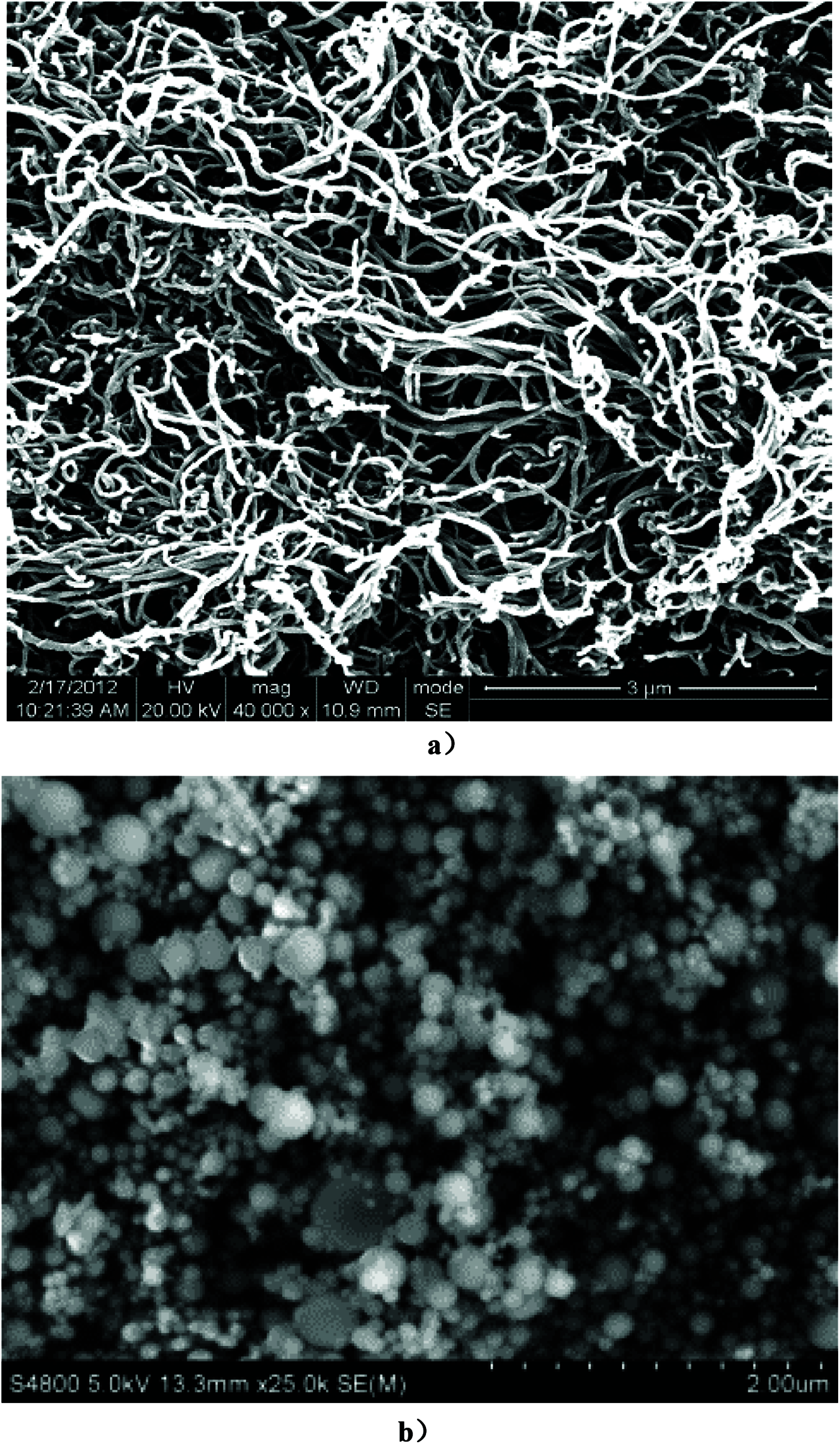
Figure 2: Microscopic morphology of two nano agents: a) Multi-walled carbon nanotube and b) Nano silicon dioxide

Based on above-mentioned raw materials, three sets of crumb rubber-nano-asphalt hybrids were prepared as shown in Fig. 3. In the sample preparation process, main steps were as follows: Firstly, heat the matrix asphalt to 170∼180°C and feed with crumb rubber powder. Secondly, shear the crumb rubber and asphalt blend at 3000∼5000 RPM for 40∼50 min at 180∼190°C; Afterwards, add the nano powder and shear the final blend at 3000∼5000 RPM for 50∼60 min at 180∼190°C. One control sample named as Terminal Blend was considered, which was 8% crumb rubber modified asphalt without adding any nano materials. Whereas the other two were crumb rubber-nano-asphalt hybrids. Each of them had a nano content of 4% and a rubber content of 8%. Both the crumb rubber dosage and nano dosage were by weight of matrix asphalt. Physical properties of the matrix, control sample and crumb rubber-nano-asphalt hybrids were tested and are presented in Table 2.

Figure 3: Preparation of crumb rubber-nano-asphalt hybrids in the laboratory

2.2 Experiments

2.2.1 Dynamic Shear Rheometer (DSR) Test

The DSR test is an effective method to characterize the rheological behavior of bituminous materials [2]. It is widely used in evaluating the performance grade (PG) of asphalt binder, which has been introduced as the main output of the Strategic Highway Research Program (SHRP) [30]. The DSR test could reveal a viscoelastic material’s rheological and mechanical behavior by implementing different testing modes such as frequency sweep, temperature sweep and strain sweep. To obtain high temperature dynamic mechanical parameters of crumb rubber-nano-asphalt hybrids, the frequency sweep mode was carried out to measure complex modulus, phase angle, and complex viscosity of the original and modified asphalts based on AASHTO T315 [31]. In this research, the TA Discovery hybrid rheometer was adopted using the parallel-plate mode, in which the diameter of the specimen was 25 mm and the plate gap was 1 mm. The frequency sweep tests were performed under the strain-controlled mode over a frequency range of 0.1∼100 rad/s at 60°C. To ensure all specimen behaviors be linear viscoelastic, an appropriate control strain should be considered. By referring to He’s research on crumb rubber modified asphalt [32], a torsional strain amplitude of 1% was applied to ensure all specimen behaviors be within the linear viscoelastic domain at the mentioned temperature range.

2.2.2 Multiple Stress Creep and Recovery (MSCR) Test

The MSCR test is a part of new Superpave grading system (AASHTO MP 19-10) which uses a DSR to provide adequate details of the rheological behaviors of modified asphalt [3,28]. The test piece in the MSCR test is subjected to creep loading and unloading cycles of 1 s and 9 s respectively at two stress levels. From the MSCR test results, the percent recovery is calculated to quantitatively evaluate the elasticity of modified asphalt binder. In this research, the MSCR test at 60°C was performed on the control and crumb rubber-nano-asphalt hybrid specimens to investigate their delayed elastic property experimentally.

3  Theoretical Basis

The present research characterized the delayed elastic properties of crumb rubber-nano-asphalt hybrids using the DSR test and material discrete relaxation spectrum calculated based on the generalized Maxwell model. The following section involves primary related theoretical basis.

3.1 The Rheodictic and Arrheodictic Generalized Series-Parallel Models

Viscoelastic theory describes strain retardation or creep, stress relaxation, steady flow viscosity and hysteresis behaviors of materials such as polymers, asphalts, and metals at high temperature. In case of small strain, the LVE theory in which final deformation of materials is the superposition of deformations induced by all previous loading stages [33–35] is predominantly applied. In such cases, the Boltzmann’s superposition principle is used to relate stress and strain in the form of hereditary integration. From the viewpoint of phenomenological theory of linear viscoelastic behavior, series and parallel combinations of elementary springs and dashpots could form mechanical models competent for better reproducing viscoelastic behavior of materials, among which are the well-known Maxwell unit, Kelvin unit, three-parameter solid model, four-parameter liquid model as well as the generalized Maxwell and Kelvin model.

3.1.1 Generalized Maxwell (GM) Model

The GM model (also called Wiechert model) is the extension of standard 4-parameter Maxwell model by adding more Maxwell units in parallel. However, this model is not invariably fixed but is fractionally adjusted to adapt two different material behaviors: rheodictic and arrheodictic. For a rheodictic material, the stress in response to a step input of strain relaxes to zero and the strain in response to a step input of stress eventually increases linearly with time. Rheodictic materials exhibit steady-state flow [36]. By contrast, a material which does not evince steady-state flow is called arrheodictic, for which the stress in response to a step input of strain relaxes to one finite value and the retarded strain in response to a step stress does not tend to infinite [36]. The GM model that describes a rheodictic behavior is schematically represented in Fig. 4a whereas that for an arrheodictic behavior is presented in Fig. 4b. In the former, the number of dashpots is equal to the number of springs; whereas in the latter the number of springs exceeds the number of dashpots by one.

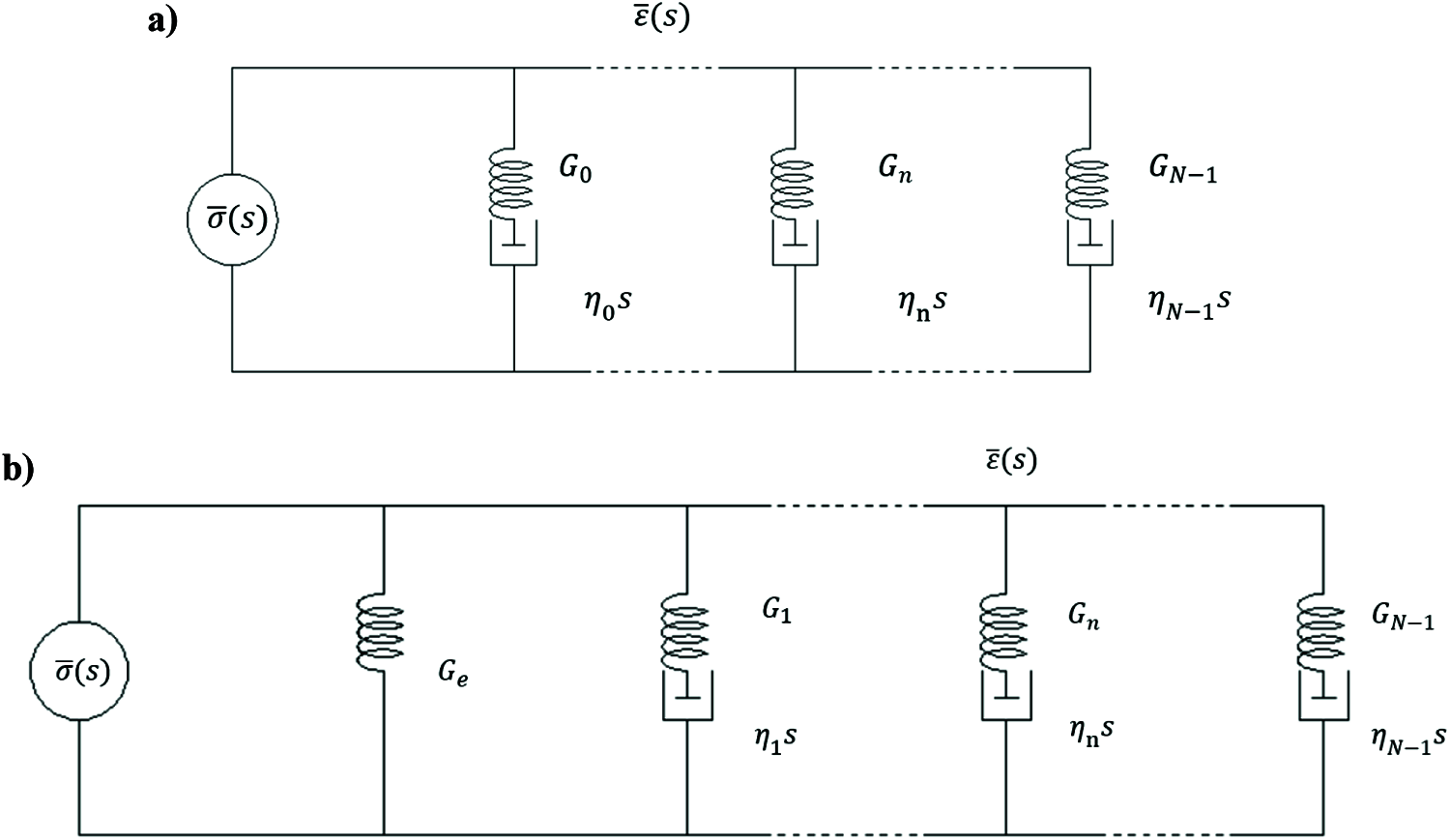
Figure 4: The GM model describing a) Rheodictic behavior; b) Arrheodictic behavior*
*Footnote: the symbols in Fig. 4 are the same to those in Eq. (1).

3.1.2 Generalized Kelvin-Voigt (GKV) Model

The GKV model is the extension of 4-parameter Kelvin model by adding further Voigt units in series. Figs. 5a and 5b represent the rheodictic and arrheodictic generalized Kelvin-Voigt model respectively. This model is the conjugate of the generalized Maxwell model according to the Alfrey’s rule.

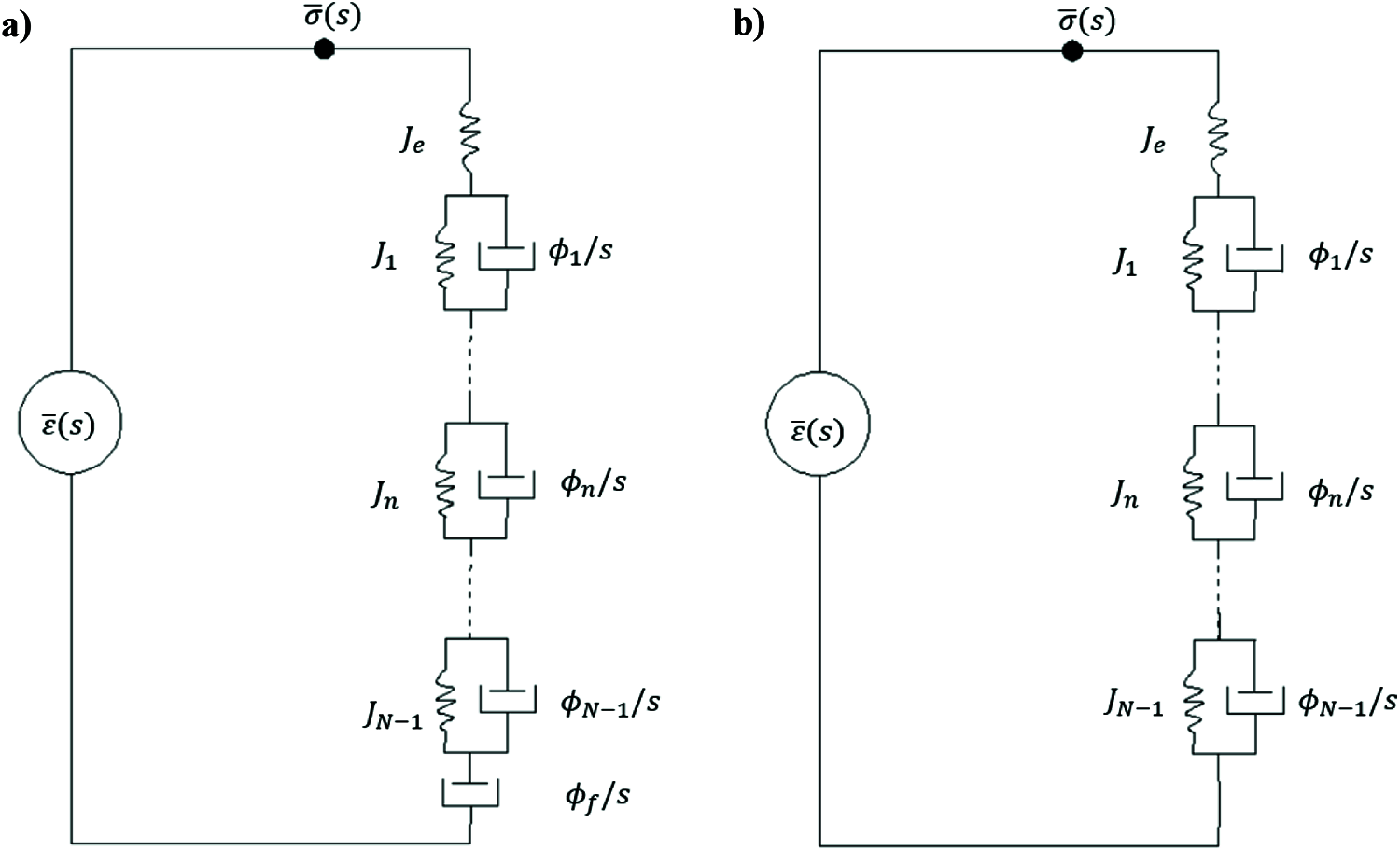
Figure 5: The GKV model describing a) Rheodictic behavior; b) Arrheodictic behavior**
**Footnote: the symbols in Fig. 4 are the same to those in Eq. (2).

3.2 Prony Series Represented Relaxation Modulus and Discrete Relaxation Spectrum

Relaxation modulus is the quotient of the resulted stress and the constant strain applied to a viscoelastic material, which is time-dependent and generally obtained from a stress relaxation test. Similarly, creep compliance is the time-dependent strain divided by the applied constant stress from a creep test. When subjecting to a step excitation, the relaxation modulus G(t) and creep compliance J(t) of the generalized Maxwell model and the generalized Kelvin-Voigt model can be derived as in Eqs. (1) and (2), respectively. It should be noted that in order to treat rheodictic and arrheodictic behaviors simultaneously, the braces are used around certain terms. In Eq. (1), the braces are omitted only when the behavior is rheodictic whereas in Eq. (2), the braces are omitted only when the behavior is arrheodictic.

G(t)={Ge}+∑i=1N⁡Gie−tτi (1)

J(t)=Jg+∑i=1N⁡Ji(1−e−tλi)=Je−∑i=1N⁡Jie−tλi+{ϕf} (2)

where, t is time (s), Ge is the equilibrium modulus (Pa) or relaxed modulus which represents the modulus when t →∞. Gi and τi = ηi/Gi are the elastic modulus and relaxation time of the ith Maxwell unit respectively. Je is the equilibrium compliance (1/Pa); Jg is the glassy compliance (1/Pa); Ji and λi = ηi/Gi are the retardation strength and retardation time of the ith Kelvin-Voigt unit, respectively; ϕf = 1/ηf is the reciprocal of the viscosity of the isolate dashpot.

Eqs. (1) and (2) represent that the modulus and compliance for a LVE material is the superposition of exponentials. Its mathematical series expression is called the Prony series or Dirichlet series. These sets of series parameters are the so-called material discrete relaxation and retardation spectra which are the most intrinsic attributes of viscoelastic materials. Once the discrete spectra are given, other material functions either in the time or frequency domain (relaxation function, creep compliance and complex modulus) will be immediately determined. Additionally, numerous finite element software packages have incorporated the Prony series as basic material input in the numerical simulation of viscoelastic behaviors [37]. Thus accurate discrete relaxation spectrum and retardation spectrum are indispensable to better characterize and numerically simulate LVE material behaviors.

3.3 Material Functions Interconversion between Time and Frequency Domain

Both the stress relaxation test and strain retardation test are instantaneous rheological tests in which the applied strain or stress changes in the form of step function versus time. Whereas the oscillation test is a dynamic test by exerting harmonic strain or stress to the test piece, from which the complex modulus or complex compliance are then obtained. In the theoretical sense, all material functions are equivalent and functions in the frequency domain can be converted into that in the time domain through the Carson transform. Due to the inconvenience in test manipulation and inadequate data smoothness encountered with the instantaneous tests, the oscillatory test is more preferred to acquire reliable material viscoelastic parameters.

The operational modulus in the Laplace-transform domain can be developed by applying the Carson transform to Eq. (1):

G~(s)=s∫0∞⁡G(t)e−stdt={Ge}+∑i=1N⁡Gisλi1+sλi (3)

where, G~(s) is the operational modulus; s is the transform variable.

As we know:

G∗(ω)=G~(s)|s=iω (4)

By replacing s with iω, we can get the complex modulus G*(ω) as follows:

G∗(ω)={Ge}+∑i=1NGiλiiω+Giλi2ω21+λi2ω2 (5)

Further, the storage modulus and the loss modulus can be derived as:

G∗(ω)=G′(ω)+iG′′(ω) (6)

G′(ω)={Ge}+∑i=1NGiλi2ω21+λi2ω2 (7)

G′′(ω)=∑i=1NGiλiω1+λi2ω2 (8)

where G′(ω) is the real part of complex modulus, called storage modulus; G′′(ω) is the imaginary part of complex modulus, called loss modulus; ω is the angular frequency; i is the imaginary unit, i2 = −1.

Similarly, the complex compliance J*(ω) storage compliance J′(ω), loss compliance J′′(ω) can be derived as follows:

J∗(ω)=J′(ω)−iJ′′(ω) (9)

J′(ω)=Je−∑i=1NJiλi2ω21+λi2ω2 (10)

J′′(ω)=∑i=1NJiλiω1+λi2ω2+{ϕfω} (11)

where J′(ω) is the real part of complex compliance, called storage compliance; J′′(ω) is the imaginary part of complex compliance, called loss compliance.

Eqs. (5)–(11) show that the material functions under instantaneous exciting and cyclic loading are not independent of each other but are interconvertible. These equations provide a very convenient way to convert frequency-domain modulus or compliance function into time-domain relaxation modulus or creep compliance.

4  Results and Discussions

The authors tested the dynamic responses of the crumb rubber-nano-asphalt hybrids and explored the feasibility of characterizing their delayed elastic properties using discrete relaxation spectrum. Prior to the calculation of asphalt discrete spectra, different configurations of the generalized Maxwell model and the generalized Kelvin-Voigt model were adopted in the data fitting process to identify the arrheodictic behavior of the hybrids. Subsequently, comparisons were made between the generalized Maxwell model and two frequently used models (Burgers model and FDM-3 fractional model) to show its effectiveness. Additionally, the effects of different nano agents on the hybrid viscoelastic characteristics were discussed. Finally, the mechanism behind good elasticity of the crumb rubber-nano-asphalt hybrids was well revealed by the discrete relaxation spectrum. This section presents the related results and discussions.

4.1 Dynamic Viscoelastic Behavior of the Crumb Rubber-Nano-Asphalt Hybrids

This subsection deals with the model fitting on the tested complex modulus and phase angle data of the foregoing hybrids to show their unique viscoelastic behaviors and to distinguish the effect of different nano agents on their viscoelastic properties. Since more parallel Maxwell units lead to better fitting on rheological data [38,39], this investigation thus utilized a minimum of 10 Maxwell units to obtain a considerable good fitting on the modulus data.

4.1.1 Arrheodictic Behavior of the Crumb Rubber-Nano-Asphalt Hybrids

As given in Fig. 6, change of the storage modulus, loss modulus as well as loss factor with angular frequency for the crumb rubber-nano-asphalt hybrids were indicated based on the DSR test results. It should be noted that for each group, three repetitions were considered in the experimental run to minimize random error. The difference between any two repeated experimental results for each group did not exceed the allowable value in the specification [29]. Subsequently, the mean modulus and loss factor value of three repetitions for each sample group were adopted to draw the modulus and loss factor versus frequency curve. Additionally, to show the deviation of test data, the standard error for three repetitions was presented in the error bar, which is attached to each curve and is presented in the form of colored strips in the graph.

Figure 6: Change of storage modulus, loss modulus and loss factor with angular frequency of the crumb rubber-nano-asphalt hybrids a) Control TB group; b) RNA1 group; c) RNA2 group

By performing the nonlinear multiple regression on the complex modulus and complex compliance data using both arrheodictic and rheodictic models, the unique viscoelastic behaviors of the hybrids were identified and discussed herein. As given in Fig. 7, fitting results on the modulus data using two kinds of generalized Maxwell models as well as that on the compliance data using two kinds of generalized Kelvin-Voigt models are illustrated respectively. It should be noted that the three sets of specimens showed very similar fitting, thus only the control TB specimen was presented in Fig. 7 to avoid redundancy.

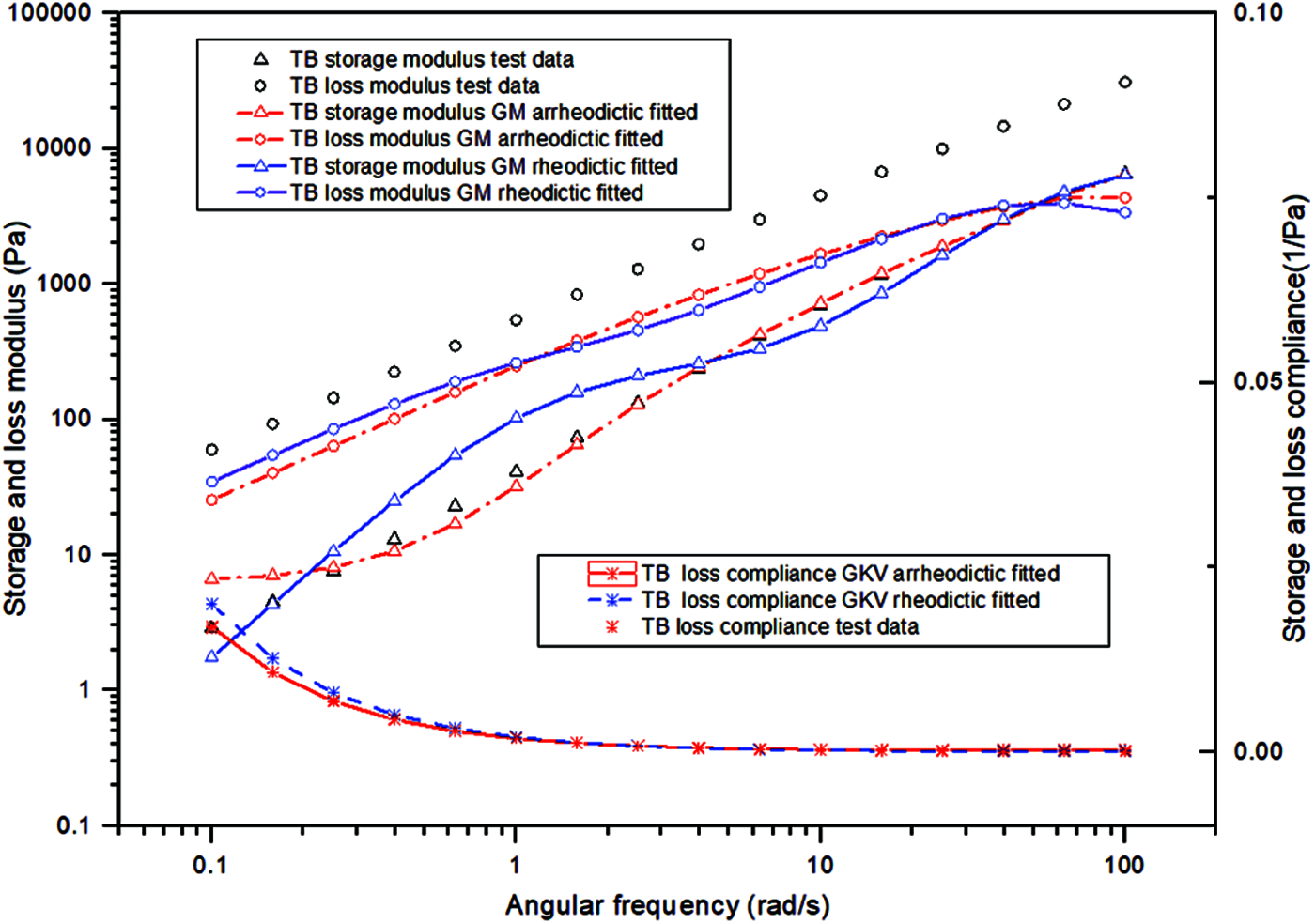
Figure 7: Rheodictic and arrheodictic generalized model fitting on the modulus and compliance data of the crumb rubber-nano-asphalt hybrids

It is readily observed from Fig. 7 that the crumb rubber-nano-asphalt hybrid showed arrheodictic behavior since the arrheodictic generalized Maxwell model fitted much better than the rheodictic one as far as the storage modulus data is concerned. Additionally, the fitting R-squares on the storage modulus data for the TB, RNA1 and RNA2 test groups are 0.9999, 0.9953 and 0.9998, respectively. This shows that 10-unit arrheodictic generalized Maxwell model was competent enough for describing true viscoelastic behavior of the prepared hybrids. However, Fig. 6 indicates that the rheodictic generalized Maxwell model showed some deviation from the test data when modeling the storage modulus of the hybrids, indicating that larger error might occur when predicting the viscoelastic behavior of crumb rubber-nano-asphalt hybrids using rheodictic model. As expected, these two models presented very close fitting results on the loss modulus data because the loss modulus function for the two models are theoretically equal.

Similar conclusions can be drawn by fitting on the complex compliance data using the arrheodictic and rheodictic 10-unit generalized Kelvin-Voigt models. Fig. 6 shows that both models fitted well on the loss compliance data for the crumb rubber-nano-asphalt hybrids. The fitting R-squares on the loss compliance data for the TB, RNA1 and RNA2 groups are 0.9649, 0.9543 and 0.9427, respectively. It can be drawn that no significant difference was found in the tested frequency range between two kinds of generalized Kelvin-Voigt models when modeling the complex compliance of the hybrid. This was primarily due to relatively small compliance values at high temperatures.

4.1.2 Effect of Nano Agents on the Dynamic Modulus and Hysteresis of Crumb Rubber-Nano-Asphalt Hybrids

Fig. 8 presents the storage modulus, loss modulus and loss factor test results of the crumb rubber-nano-asphalt hybrids to show the effect of nano agents on the dynamic modulus and hysteresis of the hybrids. The control TB sample was also discussed for comparison.

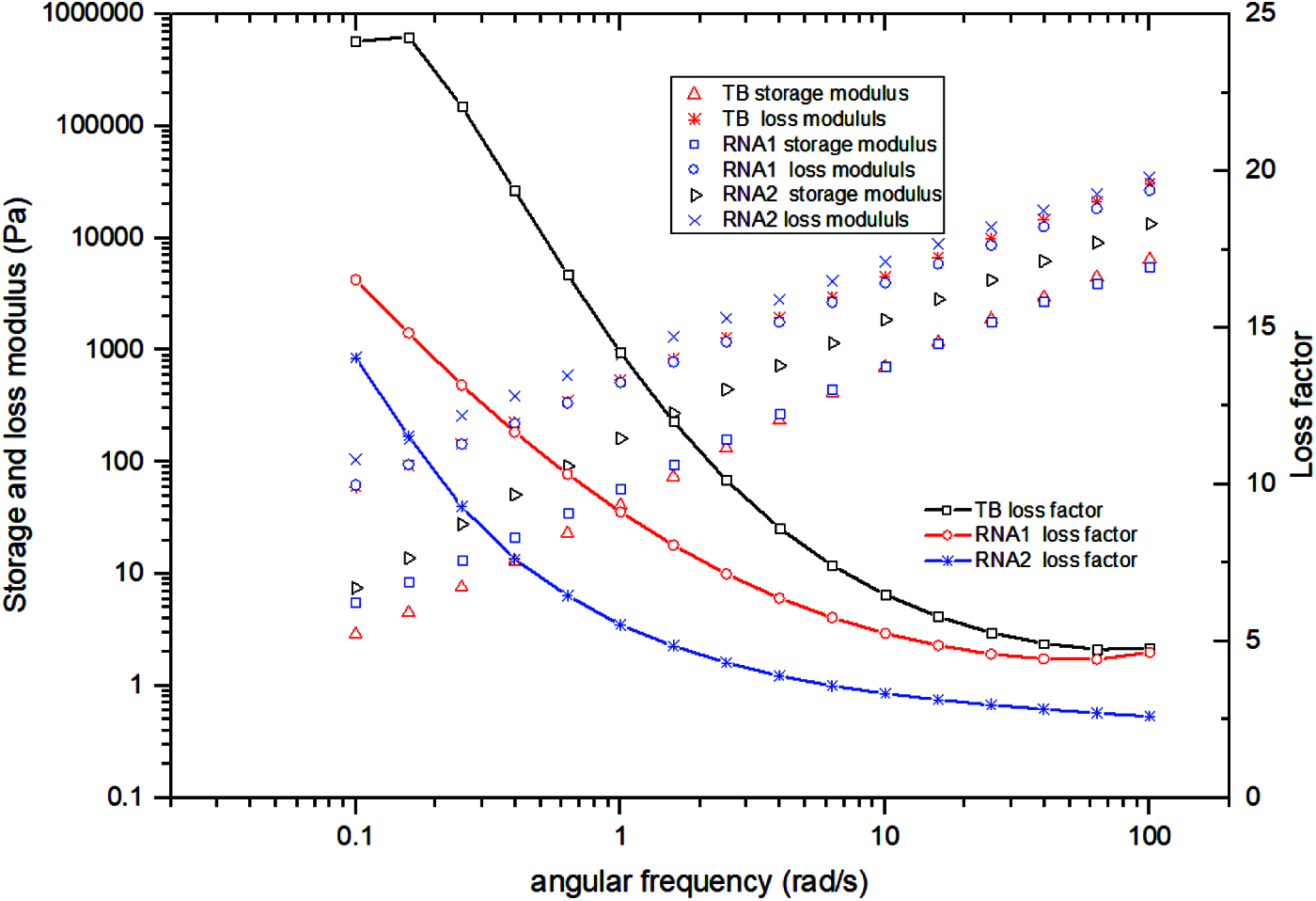
Figure 8: Effect of nano agents on the storage modulus, loss modulus and loss factor of the crumb rubber nano asphalt hybrids

It is readily seen from Fig. 8 that both nano agents showed evident effect on the storage modulus of the crumb rubber-nano-asphalt hybrids than on their loss modulus data, suggesting that adding nano materials changed the asphalt elasticity. However, different nano agents showed different effects in various frequency ranges. The RNA2 sample showed quite greater storage modulus compared to the control TB sample in all tested frequency range, which indicated that the hybrid elasticity was strengthened by adding carbon nano tubes. Moreover, the storage modulus of the RNA1 sample was also greater than the control TB sample, indicating that adding nano silicon could also improve the binder elasticity. However, the effect of nano silica on storage modulus was not significant when the frequency was greater than 10 rad/s. It can be safely inferred that the crumb-rubber-nano-asphalt hybrids would develop less permanent deformation than crumb rubber modified asphalt in case of high temperature and long time loading.

To identify the improvement in the hysteresis, the tangent of phase angle, i.e., loss factor of all samples were calculated and are shown in Fig. 8. It can be seen the loss factor of the TB sample changed sharply with frequency whereas those of the two hybrids reduced a bit slowly with the frequency. This means the susceptibility of binder modulus to frequency or temperature was reduced by adding nano agents. Furthermore, the loss factor of two groups of hybrids were much lower than that of the control sample in the low frequency range, showing that nano agents improved hybrid elasticity while reduced its viscosity in case of high temperature loading. In addition, Fig. 8 shows the loss factor of the RNA2 sample was less than that of the RNA1 sample. According to the time-temperature superposition principle, this indicated the nano carbon tubes were more effective than nano silica in improving the high temperature elasticity of the hybrids.

In traditional theory of signal and system, the Lissajous diagram is frequently adopted to measure the phase difference of two simple harmonic signals that have same frequency and are perpendicular to each other. In the DSR test of the hybrids, an analogy was made between the applied oscillatory strain, the induced oscillatory stress and two simple harmonic signals with same frequency. Then based on the frequency sweep test data, the Lissajous graphs of the crumb rubber nano asphalt hybrids at the frequency of 10 rad/s were drawn in Fig. 8 and compared with the control sample and the widely used SBS modified asphalt.

As shown in Fig. 9, all the Lissajous diagram of the TB and RNA samples were skew ellipses, which suggests obvious phase lagging between the applied strain and induced stress. Such shape of Lissajous diagram represents typical viscoelastic material behavior. According to the theory of signal and system, when the Lissajous diagram is a skew line, it represents totally elastic material behavior in a dynamic mechanical test. Whereas a horizontal ellipse or sometimes a circle represents linear viscous material behavior whose phase angle is 90°.

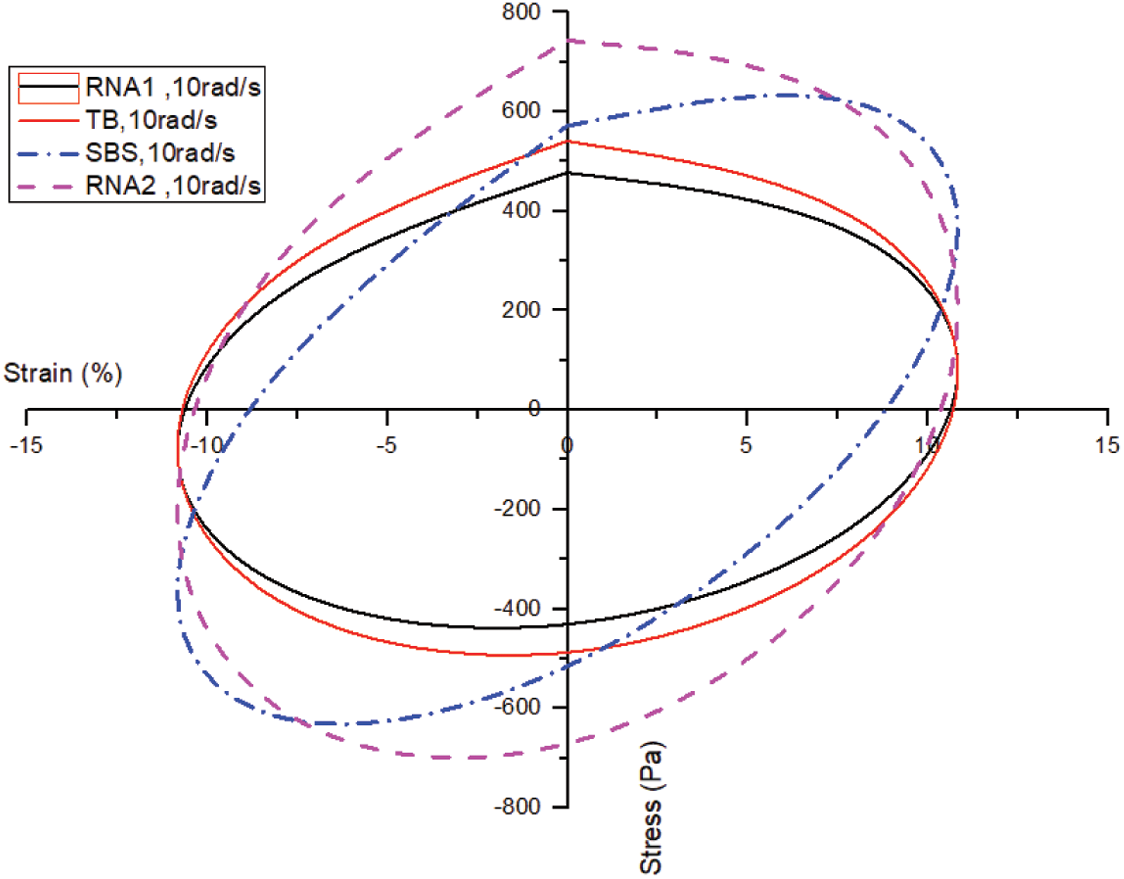
Figure 9: Lissajous graph of the crumb rubber nano asphalt hybrids

It can be seen the effect of nano carbon tubes on the shape of Lissajous diagram at 10 rad/s was more significant compared to nano silica. The Lissajous ellipse for RNA2 was much skewed than that for RNA1 sample, showing the viscoelastic behavior of the hybrid added with carbon nano tubes was more significant. Additionally, the long axis and short axis of the skew ellipse of the RNA1 sample were shorter than those of the other two samples because its complex modulus is lower than the two samples at this frequency. Fig. 9 shows the Lissajous diagram of the commonly used SBS modified asphalt was also a skew ellipses but it was more inclined due to lower phase angle.

4.2 Discrete Relaxation Spectrum of the Crumb Rubber-Nano-Asphalt Hybrids and Its Applications

As the relaxation time spectrum of a viscoelastic material plays a key role in rheology, obtaining the spectrum becomes the focus of researcher’s concern. This section involves determining the discrete relaxation spectrum of the crumb rubber-nano-asphalt hybrids using the generalized Maxwell model and applying the discrete spectrum to the predicting of stress relaxation modulus of the sample hybrids. Moreover, the possible correlation between relaxation times and zero shear viscosity was also discussed herein.

4.2.1 Comparison of the Generalized Maxwell Model with Burgers Model and FDM-3 Fractional Model

Apart from the generalized Maxwell model, previous research has reported using other models in fitting rheological data of asphalt binder. One is the Burgers model which has been widely used due to its explicit mechanical meaning and sufficient accuracy [6,9]. This model is composed of a Maxwell unit and a Kelvin unit. It is a four parameter liquid linear viscoelastic model, which has found wide application in rheology. Another one is the fractional derivative model which aimed to reduce model parameters without decreasing fitting precision [7–8,40,41]. Such models were formulated by combining fractional derivative elements such as parabolic dashpot or Abel dashpot with classical mechanical elements.

In this research, the FDM-3 fractional model [8] and the Burgers model were selected to compare with the generalized Maxwell model. Fig. 10 depicts the configuration of the FDM-3 fractional model and Eq. (12) presents its complex modulus.

G∗(iω)=1(1G+cos(rπ2)η2ωr)−(sin(rπ2)η2ωr+1η1ω)i (12)

where, G*(ω) is the complex modulus; ω is the angular frequency; G is the elastic modulus of the spring. η1 is the viscosity of the dashpot; η2 is the viscosity of the fractional unit; r is the model constant; i is the imaginary unit.

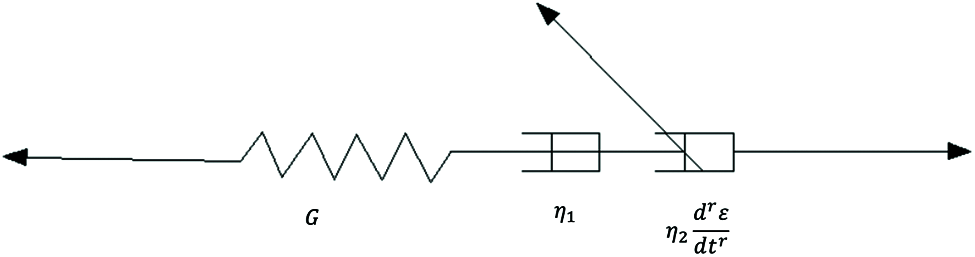
Figure 10: The FDM-3 fractional model

Fig. 11 illustrates the fitting difference of these three models on the 60°C storage modulus master curve of the TB sample. The nonlinear regression indicated that the fitting R-squares for the generalized Maxwell model, the Burgers model and the FDM-3 model were 0.9999, 0.9996 and 0.9999, respectively. Each of them had a good fitting on the master curve. However, in a double logarithmic coordinate system, a slight difference could be found especially in the low frequency range. The 10-unit generalized Maxwell model presented equally good fitting along with the FDM-3 fractional model while the Burgers model showed a slight deviation from the test data in the low frequency range. Its predicted storage modulus was lower than the tested value, implying the Burgers model would underestimate binder elasticity in case of high temperature or long time loading. Previous research has reported the fitting results of the fractional derivative Maxwell model were better than the generalized Maxwell model [8,40–42]. Yin [40] also carried out similar research on the dynamic behavior of asphalt mixtures and concluded that the fractional derivative model could describe dynamic viscoelastic behavior accurately. Our fitting confirmed that the generalized Maxwell model with at least 10 parallel Maxwell units was good enough to better characterize the highly elastic crumb rubber modified asphalt. However, although having fewer model parameters, the FDM-3 model was relatively complicated in the mathematical derivation and nonlinear fitting. Therefore, the 10-unit generalized Maxwell model was applied in the binder delayed elasticity characterization due to good accuracy and simplicity. Additionally, since the discrete relaxation spectra based on the generalized Maxwell model have been adopted as a standard material input in a number of commercial finite element software, this model was considered in order to numerically simulate the dynamic viscoelastic responses of the crumb rubber-nano-asphalt hybrids in the authors’ future research.

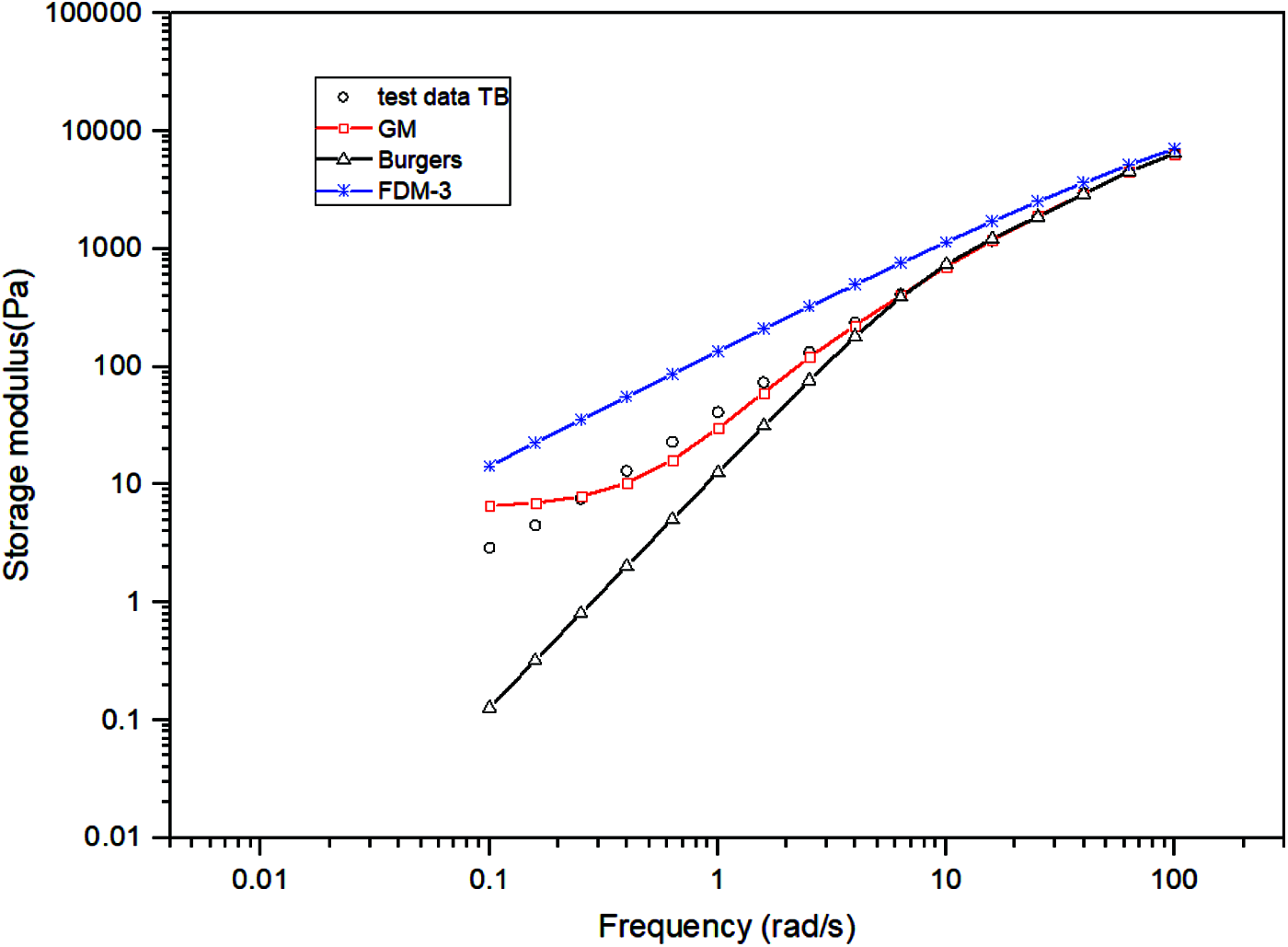
Figure 11: Comparison of the generalized Maxwell model with the Burgers model and FDM-3 fractional model

4.2.2 Prediction of High Temperature Stress Relaxation Modulus Using Discrete Relaxation Spectrum

As mentioned previously, a discrete relaxation spectrum is defined as the collection of the relaxation spectrum strength and relaxation times of n Maxwell units in the n-unit generalized Maxwell model [33]. Actually, when the unit number goes to infinity (n→∞), the discrete relaxation spectrum turns accordingly into a continuous spectrum. Relaxation spectrum and retardation spectrum are the intrinsic functions in investigating viscoelastic material’s behavior [33,35].

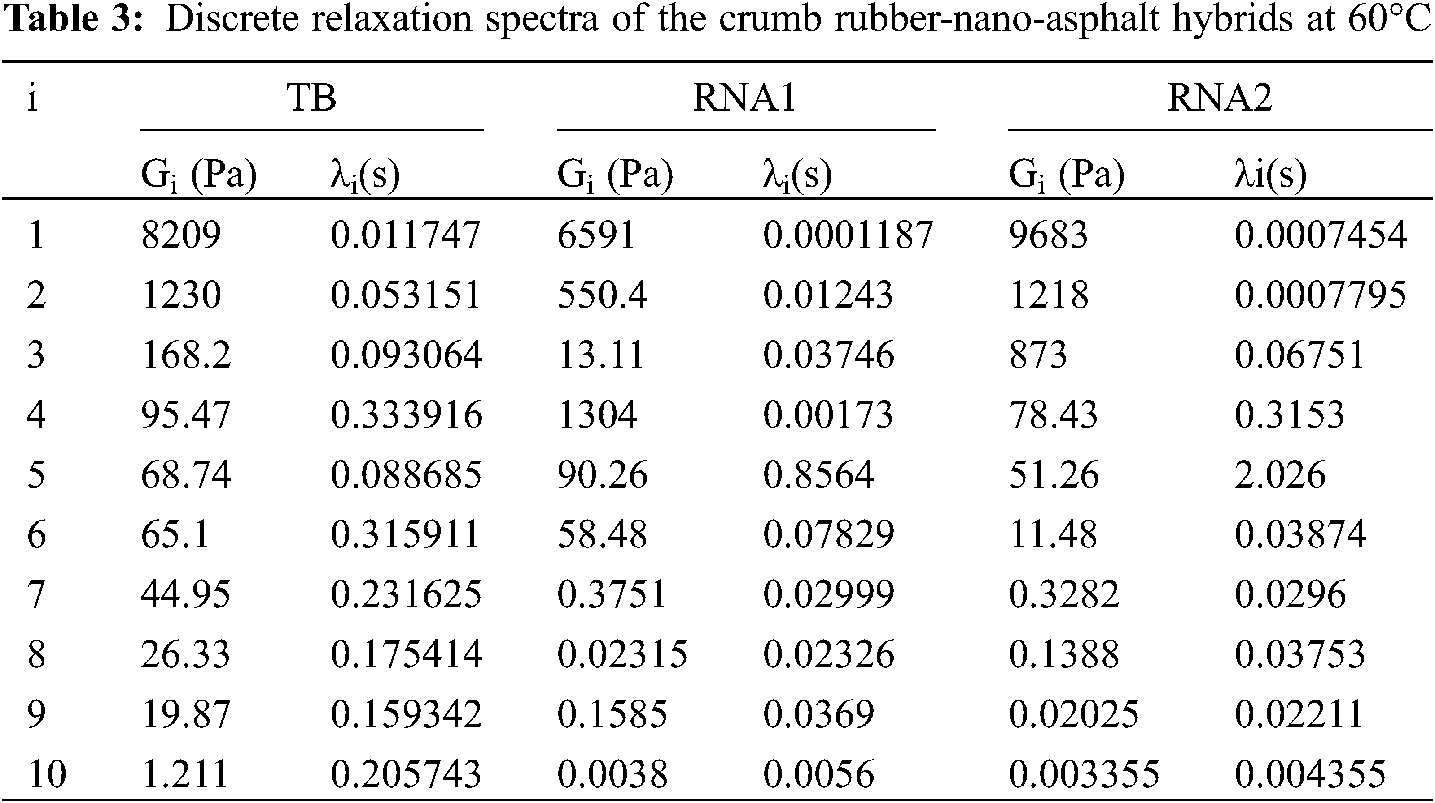
Based on the time-temperature superposition principle, the storage modulus master curves of the crumb rubber-nano-asphalt hybrids were constructed at a reference temperature of 60°C. Afterwards, the discrete relaxation spectra of the hybrids were obtained by implementing model fitting on these master curves using MATLAB CFTOOL. The calculated discrete relaxation spectra are shown in Table 3, which were then used to predict the relaxation modulus of the hybrids. They would also provide necessary input information for the finite element simulation of the hybrid’s permanent deformations.

Relaxation modulus is an important function of a viscoelastic material, which is commonly obtained from a stress relaxation test. However, this function could not be accurately obtained through a transient relaxation test since a step strain excitation is applied. Actually, the oscillatory test is more preferred to acquire reliable viscoelastic parameters. To show the high temperature stress relaxation behavior of the crumb rubber-nano-asphalt hybrids, their relaxation modulus versus time curves were predicted using the discrete relaxation spectrum as shown in Fig. 12.

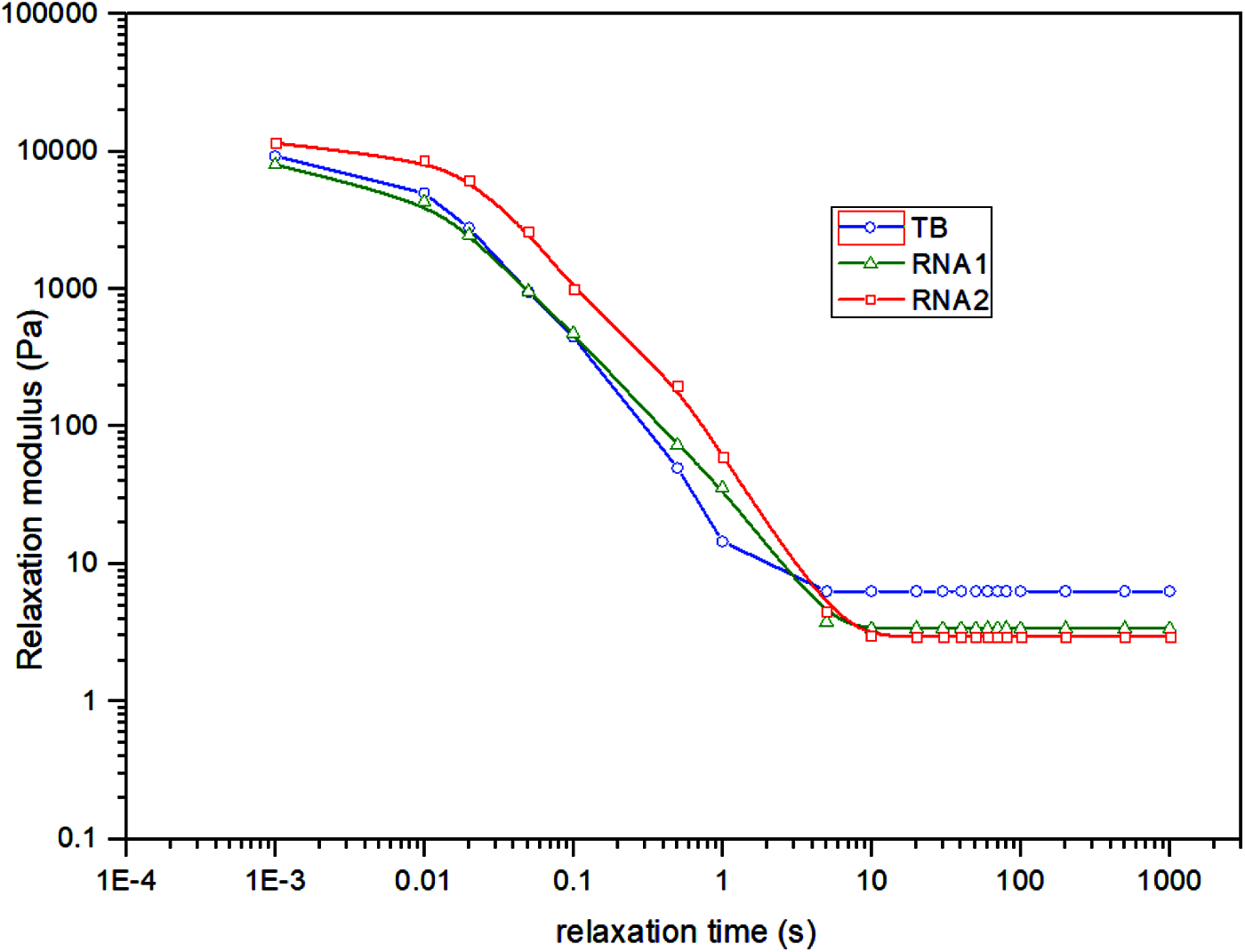
Figure 12: Relaxation modulus curve of the crumb rubber-nano-asphalt hybrids

It can be seen there existed obvious stress relaxation process for the three samples. Most stresses have already relaxed in the first second of the process. Further, all the relaxation moduli approached a nonzero value as long as the time was long enough, symbolizing apparent arrheodictic behavior. This founding was consistent with the previous fitting results shortly presented before. However, an interesting phenomenon was that the RNA1 and RNA2 samples relaxed much slowly compared to the TB control sample. This means they possessed greater zero shear viscosity than the control sample. According to rheology, there is no stress relaxation in Hooke elastic body or we can assume its relaxation time be infinity whereas the stress in a Newtonian fluid relaxes instantaneously. Longer relaxation time of a modified asphalt means closer material behavior to a Hooke elastic solid. Fig. 12 shows that the two hybrids with nano materials were more elastic than the TB control sample.

References showed the stress relaxation behavior of a material is a reflection of the combined effect of various units in the n-unit generalized Maxwell model [43]. Although the relaxation spectrum spans a wide range, the material stress relaxation process is primarily resulted from a certain unit. This is the so-called main relaxation unit and its corresponding relaxation time is called main relaxation time. Wu proposed a practical method to determine the main relaxation time experimentally. He defined the time when the stress relaxes to 0.368 times the initial stress as the main relaxation time λ0. According to polymer rheology, a series of relaxation times constitute the material relaxation time spectrum. Among them, main relaxation time is the relaxation time, which has the greatest contribution to material stress relaxation behavior. This index is defined as the time at which the stress relaxes to 0.368 (1/e = 0.368) times of original stress level. Subsequently, four secondary relaxation units were allocated by setting their relaxation times as 10−2λ0, 10−1λ0, 101λ0, 102λ0, respectively. The main and secondary relaxation units form a 5-unit model which could give very exact description on the material stress relaxation process.

This research calculated the main relaxation times and the corresponding relaxation spectrum strength of the control sample and two crumb rubber-nano-asphalt hybrids. The relaxation times spanning five orders of magnitude and their corresponding relaxation spectrum strengths are shown in Fig. 13. Fig. 13 indicates that the main relaxation times for the crumb rubber-nano-asphalt hybrids are within 10−2∼10−1 s range. Additionally, the main relaxation time of RNA2 sample is greater than those of the RNA1 and TB samples. Since longer relaxation times implies closer material behavior of elastic solid, it was then inferred the elastic effect of the hybrid added with carbon nanotubes was more significant than the other two. While similar main relaxation times of the RNA1 and TB samples mean they showed comparable solid effect as far as their stress relaxation properties are concerned.

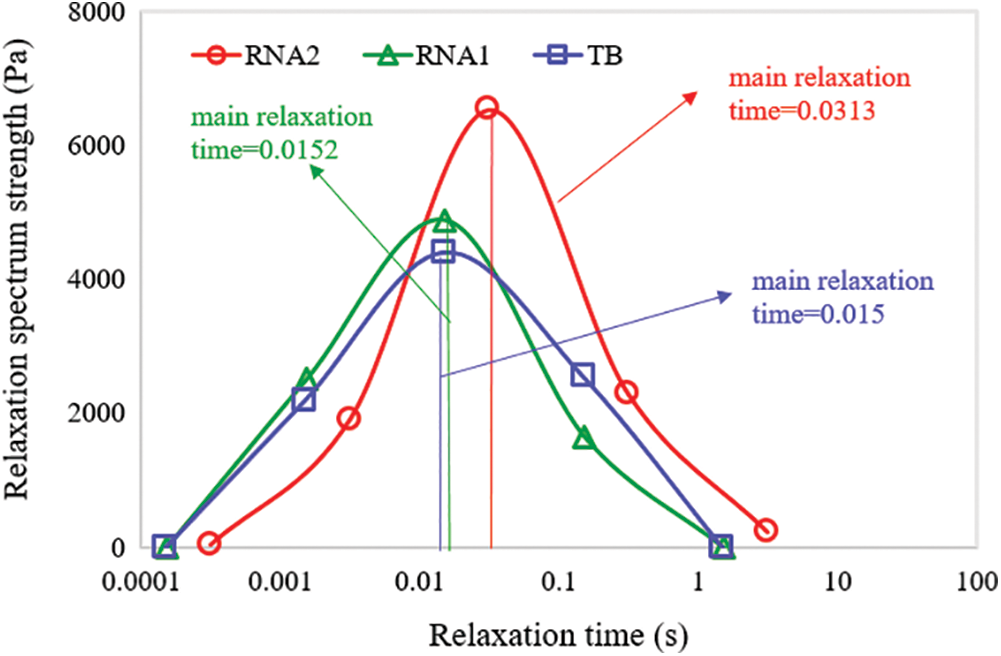
Figure 13: Main relaxation times and relaxation spectrum strengths of the crumb rubber-nano-asphalt hybrids

4.2.3 Correlation Analysis between Main Relaxation Time and Zero Shear Viscosity

Existing research has reported [2,44] that the 60°C zero shear viscosity correlated well with the anti-rutting performance of asphalt binders. From the viewpoint of polymer rheology, the zero shear viscosity is closely related to the mean molecular mass and the viscous flow activation energy of polymers, which is a reflection of the material maximum relaxation time [45]. To explore possible relationship between relaxation times and zero shear viscosity of the hybrids, model fitting on the complex viscosity versus angular frequency data was implemented to obtain the zero shear viscosity. The flow curves in terms of complex viscosity was described using the Cross model as follows [46,47]:

η∗−η∞∗η0∗−η∞∗=11+(kω)m (13)

where, η* is complex viscosity (Pas); η0∗ is zero shear viscosity (Pas); η∞∗ is limiting viscosity in the second Newtonian region (Pas); ω is angular frequency (rad/s); k and m are constant parameters.

It is an appropriate assumption that η*>> η∞∗ for frequency range used in this study. Then, the cross model can be re-written to:

η∗=η0∗1+(kω)m (14)

The tested complex viscosity data and the Cross model fitting results of various hybrids are illustrated in Fig. 14. It was found the Cross model fitted well on the complex viscosity data as the R squares for three samples are 0.9993, 0.9985 and 0.9965, respectively. With the increase in frequency, the complex viscosity of all samples decreased rapidly and then went to a steady value. Additionally, the complex viscosity of the TB and RNA1 samples were comparable whereas that of the RNA2 sample was significantly enhanced compared to the other two samples. This suggested that adding carbon nano tubes significantly improved the binder viscosity However, the effect of nano silica on complex viscosity was not evident. Fig. 14 shows the viscosity of the RNA1 samples was slightly lower than the TB sample; this may be resulted from experimental and fitting errors.

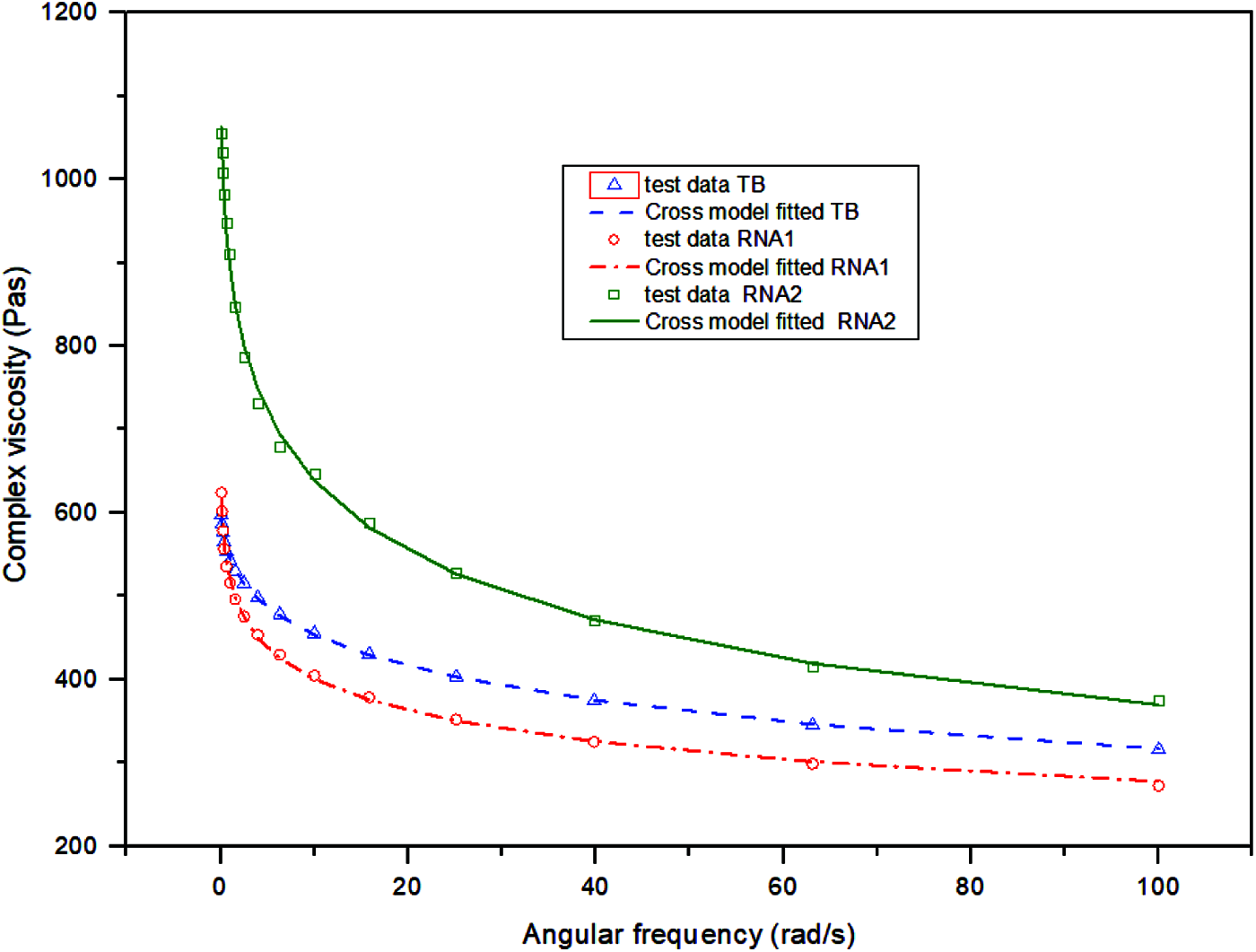
Figure 14: Complex viscosity of the crumb rubber-nano-asphalt hybrids and the Cross model fitting results

According to Eq. (14), the zero shear viscosity of the control and crumb rubber-nano-asphalt hybrids were obtained by fitting on the viscosity data and were presented in Table 4. The main relaxation time of each sample was also given in Table 4.

Table 4 shows that the zero shear viscosity of the RNA2 sample was significantly greater than the control and RNA1 samples, which suggested that carbon nano tubes was more effective than nano silica in improving the hybrid rutting resistance. Moreover, the main relaxation time of the RNA2 sample was also greater than the other two samples, which is consistent with the results of complex viscosity. In the viewpoint of rheology, zero shear viscosity is the reflection of maximum relaxation time for a viscoelastic material. The mechanism behind a stress relaxation phenomenon is that the internal stress of material experienced an evolution from non-uniformity state to uniformity state due to the anisotropy of molecular chain structure. Greater zero shear viscosity means longer main relaxation time. The results in Table 4 were in good accordance with this principle. From Table 4, it can be seen the differences in main relaxation spectrum strength of the three samples showed similar tendency to relaxation time. Longer relaxation time corresponded to greater relaxation strength in the tested sample range. However, this founding should be further confirmed in our future work by introducing more comparative samples with other nano materials.

4.3 Time-Dependent Elasticity of the Crumb Rubber-Nano-Asphalt Hybrids and the Correlation to Relaxation Spectrum

Good elasticity is one of the most important advantages of crumb rubber modified asphalt binder, which can better explain its excellent pavement performance. According to polymer physics, the total strain developed in polymers under shearing includes instantaneous elastic strain, delayed elastic strain and permanent strain. Instantaneous elastic strain is general elastic strain caused by change in the bond angle or bond length of polymer molecular chains. Whereas delayed elastic strain is entropy elastic strain and is caused by deforming, moving and rearranging of molecular chains. In the opinion of polymer conformation change theory, flexible molecular chains oriented along the flow direction under stress and the system conformational entropy decreased consequently. However, the system conformational entropy was partially restored due to thermal movement and relaxation process and thus polymers exhibit entropy elasticity.

Currently, a number of indices such as recoverable strain, die swell ratio, normal stress difference and tensile viscosity were adopted to evaluate the elastic effect of polymers. Recoverable strain is usually measured in a creep and recovery test. This index can be easily figured out using the strain-time curve in the creep and recovery test.

To evaluate delayed elastic property of the crumb rubber-nano-asphalt hybrid, the creep and recovery tests at 60°C were carried out on the hybrid samples using a control stress of 100 Pa. As discussed previously, the discrete relaxation spectrum of the hybrids had been obtained based on the dynamic modulus data. Therefore, to explore possible correlation between relaxation spectrum and delayed elastic property, comparisons were made on the main relaxation time, recoverable strain and average recovery rate.

Fig. 15 presents the creep-recovery curves of various crumb rubber-nano-asphalt hybrids after subjecting to 10 creep and recovery cycles. To reduce experimental error, the test was performed in replicate and three replicates were considered for each sample group. The mean value of three replicates was taken into account for further analysis and calculation. Data shows the experimental error for the total strain tended to increase as the number of creep and recovery cycles went up. This phenomenon might be resulted from the sample preparation technique as well the time dependent viscoelastic properties of the modified asphalt.

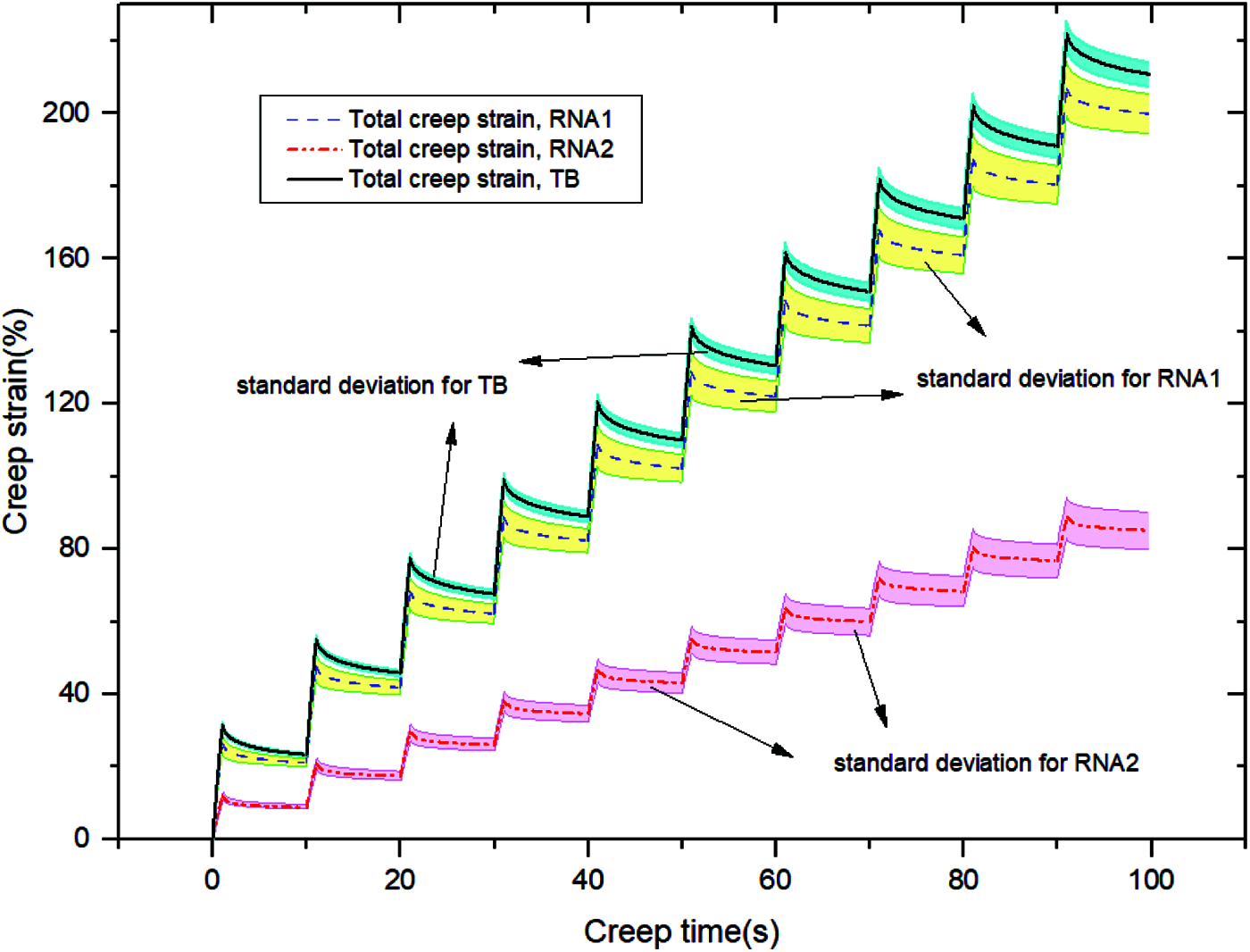
Figure 15: Creep-recovery curves of various crumb rubber-nano-asphalt hybrids

It was observed the total strain of two crumb rubber-nano-asphalt hybrids were smaller than the control sample, suggesting their creep compliance was reduced by adding nano materials. Fig. 14 shows the total creep strain of the RNA2 sample after 10 creep and recovery cycles was only 40.4% of the control sample, indicating carbon nanotubes were effective in reducing high temperature deformations of the hybrids. However, the total creep strain at the cycle end for RNA1 sample was slightly reduced compared to the control sample, suggesting nano silica was less effective compared with carbon nanotubes.

To quantitatively evaluate delayed elastic properties of the crumb rubber-nano-asphalt hybrids and to take an initial probe into the possible correlation between the discrete relaxation spectrum and asphalt delayed elasticity, the recovery rates of the hybrids were calculated based on the test data. Fig. 16 presents the recovery rate at the end of each creep and recovery cycle for various crumb rubber-nano-asphalt hybrids. Also, a comparison between the recovery rate in the 10th creep-recovery cycle and the average relaxation time was made.

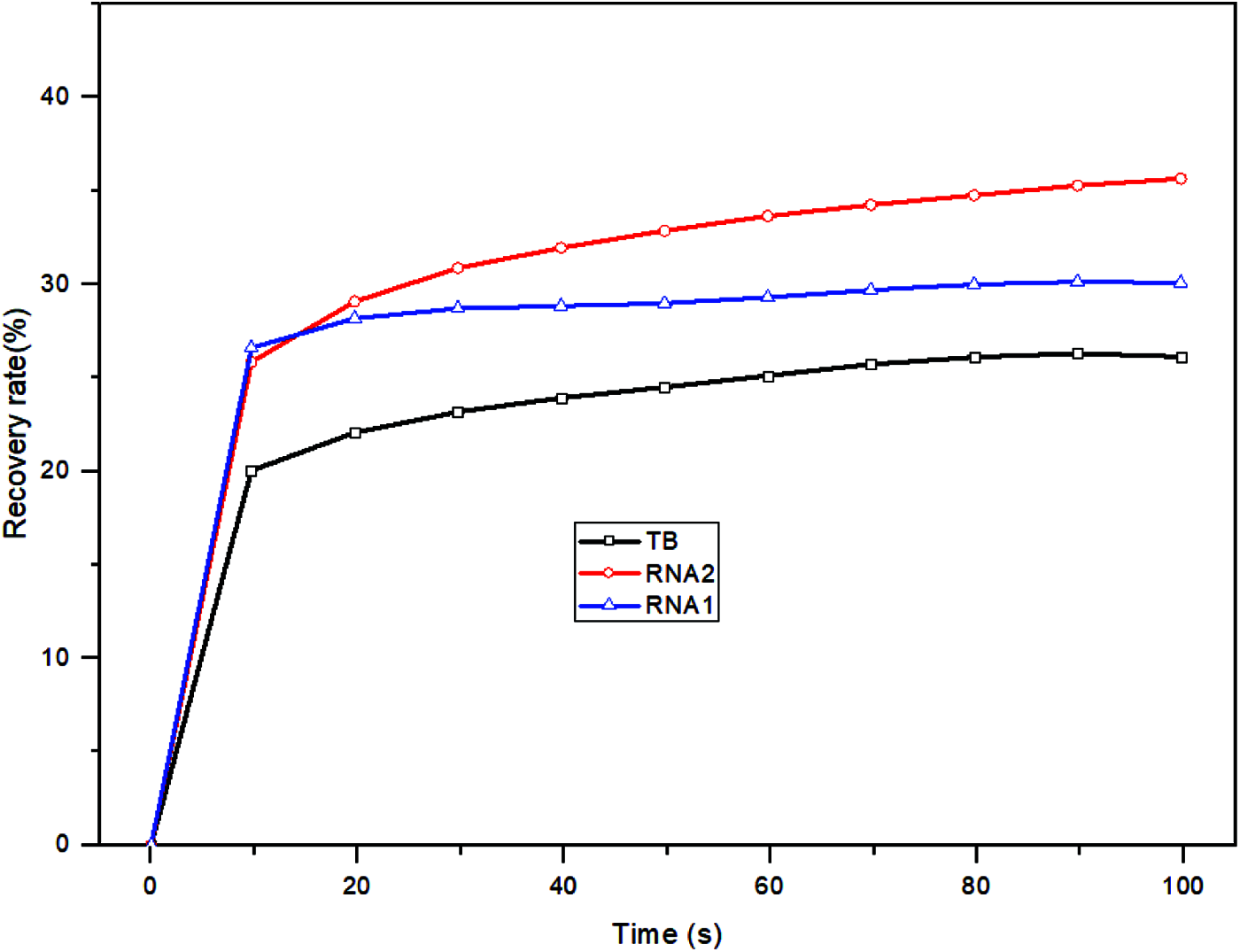
Figure 16: Change of recovery rate with time of the crumb rubber-nano-asphalt hybrids

The calculated recovery rates of the crumb rubber-nano-asphalt hybrid were shown in Fig. 16. Calculation showed that the 10th recovery rates for the control TB, RNA1 and RNA2 samples were 26.13%, 30.09% and 35.65%, respectively, which suggests that greater delayed elasticity was reached by adding nano agents to crumb rubber modified asphalt. This was consistent with the founding in Section 4.1. Fig. 15 also represented the trends of recovery rate with time for various test pieces. It can be seen clearly that the percent recovery of the control TB sample and two crumb rubber-nano-asphalt hybrids steadily increased with the increase in loading time, which means their delayed elasticities played an important role in long time loading. By comparing with the main relaxation times developed through fitting in Section 4.2.2, a conclusion that longer relaxation time led to greater delayed elastic recovery can be drawn immediately for the crumb rubber-nano-asphalt hybrids. As is commonly acknowledged, asphalt pavement rutting is the accumulation of permanent deformations developed in asphalt mixtures due to high temperature and heavy axle loads. Once the delayed elastic strain of the asphalt was improved, the viscous permanent strain would be reduced consequently. The experimental investigation at this stage of research proved that relaxation time of the crumb rubber-nano-asphalt hybrids showed high correlation to delayed elastic properties of the crumb rubber-nano-asphalt hybrids. However, this conclusion should be further validated through numerically simulating the permanent deformation of asphalt mixtures using discrete relaxation spectra obtained from the DSR test.

5  Conclusions

This study presented an experimental investigation into the high temperature delayed elastic properties of crumb rubber-nano-asphalt hybrids based on discrete relaxation spectrum obtained from fitting on the DSR test data. The generalized Maxwell model was adopted in the development of asphalt discrete relaxation spectrum and model comparisons were made to show its effect. Finally, the feasibility of characterizing the time-dependent asphalt elasticity using relaxation time was verified by the percent recovery results acquired by conducting the MSCR test at the same temperature. Some primary conclusions were drawn below:

1.    Nonlinear multiple regression on the complex modulus and compliance data using both arrheodictic and rheodictid models indicated the crumb rubber-nano-asphalt hybrids showed arrheodictic behavior since the arrheodictic generalized Maxwell model fitted much better than the rheodictic one, with high R-squares for three test groups close to 1.

2.    Significant effect of nano agents on the hybrid storage modulus than on their loss modulus suggested that nano materials improved the asphalt elasticity. Carbon nano tubes were more effective than nano silica in improving the high temperature elasticity of the hybrids. The Lissajous diagram of the hybrids was skew ellipse, which suggested obvious phase lagging between the applied strain and induced stress.

3.    The 10-unit generalized Maxwell model presented as good fitting as the FDM-3 fractional model on the complex modulus data of the hybrids. While the storage modulus predicted by the Burgers model was lower than the test data in the low frequency range, implying this model would underestimate binder elasticity in case of high temperature or long time loading.

4.    The main relaxation times of the crumb rubber-nano-asphalt hybrids were within 10−2∼10−1 s range. Additionally, the main relaxation times of samples added with nano agents were greater than the control sample, which means the elastic effect of the hybrid was intensified by introducing nano materials. A good correlation was found between the 60°C zero shear viscosity and main relaxation times of the hybrids, and greater zero shear viscosity was correlated to longer main relaxation times.

5.    The decreased total strain of two crumb rubber-nano-asphalt hybrids against the control sample in the MSCR test suggested the creep compliance was reduced by adding nano materials, and therefore less permanent deformations would be developed. Both nano agents enhanced the asphalt anti-permanent deformation performance well. Comparisons indicated good correlation between the 10th recovery rate and main relaxation time, and furthermore longer main relaxation time led to greater percent recovery for the crumb rubber-nano-asphalt hybrids.

Acknowledgement: Particular acknowledgements were extended to the “Applied Highway Technology Research and Innovation Team” for their assistance.

Funding Statement: This research was supported by the National Natural Science Foundation of China (Grant No. 52078051), the Transportation Department of Shandong Province (Grant No. Lujiaoke[2017]18), the Technology Innovation Project of Shandong Department of Industry and Information (Grant No. Lugongxinji[2020]8), the Education Department of Shaanxi Provincial Government (Grant Nos. SGH18V027, 19GG011), the Shaanxi Association of Higher Education (Grant No. XGH20379) and the Shaanxi College of Communication Technology (Grant No. YJ18008).

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.