STRASS Dehazing: Spatio-Temporal Retinex-Inspired Dehazing by an Averaging of Stochastic Samples

Zhe Yu; Bangyong Sun; Di Liu; Vincent Whannou; Margarita Khokhlova; Siyuan Wu

doi:10.32604/jrm.2022.018262

Zhe Yu1, Bangyong Sun1,3,*, Di Liu2, Vincent Whannou de Dravo1, Margarita Khokhlova4 and Siyuan Wu3

1School of Printing Packaging Engineering and Digital Media, Xi’an University of Technology, Xi’an, 710048, China
2Beijing Key Laboratory of Big Data Technology for Food Safety, Beijing Technology and Business University, Beijing, 100048, China
3Key Laboratory of Spectral Imaging Technology CAS, Xi’an Institute of Optics and Precision Mechanics, Chinese Academy of Sciences, Xi’an, 710119, China
4LASTIG, Université Gustave Eiffel, Écully, 69134, France
*Corresponding Author: Bangyong Sun. Email: sunbangyong@xaut.edu.cn
Received: 11 July 2021; Accepted: 19 August 2021

Abstract: In this paper, we propose a neoteric and high-efficiency single image dehazing algorithm via contrast enhancement which is called STRASS (Spatio-Temporal Retinex-Inspired by an Averaging of Stochastic Samples) dehazing, it is realized by constructing an efficient high-pass filter to process haze images and taking the influence of human vision system into account in image dehazing principles. The novel high-pass filter works by getting each pixel using RSR and computes the average of the samples. Then the low-pass filter resulting from the minimum envelope in STRESS framework has been replaced by the average of the samples. The final dehazed image is yielded after iterations of the high-pass filter. STRASS can be run directly without any machine learning. Extensive experimental results on datasets prove that STRASS surpass the state-of-the-arts. Image dehazing can be applied in the field of printing and packaging, our method is of great significance for image pre-processing before printing.

Keywords: Image dehazing; contrast enhancement; high-pass filter; image reconstruction

In recent years, the printing industry has increasingly pursued the concept of green printing. Green printing refers to a printing method that produces less pollution, saves resources and energy, and has little impact on the ecological environment during the printing process. Clearing the image before printing improves the visual perception of the image, which can obtain high-quality and high-definition prints. In this way, the number of substandard prints can be greatly reduced during the printing process, which means it can extremely improve production efficiency, production quality, and reduce the production of printed products cost. However, there are many suspended particles in the air such as water droplets, aerosols, dust particles in haze weather. The radius of these suspended particles is much larger than air molecules, and they have stronger shading properties. Therefore, before the scene light reaches the camera system, part of the light is attenuated in the air and be scattered or refracted by the suspended particles. As the result, the images captured in haze are often accompanied by quality degradation, which weakens the visibility of the target in the scene, and affects the normal work of subsequent computer image processing tasks. Therefore, image defogging technology is very important for both computer vision and green printing.

The first works of image dehazing began in the late 1990s and early 2000. To establish these dehazing models, one needs to combine several inputs composed of one or more images associated or not with other data. It was only barely a decade ago that the very first works with only one image input were developed. From this moment, most of the advanced algorithms are based on a single entry [1]. It can be roughly divided into two categories: algorithms that solve the problem on the basis of a physical model [1–7] and on the basis of image enhancement [8–17]. In recent years, dehazing algorithms using advanced filters with millions of parameters (deep neural network) are proposed [18–25]. However, these state-of-the-arts artificial intelligence algorithms cannot be perceived by human visual system (HVS). Hence, we try to propose a model that is close to the HVS, which is simple for human to understand.

In this paper, we mainly concern this question as follows: is it possible to propose an easy-to-understand dehazing algorithm similar to the HVS model? To solve this question, we benefit much from the random spray retinex (RSR) [26] and STRESS [27]. The idea is to build an image enhancement algorithm which is similar to STRESS model. HVS can be seen as an optical system and is affected by background illumination, texture complexity, and signal frequency. Based on the fact that different regions represent different local characteristics, we usually define this psychophysiological phenomenon as the characteristics of color perception in different local areas. Therefore, our eyes will gradually adapt to the local environment [28]. This observation is crucial since haze density changes proportionally with the depth of objects in the scene. In order to achieve image dehazing, we need to incorporate a local contrast property in our algorithm.

Note that in the definition of the Retinex algorithm, STRESS can be seen as a high-pass filter. Since the new 2-D pixel sprays will supersede the original path immediately, we regard STRESS as a heuristic for the dehazing problem [29]. Hence, the key is to choose a suitable filter that enhances the visibility of the image. To this end, we build a series of high-pass filters from RSR and STRESS. These high-pass filters are derived from well-known smoothing filters such as the mean filter, the median filter or the mode filter. In this article, we propose a practically meaningful image dehazing algorithm via contrast enhancement, called STRASS. Our method is different from the previous algorithms which were built from Retinex [15] or Retinex-inspired [29,30,31] approaches. Most of these methods are based on a different function composition, and reconstructed the dehazing model from the lightness formula. The core idea of the STRASS algorithm is similar to the principle of Retinex, while considering the influence of the human visual system. The algorithm takes one or more haze images as input, and a clear image can be obtained after a series of high-pass filtering operations. Experiments on the datasets of NTIRE 2019 and NTIRE 2020 show that STRASS outperforms the state-of-the-art, especially in practical applications and is easy to use. The contributions of our work are summed up as follows:

1) We implement a novel contrast enhancement algorithm called STRASS, which is realized by constructing an efficient high-pass filter to process haze images and taking the influence of human vision system into account in image dehazing principles. STRASS can be run directly without any machine learning, so our algorithm is more superior for practical applications. The advantage of STRASS is that it does not require complex training processes and high-cost computer equipment.

2) We design novel high-pass filters to recover image structures. The purpose of filter design is to enhance some useful image details while reducing most of the noises in image. The innovation of the proposed high-pass filter is that it improves the original low-pass filter and replaces the minimum envelope value in STRESS framework with a novel mean filter.

3) We compare the effectiveness and practical application of STRASS on both NTIRE 2019 and NTIRE 2020 datasets. The experiment results demonstrate that our proposed algorithm is superior to the state-of-the-arts in these two aspects.

Nowadays, more and more algorithms are developed to solve dehazing problems. These methods can be generally classified into three aspects.

In the early proposed algorithms, most of them exploit sophisticated solutions and need to be associated with other data of the image to achieve the fulfillment of the task. Although these methods cannot easily solve the problem of dehazing in a short time, they can be understood by humans. The work [32] did not assume that the atmospheric reflection coefficient is known, but used images taken from scattering media to predict absolute depth maps. Narasimhan et al. [33] took the same method to solve the dehazing task. They made full use of the differences between multiple images, so they could better estimate the attributes of haze images. This method is effective for both grey and color images, but the deep segmentation needs to be manually provided by the user. In addition, Caraffa et al. [34] proposed a new algorithm based on multiple images for dehazing and 3D image reconstruction tasks [35].

An alternative form of algorithm works on polarizing filters [36,37]. Schechner et al. [36] established the relationship between the image formation process and the polarization effect of atmospheric light. They first acquired multiple images of the same scene by using different polarization filters, and then used the measured polarization degree to remove the haze. Shwartz et al. [37] exploited a blind method to retrieve the necessary parameters by using polarizing filters before restoring the haze-free image.

All the methods mentioned above are based on capturing multiple images in the same scene and studying the internal connections between them. However, the real scene usually has only one image. Therefore, this type of method cannot be applied well in real scenes.

Many previous image dehazing methods have developed a variety of image prior knowledge, which is an experience (or a rule) discovered through a large number of experiments. Two assumptions are presented where the atmospheric light has the brightest value and the reflection of scene has the maximum contrast. Since they have not taken the physical principle of haze formation into consideration, color distortion usually occurs in the real image. Similarly, Tarel et al. [8] used maximum contrast priors in their work and considered that air light is normalized. Kratz et al. [2] first assumed that the scene reflection and air light were statistically independent, and then solved the dehazing equation under this premise. He et al. [1] found that most outdoor images have some pixels whose intensity has very low values on a channel. This method cannot achieve ideal results when dealing with sky areas. Meng et al. [10] stretched the concept of dark channel prior and provided a new extension for transmission map. Fattal [4] proposed the color line in a local region of the image and derived a mathematical model to explain it. Color line prior algorithm has obtained more successful results than previous methods. Berman et al. [5] used many different colors to replace the color of the haze image, and proposed a dehazing algorithm based on haze-line prior. Their algorithm can avoid artifacts in many state-of-the-art methods. Ancuti et al. [9] bring forward a global contrast enhancement method with a new dehazing algorithm based on the Gray-world color constancy. Galdran et al. [15] provided a rigorous mathematical proof on the duality relationship between image dehazing and separation problem of non-uniform lighting. Their methods do not rely on the physical meaning of the haze model.

Research [11] used the fusion principle to recover the fog-free image. Choi et al. [11] proposed a dehazing method based on image Natural Scene Statistics (NSS) and haze perception statistical features, and this method is then defined as DEFADE scheme. DEFADE was tested on darker images and denser foggy images, which obtained better results than state-of-the-art dehazing algorithms. Cho et al. [6] mixed the model-based method and the fusion-based method to perform the dehazing task, and then clarified the input image at the pixel level. However, these methods require adjustment and fusion different parameters of the image.

The effectiveness of the above methods largely depends on the accuracy of the proposed image prior knowledge. When the prior conditions do not match with the real image scene, the ideal dehazing effect cannot be obtained. Therefore, these methods tend to cause undesirable phenomenon such as color distortions.

With the wide adhibition of CNN (Convolutional Neural Networks) in the field of image processing, methods based on machine learning are gradually used in the research of single image dehazing. This type of method generally learns the parameters of the network model through supervision, or directly outputs a clear image using an end-to-end network. Among this category, we can mention the work of [18–22,38]. Cai et al. [18] proposed a dehazing algorithm based on convolutional neural networks, which combines traditional prior knowledge with deep learning in an end-to-end form. In 2017, Ancuti et al. [39] designed an effective color correction algorithm for underwater images. He et al. [23,28] proposed a pyramid deep network in 2018, which completed the dehazing task by learning the features of haze image at different scales. Guo et al. [24] won the NTIRE Dehazing Challenge in 2019 by developed two novel network architectures called At-DH and AtJ-DH. More advanced techniques in these architectures can be found in [40,41].

All of the above methods are different from prior-based methods. Deep learning-based methods are usually divided into two types: One is to embed prior knowledge into the deep network to guide the network; The other is to design an end-to-end network directly outputs clear images through feature learning.

In order to fully understand the algorithm that we have developed, we introduce it from the origin and the relationship with human visual system (HVS). The ability of HVS to perceive the color of a local area is closely related to the surrounding scene. It is not independent of the visual scene, which is strongly affected by the image content of other surrounding areas. The first mathematical model to represent the human visual system (HVS) was Land et al. [28]. Their Retinex algorithm can perfectly explain how HVS perceives colors. The model is based on three assumptions and has an intuitive representation of the brightness of the image. When we use the Retinex algorithm to process RGB images, we need to superimpose the brightness value of each pixel in the three channels of R, G, and B to get the final enhanced image. The principle of the Retinex algorithm depends on several important parameters: threshold, number of paths and iterations. Studies in [26] show that the Retinex algorithm calculates the intensity of through the following function to obtain the normalized value of brightness:

We consider a RGB image and a collection of N paths γ1, …, γNcomposed by ordered chains of pixels strating in jk and ending in i(target pixel). nk is the number of pixels traversed by the kth path γk and tk=1…nk−1 is the parameter of nk k=1…N We denote two consecutive pixels different from γk in the path as γk(tk)=xtk and γk(tk+1)=xtk+1 . Then the intensity values xtk and xtk+1 in the three channels of RGB can be expressed as I(xtk) and I(xtk+1) . Therefore, we express the ratio of them as Rtk=(I(xtk)/I(xtk+1) , where δk is an identity function, when tk = 0, δk(R0) = 1 For tk = 1, …, nk − 1, the formula is shown as follows:

δk(Rtk)={ Rtk if 0<Rtk <1−ε1 if 1−ε<Rtk <1+ε Rtk if 1+ε≤Rtk ≤ 1+ϵ∏mk = 0tk−1δk(Rmk)1∏mk = 0tk−1δk(Rmk) if Rtk>1+ε∏mk = 0tk−1δk(Rmk) (2)

where, the first and third formulas perfectly apply the ratio chain property. The second formula is suitable for the following situations: When the intensity value between two adjacent pixels changes slightly, δk(Rtk)=1 is equivalent to a threshold because it keeps the product of ratios constant. Finally, when δk(R1)δk(R2)…δk(Rtk−1)Rtk>ε+1 , the fourth formula resets the product chain to 1, so that other pixels can refer to it. Therefore, Eq. (2) realized the application of the ratio threshold reset mechanism. For such values of ε, the difference between Retinex with and without threshold has an upper bound which has negligible effects for the final lightness computation, ε > 0 being a fixed threshold.

In the construction of our dehazing framework, we neglect the threshold mechanism which allows us to simplify the significant mathematical formulation of the lightness Retinex in Eq. (1) as the following:

It is essential to find that the path is not fully applicable to every situation, especially when using Retinex model to analyze the locality of color perception. We know that image is a two-dimensional plane, but path is one-dimensional. Therefore, the path only extracts information in its specific direction, and does not travel the local neighborhood of each pixel practically. In this work, we adopt the random spray Retinex (RSR) method to solve this problem, replacing the path with the random spray of pixels, so as to achieve the purpose of traveling each pixel. The modified pixel can be expressed by the following polar coordinates:

where jx, jy represents the polar coordinates corresponding to pixel i ,f:ℝ+ → ℝ+, ρ ∈ RANDn[0, R] and θ ∈ RANDn[0, 2π]. f(ρ) represents the different radial density functions, where each different function randomly selects different pixels around i to form different types of “spray” shapes, and each “spray” has different local filtering characteristics.

In this part, we will explain our defogging algorithm in detail and define it as STRASS: “Spatio-Temporal Retinex-Inspired by an Averaging of Stochastic Samples”. Our idea is to use the random sampling method mentioned in RSR to select pixels randomly from these local areas. The main idea behind the construction of our framework is very similar to the core idea of STRESS, replacing the current pixel value by constructing a weighted average of a high-pass filter, where the original image can be enhanced in contrast within a certain range.

We assume that the radial density function is an identity (f(ρ)=ρ,0<ρ<R) for all output values of our framework. So, the only variable parameter is the radius that changes with the identity function. The simulation of the random sampling procedure is shown in Fig. 1.

Fig. 1 shows the random sampling procedure. The diameter of the sample and the number of samples collected are random, here (ix, iy) represents the central pixel, with (ix, iy) as the center, 400 samples are randomly selected in a circle with a random sampling diameter of 40. Actually, RSR, STRESS and STRASS share the same general form, but their difference lies essentially in the definition of this characteristic function:

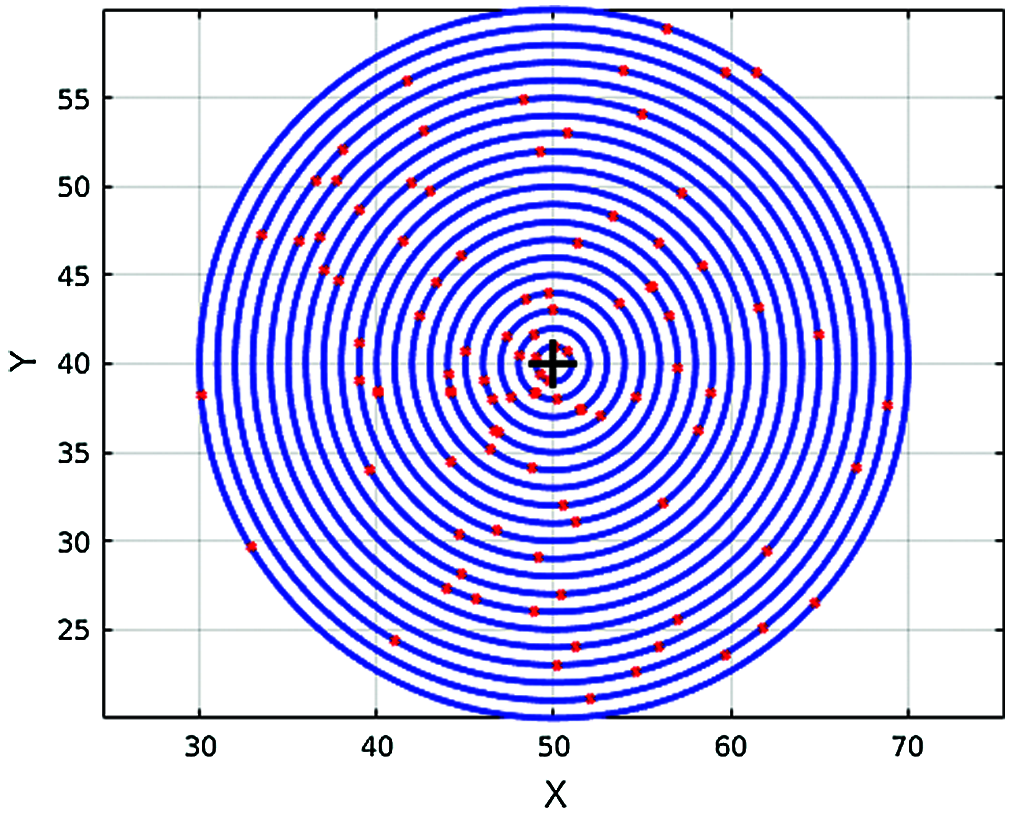
Figure 1: Simulating the random sampling procedure in Eq. (5). Here, the number of samples is M = 400, the random sampling diameter d = 40, the current pixel i0 are ixo =0iyo = 40ρ∈020 and θ ∈ [0, 2π]

In both STRESS and STRASS, the function fin is implemented as a high-pass filter. In the following, we slightly modify the notation that directly derived from [26] to adopt another notation. The pixels are randomly select M samples from a disk with radius R around the center pixel. From these samples, let us denote ximax and ximin the maximum and the minimum sample respectively from M samples for a given image unit. The following calculations are made on each channel:

where xLk represents the pixel with the lowest intensity value traversed by each γk path and xHk represents the pixel with the highest intensity value. ximax represents the maximum sample among M samples of xj, and ximin represents the minimum sample among M samples of xj. ximax and ximin can also be respectively represented by I(xHk) and I(xLk) . x0 is always one of the sample points, and ximin<x0<ximax . From here, let us call xi,R the statistical range of the samples:

In order to get a better estimate of the mean of the sample x^imean , these quantities are averaged over the M iterations:

The partial result of our High-pass filter at a given iteration is then given as:

In Eq. (10), it is easy to note that the essential difference between the high-pass filter we invented and the filter defined in [27] lies in two aspects. First, the third option indicates that the low-pass filter generated by the minimum envelope has been replaced by the low-pass mean filter designed by us. Second, the difference between the current pixel and the local filter may be negative, so the meaning of the second option is to keep this difference always positive or null. The final output of STRASS after N iterations is as the following:

In addition to the above procedure of samples selection used for dehazing tasks, we come with a new criterium for singular cases of haze situation such as dense haze scenes and nonhomogeneous haze scenes:

In those cases, we introduce a new constant K where we constrain not only the selected sample to be inside the image, but also the absolute difference between the current pixel xi in the Cartesian space and the selected sample xj in the polar space should be greater than K. After a series of image test experiments, we set the empirical value of K to 5 is more appropriate. The above constraint helps us to improve the visibility of haze particular distributions.

In this part, we will explain the meaning of the STRASS framework and its relationship with image dehazing. In [27], the core idea of the STRESS algorithm is the calculation of envelopes. The maximum envelope and the minimum envelope respectively represent the local maximum and minimum of the reference image. Based on these two extreme values, the image is restored by recalculating each pixel, which are constructed such that the image signal is always between the two. Calculated by the minimum envelope or the maximum envelope, the final output of the STRESS framework will closest to an ideal value. In [29], the author slightly modified the two formulas of envelope and conducted experiments on STRESS and hazy images. When the haze of the image in a homogeneous state, there exists a certain correlation between the haze physical model and the envelope functions, which provides a strong theoretical basis for the SRESS framework to solve the dehazing task.

Here, we replace the minimum envelope value of the sample used in [27] with the average value of the samples which is proposed in [29]. Even if we do not formally prove the link between the structure of the STRASS framework and image dehazing by establishing a solution of dehazing problem, this strong connection can be intuitively perceived through the conclusions drawn in [29]. It can be seen from Eq. (11) that the core of STRASS is to design a new high-pass filter, and replaced the characteristic function of STRESS with a new low-pass function (see Eq.(10) option 3). Since the average value of the sample takes into account the local features of the image, our improved method is more suitable for actual dehazing work. The most important thing is that our new method not only reduces the noise introduced by the envelope in STRESS, but also achieves satisfactory results when dealing with the haze of distant objects. Thus, the average filter developed by us can solve the dehazing problem more effectively than the minimum low-pass filter. Due to space issues, we did not elaborate effects of Stress, which readers can refer to [27].

The other solution that we have tried is to use a multiscale formulation for STRESS. Unlike the methods developed in [30] and [31], the multi-scale STRESS algorithm does not need to find the threshold of white pixels, nor does it require manual segmentation of the image. The algorithm can be built with 2 or more rays of the STRESS algorithm, the radiuses of rays must always be different from each other and their length must be between 1 and the diagonal of the image. Let s be the number of multiscale, x1STRESS…xsSTRESS represent a series of STRESS that operations on the image. The output of our new multiscale STRESS formulation can be defined as follows:

The experimental results show that the multiscale STRESS will occur relatively large noise in some more complicated situations (such as dense haze).

In this section, we verify the effect of the STRASS algorithm in dehazing tasks, and test its generalization ability on different datasets. The datasets we use mainly come from the NTIRE challenge. Then we show some details of the network training process. Finally, we compare the STRASS algorithm with the state-of-art methods, including Berman et al. [5], Cho et al. [6], He et al. [1], Meng et al. [10], Tarel et al. [8].

In our work, we run the code on a Linux machine with Ubuntu OS 18.04 LTS, with 8GB of memory, we conduct dehazing experiments on C++, and only one CPU is used in the training process (Intel Core i7, 2.40 GHZ x 4). We use O(MNn) to represent the complexity of the STRASS, where M represents the number of samples, N denotes the number of iterations, and the total number of pixels contained in the image is n. All the parameters in this article first set the initial threshold. In the experiment, we tested a series of images to find out the approximate range of the optimal values of these parameters through subjective evaluation and objective indicators.

We firstly show the results of the qualitative experiment on NTIRE2020 dataset in Fig. 2. The images from left to right represent the haze image and the results of the five state-of-the-art dehazing algorithms: GT, Berman et al. [5], Cho et al. [6], He et al. [1], Meng et al. [10], Tarel et al. [8] results and ours. Some dehazing methods [1,8,10] rely on prior knowledge that cannot accurately estimate the density of haze. If some areas of the image are over-processed, the dehazing results will be darker than original image, or get a brighter one. [6] showed color distortion in some areas, and there is still some remaining haze.

Figure 2: From left to right, input image, GT, Berman et al. [5], Cho et al. [6], He et al. [1], Meng et al. [10], Tarel et al. [8] and ours from NTIRE2020

In the experiment, we noticed that STRASS will amplify white noise when the haze is inhomogeneous and dense. By observing the image as shown in Fig. 3, we can clearly see that STRASS has achieved better results than other methods, it is because the haze in image 51 is relatively uniform, so the white noise of this image is not amplified, while the nonuniform haze in other images causes the appearance of white noise. So, the STRASS method is effective, and the contrast is enhanced qualitatively in the way of our visual system.

Figure 3: Visual comparison with image used in the final round of NTIRE2020. From left to right, input image, Berman et al. [5], Cho et al. [6], He et al. [1], Meng et al. [10] and ours

In order to further test the robustness and computing capabilities, we not only conducted comparative experiments on the NTIRE2020 dataset, but also on the images of NTIRE2019. Fig. 4 shows five dense haze images from the NTIRE2019 and the processing results on the state-of-art methods. By observing the first four images, we find that all methods cannot completely remove the haze, especially in areas with thick haze. It can be obviously seen that these methods are not good at handling images captured in dense haze. While compared with other algorithms, we not only get a pleasant dehazing result, but also preserve the original color of the image. The method in this article is indeed not the best on some pictures, but it is relatively better on most pictures in general. This is also the direction for us to improve in the future.

Figure 4: From left to right, input image, GT, Berman et al. [5], Cho et al. [6], He et al. [1], Meng et al. [10], Tarel et al. [8] results and ours from NTIRE2019

In order to evaluate these methods more accurately and compare the slight differences between various dehazed images, we utilize some quantitative evaluation indicators on both NTIRE2020 and NTIRE2019 as these are very difficult dehazing situations. Besides the widely adopted structural similarity indices (SSIM [42]), we also use PSNR as another important index, the average value of the experiment will be reported later. PSNR and SSIM are the most common and widely used full-reference image objective evaluation indicators. PSNR is an error-sensitive image quality evaluation. SSIM measures image similarity from three aspects: brightness, contrast, and structure. Using these two indicators in the field of image dehazing can well measure the difference between the dehazed image and the label image. It should be noted that the efficiency of dehazing algorithms can be sensitive to the density of the haze and other obscure parameters that are not necessarily related to the physical parameters of the haze. Our method has been successfully tested on many types of dry or wet particles, such as smoke, fog, dust, mist, haze as the results of the images from the databases of NTIRE2019 and NTIRE2020 attest.

For the quantitative assessment, we only considered the image datasets from NTIRE2020 and NTIRE2019 since they represent images that traditional algorithms not based on learning methods cannot easily resolve. Each image database includes 45 pairs of images taken under artificial fog and its corresponding haze-free. The number of image pairs considered for this evaluation is 90 images once the two databases have been merged. Our algorithm clearly outperform with other unsupervised algorithms as can be seen in the Tables 1 and 2. Our PSNR is the best and the second best for NTIRE2019 and for NTIRE2020 respectively. However, it seems that our SSIMs are not in agreement with the results obtained for the PSNRs. We can also notice that the results of the two metrics for our algorithm are quite close to the results obtained for the advanced methods. For the NTIRE2019 competition, several advanced algorithms as well as ours do not seem to have done better compared to the hazy image in terms of the SSIM metric. This may mean that these unusual images must be processed by algorithms based on learning methods to be effectively resolved.

Although our PSNR/SSIM value is relatively low than the state-of-the-arts, we aim to implement a fast and simple contrast enhancement-based dehazing algorithm. Therefore, we mainly consider comparative experiments with some traditional methods. The algorithm runs directly without a large number of samples, which saves a lot of time for model training, and the average running time on the NTIRE2019 and NTIRE2020 dataset as show in the Table 3. We take the influence of the human visual system (HVS) into account in image dehazing principles, making it easier for humans to understand. These state-of-the-arts artificial intelligence algorithms cannot be perceived by the HVS, so our algorithm is more superior for practical applications. On the other hand, we are also exploring the use of deep learning for dehazing, some works found that traditional algorithms are not as accurate as those based on deep learning. Therefore, this article does not compare experiments with methods based on deep learning.

We discovered the fact that the results of [5] are visually quite close to our results on all datasets (without considering the constraint for singular cases), then we can make an assumption that [5] may has some of the same properties as STRASS. This could explain why the [5] algorithm as well as ours have more white noise on the NTIRE2020 data set, while both of them have shown high visibility on the NTIRE2019 dataset.

The proposed method works quite well in general, and can even handle cases of dense and non-homogeneous haze with the introduction of the constant K (see the Eq. (12)). In those cases, our method is able to yield comparable and even better results with advanced non-learning methods. However, a limitation of our method is that it will cause the STRASS to produce white noise when the haze is inhomogeneous. As shown in Fig. 3, it got unsatisfactory results when processing dense smog images. Because the heavy haze not only greatly occludes the effective information of the image, it cannot accurately estimate the atmospheric light. Another disadvantage of this algorithm is the calculation time. When N = 150 and M = 5 the average time complexity is about 10 min, while we get almost the same output visually when N = 50 and M = 6 but the time complexity is less than 3 min and 45 s.

We try to find an effective way to solve the situation of dense and non-uniform haze as much as possible, and use another low-pass filter (such as a median filter or a mode filter) to build the STRASS framework. We will solve this complicated problem in future research.

In this paper, we propose a single image dehazing algorithm that directly utilizes the contrast enhancement principle, which works by recalculating each pixel with two envelopes. Compared with previous methods which require carefully stretching the contrast, our proposed STRASS framework considers the characteristics of HVS and is easy to implement. Inspired by STRESS and Retinex, we show that the STRASS framework can solve the task of image dehazing, where the minimum envelope value in the STRESS framework can be replaced by an average filter. In the proposed approach, we first use the random sampling method mentioned in RSR to select pixels randomly from the local areas, and then replace the current pixel value by constructing a novel high-pass filter to enhance the contrast of the original image within a certain range. The experimental results on the NTIRE dataset and real images prove the effectiveness and strong generalization ability of our method. The innovation of the proposed method is that it takes the influence of the human visual system into account in image dehazing principles and it can be run directly without any machine learning. Our method can be applied to the pre-printing image processing link, which greatly reduces the printing process and cost, and conforms to the concept of green printing.

Funding Statement: This work was supported in part by National Natural Science Foundation of China under Grant 62076199, in part by the Open Research Fund of Beijing Key Laboratory of Big Data Technology for Food Safety under Grant BTBD-2020KF08, Beijing Technology and Business University, in part by the China Postdoctoral Science Foundation under Grant 2019M653784, in part by Key Laboratory of Spectral Imaging Technology of Chinese Academy of Sciences under Grant LSIT201801D, in part by the Key R&D Project of Shaan’xi Province under Grant 2021GY-027.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. He, K., Sun, J., Tang, X. O. (2015). Single image haze removal using dark channel prior. IEEE Transactions on Pattern Analysis & Machine Intelligence, 33(12), 2341–2353. DOI 10.1109/TPAMI.2010.168. [Google Scholar] [CrossRef]

2. Kratz, L., Nishino, K. (2009). Factorizing scene albedo and depth from a single foggy image. IEEE International Conference on Computer Vision, pp. 1701–1708. DOI 10.1109/ICCV.2009.5459382. [Google Scholar] [CrossRef]

3. Tang, K., Yang, J., Wang, J. (2014). Investigating haze-relevant features in a learning framework for image dehazing. IEEE Conference on Computer Vision and Pattern Recognition, pp. 2995–3002. Columbus, USA, DOI: 10.1109/CVPR.2014.383. [Google Scholar] [CrossRef]

4. Fattal, R. (2014). Dehazing using color-lines. ACM Transactions on Graphics, 34(1), 1–14. DOI 10.1145/2651362. [Google Scholar] [CrossRef]

5. Berman, D., Treibitz, T., Avidan, S. (2016). Non-local image dehazing. IEEE Conference on Computer Vision and Pattern Recognition, pp. 1674–1682. DOI: 10.1109/CVPR.2016.185. [Google Scholar] [CrossRef]

6. Cho, Y. G., Jeong, J. Y., Ayoung, K. (2018). Model-assisted multiband fusion for single image enhancement and applications to robot vision. IEEE Robotics and Automation Letters, 3(4), 2822–2829. DOI 10.1109/LRA.2018.2843127. [Google Scholar] [CrossRef]

7. Vazquez-Corral, J., Finlayson, G. D., Bertalmio, M. (2020). Physical-based optimization for non-physical image dehazing methods. Optics Express, 28(7), 9327–9339. DOI 10.1364/OE.383799. [Google Scholar] [CrossRef]

8. Tarel, J. P., Hautière, N. (2010). Fast visibility restoration from a single color or gray level image. IEEE International Conference on Computer Vision, pp. 2201–2208. DOI 10.1109/ICCV.2009.5459251. [Google Scholar] [CrossRef]

9. Ancuti, C. O., Ancuti, C. (2013). Single image dehazing by multi-scale fusion. IEEE Transactions on Image Processing, 22(8), 3271–3282. DOI 10.1109/TIP.2013.2262284. [Google Scholar] [CrossRef]

10. Meng, G., Wang, Y., Duan, J., Xiang, S., Pan, C. (2013). Efficient image dehazing with boundary constraint and contextual regularization. IEEE International Conference on Computer Vision, pp. 617–624. DOI 10.1109/ICCV.2013.82. [Google Scholar] [CrossRef]

11. Choi, L. K., You, J., Bovik, A. C. (2015). Referenceless prediction of perceptual fog density and perceptual image defogging. IEEE Transactions on Image Processing, 24(11), 3888–3901. DOI 10.1109/TIP.2015.2456502. [Google Scholar] [CrossRef]

12. Zhu, Q., Mai, J., Shao, L. (2015). A fast single image haze removal algorithm using color attenuation prior. IEEE Transactions on Image Processing, 24(11), 3522–3533. DOI 10.1109/TIP.2015.2446191. [Google Scholar] [CrossRef]

13. Galdran, A., Vazquez-Corral, J., Pardo, D., Bertalmío, M. (2014). A variational framework for single image dehazing. Lecture notes in computer science, pp, 259–270. European Conference on Computer Vision. DOI 10.1007/978-3-319-16199-0. [Google Scholar] [CrossRef]

14. Galdran, A., Vazquez-Corral, J., Pardo, D., Bertalmío, M. (2015). Enhanced variational image dehazing. SIAM Journal on Imaging Sciences, 8(3), 1519–1546. DOI 10.1137/15M1008889. [Google Scholar] [CrossRef]

15. Galdran, A., Alvarez-Gila, A., Bria, A., Vazquez-Corral, J., Bertalmio, M. (2018). On the duality between retinex and image dehazing. IEEE/CVF Conference on Computer Vision and Pattern Recognition, pp, 8212–8221. DOI 10.1109/CVPR.2018.00857. [Google Scholar] [CrossRef]

16. Wang, Y., Fu, F., Lai, F., Xu, W., Shi, J., et al. (2018). Haze removal algorithm based on single-images with chromatic properties. Signal Processing: Image Communication, 72, 80–91. DOI 10.1016/j.image.2018.12.010. [Google Scholar] [CrossRef]

17. Xu, L. L., Han, J., Wang, T., Bai, L. F. (2019). Global image dehazing via frequency perception filtering. Journal of Circuits Systems and Computers, 28(9), 1–11. DOI 10.1142/S0218126619501421. [Google Scholar] [CrossRef]

18. Cai, B., Xu, X., Jia, K., Qing, C., Tao, D. (2016). Dehazenet: An end-to-end system for single image haze removal. IEEE Transactions on Image Processing, 25(11), 5187–5198. DOI 10.1109/TIP.2016.2598681. [Google Scholar] [CrossRef]

19. Li, B., Peng, X., Wang, Z., Xu, J., Dan, F. (2017). AOD-Net: all-in-one dehazing network. IEEE International Conference on Computer Vision, pp. 4780–4788. DOI 10.1109/ICCV.2017.511. [Google Scholar] [CrossRef]

20. Ren, W., Ma, L., Zhang, J., Pan, J., Cao, X. et al. (2018). Gated fusion network for single image dehazing. IEEE/CVF Conference on Computer Vision and Pattern Recognition, pp. 3253–3261. DOI 10.1109/CVPR.2018.00343. [Google Scholar] [CrossRef]

21. Li, R., Pan, J., Li, Z., Tang, J. (2018). Single image dehazing via conditional generative adversarial network. 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, pp. 8202–8211. DOI 10.1109/CVPR.2018.00856. [Google Scholar] [CrossRef]

22. Wang, A., Wang, W., Liu, J., Gu, N. (2019). Aipnet: Image-to-image single image dehazing with atmospheric illumination prior. IEEE Transactions on Image Processing, 28(1), 381–393. DOI 10.1109/TIP.2018.2868567. [Google Scholar] [CrossRef]

23. He, Z., Da Gi, S., Patel, V., M, V. (2018). Multi-scale single image dehazing using perceptual pyramid deep network. IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops, pp. 1015–101509. DOI 10.1109/CVPRW.2018.00135. [Google Scholar] [CrossRef]

24. Guo, T., Li, X., Cherukuri, V., Monga, V. (2019). Dense scene information estimation network for dehazing. 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops, pp. 2122–2130. DOI 10.1109/CVPRW.2019.00265. [Google Scholar] [CrossRef]

25. Chen, S., Chen, Y., Qu, Y., Huang, J., Hong, M. (2019). Multi-scale adaptive dehazing network. IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops, pp. 2051–2059. DOI 10.1109/CVPRW.2019.00257. [Google Scholar] [CrossRef]

26. Provenzi, E., Fierro, M., Rizzi, A., de Carli, L., Gadia, D. et al. (2007). Random spray retinex: A new retinex implementation to investigate the local properties of the model. IEEE Transactions on Image Processing, 16(1), 162–171. DOI 10.1109/TIP.2006.884946. [Google Scholar] [CrossRef]

27. Kolås, O., Farup, I., Rizzi, A. (2011). Spatio-temporal retinex-inspired envelope with stochastic sampling: A framework for spatial color algorithms. Journal of Imaging Science & Technology, 55(4), 40503.1–40503.10. DOI info:doi/10.2352/J.ImagingSci.Technol.2011.55.4.040503. [Google Scholar]

28. Land, E. (1971). Lightness and retinex theory. Journal of the Optical Society of America, 61(1), 1–11. DOI 10.1364/JOSA.61.000001. [Google Scholar] [CrossRef]

29. Dravo, V. W. D., Hardeberg, J. Y. (2015). Stress for dehazing. Colour and Visual Computing Symposium, pp. 1–6. DOI 10.1109/CVCS.2015.7274895. [Google Scholar] [CrossRef]

30. Dravo, V. W. D., Thomas, J. B., Hardeberg, J. Y. (2016). Multiscale approach for dehazing using the stress framework. Journal of Imaging Science and Technology, 60(1), 010409.1–010409.13. DOI 10.2352/ISSN.2470-1173.2016.20.COLOR-353. [Google Scholar] [CrossRef]

31. Dravo, V. W. D., Thomas, J. B., Hardeberg, J. Y., Khoury, J. E., Mansouri, A. (2017). An adaptive combination of dark and bright channel priors for single image dehazing. Journal of Imaging Science and Technology, 61(4), 040408.1–040408.9. DOI 10.2352/J.ImagingSci.Technol.2017.61.4.040408. [Google Scholar] [CrossRef]

32. Narasimhan, S. G., Nayar, S. K. (2002). Vision and the atmosphere. International Journal of Computer Vision, 48(3), 233–254. DOI 10.1023/A%3A1016328200723. [Google Scholar] [CrossRef]

33. Narasimhan, S. G., Nayar, S. K. (2003). Contrast restoration of weather degraded images. IEEE Transactions on Pattern Analysis & Machine Intelligence, 25(6), 713–724. DOI 10.1109/TPAMI.2003.1201821. [Google Scholar] [CrossRef]

34. Caraffa, L., Tarel, J. P. (2013). Stereo reconstruction and contrast restoration in daytime fog. In: Lecture notes in computer science, pp. 13-25. Asian Conference on Computer Vision, DOI 10.1007/978-3-642-37447-0_2. [Google Scholar] [CrossRef]

35. Li, Z., Ping, T., Tan, R. T., Zou, D., Zhou, S. Z. et al. (2015). Simultaneous video defogging and stereo reconstruction. 2015 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), pp. 4988–4997. Boston, MA, USA: IEEE. DOI 10.1109/CVPR.2015.7299133. [Google Scholar] [CrossRef]

36. Schechner, Y. Y., Narasimhan, S. G., Nayar, S. K. (2001). Instant dehazing of images using polarization. Proceedings of the 2001 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, pp. 1Boston, MA, USA: IEEE. DOI 10.1109/CVPR.2001.990493. [Google Scholar] [CrossRef]

37. Shwartz, S., Namer, E., Schechner, Y. Y. (2006). Blind haze separation. IEEE Computer Society Conference on Computer Vision and Pattern Recognition, pp. 1984–1991. New York, USA, DOI 10.1109/CVPR.2006.71. [Google Scholar] [CrossRef]

38. He, Z., Patel, V. M. (2018). Densely connected pyramid dehazing network. IEEE/CVF Conference on Computer Vision and Pattern Recognition, pp. 3194–3203. DOI 10.1109/CVPR.2018.00337. [Google Scholar] [CrossRef]

39. Ancuti, C. O., Ancuti, C., Vleeschouwer, C. D., Garcia, R. (2017). Locally adaptive color correction for underwater image dehazing and matching. IEEE Conference on Computer Vision and Pattern Recognition Workshops, pp. 997–1005. DOI 10.1109/CVPRW.2017.136. [Google Scholar] [CrossRef]

40. Ancuti, C. O., Ancuti, C., Timofte, R., Gool, L. V., Zhang, L. et al. (2018). NTIRE 2018 challenge on image dehazing: Methods and results. IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops, pp. 1004–100410. DOI 10.1109/CVPRW.2018.00134. [Google Scholar] [CrossRef]

41. Ancuti, C. O., Ancuti, C., Timofte, R., Gool, L. V., Wu, J. (2019). NTIRE 2019 image dehazing challenge report. IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops, pp. 2241–2253. DOI 10.1109/CVPRW.2019.00277. [Google Scholar] [CrossRef]

42. Wang, Z. (2004). Image quality assessment: From error visibility to structural similarity. IEEE Transactions on Image Processing, 13(4), 600–612. DOI 10.1109/TIP.2003.819861. [Google Scholar] [CrossRef]