DFT and TD-DFT Calculations of Orbital Energies and Photovoltaic Properties of Small Molecule Donor and Acceptor Materials Used in Organic Solar Cells

Daniel Dodzi; Kiran Ram; Hooman Mehdizadeh-Rad; David Ompong; Vinuthaa Murthy; Jai Singh

doi:10.32604/jrm.2022.020967

Daniel Dodzi Yao Setsoafia1, Kiran Sreedhar Ram1, Hooman Mehdizadeh-Rad1,2, David Ompong1,2, Vinuthaa Murthy1,2 and Jai Singh1,2,*

1College of Engineering, IT and Environment, Purple 12, Charles Darwin University, Darwin, NT 0909, Australia
2Energy and Resources Institute, Charles Darwin University, Darwin, NT 0909, Australia
*Corresponding Author: Jai Singh. Email: jai.singh@cdu.edu.au
Received: 21 December 2021; Accepted: 07 April 2022

Abstract: DFT and TD-DFT calculations of HOMO and LUMO energies and photovoltaic properties are carried out on four selected pentathiophene donor and one IDIC-4F acceptor molecules using B3LYP and PBE0 functionals for the ground state energy calculations and CAM-B3LYP functional for the excited state calculations. The discrepancy between the calculated and experimental energies is reduced by correlating them with a linear fit. The fitted energies of HOMO and LUMO are used to calculate the Voc of an OSC based on these donors and acceptor blend and compared with experimental values. Using the Scharber model the calculated PCE of the donor-acceptor molecules agree with the experiment. It has been found that fluorine substitution can be used to improve charge transport by reducing the electron and hole reorganization energies of the molecules. It is also found that the introduction of fluorine onto the donor pentathiophene unit of the donor molecule results in a change of polarity of the distributed charges in the molecule due to the high electronegativity of the fluorine atom. The quantum chemical potential (μ), chemical hardness (η) and electronegativity (χ), and electrostatic potential maps (EPMs) are also calculated to identify different charge distribution regions in all five molecules.

Keywords: Acceptor; donor; DFT; excitons; HOMO; LUMO; small molecule; electrophilic nucleophilic; and reorganization energy

The bulk heterojunction (BHJ) based organic solar cells (OSCs) hold a promising future for converting solar energy to electricity more economically than silicon solar cells [1–3], because of their low temperature fabrication process, light weight and flexibility [4], and their power conversion efficiency (PCE) reaching more than 18% [3,5]. BHJ OSCs are fabricated by blending donor (D) and acceptor (A) organic semiconductors as photo absorbers to form an interpenetrating network of D-A interfaces which facilitate efficient dissociation of photogenerated excitons [5,6]. Excitons are Coulomb bound excited electron and hole pairs generated in an organic semiconductor when it absorbs photons of energy equal to or more than its band gap energy [7]. The binding energy of excitons is high in organic semiconductors due to their low dielectric constant [8], hence must be dissociated into free charge carriers for the generation of electricity [7]. Two energy levels of most interest in organic semiconductors are the highest occupied molecular orbital (HOMO) and lowest unoccupied molecular orbital (LUMO) [9]. This is because the HOMO and LUMO, also referred as the frontier orbitals of a single organic molecule, act as the valence and conduction bands, respectively, in organic solids. Therefore, the energy difference between HOMO and LUMO levels become the energy gap of organic semiconductors [10]. Experimental determination of the HOMO level is achieved by cyclic voltammetry and photoemission yield spectroscopy, while the LUMO level is usually measured by cyclic voltammetry [11]. Theoretical calculations of HOMO and LUMO are usually carried out by the density functional theory (DFT) and Ab initio methods.

The dissociation of excitons in BHJ OSCs contributes to the short circuit current density ( Jsc ) and depends very critically on the HOMO and LUMO energy offsets between the donor and acceptor materials [12]. For example, if the excitons are photoexcited in the donor material, these form the charge transfer (CT) excitons by transferring electrons from the LUMO of donor to that of acceptor being at a lower energy at the donor (D) – acceptor (A) interface (D-A interface) and releasing the excess energy, ΔELUMO=ELUMOD−ELUMOA , as molecular vibrations, where ELUMOD and ELUMOA are the energies of LUMO of donor (D) and acceptor (A), respectively. If ΔELUMO≥EB , where EB is the binding energy of CT excitons, then only the CT excitons will dissociate into free charge carriers [7]. Likewise, if the excitons are excited in the acceptor then CT excitons are formed by transferring holes from the HOMO of acceptor to that of donor being at a lower energy at the D-A interface and releasing the excess energy ΔEHOMO=EHOMOA−EHOMOD as molecular vibrations, where EHOMOD and EHOMOA are the energies of HOMO of acceptor (A) and donor (D), respectively. Here again, if ΔEHOMO≥EB , then only the CT excitons will dissociate into free charge carriers. Also the open circuit voltage ( Voc ) of a BHJ OSC depends critically on the energies of LUMO and HOMO of donor and acceptor and it is usually related as [13],

Voc=1q(EHOMOD−ELUMOA)−0.3 and the power conversion efficiency, PCE=JscVocFFPin , depends directly on both Jsc and Voc , where FF and Pin are the fill factor and the incident solar power, respectively. Accordingly, it becomes very important to determine the energies of HOMO and LUMO very accurately for both donor and acceptor materials. Therefore, in this paper, we have considered four donors and one acceptor materials and used a DFT software to calculate the HOMO and LUMO energies and compared our results with the corresponding experimental results as described in the results section. The combination of four donors and one acceptor given in Fig. 1 is studied in this paper for the following two reasons. 1. The availability of experimental data for comparison with simulated results and 2. the use of small molecules as active layer material reduces the cost of fabrication of such OSCs because thiophene units which are the building blocks of the donor and acceptor materials are cheap and easy to fabricate. In addition, the selection of IDIC-4F as an acceptor provides the adequate energy offset for the efficient dissociation of excitons at the D-A interface as shown in Fig. 2.

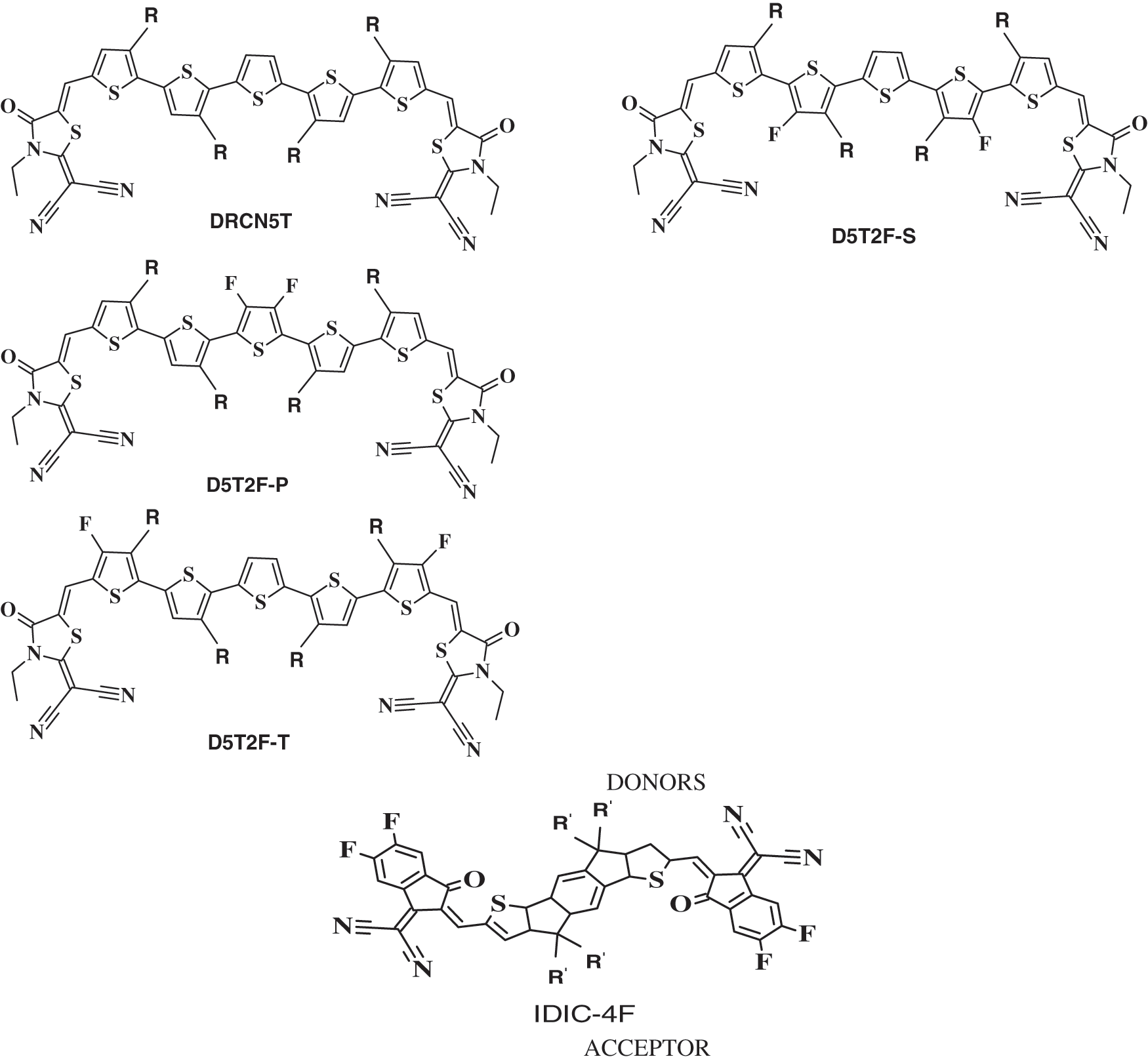
Figure 1: Molecular structures of the four donors DRCN5T, D5T2F-S, D5T2F-P, and D5T2F-T and one acceptor IDIC-4F. R and R’ represent C8H17 and C6H13, respectively

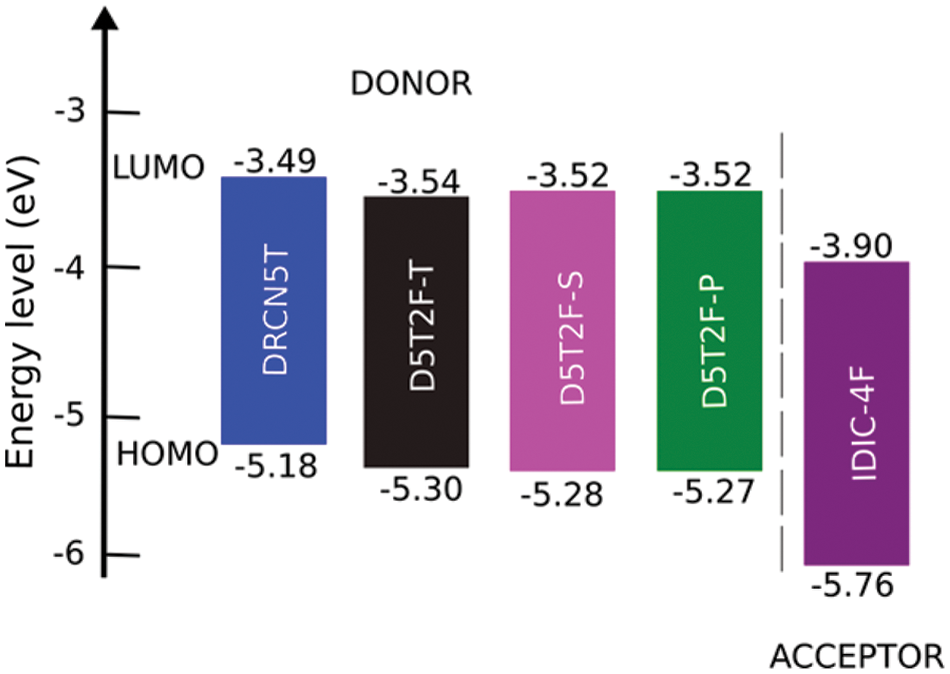
Figure 2: Energy level diagram of the studied donor and acceptor molecules calculated using DFT at the PBE0 level of theory

Organic solar cells of small molecule organic donor and acceptor materials have become research hotspot due to the ease of chemically modifying small molecules for optimizing the energy levels and the morphology of the resulting donor and acceptor materials. With the advancement of synthetic techniques, small molecule based BHJ OSCs of PCE more than 18% have been fabricated [14]. In this paper, we have performed DFT simulations to calculate the HOMO and LUMO energies of four donor type A-D-A molecules which are pentathiophene derivatives end-capped at both ends with rhodanine terminal group (2-(3-ethyl-4-oxothiazolidin-2-ylidene) malononitrile) as shown in Fig. 1. The four-donor type A-D-A molecules considered in this paper are DRCN5T, D5T2F-P, D5T2F-S, and D5T2F-T. In addition, we have also calculated the HOMO and LUMO energies of an acceptor A-D-A molecule of IDIC-4F also presented in Fig. 1. Three of the donor molecules; D5T2F-P, D5T2F-S, and D5T2F-T are fluorinated derivatives of DRCN5T. The acceptor molecule of IDIC-4F is a tetra-fluorinated derivative of 2,2 0-[(4,4,9,9-tetrahexyl-4,9-dihydro-s-indaceno[1,2-b:5,6-b0]dithiophene-2,7-diyl)bis[methylidyne(3-oxo-1H-indene-2,1(3H)-diylidene)]]bis[propanedinitrile] (IDIC) [14,15].

In our calculation, the ground state geometries of the studied molecules are optimized in chlorobenzene using DFT implemented in ORCA Program Version 4.2.1 [16]. The optimization was achieved by the implementation of the solvation continuum model by using chlorobenzene with a dielectric constant of 5.69. The electron exchange and correlation energy EXC has been approximated using Becke-3-Lee-Yang-Parr (B3LYP) [17,18], and Perdew–Burke–Ernzerhof (PBE0) hybrid functionals [19]. The electronic wave functions of all atoms in both methods were represented using the split valence polarization with diffuse functions (def2-SVP) basis sets. The basis set superposition error (BSSE) correction has been applied through Grimme’s gCP method [20]. The dispersion correction is performed using Grimme’s D3 version with the BJ damping function during the geometry optimisation process [21]. The calculation speed and better convergence criteria have been achieved by replacing the long alkyl side chains with ethyl groups. This approximation does not affect the accuracy of the results since the electronic wave functions of LUMO and HOMO are mostly located on the molecular backbone and not on the chains. The alkyl side chains mostly influence the molecular packing, which is not the focus of the current study. Even though the long alkyl side chains were truncated to enhance the computational efficiency, the correction was still implemented. This is because the four donors are structurally similar and only differ in the positional substitution of the fluorine atoms and hence minimal errors may be expected. Such minimal errors are also get corrected by using Grimme’s D3 version and accurate results are obtained. The vibrational frequencies of the optimised structures have also been calculated to ensure that the stationary point thus obtained for the optimised geometry represents a true energy minimum and not a saddle point. The chemcraft molecular visualization tool is employed for the qualitative analysis of the electrostatic potential maps of the molecules and to also visualize the HOMO and LUMO molecular structures.

Using the above two, B3LYP and PBE0, DFT functionals, the calculated energies of HOMO and LUMO of the above five molecules are listed in Table 1 along with their experimental values. The molecular orbital geometries of the five molecules corresponding to HOMO and LUMO are also shown Fig. 3. As it can be seen from Table 1, the agreement between the calculated and experimental result is poor. Such a discrepancy between the calculated and experimental results have also been found earlier [22]. Moreover, similar discrepancies between experimental and calculated orbital energies have also been reported on conjugated polymers [23,24]. Such discrepancies have been minimised by correlating the calculated data with the experimental ones [24]. The HOMO and LUMO energies obtained from the experiments are plotted as a function of the corresponding DFT calculated ones for all the five molecules and shown in Figs. 4 and 5, respectively. Using then the least square method, a linear best fit is obtained for each HOMO and LUMO energies as shown by the dotted straight line. The best fit equations thus obtained from B3LYP and PBE0 for the HOMO and LUMO energies are:

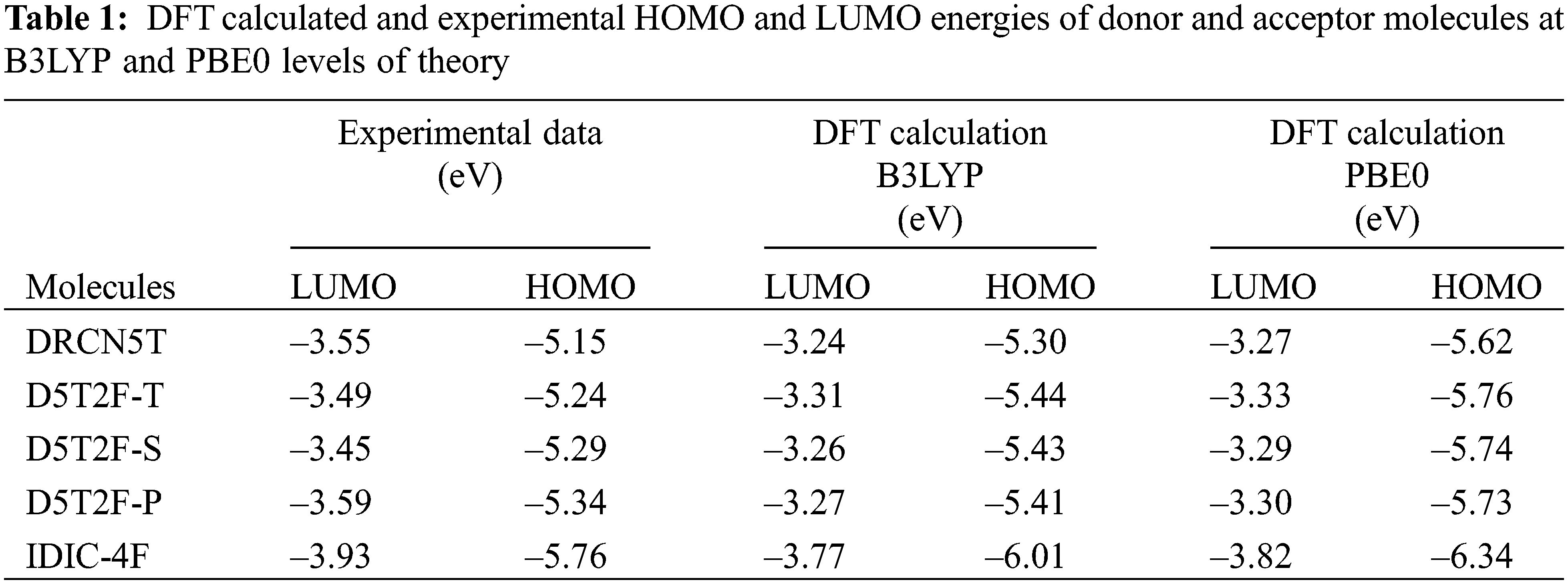
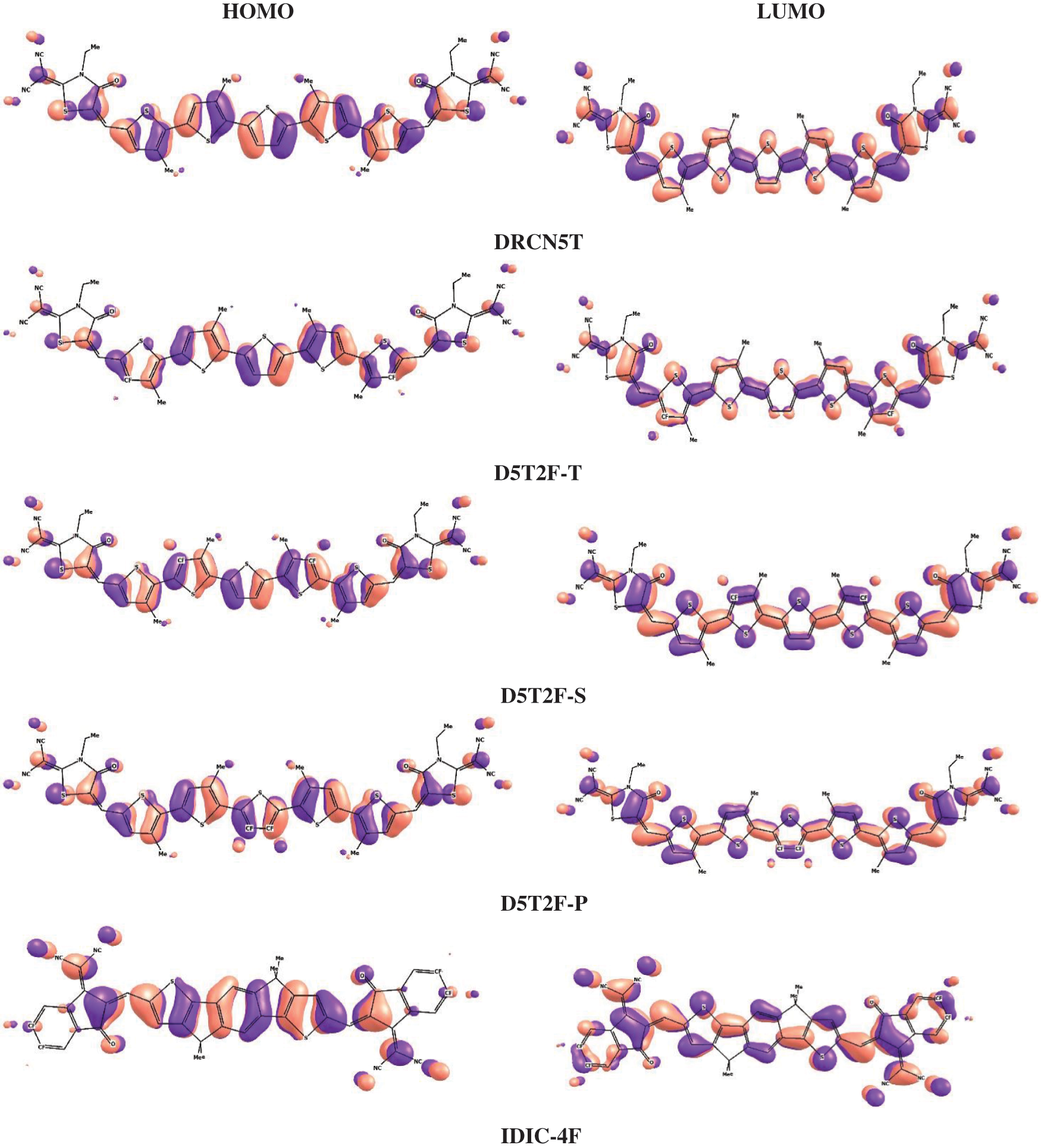
Figure 3: Countour plots of HOMO and LUMO energies of the studied molecules obtained by PBE0

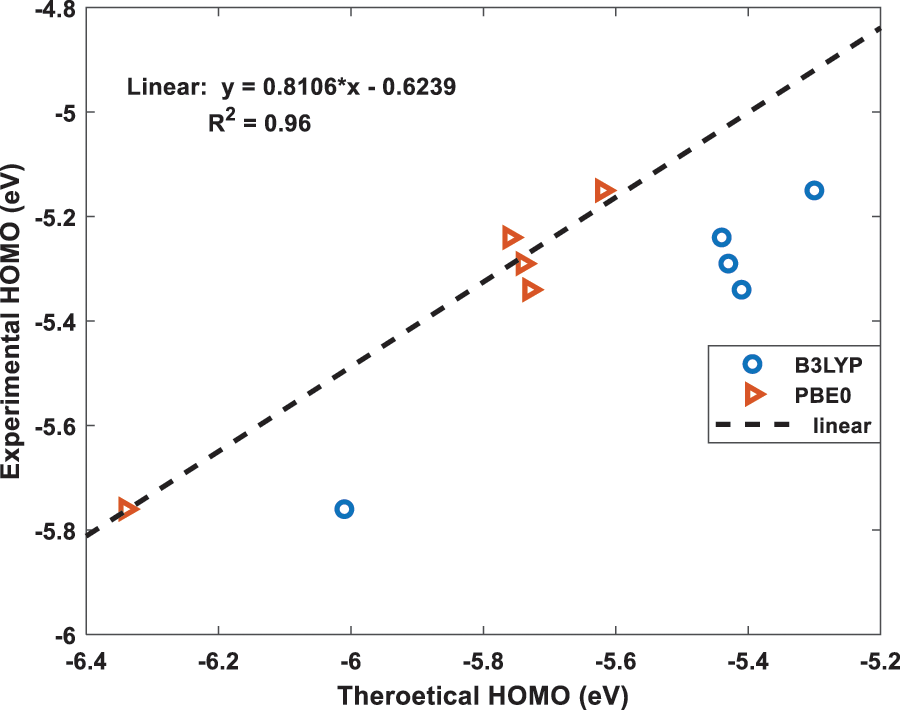
Figure 4: The best fit linear equation obtained from the experimental and calculated HOMO energies for B3LYP and PBE0 functionals. The dotted straight-line fit is only shown for PBE0 results

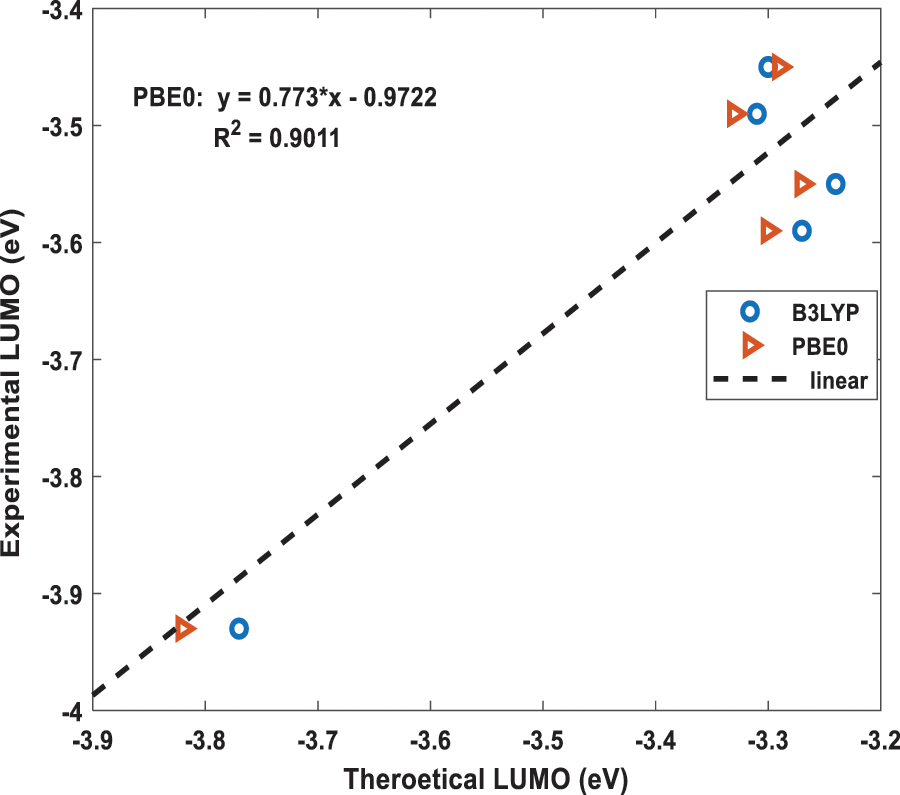
Figure 5: The best fit linear equation obtained from the experimental and calculated LUMO energies for B3LYP and PBE0 functionals. The dotted straight-line fit is only shown for PBE0 results

where the Efit(PBE0)HOMO and Efit(B3LYP)HOMO are the fitted HOMO energies and Efit(PBE0)LUMO and Efit(B3LYP)LUMO are the fitted LUMO energies obtained using PBE0 and B3LYP functionals, respectively. The energies EPBEOHOMO , EB3LYPHOMO , EPBEOLUMO and EB3LYPLUMO appearing on the right-hand sides of Eqs. (1)–(4) are the calculated HOMO and LUMO energies obtained from PBE0 and B3LYP functionals. The correlation function R2 as shown in Figs. 4 and 5 for the PBE0 functional is very close to unity representing a good correlation between the experimental and fitted energies. Using the HOMO-LUMO orbital energies obtained from the correlation results as presented in Table 2, chemical potential (μ), chemical hardness (η) and electronegativity (χ), of donor and acceptor molecules are calculated as [25]:

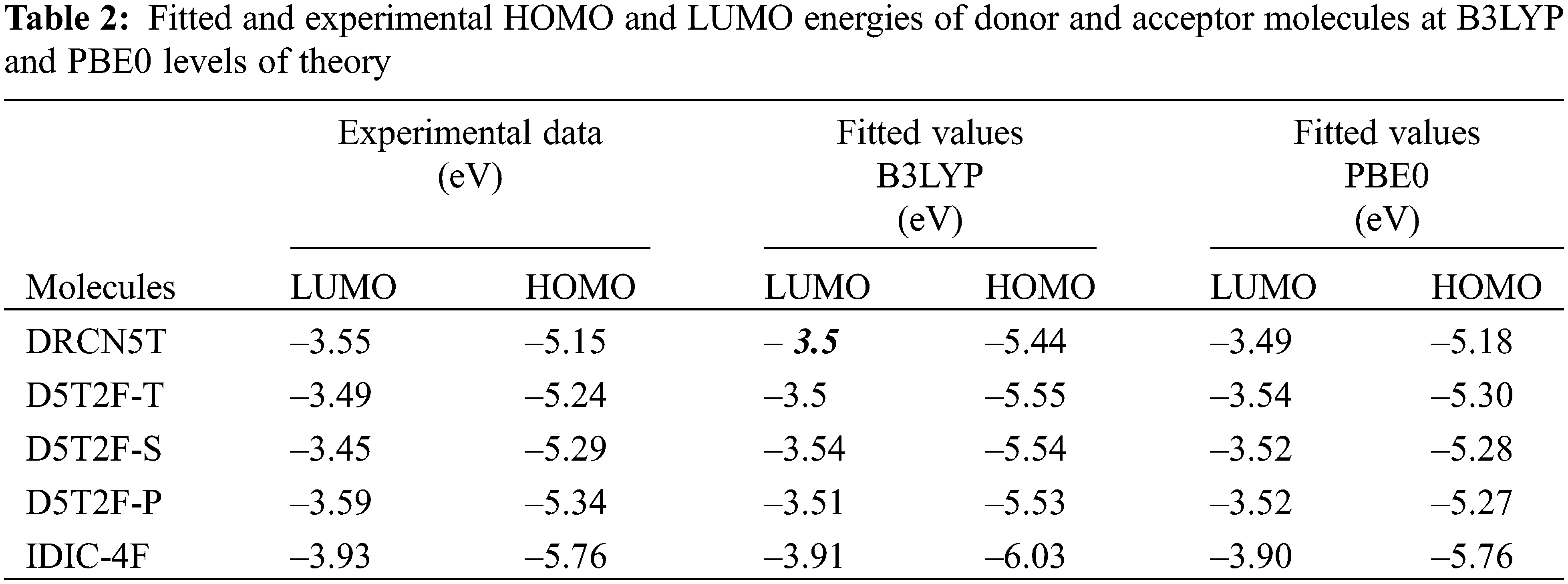
The calculated μ, η and χ = –μ from Eqs. (5) and (6) for all five molecules are listed in Table 3.

The effect of fluorine substitution on the charge transport properties of the molecules is investigated by computing the internal electron and hole reorganization energies, λe and λh , respectively, as [26]:

λe=(Eneutralgeometryanion−Eneutralgeometryneutral)+(Eaniongeometryneutral−Eaniongeometryanion) (7)

λh=(Eneutralgeometrycation−Eneutralgeometryneutral)+(Ecationgeometryneutral−Ecationgeometrycation) (8)

The hole extraction potential (HEP), electron extraction potential (EEP) [27] and the donor-acceptor energy offset ΔE [28] are then calculated as:

where Eneutralgeometryanion/cation is the energy of the anion/cation calculated using the optimized neutral geometry, Eaniongeometry/cationgeometryanion/cation is the energy of the cation calculated at the optimized geometries of the anion and cations, respectively, and Eaniongeometry/cationgeometryneutral is the energy of the neutral molecule calculated using the optimized anion and cation geometries. The results obtained for the HEP, EEP, (ΔE), λh and λh are listed in Table 4.

The Voc of the blended donor acceptor system has also been calculated using the model proposed by Scharber et al. [29]:

where q is the electronic charge, EfitLUMO(A) is the fitted energy of the LUMO of acceptor and EfitHOMO(D) is the fitted energy of HOMO of donor obtained from Eqs. (1)–(4). The calculated values of Voc from Eq. (12) for all four donors blended with the acceptor are given in Table 3 along with the corresponding experimental results for comparison. The calculated Voc is also used to estimate PCE using the Scharber model [29] for all the four donor-acceptor blends. The Scharber model has been applied to estimate the PCE of each blend by calculating Voc , and Jsc using the HOMO and LUMO energies given in Table 3. The fill factor (FF) is assumed to be 65% as and Jsc is determined as a fraction usually, 65% of the photocurrent ( Jph ) [30].

In addition, using TD-DFT and the solvation continuum model with chlorobenzene as the solvent medium, the optical properties are also simulated at the CAM-B3LYP level of theory. The electronic transitions, oscillator strengths (f) and light harvesting efficiency ( LHE=1−10−f ) are calculated using results obtained from the TD-DFT simulations.

Finally, the electrostatic potential maps (EPMs) of the studied molecules have been simulated at the PBE0/def2-SVP level of theory and plotted in Fig. 4. Molecular electrostatic potential maps illustrate the three-dimensional charge distributions within the molecule thus indicating the charged regions of the molecule and how the molecules interact with one another [31]. Using a colour scale, regions of high and low electrostatic potentials are shown within the studied molecules. Regions of low potentials (negative) represented in blue indicate the abundance of electrons and high potential regions (positive) represented by red show relative absence of electrons. The zero potential regions are represented by green colour. It has been observed that the introduction of fluorine onto the donor pentathiophene unit of the acceptor molecule results in a change of polarity of the distributed charges in the molecule due to the high electronegativity of the fluorine (F) atom. Understanding of the electrostatic potential maps can be very useful for the design of A-D-A molecules as organic photo absorbers in OSCs.

DFT calculations of the HOMO and LUMO energies are carried out using two different hybrid density functionals, B3LYP and PBE0. Using the calculated energies and corresponding experimental energies the best fits are obtained and listed in Table 3, which shows that both the methods produce fitted LUMO and HOMO energies in better agreement with the experimental results [21] for all the five molecules. The fitted LUMO and HOMO energies given in Table 3 show that introducing the fluorine in different locations of the intrinsic molecule of DRCN5T to form D5T2F-T, D5T2F-S and D5T2F-P derivatives, alters both the HOMO and LUMO energy levels. The energy level diagram of all four donors and one acceptor is shown in Fig. 2. According to Fig. 2, the change in the energy levels obtained due to the fluorine substitution is only small, a deeper HOMO level may increase the open circuit voltage. Likewise, the LUMO energies of the fluorinated derivatives become higher than that of the intrinsic DRCN5T, which enhances the band gap and hence enhances the absorption and Jsc . Thus, by fluorinating DRCN5T in different locations one may be able to achieve a higher Voc and Jsc and hence higher PCE in an OSC It may be noted that the doping concentration is not altered here and only the location of doping is different in the three different derivatives of DRCNT. It may be interesting to study the effect of changing the doping concentration in each derivative on the HOMO and LUMO energies, which we may study in future work. Shown in Fig. 3, are the molecular orbital (MO) contributions to the HOMO and LUMO energies of. MOs shown for the four donor materials are apparently similar, which is expected due to the structurally similarity in their structure.

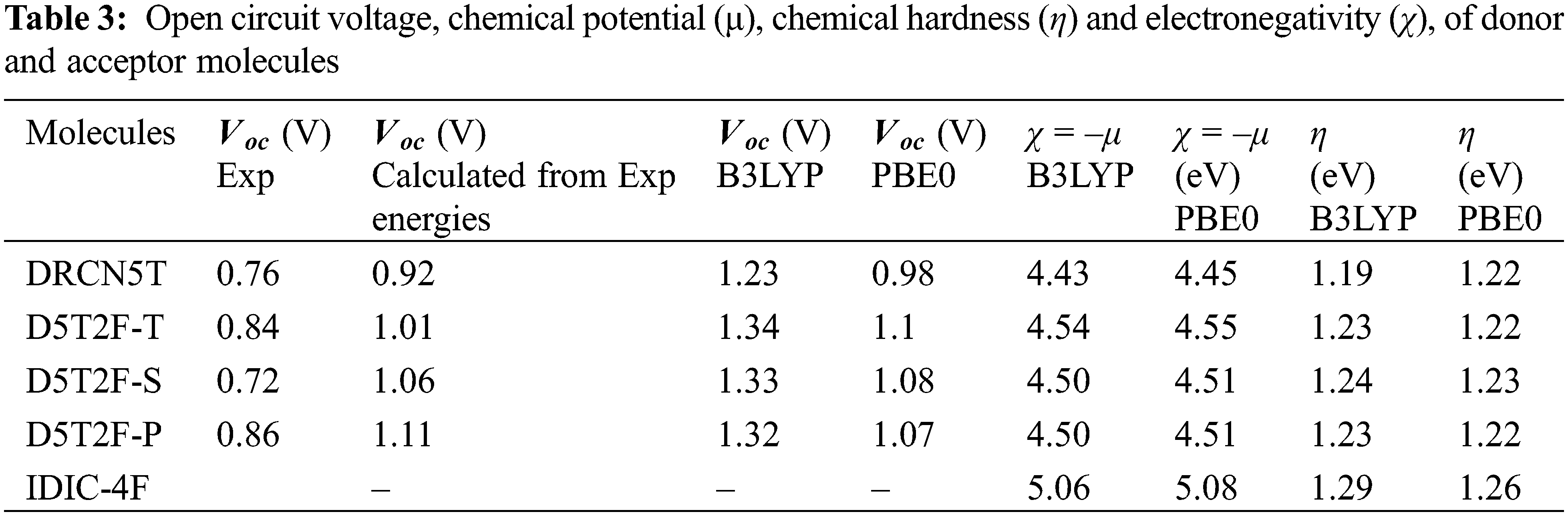
The quantum-chemical parameters μ, η and χ of the four donors and acceptor molecules are calculated from Eqs. (5) and (6), using the fitted energies listed in Table 2, and their values are listed in Table 3. According to Table 3, IDIC-4F has the smallest chemical potential (−5.06 eV), which means it can easily accept an electron transferred from the other four molecules; DRCN5T, D5T2F-T D5T2F-S and D5T2F-P [32]. In addition, the chemical hardness η of IDIC-4F molecule is the highest compared to the other four molecules, which implies that this molecule is less likely to liberate an electron in comparison with the other four molecules and hence becomes an acceptor. Likewise, the electronegativity χ = 5.06 eV of IDIC-4F is highest and hence it can easily accept electrons from the other four molecules. Such a comparative analysis of μ, η and χ is very useful and conclusively proves that IDIC-4F is an acceptor and other four molecules are donors.

The internal electron and hole reorganization energies, λe and λh , are calculated together with their hole and electron extraction potentials, HEP and EEP, are listed in Table 4. Reorganization energies λe and λh , affect the rate of charge transfer [33], and it is expected that the molecules with small reorganization energy possess high charge carrier mobility. According to Table 4, it is found that the reorganization energy λe of the three fluorine substituted donors, D5T2F-P, D5T2F-S and D5T2F-T is substantially reduced from its value in the donor DRCN5T without any fluorine. In addition, it is also found that λe and λh are nearly equal in all the five materials as given in Table 4, which implies that both the electrons and holes will have nearly similar mobility and hence better for solar cells. According to Table 4, all five materials have r EEP lower than HEP. However, the acceptor IDIC-4F has slightly higher values of EEP and HEP. The donor-acceptor offset energy ΔE in Table 4, ranges from 0.38 to 0.41 eV, which is higher than the required minimum of 0.3 eV [34] for exciton dissociation in OSCs and hence better for the efficient exciton dissociation at the D-A interface [35].

The Voc of the four different donors blended with the IDIC-4F acceptor is listed in Table 3 agrees with the experimental values [22] reasonably well. Except for the D5T2F-S derivative based OSC with a measured Voc of 0.72 V, the Voc measured for the OSCs having the fluorinated derivatives are slightly higher than that obtained for the non-fluorinated DRCNFT system. The observed increase in Voc , for the fluorinated systems is a direct consequence of the effect of the fluorine atom on the energy levels of the donor molecules [34]. The calculated values of Voc are larger than the measured ones. There is better agreement between the Voc calculated using the experimental energies and the energies predicted by the PBE0 density functional than that predicted by the B3LP functional. The low values of Vocs of the real devices can be related to the disorder induced gap tail states in organic semiconductors which serve as a favourable trap site for photogenerated carriers [13,36]. The distribution of photogenerated carriers in such gap tail states downshifts the electron quasi-Fermi level and upshifts the hole quasi-Fermi level, thereby reducing the Voc in the fabricated device. Moreover, factors such as density of states or energetic disorder, charge transfer states, D-A interface, microstructure, carrier density have all been known to influence the Voc of the fabricated OSC [37].

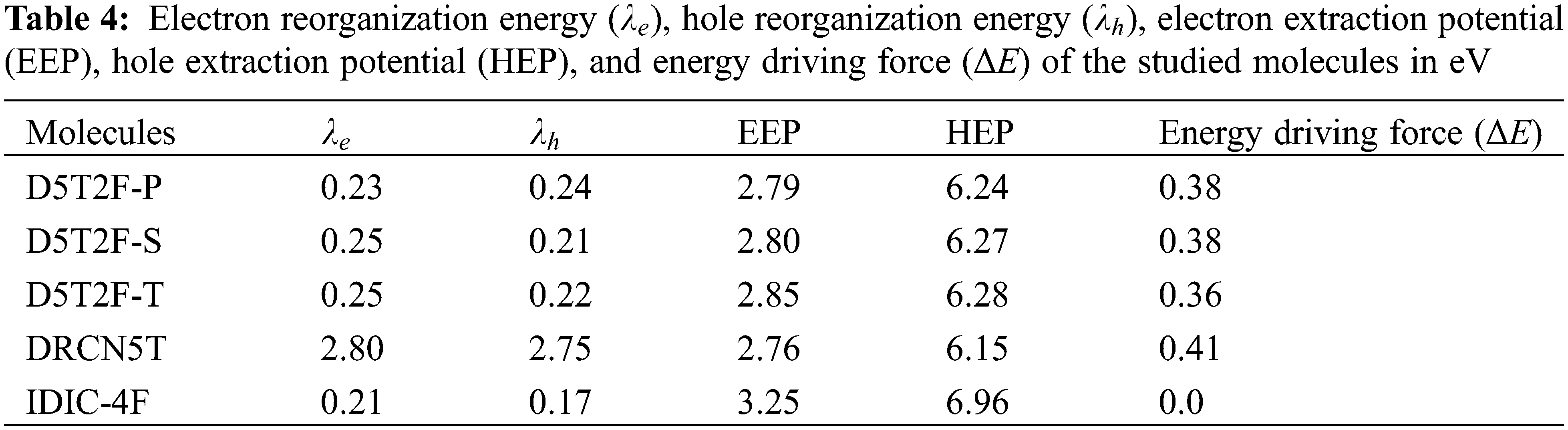
The calculated optical absorption spectra obtained by TD-DFT/CAM-B3LYP/def2-SVP are plotted together with the solar AM1.5 spectrum as shown in Fig. 6. The absorption spectra of all five molecules are peaked around 531–543 nm. The fluorinated donors have a blue shifted spectrum relative to the nonfluorinated DRCN5T molecule. The simulated absorption profiles of the donor molecules agree with the experimental results [22]. However, the simulated absorption spectrum of the acceptor molecule with peak maximum at 543 nm does not quite agree with the experimental absorption maximum found at 730 nm [32]. This discrepancy may be attributed to the use of CAM B3LYP functional in our simulation. The excited state properties of the molecules such us the electron transitions, corresponding wavelengths, excitation energies and oscillation strengths (f) as well as their assignments are listed in Table 5. The orbital transitions shown in Table 5 represent the first excited state excitation of each molecule with contributions from HOMO-LUMO orbitals. The oscillator strengths of the transitions are stronger for the fluorinated donors and acceptor molecules compared with the donor without fluorine substitution. The light harvesting efficiency calculated from the oscillator strength is nearly 100% for all the molecules.

Figure 6: Simulated absorption spectra in the donors DRCN5T, D5T2F-P, D5T2F-S, DFT2F-T and acceptor IDIC-4F plotted as a function of the wavelength along with and the solar irradiance at AM1.5 to show that absorption occurs at the peak of solar radiation

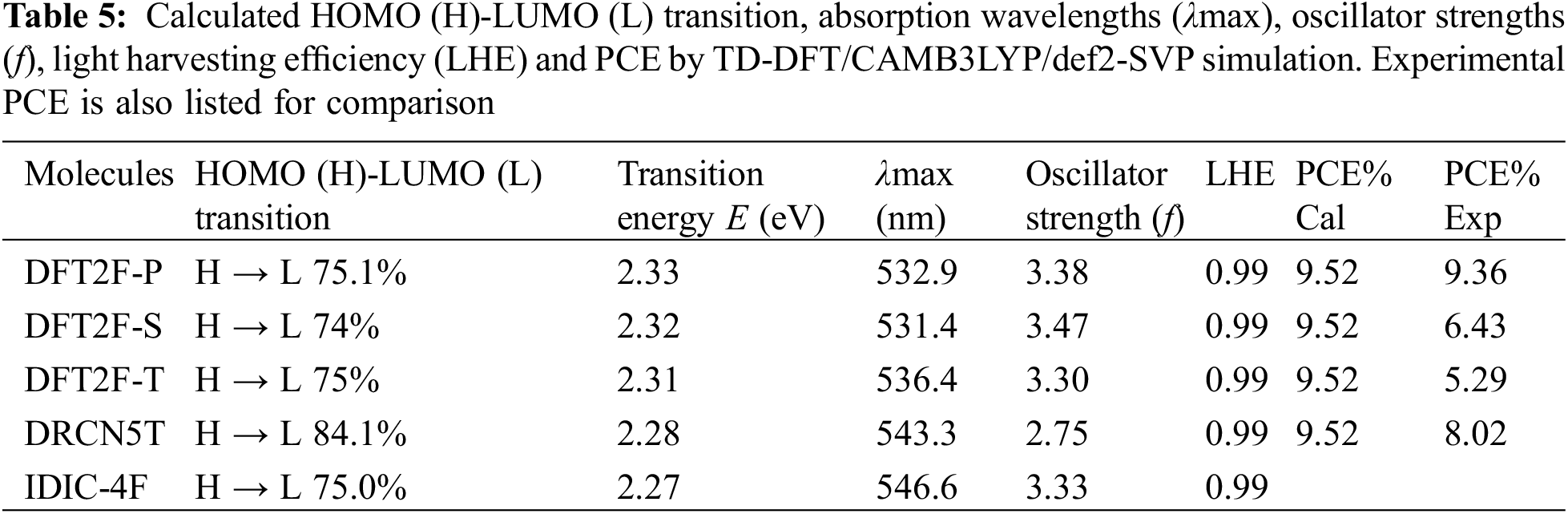
The PCE obtained for the DFT2F-P-IDIC-4F blend is consistent with that obtained from experiment [22] thus validating the accuracy of the Scharber model in predicting the PCE of OSCs. For the DFT2F-S and DFT2F-T, the PCEs obtained do not agree with the experimental results, this is because according to the experiment, the FF obtained from the OSCs fabricated using these donors are 56% and 54%, respectively. If these values are used in our simulation, then we get the PCEs in agreement with experimental values. Considering the DRCN5T-IDIC-4F system, the discrepancy between experiment and the calculated PCE can be explained as resulting from the large reorganization energies associated with both molecules as listed in Table 5.

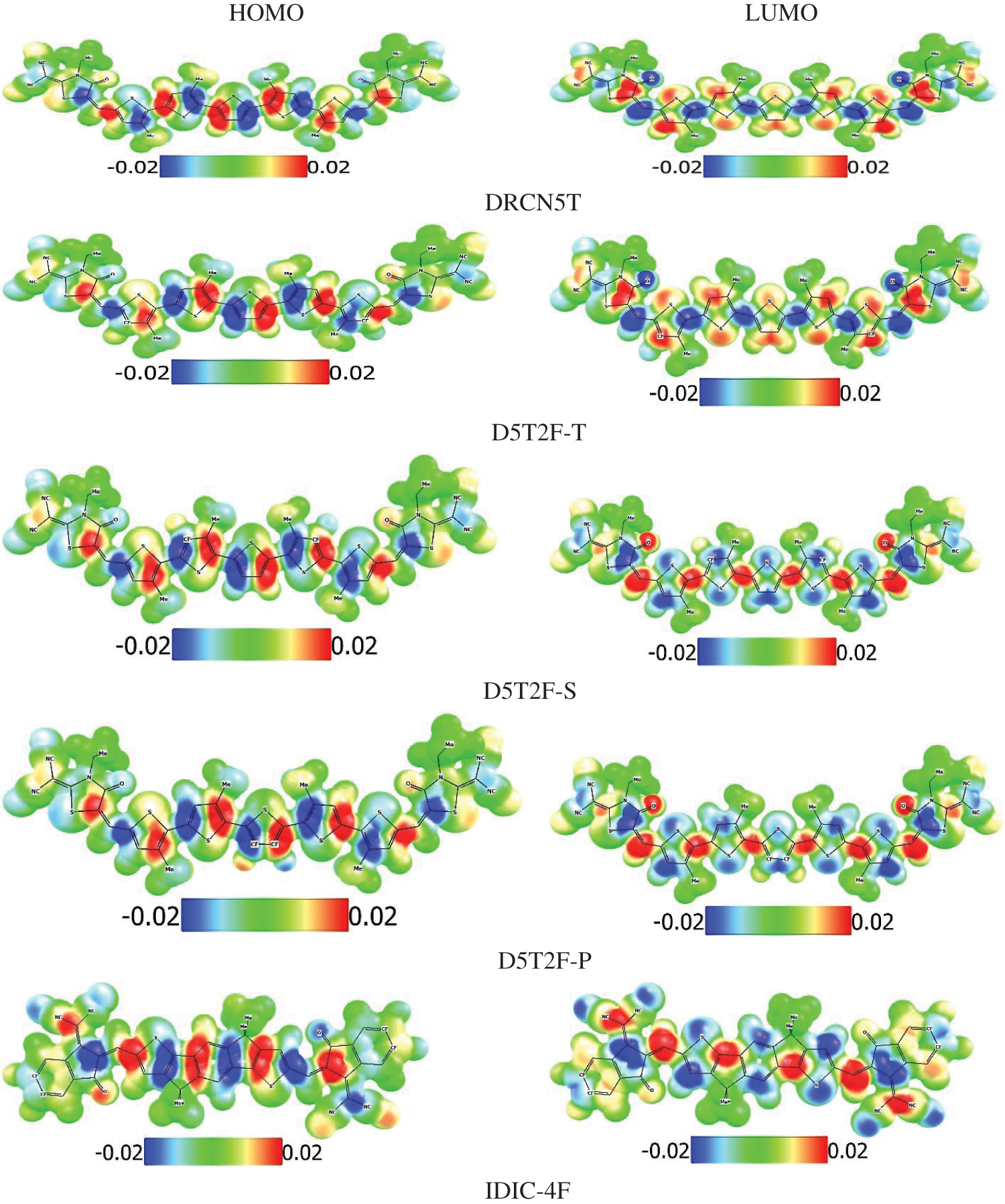
Figure 7: EPMs of the HOMO and LUMO energies of the studied molecules at the PBE0 level of theory showing electron rich (blue) and electron poor (red) regions within the molecule

Plotted EPMs in Fig. 7, enable identification of reactive regions of the molecule susceptible to electrophilic and nucleophilic attacks and the hydrogen bonding interactions [38]. The negative and positive potentials are distributed in an alternate fashion localised mostly on the double bonds. Hence these regions in the molecules are places where any chemical functionalisation can be targeted. The presence of a well-defined and alternating negative and positive potentials in a molecule indicates a region which can be used for an A-D-A design [39]. Comparing the distribution of the potentials in the fluorinated derivatives of the donor molecules shown in Fig. 7 with the non-fluorinated molecule, the ordering of the potentials in the fluorinated derivates is opposite to that observed in the parent structure. This is a direct consequence of the introduction of the highly electronegative F atoms on the donor thiophene unit hence influences the potential distribution within the molecule. This strategy can be useful in the design of molecules with the desired optoelectronic properties.

We have performed DFT calculations on pentathiophene based four donor molecules of DRCN5T, D5T2F-T, D5T2F-S, D5T2F-P and one IDIC-4F acceptor molecule using two different hybrid functionals, B3LYP and PBE0 and we have used the CAM-B3LYP functional in for the TD-DFT simulations. To achieve a better agreement between the experimental and calculated HOMO and LUMO energies, we have correlated the calculated and experimental energies to get the best fit. The calculated energies thus obtained have better agreements with the experimental results. The quantum chemical parameters, μ, η and χ calculated for all the molecules indicate that IDIC-4F is a suitable acceptor material for the donor materials. It is found that the fluorine substitution lowers the hole and electron reorganisation energies of the molecules and enhances mobilities of charges. HOMO and LUMO energies of the donors get modified due to the introduction of fluorine into the molecular structure. The Voc is calculated using the HOMO and LUMO energies for the four donors blended with the acceptor IDIC-4F. It is found that the calculated PCE of the DFT2F-P-IDIC-4F blend agrees well with the experiment results. The discrepancies observed in the DFT2F-S-IDIC-4F and DFT2F-T-IDIC-4F are because of the low FF obtained in the experiment. Also, the discrepancy between DRCN5T-IDIC-4F is because of the large reorganization energies associated with the transport of charges in the IDIC-4F acceptor. The calculated electrostatic potential maps (EPMs) show different charge distribution regions in all five molecules.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. Gurney, R. S., Lidzey, D. G., Wang, T. (2019). A review of non-fullerene polymer solar cells: From device physics to morphology control. Reports on Progress in Physics, 82(3), 036601. DOI 10.1088/1361-6633/ab0530. [Google Scholar] [CrossRef]

2. Ma, L., Yu, Z., Ma, W., Qing, S., Wu, J. (2018). Assessment and study on the impact on environment by multi-crystalline silicon preparation by metallurgical route. Silicon, 11(3), 1383–1391. DOI 10.1007/s12633-018-9937-6. [Google Scholar] [CrossRef]

3. Powell, D. M., Winkler, M. T., Choi, H. J., Simmons, C. B., Needleman, D. B. et al. (2012). Crystalline silicon photovoltaics: A cost analysis framework for determining technology pathways to reach baseload electricity costs. Energy & Environmental Science, 5(3), 5874–5883. DOI 10.1039/c2ee03489a. [Google Scholar] [CrossRef]

4. Yu, J. S., Zheng, Y. F., Huang, J. (2014). Towards high performance organic photovoltaic cells: A review of recent development in organic photovoltaics. Polymers, 6(9), 2473–2509. DOI 10.3390/polym6092473. [Google Scholar] [CrossRef]

5. Yeh, N., Yeh, P. (2013). Organic solar cells: Their developments and potentials. Renewable and Sustainable Energy Reviews, 21(1), 421–431. DOI 10.1016/j.rser.2012.12.046. [Google Scholar] [CrossRef]

6. Rafique, S., Abdullah, S. M., Sulaiman, K., Iwamoto, M. (2018). Fundamentals of bulk heterojunction organic solar cells: An overview of stability/degradation issues and strategies for improvement. Renewable & Sustainable Energy Reviews, 84, 43–53. DOI 10.1016/j.rser.2017.12.008. [Google Scholar] [CrossRef]

7. Singh, J., Narayan, M., Ompong, O., Zhu, F. (2017). Dissociation of charge transfer excitons at the donor-acceptor interface in bulk heterojunction organic solar cells. Journal of Materials Science: Materials in Electronics, 28(10), 7095–7099. DOI 10.1007/s10854-017-6443-3. [Google Scholar] [CrossRef]

8. Hughes, M. P., Rosenthal, K. D., Ran, N. A., Seifrid, M., Bazan, G. C. et al. (2018). Determining the dielectric constants of organic photovoltaic materials using impedance spectroscopy. Advanced Functional Materials, 28(32), 1801542. DOI 10.1002/adfm.201801542. [Google Scholar] [CrossRef]

9. Scharber, M. C., Sariciftci, N. S. (2021). Low band gap conjugated semiconducting polymers. Advanced Materials Technologies, 6(4), 2000857. DOI 10.1002/admt.202000857. [Google Scholar] [CrossRef]

10. Duan, C., Huang, F., Cao, Y. (2012). Recent development of push-pull conjugated polymers for bulk-heterojunction photovoltaics: Rational design and fine tailoring of molecular structures. Journal of Materials Chemistry, 22(21), 10416–10434. DOI 10.1039/c2jm30470h. [Google Scholar] [CrossRef]

11. Mainville, M., Ambrose, R., Fillion, D., Hill, I. G., Leclerc, M. et al. (2021). Theoretical insights into optoelectronic properties of non-fullerene acceptors for the design of organic photovoltaics. ACS Applied Energy Materials, 4(10), 11090–11100. DOI 10.1021/acsaem.1c01994. [Google Scholar] [CrossRef]

12. Narayan, M. R., Singh, J. (2013). Study of the mechanism and rate of exciton dissociation at the donor-acceptor interface in bulk-heterojunction organic solar cells. Journal of Applied Physics, 114(7), 073510. DOI 10.1063/1.4818813. [Google Scholar] [CrossRef]

13. Elumalai, N. K., Uddin, A. (2016). Open circuit voltage of organic solar cells: An in-depth review. Energy & Environmental Science, 9(2), 391–410. DOI 10.1039/C5EE02871J. [Google Scholar] [CrossRef]

14. Kan, B., Kan, Y., Zuo, L., Shi, X., Gao, K. (2021). Recent progress on all-small molecule organic solar cells using small-molecule nonfullerene acceptors. InfoMat, 3(2), 175–200. DOI 10.1002/inf2.12163. [Google Scholar] [CrossRef]

15. Andrea, M., Kordos, K., Lidorikis, E., Papageorgiou, D. G. (2022). Molecular description of charge transport in the IDIC non-fullerene acceptor for organic solar cells. Computational Materials Science, 202, 110978. DOI 10.1016/j.commatsci.2021.110978. [Google Scholar] [CrossRef]

16. Neese, F. (2011). The ORCA program system. WIREs Computational Molecular Science, 2(1), 73–78. DOI 10.1002/wcms.81. [Google Scholar] [CrossRef]

17. Kim, K., Jordan, K. D. (1994). Comparison of density functional and MP2 calculations on the water monomer and dimer. Journal of Physical Chemistry, 98(40), 10089–10094. DOI 10.1021/j100091a024. [Google Scholar] [CrossRef]

18. Stephens, P. J., Devlin, F. J., Chabalowski, C. F., Frisch, M. J. (1994). Ab initio calculation of vibrational absorption and circular dichroism spectra using density functional force fields. Journal of Physical Chemistry, 98(45), 11623–11627. DOI 10.1021/j100096a001. [Google Scholar] [CrossRef]

19. Perdew, J. P., Ernzerhof, M., Burke, K. (1996). Rationale for mixing exact exchange with density functional approximations. Journal of Chemical Physics, 105(22), 9982–9985. DOI 10.1063/1.472933. [Google Scholar] [CrossRef]

20. Neese, F. (2012). The ORCA program system. WIREs Computational Molecular Science, 2(1), 73–78. DOI 10.1002/wcms.81. [Google Scholar] [CrossRef]

21. Kruse, H., Grimme, S. (2012). A geometrical correction for the inter- and intra-molecular basis set superposition error in Hartree-Fock and density functional theory calculations for large systems. Journal of Chemical Physics, 136(15), 154101. DOI 10.1063/1.3700154. [Google Scholar] [CrossRef]

22. Duan, T., Gao, J., Babics, M., Kan, Z., Zhong, C. et al. (2020). Difluorinated oligothiophenes for high-efficiency all-small-molecule organic solar cells: Positional isomeric effect of fluorine substitution on performance variations. Solar RRL, 4(31900472. DOI 10.1002/solr.202070031. [Google Scholar] [CrossRef]

23. Blouin, N., Michaud, A., Leclerc, M. (2007). A low-bandgap poly(2,7-carbazole) derivative for use in high-performance solar cells. Advanced Materials, 19(17), 2295–2300. DOI 10.1002/(ISSN)1521-4095. [Google Scholar] [CrossRef]

24. Beaupré, S., Belletête, M., Durocher, G., Leclerc, M. (2011). Rational design of poly(2,7-carbazole) derivatives for photovoltaic applications. Macromolecular Theory and Simulations, 20(1), 13–18. DOI 10.1002/mats.201000061. [Google Scholar] [CrossRef]

25. Zhan, C. G., Nichols, J. A., Dixon, D. A. (2003). Ionization potential, electron affinity, electronegativity, hardness, and electron excitation energy: Molecular properties from density functional theory orbital energies. Journal of Physical Chemistry A, 107(20), 4184–4195. DOI 10.1021/jp0225774. [Google Scholar] [CrossRef]

26. Oliveira, E. F., Lavarda, F. C. (2016). Reorganization energy for hole and electron transfer of poly(3-hexylthiophene) derivatives. Polymer, 99, 105–111. DOI 10.1016/j.polymer.2016.07.003. [Google Scholar] [CrossRef]

27. Reeta Felscia, U., Rajkumar, B. J. M., Mary, M. B. (2018). Charge transport properties of pyrene and its derivatives: Optoelectronic and nonlinear optical applications. Journal of Materials Science, 53(21), 15213–15225. DOI 10.1007/s10853-018-2690-9. [Google Scholar] [CrossRef]

28. Benatto, L., Sousa, K. R. D. A., Koehler, M. (2020). Driving force for exciton dissociation in organic solar cells: The influence of donor and acceptor relative orientation. Journal of Physical Chemistry C, 124(25), 13580–13591. DOI 10.1021/acs.jpcc.0c03116. [Google Scholar] [CrossRef]

29. Scharber, M. C., Mühlbacher, D., Koppe, M., Denk, P., Waldauf, C. et al. (2006). Design rules for donors in bulk-heterojunction solar cells—Towards 10% energy-conversion efficiency. Advanced Materials, 18(6), 789–794. DOI 10.1002/adma.200501717. [Google Scholar] [CrossRef]

30. Alharbi, F. H., Rashkeev, S. N., El-Mellouhi, F., Lüthi, H. P., Tabet, N. et al. (2015). An efficient descriptor model for designing materials for solar cells. NPJ Computational Materials, 1(1), 1–9. DOI 10.1038/npjcompumats.2015.3. [Google Scholar] [CrossRef]

31. Bheema Lingam, C., Tewari, S. P. (2013). Theoretical studies on aminoborane oligomers. Computational and Theoretical Chemistry, 1020, 151–156. DOI 10.1016/j.comptc.2013.07.046. [Google Scholar] [CrossRef]

32. Tang, H., Yan, C., Karuthedath, S., Yin, H., Gao, Y. et al. (2020). Deciphering the role of fluorination: Morphological manipulation prompts charge separation and reduces carrier recombination in all-small-molecule photovoltaics. Solar RRL, 4(4), 1900528. DOI 10.1002/solr.201900528. [Google Scholar] [CrossRef]

33. Willems, R. E. M., Meskers, S. C. J., Wienk, M. M., Janssen, R. A. J. (2019). Effect of charge-transfer state energy on charge generation efficiency via singlet fission in pentacene-fullerene solar cells. Journal of Physical Chemistry C, 123(16), 10253–10261. DOI 10.1021/acs.jpcc.9b00568. [Google Scholar] [CrossRef]

34. Verstappen, P., Kesters, J., Vanormelingen, W., Heintges, G. H. L., Drijkoningen, J. et al. (2015). Fluorination as an effective tool to increase the open-circuit voltage and charge carrier mobility of organic solar cells based on poly(cyclopenta[2,1-b: 3,4-b]dithiophene-alt-quinoxaline) copolymers. Journal of Materials Chemistry A, 3(6), 2960–2970. DOI 10.1039/C4TA06054G. [Google Scholar] [CrossRef]

35. Bhattacharya, L., Sahu, S. (2019). Theoretical investigation on cyano-substituted isoindigo based copolymer for organic photovoltaics. AIP Conference Proceedings, vol. 2115, no. 1, pp. 030549. AIP Publishing LLC. DOI 10.1063/1.5113388. [Google Scholar] [CrossRef]

36. Yang, J. P., Bussolotti, F., Kera, S., Ueno, N. (2017). Origin and role of gap states in organic semiconductor studied by UPS: As the nature of organic molecular crystals. Journal of Physics D: Applied Physics, 50(42), 423002. DOI 10.1088/1361-6463/aa840f. [Google Scholar] [CrossRef]

37. Qi, B., Wang, J. (2012). Open-circuit voltage in organic solar cells. Journal of Materials Chemistry, 22(46), 24315–24325. DOI 10.1039/c2jm33719c. [Google Scholar] [CrossRef]

38. Hachi, M., Slimi, A., Fitri, A., ElKhattabi, A., Touimi Benjelloun, A. et al. (2019). New small organic molecules based on thieno[2,3-b]indole for efficient bulk heterojunction organic solar cells: A computational study. Molecular Physics, 118(81–14. DOI 10.1080/00268976.2019.1662956. [Google Scholar] [CrossRef]

39. Mun, J., Ochiai, Y., Wang, W., Yu Zheng, Y., Zheng, Y. Q. et al. (2021). A design strategy for high mobility stretchable polymer semiconductors. Nature Communications, 12(1), 1–10. DOI 10.1038/s41467-021-23798-2. [Google Scholar] [CrossRef]