Journal of Renewable Materials

DOI: 10.32604/jrm.2022.016260

ARTICLE

Intratree Variation in Viscoelastic Properties of Cell Walls of Masson Pine (Pinus Massoniana Lamb)

Shaoxiang Cai1, Yuliang Guo1 and Yanjun Li2,*

1College of Textile, Garment and Design, Changshu Institute of Technology, Suzhou, 215500, China
2College of Materials Science and Engineering, Nanjing Forestry University, Nanjing, 210037, China
*Corresponding Author: Yanjun Li. Email: lalyj@126.com
Received: 21 February 2021; Accepted: 07 May 2021

1  Introduction

Masson pine (Pinus massoniana Lamb.) is an important resource widely distributed in China’s southern provinces [1]. The Masson pine plantation wood is an important raw material for construction, polymer composites, and pulp and paper due to the beautiful grain pattern, suitable for planting in temperate and tropical climates, and the period of growing into useful timber is short [2,3]. Studying the mechanical properties of wood fibers is of great significance for pulping and papermaking. In the past few decades, scientists have done extensive research on the intratree variations in wood mechanical properties. Besides, wood physical properties have been expanded from density and tracheid morphology to anatomical parameters, microfibril angle (MFA), chemical composition, and micromechanical properties. Researchers have investigated the macroscopic mechanical properties and the anatomical variations in the wood. Compared with Pinus sylvestris, the dry density of Masson pine wood was 0.48–0.53, which was higher than that of Pinus sylvestris; And its relative cellulose content is larger, cell wall microfibril angle is smaller; The average elastic modulus and hardness of Masson pine wood cell wall are larger [4–6]. Growth in genetically improved trees under intensive management is so rapid that rotations of conttonwood and loblolly pine may be as short as 20 to 30 years. At that age, the trees contain a high proportion of lower quality juvenile wood [7]. The tensile strength of tracheids of Masson pine early wood obtained by the zero-distance tensile test method ranged from 316 to 767 MPa, which gradually increased from the pith core outwards. In the direction of height, the tensile strength gradually increases with the increase of height [6].

However, the variations in the viscoelastic properties of wood cell walls are less known, which hinders the selective utilization of wood fibers of Masson pine. In Masson pine, the differences in juvenile wood, mature wood, earlywood, and latewood are obvious. From 1th to 14th annual ring is juvenile wood, and larger than 14th annual ring is mature wood [6]. In the same annual ring, the dark part growing in autumn and winter is the late wood, and the light part is the early wood. Early wood cell wall is thin, structure is loose, density is small, and late wood cell wall is thick, structure is compact, density is large. Moreover, the anatomical structure of wood varies considerably. All properties improved markedly with age, up to nearly a tenfold increase in modulus of elasticity of one loblolly pine tree from early juvenile wood to late mature wood [7]. Average mechanical properties of juvenile wood ranged from 47% to 63% of those for mature wood in pine and from 62% to 79% in cottonwood. The age of demarcation between juvenile and mature wood varied by species and property, ranging from 13 to 20 years. At age 40, plantation trees sampled were projected to contain approximately 25% juvenile wood [7–9]. These characteristics together lead to differences in the wood cell wall mechanical properties among locations [10,11]. Intraplant variations in longitudinal viscoelasticity of Masson pine’s wood cell walls include radial variation and height variation. The elastic modulus and hardness of the cell wall of Masson pine wood were not uniform along the wall thickness direction, and the elastic modulus of the secondary wall was significantly higher than that of the composite intercellular layer. The elastic modulus and hardness of cell secondary wall of mature wood were 40% and 13% higher than those of Juvenile wood, respectively [6,11,12].

The purpose of this study was to characterize the relationship between the MFA and chemical composition of wood and the longitudinal viscoelastic properties of the cell walls in Masson pine. The mechanical properties of cell walls in different parts of Masson pine are different. Therefore, we explored the main factors affecting the viscoelastic properties. It provides theoretical basis for the segmentation utilization of masson pine and data reference for the artificial cultivation of fine masson pine seedlings. In addition, our findings will provide a theoretical basis for the selective utilization of Masson pine wood fiber.

2  Materials and Methods

2.1 Materials

Wood samples were obtained from three 40-year-old Masson pine harvested from a forest plantation located in Fujian Province, China, The geographical location is longitude 118° 85′ and latitude 27° 37′. In the first set, Wood blocks of size 10 mm × 5  mm × 5 mm (longitudinal × tangential × radial) were cut from the stem at 1, 3, 6 and 9 m height and from 6th, 8th, 10th, 14th, 16th, 18th, 20th, 24th, 30th, and 35th annual ring of the three trees. Twenty samples were made for each ring segment of each height. A small wood sample with a four prism at one end was made by a slicer/slide grater (A-1170Wien, Austria) and polished first with a glass knife and then using a diamond knife(Micro Star Tech Inc.,Huntsville, AL, USA). The sample surface was smooth with a roughness of less than 10 nm (Rz) and reflected light as a mirror. For the second set, wood blocks of size 10 mm × 10 mm × 1 mm (longitudinal × tangential × radial) were cut from the same heights and the same annual rings. The initial moisture content of dry wood was about 11%. Wood blocks were also collected, powdered, and used to measure the chemical composition after complete drying in an oven.

2.2 Microfibril Angle (MFA) Measurement

Twenty wood samples with the dimensions 10 mm × 10 mm × 1 mm (longitudinal × tangential × radial) were cut from the annual rings of the wood. As shown in Fig. 1 the MFA in the wood cell wall was measured by X-ray diffraction (XRD) to evaluate the changes of MFA at different heights. The XRD instrument (Ultima IV Rigaku, Japan) was operated at 50 kV and 25 mA and had a CCD camera. The diffraction pattern was obtained by shining the X-ray beam for 15 s [13]. The MFA was calculated following the 0.6 T method by Cave [14]. In the experiment, 15 samples were needed for each group.

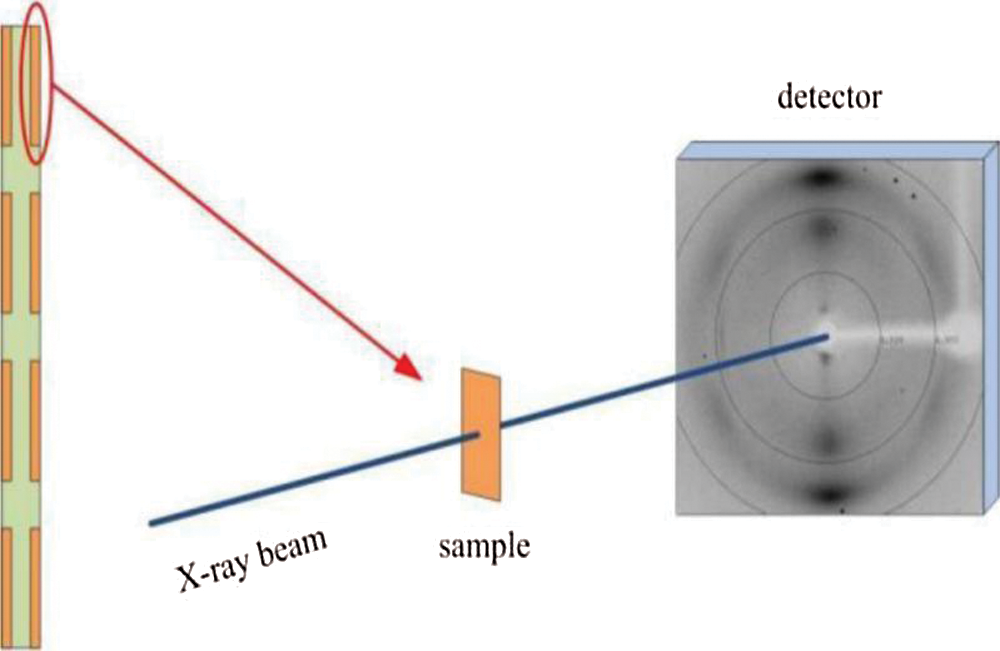
Figure 1: Sampling plan and measurement device for micro filament angle

2.3 Chemical Composition Analysis

First, wood samples of size 10 mm × 5 mm × 5 mm (longitudinal × tangential × radial) were cut from the stem at 1, 3, 6 and 9 m height, respectively. Second, wood samples of juvenile and mature woods at 3 m. Third, wood samples of earlywood and latewood parts of (10th annual ring) at 3 m. Fourth, wood samples of earlywood and latewood parts of mature wood (30th annual ring) at 3 m. The wood samples were ground in a mill to a homogeneous powder to analyze the chemical components. Samples were first ground and screened into flour of sizes between 40 and 60 mesh. Holocellulose was determined according to Wises’s sodium chlorite method, The lignin is removed by chlorination and oxidation, and the amount of residue is determined quantitatively as the holocellulose [15]. Cellulose was measured using the Kurschner-Hoffner’s nitric acid method; The samples were treated with concentrated nitric acid and ethanol solution, the lignin in the samples was nitrated and partially oxidized; At the same time, a large amount of hemicellulose is hydrolyzed and oxidized, leaving cellulose [16]. Lignin was determined following the acid-insoluble Klason lignin method (72% H2SO4; GB/T 2677.8, 1994) [17]. The hemicellulose content was calculated by subtracting the cellulose content from the holocellulose content. The relative amount of each chemical component (X) in the wood was estimated according to the following equation:

X (%)= m x   m o ×100 (1)

where m0 is the initial mass of each sample (g), and mx is the mass of the solvent extractives (i.e., holocellulose, cellulose, and lignin; g).

2.4 Quasi-Static Nanoindentation

Smaller wood samples with the dimensions 10 mm × 5 mm × 5 mm (longitudinal × tangential × radial) were cut from the juvenile wood and mature wood parts. Samples were processed with diamond cutters (Micro Star Tech Inc., Huntsville, AL, USA). The NI technology was tested on a nano-indentation meter (Hysitron Inc., Minneapolis, MN, USA) under a quasi-static loading condition as follows: holding peak load of 250 μN for 5 s and unloading within 5 s. Quasi-static nanoindentation technology was used in the measurement [11]. Five of the same samples are required for each test data. Three cell walls should be selected for each sample for testing, and five test points should be selected for each wood cell wall for nano-indentation test, and then take the average value of each test sample. The theoretical error of this indentation positioning method is 10 nm. After the indentation is finished, the indentation is automatically rescanned in the same area to obtain the actual position of indentation in the sample, which is convenient for us to evaluate the reliability of indentation experiment.Quasi-static loading and unloading at a constant rate, the maximum load is 250 μN, and the load is kept for 5 s at the maximum load to eliminate the effect of creep.The computer will automatically calculate the elastic modulus and hardness of the material. In order to stabilize the moisture content of the sample, the specimens were conditioned at temperature of 24°C and a relative humidity of 65% for 24 h. The reduced elastic modulus (Er) and hardness (H) were calculated from the load-depth curves, according to Oliver and Pharr’s method [18] as follows:

H=PmaxA (2)

where Pmax is the peak load determined at a maximum depth in an indentation cycle, and A is the projected contact area between the indenter and the sample.

Er=π2βSA (3)

where Er is the reduced elastic modulus, S is the slope of the unloading curve in the load-displacement plot, β is the correction factor correlated to indenter geometry (β = 1.034, Berkovich indenter), and A is the projected contact area between the indenter and the sample. S was determined using a linear approximation to the high-load part of the unloading curve.

Viscoelastic materials exhibit both viscous and elastic characteristics. An ideal elastic material with linear properties will work as a spring and completely recover from deformation immediately after stress removal. The stress is described by Hooke’s law as follows:

σ=Eε (4)

where E (GPa) is the elastic modulus in case of materials using NI. σ is the stress, and ε is the strain when deformation is elastic. The elastic deformation process is not due to a pure shear but due to a complex superposition of normal stress and shear [19]. On the other hand, the viscous component is described as a dashpot, which is analogous to energy dissipation. The stress-strain relationship is expressed as follows:

σ=η⋅dεdt=η⋅ε˙ (5)

where η is the viscosity of a material and dε/dt is the time derivative of the strain. The NI displacement rate could be described by the equation:

h˙=dhdt (6)

In which h is the instantaneous indenter penetrating depth, and t is the loading time. In a creep test, the creep compliance J(t) of a material held at constant stress (σ = σ0) is defined as follows:

J(t)=ε(t)σ0 (7)

Indentation creep ratio Ci is defined as the relative change in indentation depth when the applied load remains constant during the holding time [20]:

Ci( (8)

where h2 is the max penetration depth at the end of the holding segment, and h1 is the depth at the end of the loading segment.

2.5 Nano Dynamic Mechanical Analysis (Nano-DMA)

Dynamic modulus mapping was performed on the Triboindenter equipped with a nanoDMA (nano dynamic mechanical analysis) transducer. A sinusoidal force of 6 μN at a frequency of 200 Hz was superimposed on a constant quasi-static force of 12 μN during raster scanning performed over a 15 μm × 15 μm region covering the wood cell walls. Five of the same samples are required for each test. A lock-in amplifier was used to measure the phase of the resulting transducer displacement signal. A modulus map containing the dynamic modulus information was collected at a resolution of 256 × 256 pixels. The storage and loss moduli were computed based on the measured stiffness at each pixel according to the method by Asif et al. [21,22].

3  Results and Discussion

3.1 Microfibril Angle (MFA)

Fig. 2 shows the variation in MFA with tree height and among the growth rings of Masson pine latewood. For each measurement item, ten identical samples were repeated and then averaged. In the range of 1–9 m, the MFA gradually decreased with the increase in tree height and annual ring. The decrease in MFA with annual rings was more evident in the first 6–16° range, and the change was stable. We measured the MFA in the juvenile wood and mature wood parts at 1, 3, 6, and 9 m by the Cave method. Figs. 3a and 3b show that earlywood and latewood in Masson pine, the MFA at the base at 1 m was the largest, and the average value was 38.14°. The MFA decreased with the increase in tree height, and the average MFA at 9 m was 18.62°. The MFA at 1 m base of late mature wood was the largest, and the average value was 21.32°. The average value of MFA at 9 m was 11.22°. The MFA in mature wood was smaller than that in juvenile wood. The average data concerning the MFA are summarized in Figs. 2 and 3, and the deviation of MFA is small. the experimental samples are of high quality and the data meet the requirements, and the test data is accurate. Several studies have shown that the MFA in the annual rings near the young timber of the medullary heart is usually large, and it tends to decrease with the increase in tree age, and then remains relatively stable [23–25].

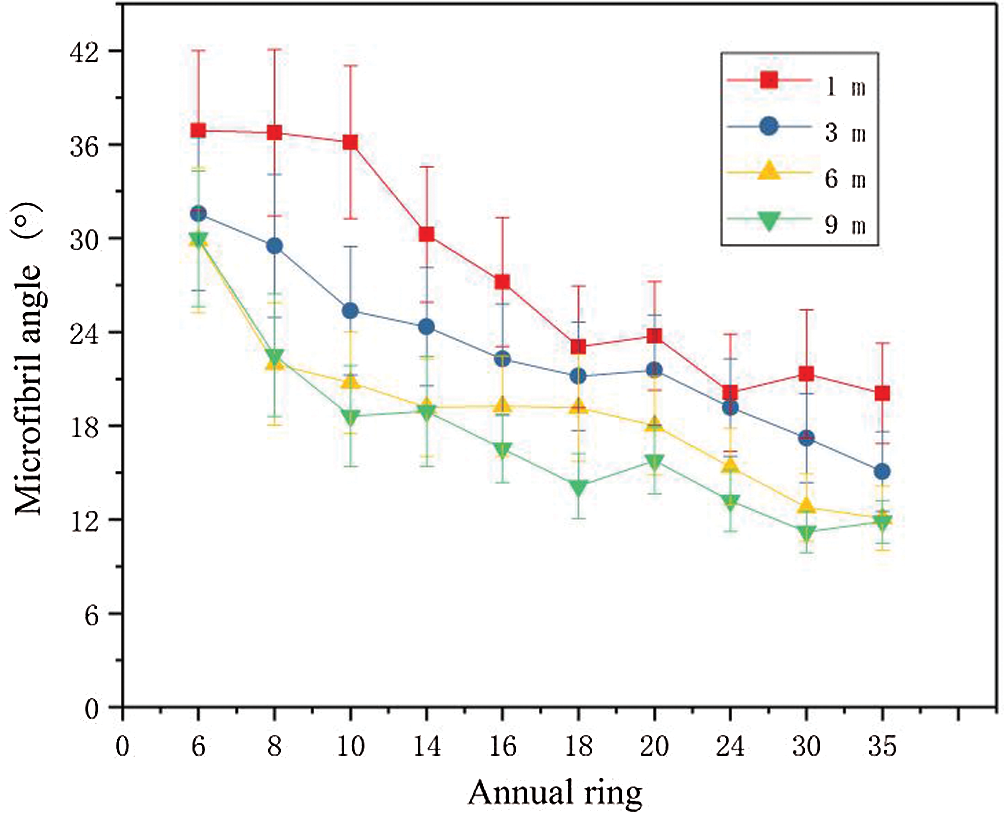
Figure 2: Changes in microfibril angle with tree height and at various growth rings of Masson pine

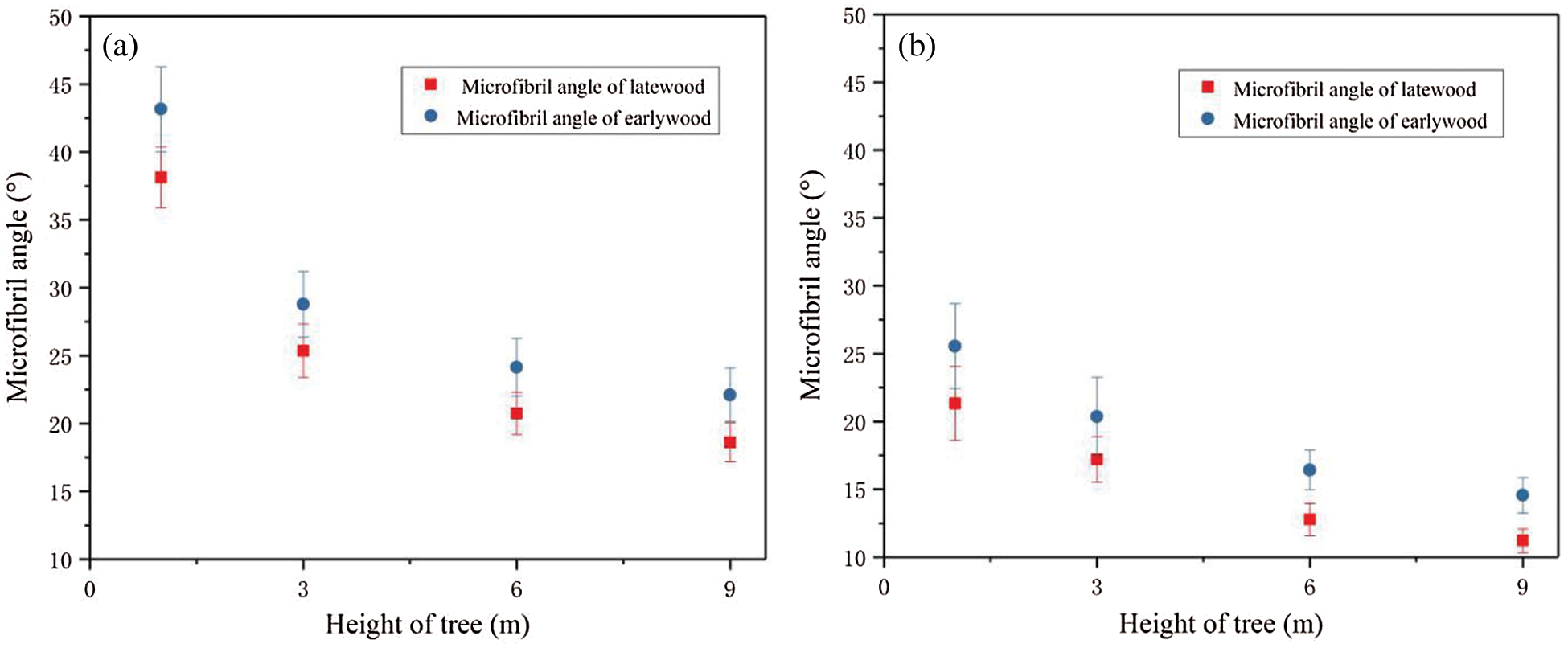
Figure 3: Microfibril angle of earlywood and latewood of juvenile (a) and mature (b) woods of Masson pine at different heights

Barnett [26] proved that at any trunk height, the MFA in Juvenile wood was larger than that in mature wood, and the MFA increased with the growth of annual rings. Similar to the earlier reports, the MFA was stable within a range between 5° and 30° [27–29]. Moreover, the wood MFA decreased with the increase in tree height, with the smallest value at 30%–50% of the tree height. Further, the MFA gradually increased to the crown [30]. We observed a decrease in the MFA of wood with an increase in tree height within the 1–9 m range.

3.2 Chemical Composition

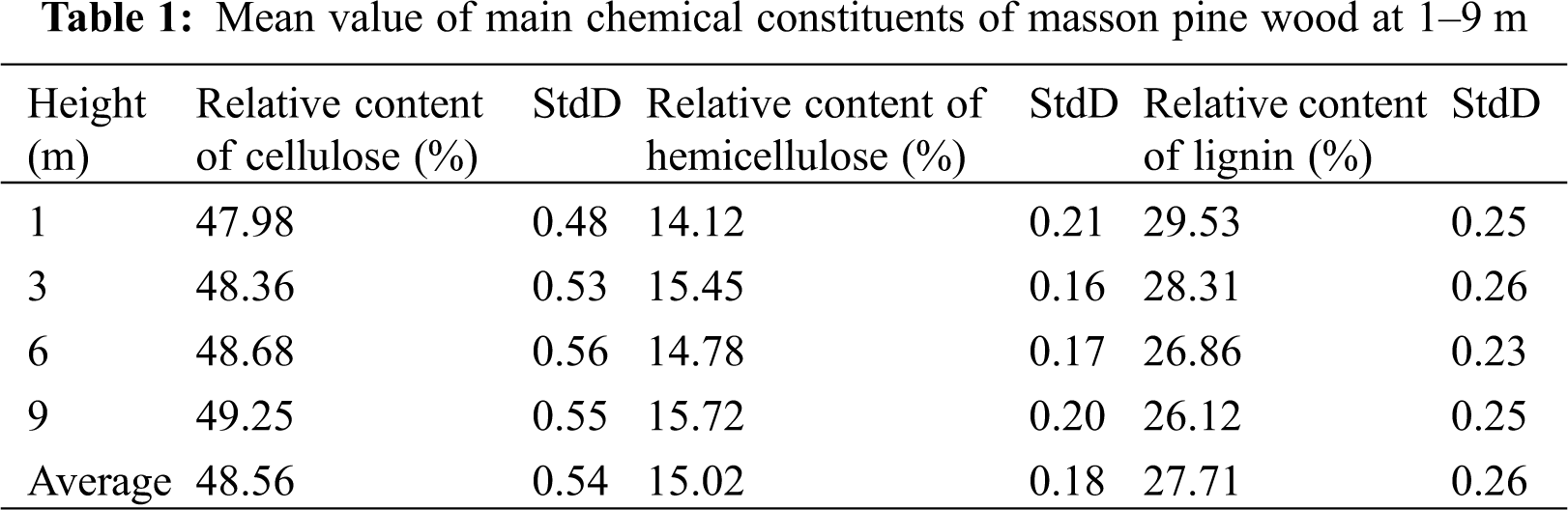
Tab. 1 shows that the cellulose and hemicellulose contents of mature wood (30th annual ring) at 3 m gradually increased with height; however, the amplitude of increase was small. Meanwhile, the lignin content decreased with the increase in height, with a smaller range of variation. This indicates that the chemical composition of mature wood change little with the change of wood height. Therefore, the chemical composition is not the main factor affecting the viscoelasticity of wood cell wall in the height direction. Changes of wood chemical composition in height direction observed in this study are consistent with the previous findings [31–33]. Tab. 2 shows that the chemical constituents of juvenile wood (10th annual ring) and mature wood (30th annual ring) were significantly different between the earlywood and latewood parts. Moreover, the relative contents of cellulose and hemicellulose in the latewood of juvenile wood were lower than that in the latewood of mature wood. In contrast, the relative content of lignin was higher. In the same annual ring, the relative contents of cellulose and hemicellulose in earlywood were lower than those in latewood. As shown by the factor analysis of Standard Deviation (StdD) in Tabs. 1 and 2, the experimental data is accurate and the experimental results meet the expectation. The chemical composition of wood change little with the wood height, the earlywood and latewood parts had a significant influence on the chemical constituents of wood. Studies have demonstrated lower cellulose and hemicellulose contents in earlywood in juvenile wood than that earlywood in mature wood (30th annual ring) [34–36].

3.3 Quasi-static Mechanics of Wood Cell Walls

3.3.1 Cell-Wall modulus and Hardness

Tab. 3 shows that the elastic modulus and hardness of the cell walls of earlywood and latewood in 30th annual ring at 1, 3, 6 and 9 m increased with the increase. The elastic modulus of the cell walls of earlywood and latewood increased by 40.8% and 28.22%, and the hardness increased by 10.7% and 7.13%, with the increase in tree height from 1 m to 9 m, respectively. As shown by the factor analysis of Standard Deviation (StdD) in Tab. 3, the experimental samples are of high quality and the data meet the requirements.The wood height, the earlywood and latewood parts had a significant influence on the elastic modulus and hardness of the wood cell walls. Combined with the change of MFA in height direction is shown in Figs. 3a and 3b which the MFA of wood decrease with an increase in tree height. The variations in elastic modulus and hardness were negatively correlated with the variation in MFA of the wood. Gindl W found that the mechanical properties of spruce wood cell wall were related to MFA [37]. Studies have shown that MFA is one of the most important factors affecting the elastic modulus of wood [38,39].

3.3.2 Creep Behavior of Wood in the Longitudinal Direction

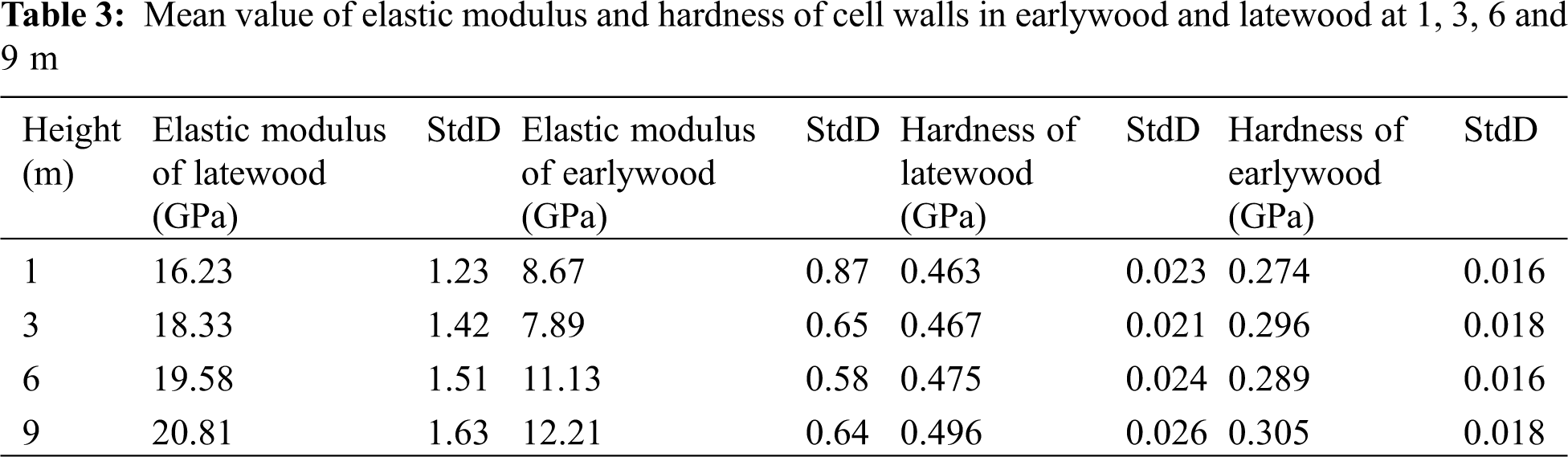
Fig. 4 shows that the creep rate of the cell walls of the latewood in the 30th annual ring decreased gradually with the increase in tree height in the 1–9 m range. The MFA also decreased with the increase in tree height, and the creep rate was positively correlated with the MFA. Page D H,s research also showed that the elastic modulus of the cell walls of wood with the same density varied with the change in MFA of the cell walls [38]. Studies have confirmed that microfibril is the most important factor influencing the mechanical properties of wood cell walls in terms of composite materials [38,39]. Fig. 5 shows that the creep compliance of the wood cell walls in the holding stage decreased ten percent with the increase in height from 1 m to 9 m. which indicates the gradual increase in the resistance of wood cell walls to creep deformation. The variation of creep compliance was related to the MFA of the cell walls. When the MFA decreased, the pressure at the end of microfibrils increased in the experiment, the deformation of wood cells will be affected. Relevant studies have shown a higher anti-deformation ability of the corner ends of microfibril in the cell walls than the lateral ends [38,39]. Therefore, in this study, the cell walls were more resistant to deformation at a lower MFA. When MFA decreased, the cell structure is more compact, the micromechanics of the cell wall increased; When the micromechanical properties of cell wall are enhanced, the macromechanical properties of wood will also be better.

Figure 4: Creep rate of Masson pine wood cell walls at different heights

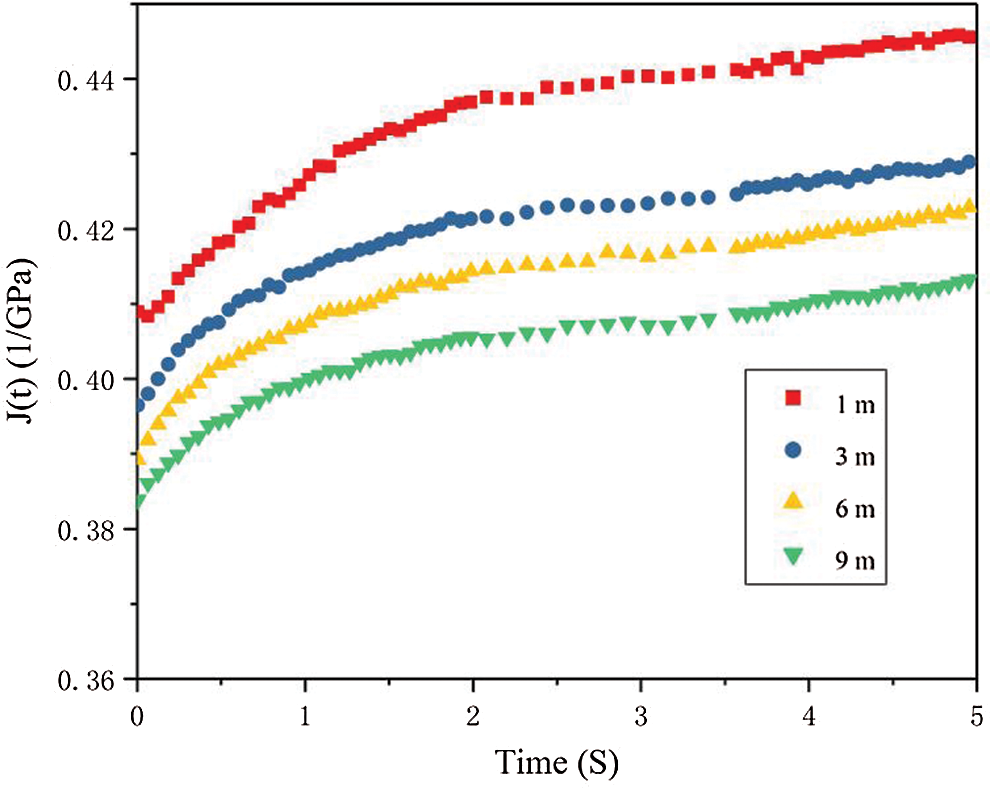
Figure 5: Creep compliance of Masson pine wood cell walls at different heights in the holding stage

3.3.3 Creep Behavior of Wood in the Radial Direction

Figs. 6 and 7 show that the elastic modulus and hardness of the wood cell walls at the same height gradually increased with the increase in annual ring, while the creep rate gradually decreased. Five of the same samples are required for each test data, and then take the average value of each test sample in 6–35th annual ring. In the Fig. 6, we can see the trend of the average value, and the deviation value is small. The elastic modulus of the cell walls in 6–14th annual rings changed a little, and the elastic modulus and hardness were significantly less than those in 16–35th annual rings. As Fig. 2 show that the MFA gradually decreased with the increase in annual ring, the MFA was negatively correlated with the elastic modulus and hardness. The creep rate gradually decreased and the deformation resistance was higher [40]. The higher the cellulose and hemicellulose contents in the wood with more annual rings in mature wood, the better the mechanical properties of the wood cell walls. Figs. 6 and 7 shows that the correlation between the wood cell walls’ mechanical properties and the annual rings observed is consistent with the previous findings [41,42]. The results showed that the static mechanical properties of cell walls were better with increasing annual rings.

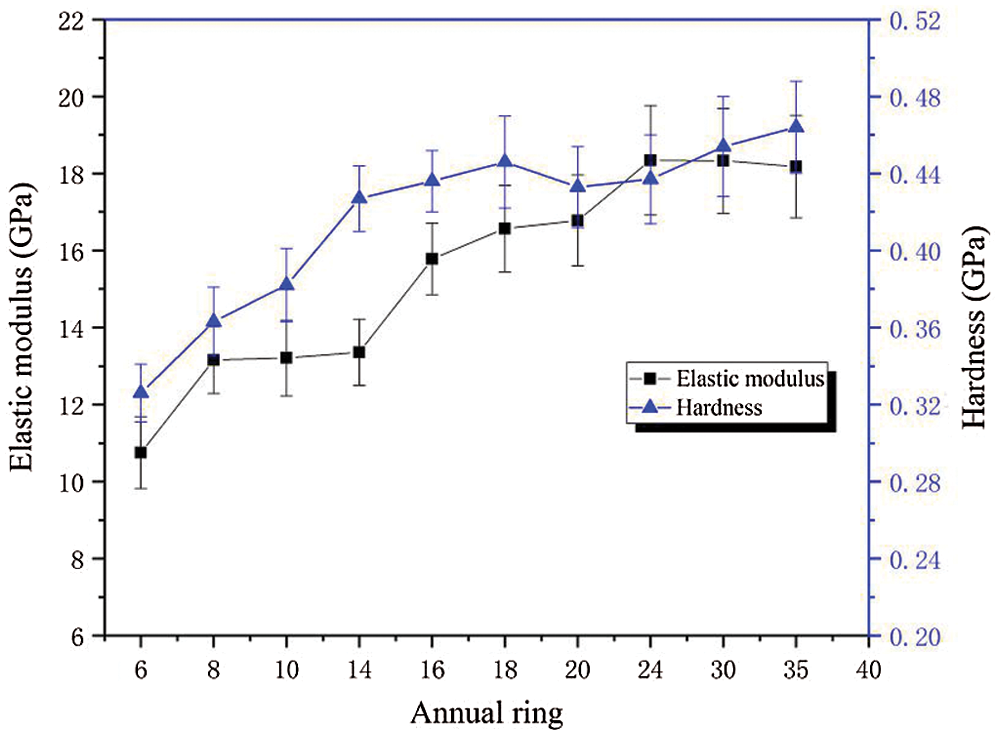
Figure 6: Radial variation in elastic modulus and hardness of Masson pine wood cell walls

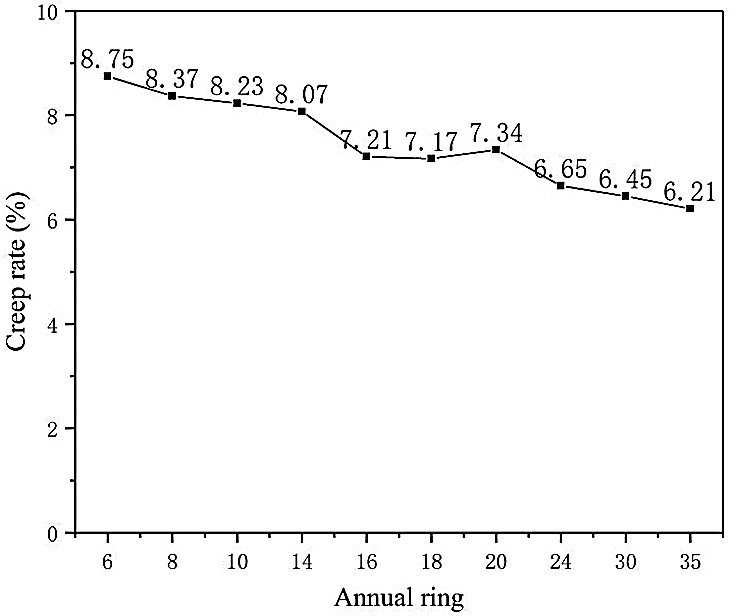
Figure 7: Radial variation in creep rate of Masson pine wood cell walls

3.4 Dynamic Mechanics Properties of Wood Cell Walls

Dynamic modulus mapping was used to test the dynamic viscoelastic properties of the wood. Fig. 8 shows the curve of the probe indentation contact force in a particular area. The average contact force was maintained at 12.02 N. The storage modulus is displayed in color in Fig. 9, and different colors represent the numerical changes. By comparing the colors in the image with the colors in the color bar, the changes in storage modulus and loss modulus were determined. Fig. 10 shows the storage modulus and loss modulus between 0 and 15 μm in the direction along the cell wall thickness. The storage modulus was between 20 and 40 GPa, and the loss modulus was less than 10 GPa.

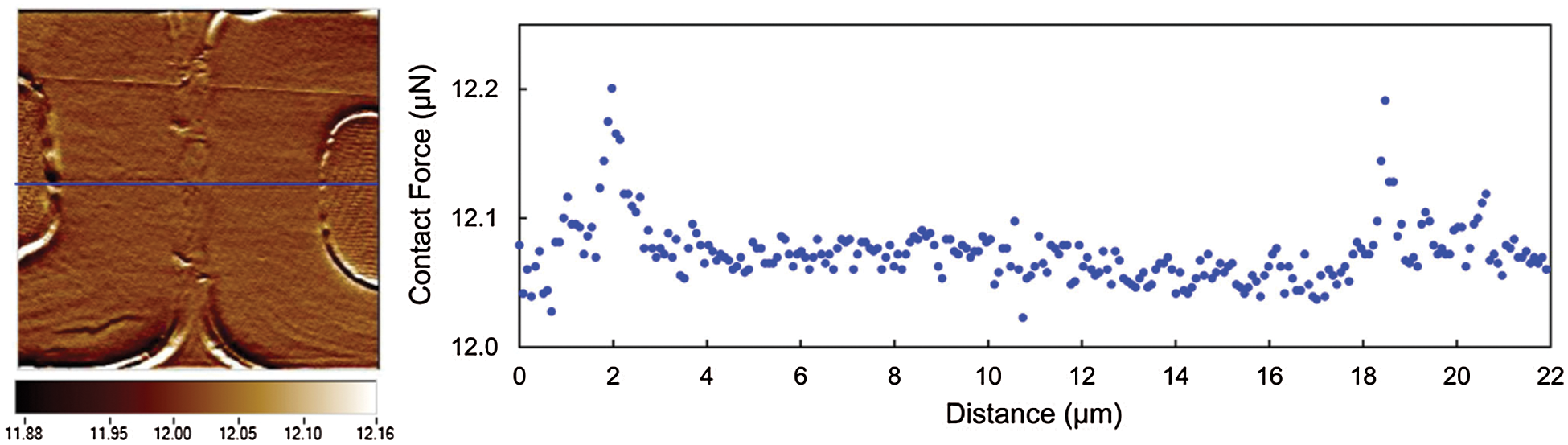
Figure 8: Scanning image and probe contact force size display

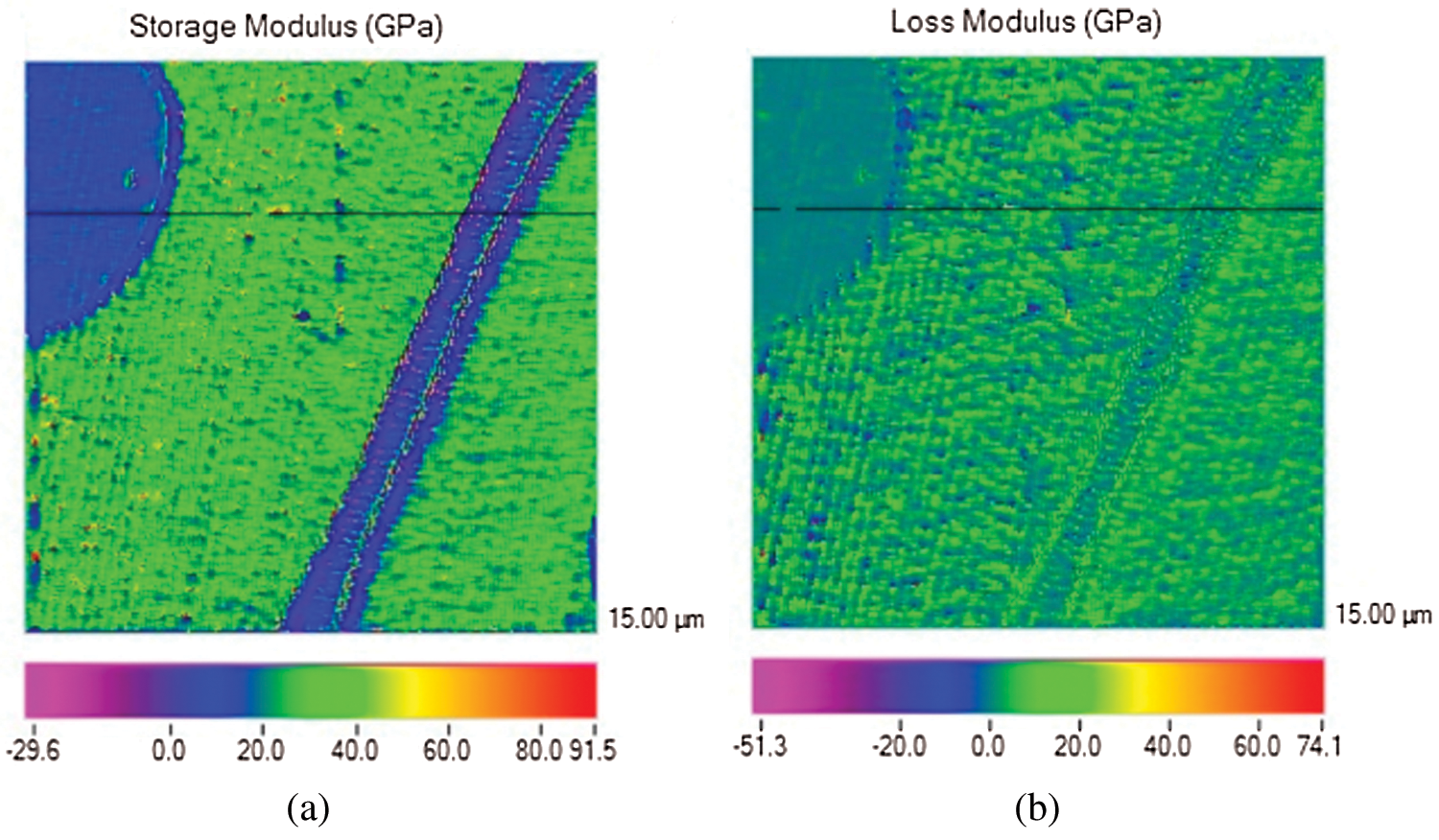
Figure 9: The effect image based on modulus mapping technique: (a) Storage modulus image; (b) Loss modulus image

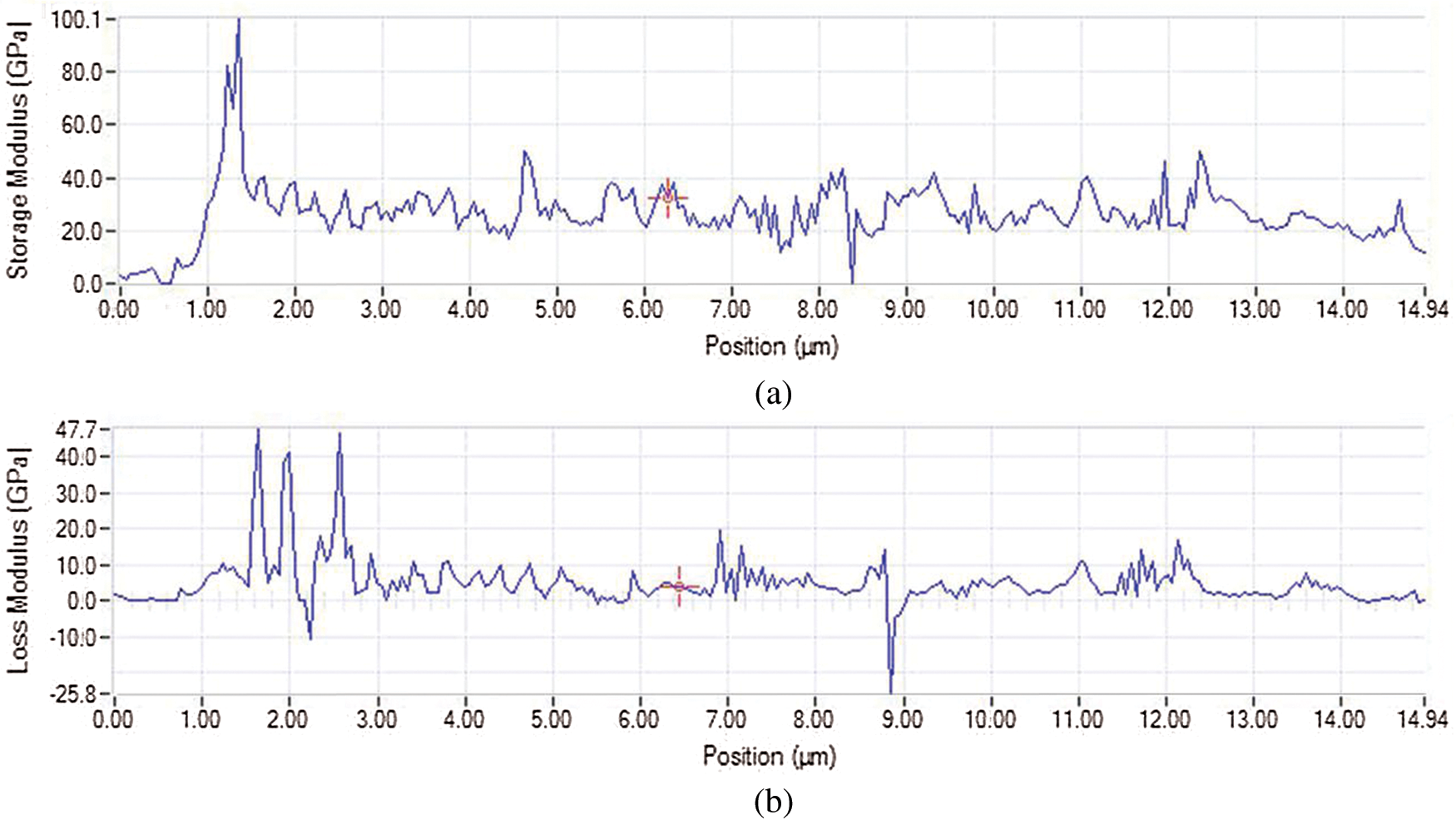
Figure 10: Experimental data curves based on modulus mapping technique: (a) Storage modulus; (b) Loss modulus

Fig. 11 shows the average values of the storage modulus and loss modulus of Masson pine wood cell walls at different heights calculated from the storage modulus and loss modulus data of dynamic modulus mapping. Five of the same samples are required at each height, and then take the average value of each test sample in the 1–9 m range. in Fig. 11, the deviation value is small, and the experimental results are accurate. Further analysis showed that the storage modulus of Masson pine cell walls increased with tree height, while the loss modulus decreased. Combined with MFA analysis, we concluded that the smaller the MFA was, the greater the storage modulus and the smaller the loss modulus were. In the 1–9 m range, the MFA gradually decreased with the increase in height. When the MFA is smaller, the microfibril in the cell wall are more tightly bound and exhibit better mechanical properties, the structure of wood cell wall was more orderly and compact, and the mechanical properties were better [19]. As a result, the storage modulus increases and the loss modulus decreases.

Figure 11: Dynamic viscoelastic properties of wood cell walls at different heights

Thus, the longitudinal stiffness component of the cell increased, and the storage modulus of the wood cell increased in the NI test. Such changes in MFA may affect the timber macro-longitudinal storage modulus [43,44].

Fig. 12 shows that with the increase in annual rings, the storage modulus increased, while the loss modulus decreased at the same wood height. The changing pattern was closely related to the change in MFA. The smaller the MFA was, the greater the storage modulus and the smaller the loss modulus were. Moreover, the MFA at 10th annual ring was larger than that at 30th annual ring. When the MFA is smaller, the microfibril in the cell wall exhibit better mechanical properties. The results of dynamic mechanics properties of this study are consistent with the previous findings [45]. The mechanical properties of wood cell wall were better when the annual ring were increased. As a result, the storage modulus is better and the loss modulus is reduced.

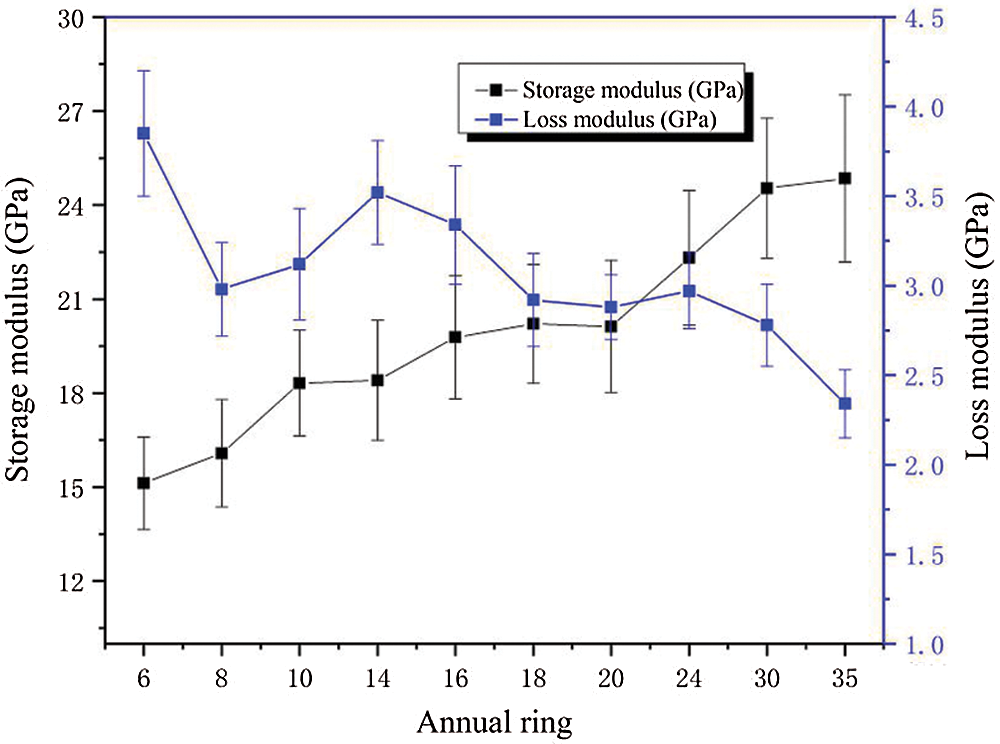
Figure 12: Radial variation trend of dynamic viscoelastic properties of wood cell walls

4  Conclusions

In Masson pine, the MFA of cell walls decreased with tree height in the 1–9 m range. In the radial direction, the MFA decreased with an increase in annual rings. The cell walls’ elastic modulus increased with the increase in height, while the hardness changed little. The creep rate and creep compliance decreased with the increase in height. The cell walls’ storage modulus increased with height, while the loss modulus decreased gradually. Besides, the elastic modulus and hardness increased with the annual rings; the storage modulus increased gradually, while the loss modulus decreased.

Funding Statement: The authors would like to gratefully acknowledge Natural Science Foundation of China (31570552).

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  Gu, H., Wang, J., Ma, L., Shang, Z., Zhang, Q. et al. (2019). Insights into the BRT (Boosted regression trees) method in the study of the climate-growth relationship of masson pine in subtropical China. Forests, 10, 228. DOI 10.3390/f10030228. [Google Scholar] [CrossRef]

 2.  He, Q., Zhan, T., Ju, Z., Zhang, H., Hong, L. et al. (2019). Influence of high voltage electrostatic field (HVEF) on bonding characteristics of masson (Pinus massoniana lamb.) veneer composites. European Journal of Wood and Wood Products, 77, 105–114. DOI 10.1007/s00107-018-1360-6. [Google Scholar] [CrossRef]

 3.  Ge, S., Ma, J., Jiang, S., Liu, Z., Peng, W. et al. (2018). Potential use of dierent kinds of carbon in production of decayed wood plastic composite. Arabian Journal of Chemistry, 11, 838–843. DOI 10.1016/j.arabjc.2017.12.026. [Google Scholar] [CrossRef]

 4.  Zobel, B. J., Buijtenen, J. P. (1989). Wood variation: Its causes and control, pp. 200. Boston: Springer-Ver, Martinus Nijhoff, Dr. W. Junk Publishers. [Google Scholar]

 5.  Yu, Y. (2003). Longitudinal mechanical properties and main influencing factors of tracheids in Chinese fir plantation. Beijing: Chinese Academy of Forestry Sciences. [Google Scholar]

 6.  Zhang, B. (2007). Study on the morphology and micromechanical properties of wood tracheids of masson pine. Beijing: Chinese Academy of Forestry Sciences. [Google Scholar]

 7.  Demartini, J. D., Wyman, C. E. (2011). Changes in composition and sugar release across the annual rings of Populus wood and implications on recalcitrance. Bioresource Technology, 102(2), 23–28. DOI 10.1016/j.biortech.2010.08.123. [Google Scholar] [CrossRef]

 8.  Dahlen, J., Jones, P. D. (2012). Bending strength and stiffness of in-grade Douglas-fir and southern pine No. 224 lumber. Canadian Journal of Forest Research, 42(5), 858–867. DOI 10.1139/x2012-041. [Google Scholar] [CrossRef]

 9.  Panshin, A. J. (1989). Textbook of wood technology, 4th edition NewYork, NY: McGraw-Hill Book Company. [Google Scholar]

10. Gindl, W., Gupta, H. S. (2002). Lignification of spruce tracheids secondary cell wall related to longitudinal hardness and modules of elasticity using nano-indentation. Canadian. Journal of Botany, 80, 1029–1033. DOI 10.1139/B02-091. [Google Scholar] [CrossRef]

11. Gindl, W., Schoberl, T. (2004). The significance of the elastic modules of wood cell wails obtained from nanoindentation measurements. Composites: Part A, 35, 1345–1349. DOI 10.1016/j.compositesa.2004.04.002. [Google Scholar] [CrossRef]

12. Gindl, W., Gupta, H. S., Schoberl, T. (2004). Mechanical properties of spruce wood cell walls by nanoindentation. Applied Physics A, 79, 2069–2073. DOI 10.1007/s00339-004-2864-y. [Google Scholar] [CrossRef]

13. Asif, S. A. S., Wahl, K. J., Colton, R. J. (1999). Nanoindentation and contact stiffness measurement using force modulation with a capacitive load-displacement transducer. Review of Scientific Instruments, 70, 2408–2413. DOI 10.1063/1.1149769. [Google Scholar] [CrossRef]

14. Cave, I. D. (1997). Thtory of X-ray measurement of microfiber angle in wood (Part 1). Wood Science and Technology, 31, 143–152. DOI 10.1007/BF00705881. [Google Scholar] [CrossRef]

15. Shi, J. H., Sheldon, Q., Michael, B. (2014). Kenaf bast fibers. Part I: Hermetical alkali digestion. International Journal of Polymer Science, 9(16), 35–43. DOI 10.1155/2011/212047. [Google Scholar] [CrossRef]

16. Browning, B. L. (1967). Method of wood chemistry, vol. II, New York, USA: Interscience/Wiley. [Google Scholar]

17. GB/T 2667.8 (1994). Fibrous raw material-Determination of acid-insoluble lignin. Standardization Administration of the People’s Republic of China, Beijing. [Google Scholar]

18. Oliver, W. C., Pharr, G. M. (1992). An improved technique for determining hardness and elastic modulus using load and displacement sensing indentation experiments. Journal of Materials Research, 7, 1564–1583. DOI 10.1557/JMR.1992.1564. [Google Scholar] [CrossRef]

19. Kirsten, I. S. (2006). Nanoindentation creep and stress relaxation tests of polycarbonate: Analysis of viscoelastic properties by different rheologicalmodels. International Journal of Materials Research, 97, 1199–1211. DOI 10.3139/146.101357. [Google Scholar] [CrossRef]

20. Konnerth, J., Gindl, W. (2006). Mechanical characterisation of wood-adhesive inter phase cell walls by nanoindentation. Holzforschung, 60, 429–433. DOI 10.1515/HF.2006.067. [Google Scholar] [CrossRef]

21. Asif, S. A. S., Wahl, K. J., Colton, R. J. (1999). Nanoindentation and contact stiness measurement using force modulation with a capacitive load-displacement transducer. Review of Scientific Instruments, 70, 2408–2413. DOI 10.1063/1.1149769. [Google Scholar] [CrossRef]

22. Asif, S. A. S., Wahl, K. J., Colton, R. J., Warren, O. L. (2001). Quantitative imaging of nanoscale mechanical properties using hybrid nanoindentation and force modulation. Journal of Applied Physics, 90, 1192–1200. DOI 10.1063/1.1380218. [Google Scholar] [CrossRef]

23. Fernandes, C., Gaspar, M. G., Pires, J. (2017). Within and between-tree variation of wood density components in Pinus sylvestris at five sites in Portugal. European Journal of Wood and Wood Products, 75, 511–526. DOI 10.1007/s00107-016-1130-2. [Google Scholar] [CrossRef]

24. Donaldson, L. A. (1993). Variation in microfiber angle among three genetic group of pinus radiata. New Zealand Jounal of Forestry Science, 23(I), 90–99. [Google Scholar]

25. Ekici, N., Fahlen, J. (2012). Ultrastructural studies on the sporogenous tissue and anther wall of Leucojum aestivum (amaryllidaceae) in different developmental stages. Anais da Academia Brasileira de Ciencias, 84(4), 951–960. DOI 10.1590/S0001-37652012005000061. [Google Scholar] [CrossRef]

26. Barnett, J. R., Bonham, V. A. (2004). Cellulose microfiber angle in the cell wall of wood fibres. Biological Reviews, 79(2), 461–472. DOI 10.1017/S1464793103006377. [Google Scholar] [CrossRef]

27. Pearson, R. G., Gilmore, R. C. (1980). Effects of fast growth rate on the mechanical properties of loblolly pine. Forest Products Journal, 30(5), 47–54. DOI 10.1016/0378-1127(80)90011-0. [Google Scholar] [CrossRef]

28. Donaldson, L. A. (1992). Within- and between-tree variation in microfiber angle in pinus radiate. New Zealand Journal of Forestry Science, 22(I), 77–86. [Google Scholar]

29. Pedini, M. (1992). The variation in the microfiberlar angle within the juvenile wood of sika spruce. LAWA Journal, 13, 261–271. [Google Scholar]

30. Donaldson, L. A. (1993). Variation in microfiber angle among three genetic group of pinus radiata. New Zealand Jounal of Forestry Science, 23(1), 90–99. [Google Scholar]

31. Li, X. J., Liu, Y. (2007). The chemical composition of loblolly pine pulp and its variation on the height of tree trunk. Journal of Central South University of Forestry & Technology, 27(4), 103–107. [Google Scholar]

32. Liang, S. Q., Luo, J. J. (2004). The chemical composition and variation of tree trunk height in the old row of rice in plantation. Journal of Central South University of Forestry & Technology, 24(5),78–83. [Google Scholar]

33. Liu, C. Q., Wang, C. G. (2017). The chemical composition and its variation in height of the wood of maplewood. Journal of Anhui Agricultural University, 44(6), 1043–1046. [Google Scholar]

34. Bendtsen, B. A., Senft, J. F. (1986). Properties in individual grownth rings of plantation grown eastern cottonwood and loblolly pine. Wood and Fiber Science, 18(1),23–28. [Google Scholar]

35. Sudo, S. (1986). Variation in tracheid length in akamatsu (Pinus densiflora.) VIU relation between tracheid length of juvenileand adult wood in akamatsu from a stand in the kansai district. Journal of the Japan Wood Research Society, 16(5), 209–212. [Google Scholar]

36. Melanie, J., Payette, S. (2014). Dynamics of active layer in wooded palsas of northern Quebec. Geomorphology, 206(1),87–96. DOI 10.1016/j.geomorph.2013.10.001. [Google Scholar] [CrossRef]

37. Gindl, W., Gupta, H. S., Schoberl, T., Lichtenegger, H. C., Fratz1, P. et al. (2004). Mechanical properties of spruce wood cell walls by nanoindentation. Applied Physics. A, 79(8), 2069–2073. DOI 10.1007/s00339-004-2864-y. [Google Scholar] [CrossRef]

38. Ye, C. M., Olavi, S., Remes, K. (1994). Microscopic transmission ellipsometry: Measurement of the fibril angle and the relative phase retardation of single, intact wood pulp fibers. Applied Optics, 33(28), 114–117. DOI 10.1364/AO.33.006626. [Google Scholar] [CrossRef]

39. Cave, I. D., Walker, J. C. F. (1994). Stiffness of wood in fast-grown plantation softwoods: The influence of microftbril angle. Forest Products Journal, 44(5), 43–48. [Google Scholar]

40. Helinska-Raczkowska, L. (1994). Variation of vessel lumen diameter in radial direction as an indication of the juvenile wood growth in oak (Quercus petraea Liebl). Annales des Sciences Forestires, 51(3), 323–329. DOI 10.1051/forest:19940307. [Google Scholar] [CrossRef]

41. Bergander, A., Branstrom, J. (2002). Fibril angle variability in earlywood of Norway spruce using soft rot cavities and polarization confocal microscopy. Journal of Wood Science, 48(4), 255–263. DOI 10.1007/BF00831344. [Google Scholar] [CrossRef]

42. Sahlberg, U., Salmén, L., Oscarsson, A. (1994). The fibrillar orientation in the S2-layer of wood fibres as determined by X-ray diffraction analysis. Wood Science and Technology, 31, 77–86. DOI 10.1007/BF00705923. [Google Scholar] [CrossRef]

43. Engelund, E. T., Svensson, S. (2011). Modelling time-dependent mechanical behaviour of softwood using deformation kinetics. Holzforschung, 65(2), 231–237. DOI 10.1515/hf.2011.011. [Google Scholar] [CrossRef]

44. Barnett, J. R., Bonham, V. A. (2010). Cellulose microfibril angle in the cell wall of wood fibres. Biological Reviews, 79, 332–340. DOI 10.1017/S1464793103006377. [Google Scholar] [CrossRef]

45. Lou, Z., Yuan, T., Wang, Q., Wu, X., Hu, S. et al. (2021). Fabrication of crack-free flattened bamboo and its macro-/MicroMorphological and mechanical properties. Journal of Renewable Materials, 9(5), 959–977. DOI 10.32604/jrm.2021.014285. [Google Scholar] [CrossRef]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.