Advancing Quantum Technology: Insights Form Mach-Zehnder Interferometer in Quantum State Behaviour and Error Correction

1  Introduction

In recent years, quantum computing has emerged as a groundbreaking and promising alternative to classical computing, with the potential to solve complex problems much more rapidly [1,2]. Quantum computing woks based on the principles of quantum mechanics and quantum bits (Qubits) to perform computations that are infeasible for classical computers to achieve [3–6]. One prominent technique in this field is Linear Optical Quantum Computing (LOQC), which utilizes photon quantum bits or qubits [7–10]. In LOQC, photonic qubits are used, which present several advantages, such as rapid operation, easy manipulation, and the ability to travel long distances without significant loss, making them highly attractive candidates for future quantum information processing systems [11–13]. However, LOQC faces significant challenges, including photon loss, decoherence, and other sources of noise [14,15].

The fragile nature of quantum states and the susceptibility of qubits to decoherence and noise present major challenges to the development of viable quantum computers. Errors in quantum operations can also stem from hardware defects, environmental interference, and the intrinsic probabilistic nature of quantum physics [16]. To address these issues, quantum error correction (QEC) techniques have been developed which enhances the robustness and reliability of systems that rely on phonic qubits [17–20]. The QEC encompasses strategies for preserving quantum states against the effects of decoherence and noise, which introduce errors in quantum operations [21–23]. The QEC systems encode information in an error-tolerant manner by distributing a quantum state across multiple qubits and incorporating redundant information to detect and correct potential faults [24,25]. By integrating QEC techniques, it is possible to construct robust and reliable quantum computers using photonic qubits [26,27].

One of the powerful tools for quantum state preparation and quantum computing within LOQC is the Mach-Zehnder interferometer (MZI) [28]. The MZI is an optical device, is a crucial component in both classical optical interferometry and quantum optics for executing various quantum operations [29–31]. Despite its advantages, MZI systems are also susceptible to errors from various sources, such as phase fluctuations, imperfect interference, and detector inefficiencies [32–34]. Error correction schemes in MZI systems, related to hardware error control strategies and random phase error correction in balanced MZIs, are discussed in [35,36]. In this paper, we optimize quantum error correction (QEC) techniques to enhance the robustness and reliability of LOQC systems. Our objective is to enhance the fault tolerance and error resilience of the LOQC system by integrating error correction techniques within the MZI framework. By meticulously designing Shor error correction schemes within the MZI-based LOQC system, we significantly reduce errors during quantum gate operations. Shor error correction is a quantum error-correcting code that correct bit-flip and phase-flip errors in quantum states [37].

This paper is structured as follows: In Section 2, we discuss the methods and approaches for any states passing through the MZI. Section 3 presents the results of our simulations and an assessment of the performance of the proposed error correction schemes. Finally, we discuss the implications and significance of our findings, followed by our conclusions.

2  Method: Mach-Zehnder Interferometry

The Mach-Zehnder interferometer (MZI) is pivotal in optical quantum computing due to its ability to perform precise quantum state manipulations and measurements. It is particularly valuable for implementing quantum error correction (QEC) because it enables accurate control over quantum states, allowing for effective detection and correction of errors in optical quantum systems. The MZI’s sensitivity to phase changes and its capability for high-fidelity operations make it an ideal tool for ensuring robust and reliable quantum computations.

The Mach-Zehnder Interferometer (MZI) is a device consisting of beam splitters and mirrors that divide an optical beam into two channels and then recombine them to produce an interference pattern based on the relative phase difference between the paths Fig. 1. In the MZI setup, the initial beam splitter serves to split singular input photons into two distinct channels. The configuration for coherent states divides a single input photon into two channels.

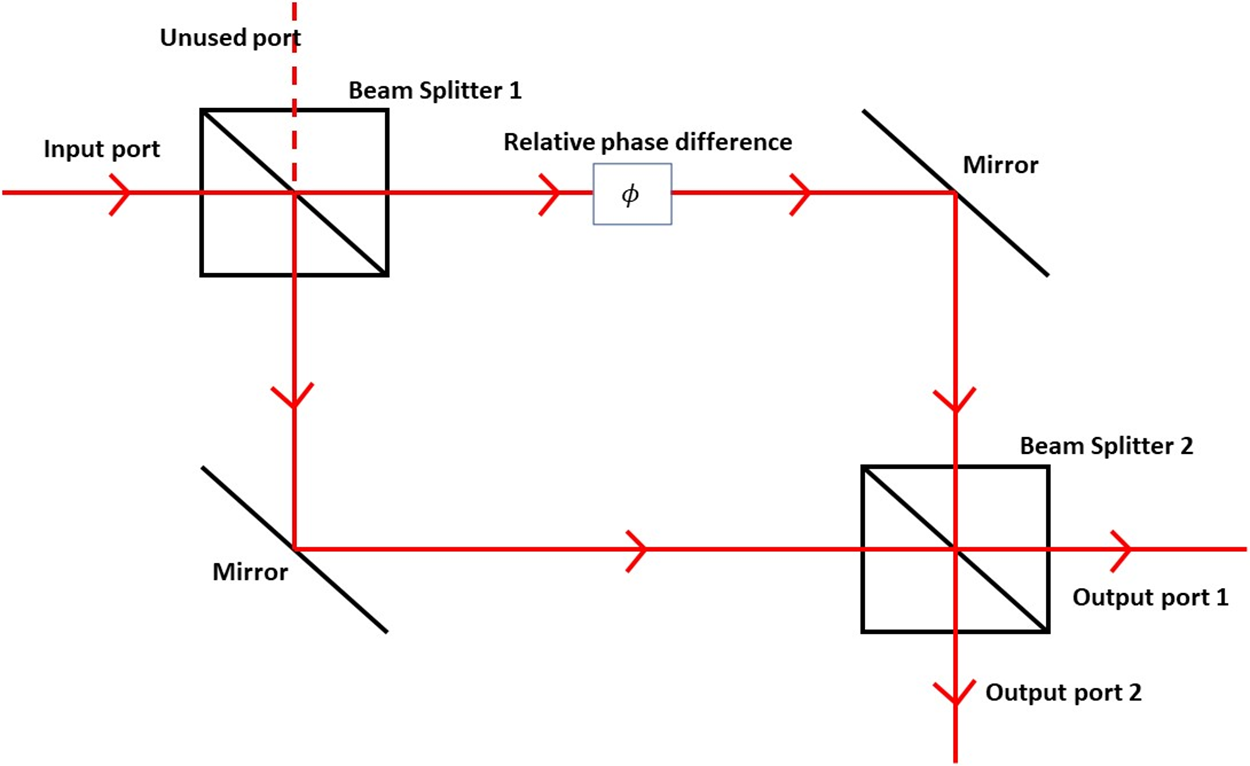
Figure 1: Schematic of the Mach-Zehnder interferometer setup

The photon then travels through the arms, where its phase may be altered due to relative phase difference, before recombining at the second beam splitter. The interference pattern visible at the MZI’s output is determined by the relative phase difference between the two arms. The phase of the coherent state could be changed by altering the path length or applying phase shifts to one of the arms, resulting in constructive or destructive interference at the output.

We examine the output probabilities for Detectors D1 and D2 using various forms of coherent state inputs, such as superposition, and unknown states, in our research. We could effectively estimate the phase shift or displacement applied to the input states by monitoring the output intensities at these detectors. The MZI with coherent states identifies minor changes in optical path length and measures external forces acting on the system. As a result, it is a versatile device for a variety of applications that require high-precision measurements and interferometric techniques. We are using Wolfram Quantum Framework for the simulation of quantum circuits, the implementation of quantum circuit for MZI is shown in Fig. 2.

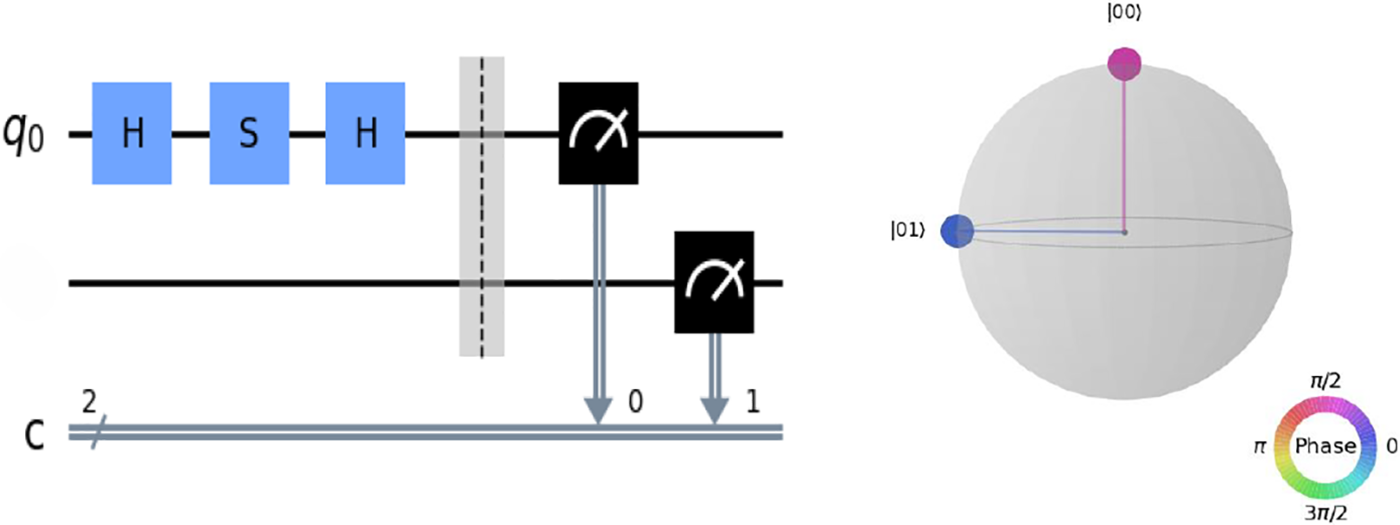
Figure 2: Left: Quantum analogue circuit of MZI, Right: Qsphere (without measurement)

The circuit starts with one qubit, represented by the labelled q0, then passes through the Hadamard gates denoted by H, its put the qubit in a superposition of 0 and 1. A phase gate S having a phase of π2 passes through another Hadamard gate operates on qubit. Further measurement is done and the output corresponds to the probability of photon in Detectors D1 and D2 as |0⟩ and |1⟩, respectively. The right-side image shows a Bloch sphere, a tool for picturing quantum state.

Superposition coherent state pass through MZI

Optical qubits are encoded in photon polarization states, represented by

|ψ⟩=α|H⟩+β|V⟩,(1)

where |H⟩ and |V⟩ are horizontal and vertical polarizations, respectively. For example, a superposition state

|ψ⟩=12|H⟩+β|V⟩,(2)

indicates an equal probability of measuring the photon in either polarization. Optical qubits excel in long-distance communication but require precise control and detection. In contrast, superconducting qubits are described by

|ψ⟩=α|0⟩+β|1⟩,(3)

where |0⟩ and |1⟩ are the ground and excited states. An example state

|ψ⟩=12|0⟩+β|1⟩,(4)

represents a superposition of these states. Superconducting qubits offer faster operations and integration with electronics but need cryogenic temperatures and are prone to decoherence. Both optical and superconducting qubits use superposition principles, represented by similar state vectors

|ψ⟩=α|0⟩+β|1⟩,(5)

but the physical systems differ in how they encode and manipulate these states.

The mathematical expression of superposition state using Dirac notation.

|ψ⟩=∑ici|ϕi⟩,(6)

where |ψ⟩ represents the superposition state, |ϕi⟩ represents the individual states forming the superposition, ci represents the probability amplitudes associated with each state, and the summation is taken over all possible states forming the superposition. The superposition state (e.g., a qubit or photon polarization state) is fed into the MZI, and the associated outcome is observed based on the behaviour of the superposition state within the MZI. The histograms presented in Fig. 3 illustrate the probabilities of the quantum states |0⟩ and |1⟩ for different coherent states.

Figure 3: Histograms showing the probabilities of the quantum states |0⟩ and |1⟩ for different coherent states specified by α. The middle left panel (second row, first column) represents the equal probability distribution where α = 1

These coherent states are specified by the complex parameter α. The dimension of the Hilbert space used for these calculations is d = 2, corresponding to the lowest two Fock states. Among the various histograms, the one located in the second row and first column (middle left panel) shows equal probabilities for |0⟩ and |1⟩. This equal probability distribution indicates a balanced superposition state. The parameter α that leads to this equal probability distribution was determined to be α = 1. This value of α represents a coherent state where the mean photon number is 1, resulting in equal probabilities of 0.5 for both |0⟩ and |1⟩.

3  Results: Circuit Evaluation and Error Correction

According to MZI quantum circuit, each qubit is susceptible to random errors introduced just before the final Hadamard gate. Specifically, each qubit has a probability p of encountering an X error, another probability p of encountering a Z error, and a probability 1–2p of experiencing no error at all. The parameter p is adjustable, allowing us to control the error rate. For instance, setting p = 0.15 indicates a 15% chance of encountering an error. To simulate these errors, we utilize a Quantum Channel box within our circuit. In the Fig. 4, MZI error scheme, we introduce errors in the first qubit between the phase operation and the final Hadamard gate, utilizing the quantum channel.

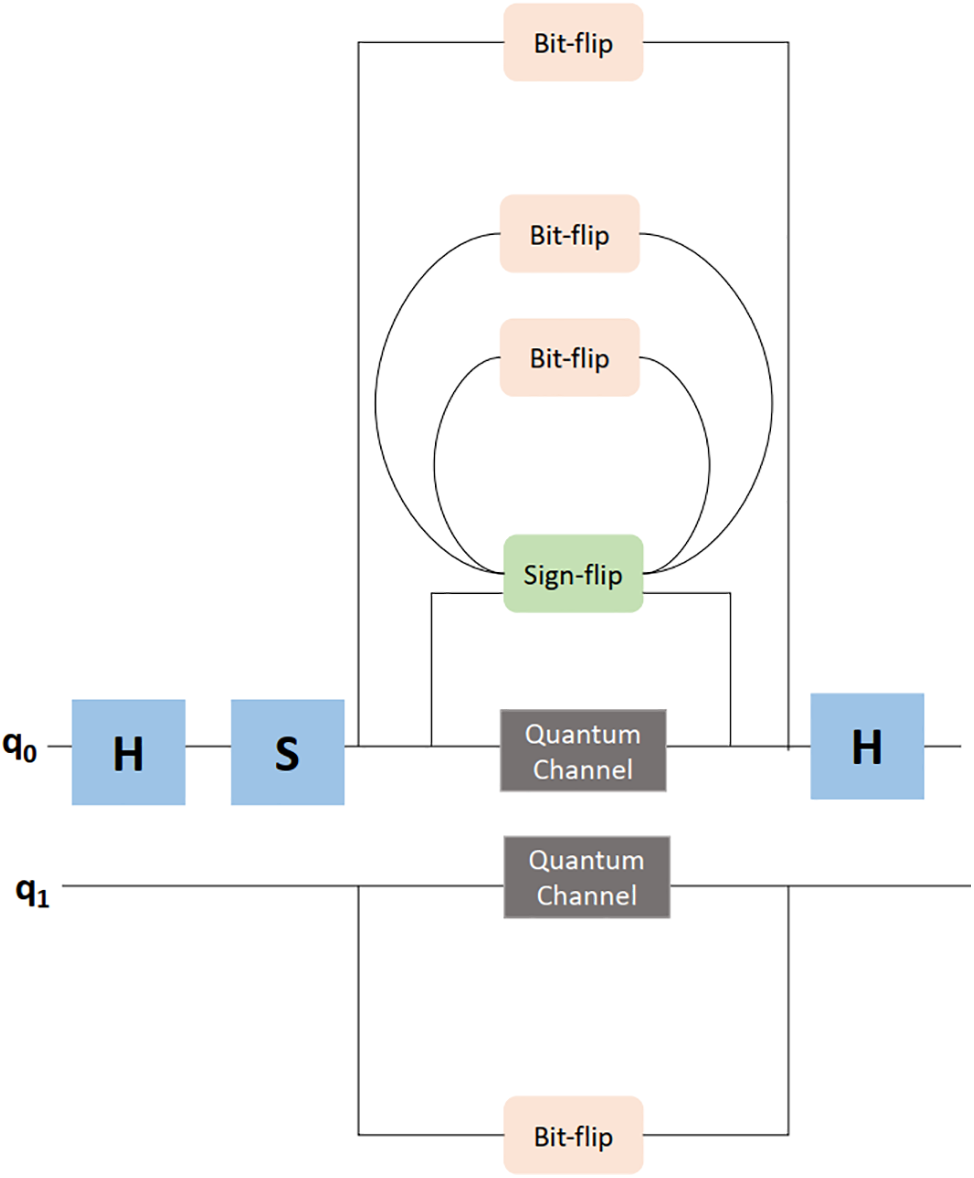
Figure 4: Error scheme using MZI setup

Quantum channels, essential for transmitting quantum information, introduce errors like decoherence and noise. Representing these channels as super operators or matrices enables precise modelling and effective quantum error correction techniques.

These errors could manifest as either bit flips or phase flips. For the second qubit, we exclusively introduce bit flip errors within the quantum channel. This represents our quantum error generation scheme, where errors are intentionally introduced to simulate real-world noise and disturbances. In The quantum circuit implementing the MZI error scheme is executed with 10,240 shots. The resulting output, highlighting the generated errors, is presented in Fig. 5.

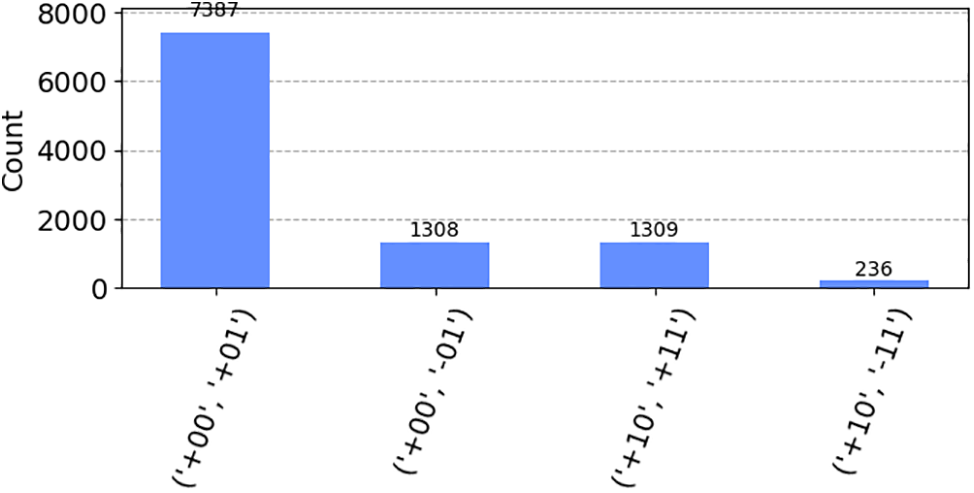
Figure 5: Quantum measurement of error-prone MZI setup

Subsequently, we employ the Shor code to rectify these errors, implementing quantum error correction techniques. The Shor code plays a pivotal role in mitigating the introduced errors, ensuring the accuracy and reliability of quantum computations within the MZI setup. For error correction, we implement the Shor code with certain assumptions:

•   Condition A: Only the 1st qubit and 2nd qubit may experience errors, including no error, bit-flip, or phase-flip errors.

•   Condition B: Any number of qubits may be subject to error without any specific restrictions.

In this approach, we introduce 8 ancillary qubits for the first logical qubit in Fig. 6, resulting in a total of 9 qubits corresponding to the first logical qubit—designated as qubits [0,2,3,4,5,6,7,8,9]. Among these, 3 qubits are allocated for bit-flip codes, while 1 qubit serves as a phase-flip code. This configuration, comprising 3 bit-flip codes and 1 phase-flip code, is widely recognized as the Shor code.

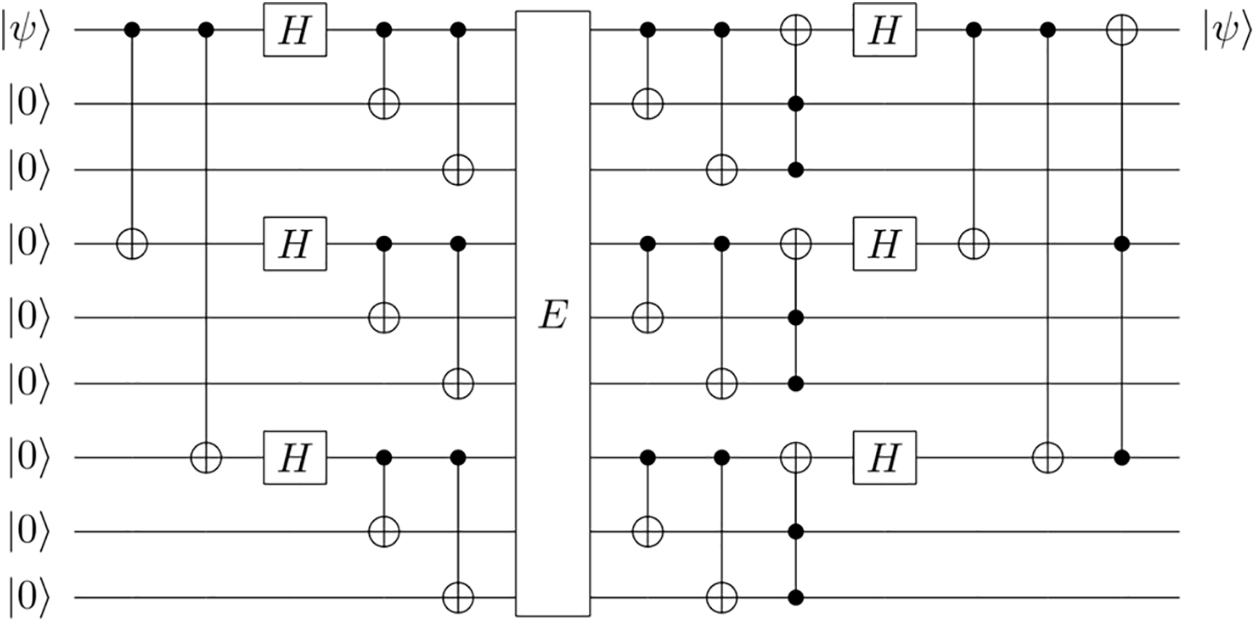
Figure 6: Error correction circuit for the shor code

The depicted quantum circuit in Fig. 7 implements the Shor code within a Mach-Zehnder interferometer to enhance error correction during interferometric measurements.

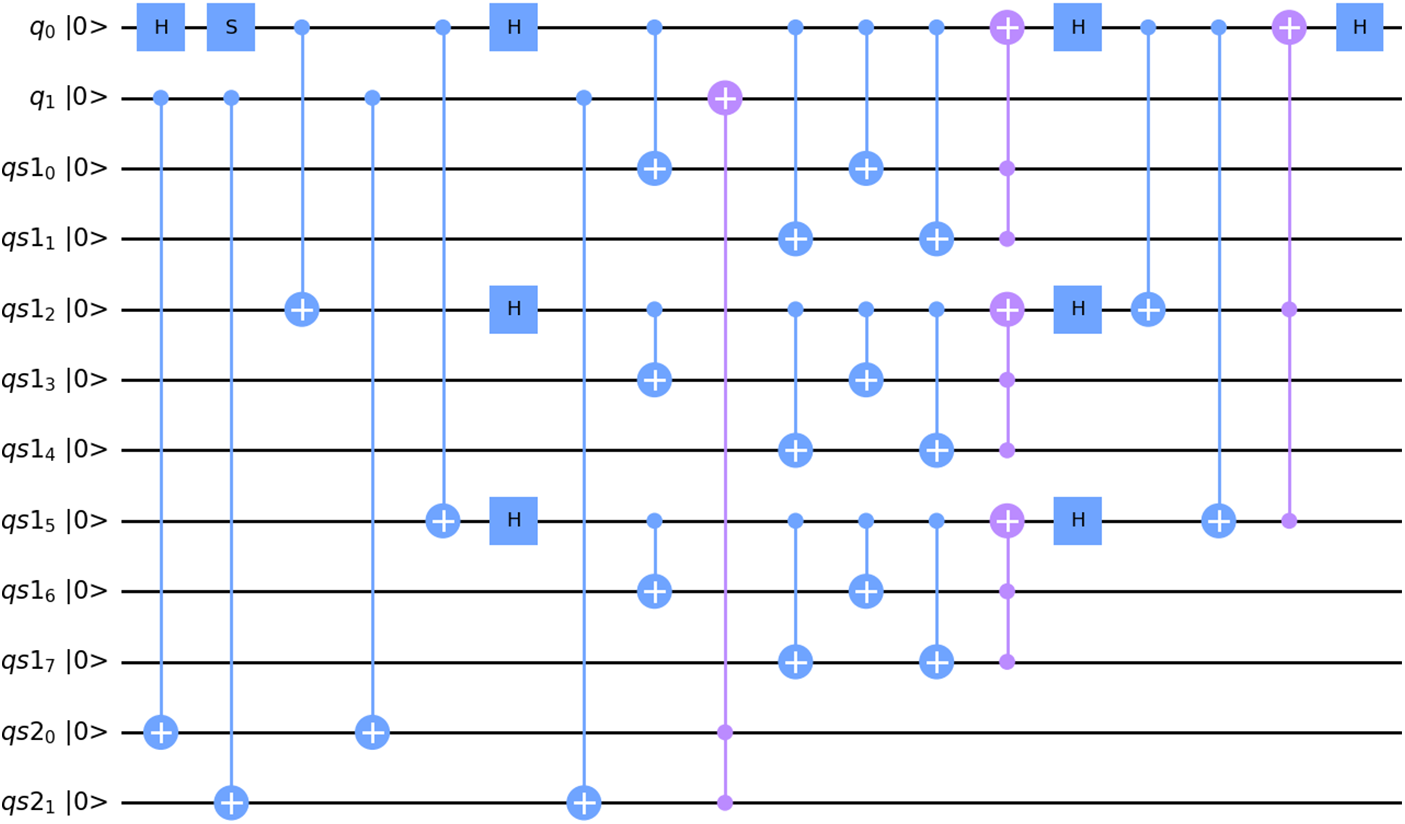
Figure 7: Shor code applied on MZI circuit

The circuit initializes 22 qubits, applies Hadamard and Phase gates to create superpositions, and uses a series of CNOT gates to entangle data qubits with ancillary qubits. This entanglement allows for the detection and correction of errors without disrupting the interferometric measurement. Ancillary qubits detect bit-flip and phase errors, which are subsequently corrected using conditional gates. This integration ensures high fidelity and coherence, demonstrating the practical application of the Shor code to improve the robustness of quantum systems in real-world scenarios.

3.1 Condition A: Only the 1st Qubit and 2nd Qubit May Experience Errors, Including No Error, Bit-Flip, or Phase-Flip Errors

We make particular assumptions about the error-prone qubits in our quantum error correction system. These assumptions imply that only the first and second qubits may encounter faults, which could be none, bit-flip errors (X), or phase-flip errors (Z). This limited error model allows us to precisely analyse the success of mistake correction.

Error Combinations

We assume that only the first and second qubits may encounter faults. These faults can be:

• None (I)

• Bit-flip errors (X)

• Phase-flip errors (Z)

Combinations Analyzed

The Shor code’s performance in minimizing these faults is assessed by applying various combinations of flaws to the first and second qubits. The combinations include scenarios where one or both qubits are affected by mistakes. The specific combinations shown in the figure are:

• X & X (bit-flip on both qubits)

• X & I (bit-flip on the first qubit, no error on the second)

• X & Z (bit-flip on the first qubit, phase-flip on the second)

• I & X (no error on the first qubit, bit-flip on the second)

• I & I (no error on both qubits)

• I & Z (no error on the first qubit, phase-flip on the second)

• Z & X (phase-flip on the first qubit, bit-flip on the second)

• Z & I (phase-flip on the first qubit, no error on the second)

• Z & Z (phase-flip on both qubits)

The results in Fig. 8 demonstrate the Shor code’s effectiveness in correcting various error combinations applied to the first and second qubits.

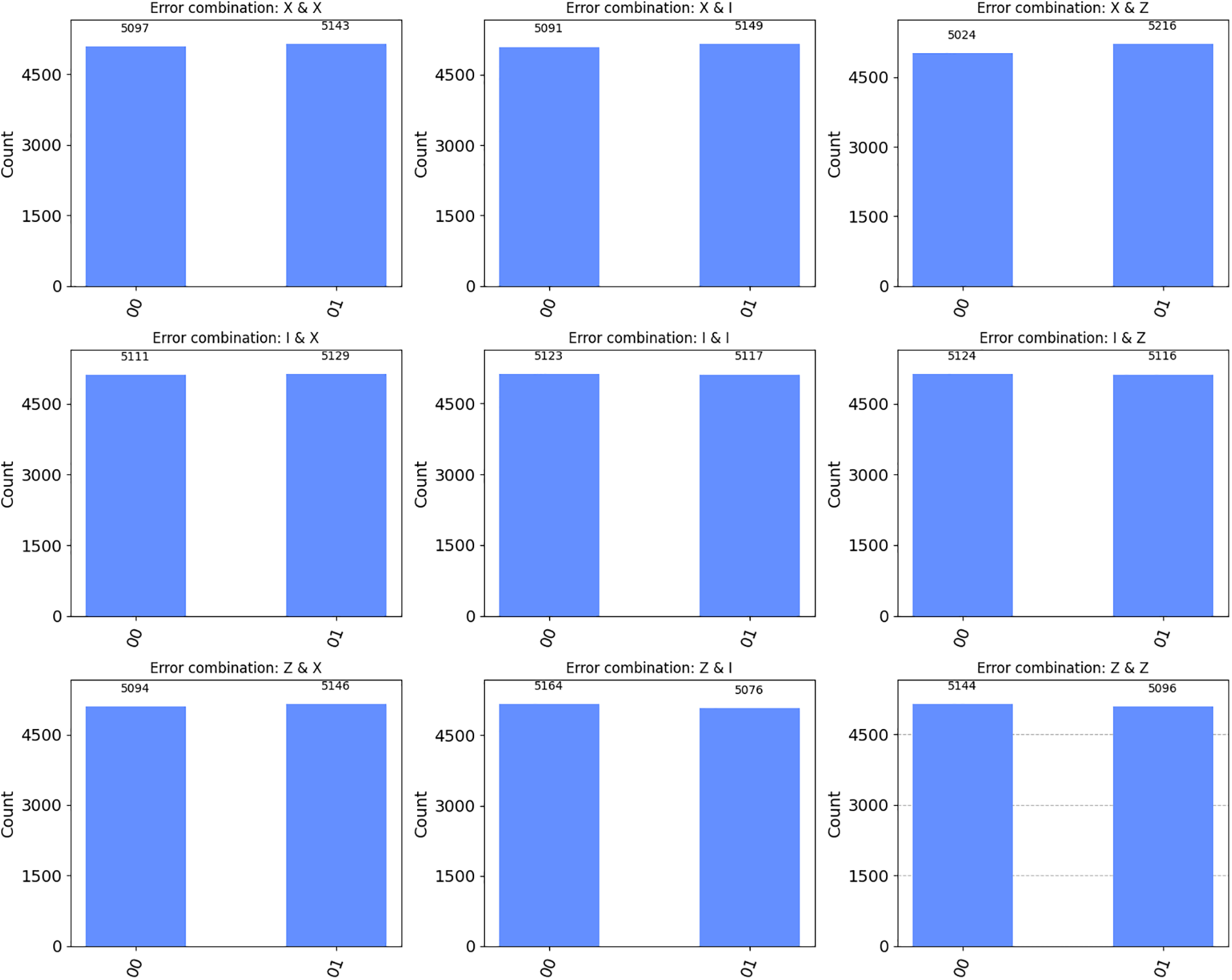
Figure 8: Error correction results with shor code

The balanced counts of “00” and “10” across all combinations suggest that the Shor code successfully mitigates the effects of these errors, aligning with the expectation of successful error correction.

3.2 Condition B: Any Number of Qubits May Be Subject to Error without Any Specific Restrictions

In this particular quantum error correction condition, there are no specific restrictions on the number of qubits that may be susceptible to errors. This condition allows for a more general and unbounded scenario, where any number of qubits could potentially be affected by errors, reflecting a realistic and challenging quantum environment.

Quantum circuit corresponding to this condition is as depicted in Fig. 9. This circuit configuration is designed to address scenarios where multiple qubits may be exposed to errors without constraints. The results obtained from this condition underscore the effectiveness of the error-correcting code in mitigating errors introduced under the condition B error scheme. It demonstrates that our error correction method performs well, even when a variable number of qubits are affected by errors.

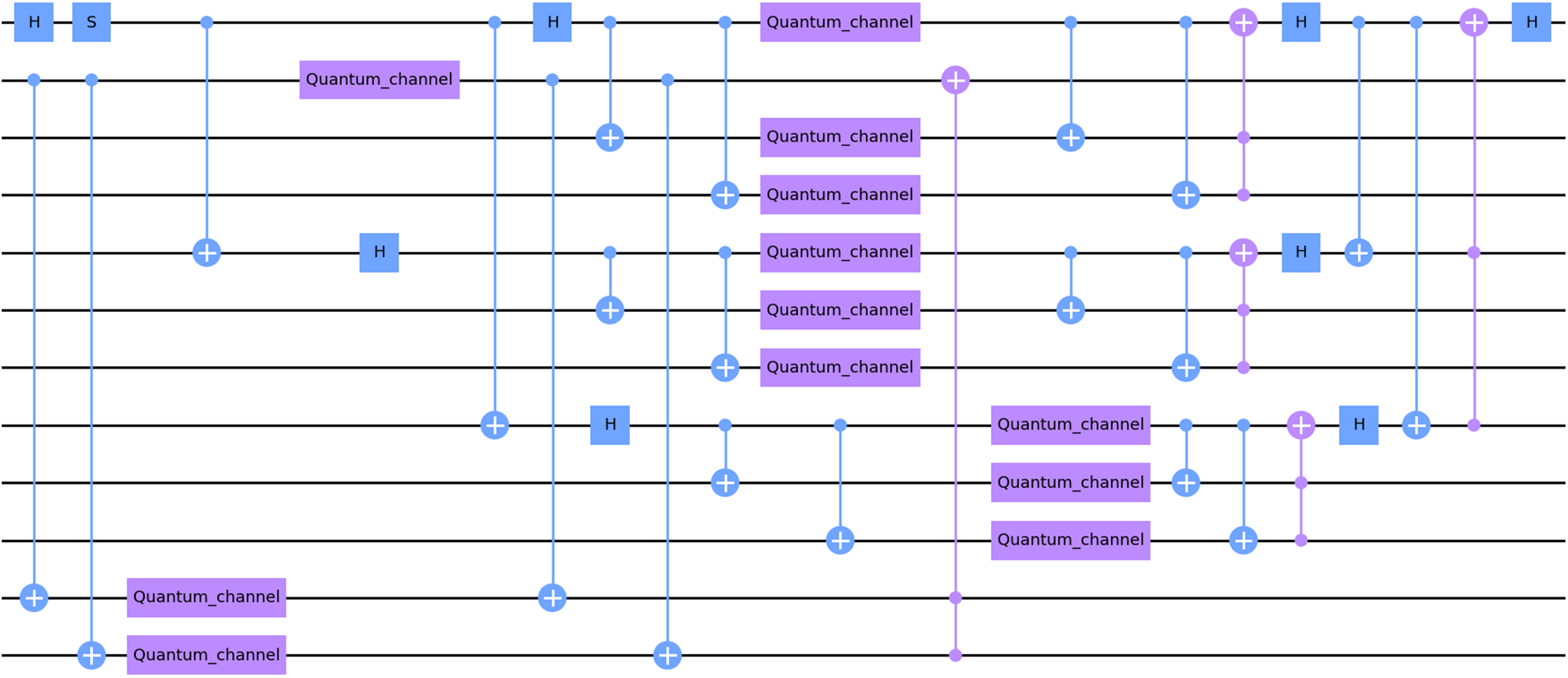
Figure 9: Quantum circuit for condition B

However, it is worth noting that there are limitations to this error-correcting scheme when errors are introduced at higher rates. This limitation becomes evident in Fig. 10, which compares the counts obtained with and without errors. Here, a 15% error rate comprising both bit-flip and phase-flip errors is examined, and the error correction method remains effective within this range.

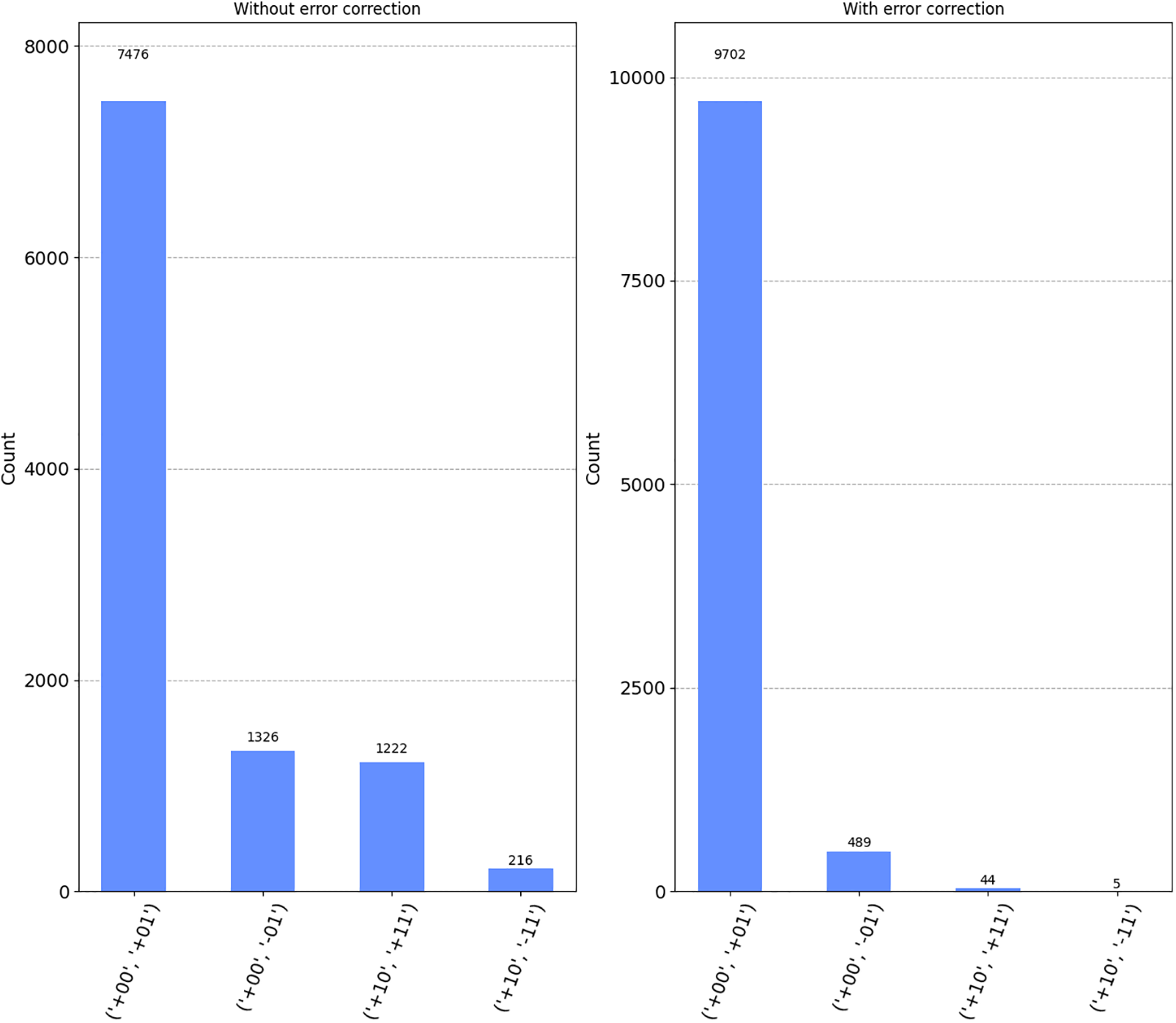
Figure 10: Left: Data with 15% error introduced, Right: Data after error correction

Moreover, in Fig. 11, we further assess the scheme’s performance and increased error rate of 25% for both bit-flip and phase-flip errors, analyzed individually. Notably, while the error correction method still effectively handles bit-flip errors, it struggles to resolve phase errors at this heightened error rate.

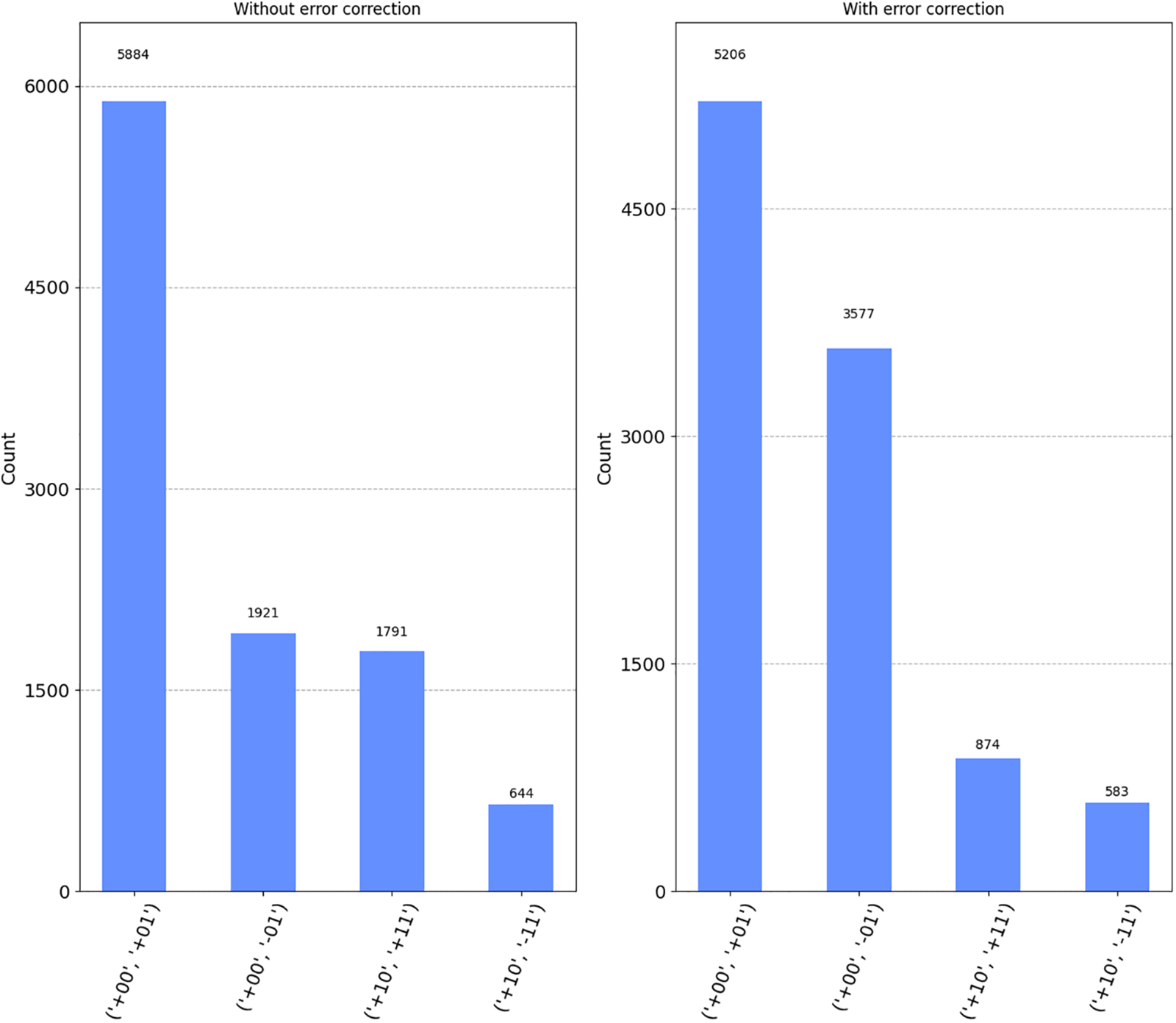
Figure 11: Left: Data with 25% error introduced, Right: Data after error correction

4  Discussion

The study presents significant advancements in understanding quantum error correction (QEC) using a Mach-Zehnder interferometer (MZI), emphasizing the nuanced interplay between coherence, interference, and error correction in quantum systems. The key finding is the demonstrated utility of the MZI in effectively correcting errors for both known and unknown coherent states, highlighting its robustness across various quantum scenarios. However, this robustness diminishes when faced with unknown superposition states, indicating a critical limitation of current QEC methods within the MZI framework. This discrepancy necessitates further research and development, such as enhanced error correction codes or alternative interferometry setups, tailored to address the complexities associated with superposition states.

The study also analyzes the output probabilities obtained from the quantum analogue circuit, which align closely with those of the classical MZI, reinforcing the validity of quantum descriptions in these systems. This alignment suggests that the quantum analogue approach is precise and reliable in studying quantum systems, facilitating the advancement of more sophisticated QEC techniques. Additionally, the research underscores the critical role of coherence and interference in quantum information processing, with the observed symmetric output probabilities and the probabilistic nature of superposition states highlighting the intricate dynamics at play. These insights pave the way for more advanced applications in quantum optics and a deeper understanding of quantum mechanics. Furthermore, the research points towards integrating advanced error correction methods, such as those proposed by Shor, to mitigate identified limitations. The interplay between bit-flip and phase-flip errors at varying rates underscores the need for adaptive and robust QEC strategies capable of handling diverse error scenarios, suggesting that future research should focus on these adaptive techniques and their practical implementations in quantum computing and communication systems.

5  Conclusion

In conclusion, we have thoroughly investigated the performance of the Mach-Zehnder interferometer (MZI) in correcting errors in known and unknown coherent and superposition states. Our findings highlight the successful correction of errors in known coherent and superposition states and unknown coherent states, while revealing the challenges posed by unknown superposition states for error correction in MZI. These insights are crucial for developing more robust quantum error correction (QEC) techniques. This study involved examining the behaviour of coherent states in an MZI and creating a quantum analogue using the Wolfram Quantum Framework. The results confirm that the quantum analogue circuit aligns with the classical MZI, supporting the application of coherent states in quantum optics and information processing. While the effectiveness of MZI-based QEC for known coherent states is evident, the significant challenges with unknown superposition states indicate a need for further research and development. Our study emphasizes the limitations of current QEC methods within the MZI framework and the importance of advancing more sophisticated and adaptive error correction strategies. By addressing these limitations and exploring new avenues, such as integrating advanced QEC methods or developing alternative interferometry setups, we can significantly enhance the reliability and efficiency of QEC systems. These advancements are essential for the progression of quantum computing and communication technologies, where robust error correction is vital for maintaining the fidelity of quantum information.

Acknowledgement: The authors are grateful for the resources and facilities made available by the Department of Physics and Astrophysics at the University of Delhi and the School of Technology at Woxsen University.

Funding Statement: The authors received no specific funding for this study.

Author Contributions: The following contributions to the work are confirmed by the authors: Priyanka, Shankar Pidishety and Ram Soorat prepared the draft paper; Priyanka, Shaik Ahmed and Damodarakurup Sajeev conceptualized and designed the study; Ram Soorat analysed and interpreted the findings. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: Upon reasonable request, the data supporting the study’s conclusions obtained from Ram Soorat, the corresponding author.

Ethics Approval: Ethics clearance was not necessary for this study because it did not use any human or animal participants.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. M. Möller and C. Vuik, “On the impact of quantum computing technology on future developments in high-performance scientific computing,” Ethics Inf. Technol., vol. 19, no. 4, pp. 253–269, 2017. doi: 10.1007/s10676-017-9438-0. [Google Scholar] [CrossRef]

2. M. A. Shafique, A. Munir, and I. Latif, “Quantum computing: Circuits, algorithms, and applications,” IEEE Access, vol. 12, pp. 22296–22314, 2024. doi: 10.1109/ACCESS.2024.3362955. [Google Scholar] [CrossRef]

3. M. A. Nielsen and I. L. Chuang, “Quantum computing,” in Quantum Computation and Quantum Information, 10th ed. Cambridge, UK: Cambridge University Press, 2010, pp. 174–231. doi: 10.1017/CBO9780511976667. [Google Scholar] [CrossRef]

4. D. Peev, “Quantum computing technology—A brief overview,” in 2024 23rd Int. Symp. Electr. Apparat. Technol. (SIELA), Bourgas, Bulgaria, 2024, pp. 1–8. doi: 10.1109/SIELA61056.2024.10637901. [Google Scholar] [CrossRef]

5. J. Preskill, “Quantum computing: Pro and con,” Proc. R. Soc. Lond. A, vol. 454, pp. 469–486, 1998. doi: 10.1098/rspa.1998.0171. [Google Scholar] [CrossRef]

J. Preskill, “Quantum Computing in the NISQ era and beyond,” Quantum, vol. 2, 2018, Art. no. 79. doi: 10.22331/q-2018-08-06-79. [Google Scholar] [CrossRef]

7. E. Knill, R. Laflamme, and G. J. Milburn, “A scheme for efficient quantum computation with linear optics,” Nature, vol. 409, pp. 46–52, 2001. doi: 10.1038/35051009. [Google Scholar] [PubMed] [CrossRef]

8. N. Budinger, A. Furusawa, and P. V. Loock, “All-optical quantum computing using cubic phase gates,” Phys. Rev. Res., vol. 6, no. 2, 2024, Art. no. 023332. doi: 10.1103/PhysRevResearch.6.023332. [Google Scholar] [CrossRef]

9. P. Kok, W. J. Munro, K. Nemoto, T. C. Ralph, J. P. Dowling and G. J. Milburn, “Linear optical quantum computing with photonic qubits,” Rev. Mod. Phys., vol. 79, no. 1, pp. 135–174, 2007. doi: 10.1103/RevModPhys.79.135. [Google Scholar] [CrossRef]

10. T. Rudolph, “Why i am optimistic about the silicon-photonic route to quantum computing,” APL Photonics, vol. 2, no. 3, 2017, Art. no. 030901. doi: 10.1063/1.4976737. [Google Scholar] [CrossRef]

11. Y. Kwon, A. Baldazzi, L. Pavesi, and B. Choi, “Quantum circuit mapping for universal and scalable computing in MZI-based integrated photonics,” Opt. Express, vol. 32, no. 7, pp. 12852–12881, 2024. doi: 10.1364/OE.520492. [Google Scholar] [PubMed] [CrossRef]

12. S. Slussarenko and G. J. Pryde, “Photonic quantum information processing: A concise review,” Appl. Phys. Rev., vol. 6, no. 4, 2019, Art. no. 041303. doi: 10.1063/1.5115814. [Google Scholar] [CrossRef]

13. J. W. Wang, F. Sciarrino, A. Laing, and M. G. Thompson, “Integrated photonic quantum technologies,” Nat. Photonics., vol. 14, no. 5, pp. 273–284, 2020. doi: 10.1038/s41566-019-0532-1. [Google Scholar] [CrossRef]

14. Y. Li, P. C. Humphreys, G. J. Mendoza, and S. C. Benjamin, “Resource costs for fault-tolerant linear optical quantum computing,” Phys. Rev. X, vol. 5, 2015, Art. no. 041007. doi: 10.1103/PhysRevX.5.041007. [Google Scholar] [CrossRef]

15. K. H. Luo et al., “Quantum optical coherence: From linear to nonlinear interferometers,” Phys. Rev. A, vol. 104, no. 4, 2021, Art. no. 043707. doi: 10.1103/PhysRevA.104.043707. [Google Scholar] [CrossRef]

16. D. Gottesman, “Theory of fault-tolerant quantum computation,” Phys. Rev. A, vol. 57, no. 1, pp. 127–137, 1998. doi: 10.1103/PhysRevA.57.127. [Google Scholar] [CrossRef]

17. E. Knill, “Quantum computing with realistically noisy devices,” Nature, vol. 434, no. 7029, pp. 39–44, 2005. doi: 10.1038/nature03350. [Google Scholar] [PubMed] [CrossRef]

18. P. W. Shor, “Scheme for reducing decoherence in quantum computer memory,” Phys. Rev. A, vol. 52, no. 4, 1995, Art. no. R2493. doi: 10.1103/PhysRevA.52.R2493. [Google Scholar] [PubMed] [CrossRef]

19. A. R. Calderbank and P. W. Shor, “Good quantum error-correcting codes exist,” Phys. Rev. A, vol. 54, no. 2, pp. 1098–1105, 1996. doi: 10.1103/PhysRevA.54.1098. [Google Scholar] [PubMed] [CrossRef]

20. D. Cruz, F. A. Monteiro, and B. C. Coutinho, “Quantum error correction via noise guessing decoding,” IEEE Access, vol. 11, pp. 119446–119461, 2023. doi: 10.1109/ACCESS.2023.3327214. [Google Scholar] [CrossRef]

21. D. A. Lidar and T. A. Brun, “Introduction to quantum error correction,” in Quantum Error Correction, 1st ed. Cambridge, UK: Cambridge University Press, 2013, pp. 1–28. doi: 10.1017/CBO9781139034807. [Google Scholar] [CrossRef]

22. J. M. Gertler, B. Baker, J. Li, S. Shirol, J. Koch and C. Wang, “Protecting a bosonic qubit with autonomous quantum error correction,” Nature, vol. 590, pp. 243–248, 2021. doi: 10.1038/s41586-021-03257-0. [Google Scholar] [PubMed] [CrossRef]

23. L. Postler et al., “Demonstration of fault-tolerant steane quantum error correction,” PRX Quantum, vol. 5, no. 3, 2024, Art. no. 030326. doi: 10.1103/PRXQuantum.5.030326. [Google Scholar] [CrossRef]

24. R. Laflamme, C. Miquel, J. P. Paz, and W. H. Zurek, “Perfect quantum error correcting code,” Phys. Rev. Lett., vol. 77, no. 1, pp. 198–201, 1996. doi: 10.1103/PhysRevLett.77.198. [Google Scholar] [PubMed] [CrossRef]

25. P. W. Shor, “Fault-tolerant quantum computation,” in Proc. 37th Annu. Symp. Foundat. Comput. Sci., Burlington, VT, USA, 1996. doi: 10.1109/SFCS.1996.548464. [Google Scholar] [CrossRef]

26. A. G. Fowler, M. Mariantoni, J. M. Martinis, and A. N. Cleland, “Surface codes: Towards practical large-scale quantum computation,” Phys. Rev. A, vol. 86, no. 3, 2012, Art. no. 032324. doi: 10.1103/PhysRevA.86.032324. [Google Scholar] [CrossRef]

27. Y. Ma et al., “Error-transparent operations on a logical qubit protected by quantum error correction,” Nat. Phys., vol. 16, no. 8, pp. 827–831, 2020. doi: 10.1038/s41567-020-0893-x. [Google Scholar] [CrossRef]

28. D. Bouwmeester, A. Ekert, and A. Zeilinger, “Experiments leading towards quantum computation,” in The Physics of Quantum Information: Quantum Cryptography, Quantum Teleportation, Quantum Computation, 1st ed. Berlin, Germany: Springer-Verlag, 2000, pp. 133–189. doi: 10.1007/978-3-662-04209-0. [Google Scholar] [CrossRef]

29. S. Bandyopadhyay, R. Hamerly, and D. Englund, “Hardware error correction for programmable photonics,” Optica, vol. 8, no. 10, pp. 1247–1255, Oct. 2021. doi: 10.1364/OPTICA.424052. [Google Scholar] [CrossRef]

30. L. Mandel and E. Wolf, “Quantum correlations and photon statistics,” in Optical Coherence and Quantum Optics, 1st ed. Cambridge, UK: Cambridge University Press, 1995, pp. 573–658. doi: 10.1017/CBO9781139644105. [Google Scholar] [CrossRef]

31. C. M. Caves, “Quantum-mechanical noise in an interferometer,” Phys. Rev. A, vol. 36, no. 8, pp. 5543– 5555, 1987. doi: 10.1103/PhysRevA.23.1693. [Google Scholar] [CrossRef]

32. S. M. R. Safaee, K. H. R. Mojaver, and O. Liboiron-Ladouceur, “Mitigating phase error accumulation in programming Mzi-based optical processors,” in 2023 Int. Conf. Photon. Switch. Comput. (PSC), Mantova, Italy, 2023, pp. 1–3. doi: 10.1109/PSC57974.2023.10297236. [Google Scholar] [CrossRef]

33. C. M. Wilkes. et al., “60 dB high-extinction auto-configured Mach-Zehnder interferometer,” Opt. Lett., vol. 41, pp. 5318–5321, 2016. doi: 10.1364/OL.41.005318. [Google Scholar] [PubMed] [CrossRef]

34. T. Kim et al., “Effect of the detector efficiency on the phase sensitivity in a Mach-Zehnder interferomete,” Phys. Rev. A, vol. 60, no. 1, 1999, Art. no. 708. doi: 10.1103/PhysRevA.60.708. [Google Scholar] [CrossRef]

35. H. H. Hou, P. F. Xu, Z. P. Zhou, and H. Su, “Hardware error correction for MZI-based matrix computation,” Micromachines, vol. 14, no. 5, 2023, Art. no. 955. doi: 10.3390/mi14050955. [Google Scholar] [PubMed] [CrossRef]

36. R. Chen et al., “Non-volatile electrically programmable integrated photonics with a 5-bit operation,” Nat. Commun., vol. 14, no. 1, 2023, Art. no. 3465. doi: 10.1038/s41467-023-39180-3. [Google Scholar] [PubMed] [CrossRef]

37. Y. X. Yang, Y. Mo, J. M. Renes, G. Chiribella, and M. P. Woods, “Optimal universal quantum error correction via bounded reference frames,” Phys. Rev. Res., vol. 4, no. 2, May 2022, Art. no. 023107. doi: 10.1103/PhysRevResearch.4.023107. [Google Scholar] [CrossRef]