IQAOA for Two Routing Problems: A Methodological Contribution with Application to TSP and VRP

1  Introduction

Quantum optimization emerges as a promising and innovative discipline with substantial potential implications in the domain of operations research. This burgeoning frontier affords the opportunity to address minimization through quantum metaheuristics, presenting a notably efficacious approach that circumvents the prevalent issue encountered by conventional local search algorithms—namely, the propensity to become trapped in local minima. The effectiveness of methods based on Simulated Annealing, a common technique in the field of operations research, relies on gradually reducing a parameter ‘t’ to zero, which aids in overcoming potential energy barriers. Different metaheuristic approaches employ diverse strategies to prevent premature convergence to local minima while maintaining robust capabilities for thorough exploration of the search space. Among these various metaheuristic techniques, which encompass a wide range of methods like memetic algorithms, GRASP (Greedy Randomized Adaptive Search Procedure), and VNS (Variable Neighborhood Search), the Simulated Annealing method stands out. Together, these metaheuristic techniques expand the toolkit available for addressing optimization challenges in the ever-evolving field of operations research.

Viewed through the lens of quantum mechanics, quantum fluctuations exhibit similarities to thermal fluctuations. What distinguishes quantum mechanics from classical methodologies is the capacity of waves to penetrate potential energy barriers—a concept elucidated by Martoňák et al. in 2004 [1]. In recent times, the quantum physics community has introduced several quantum metaheuristics, culminating in a family of quantum approximate algorithms. Among these, the Adiabatic-based Algorithms stand out, offering an approximate resolution to the Schrödinger equation formulated by Schrödinger in 1926 [2]. Recently, Reference [3] introduced a new class of algorithms centered around alternating between two distinct sets of operators: the Hamiltonian and the mixing Hamiltonian. This alternating process gives rise to Quantum Approximate Optimization Algorithms, commonly known as QAOA. These algorithms represent a hybrid approach wherein the classical computer explores the search space to optimize a set of parameters, while a quantum device handles the evaluation of probability distributions. It’s worth noting that QAOA doesn’t account for local search considerations but offers a comprehensive exploration of the entire search space. This ground-breaking work was further expanded upon in the notable publication by Hadfield in 2018 [4]. In their research, they introduced a new ansatz specifically designed to facilitate the exploration of the feasible subspace, ensuring inherent satisfaction of hard constraints. This approach bears resemblance to classical methodologies in the Operations Research (OR) community, involving a meticulous definition of classical operations, such as qubit permutations within the qubit-string used for solution modeling.

The TSP received a lot of attention for decades since it is the corner stone of all routing problems since it is emblematic of a broad category of optimization problems in classical computation, specifically within the realm of combinatorial optimization. Analysis of recent publications in quantum resolution of TSP permit to clarify the difference between the theoretical capabilities of quantum computing and the practical realities of applying these technologies to classical TSP optimization. Numerous quantum optimization algorithms have been investigated for the TSP: the recent publication of [5] propose a state-of-the-art of all QAOA based approaches investigated in gate-bases quantum computers. They provide numerical experiments with different QAOA mixer for 5 nodes TSP. Note that not only QAOA received attention, but also Grover since [6] introduces a quantum algorithm for the Traveling Salesman Problem (TSP) based on the Grover Adaptive Search (GAS). The method has been successfully applied to the resolution of one seven-node TSP using the Qiskit library. Lately, in 2024, the last investigations permit to solving 6 nodes TSP. For example, Reference [7] propose a two-step quantum search algorithm with two distinct operators for preparing the initial state and solving TSP. The algorithm first amplifies an equal superposition state of all feasible solutions of TSP and subsequently amplifies the optimal solution states among these feasible solution states. Larger instances can be addressed only by decomposition methods due to the large number of qubit required or due to the large number of gates. Reference [8] elaborate combination of two decomposition methods, namely graph shrinking and circuit cutting. Graph shrinking reduces the problem size before encoding into QAOA circuits, while circuit cutting decomposes quantum circuits into fragments for execution on medium-scale quantum computers. For a TSP with seven cities, the algorithm retrieves the optimum solution by consecutively running two 7-qubit QAOA circuits.

2  Indirect Quantum Approximate Optimization Algorithms (IQAOA)

2.1 Mapping Function in OR Field

A significant challenge in Operations Research (OR) lies in developing consistent models that exclusively represent solutions. The focused exploration of feasible subspaces has garnered attention within the Operations Research community for numerous years, proving successful in various research domains and yielding highly efficient metaheuristics. For instance, in Job-Shop Scheduling, a prevalent indirect representation relies on the Bierwith vector [9], which can be efficiently transformed (in O(n)) into an oriented disjunctive graph, thereby modeling a job-shop solution. Consequently, a Bierwith’s vector serves as the model for a solution in this context. Regarding the Vehicle Routing Problem (VRP), a widely recognized representation involves the giant trip, which, via the Split Algorithm [10,11], can be transformed into a VRP solution. The Split algorithm delineates a mapping from the set of giant trips within a Traveling Salesman Problem (TSP) to VRP solutions, with metaheuristic-based approaches adeptly manipulating the set of giant trips exclusively and efficiently. The TSP (Traveling Salesman Problem) received a lot of attention of the OR (Operational Research) community since it is the seminal problem in routing introduced first by Danzig et al. in 1959 [12]. All classical OR methods are based on partial search space enumeration, and the partial enumeration is due to the large search space. Cheng et al. in 1996 [13] made a full analysis of non-string coding in the middle of 90s and defined indirect approach and decoding mechanisms in the global context of constraint optimization. Different mappings are represented on the Fig. 1.

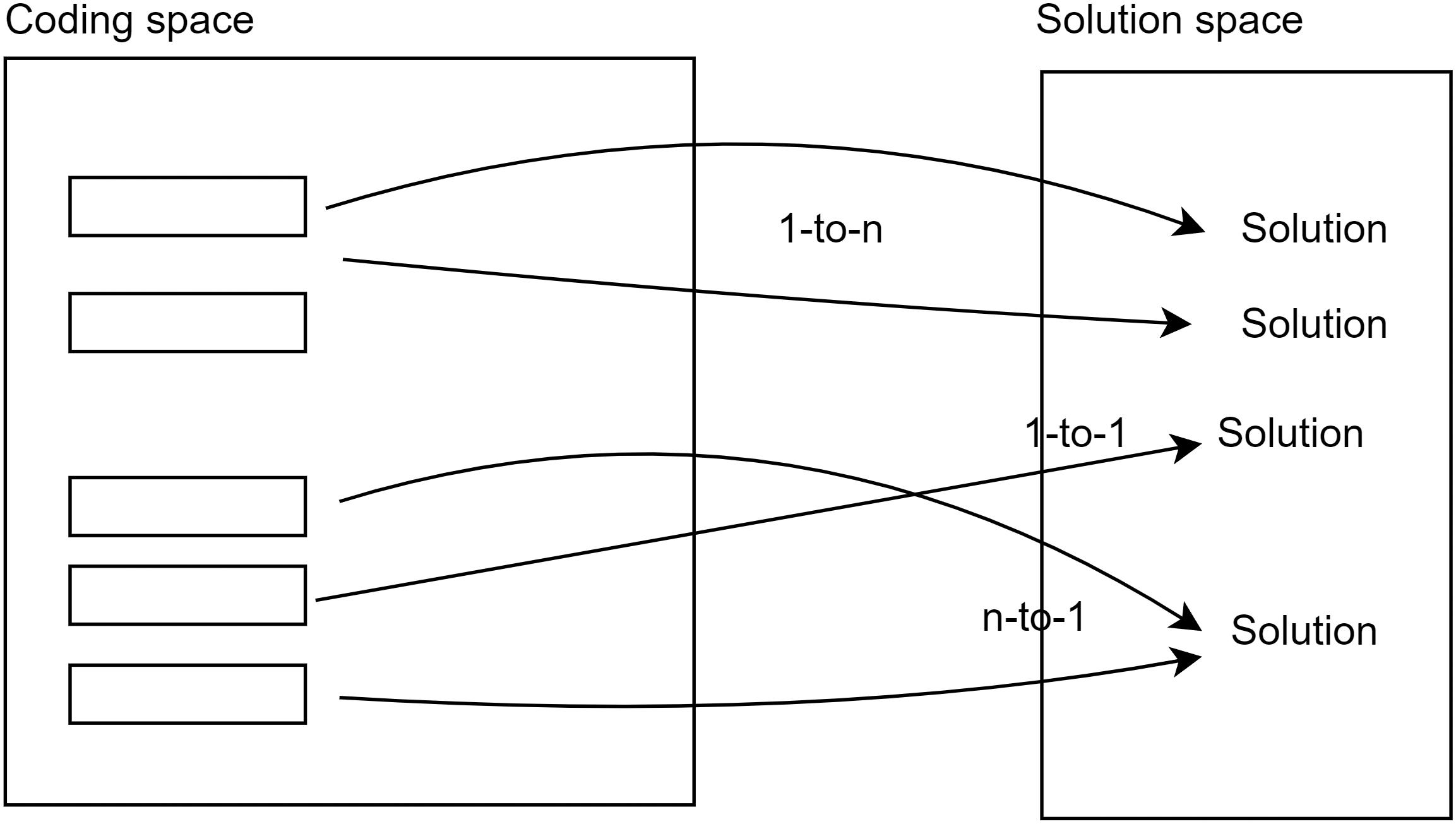
Figure 1: Mapping from coding to solution space

In summary, it is pertinent to highlight that many Operations Research (OR) problems find effective solutions through the utilization of indirect solution representations. The core concept involves exploring not the entire array of solutions, but rather a set of representations (such as the set of giant tours for VRP or the set of Bierwith’s vectors for Job-Shop, for instance). These objects, employed for indirect solution representation, typically take the form of vectors, enabling the formulation of mapping functions that operate within O(n) complexity. The primary advantage of employing these indirect representations lies in the metaheuristic’s exploration of a smaller-sized set of such representations (e.g., Bierwith’s vectors), in contrast to the larger set of solutions. This shift in focus redistributes the complexity of problem modeling away from the metaheuristic and onto the mapping function, resulting in a more manageable computational load for the metaheuristic.

2.2 Indirect Representation of Solutions: Proposition for Permutations

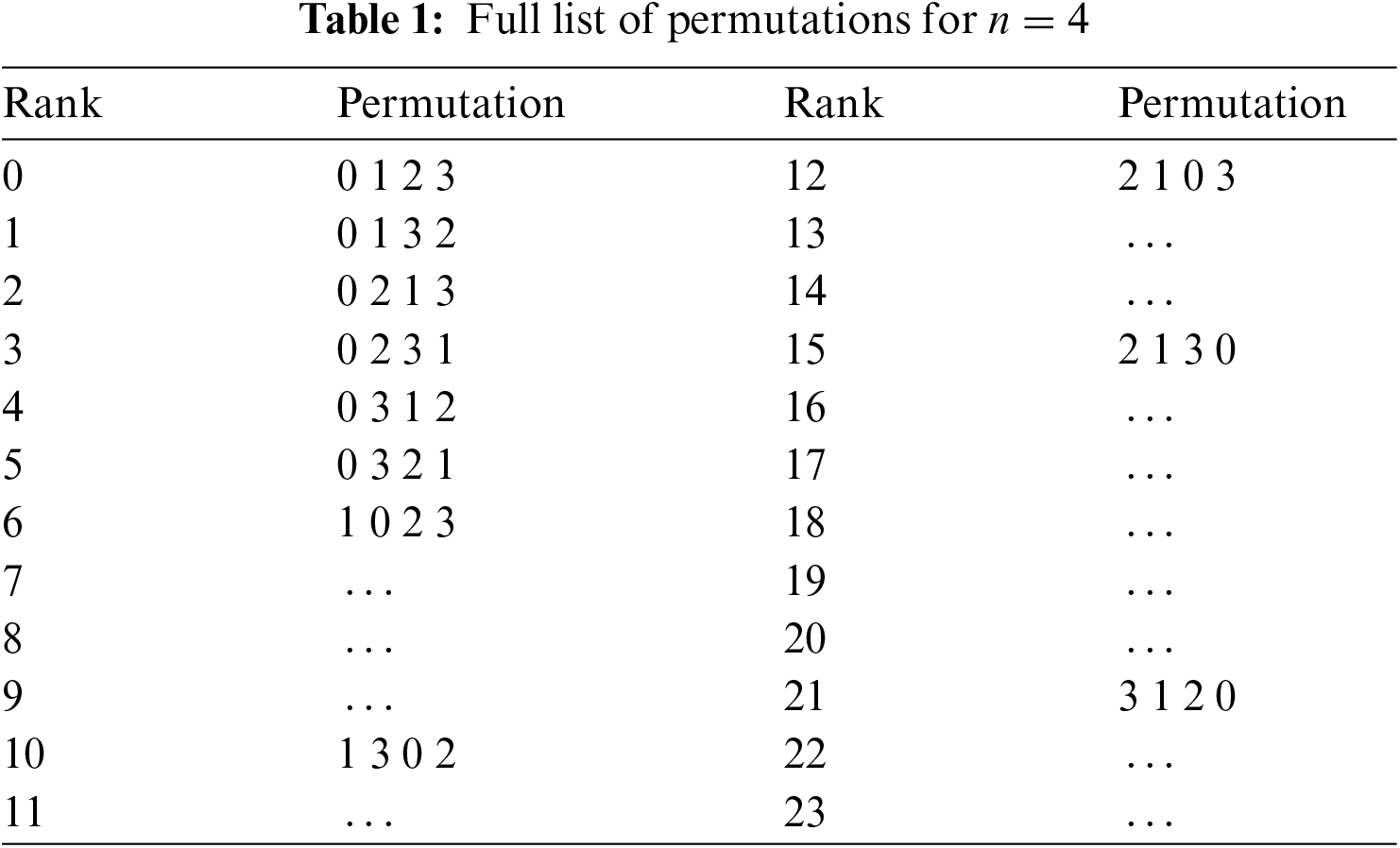
Within combinatorics, the Lehmer code offers an alternate means of encoding every possible permutation within a sequence composed of n numbers. This code serves as an exemplary system for enumerating permutations and stands as a prime illustration of an inversion table. The term “Lehmer code” honors Lehmer [14], although its existence traces back to at least 1888 [15]. Numerous methods exist for establishing this direct mapping, with the Lehmer code, also known as the inversion table, representing the most classical among them. An algorithmic depiction of this mapping was initially introduced in [16]. Indirect representations can leverage the one-to-one relationship between permutations and the so-called subexceedant functions, consequently associating a single integer number with the rank of the permutation.

Assume f is a bijection that associate each permutation over the interval [n]={0,1,…,n−1}:

f:[n]→[n](1)

f is the subexceedant [15,17] function defined by:

f(i) is the number of indices j<i such that σj<σi

Obviously the following remarks holds (subexceedant function):

∀i=1,…n,0≤f(i)≤i(2)

This property justifies the term ‘subsequent function’ a term that can be found, for example, in [17].

Moreover we have: f(0)=0

Let us note f denoted by:

f∼[f(n−1);f(n−2);…;f(1);f(0)](3)

Let us note Fn the set of functions satisfying the previous condition: Card(Fn)=n!. For example, F2={00,10} and F3={000,100,200,010,110,210}. The subexceedant function f related to σ can be obtained by iterative assignment of f[i]=σ[i]. The last elements of σ have to be decreased of one unit, to ensure that at the position i + 1 to n the number are in the interval [0;n−i] as stressed on Algorithm 1.

Algorithm 1. Conversion of σ into a subexceedant function f.

Example

Let us consider σ=[2;1;0;3]

To conclude, f=[2,1,0,0]=[f(3),f(2),f(1),f(0)] is the subexceedant function associated to σ=[2;1;0;3].

□

Conversely, given a subexceedant function f, it is possible to calculate the associated permutation using Algorithm 2.

Algorithm 2. Computation of σf.

Example

Let us σ=[5,1,4,0,2,3] and f=[_,_,_,_,_,_]

At iteration 1 the number σ[1]=5 is added to f

σ=[_,1,4,0,2,3] and f=[5,_,_,_,_,_]

At iteration 2 the number σ[2]=1 is added to f

σ=[_,_,3,0,1,2] and f=[5,1,_,_,_,_]

At iteration 3 the number σ[3]=3 is added to f

σ=[_,_,_,0,1,2] and f=[5,1,3,_,_,_]

At iteration 4 the number σ[4]=0 is added to f

σ=[_,_,_,_,0,1] and f=[5,1,3,0,_,_]

At iteration 5 the number σ[5]=0 is added to f

σ=[_,_,_,_,_,0] and f=[5,1,3,0,0,_]

At iteration 6 the number σ[6]=0 is added to f

σ=[_,_,_,_,_,_] and f=[5,1,3,0,0,0]

To conclude, f=[5,1,3,0,0,0] is the subexceedant function associated to σ=[5,1,4,0,2,3].

□

Reverse Example

Let us f=[5,1,3,0,0,0] and v=[5,4,3,2,1,0]

2.3 Indirect Representation of Solutions: Bijection with Permutation over Interval [n]

One-to-one correspondence with a permutation over the interval [n] and a function f:[n]→{0,…,n−1}.

Property

For any x∈N, we have:

x=∑i=0n−1xi.(i!)(4)

And f=(xn−1,xn−2…x0) is subexceedant for xi≤i because, if not, then xi.(i!)≥(i+1).(i!)=(i+1)!

□

Example

For example, we have:

208=1×5!+3×4!+2×3!+2×2!+0×1!+0×0!(5)

And

f=(1;3;2;2;0;0) is subexceedant

For example, we have 10=1×3!+2×2!+0×1!+0×0! and f=(1;2;0;0) is subexceedant.

For a set of n customers, we have n! permutations numbered from 0 to n!−1. Let us consider x∈[0;n!−1], i.e., a rank in the list. For a rank x∈[0;n!−1], it is possible to defined f and by consequence the permutation σ. To conclude for any rank x∈[0;n!−1] (Fig. 2):

•   we can compute the subexceedant function by decomposing x in the factorial base;

•   we can compute the permutation σf(x) associated to the subexceedant function f(x) (Algorithm 2);

•   we can compute the cost of any permutation σf(x) considering: cost= ∑i=0n−2dσi,σi+1+dσn−1,σ0, assuming di,j is the distance from customer i to customer j.

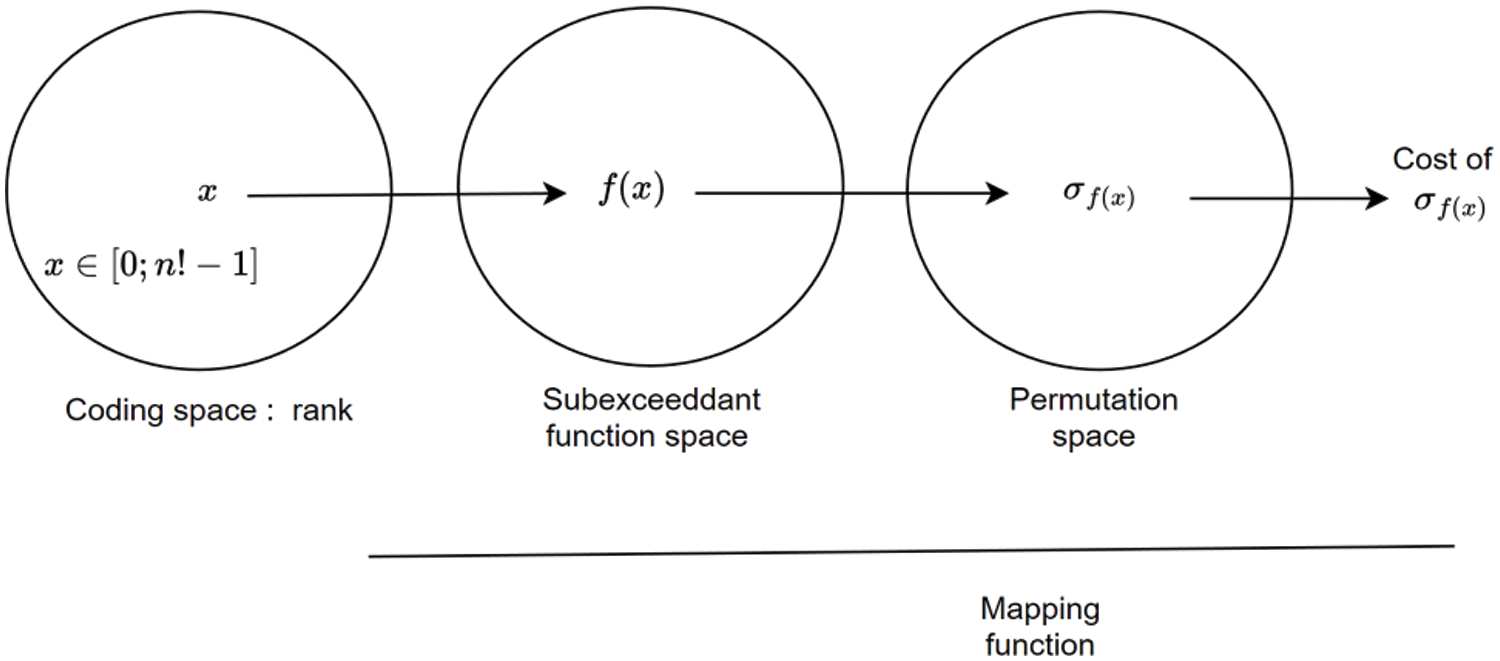
Figure 2: Mapping from coding to solution space

For convenience we denote:

m(x) as the cost of permutation σf(x) that is related to the rank x.

σx as the permutation associated with rank x whereas the correct notation should be σf(x).

This allows us to define the mapping function that associates a permutation with each rank x. Cheng et al. [13] pointed out that the most interesting mapping functions are the 1−to−1 functions, as they correspond to bijections between the two sets (the set of indirect encoding and the solutions). Note that the mapping function just defined is indeed a 1−to−1 function, unlike the functions commonly used in Operations Research, which are of the n−to−1 type (including for example the Split method in the VRP that is clearly of the n−to−1 type). By consequence, the cardinality of the code space (number of ranks) is equal to the number of permutations. For example, for n=4, we have 4!=24 permutations numbered from 0 to 23. The full list of permutations is provided on Table 1. The rank 10 is associated to the subexceedant function f=(1;2;0;0) since 10=1×3!+2×2!+0×1!+0×0!, and the subexceedant function f is associated to σ=[1;3;0;2]. The cost associated with σ is d1,3+d3,0+d0,2+d2,1, i.e., the sum of the distance from customer 1 to 3, plus the distance from customer 3 to 0, plus the distance from customer 0 to 2 plus distance from customer 2 to 1.

2.4 IQAOA Based Approach

Quantum Approximate Optimization Algorithms [18] take advantage of alternations between the cost function investigation which is modeled by a Hamiltonian HP from one side and a driver Hamiltonian operator HD. The Quantum Alternating Operator Ansatz [4] takes into consideration a general parameterized family of unitary operators and create an efficient alternative to the Adiabatic Optimization. As introduced by [2], the wave function evolution of a quantum-mechanical system is given by

∂.∂t|ψ(x,t)⟩=−iℏ.H(t).|ψ(x,t)⟩

where the energy is defined by H(t), ℏ is derived from Plank constant and |ψ(x,t)⟩ are states vectors. If H is time independent the solution is |ψt⟩=e−iℏ.t.H.|ψ0⟩. Note that the solution is |ψT⟩=e−iℏ.∫oTH(u).du.|ψ0⟩ in the general time dependent situation. Describing a problem with a Hamiltonian H and an initial state |ψ0⟩ allows to compute the ground state. The time-dependent Schrödinger’s equation can be explicitly solved in very specific situation (see [19], for one example).

2.5 Modelling Rank and Search Space Investigation

IQAOA seeks to solve a hard optimization problem i.e., minimizing or maximizing one objective function m(x) that is assumed to act on n−bits strings that model only the rank of one solution. IQAOA is based on p consecutive iterations of one Hamiltonian HP cumulated with a driver Hamiltonian HD, where this weighted sum of Hamiltonian terms varies in time. The Hamiltonian H maps the function the rank x with 2n eigenvalues that model the 2n values of the rank. The Hamiltonian is implemented into a quantum circuit by deriving UH(t)=e−i.H.t with t∈[0;2π] and using only and Z-rotations and t refers to the weight in the iterative search process of QAOA. This permits to model all the rank of the TSP.

2.6 Search Space Investigation

The β→ and γ→ parametrized a quantum state |φ(β→,γ→)⟩ which defines a solution rank x related to probability |⟨x|φ(β→,γ→)⟩|2 and related to the expectation value ⟨φ(β→,γ→)|Cp|φ(β→,γ→)⟩ estimated by sampling. Each sampling gives a measure that is a rank in the list of TSP solution that can be evaluated using the 1−to−1 function into the associated subexceedant function first, into the permutation σf(x) second and next the m(x) cost of the permutation. This sampling permit to estimate the average cost of the problem P: Cp(β→,γ→) taking advantage of the mapping function.

The quantum computer is used to construct the state:

|φ(β→,γ→)⟩=e−i.β→.HD.e−i.γ→.HP(6)

For a fixed β→,γ→, the quantum computer is used to make the stage |φ(β→,γ→)⟩ and the measure in the computational basis is achieved to get a string x and evaluated ⟨φ(β→,γ→)|Cp|φ(β→,γ→)⟩.

The binary representation of rank

rank=∑j=0nxj.2jwithxj∈{0;1}(7)

and the

HP=12∑j=0n(Id−Zj).2j(8)

Then the circuit is:

e−12∑j=0nZj.2j=Rz(20)⊗Rz(21)…Rz(2n)(9)

And to conclude:

e−i.γ→.HP=Rz(20.γ)⊗Rz(21.γ)…Rz(2n.γ)(10)

The algorithm description is illustrated in Fig. 3 that is included in a main loop iterative method introduced in the next section.

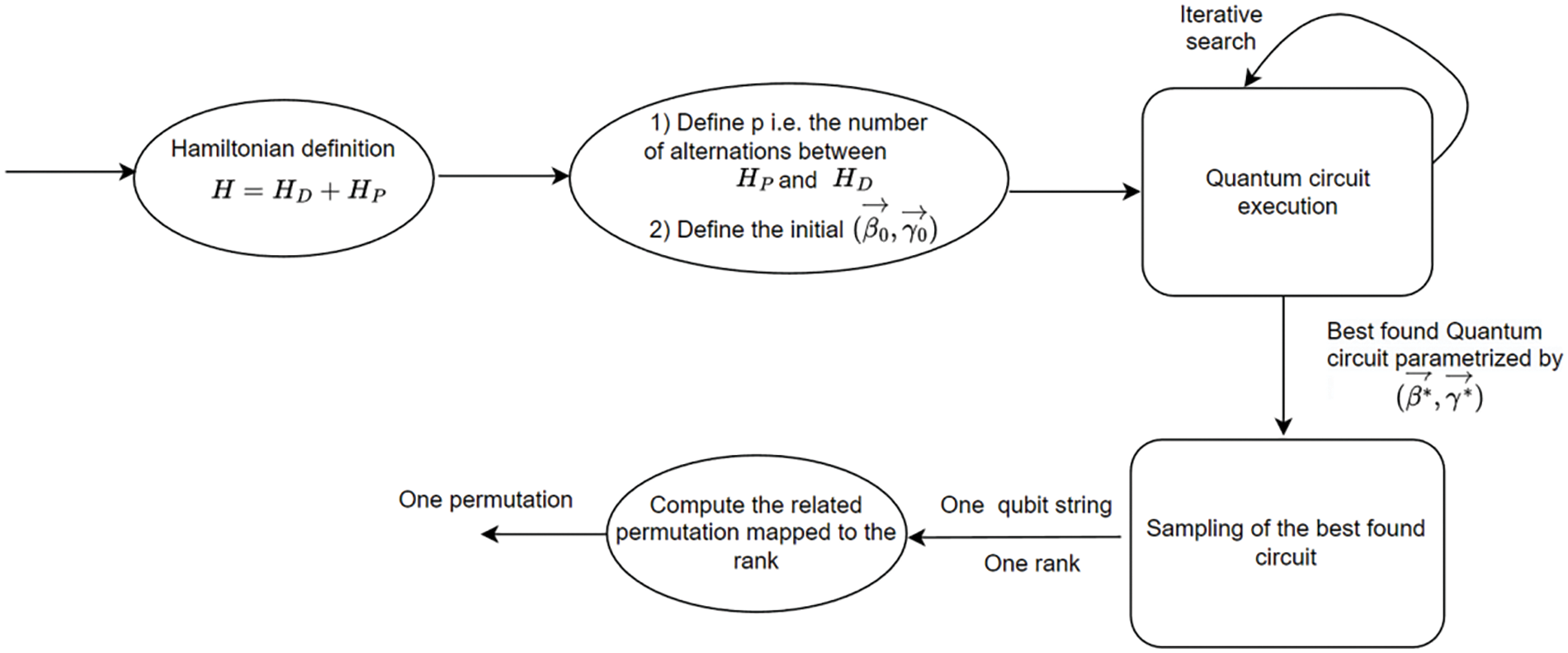
Figure 3: Partial representation of IQAOA principle

IQAOA efficiency strongly relies on some key-points:

•   The capacity to provide a significant ratio between the estimation of Cp(β→,γ→) as regards as the number of shot.

•   the last distribution |ψ(β∗→,γ∗→)⟩ must be collected on a small subset of solutions as regards avoiding a inefficient enumerations: it is suitable that the algorithm converged to high quality of solutions.

•   The availability of one dedicated methods to compute the (β∗→,γ∗→).

•   The number of qubits p such that 2p≥n! and the number of gates is very small as regards the number of qubits and gates.

Let us note that the expectation value ⟨φ(β→,γ→)|Cp|φ(β→,γ→)⟩ estimated by sampling that is the common criteria with QAOA can be replaced by more specific criteria including median, quartile or any convenient combination of this criteria depending on the objective we expect on the final distribution of probabilities. Contrary to the classical OR approaches, on a quantum computer, all the solution are simultaneously investigated giving a potential advantage as regards the partial enumeration technics.

2.7 C_GRASP × ELS for (β∗→,γ∗→) Computation

Investigation of the optimal parameters required powerful local search, or meta-heuristic based approaches including but not limited to Cobyla, Genetic Algorithm, GRASP × ELS… with performances that are related to the problem under consideration. In the OR (Operationnal Research) community the GRASP × ELS has been proved to be the more adequate for a large class of problems. The GRASP × ELS is a fusion of two powerful algorithms: GRASP (Greedy Randomized Adaptive Search Procedure) [20] and ELS (Evolutionary Local Search) [11,21]. This combination joins the strengths of both methods. The multi-start strategy of GRASP relies on a greedy randomized heuristic that generates the set of initial solutions (np solutions). These solutions are then refined through a local search procedure (Fig. 4).

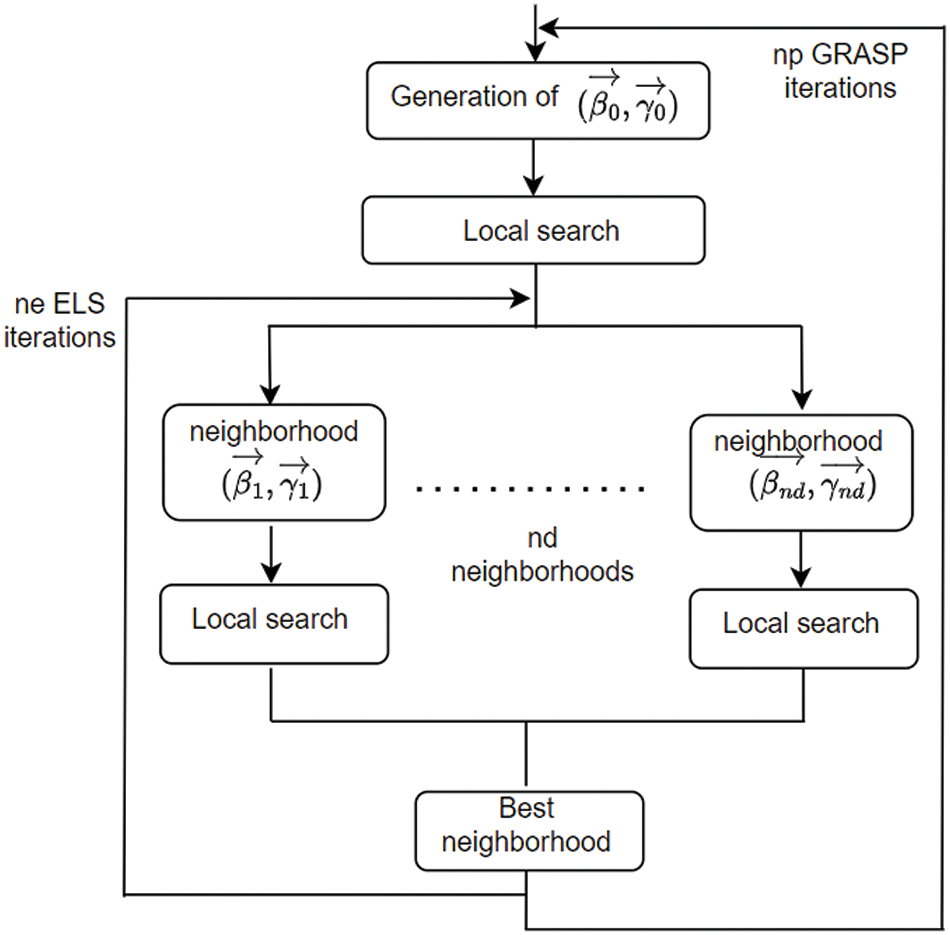
Figure 4: C_GRASP × ELS algorithm

The second component is ELS, an extension of ILS (Iterated Local Search) introduced by [22]. In each iteration (ne), a duplicate of the current solution is created, and this copy generates nd child solutions. The best-performing solution among these offspring becomes the new current solution. The overarching goal of GRASP is to enhance diversity during the exploration of the global solution space, while ELS’s purpose is to intensify the search within the vicinity of the current local optimum. Let us note that the method lies on local search and not on gradient and that suppose an ad hoc neighborhood definition. To summarize, the proposed model unites the mapping of the circuit encoding of the string into the solution space (Fig. 5) with the variational parameters optimization (GRASP×ELS) into a classical way that meet the QAOA requirement as stressed in [23] for example. Note the special role of measurement that permits to evaluate one estimation of the average cost for example [24] or any relevant criteria [25].

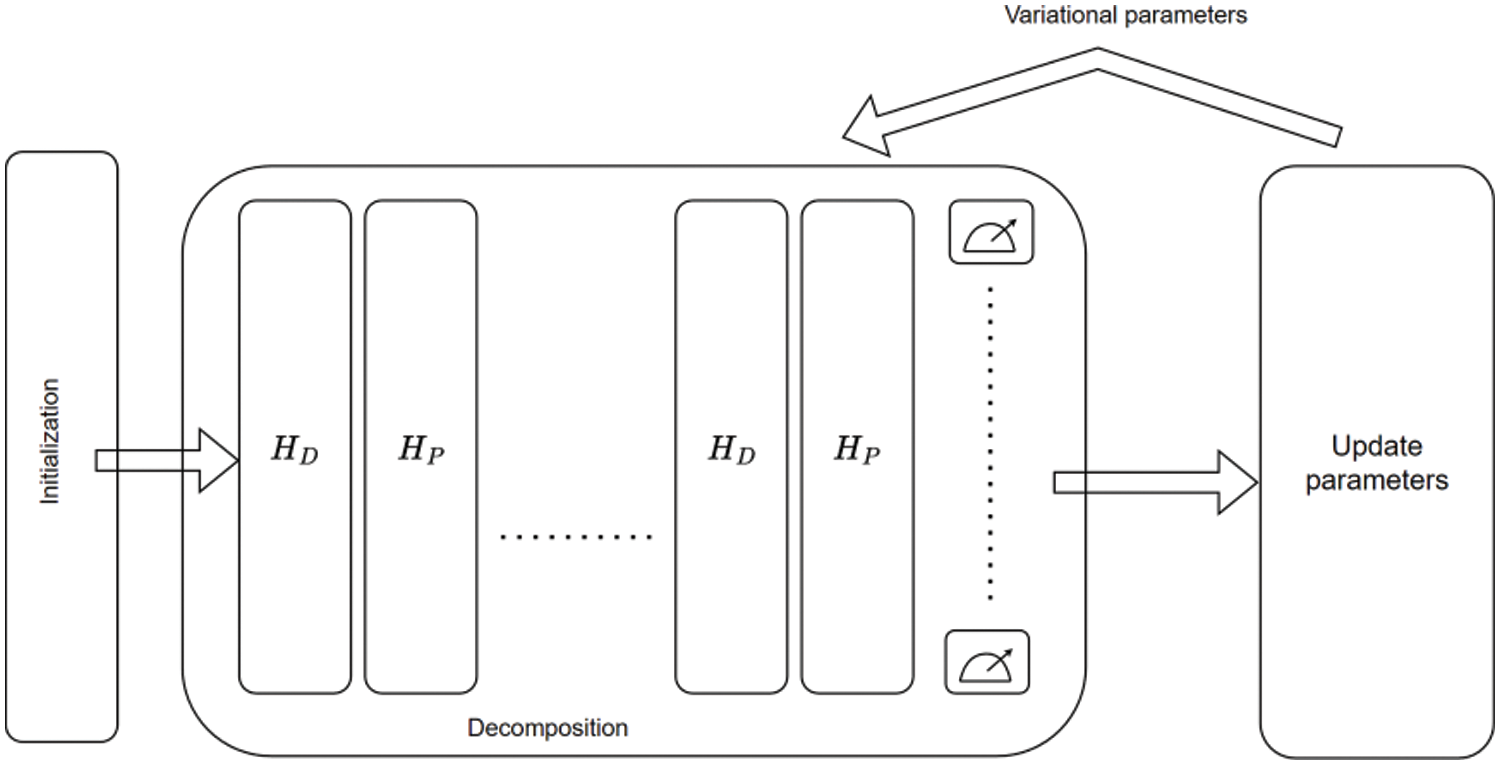
Figure 5: Classical QAOA optimization principles

Remark 1.

An efficient implementation of C_GRASP × ELS for Continuous GRASP × ELS required a neighbouring system that consists in a proper definition of Δβ→ and Δγ→.

(β→,γ→)→(β→+Δβ→;γ→+Δγ→)(11)

Remark 2.

For efficiency reason C_GRASP × ELS can be used to optimize simultaneously β→ and γ→ first and to minimize second γ→ only.

Remark 3.

Depending on the desired probability distribution, it is necessary to choose the right criteria or criteria to minimize. Among all these criteria, we can mention, without aiming to be exhaustive:

•   Minimization of the expectation value of the distribution that provides insight into the central tendency;

•   Minimization of the decile, i.e., minimization of the data set part that contain 10% of the data;

•   Minimization of the expectation value of the decile, i.e., expectation value of the data that contain 10% of the data;

•   Minimization of the quartile, i.e., minimization of the data set part that contain 25% of the data.

•   Minimization of the expectation value of the quartile, i.e., expectation value of the data that contain 25% of the data.

The quartile and the decile are used for summarizing the central tendency and spread of a dataset. Both quartile and decile provide a way to assess the distribution and variability of data while also identifying potential outliers and extreme values. To obtain a probability distribution that concentrates probabilities on low-cost solutions and avoids having a large number of values with residual probabilities, one can consider combinations of both the mean and a criterion related to the mean trend (e.g., decile or quartile, for instance). The numerical tests conducted and presented below demonstrate that it is possible to obtain a probability distribution that concentrates on high-quality solutions close to the optimal solution and even on the optimal solution itself. These tests are performed on instances ranging from 6 to 10 clients with different types of objectives to minimize and various parameters. It is worth noting that the parameters used were determined after a brief numerical study but were not subject to a specific investigation, which would be beyond the scope of this publication. The indirect QAOA we introduce permit to define very compact quantum circuit with a very small number of gates favoring the execution on real quantum computing however, in the NISQ era simulator with no noise is the common way to perform experimentation. All the experiments have been achieved using Qiskit (IBM) using the simulator. The quality of quantum gates strongly influences of all quantum algorithm.

3  Numerical Experiments

3.1 Resolution of a TSP with 6 Customers

The total number of permutations is 720 but there is only 53 different costs and the distance between customers are introduced in Table 2. A sampling of permutations permits to show that the high quality solutions have a very low probability (Fig. 6). Note that the higher probabilities are related to very low quality solutions: some solution with a cost about 800 and 900 have a probability greater than 15%.

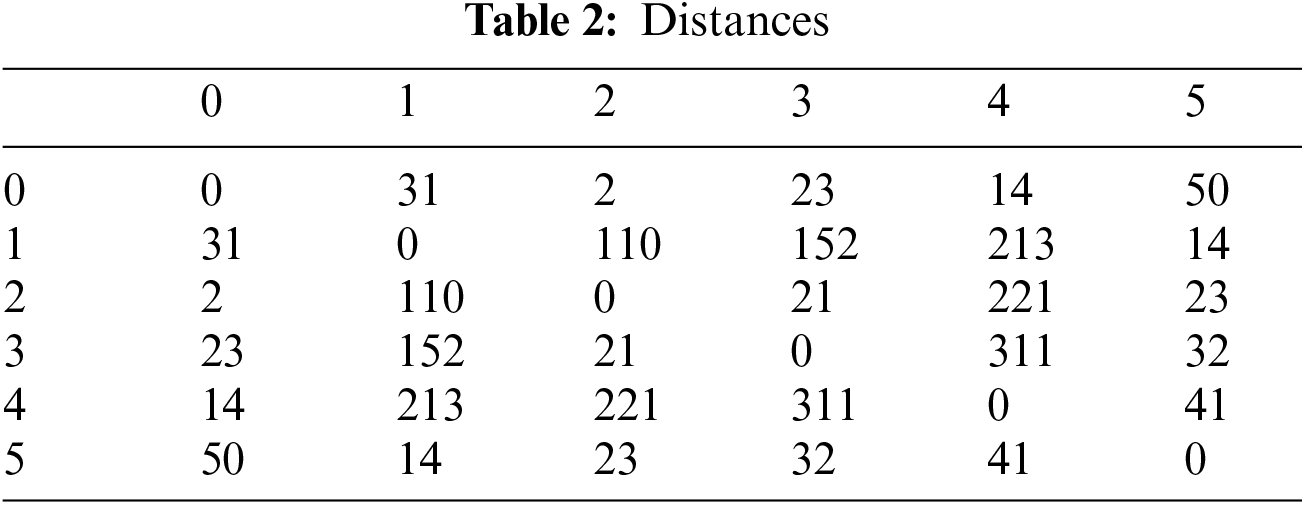
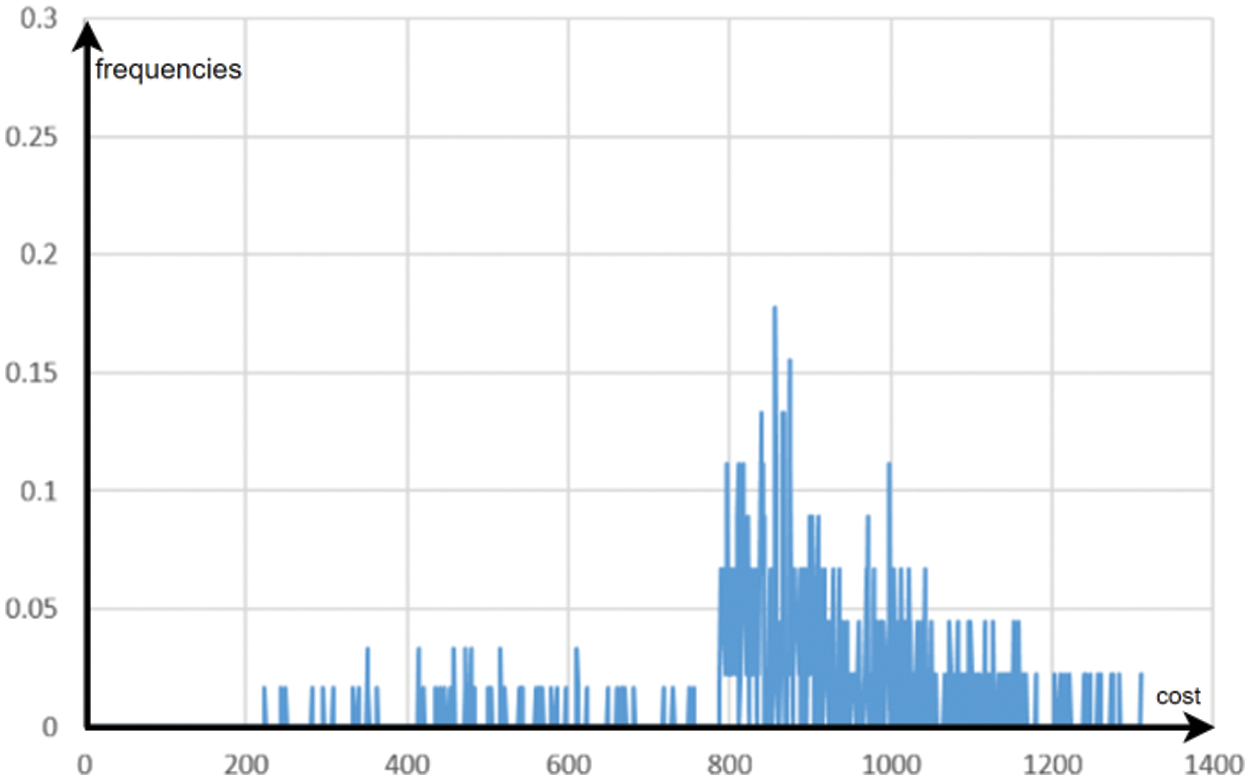
Figure 6: Initial distribution of solutions

The instance has 12 optimal solutions listed in Table 3 that shows the correspondence between rank, permutation and cost.

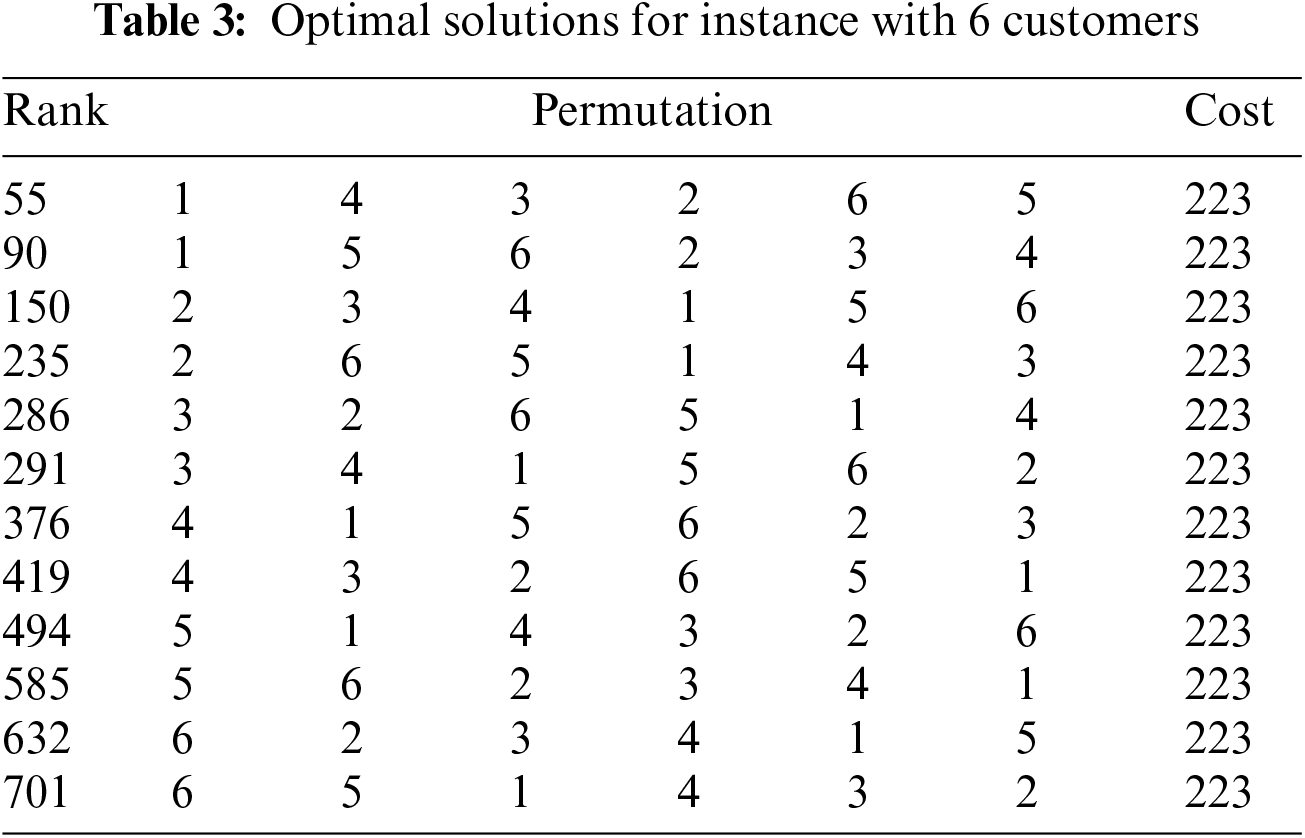
C_GRASP × ELS is executed with the following parameters:

•   Minimization of the expectation value of the decile plus the expectation value of the distribution.

•   The sampling of |φ(β→,γ→)⟩ is achieved with 50 shots.

•   The parameters np=20, ne=5, nd=3 for the first C_GRASP × ELS execution to optimize β→ and γ→.

•   The parameters np=20, ne=5, nd=5 for the second C_GRASP × ELS execution to optimize γ→.

•   Both Δβ→ and Δγ→ (in the local search) vary from 0.1 to 0.001 first at the beginning of the ELS. The value 0.001 is slowly decreased (divided by 10) at each iteration neighborhood generation.

•   The quantum circuit is parametrized with p=2.

•   40 shots are used during the optimization process to obtain a suitable evaluation of the probability distribution.

•   1000 shots are used at the end of the optimization to obtain an accurate evaluation of the probability distribution.

The landscape of the function, with ranks represented on the x-axis, is not a smooth landscape that facilitates the search for local minima (Fig. 7). However, the C_GRASP x ELS method easily, with a relatively low number of iterations, finds a minimum of the function. Likewise, it seems evident that gradient-based methods will face significant challenges with this type of problem.

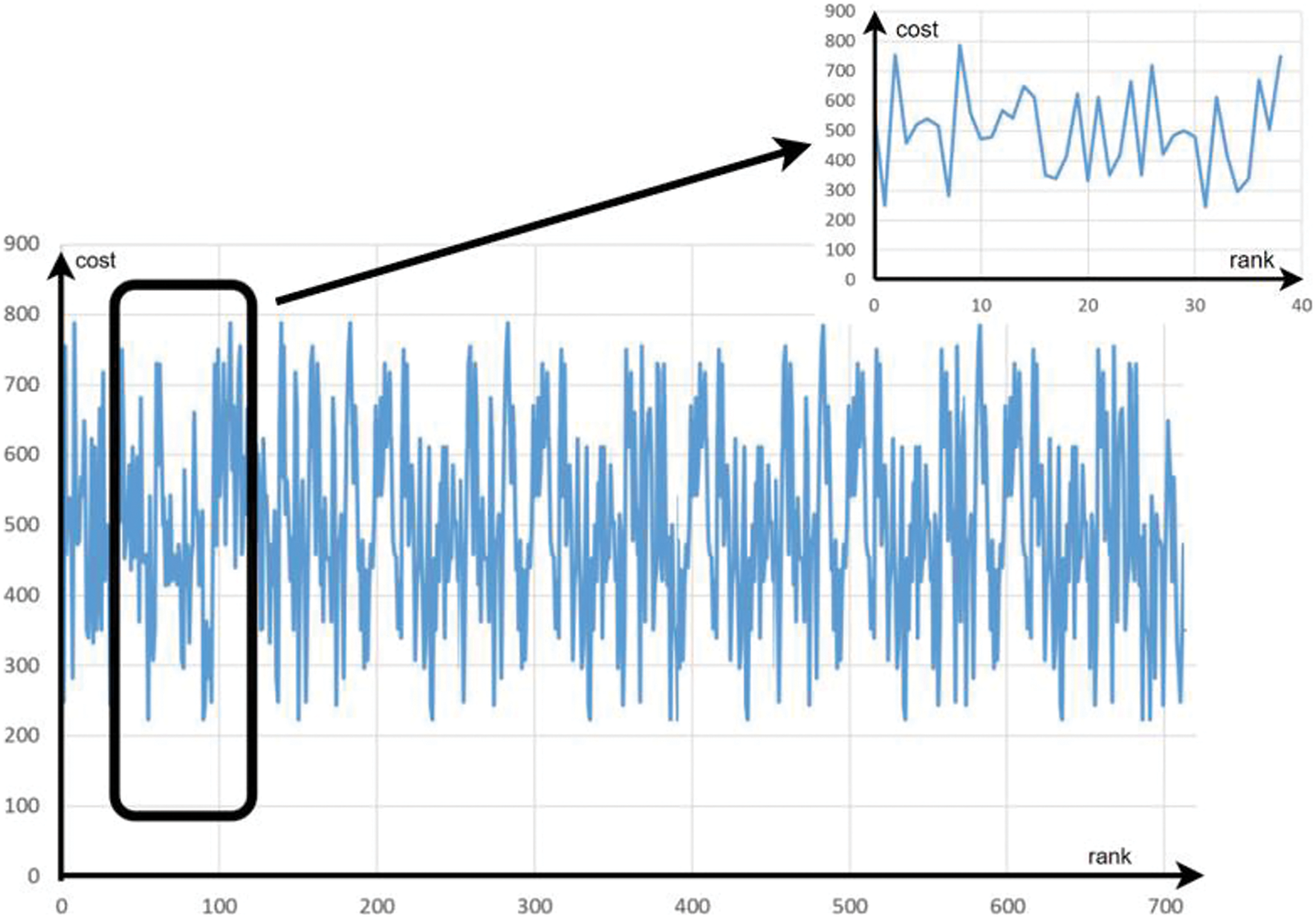
Figure 7: Function landscape

The sampling with 1000 shots gives 1010111101 with 283 shots (Fig. 8) meaning that about 28% of the probabilities is now on 1010111101 that model the rank 701 and the rank number 701 is mapped into the permutation σ=[6,5,1,4,3,2].

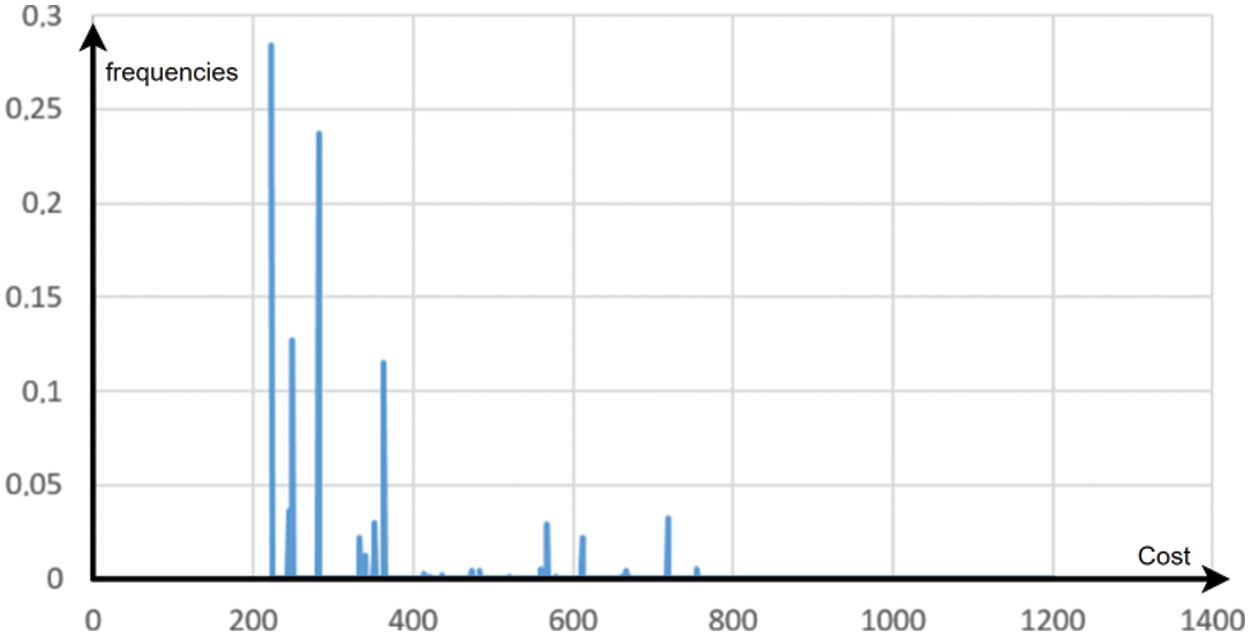
Figure 8: Final distribution of solutions

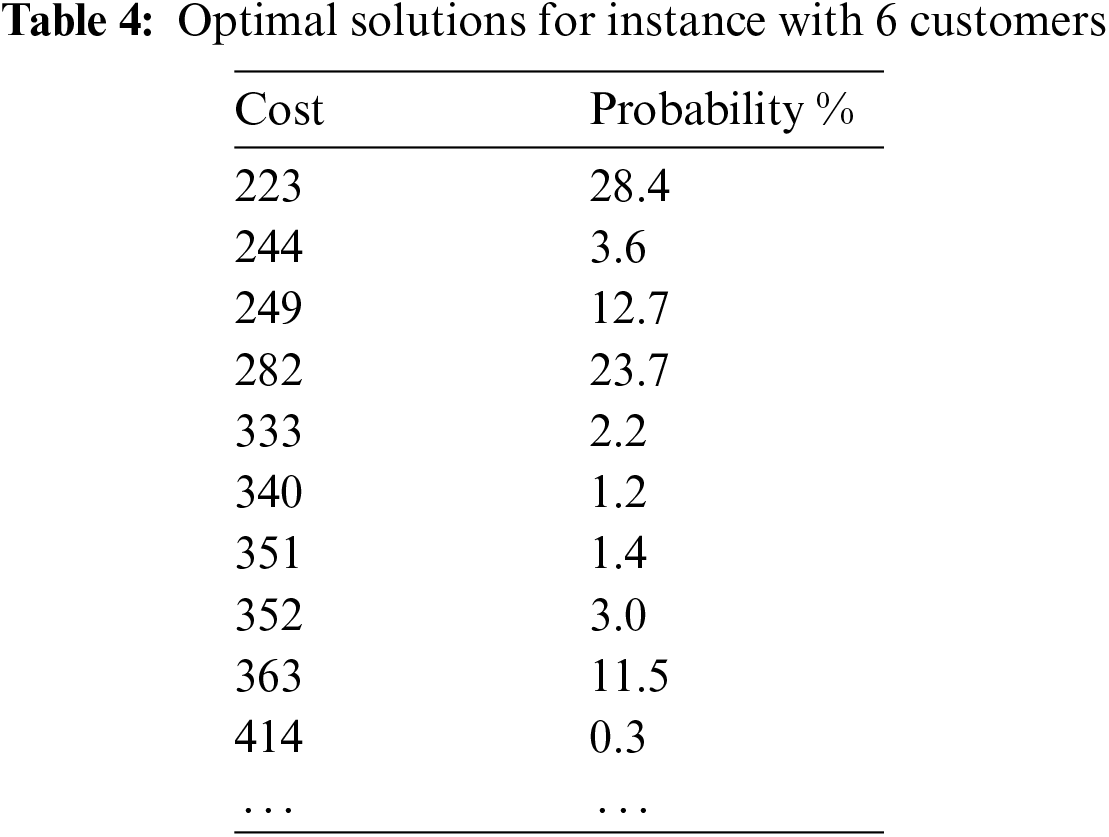
The details provided in Table 4 confirm what the visual representation suggests, namely very high probabilities concentrated on low-cost solutions, thus demonstrating the effectiveness of the IQAOA method in solving this 6-customers TSP problem.

3.2 Resolution of a TSP with 8 Customers

The total number of permutations is 40,320 but there are only 833 different costs and the distance between customers are introduced in Table 5.

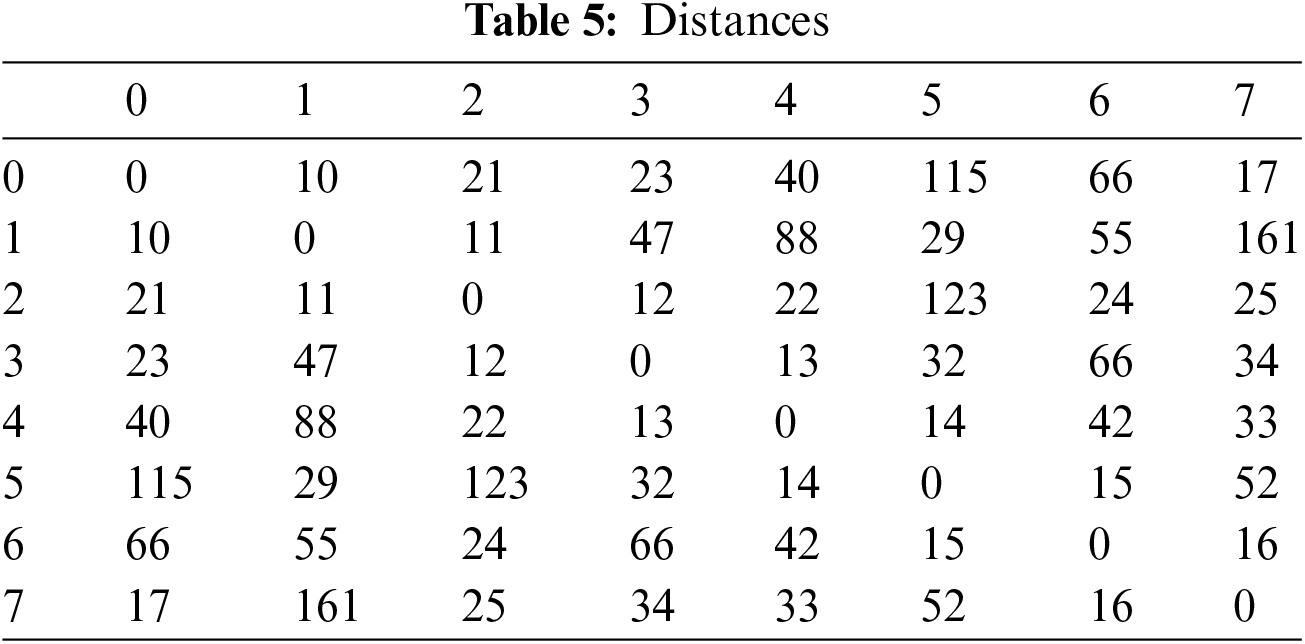
The optimal solution is 108 avec the related family permutation is: σ=[1,2,3,4,5,6,7,8].

The experiments were carried out with:

•   The parameters np=20, ne=5, nd=3 for the first C_GRASP × ELS execution to optimize simultaneously β→ and γ→.

•   The parameters np=20, ne=5, nd=5 for the second C_GRASP × ELS execution to optimize γ→.

The instance encompasses 16 optimal solutions that value 108 meaning that uniform sampling gives a probability about 0.039% to find one optimal solution (Fig. 9).

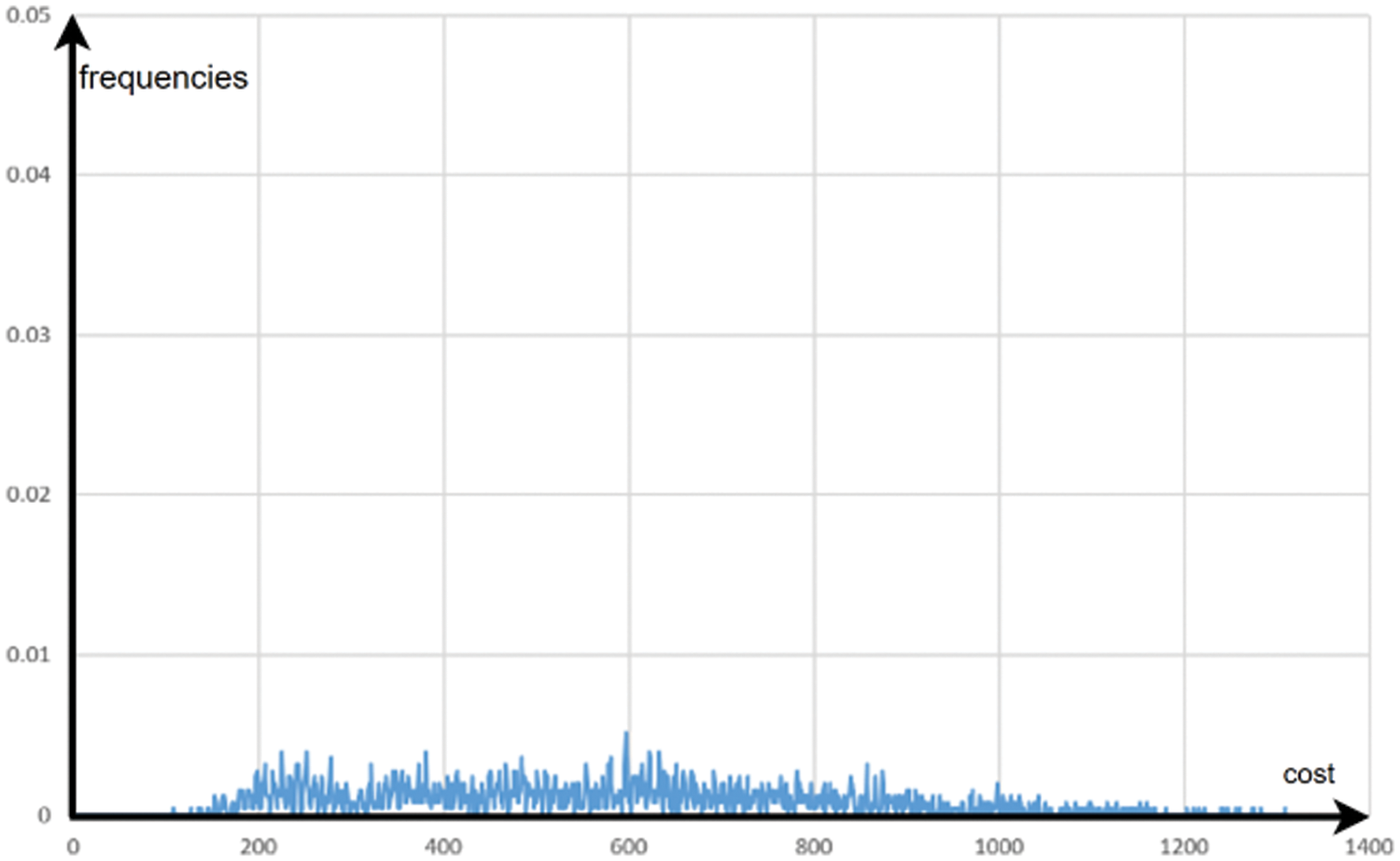
Figure 9: Initial distribution of solutions for the instance with 8 customers

The representations of the distributions in Figs. 9 and 10 show that the probability distribution has been significantly altered to concentrate on high-quality solutions. It should be noted that the median is 306, which means that 50% of the data corresponds to solutions with costs lower than 306. The final sampling achieved at the end of the optimization gives probability of 4.2% associated with 108. The fact that the probability distribution only marks certain solutions, and that this distribution is very different from a uniform distribution, is clearly visible in the diagram of Fig. 11, where the various possible ranks are represented on the x-axis.

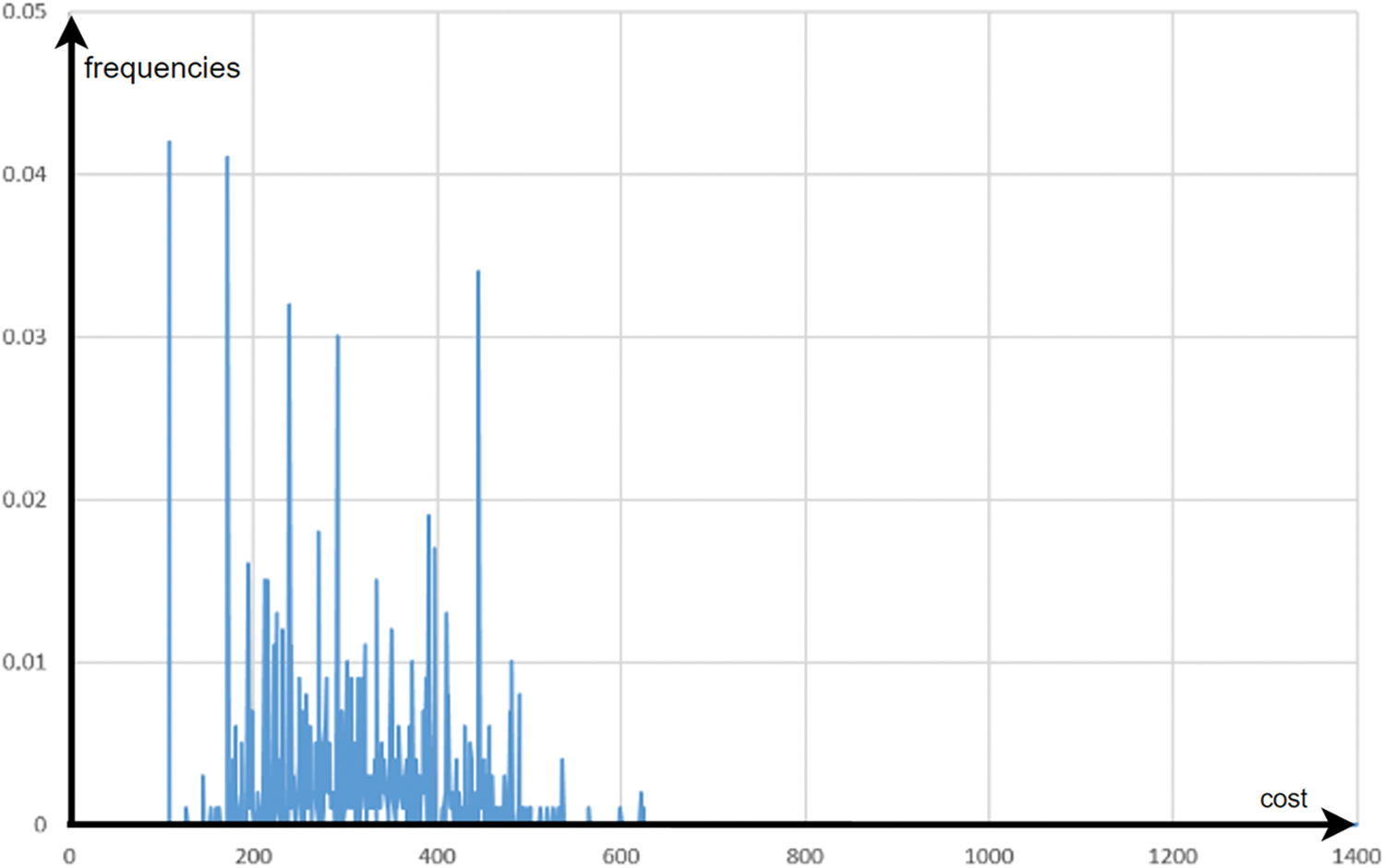
Figure 10: Final distribution of solutions for the instance with 8 customers

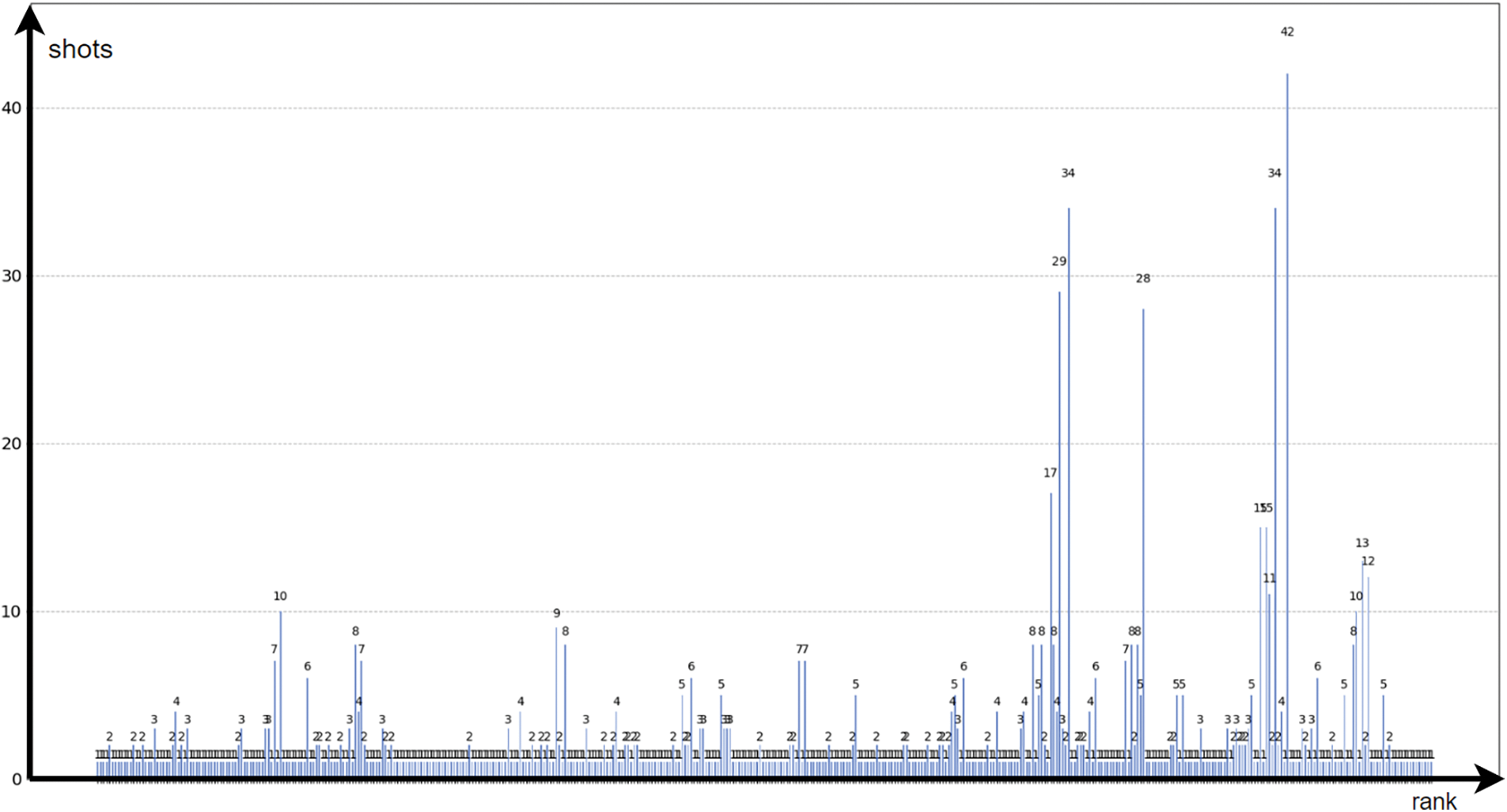
Figure 11: Final distribution of solutions for the instance with 8 customers—Qiskit vizualisation

It is difficult to give a representation of the function to minimize. However, Fig. 12 gives a partial representation of β→ with the cost, that pushes us into considering that the function encompasses numerous local minima.

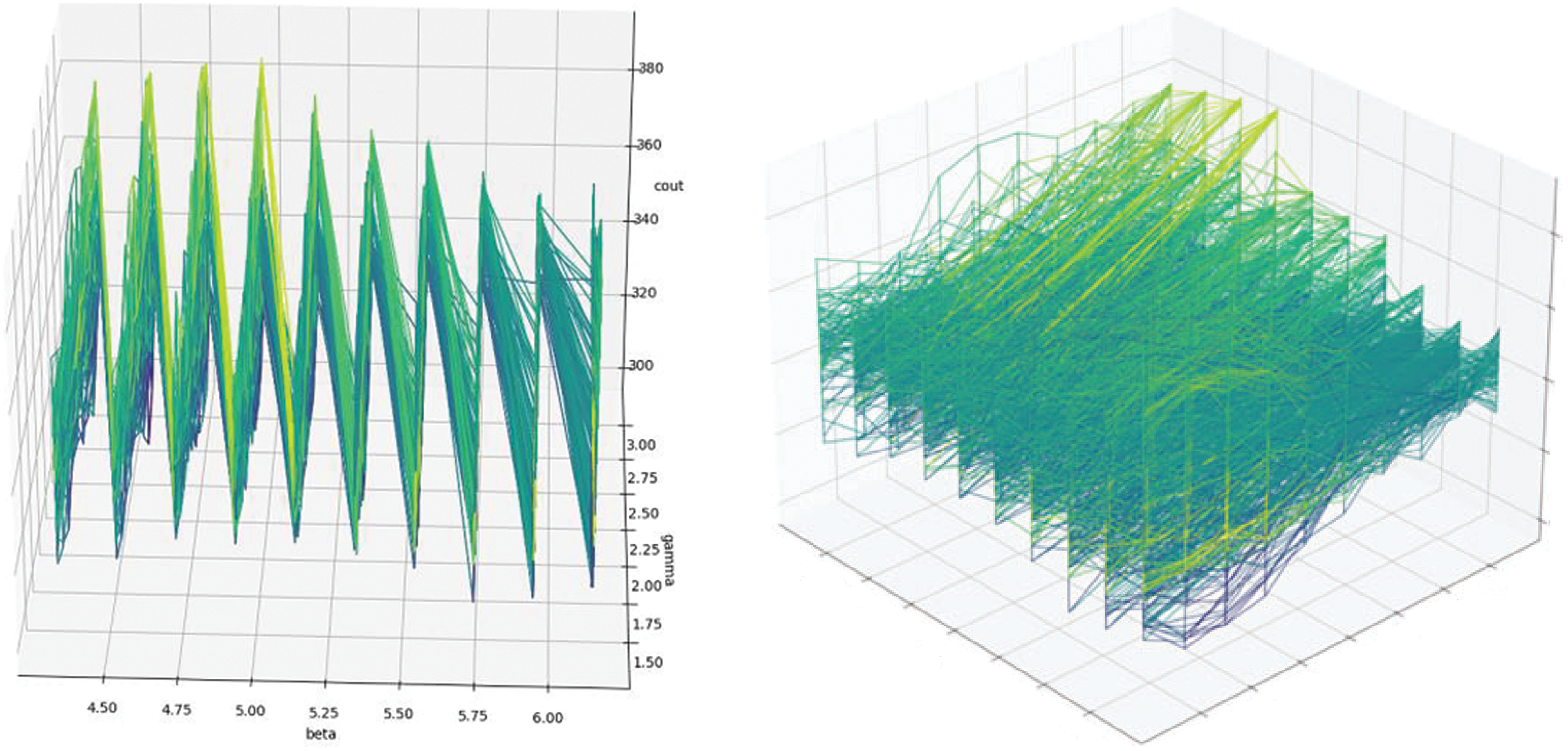
Figure 12: Partial representation of the solution landscape just around the best solution found

3.3 Resolution of a TSP with 9 Customers

The experiments were carried out with:

•   The parameters np=10, ne=10, nd=3 for the first C_GRASP × ELS execution to optimize simultaneously β→ and γ→.

•   The parameters np=10, ne=10, nd=5 for the second C_GRASP × ELS execution to optimize γ→.

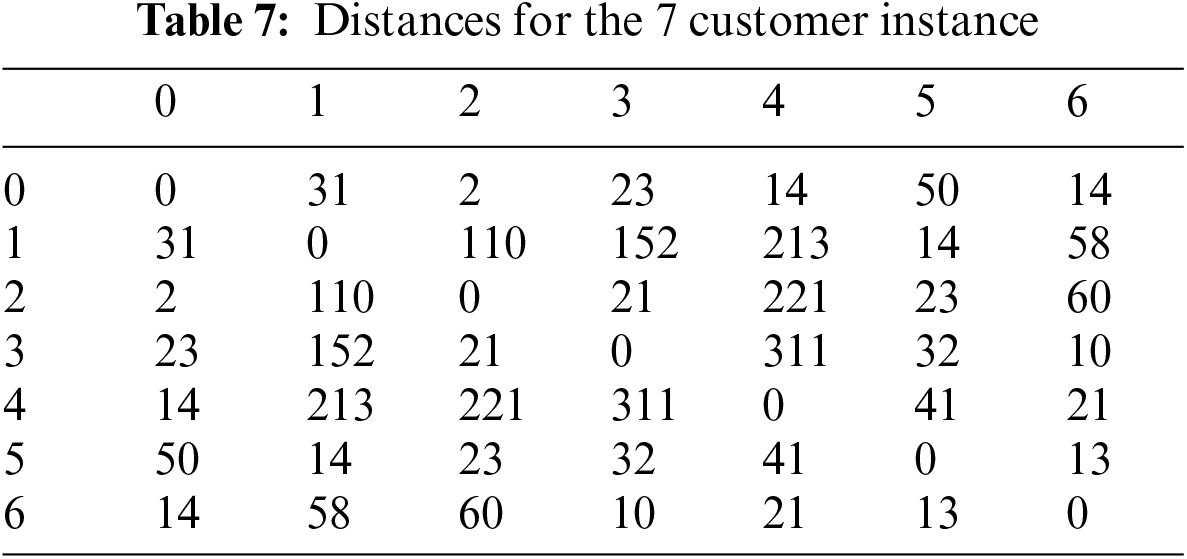
The distances used are introduced in Table 6. The optimal solution is 137 avec the related family permutation is: σ=[1,3,7,2,6,4,5,9,8]. The total number of solutions is 362,880 permutations and 310 different costs. The final sampling achieved at the end of the optimization gives probability of 0.6% associated with 108 (Fig. 13) which is 40 times better that the probability to find 108 by one uniform random sample that is only of 0.014% (there is only 54 permutations that gives 108).

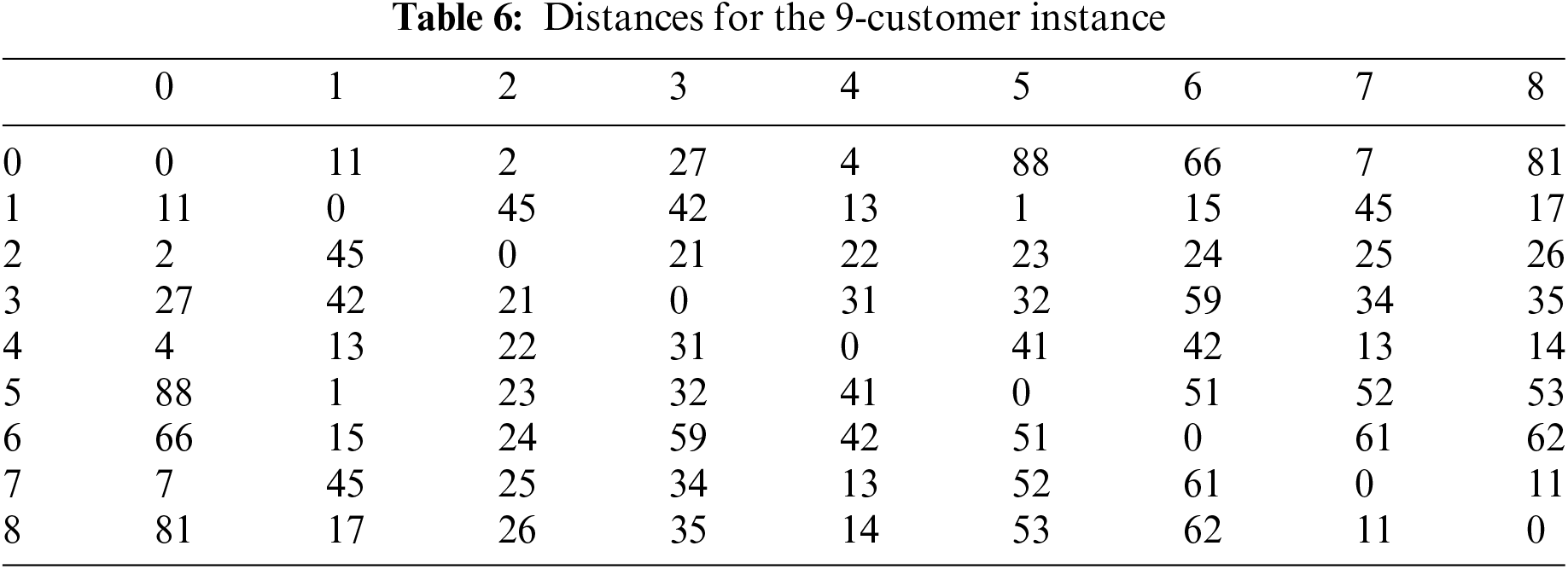
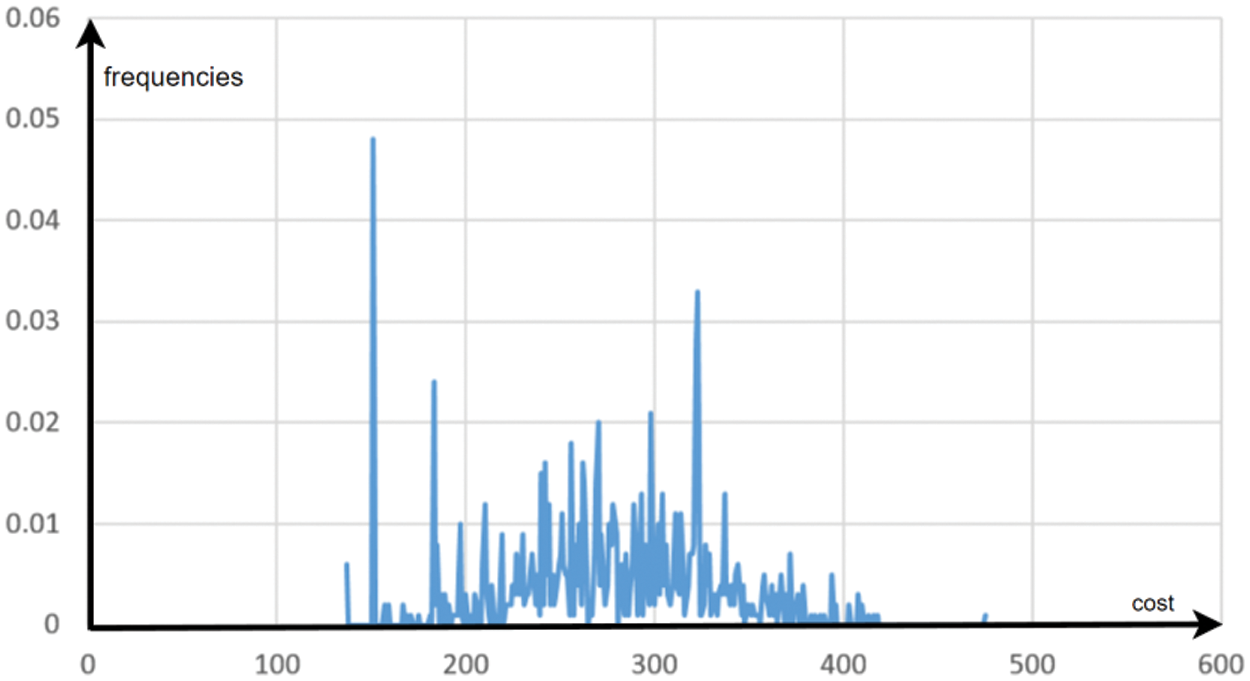
Figure 13: Final distribution of solutions for the instance with 9 customers

3.4 Resolution of a TSP with 10 Customers

A 10-customer instance is introduced in Appendix A and B results meet the results obtained with smaller instances.

3.5 VRP Resolution

The vehicle routing problem (VRP) extends the TSP by including a demand di on nodes that has to be serviced, and a fleet of vehicles of capacity W. Reference [10] introduced an algorithm to transform optimally any permutation σ into a solution of the VRP by execution on one shortest path into an auxiliary graph. Such decomposition has been intensively used in routing problem thanks to the publication of [11] which defines a metaheuristic based method that takes advantages of such decomposition. Using the Split algorithm, it is possible to transform a rank into a VRP solution. The IQAOA capability in VRP solving is evaluated on the 7 customers VRP instances introduced in Tables 7 and 8 with vehicles of capacity 10.

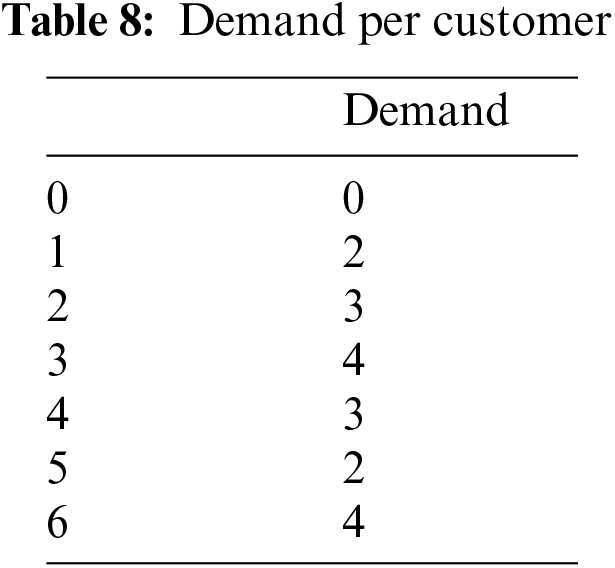
The final sampling achieved at the end of the optimization gives probability of 13% to have a solution lower than 151 (Fig. 14) which is 6 times better that the probability to find 108 by one uniform random sample (Fig. 15).

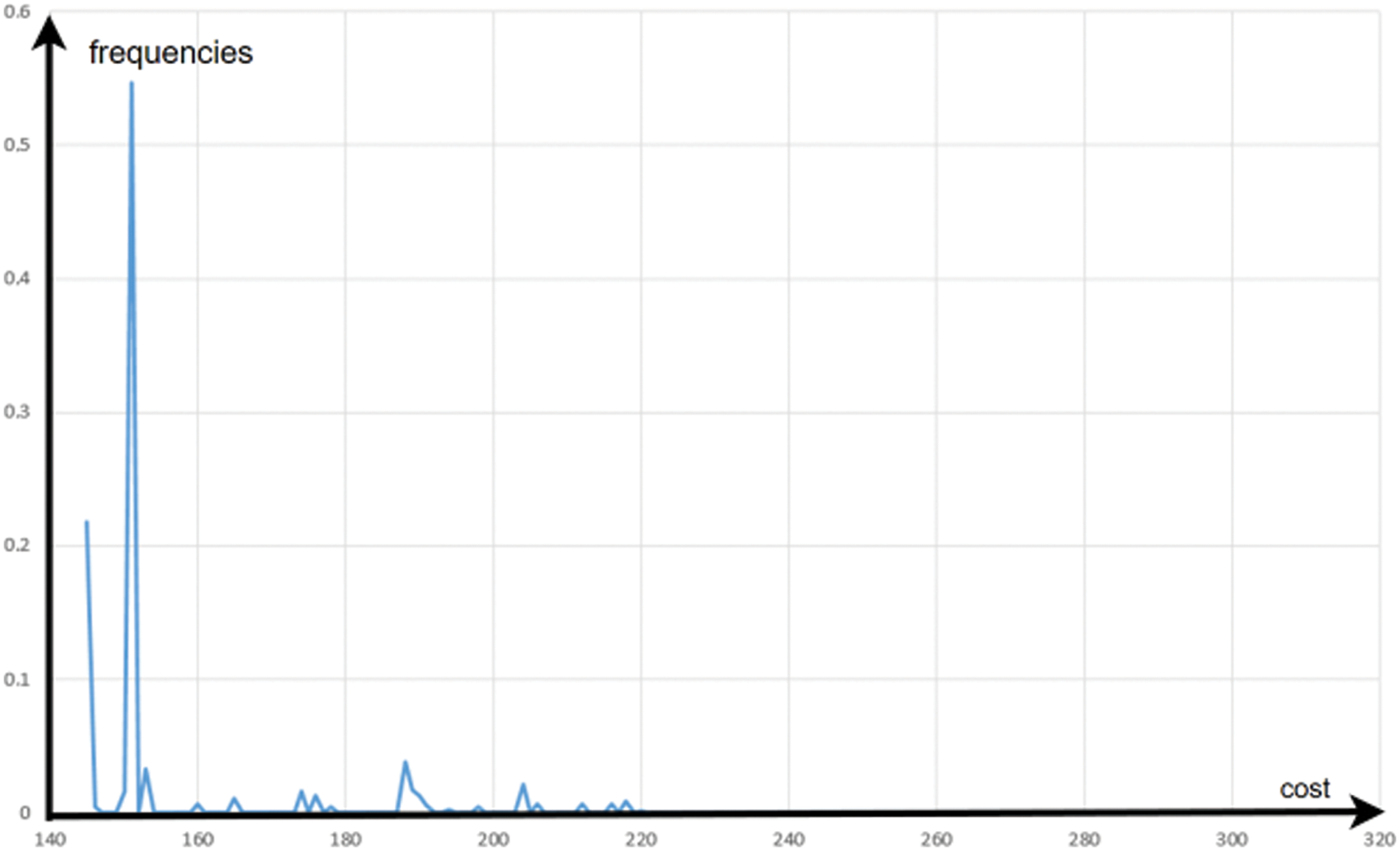
Figure 14: Final distribution of solutions for the VRP instance

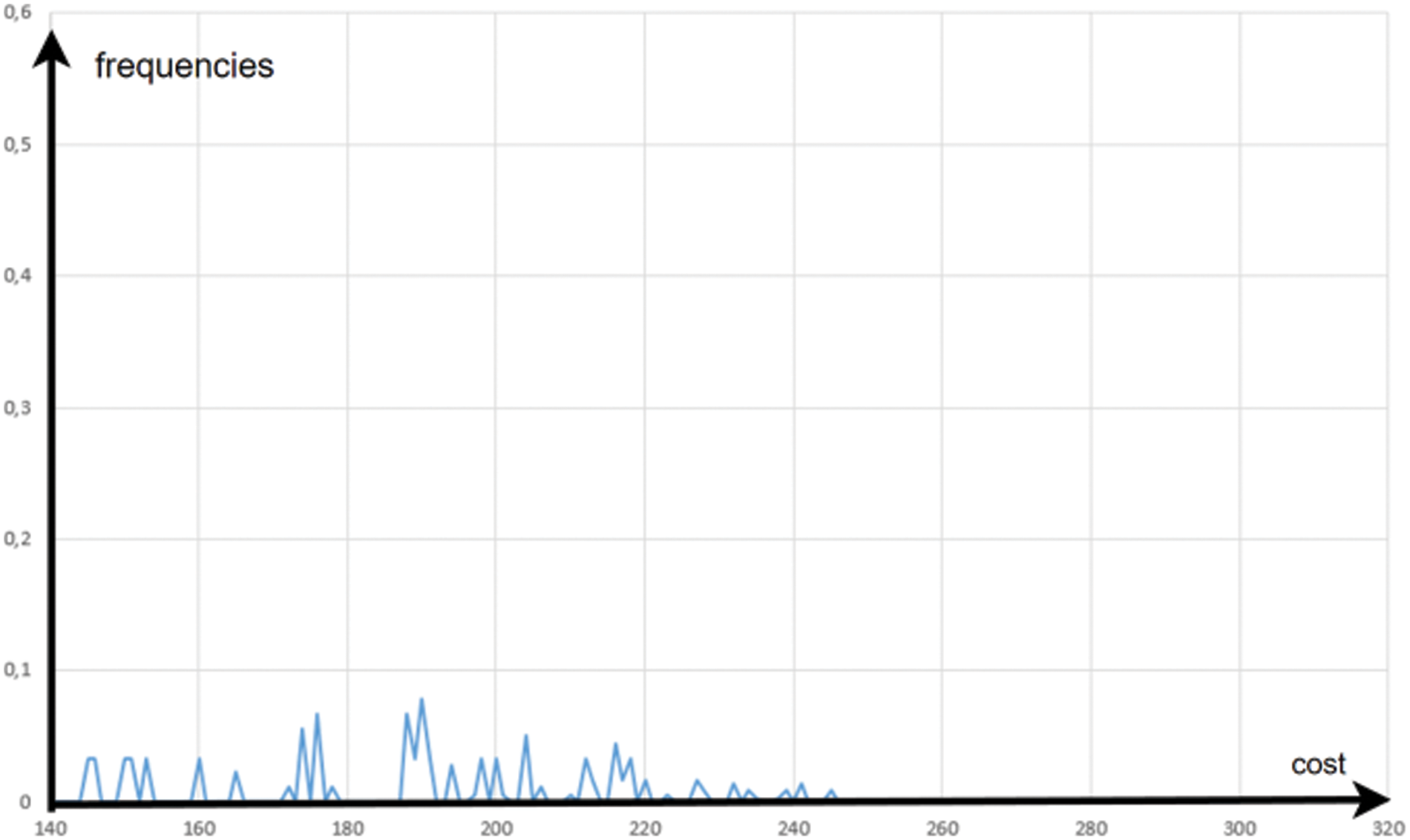
Figure 15: Initial distribution of solutions for the VRP instance

The optimal solution is σ=[0,1,5,2,3,6,4,0] which is splitted into 3 trips described in the Fig. 15 and that models a solution of cost 145. The solution is composed of 3 trips introduced in Figs. 16 and 17.

Figure 16: Optimal solution found

Figure 17: Split execution on the permutation σ=[0,1,5,2,3,6,4,0]

4  Conclusions

We have introduced the IQAOA approach, which utilizes an indirect representation of permutations. Our findings provide valuable insights into the performance of IQAOA and propose promising strategies for its practical implementation on near-term quantum devices. This is a new approach in quantum and one of the first inclusion of indirect solution modelisation into a quantum process. To the best of our knowledge, this is the first quantum solution for the 10-customer TSP. The inclusion of indirect coding within the QAOA framework gives rise to the IQAOA approach, requiring a highly specialized technique for angle optimization and the ability to leverage the potential of well-established meta-heuristics within the OR community.

Acknowledgement: Special thanks to Kevin Espiguinha and Samy Dif for preliminary discussion on Lehmer representation.

Funding Statement: The authors received no specific funding for this study.

Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: Philippe Lacomme and Eric Bourreau; data collection: all authors; analysis and interpretation of results: Gérard Fleury and Eric Bourreau; draft manuscript preparation: Philippe Lacomme and Gérard Fleury. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The data that support the findings of this study are available from the corresponding author, Philippe Lacomme, upon reasonable request.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. R. Martoňák, G. E. Santoro, and E. Tosatti, “Quantum annealing of the traveling-salesman problem,” Phys. Rev., vol. 70, no. 5, 2004, Art. no. 057701. doi: 10.1103/PhysRevE.70.057701. [Google Scholar] [PubMed] [CrossRef]

2. E. Schrödinger, “An ondulatory theory of the mechanics of atoms and molecules,” Phys. Rev., vol. 28, no. 6, pp. 1049–1070, 1926. doi: 10.1103/PhysRev.28.1049. [Google Scholar] [CrossRef]

3. E. Farhi, J. Goldstone, S. Gutmann, and L. Zh, “The quantum approximate optimization algorithm and the sherrington-kirkpatrick model at infinite size,” 2022, arXiv:1910.08187v4. [Google Scholar]

4. S. Hadfield, “Quantum algorithms for scientific computing and approximate optimization” Ph.D. thesis, Columbia University, USA, 2018. [Google Scholar]

5. W. Y. Qian, R. A. M. Basili, M. M. Eshaghian-Wilner, A. Khokhar, G. Luecke and J. P. Vary, “Comparative study of variations in quantum approximate optimization algorithms for the traveling salesman problem,” Entropy, vol. 25, no. 8, 2023, Art. no. 1238. doi: 10.3390/e25081238. [Google Scholar] [PubMed] [CrossRef]

6. J. Zhu, Y. Gao, H. Wang, T. Li, and H. Wu, “A realizable GAS-based quantum algorithm for traveling salesman problem,” 2022, arXiv:2212.02735. [Google Scholar]

7. R. Sato, G. Cui, K. Saito, H. Kawashima, T. Nikuni and S. Watabe, “Design of two-step quantum search algorithm for solving traveling salesman problems,” 2024, arXiv:2405.07129. [Google Scholar]

8. L. S. Herzog et al., “Improving quantum and classical decomposition methods for vehicle routing,” 2024, arXiv:2404.05551. [Google Scholar]

9. C. Bierwith, “A generalized permutation approach to jobshop scheduling with genetic algorithms,” OR Spektrum, vol. 17, no. 2–3, pp. 87–92, 1995. doi: 10.1007/BF01719250. [Google Scholar] [CrossRef]

10. J. E. Beasley, “Route-first cluster-second methods for vehicle routing,” Omega, vol. 11, no. 4, pp. 403–408, 1983. doi: 10.1016/0305-0483(83)90033-6. [Google Scholar] [CrossRef]

11. C. Prins, P. Lacomme, and C. Prodhon, “Order-first split-second methods for vehicle routing problems: A review,” Transp. Res. Part C: Emerg. Technol., vol. 40, no. 1, pp. 179–200, 2014. doi: 10.1016/j.trc.2014.01.011. [Google Scholar] [CrossRef]

12. G. B. Dantzig and J. H. Ramser, “The truck dispatching problem,” Manage. Sci., vol. 6, no. 1, pp. 80–91, 1959. doi: 10.1287/mnsc.6.1.80. [Google Scholar] [CrossRef]

13. A. Cheng, M. Gen, and Y. Tsumjimura, “A tutorial survey of job-shop scheduling problems using genetic algorithms–representations,” Comput. Indust. Eng., vol. 30, no. 4, pp. 983–997, 1996. doi: 10.1016/0360-8352(96)00047-2. [Google Scholar] [CrossRef]

14. D. H. Lehmer, “Teaching combinatorial tricks to a computer,” in Proc. Sympos. Appl. Math. Comb. Anal., Amer. Math. Soc., vol. 10, pp. 179–193, 1960. doi: 10.1090/psapm/010. [Google Scholar] [CrossRef]

15. C. A. Laisant, “Sur la numération factorielle, application aux permutations,” Bulletin De La Société Mathématique De France, vol. 2, pp. 176–173, 1888. doi: 10.24033/bsmf.378. [Google Scholar] [CrossRef]

16. D. Knuth, “The art of computer programming,” in Sorting and Searching, 2nd ed., USA: Addison-Wesley, 1981, vol. 3. [Google Scholar]

17. F. Rakotondrajao, “Permutation by number of fixed points and anti-excedances,” Africa Mathematica, vol. 23, no. 1, pp. 121–133, 2012. doi: 10.1007/s13370-011-0025-y. [Google Scholar] [CrossRef]

18. E. Farhi and J. Goldstone, “A quantum approximate optimization algorithm,” Quantum Phys.. arXiv:1411.4028. 2014. [Google Scholar]

19. T. Kadowaki and H. Nishimori, “Quantum annealing in the transverse Ising model,” Phys. Rev. E, vol. 58, no. 5, pp. 5355–5363, 1998. doi: 10.1103/PhysRevE.58.5355. [Google Scholar] [CrossRef]

20. T. A. Feo and M. G. C. Resende, “Greedy randomized adaptive search procedures,” J. Glob. Optim., vol. 6, no. 2, pp. 109–133, 1995. doi: 10.1007/BF01096763. [Google Scholar] [CrossRef]

21. S. Wolf and P. Merz, “Evolutionary local search for the super-peer selection problem and the p-hub median problem,” in HCI/ICCV 2007, T. Bartz-Beielstein, Ed., Springer, Heidelberg: LNCS, 2007, vol. 4771, pp. 1–15. [Google Scholar]

22. H. R. Lourenço, O. C. Martin, and T. Stutzle, “Iterated local search,” in Handbook of Metaheuristics, F. Glover and G. A. Kochenberger, Eds., Boston, MA: Springer, 2003, vol. 57. doi: 10.1007/0-306-48056-5_1. [Google Scholar] [CrossRef]

23. Y. Ruan, S. Marsh, X. Xue, Z. Liu, and J. Wang, “The quantum approximate algorithm for solving traveling salesman problem,” Comput. Mater. Continua, vol. 63, no. 3, pp. 1237–1247, 2020. doi: 10.32604/cmc.2020.010001. [Google Scholar] [CrossRef]

24. T. Stollenwerk and S. Hadfield, “Measurement-based quantum approximate optimization,” 2024, arXiv:2403.11514v1. [Google Scholar]

25. G. Fleury and P. Lacomme, “A technical note for the 91-clauses SAT resolution with indirect QAOA based approach,” 2024, arXiv:2402.00065v1. [Google Scholar]

Appendix A. Resolution of one 10-Customer Instance

The experiments were carried out with:

•   The parameters np=20, ne=5, nd=3 for the first C_GRASP × ELS execution to optimize simultaneously β→ and γ→.

•   The parameters np=20, ne=5, nd=5 for the second C_GRASP × ELS execution to optimize γ→.

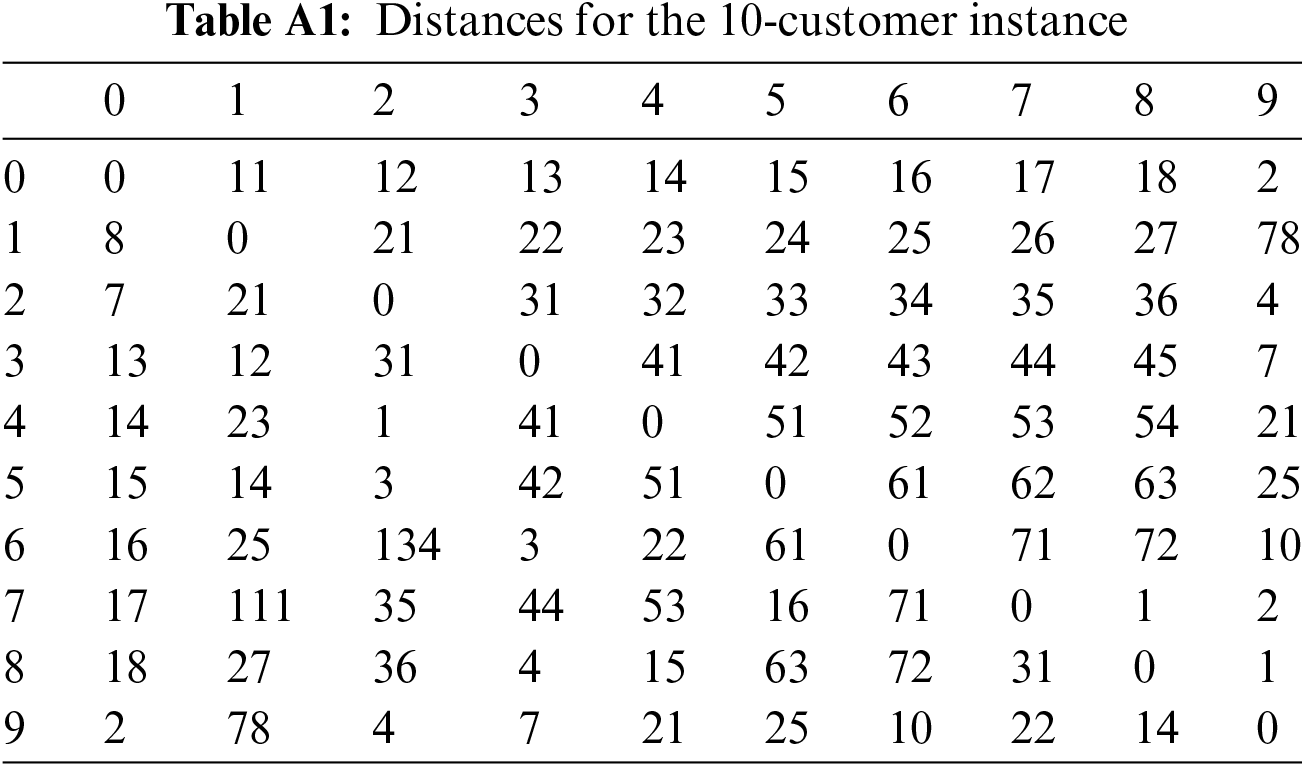
The distances used are introduced in Table A1 and they define a asymmetric TSP with 10 customers. The optimal solution is 102 avec the related family permutation is: σ=[1,6,2,8,9,5,3,10,7,4]. The total number of solutions is 3,628,800 permutations and 471 different costs and a uniform sampling (Fig. A1) gives a probability to find the optimal value 102 about 0.0005511% since we have 20 optimal permutations. The probability to have a quality solution with a cost lower than 200 is about 4.068% as stressed in Fig. A1. The cumulative final distribution introduced in Fig. A2 shows that the probability to have a solution with a cost lower than 200 is about 22.2%, i.e., 5 times higher than the initial probability.

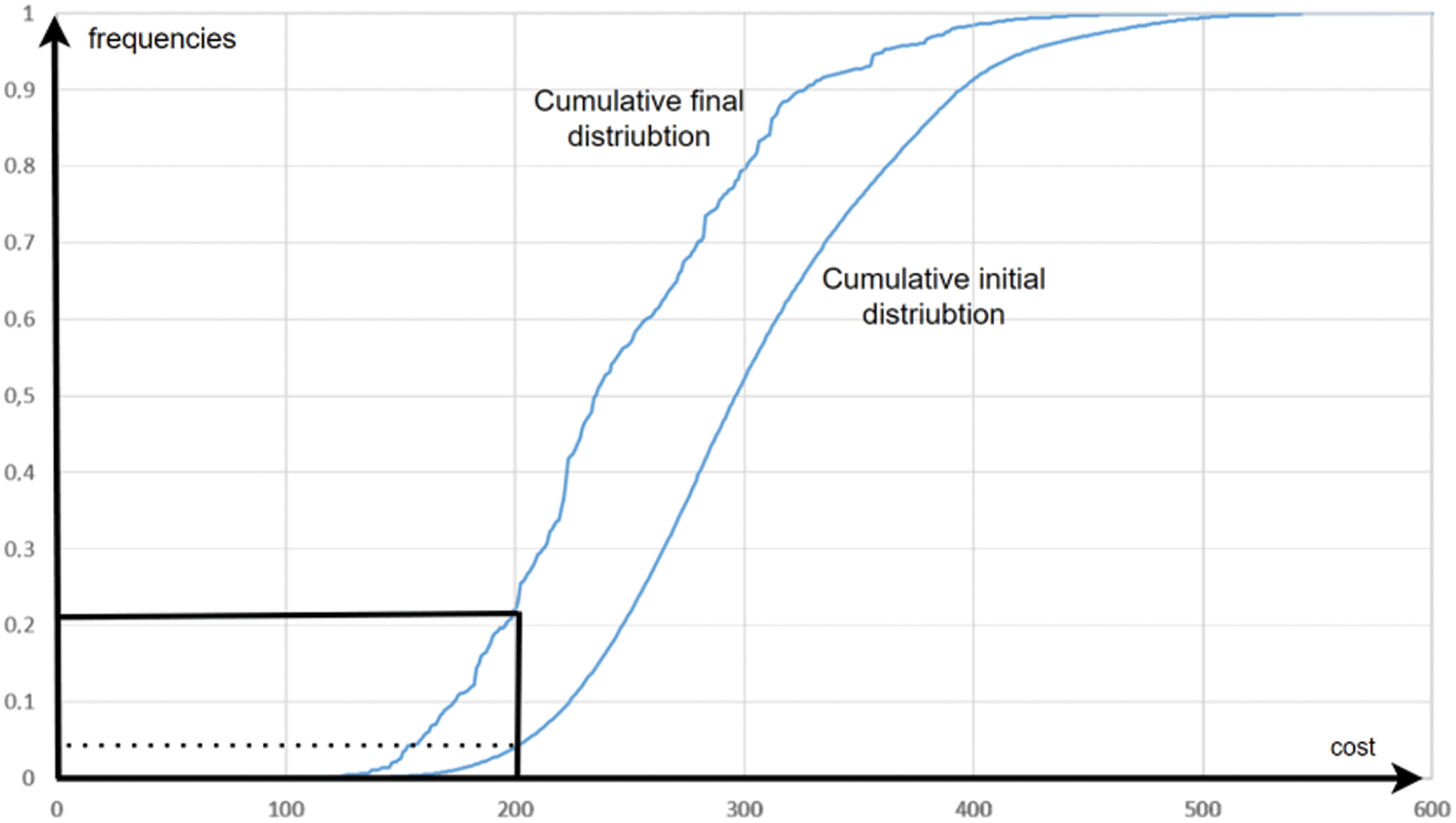
Figure A1: Cumulative final/initial distribution of solutions for the instance with 10 customers

It is worth noting that defining the number of samples based on the number of iterations makes sense. This is particularly relevant for high-quality solutions that are close to the optimal one, where the probability of making incorrect comparisons (given that we only have estimates of both quartile energy and average value) should be lower compared to situations where the solutions under consideration have lower quality. The following parameters are used:

•   The parameters np=10, ne=5, nd=3 for the first C_GRASP × ELS execution to optimize simultaneously β→ and γ→.

•   The parameters np=10, ne=5, nd=5 for the second C_GRASP × ELS execution to optimize γ→.

At each ELS iterations the number of sampling is increased of 10 units starting with 40 samplings. The results are those of Fig. A2 and are relevant even if the process of convergence should require more iterations.

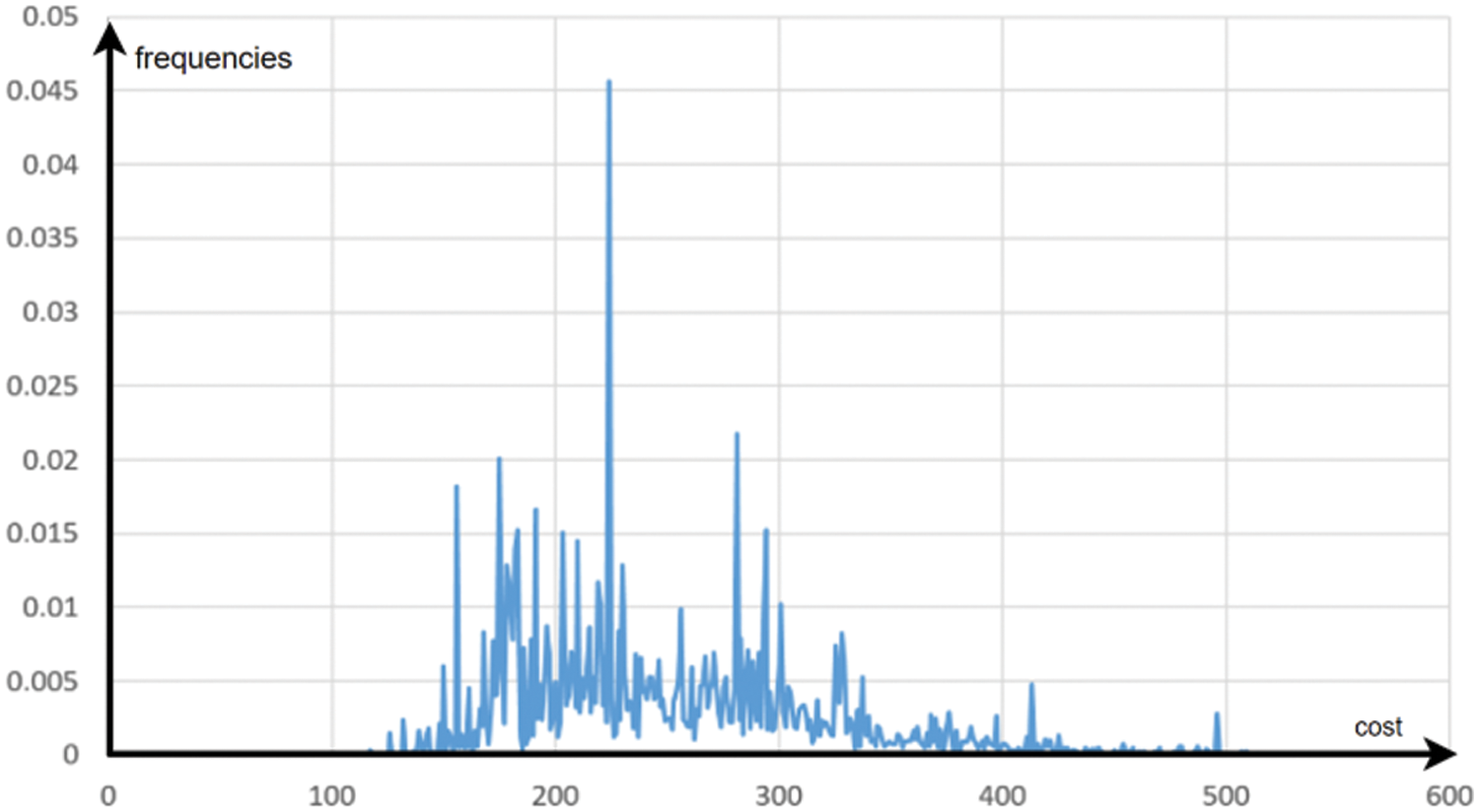
Figure A2: Final distribution of solutions for the instance with 10 customers (number of sampling varying from iterations)

Appendix B. Example of Circuits

The Fig. A3 gives the general circuit representation for rank encoding that is composed on successive application of HD (Fig. A4) and HP (Fig. A5).

It could be possible to investigate difference expression for HD including but not limited to

HD1(β)=[⊗j=0n−1RYj(β)].[⊗j=0n−2CXj,j+1]

or

HD2(β)=[⊗j=0n−1RXj(β)].[⊗j=0n−2CXj,j+1]

or

HD3(β)=[⊗j=0n−1RYj(β).RXj(β)].[⊗j=0n−2CXj,j+1]

or

HD4(β)=[⊗j=0n−2CXj,j+1].[⊗j=0n−1RYj(β)]

which are inspired by the usual VQE proposals. Depending on the instances, depending on the problems and considering the previous published works on VQE, it seems reasonable that HD mixer to claim that HD should have significant impact on the convergence rate of the method.

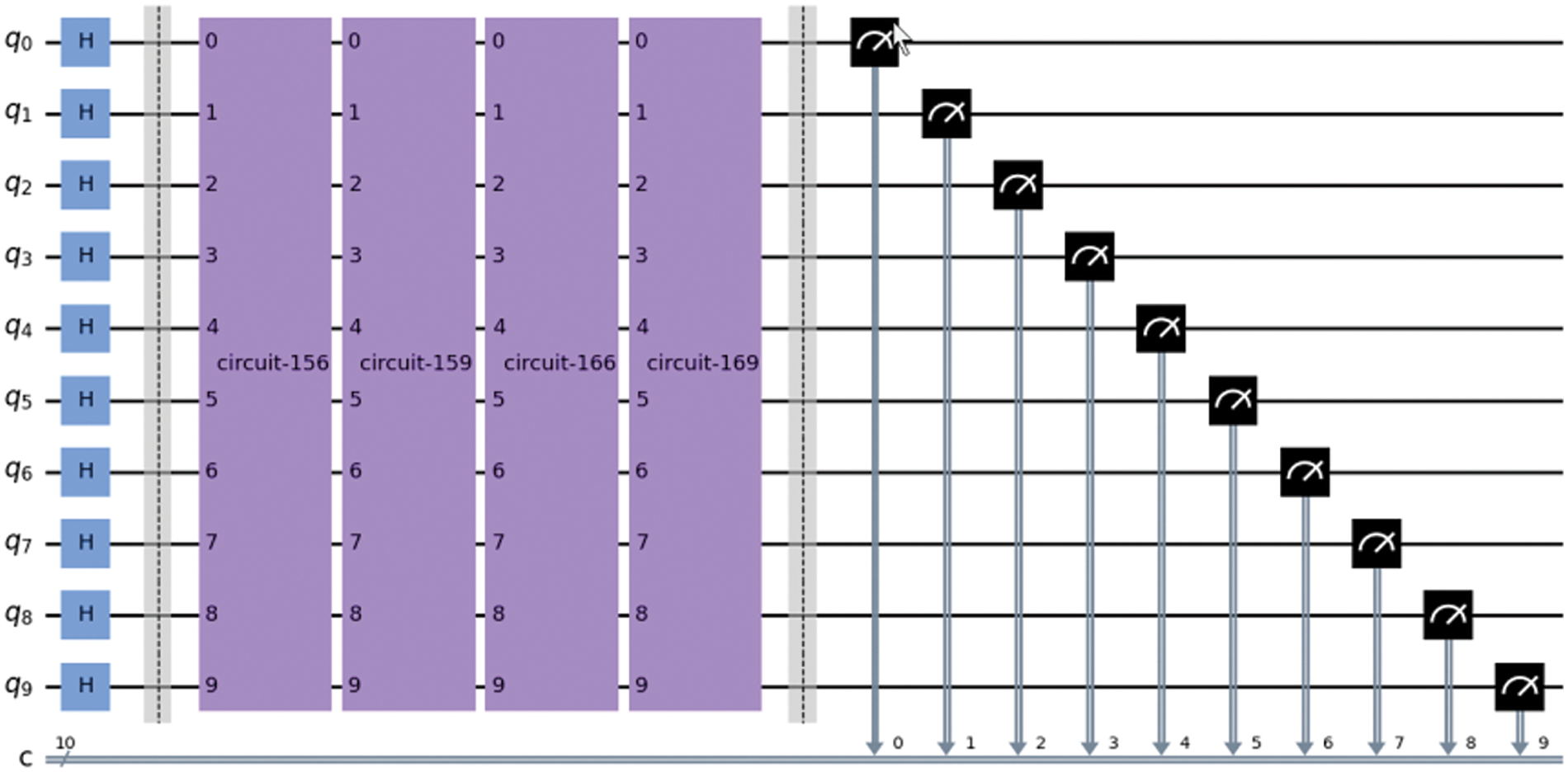
Figure A3: Example of IQAOA circuit for a 2 depth circuit (2 times the sequence of HD, HP)

Figure A4: Exemple of HD

Figure A5: HP definition