 Open Access
Open Access
ARTICLE
A Protocol for Conversion of Path-Spin to Spin-Spin Quantum Entanglement
1 Institute of Astronomy Space and Earth Science, Kolkata, 700 054, India
2 Department of Physics (UG & PG), Prabhat Kumar College, Contai, Purba Medinipur, 721 401, India
* Corresponding Author: Pradipta Panchadhyayee. Email:
Journal of Quantum Computing 2023, 5, 71-79. https://doi.org/10.32604/jqc.2023.045164
Received 19 August 2023; Accepted 07 November 2023; Issue published 14 December 2023
Abstract
The present model deals with a protocol which involves the generation and conversion of entanglement from path-spin (P-S) hybrid entanglement associated with half-spin particle to spin-spin (S-S) interparticle entanglement. This protocol finds its applications in quantum information processing via a series of operations which include a beam splitter, spin flipper, spin measurement, classical channel, unitary transformations. Finally, it leads to two particles having completely entangled spin variables, without any requirement of any simultaneous operation on the two particles.Keywords
Quantum entanglement is one of the most fascinating and unique features of quantum mechanics. It is usually accomplished by having two entangled particles emitted from a single source or by having two interacting particles. The concept of entanglement remains the focus of the EPR paradox, violations of Bell’s inequalities, and non-locality in quantum mechanics. Experimental exploration in manipulating entanglement is an important exercise that helps distribute entanglement between distant parties. One such practical scheme is entanglement swapping [1–3], which allows one to entangle two quantum systems that have never interacted directly with each other. Also, entangled pairs of particles with spatial separations find numerous applications in several other robust information processing protocols, such as Bell’s theorem-based cryptography [4–6], super-dense coding [7–9], teleportation [10–12], cheating bit commitment [13,14], testing Bell’s inequalities [15,16], etc. Meanwhile, some researchers reported various propositions of experimental demonstration of entanglement swapping [2,17,18]. Entanglement swapping may be applicable to the construction of telephone exchange [19]. The concept of entanglement in quantum mechanics was first noticed with respect to continuous variables like position and momentum [20] and then extended to discrete variables like particle spin [21] for the systems studied in Hilbert spaces dealing with discrete variables [22], etc. With the aid of shared entanglement and classical communication channels, quantum teleportation permits the transfer action of an unknown quantum state from one particle to a distant particle, bypassing the need to transfer the particle itself. Also, spatially separated multi-particle entangled states have many potential applications [23–25]. Quantum entanglement provides subtle physical insights into complex phenomena in solid-state physics, including phase transitions [26,27] and an understanding of the relation of black hole entropy with the entanglement of particles near the event horizon [28–31], etc. Lately, the idea of entanglement between properties described by mutually exclusive Hilbert spaces, such as between linear momentum and spin, is intriguing and has become an important subject of investigation for researchers. Quantum mechanical theory confirms the occurrence of entangled states in Hilbert spaces. However, the practical realization of such states is yet to be explored thoroughly.
Fascinating progress in this direction has been achieved in recent times by generating intraparticle entanglement related to various degrees of freedom (DoFs) of a single particle. For example, entanglement between the polarization of a photon and its linear momentum can be harnessed for applications like quantum key distribution in quantum cryptography. In contrast, another exciting form of intraparticle entanglement involves the entanglement between a photon’s polarization and its angular momentum. Since such entanglement is restricted to a single particle, it can be conserved effortlessly against decay effects. However, it seems cumbersome to exercise intraparticle entanglement as a tool of quantum information processing because two particles with a spatial distance between them are not intertwined by entanglement. It is, however, possible to transfer intraparticle entanglement into interparticle entanglement involving compatible DoFs of two particles that are a distance apart from each other. The first theoretical proposal [32,33] and the consequent experimental realization [34] of entanglement between the spin and path of a half spin particle have outlined protocols for creating entanglement between these different DoFs. Also, intraparticle entanglement is effectively employed in the study of neutrino oscillations [35] and to demonstrate photon non-locality [36]. Information transfer based on P-S hybrid entanglement for a single particle has also been proposed [37]. The authors of [32,33] dealt with a theoretical model for teleporting an unknown quantum state between two distant parties, Alice and Bob, creating a P-S entangled state and using a series of operations like spin-measurements, unitary operations, classical communication channel, etc. A theoretical model has been proposed by the same authors for entanglement swapping between the spin and path DoFs within a particle onto entanglement between the spins of two separate particles [38]. Our present paper involves the conversion of P-S entanglement into S-S entanglement with a new protocol. It shows the feasibility of converting the P-S intraparticle hybrid entangled state onto a S-S interparticle entangled state employing a different technique.
We consider a half-spin particle (Z1) with initial spin polarization along the + z-axis (denoted by|↑z⟩). The joint P-S state for the particle is written as |s⟩1ps=|ψ0⟩p⊗|↑z⟩s, where p and s indicate the path variable and the spin variable, respectively. The spin state |↑z⟩ of Z1 will be indicated by |0⟩1s. When Alice allows the incidence of the particle Z1 on a beam splitter BS1, it undergoes a quantum operation on its path state. The state of Z1 after ejecting from BS1 becomes |s⟩1ps=(iα1|0⟩1p+β1|1⟩1p)⊗|0⟩1s, where |0⟩1p and |1⟩1p are reflected and transmitted channels, respectively. The eigenstates of the projection operators P(|0⟩p) and P(|1⟩p) are the path states |0⟩1p and |1⟩1p. These states are mutually orthogonal and the projection operators are employed to determine the channel (reflected/transmitted) in which the Z1 is found. In this context, it is worth mentioning that the coexistence of path and spin variables enables the single particle to be considered as two qubits. Consequently, the particle corresponding to the channel |0⟩1p passes through a spin device (spin flipper) containing a steady magnetic field which acts in the +x direction and flips the spin state |0⟩1s to |1⟩1s. The P-S entangled state of Z1 becomes |s2⟩1ps=iα1|0⟩1p⊗|1⟩1s+β1|1⟩1p⊗|0⟩1s.
Our aim is to treat this entangled state of Z1 as the key element for generating S-S interparticle entanglement between the two particles (Z3 and Z4) initially occupied by another party Bob. The entire experimental setup with a schematic view is exhibited in Fig. 1. Alice holds a particle (Z2) in an unknown state given as|ψ2⟩=α2|0⟩2s+β2|1⟩2s. She performs a CNOT operation considering the Z1 particle’s spin state as the control qubit and the Z2 particle’s spin state as the target qubit. After this operation, the combined state of Z1 and Z2 is given by
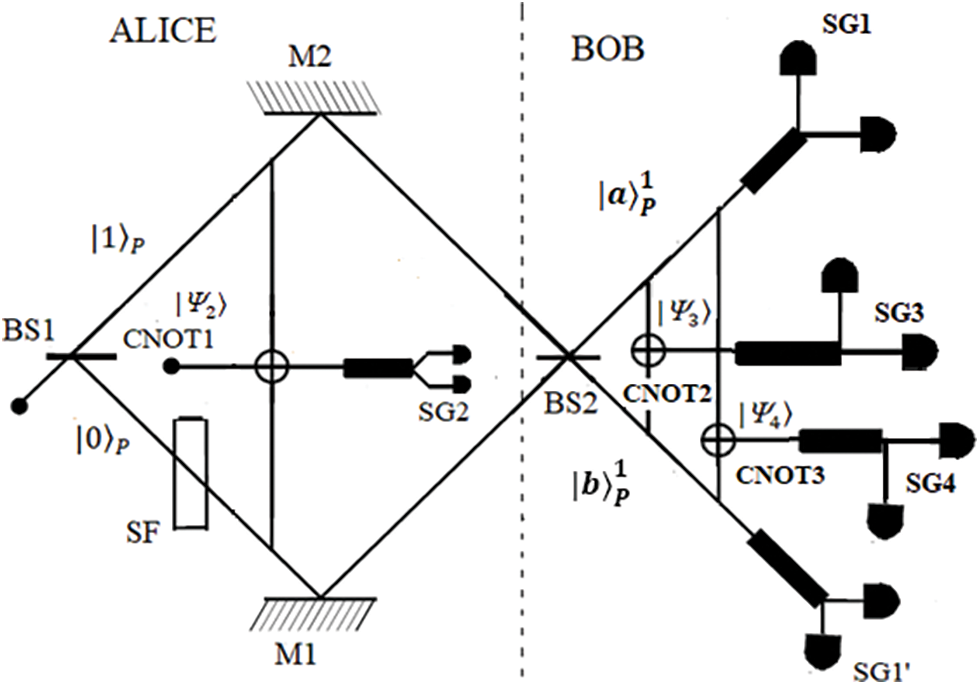
Figure 1: A particle with half spin (labeled as Z1) with a spin up polarized state can fall on a beam-splitter BS1
|s⟩12pss=iα1α2|0⟩1p|11⟩12s+iα1β2|0⟩1p|10⟩12s+β1α2|1⟩1p|00⟩12s+β1β2|1⟩1p|01⟩12s.
Alice then dispatches the particle Z1 to Bob. When Bob acknowledges the receipt of the particle, Alice performs the measurement of the spin of the particle Z2 by Stern-Gerlach (SG) device along the z-axis. In this context, it is important to highlight that SG devices play a significant role in the field of quantum computing and quantum information. The SG experiment is used to demonstrate the instantaneous and nonlocal feature related to the collapse of the wavefunction and single-particle entanglement, leading to a nonlocal effect called ‘steering’ or ‘single-particle steering’. The term ‘steering’ in quantum mechanics refers to the ability of one observer (Alice) to influence the state of a distant particle (Bob) through measurements made on her own particle. This phenomenon showcases the nonlocal nature of quantum entanglement [39]. It has been established that two successive SG experiments produce quantum nonlocality and quantum steering [40], whose relations with entanglement put a prominent footprint on our usual understanding of the experiment as a natural consequence of considering quantum correlations. Probable results of spin measurements on Alice’s Z2 particle lead to the associated states with their probabilities as given in Table 1.

Next, Alice confers with Bob classically to report the outcomes of her measurements on spin (i.e., spin up/down for Z2). Now the residual action is to be performed by Bob to generate S-S entanglement between two particles (Z3 and Z4) at his end initially. Bob has three particles in hand, Z1 (given by Alice) and Z3 and Z4 from the initial stage. The particle Z3 is in an unknown state given by |ψ3⟩=α3|0⟩3s+β3|1⟩3s whereas Z4 is in known state (in spin-up state, |0⟩4s). Based on the data which Alice sends to Bob, he adopted the following actions to reach the goal.
Case 1: Result of spin measurement of the particle Z2: |0⟩2s
When Bob receives the particle Z1 sent by Alice, he passes it via a 50-50 beam-splitter (BS2). Then BS2 transforms the states |0⟩1p and |1⟩1p in the following manner:
|0⟩1p→1√2(|a⟩1p+i|b⟩1p), and |1⟩1p→1√2(|b⟩1p+i|a⟩1p).
Next, Bob executes a CNOT operation using the spin states of Z1 and Z3 as the control and target qubits, respectively. Now the joint P-S state becomes
|S⟩13ps=iα1β2α3|0⟩1p|11⟩13s+iα1β2β3|0⟩1p|10⟩13s+β1α2α3|1⟩1p|00⟩13s+β1α2β3|1⟩1p|01⟩13s.
Bob further makes another CNOT operation taking Z1’s spin state as the qubit (control) and Z4’s spin state as the qubit (target). The resultant P-S state is expressed as
|S⟩134pss=|0⟩1p|1⟩1s(iα1β2α3|11⟩34s+iα1β2β3|01⟩34s)+|1⟩1p|0⟩1s(β1α2β3|10⟩34s+β1α2α3|00⟩34s).
Normalization leads to
|S⟩134pss=N|0⟩1p|1⟩1s(iα1β2α3|11⟩34s+iα1β2β3|01⟩34s)+N|1⟩1p|0⟩1s(β1α2β3|10⟩34s+β1α2α3|00⟩34s),
where the normalization constant, N=[(α21β22+β21α22)(α23+β23)]−12. Expressing |0⟩1s and |1⟩1s in the form of linear superposition of |0x⟩1s and |1x⟩1s as |0⟩1s=1√2(|0x⟩1s+|1x⟩1s) and |1⟩1s=1√2(|0x⟩1s−|1x⟩1s), we obtain |S⟩134pss=T1|a⟩1p|0x⟩1s+T2|a⟩1p|1x⟩1s+T3|b⟩1p|0x⟩1s+T4|b⟩1p|1x⟩1s,
where
T1=iN2(α1β2α3|11⟩34s+β1α2α3|00⟩34s)+iN2(α1β2β3|01⟩34s+β1α2β3|10⟩34s),
T2=iN2(−α1β2α3|11⟩34s+β1α2α3|00⟩34s)+iN2(−α1β2β3|01⟩34s+β1α2β3|10⟩34s),
T3=N2(−α1β2α3|11⟩34s+β1α2α3|00⟩34s)+N2(−α1β2β3|01⟩34s+β1α2β3|10⟩34s),
T4=N2(α1β2α3|11⟩34s+β1α2α3|00⟩34s)+N2(α1β2β3|01⟩34s+β1α2β3|10⟩34s).
The x-component of spin of Z1 is measured by Bob using two SG devices held in the channels of |a⟩1p and |b⟩1p. His measurement provides four probable results, i.e., |a⟩1p⊗|0x⟩1s,|a⟩1p⊗|1x⟩1s,|b⟩1p⊗|0x⟩1s, and |b⟩1p⊗|1x⟩1s. Bob carries out a corresponding unitary operation to spawn the entangled states between the particles Z3 and Z4. The results of these operations are provided in the Table 2.

The reflected channel contains a spin flipper. Alice performs one CNOT operation involving the particles Z1 and Z2, one whose state is unknown. Alice sends Z1 to Bob, and this particle is allowed by Bob to fall on another beam-splitter BS2. The spin of the Z1 is measured by Bob using two SG devices, SG 1 and SG 1′. Alice measures the z-component of the spin of Z2 using SG2. According to the results of Alice’s spin measurement (which are classically communicated to Bob), Bob performs two successive CNOT operations using particles Z1 and Z3, Z1 and Z4, and measures the P-S states of the particle Z1. Finally, Bob performs appropriate unitary operations to create the S-S entangled states between Z3 and Z4.
So far, we assume that particle Z3 is in an unknown state and the particle Z4 is in the known state. If the particle Z3 also stays in a known state, two different possibilities arise: α3=1,β3=0 and α3=0,β3=1. In such cases, Bob creates the entangled states by sorting compatible unitary transformations as presented in Tables 3 and 4, respectively.


In all cases, the normalization constant becomes N′=(α21β22+β21α22)−12.
Case 2: Spin measurement of the particle Z2: |1⟩2s
Bob repeats the procedure as described in the Case 1. He allows the particle Z1 to fall on a 50-50 beam splitter and performs two subsequent CNOT operations using the particle Z1 and two particles (Z3 and Z4) initially possessed by him. Thereafter, he measures the spin of particle Z1 using the SG device. Finally, Bob executes suitable unitary operations to generate the entangled states between the spin states of the particles Z3 and Z4 (presented in Table 5).

Here, the normalization constant, M=[(α21α22+β21β22)(α23+β23)]−12. If the particle Z3 stays in a known state (either|0⟩3s or |1⟩3s), Bob can create the entangled states by choosing suitable unitary transformations as presented in Tables 6 and 7, respectively.


Here, the normalization constant becomes M′=(α21α22+β21β22)−12.
So far as the protocol is concerned and reported in the previous literature [38], Alice makes a CNOT operation employing the second particle Z2 and then sends it to a third party, Charlie, without making a spin measurement. But, in our present work, Alice measures the spin of Z2 and informs Bob of the outcome of her measurement through a classical channel. Another point is that when we deal with the protocol, the P-S entanglement is transferred from the spin DoFs of a single particle to two different particles which are initially under the possession of Bob. Here, the entanglement is swapped to the spin DoFs of the two particles which are under the control of different parties. Although the pair of particles correlated by the S-S entanglement (when the protocol ends) are located at the same place, they can be regarded as non-interacting in the sense that the particle Z1 independently interacts with them (two consecutive CNOT operations), i.e., no combined operation is performed on the particles Z3 and Z4. Here lies the importance of the present work over others.
In this article, we propose a new protocol to convert hybrid quantum entanglement between different DoFs of a particle to spin DoFs of different parties. The principal advantage of this new protocol, apart from being an experimentally feasible novel way to perform this conversion, is the use of more friendly individual processes, such as the realization of measurements before transmissions and the use of classical communications, as well as convenient properties for the final state, such as it being shared between different parties. Furthermore, this realization requires relatively simple processes, such as CNOT gates, beam splitters, and measurement using SG devices. Our protocol, therefore, opens up the new possibility that this easier way of conversion of P-S hybrid entanglement of a particle to S-S entanglement between two spatially separated particles facilitates the tasks of information processing. Albeit, this protocol is implemented for the spin-1/2 particle, but it may be extended to photons and other optical devices optimally designed for definite operations. As is mentioned in the case of a duality quantum computer [41], it utilizes multiple qubits and exploits the particle-wave duality property for performing quantum computations. As path information could be used as a source of qubits in such computers, further study [42] ensures that entanglement quantitatively controls the degree of duality. Hence, our protocol may find potential applications in this domain of study.
Acknowledgement: We gratefully acknowledge Dr Debapriyo Syam for inspiring us to do research in this field.
Funding Statement: The authors received no specific funding for this study.
Author Contributions: Two authors equally contributed to theoretical modelling, deriving associated results, analysing and interpreting results, and final preparation of the manuscript. All authors reviewed the results and approved the final version of the manuscript.
Availability of Data and Materials: The authors confirm that the data supporting the findings of this study are available within the article.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
References
1. S. Bose, V. Vedral and P. L. Knight, “Multiparticle generalization of entanglement swapping,” Physical Review A, vol. 57, no. 2, pp. 822–829, 1998. [Google Scholar]
2. J. W. Pan, D. Bouwmeester, H. Weinfurter and A. Zeilinger, “Experimental entanglement swapping, entangled photons that never interacted,” Physical Review Letters, vol. 80, no. 18, pp. 3891–3894, 1998. [Google Scholar]
3. S. Bose, V. Vedral and P. L. Knight, “Purification via entanglement swapping and conserved entanglement,” Physical Review A, vol. 60, no. 1, pp. 194–197, 1999. [Google Scholar]
4. A. K. Ekert, “Quantum cryptography based on Bell’s theorem,” Physical Review Letters, vol. 67, no. 6, pp. 661–663, 1991. [Google Scholar] [PubMed]
5. Z. B. Chen, Q. Zhang, X. H. Bao, J. Schmiedmayer and J. W. Pan, “Deterministic and efficient quantum cryptography based on bells theorem,” Physical Review A, vol. 73, no. 5, pp. 050302(R2006. [Google Scholar]
6. A. K. Ekert, “Quantum cryptography and bell’s theorem,” Quantum Measurements in Optics, vol. 282, no. 2, pp. 413–417, 2002. [Google Scholar]
7. X. S. Liu, G. L. Long, D. M. Tong and F. Li, “General scheme for superdense coding between multipartie,” Physical Review A, vol. 65, no. 2, pp. 022304, 2002. [Google Scholar]
8. A. Harrow, P. Hayden and D. Leung, “Superdense coding of quantum state,” Physical Review Letter, vol. 92, no. 18, pp. 187901, 2004. [Google Scholar]
9. A. K. Pati, P. Parashar and P. Agrawal, “Probabilistic superdense coding,” Physical Review A, vol. 72, no. 1, pp. 012329, 2005. [Google Scholar]
10. D. Bouwmeester, J. W. Pan, K. Mattle, M. Eibl, H. Weinfurter et al., “Experimental quantum teleportation,” Nature, vol. 390, no. 6660, pp. 575–579, 1997. [Google Scholar]
11. S. Pirandola, J. Eisert, C. Weedbrook, A. Furusawa and S. L. Braunstein, “Advances in quantum teleportation,” Nature Photonics, vol. 9, no. 10, pp. 641–652, 2015. [Google Scholar]
12. M. A. Nielsen, E. Knill and R. Laflamme, “Complete quantum teleportation using nuclear magnetic resonance,” Nature, vol. 396, no. 6706, pp. 52–55, 1998. [Google Scholar]
13. L. Hardy and A. Kent, “Cheat sensitive quantum bit commitment,” Physical Review Letters, vol. 92, no. 15, pp. 157901, 2004. [Google Scholar] [PubMed]
14. H. K. Lo and H. F. Chau, “Is quantum bit commitment really possible?” Physical Review Letters, vol. 78, no. 17, pp. 3410–3413, 1997. [Google Scholar]
15. I. Šupić, R. Augusiak, A. Salavrakos and A. Acín, “Self-testing protocols based on the chained Bell inequalities,” New Journal of Physics, vol. 18, no. 3, pp. 035013, 2016. [Google Scholar]
16. H. Jeong, “Testing Bell inequalities with photon-subtracted Gaussian states,” Physical Review A, vol. 78, no. 4, pp. 042101, 2008. [Google Scholar]
17. X. S. Ma, S. Zotter, J. Kofler, R. Ursin, T. Jennewein et al., “Experimental delayed-choice entanglement swapping,” Nature Physics, vol. 8, no. 6, pp. 479–484, 2012. [Google Scholar]
18. X. Jia, X. Su, Q. Pan, J. Gao, C. Xie et al., “Experimental demonstration of unconditional entanglement swapping for continuous variables,” Physical Review Letters, vol. 93, no. 25, pp. 250503, 2004. [Google Scholar] [PubMed]
19. C. Y. Lu, T. Yang and J. W. Pan, “Experimental multiparticle entanglement swapping for quantum networking,” Physical Review Letters, vol. 103, no. 2, pp. 020501, 2009. [Google Scholar] [PubMed]
20. A. Einstein, B. Podolsky and N. Rosen, “Can quantum-mechanical description of physical reality be considered complete?” Physical Review, vol. 47, no. 10, pp. 777–780, 1935. [Google Scholar]
21. D. Bohm, Quantum Theory. Englewood Cliffs, NJ, USA: Prentice-Hall, pp. 614–623, 1951. [Google Scholar]
22. R. Horodecki, P. Horodecki, M. Horodecki and K. Horodecki, “Quantum entanglement,” Review of Modern Physics, vol. 81, no. 2, pp. 865–942, 2009. [Google Scholar]
23. D. M. Greenberger, M. A. Horne, A. Shimony and A. Zeilinger, “Bell’s theorem without inequalities,” American Journal of Physics, vol. 58, no. 12, pp. 1131–1143, 1990. [Google Scholar]
24. N. D. Mermin, “Quantum mysteries revisited,” American Journal of Physics, vol. 58, no. 8, pp. 731–734, 1990. [Google Scholar]
25. N. D. Mermin, “What’s wrong with these elements of reality?,” Physics Today, vol. 43, no. 6, pp. 9–11, 1990. [Google Scholar]
26. D. Aharonov, “Quantum to classical phase transition in noisy quantum computers,” Physical Review A, vol. 62, no. 6, pp. 062311, 2000. [Google Scholar]
27. L. A. Wu, M. S. Sarandy, D. A. Lidar and L. J. Sham, “Linking entanglement and quantum phase transitions via density-functional theory,” Physical Review A, vol. 74, no. 5, pp. 052335, 2006. [Google Scholar]
28. S. L. Braunstein and A. K. Pati, “Quantum information cannot be completely hidden in correlations, implications for the black-hole information paradox,” Physical Review Letters, vol. 98, no. 8, pp. 080502, 2007. [Google Scholar] [PubMed]
29. M. Arzano, A. Hamma and S. Severini, “Hidden entanglement at the planck scale, loss of unitarity and the information paradox,” Modern Physics Letters A, vol. 25, no. 6, pp. 437–445, 2010. [Google Scholar]
30. T. Hartman and J. Maldacena, “Time evolution of entanglement entropy from black hole interiors,” Journal of High Energy Physics, vol. 5, no. 5, pp. 14, 2013. [Google Scholar]
31. D. Kabat, “Black hole entropy and entropy of entanglement,” Nuclear Physics B, vol. 453, no. 1–2, pp. 281–299, 1995. [Google Scholar]
32. S. Basu, S. Bandyopadhyay, G. Kar and D. Home, “Bell’s inequality for a single spin-1/2 particle and quantum contextuality,” Physics Letters A, vol. 279, no. 5–6, pp. 281–286, 2001. [Google Scholar]
33. A. K. Pan and D. Home, “Contextuality within quantum mechanics manifested in subensemble mean values,” Physics Letters A, vol. 373, no. 38, pp. 3430–3434, 2009. [Google Scholar]
34. Y. Hasegawa, R. Loidl, G. Badurek, M. Baron and H. Rauch, “Violation of a Bell-like inequality in single-neutron interferometry,” Nature, vol. 425, no. 6953, pp. 45–48, 2003. [Google Scholar] [PubMed]
35. M. Blasone, F. Dell’Anno, S. de Siena and F. Illuminati, “Entanglement in neutrino oscillations,” Europhyics Letters, vol. 85, no. 5, pp. 50002, 2009. [Google Scholar]
36. B. Hessmo, P. Usachev, H. Heydari and G. Björk, “Experimental demonstration of single photon nonlocality,” Physical Review Letters, vol. 92, no. 18, pp. 180401, 2004. [Google Scholar] [PubMed]
37. T. Pramanik, S. Adhikari, A. S. Majumdar, D. Home and A. K. Pan, “Information transfer using a single particle path-spin hybrid entangled state,” Physics Letters A, vol. 374, no. 9, pp. 1121–1125, 2010. [Google Scholar]
38. S. Adhikari, A. S. Majumdar, D. Home and A. K. Pan, “Swapping path-spin intraparticle entanglement onto spin-spin interparticle entanglement,” Europhysics Letters, vol. 89, no. 1, pp. 10005, 2010. [Google Scholar]
39. L. M. A. Aguilar, “Nonlocal single particle steering generated through single particle entanglement,” Scientific Reports, vol. 11, pp. 6744, 2021. [Google Scholar]
40. E. B. Rodriguez, E. P. Martinez and L. M. A. Aguilar, “Single particle steering and nonlocality: The consecutive stern-gerlach experiment,” Physical Review A, vol. 103, no. 4, pp. 042217, 2021. [Google Scholar]
41. G. Long and Y. Liu, “Duality quantum computing,” Frontiers of Computer Science in China, vol. 2, no. 2, pp. 167–178, 2008. [Google Scholar]
42. X. F. Qian, A. N. Vamivakas and J. H. Eberly, “Entanglement limits duality and vice versa,” Optica, vol. 5, no. 8, pp. 942–947, 2018. [Google Scholar]
Cite This Article
 Copyright © 2023 The Author(s). Published by Tech Science Press.
Copyright © 2023 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF Downloads
Downloads
 Citation Tools
Citation Tools
