Design and Implementation of Quantum Repeaters: Insights on Quantum Entanglement Purification

1  Introduction

Quantum communication leverages the principles of quantum mechanics to transmit quantum information between remote locations. The quantum information is encoded in a qubit, which is the basic unit of quantum information. At the core of quantum communication is the principle of quantum entanglement, which gives rise to the phenomena of quantum teleportation as a new paradigm protocol for communication [1].

Presently, active experimental work in quantum communication channels is conducted either in optical fibres or free space. Noise affects the transmission in both of those mediums. The photon intensity is attenuated exponentially with transmission distance [2,3]. This limits long-distance communication channels. Quantum repeaters were introduced to overcome this long-distance limitation [4,5].

Quantum repeaters are devices that extend the range of quantum channels. They achieve this by distributing entangled states across distant nodes of a quantum network. Entanglement serves as a resource for long-distance quantum communication. A full-scale quantum network implementing quantum repeater technology is established through the aggregation and integration of multiple short-distance quantum communication links. The multiple short-distance quantum communication links are each carefully calibrated to have lengths shorter than the attenuation length of the quantum communication channel [6]. The quantum repeaters are positioned as intermediaries between nodes of the adjacent links, effectively bridging two communication links. The quantum repeater performs entanglement swapping between the nodes of adjacent links, thereby creating entanglement links between the endpoints or nodes of adjacent links. This process is iteratively performed across the entire expanse of the transmission channel, ultimately leading to the entanglement of the sender and receiver nodes [2,7]. Consequently, a robust quantum communication link is established between them, facilitating direct, secure and efficient quantum communication. This ability to extend quantum entanglement over long distances is essential for the practical implementation of quantum communication and quantum key distribution on a global scale.

The main components of a quantum repeater include; quantum entanglement switching for swapping entangled states between adjacent nodes, quantum memory for storing quantum states for efficient on-demand retrieval and quantum entanglement purification for enhancing the fidelity of the entangled states. These components have a few limitations arising from imperfections in the source of entangled particles, the quantum operations and the interconnecting communication channels [8].

Despite these limitations, quantum repeaters have been successfully demonstrated in experiments, such as Herbst et al., who managed to use a quantum repeater to teleport an entangled state, a photon, between the Canary Islands of La Palma to Tenerife, about 143 km [8]. The entanglement swapping experiment used two polarization-entangled photon pairs generated in two identical spontaneous parametric down-conversion (SPDC) sources using a non-linear crystal, β-barium borate (BBO) [8].

The quantum entanglement purification protocol is a key component in quantum repeaters and is necessary for first generation or near-term quantum repeaters [9]. It is the process of distilling high-quality entanglement from low-quality entanglement. It serves to ensure entangled states maintain high fidelity throughout the transmission [10], thereby compensating for the loss of fidelity incurred due to noise or imperfections in the communication channel. The two purification protocols employed in this research are: Bennett’s protocol [10] and Deutsch’s protocol [11]. Performance aspects considered for the purification protocols are the fidelity of the purified Bell pair and the success probability [12]. All protocols work towards obtaining shorter circuits that achieve higher success rates and improved final fidelity [12].

Quantum repeaters are necessary for future quantum communication technologies such as quantum internet [4,7]. They will extend the range of transmission links to an inter-continental global scale, powering the future of a global quantum network. A notable endeavour in this regard involves efforts to deploy quantum repeaters in already existing optical fibre infrastructure [13]. Experiments, such as those conducted by Hu et al., where they successfully distributed a pair of polarization-entangled states over an impressive 11 km distance using noisy multicore fibre cables [14], instil confidence in the feasibility of establishing quantum communication links within the existing optical fibre infrastructure. However, the implementation of practical full-scale quantum repeaters in the real world is a huge technological challenge. There is much ongoing research investigating the individual components and full-scale architecture of quantum repeater systems.

This study presents the full-scale architecture of a quantum repeater designed and implemented using quantum circuits executed on a quantum computer. We used the said quantum repeater implementation to study quantum entanglement purification.

2  Experimental Setup

2.1 Research Approach

This study presents a theoretical and computational approach. The architectural design of the quantum repeater is modelled based on the use of quantum optics as opposed to earth to satellite links [15]. The conceptual implementation is however, the same.

This study uses quantum backends made available by IBM Quantum. The coding was done using IBM Qiskit python library. The backends include either a native simulator, such as IBM’s Qiskit’s QASM simulator, or a real quantum computer. The environment exposed to superconducting qubits in the IBM quantum computers can ideally emulate the same environment to which quantum repeaters will be exposed to in real-world operation [6]. Each execution stage and protocol of the quantum repeater was translated into a modular quantum circuit that was independently executed on the backends. The modularity approach facilitates testing various purification strategies, protocols and components of the quantum repeater to enhance the analysis. The quantum circuits were first executed on the native simulation backend with the incorporation of a noise model that emulated one of IBM’s real quantum computers. Subsequently, the circuits were executed on physical IBM quantum computers, scheduling their execution to the least bus available backend. The findings reported herein stem from implementation on real quantum hardware. Performance analysis centres on the fidelity of the purified Bell pair. Optimisation schemes were applied to the entanglement purification circuits to analyse their performance.

2.2 Entanglement Generation

Quantum repeaters essentially teleport entangled states from one node to another. Entangled states are therefore an integral element in quantum communication. The simplest entangled states are of a two-qubit system AB in a 4-dimensional Hilbert space are the four Bell’s states. The Bell states are also known as Einstein-Podolsky-Rosen (EPR) pairs. They are expressed in terms of the computational basis states as follows:

|Φ±⟩=12(|0⟩A|0⟩B±|1⟩A|1⟩B)(1)

|Ψ±⟩=12(|0⟩A|1⟩B±|1⟩A|0⟩B)(2)

Qubits can be represented as tensor product states using the forms |A⟩⊗|B, |A⟩|B⟩ or |AB⟩. The circuit implementation that prepares and generates them takes as input two qubits and performs Hadamard and Controlled-NOT (CNOT) unitary gate operations on them as follows:

|A⟩⊗|B⟩ Hadamard→ 12(|0⟩+|1⟩)⊗|B⟩(3)

12(|0⟩+|1⟩)⊗|B⟩⟶CNOT12(|0⟩+|1⟩)⊗|12(|0⟩+|1⟩)⊕|B⟩⟩(4)

12(|0⟩+|1⟩)⊗|B⟩⟶CNOT12(|0⟩⊗|B⟩+|1⟩⊗X|B⟩)(5)

where X a Pauli gate operation that performs a bit-flip on qubits.

The Hadamard operation creates a superposition of qubits, mapping qubits from the basis states |0⟩ or |1⟩ into |+⟩=12(|0⟩+|1⟩) or |−⟩=12(|0⟩−|1⟩), respectively. The CNOT operation acts on two qubits, designating one as the control qubit and the other as the target qubit. It performs a bit flip operation on the target qubit only if the control qubit is in the basis state |1⟩.

2.3 Quantum Entanglement Distribution

To initiate the quantum repeater protocol, entangled Bell pairs must be distributed between nodes. The transfer of the qubits serves to establish entangled links between network nodes. Upon generating Alice’s and Bob’s EPR pairs, |Φ+⟩AB and |Φ+⟩CD, respectively, one qubit from each pair gets temporarily stored in a quantum memory. This distribution is emulated using SWAP gates. SWAP gates operate by exchanging the contents of the target and control qubits as follows:

|B⟩control|Q⟩target⟶SWAP|Q⟩control|B⟩target(6)

The quantum repeater protocol inherently leads to the distribution of entanglement along the transmission line from sender to receiver. This entanglement distribution relies on quantum memories, entanglement purification protocols and entanglement swapping protocols to distribute entanglement between nodes from the start of the communication link to the end. For instance, |Φ+⟩AB represents entanglement between nodes A and B, while |Φ+⟩CD represents entanglement between nodes C and D. The entanglement in AB is distributed to CD to form a new entangled links, AD and BC, before any measurements are performed. This can be shown as follows:

|Φ+⟩AB⊗|Φ+⟩CD⟶|Φ+⟩AD⊗|Φ+⟩BC(7)

2.4 Quantum Memory

Quantum memories offer on-demand reversible storage and buffering of qubits across a quantum network without losing the qubit’s quantum properties. They can also store entangled states. We momentarily store a qubit from the entangled state |Φ+⟩AB in a quantum memory, only to retrieve it when required for entanglement distribution between nodes B and C, yielding the entangled state |Φ+⟩BC. An effective quantum memory device must demonstrate the capability to endure extended storage periods with high efficiencies [16]. This attribute holds particular significance in the preservation of quantum properties, notably entanglement. Quantum memories ought to preserve entanglement just as well as they preserve qubits. However, realizing quantum memories with long coherence times remains a significant technical challenge that limits their implementation in quantum communication and computation applications [17].

The importance of quantum memory in the realization of quantum repeaters has fuelled extensive exploration of diverse technologies and different approaches in building and realizing quantum memories. Notable among these technologies are those leveraging photonic channels [18] that use optical fibres [19] and those employing diamond nanophotonic structures such as silicon-vacancy centres within diamond nanophotonic cavities [20] and those that use nuclear spins associated with nitrogen-vacancy centres [21]. One of the best and simplest quantum memories currently is a simple fibre optic loop [7]. It leverages the time delay between entry and exit of the light through the optical fibre loop. Most approaches such as polarization of atom-photon systems and atomic ensembles focus on storing single qubits of single modes. However, other approaches such as rare-earth offers possibility of storing multiple qubits and modes.

Our circuit implementation emulates quantum memory by employing SWAP gates. It is imperative to note that our present formulation does not explicitly address the introduction of decoherence errors caused by quantum memory. We emphasize that this study, in the interest of scope, deliberately omits further detailed discussion on the implementations of quantum memory.

2.5 Quantum Entanglement Purification

We focused our research on two general purification protocols: Bennett’s protocol [10] and Deutsch’s protocol [11]. Each protocol has its own complexity of implementation, providing varying fidelity levels and producing varying degrees of overhead during circuit operation. Deutsch’s protocol represents an enhancement over Bennett’s, introducing refinements to the purification process. Successful purification using these protocol results in coinciding measurement outcomes as |00⟩ or |11⟩. Any other measurement result, either |01⟩ or |10⟩, indicates a failed purification operation, requiring a fresh restart of the purification protocol. Figs. 1 and 2 depict the implementation of the two purification protocols. The quantum circuit implementing Deutsch’s protocol, depicted in Fig. 2 is an extension of the work by Das et al. [6] following the proposal made by Deutsch et al. [11]. The implementations involve three nodes: alice, charlie and bob as the communicating parties. Each node initiates the protocol by generating their respective Bell pairs. Both protocols leverage CNOT operations, utilizing the qubits of one pair as control qubits and those of the other as target qubits.

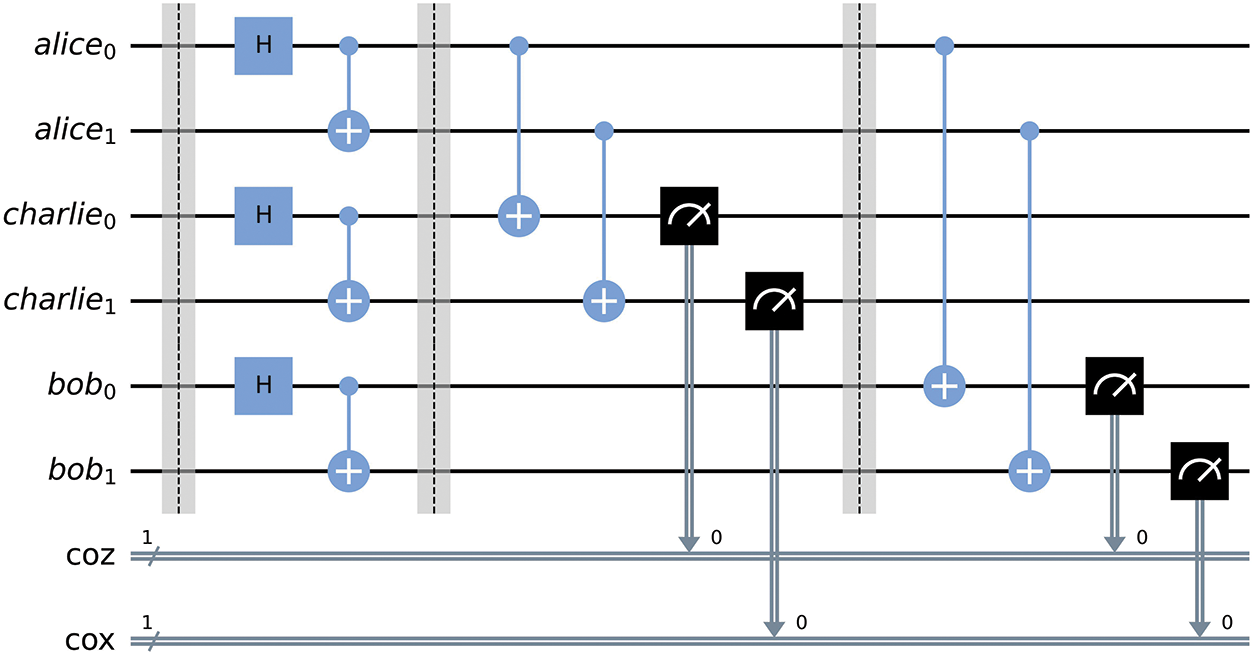
Figure 1: Quantum circuit implementation of Bennett’s purification protocol involves CNOT operations between the EPR pairs of each node. Alice’s pair serves as the control qubits while Charlie’s and Bob’s pairs acts as target qubits. CNOT operations are performed between Alice’s qubits and Charlie’s qubits. Subsequently, measurements are conducted on the target qubits. Coinciding measurement outcomes, specifically |00⟩ or |11⟩, indicate a successful purification, permitting the control qubits to advance to the next round with the subsequent node. Conversely, disparate measurement outcomes, such as |01⟩ or |10⟩, necessitate the termination of the purification attempt, requiring the discarding of all qubit pairs and a fresh restart of the purification process. The subsequent round follows a similar pattern, involving Alice and Bob’s qubits. This iterative process continues until a successful purification is achieved, or until a fresh restart is required

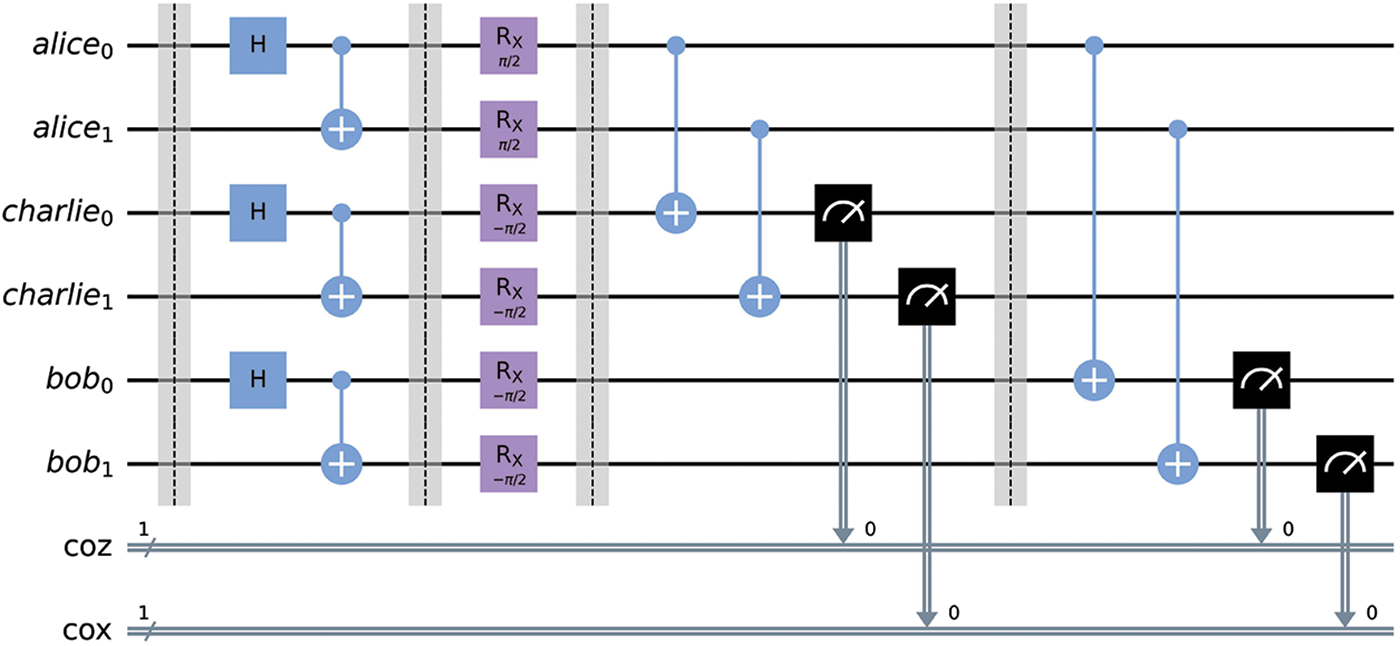
Figure 2: Quantum circuit implementation of Deutsch’s purification protocol closely resembles Bennett’s protocol but with a slight modification by introducing single-qubit rotation operations before performing CNOT operations. The node with the control qubits, Alice, performs a Rx(π2) operation on all qubits while every other corresponding node performs the inverse Rx(−π2) operation on all their qubits. The rotation operations correspond to rotations by π2 and −π2 about the x axis. Thereafter, the CNOT operations proceed as in Bennett’s procedure

2.6 Quantum Entanglement Swapping

The quantum entanglement swapping circuit has a construction approach similar to the teleportation protocol [22]. In the entanglement swapping process, one qubit of Alice’s Bell pair becomes entangled with another qubit from Bob’s Bell pair [6]. This is significant because it allows for states previously not entangled and which had never interacted with each other before to become entangled with each other. In essence, we are teleporting entanglement between nodes. This is the guiding principle to extending the length of a quantum communication link.

The elementary construction of the entanglement swapping circuit contains two Bell pairs collectively constituting a 4-qubit quantum state |ψ⟩ABCD=|Φ+⟩AB⊗|Φ+⟩CD. Bell-state measurement (BSM) operation is performed between the qubits in B and C. Based on the measurement outcomes, an appropriate Pauli correction operation I, Z, X, Y is executed on the qubit in D [6]. This results in the projection of qubits in A and D into the state |Φ+⟩AD while simultaneously establishing entanglement between nodes B and C in the state |Φ+⟩BC. The achieved entanglement distribution from A to D maintains a quantum communication link which enables direct teleportation from node A to D. The scheme described is depicted in Fig. 3. The swapping protocol is represented by the following equations:

|Ψi⟩=12(|0A0B⟩+|1A1B⟩)⊗12(|0C0D⟩+|1C1D⟩)(8)

where |Ψ_i⟩ is the initial state of the entire system involving Alice and Bob. When the Bell-state operation is performed just before measurements, we get the equation:

|Ψf⟩=12(|0A0D⟩+|1A1D⟩)⊗12(|0B0C⟩+|1B1C⟩)(9)

where |Ψf⟩ is the final state of the entire system.

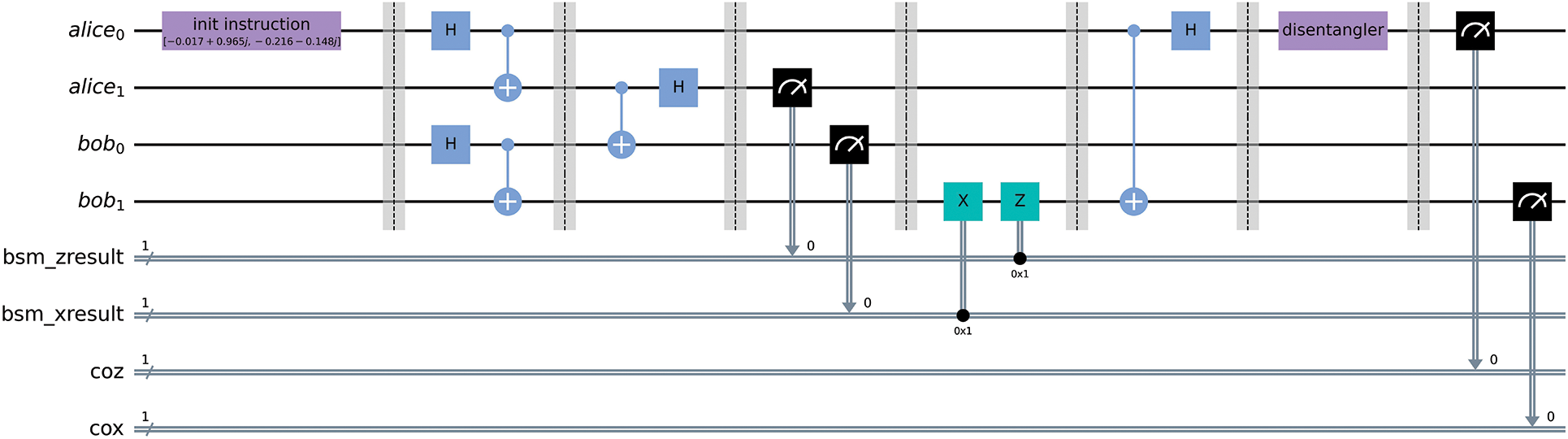
Figure 3: Quantum circuit implementation for quantum entanglement swapping protocol involves the teleportation of Alice’s quantum state |alice0⟩ to Bob. To verify the success of the protocol, a random 2-dimensional quantum state vector is used to create an initialisation instruction labelled init instruction which is applied to Alice’s qubits transforming alice0 from |0⟩ to some random state |ψ⟩. Thereafter, EPR pair generation occurs. Entanglement swapping is performed, establishing entanglement between Alice’s |alice0⟩ and Bob’s |bob1⟩ qubits while the rest of the qubits are discarded post-measurement. To validate successful entanglement, an inverse initialisation instruction labelled disentangler is applied to the entangled state |alice0bob1⟩ on |alice0⟩ which should transform the teleported qubit from |ψ⟩ to |0⟩, yielding an expected measurement outcome of |00⟩

Notably, this study employs the conventional construction of entanglement swapping that requires CNOT gates. However, there has been proposed an alternative approach that eliminates the need for CNOT gates, leveraging the quantum Zeno effect which has the potential of reducing the quantum repeater circuit complexity and potentially improving on the fidelity of quantum states [23].

The quantum circuit implementing the quantum entanglement swapping protocol extends the work by Das et al. [6]. To facilitate results analysis, we introduced initialisation and inverse initialisation instructions. The circuit, illustrated in Fig. 3, was executed on the quantum backend, and measurements were performed in the computational basis, yielding the verification results in Fig. 4 that provide insights into the success of the entanglement swapping process. An outcome of |00⟩ for Alice’s and Bob’s qubits, alice0 and bob1, respectively, indicates successful entanglement swapping. Observe that this occurs on average half the time in our case. These results are consistent with the findings of Das et al. [6] on the effect of entanglement swapping on the fidelity.

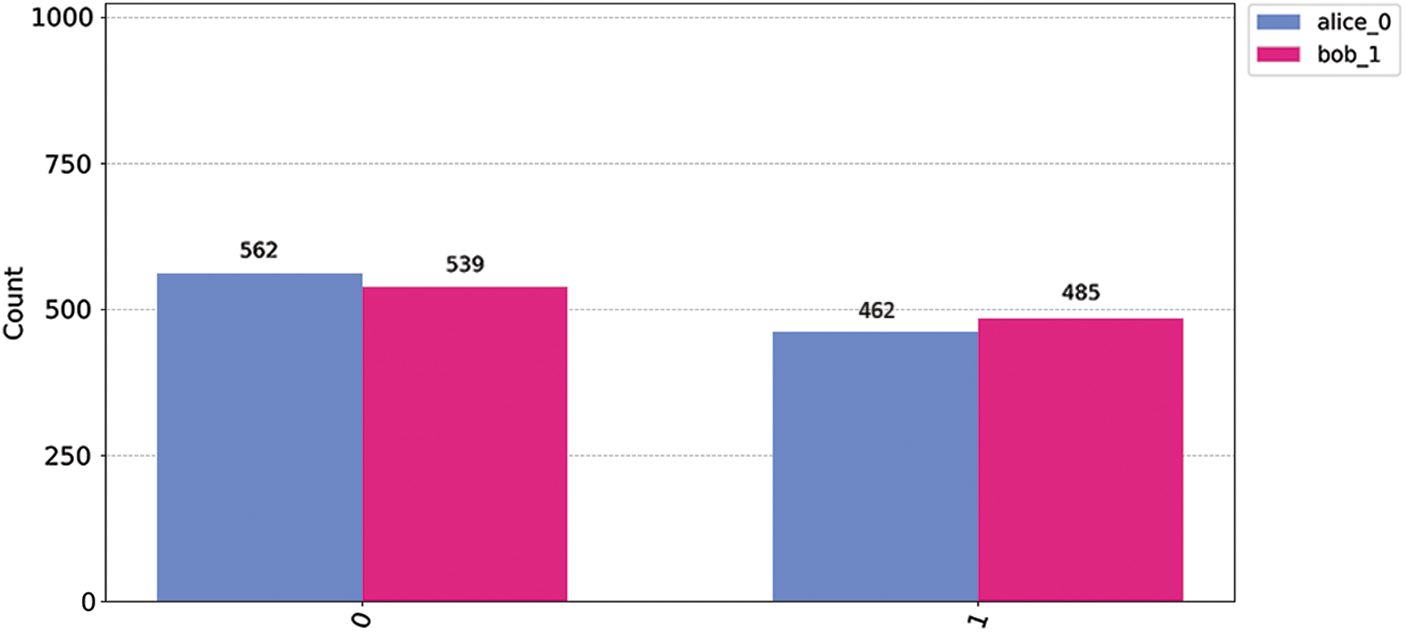
Figure 4: Results obtained for the verification of the quantum entanglement swapping protocol. Observe that for states |alice0⟩ and |bob1⟩, their measurement outcomes are measured to be in the |0⟩ state approximately half the time. This outcome indicates the successful execution of the swapping protocol on roughly half of the executions

3  Results and Discussion

3.1 Complete Quantum Repeater Architecture

By combining all the necessary components, we arrived at a complete implementation of a quantum repeater and its complimentary elements within a quantum network [24]. The circuit architecture is depicted in Figs. 5 and 6. It is important to note that the architecture presented is an extension of the works by Das et al. [6].

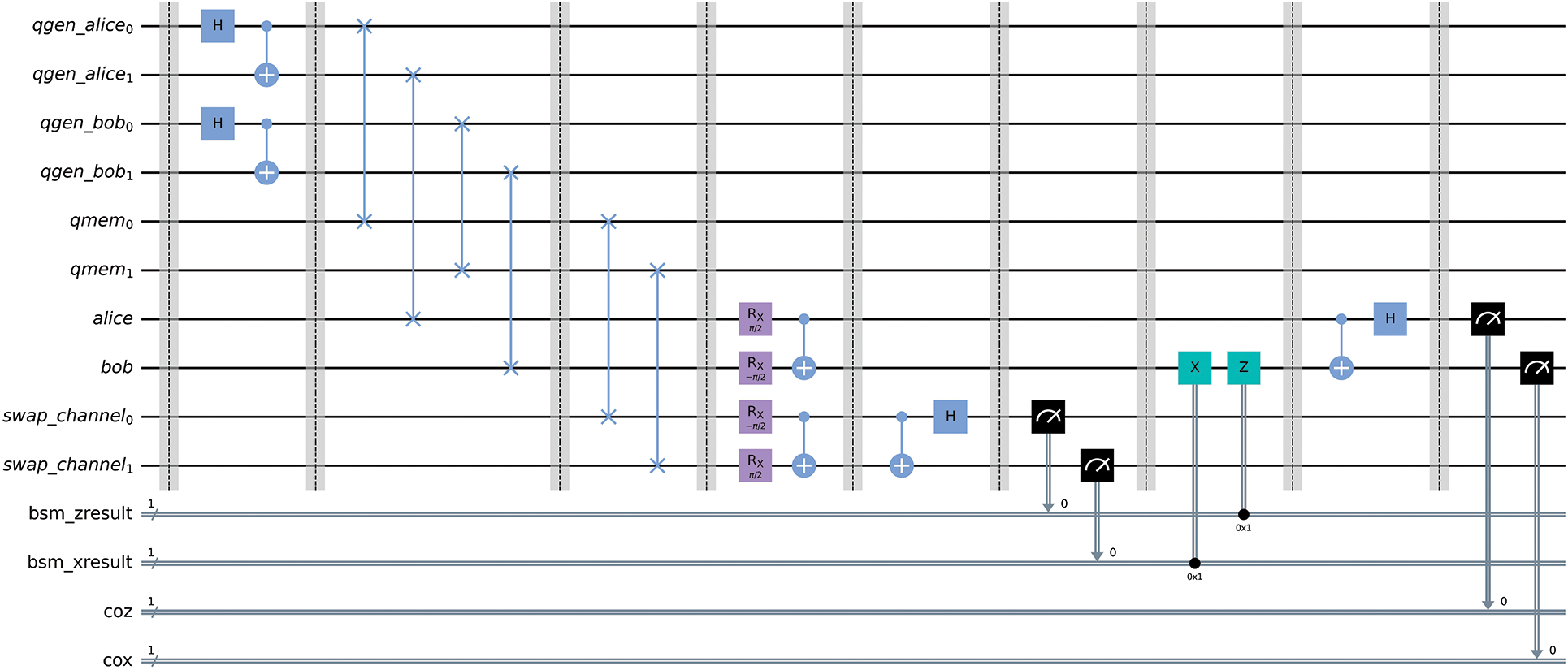
Figure 5: Quantum circuit for the full complete quantum repeater, implementing Deutsch’s purification protocol just before the swapping protocol stage. qgen_alice and qgen_bob represent the modules generating Alice’s and Bob’s entangled qubits respectively. qmem represents quantum memory devices present in a quantum repeater. The transmission of qubits through classical channels to either quantum channels of quantum memory is emulated using SWAP gates

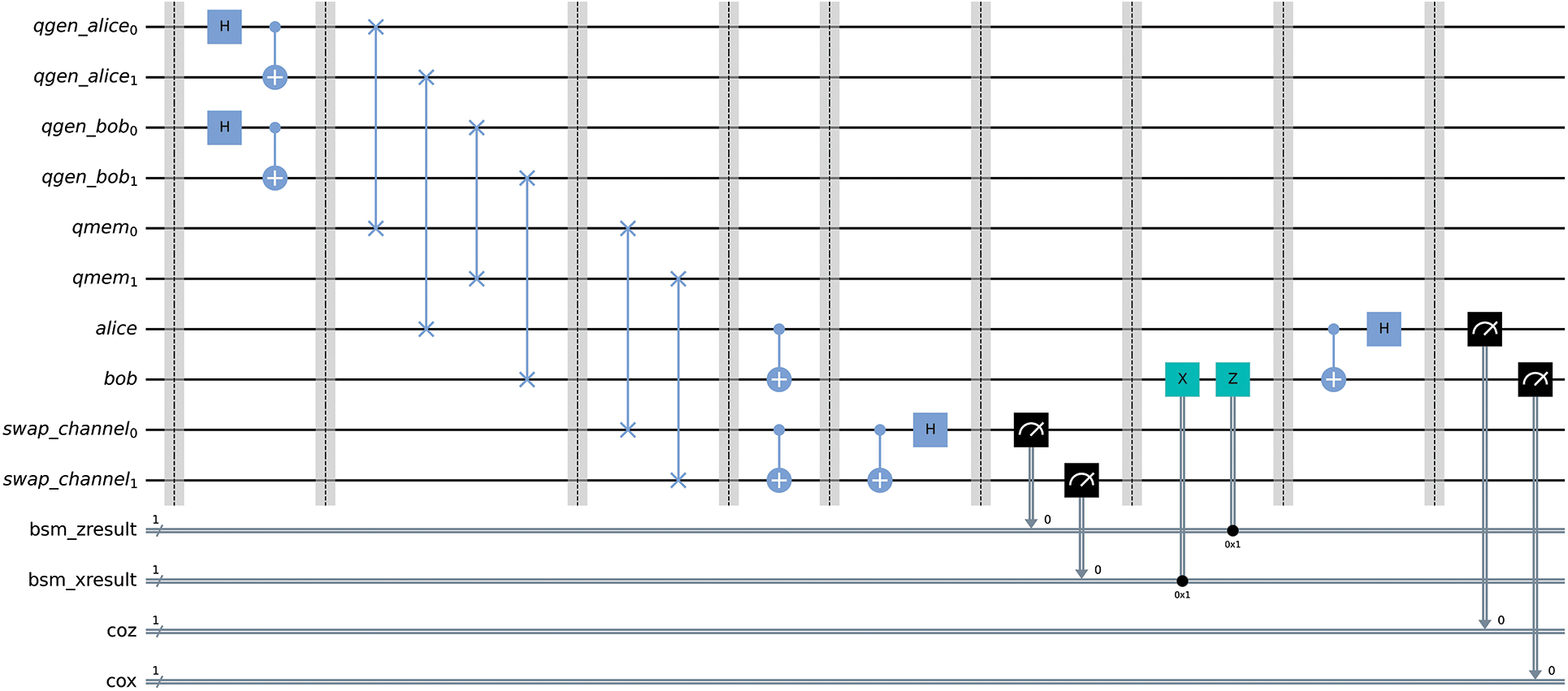
Figure 6: Quantum circuit for the full complete quantum repeater, implementing Bennett’s purification protocol just before the swapping protocol stage

Alice’s and Bob’s Bell pairs are first generated. One qubit from each Bell pair is transmitted to Alice and Bob through a classical channel. The remaining qubits from each Bell pair get transmitted through a classical channel to quantum memory devices found on the quantum repeater. The transmission of these qubits is emulated using SWAP gates. Through heralding techniques [9,25], a classical signal is sent to the repeater, indicating that Alice’s and Bob’s qubits that are in memory are ready for the swapping process [26]. The heralding helps to synchronize the swapping protocol. The qubits in the quantum memory devices are transmitted to their respective quantum channels, ready for the swapping process. This transmission is again represented by SWAP gates. As illustrated in Fig. 5, Deutsch’s purification protocol is executed just before executing entanglement swapping. Finally, Alice’s and Bob’s qubits undergo a Bell-state measurement.

The presented circuit architecture provides a real-world implementation of the quantum repeater protocol. We used it to investigate our remaining objectives regarding purification strategies and optimization schemes.

3.2 Purification Strategy

Identifying an optimal purification strategy is crucial for enhancing the operational efficiency of future practical quantum repeaters. This significance is exemplified by approaches such as the nested purification strategy, which has been experimentally demonstrated to effectively minimise unwanted noise during entanglement swapping, yielding high-fidelity entangled states [27,28].

In this study, three purification strategies are explored in the simulations. The strategies differ in terms of the application stage of the purification protocol. These strategies are: (1) post swap, performs purification after each entanglement swapping protocol; (2) repeated post swap, performs successive iterative purification instances after each entanglement swapping protocol (with three instances in our simulations); and (3) pre-and-post swap, alternating purification before and after an entanglement swapping protocol.

The simulations were exclusively conducted using Deutsch’s purification protocol, under the assumption that the outcomes would exhibit similarity across various purification protocols. This allows for variation of only the purification stage while keeping other aspects constant.

To conduct the purification strategy simulations, a compact form of the circuit in Fig. 5 was used. An initialization instruction was appended at the beginning of the circuit to perform a reset on Alice’s qubit, setting it into the state |0⟩ then applying gates to turn it into a random state |ψ⟩. After the initialization instruction followed the quantum repeater protocol after which an inverse initialization instruction was appended. The inverse initialization instruction works to revert the random state |ψ⟩ back to the state |0⟩. Thus, upon measurement on Alice’s and Bob’s qubits at the end, ideally, one should get the state |00⟩. The entire circuit was executed 20 times, resulting in 20 independent sets of measurement results each with its own set of probabilities for the states |00⟩, |01⟩, |10⟩ and |11⟩. The results were then averaged.

The averaged results obtained were used to verify that one qubit from Alice’s entangled qubit pair had indeed been teleported to Bob. Measurements on either qubit should yield either the state |0⟩ or |1⟩. The resulting plot is as illustrated in Fig. 7. Ideally, we would expect 100% probability of measuring Bob’s qubit in the state |0⟩. Higher estimated probabilities, indicate increased likelihood of successful execution of the quantum repeater protocol as theoretically expected. As observed, this success occurs approximately half the time, which is consistent with the inherent probabilistic nature of the entanglement swapping and purification processes.

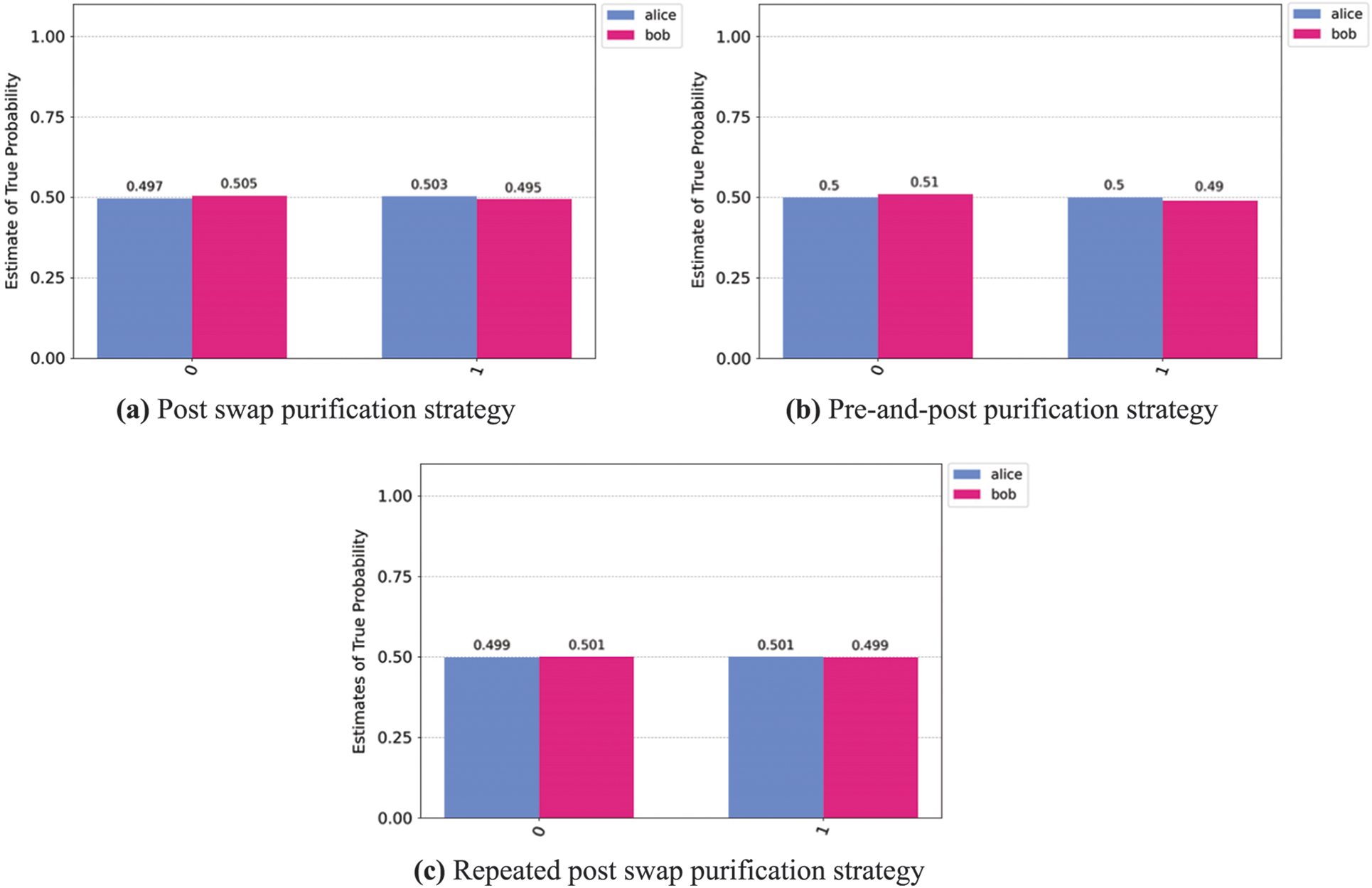
Figure 7: Results verifying the success of the teleportation of entanglement in the quantum repeater protocol between Alice and Bob under different strategies as indicated in the graph

These compelling results provide substantial evidence of the effectiveness of the employed purification strategies in achieving the teleportation of quantum information between nodes. The close alignment of the observed outcomes with theoretical predictions and prior literature, such as the work by Das et al. [6], lends robust support to the accuracy and reliability of the quantum repeater protocol strategies under investigation.

Fig. 8 presents the results depicting the impact of purification on the fidelity at different stages within the quantum repeater protocol. The considered stages include the initial distribution stage (dist), first swapping stage (aswap1), second swapping stage (aswap2) and ultimately the end of the node. To obtain fidelity measurements at each stage, the quantum circuit was duplicated up to the specific stage, executed, and measured. This process was repeated across the 20 simulation runs, resulting in 20 independent measurement sets, each containing four measurements corresponding to the four considered stages. The results were averaged before performing the Hellinger fidelity operation to obtain the fidelity between consecutive stages.

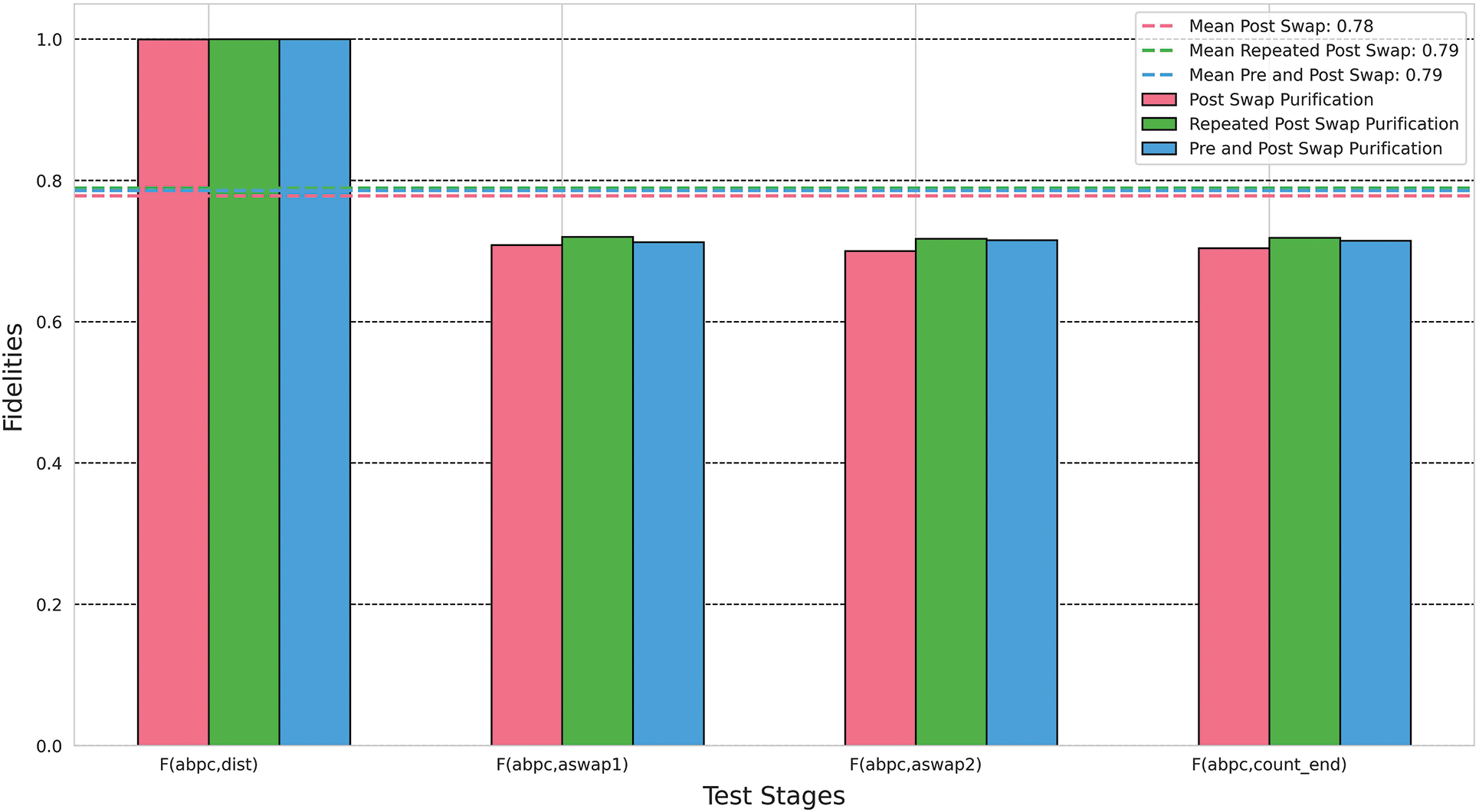
Figure 8: Effect of purification on fidelity across different purification strategies. The results were obtained from a circuit implementing an intermediate quantum repeater and hence two entanglement swapping procedures, labelled as aswap1 and aswap2

The Hellinger fidelity is used to compute and quantify the similarity between two probability distributions. It is defined as:

FH=(1−H2)2(10)

where H is the Hellinger distance. It is equivalent to the standard classical fidelity:

F(Q,P)=(∑ipiqi)2(11)

where pi and qi are two probability distributions, which in this context, are the results obtained from the circuit execution expressed as counts. The Hellinger fidelity metric helps us assess how similar the results of each stage are to the measurement results after entanglement generation.

Evidently, initial entanglement distribution has no effect on the fidelity. Realistically, fidelity loss occurs at this juncture, primarily influenced by the technology used in entanglement generation, especially when employing a parametric-down-conversion source [25], and the characteristics of the distribution channel. Heralded entanglement generation is the most practical method to suppress errors at this stage [9]. The fidelity of the Bell-pairs takes a hit during entanglement swapping.

Combining all the collected data provides valuable insights into the optimal purification strategy to be employed in practical quantum repeaters, especially in the Noisy Intermediate-Scale Quantum (NISQ) era [29], as per our formulation. All considered strategies consistently maintained a fidelity level above the minimum required threshold of 50% to sustain a quantum communication link.

Multiple analyses underscored the robustness of the purification strategies for potential application in the quantum repeater protocol. Notably, the pre-and-post swap purification strategy emerged slightly favoured, consistently achieving a higher mean fidelity value FM=0.79 at best across numerous simulation iterations. Near similar results were obtained by Behera et al. [30], where they demonstrated peak fidelity levels of up to F=0.8456. Their stages of purification from Alice to Charlie and then Charlie to Bob exhibited fidelities of FAC=0.8086 and FCB=0.7840, respectively [30]. Hu et al. proposed a high efficiency long-distance polarization entanglement purification protocol that makes use of only one pair of hyperentangled states, and which achieved fidelities of up to F=0.887 [14].

These results align with our findings, demonstrating the success of the purification protocols, even with slightly different quantum repeater designs.

We observed consistent fidelities, in contrast to demonstrations by Das et al. [6], where there was a progressively decreasing fidelity with each swap stage. Analysing the correlation between the fidelity values at different stages of the quantum repeater protocol reveals a notable positive correlation among the strategies, particularly between the pre-and-post swap and the repeated post-swap strategies. This implies that the positive impact of purification is sustained through subsequent stages.

To evaluate the consistency of each purification strategy, an analysis of the fidelity value distribution was conducted. The pre-and-post swap purification strategy not only maintained a high average fidelity but also exhibited lower variability, indicative of a more reliable performance compared to alternative strategies. This underscores the effectiveness of a purification approach that executes before and after entanglement swapping.

It is essential to acknowledge that, while there are minor differences in fidelities (see Fig. 8) and quantum repeater verification results (see Fig. 7), these differences hold limited statistical significance within the scope of our study. The main insight derived from this analysis is that we achieve nearly identical results from our purification protocols, regardless of the specific strategy employed. The pre-and-post swap strategy offers only a slight advantage, which can be attributed to its unique capability to purify both the incoming generated EPR pairs from a source and the post-entanglement swap pairs. This efficient purification circuit design balances the addressing of initialization or loss errors (arising from imperfect raw Bell pairs) and operations errors arising from imperfect local operations [12]. Furthermore, compared to the repeated post-swap strategy, the pre-and-post swap strategy necessitates purification only once. Repeated purification, as we have seen, fails to offer additional improvements and only increases circuit complexity, overhead and the likelihood of contributing to additional errors due to imperfect local operations [12].

These insights emphasize the importance of selecting an appropriate purification strategy based on the employed protocol. It is anticipated that substantial differences may arise when considering a broader and diverse array of purification protocols and strategies beyond what has been explored in this study. Further investigations into the scalability and adaptability of these strategies will be crucial for the continued development of quantum repeater systems.

3.3 Purification Optimization Scheme

The purification circuits underwent two levels of optimization—a light optimization scheme and a heavy optimization scheme. The IBM Qiskit transpiler is responsible for the optimization levels used. The purification optimization scheme was carried out for all purification strategies tested out earlier using the two major purification protocols-Bennett’s and Deutsch’s protocols.

For each of the three purification strategies, the circuit would initially implement Deutsch’s purification protocol starting with light optimization. Then execution would be repeated using heavy optimization. This was followed by implementation of Bennett’s purification protocol with both the light and heavy optimization schemes. The aim was to evaluate if the optimization schemes employed favour any of the purification protocols employed in the purification circuits in terms of efficiency and performance within the quantum repeater protocol.

There were 20 independent measurement results obtained from 20 iterations of the circuit runs per purification strategy. The probabilities were then averaged for each purification strategy to get the estimate of the true probability. These results were used for each purification strategy, in finding the difference between Deutsch’s and Bennett’s estimate of probability under the light optimization scheme then the heavy optimization scheme before plotting them as shown in Fig. 9. The differences were plotted as percentages.

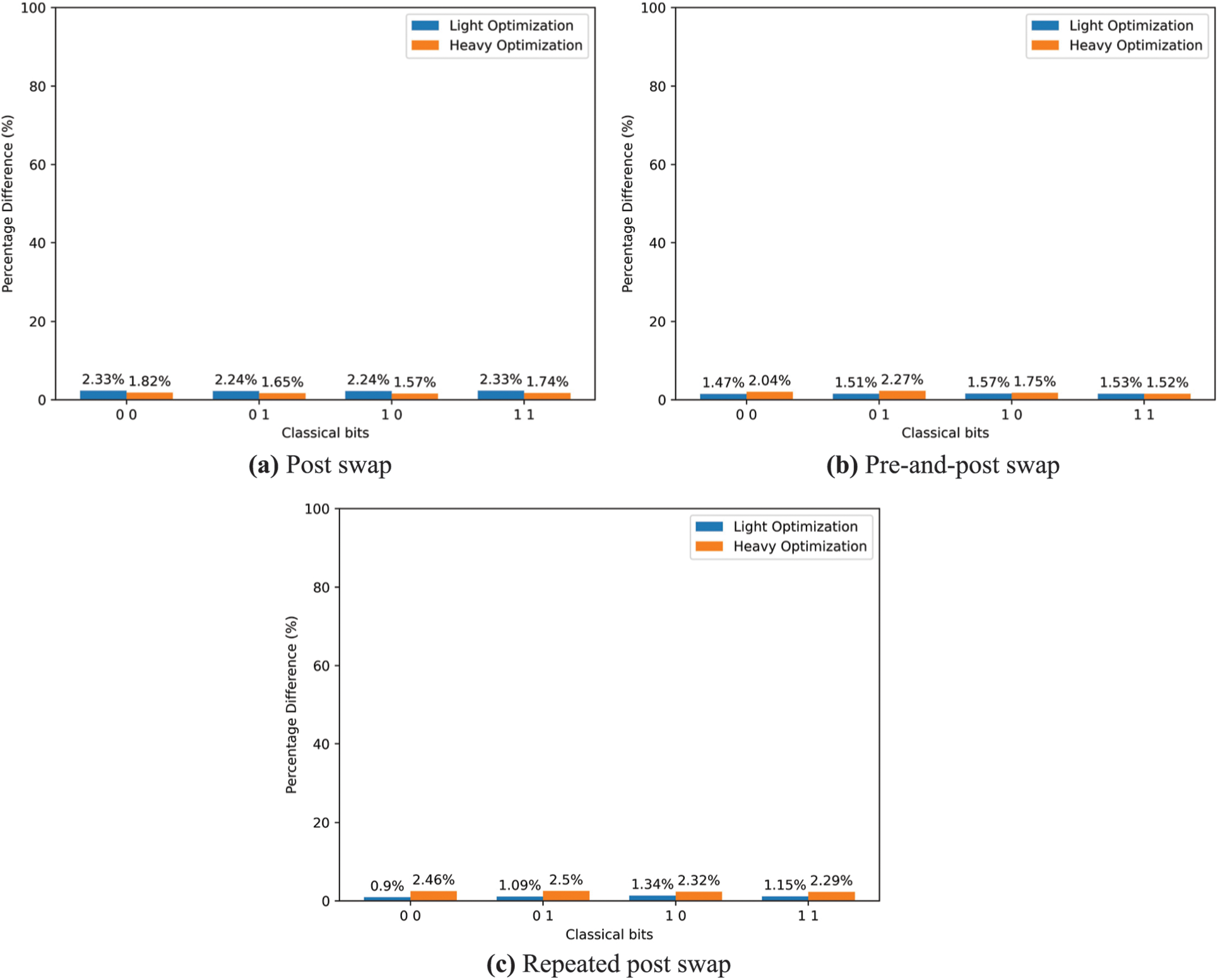
Figure 9: The results of experiments testing the differences of various purification protocols under different optimization schemes. The experiments were carried out for different purification strategies

The classical bits represent the classical states obtained after measurement by Alice and Bob at the end of the communication channel. Lower percentage values indicate less distinction in the measurement outcomes between Deutsch’s and Bennett’s purification protocols when executed under the indicated optimization scheme. Specifically, lower percentage values imply a convergence in the measurement results, demonstrating a similarity in the efficacy of the purification protocols.

The results from this experiment demonstrate and provide compelling evidence to confirm that despite the differences in experimental requirements and efficiencies, the choice of purification protocols used in this study has no significant impact on the overall purification optimization scheme employed in the purification circuits, in line with the findings by Muralidharan et al. [9]. Further research can explore the incorporation of more purification optimization schemes, such as the discrete optimization algorithms approach that can generate efficient purification circuits said to outperform many other general-purpose purification protocols [12].

4  Conclusions

This study has presented a quantum repeater design setup and its implementation, providing valuable insight into entanglement purification. We have demonstrated various entanglement purification protocol strategies and their subsequent circuit optimizations using the presented architecture. The research focused on investigating entanglement purification strategies and the impact of optimization schemes applied under two purification protocols, in the context of near-term quantum repeaters [9].

Three distinct purification strategies were tested using Deutsch’s purification protocol. The results consistently highlight the pre-and-post swap strategy as the most favourable approach in the scope of our quantum repeater studies, owing to its consistent high performance. Nevertheless, it is important to note that all strategies exhibited robustness and efficiency in preserving entanglement and optimizing quantum communication.

Notably, the purification protocols yielded similar results across various strategies employed in our study. Furthermore, the different levels of optimization had no significant impact on the performance of these purification strategies. The optimization schemes did not favour any of the employed purification protocols.

This research underscores the significance of thoughtfully considering purification strategies and optimization approaches to achieve significant improvements in quantum repeater performance, ultimately enhancing the efficiency of future practical quantum repeaters. We anticipate continued research efforts aimed at enhancing the success rate of entanglement swapping. Operational errors and loss errors remain persistent challenges in near-term quantum repeaters. It is evident that operational errors and loss errors persist as challenges in near-term quantum repeaters. Therefore, ongoing efforts should be directed toward the continual improvement and refinement of purification protocols and strategies. Through these endeavours, the realization of a practical quantum repeater operating in the NISQ era becomes an increasingly promising prospect.

Acknowledgement: This work received generous support from the University of Nairobi, Physics Department, specifically through the Astrophysics and Space Science Research Group. We are grateful to Dr. Andrew Kahonge for his invaluable input, insights and diligent feedback that greatly enriched our work. We extend our heartfelt thanks to the dedicated members of the University of Nairobi Astro Journal Club, whose insightful discussions and constructive feedback helped refine our research throughout the presentation stages. We would like to express our appreciation to the University of Nairobi’s Faculty of Science and Technology for the opportunity to present this work at the 5th Annual Conference for the Faculty of Science and Technology. Lastly, we recognise the indispensable contributions of the open-source projects Python, Jupyter and Qiskit, and the IBM Quantum Platform. These tools were instrumental in facilitating our research.

Funding Statement: The authors acknowledge support from the University of Nairobi towards making this research a success.

Author Contributions: The authors affirm their comprehensive contributions to this paper, encompassing theoretical conception and design, data collection, its analysis and interpretation, as well as the drafting of the manuscript. All authors reviewed the results, and subsequently approved the final version of the manuscript.

Availability of Data and Materials: All the data used together with the code written for this research necessary to reproduce our results is available on GitHub [31].

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. C. H. Bennett, G. Brassard, C. Crépeau, R. Jozsa, A. Peres et al., “Teleporting an unknown quantum state via dual classical and Einstein-Podolsky-Rosen channels,” Physical Review Letters, vol. 70, no. 13, pp. 1895–1899, 1993. [Google Scholar] [PubMed]

2. Q. Ruihong and M. Ying, “Research progress of quantum repeaters,” Journal of Physics: Conference Series, vol. 1237, pp. 5, 2019. [Google Scholar]

3. L. M. Duan, M. D. Lukin, J. I. Cirac and P. Zoller, “Long-distance quantum communication with atomic ensembles and linear optics,” Nature, vol. 414, no. 6862, pp. 413–418, 2001. [Google Scholar] [PubMed]

4. H. J. Briegel, W. Dür, J. I. Cirac and P. Zoller, “Quantum repeaters: The role of imperfect local operations in quantum communication,” Physical Review Letters, vol. 81, no. 26, pp. 5932–5935, 1998. [Google Scholar]

5. W. Dür and H. J. Briegel, “Entanglement purification and quantum error correction,” Reports on Progress in Physics, vol. 70, no. 8, pp. 1381, 2007. [Google Scholar]

6. S. Das, Md. S. Rahman and M. Majumdar, “Design of a quantum repeater using quantum circuits and benchmarking its performance on an IBM quantum computer,” Quantum Information Processing, vol. 20, no. 7, pp. 245, 2021. [Google Scholar]

7. N. Gisin and R. Thew, “Quantum communication,” Nature Photonics, vol. 1, no. 3, pp. 165–171, 2007. [Google Scholar]

8. T. Herbst, T. Scheidl, M. Fink, J. Handsteiner, B. Wittmann et al., “Teleportation of entanglement over 143 km,” Proceedings of The National Academy of Sciences, vol. 112, no. 46, pp. 14202–14205, 2015. [Google Scholar]

9. S. Muralidharan, L. Li, J. Kim, N. Lütkenhaus, M. D. Lukin et al., “Optimal architectures for long distance quantum communication,” Scientific Reports, vol. 6, no. 1, pp. 20463, 2016. [Google Scholar] [PubMed]

10. C. H. Bennett, G. Brassard, S. Popescu, B. Schumacher, J. A. Smolin et al., “Purification of noisy entanglement and faithful teleportation via noisy channels,” Physical Review Letters, vol. 76, no. 5, pp. 722–725, 1996. [Google Scholar] [PubMed]

11. D. Deutsch, A. Ekert, R. Jozsa, C. Macchiavello, S. Popescu et al., “Quantum privacy amplification and the security of quantum cryptography over noisy channels,” Physical Review Letters, vol. 77, no. 13, pp. 2818–2821, 1996. [Google Scholar] [PubMed]

12. S. Krastanov, V. V. Albert and L. Jiang, “Optimized entanglement purification,” Quantum, vol. 3, pp. 123, 2019. [Google Scholar]

13. J. Rabbie, K. Chakraborty, G. Avis and S. Wehner, “Designing quantum networks using preexisting infrastructure,” npj Quantum Information, vol. 8, no. 1, pp. 5, 2022. [Google Scholar]

14. X. M. Hu, C. X. Huang, Y. B. Sheng, L. Zhou, B. H. Liu et al., “Long-distance entanglement purification for quantum communication,” Physical Review Letters, vol. 126, no. 1, pp. 010503, 2021. [Google Scholar] [PubMed]

15. J. G. Ren, P. Xu, H. L. Yong, L. Zhang, S. K. Liao et al., “Ground-to-satellite quantum teleportation,” Nature, vol. 549, no. 7670, pp. 70–73, 2017. [Google Scholar] [PubMed]

16. G. Brennen, E. Giacobino and C. Simon, “Focus on quantum memory,” New Journal of Physics, vol. 17, no. 5, pp. 050201, 2015. [Google Scholar]

17. C. T. Liao, S. Bahrani, F. F. da Silva and E. Kashefi, “Benchmarking of quantum protocols,” Scientific Reports, vol. 12, no. 1, pp. 5298, 2022. [Google Scholar] [PubMed]

18. L. Childress, J. M. Taylor, A. S. Sørensen and M. D. Lukin, “Fault-tolerant quantum communication based on solid-state photon emitters,” Physical Review Letters, vol. 96, no. 7, pp. 070504, 2006. [Google Scholar] [PubMed]

19. A. I. Lvovsky, B. C. Sanders and W. Tittel, “Optical quantum memory,” Nature Photonics, vol. 3, no. 12, pp. 706–714, 2009. [Google Scholar]

20. P. J. Stas, Y. Q. Huan, B. Machielse, E. N. Knall, A. Suleymanzade et al., “Robust multi-qubit quantum network node with integrated error detection,” Science, vol. 378, no. 6619, pp. 557–560, 2022. [Google Scholar] [PubMed]

21. J. Ji, Y. F. Wu, S. C. Wein, F. K. Asadi, R. Ghobadi et al., “Proposal for room-temperature quantum repeaters with nitrogen-vacancy centers and optomechanics,” Quantum, vol. 6, pp. 669, 2022. [Google Scholar]

22. S. Pirandola, J. Eisert, C. Weedbrook, A. Furusawa and S. L. Braunstein, “Advances in quantum teleportation,” Nature Photonics, vol. 9, no. 10, pp. 641–652, 2015. [Google Scholar]

23. V. Bayrakci and F. Ozaydin, “Quantum zeno repeaters,” Scientific Reports, vol. 12, no. 1, pp. 15302, 2022. [Google Scholar] [PubMed]

24. W. Kozlowski, A. Dahlberg and S. Wehner, “Designing a quantum network protocol,” in Proc. of the 16th Int. Conf. on Emerging Networking EXperiments and Technologies (CoNEXT ‘20), Barcelona, Spain, pp. 1–16, 2020. [Google Scholar]

25. G. Z. Song, F. Z. Wu, M. Zhang and G. J. Yang, “Heralded quantum repeater based on the scattering of photons off single emitters using parametric down-conversion source,” Scientific Reports, vol. 6, no. 1, pp. 28744, 2016. [Google Scholar] [PubMed]

26. X. Liu, J. Hu, Z. F. Li, X. Li, P. Y. Li et al., “Heralded entanglement distribution between two absorptive quantum memories,” Nature, vol. 594, no. 7861, pp. 41–45, 2021. [Google Scholar] [PubMed]

27. L. K. Chen, H. L. Yong, P. Xu, X. C. Yao, T. Xiang et al., “Experimental nested purification for a linear optical quantum repeater,” Nature Photonics, vol. 11, no. 11, pp. 695–699, 2017. [Google Scholar]

28. L. Zhou, S. S. Zhang, W. Zhong and Y. B. Sheng, “Multi-copy nested entanglement purification for quantum repeaters,” Annals of Physics, vol. 412, pp. 168042, 2020. [Google Scholar]

29. J. Preskill, “Quantum computing in the NISQ era and beyond,” Quantum, vol. 2, pp. 79, 2018. [Google Scholar]

30. B. K. Behera, S. Seth, A. Das and P. K. Panigrahi, “Demonstration of entanglement purification and swapping protocol to design quantum repeater in IBM quantum computer,” Quantum Information Processing, vol. 18, no. 4, pp. 1–10, 2019. [Google Scholar]

31. Quantum Repeater Design. https://github.com/Phystro/Quantum-Repeater-Design/ (accessed on 08/11/2023). [Google Scholar]