Pancreatic Cancer Data Classification with Quantum Machine Learning

1  Introduction

The term ‘Quantum computing’ encompasses the utilization of quantum mechanics principles to devise algorithms based on the fundamental laws of physics. These algorithms operate differently from classical computer operations [1]. Quantum computing, in particular, holds the promise of providing potential solutions for intricate problems that necessitate exponential time for computation. These problems typically center around combinatorial tasks such as optimization, simulation and graph searches. Quantum computers leverage the principles of quantum mechanics to conduct computations, capitalizing on the characteristics of quantum states at the atomic and subatomic tiers of matter such as superposition, interference, and entanglement [2]. Quantum computing constitutes a sub-field within quantum information science that delves into the integration of quantum phenomena with the realm of information science [3]. In addition to quantum computing, other subfields of quantum information science, such as like error correction, cryptography, communication, and teleportation, also utilize quantum computing along with the hardware circuits [4]. The concept of quantum computing evolved in 1980s with the proposal of a quantum mechanical model of the Turing machine and the execution of simulations on quantum model. This exhibited the potential to outpace classical models in terms of speed and efficiency [5]. Subsequently, a few quantum algorithms, such as Shor’s algorithm for the factorization of large numbers and the Grover’s algorithm for quantum search were developed [6,7]. Several technological breakthroughs geared towards achieving ‘Quantum supremacy’ have propelled the field of quantum computing into the spotlight and opened various avenues for extensive research. Quantum supremacy is a demonstration of a programmable quantum device that can solve a problem which no classical computer can solve within a finite amount of time. This achievement essentially entails performing calculations at an exponential rate on a quantum processor [8,9]. Following the attainment of quantum supremacy, the field of quantum computing has witnessed a surge in exploration and collaboration, driven by the prospect of addressing complex challenges previously deemed intractable. This achievement not only marks a critical milestone in quantum technology but also paves the way for revolutionary advancements in diverse domains, including optimization, material science, cryptography, and artificial intelligence. As research and development continue, the interplay between hardware innovation, algorithmic breakthroughs, and quantum software refinement remains integral to fully harnessing the potential of quantum computing for real-world applications.

In a classical computer, the computation manipulates the bits that can be 0 or 1. In the quantum model, the quantum bit, referred to as qubit, can be in any amount of superposition of the states |0⟩ and |1⟩ denoted by |ψ⟩=α|0⟩+β|1⟩, where α,β,∈,C and α2+β2=1. The complex values α and β are the amplitude values of the respective states. In quantum mechanics, the act of measuring a qubit, which is the fundamental unit of quantum information, results in the collapse of its quantum state into a definite value. Prior to measurement, a qubit exists in a superposition of multiple states, embodying a blend of all possible states simultaneously. However, upon measurement, the qubit takes on a specific state, typically one of its constituent states, as determined by the measurement outcome. This phenomenon is a core principle of quantum mechanics and distinguishes it from classical physics. Quantum manipulations are accomplished through the application of various quantum gates, which alter the state of qubits in a controlled manner. Mathematically, these operations involve complex numbers, linear algebra, and the multiplication of unitary matrices to represent various quantum logic gates. These gates enable transformations and interactions between qubits, forming the foundation for quantum algorithms and computations. The diverse array of single and multi-qubit logic gates plays pivotal roles in the landscape of quantum computing. Identity gate preserves the quantum state intact. Pauli gates (X, Y, Z) orchestrates rotation about x, y, z axes in a Bloch sphere by π radians, resulting in phase and amplitude transformations. Hadamard gate (H) induces superposition states within a single qubit. Control gate or CNOT gate empowers some qubits to control the operation of other qubits and is also used to represent entanglement. Phase shift gates (Z, S, T) change the phase of the quantum state but the probability of measurement remains unchanged. Rotation operator gates (Rx(θ), Ry(θ), Rz(θ)) denote rotation by θ degrees in Euclidean space. Toffoli or CCNOT gate acts as controlled gate for three qubits. CSWAP gate performs a controlled swap operation on three qubits. These gates can be systematically combined in a serial or parallel manner tailored to the specific demands of the given problem [4].

A quantum algorithm is described in terms of the quantum circuit model, where the circuit is a layout of quantum gates acting on the predetermined number of input qubits. The process culminates with measurements taken to yield the desired output. The circuit design forms a sequential sequence of quantum gates, akin to a pipeline. This assembly can be replicated and evaluated on a quantum simulator by conducting vector multiplications involving unitary matrices, corresponding to the quantum gates. The circuit's execution is reiterated multiple times, as the result entails probability values for diverse potential outcomes. These iterative executions are termed as “shots”. Hence, the quantum algorithm workflow encompasses the following steps: a. Formulation of the quantum circuit tailored to the specific requirements of the problem; b. Repetitive execution of the circuit for a designated count of trails and capturing the output measurements; and c. Evaluate the collected outputs, culminating in the presentation of conclusive results [10].

1.1 Quantum Machine Learning

Machine Learning is a sub-field of Artificial Intelligence that employs a number of algorithms to learn the patterns out of data and use it for data analysis, its classification, and further predictions [11]. The algorithms make use of mathematics and statistics to build training models from the data itself. These models undergo rigorous testing and validation using a portion of the data. Once validated, these models can be applied to process new data effectively. Machine Learning algorithms are categorized as supervised learning, unsupervised learning, and reinforcement learning [12]. In supervised learning, the input data or training data is annotated or labelled, enabling the data model to be trained to produce the desired outputs. After the training phase, the model is able to predict the output for new and unseen data. Supervised learning is used for data classification (predicting the class of new data based on the training with class labelled data) and prediction (determining the output value for new data based on the mathematical regression patterns found in existing data). These algorithms are useful for similarity-based applications like recommendation systems, annotation systems, and verification systems [13]. The unsupervised learning algorithms work on unlabeled data with an aim to find some underlying pattern in the groups of data and try to create clusters of somewhat similar data. This process permits the categorization of unknown or new data into a cluster by gauging the similarity of input features with those existing in the established clusters. Unsupervised learning is used for clustering, feature learning, and dimension reduction related problems [14]. Reinforcement learning employs a feedback mechanism to train the data model. The model is rewarded for correct output and penalized for incorrect output and hence facilitates learning through accumulated experience. Reinforcement learning is applied in areas like game theory and automated driving [15].

Quantum machine learning amalgamates the power of classical machine learning algorithms using the quantum systems, yielding enhanced computational capabilities [16]. The exponential acceleration of linear algebra operations leads to substantial speed improvements [17]. A diverse range of quantum machine learning algorithms have been designed and implemented to work in high dimension vector spaces, e.g., Quantum Principal Component Analysis (QPCA), Quantum enhanced reinforcement learning, Hidden Quantum Markov Model (HQMM), Quantum neural networks (QNN), and Quantum Support Vector Machine (QSVM) [18]. These advancements hold the potential to revolutionize various fields by harnessing the unique power of quantum systems for complex data analysis and prediction. The QSVM algorithm is discussed in detail in the next section. The remaining algorithms are out of scope for the current work.

1.2 Quantum Support Vector Machine

Support Vector Machine (SVM) is a type of supervised machine learning algorithm used for classification problems [19]. Support Vector Machine (SVM) relies on establishing a ‘hyperplane’ to segregate the input dataset into distinct classes. Given the multiple potential ways of segmenting data, the objective is to pinpoint the optimal hyperplane using support vectors, which are the closest points to their respective classes. The most effective hyperplane ensures maximal distance from the nearest data points on both sides. In essence, SVM constructs a maximum margin hyperplane from the provided input data, to facilitate the classification of new data points, as illustrated in Fig. 1. This approach demonstrates the SVM’s capability to robustly classify data by creating a clear boundary between classes [19].

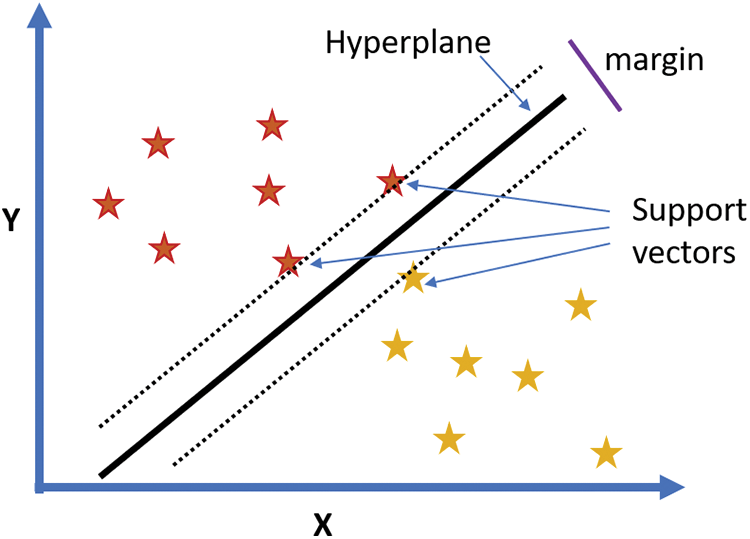
Figure 1: A hyperplane with maximized margin and support vectors for the given data

SVM algorithms make use of mathematical kernel functions that can transform the input data into higher dimension space [20]. The training dataset of input size n can be described as a set of (x1, y1), (x2, y2),…, (xn, yn) distinct values. Each element xi is a vector of size f (number of features). The label yi is mapped to {+1, −1} values for classification. So, the job of hyperplane is to divide the set into two classes for which yi is either +1 or −1. The hyperplane is represented by the equation wT.x – b = 0, where w is a normal vector to the hyperplane and b is the offset of hyperplane from origin in the direction of normal. ‖W‖ should be minimized to obtain the maximum distance from the hyperplane. This results in the optimization problem to minimize ‖W‖ for yi (wT.xi – b) ≥ 1 for 1≤ i ≤ n. The xi that are closest to the hyperplane influence it the most and are known as support vectors. If the dataset is not linearly separable, nonlinear kernel functions are used. They support maximizing the margin hyperplane in a transformed feature space. The hyperplane in non-linear classification corresponds to a linear classification in the transformed vector space. Some nonlinear kernels and their equations are given below:

a.Polynomial:K (xi,xj)=(xi.xj+1)d;d−degree of polynomial(1)

b.Gaussian:K(xi,xj)=exp⁡(−||xi−xj||2/2σ2);σ parameter is optimized(2)

c.Radial basis function:K (xi,xj)=exp⁡(−γ||xi−xj||2)(3)

d.Sigmoid:K(xi,xj)=tanh⁡(αxjTxj+c)for some α>0 andc<0(4)

e.ANOVA radial basis function:K(xi,xj)=∑exp⁡(−σ(xi2−xj2)2)d(5)

Quantum SVM (QSVM) algorithm implements the classical SVM algorithm in quantum systems. QSVM uses ‘kernel trick’ to construct the hyperplane that divides the data into respective classes by using linear or non-linear transformation functions also known as feature map in feature space [21]. The ‘kernel’ is the collection of inner products calculated for all the pairs of data points for the purpose of classification of data points in the feature space. The QSVM algorithms are beneficial for the classification problems where the classical computation of the kernel function is not efficient and need the feature maps to run on quantum systems. QSVM follows the same steps of training and testing as in supervised learning algorithms. Apart from the binary classification, QSVM also provides multiclass extension algorithms for classifying datasets into multiple classes.

Hence, for the classification problem, the input datapoints are represented in the higher dimension quantum feature space with the help of a kernel function as k(xi→,xj→)=⟨f(xi→),f(xj→)⟩. Here, xi→,xj→ are the data points of dimension n, f is the mapping from original n dimension space to the m (higher) dimension space, k is kernel function and represents the dot product as shown in the equation above and can also be written as Kij=k(xi→,xj→).

In QSVM, quantum feature map ψ(x→) is used to map the classical feature vector to the quantum Hilbert space |ψ(xi→)⟩⟨ψ(xj→)| and Kij=|⟨ψt(xj→)|ψ(xi→)⟩xi→,xj→|2 [18].

2  Methodology

In the current study, we have employed both the classical and quantum-based classification algorithms for a comparative analysis. The SVM and QSVM algorithms have been implemented for a multiclass classification of the pancreatic cancer biomarker data. Anaconda Python distribution with Python 3.9.4 on Windows 10 has been used for code development. The Python modules, numpy and pandas were used for storing and processing the dataset. The modules matplotlib and seaborn were used for visualization. The machine learning component was executed using the scikit-learn (sci-kit learn) module, a comprehensive toolkit specifically designed for machine learning tasks.

Incorporating the quantum dimension into our study, we embraced Qiskit and the qiskit_machine_learning modules. These tools play a pivotal role in orchestrating various aspects of quantum machine learning. This encompasses establishing the quantum instance, designing quantum circuits tailored for the classification task, establishing connections to the quantum backend, and ultimately executing the classification algorithms on the quantum hardware.

This holistic approach, combining both classical and quantum techniques, has enabled us to tackle the intricate task of classifying pancreatic cancer data effectively. By leveraging the capabilities of the chosen Python libraries and Qiskit, we have not only demonstrated the potential of quantum-assisted machine learning but also showcased the seamless integration of classical and quantum computing frameworks for solving real-world challenges [22,23].

2.1 Pancreatic Cancer Dataset

Pancreatic ductal adenocarcinoma (PDAC) originates in the part of pancreas that secretes digestive enzymes and accounts for about 90% of the pancreatic cancer [24]. Symptoms are typically absent during the early stages of mass formation in the pancreas, and noticeable indicators emerge as the disease advances. PDAC tends to develop later in life and bears a grim prognosis. It is one of the deadliest type of cancers with less than 10% five-year survival rate. Reference [24] discussed a urinary protein biomarker panel that can be useful for early detection of PDAC. This biomarker panel has been reported to hold crucial insights for timely identification. The biomarker panel reading is obtained from the urine of three groups of patients: 1. healthy controls, 2. patients with non-cancerous pancreatic conditions, and 3. patients with PDAC. The case study related data, e.g., sample collection details, test readings for the biomarker panel and the classification of results, etc., has been made available in the public domain through Kaggle platform [25]. The dataset has 590 rows and 14 columns. The columns in the dataset are: sample id (unique for sample identification), patient cohort, sample origin, age, gender, diagnosis, stage (in case of cancer), benign sample diagnosis (for non-cancerous case), plasma_ca19_9 (blood plasma levels of monoclonal antibody CA19-9), urinary levels in ng/ml of LYVE1, REG1B, TFF1 and REG1A. The biomarker panel consists of LYVE1, REG1B and TFF1 proteins. LYVE1 (lymphatic vessel endothelial hyaluronan receptor 1) protein is related to cancer metastasis, REG1A and REG1B are REG family proteins associated with accelerated cell proliferation and tumor growth and TFF1 (Trefoil Factor 1) protein is linked with cancer cell invasion and growth. The diagnosis column contains labels 1, 2 or 3 where 1 denotes control or no pancreatic disease, 2 denotes benign (non-cancerous pancreatic disease) and 3 denotes PDAC.

2.2 Classical SVM

The initial stage of the analysis involved data preprocessing, wherein several essential steps were undertaken. Initially, columns housing text-based annotation data pertaining to the samples were excluded from the dataset. Following this, a correlation analysis was conducted to identify and retain the most pertinent features for further investigation. Fig. 2 is the heatmap generated that shows the correlation among the selected features of the dataset. Features with correlation more than 0.3 were identified. This cut-off is introduced to select the biomarker associated data. The biomarkers LYVE1, REG1B and TFF1 show a good correlation score of 0.54, 0.38 and 0.39 with diagnosis. REG1A, plasma_ca19_9 and creatinine are weakly correlated with diagnosis. The age column was also removed to study only the biomarker panel. The values for the features corresponding to these biomarkers were subjected to scaling and transformation using the sci-kit learn (sklearn) module libraries StandardScaler and Principal Component Analysis (PCA) respectively and individual explained variance of 0.77 and 0.23 were obtained.

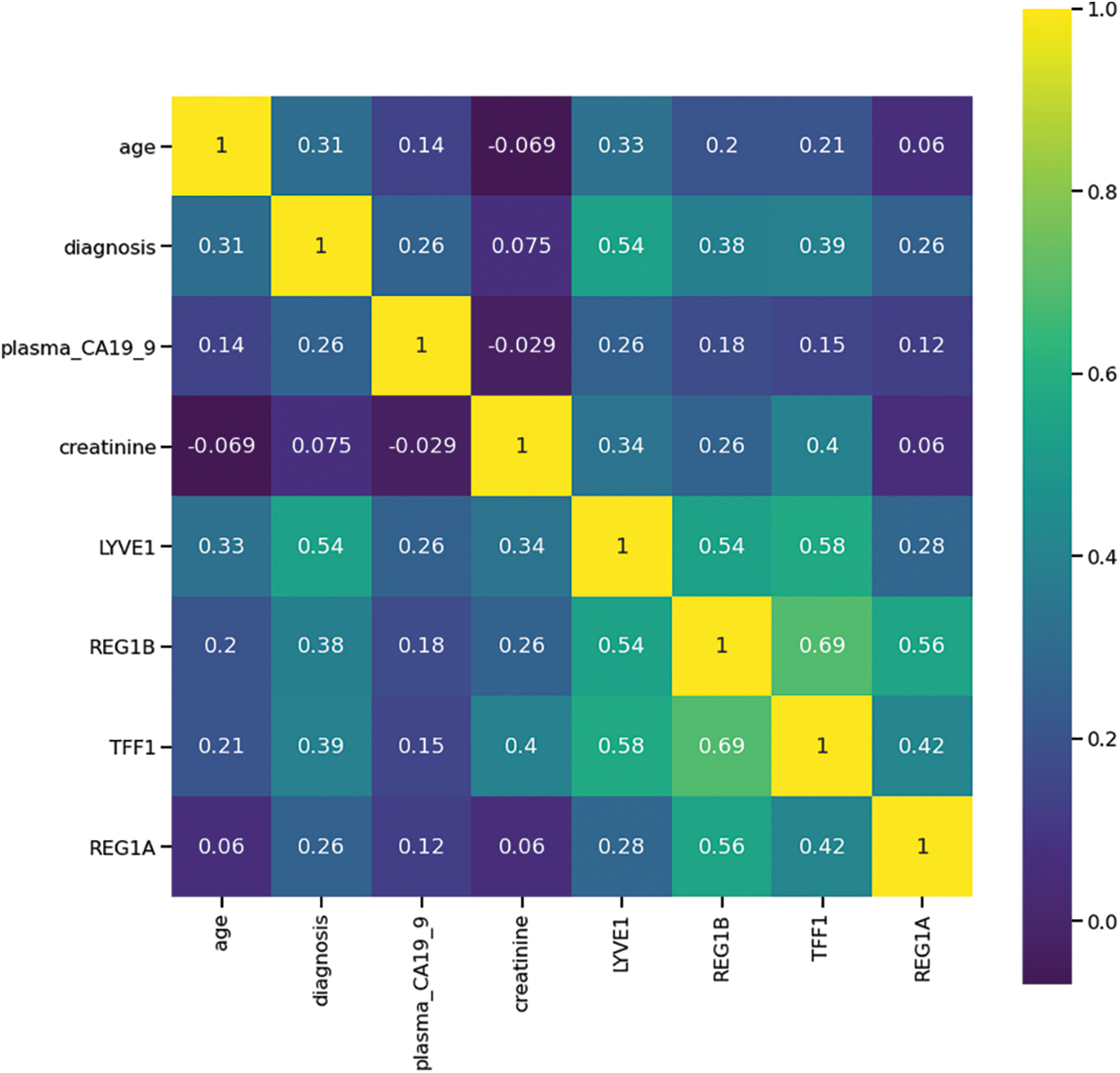
Figure 2: Heatmap showing correlation among important features of the Pancreatic Cancer dataset

The dataset was split into training and test subset with a test size of 20% using the train_test_split function of the model_selection module. The SVM module from sklearn library was used to apply SVC function on the data. The SVC (C-support vector classification) is a libsvm based implementation. Multiclass classification according to one vs. one scheme was carried out by setting the decision_function_shape parameter to ‘ovo’. Regularization parameter C was set to 10 and gamma kernel function was set to ‘auto’. Among the available kernels (linear, polynomial, radial basis function, and sigmoid), the linear kernel yielded the highest accuracy. So, the linear kernel function was chosen for the quantum implementation. The model was trained on the training dataset followed by predictions on the test dataset to acquire the anticipated output. The assessment of the trained model's accuracy was accomplished using the metrics module from the sklearn package. This rigorous evaluation facilitated the determination of the model's efficacy in classification.

2.3 Quantum SVM

In the domain of quantum-assisted machine learning, Qiskit and its qiskit_machine_learning modules offer a range of submodules that facilitate the integration of quantum algorithms. These encompass tools for harnessing quantum circuit libraries, implementing quantum kernels, developing neural networks, and accessing a collection of built-in datasets. These versatile submodules contribute to the effective utilization of quantum resources for enhancing machine learning tasks. The ‘AllPairs’ Multiclass classification is supported by the aqua module of Qiskit. This functionality within the module caters to multiclass classification tasks by employing an “all-pairs” strategy to transform the problem into a series of binary classifications. This approach aids in effectively handling complex classification scenarios involving multiple classes. Classical SVC can also be executed using quantum kernel in a quantum instance. The quantum support vector classifier (QSVC) class in qiskit_machine_learning module extends the sklearn module’s SVC class. A separate module QSVM is provided that runs the algorithm on quantum circuit on either the simulator or a real quantum processor by connecting to either of these backends, defining the circuit, providing the training and test input, and finally executing the quantum instance.

A feature map is a pivotal component in quantum machine learning, responsible for translating classical data into a quantum format suitable for manipulation by quantum circuits. This transformation bridges the gap between classical and quantum domains, allowing quantum algorithms to glean insights from classical datasets. The PauliFeatureMap implements the Pauli expansion circuit. In quantum mechanics, Pauli matrices (X, Y, Z) are fundamental operators that describe the quantum observables. The PauliFeatureMap uses combinations of these Pauli operators to create a quantum circuit that transforms classical input data into a quantum state. By applying these Pauli matrices to different qubits and utilizing their tensor products, the PauliFeatureMap encapsulates complex relationships between features. This facilitates the encoding of classical data into a multi-qubit quantum state, allowing quantum algorithms to operate on this state for various machine learning tasks. ZFeatureMap implements the first order Pauli-Z evolution circuit. This gate induces phase shifts in the quantum state based on the classical input features. This approach encodes the input data as distinct quantum phases, preserving important information while translating classical data into quantum states. ZZFeatureMap implements the second order Pauli-Z evolution circuit. This expanded feature map allows for the encoding of more intricate correlations present in the classical data. By using the tensor product of Pauli-Z operators on pairs of qubits, the ZZFeatureMap effectively encodes both linear and quadratic interactions, resulting in a richer quantum state representation of the classical data. In essence, these feature maps are quantum circuits designed to transform classical data into quantum states by exploiting the properties of Pauli matrices and gates. Each feature map varies in complexity, capturing different levels of relationships between classical features and quantum states. The choice of feature map depends on the complexity of the dataset and the specific quantum algorithm being employed.

The qasm_simulator was used as the backend for execution. A quantum instance was created to run on the backend and the number of shots was set to 1024. The quantum instance and a feature map were supplied to quantum kernel and the classification algorithms were provided with the training and testing datasets.

The time taken to execute the model fitting in both the environments was measured by the calling the time function in Python just before start of fitting the model on training data set and just after the prediction on test data set of the same sizes.

3  Results and Discussions

The Pancreatic Cancer dataset was employed to both train and assess the accuracy of the Support Vector Machine (SVM) classification model within both the classical and quantum computational settings. This comparative evaluation across two environments provided insights into the potential benefits and performance enhancements brought about by quantum-assisted machine learning techniques. As already discussed, the biomarker panel produces the readings of three proteins. The diagnosis feature was used for classification. The data points were classified as 1-healthy control, 2-patients with non-PDAC pancreatic conditions and 3-patients with PDAC. After the correlation analysis and feature selection process, the features dataset was subjected to scaler transform using the scaler.fit_transform function of StandardScalar module of sklearn.preprocessing library. It was followed by the Principal Component Analysis (PCA) transform using the pca.fit_transform function of the PCA module of sklearn.decomposition library. Fig. 3 shows one instance of training and test datapoints from PCA dimension reduced Pancreatic Cancer dataset. The datapoints are colored according to the diagnosis label value and the Fig. 4 shows one instance of the training set and test set split.

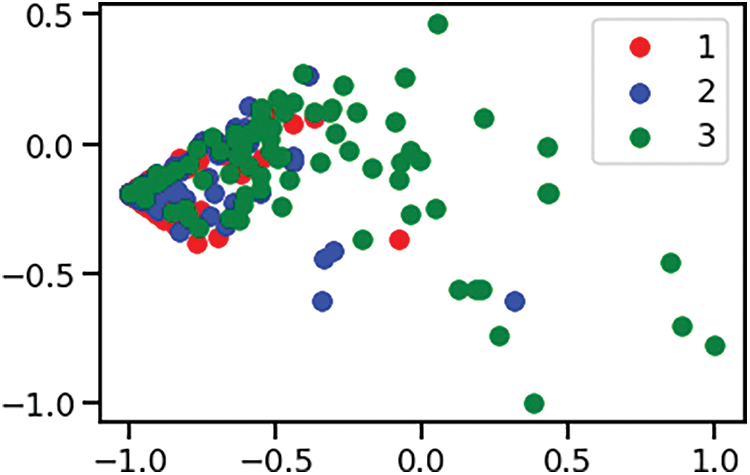
Figure 3: PCA dimension reduced dataset with training and test data points

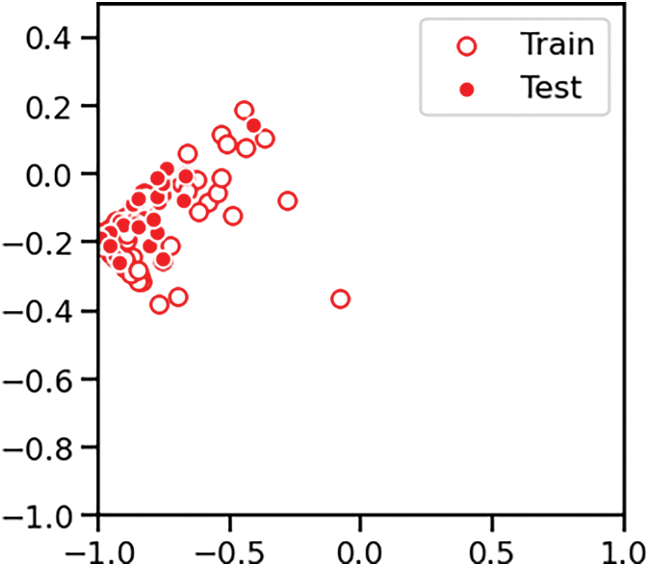
Figure 4: Dataset split into training and test subsets for classification

The three different feature maps were designed next by selecting the appropriate quantum gates and arranging them on qubits to encapsulate distinct relationships present in the classical data. The screenshots of the circuit designs for the three types of feature maps (ZZFeatureMap, ZFeatureMap and PauliFeatureMap) used for data encoding are shown in the Figs. 5–7 below. These feature maps were designed for 3 input qubits q_0, q_1 and q_2 (corresponding to the 3 features in the dataset) and the circuit is repeated twice (specified by parameter reps = 2).

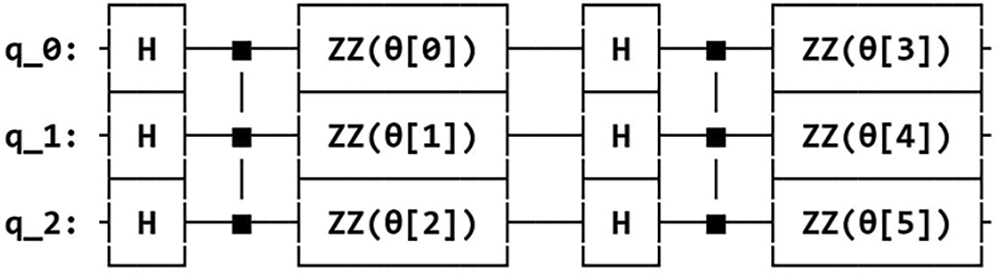
Figure 5: ZZFeatureMap circuit design for feature dimension = 3, repetitions = 2 and entanglement = full

Figure 6: ZFeatureMap circuit design for feature dimension = 3 and repetitions = 2

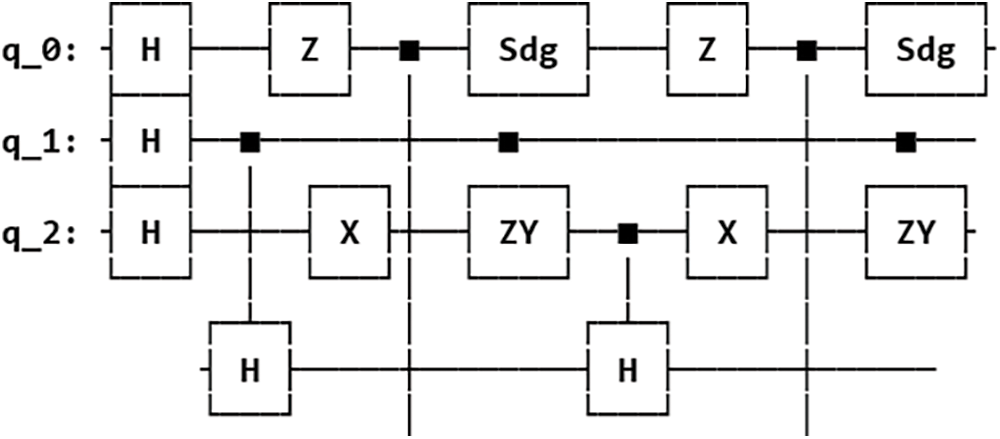
Figure 7: PauliFeatureMap circuit design for feature dimension = 3, repetitions = 2 and Paulis matrices = (Z, X, ZY)

For the ZZFeatureMap, each qubit is first prepared in the |+⟩ state (Hadamard gate) to initialize the quantum state. For each feature, a ZZ interaction gate is applied between all pairs of qubits (full entanglement). The angles θ [0] to θ [5] represent the parameters of the ZZ interaction gates that determines the amount of phase shift applied to the |11⟩ state.

For the ZFeatureMap, each qubit is first prepared in the |+⟩ state (Hadamard gate) to initialize the quantum state. For each feature, a Z gate is applied on each qubit. Applying a Z gate to a qubit has the effect of flipping the phase of the |1⟩ state, while leaving the |0⟩ state unchanged.

For the PauliFeatureMap, each qubit is prepared in the |+⟩ state (Hadamard gate) to initialize the quantum state. For each feature, the corresponding Pauli operation gates are applied to the qubits. The gate “Sdg” refers to the square root of the Z gate, represented as the “u1” gate with a parameter of π/2. The Sdg gate is equivalent to applying a phase of −π/2 to the qubit state. The X gate represented by the Pauli-X matrix, also known as the ``bit-flip'' gate effectively flips the state of the qubit. ZY gate combines the Pauli-Z and Pauli-Y gates to introduce a phase shift and a state flip simultaneously.

In machine learning algorithms like Support Vector Classification, a kernel is an essential tool that allows to transform data into higher-dimensional spaces. This transformation can make it easier to find decision boundaries between different classes of data. The sci-kit learn SVC algorithm permits the kernel to be defined either as a callable function or as a precomputed matrix. The callable function maps the original data into a higher-dimensional quantum space, allowing SVC to find decision boundaries more effectively. Instead of using raw data to compute the kernel during training and testing, the kernel matrices can also be precomputed for both training and testing data pairs using the kernel.evaluate function. This allows the kernel values to be calculated in advance and is stored in matrices. Each element (i, j) of the training kernel matrix represents the similarity between the ith and jth training data points. Similarly, the testing kernel matrix stores the similarity values between testing data pairs. These precomputed kernel matrices essentially encapsulate the information required for the SVC algorithm to operate in the transformed space. The kernel was provided as a callable function by using Quantum kernel. The training and testing kernel matrices were precomputed using kernel.evaluate function. Fig. 8 shows a plot of precomputed training and testing kernel matrices as colormaps.

Figure 8: Plot of precomputed training and test kernel matrices

Following the preprocessing and feature map preparation steps, different algorithms were applied. The classical SVC algorithm was called first using the SVC model of svm module of sklearn library. Linear kernel with regularization parameter value of 10 was used. QSVM models from Qiskit Aqua module were set using the three different feature maps as designed above. Aer quantum simulator was chosen as backend for the quantum computations and hence simulated the quantum circuits on a classical computer. Three different QuantumInstances were created for running the QSVM algorithm. The classification methods were evaluated using different implementations, including classical and quantum-inspired approaches. The performance of each method was assessed based on accuracy and the time taken for execution. The accuracy of support vector machine classification in classical and quantum environments for executing one instance of training and test data set is reported in Table 1 below.

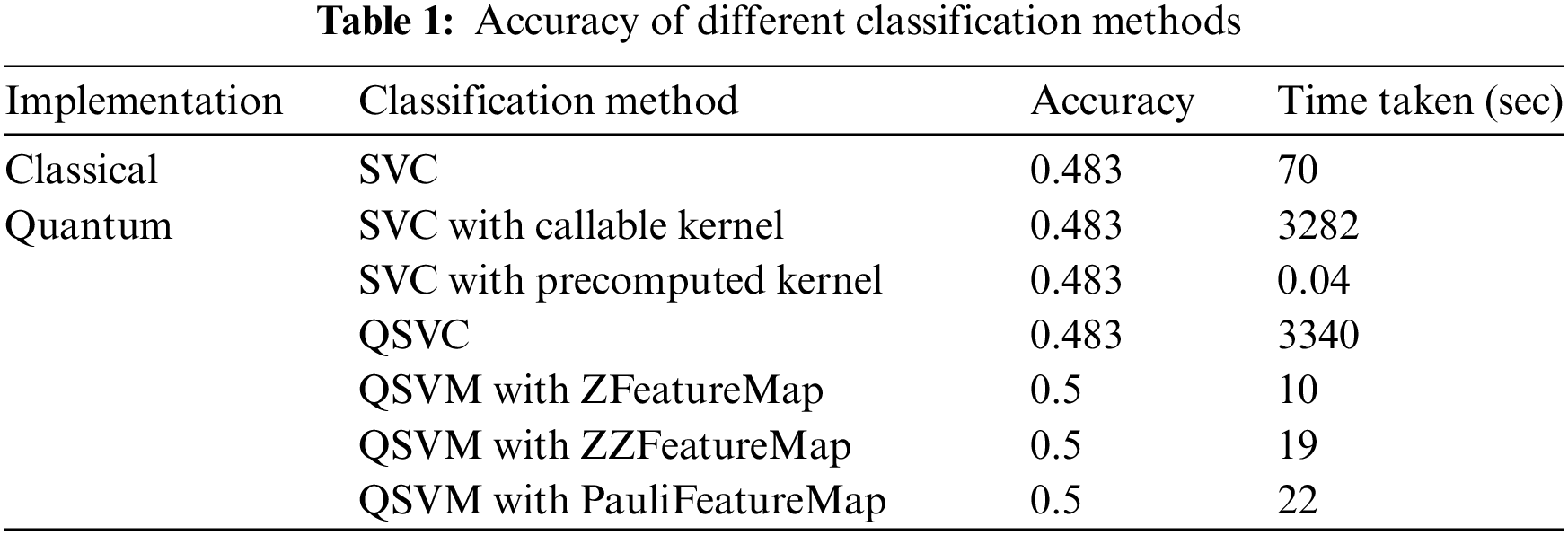
The classification accuracy achieved across all methods was found to be consistent, ranging between 48.3% and 50%. This consistency implies that each method was capable of capturing similar underlying patterns within the dataset. The time taken varies significantly across the implementations. The “Quantum SVC with callable kernel” and “QSVC” methods took the longest time due to the computational complexity of quantum computations. This can be attributed to the inherent complexity and resource-intensive nature of quantum computations. Quantum simulations require substantial computational overhead due to intricate quantum state manipulations. This was primarily due to the need to simulate quantum circuits for each data point pair, accompanied by complex quantum operations and calculations. The callable function’s complexity, along with quantum state transformations, contributed to the overall execution time. Notably, the “QSVM with ZFeatureMap,” “QSVM with ZZFeatureMap,” and “QSVM with PauliFeatureMap” methods achieved a slightly improved accuracy of 50%, potentially due to the utilization of quantum-inspired feature maps. Despite this improvement, these quantum-inspired methods necessitated a moderate execution time, further underlining the trade-off between accuracy and computational efficiency. The “SVC with precomputed kernel” demonstrated the shortest execution time which indicates the usefulness of precomputed kernels. These results collectively contribute to a comprehensive understanding of the performance variations between classical and quantum-inspired machine learning methods, emphasizing the need to balance accuracy aspirations with practical computational considerations.

4  Conclusion

In the current study, we undertook a comprehensive exploration of classification methodologies, encompassing both classical and quantum-inspired approaches, to address a pancreatic cancer data classification task. The goal was to assess the accuracy and computational efficiency of various implementations, shedding light on the trade-offs between accuracy enhancements and computational complexity in the realm of quantum machine learning. The choice of implementation should be determined by the trade-offs between accuracy and computational efficiency, tailored to the specific problem's demands and available resources. While quantum-inspired methods hold the promise of enhanced accuracy, their current computational overhead must be carefully weighed against their benefits.

Refining the quantum computation methodologies and harnessing quantum strengths could pave the way for more streamlined and precise solutions to the current computational challenges.

Acknowledgement: The authors acknowledge the access to IBM Quantum cloud and Qiskit documentation and tutorials. SS acknowledges Savitribai Phule Pune University and AS acknowledges Ministry of Electronics and Information Technology (MeitY), Government of India for infrastructural support.

Funding Statement: The authors received no specific funding for this study.

Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: A. Saxena, S. Saxena; data collection: A. Saxena; analysis and interpretation of results: A. Saxena, S. Saxena; draft manuscript preparation: A. Saxena, S. Saxena. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The dataset used in this study can be accessed through the Kaggle website as mentioned in the reference section. Access to this dataset is subject to Kaggle's terms of use, and interested parties should refer to Kaggle's platform for data access and usage guidelines.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. G. Brassard, I. Chuang, S. Lloyd and C. Monroe, “Quantum computing,” in Proc. of the National Academy of Sciences of the United States of America, vol. 95, no. 19, pp. 11032–11033, 2000. [Google Scholar]

2. C. H. Bennett, E. Bernstein, G. Brassard and U. Vazirani, “Strengths and weaknesses of quantum computing,” SIAM Journal on Computing, vol. 26, no. 5, pp. 1510–1523, 1997. [Google Scholar]

3. B. P. Lanyon, M. Barbieri, M. P. Almeida and A. G. White, “Experimental quantum computing without entanglement,” Physical Review Letters, vol. 101, no. 20, pp. 200501, 2008. [Google Scholar] [PubMed]

4. M. A. Nielson and I. L. Chuang, “Quantum circuits,” in Quantum Computation and Quantum Information. New York, USA: Cambridge University Press, pp. 171–211, 2010. [Google Scholar]

5. D. Deutsch, “Quantum theory, the Church-Turing principle and the universal quantum computer,” in Proc. of the Royal Society A. Mathematical, Physical and Engineering Sciences, vol. 400, no. 1818, pp. 97–117, 1985. [Google Scholar]

6. P. W. Shor, “Polynomial-time algorithms for prime factorization and discrete logarithms on a quantum computer,” SIAM Review, vol. 41, no. 2, pp. 303–332, 1999. [Google Scholar]

7. G. L. Long, “Grover algorithm with zero theoretical failure rate,” Physical Review A, vol. 64, no. 2, pp. 022307, 2001. [Google Scholar]

8. F. Arute, K. Arya, R. Babbush, D. Bacon, J. C. Bardin et al., “Quantum supremacy using a programmable superconducting processor,” Nature, vol. 574, no. 7779, pp. 505–510, 2019. [Google Scholar] [PubMed]

9. B. Villalonga, D. Lyakh, S. Boixo, H. Neven, T. S. Humble et al., “Establishing the quantum supremacy frontier with a 281 pflop/s simulation,” Quantum Science and Technology, vol. 5, no. 3, pp. 034003, 2020. [Google Scholar]

10. I. L. Chuang, L. M. Vandersypen, X. Zhou, D. W. Leung and S. Lloyd, “Experimental realization of a quantum algorithm,” Nature, vol. 393, no. 6681, pp. 143–146, 1998. [Google Scholar]

11. M. I. Jordan and T. M. Mitchell, “Machine learning: Trends, perspectives, and prospects,” Science, vol. 349, no. 6245, pp. 255–260, 2015. [Google Scholar] [PubMed]

12. R. Sathya and A. Abraham, “Comparison of supervised and unsupervised learning algorithms for pattern classification,” International Journal of Advanced Research in Artificial Intelligence, vol. 2, no. 2, pp. 34–38, 2013. [Google Scholar]

13. R. Caruana and A. Niculescu-Mizil, “An empirical comparison of supervised learning algorithms,” in Proc. of Int. Conf. on Machine Learning, Pittsburgh, PA, USA, pp. 161–168, 2006. [Google Scholar]

14. H. B. Barlow, “Unsupervised learning,” Neural Computation, vol. 1, no. 3, pp. 295–311, 1989. [Google Scholar]

15. C. Szepesvári, “Algorithms for reinforcement learning,” Synthesis Lectures on Artificial Intelligence and Machine Learning, vol. 4, no. 1, pp. 1–103, 2010. [Google Scholar]

16. M. Schuld, I. Sinayskiy and F. Petruccione, “An introduction to quantum machine learning,” Contemporary Physics, vol. 56, no. 2, pp. 172–185, 2015. [Google Scholar]

17. P. Wittek, “Machine learning,” in Quantum Machine Learning: What Quantum Computing Means to Data Mining. USA: Academic Press, pp. 11–24, 2014. [Google Scholar]

18. M. Schuld and N. Killoran, “Quantum machine learning in feature Hilbert spaces,” Physical Review Letters, vol. 122, no. 4, pp. 040504, 2019. [Google Scholar] [PubMed]

19. D. Anguita, S. Ridella, F. Rivieccio and R. Zunino, “Quantum optimization for training support vector machines,” Neural Networks, vol. 16, no. 5, pp. 763–770, 2003. [Google Scholar] [PubMed]

20. J. A. Suykens, “Support vector machines: A nonlinear modelling and control perspective,” European Journal of Control, vol. 7, no. 2–3, pp. 311–327, 2001. [Google Scholar]

21. P. Rebentrost, M. Mohseni and S. Lloyd, “Quantum support vector machine for big data classification,” Physical Review Letters, vol. 113, no. 13, pp. 130503, 2014. [Google Scholar] [PubMed]

22. M. Steffen, D. P. DiVincenzo, J. M. Chow, T. N. Theis and M. B. Ketchen, “Quantum computing: An IBM perspective,” IBM Journal of Research and Development, vol. 55, no. 5, pp. 13:1–13:11, 2011. [Google Scholar]

23. A. Cross, “The IBM Q experience and QISKit open-source quantum computing software,” in Proc. of the American Physical Society (APS) March Meeting, Los Angeles, CA, USA, pp. L58-003, 2018. [Google Scholar]

24. S. Debernardi, H. O’Brien, A. S. Algahmdi, N. Malats, G. D. Stewart et al., “A combination of urinary biomarker panel and PancRISK score for earlier detection of pancreatic cancer: A case-control study,” PLoS Medicine, vol. 17, no. 12, pp. e1003489, 2020. [Google Scholar] [PubMed]

25. Urinary Biomarkers for Pancreatic Cancer, “Kaggle,” 2023. [Online]. Available: https://www.kaggle.com/johnjdavisiv/urinary-biomarkers-for-pancreatic-cancer [Google Scholar]