T_GRASP: Optimization Algorithm of Ship Avoiding Typhoon Route

1  Introduction

The typhoon significantly affects how ships navigate. When a typhoon strikes a sailing ship, the storm’s enormous waves cause the hull to shake violently, slow down, move in an unstable direction, and present other different navigational challenges. Unexpected dangers, such as hull breakage and capsizing, may also occur.

At the moment, manual intervention and the method of avoiding navigation are used most frequently in China. Based on his navigational expertise, the skipper manually evaluates the weather data obtained to avoid typhoons. The ship can adjust its route and speed in line with the dynamics and power of the typhoon without losing the chance to keep its location outside of the high wind range of the wind level that the ship can tolerate.

Typhoon avoidance has been the subject of numerous productive types of research in recent years by relevant academics. The secret to guaranteeing the safety of ships is identifying the typhoon’s hazardous areas so that they can avoid them. The massive wind and wave distribution caused by the typhoon will alter dynamically as it moves and changes the surrounding large-scale pressure field, which objectively makes it more difficult for ships to steer clear of the wind. Liu et al. [1] determined tropical cyclones in dangerous areas on the basis of multi-source forecasting; Zhang et al. [2] used the multi-level decision-making method to design the route to avoid typhoons. In addition, designing an efficient and stable typhoon avoidance route optimization algorithm based on ship motion control and typhoon information is also the key to safe and scientific typhoon avoidance for ships [3–5]. By evaluating the benefits of the navigation plan for ships to avoid tropical cyclones, it can provide a reference for shipping companies to avoid typhoons and improve the economic benefits of enterprises [6]. By plotting the relative movements of ships and tropical cyclones in the future, it is convenient for ship drivers to formulate new routes to avoid tropical cyclones [7].

We take the guarantee of safe navigation of the ship, the shortest sailing time, and the minimum fuel consumption as the optimization goals, carry out multi-objective optimization, establish a GRASP-based ship avoiding typhoon route optimization model, and propose an optimization algorithm based on the GRASP algorithm, that is, the ship avoiding typhoon route optimization algorithm T_GRASP.

The T_GRASP algorithm improves the GRASP algorithm. The modification points are mainly reflected in the construction of the candidate set. For the construction of the candidate set, the shortest route time function, the lowest risk function, and the least fuel consumption function are taken into consideration, so that the algorithm ensures that the ship can avoid the typhoon, that is, the safety of navigation, while also ensuring the efficiency of the route.

Most of the current research shows that for route planning problems, researchers tend to use the A* algorithm or Ant Colony Algorithm as a basis for research, and the use of the GRASP algorithm to solve route planning problems is currently an untouched field. This paper is based on the optimization algorithm of the GRASP algorithm, the ship avoidance route optimization algorithm T_GRASP. Through actual simulation experiment verification, the final test result is similar to the result of the traditional A* algorithm and better than the Ant Colony Algorithm, but we carried out multi-objective planning when designing the model. The shortest route time function, the lowest risk function, and the least fuel consumption function are added to the GRASP algorithm for consideration. As a result, the T_GRASP algorithm has more advantages in solving the problem of route planning to avoid typhoons.

The remainder of this article is organized as follows. In Section 2, we provide a general overview of related works. In Section 3, we introduce our optimal modeling of ship avoiding typhoon route based on GRASP. In Section 4, we introduce our T_GRASP algorithm. In Section 5, we provide a simulation verification test. In Section 6, we provide our conclusion.

2  Related Works

2.1 Related Research

Numerous studies have been conducted by academics both domestically and internationally regarding weather navigation and route optimization. There are approximately three types of ship route planning techniques that take maritime weather conditions into account: conventional algorithms, intelligent bionic algorithms, and graphical algorithms.

2.1.1 Traditional Algorithm

The traditional method is a route planning approach based on a large number of meteorological papers and invaluable prior navigating experience. The James isochrone approach, which maximizes time to find a path with the least amount of fuel consumed, is the earliest.

In order to address the issue of difficulties in avoiding obstacles and “isochronous loops,” Roh [8] updated the isochronous approach in 2013. Later, the isochronous technique was improved again using dynamic programming and its better algorithm. For instance, reference [9] provides a three-dimensional dynamic planning algorithm based on weather forecast maps, which refers to ship navigation as multi-stage decision-making, and takes the lowest fuel usage in navigation as the aim. The approach reduces the path to a set of finite waypoints, and the best route is determined by allocating the waypoints and their travel times while maintaining a constant ship speed.

2.1.2 Bionic Intelligent Algorithm

By mimicking different aspects of natural animal life, bionic intelligent algorithms are created. The genetic algorithm, the neural network algorithm, the ant colony algorithm, and the particle swarm optimization algorithm are a few examples.

The ant colony algorithm was first put forth by Marco Dorigo in 1992. The algorithm was influenced by how ants forage in the wild. It involves getting good feedback. There are more ants on the shorter path because more pheromones are emitted when the path is shorter. The ant colony algorithm has significant robustness and the capacity to seek out better solutions based on the performance of the solutions. The ant colony algorithm is also simple to parallel-solve. The algorithm’s modest rate of convergence, particularly in the early stages, and the ease of settling into the local optimum are both caused by the lack of an initial pheromone.

In order to provide a collection of ideal solutions, Szlapczynska [10] created a multi-objective weather path algorithm that used the genetic algorithm’s population iterative development process. A real-coded genetic algorithm (Genetic Algorithm, GA) was proposed by Wang et al. [11] to discover the route with the least flying time. The algorithm considerably simplifies adaptation by allocating fitness based on the individual’s position in the sorted group. The degree value computation and the addition of a hybrid mutation operator improve the pursuit of the ideal outcome and preserve population diversity. Some researchers [12,13] develop ship routes using intelligent control algorithms like the ant colony algorithm and then implement them using simulation techniques.

2.1.3 Graphics Algorithm

The graphics method is a route planning technique based on environmental modeling. By rasterizing the navigation environment and fusing it with the appropriate algorithms, this technique optimizes the navigation route.

The Dijkstra algorithm is a well-known graphical algorithm that is frequently used to address the route planning issue.

The A* algorithm is another well-liked option to optimize routes. To study the method of ship weather route design, for instance, reference [14] uses the A* algorithm, which significantly reduces the number of search nodes that must be searched while the algorithm is running. However, the empirical formula used there differs to some extent from the stall analysis of wind and wave navigation and the actual ship stall. And there is no fuel consumption simulation. It simply takes into account the two optimization goals of sailing time and sailing danger. A purposeful collision avoidance trajectory planning method [15] was presented, based on the A* algorithm, taking maneuverability, static and moving impediments, and the limitations of the international maritime collision avoidance regulations into consideration. The optimal route problem for ships was resolved by Sen et al. Reference [16] using grid method modeling, and a generic weather route solution was proposed using an enhanced Dijkstra algorithm.

3  Optimal Modeling of Ship Avoiding Typhoon Route Based on GRASP

3.1 Problem Description

The route affects a journey’s economic advantages and safety. A smart route can lower costs and minimize the loss of ships and cargo, resulting in significant financial gains and minimizing casualties. Typhoon avoidance route optimization aims to arrange a route based on weather and ocean forecast data that gets to the destination within the anticipated arrival time and avoids the typhoon in advance, which might result in larger economic benefits.

An ocean cruise will cost money because of fuel use, equipment upkeep, consumption of daily essentials, and crew wages. A lot of money is spent every day. Therefore, the quickest possible travel time is required for an optimal route. An ideal route must also aspire to low fuel usage because it makes up a significant portion of daily costs. Wind, waves, and typhoons are the primary variables that cause marine accidents, and the safety of the crew is also a crucial issue.

As a result, the objective of this model and the issue that it is intended to address is the ability to avoid typhoons in advance based on weather, ocean forecasts, and other data, employing algorithms, and guaranteeing that the route can bring about the highest economic gains. The ship should be able to turn at point T, which is outside the blue typhoon danger zone, forsake the general black course, and select the red route, as indicated in Fig. 1.

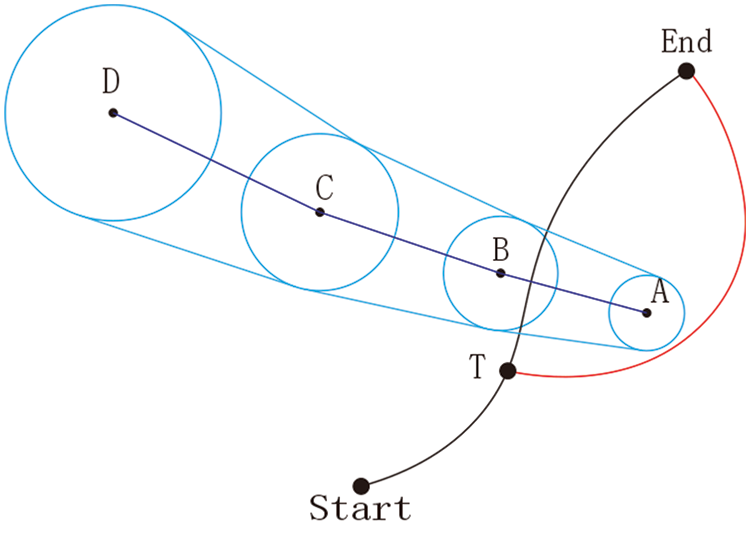
Figure 1: Typhoon avoidance diagram

3.2 Objective Function

3.2.1 Shortest Sailing Time

When designing a route, the route is divided into multiple segments, so the total sailing time is the sum of the sailing time of each channel, as shown in Eq. (1).

Tvoyage=∑i=1nSi/Vi(1)

Among them, Tvoyage shows the shortest sailing time of the ship (h); Si shows the range of each flight segment (nm); Vi shows the actual sailing speed of each flight segment (kn).

Considering the influence of wave height, wind speed, and wind direction on the ship’s stall, the ship’s stall formula is derived by analyzing a large amount of sailing data, and the actual sailing speed of the ship is obtained, V is shown in Eq. (2) [17].

V=V0−(a1h−a2qh+a3Fcos⁡α)(1−a4DV0)(2)

Among them, V represents actual sailing speed, V0 represents still water ship speed, h represents wave height, q represents relative wave direction, F represents wind speed, α represents relative wind direction, D represents displacement,  ai represents coefficient.

3.2.2 Lowest Risk

The hazard of a ship during navigation can be expressed by the ratio of the time within the typhoon danger radius to the total navigation time, as shown in Eq. (3).

D=Talarm/Tvoyage(3)

Among them, D represents the navigation risk index; Talarm represents the time the ship is within the typhoon danger radius (h); Tvoyage represents the shortest total navigation time of the ship (h).

3.2.3 Minimum Fuel Consumption

The fuel consumption of a ship during navigation can be obtained by adding up the fuel consumption of each segment, as shown in Eq. (4).

G=∑i=1n(Si/Vi∗g(v))(4)

Among them, G represents the total fuel consumption of the ship during navigation (t), Si/Vi represents the travel time of each segment, and g(v) represents the fuel consumption per hour (t/hour) of the ship in that segment.

3.3 Weight Analysis

The purpose of this model is to find a safe, fast, and economical route, so the total value of the route is set as f, which is obtained by weighting the risk D, sailing time Tvoyage, and fuel consumption G, as shown in Eq. (5).

f(x)=αD+βTvoyage+γG(5)

The sum of the weighting coefficients is 1, that is α+ β+ γ= 1. According to the different importance of the above three influencing factors, different weights are assigned.

3.4 Restrictions

3.4.1 Speed

The speed of the ship cannot exceed the speed range of the ship’s design, as shown in Eq. (6).

Vmin<Vi<Vmax(6)

Among them, Vmin and Vmax represents the minimum and maximum still water set speed that the ship can reach.

3.4.2 Time

The ship should arrive within the specified time frame, as shown in Eq. (7).

t0−△t<Tvoyage<t0+△t(7)

Among them, t0−△t represents the minimum value of the ship’s sailing time within the acceptable range, and t0+△t represents the maximum value of the ship’s sailing time within the acceptable range.

4  T_GRASP Algorithm

This paper’s algorithm is based on the GRASP algorithm. The GRASP algorithm was developed to address the issue of combinatorial optimization. We use it to tackle the issue of route optimization and discover some of its benefits.

4.1 GRASP Algorithm

The overall framework of the GRASP algorithm consists of two stages, the construction stage, and the local search stage.

In the construction stage, a feasible solution is produced. The process is as follows. Initialize the feasible solution set S to be empty, and initialize the candidate set C. When the candidate set is not empty, repeat the following actions. Evaluate each element of the candidate set as a basis for entering the restricted candidate list. Select some elements from the candidate set to form a restricted candidate list RCL. Each time an element is randomly selected from the restricted candidate list RCL to merge with the feasible solution S, the elements of the candidate set C are updated, and each element in it is re-evaluated.

In the local search stage, the locally optimal solution is found. The process is as follows. Searching for the optimal solution to replace it in the neighborhood of the current feasible solution in a continuous iterative manner, until the locally optimal solution is found. The strategies for selecting adjacent solutions include optimal adaptation and first adaptation. The optimal adaptation strategy requires that all adjacent solutions are examined and then the adjacent solutions of the optimal solution are replaced with feasible solutions. The first adaptation strategy is that when a neighboring explanation that is better than a feasible solution is searched for the first time, the feasible solution is replaced by the neighboring solution, and the local search is performed using this as a new starting point.

4.2 T_GRASP Algorithm Ideas

Enter initial parameters, such as ship parameters, wind, wave, and other information. Algorithm 1 shows the overall flow of the algorithm.

Enter the construction stage, determine the starting point of the route, add the starting point of the route to the feasible set, and initialize the candidate set; calculate the Tvoyage, D, and G of each candidate segment, and select some route points from the candidate set that can form a high total profit segment. Candidate list RCL: randomly select a route point from the RCL, add it to the feasible set, and update the candidate set at the same time; if the candidate set is not empty at this time, repeat the above process. Algorithm 2 shows the construction stage.

Otherwise, enter the local search stage to determine whether the current feasible flight segment is the optimal flight segment, if not, search for a better flight segment in the neighborhood of the current feasible flight segment. Algorithm 3 shows the local search stage.

Otherwise, it is judged whether the termination condition is met, and if it is still not, it will enter a new round of construction stage again. If the termination conditions have been met, the best route will be output.

The algorithm flow chart is shown in Fig. 2.

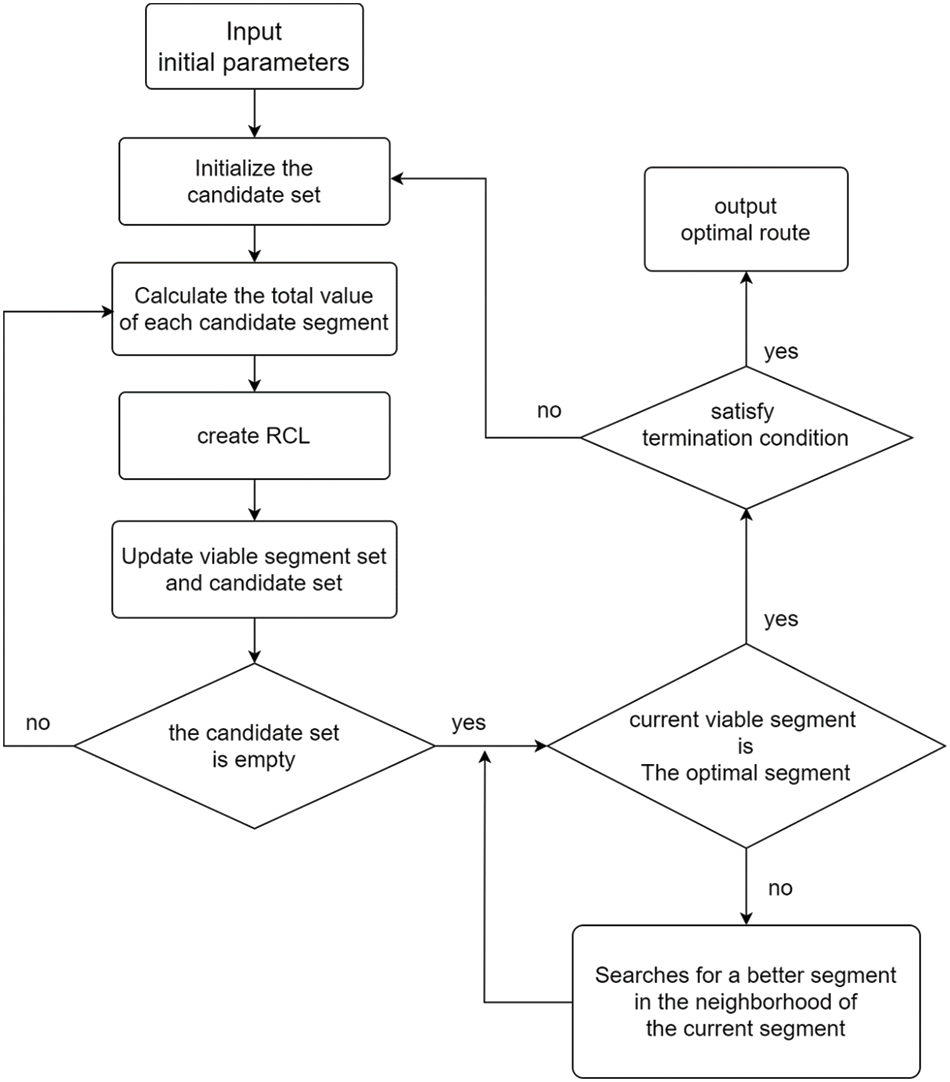
Figure 2: T_GRASP flow chat

5  Simulation Verification Test

This section compares the simulation of the A* algorithm and the Ant Colony Algorithm with the improved T_GRASP algorithm of the GRASP algorithm in order to demonstrate the effectiveness of our improved T_GRASP algorithm. The safety of the ship’s navigation, the amount of time it takes to navigate, and the amount of fuel it uses are all taken into account in this simulation. In this experiment, Boston, located at 70°W and 42°N, serves as the starting point and Porto, located at 9°W and 41°N, serves as the destination. A class 4 typhoon is active about 1000 meters away. The angle between the typhoon’s path and the ship’s course is around 27°. The typhoon data is updated in real time with the movement of the typhoon. The European Medium-term Meteorological Prediction Center provided the meteorological data for this experiment, which included the effective wave height, average wave direction, horizontal wind speed component at 10 meters above the sea surface, and vertical wind speed component at 10 meters above the sea surface.

The route from Boston (70°W, 42°N) to Porto (9°W, 41°N) was drawn using the simulation tool and the T_GRASP algorithm, as shown in Fig. 3.

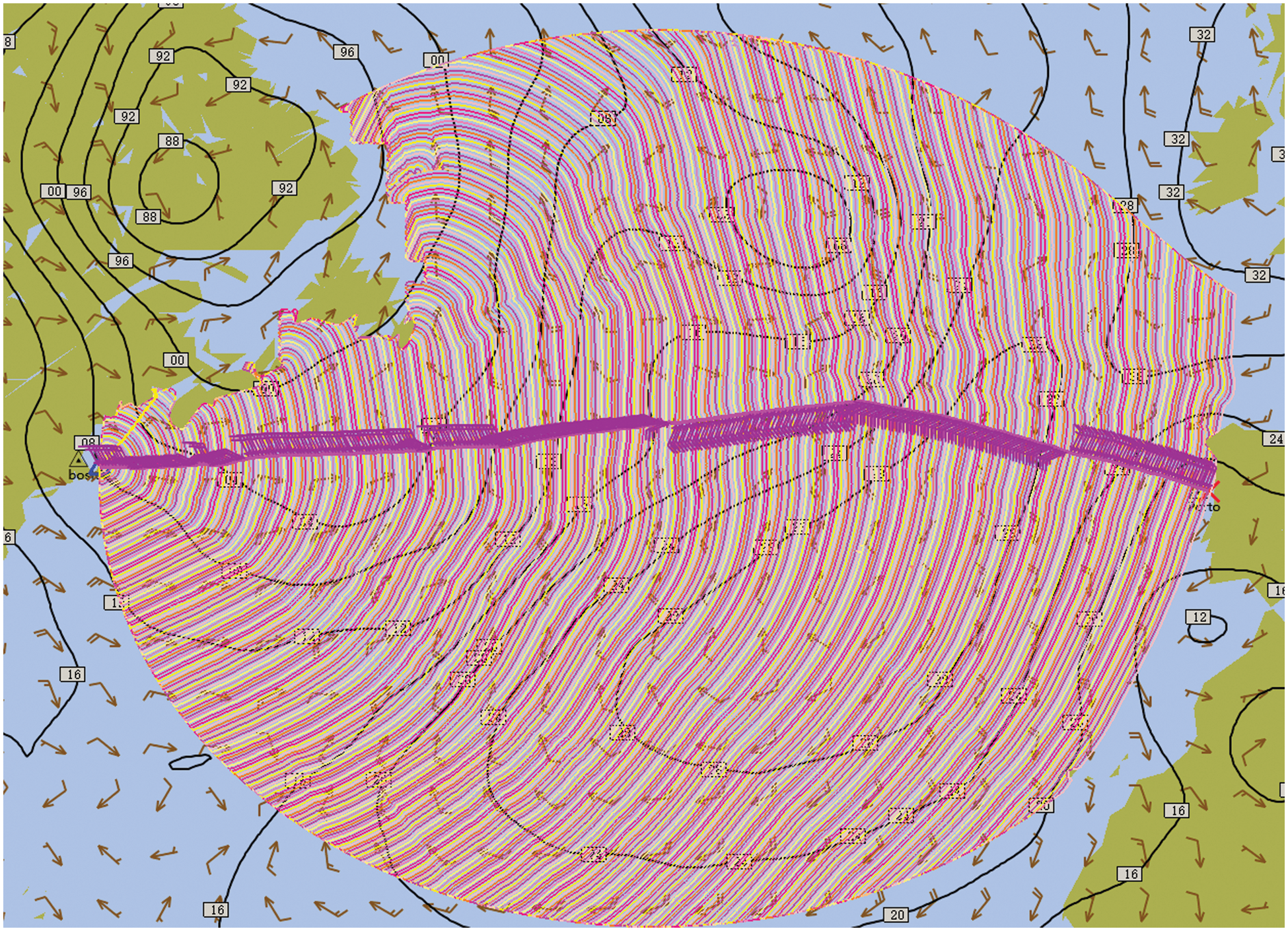
Figure 3: T_GRASP algorithmic route planning diagram

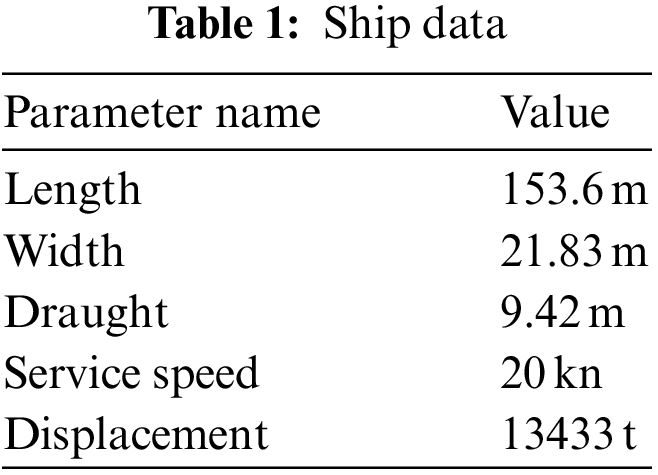
The parameters of the ship selected in this article are shown in Table 1. The ship type of the selected ship is suitable for the empirical formula of the ship stall, so the actual speed of the ship can be calculated.

Using the basic multi-objective A* algorithm, Ant colony algorithm, and T_GRASP algorithm to execute on a standard PC machine to get the following Tables 2 and 3.

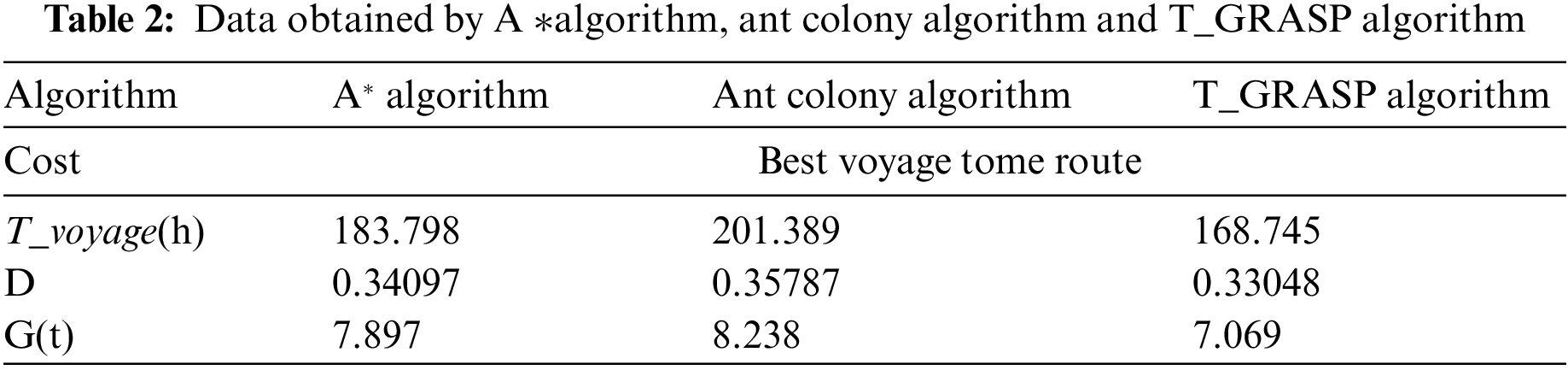
As was previously said, for the optimal navigation route to avoid typhoons, the T_GRASP algorithm’s route took less time to complete than the A* algorithm or Ant Colony Algorithm, and since there was less chance that the ship would run afoul of the typhoon, less fuel was used. The T_GRASP algorithm outperforms the A* algorithm and the ant colony algorithm, according to the simulation findings.

The number of iterations required to identify the ideal ship route planning strategy serves as the performance assessment index used to gauge how effectively the algorithm is implemented. In both the navigation environment without typhoons and the navigation environment with typhoons, the iteration times of the T_GRASP algorithm are similar to those of the A* algorithm but smaller than those of the ant colony algorithm.

6  Conclusion

Route planning is a crucial component of route transportation, and typhoon weather frequently occurs in the coastal regions of China. The development of the maritime transport industry has an impact on the growth of the national economy of China. In allied academic areas, the planning of navigational routes is currently a prominent topic. It is uncommon to find route planning based on the GRASP algorithm in the current related research. We present an enhanced T_GRASP algorithm to assure the safe navigation of ships, with the quickest sailing time and least amount of fuel consumption as the optimization goals, through research and expansion of the GRASP algorithm framework. We constructed a multi-objective function model with the objectives of danger, sailing time, and fuel consumption, and then simulated it with the goal of being better than the A* algorithm and the ant colony algorithm. The final simulation results came to the conclusion that the T_GRASP algorithm is slightly better than the A* algorithm and the ant colony algorithm.

Future ships can avoid typhoon issues by using the T_GRASP algorithm, which is advantageous for the maritime transport sector and advances the economic growth of China.

Funding Statement: The authors received no specific funding for this study.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. D. G. Liu, Z. J. Liu and Z. L. Wu, “Determining method of dangerous areas around tropical cyclone based on multisource forecasts,” Journal of Traffic and Transportation Engineering, vol. 8, no. 2, pp. 80–84, 2008. [Google Scholar]

2. W. J. Zhang, S. Y. Wei, Q. Li, D. G. Liu and Z. J. Liu, “Multilevel decision method of ship’s tropical cyclone avoidance route multisource track forecast,” Journal of Traffic and Transportation Engineering, vol. 10, no. 3, pp. 122–126, 2010. [Google Scholar]

3. Y. F. Guo, C. G. Ma, X. F. Liu and D. G. Liu, “Disaster weather avoiding and optimal sailing route selecting system,” Journal of Dalian Maritime University, vol. 35, no. 4, pp. 21–24+29, 2009. [Google Scholar]

4. Q. H. Tang, G. Chen and Y. Y. Liu, “An intelligent method for route planning of typhoon avoidance,” Periodical of Ocean University of China, vol. 41, no. 6, pp. 104–108, 2011. [Google Scholar]

5. Z. J. Gao, Y. J. Zhang, F. X. Zhu, H. L. Li and Y. K. Li, “Routing design method for ocean ship avoiding the typhoon journal, Journal of Dalian Maritime University, vol. 39, no. 1, pp. 39–42, 2013. [Google Scholar]

6. J. L. Wu, K. X. Ma, Z. Z. Zhou, D. G. Liu and Z. J. Liu, “Benefit evaluation for ship’s avoidance routing of tropical cyclone,” Journal of Dalian Maritime University, vol. 36, no. 2, pp. 31–34+38, 2010. [Google Scholar]

7. J. J. Wu, C. J. Bai, D. G. Liu, J. W. Chen and H. H. Luo, “Ship-TC dynamic plotting system,” Navigation of China, vol. 36, no. 2, pp. 114–119, 2013. [Google Scholar]

8. M. Roh, “Determination of an economical shipping route considering the effects of sea state for lower fuel consumption,” International Journal of Naval Architecture and Ocean Engineering, vol. 5, no. 2, pp. 246–262, 2013. [Google Scholar]

9. R. Zaccone, E. Ottaviani, M. Figari and M. Altosole, “Ship voyage optimization for safe and energy-efficient navigation: A dynamic programming approach,” Ocean Engineering, vol. 153, no. 1, pp. 215–224, 2018. [Google Scholar]

10. J. Szlapczynska, “Multicriteria evolutionary weather routing algorithm in practice,” Trans. Nav.: International Journal on Marine Navigation and Safety of Sea Transportation, vol. 7, no. 1, pp. 61–65, 2013. [Google Scholar]

11. H. B. Wang, X. G. Li, P. F. Li, E. I. Veremey and M. V. Sotnikova, “Application of real-coded genetic algorithm in ship weather routing,” Journal of Navigation, vol. 71, no. 4, pp. 989–1010, 2018. [Google Scholar]

12. X. Y. Li, “Mathematical modeling and artificial intelligence algorithm for ship route planning,” Ship Science and Technology, vol. 43, no. 4, pp. 34–36, 2021. [Google Scholar]

13. M. F. Gong, H. X. Xu and H. Feng, “Intelligent ship path planning based on improved ant colony algorithm,” Journal of Wuhan University of Technology (Transportation Science & Engineering), vol. 44, no. 6, pp. 1072–1076, 2020. [Google Scholar]

14. Z. H. Shen, “Research on ship meteorological route design method based on A* algorithm,” M.S Thesis Jilin University, China, 2018. [Google Scholar]

15. C. Qin and R. W. Yang, “Complicated water area deliberate collision avoidance trajectory planning,” Journal of Shanghai Maritime University, vol. 41, no. 3, pp. 12–18, 2020. [Google Scholar]

16. D. Sen and C. P. Padhy, “An approach for development of a ship routing algorithm for application in the North Indian ocean region,” Applied Ocean Research, vol. 50, pp. 173–191, 2015. [Google Scholar]

17. H. C. Zhao, “Dynamic route planning method based on live weather,” M.S Thesis, Harbin Engineering University, 2017. [Google Scholar]