Hybrid Metaheuristic Lion and Firefly Optimization Algorithm with Chaotic Map for Substitution S-Box Design

Glossary/Nomenclature/Abbreviations

1  Introduction

Substitution boxes (S-boxes) are crucial components in contemporary cryptographic systems. An S-box functions as a nonlinear transformation, denoted by S(y):GF(2a)→GF(2b), or equivalently, as a Boolean function g(y)=(g1(y),g2(y),…,gb(y)). The primary importance of S-boxes in symmetric key algorithms is to obscure the connection between the input key and output code [1,2], thereby playing a critical role in ensuring the security of the algorithm.

Attacks, such as parallel brute forcing and linear cryptanalysis, can break an encoder if the quality of the S-box is inadequate. The DES [3] uses eight 6 × 4 S-boxes that are ultimately weak. The AES, which was introduced in 2000 as a successor to DES, uses an S-box that is resistant to linear and differential cryptographic analyses [4]. However, the use of a static S-box in AES remains unchanged despite significant variations in the input, making the algorithm more predictable and vulnerable to ciphertext-mating attacks [5]. Key-dependent S-boxes offer enhanced security; however, designing systematic methodologies for dynamic S-boxes remains an open challenge, which was partially addressed in [6]. However, large design gaps still exist in developing S-boxes that can balance high nonlinearity with strong resistance to differential attacks, necessitating the investigation of advanced metaheuristic techniques to overcome these limitations [7]. Most previous studies on metaheuristic-based S-box designs, including the use of the FA and other optimization techniques, have shown promising results in improving cryptographic properties; however, they often present limitations. Poor search diversity, particularly early convergence, is a major obstacle to achieving optimum cryptographic robustness. As a typical example, although the FA is effective in performing a search in space, it tends to converge prematurely and hence may yield suboptimal S-box designs with lower nonlinearities and weak resistance to differential attacks. In addition, most previous methods cannot balance exploration and exploitation in a complicated search space, which significantly influences the comprehensive security characteristics of the generated S-boxes. These challenges underscore the application of an advanced approach; hence, the proposed ML-F algorithm combines the strengths of the FA with the LOA for better performance in S-boxes. The motivation for this study is the increased S-box design requirements required for stronger robustness against cryptanalytic attacks in terms of higher nonlinear order and stronger resistance properties. Existing metaheuristics, such as FA have demonstrated potential; however, in practice, early convergence reduces diversity and search capability, compromising their eventual results for optimal cryptographic properties. The proposed ML-F algorithm addresses these shortcomings by combining the strengths of the LOA and FA, enhancing search capabilities, and ensuring more reliable S-box performance for secure encryption systems.

The ideal cryptographic S-box remains elusive and requires a balance between the desired properties [8,9]. There are three major design methodologies [10]: algebraic, random search, and metaheuristic methods. Each method has its advantages and disadvantages. A random search is the simplest method; however, it mostly results in S-boxes with inferior cryptographic properties [11]. Algebraic methods yield S-boxes with improved properties; however, generating large sets of strong S-boxes is difficult [12]. Another approach, metaheuristic algorithms, has been widely studied in S-box design and offers good hardware and software performances. Despite these promising approaches, several difficulties still affect S-box design and analysis [13]. For instance, early convergence and lower search diversity were major drawbacks of previous FA applications, making them unfeasible or ineffective in reaching optimality regarding cryptographic properties [14]. Nature-inspired population-based metaheuristics commonly experience poor balancing of global and local search capabilities, which results in slow convergence and premature entrapment into local optima [15]. The study proposes the ML-F algorithm, which constitutes a hybrid of the LOA and FA necessary for addressing issues. The newly developed ML-F introduces fresh search dynamics instigated by the chaotic exploration behavior of the FA and the structured search capabilities of the LOA for better scalability and performance of the S-box design. This study focuses on developing a new and improved methodology for designing an S-box that will further enhance cryptographic robustness and overcome some of the limitations found in previous metaheuristic approaches. This study outlines a strategy for overcoming two significant issues, early convergence and bounded search diversity, which are traditionally encountered in algorithms such as FA. ML-F combines the superior qualities of the LOA in enhancing features, such as nonlinearity and differential resistance, in the S-box design with those of the FA. S-boxes are relevant to secure encryption systems. Thus, the proposed approach generated S-boxes with the best cryptographic properties, possessing higher resistance against differential and linear cryptanalysis. The remainder of this paper is structured as follows: Related works on metaheuristic-based S-box design are presented in Section 2. In Section 3, a cryptographic criterion essential for a good S-box performance is elaborated. The proposed algorithm-namely, including its structure and several enhancements, is presented in Section 4. Section 5 compares the proposed approach with existing approaches, and Section 6 analyzes the cryptographic properties of the generated S-boxes. Section 7 presents the limitations of the study, and Section 8 discusses directions for future research. Finally, conclusions, key findings, and recommendations are presented in Section 9.

2  Related Works

Numerous studies have explored metaheuristic algorithms for designing S-boxes, emphasizing the effectiveness of generating S-boxes with strong cryptographic properties. Various optimization techniques have been examined to enhance the security of cryptographic systems using robust S-box designs. SA is an optimization algorithm employed to create S-boxes with high nonlinearity and favorable autocorrelation properties [16]. The iterative nature of SA, with accepted solutions based on improvement or calculated probability, improves the S-box characteristics that are crucial for cryptographic security. However, SA has limitations, particularly in terms of execution time and risk of premature convergence. In addition to these cryptographic criteria, recent research has shown that S-boxes without fixed points, reverse fixed points, or short-period rings are stronger and more resistant to certain types of attacks. In [17], methods for generating S-boxes that avoid fixed points and reverse fixed points were discussed. These methods enhance security by eliminating various types of vulnerabilities caused by repetitive or predictable mappings. This study proposes methods for detecting and removing these properties in S-box designs to avoid weaknesses in cryptographic applications. To address these limitations, researchers have explored combinations of optimization techniques with other methods. One study proposed a method that merges ACO with chaos-based techniques to optimize the S-boxes [18]. This approach leverages the ACO’s ability to find optimal solutions by incorporating chaos for enhanced randomness and security, generating S-boxes that meet the essential cryptographic criteria. The use of ABC optimization alongside chaotic maps has also been investigated to construct robust S-boxes [19]. This method involves the generation of initial S-boxes using chaotic maps, which are subsequently refined using ABC optimization. This process ensures the creation of dynamic S-boxes with superior cryptographic performance compared with existing techniques. Additionally, FA, inspired by the flashing behavior of fireflies, has been explored for S-box designs. The FA was combined with a discrete chaotic map to improve the search capability and performance [20]. The results demonstrate the effectiveness of this approach in generating S-boxes that satisfy various security criteria, thereby enhancing security in symmetric ciphers. Building on these advancements, another study introduced a method that combined chaotic maps with the MSAA for efficient S-box generation [21]. This approach exhibited superior performance compared with existing methods, reducing the execution time and cost while achieving high cryptographic properties. The potential of the GFA combined with chaos theory has also been explored for designing robust S-boxes [22]. This method was evaluated against various cryptographic criteria, demonstrating its effectiveness in generating S-boxes that satisfy the necessary security requirements. Another study integrated discrete chaotic maps with a CS algorithm to enhance the S-box cryptographic properties [23]. The findings suggest that this combined method improves S-box characteristics, such as nonlinearity. Further advancements include the AAHC for S-box design [24], which dynamically allocates agents and uses a swap operator to refine the solutions, and a multiswarm PSO algorithm with a chaotic tent map for S-box design, which results in superior performance [25]. Finally, 3D chaotic maps combined with the WOA [26] for the S-box design showed better results in terms of execution time and cost, along with superior cryptographic properties, underscoring the need for new techniques to build robust and secure S-boxes. In addition to these algorithmic approaches, other studies have explored broader techniques for synchronization and robustness against uncertainties in chaotic systems, thereby providing useful insights into the design of cryptographic systems that are more stable and resilient. For example, the study of the sliding mode synchronization of multiple chaotic systems under uncertainties and disturbances explored techniques for maintaining system stability in the presence of dynamic variations and disturbances [27]. Such methodologies are relevant to the design of S-boxes in cryptographic systems, which inherently require the satisfaction and conservation of secure and robust properties against disruptions. In contrast, chaotic systems introduce controlled chaos into the ML-F algorithm as one of the key ways of improving exploration and convergence properties with integrated chaotic maps; therefore, the stability issues that are pertinent in classic FA and LOA are mitigated here. This agrees well with the results of research on chaotic system synchronization and allows ML-F to balance exploration and exploitation, enhance the resilience of the S-box, and ensure cryptographic robustness.

3  Problem Description

This study addresses the challenge of designing a robust S-box by evaluating it against established cryptographic criteria: bijective property, nonlinearity, SAC, BIC, DP, and MELP [18,28]. While these criteria are standard in the S-box design, achieving an optimal balance across all criteria simultaneously has proven challenging, as numerous studies have prioritized individual properties rather than holistic optimization. A new assumption of this study is the involvement of controlled chaotic dynamics in the optimization process. Traditionally, chaotic maps have been used either independently or alone in the frames of single algorithms, and chaos is introduced directly into the hybrid ML-F algorithm to enhance both the global and local search capabilities in this study [18,28]. Furthermore, it is assumed that the hybridization of the FA-LOA would reduce the limitations observed in the literature for both algorithms, as the former converges prematurely and the latter may fail to balance exploration with exploitation [8–10]. In this context, a chaotic mapping-based hybrid FA-LOA can result in more consistent performance in the S-box generated through a set of cryptographic criteria, thus reducing the gaps identified in earlier sections regarding the balanced robust cryptographic S-box [29]. Based on these standards, the S-box design creates a bijective S-box that maximizes nonlinearity and BIC, minimizes the SAC offset value, and reduces the maximum DP and MELP values. Previous studies have often focused on improving a single criterion, such as nonlinearity, with other standards serving primarily as filters for the resulting S-boxes [8–10]. However, this study aims to optimize all the criteria using new assumptions integrated into the ML-F algorithm.

3.1 Bijective Property

In an 8×8 S-box, the bijective property is satisfied when each input value is uniquely mapped to an output value covering the range of 0–255.

3.2 Nonlinearity

The nonlinearity of the Boolean function f(x) can be expressed using the Walsh spectrum as follows:

Nf=2m−1(1−2−mmaxv∈GF(2m)|Wf(v)|)(1)

The Walsh Spectrum of f(x) is defined as:

Wf(v)=∑u∈GF(2m)(−1)f(u)⊕u⋅v(2)

where v∈GF(2m) and u⋅v denotes the dot product of u and v, computed as u1v1⊕u2v2⊕⋯⊕umvm.

3.3 Strict Avalanche Criterion

SAC, originally proposed by Webster and Tavares [18,28], mandates that each output bit undergoes a 0.5 probability change when a single input bit is complemented. The SAC of the S-box is determined using a dependency matrix. The S-box approximately satisfies the SAC if every element in the matrix is close to the ideal value of 0.5. The SAC offset value was calculated as follows:

𝒮(f)=1m2∑1≤i,j≤m|0.5−Pi,j(f)|(3)

3.4 Bit Independence Criterion

The BIC, which was also proposed by Webster and Tavares [18,28], evaluates the pairwise independence of all avalanche vectors generated by single-bit complements in plain text. For an S-box with Boolean functions g1,g2,…,gm, the BIC is satisfied if the XOR of any two different functions gj⊕gk (for j≠k, 1≤j,k≤m) meets the avalanche criterion and is highly nonlinear.

3.5 Differential Probability

S-box is a nonlinear component of encryption algorithms. Ideally, it should exhibit differential uniformity to ensure that the input differential maps uniquely onto the output differential. The differential approximation probability is expressed as [30]:

ΔP(δx→δy)=|{x∈X:S(x)⊕S(x⊕δx)=δy}|2m(4)

where δx and δy represent the input and output differentials, respectively.

3.6 Maximum Expected Linear Probability

The MELP quantifies the maximum event imbalance by applying two masks, Λx and Λy. The input and output bit parity is determined by the parity matrix [31]. The MELP of an S-box is expressed as:

LP=maxΛx,Λy≠0||{x:x⋅Λx=S(x)⋅Λy}|2m−0.5|(5)

where X represents the set of all possible inputs and 2m denotes the number of elements in this set.

Based on these standards, the S-box design creates a bijective S-box that maximizes the minimum values of nonlinearity and BIC, minimizes the SAC offset value, and minimizes the maximum values of DP and MELP. In previous studies [32], nonlinearity was often emphasized as the primary improvement goal along with bijectivity, with other standards primarily serving as filters for the resulting S-boxes.

4  Proposed Algorithms

Owing to the need for robust cryptographic measures, this study extends the design criteria of S-boxes to not only achieve high nonlinearity, potentially up to values, such as 116, but also ensure that there are no fixed points, reverse fixed points, and short-period rings. The fixed points in an S-box and reverse fixed points reduce the unpredictability of secure cryptographic operations. Short-period rings are pairs that, through successive applications of an S-box, quickly transform an input to its original value, and tend to destroy the effectiveness of resistance to these types of cryptanalytic attacks. In the case of ML-F, the algorithm checks and eliminates them through optimization. This algorithm combines chaotic maps and dynamic feedback systems to iteratively update the entries of the S-boxes such that none of the conditions for fixed points or short-period cycles are satisfied, simultaneously ensuring optimum nonlinearity. This approach not only strengthens the security features of the generated S-boxes but also makes them implementable for environments requiring a high degree of cryptographic applicability.

This section provides an overview of the metaheuristic LOA and FA, followed by a detailed introduction to the proposed hybrid ML-F optimization algorithm. Additionally, a discrete chaotic map, which is used to introduce the randomness required in the ML-F hybrid algorithm, is discussed. Finally, methods for generating S-boxes using these algorithms are presented.

4.1 Discrete Chaotic Map

Let σ=σ0σ1…σm−1 denote a permutation of the set {0,1,…,m−1}. The permutation σr=σm−1σm−2…σ1σ0 is the reverse permutation of σ. The composition ϕ=α∘β of two permutations α and β of the same set A is the permutation mapping of each z∈A into ϕ(z)=α(β(z)).

λ(σ)=∑0≤i<mci(m−1−i)!(6)

where σ∈Sm and ci represents the number of elements of the set {j>i∣σj<σi}.

The inverse Lehmer code is a bijective function defined as λ−1:{0,1,2,…,m!−1}→Sm. The one-dimensional discrete chaotic map is defined in [33] as:

Zi+1=Zi∘f(Zi,C)(7)

where Zi,C∈Sm and f:Sm→Sm. If zi=λ(Zi) and c=λ(C), this map can also be expressed as:

zi+1=λ[λ−1(zi)∘F(λ−1(zi),λ−1(c))](8)

f(Zi,C)=λ−1(|λ(C∘Zi)−λ((C∘Zi)r)|)(9)

Based on [33], we obtained a map Fm:{0,1,2,…,m!−1}→{0,1,2,…,m!−1} defined by:

Fm(z)=λ(λ−1(z)∘λ−1(|λ(C∘λ−1(z))−λ([C∘λ−1(z)]r)|))(10)

This map can also be expressed as:

zi+1=λ−1(|λ(C∘Zi)−λ((C∘Zi)r)|)(11)

4.2 Metaheuristic Lion Optimization Algorithm

The LOA is a stochastic metaheuristic approach used to solve optimization problems [34]. Metaheuristic algorithms generate effective solutions at each iteration. LOA begins by randomly generating a population within the solution space. In this context, each solution is referred to as a “lion,” represented as follows:

L=(y1,y2,y3,…,yNd)(12)

Here, y1,y2,y3 represent the positions of individual lions, and yNd denotes the number of dimensions in the search space. A certain fraction P of the population consisted of randomly generated nomadic lions, whereas the remainder consisted of resident lions. The position of each lion, denoted by y, includes n elements (y1,y2,…,yn). This position corresponded to a candidate solution in the search space, and the algorithm evaluated the fitness value of each lion. The fitness function assesses the performance of a candidate solution to the problem at hand. The LOA proceeds through the following steps [35]:

Step 1: Initialization: The population is generated randomly within the solution space, and the positions of the lions are stored in a matrix. The fitness value of each lion is computed using an objective function, and is then sorted and stored in a matrix as follows:

g(L)=g(y1,y2,…,yNd)(13)

where g(L) represents the fitness value and yNd denotes the dimensions of the search space.

Step 2: Mating: This step involves creating new solutions by combining existing solutions through processes, such as mutation and crossover, with the weaker solutions eliminated to retain the best solutions.

Step 3: Territory Defense: This step compares the fitness values of the nomadic and resident lions. If a nomadic lion exhibited a better fitness value than a resident lion, then the resident lion was replaced by the nomadic lion.

Step 4: Territory Takeover: In this step, all resident lions (cubs and males) are sorted based on their fitness values. Weaker males are expelled from pride and become nomads, whereas stronger males remain resident lions.

The LOA is effective for selecting relevant features and enhancing the generalization of classification models.

4.3 Firefly Optimization Algorithm

The FA is inspired by the behavior of fireflies, particularly their varying light intensity and attraction. The attractiveness of fireflies is determined by their brightness, which is related to their objective function [36]. At a specific location y, the brightness of a firefly is proportional to the value of the objective function h(y), which is expressed as:

J(y)∝h(y)(14)

in the maximization problem. The relative attractiveness β between two fireflies depends on the distance dij between them, where i and j refer to different fireflies. The intensity of the light decreases with distance because of its absorption by the medium, and the light intensity J(d) follows the inverse squared law:

J(d)=J0d2(15)

J=Jie−δd(16)

J=Jie−δd2(17)

The attractiveness β of a firefly is proportional to the observed light intensity and is described as:

β=β01+δd2(18)

where β0 represents the baseline attractiveness; δ represents the light absorption coefficient; and d represents the distance between fireflies. The relationship between attractiveness and distance is further described by:

β(d)=β0e−m(m≥1)(19)

τ=δ−1/m→1 as m→∞(20)

The distance between two fireflies is calculated using the Cartesian distance formula:

dij=|Yi−Yj|=∑k=1D(yi,k−yj,k)2(21)

where yi,k denotes the k-th component of the spatial coordinates, and Yi denotes the position of the i-th firefly.

4.4 Proposed Hybrid ML-F Optimization Algorithm

In the proposed hybrid ML-F optimization approach, the population was initially generated randomly within the search space. A percentage P of the randomly generated solutions is designated as nomadic lions based on the light intensity I and attractiveness β obtained from the firefly algorithm [37]. The attractiveness of nomadic lions is determined by their brightness, which is related to their objective functions. At a particular location, the brightness of the nomadic lions was selected to maximize the objective. Attractiveness varies with distance, as perceived for other nomadic lions. The remaining randomly generated populations were divided into pride groups. Within each pride, female lions hunt for prey in groups to provide pride. During the hunt, each lion adjusts its position based on its location within the group and its individual positions.

Male lions patrol their territories with pride. To mimic this roaming behavior, randomly selected male residents visited various locations. If a new location is better than the current best, it becomes the new best, allowing weaker nomads to have a higher probability of escaping from less favorable areas. A mating process then occurs, which ensures the survival of lions and allows the exchange of information among the pride members. As male lions matured, they became more aggressive and challenged other males with pride. Defeated males leave pride and become nomadic; if a nomadic male is stronger, it may take over pride by defeating a resident male. This migration behavior includes lions moving from one pride to another, or a resident female becoming nomadic, and vice versa.

The algorithm begins by initializing the population and objective function, which is a process that is uniform in both embodiments of the S-box design approach. The initialization process is executed as follows. Every individual lion (S-box) in the swarm is assigned random numbers drawn from the range of 0 to 1. For each lion, 256 random numbers were required and computed as follows:

Zi=(Umax−Lmin)×rand(0,1)+Lmin(22)

where Umax and Lmin represent the upper (1.0) and lower (0.0) bounds, respectively. These generated sequences were converted into integer values within the range [0,255] using the following equation:

Wi=round(Zi×255)(23)

Here, the swarm size may have values of 15, 20, 25, or 50, with each lion representing an S-box, and Wi an element of the S-box. The objective function is defined as follows:

ϵ=112−NL(gi)(24)

where 112 represents the optimal AES nonlinearity value [38], and NL denotes the nonlinearity function of the lion agent. During each iteration, the S-box with the lowest error value is considered the best agent in terms of fitness. The intensity of the light emitted by each firefly in the swarm is then determined as

I(gi)=11+ϵ2(25)

where I and gi denote the S-box and light intensity, respectively.

4.5 Adaptation

An 8 × 8 S-box can be visualized as a sequence of 256 unique elements. The bijectivity property requires the elements in the S-box to be distinct. However, fireflies generated through swarm operations do not always satisfy this criterion. Thus, the adjustment process for each firefly S-box is as follows:

1.    The entire S-box is thoroughly scanned and duplicate values are identified. The positions of these duplicates are stored in sequence R. All repeated values, except for the first occurrence, are replaced with a placeholder. Missing values in the S-box are identified during the scan.

2.    The missing values are then sorted randomly and their positions are saved. These sorted values define a new sequence R2.

3.    Finally, the positions in sequence R are randomly filled with the corresponding values from R2. This ensures that the S-box generated by the Swarm FA is adjusted to satisfy the bijectivity requirement. The overall process for generating an S-box using the FA is illustrated in Algorithm 1, and the process for the ML-F approach is shown in Algorithm 2.

5  Evaluation of the Proposed Algorithms

To evaluate the effectiveness of the proposed algorithms, a series of experiments focusing on S-box generation were conducted using different swarm sizes (15, 20, 25, and 50) and iterations (200, 400, and 750) on a system equipped with an Intel (R) Core (TM) i7-8565U CPU operating at 1.80 GHz with 16 GB of RAM, Windows 10, and MATLAB R2013a. Each experiment was repeated 25 times to ensure the reliability.

The performance of swarm intelligence algorithms is highly dependent on the parameter settings, particularly because the focus of this study was to enhance the FA movement strategy. Therefore, the parameters for FA and ML-F were set as follows: β0=0.1, βmin=0.1, γ=1.0, α=0.2, and δ=0.96, in line with the recommendations from previous research [36]. Here is a refined version of the paragraph, aligned with the updated Table 1.

Table 1 illustrates the nonlinearity of the S-boxes constructed using the FA and ML-F for different swarm sizes and iteration counts. The “Best Nonlinearity” column yields the best nonlinearity in each experiment, the “Worst Nonlinearity” column yields the lowest value, and the “Average Nonlinearity” column provides the average of the fitness score over all configurations. At 200 iterations, ML-F outperformed slightly in terms of stability, yielding a higher “Worst Nonlinearity” and more consistent “Average Nonlinearity” for different swarm sizes. When the number of iterations was increased to 400 and 750, the difference in performance between ML-F and FA became evident. For example, at 400 iterations with a swarm size of 25, ML-F reached a “Best Nonlinearity” score of 120, while FA reached only 119.2, which shows the stronger capability of ML-F in achieving high nonlinearity values. Both algorithms improved the nonlinearity with an increase in the swarm size. However, greater scalability was observed with ML-F, which maintained higher nonlinearity values with increased swarm size and iteration count. The best “Best Nonlinearity” value of ML-F was 120 when the number of iterations was 750 with a swarm size of 50. Furthermore, it maintained a stable and reliable performance through configurations, whereas its “Worst Nonlinearity” was 119.5. In contrast, a significant drop in the nonlinearity scores for several configurations was observed in the FA. For example, when the number of iterations was 200 and the swarm size was 15, the worst nonlinearity score for FA was 115.0, whereas ML-F had a minimum score of 117.5, which underlines the robustness of ML-F and its lower tendency toward generating weaker S-boxes. The average fitness values confirm the dominance of ML-F: at 400 iterations and a swarm size of 25, ML-F managed to get an “Average Nonlinearity” of 119.3, against 118.7 obtained by FA. This trend of higher averages in the scores across all iteration counts signifies the capability of ML-F to create S-boxes with consistently better nonlinearity. The best overall results were observed at 750 iterations-run with a swarm size of 50 for ML-F: it achieved a “Best Nonlinearity” value of 120 and “Average Nonlinearity” of 119.8. The results in Table 1 indicate the advantage that ML-F has over FA in generating better and higher nonlinear S-boxes for different swarm sizes and iterations. The performance of ML-F resulted not only in higher best-case nonlinear scores but also was more resistant to worst-case scenarios. Similarly, its capability of having higher average fitness values while providing scalability with a larger swarm size establishes it as more robust and efficient in cryptographic applications.

The results in Tables 2 and 3 indicate that increasing the swarm size improves the quality of the generated S-box to some extent, although the nonlinearity gains in the FA are modest relative to the required increase in swarm size. By contrast, ML-F exhibited substantial improvements, particularly between 200 and 400 iterations. However, further increasing to 750 iterations did not significantly enhance the best S-box nonlinearity.

6  Performance Assessment of the Generated S-box

A robust S-box satisfies the criteria described in Section 2. The performances of the S-boxes generated by the two methods were compared with those of other metaheuristic approaches, such as FA, BFO [39], GA [28], ABC [7], TLO [40], LFM [41], SA [42], ACO [18], and CFA [20], which also used nonlinearity as an objective function.

6.1 Bijective Property

The S-boxes generated by both methods produced distinct output values ranging from 0 to 255, thereby satisfying the bijectivity requirement.

6.2 Nonlinearity

Table 4 presents a comparative analysis of the nonlinearity scores of the eight Boolean functions from the S-boxes generated using the different optimization methods. The ML-F method stands out, consistently achieving higher nonlinearity scores ranging from 108 to 110, with an average score of 108.5, and demonstrating its effectiveness in producing robust S-boxes with superior cryptographic properties.

In contrast, FA generated nonlinearity scores within the range of 100–108, with a mean of 105.25, indicating less consistency and effectiveness than ML-F. Other methods, such as SA, GA, ABC, TLO, and BFO, can generate S-boxes whose average nonlinearity scores lie in the range of 105–107.66. However, none of them generated consistency or a higher performance than that generated by ML-F. ACO and CFA also produced respectable results, with an average of approximately 107.16. However, neither outperformed the above-mentioned ML-F in terms of consistency and nonlinearity. Among them, the ML-F method achieved the best performance and was the most effective method for generating S-boxes with high and consistent nonlinearity values.

6.3 Strict Avalanche Criterion

SAC is a critical measure for assessing the robustness of an S-box and is represented by a dependency matrix. Table 5 lists the SAC values for the S-box generated using the ML-F method, and Table 6 lists the SAC values for the S-box generated using the FA method. The mean SAC values for the S-boxes generated by ML-F and FA were 0.496 and 0.493, respectively, both close to the ideal value of 0.5. This indicates the good diffusion properties of the generated S-boxes. Table 7 compares the SAC results obtained using different methods. The dependency matrix offset values for the S-boxes generated by ML-F and FA were 0.03048 and 0.02837, respectively. These results indicate that both ML-F and FA produced S-boxes with acceptable SAC properties, with ML-F showing a slight edge closer to the ideal SAC values.

6.4 Output Bits Independence Criterion

The BIC results for the S-boxes generated using the two methods are listed in Tables 8 and 9. The minimum BIC nonlinearity scores were 97 and 101 for the ML-F-based and FA-based S-boxes, respectively. Table 10 presents a comparison of the BIC results with those of previous studies. The average BIC nonlinearity for the ML-F-based S-box is 103.25, which outperforms those obtained from methods, such as the GA and ABC, although it is slightly lower than that obtained by the S-box from the FA, which had an average of 104.05. This implies that, whereas ML-F performed well in this area, FA produced slightly better results with regard to BIC nonlinearity.

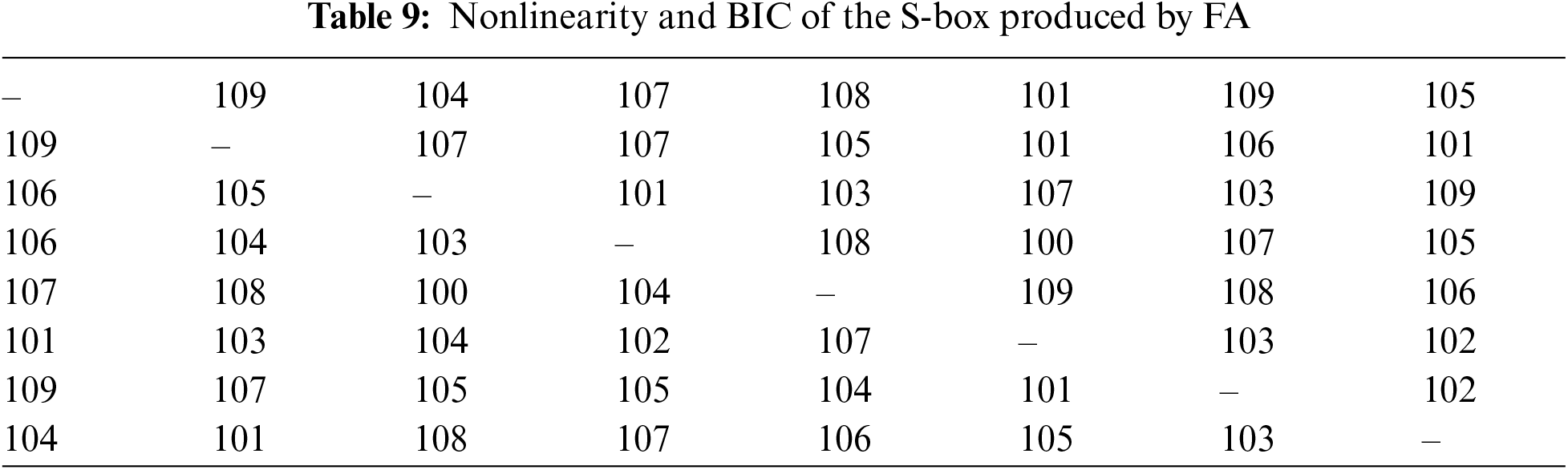
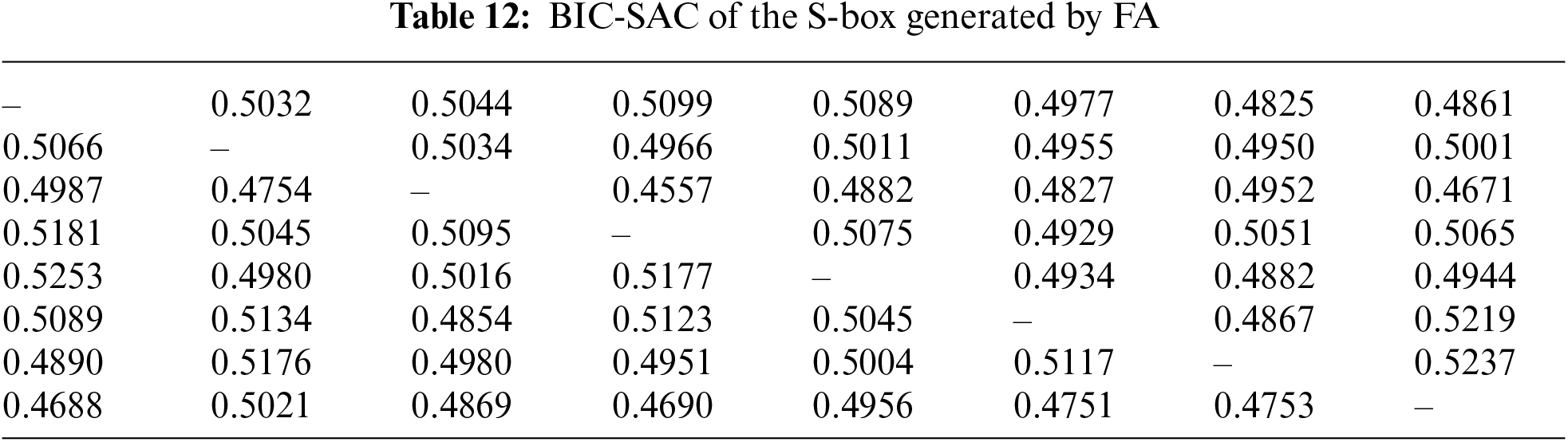
Tables 11 and 12 list the average values of BIC-SAC for S-boxes generated using both methods. The average BIC-SAC value of the ML-F-based S-box was 0.5036, whereas that of the LOA-based S-box was 0.4954 (Table 13). These results indicate that the ML-F method was more successful in achieving BIC-SAC values closer to the ideal value, indicating better overall performance in maintaining the balance between input and output bit dependencies and nonlinearity.

6.5 Differential Harmonization Probability

The S-boxes were analyzed using the DP method, and the results are presented in Tables 14 and 15. Each table element represents the DP of the generated S-box. The analysis showed that both ML-F and FA produced S-boxes with DAP values mostly concentrated around 6–8 with occasional values of 10. As shown in Table 16, both the ML-F and FA S-boxes are produced with a maximum DP value of 11, which is consistent with other high-performance methods reported in the literature. This consistency between the different optimization techniques, including ML-F and FA, shows that these methods are effective in generating S-boxes with strong resistance to differential attacks, thus maintaining a uniform distribution of differential opportunities.

6.6 Maximum Expected Linear Probability

Table 17 compares the MELP results for the S-boxes generated using the proposed method with those generated using various other techniques. The MELP value for the ML-F-based S-box is 0.0789, which is similar to the values obtained using methods, such as SA and GA, and slightly lower than the value achieved by the FA-based S-box (0.0873), which is similar to those obtained using ACO and ABC. The results show that both the ML-F and FA approaches produce S-boxes that meet the MELP criterion, demonstrating a strong performance in maintaining a linear probability distribution comparable to that of other high-performance methods.

7  Threats to Validity

Empirical research is often subject to various validity threats, both external and internal. External validity threats emerge when experimental results cannot be generalized to real-world applications. In this study, such threats were mitigated by employing widely accepted benchmarks from the literature that reflect realistic and commonly encountered cryptographic configurations. Internal validity threats arise from factors that can inadvertently influence the outcomes of the study, including variations in the population size, number of iterations, and specific parameters used for each algorithm. Considering that the source code for all the methods was not available, it would be challenging to confirm whether the ML-F and LOA methods were evaluated using an identical number of fitness functions. Nonetheless, the comparisons presented in this study are considered valid because the published S-box results were obtained using optimal control parameter settings, thereby minimizing the impact of external factors. In addition, the performance was evaluated based on the averaged results to account for the stochastic nature of each metaheuristic run. Comparing ML-F with methods such as TLO could be misleading because of the inherent differences in their operational mechanisms, such as the dual phases of TLO, which require a greater number of fitness function evaluations. Moreover, although TLO is often cited as parameter-free, it still requires careful tuning of the iteration counts and population sizes. Recent scrutiny of TLO has highlighted concerns about unreported implementation steps that can result in unfair comparisons. Another internal validity threat involves the generation time, which is significantly influenced by the computational environment. A fair comparison of generation times necessitates that all methods are executed under identical conditions.

Limitations

Although the performed study illustrates that the ML-F algorithm provides an effective way of generating highly nonlinear and robust S-boxes, there are specific limitations. The first is that a larger swarm size with an increase in iterations requires more computation time and execution, which is perhaps not feasible in real-time or resource-constrained conditions. Although the algorithm has been tested for a range of swarm sizes and iterations, the configurations are still limited, and further research is required to explore its performance under different environmental parameters or on different hardware configurations. More importantly, although the optimization in this study focused on nonlinearity and resistance to linear and differential cryptanalysis, not all types of cryptographic weaknesses, such as fixed points or reverse fixed points, were considered. The performance has a large remaining margin, which will allow refinement towards fully comprehensive cryptographic strength. The results of this study are obtained from simulations. Real implementations may have completely different performances because of additional factors unrelated to this study, such as hardware variability or specific operating limitations. Future studies may thus overcome these two limitations, with a primary focus on ML-F optimization in terms of computational efficiency and the assessment of its real performance against practical cryptographic requirements.

8  Conclusion

S-boxes play a crucial role in symmetrical cryptosystems by providing essential confusion, as highlighted by Shannon, to obscure the relationship between the encryption key and plaintext, thereby enhancing the resistance of the cryptosystem to attacks. In this study, we introduced a novel method for generating S-boxes based on a hybrid ML-F optimization algorithm. This approach leverages the exploration and exploitation capabilities of both the LOA and FA, which jointly address limitations, such as early convergence and limited search diversity often observed in standalone metaheuristic algorithms. These experimental results confirm that the proposed ML-F algorithm is satisfactory for some important cryptographic attacks, such as nonlinearity analysis, BIC, SAC, DP, and MELP. The ML-F-based generated S-boxes maintained their nonlinearity scores highly in comparison to the S-boxes generated by FA and other compared algorithms each time while varying the swarm sizes and iteration counts used in ML-F. From these experimental results, it can be concluded that ML-F obtains better S-boxes with higher resistance to both linear and differential crypt analyses.

One of the striking features of ML-F is its scalability, with an increase in iterations and swarm size, yielding robust performance under larger configurations. In contrast, the FA demonstrated greater fluctuation and vulnerability to local optima, particularly for smaller iterations. This consistency in producing high values of best-case, worst-case, and average metrics indicates the reliability of ML-F for cryptographic applications. However, this study has some limitations. One major limitation is that the increased swarm size and number of iterations boost the computational time, which might limit the practice of ML-F in real-world applications with reduced resources or in real time. Moreover, this study focused only on the optimization of important cryptographic properties, such as nonlinearity and resistance against differential attacks. Other possible vulnerabilities include fixed points or reverse fixed points, which are other important aspects of cryptographic strength. These limitations include avenues for further research, in which better computational efficiency and more cryptographic criteria may be integrated to enhance the applicability of ML-F. This implies that, eventually, ML-F is an effective and promising approach toward the optimization of S-box properties because of its persistent improvement in nonlinearity, along with the general cryptographic security of various configurations. Further research might address improving the computational efficiency of ML-F and exploring methods for adaptive tuning to optimize the ML-F performance. In addition, other practical cryptographic applications may be promising avenues to which the ML-F algorithm might be deployed, considering the great potential that this can provide for the robustness and scalability of cryptographic systems. Extending the scope of the application of ML-F by real-time tests and investigating its hardware implementation could provide a more solid basis for establishing the practicality and effectiveness of the proposed MLF on modern cryptography.

9  Future Research Directions

This paper presents the ML-F algorithm as an efficient way of generating highly nonlinear and robust S-boxes, although a few avenues for future research remain open. Future work may be undertaken to enhance the computational efficiency of ML-F, especially to optimize its performance for real-time applications and resource-constrained environments. Adaptive tuning techniques for parameters or exploring parallel processing may reduce the execution time without compromising cryptographic strength. In addition, it can be extended further to enhance the robustness of the S-boxes generated by ML-F with more security criteria beyond nonlinearity, bit independence, and the properties of differential approximation. Other possible lines of research work may also include resistance against fixed points, reverse fixed points, and short-period cycles, which are important for several advanced cryptographic applications. Further investigations were conducted to test the ML-F algorithm in practical cryptographic contexts, such as encryption schemes for secure communications, image encryption, and IoT security. In addition, based on recent studies related to the design of S-boxes, such as weighted Loeplitz matrices for data encryption and corner-modified symmetric Toeplitz matrices for image encryption, one can gain insight into some feasible and new applications of the ML-F algorithm in cryptographic infrastructure. Addressing these issues will refine the ML-F approach in future research, thereby expanding its application and further increasing its viability in various cryptographic settings.

Acknowledgement: We extend our gratitude to the Department of Mathematics at the Open Educational College, Kirkuk Branch, for its invaluable support throughout this study.

Funding Statement: This research did not receive any specific grants from funding agencies in the public, commercial, or not-for-profit sectors.

Availability of Data and Materials: Data and materials for this study can be made available through an inquiry managed by Arkan Kh. Shakr Sabonchi, under data and privacy guidelines and access, could be subject to limitations for confidentiality purposes, according to ethical and legal standards.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

References

1. A. F. Webster and S. E. Tavares, “On the design of S-boxes,” in Advances in Cryptology CRYPTO’85 Proceedings, H. C. Williams, Ed. Berlin, Heidelberg: Springer, 1985, vol. 218, pp. 523–534. doi: 10.1007/3-540-39799-X_41. [Google Scholar] [CrossRef]

2. M. Matsui, “On correlation between the order of S-boxes and the strength of DES,” in Advances in Cryptology-EUROCRYPT’94, A. De Santis, Ed. Berlin, Heidelberg: Springer, 1995, vol. 950. doi: 10.1007/BFb0053451. [Google Scholar] [CrossRef]

3. W. Gao, B. Idrees, S. Zafar, and T. Rashid, “Construction of nonlinear component of block cipher by action of modular group PSL(2, Z) on projective line PL(GF(28)),” IEEE Access, vol. 8, pp. 136736–136749, 2020. doi: 10.1109/ACCESS.2020.3010615. [Google Scholar] [CrossRef]

4. E. F. Brickell, J. H. Moore, and M. R. Purtill, “Structure in the S-boxes of the DES (extended abstract),” in Advances in Cryptology-CRYPTO’ 86, A. M. Odlyzko, Ed. Berlin, Heidelberg: Springer, 1987, vol. 263. doi: 10.1007/3-540-47721-7_1. [Google Scholar] [CrossRef]

5. A. Y. Al-Dweik, I. Hussain, M. Saleh, and M. T. Mustafa, “A novel method to generate key-dependent s-boxes with identical algebraic properties,” J. Inf. Secur. Appl., vol. 64, no. 14, 2022, Art. no. 103065. doi: 10.1016/j.jisa.2021.103065. [Google Scholar] [CrossRef]

6. S. Murphy and M. J. B. Robshaw, “Key-dependent S-boxes and differential cryptanalysis,” Des. Codes Cryptogr., vol. 27, no. 3, pp. 229–255, 2002. doi: 10.1023/A:1019991004496. [Google Scholar] [CrossRef]

7. Y. Tian and Z. Lu, “S-box: Six-dimensional compound hyperchaotic map and artificial bee colony algorithm,” J. Syst. Eng. Electron., vol. 27, no. 1, pp. 232–241, 2016. doi: 10.1109/JSEE.2016.7400771. [Google Scholar] [CrossRef]

8. V. M. Silva-García, R. Flores-Carapia, C. Rentería-Márquez, B. Luna-Benoso, and M. Aldape-Pérez, “Substitution box generation using chaos: An image encryption application,” Appl. Math. Comput., vol. 332, pp. 123–135, 2018. doi: 10.1016/j.amc.2018.02.013. [Google Scholar] [CrossRef]

9. K. Z. Zamli, A. Kader, F. Din, and H. S. Alhadawi, “Selective chaotic maps Tiki-Taka algorithm for the S-box generation and optimization,” Neural Comput. Appl., vol. 33, no. 23, pp. 16641–16658, 2021. doi: 10.1007/s00500-020-04753-1. [Google Scholar] [CrossRef]

10. S. Picek, D. Jakobovic, J. F. Miller, L. Batina, and M. Cupic, “Cryptographic Boolean functions: One output, many design criteria,” Appl. Soft Comput., vol. 40, no. 3, pp. 635–653, 2016. doi: 10.1016/j.asoc.2015.10.066. [Google Scholar] [CrossRef]

11. J. S. Khan, J. Ahmad, S. S. Ahmed, H. A. Siddiqa, S. F. Abbasi and S. K. Kayhan, “DNA key based visual chaotic image encryption,” J. Intell. Fuzzy Syst., vol. 37, no. 2, pp. 2549–2561, 2019. doi: 10.3233/JIFS-182778. [Google Scholar] [CrossRef]

12. S. Tiwari and D. Sharma, “On higher order nonlinearities of Boolean functions,” Cryptogr. Commun., vol. 15, no. 4, pp. 821–830, 2023. doi: 10.1007/s12095-023-00643-5. [Google Scholar] [CrossRef]

13. G. Ivanov, N. Nikolov, and S. Nikova, “Reversed genetic algorithms for generation of bijective S-boxes with good cryptographic properties,” Cryptogr. Commun., vol. 8, no. 2, pp. 247–276, 2016. doi: 10.1007/s12095-015-0170-5. [Google Scholar] [CrossRef]

14. L. Cao, K. Ben, H. Peng, and X. Zhang, “Enhancing firefly algorithm with adaptive multi-group mechanism,” Appl. Intell., vol. 52, pp. 9795–9815, 2022. doi: 10.1007/s10489-021-02766-9. [Google Scholar] [CrossRef]

15. X. -S. Yang, S. Deb, Y. -X. Zhao, S. Fong, and X. He, “Swarm intelligence: Past, present and future,” Soft Comput., vol. 22, no. 18, pp. 5923–5933, 2018. doi: 10.1007/s00500-017-2810-5. [Google Scholar] [CrossRef]

16. J. A. Clark, J. L. Jacob, and S. Stepney, “The design of S-boxes by simulated annealing,” New Gener. Comput., vol. 23, no. 3, pp. 219–231, 2005. doi: 10.1007/BF03037656. [Google Scholar] [CrossRef]

17. H. Liu, A. Kadir, and C. Xu, “Cryptanalysis and constructing S-box based on chaotic map and backtracking,” Appl. Math. Comput., vol. 376, no. 3, 2020, Art. no. 125153. doi: 10.1016/j.amc.2020.125153. [Google Scholar] [CrossRef]

18. M. Ahmad, D. Bhatia, and Y. Hassan, “A novel ant colony optimization based scheme for substitution box design,” Procedia Comput. Sci., vol. 57, no. 2, pp. 572–580, 2015. doi: 10.1016/j.procs.2015.07.394. [Google Scholar] [CrossRef]

19. M. Ahmad, M. N. Doja, and M. M. S. Beg, “ABC optimization based construction of strong substitution-boxes,” Wirel. Pers. Commun., vol. 101, no. 3, pp. 1715–1729, 2018. doi: 10.1007/s11277-018-5787-1. [Google Scholar] [CrossRef]

20. H. A. Ahmed, M. F. Zolkipli, and M. Ahmad, “A novel efficient substitution-box design based on firefly algorithm and discrete chaotic map,” Neural Comput. Appl., vol. 31, no. 11, pp. 7201–7210, 2019. doi: 10.1007/s00521-018-3557-3. [Google Scholar] [CrossRef]

21. J. Wang, Y. Zhu, C. Zhou, and Z. Qi, “Construction method and performance analysis of chaotic S-box based on a memorable simulated annealing algorithm,” Symmetry, vol. 12, no. 12, 2020, Art. no. 2115. doi: 10.3390/sym12122115. [Google Scholar] [CrossRef]

22. H. S. Alhadawi, D. Lambić, M. F. Zolkipli, and M. Ahmad, “Globalized firefly algorithm and chaos for designing substitution box,” J. Inf. Secur. Appl., vol. 55, no. 1, 2020, Art. no. 102671. doi: 10.1016/j.jisa.2020.102671. [Google Scholar] [CrossRef]

23. H. S. Alhadawi, M. A. Majid, D. Lambić, and M. Ahmad, “A novel method of S-box design based on discrete chaotic maps and cuckoo search algorithm,” Multimed. Tools Appl., vol. 80, no. 5, pp. 7333–7350, 2021. doi: 10.1007/s11042-020-10048-8. [Google Scholar] [CrossRef]

24. K. Z. Zamli, “Optimizing S-box generation based on the adaptive agent heroes and cowards algorithm,” Expert. Syst. Appl., vol. 182, no. 11, 2021, Art. no. 115305. doi: 10.1016/j.eswa.2021.115305. [Google Scholar] [CrossRef]

25. H. S. Alhadawi, S. Q. Salih, and Y. D. Salman, “Chaotic particle swarm optimization based on meeting room approach for designing bijective S-boxes,” in Proc. Int. Conf. Emerging Technol. Intell. Syst., M. Al-Emran, M. A. Al-Sharafi, M. N. Al-Kabi, K. Shaalan, Eds. Cham: Springer, 2022, vol. 322. doi: 10.1007/978-3-030-85990-9_28. [Google Scholar] [CrossRef]

26. F. Artuğer, “A new S-box generator algorithm based on 3D chaotic maps and whale optimization algorithm,” Wirel. Pers. Commun., vol. 131, no. 2, pp. 835–853, 2023. doi: 10.1007/s11277-023-10456-7. [Google Scholar] [CrossRef]

27. X. Chen, J. H. Park, J. Cao, and J. Qiu, “Sliding mode synchronization of multiple chaotic systems with uncertainties and disturbances,” Appl. Math. Comput., vol. 308, pp. 161–173, 2017. doi: 10.1016/j.amc.2017.03.012. [Google Scholar] [CrossRef]

28. Y. Wang, K. -W. Wong, C. Li, and Y. Li, “A novel method to design S-box based on chaotic map and genetic algorithm,” Phys. Lett. A, vol. 376, no. 6–7, pp. 827–833, 2012. doi: 10.1016/j.physleta.2012.01.009. [Google Scholar] [CrossRef]

29. M. H. Dawson and S. E. Tavares, “An expanded set of S-box design criteria based on information theory and its relation to differential-like attacks,” in Advances in Cryptology-EUROCRYPT’91, D. W. Davies, Ed. Berlin, Heidelberg: Springer, 1991, vol. 547. doi: 10.1007/3-540-46416-6_30. [Google Scholar] [CrossRef]

30. Y. Li and M. Wang, “Constructing differentially 4-uniform permutations over GF(22m) from quadratic APN permutations over GF(22m+1),” Des. Codes Cryptogr., vol. 72, no. 2, pp. 249–264, 2014. doi: 10.1007/s10623-012-9760-9. [Google Scholar] [CrossRef]

31. A. A. Alzaidi, M. Ahmad, H. S. Ahmed, and E. Al Solami, “Sine-cosine optimization-based bijective substitution-boxes construction using enhanced dynamics of chaotic map,” Complexity, vol. 2018, no. 1, 2018, Art. no. 9389065. doi: 10.1155/2018/9389065. [Google Scholar] [CrossRef]

32. H. S. Alhadawi, M. F. Zolkipli, S. M. Ismail, and D. Lambić, “Designing a pseudorandom bit generator based on LFSRs and a discrete chaotic map,” Cryptologia, vol. 43, no. 3, pp. 190–211, 2019. doi: 10.1080/01611194.2018.1548390. [Google Scholar] [CrossRef]

33. D. Lambić, “A new discrete chaotic map based on the composition of permutations,” Chaos Solitons Fractals, vol. 78, no. 2, pp. 245–248, 2015. doi: 10.1016/j.chaos.2015.08.001. [Google Scholar] [CrossRef]

34. M. Yazdani and F. Jolai, “Lion optimization algorithm (LOAA nature-inspired metaheuristic algorithm,” J. Comput. Des. Eng., vol. 3, no. 1, pp. 24–36, 2015. doi: 10.1016/j.jcde.2015.06.003. [Google Scholar] [CrossRef]

35. E. S. P. Krishna and A. Thangavelu, “Attack detection in IoT devices using hybrid metaheuristic lion optimization algorithm and firefly optimization algorithm,” Int. J. Syst. Assur. Eng. Manag., vol. 12, no. 4, pp. 999–1010, 2021. doi: 10.1007/s13198-021-01150-7. [Google Scholar] [CrossRef]

36. X. S. Yang, “Firefly algorithms for multimodal optimization,” in Stochastic Algorithms: Foundations and Applications, O. Watanabe, T. Zeugmann, Eds. Berlin, Heidelberg: Springer, 2009, vol. 5792. doi: 10.1007/978-3-642-04944-6_14. [Google Scholar] [CrossRef]

37. I. Fister, X. -S. Yang, J. Brest, and I. Fister, “Modified firefly algorithm using quaternion representation,” Expert Syst. Appl., vol. 40, no. 18, pp. 7220–7230, 2013. doi: 10.1016/j.eswa.2013.06.070. [Google Scholar] [CrossRef]

38. J. Daemen and V. Rijmen, The Design of Rijndael. New York: Springer-Verlag, 2002. [Google Scholar]

39. Y. Tian and Z. Lu, “Chaotic S-box: Intertwining logistic map and bacterial foraging optimization,” Math. Probl. Eng., vol. 2017, no. 1, 2017, Art. no. 6969312. doi: 10.1155/2017/6969312. [Google Scholar] [CrossRef]

40. T. Farah, R. Rhouma, and S. Belghith, “A novel method for designing S-box based on chaotic map and teaching-learning-based optimization,” Nonlinear Dyn, vol. 88, no. 2, pp. 1059–1074, 2017. doi: 10.1007/s11071-016-3295-y. [Google Scholar] [CrossRef]

41. I. Hussain, T. Shah, M. A. Gondal, W. A. Khan, and H. Mahmood, “A group theoretic approach to construct cryptographically strong substitution boxes,” Neural Comput. Applic., vol. 23, no. 1, pp. 97–104, 2013. doi: 10.1007/s00521-012-0914-5. [Google Scholar] [CrossRef]

42. G. Chen, “A novel heuristic method for obtaining S-boxes,” Chaos Soliton. Fract., vol. 36, no. 4, pp. 1028–1036, 2008. doi: 10.1016/j.chaos.2006.08.003. [Google Scholar] [CrossRef]