Ensuring Information Security in Electronic Health Record System Using Cryptography and Cuckoo Search Algorithm

1  Introduction

The Electronic Health Record System (EHRS) serves as a digital repository for a patient’s comprehensive health information, including medical history, diagnoses, medications, allergies, immunization dates, laboratory test results, and other relevant clinical data [1]. EHRs aim to provide healthcare professionals with real-time access to updated patient information, enabling informed decision-making in diagnosis, treatment, and care. Additionally, EHRs facilitate communication and collaboration among healthcare providers, resulting in improved patient safety, enhanced quality of care, and reduced administrative tasks such as paperwork and duplicate testing [2]. These records are securely stored in electronic databases, accessible only to authorized healthcare professionals involved in patient care. EHRs can be shared electronically across healthcare settings to support coordinated care [3]. However, to realize universal accessibility, standardization of electronic usage and protocols is crucial. Safeguarding patient privacy and security is paramount to uphold medical ethics and societal expectations, including access control, secure storage, transmission, and regulatory policies [4]. In an effort to enhance EHR data security, a hybrid model has been proposed, suggesting the combined use of SHA-256, ECC, and CS algorithms. The private key for ECC is generated using a CS-based algorithm, which then applies SHA-256 hashing to the data. The CS Algorithm draws inspiration from the behavior of cuckoo birds and serves as an optimization algorithm. It iteratively enhances candidate solutions within the population, explores new solutions through random walks, and generates fresh solutions using the cuckoo egg replacement mechanism [5]. Over time, the algorithm converges to the optimal solution, progressively improving the quality of solutions in the population. ECC, a public-key encryption technique that employs elliptic curves over finite fields, is gaining popularity due to its robust security, computational efficiency, and smaller key sizes compared to other encryption methods. ECC finds application in secure messaging, digital signatures, and secure key exchange. Notably, ECC’s key sizes are considerably shorter, leading to improved computational and memory efficiency [6]. SHA-256, a widely used cryptographic hash function, generates a fixed-size 256-bit output regardless of the input size [7]. It ensures data integrity by detecting any modifications during transmission. Even a single bit change in the data would result in a different hash value, indicating tampering [8]. Utilizing ECC for key exchange and digital signatures, along with SHA-256 for data integrity, guarantees secure communication over the Internet. By incorporating these hybrid approaches to enhance EHR data security, healthcare systems can ensure both privacy and the seamless exchange of patient information, promoting efficient and reliable healthcare delivery.

1.1 Motivation

Ensuring the security of Electronic Health Record Systems (EHRS) data against unauthorized access is of utmost importance, and this objective can be accomplished by employing strong encoding algorithms for data storage and transmission. The violation of data security could result in substantial difficulties in upholding the confidentiality and accuracy of user data within EHRS. Consequently, the encoding of data before transmission becomes an essential aspect. This study presents a viable method to enhance data security by leveraging the Cuckoo Search (CS) algorithm to generate a private key for Elliptic Curve Cryptography (ECC), while also incorporating the SHA-256 algorithm.

1.2 Contributions

This research presents four primary outcomes. First, it proposes a novel approach to secure EHRS data, which involves the utilization of ECC, CS algorithm, and SHA-256. Second, it devises an efficient private key for ECC with the use of the CS algorithm. Third, it enhances data security by encrypting the ciphertext based on ECC-CS with SHA-256. Finally, the effectiveness of the proposed method is demonstrated by comparing it with other existing models through empirical evaluation.

1.3 Organization

The paper is structured as follows: Related works are reviewed in Section 2. The CS algorithm and ECC are explained in Section 3. Section 4 presents the proposed model. Section 5 provides an evaluation and comparison of the proposed model with the other models. Finally, Section 6 concludes the study and discusses future work.

2  Related Works

In recent years, the healthcare industry has witnessed increasing concerns regarding the security and privacy challenges inherent in Electronic Health Record Systems (EHRS). Consequently, researchers have proposed various innovative methodologies to address these issues and ensure the confidentiality, integrity, and availability of medical data. For instance, one approach suggested in [9] involved the utilization of robust authentication and anonymity measures to protect user privacy in telecare medical information systems. This system employs biometrics and pseudonyms to maintain the confidentiality of patients’ identities while enabling authorized users to access medical data. Similarly, study [10] introduced a privacy-preserving data aggregation scheme that employs the bilinear ElGamal cryptosystem to secure patient privacy and data confidentiality during the aggregation of data from multiple patients. In [11], a unique method was proposed for securing ECG data in telecare medical information systems. The authors suggest encrypting the data using the singular value decomposition method and subsequently compressing the encrypted data to enhance data security without compromising its quality during transmission. This approach not only offers a high level of security but also ensures the integrity of the data. Additionally, study [12] presented a fragile watermarking scheme for medical images, allowing for the detection of tampered images. This technique utilizes discrete wavelet transform and singular value decomposition to embed a watermark in medical images, enabling the identification of any alterations made to the image. Consequently, the integrity of the data is preserved. Another study [13] proposed two approaches to protect patient privacy in IoT-based healthcare systems. The first approach, known as the PrivacyProtector mechanism, ensures that data collection occurs without revealing the patient’s identity. The second approach employs a quantum information hiding scheme, utilizing quantum entanglement and quantum teleportation to securely transmit medical images over unsecured channels. This technique safeguards the medical data from unauthorized access during transmission. In [14], a smart card-based cancelable finger-vein biocryptosystem is proposed to enhance mobile healthcare data security while preserving user privacy. This method generates a cancelable biometric template based on a user’s finger vein pattern, facilitating authentication without divulging the user’s identity. As a result, user privacy is maintained while authorized access to medical data is upheld. Furthermore, study [15] introduced an efficient design for a novel public key scheme for medical data protection using the NanoPi Fire platform. This scheme offers enhanced security and faster computation time, enabling real-time encryption and decryption of medical data. Moreover, study [16] proposed an audio transmission approach for medical reports in visa processing to mitigate the spread of communicable diseases among the immigrant population. This approach enhances data security and privacy while improving immigrants’ access to healthcare services. It ensures the secure transmission of medical data while maintaining the privacy of the immigrant population. Finally, study [17] presented a secured cloud computing approach for medical data, incorporating watermarking and encryption to enhance data confidentiality and integrity while enabling efficient and secure data sharing. This approach ensures the secure storage of medical data in the cloud while permitting authorized users to access the data securely. Collectively, these innovative approaches have facilitated efficient and secure sharing of medical data while preserving user privacy and data confidentiality. By employing a combination of techniques such as biometrics-based authentication, secure data aggregation, encryption and compression of medical data, watermarking, quantum information hiding, and cancelable biometric templates, researchers have effectively addressed the security and privacy challenges associated with EHRS [18].

3  Preliminaries

This section presents an overview of the CS and ECC algorithms.

3.1 Cuckoo Search Algorithm

The Obligate Interspecific Brood Parasites comprise a group of avian species, among which the cuckoo is prominent, exhibiting a parasitic behavior driven by the cuckoo’s efficient egg-laying process. This behavior entails depositing their eggs in the nests of other bird species and leaving them to hatch and develop without any parental care. Consequently, the reproductive success of the host birds is compromised, as their nesting success diminishes through various mechanisms. For instance, female parasites may potentially remove or damage host eggs, while young parasites can evict or kill host offspring following hatching. To address optimization problems inspired by natural phenomena, the Cuckoo Search (CS) algorithm [5] was developed. This algorithm generates solutions within nests and then improves them by modifying specific components of the solution while eliminating weaker nests. Leveraging Lévy flights and Markov chain random walk, the CS algorithm creates new solutions that are further optimized and efficient.

The term “Lévy flights” was originally coined by the French mathematician Paul Pierre Lévy in the 1930s. Lévy flights refer to a type of random walk wherein movement lengths conform to a probability distribution characterized by a power law tail. This distribution allows for infrequent yet substantial movements, a pattern observed in various natural systems, such as the foraging behavior of spider monkeys and the flight patterns of certain mammals. The power law distribution signifies that occasional long-distance movements can yield greater benefits compared to numerous short movements. Despite appearing random, Lévy flights have demonstrated efficacy in optimizing certain search algorithms, leading to their application in diverse fields, including finance and biology [19]. Lévy [20] discovered that the equation y = |x|−α, where α is between 1 and 2, leads to a stable and balanced distribution. Mantegna [21] created an algorithm to simulate this distribution, and the size of each step is determined by a random variable described in Eq. (1).

η=x|y|1/β(1)

The standard deviation of the variable σx can be determined by applying Eq. (2) when the variables x and y follow a normal distribution with a mean of 0 and the standard deviation of σy is 1.

σx={Γ(1+β)sin⁡(πβ2)[Γ(1+β)/2]β2(β−1)/2}1/β(2)

According to a recommendation made in [21], when the standard deviation of x (σx) is 0.6965 and the standard deviation of y (σy) is 1, it is advised to use β = 1.5 in Eq. (2). Under these conditions, when the absolute value of ƞ is greater than or equal to 10, the probability distributions of ƞ and the symmetrical Lévy stable process exhibit similar asymptotic behavior. In [22], the performance of three different methods for generating Lévy noise was compared, and Mantegna’s algorithm was found to be the fastest. The proposed data security model incorporates multiple algorithms, such as the CS, ECC, and SHA-256. The CS algorithm generates private keys for ECC, while SHA-256 ensures privacy and security. This comprehensive solution ensures the confidentiality, integrity, and authenticity of data, which makes it suitable for a variety of applications requiring high-level security, such as online banking, e-commerce, and government systems.

3.2 Elliptic-Curve Cryptography

ECC is a cryptographic technique that employs mathematical operations on small fields to provide security. It is faster than other encoding techniques because of its short key length. The security of ECC is maintained due to the complex exponential discrete logarithm problem [6]. To apply ECC, two numbers (a and b) are necessary from a particular set called Fp. Moreover, an elliptical curve has a set of points denoted as E (Fp), with Q being one of these points as shown in Eq. (3).

y2=x3+ax+b(3)

The process of encrypting data using ECC involves selecting a random number x from the Fp set, between 1 and n−1, as a private key. The plaintext is first converted into bits and then mapped onto an elliptic curve as (x, y) points. These points are subsequently encrypted and converted back into bits. The process of encrypting an elliptic curve involves the following steps:

1.    Initialization: The encoding algorithm is initialized by selecting appropriate parameters and initializing necessary data structures, such as E, Q, and p. In some cases, this step may require generating random numbers or other initial values.

2.    Public Key Generation: A cryptographic key pair consisting of a public key and a private key is created. The public key is used for data encoding, while the private key is used for decoding. The keys are generated in a way that makes it computationally infeasible to derive the private key from the public key. The private key, x, is used to determine the public key (H), which is determined by the equation H = x.Q.

3.    Encoding: Once the public key is generated, the plaintext data is encrypted using the public key. Encoding involves transforming the original data into an unreadable form without the corresponding private key, as depicted in Eq. (4), where r represents a random number.

Ciphertext=Enc(data)={Ciphertext1=r.QCiphertext2=data+r.H(4)

4.    Decoding: The encrypted data is decoded using the private key, as shown in Eq. (5). Decoding is the process of reversing the encoding process and transforming the encrypted data back into its original form. Only the owner of the private key can decrypt the data, ensuring confidentiality and security.

Dec(Ciphertext)=Ciphertext2−x.Ciphertext1=data+r.H−x.r.Q=data+x.r.Q−x.r.Q=data(5)

4  The Proposed Model

In order to ensure the secure encoding and decoding of data using ECC, it is necessary to generate a random private key. To address this requirement, a proposed approach utilizes CS optimization to generate such a key. The quality of the encoding for sensitive data in ECC is significantly impacted by the randomness of the key used in the encoding process. CS is a mathematical technique that searches for solutions in the search space, which is analogous to the discrete nests or eggs of host birds. In this context, the objective of the CS algorithm is to identify the optimal private key (Pr) for ECC, which can allow for accurate and secure decoding of the ciphertext to the original plaintext. The fitness of a solution, i.e., a private key, is determined by comparing the decrypted plaintext with the original plaintext, and evaluating a fitness value based on the accuracy and security of the decoding. The objective function for the CS algorithm in this context can be formulated as follows:

f(Pr)=−h(Dec(CP,Pr),B)(6)

where, CP is the ciphertext obtained after encoding, B is the original plaintext, Dec(CP, Pr) is the decoding of the ciphertext CP using the private key Pr, h(x, y) is a function that measures the similarity or distance between the decrypted plaintext x and the original plaintext y.

In this case, the negative sign is used to convert the fitness function into a minimization problem where the goal is to minimize the distance between the decrypted plaintext and the original plaintext.

The following steps are involved in the proposed model:

1.    The Cuckoo Search method starts by setting certain values: the number of nests (n), the size of each nest (m), the chance of finding foreign eggs (pa), the step size (α = 0.01), and the maximum number of iterations.

2.    The host bird’s eggs are set up by picking a random sequence of numbers with the same length as the private key. For ECC, the private key is 256 bits long.

3.    New eggs are created using Eq. (1), except for the best egg, which stays the same. If the new eggs are better than the current ones, they are selected randomly using Eq. (6).

4.    Bad nests are removed by finding alien eggs through a process of generating a random number and comparing it to the chance of discovering alien eggs (pa). If the random number is less than pa, a new solution is created. If it is better than the current nests, it replaces them by taking small steps from their current positions.

5.    The creation of new nests and the finding of alien eggs are repeated until either the maximum number of attempts is reached, or the best nest reaches the desired quality level. The values of n, pa, and α are determined through experimentation.

The new method saves time by automatically assigning strings without user input. It uses the CS algorithm to find the private keys for users 1 and 2, while the public key is based on Q and the private key. The algorithm runs for a maximum of 175 iterations.

Algorithm 1 initializes variables and functions. It starts by defining the ECC curve equation and calculating point Q. During encoding, the function CS() finds the best discrete nests or eggs for the private key, and then SHA-256 is used to hash and encrypt texts. During decoding, the hash function is applied first, employing XOR, and right-shift, and left-shift procedures, to modify the initial hash values. ECC decoding is then performed. The proposed method offers many benefits: it automates the string assignment process, reduces time, and ensures secure communication. It also uses CS to optimize the solution and employs hash functions for extra security.

Overall, this new model is an efficient and secure way to assign strings and transmit data between users. To increase data confidentiality, the suggested approach follows ECC encoding with the XOR and shift-left operators. There are four ECC-based phases in these operators: Encoding (1), Encoding (2), Decoding (1), and Decoding (2). This strengthens the model’s core and ensures secure message transmission. During decoding, the encrypted text undergoes shift-left operations and XOR before using the ECC algorithm.

5  Evaluation and Results

This section aims to evaluate the encoding and decoding throughput and speed of the proposed model. The experiments were executed on a Windows 10 Pro machine, utilizing C# programming language via Microsoft Visual Studio 2012. The computer was equipped with an AMD E-350 Processor, running at a frequency of 1.60 GHz, and 4 GB of RAM.

The initial population size, randomly chosen by the algorithm, was influenced by the key length. In this specific model, the key length was determined by selecting random integers between 0 and 127. The size of the initial population was therefore dependent on this key length. The performance evaluation of the encoding and decoding process was based on these experimental settings.

5.1 Performance Analysis

5.1.1 Decoding and Encoding Times

This section presents an evaluation of the encoding and decoding speeds of the proposed model. The results are depicted in Figs. 1 and 2, respectively. Fig. 1 displays the encoding time (measured in milliseconds) of the proposed model at different iterations with an initial population of 25. The data indicates that the encoding time decreases as the number of iterations increases, with the lowest encoding time observed at 75 iterations. For instance, when encoding a file of 75,000 KB, the encoding time is 8,125 ms for 25 iterations, 7,635 ms for 75 iterations, and 7,930 ms for 175 iterations. The findings are supported by the data presented in the figures, which were obtained through a comprehensive experimental study conducted on the proposed model.

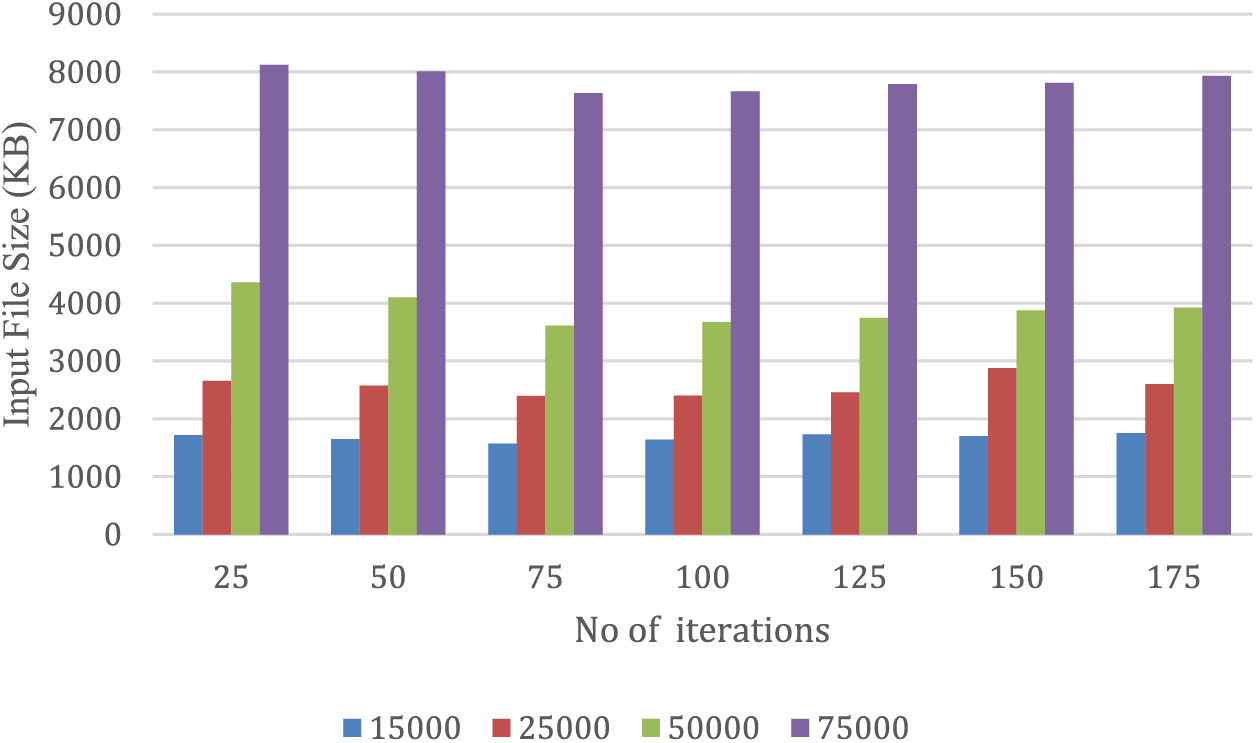
Figure 1: Encoding time based on iterations

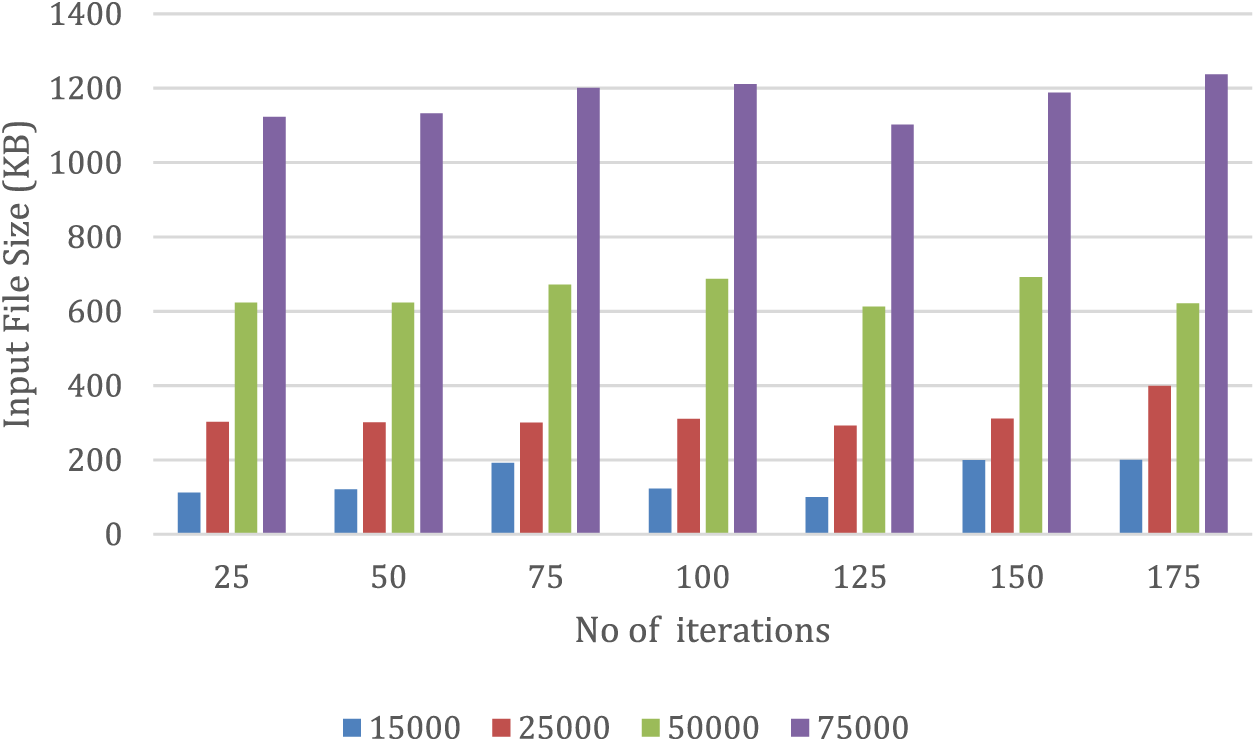
Figure 2: Decoding time based on iterations

In contrast, Fig. 2 displays the decoding time in milliseconds of the suggested model at different iterations while using an initial population of 25. The optimal condition is when the decoding time is less than the encoding time, which results in a prompt and efficient system. The results reveal that the decoding time reaches its minimum at 125 iterations. For example, when decrypting a file of 75,000 KB, the decoding time measures at 1123.201 ms for 25 iterations, 1102.012 ms for 125 iterations, and 1237.072 ms for 175 iterations.

The findings depicted in Fig. 3 show that the proposed model exhibits varying mean encoding and decoding times at different iterations. The most efficient encoding time is observed at the 75th iteration, while the optimal decoding time is achieved at the 125th iteration. These results suggest that the proposed model meets the desired security level while also demonstrating improved execution time.

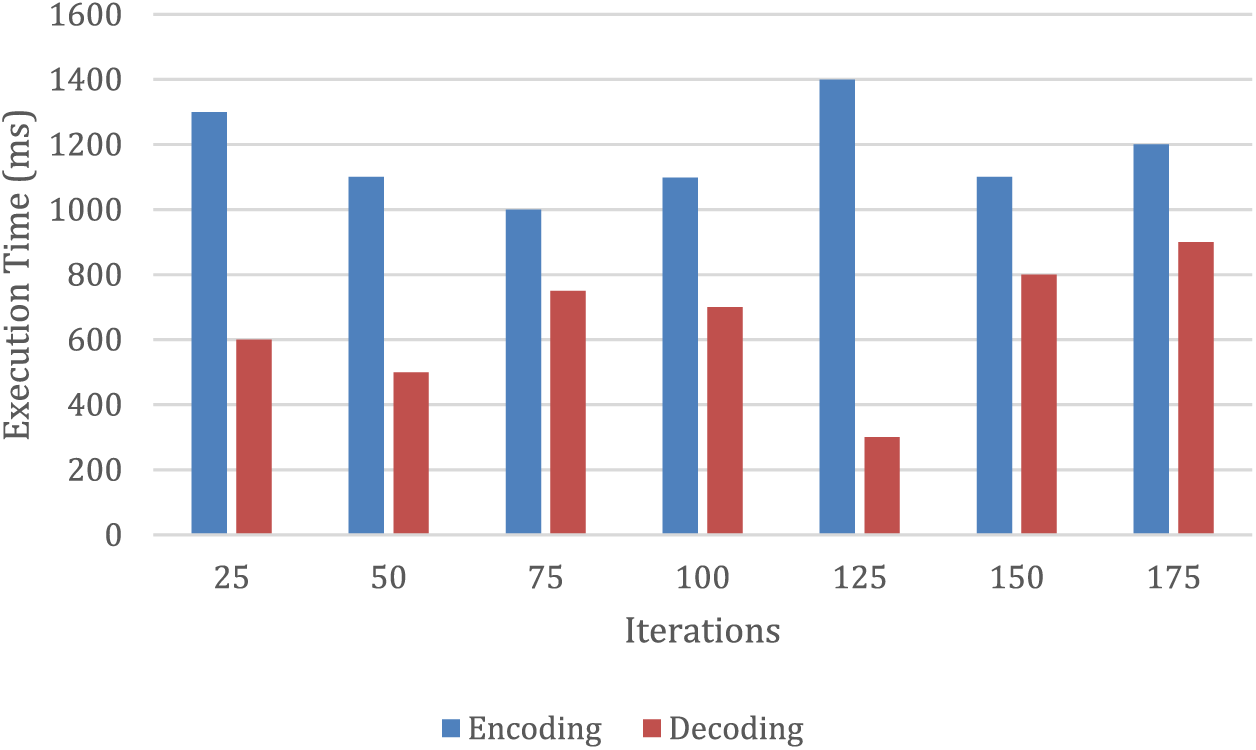
Figure 3: Times on average for encoding and decoding at various iterations

Therefore, it can be concluded that the proposed model is a viable solution for achieving secure and efficient data encoding and decoding. The outcomes of this evaluation indicate that the suggested model is effective in terms of both encoding and decoding speed. The optimal number of iterations for minimizing encoding time is 75, while the optimal number for minimizing decoding time is 125. These results have significant implications for the development of more efficient and effective encoding algorithms in the future and contribute to the advancement of the field of cryptography. Additionally, the proposed model’s improved execution time can provide practical benefits for various applications, particularly those involving large file sizes.

5.2 Comparison and Evaluation

This section provides a comparative analysis between the proposed model and AES, RSA [23], based on the evaluation of 14 files with varying sizes and a 128-bit key length using Visual Studio.

5.2.1 Encoding and Decoding Based on AES and Proposed Model

As presented in Table 1. The main aim of this study was to compare the efficiency of the proposed model with AES in terms of encoding and decoding time. The results reveal that the suggested model outperforms AES, particularly when dealing with a data size of 50 MB. The encoding time of AES in this scenario is 7.009 s, while the proposed model only takes 4.62 s, indicating a significant improvement in processing time. As shown in Fig. 4, the proposed model’s encoding time is considerably shorter than that of AES, resulting in a reduction of about 34.17% in the execution time of encoding on a file size of 50 MB. Additionally, the proposed model has been demonstrated to outperform AES, establishing its superiority over the current AES approach in terms of efficiency.

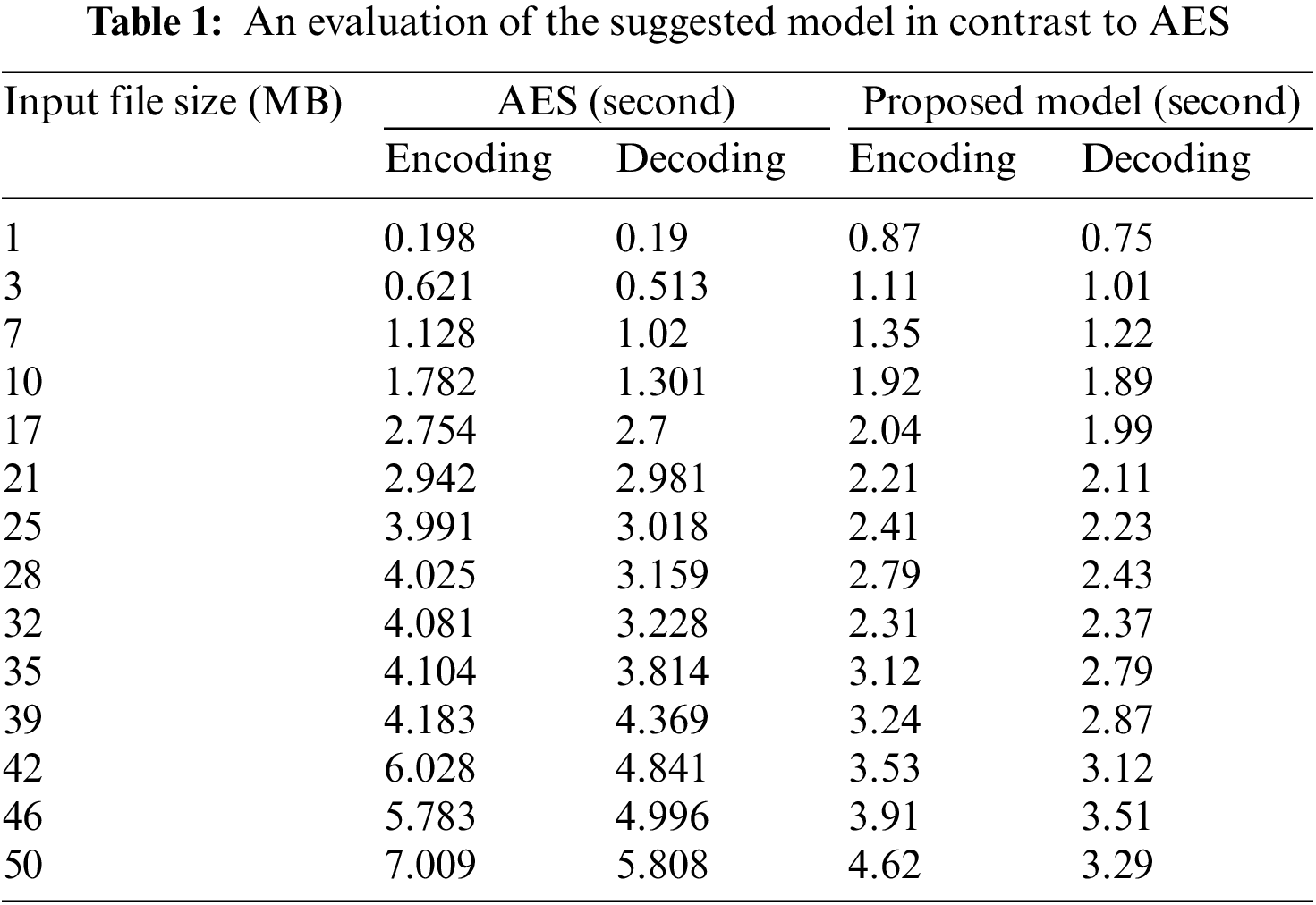
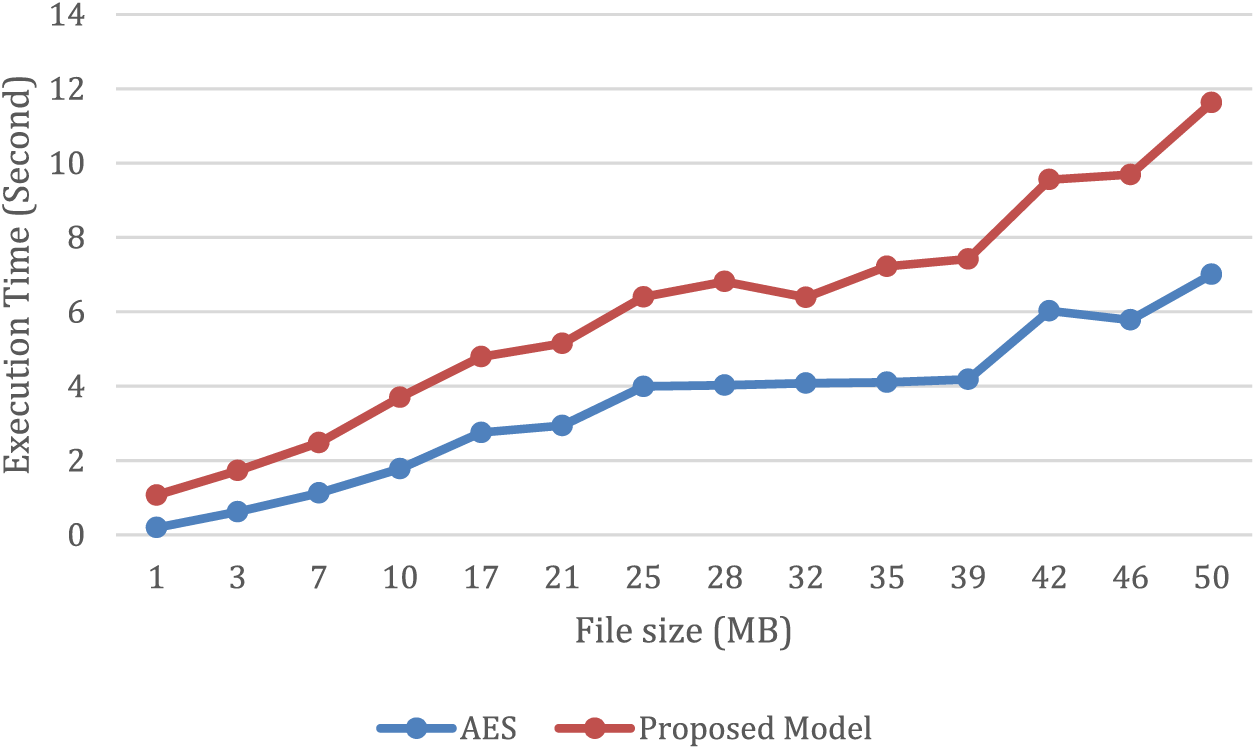
Figure 4: A comparison of the suggested model’s and AES’s encoding times

Regarding decoding time, the comparison between the proposed model and AES is illustrated in Fig. 5, indicating that the proposed model outperforms AES in terms of speed. The proposed model requires fewer computations during its encoding and decoding processes, resulting in faster processing speeds when compared to AES. The findings indicate that the proposed model’s encoding time is considerably shorter, resulting in a reduction of about 43.32% in the execution time of encoding on a file size of 50 MB.

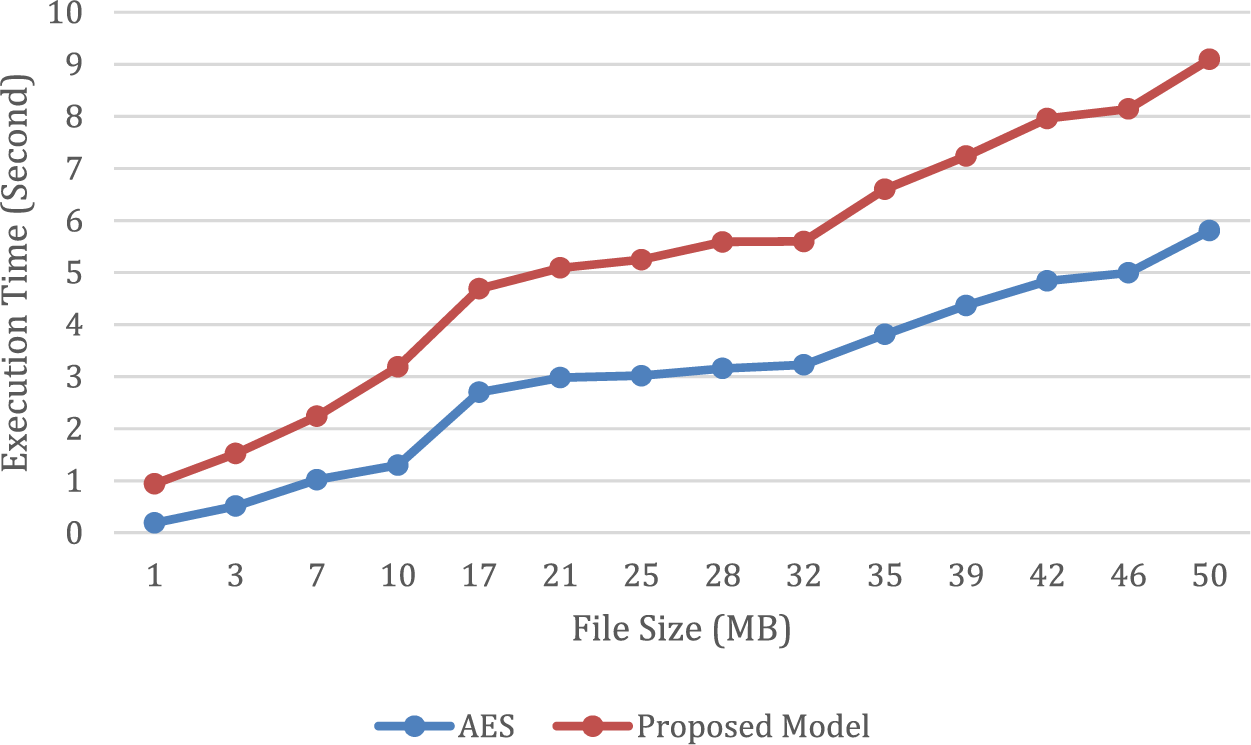
Figure 5: Evaluating the differences between the suggested model’s and AES’s decoding times

Overall, the proposed model in this study is superior to AES in both encoding and decoding speed, making it a more efficient and feasible alternative for cryptographic applications, particularly in situations with limited resources. The use of ECC in the suggested model reduces the computational burden, making it more rapid and well-suited for real-time scenarios. These advantages make the proposed model a promising solution for secure data communication.

In brief, the model suggested in this study surpasses AES in both encoding and decoding speed, thereby proving to be a more efficient and feasible alternative for cryptographic applications, particularly in situations with limited resources. The utilization of ECC in the suggested model curtails the computational burden, rendering it more rapid and well-suited for real-time scenarios. These advantages make the proposed model a promising solution for secure data communication.

5.2.2 Encoding and Decoding Based on RSA and Proposed Model

This section offers a comparative evaluation between a newly suggested model and RSA, which was discussed in the work of [23]. The main objective of the analysis was to assess the efficiency of the proposed model against RSA in terms of both encoding and decoding time. The findings, which are summarized in Table 2, reveal that the proposed model demonstrates superior performance compared to RSA, especially when dealing with large data sets of 50 MB. The results indicate that RSA’s encoding time for this data size is 475.128 s, whereas the proposed model only requires 3.29 s, representing a significant enhancement in processing time. RSA is a heavyweight cryptography system due to its large key size, while the ECC offers a more efficient alternative with a smaller key size, resulting in faster processing speeds and less memory usage, as mentioned in [24]. Therefore, implementing the ECC on devices with limited resources can lead to quicker computations in real-time.

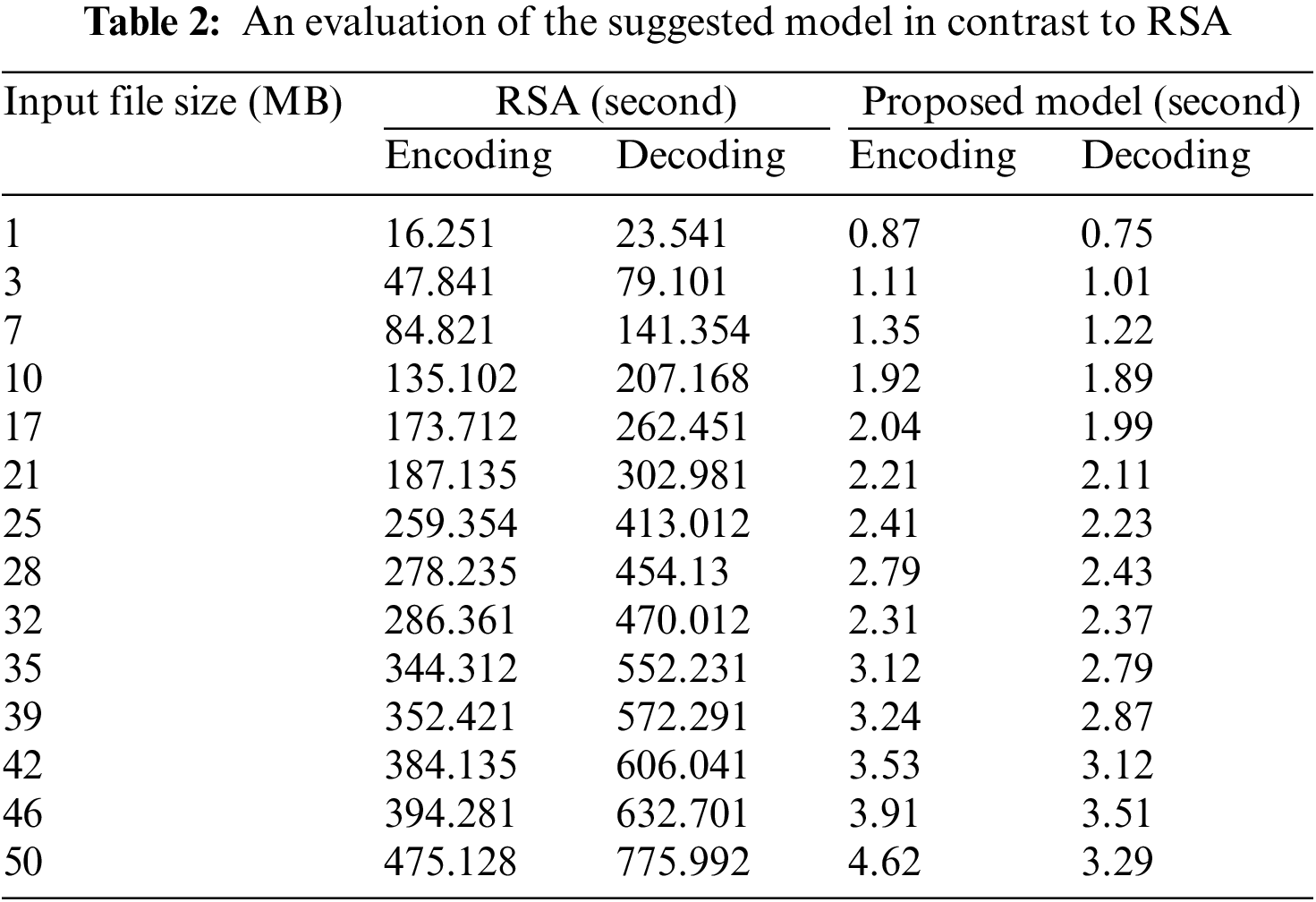
Fig. 6 presents a comparison of the proposed model’s encoding time with RSA, demonstrating that the proposed model’s encoding time is considerably shorter, resulting in a reduction of about 0.99% in the execution time of encoding on a file size of 50 MB. Additionally, the proposed model has been shown to outperform RSA, establishing its superiority over RSA in terms of efficiency.

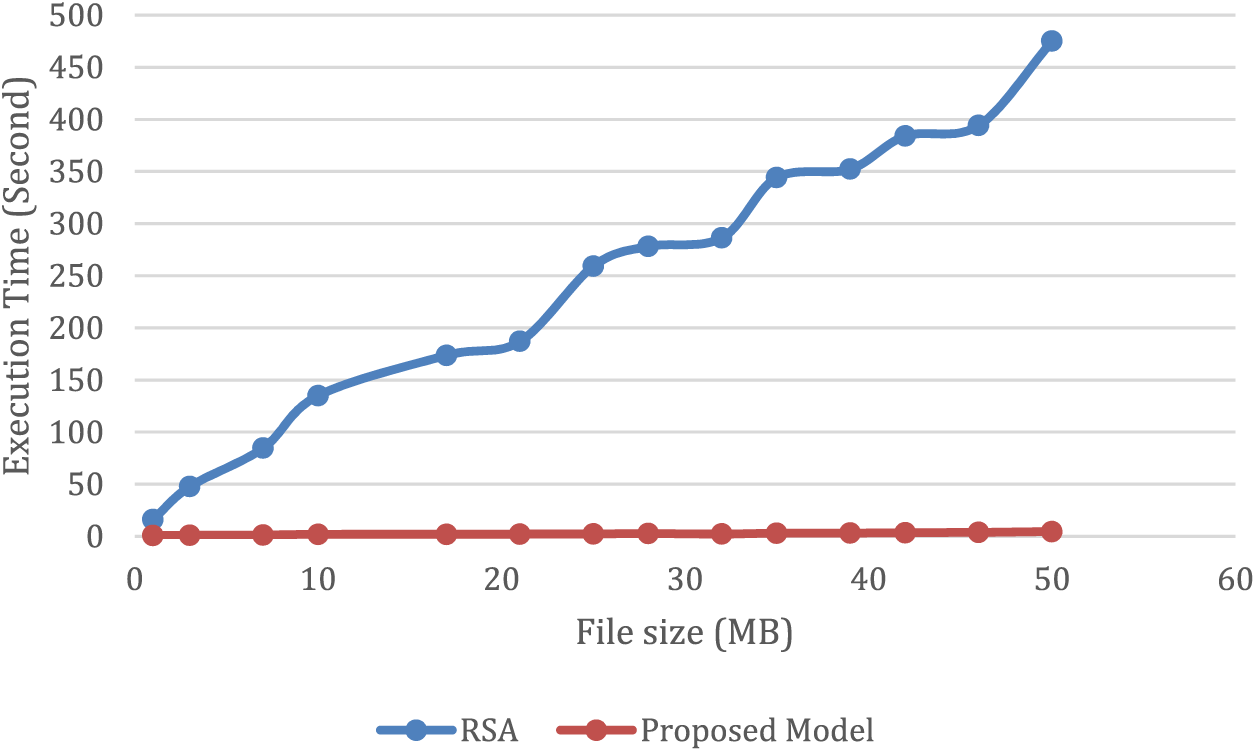
Figure 6: A comparison of the suggested model’s and RSA’s encoding times

Fig. 7 compares the decoding time between the proposed model and RSA, indicating that the proposed model outperforms RSA in terms of speed. RSA’s slower performance can be attributed to its computationally intensive encoding and decoding processes, which require modular exponentiation operations and private key exponent calculations, resulting in slower processing speed. Conversely, the proposed model requires fewer computations during its encoding and decoding processes, resulting in faster processing speeds when compared to RSA. The proposed model’s superior performance is therefore attributed to its reduced computational requirements.

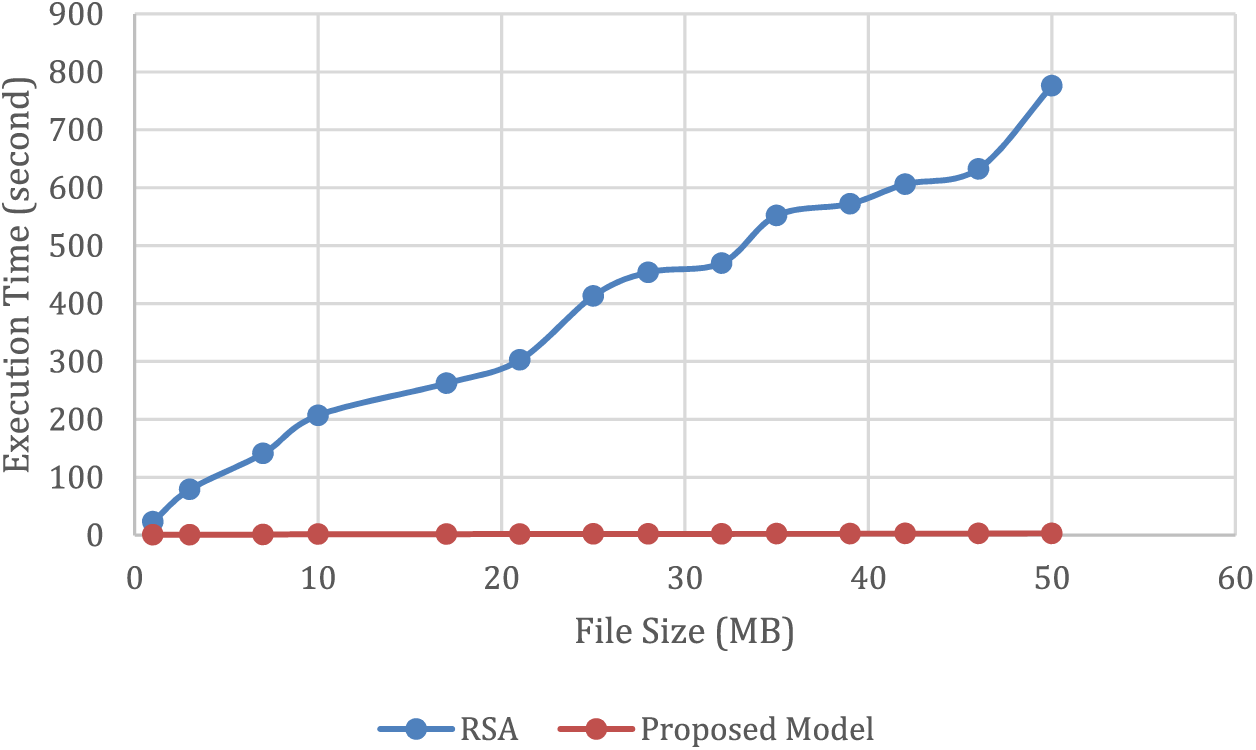
Figure 7: Evaluating the differences between the suggested model’s and RSA’s decoding times

In brief, the model suggested in this study surpasses AES-RSA in both encoding and decoding speed, thereby proving to be a more efficient and feasible alternative for cryptographic applications, particularly in situations with limited resources. The utilization of ECC in the suggested model curtails the computational burden, rendering it more rapid and well-suited for real-time scenarios. These advantages make the proposed model a promising solution for secure data communication.

5.2.3 Encoding and Decoding Based on GA, and Proposed Model

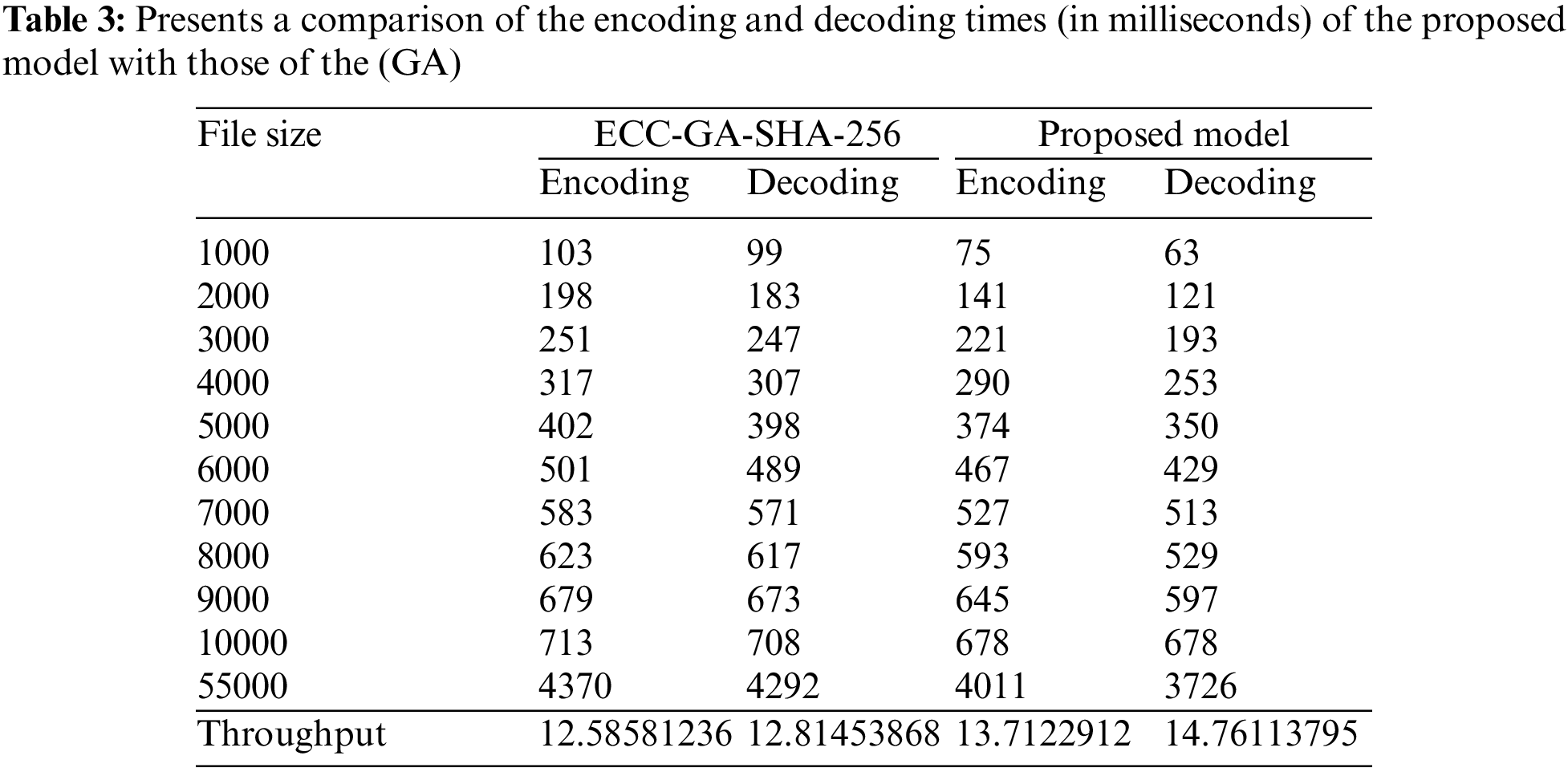
This section provides a comparative analysis of the metaheuristic Genetic Algorithm (GA) [25], combined with the proposed model for generating ECC keys. These algorithms utilize selection, crossover, and mutation operators to search for the optimal ECC solution. The results, presented in Table 3, indicate that the proposed CS algorithm outperforms GA in terms of encoding and decoding times, resulting in better solutions, search, and power convergence. Specifically, when encoding a 10,000 KB file, the proposed CS algorithm demonstrated faster encoding and decoding times than GA. ECC-GA-SHA-256 required 4370 ms for encoding and 4292 ms for decoding, while the proposed model exhibited encoding and decoding times of 4011 and 3726 ms, respectively.

The results presented in Figs. 8 and 9 offer additional evidence that the proposed model outperforms other methods in terms of both execution time and encoding efficiency. Thus, the proposed model is a superior choice when compared to existing techniques for generating ECC keys within the context of the CS algorithm. These findings strongly suggest that the implementation of the proposed CS algorithm leads to an increase in the security and efficiency of cryptographic systems.

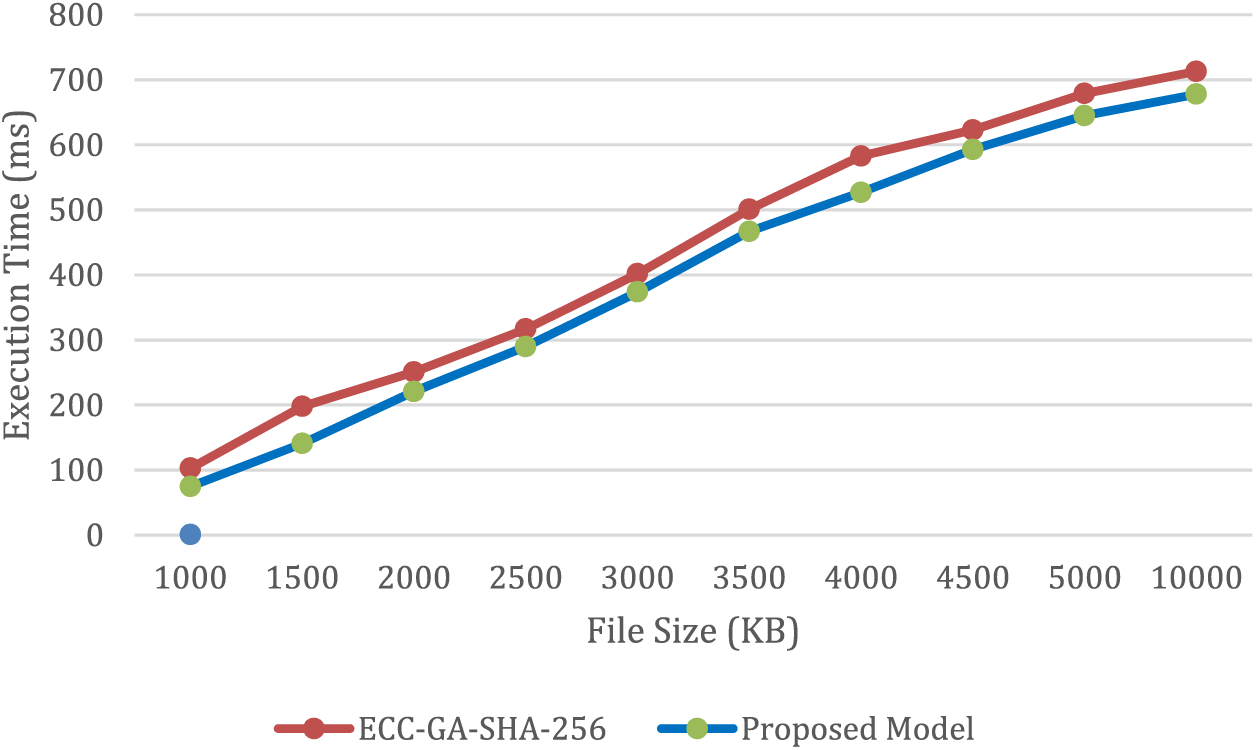
Figure 8: Illustrates a comparison of the encoding time between the proposed model and GA

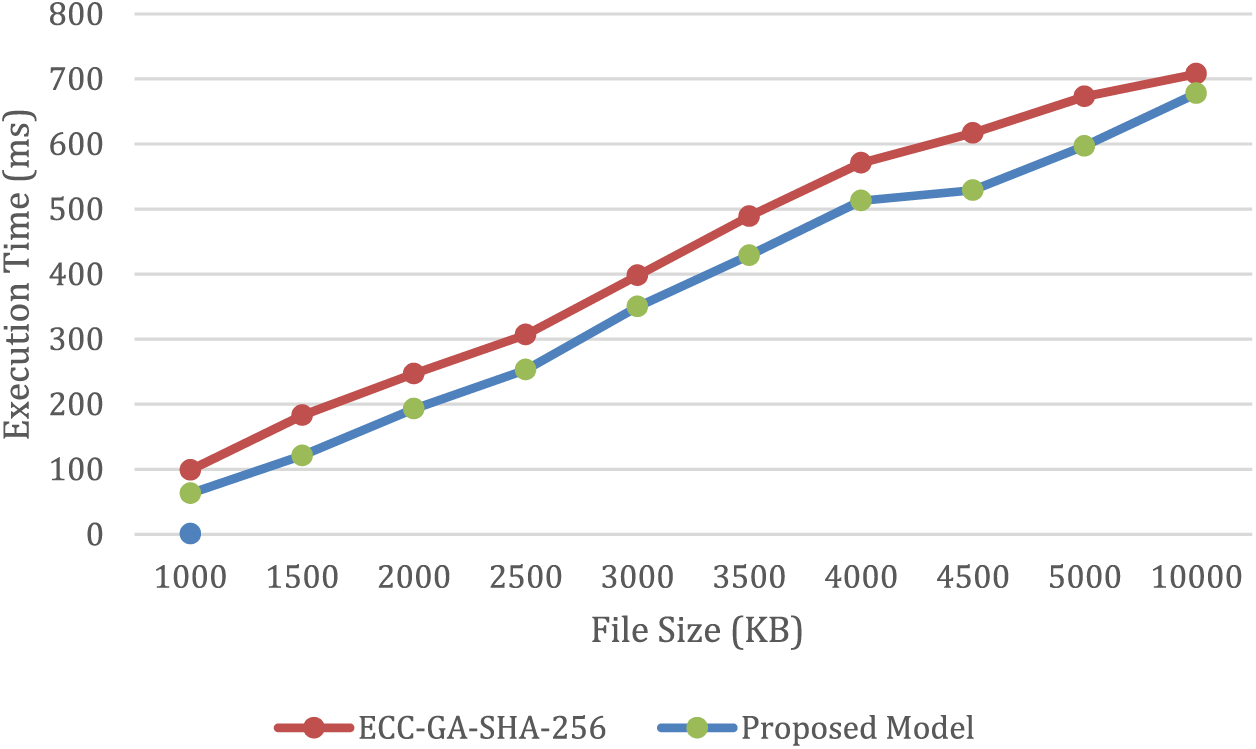
Figure 9: Illustrates a comparison of the decoding time of the proposed model with that of GA

5.3 Throughput

This investigation focused on examining the encoding and decoding capabilities of a proposed model, as measured by its speed, using Eqs. (7) and (8) [26], as the determining factors. A higher speed reading indicated a superior model. To assess the model’s effectiveness, a 55000 KB file was utilized for testing, and the resulting data was compared against that of the (ECC-GA-SHA-256) model. The proposed model demonstrated encoding and decoding throughputs of 13.71 and 14.76 ms, respectively, whereas the (ECC-GA-SHA-256) model exhibited encoding and decoding throughputs of 12.58 and 12.81 ms, respectively. Consequently, the proposed model outperformed the (ECC-GA-SHA-256) model, as well as the other comparison models, in terms of encoding and decoding speed.

Encoding Throughput =Σ(Input File)/Σ(Encoding Time)(7)

Decoding Throughput =Σ(Input File)/Σ(Decoding Time)(8)

According to the results, the proposed model demonstrated approximately 8.95% improvement in encoding throughput and 15.17% improvement in decoding throughput over the (ECC-GA-SHA-256) model. These outcomes reveal that the proposed model offers a significantly more efficient and effective approach to encoding and decoding data quickly and securely compared to the other models examined.

6  Conclusion and Future Works

In contemporary times, the availability of health information on the internet and mobile devices has increased significantly. However, maintaining the confidentiality of patients’ medical information remains a crucial concern when sharing it with healthcare professionals. Despite the convenience offered by electronic records and the internet for medical information sharing, concerns about data security persist. To ensure the safety of medical information, certain security methods prove more effective than others. This research paper introduced a novel approach to enhance the security of electronic health records (EHRS) by employing a combination of ECC, SHA-256, and the CS algorithm. The proposed approach demonstrates swiftness and efficiency, resulting in shorter encoding and decoding times. Through simulations, the study concludes that employing 75 iterations for encoding and 125 iterations for decoding yields optimal results. When compared to other techniques, the newly proposed method showcases a 15.17% increase in efficiency and offers robust protection against attacks. This makes it a suitable option for devices with limited resources. However, it is important to acknowledge the limitations of this study.

While this research provides valuable insights into enhancing EHR data security, it is important to note some limitations. Firstly, the evaluation and simulations were conducted under specific scenarios and assumptions. The performance and effectiveness of the proposed method may vary in different environments or real-world implementations. Additionally, the study focused on a specific set of security algorithms, and further exploration of alternative encryption and key generation methods could be beneficial.

Building upon this study, future research should investigate additional encoding techniques and novel approaches to creating private keys for EHRs. Exploring the integration of emerging technologies, such as blockchain or secure multi-party computation, could further enhance the security and privacy of electronic health records. Additionally, conducting real-world trials and assessments to evaluate the proposed method’s effectiveness in diverse healthcare settings would provide valuable insights and validate its practicality.

By addressing these limitations and pursuing these future directions, researchers can continue to advance the field of EHR security, ultimately ensuring the confidentiality, integrity, and accessibility of patients’ health information.

Acknowledgement: Grateful thanks to the Department of Mathematics, Open Educational College, Kirkuk Branch, and Mutafaweqat High School for Girls, Kirkuk Branch, for their invaluable support.

Funding Statement: The authors received no specific funding for this study.

Author Contributions: The authors confirm their contributions to the paper as follows: study conception and design: Arkan Kh Shakr Sabonchi, Zainab Hashim Obaid; data collection: Zainab Hashim Obaid; analysis and interpretation of results: Arkan Kh Shakr Sabonchi, Zainab Hashim Obaid; draft manuscript preparation: Zainab Hashim Obaid. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The data and materials utilized in this study are available upon request from the corresponding author, in compliance with the relevant data protection and privacy regulations. Due to confidentiality and ethical considerations, certain data may not be made publicly accessible. However, efforts have been made to ensure transparency and reproducibility, and interested researchers can contact the corresponding author to discuss access to the data within the bounds of ethical and legal restrictions.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. T. Seymour, D. Frantsvog and T. Graeber, “Electronic health records (EHR),” American Journal of Health Sciences (AJHS), vol. 3, no. 3, pp. 201–210, 2012. [Google Scholar]

2. R. Hoover, “Benefits of using an electronic health record,” Nursing, vol. 46, no. 7, pp. 21–22, 2016. [Google Scholar]

3. I. Keshta and A. Odeh, “Security and privacy of electronic health records: Concerns and challenges,” Egyptian Informatics Journal, vol. 22, no. 2, pp. 177–183, 2021. [Google Scholar]

4. P. M. Chanal and M. S. Kakkasageri, “Security and privacy in IOT: A survey,” Wireless Personal Communications, vol. 115, pp. 1667–1693, 2020. [Google Scholar]

5. X. S. Yang and S. Deb, “Cuckoo search via Lévy flights,” in 2009 World Congress on Nature & Biologically Inspired Computing (NaBIC), Coimbatore, India, pp. 210–214, 2009. [Google Scholar]

6. V. S. Miller, “Use of elliptic curves in cryptography,” in Conf. on the Theory and Application of Cryptographic Techniques, Berlin, Heidelberg, pp. 417–426, 1986. [Google Scholar]

7. H. Yoshida and A. Biryukov, “Analysis of a SHA-256 variant,” in 12th Int. Workshop: Selected Areas in Cryptography SAC, Kingston, Canada, pp. 245–260, 2005. [Google Scholar]

8. S. R. Prasanna and B. S. Premananda, “Performance analysis of MD5 and SHA-256 algorithms to maintain data integrity,” in 2021 Int. Conf. on Recent Trends on Electronics, Information, Communication & Technology (RTEICT), Bangalore, India, pp. 246–250, 2021. [Google Scholar]

9. H. Xiong, J. Tao and C. Yuan, “Enabling telecare medical information systems with strong authentication and anonymity,” IEEE Access, vol. 5, pp. 5648–5661, 2017. [Google Scholar]

10. A. Ara, M. Al-Rodhaan, Y. Tian and A. Al-Dhelaan, “A secure privacy-preserving data aggregation scheme based on bilinear ElGamal cryptosystem for remote health monitoring systems,” IEEE Access, vol. 5, pp. 12601–12617, 2017. [Google Scholar]

11. T. Liu, K. Lin and H. Wu, “ECG data encryption then compression using singular value decomposition,” IEEE Journal of Biomedical and Health Informatics, vol. 22, no. 3, pp. 707–713, 2018. [Google Scholar]

12. A. Shehab, M. Elhoseny, K. Muhammad, A. Sangaiah, P. Yang et al., “Secure and robust fragile watermarking scheme for medical images,” IEEE Access, vol. 6, pp. 10269–10278, 2018. [Google Scholar]

13. E. Luo, M. Z. A. Bhuiyan, G. Wang, M. A. Rahman, J. Wu et al., “PrivacyProtector: Privacy-protected patient data collection in IoT-based healthcare systems,” IEEE Communications Magazine, vol. 56, no. 2, pp. 163–168, 2018. [Google Scholar]

14. A. A. El-Latif, B. Abd-El-Atty, M. Hossain, M. Rahman, A. Alamri et al., “Efficient quantum information hiding for remote medical image sharing,” IEEE Access, vol. 6, pp. 21075–21083, 2018. [Google Scholar]

15. W. Yang, S. Wang, J. Hu, G. Zheng, J. Chaudhry et al., “Securing mobile healthcare data: A smart card based cancelable finger-vein bio-cryptosystem,” IEEE Access, vol. 6, pp. 36939–36947, 2018. [Google Scholar]

16. D. Abbasinezhad-Mood and M. Nikooghadam, “Efficient design of a novel ECC-based public key scheme for medical data protection by utilization of NanoPi fire,” IEEE Transactions on Reliability, vol. 67, no. 3, pp. 1328–1339, 2018. [Google Scholar]

17. B. Datta, P. Pal and S. Bandyopadhyay, “Audio transmission of medical reports for visa processing: A solution for the spread of communicable diseases by the immigrant population,” IEEE Consumer Electronics Magazine, vol. 7, no. 5, pp. 27–33, 2018. [Google Scholar]

18. M. Boussif, N. Aloui and A. Cherif, “Secured cloud computing for medical data based on watermarking and encryption,” IET Networks, vol. 7, no. 5, pp. 294–298, 2018. [Google Scholar]

19. D. W. Sims, D. Righton and J. W. Pitchford, “Minimizing errors in identifying Lévy flight behaviour of organisms,” Journal of Animal Ecology, vol. 76, no. 2, pp. 222–229, 2007. [Google Scholar]

20. P. Lévy, “Théorie de l’addition des variables aléatoires,” Bulletin De La Société Mathématique De France, vol. 67, pp. 1–41, 1939. [Google Scholar]

21. X. S. Yang and S. Deb, “Engineering optimisation by cuckoo search,” International Journal of Mathematical Modelling and Numerical Optimisation, vol. 1, no. 4, pp. 330–343, 2010. [Google Scholar]

22. M. Conti, N. Dragoni and V. Lesyk, “A survey of man in the middle attacks,” IEEE Communications Surveys & Tutorials, vol. 18, no. 3, pp. 2027–2051, 2016. [Google Scholar]

23. L. Zou, M. Ni, Y. Huang, W. Shi and X. Li, “Hybrid encryption algorithm based on AES and RSA in file encryption,” in Frontier Computing: Theory, Technologies and Applications (FC 2019). Singapore: Springer, pp. 541–551, 2020. [Google Scholar]

24. M. Bafandehkar, S. M. Yasin, R. Mahmod and Z. M. Hanapi, “Comparison of ECC and RSA algorithm in resource constrained devices,” in 2013 Int. Conf. on IT Convergence and Security (ICITCS), Macao, China, pp. 1–3, 2013. [Google Scholar]

25. J. H. Holland, “Genetic algorithms,” Scientific American, vol. 267, no. 1, pp. 66–73, 1992. [Google Scholar]

26. A. Lemma, M. Tolentino and G. Mehari, “Performance analysis on the implementation of data encryption algorithms used in network security,” International Journal of Computer and Information Technology, vol. 4, no. 4, pp. 711–717, 2015. [Google Scholar]