Research on the Electric Energy Metering Data Sharing Method in Smart Grid Based on Blockchain

1  Introduction

Smart grid is to achieve the goal of reliability, safety, economy and efficiency through the application of advanced sensing and measurement technology, control methods and decision support system technology [1,2]. The U.S. Department of Energy’s “Grid 2030” emphasizes: a fully automated power transmission network that can monitor and control each user and grid node to ensure the information and electrical energy between all nodes in the entire transmission and distribution process from the power plant to the end user Two-way flow [3]. In the big data environment, the electric energy metering device in the smart grid will generate a large amount of data information [4]. Electric energy measurement is not only the basic technical support and basic data source for power market transactions and marketing, but also the basic data source for production technology units to judge whether the equipment is operating economically. Researchers can analyze whether the loss of power grid equipment such as power transformers in operation exceeds the allowable value through accurate measurement and calculation, and process or replace high-loss power grid equipment to reduce the unit energy consumption of the enterprise [5]. However, various data information of the power grid is intricate and complicated, and the management of electric energy metering big data faces new challenges. Due to the isolation of isolated microgrids and different standards, the data between various departments has always lacked effective integration, resulting in the formation of “data islands”, and a large number of valuable data resources cannot play a greater role [6]. How to achieve credible sharing of energy metering data is an important challenge in the development of smart grids.

2  Progress of Research

The last ten years, owing to its characteristics of decentralization, anonymity and trust, blockchain technology has attracted growing attention and research work in the context of smart grid [7,8]. The emerging blockchain can establish a stable trust system between participants, and the distributed ledger ensures that all data and operating processes on the chain are open and transparent [9,10]. Blockchain can promote the establishment of a safe, credible and decentralized smart grid ecosystem and solve the problem of data sharing [11].

The traditional principal-agent architecture commonly used in federated learning is not efficient and does not prioritize privacy protection and trustworthiness. Zhou et al. [12] suggested using blockchain technology to address these challenges. They propose an autonomous and reliable federated extreme gradient boosting learning algorithm (FedXGBoost) to crack the data isolation problem and provide privacy protection and verifiability. They also introduce a secure and trusted data sharing and trading mechanism that ensures secure on-demand controlled data sharing and fair trading. However, the model does not take into account the differences in the relationships and identities of the different participants, leading to possible problems in their allocation of entitlements. The model does not set out detailed rules for this situation.

Wu et al. [13] presented detailed data exchange protocols for data insertion and retrieval operations in MapChain-D and provides theoretical analyses of its space, time, and communication complexities compared to conventional single-chain frameworks. The authors implemented a prototype of MapChain-D using open-source communication protocols and blockchain platforms and show that it is more suitable for resource-constrained IIoT devices. Isaja et al. [14] designed a heterogeneous encrypted data sharing scheme supported by blockchain, which is used for tucker decomposition to protect privacy when the homomorphic encryption method extracts knowledge.

Feng et al. [15] emphasized the significance of data analysis and the sharing of data between stakeholders in order to achieve greater values. The document introduces the concept of a Product-Process-Data (PPD) quality hallmark and a distributed ledger-based Trusted Framework (TF) to address these challenges. It proposes the use of blockchain technology to ensure trustworthy and traceable quality data sharing in the product supply chain. However, it is worth noting that the article mainly focuses on the theoretical aspects of their blockchain-based framework for trusted quality data sharing towards zero-defect manufacturing. The document provides a proof-of-concept for publishing quality data, but there is no discussion on the practical implementation or challenges that may arise during the implementation process. Additionally, while the article highlights the importance of data analysis and the sharing of data between stakeholders, it does not delve into potential privacy or security concerns that may arise when sharing sensitive data using blockchain technology.

These research results provide new ideas for the wide application of blockchain, and also provide a safe and reliable method for data sharing in smart grids.

Research on data sharing of smart grid, mining the effective value of big data, breaking data islands is an effective way to improve the efficiency of smart grid operation. In this article, we propose a blockchain-based smart grid energy metering data sharing architecture to ensure the security of data sharing. Furthermore, we propose a data sharing model based on evolutionary games. The main contributions are as follows:

1) We propose a blockchain-based grid data sharing architecture. The architecture makes full use of the advantages of blockchain decentralization and de-trust, and establishes a Pointer-to-Pointer (P2P) network-based transaction model between data providers and data demanders, and promotes the interconnection of grid data.

2) We propose a data sharing model based on dynamic evolutionary game theory. We have established a value rule for data transactions and proposed a piecewise function whose value changes with the volume of transactions. The evolutionary game model between data providers and data demanders is further constructed. The conditions of the optimal stable strategy of the data provider are analyzed. The platform can formulate rules based on this condition to motivate the data owner to analyze the data.

The remainder of this paper is organized as follows. In Section 2, we introduce the system model. Section 3 establishs data sharing based on evolutionary game model. In Section 4, we evaluate the performance of data sharing model. Finally, Section 6 concludes this paper.

The subsequent sections of this paper are meticulously structured to present a comprehensive understanding of the proposed framework. Section 2 provides an in-depth exposition of the system model, elucidating its fundamental components and intricacies. In Section 3, we expound upon the establishment of data sharing, leveraging an evolutionary game model to underpin the conceptual framework. Building upon this foundation, Section 4 undertakes a rigorous evaluation of the performance exhibited by the data sharing model, probing its efficacy, reliability, and efficiency through empirical analysis. Conclusively, Section 6 synthesizes the findings and discussions, encapsulating the essence of this research endeavor and charting potential avenues for future exploration.

3  System Model

Blockchain has the main advantages of decentralization, trustlessness, traceability, collective maintenance, security and non-tampering, openness, anonymity, etc. We propose a smart grid energy metering data sharing system model based on blockchain technology, see Fig. 1 below. Data providers mainly include power supply enterprises and users. Data demanders mainly include colleges and universities, academies, and government departments. Data providers sell data to data demanders as a research basis. Through effective analysis of data, researchers can ensure uninterrupted production, sales and service levels at the lowest cost, thereby improving the management level of power supply companies. Advanced data analysis technology can improve the productivity and efficiency of power plant operation activities, and can optimize energy according to business and customer needs. Data demanders and power supply companies, as strong nodes of the blockchain, keep complete data and transaction records. Due to their weak storage and computing capabilities, individual users, as light nodes of the blockchain, only provide data, and do not store data and transaction records.

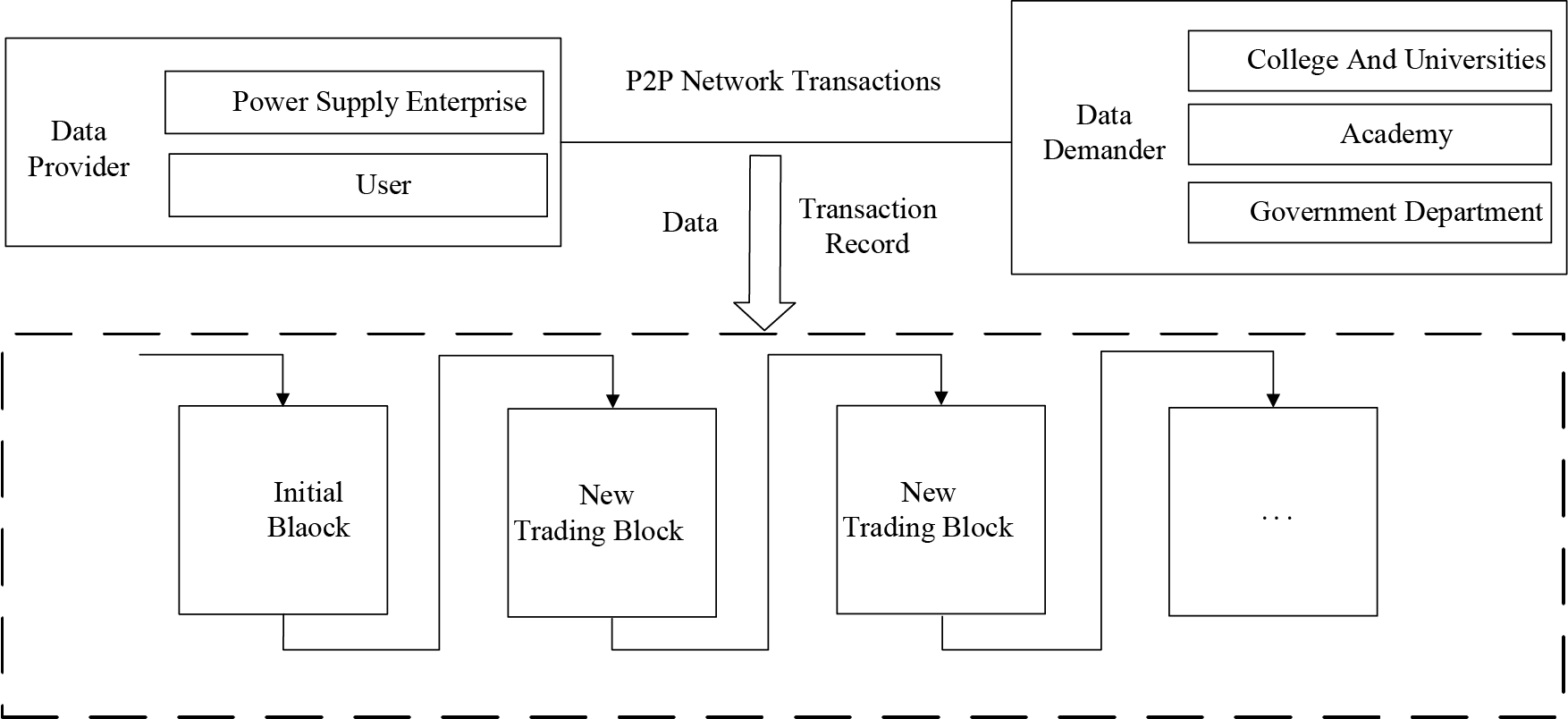
Figure 1: System model

Blockchain-based data transactions are carried out on the P2P network, and the process is as follows:

1.    First, the data provider creates a new transaction and makes a transaction order.

2.    Second, the data provider broadcasts the new data record to the entire network.

3.    Third, the receiving node records and verifies the integrity of the received the electric energy metering data.

4.    Fourth, all accepting nodes in the entire network execute a consensus algorithm on the block.

5.    Fifth, the block is officially included in the blockchain for storage after passing the consensus algorithm process, and all strong nodes keep complete transaction records.

Data owners can adopt two trading strategies: sharing data or not sharing data. Shared data means that the data is provided to the blockchain platform, and all strong nodes that join the shared platform can download and save the data. Similarly, data demanders also have two strategies, join a shared platform, or buy data directly. We aim to establish a suitable sharing mechanism, promote the interconnection of data, provide the most basic data source for enterprise optimization and scientific research, and give play to the potential value of data.

4  Data Sharing Based on Evolutionary Game Model

Evolutionary game theory was first introduced by biology. In traditional game theory, the strategy of a rational person is to choose a strategy from the perspective of maximizing benefits, while the strategy in biological phenomena is determined by genes. In the long-term natural selection process, genes suitable for survival undergo continuous self-replication, and through continuous reproduction and adaptation, the stable survival of genes gradually determines the behavior of individual organisms. This stable behavior is ESS. The actors in traditional game theory are completely rational. Generally, under the assumption of complete rationality, if the Nash equilibrium exists, then the two sides of the game can directly reach the Nash equilibrium in one game. This result does not depend on the initial state of the market, so there is no need for any dynamic adjustment process. On the contrary, the evolutionary game theory believes that the Nash equilibrium should be reached after multiple games, and a dynamic adjustment process is required. The achievement of the equilibrium depends on the initial state and path. Next, we have to establish data trading rules.

The value growth of data is related to the amount of investment of data producers [16]. Generally, the utility reward to the data producer is dependent only on its investment, which can be written as the variant of logarithmic function alog(1+x), where x is the amount of investment made and a Is a scale factor [17]. Without loss of generality, let us take a=2 as an example and draw the curve of the utility reward with the investment amount, see Fig. 2 below. The variant of logarithmic function, which reflects the trend of income changes with the amount of investment is first fast and then slow, and then tends to be basically saturated. This macro trend is in line with the general law that returns change with investment.

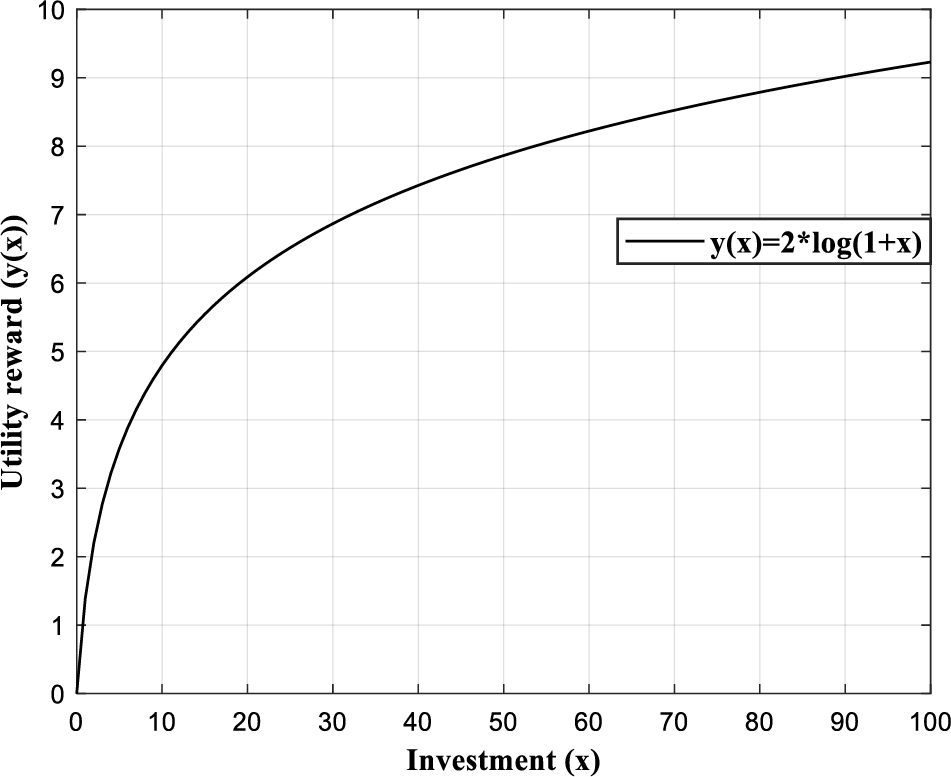
Figure 2: The curve of the utility reward with the investment amount

In this paper, we propose a new trading rule that revenue depends on the amount of data. The specific functional relationship expression is as follows:

f(x)={k1x+b1,[x1,x2),k2x+b2,[x2,x3),k3x+b3,[x3,x4),(1)

where b1, b2, and b3 are positive numbers, and 0<k1<k2<k3. The function graph can be seen in Fig. 3 below.

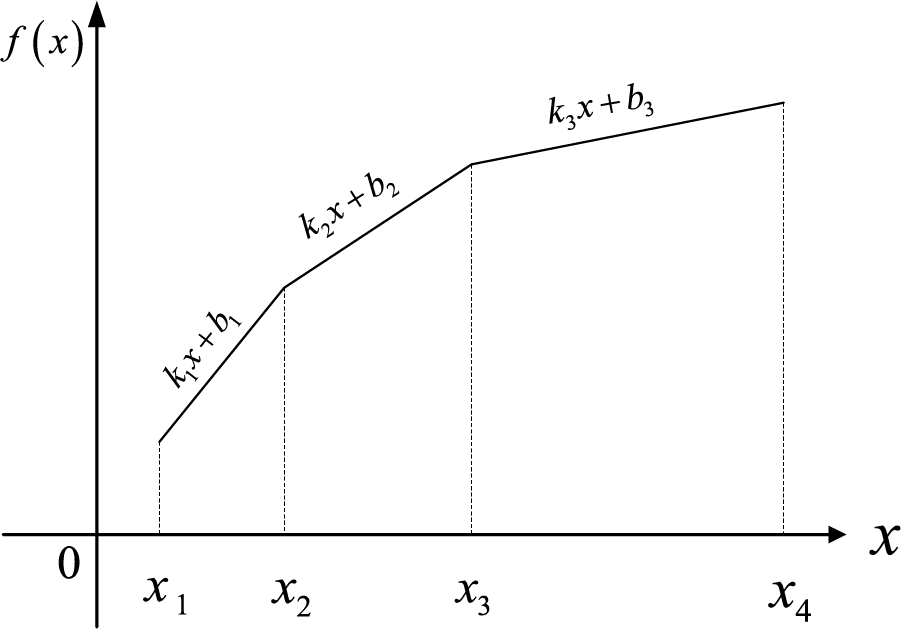
Figure 3: Data value function

The value growth of data is mainly divided into three stages. The first stage has the largest growth rate, which aims to encourage data providers to provide more valuable data. The value growth in the second stage is relatively flat, but there is still a way to ensure that the data owner is profitable. The third stage of growth is particularly slow and belongs to the saturation period. In summary, income will not increase rapidly with the increase in transaction volume, it should be fast first, then slow, and then tend to be saturated. In particular, the data volume of a single transaction must be within an upper limit. For example, the platform stipulates that data greater than a certain threshold x4 will not be traded. Data providers can split large data packets into small data packets for multiple transactions, which can alleviate the bandwidth pressure caused by data transmission. In addition, notice that when the amount of data is less than the threshold x1, the platform also refuses to trade.

In order to promote the sharing of smart grid data, we establish sharing rules with reward factors. For data providers, they can trade data with a sharing strategy, and the benefits is af(x)−c, where α is the sharing gain coefficient and c is the cost of joining the sharing platform. For data demanders, they can also freely choose whether to join the sharing platform. If the data demander joins the sharing platform, it can download and store all transaction data to realize resource sharing. If the data demander does not join the sharing platform, then they only need to buy the data that they are most interested in. In particular, if both the data provider and data demander in a transaction join the sharing platform, the platform will give both parties economic rewards δ. Under such trading rules, in view of the dynamic evolutionary game theory [18], we give the payoff matrix of data transactions as follows, see Table 1.

We assume that there is a total of N data provider nodes in the network, and we mainly study the evolutionary game model between this N data owner nodes. Data providers can adopt two strategies: S1 (Participate and Share) and S2 (Not Participate). We assume p1 and p2 are the proportions of total N population taking strategies S1 and S2, respectively, p1+p2=1, we assume that the proportion of data needs to adopt different strategies is also the same. Letting E[Ush] is the expected utility of a player for participating and sharing, E[Uno] is the expected utility of a player for not participate, then we can get

E[Ush]=p1(αf(x)−c+δ)+p2(f(x)−c), E[Uno]=f(x)(2)

Further, we can calculate the average utility of the data providers

E[Ush]=p1(αf(x)−c+δ)+p2(f(x)−c)(3)

E[Uno]=f(x)=(αf(x)−c+δ)p12+(f(x)−c)p1p2+f(x)p2

According to dynamic evolutionary game theory [19], we can get the dynamic equation of replication of data providers under different strategies as

dp1dt=p1[E(Ush)−E(Uavg)](4)

dp2dt=p2[E(Uno)−E(Uavg)]

That is

dp1dt=p1[(αf(x)−c+δ)p12+p1((c−f(x))p2+αf(x)−c+δ)−cp2]=g1(p1,p2)(5)

dp2dt=p2[(−αf(x)+c−δ)p12+(c−f(x))p1p2−p2f(x)+f(x)]=g2(p1,p2)

In order to obtain the EES that replicator dynamics equations, we first solve its equilibrium.

Let g1(p1,p2)=g2(p1,p2)=0, Eq. (5) with up to three stable states, which are

E0=(1,0),E1=(0,1)(6)

E2=(cf(x)α+α−f(x),f(x)α+α−f(x)−cf(x)α+α−f(x))

Regarding the EES that replicator dynamics equations, we have the following theorem:

Theorem 1 For the replicator dynamics equations, the following conclusions hold:

1) If the conditions c<f(x)+δ and c+f(x)<f(x)α+δ are satisfied, then the no participate strategy is EES for data providers;

2) If the conditions c>0 and f(x)>0 are satisfied, then the no Participate strategy is EES for data providers.

Proof: We can calculate the Jacobian matrix of the replicator dynamics equations at any point as follows:

J|(p1,p2)=[∂g1(p1,p2)∂p1∂g1(p1,p2)∂p2∂g2(p1,p2)∂p1∂g2(p1,p2)∂p2](7)

where

∂g1(p1,p2)∂p1=3p12(c−f(x)α−δ)−cp2+p1(−c+f(x)α+δ+(c−f(x))p2)(8)

∂g1(p1,p2)∂p2=p1(p1(c−f(x))−c)

∂g2(p1,p2)∂p1=p1(2p1(c−f(x)α−δ)+p2(c−f(x)))

∂g2(p1,p2)∂p2=p12(c−f(x)α−δ)−2(c−f(x))p1p2−2f(x)p2+f(x)

In view of the Jacobian matrix, we can get the Jacobian matrix at the three stable states as follows:

J|(1,0)=[c−f(x)−δ−f(x)0c+f(x)−f(x)α−δ], J|(1,0)=[−c0c−f(x)−f(x)](9)

J|(cf(x)α+α−f(x),f(x)α+α−f(x)−cf(x)α+α−f(x))=

[c(c2+c(f−2f(x)α−2δ)+(f(x)(α−1)+δ)2)(f(x)(α−1)+δ)2c2(c−f(x)α−δ)(f(x)(α−1)+δ)2(f(x)(α−1)−c+δ)(f(x)(α−1)−c2+δ)(f(x)(α−1)+δ)2c3+f(x)(f(x)(α−1)+δ)2−c2(f(x)α+δ)(f(x)(α−1)+δ)2].

To demonstrate stability of stable states mathematically, we must show that the eigenvalues of the corresponding Jacobian matrix have negative real part. We need to solve the eigenvalues of these three matrices. Obviously, the matrices J|(1,0) and J|(0,1) are upper and lower triangular matrices, respectively, so the eigenvalues of J|(1,0) are c−f(x)−δ and c+f(x)−f(x)α−δ, and the eigenvalues of J|(0,1) are −c and −f(x). In addition, in our shared architecture, the cost can be positive or negative. If the cost is negative, it is a disguised incentive measure. Obviously, the conclusion in the theorem is correct. The stability of the positive equilibrium point is too complicated, we will not discuss it. The proof is completed.

Realizing data sharing make more users use of existing data resources, reduce duplication of labor and corresponding costs such as data collection, and focus on the development of novel applications and system optimization.

In Theorem 1, we obtain the sufficient condition that the equilibrium point (1,0) is EES. This condition involves three factors, the cost of joining the platform, sharing gains, sharing rewards. Reducing sharing costs, increasing sharing gains and sharing rewards are effective ways to motivate data owners to sharing data. In addition, the introduction of blockchain technology has fully guaranteed the security, traceability and other advantages of grid data sharing. In the next section, we will use numerical simulation to verify the effectiveness of the sharing model in this paper.

5  Numerical Results

We mainly verify the correctness of the conclusion in Theorem 1, i.e., verify that the dynamic evolutionary game converges to different EES under different conditions. Note that there are three key parameters in the dynamic evolution game model, the cost of joining the platform, sharing gains, and sharing rewards. Shared gain is generally determined by the platform and the market, and is relatively stable. Here, we take a=1.2, which means that sharing data can increase revenue for data providers by 20%. The cost of participating in the platform and reward factor will be determined later as two dynamically quantities. In particular, in our evolutionary game model, revenue and data transaction volume satisfy a unique functional relationship. As an example, without loss of generality, we take f(x)=10.

See Fig. 4 below, we simulated the average utility in which data owners participate in sharing under four different conditions. In the first group, we take c=−4 and δ=2, which means that you do not need to pay for participating in the sharing platform, but you can get rewards. Under this mechanism, it is clear that the average utility of sharing strategies are greater than those of non-sharing strategies. Therefore, the equilibrium (1,0) is the EES of the evolutionary game model, see Fig. 5 below. For the second group, we take c=0 and δ=2. Although the cost and reward are equal, but, the reward and gain can only be obtained under certain probability conditions. Therefore, what kind of strategy an individual adopts needs to be observed, and it needs to refer to the behavior of other players to determine its own behavior and make it possible to obtain the best benefits. Under this condition, the initial value condition also affects the final convergence state of the model. The third group: we take c=0 and δ=0, it means that the benefits obtained under the two different strategies are the same. The fourth group: we take c=6 and δ=2. Since the reward is greater than the cost, the data owner adopts a shared data strategy to obtain the optimal benefit. Fig. 6 below shows the evolution of population dynamics under this condition. The equilibrium (1,0) is EES of model.

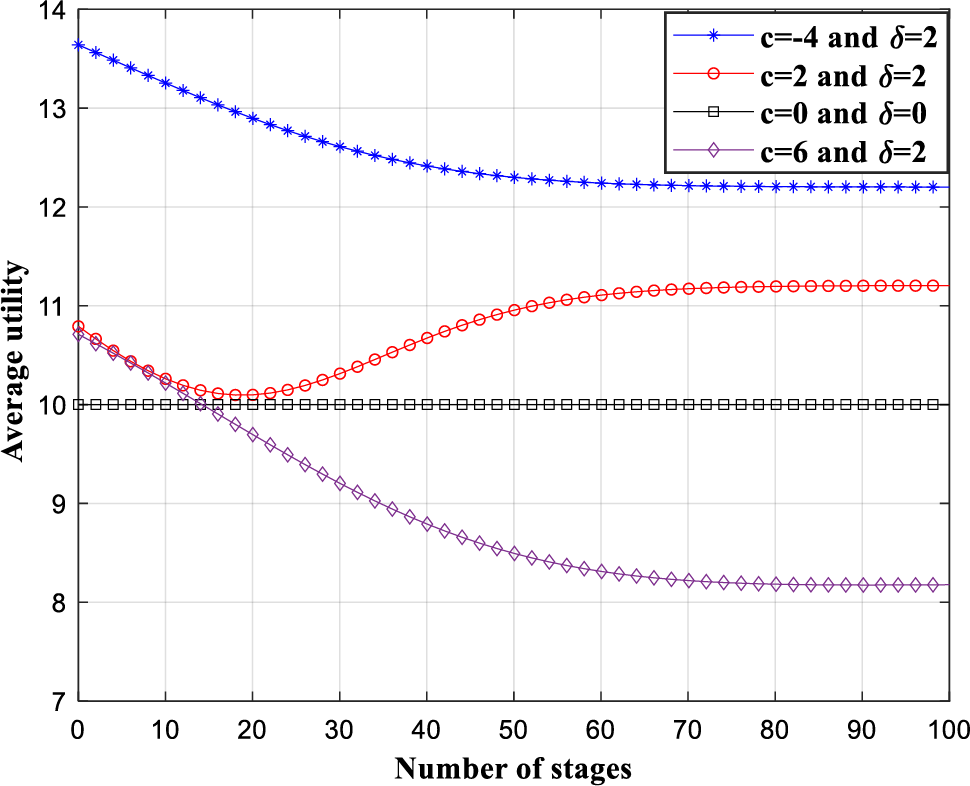
Figure 4: Average utility of participating population under different conditions

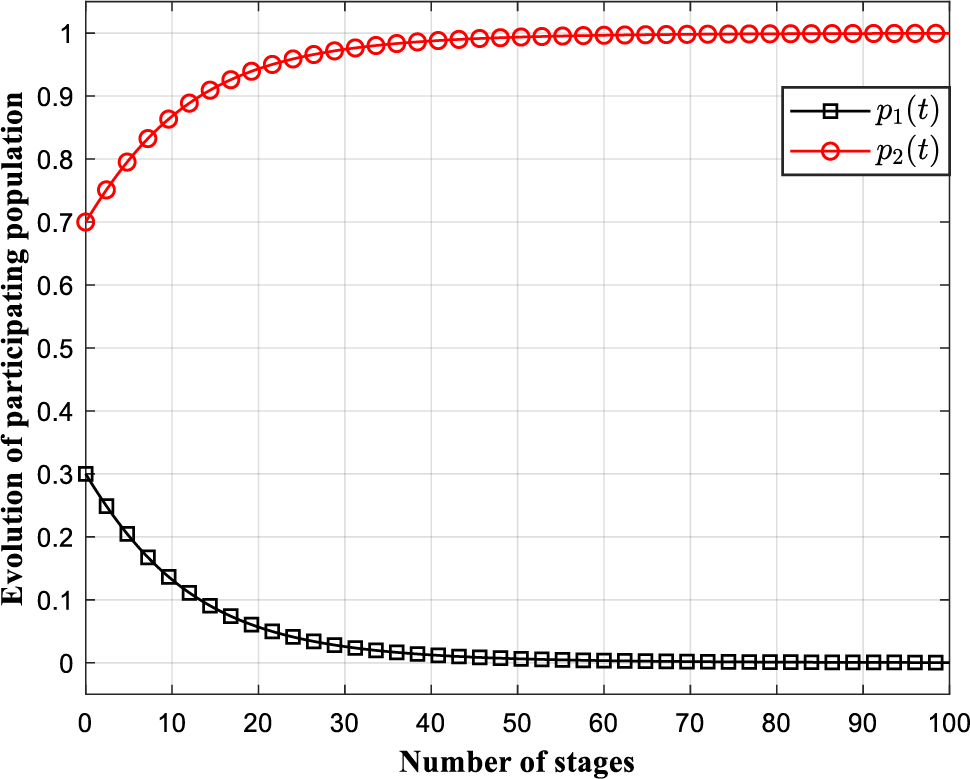
Figure 5: Evolution dynamics of participating population

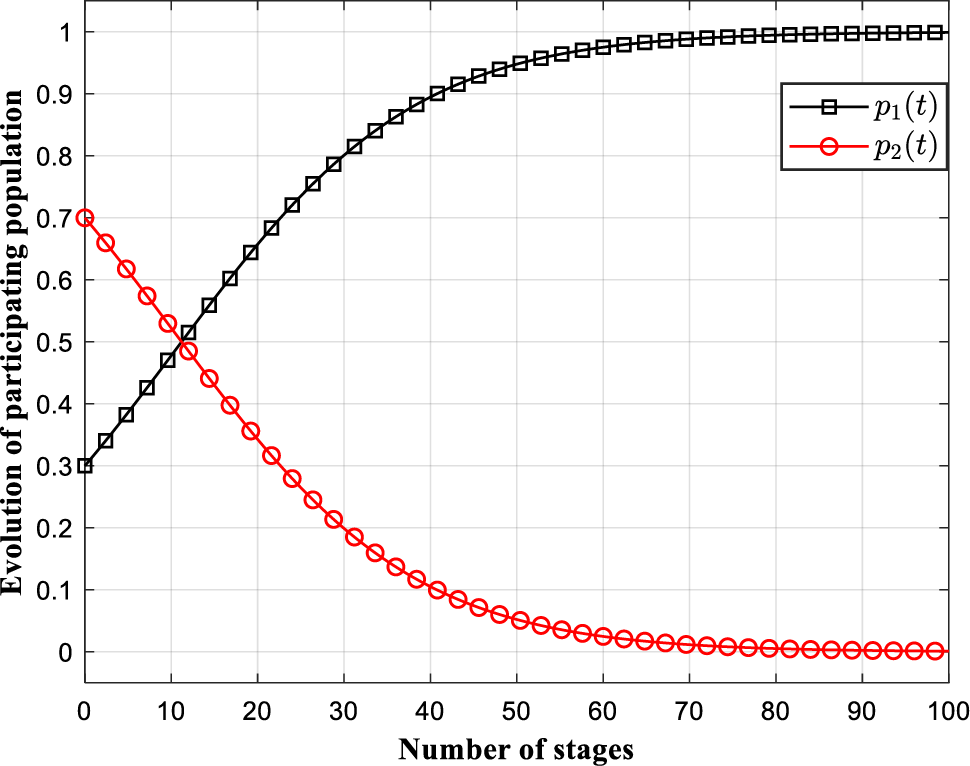
Figure 6: Evolution dynamics of participating population

6  Conclusion

The smart grid embodies the remarkable characteristics of a high degree of integration of power flow, information flow and business flow. The main advantage of the smart grid is to achieve high integration, sharing and utilization of real-time information, and to display a comprehensive, complete and refined grid operation state diagram for operation management. Therefore, the realization of data sharing is a necessary condition for the development of smart grid. In the current smart grid environment, in this paper, we proposed an energy metering data sharing architecture based on blockchain technology. We analyzed the growth law of data value and constructed a piecewise function to describe the growth of data value with the change of transaction volume. Further, we proposed a data sharing model based on evolutionary game theory. Applying the Lyapunov stability theory, the sufficient conditions of the EES for data providers are obtained. Numerical results show that the scheme studied in this paper has application value.

Acknowledgement: None.

Funding Statement: The authors received no specific funding for this study.

Author Contributions: Conceptualization, SCW; methodology, HHL; validation, XWC; formal analysis, TL; investigation, JPR; writing—original draft preparation, JL; writing—review and editing, QHG; supervision, PZ. All authors read and approved the fnal manuscript.

Availability of Data and Materials: The authors do not provide supplementary data and material.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. G. Dileep, “A survey on smart grid technologies and applications,” Renewable Energy, vol. 146, pp. 2589–2625, 2020. [Google Scholar]

2. J. Tsai and N. Lo, “Secure anonymous key distribution scheme for smart grid,” IEEE Transactions on Smart Grid, vol. 7, no. 2, pp. 906–914, 2016. [Google Scholar]

3. D. Bugden and R. Stedman, “Unfulfilled promise: Social acceptance of the smart grid,” Environmental Research Letters, vol. 16, no. 3, pp. 1–10, 2021. [Google Scholar]

4. L. Fan, J. Li, Y. Pan, S. Wang, C. Yan et al., “Research and application of smart grid early warning decision platform based on big data analysis,” in 2019 4th Int. Conf. on Intelligent Green Building and Smart Grid (IGBSG), Hubei, China, pp. 645–648, 2019. [Google Scholar]

5. M. H. Yaghmaee and H. Hejazi, “Design and implementation of an Internet of Things based smart energy metering,” in 2018 IEEE Int. Conf. on Smart Energy Grid Engineering SEGE, Oshawa, ON, Canada, pp. 191–194, 2018. [Google Scholar]

6. F. Guzzi, D. Neves and C. A. Silva, “Integration of smart grid mechanisms on microgrids energy modelling,” Energy, vol. 129, no. 15, pp. 321–330, 2017. [Google Scholar]

7. H. Hui, X. An, H. Wang, W. Ju, H. Yang et al., “Survey on blockchain for Internet of Things,” Journal of Internet Services and Information Security, vol. 9, no. 2, pp. 1–30, 2019. [Google Scholar]

8. A. Davenport and S. Shetty, “Air gapped wallet schemes and private key leakage in permissioned blockchain platforms,” in 2019 IEEE Int. Conf. on Blockchain (Blockchain), Atlanta, GA, USA, pp. 541–545, 2019. [Google Scholar]

9. F. D. Giraldo, C. B.Milton and C. E. Gamboa, “Electronic voting using blockchain and smart contracts: Proof of concept,” IEEE Latin America Transactions, vol. 18, no. 10, pp. 1743–1751, 2020. [Google Scholar]

10. Y. Qu, S. R. Pokhrel, S. Garg, L. Gao and Y. Xiang, “A blockchained federated learning framework for cognitive computing in Industry 4.0 networks,” IEEE Transactions on Industrial Informatics, vol. 17, no. 4, pp. 2964–2973, 2021. [Google Scholar]

11. F. Zhang, X. Li, Y. Li, S. Zhang, H. Yu et al., “Blockchain-enabled secure and transparent cross-regional model updating and sharing approach in smart grid,” in IEEE 10th Data Driven Control and Learning Systems Conf. (DDCLS), Suzhou, China, pp. 959–963, 2021. [Google Scholar]

12. Z. Zhou, Y. Tian, J. Xiong, J. Ma and C. Peng, “Peng blockchain-enabled secure and trusted federated data sharing in IIoT,” IEEE Transactions on Industrial Informatics, vol. 19, no. 5, pp. 6669–6681, 2022. [Google Scholar]

13. T. Wu, G. Jourjon, K. Thilakarathna and P. L. Yeoh, “MapChain-D: A distributed blockchain for IIoT data storage and communications,” IEEE Transactions on Industrial Informatics, vol. 19, no. 9, pp. 9766–9776, 2023. [Google Scholar]

14. M. Isaja, P. Nguyen, A. Goknil, S. Sen, J. E. Husom et al., “A blockchain-based framework for trusted quality data sharing towards zero-defect manufacturing,” Computers in Industry, vol. 146, pp. 103853, 2023. [Google Scholar]

15. J. Feng, L. T. Yang, R. Zhang and B. S. Gavuna, “Privacy-preserving tucker train decomposition over blockchain-based encrypted industrial IoT data,” IEEE Transactions on Industrial Informatics, vol. 17, no. 7, pp. 4904–4913, 2021. [Google Scholar]

16. P. D. Taylor and L. B. Jonker, “Evolutionary stable strategies and game dynamics,” Mathematical Biosciences, vol. 40, no. 1, pp. 145–156, 1978. [Google Scholar]

17. S. Sengupta and M. Chatterjee, “An economic framework for dynamic spectrum access and service pricing,” IEEE/ACM Transactions on Networking, vol. 17, no. 4, pp. 1200–1213, 2009. [Google Scholar]

18. D. Tosh, S. Sengupta, C. A. Kamhoua and K. A. Kwiat, “Establishing evolutionary game models for cyber security information exchange (cybex),” Journal of Computer and System Sciences, vol. 98, pp. 27–52, 2018. [Google Scholar]

19. J. Hofbauer and K. Sigmund, “Evolutionary game dynamics,” Bulletin of the American Mathematical Society, vol. 40, no. 4, pp. 479–519, 2003. [Google Scholar]