Continuous Monitoring of Multi-Robot Based on Target Point Uncertainty

1  Introduction

Multi-robot continuous monitoring is a typical multi-robot cooperative task that appears in many practical monitoring applications, such as border patrol, monitoring, search and rescue in disaster areas, and visits and monitoring of important areas.

At present, continuous monitoring by multi-robots has aroused widespread concern in the field of robot research. Kobayashi et al. [1] proposed that multi-robot patrolling is the potential application to robotic systems to survey wide areas efficiently without human burdens and mistakes. However, such systems have few examples of real-world applications due to their lack of human predictability. This paper proposes an algorithm: Local Reactive (LR) for multi-robot patrolling. Song et al. [2] studied maps with appropriate circular patrol paths, where homogeneous robots can maintain a certain time interval to access the patrol area, but the effect of heterogeneous robots working together under this communication condition is not good. Determining multi-robot motion strategies for persistently monitoring an area, subject to limited sensing, communication, and localization constraints. Mishra et al. [3] considered a heterogeneous robotic system composed of two types of agents: anchor agents with accurate localization capabilities and auxiliary agents with lower localization accuracy. Palacios-Gasós et al. [4] considered the problem of using unmanned aerial vehicles for persistent surveillance, in order to constantly check the mission area and minimize the interval between visits to it. The monitoring area is closely related to multi-robot continuous monitoring, including multi-robot patrol and dynamic coverage. Cassandras et al. [5] used external monitors to detect the access of each vertex and adjust the task allocation among robots through an auction mechanism to better balance the effective load of the robots. At the same time, the robustness of the system is improved due to the introduction of online decision-making. The Cyber-physical system (CPS) architecture proposed in the article has made significant improvements in the collaborative operation of multi-robot systems, remote environmental perception and mapping, and the design of scalable and low-latency communication networks [6].

Zhou et al. [7] studied the need for robots to repeatedly access the task area or a set of predefined detection locations in multi-robot patrols. Uchimura et al. [8] proposed an optimal cooperative patrol algorithm to minimize reconstruction time and delay criteria, which refers to the time difference between two visits to the same location, also known as access vertex idle time. Frequency-based continuous monitoring was addressed by Bartolini et al. [9], where the optimal closed path to all points in the task area is constructed to optimize the frequency of access to those point Zhai et al. [10] proposed a decentralized algorithm to solve the dynamic coverage problem of multi-robots in areas with uncertain workload density, and also estimated the upper bound of the difference between the actual coverage time and the optimal coverage time. Jiang et al. [11] solved the problem of continuous perceptual coverage for networked mobile sensors with potential loss of sensing capability. In the case of constraints during continuous coverage, if a set of linear inequalities has a solution, the continuous coverage task can be completed. To explore the advantages of multi-robot systems in dealing with uncertainty and imprecision in different heterogeneous environments. The method proposed in the article provides an effective task allocation strategy in such environments [12]. However, it also presents challenges in terms of computational resource requirements and system design complexity. In practical applications, it is necessary to weigh the pros and cons based on specific application scenarios and system resources.

With recent advances in robotic technology, it is now possible to use mobile sensors for field coverage. Due to the dynamics arising from the continuous movement of sensors, the problem of area coverage in mobile sensor networks has become more complex. Varposhti et al. [13] proposed a distributed learning algorithm to coordinate the movement of sensors in the field and proves its convergence to equilibrium states. Song et al. [14] in the case of a given path, optimized the initial position and speed of the machines, using an uncertainty model that varies nonlinearly with time as the evaluation standard for continuous monitoring. Kimura et al. [15] employed an uncertainty model that varies linearly with time as an evaluation index for continuous monitoring of multi-robot systems. The perceptual coverage model of mobile sensor networks mentioned by Wang and Hussein can also be considered a special nonlinear uncertainty model [16]. Faced with communication constraints in robotic scenarios. The article [17] investigates the path-following control problem for Autonomous Underwater Vehicles (AUVs) that are subject to external disturbances and unknown model parameters. An Event-Triggered Model-Free Adaptive Control (ETMFAC) method is designed, and an event-triggering mechanism is proposed to reduce the communication and computational burden on the control system, thereby addressing the communication issues of underwater vehicles.

Currently, in order to enhance multi-robot systems in terms of optimized resource allocation and improved energy efficiency and performance, Peng et al. [18] have proposed using cognitive computing to predict the flow status of flexible rectifiers. This approach has shown significant improvements over the original literature that only focused on centralized resource allocation and system performance. Song et al. [19] introduced two dynamic task allocation algorithms: the greedy baseline strategy (DTAG) and the market-based continuous single-item auction strategy (DTAP), to address the problem of online coordination in multi-robot patrols. The DTAP algorithm considers both local instantaneous idle time and instantaneous idle time received from other robots to make decisions, selecting the next access target point based on a maximum utility function. Cortes et al. [20] proposed two distributed multi-robot patrol algorithms based on a Bayesian mathematical framework: the greedy Bayesian strategy (GBS) and the state exchange Bayesian strategy (SEBS). While the GBS strategy performs well in most cases, it suffers from increased conflicts between robots competing for the same vertex in regions with a large number of robots, leading to degraded system performance. To overcome this limitation of the GBS strategy, the SEBS strategy considers interactions between robots, mitigating conflicts to some extent and outperforming the GBS algorithm.

By analyzing and comparing the aforementioned literature, this paper adopts an approach in multi-robot systems that enhances the efficiency and performance of continuous monitoring tasks through online decision-making and optimization of the uncertainty of target points and idle time.

2  Description and Perception Model of the Problem

2.1 Problem Description

Consider a mobile sensor network operating within a workspace of , where denotes the position of the the robot, and represents the set of robots. The task area D is a closed, fixed, and convex polygon, within which any point is denoted by , and is a predefined set of target points located within the monitoring area D.

Based on the papers [11,12], a full perception model is utilized for modeling, which can be formulated as:

(1)

where represents the peak induction of the sensor at the monitoring node . When = = 0, the induction peak reaches its maximum value, where = 1. The probability perception model when the robot induction radius = 5 is shown in Fig. 1. Obviously, is the limited perceptual range. Assuming that the robot satisfies a uniform perception range, represents the distance from the robot to any point in the monitoring area, and represents the peak value of the robot reaching the target point, .

Figure 1: Probabilistic perception models

Furthermore, consider the problem of coverage related to the uncertainty of target points within the monitoring area by the robot. Assuming there is a predefined set of access points P in the task area Fig. 2, an uncertainty function is used to evaluate the access of multiple robots to each target point in the monitoring area. When , it indicates that the robot has not monitored the desired target point. will accumulate as the number of target points in the monitoring area that are not covered increases. For each target point in the monitoring area, .

Figure 2: Target point topology

The differential equation of the uncertainty function can be expressed as:

(2)

(3)

where . is a constant value, is a constant, and represents the impact of the current value of the target point uncertainty function on the rate of change of . represents the initial uncertainty of the target point .

The uncertainty associated with the target points of interest is nonlinear and time-varying, distinct from the linear uncertainty model referenced in [3]. The reality is complex and dynamic, and the presence of nonlinear uncertainty is more representative. The rate of change in the number of target points of interest is intimately linked to the current number of target points. Not all points within the actual monitoring area possess equal importance. Furthermore, given the constraints on robot resources and monitoring capabilities, it is challenging to maintain comprehensive surveillance over the entire area. Consequently, during the monitoring process, it is crucial to prioritize ensuring the monitoring efficiency of target points of interest, thereby enhancing the surveillance of vital nodes.

Idle time pertains to the duration between consecutive visits to a particular node. The multi-robot system visits any target point within the monitoring area at a time interval denoted as , which can be represented as:

(4)

The time interval for accessing the target points of interest, denoted as , can be reframed as an optimization problem aimed at minimizing the idle time for robots to access each target point. By discretizing Eq. (3), we can deduce that:

(5)

where represents the initial time for the robot to access the target point, and represents the travel time for the robot to access each interest target point.

During the monitoring process, the objective is to monitor and patrol all target points within the monitoring area [21,22] and to surveil the entire area as frequently as feasible. To accomplish this, the robot must initially assess the uncertainty of adjacent target points while simultaneously ensuring that the interval between visits to adjacent target points across the entire task domain is as short as possible.

3  Optimal Control Algorithms

This paper employs a distributed control strategy grounded in target point uncertainty to enhance the efficiency of accessing the monitoring area. When robot arrives at a vertex within the topology graph G of the monitoring area, the robot engages in a decision-making process, during which each robot’s access to target points is progressively established. The robot autonomously selects the next target of interest to access based on information about target points within the task domain and the maximization of a utility function.

In the process of robot monitoring, the situation is complex and variable. To avoid unpredictable situations, it is assumed that the robot calculates and compares adjacent target points. Once the access target point is determined, the robot shares its own location information and the subsequent target point to be accessed with other robots via wireless networks. This enables avoiding repeated access to the same target of interest, prevents robot conflicts, and enhances the frequency of target point access. During the decision-making process, each robot maintains a set, Q, which comprises the idle times of target points accessed by other robots. Throughout the decision-making process, set Q is updated in real time to eliminate information about outdated target points resulting from communication delays or robot failures.

During the decision-making process, the robot initially calculates and evaluates the adjacent target points surrounding the current target point. Then, it assesses the travel time required for the robot to access the target point , which is expressed as:

(6)

where represents the length of the path from the current target point to the adjacent target point . represents the average speed of robots along different paths.

In order to prevent robots from repeatedly accessing adjacent target points, a lower bound value of is set as:

(7)

where represents the weight of edge , and represents the average weight of all edges in the topology graph G.

The time for the robot to reach the next target point is:

(8)

where represents the time at which the target point will be accessed, and represents the current time of the robot relative to the target point.

The time expression for the robot to access the current target point is:

(9)

where represents the time when the target point was last visited by any robot, and represents the travel time when another robot visited the target point . In order to evaluate the frequency of robot visiting to the target point of interest, the instantaneous idle time of the target point at time can be defined as:

(10)

(11)

For the sake of intuition and simplicity in calculation, the travel time is utilized instead of the path length to represent the utility function. Based on Formulas (5), (6), and (9), it can be inferred that:

(12)

to further simplify the formula, it is derived from Formulas (7)–(9):

(13)

(14)

where represents the uncertainty of the target point at time .

The algorithm based on the uncertainty of target points, minimizes the uncertainty and instantaneous idle time of all target points within the task domain through online decision-making. With this design approach, the robot maintains a certain frequency in the monitoring area, and the algorithm needs to be further optimized to achieve global optimality under specific conditions.

In the utility function, absolute values are employed to signify that the current robot’s time of accessing the next target point, , may be either greater than or less than the time of accessing the previous target point, . This implies that the robot may arrive earlier or later than other robots at the target point of interest.

Furthermore, during the continuous monitoring process within the task domain, the robot must also take into account the issue of interference. Interference is defined as the collision between two approaching robots or the interaction between the robot and environmental obstacles. During continuous monitoring, robots frequently encounter various interference scenarios. To mitigate interference, robots utilize internal obstacle avoidance modules to prevent it and enhance the efficiency of robot monitoring.

Assuming that the robots are 2 m apart, this is recorded as one instance of interference. The variable is used to represent the interference rate of the robots per minute. It is expressed as:

(15)

where represents the total number of interferences, and represents the total travel time.

The algorithm proposed in this paper encourages robots to prefer target points that have not been accessed, possess high accumulated uncertainty over time, or offer longer idle time for access. The robots make online decisions, with each robot in the team making independent choices. The robot will disseminate access messages to other robots, guiding them to these target points. Upon reaching the target point of interest, the robot promptly updates and publishes the list of target points of interest and access time lists in real time.

4  Experiment and Conclusion Analysis

4.1 Simulation

To validate the feasibility of the algorithm, a multi-robot simulation platform was established utilizing the Stage simulator within the Robot Operating System(ROS) environment. To control variations in environmental complexity, the simulation environment is meticulously designed to reduce the impact of environmental complexity on the experimental results. For instance, the number and types of obstacles in the environment can be limited, or a standardized environmental layout can be used to control the complexity. In the simulation environment, the robots used are Turtlebot3, and the primary sensors are Light Detection and Ranging(LIDAR) rangefinders for real time scanning of the map and environmental obstacles. To prevent collisions between robots and obstacles or other robots due to communication delays during motion, the Stage simulator in the ROS environment introduces delays into the communication protocols. For example, specific publishing and subscribing frequencies can be set in ROS topic communication to simulate the communication delays that might be encountered in real environments. Assuming a varying number of robots N (4, 8, 12), with each robot being isomorphic and possessing a perception radius of , where , the feasibility of the algorithm is verified through three types of maps: Cumberland, Grid, and Lab. The topologies of their respective environments are depicted in Fig. 3.

Figure 3: Simulation experiment topology

For simplicity, Table 1 presents detailed information such as the number of vertices P, the number of edges , the Fiedler value (indicating the connectivity of the topology), the region area, and the uncertainty X of the target points in each graph within the environment’s topology map mentioned above.

To validate our algorithm, we employed varying numbers of robots and compared it with the GBS, DTAG, and DTAP algorithms. In the experiments, the average speed of the robots was set to m/s, and each set of experiments typically ran for 1 h.

In order to assess and contrast the merits and drawbacks of these algorithms, we used not only the uncertainty of the target point’s nonlinear change over time and the idle time for accessing the target point as measurement criteria but also considered the maximum value of the system’s instantaneous idle time , the robot interference rate , and the standard deviation . serves as an evaluation of the balance in accessing target points.

At the same time, for different map topologies (Cumberland, Grid, Lab), the algorithm was also analyzed in terms of scalability and applicability. By changing the number of robots (for example, N = 4, 8, 12), the scalability of the algorithm in different scale scenarios can be tested. This helps to understand whether the algorithm can adapt to monitoring areas of different sizes and how its performance changes with an increase in the number of robots. Regarding the adaptability of the algorithm, the algorithm’s path planning and obstacle avoidance capabilities on different maps can be observed to assess its adaptability to environmental changes. This includes the algorithm’s ability to adjust in the face of different obstacle distributions and spatial constraints. However, under specific conditions, the algorithm may exhibit instability. These issues are identified through detailed log recording and performance metric analysis and are further addressed by adjusting algorithm parameters and improving algorithm adaptability.

Generally, the lower the standard deviation value and the number of interferences, the better the robot’s monitoring effectiveness, enabling the robot to reach the target point to be monitored more swiftly, thereby reducing the instantaneous idle time between adjacent target points. Therefore, can also be utilized as a metric for evaluating system performance.

Based on the analysis presented in Tables 2 and 3, when the number of robots (N) equals 4, the values of , , , and X for these algorithms are relatively high. As the number of robots increases to , the parameter values actually decrease, indicating that with more robots, the frequency of accessing and interfering with target points in the task domain increases.

When , the various indicators of the algorithm proposed in this paper are not optimal compared to other algorithms. Nevertheless, with the increase in the number of robots, this situation improves significantly, and the TPUAF algorithm’s parameters reach their optimal values compared to the other algorithms. Consequently, the algorithm presented in this paper exhibits greater advantages over the other algorithms.

The box plots in Fig. 4 compare the performance of different algorithms in two distinct environments when the number of robots . The blue rectangular box in the figure signifies the interquartile range (IQR). A smaller IQR indicates a more concentrated distribution of the target point’s idle time. The closer the position of the box to the bottom of the graph, the smaller the idle time, suggesting a higher access frequency. The red line represents the median, the X marks the average, the two black lines above and below indicate the maximum and minimum values within the non-outlier range, and the circles represent outliers (uncertainty of the target point).

Figure 4: Box graph with different algorithms in Cumberland and grid environment

When , Fig. 4a,d shows that the idle time of target points for the four algorithms in the Cumberland environment is relatively dispersed, whereas in the Grid environment, it is more concentrated. In Cumberland, the outliers and idle time of the DTAP and GBS algorithms are more scattered, whereas in the TPUAF algorithm, they are more concentrated, indicating better overall system stability.

When , as depicted in Fig. 4b,e,c,f, as the number of robots increases, the TPUAF algorithm exhibits a more concentrated distribution of idle times, with lower average values and uncertainties compared to other algorithms. This enhancement improves the access efficiency of target points and reduces the access cycle within the task area.

4.2 Physical Experiments

To validate the superior performance of our algorithm, we conducted physical experiments using the Turtlebot 3 as the experimental carrier in a self-built indoor environment with an area of 3.0 2.6 , as depicted in Fig. 5. Throughout the experiments, the Rviz interface was continuously monitored, as shown in Fig. 6. Additionally, the topology diagram of the experimental environment is presented in Fig. 3.

Figure 5: Indoor entity monitoring environment

Figure 6: Physical experiment

Fig. 6 illustrates the operational results of varying numbers of robots at different time intervals, and the corresponding parameters are summarized in Table 4. These experiments serve to verify the TPUAF algorithm’s performance optimization for task domain monitoring within this specific environment.

In the physical experiment, the average speed of the robots was set to 0.1 m/s, and each robot experiment ran for 15 min. Upon completion of one cycle by the system, all target points in the environment were visited at least once before global information was recorded in the task space. As the number of robots increased, the values of , , , and X decreased, which aligns with the observations from the simulation experiment, demonstrating consistency between the two.

Fig. 7 displays the curves of the performance evaluation indicators , , , and X over time for varying numbers of robots. Based on the graph analysis, as and gradually stabilize with the progression of monitoring time, the instantaneous idle time and the uncertainty associated with the visited target points also tend to synchronize with the monitoring duration. The robots continuously monitor each targeted point of interest at a consistent frequency.

Figure 7: Robot performance evaluation in solid environment

Furthermore, the cumulative uncertainty of each target point within the monitoring area continually evolves in response to the total idle time of each target. When certain target points in the task area remain unvisited by the robots for an extended period, their uncertainty accumulates and increases over time. This scenario prompts the robots to make online decisions, leveraging utility functions to prioritize and monitor target points with high cumulative uncertainty. Upon visiting such a target point, its uncertainty diminishes towards zero.

Additionally, the total idle time and uncertainty of target points within the task domain fluctuate according to the number of robots involved. Notably, as the multi-robot system achieves equilibrium with increased monitoring time, also converges to a constant value, remaining stable despite further increments in monitoring duration.

5  System Stability and Scalability

Further analysis is conducted to evaluate the stability and scalability of robots within the laboratory environment. The stability of the system can be discerned by examining the trends in instantaneous idle time and standard deviation over time. Fig. 7 presents a discussion of the system’s performance for varying numbers of robots, specifically , and , respectively. When the number of robots is small, and in Fig. 7a tend to stabilize at . Due to the limited number of robots, the various system indicators are not optimal. However, as the number of robots increases, this situation undergoes significant improvement. From Fig. 7b–d, it is evident that and reach a stable state in a shorter duration, with the number of robots directly correlating to the values of and , thus demonstrating the superiority of this algorithm.

Analyze the scalability of various algorithms across different environments. Scalability is a crucial aspect of continuous monitoring algorithms for robots, and an optimal monitoring algorithm should remain unaffected by the number of robots or the environmental graph structure. Typically, as the number of robots increases, the efficiency of monitoring within the system also enhances. Nevertheless, due to constraints within the task space, the proliferation of robots can lead to increased collisions, interference, and competition among robots for access to the same target point during the monitoring process, thereby adversely affecting monitoring efficiency to some extent. Consequently, the acceleration ratio is adopted as the standard for evaluating scalability. Meantime with the increase in the number of robots, in order to maintain efficient operation of the multi-robot system, dynamic adjustment of resource allocation, communication protocols, and computational loads is achieved through distributed control strategies, online decision-making, utility function optimization, internal obstacle avoidance modules, and adaptive adjustment of access frequency.

Fig. 8 depicts the acceleration ratio of a multi-robot system. In general, a higher acceleration ratio signifies enhanced robot efficiency and improved scalability of the multi-robot system. Based on the analysis presented in Fig. 8a–c, the acceleration ratio of the GBS algorithm gradually decreases as the number of robots increases, while the DTAG and DTAP algorithms exhibit a system acceleration ratio that exceeds 1 when the number of robots is low. When the acceleration ratio surpasses 1, the system is classified as super-linear; conversely, when it equals 1, the system is deemed linear. As the number of robots increases, the acceleration ratios of these two algorithms actually decrease. Although the TPUAF algorithm may not initially exhibit the optimal acceleration ratio with a small number of robots, its acceleration ratio remains relatively stable compared to other algorithms. Notably, as the number of robots increases, the acceleration ratio of the TPUAF algorithm increases significantly.

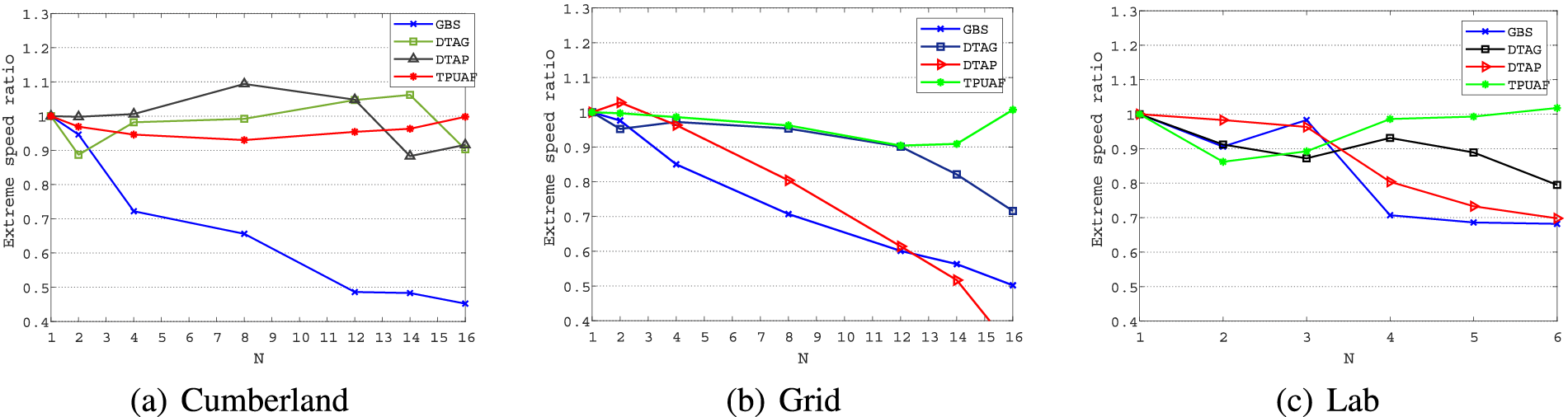
Figure 8: Acceleration ratio of multi robot systems

6  Discussion

This article explores the following aspects:

1. Algorithm performance: The performance of the proposed multi-robot continuous monitoring algorithm in handling target point uncertainty was discussed, as well as how to effectively solve the efficiency challenge of multi-robot access to monitoring areas through online decision-making.

2. Experimental analysis: By comparing with several existing algorithms, it was analyzed that the system performance is moderate when the number of robots is small, but the overall performance of the system significantly improves with the increase of the number of robots.

3. Stability and Scalability: An in-depth analysis was conducted on the stability and scalability of multi-robot systems in experimental environments. The stability of the system can be identified by monitoring the trend of instantaneous idle time and standard deviation, and how the scalability of the algorithm improves with the increase of the number of robots.

4. Algorithm optimization: We discussed how to improve the performance of multi-robot systems by optimizing the cumulative uncertainty and instantaneous idle time of target points, as well as how to use utility functions to determine the next optimal target point for access.

5. Future work: Future research directions may also be discussed, including further optimizing algorithms, exploring their applications in monitoring areas of different types and scales, and addressing potential challenges such as communication and coordination issues between robots.

7  Conclusion

This paper a multi-robot continuous monitoring algorithm that addresses target point uncertainty, effectively tackling the efficiency challenge of multi-robot access to monitoring areas through online decision-making. It employs the cumulative uncertainty and instantaneous idle time of target points as evaluation metrics for multi-robot systems, aiming to minimize the uncertainty and instantaneous idle time of all target points within the task domain while maintaining a specific number of visits at predefined intervals. During the monitoring process, the robot pre-evaluates the cumulative uncertainty and instantaneous idle time of adjacent target points through online decision making, utilizing a utility function to identify the next optimal target point for access, incorporating the updated list of visited target points. In general, the target point with the highest cumulative uncertainty and utility function value is considered the optimal choice. Through the experimental analysis and comparison of several algorithms, it was observed that the overall performance of the multi-robot system was moderate when the number of robots was low. However, as the number of robots increased, the system’s overall performance improved significantly. The paper concludes with an insightful analysis of the stability and scalability of multi-robot systems.

Acknowledgement: The authors thank Jie Xie for assistance with the experiments and valuable discussion. This work was supported in part by the National Nature Science Foundation of China.

Funding Statement: The National Nature Science Foundation of China under Grant 62106186. Initials of Jin Xie received the grant.

Author Contributions: All authors contributed to the study conception and design. Material preparation, data collection and analysis were performed by Jin Xie and Guodong Yuan. The first draft of the manuscript was written by Guodong Yuan and all authors commented on previous versions of the manuscript. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: Data available within the article or its supplementary materials. The authors confirm that the data supporting the findings of this study are available within the article or its supplementary materials.

Ethics Approval: This study does not involve human or animal subjects.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

References

1. Kobayashi K, Ueno S, Higuchi T. Multi-robot patrol algorithm with distributed coordination and consciousness of the base station’s situation awareness. arXiv:2307.08966. 2023. [Google Scholar]

2. Song C, Liu L, Feng G, Wang Y, Gao Q. Persistent awareness coverage control for mobile sensor networks. Automatica. 2013;49(6):1867–73. doi:10.1016/j.automatica.2013.02.048. [Google Scholar] [CrossRef]

3. Mishra M, Poddar P, Agrawal R, Chen J, Tokekar P, Sujit PB. Multi-agent deep reinforcement learning for persistent monitoring with sensing, communication, and localization constraints. IEEE Trans Autom Sci Eng. 2024. doi:10.1109/TASE.2024.3385412. [Google Scholar] [CrossRef]

4. Palacios-Gasós JM, Talebpour Z, Montijano E, Sagüés C, Martinoli A. Optimal path planning and coverage control for multi-robot persistent coverage in environments with obstacles. In: 2017 IEEE International Conference on Robotics and Automation (ICRA); 2017 May 29–Jun 3; Singapore: IEEE; p. 1321–7. [Google Scholar]

5. Cassandras CG, Lin X, Ding X. An optimal control approach to the multi-agent persistent monitoring problem. IEEE Trans Automat Contr. 2022;58(4):947–61. doi:10.1109/TAC.2012.2225539. [Google Scholar] [CrossRef]

6. Kivrak H, Karakusak MZ, Watson S, Lennox B. Cyber-physical system architecture of autonomous robot ecosystem for industrial asset monitoring. Comput Commun. 2024;218(9):72–84. doi:10.1016/j.comcom.2024.02.013. [Google Scholar] [CrossRef]

7. Zhou N, Yu X, Andersson SB, Cassandras CG. Optimal event-driven multi-agent persistent monitoring of a finite set of targets. In: 2016 IEEE 55th Conference on Decision and Control (CDC); 2016 Dec 12–14; Las Vegas, NV, USA: IEEE; 2016. p. 1814–9. [Google Scholar]

8. Uchimura Y, Imaizumi T, Murakami H. Mobile robot deployment based on Voronoi diagram. In: 2011 1st International Symposium on Access Spaces (ISAS); 2011 Jun 17–19; Yokohama, Japan: IEEE; 2011. p. 71–6. [Google Scholar]

9. Bartolini N, Bongiovanni G, La Porta TF, Silvestri S. On the vulnerabilities of the virtual force approach to mobile sensor deployment. IEEE Trans Mob Comput. 2014;13(11):2592–605. doi:10.1109/TMC.2014.2308209. [Google Scholar] [CrossRef]

10. Zhai C, Hong Y. Decentralized sweep coverage algorithm for multi-agent systems with workload uncertainties. Automatica. 2013;49(7):2154–9. doi:10.1016/j.automatica.2013.03.017. [Google Scholar] [CrossRef]

11. Jiang P, Wang X, Liu J. A sensor redeployment algorithm based on virtual forces for underwater sensor networks. Chin J Electron. 2018;27(2):413–21. doi:10.1049/cje.2017.10.003. [Google Scholar] [CrossRef]

12. Khelifa R, Hamza T, Fatma B. Fuzzy task assignment in heterogeneous distributed multi-robot system. Artif Intell Rev. 2024;58(1):14. doi:10.1007/s10462-024-10977-y. [Google Scholar] [CrossRef]

13. Varposhti M, Hakami V, Dehghan M. Distributed coverage in mobile sensor networks without location information. Auton Robots. 2020;44(3):627–45. doi:10.1007/s10514-019-09859-y. [Google Scholar] [CrossRef]

14. Song C, Feng G, Fan Y, Wang Y. Decentralized adaptive awareness coverage control for multi-agent networks. Automatica. 2011;47(12):2749–56. doi:10.1016/j.automatica.2011.09.006. [Google Scholar] [CrossRef]

15. Kimura H, Motoi N. Virtual force generation method for remote control system in mobile robot. In: IECON 2016-42nd Annual Conference of the IEEE Industrial Electronics Society; 2016 Oct 23–26; Florence, Italy: IEEE; 2016. p. 6193–8. [Google Scholar]

16. Wang Y, Hussein II. Awareness coverage control over large-scale domains with intermittent communications. IEEE Trans Automat Contr. 2020;55(8):1850–9. doi:10.1109/TAC.2010.2042346. [Google Scholar] [CrossRef]

17. Zhou G, Xiang X, Liu C. Parameter identification and model prediction path following control of underactuated AUV: methodology and experimental verification. Control Eng Pract. 2023;141:105729. doi:10.1016/j.conengprac.2023.105729. [Google Scholar] [CrossRef]

18. Peng Y, Yang X, Li D, Ma Z, Liu Z, Bai X, et al. Predicting flow status of a flexible rectifier using cognitive computing. Expert Syst Appl. 2025;264(1):125878. doi:10.1016/j.eswa.2024.125878. [Google Scholar] [CrossRef]

19. Song C, Feng G, Huang Y. Optimal awareness coverage control for networked mobile sensors with awareness loss. In: IEEE International Conference on Control and Automation (ICCA); 2013 Jun 12–14; Hangzhou, China: IEEE; 2013. p. 129–34. [Google Scholar]

20. Cortes J, Martinez S, Karatas T, Bullo F. Coverage control for mobile sensing networks. IEEE Trans Robot Autom. 2004;20(2):243–55. doi:10.1109/TRA.2004.824698. [Google Scholar] [CrossRef]

21. Wu QP, Zhou SL, Liu W, Yin GY. Multi-unmanned aerial vehicles cooperative search based on central-distributed model predictive control. Control Theo Appl. 2015;32(10):1414–21. doi:10.7641/CTA.2015.50482. [Google Scholar] [CrossRef]

22. Jiang W, Wang D, Wang Y. A vector field based method for multi-UAV simultaneous arrival. Control Theo Appl. 2018;35(9):1215–28. doi:10.7641/CTA.2018.70225. [Google Scholar] [CrossRef]