A Performance Analysis of Machine Learning Techniques for Credit Card Fraud Detection

1  Introduction

Internet use is growing in all parts of people’s lives, from business to banking. As a result, more information is being virtualized and integrated. In contemporary times, there has been a discernible rise in the frequency and scale of online transactions, resulting in an expanding population of persons employing the Internet as a medium for engaging in commercial activities. Concurrently, an increasing tendency is observed in the magnitude of online transactions. These circumstances create a favourable setting for the expansion of transactional fraud. Fraudulent persons often adopt various methods to illicitly get user information and quickly transfer large amounts of money, leading to enormous financial losses for users and institutions. Transaction fraud is a common anomaly often camouflaged inside typical financial transactions. There is a widespread tendency to utilize machine learning and data mining methodologies to address significant labour costs to detect unusual trade trends. The system employs detection approaches mostly based on classification [1–5]. Several data mining techniques associated with transaction fraud tasks have been employed to efficiently manage a significant amount of data [2,6–10].

Fraud in the financial industry, both in firms and in government, is a widespread problem with far-reaching consequences. Two distinct categories of fraudulent conduct can be associated with credit cards: internal and external card fraud. Utilizing a pilfered credit card to acquire funds through illicit means can be classified as internal card fraud, whilst utilizing a pilfered credit card itself constitutes external card fraud. Inside card fraud arises when cardholders and financial institutions collide to perpetrate fraudulent activities by assuming a fabricated identity. Extensive study has been conducted on detecting and preventing external card fraud, which accounts for most credit card fraud cases. The conventional methods employed in the past for identifying fraudulent transactions have proven to be labour-intensive and ineffective. Consequently, the implementation of big data has made manual procedures increasingly unfeasible. In contrast, financial institutions have redirected their focus towards contemporary computational techniques to address the problem of fraudulent credit card utilization.

The primary objective of this research is to evaluate the efficacy of cutting-edge machine-learning approaches in identifying fraudulent credit card transactions using a publicly available dataset. These machine learning algorithms are evaluated using different metrics, including accuracy, recall, and F1 score. Furthermore, the confusion matrix of the machine learning models for training and test results and the computational time are evaluated. To the best of our knowledge, this dataset is not implemented by any other study to compare machine learning technique performance for fraudulent detection.

The rest of this paper is organized as follows: In Section 2, a comprehensive literature on credit card fraud, including an overview of the models, is provided. Section 3 discusses the methodology and dataset for detecting credit card fraud. The findings of the experiments are presented in Section 4, along with a discussion regarding the comparative analysis. The comparative analysis is ended in Section 5, which also suggests further research.

2  Related Work

Credit card fraud detection is the technique of categorizing fraudulent transactions as real (genuine) or fraudulent [4]. Credit card transactions can be classified as either genuine or fraudulent. The identification of fraudulent activity on a credit card can be accomplished by analyzing the cardholder’s spending patterns. Artificial neural networks (ANNs) [11], genetic algorithms [12,13], support vector machines (SVM) [14], frequent item mining [15], decision trees [16], migrating birds optimization algorithms [17], and Naïve Bayes [18].

Ng et al. [19] compared Naïve Bayes and logistic regression models. Current research is being performed to evaluate the effectiveness of decision trees, neural networks, and logistic regression in detecting fraudulent activity [20]. Reference [21] analysed the performance of two modern data mining approaches, support vector machines, and random forests, alongside logistic regression, as part of an effort to better detect credit card fraud. On the other hand, reference [22] addressed the subject of credit card fraud detection using neural networks and logistic regression approaches. Detecting credit card theft presents several issues in the area. These difficulties include limited availability and severe imbalance within credit card transaction datasets, finding suitable features for modeling purposes, and selecting relevant metrics to evaluate technique success while dealing with imbalanced credit card fraud data.

Şahin et al. [23] investigated the use of decision trees and support vector machines for credit card fraud detection in their work. Their findings demonstrated that decision tree classifiers outperformed SVM approaches in handling the specific issue under consideration. The ability of the SVM-based model to detect fraud approached the accuracy level attained by decision tree-based models as the volume of training data rose. Nonetheless, the SVM model fell short of recognizing many fraudulent cases in the context of credit card fraud detection. Bhattacharyya et al. [21] compared logistic regression’s efficacy against two current data mining methods, support vector machines and random forests. The study found that varied levels of under-sampling did not affect the effectiveness of logistic regression. In contrast, SVM performance improved as the proportion of false cases in the training dataset declined. SVM models with varied kernels regularly outperformed logistic regression models. Reference [22] used ANN and logistic regression to create and implement classification models to address the problem of credit card fraud detection. The data used in this analysis was extremely unbalanced. When dealing with the topic under consideration, the results showed that the ANN classifiers outperformed the logistic regression classifiers in this study. As the number of iterations increased, the logistic regression classifiers tended to overfit the training data, a problem attributed to the study’s poor sampling. The data used in this study was highly imbalanced. The findings indicate that the ANN classifiers presented in this study exhibit superior performance compared to the logistic regression classifiers in addressing the problem under examination. Logistic regression classifiers tend to overfit the training data as iterations grow. This issue can be attributed to insufficient sampling in the study. In [24], Decision trees, neural networks, and Naïve Bayes classifiers were among the methodologies used. It was shown that when applied to larger databases, neural network classifiers performed optimally but with lengthy training cycles to create the model. During the training phase, Bayesian classifiers demonstrated greater accuracy and efficiency, making them well-suited for datasets of varying sizes. However, when applied to novel instances, their performance may be slower.

In [25], the performance of Logistic Regression, Random Forest, Decision Tree, and SVM was investigated. The proposed system shows results according to the accuracy, sensitivity, specificity, and precision of the above techniques. Transactions in the dataset are heavily right-skewed. In [26], popular supervised and unsupervised machine learning algorithms have been applied to detect credit card fraud in a highly imbalanced dataset. It was found that unsupervised machine learning algorithms can handle the skewness and give the best classification results. In [27], three machine learning algorithms, namely logistic regression, Naïve Bayes and K-nearest neighbour. The performance of these algorithms is recorded with their comparative analysis. The overview of related work is provided in Table 1.

The literature uses only a few machine learning models and ignores the boosting models, including XGBoost, LGBM and CatBoost; most compare the performance of only two models using a single dataset. However, multiple machine learning models’ performance evaluation using a single dataset can be helpful in comparing the performance of the models using evaluation metrics, including accuracy, precision and F1 score, along with the computational time.

The sampling approach significantly impacts the performance of detecting fraudulent activity on credit cards, the selection of variables, and the applied detection techniques. Many machine-learning techniques have been created and used in various experimental research to detect fraudulent activity on credit cards. However, a comprehensive analysis of machine learning techniques for credit card fraud detection is helpful for the researchers to study. The machine learning techniques used in this research include Regression and Boosting methods, including Logistic Regression, Random Forest, Extra Trees, XGBoost, Light Gradient Boosting, and Categorical Boosting, which are briefly highlighted in this section.

2.1 Machine Learning Models

The machine learning models used in this work are as follows.

2.1.1 Logistical Regression

Logistic regression is a statistical technique used in machine learning to address binary classification problems such as credit card fraud detection. The model determines whether a particular set of input features correlates with the chance of an occurrence being classed as fraudulent or authentic. In the context of credit card fraud detection, input features include a wide range of variables such as transaction amount, location, time, and historical transaction data. The Logistic Regression model calculates a weighted sum of the given features and subsequently uses a sigmoid function to estimate the chance of a fraudulent transaction, which falls from 0 to 1. Based on the aforementioned probability, it is possible to establish a threshold for categorizing transactions into fraudulent or lawful categories. For instance, when the likelihood of a transaction being fraudulent exceeds 0.5, it is categorized as fraudulent. The method presented herein offers a straightforward yet efficient approach for financial institutions to detect possibly fraudulent transactions by leveraging historical data trends and transaction features.

2.1.2 Random Forest

The Random Forest algorithm is one of the most popular ensembles learning techniques in machine learning. It has proven effective in various categorization tasks, including detecting credit card fraud. The system generates numerous decision trees, each with a randomized subset of the training data and a randomized subset of the input attributes. The predictions generated by each tree are subsequently aggregated to provide a conclusive decision. Within credit card fraud detection, every decision tree can scrutinize several transaction attributes, including but not limited to temporal aspects, geographical information, monetary value, and records. Using Random Forest, through aggregating outputs from multiple separate trees, has proven to be an efficient method of detecting fraudulent transactions. For instance, consider a scenario where one decision tree classifies a transaction as suspicious based on its geographical location while another tree flags it owing to an atypical transaction amount. In this scenario, the Random Forest algorithm can assign weights to different signals, enhancing the precision of fraud detection and demonstrating resilience towards noisy or irrelevant information.

2.1.3 Extra Trees

The Extra Trees algorithm, also known as Extremely Randomized Trees, is a widely employed ensemble learning method in machine learning. It finds application in several applications, including detecting credit card fraud. The proposed approach expands on the foundational idea of decision trees by constructing an ensemble of independent decision trees. The distinguishing characteristic of Extra Trees lies in its highly random tree creation technique. The algorithm employs a random selection process during each split to choose the features to be utilized and utilizes random subsets of the data to construct each tree. The use of randomness in the Extra Trees algorithm mitigates the overfitting issue, hence decreasing its susceptibility to noise in the dataset. In the context of credit card fraud detection, this can provide significant value. When examining transaction data, the Extra Trees algorithm may consider many transaction characteristics such as time, location, amount, etc. It randomly selects subsets of these qualities and performs splits based on them. This methodology facilitates the detection of complex patterns and irregularities within the dataset that could potentially signify fraudulent activity, all while ensuring resilience against noisy or extraneous variables.

2.1.4 XGBoost (XGB)

XGBoost, or Extreme Gradient Boosting, is a robust machine learning method that has demonstrated significant efficacy in credit card fraud detection and other classification tasks. This algorithm is a member of the gradient-boosting family, which involves the aggregation of numerous weak learners, often in the form of decision trees, to construct a robust prediction model. XGBoost enhances conventional gradient boosting techniques using a regularized objective function and an exceptionally effective tree-growing procedure. XGBoost, a machine learning algorithm, can be utilized in the context of credit card fraud detection to analyze transaction data. This analysis examines many factors, including transaction time, location, amount, and historical data. The process optimizes the amalgamation of decision trees to detect minor trends and abnormalities that indicate fraudulent activity. For example, when one decision tree emphasizes the atypical timing of a transaction while another prioritizes the transaction’s location, XGBoost effectively combines these perspectives to improve the precision of fraud detection. This approach provides a resilient and high-performing method for identifying fraudulent activities.

2.1.5 Light Gradient Boosting Machine (LGBM)

LightGBM, also known as Light Gradient Boosting Machine, is an advanced gradient boosting framework demonstrating exceptional credit card fraud detection performance. The system has been purposefully engineered to possess high efficiency and scalability, rendering it an optimal selection for managing extensive datasets and real-time applications. The LightGBM framework employs a learning method based on histograms, resulting in accelerated training and enhanced compatibility with categorical information. LightGBM can be utilized in credit card fraud detection to examine transaction data, encompassing attributes like transaction time, location, amount, and historical data. The algorithm constructs a collection of decision trees to improve their configuration to detect fraudulent transactions accurately. As an illustration, let us consider a scenario wherein one tree algorithm identifies instances of fraud by analyzing the geographical information associated with a transaction. In contrast, another tree algorithm prioritizes the examination of transaction amounts. In this context, LightGBM successfully incorporates these discoveries, offering a remarkably precise and efficient approach for identifying instances of credit card fraud, especially in situations characterized by extensive and swiftly evolving datasets.

2.1.6 Categorical Boosting (CatBoost)

CatBoost, also known as Categorical Boosting, is a very effective gradient-boosting algorithm that exhibits strong suitability for various applications, such as identifying credit card fraud. The software demonstrates exceptional proficiency in managing categorical characteristics and effectively addresses missing data, rendering it a suitable option for real-world datasets. The CatBoost algorithm constructs a collection of decision trees to optimize their configuration to classify transactions as either fraudulent or valid accurately. Credit card fraud detection involves many features, including transaction timing, location, amount, and historical data. CatBoost has demonstrated its ability to accurately capture intricate associations among various features and detect small patterns that may indicate fraudulent behaviour. For example, it is possible to ascertain that specific combinations of transaction features exhibit a higher likelihood of being linked to fraudulent activities. Using CatBoost, which can effectively handle categorical data and its rapid training procedure, is a valuable solution for improving fraud detection accuracy. This enables financial institutions to enhance their ability to safeguard consumers from fraudulent actions.

3  Methodology

A credit card transaction is considered fraudulent when another individual uses your card without authorization. Criminals commit fraud by stealing the personal identification number (PIN) associated with a credit card or the account details and then using this information to make illicit purchases without taking possession of the card. With the help of the credit card fraud detection system, we can determine whether the newly processed transactions are fraudulent or legitimate. The card, which might be a credit card or a debit card, could be involved in the fraudulent activity that is taking place. When anything like this happens, the card becomes a fraudulent transaction source. It is possible that you committed the crime intending to get the products without paying for them or getting your hands on the ill-gotten money. Credit cards present an attractive opportunity for fraudulent activity. This is because a significant amount of money can be made quickly without incurring many risks, and it will take quite some time before criminal activity is discovered.

Many techniques are used to detect fraudulent activities in credit card transactions. However, in this research, state-of-the-art machine learning algorithms, including Logistic Regression, Random Forest, Extra Trees, XGB, LGBM, and CatBoost are utilized for performance analysis using the dataset. The algorithms’ performance, accuracy, precision, and recall are compared, along with the confusion matrix for the analysis and the computational time. Fig. 1 shows the implementation and evaluation process of the machine learning models.

Figure 1: Implementation and evaluation process

3.1 Dataset

The dataset used in this research work includes around 550,000 records of credit card transactions carried out in Europe in 2023 by cardholders, all of which have been anonymized to secure the cardholders’ privacy and keep their identities secret. The major purpose of this dataset is to make it easier to construct algorithms and models to detect possibly fraudulent transactions. The dataset includes the following features:

•   Id: A one-of-a-kind identification that is assigned to every single transaction.

•   V1–V28: Anonymized features reflecting various transaction attributes (such as time, location, and so on).

•   Amount: the total dollar value of the transaction.

•   Class: A binary label that indicates whether the transaction is fraudulent, with a value of either (1) or (0).

The dataset contains two classes: 0, i.e., not fraud and 1, i.e., fraud, as the number of transactions for each class is shown in Fig. 2.

Figure 2: Dataset class

The dataset is divided into two parts: train and test with 0.70 and 0.30 split. The dataset for the training set contains 50% fraudulent and 50% non-fraudulent transactions, also for the test set, the fraudulent have 50% and non-fraudelent activites are also 50% transactions data. The dataset for test set contains the fraudulent transactions as non-fraudulent, and non-fraudulent transactions are considered fraudulent. Fig. 3 depicts the distribution of training and test sets.

Figure 3: Train and test set distribution

4  Evaluation Metrics

Truly Positive (TN), False Negative (FN), True Positive (TP), and False Positive (FP) are the primary components of the evaluation metrics that are employed to assess the performance of ML algorithms. The definition of each of these entities is shown in Fig. 4. To assess the efficacy of the models, this study employs the utilisation of the confusion matrix, which offers a comprehensive perspective on the algorithm’s performance.

Figure 4: Evaluation metric

4.1 Accuracy

When analysing the performance of ML algorithms, it is one of the most widely used assessment measures. This can be attributed partly to its simplicity and ease of implementation [19]. Accuracy can be conceptualised as quantifying the extent to which test data points have been correctly classified, typically represented as a percentage. Nevertheless, it is advisable to refrain from measuring accuracy solely on the training data due to the potential for overfitting. This is because the accuracy rate may frequently appear greater than its true value, leading to an incorrect outcome. Mathematical correctness can be quantified as follows:

Accuracy =TP+TN/P+N(1)

One significant limitation of accuracy is its inability to distinguish between False Positives (FP) and False Negatives (FN) [19]. Consequently, it becomes challenging to identify the specific areas where the algorithm is making errors, potentially resulting in more severe issues depending on the context in which the method is applied.

4.2 Precision and Recall

Precision and recall are frequently considered in tandem due to their inherent correlation. Precision is a metric that quantifies the proportion of positive predictions that accurately belong to the positive class. Recall refers to the ratio of correctly predicted positive cases to the total number of positive instances. The mathematical formulas for both precision and recall are presented in Eqs. (2) and (3).

Precision=TP/TP+FP(2)

Recall=TP/P(3)

Precision and recall, like accuracy, are frequently employed in several domains because of their ease of implementation and comprehensibility, which is their primary advantage. One of the primary limitations associated with precision and memory is the omission of True Negatives (TN). This implies that the correctly categorised negatives do not influence the overall score of either criterion. Hence, the omission of True Negative (TN) ratings in evaluating algorithm performance can result in an overall skewed perspective, and it is imperative to use TN scores only when their relevance is deemed necessary.

4.3 F1 Score

The F1 score, sometimes called the F-Measure, is a composite metric that combines accuracy and recall through a weighted average. This metric yields a singular comprehensive score for evaluating the performance of a classification model. The F1 score can be formally described in mathematical terms as shown in Eq. (4):

F=2(Precision×Recall)/(Precision+Recall).(4)

5  Performance Evaluation

In this section, the performance of each model, including the evaluation metrics and confusion matrix, is discussed, along with the computational time.

5.1 Logistic Regression Performance

In the training set for the credit card fraud detection, the logistic regression model exhibits a precision of 0.95 for class 0 (legitimate transactions) and 0.98 for class 1 (fraudulent transactions), indicating the proportion of true positive predictions among all positive predictions made for each class. The recall for class 0 is 0.98, which suggests that the model is able to identify 98% of the non-fraud cases correctly. However, the recall for class 1 is slightly lower at 0.95, pointing to a small percentage of fraudulent activities that the model might not capture. The F1 score, a harmonic mean of precision and recall, is 0.97 for both classes, reflecting a balance between the precision and recall for the model on the training data.

For the test dataset, the precision values remain consistent with the training data, at 0.95 for class 0 and 0.98 for class 1. The recall scores show a fractional decrease for both classes, with class 0 at 0.98 and class 1 at 0.95, indicating a slight reduction in the model’s ability to detect all relevant instances in an unseen dataset. The F1 scores are also marginally lower for class 1 in the test data, standing at 0.96, compared to the training phase. The macro averages for precision, recall, and the F1 score are 0.97, suggesting that the model’s overall performance metrics do not exhibit substantial variance between the training and testing phases. The classification report for the train set and test set for logistic regression is shown in Fig. 5.

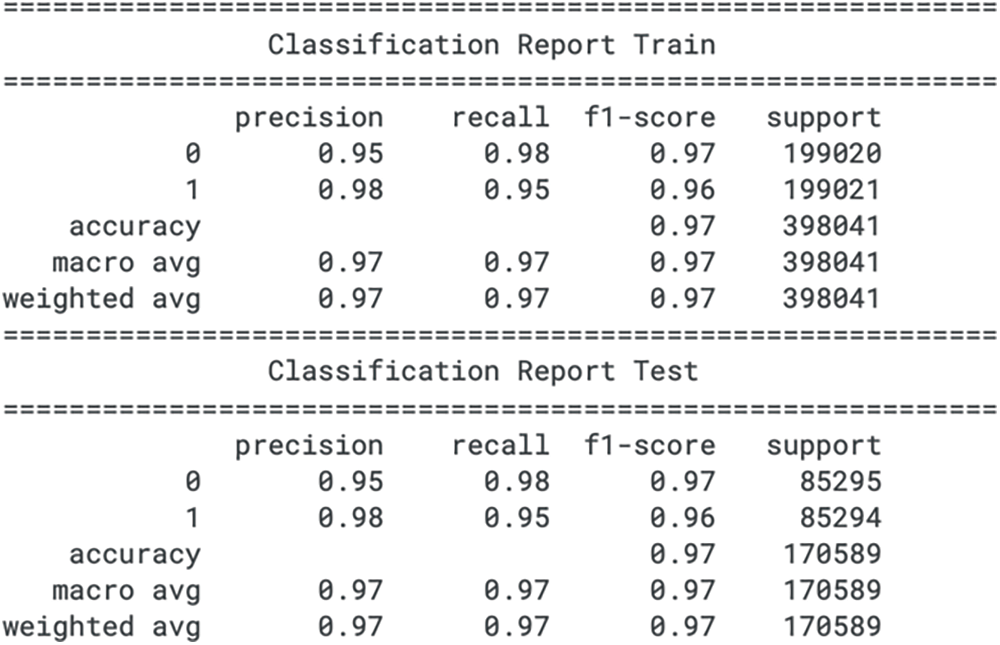
Figure 5: Logistic regression confusion matrix

The confusion matrix for logistic regression using train and test sets is shown in Fig. 6.

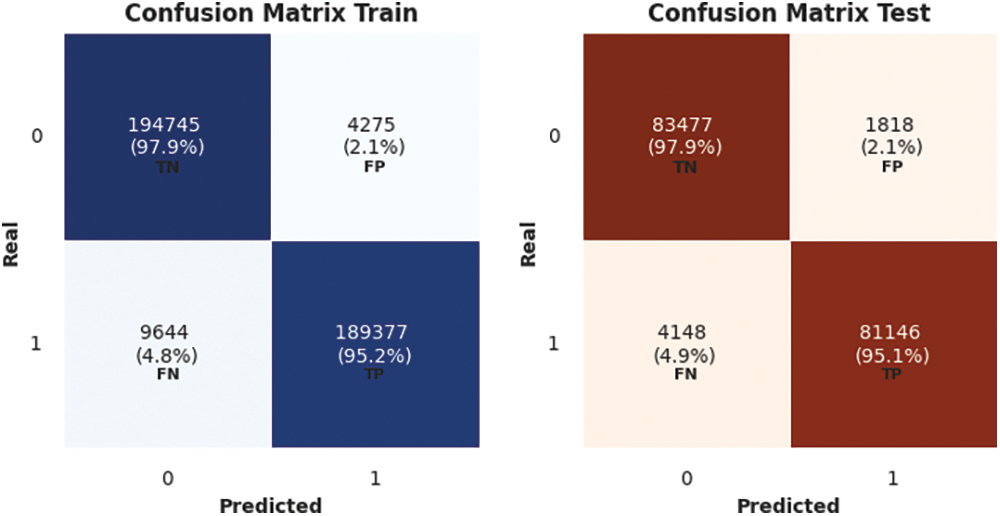
Figure 6: Logistic regression confusion matrix

5.2 Random Forest Performance

For the training set of the credit card fraud detection dataset, the random forest model has achieved a precision, recall, and F1 score of 1.00 for both classes, indicating that every instance was classified correctly according to the model. Class 0, representing legitimate transactions, and class 1, representing fraudulent activities, show an absolute score, typically suggesting that the model has perfectly distinguished between the two. However, such perfect metrics could indicate potential overfitting to the training data.

In the test set, the model also reports precision, recall, and F1 scores of 1.00 for both classes. This implies that the model has classified all test instances without error. While these results appear ideal, such perfection is uncommon in practical scenarios. It might warrant further investigation for issues such as data leakage, overfitting, or an error in the evaluation process, as real-world data often contains noise and anomalies that prevent such flawless performance. It is also noted that the F1 score is not provided in the report. It could give additional insights into the model’s ability to balance recall against precision, especially in the imbalanced classes typical of fraud detection datasets. The classification report for the train set and test set for the random forest is shown in Fig. 7.

Figure 7: Random forests classification report for train and test sets

The confusion matrix for random forests using train and test sets is shown in Fig. 8.

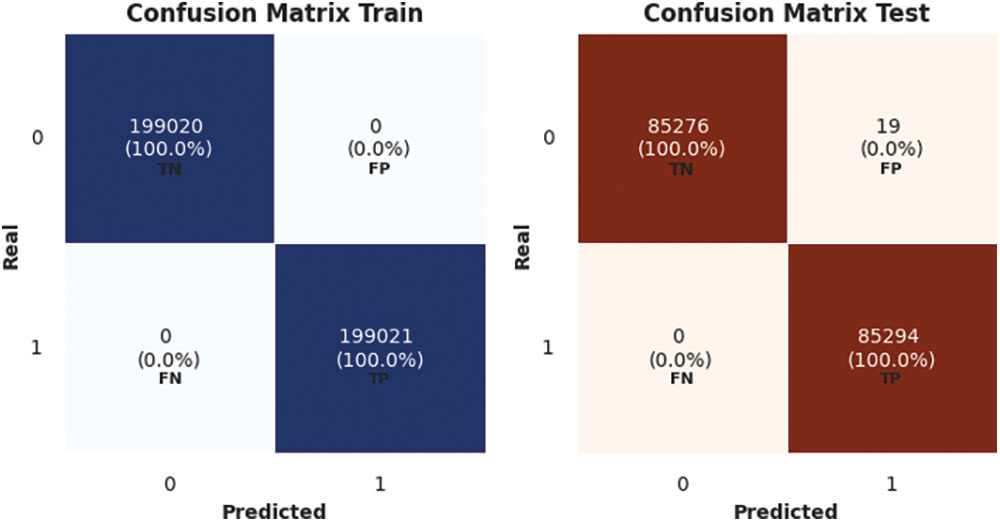
Figure 8: Random forest confusion matrix for train and test sets

5.3 Extra Trees Performance

For the training set, the Extra Trees model applied to the credit card fraud detection dataset indicates precision, recall, and an F1 score of 1.00 for both classes. While these results suggest that the model has classified every instance correctly as either class 0 (non-fraudulent) or class 1 (fraudulent), they also raise concerns about overfitting. It is atypical for any model to achieve such perfect metrics on real-world data, which often contains some level of noise and complexity.

In the test set, the model continues to display precision, recall, and F1 score of 1.00 for both classes, suggesting no loss in performance from the training set to the unseen data. This perfection in the test metrics, as with the training metrics, is unusual and could suggest issues such as data leakage, over-optimistic evaluation, or an overly simplistic test set that does not capture the complexities of real-world data. Furthermore, the lack of an F1 score, which places more emphasis on recall, limits the evaluation of the model’s performance in scenarios where failing to detect fraud (a false negative) is more detrimental than incorrectly flagging a legitimate transaction as fraudulent (a false positive). Thus, while the reported metrics are ideal, the practicality of such results in a real-world application should be critically assessed. The classification report for the train set and test set for extra trees is shown in Fig. 9.

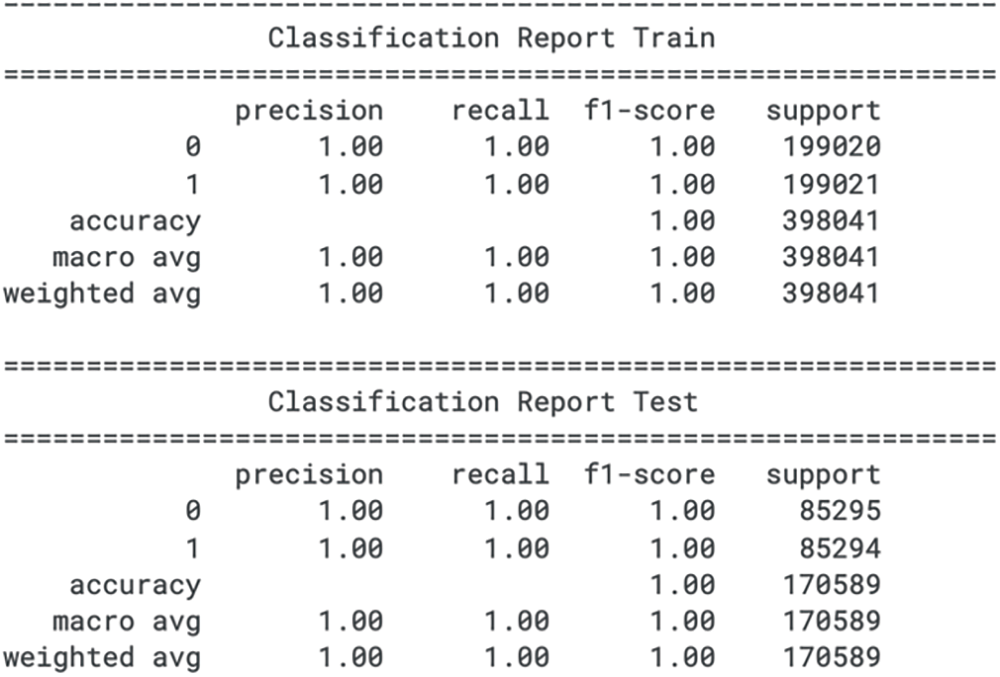
Figure 9: Extra trees classification report for train and test sets

The confusion matrix for extra trees using train and test sets is shown in Fig. 10.

Figure 10: Extra trees confusion matrix for train and test set

5.4 XGBoost (XGB) Performance

The classification report for the XGBoost model on the credit card fraud detection dataset presents metrics for the training set with precision, recall, and F1 score at 1.00 for both classes, 0 (non-fraudulent) and 1 (fraudulent). These scores imply that the model has classified all instances of the training set correctly. While such results would typically be considered excellent, in the context of a real-world application like fraud detection, they may suggest a model that is overly fitted to the training data.

Similarly, for the test set, the model also scores a precision, recall, and F1 score of 1.00 for both classes. This indicates that the model has classified the test data without any errors. Nonetheless, such perfect performance on the test set is unusual and may warrant further investigation. This could involve checking for data leakage, ensuring the test set is representative of real-world scenarios, and validating the robustness of the model against different datasets. An F1 score, which is not provided in the report, would be useful for understanding the model’s performance in terms of recall, which is crucial in fraud detection to minimize the number of fraudulent transactions that go undetected. Without an F1 score, it is harder to evaluate the model’s utility in operational settings where false negatives can have significant consequences. The classification report for the train set and test set for XGB is shown in Fig. 11.

Figure 11: XGB classification report for train and test sets

The confusion matrix for XGB using train and test sets is shown in Fig. 12.

Figure 12: XGB confusion matrix for train and test sets

5.5 Light Gradient Boosting Machine (LGBM) Performance

For the training set, the LGBM model achieves a precision, recall, and F1 score of 1.00 for both the non-fraudulent (class 0) and fraudulent (class 1) classes. These metrics suggest that the model has classified every instance correctly during training. While these results show no indication of classification error, they may not indicate the model’s expected performance in a real-world scenario, where data is rarely perfect, and models may not perform with absolute accuracy.

In the test set, the model also reports precision, recall, and an F1 score of 1.00 for both classes, maintaining the same level of performance observed in the training set. Such high scores across the test set suggest that the model is potentially overfitted, as it is uncommon for models to achieve perfect generalization on unseen data, especially in complex tasks like fraud detection. The lack of an F1 score, which gives more weight to recall, prevents a deeper insight into the model’s ability to prioritize correctly identifying fraudulent transactions over non-fraudulent ones. These perfect metrics warrant carefully examining the model’s evaluation process to ensure its validity and applicability in operational environments. The classification report for train set and test set for LGBM is shown in Fig. 13.

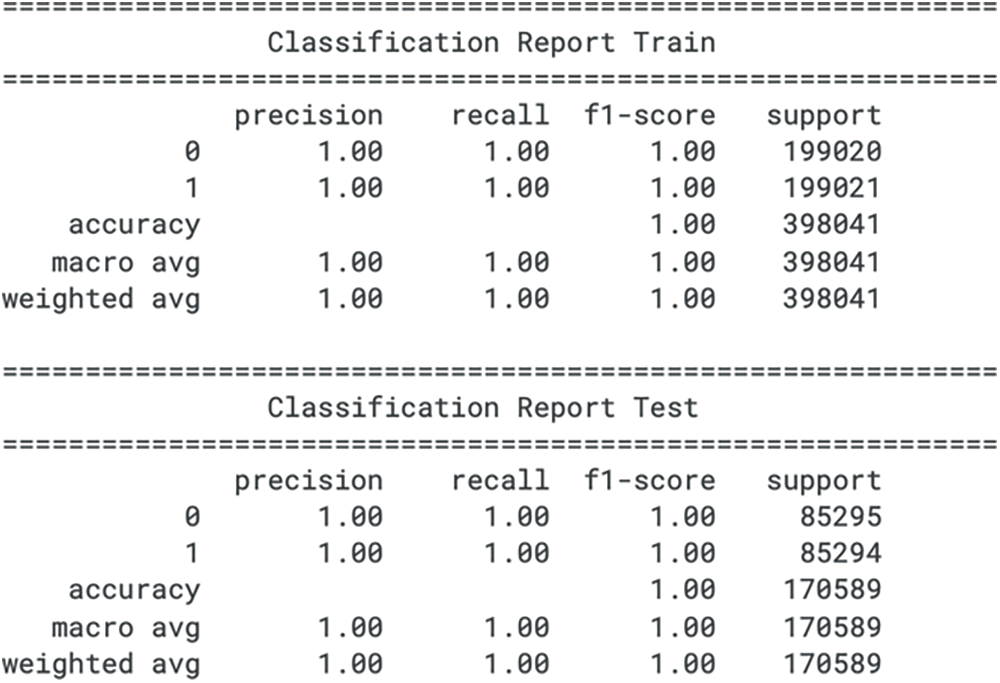
Figure 13: LBGM classification report for train and test sets

The confusion matrix for LBGM using train and test sets is shown in Fig. 14.

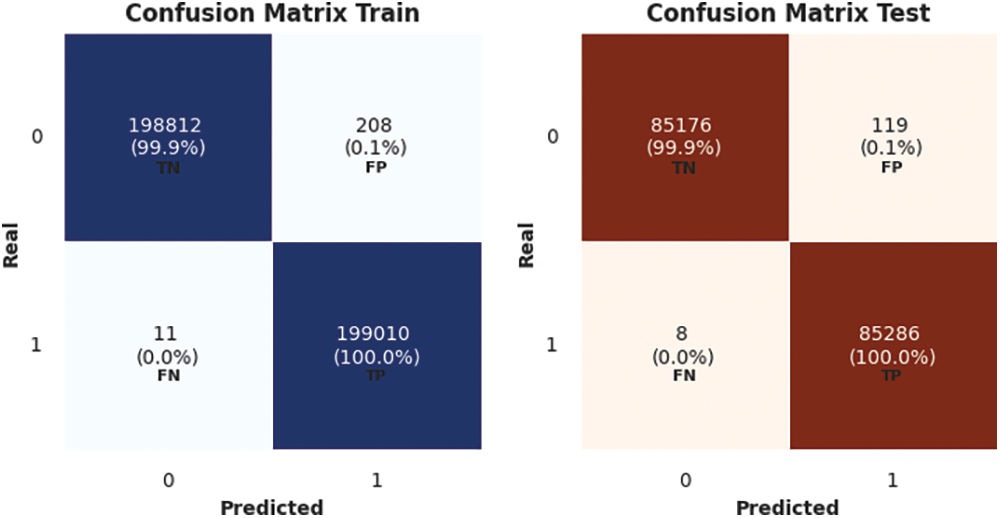
Figure 14: LBGM confusion matrix for train and test sets

5.6 Categorical Boosting (CatBoosting) Performance

The classification report for the Light Gradient Boosting Machine (LGBM) model on the credit card fraud detection dataset shows precision, recall, and F1 score of 1.00 for both class 0 (not fraud) and class 1 (fraud) in the training set. These metrics would typically indicate that the model has achieved perfect classification on the training data. However, such perfect scores across all metrics raise questions about the model’s generalizability, as they could suggest that the model is overfitting to the training set.

On the test set, the LGBM model retains the precision, recall, and F1 score of 1.00 for both classes, suggesting that it has perfectly classified the unseen data. While this could indicate the model’s robustness, it is rare to achieve such results in a real-world scenario, particularly for fraud detection where data is inherently imbalanced and noisy. The perfect scores on the training and test sets could indicate data leakage, an overly simplistic test set, or other evaluation methodology problems. Additionally, the F1 score, which emphasises recall, is not reported. This is a significant omission, as the F1 score is particularly relevant in fraud detection, where the cost of false negatives (failing to identify fraudulent transactions) is often much higher than that of false positives (incorrectly flagging a transaction as fraudulent). Without the F1 score, evaluating the model’s true performance in prioritizing recall is incomplete. Therefore, these results should be interpreted cautiously, and further validation should be conducted to confirm the model’s effectiveness in a practical setting. The classification report for train set and test set for CatBoost is shown in Fig. 15.

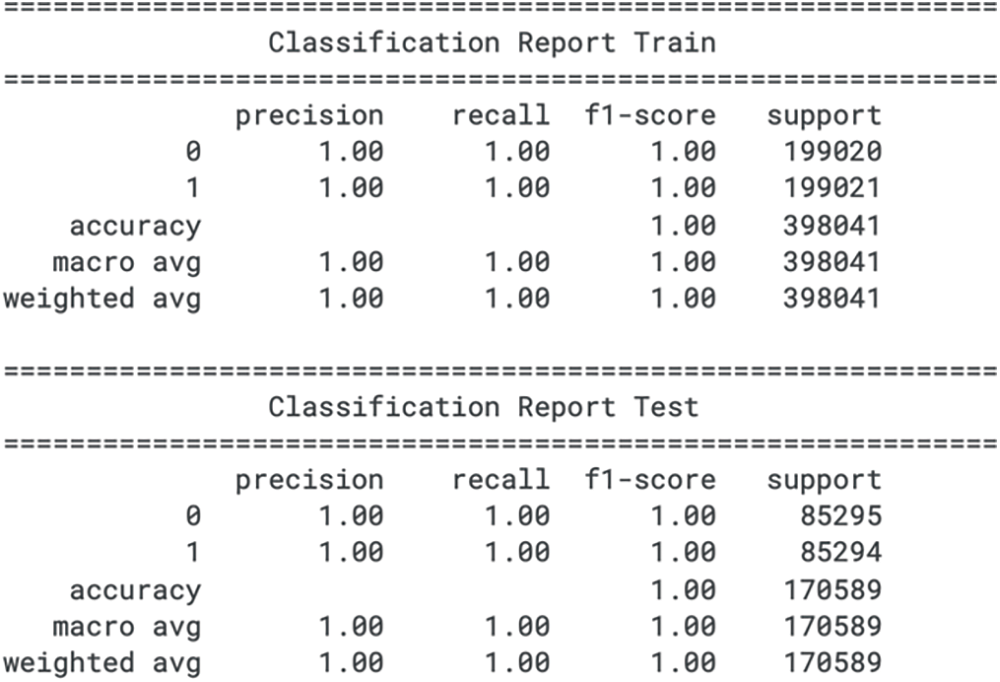
Figure 15: CatBoost classification report for train and test sets

The confusion matrix for CatBoost using train and test sets is shown in Fig. 16.

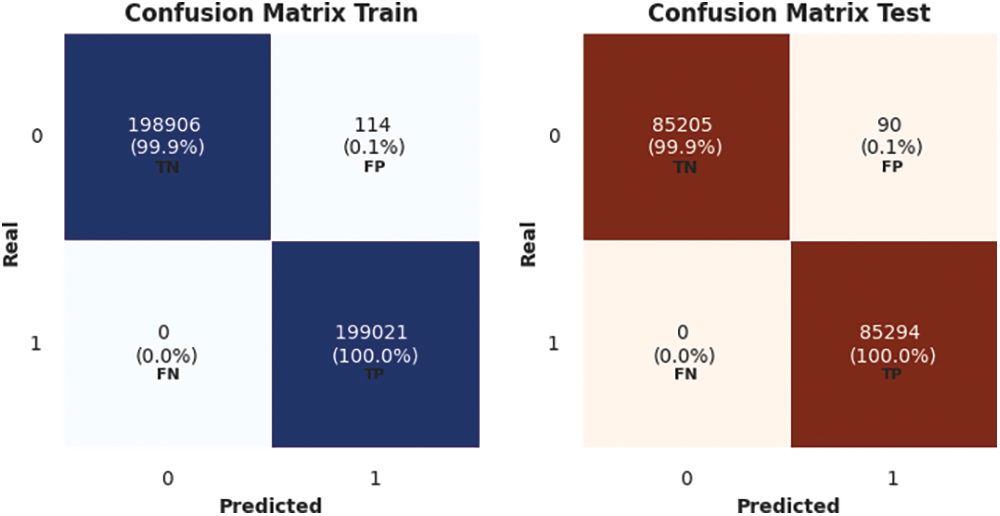
Figure 16: CatBoost confusion matrix for train and test sets

6  Discussion and Analysis

This section provides a performance overview of the machine learning models using accuracy, recall, F1 score, and model training time.

6.1 Accuracy Comparison

According to the test results using the dataset, logistic regression, random forest, extra trees, and Light Gradient Boosting Machine (LGBM) models on a credit card fraud detection dataset indicate that each model has achieved a test accuracy of 1.00 for both classes, class 0 (non-fraudulent transactions) and class 1 (fraudulent transactions). This suggests that on the test set, every model could correctly classify all instances without error. The comparison of accuracy is shown in Fig. 17.

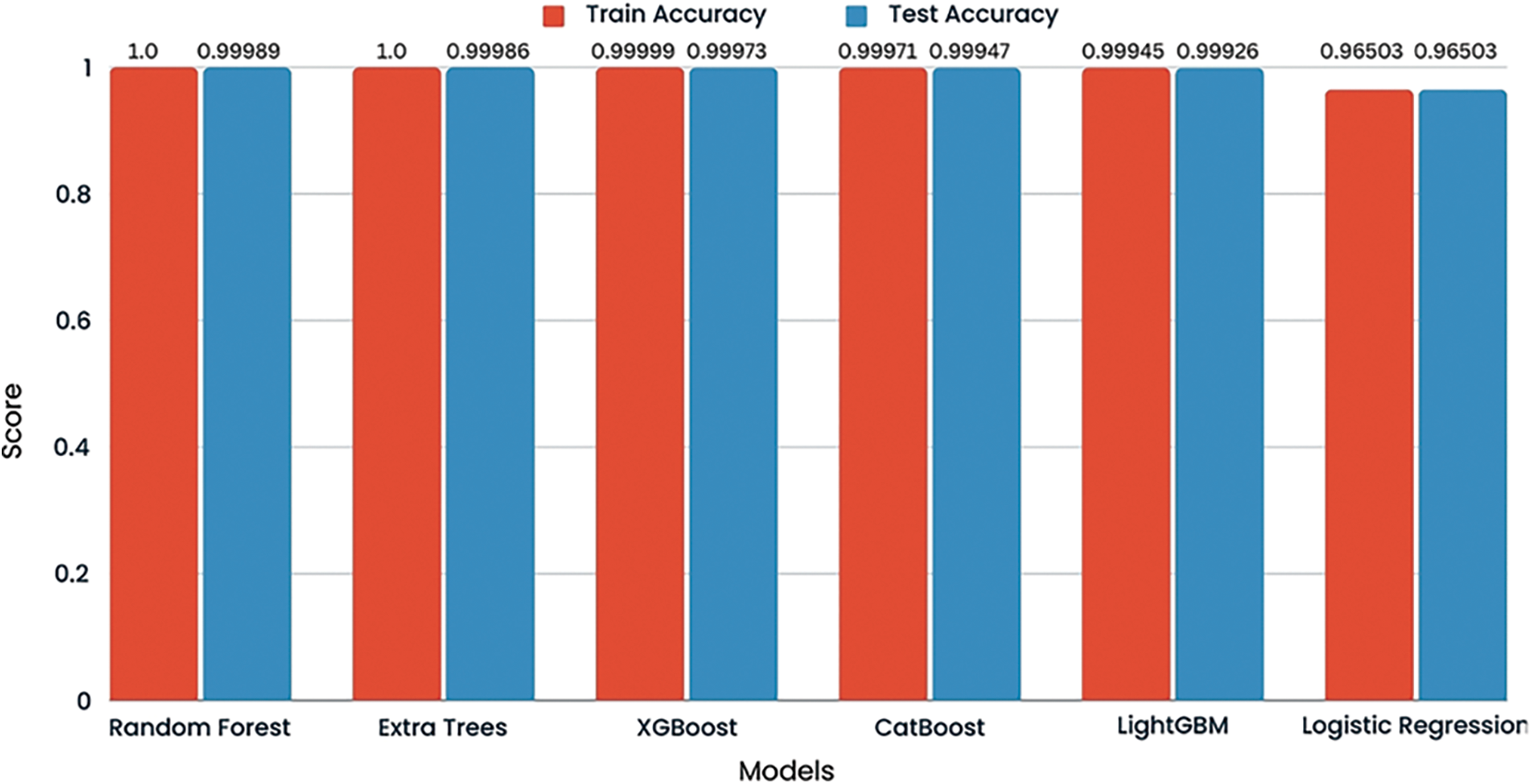
Figure 17: Accuracy comparison

6.2 Recall Comparison

The recall for logistic regression, random forest, extra trees, and LGBM on the credit card fraud detection dataset is reported to be 1.00 for class 0 (non-fraud) and class 1 (fraud) on the test set. This indicates that each model has a recall rate of 100%, signifying that they all have correctly identified every instance of fraudulent and legitimate transactions without missing any actual fraud cases. The comparison of recall is shown in Fig. 18.

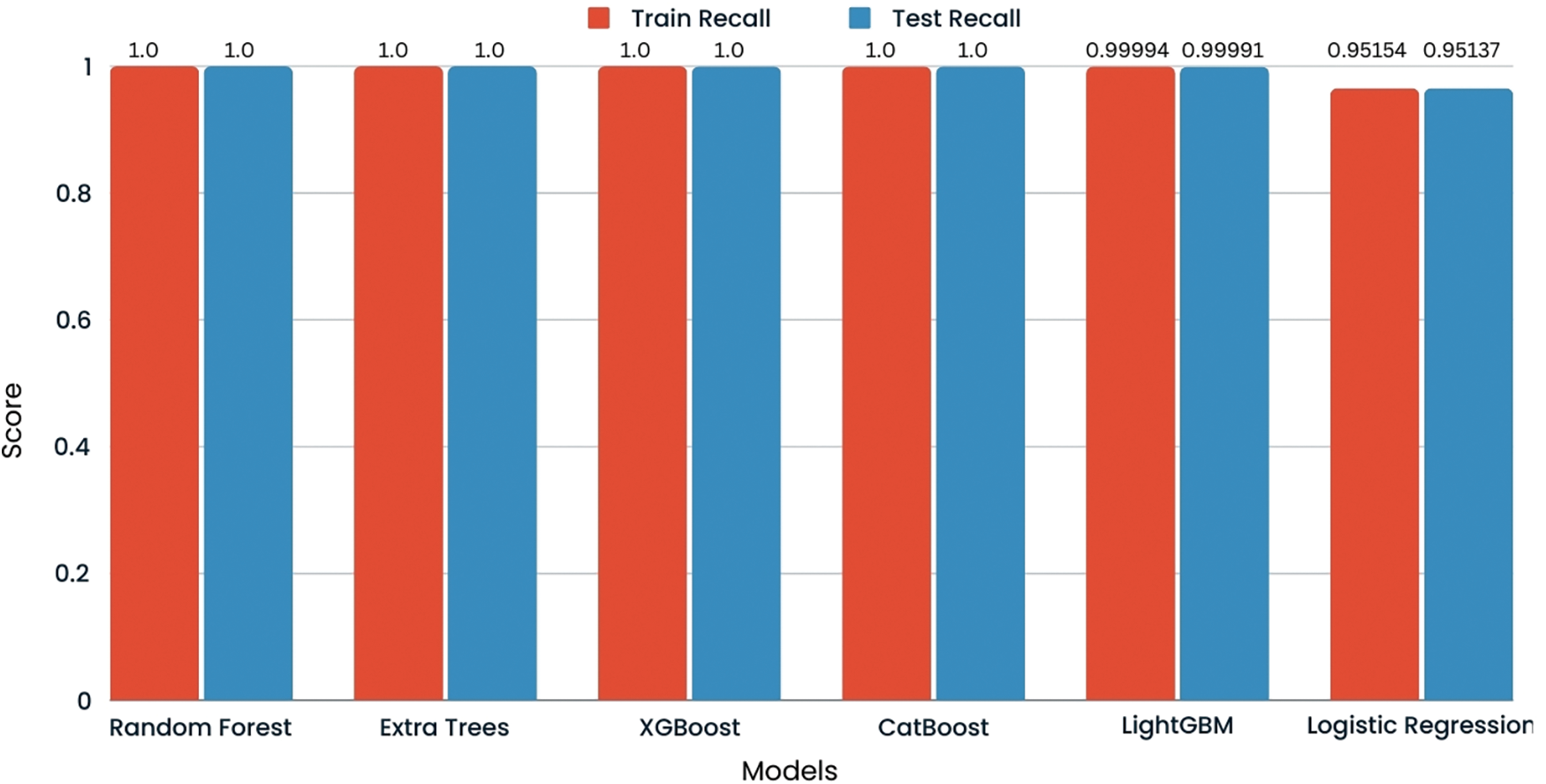
Figure 18: Recall comparison

6.3 F1 Score Comparison

The F1 score for the test set across all model’s logistic regression, random forest, extra trees, and LGBM is consistently reported as 1.00 for both classes in the credit card fraud detection dataset. The F1 score, the harmonic means of precision and recall, at a perfect score indicates that each model is achieving the highest possible performance in precision and recall. This suggests that the models are not only identifying all actual positive cases (recall) but also that all their positive predictions are correct (precision). The comparison of F1 score is shown in Fig. 19.

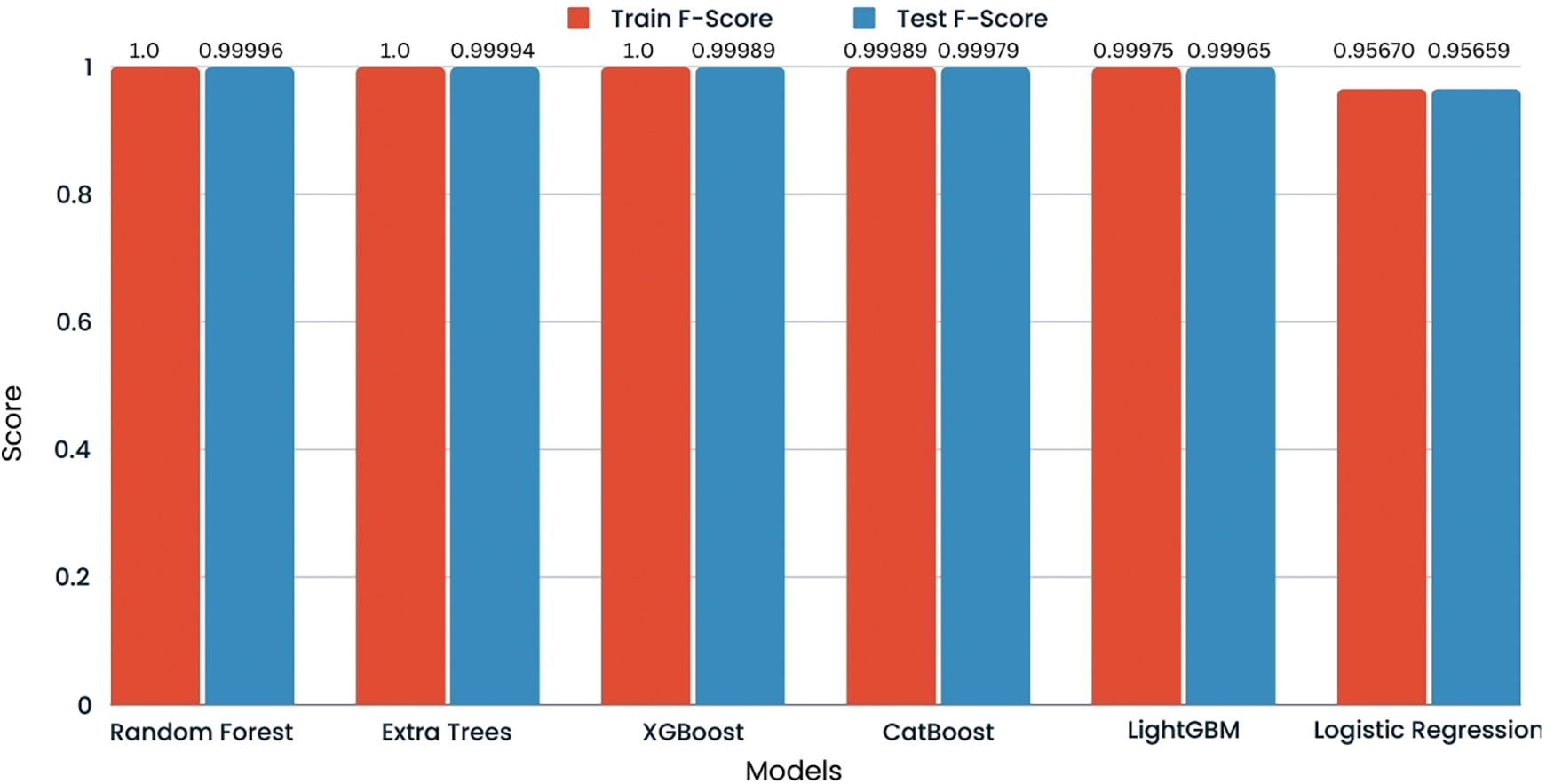
Figure 19: F1 score comparison

A significant difference in computing efficiency may be seen when comparing the training times for the various machine-learning models. Logistic Regression and LightGBM stand out as the quickest, with just a few seconds of training times. Because of this, they are perfect for situations that call for rapid iteration and speedy model construction. Since Random Forest and XGBoost are both ensemble learning methods, they require much longer to train, with some training sessions lasting more than several minutes. While these models may be more time-consuming, they frequently yield great predictive performance. Because of this, they are appropriate for applications in which model accuracy is of the utmost importance and computational resources are in abundance. The training times for Extra Trees and CatBoost are somewhere in the middle, taking somewhat longer than those for Logistic Regression and LightGBM but less time than those for Random Forest and XGBoost. When selecting the appropriate model, one should consider the time needed for training and the demands and objectives of the machine learning activity. This strikes a balance between the requirement for computational efficiency and the desire for predictive power. Table 2 shows the training time for all the models.

Both Logistic Regression and LightGBM demonstrate remarkable efficiency, as their training times are on the scale of seconds. They provide an appealing option for use cases requiring quick model creation and iteration, especially in real-time or time-sensitive fraud detection. On the opposite side of the continuum, models like Random Forest and XGBoost demonstrate extended training durations, surpassing several minutes. Ensemble approaches frequently exhibit enhanced prediction performance but at the cost of increased computational resource requirements. The appropriateness of their suitability may be most closely associated with situations in which precision is of utmost importance and computational resources are accessible to facilitate the longer duration required for training. The Extra Trees and CatBoost algorithms are positioned between these extremes, providing a harmonious trade-off. Although the training durations of these models are somewhat lengthier compared to Logistic Regression and LightGBM, they offer a favourable trade-off between predicted accuracy and computational effectiveness.

7  Conclusion

In the case of credit card fraud detection, the choice of a machine learning model must consider not just prediction performance but also the practical factor of training time. The evaluation of the various models reveals a trade-off between the time spent on training and the accuracy of the results. Logistic Regression and LightGBM are extraordinarily effective alternatives, with training times on the order of seconds. When it comes to situations in which rapid model creation and iteration are crucial, such as when dealing with real-time or time-sensitive fraud detection, they offer an appealing choice as a potential solution. On the opposite end of the spectrum are the models with longer training times, such as Random Forest and XGBoost, which can last several minutes or longer. These ensemble approaches frequently improve prediction performance despite the increased processing resources they require. Their applicability may be best matched with circumstances in which precision is of the utmost importance and when sufficient computational resources are available to support the prolonged training timeframes.

Extra Trees and CatBoost provide a reasonable middle ground by mediating between the two perspectives. Even though their training times are moderately longer than those of Logistic Regression and LightGBM, they offer a decent balance between their models’ predictive strength and computational efficiency. In the end, the decision of which machine learning model to use for the detection of credit card fraud should be made under the requirements and limitations of the application. When time is of importance, it is possible that more straightforward models, such as Logistic Regression and LightGBM, will be preferred. On the other hand, ensemble models such as Random Forest and XGBoost might be better appropriate for jobs that require the highest possible accuracy as well as the availability of resources. To combat credit card fraud effectively, the decision should be based on an in-depth analysis of performance, training time, and available resources, striking the optimal balance between the three factors.

Machine learning techniques help detect fraudulent activities. This study provides a comparative analysis of Regression and Boosting models, including Linear Regression, Random Forest, Extra Trees, XGBoosting, LightGBM, and CatBoost. The study is helpful for beginner researchers to understand the performance of the machine learning models for fraudulent transaction detections using a public dataset. In future, the evaluation of these machine learning models can be performed using multiple datasets. Also, the deep learning models can be applied for credit card fraud detection using the same dataset, along with other datasets, to compare the performance of machine learning and deep learning models.

Acknowledgement: None.

Funding Statement: The authors received no specific funding for this study.

Author Contributions: The authors confirm their contribution to the paper as follows: models implementation: Adil Hussain; data collection: Ayesha Aslam; interpretation of results: Adil Hussain, Ayesha Aslam; draft manuscript preparation: Adil Hussain. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The data will be provided on request.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. L. Duan, L. Xu, Y. Liu, and J. Lee, “Cluster-based outlier detection,” Ann. Oper. Res., vol. 168, pp. 151–168, 2009. [Google Scholar]

2. E. A. Minastireanu and G. Mesnita, “Light GBM machine learning algorithm to online click fraud detection,” J. Inform. Assur. Cybersecur., vol. 2019, pp. 263928, 2019. [Google Scholar]

3. Y. Fang, Y. Zhang, and C. Huang, “Credit card fraud detection based on machine learning,” Comput. Mater. Contin., vol. 61, no. 1, 2019. [Google Scholar]

4. S. Maes, K. Tuyls, B. Vanschoenwinkel, and B. Manderick, “Credit card fraud detection using Bayesian and neural networks,” in Proc. 1st Int. Naiso Congress Neuro Fuzzy Technol., vol. 261, pp. 270, 2002. [Google Scholar]

5. M. Wang, J. Yu, and Z. Ji, “Credit fraud risk detection based on XGBoost-LR hybrid model,” in Proc. 18th Int. Conf. Electron. Bus., Guilin, China, Dec. 2–6, 2018, pp. 336–343. [Google Scholar]

6. S. Dhingra, “Comparative analysis of algorithms for credit card fraud detection using data mining: A review,” J. Adv. Database Manag. Syst., vol. 6, no. 2, pp. 12–17, 2019. [Google Scholar]

7. A. C. Bahnsen, D. Aouada, A. Stojanovic, and B. Ottersten, “Feature engineering strategies for credit card fraud detection,” Expert Syst. Appl., vol. 51, pp. 134–142, 2016. [Google Scholar]

8. Y. Zhang, J. Tong, Z. Wang, and F. Gao, “Customer transaction fraud detection using xgboost model,” in Int. Conf. Comput. Eng. Appl. (ICCEA), IEEE, Guangzhou, China, 2020, pp. 554–558. [Google Scholar]

9. V. Bhusari and S. Patil, “Study of hidden markov model in credit card fraudulent detection,” Int. J. Comput. Appl., vol. 20, no. 5, pp. 33–36, 2011. [Google Scholar]

10. N. Carneiro, G. Figueira, and M. Costa, “A data mining based system for credit-card fraud detection in e-tail,” Decis. Support Syst., vol. 95, pp. 91–101, 2017. [Google Scholar]

11. F. N. Ogwueleka, “Data mining application in credit card fraud detection system,” J. Eng. Sci. Technol., vol. 6, no. 3, pp. 311–322, 2011. [Google Scholar]

12. K. RamaKalyani and D. UmaDevi, “Fraud detection of credit card payment system by genetic algorithm,” Int. J. Sci. Eng. Res., vol. 3, no. 7, pp. 1–6, 2012. [Google Scholar]

13. P. Meshram and P. Bhanarkar, “Credit and ATM card fraud detection using genetic approach,” Int. J. Eng. Res. Technol. (IJERT), vol. 1, no. 10, pp. 1–5, 2012. [Google Scholar]

14. G. Singh, R. Gupta, A. Rastogi, M. D. Chandel, and R. Ahmad, “A machine learning approach for detection of fraud based on SVM,” Int. J. Sci. Eng. Technol., vol. 1, no. 3, pp. 192–196, 2012. [Google Scholar]

15. K. Seeja and M. Zareapoor, “FraudMiner: A novel credit card fraud detection model based on frequent itemset mining,” Sci. World J., vol. 2014, pp. 252797, 2014. [Google Scholar]

16. J. R. Gaikwad, A. B. Deshmane, H. V. Somavanshi, S. V. Patil, and R. A. Badgujar, “Credit card fraud detection using decision tree induction algorithm,” Int. J. Innov. Technol. Explor. Eng. (IJITEE), vol. 4, no. 6, pp. 2278–3075, 2014. [Google Scholar]

17. E. Duman, A. Buyukkaya, and I. Elikucuk, “A novel and successful credit card fraud detection system implemented in a Turkish bank,” in 2013 IEEE 13th Int. Conf. Data Mining Workshops, IEEE, Dallas, TX, USA, 2013, pp. 162–171. [Google Scholar]

18. A. C. Bahnsen, A. Stojanovic, D. Aouada, and B. Ottersten, “Improving credit card fraud detection with calibrated probabilities,” in Proc. 2014 SIAM Int. Conf. Data Mining, SIAM, 2014, pp. 677–685. [Google Scholar]

19. A. Ng and M. Jordan, “On discriminative vs. generative classifiers: A comparison of logistic regression and Naïve Bayes,” in Adv. Neural Inf. Process. Syst., 2001, pp. 841–848. [Google Scholar]

20. A. Shen, R. Tong, and Y. Deng, “Application of classification models on credit card fraud detection,” in 2007 Int. Conf. Serv. Syst. Serv. Manag., IEEE, Chengdu, China, 2007, pp. 1–4. [Google Scholar]

21. S. Bhattacharyya, S. Jha, K. Tharakunnel, and J. C. Westland, “Data mining for credit card fraud: A comparative study,” Decis. Support Syst., vol. 50, no. 3, pp. 602–613, 2011. [Google Scholar]

22. Y. Sahin and E. Duman, “Detecting credit card fraud by ANN and logistic regression,” in 2011 Int. Symp. Innov. Intell. Syst. Appl., IEEE, Chengdu, China, 2011, pp. 315–319. [Google Scholar]

23. Y. G. Şahin and E. Duman, “Detecting credit card fraud by decision trees and support vector machines,” in Proc. of the Int. MultiConf. of Eng. and Comp. Sci., 2011, 2011, pp. 442–447. [Google Scholar]

24. K. Sherly, “A comparative assessment of supervised data mining techniques for fraud prevention,” TIST Int. J. Sci. Tech. Res, vol. 1, no. 1, pp. 1–6, 2012. [Google Scholar]

25. S. Mittal and S. Tyagi, “Performance evaluation of machine learning algorithms for credit card fraud detection,” in Proc. IEEE Confluence, Noida, India, 2019, pp. 320–324. [Google Scholar]

26. A. H. Nadim, I. M. Sayem, A. Mutsuddy, and M. S. Chowdhury, “Analysis of machine learning techniques for credit card fraud detection,” in Proc. IEEE iCMLDE, Taipei, Taiwan, 2019, pp. 42–47. [Google Scholar]

27. F. Itoo, Meenakshi, and S. Singh, “Comparison and analysis of logistic regression, Naïve Bayes and KNN machine learning algorithms for credit card fraud detection,” Int. J. Inf. Technol., vol. 13, pp. 1503–1511, 2021. [Google Scholar]