An Example of a Supporting Combination by Using GA to Evolve More Advanced and Deeper CNN Architecture

1  Introduction

Deep Neural Networks (DNNs) have garnered substantial attention in recent years due to their potential in various applications. The architecture and hyper parameter configuration of DNNs play a pivotal role in their overall performance. Presently, DNN models are meticulously crafted by experts from diverse domains in machine learning, tailored to address specific problem domains or datasets. For instance, Convolutional Neural Networks (CNNs) find widespread use in a myriad of computer vision applications, particularly those related to images [1]. While techniques like transfer learning can be employed to adapt existing state-of-the-art DNNs to similar tasks as found in the literature, it is crucial to acknowledge that a one-size-fits-all network architecture is seldom optimal for all scenarios. Hence, the need arises to design DNNs that are custom-tailored to the specific problem at hand to achieve optimal performance. Consequently, a growing number of researchers are actively developing automated methods capable of identifying the most suitable DNN architecture and hyper parameters for a given task. Evolutionary algorithms (EAs), a category of population-based meta-heuristic optimization methods, are valuable tools for uncovering the optimal network design and hyper parameters [2]. Notably, there have been notable endeavors in the scientific literature to address diverse optimization challenges by utilizing various evolutionary algorithm variants, such as Genetic Algorithms (GAs) and Particle Swarm Optimization (PSO) [3]. Given the promise exhibited by evolutionary algorithms and Artificial Neural Networks (ANNs) across a spectrum of machine learning tasks, researchers have been diligently exploring effective approaches to amalgamate these two methodologies. This exploration has led to the detailed examination of two fundamental combination techniques, namely supportive combinations and collaborative combinations [4]. Supportive combinations employ genetic algorithms to facilitate the development of neural networks, allowing the networks to dynamically adapt their parameters and acquire new rules. In contrast, collaborative combinations employ genetic algorithms to determine the neural network’s topology, weights, or both. In a supportive combination, Genetic Algorithms assist in selecting features for neural networks, while in a collaborative combination, Genetic Algorithms are instrumental in crafting the architecture of an ANN.

There is a growing interest in leveraging evolutionary algorithms (EAs) to construct and train Deep Neural Networks (DNNs), which have emerged as highly effective tools for tackling a wide array of challenges in machine learning. Historically, training DNNs using EAs has garnered relatively less attention, partly due to the rapid advancement of gradient-based methods and the formidable challenges posed by the vast search space. Research efforts have primarily concentrated on two core areas: the creation of deep neural network (DNN) architectures and the identification of optimal hyper parameter configurations for various regression and classification tasks [2].

While Genetic Algorithms (GA) have been employed for training DNNs in reinforcement learning, such endeavors, although notable, have been somewhat overshadowed by the predominant research focus on the aforementioned topics [5]. Convolutional Neural Networks (CNNs) stand out as highly efficient deep architectures, demonstrated by their remarkable performance across numerous practical applications. The development of modern CNN designs, exemplified by VGG-Net, Res-Net, and Google-Net, represents a domain reserved for seasoned researchers with substantial subject knowledge and neural network design expertise.

However, for novice researchers and application engineers, devising an appropriate architecture tailored to the specific problem and dataset often proves to be a challenging endeavor, given these prerequisites. As a response to these challenges, recent years have witnessed numerous endeavors that employ evolutionary algorithms to autonomously generate CNN structures and optimize network hyper parameters, making this powerful technology more accessible to a broader audience.

In this research, we designed and fine-tuned Convolutional Neural Network (CNN) architectures using a conventional Genetic Algorithm (GA), aiming to identify the optimal combination of hyper parameters for the task of image classification on the MNIST dataset. Our focus was on optimizing the traditional CNN architecture, structured as a sequence of convolutional layers, and inspired by VGG-like networks. The study involved the optimization of both the number of convolutional blocks and the number of layers within each block through the proposed GA. We explored a flexible search space for CNN architectures, allowing for a variable number of layers while employing a fixed-sized chromosome representation. Furthermore, the algorithm systematically sought out the most suitable set of hyper parameters for the network from predefined parameter ranges.

A significant challenge encountered in the evolution of various Deep Neural Networks (DNNs) is the substantial computational burden. The fitness evaluation of each individual within an evolutionary algorithm necessitates the training of numerous deep neural networks, resulting in a considerable computational load. Recent research has introduced the concept that only partial training is required to estimate the quality of a Convolutional Neural Network (CNN) architecture [6,7]. In this study, we adopted this approach, implementing it by training the CNN architectures for a limited number of epochs during the evolutionary phase. Subsequently, the most promising CNN model underwent comprehensive training to assess its overall performance.

Our approach employed a Genetic Algorithm (GA) on a well-established dataset, and the CNN model that emerged from this evolutionary process was compared against a range of other autonomously generated models, highlighting its effectiveness.

The subsequent sections of this paper are organized as follows: In Section 2, an extensive review of the pertinent literature is presented. Section 3 offers an in-depth exploration of the proposed Genetic Algorithm. Section 4 outlines the details of the experimental setup. Section 5 delves into the presentation of the experimental results. Section 6 provides a concise discussion of the results. Finally, Section 7 brings the study to a conclusion.

2  Related Works

Convolutional Neural Networks (CNNs), inspired by the structural brotherhood of the bestial layer [8], are typically employed for processing two dimensional inputs, such as images. Convolutional Neural Networks (CNNs) consist of three primary types of coats: convolutional, pooling, and fully-connected layers. These layers rely on three fundamental concepts—equivariant representations, parameter-sharing, and sparse interactions—to drive their learning processes [9].

In traditional artificial neural networks (NNs), matrix multiplication determines the connections between input and output components, incurring substantial computational costs. However, CNNs drastically reduced this computational burden by utilizing sparse interactions, employing smaller kernels compared to the input size, and applying them across the entire image. To enhance the feature-capturing capabilities of convolutional layers, pooling layers are frequently incorporated to reduce dimensionality. Parameter sharing further streamlines training by ensuring that a single set of parameters is used across all locations, contributing to CNNs’ superior performance compared to standard NNs. The core components of a multi-layer neural network, the CNN, predominantly comprise convolutional and pooling layers. When designing a CNN architecture, various hyper parameters must be considered, including the stride size of the pooling layer, kernel size, type of pooling operation, number of layers in a convolutional block, the configuration of fully connected layers, the size of the convolution layer channels, and more. In human-designed Convolutional Neural Networks, these hyper parameters are typically determined through a process of trial and error, often guided by existing literature and established practices in layer design.

The field of evolutionary computation has recently witnessed a surge in interest regarding the evolution of Deep Neural Network (DNN) architectures and their associated hyper parameters. In a notable contribution, David and Greental [10] introduced a straightforward genetic algorithm (GA)-assisted approach for optimizing auto encoders on the MNIST dataset, resulting in the creation of sparser networks and improved performance. In their method, multiple sets of weights (W) are maintained for the layers. Each chromosome within the GA population represents a unique set of weights for the auto encoder. The root mean squared error (RMSE), calculated as the difference between input and output layer values for each training sample, serves as the fitness metric for each chromosome. All chromosomes receive fitness scores, leading to their ranking from most fit to least fit. Backpropagation is utilized to update the weights of the top-ranked chromosomes, while the lower-ranked chromosomes are removed from the population. The elimination of low-ranking members is solely determined by their fitness scores, and selection is carried out uniformly and consistently across all promising chromosomes. The authors demonstrated that this GA-assisted technique surpasses conventional backpropagation in terms of both reconstruction error and network sparsity, thereby enhancing the performance of auto encoders.

Suganuma et al. [6] presented a method for crafting Convolutional Neural Network (CNN) architectures based on Cartesian Genetic Programming (CGP). In this approach, CNN architectures are represented as directed acyclic graphs, with each node representing functional modules such as convolutional blocks and tensor operations, and each edge denoting layer connections. An evolutionary process is employed to optimize the design, aiming to maximize classification accuracy using a validation dataset. Their experiments on the CIFAR10 and CIFAR100 datasets illustrate that this method can identify CNN architectures that compete effectively with state of the art approaches in image classification.

In a separate contribution, Zhou et al. [11] proposed the utilization of the Covariance Matrix Adaptation Evolution Strategy (CMA-ES), renowned for its advanced performance in derivative-free optimization—the method they advocate for. CMA-ES facilitates concurrent evaluations of solutions and possesses valuable invariance properties. To demonstrate a comparison between CMA-ES and contemporary Bayesian optimization techniques when fine-tuning hyper parameters for a convolutional neural network using 30 GPUs concurrently, a toy example is provided.

In a separate study, Sun et al. [12] harnessed the power of a Genetic Algorithm to autonomously craft Convolutional Neural Network (CNN) architectures for image categorization. Their approach incorporated skip layers, enhancing the network structure, which featured two convolutional layers and a skip connection inspired by Res-Net [13]. Moreover, they used their method to determine the number of feature maps while maintaining consistent filter sizes and strides across convolutional layers. In their model, they replaced fully connected layers with pooling layers. They gauged the effectiveness of their methodology through extensive benchmarking, including well-known datasets like CIFAR-10 and CIFAR-100.

In a related work by Sun et al. [14], they leveraged Res-Net and Dense-Net blocks [15] to autonomously evolve CNN designs. Their approach involved the synthesis of CNN architectures using three distinct units: Res-Net block units, Dense-Net block units, and pooling layer units. Each Res-Net or Dense-Net unit comprised numerous Res-Net and Dense-Net blocks, enabling adjustments to the network’s depth and heuristic search efficiency by modifying its depth. By analyzing their model’s performance against 18 state of the art algorithms on CIFAR10 and CIFAR100 datasets, they showcased the superiority of their approach.

Another noteworthy contribution was made by Bakhshi et al. [16], who suggested a Genetic Algorithm (GA) model for the automatic determination of optimal CNN architectures and the corresponding hyper parameters, describing it as a deep evolutionary technique. They employed a traditional genetic algorithm named fast-CNN to identify the optimal combination of CNN hyper parameters, including the number of layers, feature maps, learning rate, weight decay factor, and momentum. Although the CNN model was developed using the CIFAR10 dataset, its performance was evaluated on both the CIFAR10 and CIFAR100 datasets. They conducted a comprehensive comparison, pitting the performance of the developed fast-CNN model against 13 cutting-edge algorithms, considering classification accuracy, GPU usage, and parameter setup techniques.

Furthermore, Sun et al. [7] employed an effective variable-length gene encoding strategy to determine the optimal depth of the CNN. They presented a novel approach for initializing the interconnection of weights of the Deep Neural Networks (DNNs) to mitigate issues with local minima, a significant challenge in gradient-based training. Their work was subjected to rigorous evaluation on nine widely recognized image classification tasks, where they compared their results against 22 existing algorithms, utilizing cutting-edge models to demonstrate the effectiveness of their proposed methodology.

3  The Suggested GA

In this research, we harnessed the power of a Genetic Algorithm (GA) to create an optimal Convolutional Neural Network (CNN) architecture, fine-tuning hyper parameter settings for maximum performance. Our approach assumed that the Convolutional Neural Network (CNN) architecture consisted of various layers, including fully connected and normalization layers, and effectively navigated within the realm of VGG-like structures. The Genetic Algorithm (GA) enhanced the convolutional blocks, individual convolutional layers within every block, and a selection of hyper parameters vital to CNN architecture. It is worth noting that our Genetic Algorithm (GA) was designed with certain limitations in mind, restricting the scope of CNN architectures to standard modules. More intricate elements like residual-blocks [17] or inception-modules [18] were not part of the options due to these constraints. Nonetheless, our proposed Genetic Algorithm demonstrated its ability to construct Convolutional Neural Networks (CNNs) that rival cutting-edge models, even within this constrained search space.

The suggested algorithm for improving Convolutional Neural Network (CNN) architectures operates within the broader Genetic Algorithm (GA) framework, following standard GA procedures, as depicted in Fig. 1. To initiate the algorithm, an initial population is generated by randomly selecting sets of genes for each individual. An individual’s chromosome uniquely defines the Convolutional Neural Network (CNN) design and specific hyper parameters. After training and validating each Convolutional Neural Network (CNN) model on the training dataset, we calculate an individual’s fitness score based on the network’s average classification accuracy during the validation phase. The individuals within the population are then sorted in descending order of their fitness scores. Subsequently, the next generation of the population is created through a sequence of genetic operations, including elite selection, random selection, and the breeding of new members. This process continues until the termination criterion is met. In Algorithm 1, the pseudocode for the evolutionary algorithm dedicated to CNN architecture optimization is presented, with subsequent subsections providing detailed information on each component.

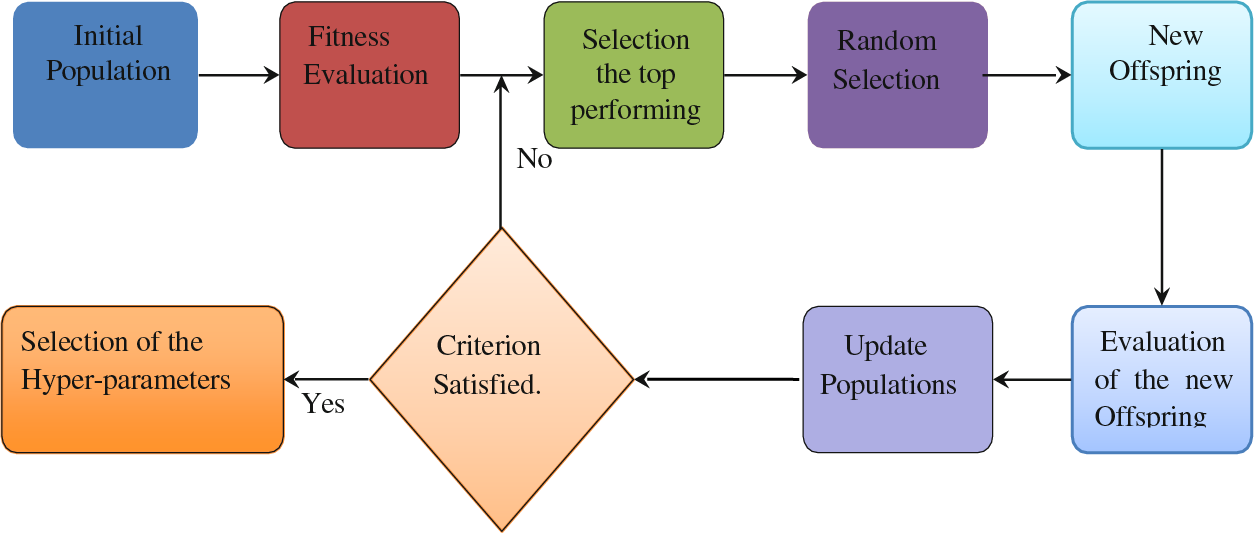
Figure 1: The genetic algorithm flowchart for the evolutionary development of a Convolutional Neural Network (CNN) model

3.1 The Initialization of the Population

As previously mentioned, the proposed Genetic Algorithm (GA) is employed to navigate the landscape of conventional Convolutional Neural Network (CNN) architectures in search of the optimal Convolutional Neural Network (CNN) model. We have constrained the Convolutional Neural Network (CNN) design to comprise a maximum of 20 convolutional layers, organized into no more than five distinct blocks, labeled as Block 1, Block 2, Block 3, Block 4, and Block 5. Each of these blocks may contain any number of layers ranging from 0 to 4. The GA is tasked with optimizing the number of filters (NF) for each block, with available options of 32, 64, 128, 256, or 512.

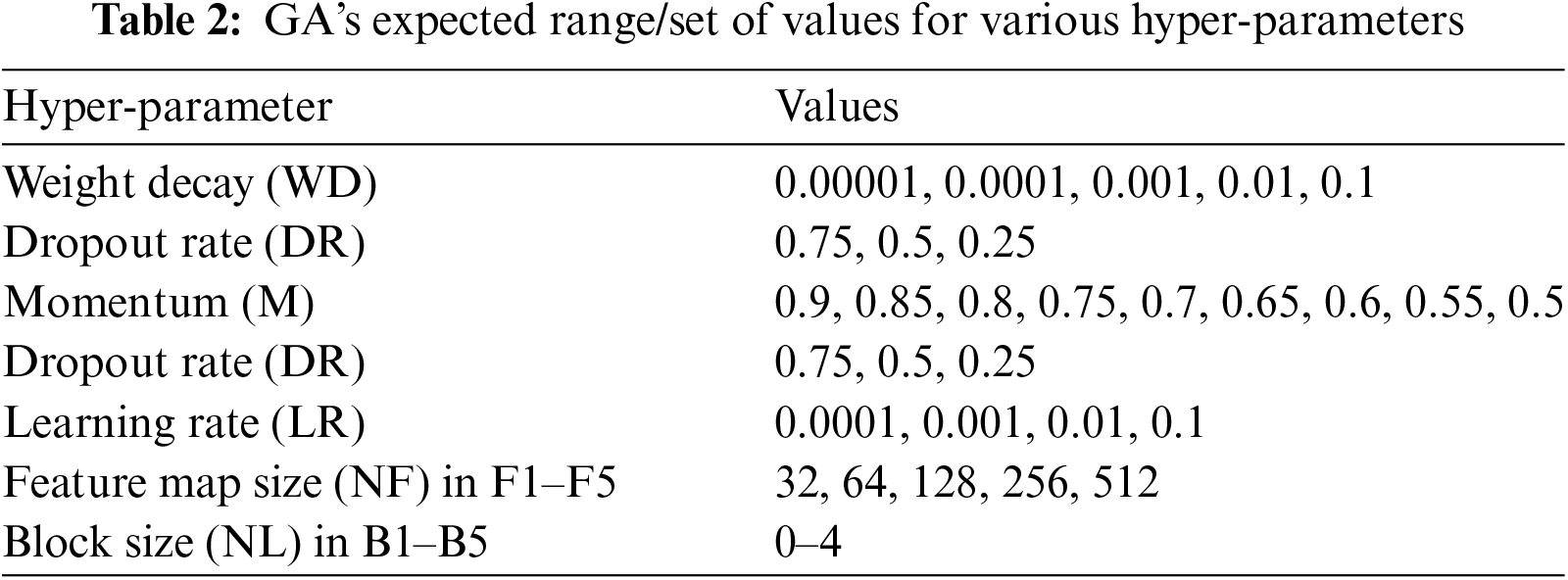
Furthermore, our GA is responsible for optimizing several critical hyper parameters, including weight decay (WD), dropout rate (DR), momentum (M), and learning rate (LR). The chromosome structures are detailed in Table 1, illustrating the genetic encoding used in our approach.

The structure of the chromosomes employed in our approach highlights the utilization of fixed-size chromosomes within the proposed Genetic Algorithm (GA). This GA has the capacity to discover diverse Convolutional Neural Network (CNN) models with varying lengths, encompassing multiple blocks, and accommodating any number of layers ranging from 0 to 20, even permitting a block size of zero.

To illustrate, Table 1 showcases an example of a Convolutional Neural Network (CNN) architecture with 11 layers. In this example, the initial block comprises two convolutional layers with 256 feature maps, while there is no second block. Subsequently, the third, fourth, and fifth blocks contain three, two, and four layers, respectively, each characterized by feature map sizes of 32, 512, and 256. This demonstrates the flexibility of our approach in creating CNN architectures tailored to specific requirements.

Additional layers have been integrated into each Convolutional Neural Network (CNN) model to facilitate the mapping from genotype to phenotype. Following each convolutional block within the network, we have introduced an average-pooling layer with a kernel size of 2 and a stride size of 1, a max-pooling layer with a kernel size of 2 and a stride size of 2, and a linear fully connected layer. Furthermore, within each convolutional block, we have included a dropout layer, while after each convolutional layer, a sequence of layers follows, comprising batch normalization [19] and a ReLU layer [20]. These architectural elements enhance the overall capabilities of the CNN models.

Algorithm 2 provides an overview of the population initialization process within the Genetic Algorithm (GA). Each chromosome contains multiple genes, each of which can take on various alternative values. The proposed GA employs the evolutionary process to determine the perfect sequence of these gene values. The interval values amount to every gene, as reported in Table 2, were chosen based on past successes in using Convolutional Neural Networks (CNN) for classifying diverse scenarios.

In the construction of the CNN architecture, the hyper parameters are chosen randomly, and there are no constraints on the number or arrangement of feature maps or convolutional layers. In contrast, when designing Convolutional Neural Network (CNN) structures manually, a common approach is to add more feature mappings to subsequent convolutional blocks, illustrating the flexibility and adaptability of the evolutionary approach.

The chromosomal structure and the associated algorithm demonstrate a high degree of flexibility, enabling the optimization of additional hyper parameters like the choice of activation functions and the use of distinct kernel sizes for individual convolutional blocks. This adaptability aims to make the approach more versatile and applicable across a broader spectrum of tasks. However, it is important to note that extending the search space to include these additional hyper parameters will necessitate more comprehensive exploration and increase computational demands.

To mitigate the computational burden, we initially conducted preliminary research using various types of chromosomes but subsequently fixed certain hyper parameter values. For example, we set the kernel size for convolutional layers to a fixed value of 3. This approach strikes a balance between flexibility and computational efficiency, ensuring that the optimization process remains manageable.

3.2 Fitness Evaluation

To evaluate the model’s quality, we undertake the training and assessment of a Convolutional Neural Network (CNN) model created from an individual’s chromosomes, particularly focusing on its classification performance. Notably, the most resource-intensive phase in any deep neuro-evolution method is the training and evaluation of deep neural networks. Recent research has unveiled the possibility of roughly gauging the architectural quality of a Convolutional Neural Network (CNN) model based on its performance following partial training [6,7]. In light of this insight, we opted to assess the performance of CNN networks during the evolutionary process after subjecting them to just Nepoch = 15 of partial training, significantly expediting the evolution of our algorithm.

The fitness score for the respective individual is determined based on the typical accuracy of validation achieved by the evolved Convolutional Neural Network (CNN) model. During the training phase, 90% of the training data is utilized, with the remaining 10% reserved for validation purposes. After the Convolutional Neural Network (CNN) models, generated by the individual, have undergone training using the SGD method [21] for a fixed number of epochs (Nepoch = 15), the individual’s fitness score is computed by assessing the typical accuracy of classification during the time of validation.

Throughout each experiment, the cross-entropy loss function is applied during the training phase. Additionally, the LR is systematically shortened by a factorization of 15 in every 15 epochs after the evolutionary phase. For a comprehensive understanding of how an individual’s fitness is evaluated, please refer to the details provided in Algorithm 3.

3.3 Creation of a New Generation

In our proposed Genetic Algorithm, we employ a combination of random selection, offspring generation, and elite selection to generate the subsequent generation of the population from the existing one. Initially, the members of the current generation are sorted based on their fitness levels. The elite individuals, typically representing the top e% of the population, are chosen amount the present population and carried over to the later procreation. In addition to these elite individuals, random individuals are introduced into the later procreation for maintaining population diversification and limiting incomplete merging, a strategy supported by research [22,23].

These randomly chosen individuals are selected from the remainder of the current population with a probability of pr and are integrated into the succeeding generations. The parent pool is the combination of random individuals and elite, from which the offspring are generated. This approach ensures that the genetic diversity of the population is sustained and that potential variations are explored for evolutionary progress.

4  Experimental Setup

4.1 Dataset

The MNIST database encompasses an extensive collection of handwritten numerical characters [24]. This database comprises a training set, consisting of 60,000 examples, and a test set, comprising 10,000 examples. It is derived from two larger datasets known as NIST Special Databases 1 and 3, featuring handwritten digits created by employees of the US Census Bureau and high school students, respectively. These numerical characters have undergone a standardization process, where they are centered within a fixed-size image and size-normalized.

To achieve this standardization, the original NIST images, which were initially 20 × 20 pixels in size, were resized while preserving their aspect ratio. The normalization procedure employed an anti-aliasing technique, resulting in images with varying shades of gray. Furthermore, the images were centered by calculating the center of mass of the pixels and subsequently translating the image to position this center point at the center of a 28 × 28 field, ensuring uniformity and consistency in their presentation.

4.2 Experimental Environment

Throughout this research, all experiments and tests were carried out using Python programming language version 3.7. The execution of the algorithms was performed on both the DGX station machine and High-Performance Computing (HPC) facilities. At each stage of the study, which encompassed the development of diverse Convolutional Neural Network (CNN) architectures, comprehensive training of the selected model over an extended number of epochs, and the evaluation of the most promising models, all scripts were executed on a computing environment equipped with two GPUs.

4.3 The Selection of Parameters

As previously highlighted, our proposed framework offers a high degree of flexibility for extending the search space. In essence, the suggested Genetic Algorithm framework can be configured to optimize a wide range of hyper parameters. However, due to computational resource limitations, we have focused on a specific subset of hyper parameters in our development.

Furthermore, informed by the findings from our previous experiments, it is notable that the Genetic Algorithm consistently selects particular values for the activation function and optimizer hyper parameters. Consequently, we have maintained the use of the SGD optimizer and the ReLU activation function for all our testing.

In the specific context of our convolutional layers, we have adjusted the kernel sizes to range from 1 to 3, while the convolutional layers’ stride size and the max pooling layer have been uniformly fixed to 2. This approach helps strike a balance between versatility and efficient resource utilization.

We configured the parameters of the Genetic Algorithm with the following values: a population size of NP = 30, an elite retention rate of e = 40%, a maximum number of generations set to Gmax = 40, a mutation probability of Pm = 0.2, and an individual retention probability for non-elite members of Pr = 0.1. These parameter values were chosen based on references in the literature and our own expertise with evolutionary algorithms. To streamline computation and expedite the process, the training of the networks during the evolutionary phase was performed over a reduced number of epochs (Nepoch = 15).

Upon the completion of the mutative period, the top-performing Convolutional Neural Network (CNN) model was fully trained, and used the test dataset for rigorous testing. Furthermore, the top performance generated by the Genetic Algorithm undergoes specialized training using the entire training set, over a more extensive number of epochs (Nepoch = 350), to further enhance its performance.

5  Experimental Results

In this research, the proposed Genetic Algorithm has been applied to evolve CNN architectures specifically for a single dataset. Given the theoretical description of the approach, each experiment was conducted five times. Subsequently, after every experiment the obtained top-performance model underwent comprehensive training on the relevant dataset and was subjected to evaluation. The outcomes pertaining to the evolving model’s performance on the dataset, including average accuracy, worst accuracy, best accuracy, and standard deviation, are presented in Table 3.

It is noteworthy that the CNN model created by the Genetic Algorithm displayed outstanding performance on the dataset. The values in Table 3, including average, best, and worst accuracies and the standard deviations, collectively demonstrate that the evolutionary technique consistently identified CNN models of comparable quality across multiple trial runs.

The network underwent an extensive training phase spanning 350 epochs.

Fig. 2 illustrates the successful improvement of the overall fitness level within the population by the proposed algorithm. Initially, over the first nine generations, there was a rapid increase in population fitness. Subsequently, this rate of improvement gradually slowed down. This deceleration in fitness growth can be anticipated due to the significant selection pressure introduced by the elitism strategy and the contribution of elite individuals in the procreation of offspring.

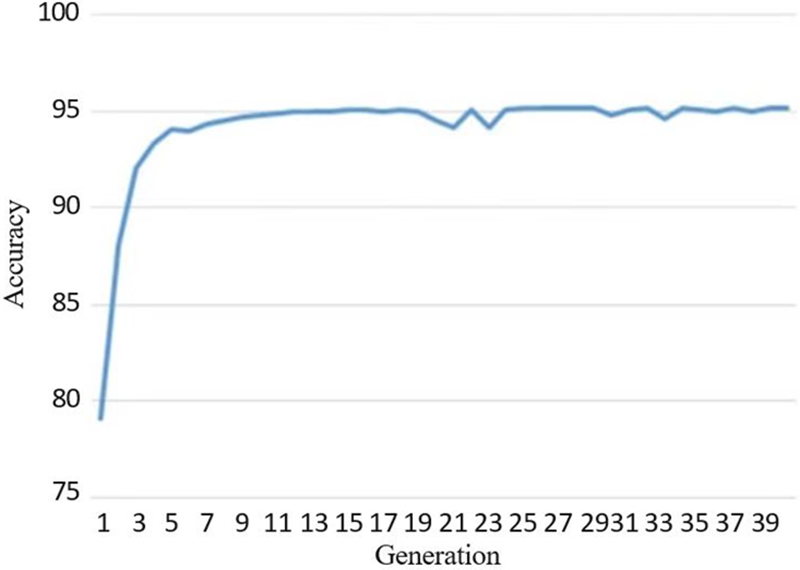
Figure 2: The average convergence graph for the GA population from the MNIST dataset

Table 4 provides an overview of the architectures for the top-performing networks that were generated through multiple runs of the Genetic Algorithm for the given dataset. The Convolutional Neural Network (CNN) architectures are presented in each row of Table 4, specifying the number of blocks, convolutional layers within each block, and the number of feature maps (NF) for those blocks. Additionally, the number of layers (NL) and the NF for layers within each block are listed, with the values separated by commas.

For instance, consider the first convolutional block of the Convolutional Neural Network (CNN) in the initial row of the table, which is represented as “3 (512)”—indicating that it comprises three convolutional layers, the first two each have 512 feature maps (NFs) and 256 for the last convolutional layer.

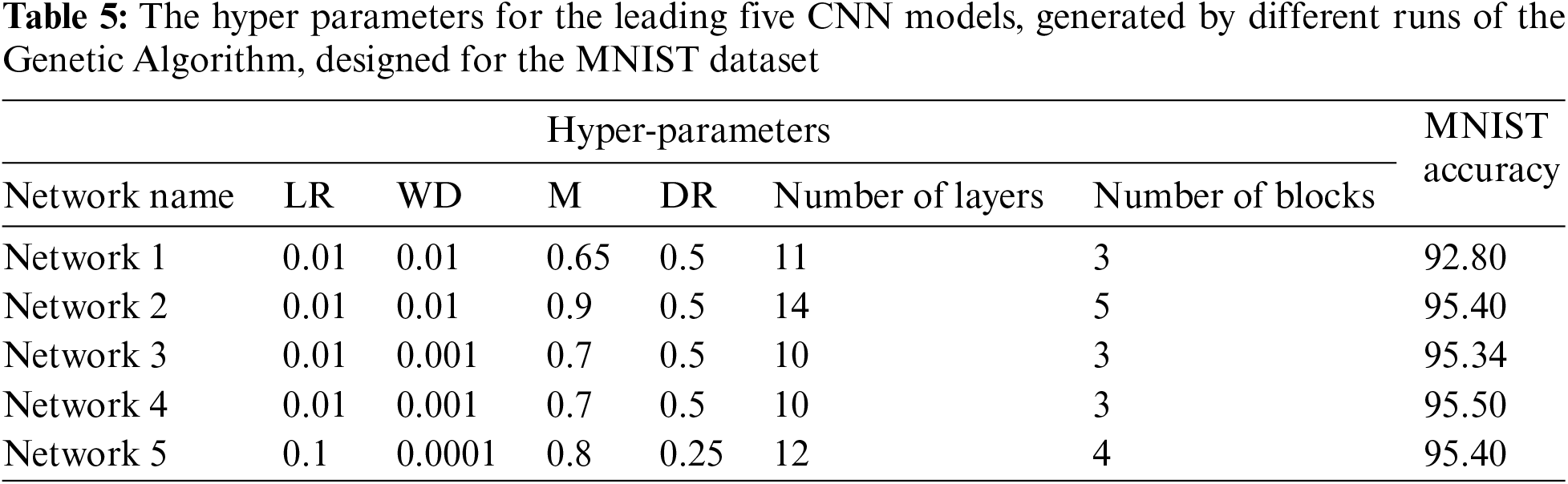
To assemble the complete CNN model, we incorporated BN (Batch Normalization), an average pooling layer, ReLU activation, dropout, and fully connected layers. Additionally, Table 5 provides information about the number of trainable parameters for the various models that were developed. Furthermore, Table 5 presents details regarding the additional hyper parameters for each of the evolved networks designed for the MNIST dataset.

For a visual representation of the top-performing Convolutional Neural Network (CNN) models developed through the Genetic Algorithm across five iterations, please refer to Fig. 3.

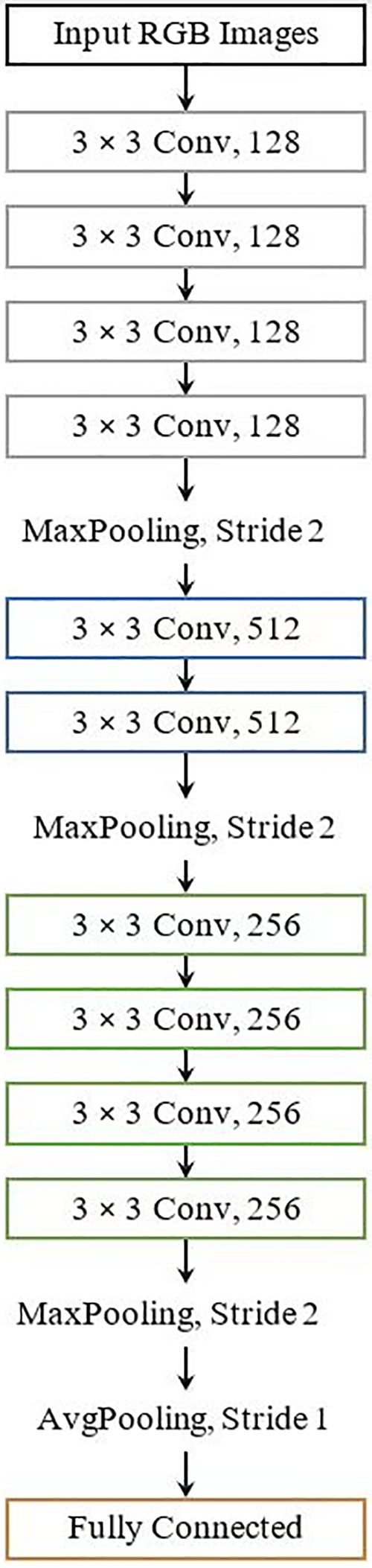
Figure 3: The top CNN model architectures created through the Genetic Algorithm (MNIST dataset)

Table 4 vividly illustrates that multiple runs of the evolutionary process yielded CNN architectures that displayed significant diversity concerning the number of layers, trainable parameters, and the number of blocks. An intriguing observation made by the Genetic Algorithm is the variation in feature map magnitudes within different blocks of evolving architectures. This feature map progression, as typically observed in many VGG models and human-designed architectures, often sees an increase in feature map size across successive convolutional blocks. While certain evolved models maintain this trend (e.g., Network 5), the order is not consistently upheld in the designed models. In some instances, architectures exhibit a descending order (e.g., Network 2), while others do not adhere to a specific pattern (e.g., Network 4). This finding leads us to the conclusion that the inclusion of larger feature maps in later convolutional blocks is not an absolute requirement for an effective Convolutional Neural Network architecture.

To assess the models’ quality, we employed the MNIST dataset for training each evolving model and evaluating its accuracy. Table 5 provides a detailed breakdown of the best-evolved models specific to this dataset.

To reduce computational demands, some of the models underwent partial training, involving a limited number of epochs, during the evolutionary phase. Previous researches [6,7] and [16] have shown that minimal training may be sufficient for evaluating network architectures in image categorization. In our study, we opted to train the network for a mere 15 epochs, seeking to explore this concept further. This approach significantly accelerated the evolutionary process, resulting in an average evolution time of just 6 GPU days.

Finally, we conducted a comparative analysis to determine the performance of the evolved model against some state of the art Convolutional Neural Network (CNN) models, as presented in Table 6 (Bold highlights indicate the top results). Our evaluation encompassed three different classes of neural networks, namely humanly designed, semi-automatic generated, and fully mechanically constructed networks [12]. Within the manually designed category, models such as Maxout [25], Dense-Net [15], VGG19 [13], Res-Net101 [17], and VGG16 [13] were considered. Semi-automatically constructed networks included Genetic CNN, Hierarchical Evolution, and Block-QNN-S, while fully automatically designed networks consisted of Large-scale Evolution, CGP-CNN, NAS, Meta-QNN, CNN-GA, and Fast-CNN [16].

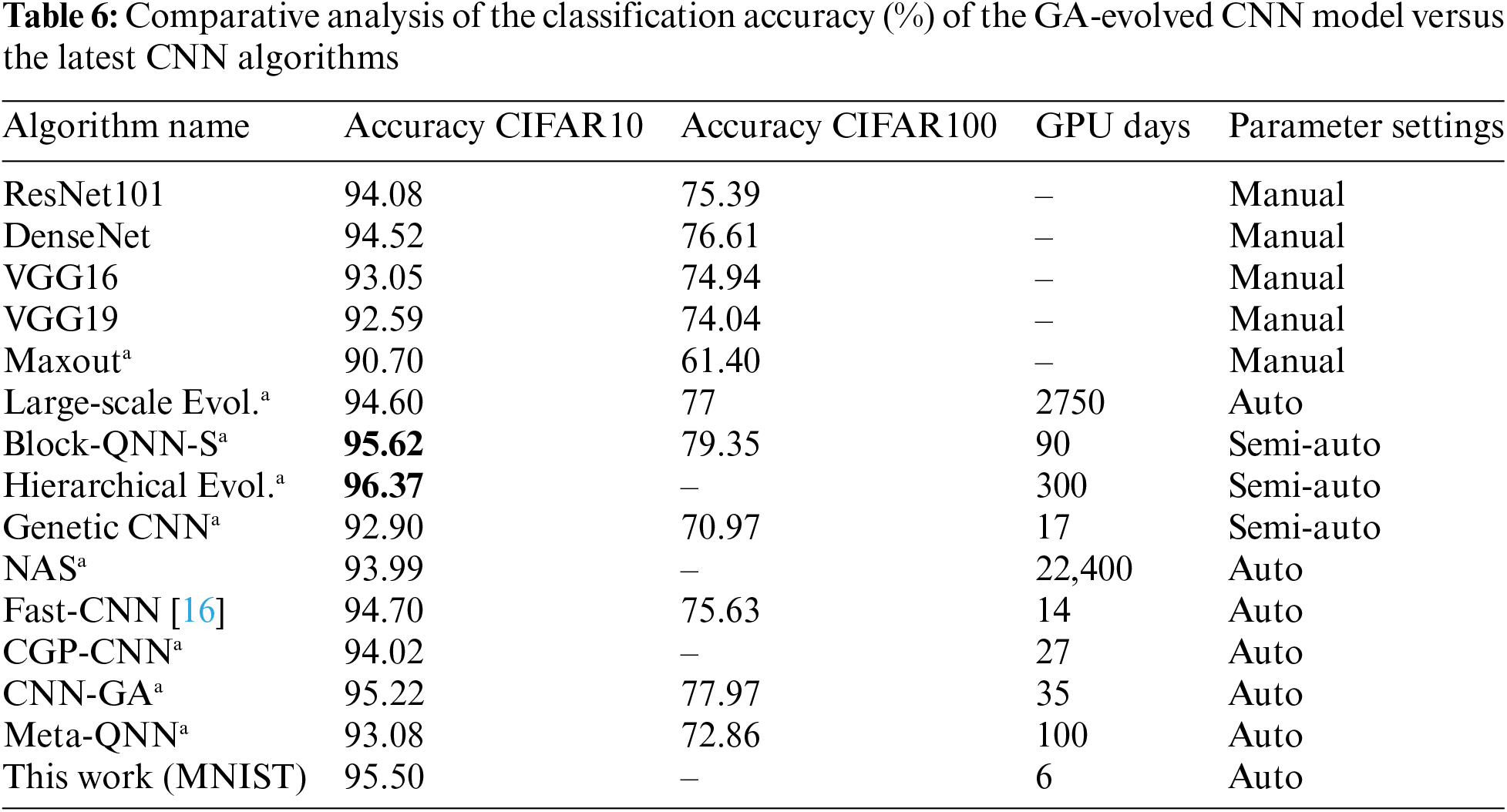
For the MNIST dataset, we correlated the top-performing model generated by the suggested Genetic Algorithm. In addition to assessing the accuracy of autonomously generated networks, we also compared these models in terms of the number of GPU days required to generate them. GPU days provide a rough estimate of the algorithm’s efficiency, although it is important to note that this metric does not apply to manually created models.

It is worth emphasizing that while some results were independently replicated by us, others were obtained from [12].

Table 6 clearly demonstrates that the Convolutional Neural Network model, crafted by our proposed Genetic Algorithm, outperformed VGG models and various human-designed Convolutional Neural Network models when evaluated on the CIFAR10 dataset. Notably, it even outperformed every other automatically generated model, securing a place within the top three performers on the CIFAR10 dataset. The model resulting from hierarchical evolution, which was created semi-automatically, exhibited the highest performance in this dataset.

For the CIFAR-100 dataset, the evolving model utilized in this study surpassed every other’s Convolutional Neural Network (CNN) models, regardless of even if they were human designed, semi-automatic designed, or mechanically designed. Last but not least, the suggested Genetic Algorithm proved to be remarkably efficient in terms of computational speed, demanding only 6 GPU days to produce the optimal Convolutional Neural Network. While it is true that the Hierarchical Evolutionary model outperformed the GA-evolved model in classification accuracy, the latter’s computational requirements were just a fraction, being 50 times less.

6  Discussion

This study primarily delves into the viability of evolving an optimized Convolutional Neural Network (CNN) model, inspired by the VGG architecture, for image classification using a Genetic Algorithm (GA). Our proposed GA scrutinizes CNN designs employing a fixed-length chromosome while accommodating a variable number of layers distributed across multiple blocks. The innovative aspect of our GA lies in its capacity to generate CNN models optimized not only in terms of their structural layout but also their hyper parameters. The CNN model born from our GA outperformed both conventional VGG models and a diverse spectrum of human-engineered CNN architectures. Notably, the GA-crafted model demonstrated competitiveness against cutting-edge CNN models developed using semi-automatic and automatic methodologies, despite adhering to a VGG-like architecture. It is noteworthy that the CNN model synthesized by the GA occasionally exhibited distinctive structural characteristics compared to human-designed models. The superior performance of these GA-optimized architectures is vividly illustrated by the high-quality results achieved by the models. These findings strongly suggest that our proposed GA has the potential to significantly enhance the performance of conventional CNN models, paving the way for more efficient image classification.

7  Conclusion

In this research, we present an innovative approach to the automatic discovery of optimized Convolutional Neural Network (CNN) models, employing a straightforward genetic algorithm (GA). The core focus of our work revolves around optimizing critical training-related hyper parameters, including the LR, WD, M, and DR. To achieve this, our proposed GA meticulously navigates the search space encompassing conventional CNN models, adjusting parameters such as the number of convolutional blocks, the number of layers (NLs) within each block, and the number of filters (NFs) for each block. We introduce an efficient strategy of partially training the models during the evolutionary process, a practice aimed at alleviating the computational demands typically associated with deep neuro-evolutionary algorithms. Our GA demonstrates its prowess through a series of iterations, culminating in the development of highly superior CNN models. To assess the performance of these enhanced CNN models, we rigorously evaluate them in terms of classification accuracy and computational resource expenditure, specifically GPU days. In this comparative analysis, our best-performing CNN model, boasting an impressive accuracy of 95.50%, emerges as a standout achiever. Notably, it outperforms 14 state of the art models selected amount various classes. Equally remarkable is the efficiency of our approach; the optimal CNN model was evolved within a mere 6 GPU days, a result that positions it as a strong contender against manually or automatically generated CNN models.

Acknowledgement: I wish to extend my heartfelt appreciation to all those who have generously contributed their unwavering support and invaluable insights. Their unparalleled expertise and unwavering dedication have played a pivotal role in elevating the quality of this paper. Additionally, my gratitude goes out to the diligent reviewers whose constructive feedback has contributed to the refinement of this work. I am deeply indebted to my colleagues for their encouragement and assistance, without which this publication would not have come to fruition.

Funding Statement: The author received no specific funding for this study.

Author Contributions: The author confirms his contribution to the paper as follows: study conception and design: Bah Mamoudou; data collection: Bah Mamoudou; analysis and interpretation of results: Bah Mamoudou; draft manuscript preparation: Bah Mamoudou.

Availability of Data and Materials: The code utilized and/or examined in the course of this research can be obtained from the corresponding author upon a reasonable request.

Conflicts of Interest: I hereby provide this statement as an assurance that the author has thoroughly reviewed and endorsed the manuscript being submitted, while also confirming the absence of any conflicts of interest or personal associations that may impact the integrity and impartiality of this paper.

References

1. E. Selvi, M. Adimoolam, G. Karthi, K. Thinakaran, N. M. Balamurugan et al., “Suspicious actions detection system using enhanced CNN and surveillance video,” Electronics, vol. 11, no. 24, pp. 1–20, 2022. [Google Scholar]

2. A. Darwish, A. E. Hassanien and S. Das, “A survey of the swarm and evolutionary computing approaches for deep learning,” Artificial Intelligence Review, vol. 53, pp. 1767–1812, 2019. [Google Scholar]

3. M. Azab, “Design approach and performance analysis of trap filter for three-phase PV grid integration systems using evolutionary search algorithms,” Journal of King Saud University—Engineering Sciences, vol. 33, no. 7, pp. 491–506, 2021. [Google Scholar]

4. A. Bakhshi, S. Chalup and N. Noman, “Fast evolution of CNN architecture for image classification,” in Natural Computing Series, pp. 209–229, 2020. [Google Scholar]

5. F. P. Such, V. Madhavan, E. Conti, J. Lehman, K. O. Stanley et al., “Deep neuro-evolution: Genetic algorithms are a competitive alternative for training deep neural networks for reinforcement learning,” arXiv:1712.06567, 2017. [Google Scholar]

6. M. Suganuma, S. Shirakawa and T. Nagao, “A genetic programming approach to designing convolutional neural network architectures,” in Proc. of the Genetic and Evolutionary Computation Conf., New York, USA, pp. 497–504, 2017. [Google Scholar]

7. Y. Sun, B. Xue, M. Zhang and G. G. Yen, “Evolving deep convolutional neural networks for image classification,” IEEE Transactions on Evolutionary Computation, vol. 24, no. 2, pp. 394–407, 2020. [Google Scholar]

8. M. Matsugu, K. Mori, Y. Mitari and Y. Kaneda, “Subject-independent facial expression recognition with robust face detection using a convolutional neural network,” Neural Network, vol. 16, no. 5, pp. 555–559, 2003. [Google Scholar]

9. I. Goodfellow, Y. Bengio, A. Courville and A. Bengio, Deep Learning, vol. 1, Cambridge: MIT Press, 2016. [Google Scholar]

10. O. E. David and I. Greental, “Genetic algorithms for evolving deep neural networks,” in Proc. of the Companion Publication of the 2014 Annual Conf. on Genetic and Evolutionary Computation, New York, USA, pp. 1451–1452, 2014. [Google Scholar]

11. Y. Zhou, Y. Jin and J. Ding, “Surrogate-assisted evolutionary search of spiking neural architectures in liquid state machines,” Neurocomputing, vol. 406, pp. 12–23, 2020. [Google Scholar]

12. Y. Sun, B. Xue, M. Zhang, G. G. Yen and J. Lv, “Automatically designing CNN architectures using the genetic algorithm for image classification,” IEEE Transactions on Cybernetics, vol. 50, no. 9, pp. 3840–3854, 2020 [Google Scholar] [PubMed]

13. K. Simonyan and A. Zisserman, “Very deep convolutional networks for large-scale image recognition,” arXiv:1409.1556, 2014. [Google Scholar]

14. Y. Sun, B. Xue and M. Zhang, “Automatically evolving CNN architectures based on blocks,” arXiv:1810.11875, 2018. [Google Scholar]

15. G. Huang, Z. Liu, L. van der Maaten and K. Q. Weinberger, “Densely connected convolutional networks,” in 2017 IEEE Conf. on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, pp. 2261–2269, 2017. [Google Scholar]

16. A. Bakhshi, N. Noman, Z. Chen, M. Zamani and S. Chalup, “Fast automatic optimization of CNN architectures for image classification using genetic algorithm,” in 2019 IEEE Congress on Evolutionary Computation (CEC), Wellington, New Zealand, pp. 1283–1290, 2019. [Google Scholar]

17. K. He, X. Zhang, S. Ren and J. Sun, “Deep residual learning for image recognition,” in Proc. of the IEEE Conf. on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, pp. 770–778, 2016. [Google Scholar]

18. C. Szegedy, W. Liu, Y. Jia, P. Sermanet, S. Reed et al., “Going deeper with convolutions,” in 2015 IEEE Conf. on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, pp. 1–9, 2015. [Google Scholar]

19. S. Liang, Y. Khoo and H. Yang, “Drop-activation: Implicit parameter reduction and harmonious regularization,” Communications on Applied Mathematics and Computation, vol. 3, no. 2, pp. 293–311, 2021. [Google Scholar]

20. L. Gu, “Object tracking algorithm based on adaptive deep sparse neural network,” IOP Conference Series: Materials Science and Engineering, vol. 490, no. 4, pp. 1–7, 2019. [Google Scholar]

21. J. R. Shi, D. Wang, F. H. Shang and H. Y. Zhang, “Research advances on stochastic gradient descent algorithms,” Zidonghua Xuebao/Acta Automatica Sinica, vol. 47, no. 9, pp. 2103–2119, 2020 (In Chinese). [Google Scholar]

22. C. Bu, F. Liu, Z. Cao, L. Li, Y. Zhang et al., “Cognitive diagnostic model made more practical by genetic algorithm,” IEEE Transactions on Emerging Topics in Computational Intelligence, vol. 7, no. 2, pp. 1–15, 2023. [Google Scholar]

23. S. Malik and S. Wadhwa, “Preventing premature convergence in the genetic algorithm using DGCA and elitist technique,” International Journal of Advanced Research in Computer Science and Software Engineering, vol. 4, no. 6, pp. 1–9, 2014. [Google Scholar]

24. O. Nocentini, J. Kim, M. Z. Bashir and F. Cavallo, “Image classification using multiple convolutional neural networks on the fashion-MNIST dataset,” Sensors, vol. 22, no. 23, pp. 1–14, 2022. [Google Scholar]

25. I. J. Goodfellow, D. Warde-Farley, M. Mirza, A. Courville and Y. Bengio, “Maxout networks,” arXiv:1302.4389, 2013. [Google Scholar]