Computers, Materials & Continua DOI:10.32604/jai.2022.029141
Article

Tibetan Sorting Method Based on Hash Function

AnJian-CaiRang1,2, Dawei Song3,4,*

1College of Intelligence and Computing, Tianjin University, Tianjin, 300350, China
2The Computer College, Qinghai Minzu University, Qinghai, 810007, China
3School of Computer Science, Beijing Institute of Technology, Beijing, 10008, China
4School of Computing and Communications, The Open University, Walton Hall, Milton Keynes, MK7 6AA, United Kingdom
*Corresponding Author: Dawei Song. Email: dwsong@bit.edu.cn
Received: 26 February 2022; Accepted: 21 April 2022

Abstract: Sorting the Tibetan language quickly and accurately requires first identifying the component elements that make up Tibetan syllables and then sorting by the priority of the component. Based on the study of Tibetan text structure, grammatical rules and syllable structure, we present a structure-based Tibetan syllable recognition method that uses syllable structure instead of grammar. This method avoids complicated Tibetan grammar and recognizes the components of Tibetan syllables simply and quickly. On the basis of identifying the components of Tibetan syllables, a Tibetan syllable sorting algorithm that conforms to the language sorting rules is proposed. The core of the Tibetan syllable sorting algorithm is a hash function. Research has found that the sorting of all legal Tibetan syllables requires eight components of information. The hash function is based on this discovery and can be assigned corresponding weights according to different sorting verify the effectiveness of the Tibetan sorting algorithm, we established an experimental corpus using the Tibetan sorting standard document recognized by the majority of Tibetan users, namely the New Tibetan Orthographic Dictionary. Experiments show that this method produces results completely consistent with standard reference works, with an accuracy of 100%, and with minimal computational time.

Keywords: Hash function; Tibetan; component element; priority

1  Introduction

Research into sorting the Chinese and English languages is both mature and widely used, but similar research for the Tibetan language is still immature. Tibetan sorting differs from sorting Chinese and English. English and Chinese sorting algorithms are not usable with Tibetan, as the order of Tibetan does not depend upon the order of consonants and vowels in Tibetan syllables. It is necessary to combine Tibetan syllabification, grammatical rules, and component priority in conjunction with the root characters to sort the words properly.

Tibetan information processing scholars have previously explored the ordering of Tibetan languages. The first attempt at automated sorting proposed an implementation for Tibetan syllable ordering but did not provide test data [1]. Other methods analyze the characteristics of Tibetan characters, structure, traditional character sequence, length, and layer height of Tibetan syllables and construct a mathematical model of Tibetan ordering that assigns a numerical value for each type of Tibetan components and sorts words by numerical value [2–5]. This method has difficulty assigning values to Tibetan components, the sorting work is closely integrated with the grammar of Tibetan syllables and is complicated, and no test data are provided. Another method finds the sorting code of each character from the Default Unicode Collation Element Table (DUCET) [6–8], generates the sorting code string of Tibetan syllables, and finally performs the sorting of Tibetan syllables by comparing the sorting code strings. However, this method does not consider the differences between Tibetan alphabetic characters and main characters. For example, the sort code of the Tibetan alphabetic character ‘ཁ’ is smaller than the sort code of the main character ‘ྐ’. The sorted result is ‘ཁ’ in the front and ‘ྐ’ in the back by this method, a result that is completely inconsistent with traditional expected sorting results. No test data are available for the method provided in the article. A method for sorting Tibetan according to the Tibetan national coding standard has also been proposed [9], but the results differ greatly from traditional sorting results. As with the others, no test data are available. Another technique normalizes the number of Tibetan components to seven, using spaces to fill in missing Tibetan syllable components, and then compares the normalized syllables to perform sorting [10]. However, the sorting rules of this method differ from standard sorting conventions, and the method does not address special situations such as double-subscript characters or suffixes in Tibetan syllables. The test experiment for this method only demonstrated its work with four Tibetan syllables, which is not representative. Another approach converts Tibetan syllables into one-dimensional letter strings, recognizing base characters and adjusting the order of letters (components) that constitute Tibetan syllables: root character, superscript character, prefix character, subscript character, vowel character, suffix character, and additional suffix character, with spaces added for missing components [11]. The method then uses the quick sort method to sort the resulting strings, but the sorting results remain inconsistent with general Tibetan sorting rules. Moreover, the included test experiment only gives examples for illustration without any specific actual data.

In summary, the existing sorting methods of Tibetan syllables must all adjust the order of components in Tibetan syllables. However, other syllable components in Tibetan syllables, except the root component, can be omitted, which causes the structure of Tibetan syllables to be complex and the length to be un-fixed; in addition, the complexity of the Tibetan syllable sorting rules is increased. Thus, it is difficult and unsatisfactory to perform Tibetan sorting by only adjusting the composition order of Tibetan syllables. Tibetan syllables are composed of seven components, and different components have different sorting functions. According to this feature, a hash function of Tibetan syllables is constructed and the corresponding hash value is generated to solve the problem of sorting Tibetan syllables.

To successfully sort Tibetan words, we must first correctly identify the component elements that make up a Tibetan syllable. One method for doing this includes a modern Tibetan component element recognition algorithm based on a study of Tibetan character structure, writing rules, and grammatical rules [12]. A second method uses Tibetan syllables’ glyph, collocation rules, and syllable length characteristics, combined with Tibetan grammar rules to design a root character recognition algorithm to help determine the position of other characters in the syllable [13]. Other works comprehensively consider many features such as syllable length and script collocation rules when identifying the component elements of Tibetan syllables [6,5,10]. However, the rules for Tibetan script are complicated and strict. The resulting algorithms are complex and difficult to use.

Based on the shortcomings and limitations of existing Tibetan component element recognition algorithms, we present a structure-based recognition design that does not rely on Tibetan grammar.

2  Structure-based Recognition Algorithm for Tibetan Syllable Components

The Tibetan language consists of horizontally linear and vertically superimposed alphabetic characters, spelled out using 30 consonants and 4 vowels [14,15]. Any collection of scripts or syllables can then be spelled with seven components, as shown in Fig. 1. Each component includes its own elements and must satisfy strict constraints [15,16], e.g., the prefix must be one of the four Tibetan letters ‘ག’,’ ད’, ‘བ’, ‘མ’, ‘འ’, and the Superscript must be one of ‘ར’, ‘ལ’, ‘ས’. However, as the prefix is ‘ག’, there can be no superscript, but as the prefix is ‘བ’, there can be a superscript, and so on. Our previous research has suggested that Tibetan grammatical rules are mainly used for the proper writing of Tibetan syllables. Once a syllable is generated, the positions of its components are fixed and no longer depend on grammar.

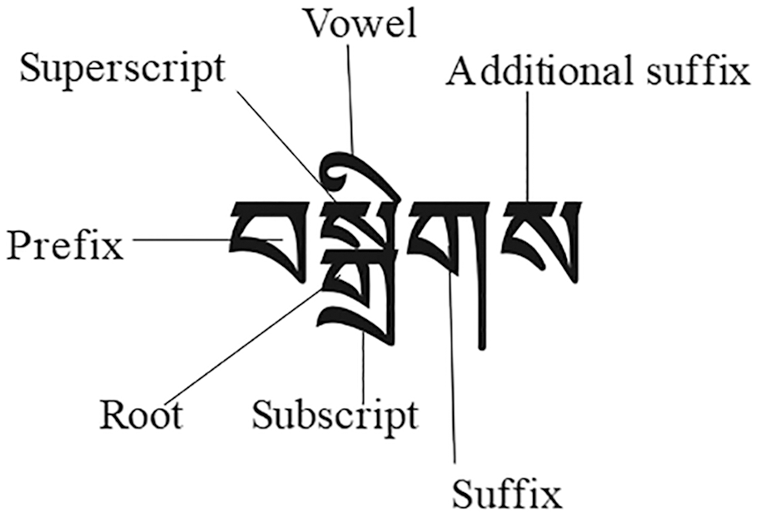
Figure 1: Tibetan syllable composition

2.1 Converting Tibetan Syllables into Syllable Structures (CTSISS)

Syllables in the National Standard Tibetan Basic Set [14] are divided into two types: alphabetic and main characters. The number of Tibetan scripts and syllables is relatively large and the recognition of components is correspondingly complicated. To simplify this complexity, we converted Tibetan syllables into syllable structures using an algorithm that can be described as follows. Strings in Tibetan syllables were scanned in order and alphabetic characters were replaced with `` T” The characters “ྲ, ླ, ྱ, ྭ” were replaced by `` D”, other main characters were substituted with `` M”, and vowels were replaced by `` Y”. For example, supposing that the Tibetan syllable T is represented by t0,…,tm, where m = length (syllable) –1 and 0≤i≤m, gives

y=s(T)=s(t0…tm)=s0…sm,(1)

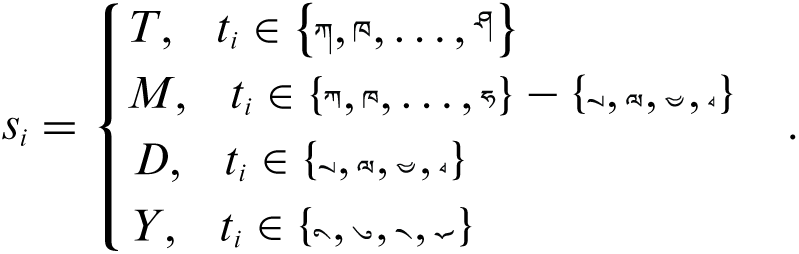
This CTSISS algorithm was applied to 17,525 Tibetan syllables to produce 60 different syllable structures, as shown in Tab. 1.

Theorem 1: After a Tibetan syllable is generated, the positions of its components are fixed, do not depend on syllable grammar, and do not include TTY or TTT structures.

Proof: The exhaustive method.

There are 17,525 Tibetan syllables [15]. Analyzing the structure of each suggested that there are only 60 structural types, with fixed component positions that are equivalent for syllables with the same structure. However, components such as གནད, དགས, དབས, དངས, དམས, བགས, མགས, མནད, མངས, འགས, and འབས are ambiguous and cannot be used to determine component position. In addition, TTY types, such as  and , have the same structure, but the position of its components cannot be uniquely determined by the structure. TTT types, such as གངས and ཟགས, have the same structure, but the position of each component is different and must be addressed separately. A sample syllable component for མངས  is shown in Fig. 2.

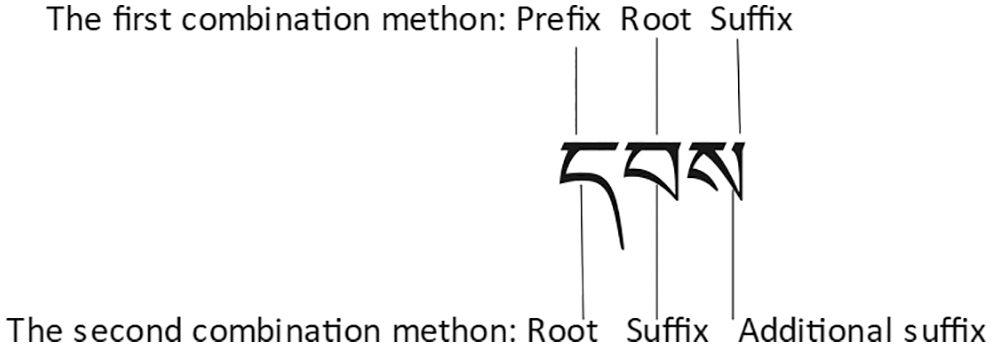
Figure 2: Special syllables

2.2 Technique for Addressing Positional Ambiguity of TTY and TTT Tibetan Syllable Structural Components (TAPATTTSSC)

Given the Tibetan syllable tibetword, with a length of three characters, the following can be inferred for tibetword [0], tibetword [1], and tibetword [2].

(1) TTY structure. Thus, if one of the elements in the last two-character combination sets is given by 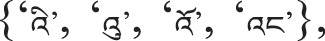then t6 = tibetword [0], t5 = ‘ε’, t4 = ‘ε’, t3 = ‘ε’, t2 = ‘ε’, t1 = tibetword [1], and t0 = tibetword [2]. Otherwise, t6 = tibetword [2], t5 = tibetword [0], t4 = tibetword [1], t3 = ‘ε’, t2 = ‘ε’, t1 = ‘ε’, and t0 = ‘ε’.

(2) TTT structure

Step 1: If the TTT syllable is  གནད, དགས, དབས, དངས, དམས, བགས, མགས, མནད, མངས, or འགས, processing proceeds as prefix, root, and superscript; namely, T6 = tibetword [1], t5 = tibetword [0], t4 = ‘ε’, t3 = ‘ε’, t2 = ‘ε’, t1 = tibetword [2], and t0 = ‘ε’. Otherwise, proceed to step 2.

Step 2: If tibetword [0] is one of the elements found in the prefix set f = {‘ག’,‘ད’,‘བ’,‘མ’,‘འ’}, and the first and second characters (tibetword [0] and tibetword [1]) are not in the same group of letters, the three Tibetan characters consist of a prefix, root, and suffix. Specifically, t6 = tibetword [1], t5 = tibetword [0], t4 = ‘ε’, t3 = ‘ε’, t2 = ‘ε’, t1 = tibetword [2], and t0 = ‘ε’. Otherwise, the three characters form a root, suffix, and suffix; namely, t6 = tibetword [0], t5 = ‘ε’, t4 = ‘ε’, t3 = ‘ε’, t2 = ‘ε’, t1 = tibetword [1], and t0 = tibetword [2].

2.3 Structure-based Recognition Algorithm for Tibetan Syllable Components (SBRATSC)

The proposed structural component recognition algorithm can be implemented using the following steps.

Step 1: Convert syllables into their corresponding structures using the CTSISS algorithm.

Step 2: If the Tibetan syllable structure is not TTY or TTT, reference Tab. 1 to acquire position information p = (p6, p5, p4, p3, p2, p1, p0) for all components. The value of p can then be used to obtain corresponding characters t = (t6, t5, t4, t3, t2, t1, t0) for each component of the syllable string. Otherwise, proceed to Step 3.

Step 3: Process the TTY and TTT syllable structures using TAPATTTSSC. A flowchart for the SBRATSC algorithm is provided in Fig. 3.

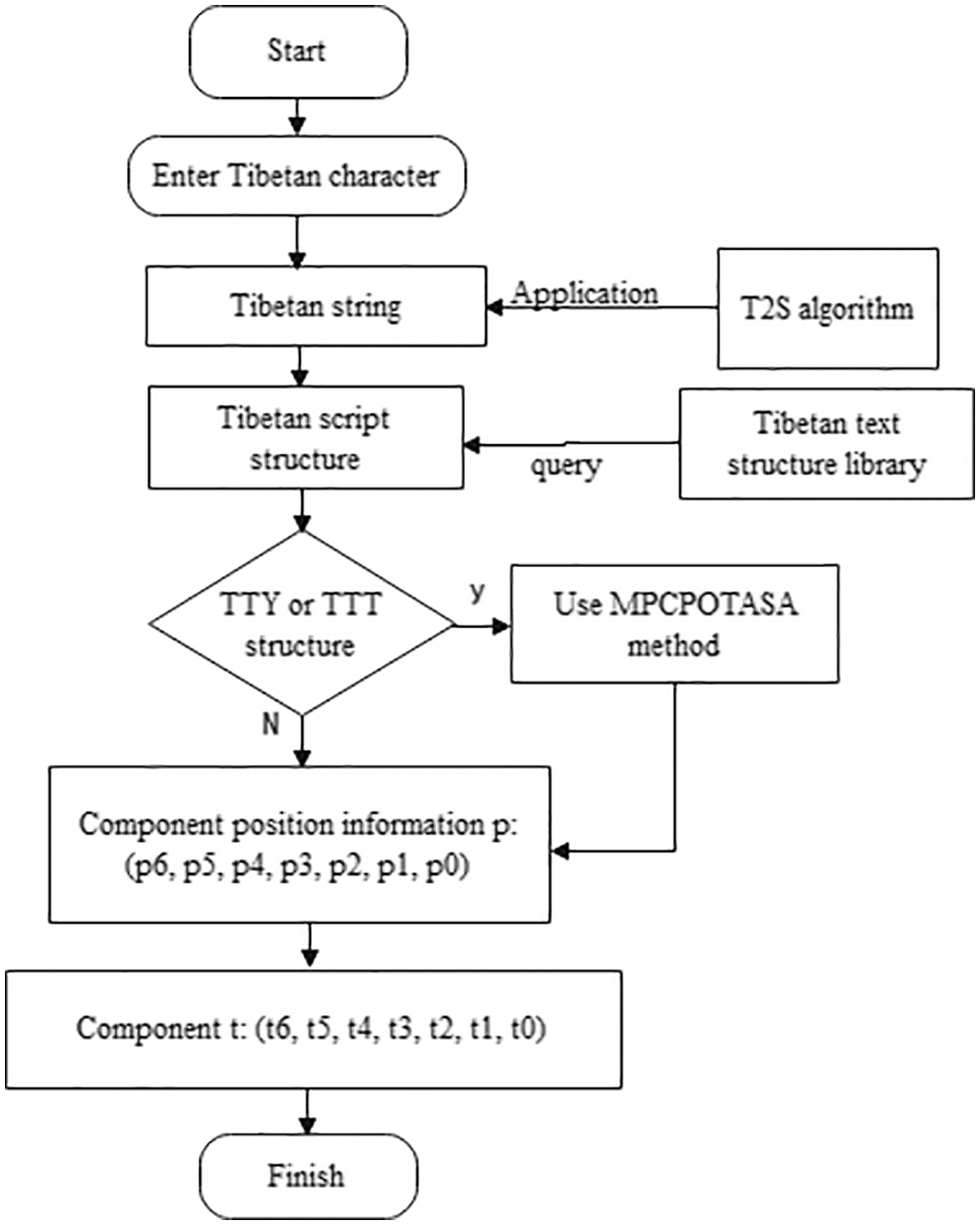
Figure 3: A Flowchart of structural Tibetan syllable component recognition algorithm

As an example, the process of applying the CTSISS algorithm to convert འརྒྱགས into its corresponding syllable structure can be described as follows.

Step 1: Convert འ  to T, ར  to T, ྒ  to M, ྱ  to D, and  ག and  ས  to T. The final structure of   is then given by TTMDTT.

Step 2: TTMDTT is not a TTY-or TTT-type structure. As such, Tab. 1 can be used to acquire the component position information: p6 = 2, p5 = 0, p4 = 1, p3 = 3, p2 = −1, p1 = 4, and p0 = 5. The components of  are given by t6 = ྒ, t5 = འ, t4 = ར, t3 = ྱ, t2 = ε, t1 = ག, and t0 = ས.

3  Hash Function of Tibetan Syllables

3.1 Position Weights of Tibetan Syllable Components

Tibetan characters are formed by combining four vowels and 30 consonants in accordance with grammatical rules [15]. Tibetan scripts are composed of seven letters in order: prefix, superscript characters, root characters, subscript characters, vowels, suffix characters, and additional suffix. The same Tibetan letter has different significance based on its position, just like a numerical value. Additionally, only the root character is absolutely required; the others may be present or not.

According to the sorting rule (SR) of Tibetan characters in the book New Tibetan Orthographic Dictionary [17], sorting takes place according to (in order): root character, superscript character 1, prefix character, superscript character 2, subscript character, vowel character, suffix character, and additional suffix character. Ordering Tibetan syllables requires eight comparisons, with the superimposed characters participating in two comparisons. In order to distinguish the superscript character participating in the second comparison, we denote the superscript character of the first comparison as superscript character 1 and the superscript character of the second comparison as superscript character 2. The two comparisons have different functions. Superscript character 1 divides the syllables that need to be sorted into a syllable group with top characters and a group without top characters. Superscript character 2 sorts the syllables according to their size.

The steps in our Tibetan sorting method are as follows. (Tibetan syllables with the same base character are put into a set).

1) First, sort the Tibetan syllables according to the size of the root character. At the same time, Tibetan syllables with the same root character are put into a set Si (1 ≤ i ≤ 30). In this way, the Tibetan syllables that need to be sorted are divided into a maximum of 30 sets according to the order of the root characters.

2) For each set Si, use the presence or absence of the superscript character to divide Si into two sets. Syllables without the superscript character are placed in set Si0, and syllables with the superscript character are placed in set Si1.

3) Finally, sort the elements of the sets Sij (where j is 0 or 1) in order of prefix character, superscript character, subscript character, vowel character, suffix character, and additional suffix character.

Eight comparisons are required to accomplish the sorting in step 3, with weights assigned for each comparison according to the position of the component. The position weight distribution is shown in Tab. 2 and Fig. 4.

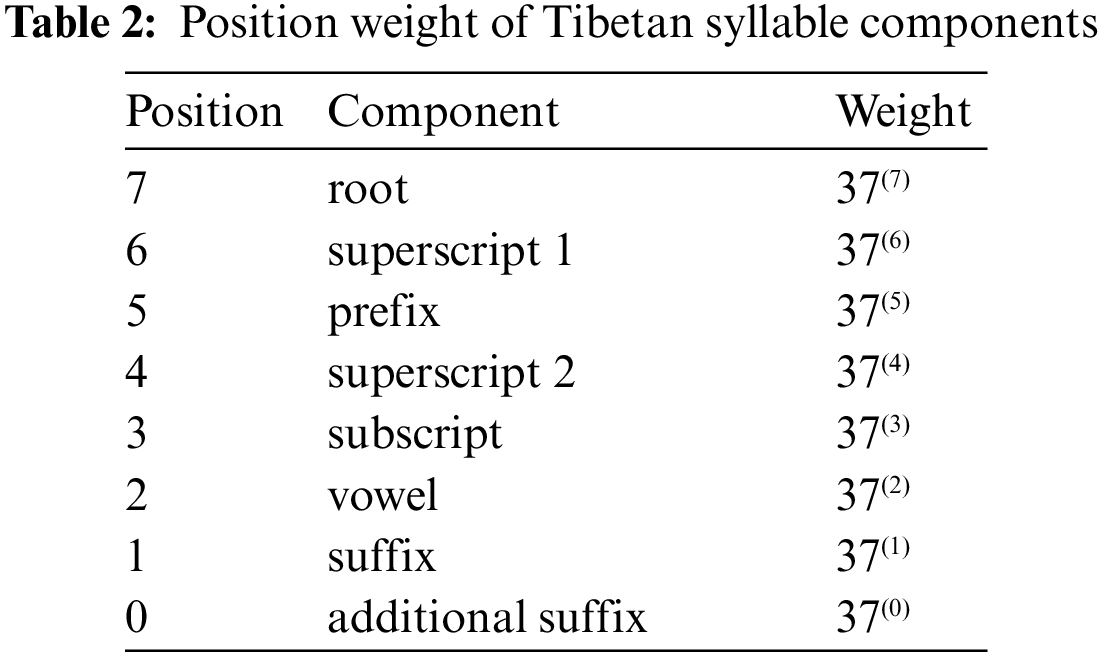
Figure 4: The distribution of position weights of Tibetan script components

3.2 Conversion between Tibetan Alphabetic Characters and Tibetan Main Characters

In the National Standard Tibetan Basic Set [14], the traditional Tibetan syllable alphabet is divided into t Tibetan alphabetic characters and Tibetan main characters, with the syllables sorted according to the alphabetic representations. Therefore, when sorting Tibetan syllables, it is necessary to convert Tibetan main characters into Tibetan alphabetic characters. The Tibetan code shows that the gap between alphabetic and main characters is 80. The conversion algorithm between the two types of characters is as follows.

First, we denote the Tibetan main character as 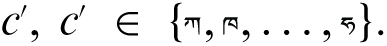The function f(c′) of the alphabetic character y is

g=g(m)    =m−80(3)

The function h(c) finds the code point of the character c. The function g() converts the code point h(c) to the code point of the Tibetan alphabetic character. 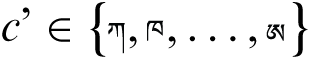h−1() is the inverse of h(c), converting the code point back to the original character. In addition, ,and c=f(c′)=c′.

The encoding of Tibetan characters is relatively large, and it is inconvenient to compare two Tibetan syllables directly. To solve this problem, we convert the encoding of Tibetan characters into relatively small eigenvalues. The eigenvalues of Tibetan characters are calculated as follows:

where c is the Tibetan alphabetic character, and v(c) denotes the eigenvalues of c.

The Tibetan characters and their corresponding feature values are shown in Tab. 3.

3.3 Hash Function of Tibetan Syllables

For the Tibetan syllable Ti, we use the set {ti6,ti5,ti4,ti3,ti2,ti1,ti0} to represent the combination of the root, prefix, superscript, subscript, vowel, suffix, and additional suffix characters. The set of values {vi6,vi5,vi4,vi3,vi2,vi1vi0} are their corresponding feature values. We then define the hash function h of the Tibetan syllable script Ti as

h(Ti)=∑j=0537j×vij+377×vi6+376×(1−α),(5)

where α=0 when vi4≠0, and α=1 when vi4=0 (when there is a superscript character, α = 1; α = 0 otherwise); vij represents the feature value of the j-th component of the i-th Tibetan character, and 37j represents the position weight of the component.

Using this hash function provides all Tibetan syllables with a unique hash value having a maximum value of 55,148,011,380 and a minimum value of 1,838,265,625. However, these hash values are too large. By subtracting the minimum value of 1,838,265,625 from the function h(Ti) and taking its log, Formula (5) becomes Formula (6):

h(Ti)=log⁡(∑j=0537j×vij+377×vi6+376×(1−α)−1838265625)(6)

The modified h(Ti) is a logarithmic function with strong functional properties. Its inverse function is straightforward, with the corresponding Tibetan syllables and components obtainable using the inverse function on the hash value.

4  Sorting Method of Tibetan Syllables Based on Hash Function (SMTSBHF)

4a: Enter the Tibetan syllable string to be sorted: T0, T1, T2, …, Tn.

4b: Use the SBRATSC algorithm to identify the components of the Tibetan syllable Ti as ti0,ti1,ti2,ti3,ti4,ti5,ti6.

4c: Use Formula (2) to calculate the Tibetan alphabet characters ti0,ti1,ti2,ti3,ti4,ti5,ti6:

ti0=f(ti0)ti1=f(ti1)ti2=f(ti2)ti3=f(ti3)ti4=f(ti4)ti5=f(ti5)ti6=f(ti6).

Use Formula (3) to obtain the feature values of the characters ti0,ti1,ti2,ti3,ti4,ti5,ti6:

vi0=v(ti0)vi1=v(ti1)vi2=v(ti2)vi3=v(ti3)vi4=v(ti4)vi5=v(ti5)vi6=v(ti6).

Use Formula (4) to calculate the hash value h(Ti) of Tibetan syllable Ti:

hi=h(Ti)=log⁡(∑j=0537j×vij+377×vi6+376×(1−α)−1838265625)

Calculate the hash values of the other Tibetan syllables in turn.

The calculations in this third step can be expressed as a single expression:

hi=h(Ti)=log⁡(∑j=0537j×v(f(tij))+377×v(f(ti6))+376×(1−α)−1838265625)

4d: Sort the hash values h(T0), h(T1), h(T2), …, h(Tn) of the Tibetan syllables, and then, adjust the corresponding Tibetan syllables to obtain the sort sequence of Tibetan syllables.

The pseudo-code of the sorting method of Tibetan syllables based on the hash function is as follows:

5  Experiment and Analysis

5.1 Experiment

In order to verify our algorithm’s abilities, we collected an experimental corpus consisting of a total of 4268 standardized modern Tibetan syllables taken from the New Tibetan Orthographic Dictionary [17], which is an authoritative Tibetan dictionary published by Qinghai Ethnic Publishing House and recognized by Tibetan scholars. We sorted the syllables according to the sorting rules of that dictionary. We term this original set S1. We then shuffled this set, denoting the unsorted result as S2.

The experimental hardware environment included a processor with six cores and an Intel®Core™ i5-9400F CPU@ 2.90 GHz, with 16 GB of memory, an 11-GB GPU, running the Ubuntu20.10 operating system. All software was developed in Anaconda 3 using Python 3.9.

In the experiment, we compared our method (called method C) to method A [6] and method B [13] when sorting S2. Method A finds the sorting code of each character from the Default Unicode Collation Element Table (DUCET) [6–8], generates the sorting code string of Tibetan syllables, and finally performs the sorting of Tibetan syllables by comparing the sorting code strings. Method B establishes the Tibetan spelling rule function, defines the priority of Tibetan components, and uses the Cartesian product mathematical model to achieve the sorting of Tibetan syllables. The experimental results are shown in Tab. 4.

5.2 Analysis

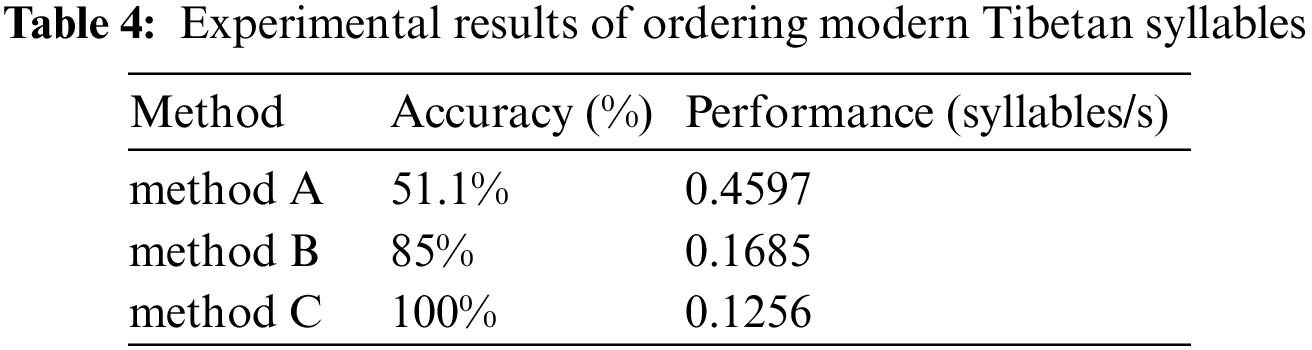
The experimental results show that our method efficiently and conveniently completed the sorting process with an accuracy rate of 100% and using the least time per syllable. Method A was only 51.1% accurate, largely because its sorting rules are defective (Its sorting rules are: root character, prefix character, superscript character, subscript character, vowel character, suffix character, and additional suffix character. This sorting rule is not completely consistent with the rule in the New Tibetan Dictionary.). Method A also did not consider the difference between the alphabetic and traditional Tibetan characters, and its handling of the adhesive affix  was not entirely correct. The accuracy of method B was only 85%, also because of its flawed rules (Its sorting rules are: root character, superscript character, prefix character, subscript character, vowel character, suffix character, and additional suffix character. As with method A, this sorting rule differs from the sorting rule in the New Tibetan Dictionary.). In addition, when the superscript character participated in the sorting for the first time, S2 was sorted directly according to the superscript character size. However, the actual sorting rules require that the superscript character participates in the sorting for the first time only considering whether the superscript character exists; its size should not be used in sorting. In addition, the ordering of Tibetan syllables with double-suffix characters was also insufficiently considered.

6  Concluding Remarks

Currently, Tibetan information processing technology lags behind Chinese information processing technology, and Chinese and English sorting technology is not applicable to Tibetan. By studying the grammar and character formation rules of Tibetan syllables, we propose a method of sorting Tibetan syllables using a hash function. This method is useful in research and in practical applications connected with Tibetan language analysis, text recognition, speech recognition, publishing, and printing.

Acknowledgement: We thank Accdon (www.accdon.com) for its linguistic assistance during the preparation of this manuscript.

Funding Statement: This work was supported by the National Natural Science Foundation of China (No. 61862054) and Applied Basic Research Project of Qinghai Province (No. 2019-ZJ-7066).

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  Cereng-Zhaxi, “The sorting rules of Tibetan language and the realization of automatic sorting by computer,” China Tibetology, vol. 12, no. 4, pp. 128–135, 1999. [Google Scholar]

 2.  D. Jiang and C. J. Kang, “The sorting mathematical model and algorithm of written Tibetan language,” Chinese Journal of Computer, vol. 27, no. 4, pp. 524–529, 2004. [Google Scholar]

 3.  D. Jiang and J. W. Zhou., “On the sequence of Tibetan words and the method of making sequence,” Journal of Chinese Information Processing, vol. 14, no. 1, pp. 56–64, 2000. [Google Scholar]

 4.  D. Jiang, “The current status of sorting order of tibetan dictionaries and standardization,” in The 20th Pacific Asia Conf. on Language, Information and Computation, Wuhan, China, 2006. [Google Scholar]

 5.  Tshedpa, “Research on the automatic recognition and sorting of Tibetan word components on the unicode,” Journal of Tibet University, vol. 29, no. 2, pp. 81–86, 2014. [Google Scholar]

 6.  H. M. Huang and C. X. Zhao., “A ducet-based Tibetan sorting algorithm,” Journal of Chinese Information Processing, vol. 22, no. 4, pp. 109–113, 2008, 2008. [Google Scholar]

 7.  Z. X. Zhong and H. M. Huang, “The design and implementation of a Tibetan syllables sorting rule based on VBA,” Journal of Qinghai Normal University (Natural Science), vol. 33, no. 3, pp. 46–49, 2011. [Google Scholar]

 8.  H. M. Huang and C. X. Zhao, “Introducing sort code to realize Tibetan characters’ sort,” Computer Technology and Development, vol. 18, no. 10, pp. 68–74, 2008. [Google Scholar]

 9.  Zhujie and Erzhu, “Research on Tibetan sorting method based on Tibetan code GB,” Journal of Tibet University (Natural Science Edition), vol. 23, no. 2, pp. 33–35, 2008. [Google Scholar]

10. W. L. Wang and S. C. Wang, “Implementation method and process of Tibetan basic characters positioning,” China Tibetology, vol. 32, no. 4, pp. 215–221, 2019. [Google Scholar]

11. P. Liu and H. M. Huang, “Algorithm design of local Tibetan syllable sorting,” Journal of Northwest Normal University (Natural Science), vol. 48, no. 6, pp. 44–47, 2012. [Google Scholar]

12. Wanme-Zhaxi and Nima-Zhaxi, “Research about Tibetan-sort based on ISO/IEC 10646(Tibetan),” Computer Engineering and Applications, vol. 49, no. 8, pp. 146–150, 2013. [Google Scholar]

13. Bianba-Wangdui, Zhuoga, Z. C. Dong and Q. Wu, “Study on the sorting algorithm of Tibetan dictionary,” Journal of Chinese Information Processing, vol. 29, no. 1, pp. 191–196, 2015. [Google Scholar]

14. of PRC, “National standard,” Information Technology, Tibetan Coded Character Sets for Information Interchange, Basic Set (GB169592-1997). Beijing: Standards Press of China, 1998. [Google Scholar]

15. Caidan-Xiarong, “Explanation of Tibetan related forms,” Detailed Explanation of Tibetan Grammar. Qinghai, China: Qinghai Ethnic Publishing House, 1954. [Google Scholar]

16. E. Roux and H. Hildt, “Algorithmic description of the decomposition and checking of a Classical Tibetan syllable,” Himalayan Linguistics, vol. 17, no. 1, pp. 50–66, 2018. [Google Scholar]

17. Dictionary writing group, New tibetan orthographic dictionary. Qinghai, China: Qinghai Ethnic Publishing House, 1978. [Google Scholar]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.