Journal on Artificial Intelligence DOI:10.32604/jai.2022.027839
Article

Optimizing the Multi-Objective Discrete Particle Swarm Optimization Algorithm by Deep Deterministic Policy Gradient Algorithm

Sun Yang-Yang, Yao Jun-Ping*, Li Xiao-Jun, Fan Shou-Xiang and Wang Zi-Wei

Xi an High-Tech Institute, Xi an, 710025, China
*Corresponding Author: Yao Jun-Ping. Email: junpingy200225@163.com
Received: 26 January 2022; Accepted: 09 March 2022

Abstract: Deep deterministic policy gradient (DDPG) has been proved to be effective in optimizing particle swarm optimization (PSO), but whether DDPG can optimize multi-objective discrete particle swarm optimization (MODPSO) remains to be determined. The present work aims to probe into this topic. Experiments showed that the DDPG can not only quickly improve the convergence speed of MODPSO, but also overcome the problem of local optimal solution that MODPSO may suffer. The research findings are of great significance for the theoretical research and application of MODPSO.

Keywords: Deep deterministic policy gradient; multi-objective discrete particle swarm optimization; deep reinforcement learning; machine learning

1  Introduction

Particle swarm optimization (PSO), a swarm intelligence algorithm, was proposed by Bai et al. [1] in 1995. PSO is inspired by foraging behaviors of bird, information about the food will be shared among these birds. PSO can solve optimization problems with a continuous solution space, but it is invalid in discrete solution space optimization problem. Therefore, Zheng [2] proposed binary particle swarm optimization (BPSO) in 1997, and later, a variant of BPSO called discrete particle swarm optimization (DPSO) was put forward. For BPSO cannot solve combination optimization problem with ordered structure expression and constraint condition [3], therefore DPSO is more widely used than BPSO. However, DPSO cannot solve multi-objective problems in practical applications. Drawing lessons from the multi-objective particle swarm optimization (MOPSO) proposed by Feng et al. [4] in 2002, the multi-objective discrete particle swarm optimization (MODPSO) combines DPSO with MOPSO, can make up for the shortcomings of DPSO.

The static hyperparameter configuration has been proved to be an important factor constraining the performance of PSO, especially in convergence speed and local optimal solution. Therefore, Lu et al. [5] explored dynamic setting of PSO hyperparameters based on deep deterministic policy gradient (DDPG) in 2021.

The configuration of hyperparameters of MODPSO and PSO is static. For example, value of the positive acceleration constant [6] is usually 2 in MODPSO [7] and PSO [8], this means static hyperparameter configuration of MODPSO may be an important factor constraining the performance of the algorithm as well as PSO. Therefore, determining whether DDPG can improve the performance of MODPSO is of great significance for promoting the theoretical research and real-world application of MODPSO.

In this logic, this paper explored whether DDPG could improve the performance of MODPSO, basic idea is that DDPG initially generates random hyperparameters for MODPSO, MODPSO gives good or bad reward to DDPG after adopting these hyperparameters, DDPG will generates new hyperparameters for MODPSO according to the reward from MODPSO. Steps of MODPSO are presented in Section 2. Frame of DDPG is presented in Section 3. Steps of deep deterministic policy gradient multi-objective discrete particle swarm optimization (DDPGMODPSO) is presented in Section 4, which is the development of MODPSO. Experimental results are presented in Section 5. Conclusion is presented in Section 6.

2  MODPSO

To compare DDPGMODPSO and MODPSO, the fitness function proposed by Sun et al. [7] was adopted, and the calculation method is as follow.

{Min(Cost)=Min{ ∑i=1mTi,process×[3.66+0.002×(∑j=1nSdj,memory+∑k=1hSmk,memory)]}Min(Time)=Min(∑i=1mTi,process)(1)

Materialized view is an important term in database and data house, the above multi-objective function is about to reduce cost and time of materialized view. i represents the ith query, j represents the jth base table, k represents the kth materialized view, Ti,process represents time used for the ith query, Sdj,memory represents storage used for the jth base table, Smk,memory represents storage used for the kth materialized view.

The MODPSO process designed by Sun et al. [7] is as follows.

Input: Discrete solution space;

      positive acceleration constants c1 and c2;

      number of particles;

      number of training epochs.

Output: Optimal solution.

Step 1: Initialize the particle swarm, determine particle speed and position randomly, and deal with the illegal position.

Step 2: Calculate individual fitness values Cost(xi(t)) and Time(xi(t)).

Step 3: If individual fitness values greater than individual optimal fitness values, update the individual optimal fitness values as follows.

{Cost(pbesti)>Cost(xi(t))Time(pbesti)>Time(xi(t))(2)

{Cost(pbesti)=Cost(xi(t))Time(pbesti)=Time(xi(t))pbesti=xi(t)(3)

Step 4: If individual optimal fitness values greater than global optimal fitness values, update the global optimal fitness values as follows.

{Cost(gbesti)>Cost(xi(t))Time(gbesti)>Time(xi(t))(4)

{Cost(gbesti)=Cost(xi(t))Time(gbesti)=Time(xi(t))gbesti=xi(t)(5)

Step 5: Update velocity for each particle.

vi(t)=vi(t−1)+ρ1×(xpbesti−xi(t))+ρ2×(xgbest−xi(t))(6)

where random number ρ1=r1×c1, ρ2=r2×c2, r1∼U(0, 1), r2∼U(0, 1).

Step 6: Update particle position as follows.

{xi(t)=xi(t−1)+vi(t)t=t+1(7)

Deal with the illegal position.

Step 7: Judge whether the training is terminated. If it is terminated, output the result; otherwise, go to Step 2.

It is necessary to noted that illegal position means position not in the discrete solution space, the way we deal with illegal position is replace it by the nearest position in the discrete solution space.

3  DDPG

DDPG was proposed by Zhao et al. [9] in 2015, it combines deterministic policy gradient (DPG) and deep Q-network (DQN) with the actor-critic algorithm as a framework. Fig. 1 shows the structure of DDPG, which is mainly composed of Environment (MODPSO), Agent (Actor Network and Critic Network), State (st and st+1), Action (at) and Reward (rt).

Figure 1: Structure of DDPG

The components of the DDPG are specified as follows.

(1)   Environment

Actor network and critic network obtain the optimal hyperparameters c1 and c2 by continuously interacting with MODPSO, and then apply c1 and c2 to MODPSO, so MODPSO is set as the Environment here.

(2)   Agent

Since actor network and critic network are the only elements that can interact with the Environment, the actor network and the critic network are used as Agent here.

(3)   Action

Actions are c1 and c2.

(4)   State

State have six dimensions. The first five dimensions represent the change in the average fitness value of MODPSO in the past, and the last dimension represents the current number of training epochs of MODPSO. The calculation method is as follows.

sit=fitmeant+4−i−fitmeant+3−i(8)

s5t=tTmax(9)

where sit represents state vector of the t-th training epoch and the i-th dimension. The value range of i is [0, 4]. Where Tmax indicates the maximum number of training epochs and fitment indicates the average fitness value of particles in the t-th training epochs of MODPSO.

(5)   Reward

State of the Environment is transferred, and Environment then gives Reward to Agent according to Agent's action. The setting of Reward is related to whether the global optimal fitness value has changed. The calculation method is as follows.

ri={1,Global optimal fitness value changed−1,Global optimal fitness value not changed(10)

4  DDPGMODPSO

Inspired by deep deterministic policy gradient particle swarm optimization (DDPGPSO) proposed by Lu et al. [5], this paper proposed DDPGMODPSO. DDPG initially generates random hyperparameters for MODPSO, MODPSO gives good or bad reward to DDPG after adopting these hyperparameters, then DDPG will generates new hyperparameters for MODPSO according the reward from MODPSO.

The DDPGMODPSO process designed in the this work is as follows.

Input: Discrete solution space;

      the number of particles;

      number of training epochs for MODPSO Tmax;

      number of training epochs for DDPG Trainmax.

Output: Optimal solution.

Step 1: Randomly initialize the parameters of the current policy network μ(s|θμ) and current Q-network Q(s,a|θQ), i.e., θμ, and θQ.

Step 2: Randomly initialize the parameters of target policy network μ(s|θμ′) and target Q-network Q(s,a|θQ′): θμ′←θμ, θQ′←θQ.

Step 3: Initialize experience replay pool R.

Step 4: Execute Step 1 to Step 4 of the MODPSO algorithm.

Step 5: While episode is less than Trainmax.

Step 6: Initialize a random process to explore Action;

Step 7: Receive initial observations s1 of Environment (particle swarm).

Step 8: While t is less than Tmax.

Step 9: Choose Action according to the current strategy and explore noise. The specific process is as follows.

at=μ(st|θμ)+Nt(11)

Step 10: Execute Action at in Environment, then observe Reward rt and new State st+1;

Step 11: Save (st, at, rt, st+1) to R as a data set for training the current network;

Step 12: Randomly sample a minimum batch of N groups of data from R as training data of the current Q-network, and set yi.

yi=ri+γQ′(si+1,μ′(si+1|θμ′)|θQ′)(12)

Step 13: Update current Q-network by minimizing the loss function, and the minimum loss function is expressed as follows.

L=1N∑i=0N(yi−Q(si,ai|θQ))2(13)

Step 14: Use the gradient of the sample to update actor network as follows.

∇θμJ≈1N∑i(∇aQ(s,a|θQ)|s=si,a=μ(si)⋅∇θμμ(s|θμ)|s=si)(14)

Step 15: Update target network.

θQ′←τθQ+(1−τ)θQ′(15)

θμ′←τθμ+(1−τ)θμ′(16)

where τ is the parameter update rate, which is generally set at 0.0001.

Step 16: t++.

Step 17: episode++.

Step 18: Save the weights of the trained actor network;

Step 19: Execute Step1 to Step 4 of the MODPSO algorithm;

Step 20: While t is less than Tmax.

Step 21: Calculate the current State and update the global optimal fitness value.

Step 22: According to current policy network μ(s|θμ) and current State, get the current Action, calculate c1 and c2;

Step 23: Execute Step 5 to Step 6 of the MODPSO algorithm.

Step 24: t++.

5  Experimental Results and Analysis

5.1 Experimental Setup

The discrete solution space (the experimental data) in this paper is the same as Sun et al. [7]. Tab. 1 shows the specifics of the data.

Tab. 2 shows the setup of MODPSO.

Tab. 3 shows the setup of actor network.

Tab. 4 shows the setup of critic network.

5.2 Result and Analyses

Ten sets of experiments were carried out on MODPSO and DDPGMODPSO separately, experimental result is showd in Tab. 5.

As showed in Fig. 2, DDPGMODPSO outperformed MODPSO.

As showed in Fig. 3, Among the 10 experiments, MODPSO only found the global optimal value in two experiments, while DDPGMODPSO found the global optimal value in seven experiments. Therefore, DDPGMODPSO is significantly better than MODPSO in finding the global optimal fitness value.

As is showed in Fig. 4, In the two experiments in which MODPSO found the global optimal fitness value, MODPSO took an average of 56 steps to reach the global optimal fitness value; in the seven experiments in which DDPGMODPSO found the global optimal fitness value, DDPGMODPSO took an average of 41 steps. Therefore, DDPGMODPSO converges faster than MODPSO.

Figure 2: Experimental result

Figure 3: Number of times the global optimal value was found

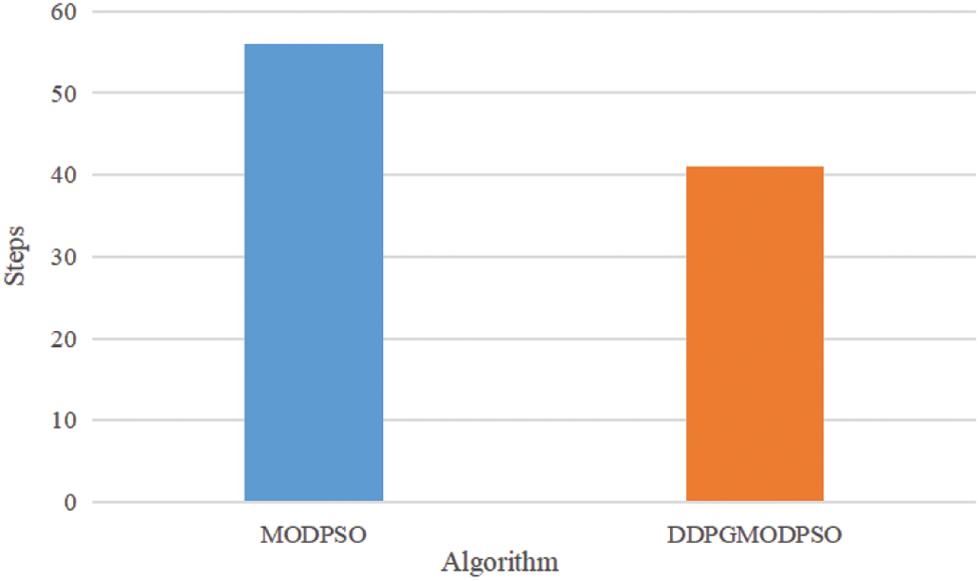
Figure 4: Average number of steps the global optimal value was found

6  Conclusion

In the present work, we explored how the DDPG can improve the performance of MODPSO. Experiments revealed that DDPGMODPSO outperformed MODPSO in discovering the optimal fitness value and converged faster than the latter. Therefore, it was verified that DDPG can significantly improve the global optimal fitness value discovery capability and convergence speed of MODPSO.

Funding Statement: The authors received no specific funding for this study.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  B. Bai, Z. W. Guo, C. Zhou, W. Zhang and J. Y. Zhang, “Application of adaptive reliability importance sampling-based extended domain PSO on single-mode failure in reliability engineering,” Information Sciences, vol. 546, pp. 42–59, 2020. [Google Scholar]

 2.  R. Z. Zheng, “An improved discrete particle swarm optimization for airline crew rostering problem,” in Proc. of the 2020 IEEE Congress on Evolutionary Computation, Piscataway, USA, pp. 1–7, 2020. [Google Scholar]

 3.  L. C. Shen, X. H. Huo and Y. F. Niu, “Survey of discrete particle swarm optimization algorithm,” Systems Engineering and Electronics, vol. 30, no. 10, pp. 1986–1990, 2008. [Google Scholar]

 4.  Q. Feng, Q. Li, W. Quan and M. Pei, “Research review of multi-objective particle swarm optimization algorithm,” Chinese Journal of Engineering, vol. 43, no. 6, pp. 745–753, 2021. [Google Scholar]

 5.  H. X. Lu, S. Y. Yin, G. L. Gong, Y. Liu and G. Chen, “Particle swarm algorithm based on depth deterministic policy gradient,” Journal of University of Electronic Science and Technology of China, vol. 50, no. 2, pp. 199–206, 2021. [Google Scholar]

 6.  Z. X. Cai, L. Y. Liu, J. F. Cai and B. F. Chen Artificial Intelligence and its Applications, 5st ed., Beijing, China: Tsinghua University Press, pp. 184–189, 2016. [Google Scholar]

 7.  Y. Y. Sun, J. P. Yao, X. J. Li and Y. J. Wang, “Materialized view selection in cloud environment based on multi-objective discrete particle swarm optimization,” Journal of China Academy of Electronics, vol. 16, no. 7, pp. 661–668, 2021. [Google Scholar]

 8.  Y. P. Lin, L. L. Chen and J. Z. Zou, “Application of hybrid feature selection algorithm based on PSO in fatigue driving,” Computer Engineering, vol. 45, no. 2, pp. 278–283, 2019. [Google Scholar]

 9.  X. Y. Zhao and S. F. Ding, “A review of deep reinforcement learning research,” Computer Science, vol. 45, no. 7, pp. 1–6, 2018. [Google Scholar]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.