Open Access

PROCEEDINGS

Damage Identification Algorithm of Composite Structure Based on Displacement Field

Xiaoyang Shen¹, Xiaojing Zhang^1,*

1 School of Astronautic and Aeronautic, Shanghai Jiao Tong University, Shanghai, 201100, China

* Corresponding Author: Xiaojing Zhang. Email:

The International Conference on Computational & Experimental Engineering and Sciences 2023, 28(1), 1-3. https://doi.org/10.32604/icces.2023.010519

Abstract

1 General Introduction
Reliable structural health monitoring with high detection probability is very important [1]. Therefore, the method of finite element simulation was adopted. Based on the basic equation of material mechanics and stiffness degradation theory, to detect the damage of composite laminates, and further improves the intelligence of the detection process through the method of visual detection neural network.

2 Theoretical derivation and simulation
2.1 Equations for buckling
In the stratified damage area, each layer bears the load independently, and the bearing capacity is determined by the stiffness there: the larger the axial stiffness, the stronger the bearing capacity at the stratified area. [2] The higher the bending stiffness, the greater the critical buckling load. When the layer with lower bending stiffness reaches the buckling load, the layer will no longer bear the load, and the load will continue to be borne by the damage site with higher stiffness.[3] When the layer with the maximum stiffness also reaches the buckling load, local buckling will occur in each layer of the sub-plate at the same time. Based on this conclusion, the load can be calculated using the known stiffness of the substrate Amp (1) and the critical strain of another substrate .

.

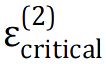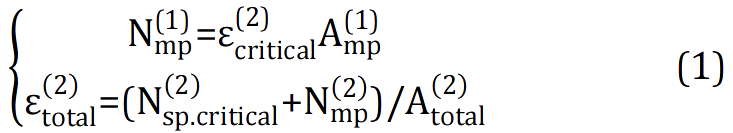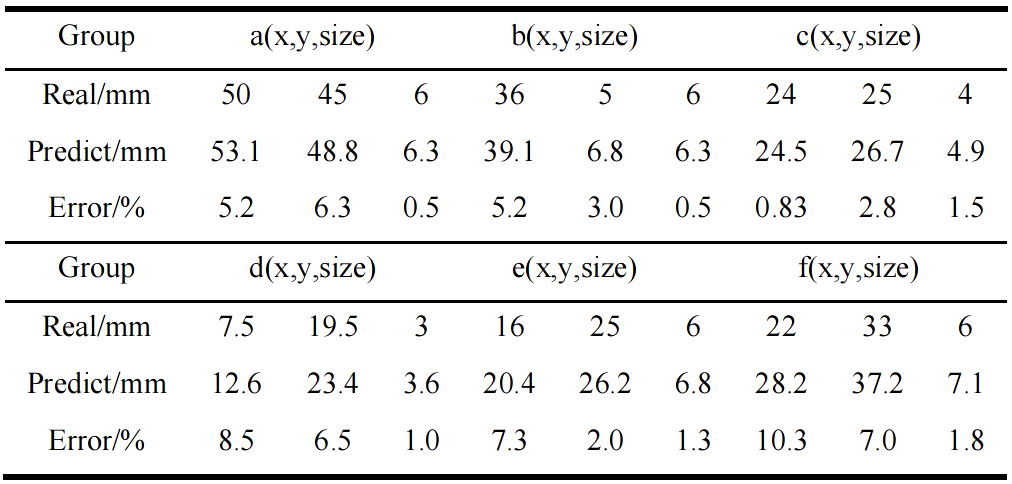
Compared the predicted parameters with the actual parameters, the results are shown in Table 2. The average relative error of the neural network model for coordinate prediction is 5.41%, and the prediction effect is good, which is larger than the actual value, which proves that there is still room for adjustment. The average relative error of the model for predicting the damage size is 1.1%, and the prediction effect is quite in line with the expectation.

2.2 Preparation for simulation
The size of the model selected in this work is 60mm×60mm, and the layup of the laminate is [0°/45°/- 45°/90°]s. Compression load of 1mm was loaded to make the laminates deform in the direction out of plane. In order to simulate the interlayer force in Abaqus, a cohesive force unit with a thickness of 0 is biased between adjacent layers, and the interlayer damage simulated by the stiffness reduction method is shown in Table.1.

2.3 Database of the simulation
On the basis of parameterized modeling using Python, 700 groups of models containing damage were established through for loop which randomly assigns the size and location of damage through random function. The damage radius is controlled within 2-8mm, and the damage may occur at any interlayer position.

3 Analysis and algorithm
3.1 Analysis of database
The cloud image is derived as shown in Figure.1. The color difference in the cloud image can better reflect the damage appearance of the laminates. It should be noted that different cloud images need to unify the color range in Abaqus software. From the photo gallery, it can be roughly seen that the colors of different pictures are relatively uniform, and there are no obvious inappropriate samples.

3.2 Image processing
During the image processing, the non-maximum suppression algorithm was used to select the box with the highest evaluation and suppress the box with the lower evaluation. This process is an iterative elimination process shown in Figure.2.

4 Conclusion
Figure.3 shows the relationship curve between accuracy and recall of the model. The average accuracy of this model is 0.89. If the 45° reference line is taken as the equilibrium point of P=R, it can be found that the equilibrium point of this model is very high, indicating that the algorithm is suitable for this work.

Table 1: Cloud image of displacement field



Figure 1: Cloud image of displacement field


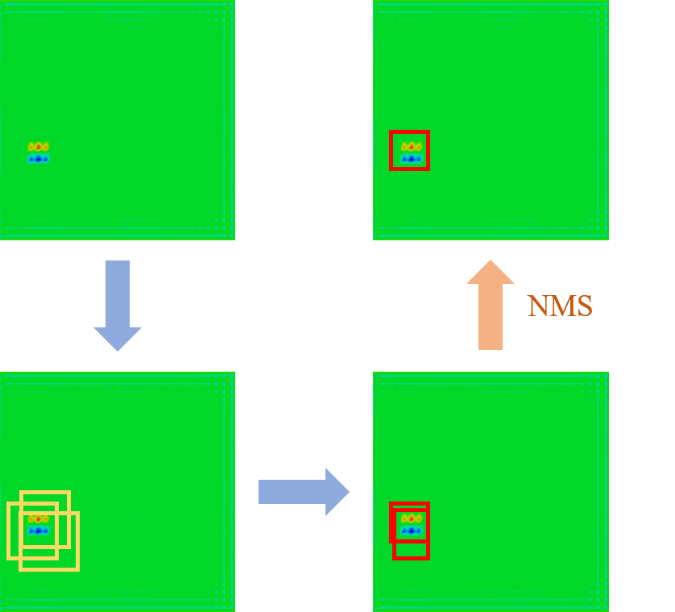
Figure 2: Non-maximum suppression algorithm


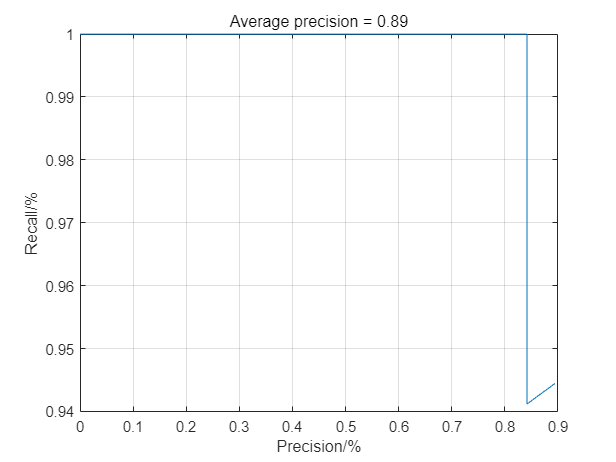
Figure 3: Cloud image of displacement field

Table.2: Predicted parameters and errors

---