Innovative Lightweight Encryption Schemes Leveraging Chaotic Systems for Secure Data Transmission

1  Introduction

Big data encompasses structured and unstructured data derived from social media, sensors, and transactions [1]. Such heterogeneous data required sophisticated techniques for storage and processing [2]. It facilitates data-driven decision-making and enables industries to gain profound insights by revealing previously unachievable patterns and trends [3]. To fully realize its disruptive capabilities, it is imperative to tackle data privacy and security issues and develop a scalable infrastructure [4].

In real-time data transmission, securing data in the transiting phase requires lightweight encryption to safeguard critical information in secure transaction data [5]. Conventional encryption techniques may be ineffective and require many resources because of the data’s fast pace and diverse nature [6]. Efficient encryption guarantees the protection of data while maintaining optimal performance and scalability [7]. Swift encryption and decryption are vital in real-time processing and analysis such as efficiently safeguarding transaction data integrity and confidentiality in the banking, healthcare, and e-commerce industries [7,8]. Also, another field where lightweight encryption is demanded is cloud computing where enormous small but sensitive data are stored and retrieved in frequent and repetitive forms [9].

While focusing on securing data while transmitted in real-time, a stream cipher is the commonly employed encryption algorithm [10]. These ciphers generate a key stream that combines with plaintext bytes using the bitwise exclusive-or (XOR) operation, creating encrypted data [11]. Stream ciphers are implemented across various security protocols to protect transmitted data, such as secure SMS with A5/1 for Global System for Mobile Communications, Virtual Private Network (VPN) technologies using Layer Two Tunneling Protocol, and Wi-Fi security through Cipher Block Chaining Message Authentication Code Protocol [12]. Other researchers implemented such lightweight algorithms to encrypt -decrypt the data at the network layer [13], by replacing the old A5/1 stream cipher with a new stream cipher called Grain-128PLE.

1.1 Chaotic Map

A chaotic map is a mathematical function that sensitively depends on initial conditions. It allows the scrambling and deconstruction of digital information, which is essential for secure communication. Modern chaotic systems have been employed in encryption to maintain the confidentiality of sensitive information.

Chaotic maps used in ASCII encoding can also serve as key generators for one-time pad ciphers, known for their unbreakability if the pad is truly random and never reused [14].

Lightweight encryption depends on chaotic maps in resource-limited environments including IoT devices and wireless sensor networks [15]. These maps provide complex encryption keys and sequences employing their sensitive dependency on initial conditions and pseudo-random behavior [16]. Chaotic-based encryption methods improve security without raising computational costs by using the unpredictable and nonlinearity of chaotic systems [17]. For uses with minimal resources and processing capability, they are thus perfect. While keeping real-time data transmission efficiency, chaos maps in lightweight encryption offer excellent security that questions brute force and differential analysis [18].

The authors of [19] employed Chaotic and Henon maps for low processing overhead using the intrinsic features of chaotic systems—such as sensitivity to beginning circumstances, pseudo-randomness, and nonlinearity for encrypting grayscale images. The logistic chaotic map and multidimensional and hybrid chaotic maps are widely used for securing text and image data [20]. The chaotic map is also utilized in block cipher to generate s-box due to the high sensitivity of the chaotic system for the initials, making it suitable for implementation in resource-constrained devices [21]. For constructing next-generation lightweight cryptographic systems, then, chaotic maps are becoming appealing. In lightweight encryption, chaotic maps have proven especially valuable for securing data in resource-limited environments, such as IoT devices and wireless sensor networks [13]. Chaotic maps generate complex encryption keys and sequences by leveraging their sensitivity to initial conditions and pseudo-random behavior [14]. The inherent unpredictability and nonlinearity of chaotic systems strengthen encryption while keeping computational costs low, making them ideal for devices with limited resources and processing capabilities [15]. Moreover, chaotic maps provide strong security against brute force and differential analysis, supporting efficient real-time data transmission while resisting advanced attacks [16]. The logistic chaotic map is expressed as:

yt+1=r.yt(1−yt)(0≤yt,0≤r≤4).(1)

Logistic map sensitivity to initial conditions and parameter r makes it highly applicable in encryption. Bifurcation analysis reveals that the map’s behavior changes significantly with variations in r, displaying periodic windows and chaotic orbits as r increases.

1.2 Bifurcation and Its Role in Chaotic Systems

Bifurcation is a critical phenomenon in chaotic systems that significantly affects system behavior. The system transitions between dynamic regimes by varying a parameter, such as (r) in the logistic map (see Eq. (1)). This sensitivity to parameter changes makes chaotic maps ideal for pseudorandom number generation and encryption, as slight variations in parameters ensure unpredictability and enhanced security [22].

Behavior as r increases:

1. Stable Fixed Point (0 < r ≤ 3): For small r, the population approaches a singular stable value.

For instance, if r = 2.5, the system attains stability at a given location.

2. Periodic Oscillations (3 < r ≤ 3.45): Beyond r = 3, the system exhibits oscillations between two values, characterized by period-2 behavior.

As r grows, the oscillations bifurcate into 4, 8, 16, and so forth, resulting in periodic windows (e.g., period-4 at r ≈ 3.5).

3. Chaos (r > 3.57): For r > 3.57, the system exhibits chaotic behavior characterized by non-repeating values and extreme sensitivity to initial conditions.

The system displays “chaotic bands” characterized by seemingly random values.

4. Periodic Windows in Chaos: Within chaotic regions, narrow periodic activity intervals exist (e.g., period-3 cycles at r ≈ 3.83).

5. Complete Chaos (r = 4): At r = 4, the system exhibits complete chaos, with values encompassing nearly the whole interval [0, 1].

Fig. 1 represents the bifurcation diagram, which illustrates the alterations in the long-term dynamics of the Logistic map as (r) escalates.

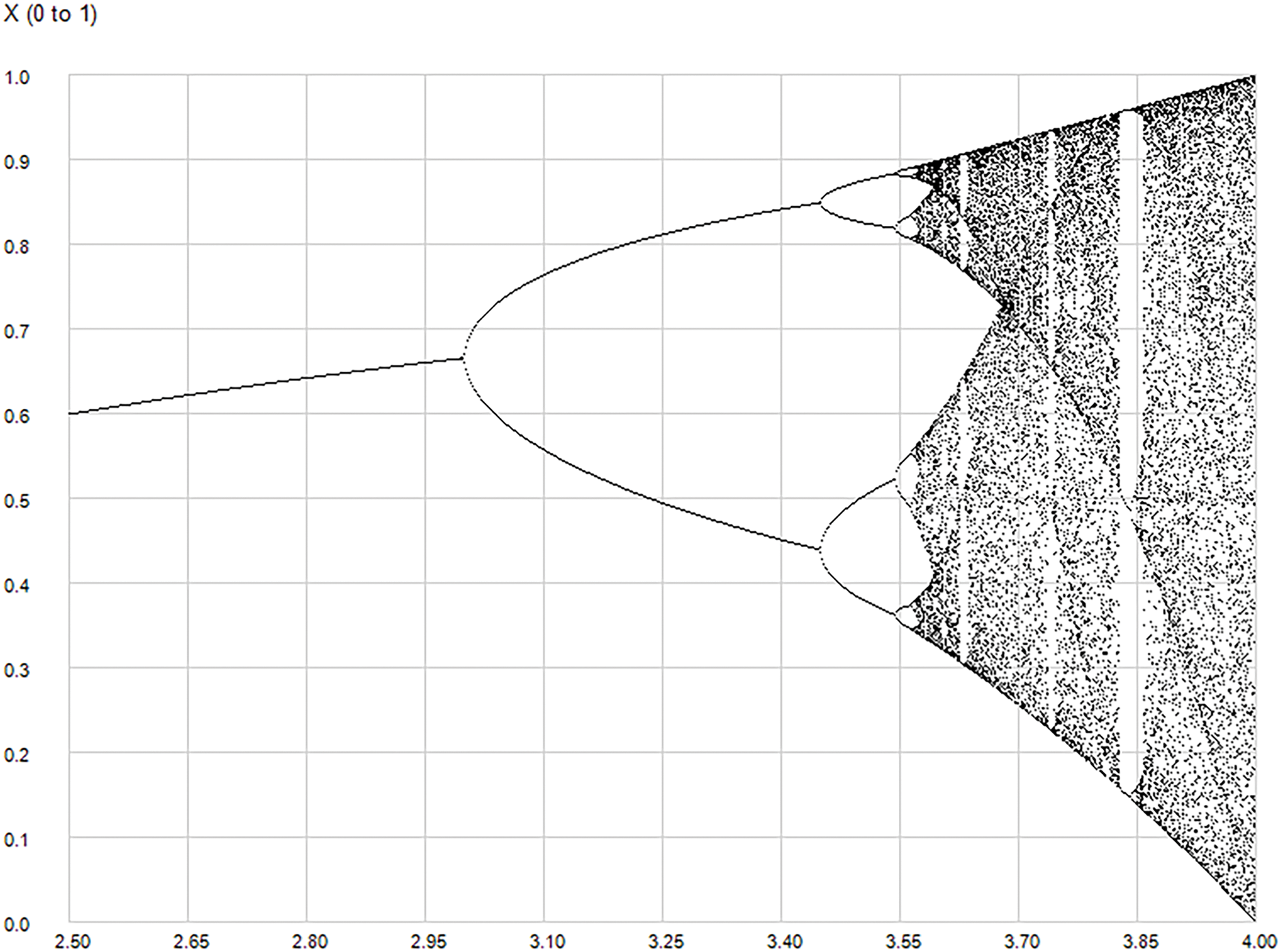
Figure 1: Bifurcation diagram of the logistic map

1.2.1 The Lyapunov Exponent in Chaotic Systems

Lyapunov exponent explains the system’s unpredictability and robustness, confirming that a well-constructed logistic map ensures secure communication [23]. Lyapunov Exponent calculated using Eq. (2).

λ=1n∑1=1nln|df(x)dx|,(2)

where: X-axis represents r. Y-axis represents x values.

It measures the sensitivity of a system to initial conditions, making it a key indicator of chaos. A positive Lyapunov exponent indicates exponential divergence of trajectories, signifying chaos, while a negative exponent denotes stability, as stated in Fig. 2. In encryption, the Lyapunov exponent helps evaluate the robustness of chaotic systems, with higher values indicating greater security. For the logistic chaotic map, the Lyapunov exponent is particularly useful in assessing the unpredictability and complexity of the encryption process. The exponent also aids in brute-force cryptanalysis by demonstrating the difficulty of replicating chaotic behavior [24].

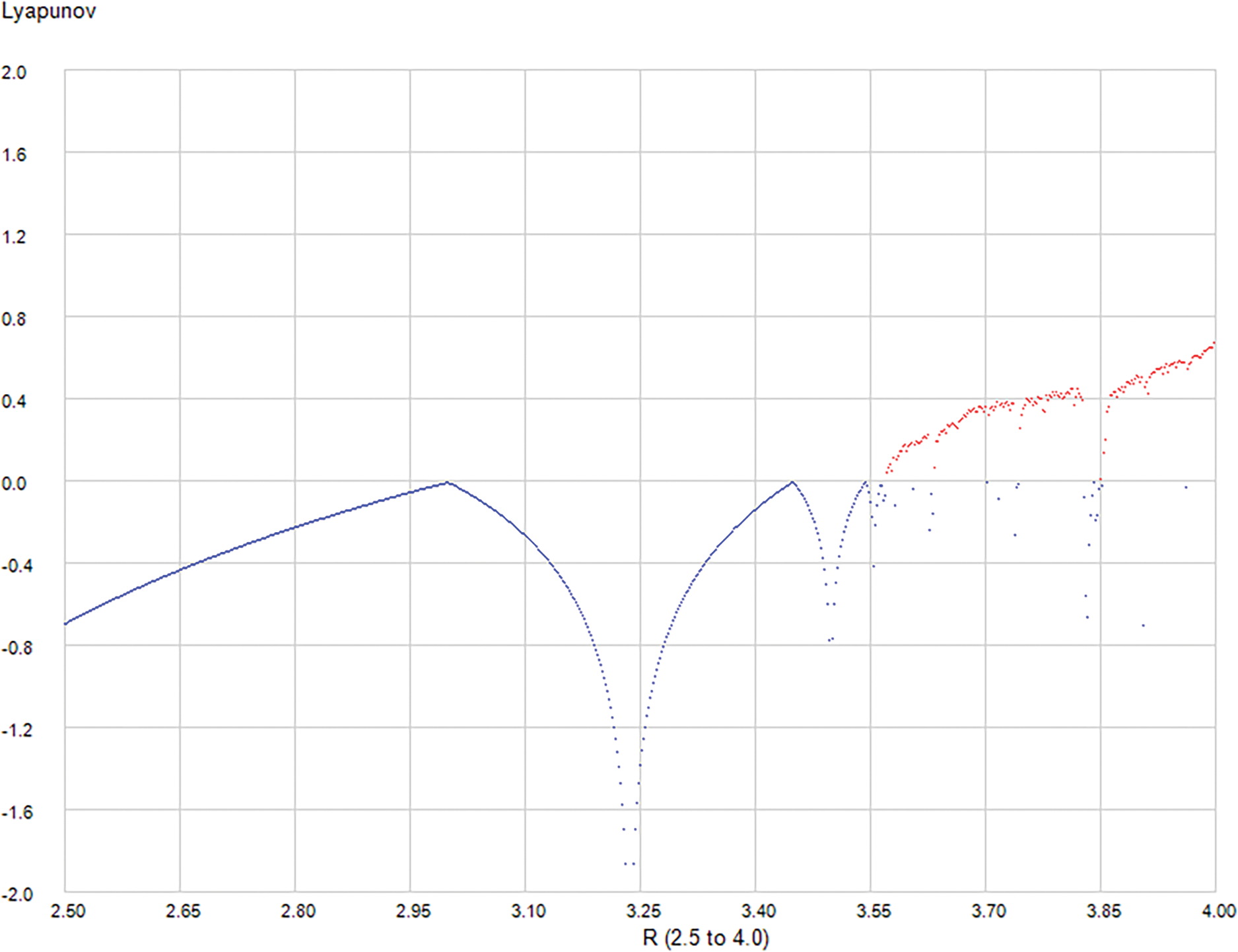
Figure 2: Lyapunov exponent of the logistic map

This paper explores lightweight encryption, stream ciphers, and chaotic maps as essential techniques for secure real-time data transmission, examining their individual and combined capabilities to meet modern security challenges effectively. The rest of the paper is structured into multiple sections to convey the research and its results methodically. Section 3 examines the pertinent literature, providing context and background for the research. Section 4 delineates the problem statement, highlighting the principal challenges addressed by the research. Section 5 outlines the study objectives, elucidating the aims of the offered solutions.

2  Related Works

In contexts with limited resources, chaotic map-based lightweight encryption systems are extensively applied to guarantee effective and safe data protection. Though chaotic maps have a deterministic and unpredictable character [25], they improve the resistance of encryption systems against attacks by increasing the diffusion and confusion processes [26]. Their adaptation for secure encryption [27] comes from their sensitivity to basic conditions and intricate dynamics. Chaos maps find use in many disciplines, including biometric authentication [28], picture and video encryption [29,30], and identity-based authentication [31]. Using chaotic maps improves security and efficiency, according to research. Therefore, they are fit for modern lightweight cryptographic applications in the Internet of Things (IoT), edge computing, and cloud computing. Considered one of the primary sources of big data kinds, scientists used a type of encryption that is not heavy to protect digital photos, categorized as considerable volumes of data, and thus safeguarded.

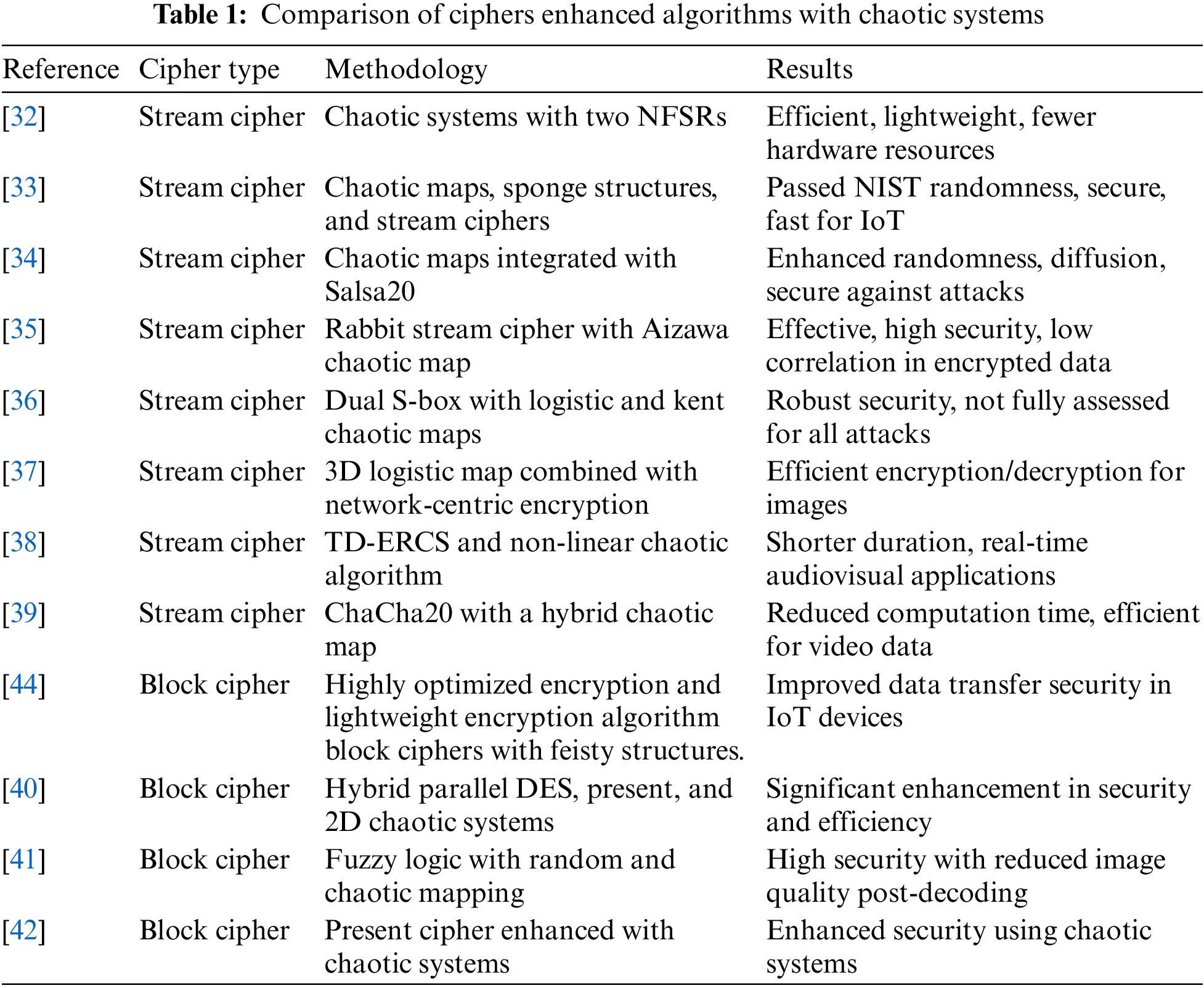
According to [32], the researchers addressed the construction and analysis of a novel stream cipher integrating chaotic systems for usage in environments with restricted resources. Designed for devices with limited processing capability, such as smart cards and wireless sensors, the cipher combines a chaotic system with two Nonlinear Feedback Shift Registers (NFSRs) to create a lightweight stream cipher labeled Logic. The design is hardware-oriented, so minimum resources are required to provide strong encryption. A comparative study of lightweight stream ciphers, such as Trivium and Grain, indicates that the Logic cipher requires fewer hardware resources while maintaining competitive throughput. The author of [33] presents a lightweight authentication encryption method tuned for IoT. Proposed is a lightweight encryption method employing sponge structures, chaotic maps, and stream ciphers. This approach manages IoT device problems, including limited memory and processing capability. The method passes security, NIST randomness, and speed testing. It used memory efficiently, making it suited for resource-constrained settings. The proposed encryption method is faster and uses less memory than ASCON and Beetle, making it ideal for resource-constrained IoT applications. As noted by [34], the research presents an enhanced Salsa20 stream cipher that uses chaotic maps like the Henon, Lorenz, Rabinovich-Fabrikant, and Chua circuit maps to generate keys and increase randomness and diffusion, strengthening its security against known attacks. This increases cipher security by increasing unpredictability and complexity. The new method fixes weaknesses in Salsa20/7 and Salsa20/12, which were no longer secure. Increased diffusion and chaotic map unpredictability protect the proposed technique from cryptanalytic attacks. The lightweight, efficient cipher is ideal for real-time applications on resource-constrained devices like IoT systems, notwithstanding security and dispersion improvements. According to [35], the research employed the Rabbit algorithm, a lightweight stream cipher, in conjunction with the Aizawa chaotic map to provide dynamic keys for picture encryption. The findings demonstrate that the encryption method is effective. There is minimal correlation between the original and encrypted photos, indicating high security. The encryption keys produced with the hybrid method successfully met the NIST randomness criteria, demonstrating their resilience against attacks.

The researchers of [36] reported utilizing dual S-box encryption system “Logistic and Kent” chaotic maps to build sub-chaotic matrices, ensuring robust security for transmitting medical data in wireless body area networks. The study does not entirely assess the system’s effectiveness in handling various scenarios or intensive attacks. Authors of [37] suggested a hybrid chaotic encryption system combining network-centric encryption with a 3D logistic map. The primary results indicate efficiently applying encryption and decryption techniques to photographs.

As described by [38], the proposed technique utilizes the Tangent-Delay Ellipse Reflecting Cavity-Map System and the Non-linear Chaotic algorithm for encryption. It attains a shorter duration, which makes it appropriate for real-time applications in audiovisual hearing aids. Expanding the critical space makes it more resistant to brute-force attacks. The article by [39] integrated the ChaCha20 stream cipher and a hybrid chaotic map to secure video data. The technique reduces computation time and data required, enhancing the encryption efficiency. In the research of [41], efficient block ciphers like Highly Optimized Encryption and Lightweight Encryption Algorithms are incorporated to improve data transfer security between IoT devices by employing a blend of feisty structures and fundamental operations like XOR, addition, and rotation. As stated by [40], the suggested hybrid parallel technique combines the DES, present, and 2D chaotic systems. This pioneering method significantly enhances the security and efficiency of image encryption, offering a promising solution to current challenges. In the research of [41], efficient block ciphers like Highly Optimized Encryption and Lightweight Encryption Algorithms are incorporated to improve data transfer security between IoT devices by employing a blend of feisty structures and fundamental operations like XOR, addition, and rotation. The data presented by [41] showed an innovative and efficient chaotic encryption technique incorporating fuzzy logic for access management. The suggested system utilized random and chaotic mapping techniques using a designated password key supported by fuzzy logic shifts to manipulate the image pixels. The primary constraint is decreased image quality following decoding and computation capabilities. The findings of [42] employed the chaos-based present cipher as an innovative encryption technique that enhances security by utilizing chaotic systems. The study by [43] improves resource-constrained device security and efficiency with ASCON authenticated encryption and ECC. The proposed system protects against impersonation, replay, man in the middle, and credential leakage threats by checking mobile user identity before network access and providing a secure communication channel, as verified by Random Oracle Model analysis. Despite its computational and communication efficiency, the proposed system requires more storage and complexity owing to multi-factor authentication (password, biometrics, and device). Due to protected hardware, physical assaults like power analysis could offer hazards if an attacker acquires device access. SAF-MCN is ideal for secure situations with low computing resources. Table 1 briefly describes the related work.

2.1 Problem Statement

After carefully reviewing the available literature, it is clear that many studies have used chaotic algorithms to create encryption keys. Nevertheless, these methods frequently demand significant computational time for the requisite computations. To rectify this inefficiency, the proposed research suggests employing chaos theory to execute a transposition procedure. The suggested technique will generate random numbers to be utilized as the arrangement of the original character indices before executing the XOR operation, which has the potential to decrease the overall computing time and improve the efficiency of the encryption procedure.

2.2 Aims

The growing demand for safe communication in the modern digital age has driven significant research on encryption technologies. Although secure, conventional encryption methods usually rely on chaotic algorithms for key creation, which use a lot of processing power and take a long time. This work addresses this challenge by introducing a novel approach using chaos theory to undertake a transposition process, generating a random rearranging of character indices before the XOR operations. This work presents a more effective and pragmatic encryption method that lowers processing time while preserving good security, providing strong protection for private data during the transmission. The following lists the goals of the present research:

1. Execute a transposition process grounded in chaos theory to produce a randomized character index arrangement, thereby providing an efficient, lightweight encryption mechanism.

2. To Improve computation Efficiency: Calculate the computing efficiency of the suggested approach relative to standard chaotic key-generating techniques to significantly lower the encryption times.

3  Methodology

The general phases in the encryption process must contain two major processes: Permutation and Substitution [45] in addition to the input and output, as depicted in Fig. 3. Two algorithms have been implemented to achieve the permutation process, utilizing first-order chaotic maps. On the other hand, the XOR process is used to achieve the substitution process.

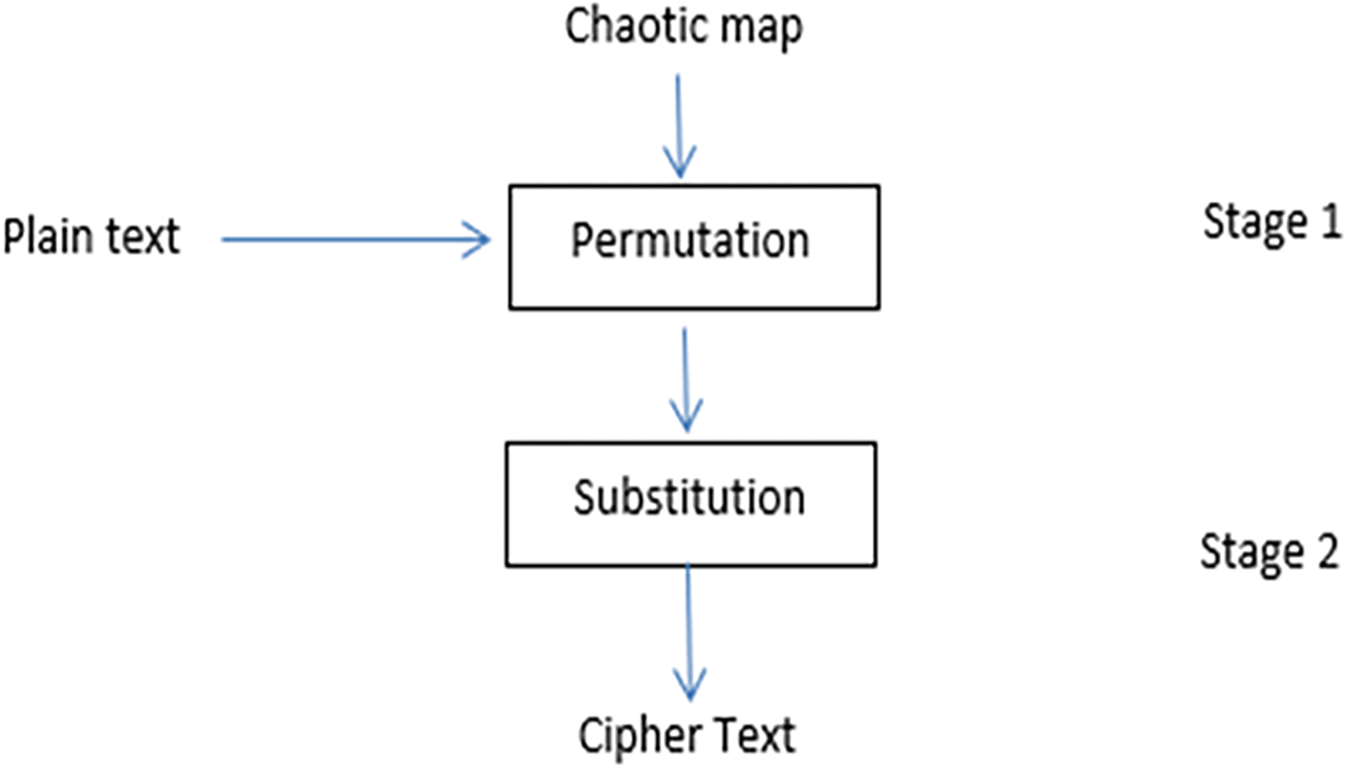
Figure 3: Encryption process

3.1 First Algorithm: Double Chaotic

The technique generates extremely random sequences with different seeds from two chaotic functions, improving security and complexity. The chaotic functions and plain text to be encrypted are the input, and the output is ciphered text. This algorithm has three steps. In the first stage, a one-dimensional chaotic algorithm creates fractional random integers for each plain text letter. These integers are sorted in ascending order in an array while preserving their places. The plain text characters are altered to match the new sequence, which confuses. ASCII encoding converts characters into numbers for mathematical processes.

In the second stage, a new chaotic function generates another set of random numbers in blocks of 256 values. Sorting these integers in ascending order creates a new reordering sequence. This sequence underpins the XOR operation, bringing randomness and diffusion to encryption.

In the third and final stage, the encryption process is implemented by XORing the numeric values of the rearranged characters from the first stage and the random numbers from the second stage. Chaotic randomization, reordering, and XOR ensure considerable output changes for tiny input alterations, making encryption resilient and secure. Table 2 contains an example of (9) randomly generated numbers and the same numbers after implementing the reordering process presented in Table 3.

For more practical implementation, a plaintext “PRESIDENT” is suggested as a sequence of characters arranged from positions 0 to 8, each character holding a unique position as shown in Table 4. The initial position is given by the coordinates (0, 1, 2, 3, 4, 5, 6, 7, 8). Each character in the plaintext corresponds to a specific position specified in this row. For instance, the character ‘P’ was initially located at position 0, ‘R’ at position 1, and so forth.

Another Chaotic equation with different inputs generates a collection of fractional random numbers. The second chaotic equation is suggested to ensure the process’s robustness. The fractional random values are converted into integer numbers between 0 and 255 utilizing Eq. (2) and sorted ascending. The multiplication by (255) ensures the range of the output between (0–255), while the “round” process converts the fractional number into an integer.

y=round (x0×255).(3)

Finally, the characters and symbols of the original text are transformed into numerical values using the ASCII table. Then, an XOR operation is executed between the numerical values of the characters in the new places and the numerical values representing the new location of the fractional values generated by the second chaotic map function.

The key length in the first and second logistic maps is 80 bits. Each logistic map provided 64 bits for initial value and 16 bits for iteration. The key space of an encryption method generally defines the number of possible keys that could be employed. The security of the encryption process depends critically on a strong key space for both the Double Chaotic and Single Chaotic methods. The first suggested algorithms have a key length of 160, which offers a key space of (2^160). The first suggested algorithm is explained below (Algorithm 1):

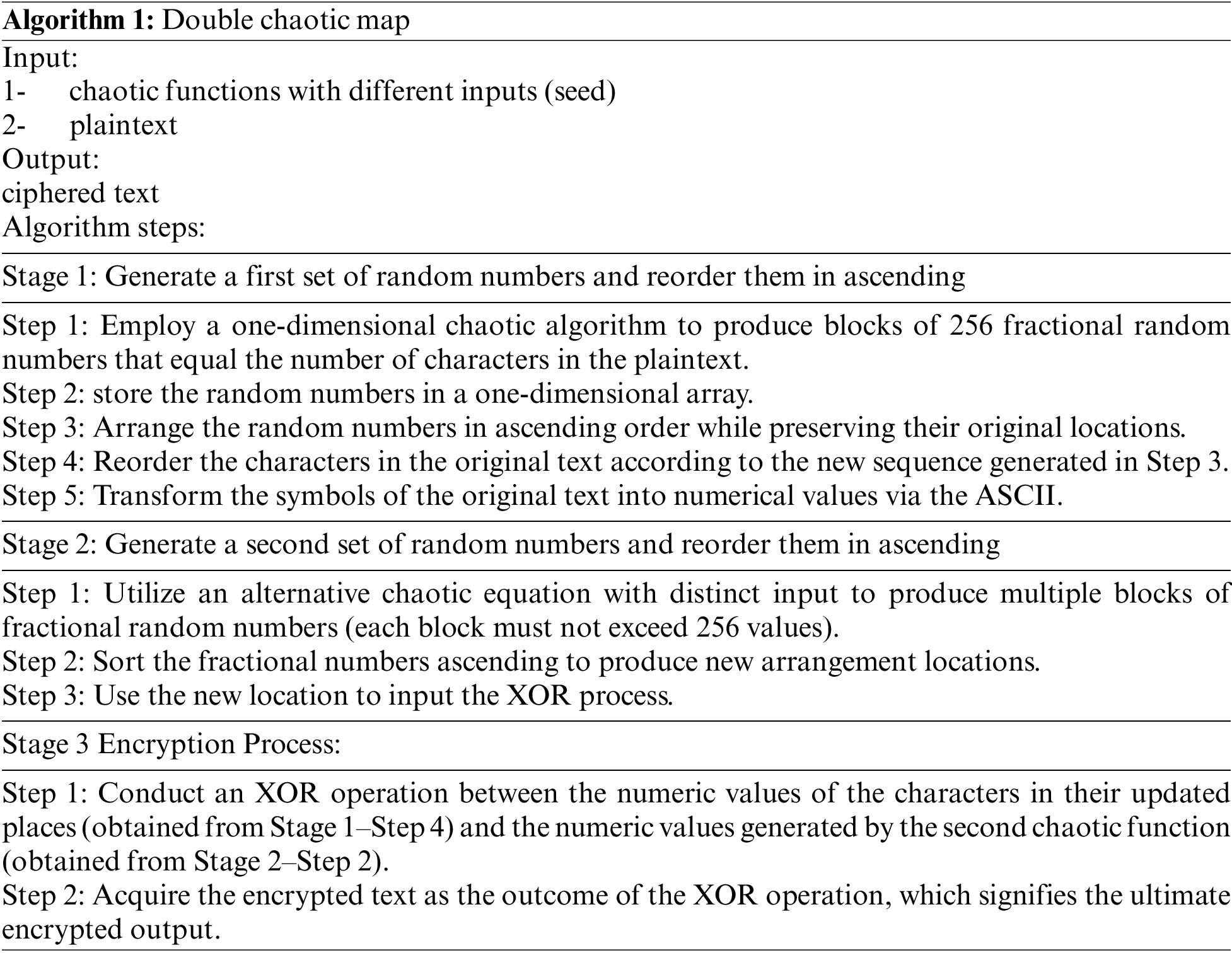
To present a fully accurate understanding of the steps in the suggested algorithm, detailed discussion for all steps in each stage separately:

Stage 1: Generate a first set of random numbers and reorder them in ascending

In Step 1, a one-dimensional chaotic map is utilized to generate blocks of 256 random fractional numbers. The generated random numbers are equal to the length of the plaintext.

Step 2: The random numbers are stored in an array for efficient manipulation. This structure is essential for sorting and maintaining the connection between characters in the plaintext and their corresponding random values.

Step 3: For each block of 256 of the random numbers, sort them in ascending order to establish a new sequence, although the original indices of these numbers remain essential and are maintained. For instance, assume [0.43, 0.12, 0.78] as arbitrary numbers with indices [0, 1, 2]. Upon sorting, the sequence is transformed to [0.12, 0.43, 0.78], while the indices are rearranged to [1, 0, 2].

Step 4: In this step, the plaintext characters are reordered according to the sequence obtained from Step 3. For instance, if the plaintext is “ABC,” taking the original indices [0, 1, 2] and the random indices from sorting is ‘[1, 0, 2]’, the resultant arrangement is “BAC.”

Step 5: In the final step, which belongs to Stage 1, every character in the reordered plaintext is transformed into its ASCII representation, resulting in a series of numerical numbers. ASCII defines the string ‘BAC’ as ‘[66, 65, 67]’.

Discussion of the second stage: Produce a Second Set of Random Numbers and Arrange Them in Ascending Order.

Step 1: in this step, the research employed another chaotic map equation with different inputs to generate several blocks of fractional random numbers for each number.

Step 2: In this step, the fractional numbers generated in Step 1 are organized in ascending order to get new arrangement positions. These arbitrary integers are arranged, resulting in an additional set of ordered indices as sorted in Stage 1. The new indices will subsequently ascertain the position of characters during the XOR process.

Step 3: The indices obtained in Step 2 serve as input to map the numerical plaintext values for the XOR operation, guaranteeing a shuffled sequence before encryption.

Stage 3: Encryption procedure

Step 1: Perform an XOR operation between the numeric values of the reordered characters (produced by Stage 1, Step 5) and those made by the second chaotic function (Stage 2, Step 2).

This procedure integrates two autonomous layers of randomness, hence augmenting security.

Step 2: The outcome of the XOR procedure is the conclusive encrypted numeric sequence. This sequence can be reverted to characters via ASCII or maintained as numeric values for transmission or storage.

Fig. 4 represents the activity diagram for the encryption process relating to Algorithm 1.

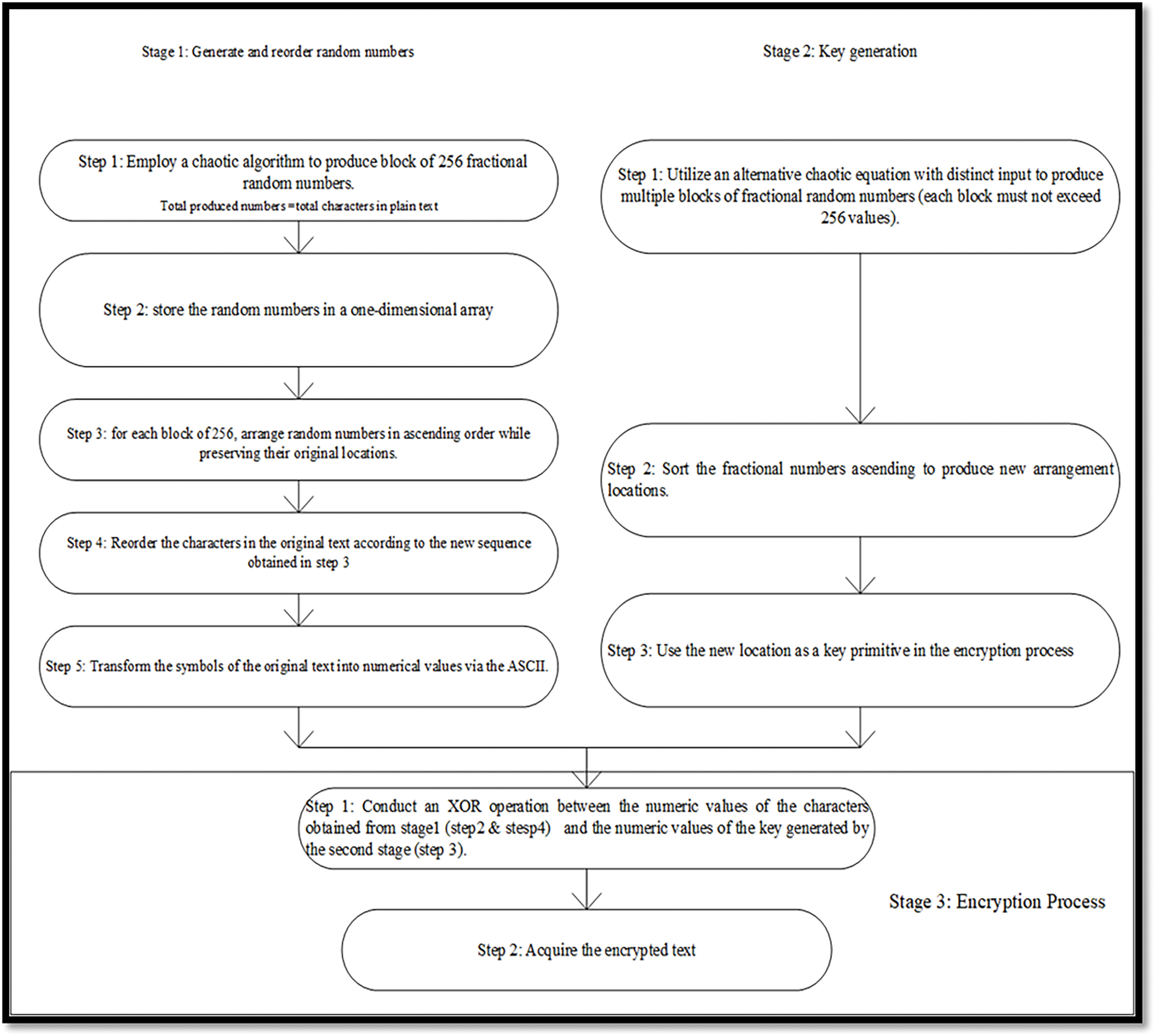
Figure 4: Activity diagram for the suggested Algorithm 1

3.2 Second Algorithm: Single Chaotic

The described lightweight encryption scheme uses chaotic functions and XOR operations to cipher plain text. The method takes a chaotic function with seeds and plain text to encrypt as inputs and outputs the encrypted content.

Starting with a one-dimensional chaotic method, a sequence of random integers equal to the plain text’s characters is generated. A one-dimensional array stores these fractional random numbers for processing. Next, the random numbers are broken into 256-value sequences and reordered in ascending order while preserving their original places, providing a unique sequence for each block.

Plain text is read as ASCII values and stored in a separate array. The random number sorting sequence reorders these values. This stage scrambles the text using the chaotic sequence, improving security. In the final stage, XORing the reordered ASCII values of the characters and the new location values from the random numbers completes the encryption. The encrypted output is produced by XORing the chaotic system’s unpredictability with the scrambled text. XOR produces the final ciphered text, providing a secure and efficient encryption approach for the lightweight algorithm.

This approach combines chaotic systems with cryptographic processes to accomplish encryption through randomization and reordering. The following is a detailed sequential analysis of its functionality.

Below paragraph explain the Algorithm 2 in more details:

In Step 1, the research utilized a one-dimensional chaotic method to generate blocks of 256 random numbers corresponding to the plaintext’s character count. The produced random numbers are fractional and directly correlate to each character in the plaintext. The total generated random numbers must equal the number of plaintext characters.

Step 2: The random numbers are stored in a one-dimensional array for efficient access and manipulation. This array functions as a mapping framework for subsequent stages, facilitating the incorporation of chaotic characteristics into the encryption procedure.

Step 3: The random integers are arranged in ascending order for each block while preserving their original indices. This process will establish a mapping that determines the rearrangement of characters in the plaintext. For example, random numbers: [0.43, 0.12, 0.78] sorted as: [0.12, 0.43, 0.78] according to the initial indices: [1, 0, 2].

Step 4: Each plaintext character is transformed into its respective ASCII value. ASCII defines the plaintext ‘ABC’ as ‘[65, 66, 67]’. The numeric values are retained in a one-dimensional array, maintaining their sequence.

In Step 5, the plaintext array from Step 4 is reorganized according to the mapping established in Step 3. Utilizing the illustration from Step 3: Original plaintext: ‘ABC’ → Numeric representations: [65, 66, 67]. So random sequence indices: [1, 0, 2] → Rearranged plaintext: [66, 65, 67] (equivalent to “BAC”).

Step 6: Execute an XOR operation between the new location value derived from Step 3 and the numeric values of the characters in their revised positions (obtained by Step 5).

In the final step (number 7), the XOR outcomes represent the ultimate encrypted numerical values. These can be reverted to characters utilizing ASCII (if necessary) or transmitted/stored in their current form. Implementing chaotic algorithms results in significant unpredictability owing to their sensitivity to starting seeds. This improves security, as the random sequences are distinct for various seeds. The rearranging of the plaintext before executing XOR introduces complexity, obscuring trends in the ciphertext. The XOR technique guarantees reversibility, an essential characteristic of decryption. Managing 256-character blocks is consistent with established cryptographic practices (e.g., byte-oriented processing) and guarantees scalability for extended plaintexts.

Fig. 5 represents the block diagram for the encryption process relating to Algorithm 2.

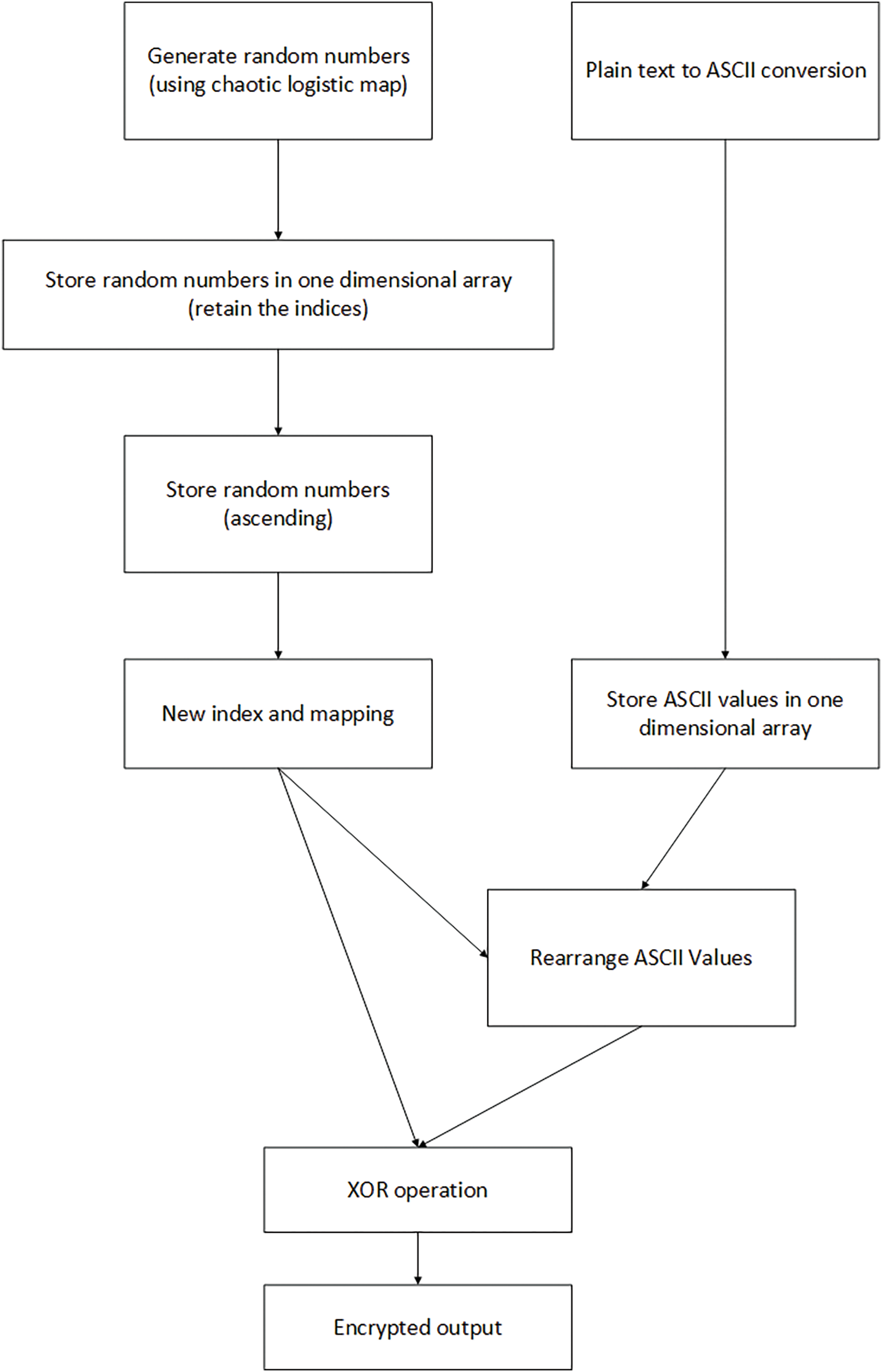
Figure 5: Algorithm 2 encryption

4  Results

The practical tests were made using a computer equipped with Processor Intel (R) Core (TM) i5-4200U CPU @ 1.60 GHz, 2.30 GHz, RAM, 12.0 GB, and Microsoft Windows 10 type 64-bit operating system, x64-based processor. The practical results demonstrate a high and acceptable level of randomness in the encryption data, indicating the robustness of the two proposed algorithms. However, there is a slight preference between them. These algorithms were applied to text files of varying sizes, such as 80,000, 120,000, and 140,000 bytes, and the results were encouraging.

The results concern calculating and comparing entropy and NIST statistical tests as evidence of the strength of suggested algorithms. They also compute and compare the encryption time. All comparisons are made using only research in related work.

4.1 Entropy

Table 5 compares the practical results of the two algorithms when applied to data files ranging from 80,000 to 140,000 bytes.

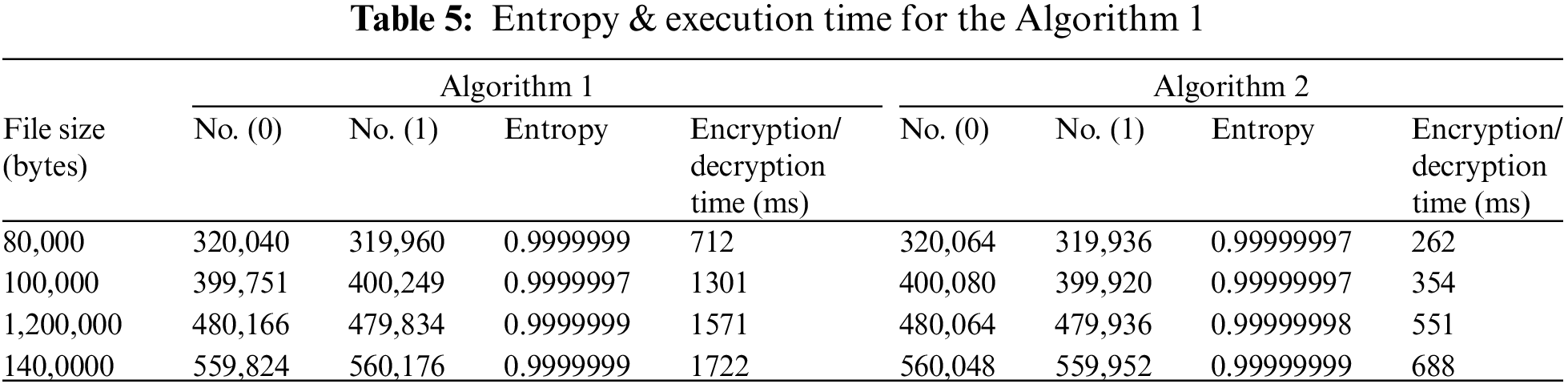
Table 6 briefly compares the proposed two algorithms (when applied to 140,000 bytes of data) and some related works that used entropy to measure the randomness of encrypted data.

4.2 NIST Statistical Test

The tests assess randomness, with findings expressed as p-values, indicating the probability that the tested sequence demonstrates adequate randomness. Table 7 compares the outcomes of statistical tests conducted on different cryptographic algorithms, emphasizing the proposed Algorithm 1 (Double Chaotic) and Proposed Algorithm 2 (Single Chaotic). The Double Chaotic algorithm typically outperforms the Single chaotic algorithm in most assessments, especially in the Frequency (mono bit), Cumulative Sum, Runs, and linear complexity tests demonstrating elevated p-values, signifying superior randomness. Fig. 6 demonstrates the visual results recorded in Table 7.

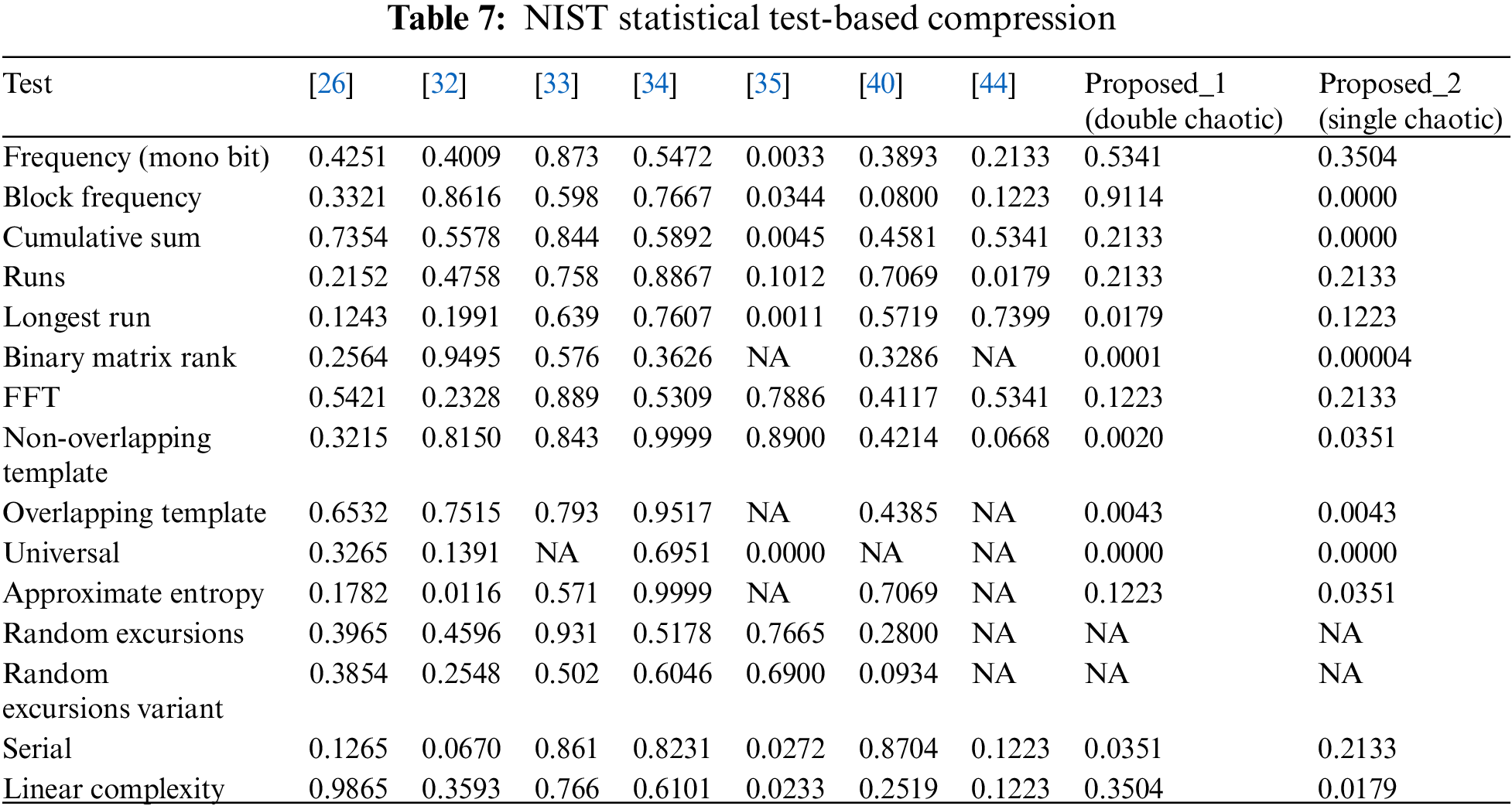
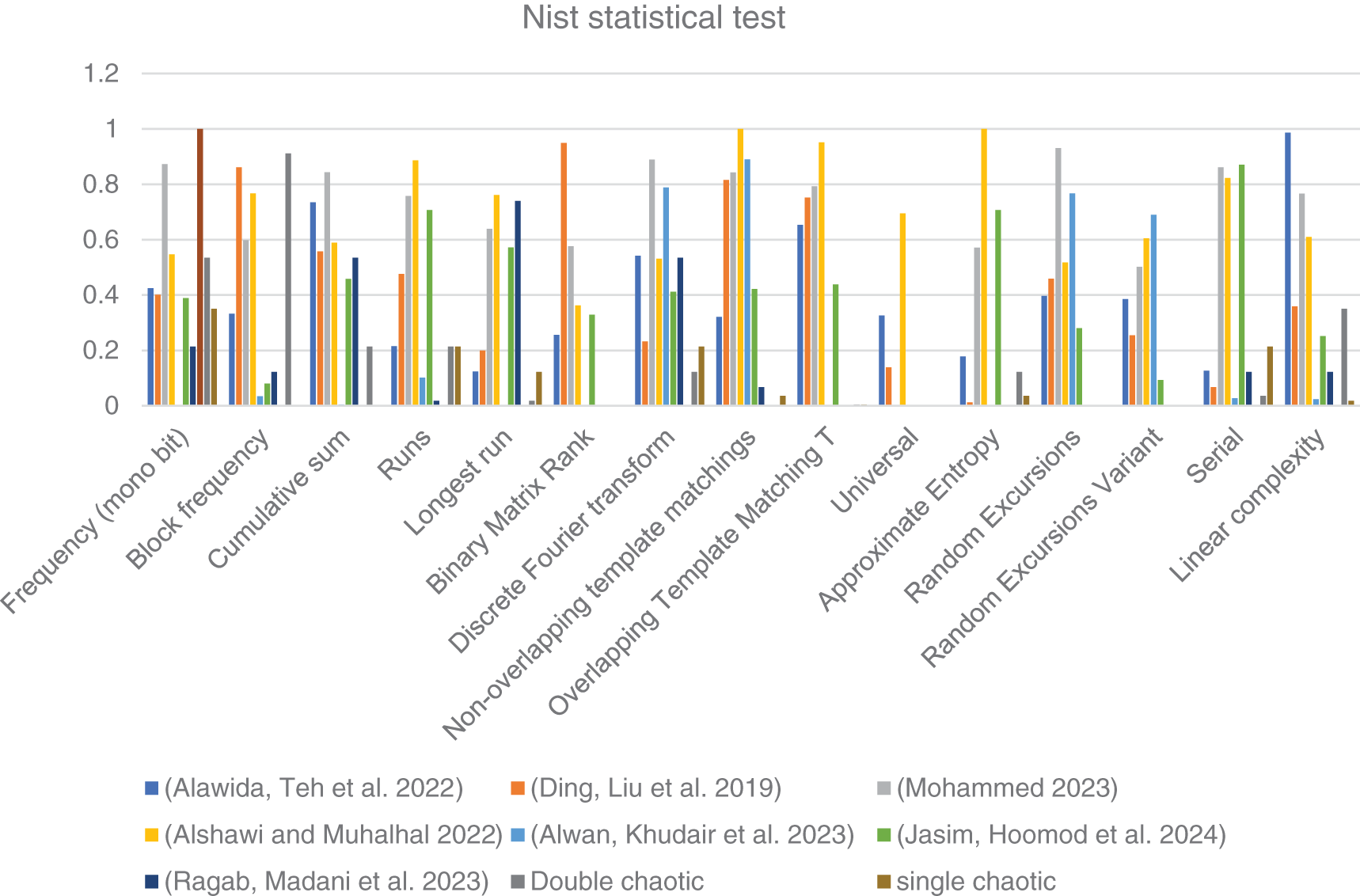
Figure 6: NIST statistical test-based compression [26,32–35,40,44]

4.3 Execution Time

Table 8 displays compassion between the proposed algorithm and related work according to an exciting time.

Table 8 compares the encryption duration, size of encrypted data, time per kilobyte (ms/kB), CPU frequency (GHz), RAM capacity (GB), and key length for various cryptographic algorithms, including Proposed_1 (Double Chaotic), Proposed_2 (Single Chaotic), and several reference algorithms denoted by numbers. The methods are assessed on performance, focusing on encryption duration, resource consumption (CPU, RAM), and the volume of the encrypted data.

Proposed_1 (Double Chaotic) exhibits a significantly longer encryption duration (712 ms) than proposed_2 (Single Chaotic) (262 ms) for an identical data size of 80,000 bytes. When normalized by ms/kB, proposed_2 demonstrates superior efficiency, requiring 3.35 ms per kilobyte, but proposed_1 necessitates 9.11 ms per kilobyte. This shows that the single chaotic approach is faster than the dual chaotic alternative in speed. Both methods have key lengths of 160 and 80 bits, respectively, and use the same CPU and RAM resources (2.3 GHz, 4 GB RAM). The double chaotic system’s complexity helps one explain the performance difference.

Regarding encryption speed, proposed_2 (Single Chaotic) trumps proposed_1 (Double Chaotic), providing higher efficiency for real-time uses. Nevertheless, a perhaps strong chaotic system, the proposed_1 method, might offer improved security at the price of performance.

4.4 Key Sensitivity

Hamming distance is one of the concepts in cryptography that was abandoned in the domain of information theory. Hamming distance is one of the non-linear properties supported by any security cryptosystem domain, which measures the distance between two strings of equal length [47]. The Hamming distance between two equal-length strings is the number of bit positions at which the corresponding bits differ. Hence, it can be used for error detection when two strings are comparable bit by bit [48]. In general, it is also used to analyze the sensitivity of the keys of selected cryptographic algorithms. When initials were used in the first algorithm (where two logistic maps were used in the encryption process), changing only the x0 for one out of two equations from x0 = 0.1 to x0 = 0.2 obtained hamming distance = 79,349 bits for two ciphered files, each of 80,000 characters, on the other hand, for the second approach, when only one logistic map was utilized for the encryption process, results showed that when initially changed from (x0 = 0.1 to x0 = 0.2), a considerable value of hamming distance obtained reaching 104,239 bits calculated for two cipher texts both of 120,000 characters. According to [49], the greater the value of Hamming, the greater the sensitivity of the key, it is notable that both approaches are practicing well and producing different cipher text when implementing small changes to the utilized key values. These hamming distances indicate changes in the ciphertext when changing only three bits for both algorithms ((3 out of 160) bits for the first algorithm and (3 out of 80) bits for the second algorithm).

The results indicate that Chaotic algorithms are computationally efficient and exhibit superior pseudo-random characteristics, rendering them suitable for resource-limited settings such as IoT devices. Rearranging characters and using XOR with an extra layer of randomization guarantees that minor alterations in the plaintext or key significantly impact the ciphertext (avalanche effect). Finally, the multi-stage architecture incorporates nonlinear dependencies, rendering it impervious to linear and differential cryptanalysis.

5  Conclusions

The work shows that chaotic algorithms for lightweight encryption are effective and robust, especially for high-randomness and secure applications. Practical outcomes like entropy, NIST statistical tests, and execution time measurements show the two techniques’ benefits and weaknesses.

1. Randomness and Entropy Performance: Both methods produced near-perfect entropy values across file sizes, proving their randomness. The Double Chaotic (Algorithm 1) and Single Chaotic (Algorithm 2) algorithms maintained entropy levels of 7.999, exceeding other algorithms in the literature.

2. NIST Statistical Test Results: In Frequency, Cumulative Sum, Runs, and Linear Complexity tests, the Double Chaotic algorithm outperformed the Single Chaotic technique. This suggests that the Double Chaotic approach provides slightly more random sequences, which may protect against predictability assaults.

3. Performance and Execution Time: The Double Chaotic algorithm (Algorithm 1) provides more unpredictability but takes 9.11 ms/kB longer than the Single Chaotic algorithm (3.35 ms/kB). This makes the Single Chaotic method better for real-time applications prioritizing speed, whereas the Double Chaotic method may be better for security-focused applications.

4. Security-Performance Trade-off: The Double Chaotic algorithm’s more complicated structure and higher processing requirements boost its security potential, making it a good choice for environments that emphasize security above performance. The Single Chaotic algorithm is faster, more efficient, and highly random, making it suitable for resource-constrained IoT and embedded systems.

In conclusion, both algorithms have strengths for distinct applications. The efficient Single Chaotic technique is ideal for real-time or resource-constrained applications, whereas the Double Chaotic approach is better for secure applications. These findings demonstrate chaotic encryption’s adaptability for lightweight cryptographic methods, enabling secure data transport in modern computational contexts. However, a fixed block size limits adaptation, sorting operations are computationally expensive, and chaotic map seeds are required for security. Future work should introduce dynamic block sizing for flexibility, optimize computational stages to reduce overhead, create safe seed management mechanisms, and use parallel processing to boost efficiency. Lightweight algorithm adaptations are needed for resource-constrained contexts like IoT devices. These changes will make the algorithm more practical and secure for current cryptography.

Acknowledgement: This work was supported by “The Informatics Institute for Postgraduate Studies and the Iraqi Commission for Computers and Informatics.”

Funding Statement: The authors received no specific funding for this study.

Author Contributions: The authors confirm their contributions to the paper as follows: study conception and design: Haider Al-Mahmood and Saad Alsaad; data collection: Haider Al-Mahmood and Saad Alsaad; analysis and interpretation of results: Haider Al-Mahmood and Saad Alsaad; draft manuscript preparation: Haider Al-Mahmood and Saad Alsaad. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The datasets generated and/or analyzed during the current study are available from the corresponding author upon reasonable request.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

References

1. S. B. Abkenar, M. H. Kashani, E. Mahdipour, and S. M. Jameii, “Big data analytics meets social media: A systematic review of techniques, open issues, and future directions,” Telematics Inform., vol. 57, 2021, Art. no. 101517. [Google Scholar]

2. K. Sharma, A. Agrawal, D. Pandey, R. A. Khan, and S. K. Dinkar, “RSA based encryption approach for preserving confidentiality of big data,” J. King Saud Univ.-Comput. Inf. Sci., vol. 34, no. 5, pp. 2088–2097, 2022. doi: 10.1016/j.jksuci.2019.10.006. [Google Scholar] [CrossRef]

3. U. Awan, S. Shamim, Z. Khan, N. U. Zia, S. M. Shariq and M. N. Khan, “Big data analytics capability and decision-making: The role of data-driven insight on circular economy performance,” Technol. Forecast. Soc. Change, vol. 168, no. 1, 2021, Art. no. 120766. doi: 10.1016/j.techfore.2021.120766. [Google Scholar] [CrossRef]

4. Z. Lashkaripour, “The era of big data: A thorough inspection in the building blocks of future generation data management,” Int. J. Sci. Technol. Res., vol. 9, pp. 321–330, 2020. [Google Scholar]

5. D. Tiwari, B. Mondal, S. K. Singh, and D. Koundal, “Lightweight encryption for privacy protection of data transmission in cyber physical systems,” Cluster Comput., vol. 26, no. 4, pp. 2351–2365, 2023. doi: 10.1007/s10586-022-03790-1. [Google Scholar] [CrossRef]

6. M. J. Saddam, A. A. Ibrahim, and A. H. Mohammed, “A lightweight image encryption and blowfish decryption for the secure internet of things,” in 2020 4th Int. Symp. Multidiscip. Stud. Innov. Technol. (ISMSIT), Oct. 22–24, 2020, vol. 2020, pp. 1–5. doi: 10.1109/ISMSIT50672.2020.9254366. [Google Scholar] [CrossRef]

7. D. Clemente-Lopez, J. de Jesus Rangel-Magdaleno, and J. M. Muñoz-Pacheco, “A lightweight chaos-based encryption scheme for IoT healthcare systems,” Internet Things, vol. 25, no. 24, 2024, Art. no. 101032. doi: 10.1016/j.iot.2023.101032. [Google Scholar] [CrossRef]

8. G. S. Shyaa and M. Al-Zubaidie, “Utilizing trusted lightweight ciphers to support electronic-commerce transaction cryptography,” Appl. Sci., vol. 13, no. 12, 2023, Art. no. 7085. doi: 10.3390/app13127085. [Google Scholar] [CrossRef]

9. S. Mohammed, S. Nanthini, N. B. Krishna, I. V. Srinivas, M. Rajagopal and M. A. Kumar, “A new lightweight data security system for data security in the cloud computing,” Meas.: Sens., vol. 29, 2023, Art. no. 100856. doi: 10.1016/j.measen.2023.100856. [Google Scholar] [CrossRef]

10. S. -T. Wu, “A key-based multi-mode clock-controlled stream cipher for real-time secure communications of IoT,” Electronics, vol. 12, no. 5, 2023, Art. no. 1076. doi: 10.3390/electronics12051076. [Google Scholar] [CrossRef]

11. T. Liu, Y. Wang, Y. Li, X. Tong, L. Qi and N. Jiang, “Privacy protection based on stream cipher for spatiotemporal data in IoT,” IEEE Internet Things J., vol. 7, no. 9, pp. 7928–7940, 2020. doi: 10.1109/JIOT.2020.2990428. [Google Scholar] [CrossRef]

12. E. N. Ekwonwune and V. C. Enyinnaya, “Design and implementation of end to end encrypted short message service (SMS) using hybrid cipher algorithm,” J. Softw. Eng. Appl., vol. 13, no. 3, pp. 25–40, 2020. doi: 10.4236/jsea.2020.133003. [Google Scholar] [CrossRef]

13. M. de Ree, G. Mantas, and J. Rodriguez, “Grain-128PLE: Generic physical-layer encryption for IoT networks,” in 2023 IEEE Globecom Workshops (GC Wkshps), IEEE, 2023, pp. 1844–1849. [Google Scholar]

14. H. T. Mangi, S. A. Ali, and M. J. Jawad, “Encrypting of text based on chaotic map,” J. Univ. Babylon Pure Appl. Sci., pp. 25–39, 2023. doi: 10.29196/jubpas.v31i1.4526. [Google Scholar] [CrossRef]

15. H. Liu, B. Zhao, J. Zou, L. Huang, and Y. Liu, “A lightweight image encryption algorithm based on message passing and chaotic map,” Secur. Commun. Netw., vol. 2020, no. 1, 2020, Art. no. 7151836. doi: 10.1155/2020/7151836. [Google Scholar] [CrossRef]

16. M. A. Midoun, X. Wang, and M. Z. Talhaoui, “A sensitive dynamic mutual encryption system based on a new 1D chaotic map,” Opt. Lasers Eng., vol. 139, no. 1, 2021, Art. no. 106485. doi: 10.1016/j.optlaseng.2020.106485. [Google Scholar] [CrossRef]

17. A. V. Tutueva, E. G. Nepomuceno, A. I. Karimov, V. S. Andreev, and D. N. Butusov, “Adaptive chaotic maps and their application to pseudo-random numbers generation,” Chaos Soliton. Fract., vol. 133, no. 1, 2020, Art. no. 109615. doi: 10.1016/j.chaos.2020.109615. [Google Scholar] [CrossRef]

18. Y. Dou and M. Li, “An image encryption algorithm based on a novel 1D chaotic map and compressive sensing,” Multimed. Tools Appl., vol. 80, no. 16, pp. 24437–24454, 2021. doi: 10.1007/s11042-021-10850-y. [Google Scholar] [CrossRef]

19. S. Ullah, X. Liu, A. Waheed, S. Zhang, and S. Li, “Novel grayscale image encryption based on 4D fractional-order hyperchaotic system, 2D Henon map and knight tour algorithm,” Phys. Scr., vol. 99, no. 9, 2024, Art. no. 095248. doi: 10.1088/1402-4896/ad6d0e. [Google Scholar] [CrossRef]

20. F. Naz, I. A. Shoukat, R. Ashraf, U. Iqbal, and A. Rauf, “An ASCII based effective and multi-operation image encryption method,” Multimed. Tools Appl., vol. 79, no. 31–32, pp. 22107–22129, 2020. doi: 10.1007/s11042-020-08897-4. [Google Scholar] [CrossRef]

21. S. Ullah, X. Liu, A. Waheed, and S. Zhang, “An efficient construction of S-box based on the fractional-order Rabinovich-Fabrikant chaotic system,” Integration, vol. 94, no. 3, 2024, Art. no. 102099. doi: 10.1016/j.vlsi.2023.102099. [Google Scholar] [CrossRef]

22. U. Zia et al., “Survey on image encryption techniques using chaotic maps in spatial, transform and spatiotemporal domains,” Int. J. Inf. Secur., vol. 21, no. 4, pp. 917–935, 2022. doi: 10.1007/s10207-022-00588-5. [Google Scholar] [CrossRef]

23. S. Liu, L. Liu, and M. Pang, “Encryption method and security analysis of medical images based on stream cipher enhanced logical mapping,” Technol. Health Care, vol. 29, no. S1, pp. 185–193, 2021. doi: 10.3233/THC-218019. [Google Scholar] [PubMed] [CrossRef]

24. A. JarJar, “Vigenere and genetic cross-over acting at the restricted ASCII code level for color image encryption,” Med. Biol. Eng. Comput., vol. 60, no. 7, pp. 2077–2093, 2022. doi: 10.1007/s11517-022-02566-4. [Google Scholar] [PubMed] [CrossRef]

25. Q. Zhou, “Constructing a non-degenerate 2D chaotic map with application in irreversible PRNG,” Multimed. Tools Appl., vol. 120, no. 12, pp. 1–14, 2024. doi: 10.1007/s11042-024-19787-4. [Google Scholar] [CrossRef]

26. M. Alawida, J. S. Teh, A. Mehmood, and A. Shoufan, “A chaos-based block cipher based on an enhanced logistic map and simultaneous confusion-diffusion operations,” J. King Saud Univ.-Comput. Inf. Sci., vol. 34, no. 10, pp. 8136–8151, 2022. doi: 10.1016/j.jksuci.2022.07.025. [Google Scholar] [CrossRef]

27. M. K. Khairullah, A. A. Alkahtani, M. Z. Bin Baharuddin, and A. M. Al-Jubari, “Designing 1D chaotic maps for fast chaotic image encryption,” Electronics, vol. 10, no. 17, 2021, Art. no. 2116. doi: 10.3390/electronics10172116. [Google Scholar] [CrossRef]

28. F. Wang, G. Xu, and G. Xu, “A provably secure anonymous biometrics-based authentication scheme for wireless sensor networks using chaotic map,” IEEE Access, vol. 7, pp. 101596–101608, 2019. doi: 10.1109/ACCESS.2019.2930542. [Google Scholar] [CrossRef]

29. A. S. Saljoughi and H. Mirvaziri, “A new method for image encryption by 3D chaotic map,” Pattern Anal. Appl., vol. 22, no. 1, pp. 243–257, Feb. 01, 2019. doi: 10.1007/s10044-018-0765-5. [Google Scholar] [CrossRef]

30. C. Rupa, M. Harshitha, G. Srivastava, T. R. Gadekallu, and P. K. R. Maddikunta, “Securing multimedia using a deep learning based chaotic logistic map,” IEEE J. Biomed. Health Inform., vol. 27, no. 3, pp. 1154–1162, 2022. doi: 10.1109/JBHI.2022.3178629. [Google Scholar] [PubMed] [CrossRef]

31. L. Zhang, Y. Zhu, W. Ren, Y. Wang, K. -K. R. Choo and N. N. Xiong, “An energy-efficient authentication scheme based on Chebyshev chaotic map for smart grid environments,” IEEE Internet Things J., vol. 8, no. 23, pp. 17120–17130, 2021. doi: 10.1109/JIOT.2021.3078175. [Google Scholar] [CrossRef]

32. L. Ding, C. Liu, Y. Zhang, and Q. Ding, “A new lightweight stream cipher based on chaos,” Symmetry, vol. 11, no. 7, 2019, Art. no. 853. doi: 10.3390/sym11070853. [Google Scholar] [CrossRef]

33. R. S. Mohammed, “Design a lightweight authentication encryption based on stream cipher and chaotic maps with sponge structure for internet of things applications,” Int. J. Intell. Eng. Syst., vol. 16, no. 1, pp. 532–547, Feb. 2023. doi: 10.22266/ijies2023.0228.46. [Google Scholar] [CrossRef]

34. I. Alshawi and L. Muhalhal, “Improved Salsa20 stream cipher diffusion based on random chaotic maps,” Informatica, vol. 46, no. 7, 2022. doi: 10.31449/inf.v46i7.4279. [Google Scholar] [CrossRef]

35. M. G. Alwan, E. T. Khudair, and E. F. Naser, “A hybrid algorithms based on the Aizawa attractor and rabbit-lightweight cipher for image encryption,” Iraqi J. Sci., pp. 6534–6547, 2023. doi: 10.24996/ijs.2023.64.12.35. [Google Scholar] [CrossRef]

36. B. Patil and S. R. Biradar, “Light weight hybrid chaotic based encryption scheme for image transmission in wireless multimedia sensor network,” Indian J. Comput. Sci. Eng., vol. 12, no. 6, pp. 1601–1610, Dec. 2021. doi: 10.21817/indjcse/2021/v12i6/211206303. [Google Scholar] [CrossRef]

37. G. Suseela, Y. A. V. Phamila, G. Niranjana, K. Ramana, S. Singh and B. Yoon, “Low energy interleaved chaotic secure image coding scheme for visual sensor networks using pascal’s triangle transform,” IEEE Access, vol. 9, pp. 134576–134592, 2021. doi: 10.1109/ACCESS.2021.3116111. [Google Scholar] [CrossRef]

38. A. A. Shah et al., “A novel chaos-based light-weight image encryption scheme for multi-modal hearing aids,” in 2022 IEEE Conf. Dependable Secure Comput. (DSC), IEEE, 2022, pp. 1–6. [Google Scholar]

39. A. T. Maolood, E. K. Gbashi, and E. S. Mahmood, “Novel lightweight video encryption method based on ChaCha20 stream cipher and hybrid chaotic map,” Int. J. Electr. Comput. Eng., vol. 12, no. 5, pp. 4988, 2022. doi: 10.11591/ijece.v12i5.pp4988-5000. [Google Scholar] [CrossRef]

40. S. H. Jasim, H. K. Hoomod, and K. A. Hussein, “Image encryption based on hybrid parallel algorithm: DES-present using 2D-chaotic system,” Int. J. Saf. Secur. Eng., vol. 14, no. 2, pp. 633–646, 2024. doi: 10.18280/ijsse.140229. [Google Scholar] [CrossRef]

41. A. M. N. Gilmolk and M. R. Aref, “Lightweight image encryption using a novel chaotic technique for the safe internet of things,” Int. J. Comput. Intell. Syst., vol. 17, no. 1, 2024, Art. no. 146. doi: 10.1007/s44196-024-00535-3. [Google Scholar] [CrossRef]

42. A. Abdelli, W. El Hadj Youssef, F. Kharroubi, L. Khriji, and M. Machhout, “A novel enhanced chaos based present lightweight cipher scheme,” Phys. Scr., vol. 99, no. 1, 2024, Art. no. 016004. doi: 10.1088/1402-4896/ad1560. [Google Scholar] [CrossRef]

43. A. Aldosary et al., “A secure authentication framework for consumer mobile crowdsourcing networks,” IEEE Trans. Consum. Electron., pp. 1–1, 2024. doi: 10.1109/TCE.2024.3473930. [Google Scholar] [CrossRef]

44. A. A. M. Ragab, A. Madani, A. Wahdan, and G. M. Selim, “Design, analysis, and implementation of a new lightweight block cipher for protecting IoT smart devices,” J. Ambient Intell. Humaniz. Comput., vol. 14, no. 5, pp. 1–18, 2023. doi: 10.1007/s12652-020-02782-6. [Google Scholar] [CrossRef]

45. J. Arif et al., “A novel chaotic permutation-substitution image encryption scheme based on logistic map and random substitution,” IEEE Access, vol. 10, no. 2, pp. 12966–12982, 2022. doi: 10.1109/ACCESS.2022.3146792. [Google Scholar] [CrossRef]

46. A. H. Fadel, R. S. Hameed, J. N. Hasoon, S. A. Mostafa, and B. A. Khalaf, “A light-weight ESalsa20 ciphering based on 1D logistic and chebyshev chaotic maps,” Solid State Technol., vol. 63, no. 1, pp. 1078–1093, 2020. [Google Scholar]

47. M. D. Gietaneh and T. B. Akele, “Enhancing the Hill Cipher algorithm and employing a one time pad key generation technique,” Abyssinia J. Eng. Comput., vol. 3, no. 1, pp. 1–10, 2023. [Google Scholar]

48. A. Abba, J. S. Teh, and M. Alawida, “Towards accurate keyspace analysis of chaos-based image ciphers,” Multimed. Tools Appl., vol. 83, no. 33, pp. 1–20, 2024. doi: 10.1007/s11042-024-18628-8. [Google Scholar] [CrossRef]

49. S. Zhu, C. Zhu, and H. Yan, “Cryptanalyzing and improving an image encryption algorithm based on chaotic dual scrambling of pixel position and bit,” Entropy, vol. 25, no. 3, 2023, Art. no. 400. doi: 10.3390/e25030400. [Google Scholar] [PubMed] [CrossRef]