Fusion of Type-2 Neutrosophic Similarity Measure in Signatures Verification Systems: A New Forensic Document Analysis Paradigm

1  Introduction

A forensic document analysis system (FDAS) is software created to help forensic document examiners assess handwriting, signatures, paper, printing methods, and other relevant characteristics of documents [1]. Analysis of signatures and handwriting is one of the most often used uses of such a technology. Using the unique characteristics of a signature, a biometric signature verification system (BSVS) enables forensic investigators to compare and analyze signatures for document authorship tracking, fraud detection, or validity. But many issues must be resolved if BSVS is to be used widely and successfully. It is difficult to create a consistent baseline for comparison since signatures might vary significantly over time because of variables such as mood, health, exhaustion, or age. Furthermore, it would be possible to conduct fraud attacks against BSVS using counterfeit or duplicated signatures to trick the system [2,3].

Uncertainty in describing signature features is one of the main problems BSVS is encountering. Standardizing the analysis method is difficult since many signature features are qualitative and subjective (like style or fluency), while others may be measured scientifically (like stroke length or angle). Variations in measuring methods may cause variations in the description and assessment of signature characteristics [4]. Because of inherent handwriting variations, signatures from the same person may often show considerable intra-class diversity, making it difficult to construct a consistent template for verification. It is further difficult to distinguish between real and fake signatures since signatures from various people may have similar characteristics. Many techniques may be used to reduce the ambiguity in the BSVS definition of signature features. Fuzzy rule-based decision systems are one of the most widely utilized techniques; they provide a strong foundation for signature verification by using fuzzy logic to manage the underlying uncertainties and ambiguities in signature analysis [5].

High uncertainty associated with signature features’ descriptions increases the risk of receiving false positives or false negatives in signature verification. Fuzzy methods may struggle to distinguish genuine signatures from fakes when high-level uncertainty is considerable. The capabilities of traditional fuzzy logic are expanded by the explicit handling of truth, indeterminacy, and falsity by neutrosophic logic [6,7]. Neutrosophic logic (NL) makes modeling of circumstances in which there is a large degree of indeterminacy, an uncertain truth value, or a significant degree of falsity in the data [6]. NL explicitly accounts for indeterminacy as a separate dimension, which is particularly useful in situations where information is ambiguous or contradictory. This helps to distinguish between different sources and types of uncertainty. NL is very helpful in the context of signature verification when managing uncertain signatures where the degree of truthfulness, indeterminacy, and falsify might vary.

Type-2 Neutrosophic Logic (T2NL) with the Footprint of Uncertainty (FOU) provides many advantages when uncertainty is frequent and has to be accurately modeled. FOU inclusion makes it possible to show uncertainty more fully by including not just the degree of membership but also the associated uncertainty [7]. Compared to Type-1 Neutrosophic Logic (T1NL), T2NL offers a stronger foundation for handling imprecision and uncertainty as T2NL simulates uncertainty at the level of the membership function as much as the membership values (see Fig. 1). This makes T2NL more sophisticated in its depiction of complex uncertain data by enabling it to record uncertainty about uncertainty. Higher degrees of uncertainty in the membership functions provide better representations of situations with ambiguous boundaries between several categories [8–11]. Using a type-2 Neutrosophic Engine for the BSVS task enhances the system’s ability to manage uncertainty and variability in signatures. By allowing indeterminacy to be a function, this method can handle ambiguous cases where signatures might be partially matched, which is common in real-world scenarios. Furthermore, the methodology can be scaled to handle large datasets and complex verification scenarios, making it suitable for large-scale applications like banking and legal systems.

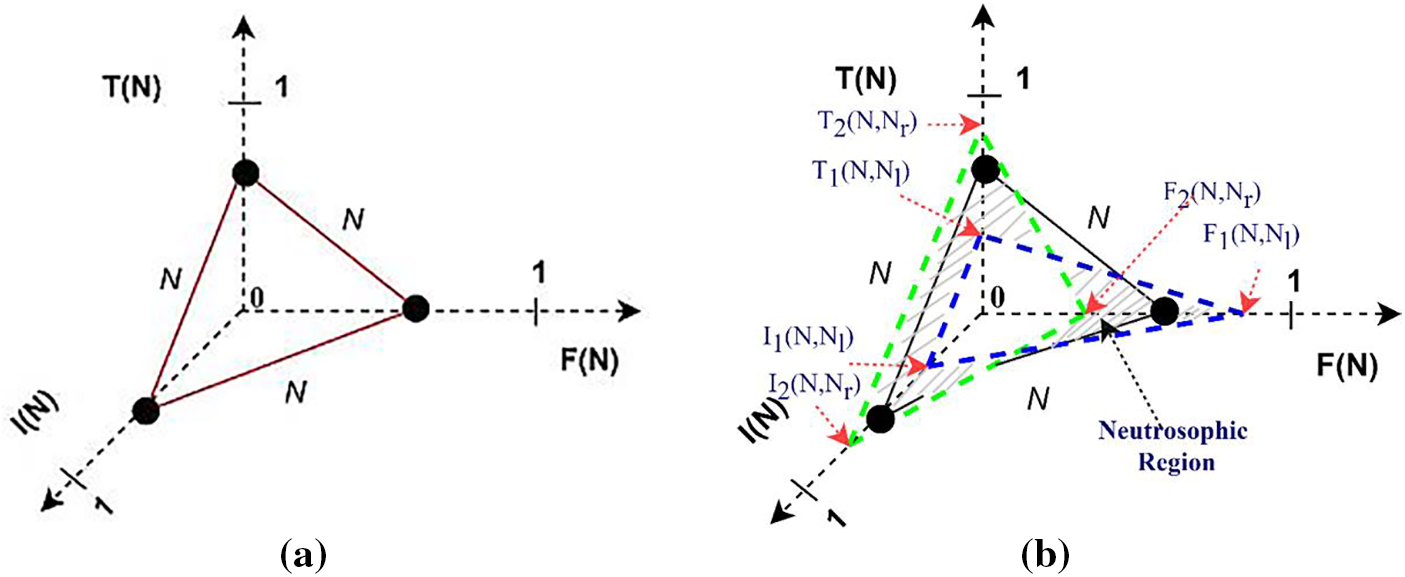
Figure 1: (a) Type-1 Neutrosophic truth T(N), indeterminacy I(N), and falsity membership functions F(N). (b) Type-2 neutrosophic set membership functions; the blurred region in T2NS provides two extra memberships for truth, indeterminacy, and falsify membership functions TM, IM, and FM. The two extra memberships are Nl, Nr, l, and r are left and right shifts [7]

T2NL is an advanced framework for dealing with uncertainty, imprecision, vagueness, and inconsistency. This approach provides a more flexible and precise method for handling higher levels of uncertainty and complex information. A neutrosophic set is characterized by three functions: truth-membership (T), indeterminacy-membership (I), and falsity-membership (F). In T2NL, these functions are not single values but ranges (intervals) [7,8]. Truth (T) represents the degree to which an element is true. In type-2 neutrosophic logic, it is an interval [TL,TU],0≤TL≤TU≤1. Indeterminacy (I) represents the degree of indeterminacy or uncertainty. It is an interval [IL,IU],0≤IL≤IU≤1. Falsity (F) represents the degree to which an element is false. It is an interval [FL,FU],0≤FL≤FU≤1. A Type-2 neutrosophic set A in a universe of discourse X is defined as A={⟨x,(F(x),I(x),F(x))⟩:x∈X},∀x∈X,T(x)=[TL(x),TU(x)],I(X)=[IL(x),IU(x)],F(X)=[FL(x),FU(x)].

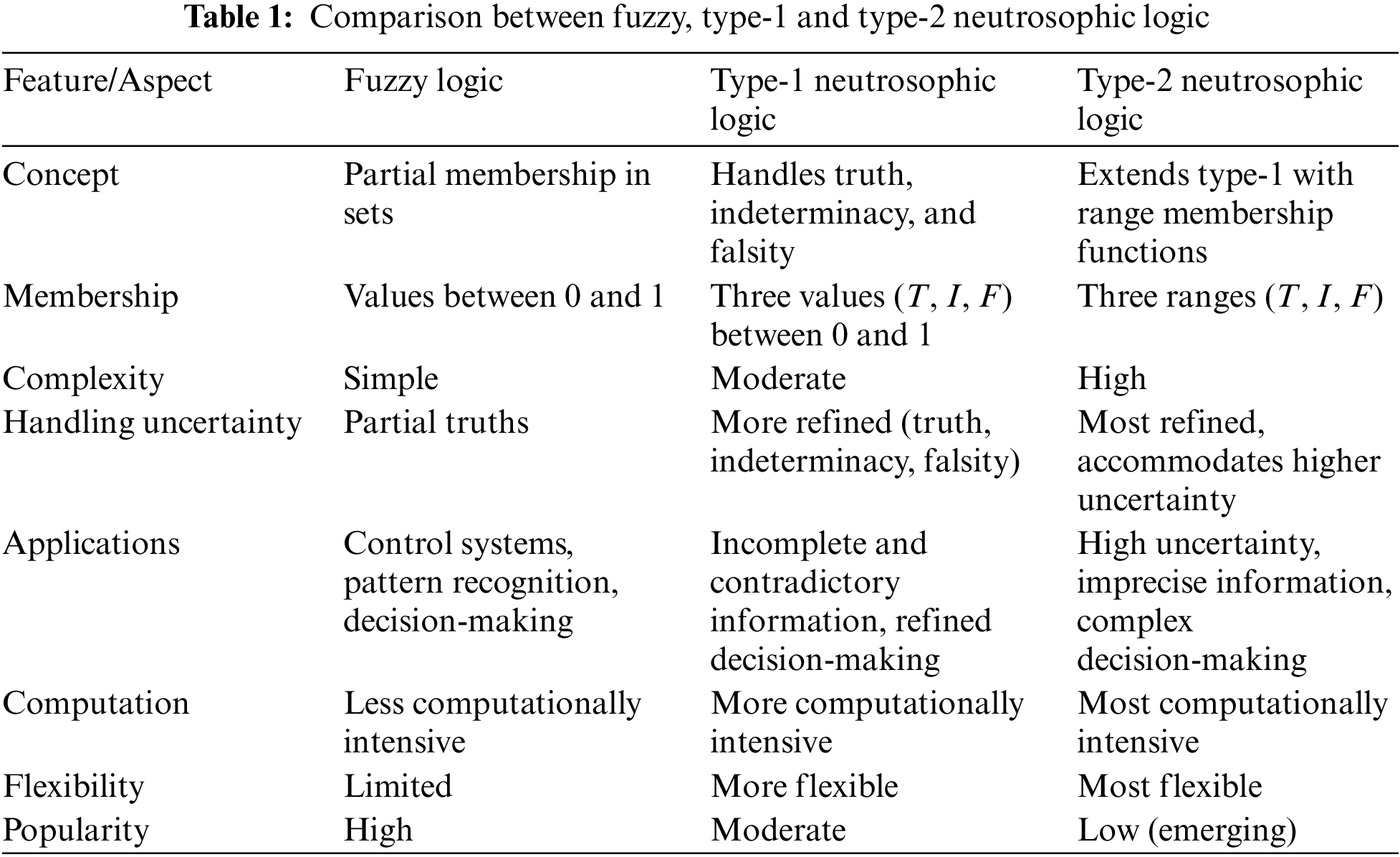
T2NL introduces the concept of the FOU to provide a more robust framework for dealing with high levels of uncertainty. This approach enhances traditional fuzzy and T1NL by allowing each membership function (truth, indeterminacy, and falsity) to be represented as intervals rather than single values. A comparison of fuzzy logic, type-1 neutrosophic logic, and type-2 neutrosophic logic is shown in Table 1. By representing truth, indeterminacy, and falsity as intervals, T2NL can more accurately capture the variability and vagueness inherent in uncertain information. This interval representation acknowledges that the exact degree of membership is often not precisely known. The range of values (the foot of uncertainty) provides a buffer zone that accommodates fluctuations and uncertainties in the data, leading to more robust decision-making processes. FOU helps to absorb and mitigate the impact of noise and variability in the input data, leading to more stable and reliable outputs. By analyzing the width of the intervals, it is possible to gain insights into the degree of uncertainty present in the system, facilitating more informed and precise analyses [9–11].

1.1 Problem Statement and Motivation

Signature verification systems ensure the authenticity of documents in the financial, legal, and government sectors among others. Nevertheless, conventional techniques for verifying signatures sometimes find it challenging to sufficiently capture and convey the ambiguity and inherent uncertainty related with signature characteristics and the similarity score in the matching algorithm. In tasks requiring signature verification, aging effects, intentional efforts at forgery, and differences in writing style may cause variable degrees of uncertainty in judging the authenticity of the signature. Fuzzy logic and T1NL are two instances of traditional methods that could not have sufficient granularity to sufficiently explain and reason around this uncertainty. Higher degrees of uncertainty must thus be managed by a more dependable and complete signature verification mechanism. A practical solution is provided by the representation of uncertainty in the membership functions by T2NL. Including T2NL in signature verification systems makes it easy to reason and express uncertainty at many levels, including uncertainty about uncertainty. Consequently, verification results are more precise even in situations where signatures include complex and imprecise characteristics.

1.2 Contribution

The main contribution of the suggested work lies in fusing a type-2 neutrosophic similarity measure (for the first time) with biometric signature verification, which enables decision-making by capturing not only the degree of match between signatures but also the degree of uncertainty associated with the match. This allows for more informed decisions, especially in cases where the signature’s characteristics are ambiguous. In our model, when comparing a given signature against a reference (genuine) signature, a matching algorithm is employed to compute the degree of the match using type-2 neutrosophic similarity measures. Based on the computed similarity score, a thresholding mechanism is applied to determine whether the given signature is genuine or forged. This thresholding approach gives an alternative along with matching confidence ratings with regard to the uncertainty in the similarity score. Type-2 neutrosophic similarity scores measure the degree of matching between signatures as well as the degree of uncertainty related to the matching via efficient management of the uncertainty related to the intrinsic variability of signatures.

The structure of this article is as follows: The relevant literature is presented in Section 2. The suggested T2NL-based signature verification system’s design is presented in Section 3. Results from experiments and comparisons to relevant literature and the suggested methodology are presented in Section 4. The conclusion and plans for further research are summarized in Section 5.

2  Related Work

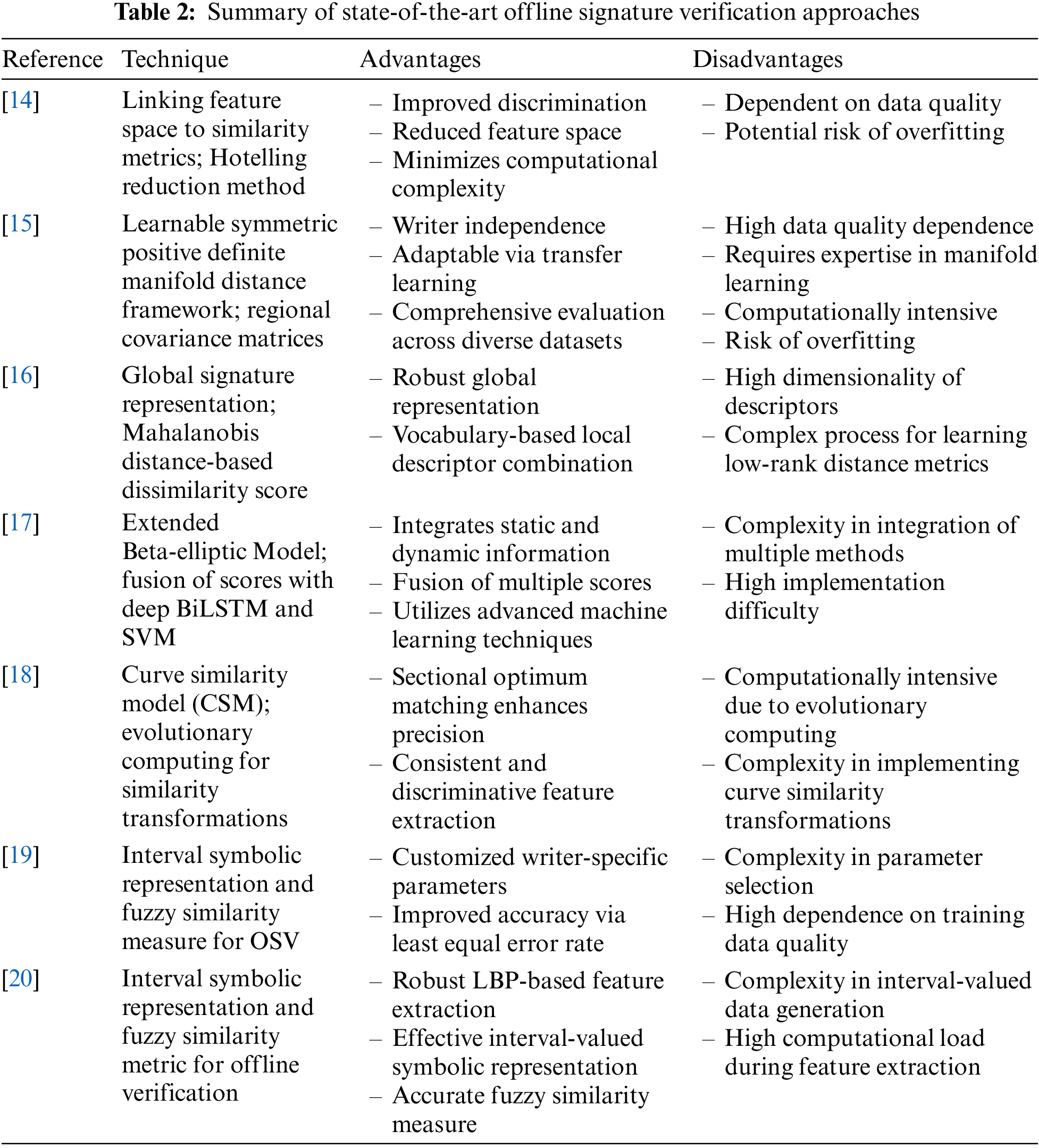
Current similarity measurements in signature verification involve a combination of feature extraction, pattern recognition, and machine learning techniques. The kind of features (static or dynamic), the comparison algorithms (pointwise and structural comparison or statistical and machine learning methods), and the actual verification systems (forensic analysis software or automated signature verification systems) to which these techniques are applied allow for categorization of these approaches [12,13]. Based on the dynamic features of a certain signature, the authors in Reference [14] provided a technique for person verification. One way to do signature verification using this method is to link the feature space to a collection of similarity metrics. Novel signature features are generated by combining features with connected similarity coefficients. The Hotelling reduction method, which uses multivariate statistics to analyze the differences between mean vectors, finds the best features and unique similarity metrics for each individual before reducing the composed features. As a last result, the space of assembled signature features is reduced. The suggested method automatically chooses the most effective discriminating features and similarity metrics in comparison to competing methods.

In Reference [15], the authors advocated using a learnable symmetric positive definite manifold distance framework in offline signature verification literature to construct a global signature verification classifier that is independent of writers. As visual descriptors, the use of regional covariance matrices of handwritten signature images translates them into the symmetric positive definite manifold, which is the fundamental building component of the framework. Using four well-known signature datasets from Asia and the West, the learning and verification methodology investigates blind intra- and blind inter-transfer learning frameworks. To distinguish between genuine signatures and well faked ones, the suggested method in Reference [16] used a new global signature representation and then the Mahalanobis distance-based dissimilarity score. The combination of local descriptors using a vocabulary forms the basis of the global representation of a signature-containing image. Due to the large dimensionality of the descriptor, learning a low-rank distance metric using the global descriptors from the two images is not a simple process.

A new biometric method for signature verification was introduced in the paper cited in Reference [17]. Integrating the fuzzy elementary perceptual codes (FEPC) to extract static and dynamic information, the authors developed a novel model called the extended beta-elliptic model. Utilizing a fusion employing the sum rule combiner of three scores, they investigated the possibility of using deep bidirectional long short-term memory (deep BiLSTM), support vector machine (SVM) with dynamic time warping (DTW), and SVM with a newly suggested parameter comparator to distinguish between genuine and counterfeit user signatures. The authors in Reference [18] presented a novel method for matching elastic curves that only requires one reference signature, which we call the curve similarity model (CSM). In order to find the similarity distance between two curves, they used evolutionary computing (EC) to look for the best possible match under various similarity transformations. Referring to the geometric similarity property, curve similarity may translate, stretch, and rotate across curves to account for the unpredictable signature size, location, and rotation angle. They developed a sectional optimum matching method for the matching of signature curves. Using this information as a starting point, they created a novel approach to fusion feature extraction that is both consistent and discriminative, with the goal of detecting signature curve similarities.

Due to significant intra-individual variability, the authors in Reference [19] presented a new technique for online signature verification (OSV) based on an interval symbolic representation and a fuzzy similarity measure based on writer-specific parameter selection. The two parameters, the writer-specific acceptance threshold and the ideal feature set to be utilized for authenticating the writer, are chosen based on the least equal error rate (EER) obtained during the parameter resolving phase using the training signature samples. This is an extended version on existing OSV approaches, which are essentially writer-independent and use a common set of characteristics and acceptability thresholds. In Reference [20], an efficient off-line signature verification approach using an interval symbolic representation and a fuzzy similarity metric is presented. During the feature extraction process, a collection of local binary pattern (LBP)–based features is generated from both the signature image and its under-sampled version. Interval-valued symbolic data is then generated for each feature in each signature class. As a consequence, each individual’s handwritten signature class is represented by a signature model made up of a collection of interval values (equal to the number of features). To verify the test sample, a new fuzzy similarity measure is offered that computes the similarity between a test sample signature and the appropriate interval-valued symbolic model.

There are several studies in the literature that discuss T2NL’s applicability in various disciplines. The authors in Reference [21] have developed and examined an enhanced scoring function for interval neutrosophic numbers to manage traffic flow. The authors developed this function by determining which junction has a greater number of cars. This enhanced scoring function uses the score values of triangular interval type-2 fuzzy numbers. The expanded Efficiency Analysis Technique with Input and Output Satisficing (EATWIOS) technique, which is based on type-2 Neutrosophic Fuzzy Numbers (T2NFNs), was addressed by the authors in Reference [22]. Following that, the T2NFN-EATWIOS is used to solve a real-world evaluation challenge that is present in container shipping businesses.

In order to deal with uncertainty in real-time deadlock-resolving systems, the work that was given in Reference [23] used type-2 neutrosophic logic, which is an extension of type-1 neutrosophic logic. In this context, the level of uncertainty that occurs in the value of a grade of membership is represented by the footprint of uncertainty (FOU) for truth, indeterminacy, and falsehood. The simulations were carried out by the authors with the assistance of a distributed real-time transaction processing simulator, and the tests were carried out using the Pima Indians diabetes dataset (PIDD) serving as the benchmark. According to the execution ratio scale, the performance of the resolution that is based on type-2 neutrosophic is superior to the performance of the approach that is based on type-1 neutrosophic. An investigation into the multi-objective supplier selection problem (SSP) with type-2 fuzzy parameters was carried out in the work that was presented in Reference [24]. All of the involved parameters, including aggregate demand, budget allocation, quota flexibility, and rating values, were represented as type-2 triangular fuzzy (T2TF) parameters. Additionally, an interval-based approximation method was developed for the purpose of defuzzifying the T2TF parameters. Furthermore, a novel interactive neutrosophic programming approach was suggested as a means of solving the deterministic multi-objective SSP.

In Reference [25], Hausdorff, Hamming, and Euclidean distances are used to present several distance measurement techniques for type-2 single-valued neutrosophic sets, and certain features of these distance measurement methods are examined. In addition, a multi-criteria group decision-making technique is created under the terms of the type-2 single-valued neutrosophic environment. This method is based on the Technique for Order Preference by Similarity to the Ideal Solution (TOPSIS) approach. In the research that has been done on intelligent transportation systems, a type-2 neutrosophic number, also known as a T2NN, is used in the process of performing advantage prioritizing in order to cope with uncertainty [26]. In order to facilitate flexible decision-making, the T2NN model has included an innovative aggregation function. This function simulates a variety of situations throughout the sensitivity analysis process. The technique that has been provided has a higher degree of generality and objectivity when it comes to the processing of group information in comparison to the conventional multi-criteria models.

For the purpose of selecting an appropriate chemical tanker, which is a complex process that requires overcoming a great deal of ambiguity and taking into consideration a great deal of conflicting criteria, the authors in Reference [27] presented a new and integrated Multi-Criteria Decision Making (MCDM) approach that was based on type-2 Neutrosophic fuzzy sets. In this research, fourteen distinct selection criteria were established for the purpose of evaluating the chemical tanker ships. A detailed sensitivity analysis was performed in order to verify the validity and application of the model that was suggested. The results of the sensitivity study supported the validity, robustness, and applicability of the model. In Reference [28], the authors presented an approach for performance analysis of domestic energy usage in European cities that was based on type-2 neutrosophic numbers. This approach identifies the criteria weights by utilizing the CRiteria Importance Through Intercriteria Correlation (CRITIC) technique. Additionally, the authors rank the alternatives with the assistance of the Multi-Attribute Utility Theory (MAUT) approach. By carrying out a detailed sensitivity analysis that was comprised of three steps, the validity of the suggested mixed approach was examined, and the results that were obtained demonstrate that the model is both valid and applicable.

The authors of Reference [29] presented a two-stage hybrid multi-criteria decision-making model that is based on type-2 neutrosophic numbers (T2NNs) for the purpose of determining the level of security that fog and Internet of Things devices provide. In the T2NN environment, the first phase of this procedure involves establishing the weights of the criteria via the use of the Analytic Hierarchy procedure (AHP) approach. For the second step, the T2NN-based Multi-Attributive Border Approximation Area Comparison (MABAC) approach is used in order to rate the different fog security solutions that are based on the Internet of Things. As a result of the comparative research, it has been shown that the combined AHP and MABAC-based type-2 neutrosophic model has a high level of dependability and robustness. In Reference [30], a hybrid model that is based on the T2NNs, CRITIC, and MABAC is presented in order to assess the green-oriented supplier. The suggested model has practical implications for the selection of suppliers in the micro-mobility services industry. Table 2 summarizes the key aspects of each reference, highlighting their main techniques, advantages, and disadvantages.

2.1 The Need to Extend the Related Work

In signature verification, similarity measures play a crucial role in comparing a new signature against stored templates to determine authenticity. Effective handling of uncertainty is necessary to improve the robustness and dependability of these systems. The underlying uncertainties and variances in signature data are managed in signature verification using fuzzy similarity measures. These measures have numerous problems even if they have some benefits. It is not up to handling indeterminacy and contradicting facts. At the expense of extra complexity and computing overhead, neutrosophic logic provides a more flexible solution to uncertainty with its three-component structure. We show that type-2 neutrosophic similarity measures with the FOU, provide a powerful framework for managing large degrees of uncertainty in signature verification. For sophisticated signature verification systems in particular, their capacity to capture a comprehensive and adaptable representation of uncertainty, along with their resilience against noise and flexibility to variability, makes them very well-suited.

3  Proposed Methodology

A systematic method including signature samples acquisition and pre-processing, feature extraction, type-2 neutrosophic representation, uncertainty modeling using FOU, similarity measure calculation, and decision-making is needed to build the suggested signature verification system based on uncertainty similarity measures. The steps of the proposed model consist of (1) getting samples of user signatures initially to guarantee diversity in signature styles with different conditions. (2) Take out signature features like gravity distance, normalized area, pixel density, and width-to-height ratio. The suggested model utilizes a geometric method for extracting signature features. (3) Embedding uncertainty in the feature values; represent each signature sample as a type-2 neutrosophic set. (4) Establish the upper and lower membership functions for each component (truth, indeterminacy, and falsehood) of the type-2 neutrosophic sets to determine the FOU. We determine the similarity between pairs of these sets using uncertainty-incorporating similarity measures, such as Jaccard similarity, adapted for type-2 neutrosophic sets. (5) After totalling up the similarity ratings from many pairs of claimed and genuine signatures, decide at what point to accept or reject a signature (decision-making). In Fig. 2, we can see the general architecture of the proposed verification system, and in the following sections, we will go over each individual phase.

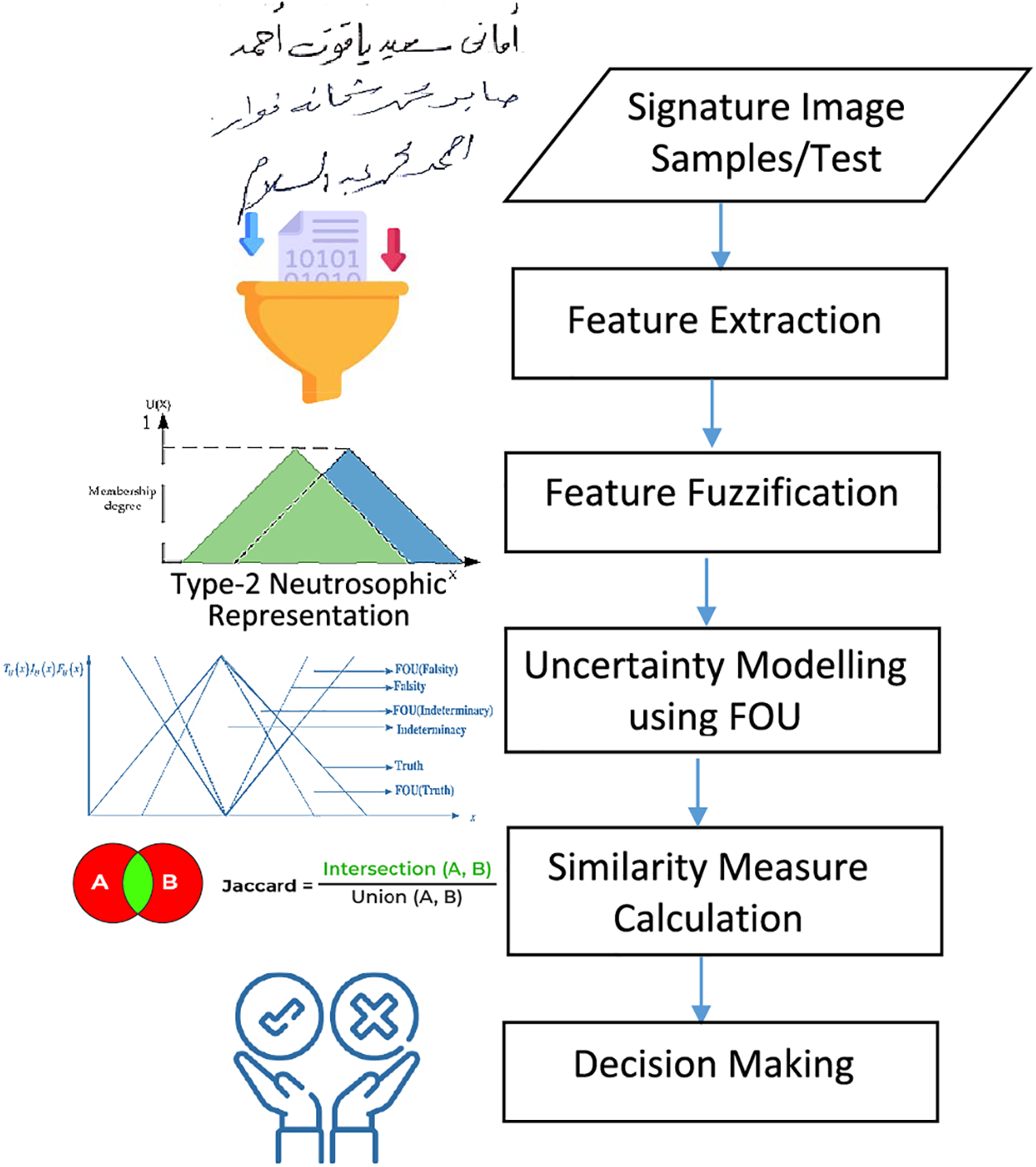
Figure 2: The proposed Arabic offline signature verification system based on type-2 neutrosophic similarity measure

Step 1: Signature Samples Acquisition and Pre-Processing

The first step include gathering numerous samples of the person’s signature to find a pattern and to allow for natural variances. To get different samples, ask the person to sign their name several times on a single sheet of paper. Next, scan hard copy signature samples with a high-resolution scanner and take into account that signature images are of high quality and well illuminated [31]. In the next step, data pre-processing is carried out. Data pre-processing has a substantial impact on the efficacy and accuracy of signature verification systems. It involves the transformation of raw signature data into a format that is both clear and normalized, making it suitable for analysis and comparison. This encompasses (1) Filtering: the implementation of filters to enhance the quality of the input data and normalize the signature curves. (2) Size Normalization: this step allows for the comparison of signatures of varying sizes by adjusting the signature’s size to a standard scale. (3) Position Alignment: ensure that the signature is centered and aligned within the image frame to ensure consistent positioning across all samples. (4) Binarization: the signature image is converted to binary form (black and white) to emphasize the signature in contrast to the background. (5) Thinning: to emphasize the signature’s shape and structure, the breadth of the signature strokes is reduced to a single pixel. (6) Rotation Correction: identify and rectify any rotation in the signature to guarantee its proper orientation and vertical position. (7) Scaling: ensure that the signature is scaled consistently to correspond to a standard size [32].

Step 2: Signature Geometric Features Extraction

A key step in signature verification systems is feature extraction. Among its tasks is extraction of significant features from signature samples that may be used to distinguish between real and fake signatures. Three basic groups can be distinguished among the features: geometric, statistical, and dynamic features [33]. By extracting important features, the dimensionality of the data is reduced, simplifying the problem and making it easier to visualize and understand. The suggested model employs geometric features that analyse the spatial and structural properties of a signature. These features capture the overall shape, local structures, and global properties of the signature. The following features will be utilized to represent the signature:

- f1:Aspect Ratio(ARglobal)=WidthoftheBoundingBoxHeightoftheBoundingBox,(1)

 Width=xmax−xmin,(2)

 Height=ymax−ymin,(3)

(xmin,ymin), (xmax,ymax) are the coordinates of the bottom-left and top-right corners of the bounding box.

- f2:NormalizedArea(NAglobal)=ASignatureABoundingBox,(4)

 ABoundingBox=Width×Height,(5)

 ASignature=NumberofpixelsintheSignaturebinaryimage,(6)

- f3:Pixel Density(PDlocal)=NblackNtotal×100%,(7)

Let Asector is the sector’s area:

 Asector=θ360o×πr2,(8)

Nblack is the count of sector’s black pixels, and Ntotal is the sector’s total number of pixels.

- f4:Gravity Distance (GDlocal)=dcgr,(9)

dcg is the Euclidean distance between the center of gravity (xcg,ycg) and the center of the circular grid (xcenter,ycenter)

 dcg=(xcg,xcenter)2−(ycg,ycenter)2.(10)

Step 3: Type-2 Neutrosophic Features Representation

Signature data frequently exhibits varying degrees of imprecision and uncertainty in the representation of features. Type-2 neutrosophic sets are more effective in modeling this complexity than traditional methods. The reliability and variability of each feature can be comprehensively understood through the degrees of truth, indeterminacy, and falsity, which can be represented by a type-2 neutrosophic set in our scenario. Considering the whole range of data uncertainty and imprecision will help one make more reliable and well-informed decisions. Membership functions are applied to the features of each signature to ascertain how closely each input fits the proper neutrosophic set. The degree of membership is between 0 and 1. In our scenario, they all have three linguistic levels, “Low,” “Medium,” and “High,” with linear trapezoidal membership functions. A linear trapezoidal neutrosophic number is defined as A~Neu=(a,b,c,d;e,f,g,h;i,j,k,l) whose truth, indeterminacy and falsity membership is defined as [6,33], where 0≤TA~Neu(x)+IA~Neu(x)+IA~Neu(x)≤3,x∈A~Neu. The pictorial view is shown in Fig. 3.

Truthmembershipfunction=TA~_Neu={0x<ax−ab−aa≤x<b1b≤x<cd−xd−cc≤x≤d0x>d(11)

Indeterminacymembershipfunction=IA~_Neu={1x<ef−xf−ee≤x<f0f≤x<gx−gh−gg≤x≤h1x>h(12)

Falsitymembershipfunction=FA~_Neu={1x<ij−xj−ii≤x<j0j<x<kx−kl−kk≤x≤l1x>l(13)

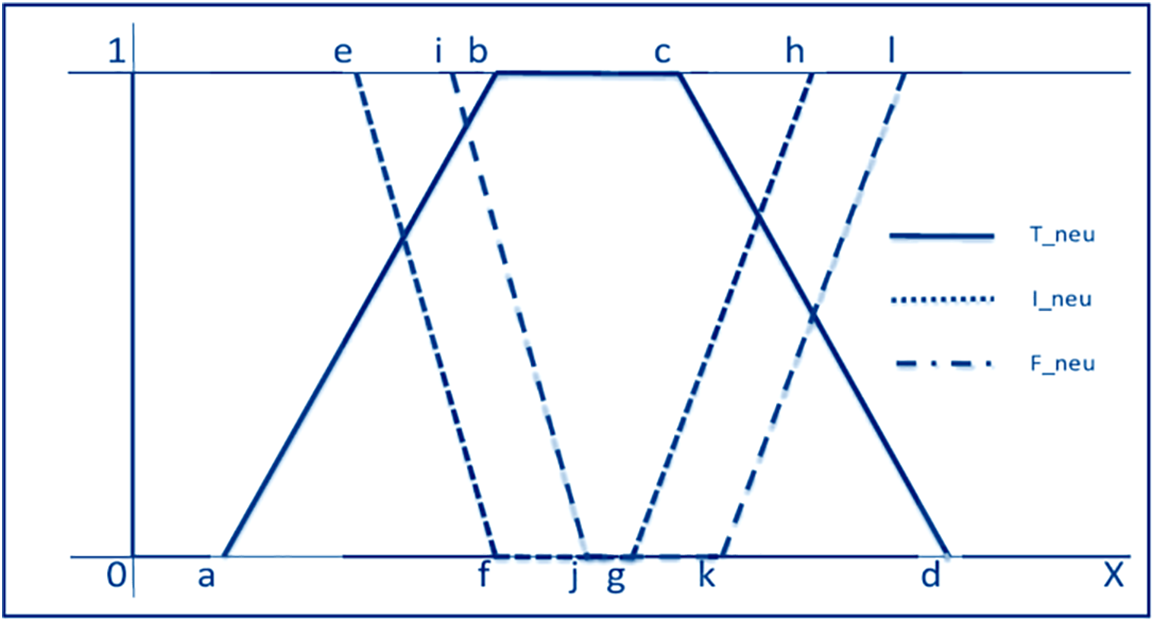
Figure 3: Linear trapezoidal neutrosophic number [23]

Step 4: Uncertainty Modelling using FOU

The Footprint of Uncertainty (FOU) is an essential term in type-2 neutrosophic logic, especially in applications like signature verification. Forgeries are distinguished by a higher level of variety, while authentic signatures generally display consistent patterns within the signatures of the same person. By designating appropriate intervals to T, I, and F for each feature, type-2 neutrosophic sets can model these patterns, thereby aiding in the differentiation between genuine and forged signatures. The FOU is a representation of the range of uncertainty in the membership functions of type-2 fuzzy sets, and its adaptation to type-2 Neutrophobic sets enables more precise modeling of the inherent variability and imprecision in biometric signatures data [8,11]. The type-2 neutrosophic membership function is graphically represented in Fig. 4 [7].

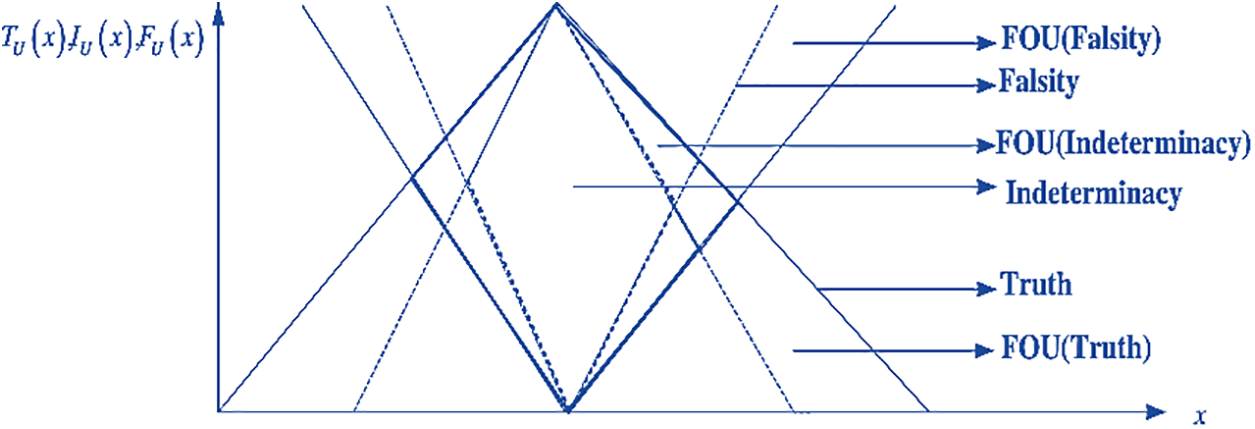
Figure 4: Graphical representation of type-2 neutrosophic membership function [7]

Formally, a single-valued neutrosophic set (SVNS) S˘ on universal set U is characterized by truth membership function TMF(ϑS˘), indeterminacy membership function IMF(ϑS˘) and falsity membership function FMF(ϑS˘), respectively, in the following way [32]:

S˘={⟨ξ,(ϑS˘(ξ),ψS˘(ξ),φS˘(ξ))⟩:ξ∈U,ϑS˘(ξ),ψS˘(ξ),φS˘(ξ)∈[0,1]}(14)

Such that 0≤ϑS˘(ξ),ψS˘(ξ),φS˘(ξ)≤3. Let S˘(ξ)=[S˘U(ξ),S˘L(ξ)] be an interval type-2 neutrosophic set (IT2NS) on universal set U where ξ∈U and S˘U:U→[0,1] and S˘L:U→[0,1] are two type-1 neutrosophic sets (T1NSs) known as upper and lower neutrosophic sets respectively having the condition 0≤S˘L(ξ)≤S˘U(ξ)≤1 defined as follows [19]:

S˘={⟨ξ,([ϑS˘U(ξ),ϑS˘L(ξ)],[ψS˘U(ξ),ψS˘L(ξ)],[φS˘U(ξ),φS˘L(ξ)])⟩:ξ∈U}(15)

[ϑS˘U(ξ),ϑS˘L(ξ)],[ψS˘U(ξ),ψS˘L(ξ)],[φS˘U(ξ),φS˘L(ξ)]∈[0,1](16)

ϑS˘(ξ)={(ξ−S˘1)ϑS˘S˘2−S˘1S˘1≤ξ≤S˘2θS˘S˘2≤ξ≤S˘3(S˘4−ξ)ϑS˘S˘4−S˘3S˘3≤ξ≤S˘40otherwise(17)

ψS˘(ξ)={S˘2−ξ+(ξ−S˘1)ψS˘S˘2−S˘1S˘1≤ξ≤S˘2ψS˘S˘2≤ξ≤S˘3ξ−S˘3+(S˘4−ξ)ψS˘S˘4−S˘3S˘3≤ξ≤S˘41otherwise(18)

φS˘(ξ)={S˘2−ξ+(ξ−S˘1)φS˘S˘2−S˘1S˘1≤ξ≤S˘2φS˘S˘2≤ξ≤S˘3ξ−S˘3+(S˘4−ξ)φS˘S˘4−S˘3S˘3≤ξ≤S˘41otherwise(19)

where ϑS˘=[ϑS˘U,ϑS˘L],ψS˘=[ψS˘U,ψS˘L]and φS˘=[φS˘U,φS˘L] interval type-2 neutrosophic are numbers (IT2NNs). The number S˘ can be represented as (see Fig. 5):

S˘=[S˘U,S˘L]=[(S˘1U,S˘2U,S˘3U,S˘4U;ϑS˘U,ψS˘U,φS˘U),(S˘1L,S˘2L,S˘3L,S˘4L;ϑS˘L,ψS˘L,φS˘L)](20)

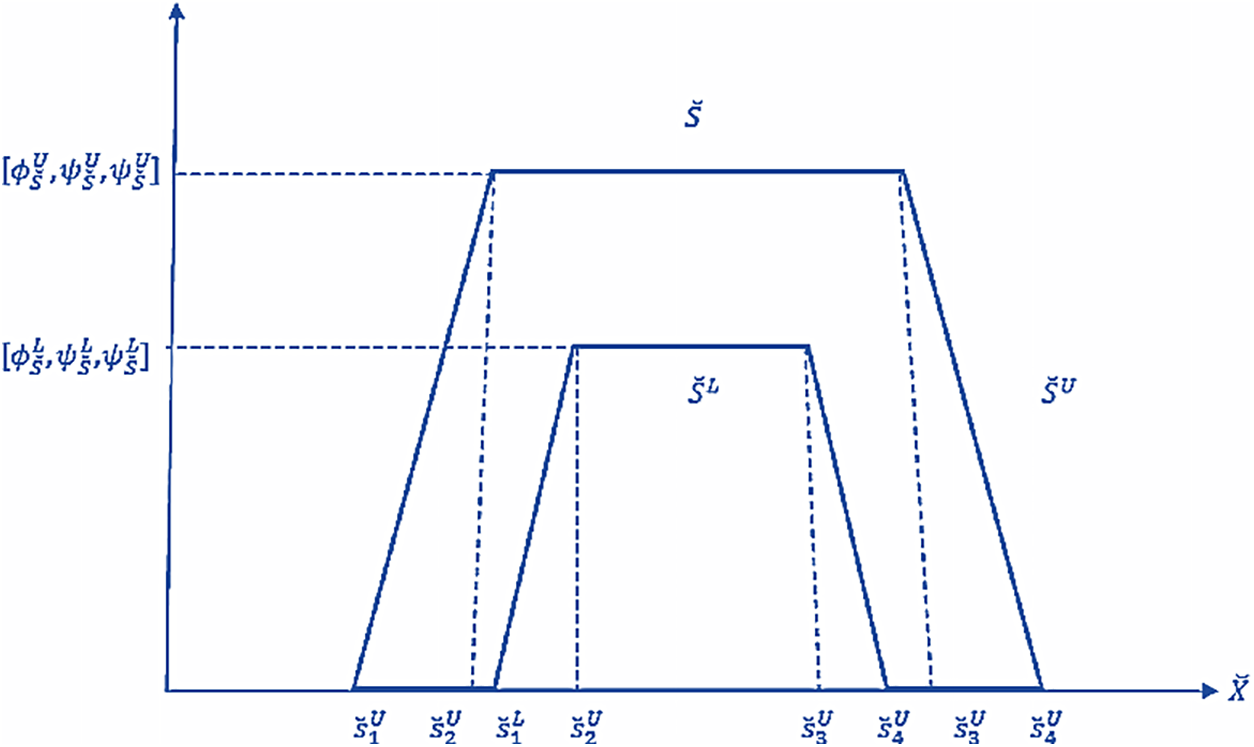
Figure 5: An interval type-2 trapezoidal neutrosophic number [23]

It is called interval type-2 trapezoidal neutrosophic logic number (IT2TrNN) where

0≤S˘1U≤S˘2U≤S˘3U≤S˘4U≤1,0≤S˘1L≤S˘2L≤S˘3L≤S˘4L≤1,

0≤ϑS˘L≤ϑS˘U≤1,0≤ψS˘L≤ψS˘U≤1,0≤φS˘L≤φS˘U≤1(21)

Step 5: Similarity Measure Calculation

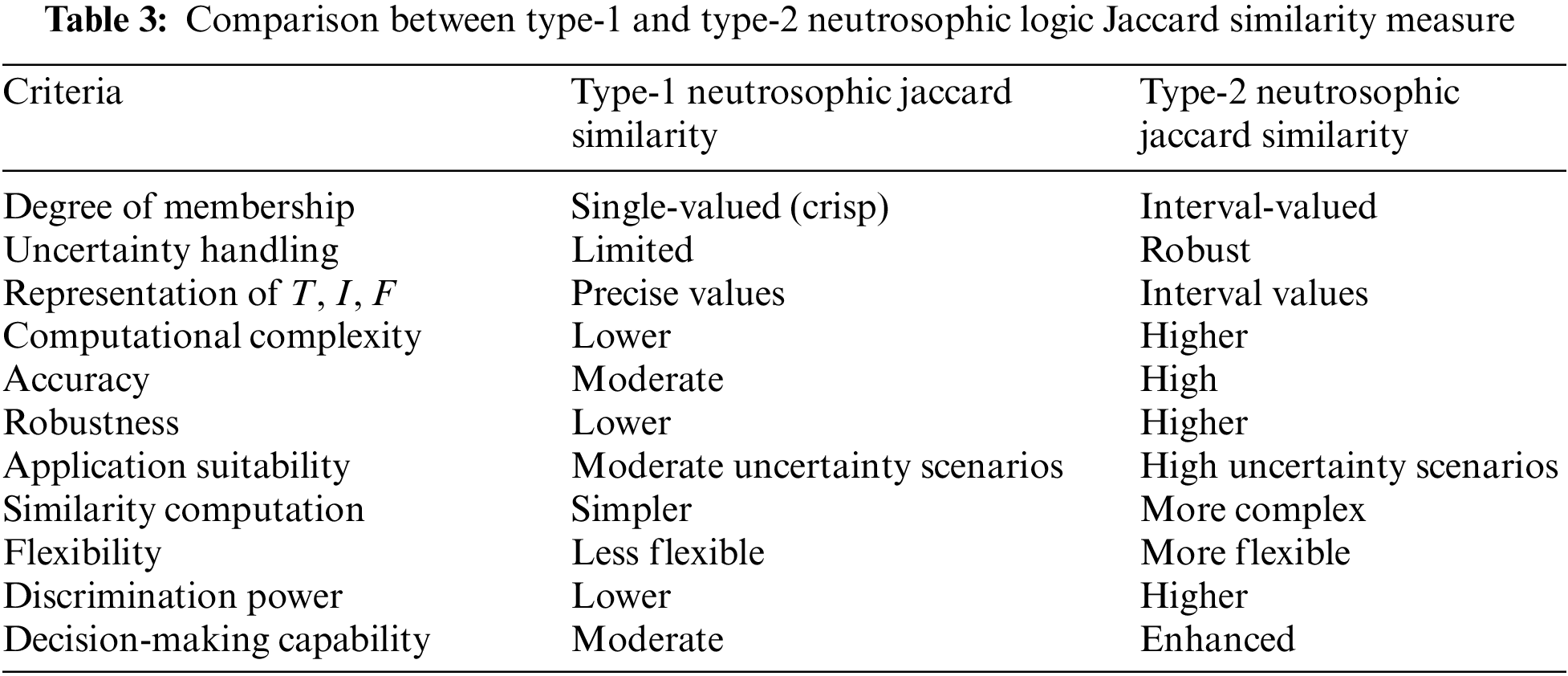
Conventional similarity measurements can face challenges because of the inherent ambiguity and variability in signature data. One can use similarity measures based on type-2 neutrosophic logic to assess the overlap and distance between the intervals of T, I, and F for the corresponding aspects of two signatures. These sophisticated measurements account for the entire uncertainty spectrum, which leads to more precise and robust similarity assessments. In our case, the Jaccard similarity index is used, that is a measure of similarity between two sets, defined as the size of the intersection divided by the size of the union of the sets. Table 3 discusses the difference between type-1 and type-2 neutrosophic logic-based Jaccard similarity measures.

Formally, let A={(x,[TA(x),IA(x),FA(x)])} and B={(x,[TB(x),IB(x),FB(x)])} be to type-2 neutrosophic sets. For each component (T,I,F) we have upper and lower membership functions denoted as U and l, respectively. UT(x) is the upper membership function for truth component, and LT(x) is the lower membership function for truth component. The FOU for each component is calculated as the difference between the upper and lower membership functions [34]:

FOUT(x)=UT(x)−LT(x),for Truth component T,UT(x)=TA(x)+12×FOUT(x),LT(x)=TA(x)−12×FOUT(x).(22)

FOUI(x)=UI(x)−LI(x),for Indeterminacy component I,UI(x)=IA(x)+12×FOUI(x),LI(x)=IA(x)−12×FOUI(x).(23)

FOUF(x)=UF(x)−LF(x),for Falsity component F,UF(x)=FA(x)+12×FOUF(x),LF(x)=FA(x)−12×FOUF(x).(24)

The Jaccard similarity between two T2NS sets A and B can be computed by determining the intersection and union of the sets while accounting for the FOU. Let’s call the functions that determine the degree of truth, indeterminacy, and falsity of sets TA(x), IA(x), FA(x) and TB(x), IB(x), FB(x). The lower and higher approximations of the T2NS sets A and B are precisely stated as:

AU_={x|TA(x)>0,IA(x)>0,FA(x)=0},AU¯={x|TA(x)=1,IA(x)=1,FA(x)<1},BU_={x|TB(x)>0,IB(x)>0,FB(x)=0},BU¯={x|TB(x)=1,IB(x)=1,FB(x)<1},(25)

Then, the intersection and union of the sets A and B with respect to the FOU can be calculated as:

(A∩B)U_=AU_∩BU_,(A∩B)U¯=AU¯∩BU¯,(A∪B)U_=AU_∪BU_,(A∪B)U¯=AU¯∪BU¯,(26)

Finally, the Jaccard similarity can be computed as:

J(A,B)=|(A∩B)U_∩(A∩B)U¯||(A∪B)U_∪(A∪B)U¯|(27)

where ∣⋅∣ denotes the cardinality of a set.

Step 6: Decision-Making

Typically, systems that utilize type-2 neutrosophic Jaccard similarity can make more informed decisions by taking into account the complete spectrum of uncertainty in the data. This results in more resilient decision-making processes, which are less susceptible to being misguided by irrelevant or insufficient information. In classification tasks, for example, the FOU allows classifiers to make more informed decisions by considering the range of possible values for each feature rather than relying on precise, but potentially inaccurate, single values [34]. In our model, if the output of Jaccard similarity J≥0.7 then the signature is genuine. In general, determining the best value of the threshold for similarity measures in signature verification involves a systematic process that balances the trade-off between false positives (accepting a forgery as genuine) and false negatives (rejecting a genuine signature). Herein, we establish a range of possible threshold values. This range is based on initial experiments; we perform a preliminary analysis to understand the distribution of similarity scores for genuine and forged signatures.

4  Results and Discussions

The effectiveness of the suggested verification approach was examined using an implementation of MATLAB (Release 2022a). Fig. 6 shows the screen snapshot of the proposed signature verification system. The following configuration of a Dell PC machine was used to test a modularly created prototype verification approach: A 4 GB of RAM and an Intel (R) Core (TM) i7 CPU (L640) running at 2.31 GHz are necessary for this setup. System requirements: 64-bit OS. Running Microsoft Windows 8.1 Enterprise on a 500 GB disk. In the training phase of this investigation, 40 images of signatures were used, with four features given to each signature. Ten real signatures and ten forged signatures were included in the twenty historical signature images used for testing (see Fig. 7). Two measures, the False Acceptance Rate (FAR) and the False Rejection Rate (FRR), are used to quantify the efficacy of a signature verification approach [35].

Figure 6: Output screen showing classification results of forged signature

Figure 7: A sample of signatures for a group of people (top) original and (bottom) forged

The primary aim of the first set of tests is to assess the efficacy of type-1 and type-2 neutrosophic similarity measures in differentiating genuine signatures from forgeries ones. The verification system is compared in Table 4. The results indicate that the type-2 neutrosophic similarity measure performs better than the type-1 measure when it comes to signature verification. The higher accuracy rate and the lower of both FRR and FAR justify the use of type-2 measures for more reliable and secure biometric verification systems. These results suggest that incorporating more sophisticated uncertainty modeling in neutrosophic logic can substantially enhance the performance of similarity measures in verification applications. An explanation for this result could be that type-2 neutrosophic sets offer an extra level of uncertainty management in comparison to type-1 neutrosophic sets. Type-1 sets express uncertainty by considering truth, indeterminacy, and falsity values. On the other hand, type-2 sets introduce a more complex level of uncertainty, encompassing a wider range of possibilities. This increased level of detail enables a more accurate representation of the inherent uncertainties in signature data, particularly in situations where signatures may be intricate or exhibit minor differences.

Type-2 neutrosophic measures improve the discriminatory power between forgeries and similar-looking genuine signatures by integrating a second level of uncertainty. This is due to the fact that type-2 measures are capable of detecting subtle differences that type-1 measures may neglect, resulting in improved differentiation and a reduced number of false positives and false negatives. Moreover, differences in handwriting often lead to significant uncertainty in the process of verifying signatures. Type-2 Neutrosophic sets assign a range of values to the indeterminacy component in order to better represent its nature. The benefits of type-2 neutrosophic Jaccard similarity measures make them highly successful for complicated applications like signature verification. These measures are particularly useful for capturing subtle variations and handling variability, which are crucial for achieving precise and dependable findings [8–11].

To show the relationship between signature verification accuracy and the similarity index threshold using Type-2 Neutrosophic-based Jaccard similarity measures, we conduct an experiment that varies the threshold for classifying a signature as genuine or forged. We define a range of similarity index thresholds from 0.1 to 0.9 in increments of 0.1. For each threshold, classify signatures as genuine if their similarity index is above the threshold and as forged if it is below the threshold. Below is a table of results (see Table 5) to illustrate the relationship between the similarity index threshold and the performance metrics. Accuracy increases as the threshold is raised from 0.1 to 0.9, reaching its peak in the 0.6–0.7 range, and then marginally decreases. Due to a decrease in the number of authentic signatures that satisfy the higher similarity index criterion, the True Positive Rate (TPR) decreases as the threshold increases. As a consequence of increasing the threshold value, only signatures that demonstrate an exceptionally high degree of similarity are classified as authentic, thereby reducing the number of true positive identifications. With an increase in the threshold, the false positive rate (FPR) decreases, leading to a decrease in the number of forgeries that are mistakenly identified as genuine. Improving the threshold level reduces the probability of incorrectly identifying counterfeit items as authentic, thereby improving the security of the system. The optimal threshold is established by achieving a balance between the TPR and the FPR to improve accuracy. According to this scenario, it appears that a threshold of approximately 0.6–0.7 achieves the most favorable balance, resulting in the highest level of accuracy. The computational cost of this similarity index remains linear, denoted as O(n); the total number of signature samples is denoted by n, despite the fact that the process of generating it has become more complex in order to address uncertainty. These signature verification applications are economically and scalable due to their linear complexity.

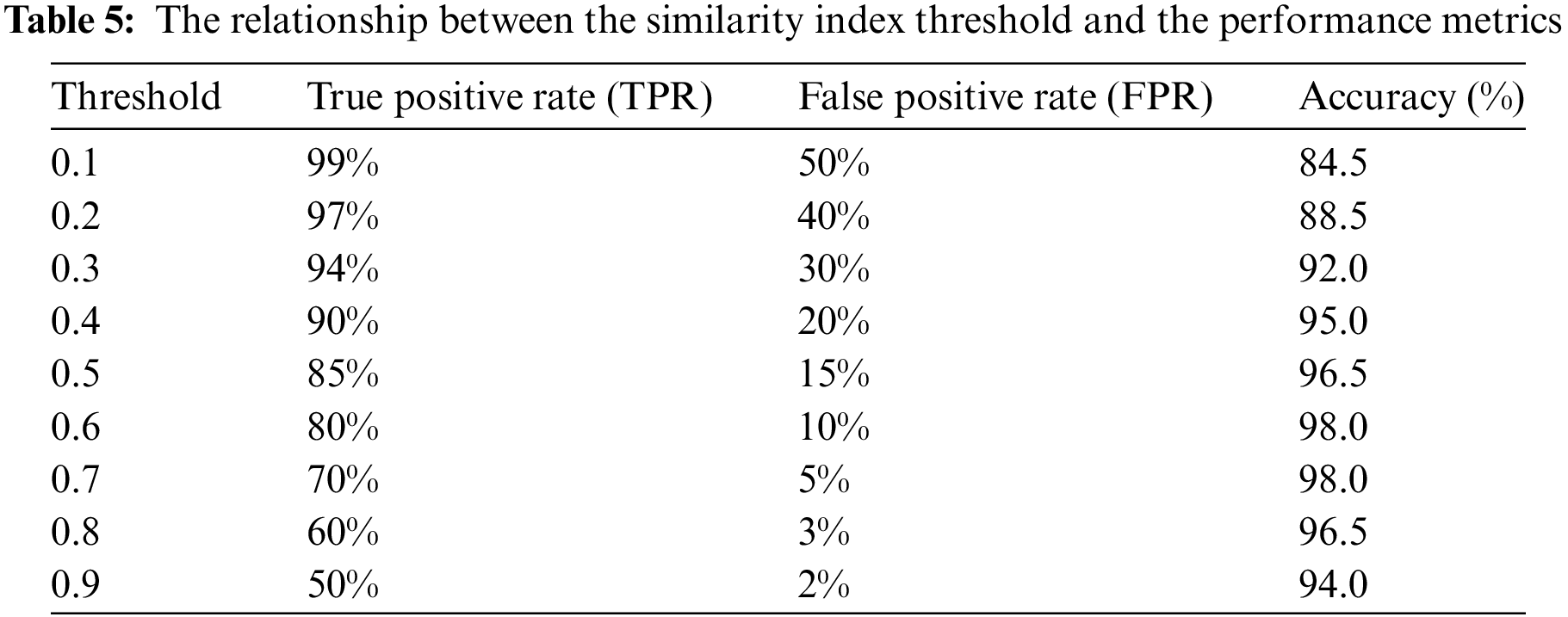
In the domain of offline signature verification, both Deep Neural Networks (DNNs) [36–38] and type-2 Neutrosophic Logic (T2NL) similarity measure have shown promising results. While DNNs are renowned for their high accuracy in complex pattern recognition tasks, T2NL classifiers offer unique advantages in handling uncertainty and imprecision. While DNNs are highly effective in feature extraction and complex pattern recognition, their performance is heavily dependent on the availability of large datasets and substantial computational resources. T2NL classifiers, on the other hand, offer distinct advantages in handling uncertainty, noise, and computational efficiency. This makes T2NL a preferable choice in scenarios with high variability, noise, and limited data or computational resources.

The aim of the last set of experiments is to compare the two advanced techniques: DNNs and T2NL-based similarity measures for offline signature verification. The performance of both methods is evaluated based on their accuracy, robustness, and computational efficiency. The results are summarized in Table 6 for populations with high variability in signature styles; furthermore, Figs. 8 and 9 visually demonstrate the superiority of the suggested model in terms of accuracy (on average 2.5% increase), FAR, and FRR. T2NL classifiers are more robust to noisy data. In scenarios where signatures are scanned in less-than-ideal conditions, T2NL can maintain performance by leveraging its ability to process and classify data with high levels of noise and uncertainty. Furthermore, T2NL models generally require less computational power and time to train compared to DNNs. This makes them suitable for applications with limited computational resources or where rapid deployment is necessary. For populations with high variability in signature styles (e.g., different cultural handwriting styles), T2NL’s capability to manage a wide range of variations and uncertainties can lead to better performance compared to DNNs, which might struggle with overfitting or underfitting.

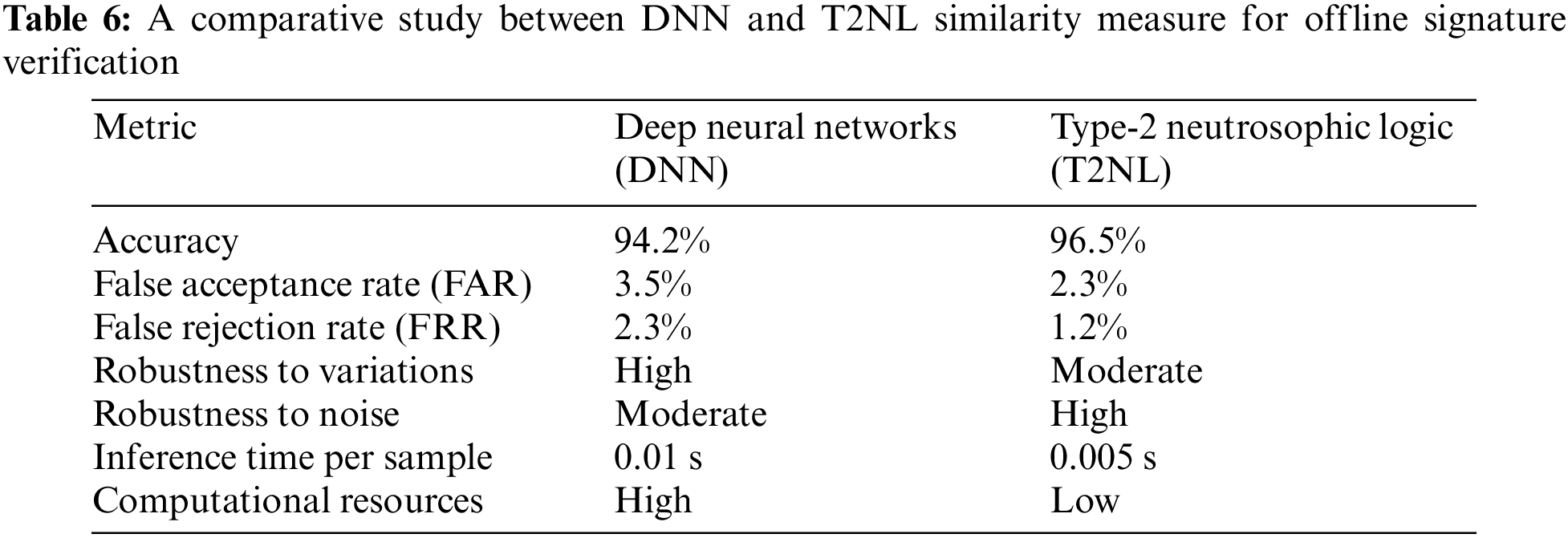
Figure 8: A comparative study between DNN and T2NL–based signature verification in terms of accuracy

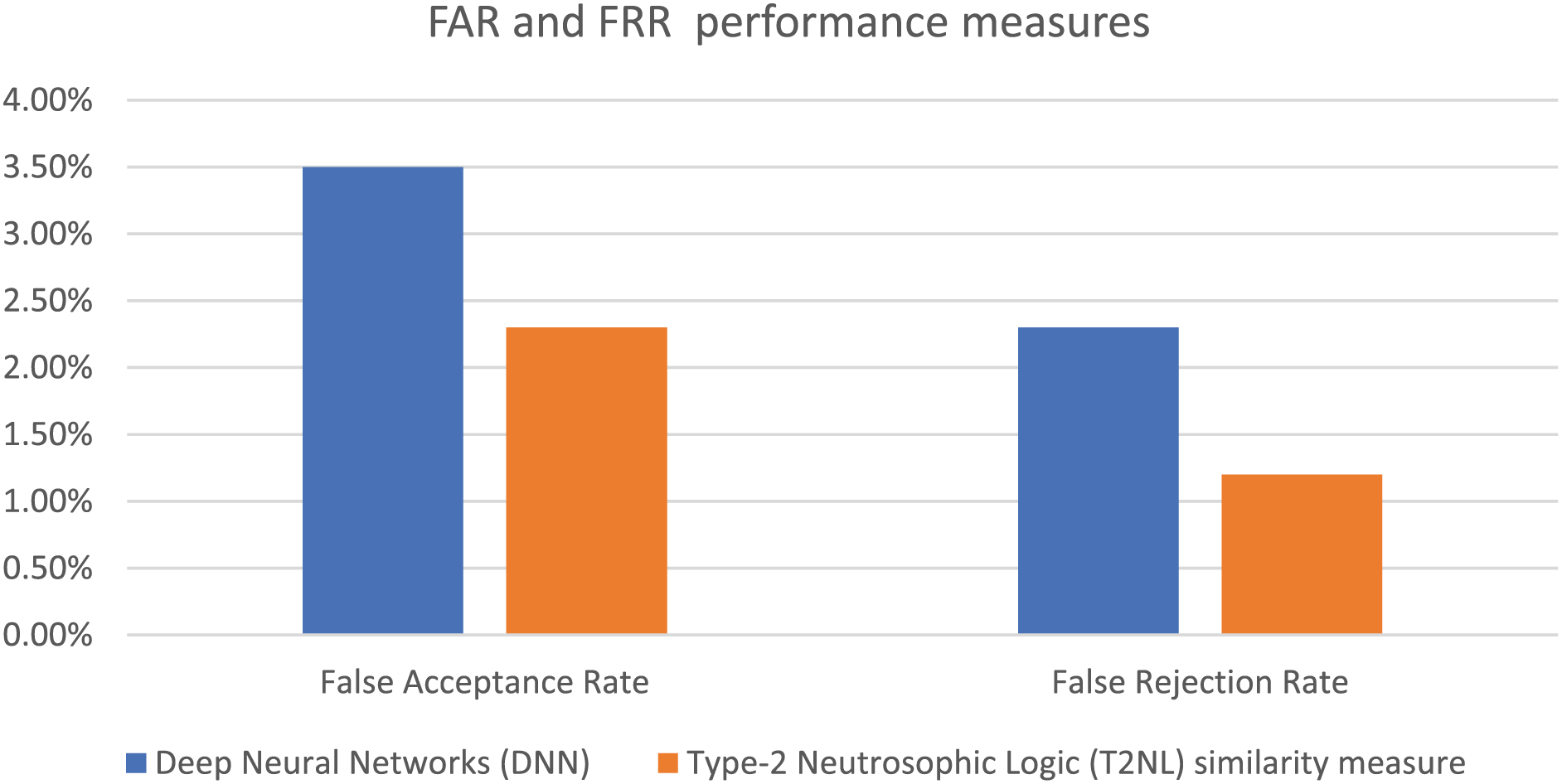
Figure 9: A comparative study between DNN and T2NL–based signature verification in terms of FAR and FRR

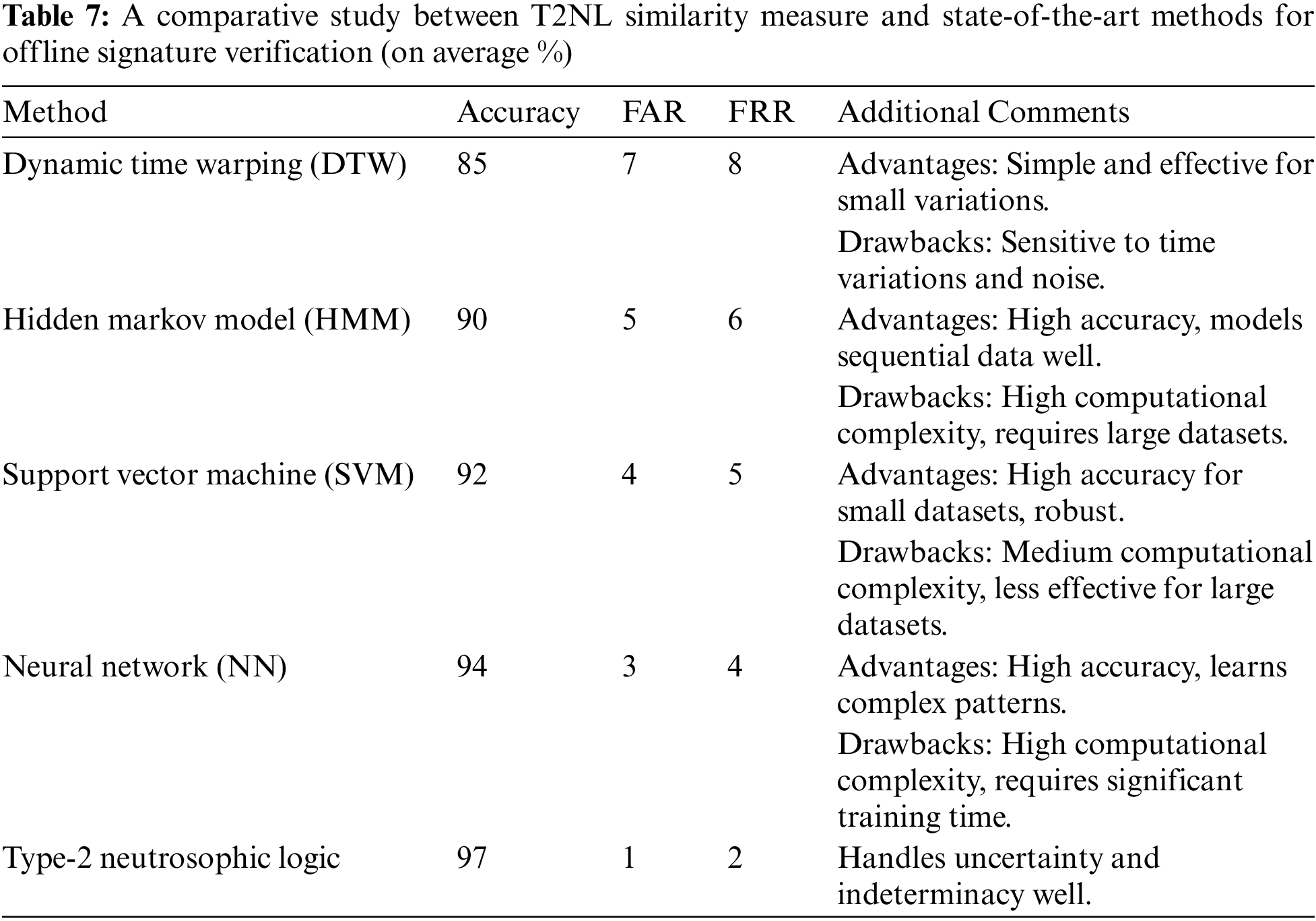
Furthermore, Table 7 provides a comparison of type-2 neutrosophic logic-based signature verification with existing methods that include Dynamic time warping (DTW) [39], Hidden Markov Model (HMM) [40], Support Vector Machine (SVM) [41], and Neural Network (NN) -based offline signature verification [42] in terms of accuracy, false acceptance rate (FAR), and false rejection rate (FRR). As revealed in Table 7, type-2 neutrosophic logic often outperforms other methods due to its ability to handle uncertainty. The FAR is significantly lower in type-2 neutrosophic logic-based systems because they can better manage the variability and uncertainty in signatures. Similarly, the FRR is lower in type-2 neutrosophic logic-based systems as they can accurately distinguish between genuine and forged signatures even in the presence of minor variations.

5  Conclusions

Utilizing type-2 neutrosophic logic for similarity measures in signature verification provides a robust method for dealing with the inherent uncertainty and variability in biometric signature data. This strategy enhances accuracy and decision-making abilities by utilizing the interval-valued representation of truth, indeterminacy, and falsity. Type-2 neutrosophic-based similarity measures provide robustness against variations in signature characteristics, such as different writing styles or environmental conditions, by accurately capturing the uncertainty linked to these elements. The increased discriminatory capability of measures based on type-2 neutrosophic logic results in a decrease in both false positives (incorrectly accepting forgeries as genuine) and false negatives (incorrectly rejecting authentic signatures), leading to more dependable verification results. Experimental results indicate that type-2 procedures are more effective than type-1 measures in managing uncertainty and variability in signature data, resulting in more dependable verification results. In addition, type-2 measures may demonstrate a lower degree of sensitivity to threshold changes than type-1 measures, as they inherently incorporate uncertainty into interval-based representations. Future research should mostly concentrate on how to improve the feature extraction and classification in signature verification by including type-2 Neutrophobic similarity measurements into deep learning algorithms. Develop optimization techniques as well to make type-2 neutrosophic similarity calculations less computationally complex and so enable their effective application in settings with restricted resources.

Acknowledgement: Not applicable.

Funding Statement: The authors received no specific funding for this study.

Author Contributions: Conceptualization, Saad M. Darwish, Shahlaa Mashhadani, and Oday Ali Hassen; methodology, Saad M. Darwish, Shahlaa Mashhadani, and Oday Ali Hassen; software, Wisal Hashim Abdulsalam, and Oday Ali Hassen; validation, Saad M. Darwish, Shahlaa Mashhadani, and Wisal Hashim Abdulsalam; formal analysis, Saad M. Darwish, Shahlaa Mashhadani, and Wisal Hashim Abdulsalam; investigation, Saad M. Darwish, and Oday Ali Hassen; resources, Wisal Hashim Abdulsalam, and Shahlaa Mashhadani; data curation, Wisal Hashim Abdulsalam, and Shahlaa Mashhadani; writing—original draft preparation, Saad M. Darwish, and Oday Ali Hassen; writing—review and editing, Saad M. Darwish, Shahlaa Mashhadani, and Wisal Hashim Abdulsalam; visualization, Wisal Hashim Abdulsalam; supervision, Saad M. Darwish, and Oday Ali Hassen; project administration, Wisal Hashim Abdulsalam, and Shahlaa Mashhadani; funding acquisition, Wisal Hashim Abdulsalam, and Shahlaa Mashhadani. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The data that support the findings of this study are available from the corresponding author, Shahlaa Mashhadani, upon reasonable request.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. S. Gupta and M. Kumar, “Forensic document examination system using boosting and bagging methodologies,” Soft Comput., vol. 24, no. 7, pp. 5409–5426, 2020. doi: 10.1007/s00500-019-04297-5. [Google Scholar] [CrossRef]

2. J. Huang, Y. Xue, and L. Liu, “Dynamic signature verification technique for the online and offline representation of electronic signatures in biometric systems,” Processes, vol. 11, no. 1, pp. 1–18, 190, 2023. [Google Scholar]

3. H. Kaur and M. Kumar, “Signature identification and verification techniques: State-of-the-art work,” J. Ambient Intell. Humaniz. Comput., vol. 4, no. 2, pp. 1027–1045, 2023. doi: 10.1007/s12652-021-03356-w. [Google Scholar] [CrossRef]

4. I. Priya and N. Chaurasia, “Estimating the effectiveness of CNN and fuzzy logic for signature verification,” in Proc. Third Int. Conf. Secur. Cyber Comput. Commun., IEEE, 2023, pp. 1–6. [Google Scholar]

5. A. Varshney and V. Torra, “Literature review of the recent trends and applications in various fuzzy rule-based systems,” Int. J. Fuzzy Syst., vol. 25, no. 6, pp. 2163–2186, 2023. doi: 10.1007/s40815-023-01534-w. [Google Scholar] [CrossRef]

6. S. Pai and R. Gaonkar, “Safety modelling of marine systems using neutrosophic logic,” J. Eng. Marit. Environ., vol. 235, no. 1, pp. 225–235, 2021. doi: 10.1177/1475090220925733. [Google Scholar] [CrossRef]

7. A. Bakali, S. Broumi, D. Nagarajan, M. Talea, M. Lathamaheswari and J. Kavikumar, “Graphical representation of type-2 neutrosophic sets,” Neutrosophic Sets Syst., vol. 42, no. 2, pp. 28–38, 2021. [Google Scholar]

8. M. Touqeer, R. Umer, A. Ahmadian, and S. Salahshour, “A novel extension of TOPSIS with interval type-2 trapezoidal neutrosophic numbers using (α, β, γ)-cuts,” RAIRO-Oper. Res., vol. 55, no. 5, pp. 2657–2683, 2021. doi: 10.1051/ro/2021133. [Google Scholar] [CrossRef]

9. I. Alrashdi, “An intelligent neutrosophic type-II model for selecting optimal internet of things (IoT) service provider: Analysis and application,” Neutrosophic Sets Syst., vol. 66, no. 2, pp. 204–217, 2024. [Google Scholar]

10. V. Simić, B. Milovanović, S. Pantelić, D. Pamučar, and E. Tirkolaee, “Sustainable route selection of petroleum transportation using a type-2 neutrosophic number based ITARA-EDAS model,” Inf. Sci., vol. 622, no. 4, pp. 732–754, 2023. doi: 10.1016/j.ins.2022.11.105. [Google Scholar] [CrossRef]

11. M. Abdel-Basset, N. Mostafa, K. Sallam, I. Elgendi, and K. Munasinghe, “Enhanced COVID-19 X-ray image preprocessing schema using type-2 neutrosophic set,” Appl. Soft Comput., vol. 123, 2022, Art. no. 108948. doi: 10.1016/j.asoc.2022.108948. [Google Scholar] [CrossRef]

12. T. Dhieb, H. Boubaker, S. Njah, M. Ben, and A. Alimi, “A novel biometric system for signature verification based on score level fusion approach,” Multimed. Tools Appl., vol. 81, no. 6, pp. 7817–7845, 2022. doi: 10.1007/s11042-022-12140-7. [Google Scholar] [CrossRef]

13. S. Bhavani and R. Bharathi, “A multi-dimensional review on handwritten signature verification: Strengths and gaps,” Multimed. Tools Appl., vol. 83, no. 1, pp. 2853–2894, 2024. doi: 10.1007/s11042-023-15357-2. [Google Scholar] [CrossRef]

14. R. Doroz, P. Porwik, and T. Orczyk, “Dynamic signature verification method based on association of features with similarity measures,” Neurocomputing, vol. 171, no. 27, pp. 921–931, 2016. doi: 10.1016/j.neucom.2015.07.026. [Google Scholar] [CrossRef]

15. E. Zois, D. Tsourounis, and D. Kalivas, “Similarity distance learning on SPD manifold for writer independent offline signature verification,” IEEE Trans. Inf. Forensics Secur., vol. 19, no. 11, pp. 1342–1356, 2023. doi: 10.1109/TIFS.2023.3333681. [Google Scholar] [CrossRef]

16. M. Hanif and M. Bilal, “A metric learning approach for offline writer independent signature verification,” Pattern Recognit. Image Anal., vol. 30, no. 10, pp. 795–804, 2020. doi: 10.1134/S1054661820040173. [Google Scholar] [CrossRef]

17. T. Dhieb, S. Njah, H. Boubaker, W. Ouarda, M. Ayed and A. Alimi, “An extended Beta-Elliptic model and fuzzy elementary perceptual codes for online multilingual writer identification using deep neural network,” 2018, arXiv:1804.05661. [Google Scholar]

18. H. Hu, J. Zheng, E. Zhan, and J. Tang, “Online signature verification based on a single template via elastic curve matching,” Sensors, vol. 9, no. 22, pp. 1–23, 2019, Art. no. 4858. doi: 10.3390/s19224858. [Google Scholar] [PubMed] [CrossRef]

19. A. Alaei, S. Pal, U. Pal, and M. Blumenstein, “An efficient signature verification method based on an interval symbolic representation and a fuzzy similarity measure,” IEEE Trans. Inf. Forensics Secur., vol. 12, no. 10, pp. 2360–2372, 2017. doi: 10.1109/TIFS.2017.2707332. [Google Scholar] [CrossRef]

20. V. Sekhar, P. Mukherjee, D. Guru, and V. Pulabaigari, “Online signature verification based on writer specific feature selection and fuzzy similarity measure,” 2019, arXiv:1905.08574. [Google Scholar]

21. D. Nagarajan, M. Lathamaheswari, S. Broumi, and J. Kavikumar, “A new perspective on traffic control management using triangular interval type-2 fuzzy sets and interval neutrosophic sets,” Oper. Res. Perspect., vol. 6, no. 2, pp. 1–13, 2019, Art. no. 100099. doi: 10.1016/j.orp.2019.100099. [Google Scholar] [CrossRef]

22. S. Zolfani, Ö. Görçün, M. Çanakçıoğlu, and E. Tirkolaee, “Efficiency analysis technique with input and output satisficing approach based on type-2 neutrosophic fuzzy sets: A case study of container shipping companies,” Expert. Syst. Appl., vol. 218, pp. 1–21, 2023, Art. no. 119596. [Google Scholar]

23. M. Hassan, S. Darwish, and S. Elkaffas, “Type-2 neutrosophic set and their applications in medical databases deadlock resolution,” Comput. Mater. Contin., vol. 74, no. 2, pp. 4417–4434, 2023. doi: 10.32604/cmc.2023.033175. [Google Scholar] [CrossRef]

24. S. Ahmad, F. Ahmad, and M. Sharaf, “Supplier selection problem with type-2 fuzzy parameters: A neutrosophic optimization approach,” Int. J. Fuzzy Syst., vol. 23, no. 2, pp. 755–775, 2021. doi: 10.1007/s40815-020-01012-7. [Google Scholar] [CrossRef]

25. F. Karaaslan and F. Hunu, “Type-2 single-valued neutrosophic sets and their applications in multi-criteria group decision making based on TOPSIS method,” J. Ambient Intell. Humaniz. Comput., vol. 11, no. 3, pp. 4113–4132, 2020. doi: 10.1007/s12652-020-01686-9. [Google Scholar] [CrossRef]

26. M. Deveci, I. Gokasar, D. Pamucar, A. Zaidan, X. Wen and B. Gupta, “Evaluation of cooperative intelligent transportation system scenarios for resilience in transportation using type-2 neutrosophic fuzzy VIKOR,” Transp. Res. Part A: Policy Pract., vol. 172, pp. 1–14, 2023, Art. no. 103666. doi: 10.1016/j.tra.2023.103666. [Google Scholar] [CrossRef]

27. Ö. Görçün, “A novel integrated MCDM framework based on Type-2 neutrosophic fuzzy sets (T2NN) for the selection of proper Second-Hand chemical tankers,” Transp. Res. Part E: Logist. Transp. Rev., vol. 163, pp. 1–26, 2022, Art. no. 102765. [Google Scholar]

28. Ö. Görçün and H. Küçükönder, “Performance analysis of domestic energy usage of European cities from the perspective of externalities with a combined approach based on type 2 neutrosophic fuzzy sets,” in Advancement in Oxygenated Fuels for Sustainable Development. The Netherlands: Elsevier, 2023, pp. 331–361. [Google Scholar]

29. M. Alshehri, “An integrated AHP MCDM based type-2 neutrosophic model for assessing the effect of security in fog-based IoT framework,” Int. J. Neutrosophic Sci., vol. 20, no. 2, pp. 55–67, 2023. doi: 10.54216/IJNS.200205. [Google Scholar] [CrossRef]

30. İ. Önden et al., “Supplier selection of companies providing micro mobility service under type-2 neutrosophic number based decision making model,” Expert. Syst. Appl., vol. 245, pp. 1–20, 2024, Art. no. 123033. [Google Scholar]

31. M. Stauffer, P. Maergner, A. Fischer, and K. Riesen, “A survey of state of the art methods employed in the offline signature verification process,” in New Trends in Business Information Systems and Technology: Digital Innovation and Digital Business Transformation. Salmon Tower Building, New York City, USA: Springer, 2020, vol. 294, pp. 17–30. [Google Scholar]

32. M. Saleem, C. Lia, and B. Kovari, “Systematic evaluation of pre-processing approaches in online signature verification,” Intell. Decis. Technol., vol. 17, no. 3, pp. 655–672, 2023. doi: 10.3233/IDT-220247. [Google Scholar] [CrossRef]

33. S. Basha, A. Tharwat, A. Abdalla, and A. Hassanien, “Neutrosophic rule-based prediction system for toxicity effects assessment of bio transformed hepatic drugs,” Expert. Syst. Appl., vol. 121, no. 4, pp. 142–157, 2019. doi: 10.1016/j.eswa.2018.12.014. [Google Scholar] [CrossRef]

34. Ş. Özlü and F. Karaaslan, “Hybrid similarity measures of single-valued neutrosophic type-2 fuzzy sets and their application to MCDM based on TOPSIS,” Soft Comput., vol. 26, no. 9, pp. 4059–4080, 2022. doi: 10.1007/s00500-022-06824-3. [Google Scholar] [CrossRef]

35. B. Rajarao, M. Renuka, K. Sowjanya, K. Krupa, and M. Babbitha, “Offline signature verification using convolution neural network,” Ind. Eng. J., vol. 52, no. 4, pp. 1087–1101, 2023. [Google Scholar]

36. R. Ghosh, “A recurrent neural network based deep learning model for offline signature verification and recognition system,” Expert. Syst. Appl., vol. 168, no. 5, pp. 1–13, 2021, Art. no. 114249. doi: 10.1016/j.eswa.2020.114249. [Google Scholar] [CrossRef]

37. J. Lopes, B. Baptista, N. Lavado, and M. Mendes, “Offline handwritten signature verification using deep neural networks,” Energies, vol. 15, no. 20, pp. 1–15, 2022, Art. no. 7611. doi: 10.3390/en15207611. [Google Scholar] [CrossRef]

38. Z. Hashim, H. Mohsin, and A. Alkhayyat, “Signature verification based on proposed fast hyper deep neural network,” Int. J. Artif. Intell., vol. 3, no. 1, pp. 961–973, 2024. [Google Scholar]

39. M. Stauffer, P. Maergner, A. Fischer, R. Ingold, and K. Riesen, “Offline signature verification using structural dynamic time warping,” in Proc. Int. Conf. Doc. Anal. Recognit., 2019, pp. 1117–1124. [Google Scholar]

40. M. Chavan, “Handwritten online signature verification and forgery detection using hybrid wavelet transform-2 with HMM classifier,” J. Electr. Syst., vol. 20, no. 4s, pp. 2463–2470, 2024. doi: 10.52783/jes.2799. [Google Scholar] [CrossRef]

41. F. Batool et al., “Offline signature verification system: A novel technique of fusion of GLCM and geometric features using SVM,” Multimed. Tools Appl., vol. 83, no. 2, pp. 14959–14978, 2024. doi: 10.1007/s11042-020-08851-4. [Google Scholar] [CrossRef]

42. P. Kiran, B. Parameshachari, J. Yashwanth, and K. Bharath, “Offline signature recognition using image processing techniques and back propagation neuron network system,” SN Comput. Sci., vol. 2, no. 3, pp. 1–8, 2021, Art. no. 196. [Google Scholar]