Mathematical Named Entity Recognition Based on Adversarial Training and Self-Attention

1  Introduction

With the rapid development of big data and artificial intelligence, it is significant to promote intelligent education in mathematics subjects, by using computers to process mathematical knowledge and develop applications such as knowledge recommendation, machine problem solving, intelligent education, and intelligent computing informally and intelligently [1]. The basic tasks of NLP include word division, part-of-speech (POS) tagging, Named Entity Recognition (NER), and syntactic analysis [2]. Mathematical Named Entity Recognition (MNER) aims to extract specific entities (such as mathematical proper names, alphabets, special symbols, and formulas, etc.) from mathematical texts and annotate them with symbols. Different from English mathematics texts, Chinese mathematics has no obvious word boundary and has a complex structure of Chinese characters, numbers, English letters, special mathematical symbols, formulas, and images, such as “△ABC”, “X”, “ (circle)”, etc. In particular, there are long and rare mathematical proper nouns, which have different meanings when processing different participles at the word level. Furthermore, the field of mathematical research has not yet matured, with few opening mathematics data sets. Therefore, it is a great challenge to accurately identify mathematical entities from Chinese mathematical texts.

With the development of deep learning, the research of NER has gradually shifted to neural networks. The most representative neural networks were convolutional neural networks (CNN) [3] and recurrent neural networks (RNN) [4]. In recent years, natural language processing (NLP) has made great progress in the field of mathematics, especially in the recognition of handwritten or printed symbols in English mathematics. Vanetik et al. [5] studied the problem of automatic detection of single-sentence definitions in mathematical texts, applying deep learning methods such as CNN and RNN to recognize mathematical definitions. Experiments proved the merits of combining CNN and RNN in syntactic-rich input representation. Wang et al. [6] proposed a deep neural solver that automatically solved mathematical word problems, They used RNN to transform mathematical word problems into equation templates and reduced complex engineering compared to traditional methods. POS tagging [7] was introduced in mathematical text processing and transformed mathematical formulas into character sequences to improve the accuracy of extracting mathematical entities. Ferreira et al. [8] proposed a method to extract mathematical theorems, axioms, and definitions using CNN, and the experimental results showed that the F1-score was 41 higher than BERT. For Chinese mathematics, from traditional methods to deep learning methods, researchers replaced mathematical formulas in Chinese mathematical texts with special symbols and used neural network models to learn and extract features. The model that integrated word embedding, speech (POS) tag embedding, BiLSTM, and attention, and the experiments achieved good results in different language datasets [9]. However, there was a problem with the fuzzy entity boundary. Zhang et al. [10] proposed a method that is used for identifying primary mathematical named entities based on the BERT-BiLSTM-IDCNN-CRF. The results of the F1-score reached 93.91%. Although the processing of mathematical texts in the above studies has achieved promising successes, there are still dependency problems among long-distance mathematical entities.

In the NER task, only short-range dependencies can be established due to the capacity of information transmission and the vanishing of the gradient in RNN. Although the number of network layers can be increased or the fully connected network can be used to establish long-distance dependencies between entities, longer sequential tasks cannot be processed. To address this problem, it is effective to dynamically generate weights for different connections to obtain more relevant semantic information by introducing a self-attention model. For example, Lin et al. [11] realized that self-attention had no dependency on the downstream task, and used self-attention for sentence embedding to enhance the semantic relationships of sentences. Li et al. [12] introduced a self-attention mechanism in their study of NER for network security. Moreover, The self-attention and neural network model for NER to extract relevant semantic information from characters of different granularity and obtain the correlation between characters in the sequence [13]. Self-attention was used to establish a direct connection between each character to learn long sequence dependencies and complete the identification and naming of entities in electronic medical records [14]. We find that if the self-attention mechanism is implemented in the task of MNER, it can dynamically learn inter-character features and obtain better features, and can solve the long-distance semantic problem of mathematical entities.

Additionally, improving the stability and robustness of NER models is also important in MNER. There are some rare proper nouns and a large number of fuzzy entity boundaries in mathematical texts that inevitably lead to the existence of local instability using the current network model.

A lot of work on adversarial training targets the issue of NER model robustness and entity boundary ambiguity. To solve the problem of irregular entity representation and insignificant boundary, a method of adverse drug reaction entity identification based on adversarial transfer learning was proposed, their F1 value reached 91.35% [15]. For the problem of inaccurate semantic and entity boundaries, an industrial person entity recognition model based on word fusion and adversarial training was proposed. Added perturbation to generate adversarial samples after fusing word features to improve the effect of entity recognition [16]. Dong et al. [17] adopted a food domain NER method based on BERT and adversarial training, which used the shared information of Chinese word segmentation and NER to improve the accuracy of the entity boundary.

To solve the above problems in MNER, we propose an AT-BSAC model that integrates Adversarial Training [18], a self-attention mechanism [19], and BiLSTM-CRF [20]. This method takes BiLSTM-CRF as the basic model and adds adversarial training in the embedding layer to improve the robustness of the model to small perturbations. Then, a self-attention mechanism is introduced after the BiLSTM [21] layer to give different weights to features and learn features with stronger local correlation, to identify mathematical entities more accurately and achieve a better MNER effect.

The primary contributions of this study are outlined as follows:

1. Considering the unpublished Chinese mathematics domain data sets, this study self-constructs Chinese mathematics data sets and proposes an MNER method with prior knowledge and a few annotated data sets. The method extracts features through model training and adds disturbance to the model to optimize the model, which in turn compensates to a certain extent for the problem of entity boundary ambiguity and improves the accuracy of model identification.

2. The Adversarial Training-BiLSTM-Selfattention-CRF (AT-BSAC) model is used in this paper to dynamically extract the features and capture the long-distance dependency features within longer Chinese mathematical entities.

3. A series of experiments on a manually labeled dataset received an F1-score of 93.74%. The results show that the proposed method performs better than other methods in identifying Chinese mathematical entities.

2  Related Work

2.1 Named Entity Recognition

Named entity recognition (NER) methods mainly include rule-based, based on statistical machine learning, and based on deep learning. The method based on rule requires experts to make rules and dictionaries manually, which has high labor costs, strong subjectivity, and poor portability [22]. With the emergence of machine learning, researchers treat NER as a sequential labeling problem. Many achievements have been made on the model Maxim Entropy (ME), Hidden Markov Models (HMM), and Conditional Random Field (CRF) [23]. Although the method built upon statistical machine learning does not require manual construction of rules and templates, tedious feature engineering also requires a lot of manpower. Compared with traditional methods, the methods based on deep learning reduce the tedious feature engineering and also have strong generalization ability. Especially, the BiLSTM-CRF model, coupled with an attention mechanism, is widely used in research on named entity recognition across various fields. For example, Liu et al. [24] introduced the BERT-BiLSTM-CRF model, which exhibits enhanced accuracy and efficiency in extracting entities from vast historical and cultural information datasets. Huang et al. [25] studied the recognition of Chinese-named entities in the judicial field, and proposed a model that used character vectors, and sentence vectors trained by distributed memory model of paragraph vectors (PV-DM). Liu et al. [26] used a two-stage fine-tuning method to accurately identify entities in geographic texts, and accomplished the task of geological naming entity recognition (Geo-NER). Ma et al. [27] employed two weakly supervised learning techniques, namely sampling-based active learning and parameter-based transfer learning, in order to address a specific research challenge or objective, the experimental results show that the model obtained an F1-score of 89.21%.

Compared with English mathematical entities, Chinese mathematical entities have no obvious entity boundary, and different participles have different meanings. In addition, there are many kinds of entities in mathematical texts and their structures are complex. The mathematical language is professional and rigorous. There are often entity nesting, semantic ambiguity, and unknown entity reference problems in MNER tasks through literature analysis. Therefore, this paper takes BiLSTM-CRF as the basic model to introduce a self-attention mechanism to improve the accuracy rate of mathematical entity recognition.

2.2 Adversarial Training

Adversarial training originally appeared in the realm of computer vision. Generative Adversarial Networks (GAN) [28] enhance the robustness of the model through adversarial attacks and generative defense of the model. Later, it was widely used in the field of NLP. Adversarial training generates adversarial samples by introducing noise [29], and after training and learning, it identify adversarial samples. As a regularization method, adversarial training improves the generalization ability and robustness of the model. The Fast Gradient Method (FGM) and Projected Gradient Descent (PGD) are two common methods to calculate the perturbation value. They are obtained by calculating the gradient of the word vector after the embedding and then standardizing the gradient. FGM only needs to calculate the perturbation value once, while PGD calculates the perturbation value through multi-step iteration. So PGD requires more computing resources. Li et al. [30] proposed Metabdry, a novel domain generalization approach for entity boundary detection without requiring any access to target domain information, and adopted adversarial learning to encourage domain-invariant representations. Finally, good experimental results were obtained. Wang et al. [31] introduced perturbations to network variables during training as a means to diversify these variables, ultimately enhancing the model’s generalization capabilities and robustness. An Adversarial Trained LSTM-CNN (ASTRAL) system and a specific adversarial training method were proposed. Yu et al. [32] proposed the GAN-bidirectional long short-term memory conditional random field (GANBiLSTM-CRF) and the GAN-based bidirectional encoder representations from transformers-conditional random field (GAN-BERT-CRF) models, aiming to tackle the issue of annotation inconsistency in the biomedical annotation field.

Adversarial training can add small perturbations to the model, which can represent rare proper nouns and fuzzy boundary entities in mathematical texts. The perturbations and the original word vector can be trained together in the model to make the model have the ability to identify them, and thus enhance the robustness and robustness of the model.

In the MNER task, there are many uncommon mathematical entities in the data set, and the amount of data is limited. Using the multi-layer deep neural network model, it is easy to have the problem of overfitting. Therefore, to solve problems such as robustness and entity boundary ambiguity of the model, adversarial training is introduced in this paper. Small perturbations are added to the word vector to generate adversarial samples to train model learning and improve the generalization ability and robustness of the model.

2.3 Self-Attention Mechanisms

The fundamental idea behind attention mechanisms is to allocate varying degrees of significance to input items, selecting the most crucial information from input sequences for the current task. The objective is to prioritize relevant segments of the input data while disregarding irrelevant portions, ultimately enriching the extracted feature set. Initially, attention mechanisms were integrated with neural networks to address image classification tasks, enabling their application in the field of visual imagery. Subsequently, researchers extended attention mechanisms to natural language processing, significantly enhancing the accuracy of text translation. In recent years, with the widespread adoption of pre-trained BERT models, numerous improved models have emerged, many of which rely on Transformer models based on self-attention mechanisms, making attention mechanisms a current research hotspot. Currently, self-attention mechanisms have been successfully applied in various fields such as medical electronic records, agriculture, law, and military weaponry to address long-distance semantic issues among entities.

Self-attention mechanisms represent a variant form of attention mechanisms, where the basic idea is to assign weights to input items based on their relationships, allowing each input item’s weight to depend on the relationships between input items. In natural language processing tasks, input sequences of varying lengths exhibit different connection weightings, in such cases, self-attention models can dynamically generate different connection weights, reducing reliance on external dependency information and improving their ability to capture semantic information within sentences.

3  Model Design

As depicted in Fig. 1, the AT-BSAC model comprises an Input, an Embedding layer, a BiLSTM layer, a Self-attention layer, a CRF layer, and an Output. The overall workflow is as follows: in Fig. 1, the initial conversion of the input sequence into a vectorized representation, yielding the set v = {v1, v2, ..., v6}, is performed by the Embedding layer. Adversarial training is then added to generate adversarial samples with small perturbations for iterative training. Secondly, the output word vectors of the embedding layer are fed into the BiLSTM layer along with the adversarial samples, and the bi-directional LSTM globally extracted features. Then a self-attentive mechanism layer is introduced after the BiLSTM layer to learn and acquire better features. Finally, the CRF layer learns the conditions of the label constraints to get the correct sequence labels.

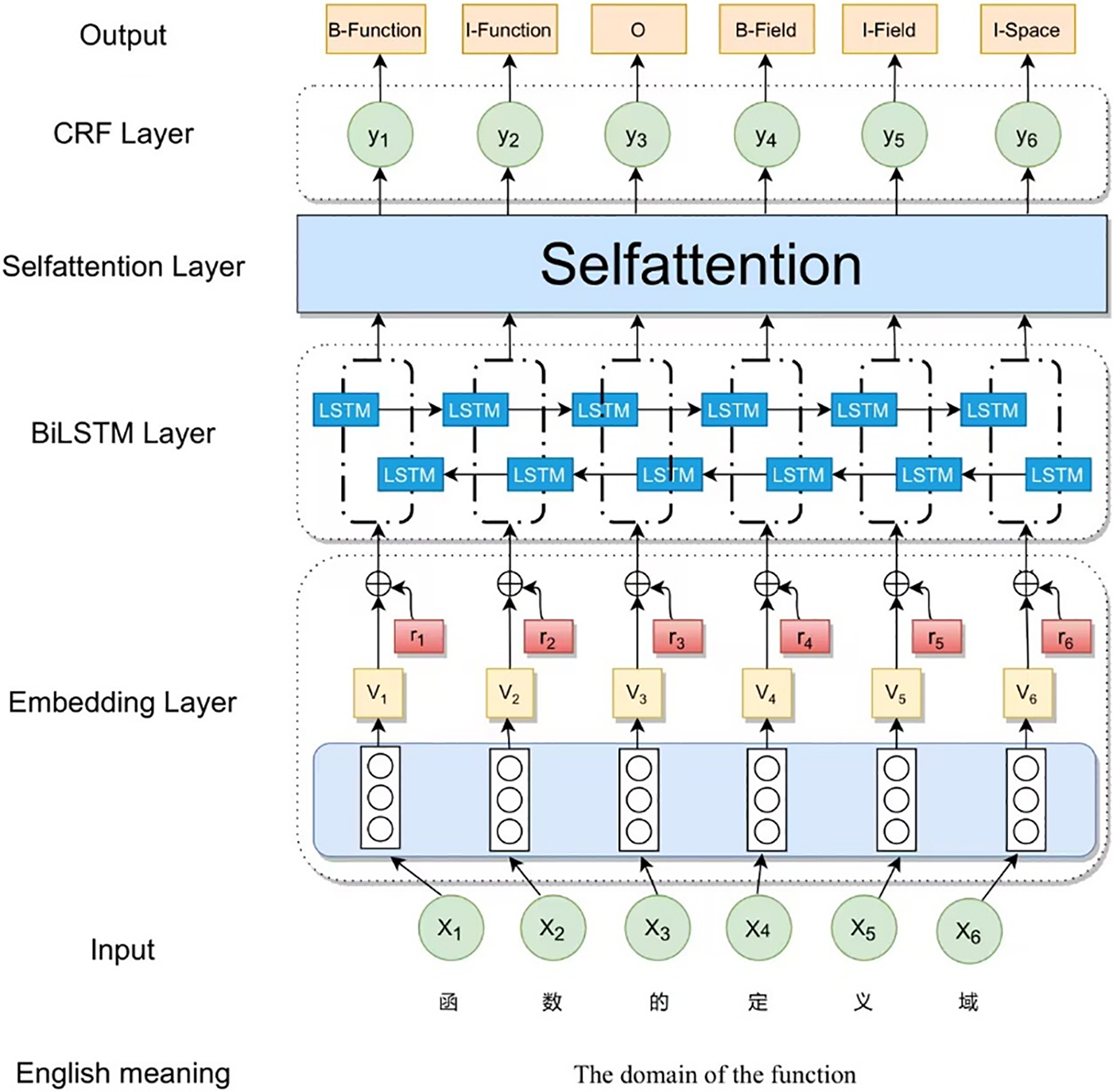
Figure 1: AT-BSAC model structure

3.1 Embedding Layer

The mathematical text is preprocessed to get, word vectors by using embedding mapping in PyTorch. To improve the accuracy, adversarial training is introduced after the word vectors are generated so that the multilayer neural network can optimize the parameters in the model training to improve the recognition performance of the model. Adversarial Training (AT) can generate adversarial samples by introducing small perturbations into the word vectors of embedded layers in the recognition task.

In this paper, based on the core idea of adversarial training in the above literature, we use a gradient ascent on the input to find the perturbation values and another gradient descent on the parameters to find the parameters of the model. After the word vectors are generated by embedding, the forward loss corresponding to each vector is first calculated according to the word vectors, the labels corresponding to the word vectors, and the model parameters. After that, the corresponding gradients are obtained according to the backpropagation. And finally, the perturbation values are integrated and calculated. The perturbation values and word vectors are summed to obtain the adversarial samples, which are then fed into the neural network together with the original word vectors to update the model parameters. The mathematical equation is shown below:

minE (x, y)∼D ⌊maxΔx∈ΩL (x+r, y; θ)⌋(1)

where x is the input, y is the label, D is the training set, r is the perturbation value, ω is the perturbation space, Δx is the perturbation added to the input, and θ is the model parameter.

The procedure for calculating the perturbation value r is shown below:

r=ε⋅g‖g‖2(2)

g=∇xL (xt, y, θ)(3)

x←x+r(4)

where ε is the scaling factor, L is the loss function, and g is the partial derivative of the loss function concerning for to x, i.e., the gradient. To find a better adversarial sample, we use the idea of “small steps, more steps” to get the optimal point. The term “small steps, more steps” refers to the strategy of employing smaller step sizes but conducting a greater number of iterations during the optimization process.

xt+1=∏x+s (xt+αg (xt)‖g (xt)‖2)(5)

g(xt)=∇xL (xt, y, θ)(6)

α is the step size xt,xt+1 is the vector of the previous and the next time, and s=r∈rd:∥r∥2<ε is the perturbation constraint space, which aims to limit the magnitude of adversarial perturbations to ensure that the generated adversarial samples fall within a certain range, thereby avoiding excessive interference with the original input.

3.2 Bilstm Layere

LSTM improves on the RNN model, it calculates the forgetting gate, input gate, current moment cell state, output gate, and hidden layer state in turn, and the formula is as Eqs. (7)–(9). x and y are the hidden layer state value and cell state value at time t−1, respectively. By adding input gates, forgetting gates, output gates, and a cell state to solve the gradient vanishing or exploding problem of RNN. It can control the degree to which information is forgotten or retained, as well as preserve information about the state from the beginning of the sequence to the current moment. BiLSTM is composed of a bi-directional Long Short Memory Network (LSTM), as shown in Fig. 2.

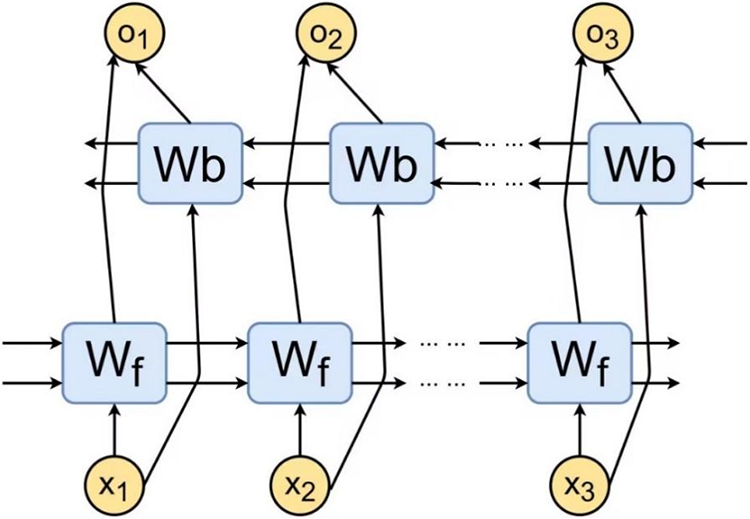
Figure 2: BiLSTM model structure

Long-distance dependencies often occur in Chinese mathematical texts, and it is not accurate enough to identify entities by word-level information only. As a result, we use BiLSTM to extract features and capture sentence-level information, we splice the adversarial samples and the obtained word vectors and feed them into BiLSTM to capture contextual information with two feature vectors h→t, h←t, the vector h→t is the forward vector, while h←t is the backward vector. Finally, we splice these two vectors as ht=h→t⊕h←t into the lower layer model.

[ftitotc∼t]=[σσσtan⁡h](W[xtht−1]+b)(7)

ct=ft∗ct−1+it∗c∼t(8)

ht=ot∗tan⁡h (ct)(9)

where xt is the input at moment t, ht−1, ct−1 are the hidden layer state values, cell state values at moment t−1, respectively, W and b are trainable parameters, ft, it, c∼t, ct, ot, ht are the forgetting gate, input gate, temporary cell state, cell state, output gate, and hidden layer state, respectively, σ is sigmoid function and tanh is hyperbolic tangent function.

Although BiLSTM can extract contextual information, it cannot fully express the potential semantic correlation between current information and contextual information. Therefore, the Selfattention layer is added after the BiLSTM layer.

3.3 Selfattention Layer

The BiLSTM layer extracts global features and then adds a self-attentive mechanism layer, which can dynamically learn the dependency between any two characters in a sentence and can compensate for the shortage of BiLSTM to extract local features. For example, in the sentence “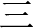, 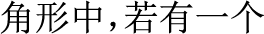60 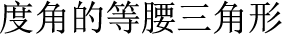, 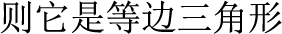(In a triangle, if there is an isosceles triangle with an angle of 60 degrees, it is an equilateral triangle)”, “ 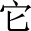(it)” might refer to “ (triangle)”, “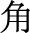 (angle)”, or “ 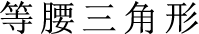(isosceles triangle)”, where the process of entity identification will have semantic ambiguity. The selfattentive mechanism model focuses on the important features in the sentence according to the relevance of “ 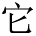(it)” to each word and thus enhances the precision of recognition. The obtained feature vectors will be fed into the CRF layer for label prediction.

The essence of the self-attention mechanism is weight allocation. By calculating the similarity between words in a sentence, different weights are given to feature vectors to obtain the potential semantic information of the text. The calculation process of the self-attention mechanism is shown in Fig. 3. When output H=[h1, h2, …, hn]∈RDh×n, the self-attentive mechanism model maps it to three different spaces, the query vector qi∈RDk, key vector ki∈RDk, value vector vi∈RDv are obtained, respectively:

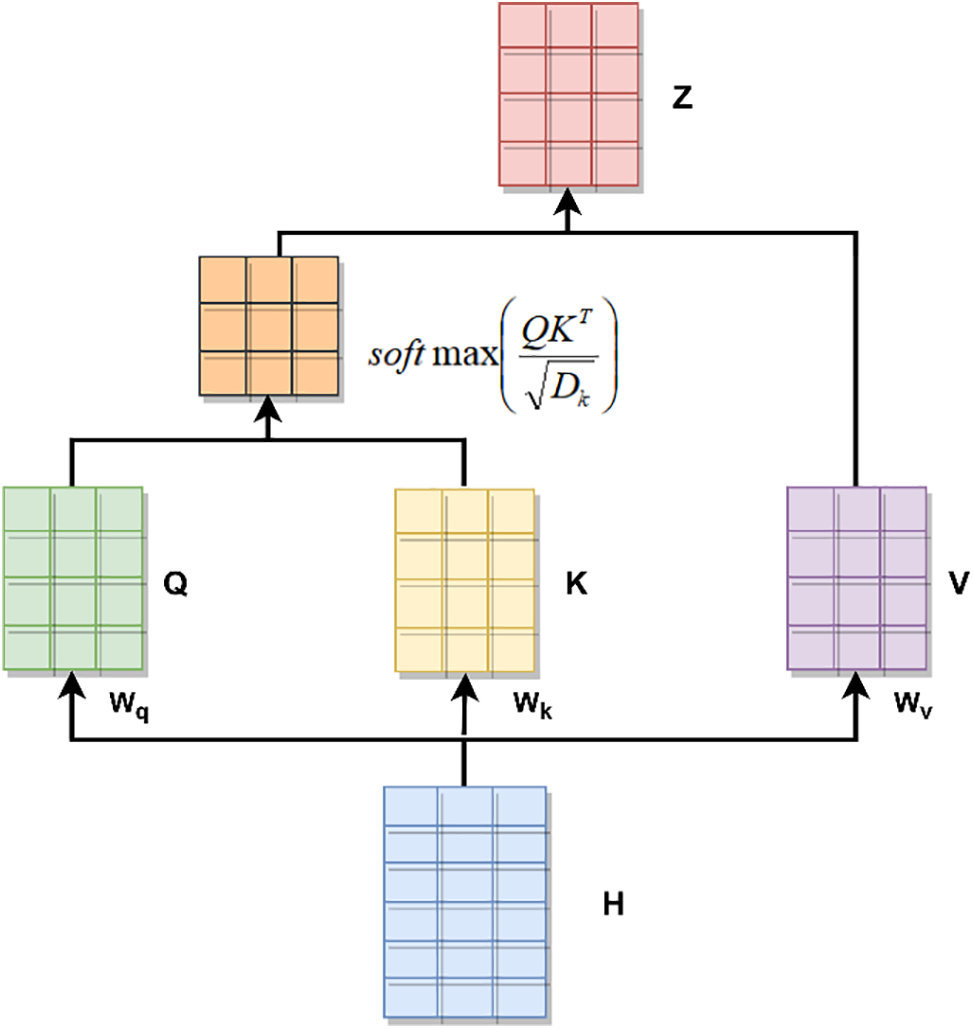
Figure 3: Flow chart of the calculation of the self-attentive mechanism

Q=WqH(10)

K=WkH(11)

V=WvH(12)

where Wq∈RDk×Dh, Wk∈RDk×Dh, Wv∈RDv×Dh are the linear mapping matrices, Q=[q1, q2, …, qn]∈RDk×n, K=[k1, k2, …, kn]∈RDk×n, V=[v1, v2, …, vn]∈RDv×n are Query matrix, Key matrix, and Value matrix, respectively. We use a scaled dot product model to calculate the attention scores, which can avoid the variance of the model being too large when the dimensionality of the input vectors is too high and the gradient of the function softmax is too small:

score(Q, K)=softmax (QKTDk)(13)

where Dk for K dimension. The result of the softmax activation function is dotted with V and then summed to obtain the output sequence Z=[z1, z2, …, zn]∈RDv×n.

Z=softmax (QKTDk)V(14)

3.4 CRF Layer

Considering the dependency problem between continuous tags in Chinese mathematical texts, this paper selects CRF to learn the relationship between tags for sequence annotation. For an input sequence x={x1,x2,…,xn}, the prediction sequence obtained in the named entity identification task is y={y1, y2, …, yn}, define as the predictive score function S as follows:

S(x,y)=∑i=0nAy1, yi+1+∑i=1npi, yi(15)

where pi,yi represents the probability that the character xi is marked as xi, Ay1,yi+1 represents the probability that xi+1 is labeled as yi+1 when xi is tagged as yi.

For each training sample x, the fraction S of the labeled sequence y representing each possibility is found, and the probability distribution about the output sequence y is obtained by normalizing all sequence paths, as shown in Eq. (16).

p(y|x)=eS(x, y∼)∑y∼∈YXeS(x, y∼)(16)

where y∼ denotes the set of all tags, YX denotes the sequence of all occurrences of tags, and S(x, y∼) denotes the score of the correct tag.

According to the principle of maximum likelihood estimation, the likelihood function is obtained by the logarithm of the predicted sequence y.

Loss=log⁡(∑y∼∈YXeS(x, y∼))−S(x, y)(17)

Finally this paper we use the Viterbi algorithm [33] in decoding to find the highest-scoring tag sequence y∗ to obtain the optimal labeling result, which is calculated as follows:

y∗=argy∼∈YXmax S (x, y∼)(18)

4  Experimental Results and Analysis

4.1 Datasets and Annotation Strategies

The public mathematical data on Wikipedia, Baidu Baike, and mathematical websites were used, including some mathematical theorems, definitions, formulas, exercises, etc. The data were pre-processed to create a usable dataset by removing irrelative information text, special symbols, and formulas, and splitting based on punctuation. 35,485 words of data text were obtained and annotated.

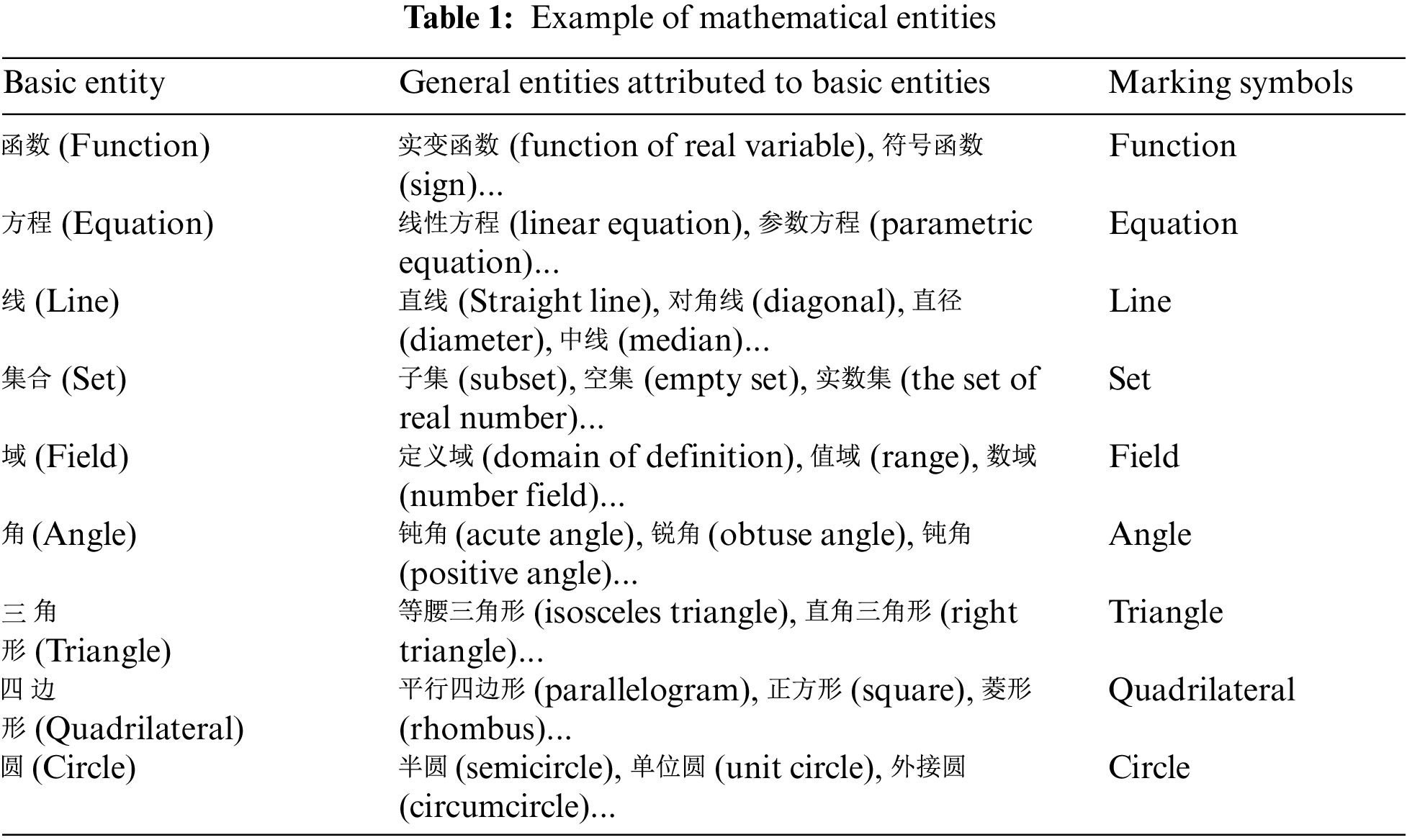
Based on the Mathematics Handbook [34], the classification of mathematical knowledge is described, the corresponding annotation symbols are defined, and the descriptions and examples of some mathematical entities are shown in Table 1.

In this paper, we use the BIO tag schema to annotate the data. Examples of mathematical entity annotation are shown in Table 2. 3947 mathematical entities were marked in the experiment. And the data set was sorted, and each type of entity was divided into the training set, test set, and verification set according to 6:2:2.

4.2 Experimental Environment and Parameter Settings

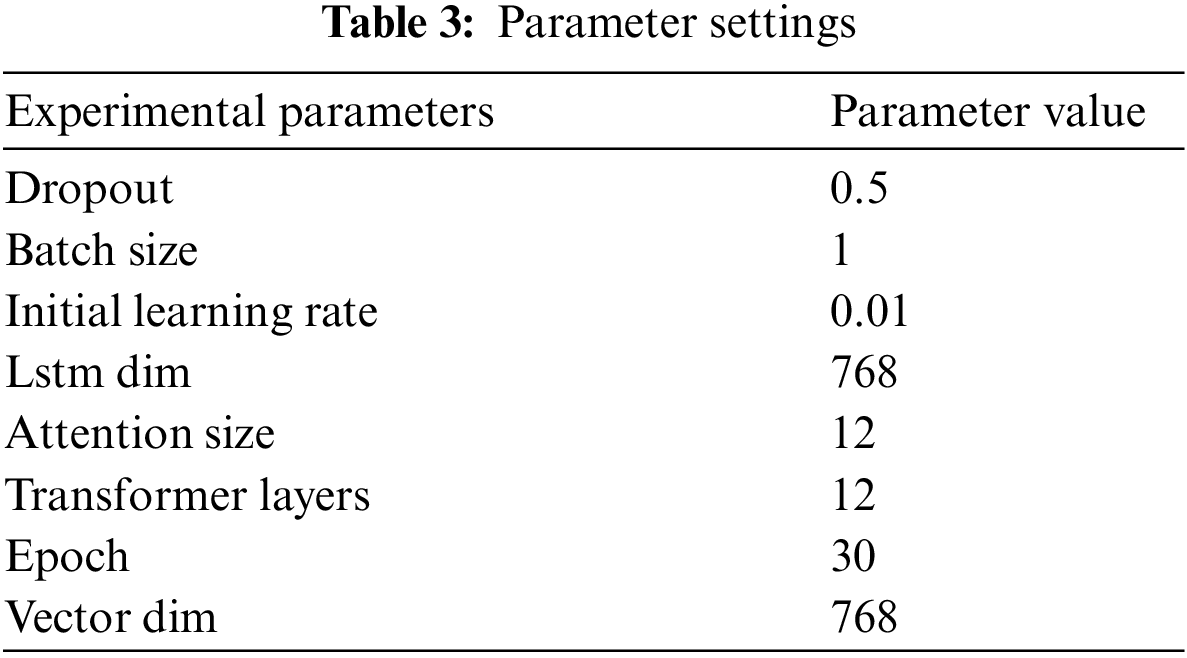
Our experimental configuration is outlined as: the operating system is Debian, the CPU is intel Zhiqiang, the memory is 32 G, and the programming languages Python3.9, and Pytorch1.10.1. The parameters are shown in Table 3.

4.3 Evaluation Metrics

We leverage precision (P), recall (R), and the F1-score as metrics to assess the performance of our model on the test data set. We can calculate them as follows:

P=TPTP+FP×100%(19)

R=TPTP+FN×100%(20)

F1=2PRP+R×100%(21)

where TP represents the true positive, FP represents the false positive, and FN represents the false negative.

4.4 Analysis of Experimental Results

To validate the effectiveness of introducing adversarial training and self-attentive mechanism models in MNER tasks, three groups of experiments were carried out on the same mathematical data set. The first group analyzed the effectiveness of the adversarial training model, the second group analyzed the effectiveness of the self-attention mechanism, and the third group analyzed the effectiveness of both the adversarial training and the self-attention mechanism model. The analysis of the results from the three sets of experiments is presented separately in Sections 4.4.1 and 4.4.2. The experiment results are shown in Table 4, Figs. 4, and 5.

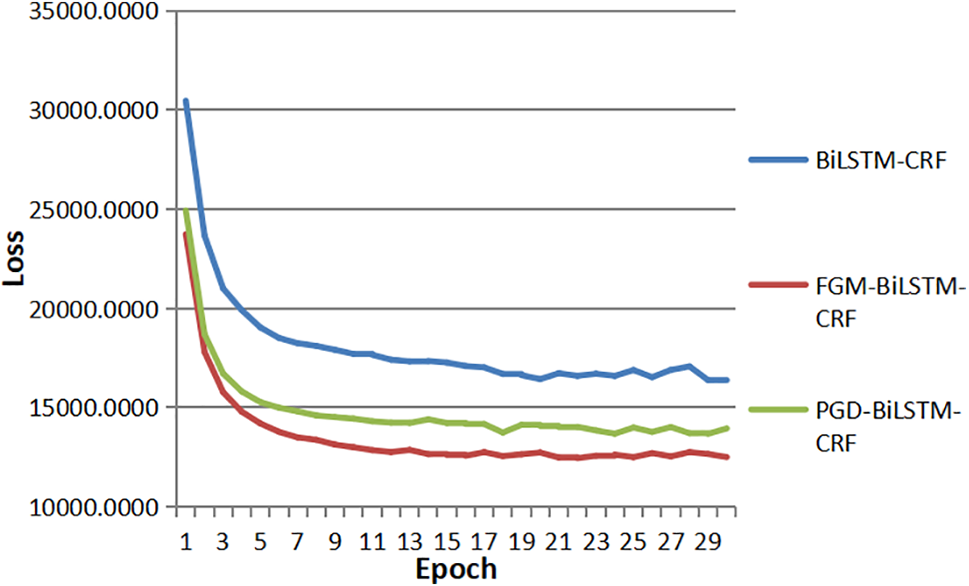
Figure 4: Comparison of loss analysis among different models

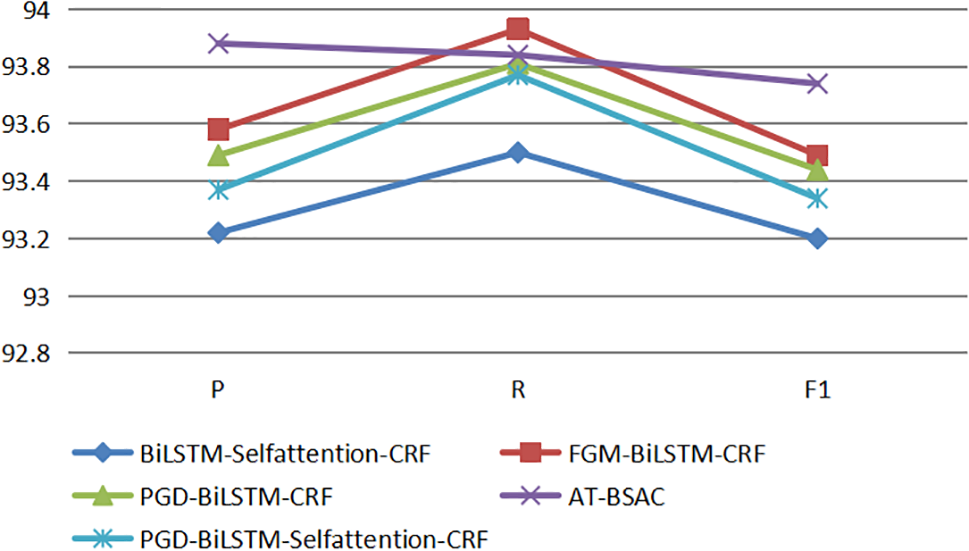
Figure 5: Compared P, R, and F1-score of different models

4.4.1 Experimental Analysis of BiLSTM-CRF Introduced into the Adversarial Training Model

Table 4 presents the P, R, and F1-scores of different models. After introducing the Fast Gradient Method (FGM) and Projected Gradient Descent (PGD) models into the BiLSTM-CRF benchmark model, all three scores of the model have improved, indicating an enhancement in the model’s recognition effect and recognition accuracy. Fig. 4 depicts the loss of the model after introducing FGM or PGD, it can be observed that the loss decreases rapidly upon the introduction of FGM or PGD. The main reason is that adversarial training can generate adversarial samples against model attacks. After learning and training, the robustness of the model can be improved when getting adversarial samples. However, the experiment results of different adversarial training models were different, and the P, R, and F1-score with FGM were slightly higher than those with PGD. The P, R, and F1-score of FGM reached 93.58%, 93.93%, and 93.49%. It shows that different perturbation values of the adversarial samples will influence the results. FGM has better recognition performance and robustness for mathematical entities in this experiment.

4.4.2 Experimental Analysis of BiLSTM-CRF Introducing Self-Attention Mechanism Model

As shown in Table 4 and Fig. 5, based on the BiLSTM-CRF model, the presence of a self-attention mechanism has a significant impact on the results. BiLSTM-Selfattention-CRF has a higher P, R, and F1score than the BiLSTM-CRF model. In particular, the F1-score of the BiLSTM-Selfattention-CRF model reaches 93.20%, which is 8.19% higher than that of BiLSTM-CRF. This is mainly because the presence of the self-attentive mechanism can dynamically and globally acquire features and solve the long-range semantic problem, and thus improve the results of MNER. Also, the results show that the adoption of scaled dot product calculation methods in the self-attention mechanism can increase accuracy.

4.4.3 Experimental Analysis of BiLSTM-CRF with Simultaneous Introduction of Adversarial Training and Self-Attention Mechanism Models

We further verify the effectiveness of the AT-BSAC model for named entity recognition in mathematics. Based on the results in experiments 1 and 2, introducing the adversarial training and self-attention mechanism models separately has already increased the P, R, and F1-score. As a result, we introduce both the adversarial training and self-attention mechanism models to compare the experimental results of BiLSTM-Selfattention-CRF, FGM-BiLSTM-CRF, PGD-BiLSTM-CRF, FGM-BiLSTM-Self-attentionCRF (AT-BSAC), and PGD-BiLSTM-Selfattention-CRF models in a mathematical named entity recognition task. As shown in Fig. 5, the F1-score of model AT-BSAC is about 93.74%, and is higher than all other models including BiLSTM-Selfattention-CRF, FGM-BiLSTM-CRF, PGD-BiLSTM-CRF, and PGDBiLSTM-Self-attention-CRF, specifically respectively improved by about 0.54%, 0.25%, 0.30%, and 0.40%. This indicates that the FGM and self-attention mechanism model should be integrated into the basic model BiLSTM-CRF at the same time, rather than separately. This is mainly because the AT-BSAC model can not only enhance the robustness of neural networks but also dynamically capture features in sentences to improve the performance of local instability of models and long-distance dependence among mathematical entities in mathematical named entity recognition tasks.

5  Conclusions

In this paper, the AT-BSAC model is constructed by introducing adversarial training and self-attention mechanisms to address the problems of model local instability, entity boundary ambiguity, and long-distance dependence among entities in the study of named entity recognition of mathematical text. The experimental results show that the AT-BSAC model in this paper achieves better results in terms of P, R, and F1-score compared with other comparative models, with the F1-score improving by 8.73% compared with the base model. The word vector is obtained by Pytorch, and after embedding, adversarial training is introduced to generate adversarial samples. The samples are fed into the BiLSTM model together with the word vector to extract local features. At the same time, the self-attentive mechanism model is introduced to obtain global features further and solve the problems of entity boundary ambiguity and long-distance dependence between entities to a certain extent. The accuracy of mathematical entity recognition has been improved. And our work can have a significant influence on mathematical formula text recognition.

Acknowledgement: The assistance provided by Cheng in code development is greatly appreciated.

Funding Statement: The authors received no specific funding for this study.

Author Contributions: The authors confirm their contribution to the paper as follows: study conception and design: Lei Yang, Chun Yang; data collection: Wang Kang, Delin Zhang; code development: Wang Kang; analysis and interpretation of results: Lei Yang; draft manuscript preparation: Lei Yang, Qiuyu Lai. The author Wang Kang is from the Chengdu State-Owned Jinjiang Machine Factory. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The data used to support the findings of this study are available from the corresponding author upon request.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. B. Nye, P. Pavlik Jr, A. Windsor, A. Olney, and M. Hajeer, “Skope-it (shareable knowledge objects as portable intelligent tutorsOverlaying natural language tutoring on an adaptive learning system for mathematics,” Int. J. STEM Educ., vol. 5, 2018. doi: 10.1186/s40594-018-0109-4. [Google Scholar] [PubMed] [CrossRef]

2. L. Liu and D. W, “A review of named entity identification studies,” J. Intell., vol. 37, no. 3, pp. 329–340, Sept. 2018. [Google Scholar]

3. S. Hochreiter and J. Schmidhuber, “Long short-term memory,” Neural Comput., vol. 9, no. 8, pp. 1735–1780, Aug. 1997. doi: 10.1162/neco.1997.9.8.1735. [Google Scholar] [PubMed] [CrossRef]

4. R. Collobert, J. Weston, L. Bottou, M. Karlen, K. Kavukcuoglu and P. Kuksa, “Natural language processing (almost) from scratch,” J. Mach. Learn. Res., vol. 12, pp. 2493–2537, Nov. 2011. doi: 10.5555/1953048.2078186. [Google Scholar] [CrossRef]

5. N. Vanetik, M. Litvak, S. Shevchuk, and L. Reznik, “Automated discovery of mathematical definitions in text,” in Proc. Twelfth Lang. Resour. Eval. Conf., Marseille, France: European Language Resources Association, May 11–16, 2020. [Google Scholar]

6. Y. Wang, X. Liu, and S. Shi, “Deep neural solver for math word problems,” in Proc. 2017 Conf. Empirical Methods Nat. Lang. Process., Copenhagen, Denmark: Association for Computational Linguistics, Sep. 7–11, 2017. [Google Scholar]

7. U. Schöneberg and W. Sperber, “POS tagging and its applications for mathematics: Text analysis in mathematics,” in Intelligent Computer Mathematics, Springer, pp. 213–223, 2014. doi: 10.1007/978-3-319-08434-3_16. [Google Scholar] [CrossRef]

8. D. Ferreira and A. Freitas, “Natural language premise selection: Finding supporting statements for mathematical text,” presented at the Twelfth Lang. Resour. Eval. Conf., Marseille, France, May 11–16, 2020. [Google Scholar]

9. V. Liyanage and S. Ranathunga, “Multi-lingual mathematical word problem generation using long short term memory networks with enhanced input features,” presented at the Twelfth Lang. Resour. Eval. Conf., Marseille, France, May 11–16, 2020. [Google Scholar]

10. Y. Zhang, S. Wang, and B. He, “A BERT-based method for recognizing named entities in primary mathematical texts,” Comput. Appl., vol. 42, pp. 433–439, 2022. doi: 10.3778/j.issn.1002-8331.2111-0023. [Google Scholar] [CrossRef]

11. Z. Lin et al. “A structured self-attentive sentence embedding,” presented at the 5th Int. Conf. Learn. Representations, ICLR 2017, Toulon, France, Apr. 24–26, 2017. [Google Scholar]

12. T. Li, Y. Guo, and A. Ju, “A self-attention-based approach for named entity recognition in cybersecurity,” presented at the 2019 15th Int. Conf. Comput. Intell. Secur. (CIS), Macao, China, 2019, vol. 9, pp. 147–150. doi: 10.1109/CIS.2019.00039. [Google Scholar] [CrossRef]

13. C. Song, Y. Xiong, W. Huang, and L. Ma, “Joint self-attention and multi-embeddings for Chinese named entity recognition,” presented at the 2020 6th Int. Conf. Big Data Comput. Commun. (BIGCOM), Deqing, China, 2020, pp. 76–80. doi: 10.1109/BigCom51056.2020.00017. [Google Scholar] [CrossRef]

14. G. Wu, G. Tang, Z. Wang, Z. Zhang, and Z. Wang, “An attention-based BiLSTM-CRF model for Chinese clinic named entity recognition,” IEEE Access, vol. 7, pp. 113942–113949, 2019. doi: 10.1109/ACCESS.2019.2935223. [Google Scholar] [CrossRef]

15. P. Han, Y. Zhong, H. Lu, and S. Ma, “A study on entity identification in adverse drug reactions based on adversarial transfer learning,” Data Anal. Knowl. Discov., vol. 7, pp. 131–141, 2023. [Google Scholar]

16. H. Zhu, H. Niu, and T. Zhu, “Entity recognition of industry figures based on character and word fusion and adversarial training,” Comput. Eng., vol. 49, pp. 56–62, 2023. [Google Scholar]

17. Z. Dong, R. Shao, Y. Chen, and J. Chen, “Named entity recognition in the food field based on BERT and adversarial training,” presented at the 2021 33rd Chinese Control and Decision Conf. (CCDC), Kunming, China, 2021, pp. 2219–2226. doi: 10.1109/CCDC52312.2021.9601522. [Google Scholar] [CrossRef]

18. I. Goodfellow et al., “Generative adversarial networks,” Commun. ACM, vol. 63, no. 11, pp. 139–144, Nov. 2020. doi: 10.1145/1122445.1122456. [Google Scholar] [CrossRef]

19. A. Vaswani et al., “Attention is all you need,” arXiv preprint arXiv:1706.03762, 2017. [Google Scholar]

20. Z. Huang, W. Xu, and K. Yu, “Bidirectional LSTM-CRF models for sequence tagging,” arXiv preprint arXiv:1508.01991, 2015. [Google Scholar]

21. M. Schuster and K. Paliwal, “Bidirectional recurrent neural networks,” IEEE Trans. Signal Process., vol. 45, no. 11, pp. 2673–2681, Nov. 1997. doi: 10.1109/78.650093. [Google Scholar] [CrossRef]

22. Z. Sun and H. Wang, “A review of advances in named entity identification research,” Data Anal. Knowl. Discov., vol. 42, pp. 42–47, 2010. doi: 10.3969/j.issn.1002-8331.2010.02.008. [Google Scholar] [CrossRef]

23. Y. Benajiba, M. Diab, and P. Rosso, “Arabic named entity recognition: A feature-driven study,” IEEE Trans. Audio, Speech, Lang. Process., vol. 17, no. 5, pp. 926–934, Sept. 2009. doi: 10.1109/TASL.2009.2019927. [Google Scholar] [CrossRef]

24. S. Liu, H. Yang, J. Li, and S. Kolmanic, “Chinese named entity recognition method in history and culture field based on BERT,” Int. J. Comput. Intell. Syst., vol. 14, 2021. doi: 10.1007/s44196-021-00019-8. [Google Scholar] [CrossRef]

25. W. Huang, D. Hu, Z. Deng, and J. Nie, “Named entity recognition for Chinese judgment documents based on BiLSTM and CRF,” J. Image Video Process., vol. 2020, no. 1, 2020. doi: 10.1186/s13640-020-00539-x. [Google Scholar] [CrossRef]

26. H. Liu, Q. Qiu, L. Wu, W. Li, B. Wang, and Y. Zhou, “Few-shot learning for named entity recognition in geological text based on GeoBERT,” Earth Sci. Informatics, vol. 15, no. 2, pp. 979–991, Jun. 2022. [Google Scholar]

27. L. L. Ma, J. Yang, B. An, S. Liu, and G. Huang, “Medical named entity recognition using weakly supervised learning,” Cogn. Comput., vol. 14, 2022. doi: 10.1007/s12559-022-10003-9. [Google Scholar] [CrossRef]

28. C. Wang, C. Xu, X. Yao, and D. Tao, “Evolutionary generative adversarial networks,” IEEE Trans. Evol. Comput., vol. 23, no. 6, pp. 921–934, Dec. 2019. doi: 10.1109/TEVC.2019.2895748. [Google Scholar] [CrossRef]

29. C. Szegedy et al., “Intriguing properties of neural networks,” in Proc. 2nd Int. Conf. Learn. Representations, ICLR 2014, Banff, AB, Canada, Apr. 14–16, 2014. [Google Scholar]

30. J. Li, S. Shang, and L. Chen, “Domain generalization for named entity boundary detection via meta-learning,” IEEE Trans. Neural Netw. Learn. Syst., vol. 32, no. 9, pp. 3819–3830, Sept. 2021. doi: 10.1109/TNNLS.2020.3015912. [Google Scholar] [PubMed] [CrossRef]

31. J. Wang, W. Xu, X. Fu, G. Xu, and Y. Wu, “ASTRAL: Adversarial trained LSTM-CNN for named entity recognition,” Knowl.-Based Syst., vol. 197, Jan. 2020, Art. no. 105842. doi: 10.1016/j.knosys.2020.105842. [Google Scholar] [CrossRef]

32. G. Yu et al. “Adversarial active learning for the identification of medical concepts and annotation inconsistency,” J. Biomed. Inform., vol. 108, Apr. 2020, Art. no. 103481. doi: 10.1016/j.jbi.2020.103481. [Google Scholar] [PubMed] [CrossRef]

33. S. Liu, T. He, and J. Dai, “A survey of CRF algorithm based knowledge extraction of elementary mathematics in Chinese,” Mob Netw. Appl., vol. 26, pp. 1891–1903, 2021. doi: 10.1007/s11036-020-01725-x. [Google Scholar] [CrossRef]

34. Q. Ye and Y. Shen, Practical Mathematics Handbook, 2nd ed. Beijing, China: Science Press; 2006. [Google Scholar]